Constant pH Molecular Dynamics with Proton Tautomerism

Abstract

The current article describes a new two-dimensional λ-dynamics method to include proton tautomerism in continuous constant pH molecular dynamics (CPHMD) simulations. The two-dimensional λ-dynamics framework is used to devise a tautomeric state titration model for the CPHMD simulations involving carboxyl and histidine residues. Combined with the GBSW implicit solvent model, the new method is tested on titration simulations of blocked histidine and aspartic acid as well as two benchmark proteins, turkey ovomucoid third domain (OMTKY3) and ribonuclease A (RNase A). A detailed analysis of the errors inherent to the CPHMD methodology as well as those due to the underlying solvation model is given. The average absolute error for the computed pK_a values in OMTKY3 is 1.0 pK unit. In RNase A the average absolute errors for the carboxyl and histidine residues are 1.6 and 0.6 pK units, respectively. In contrast to the previous work, the new model predicts the correct sign for all the pK_a shifts, but one, in the benchmark proteins. The predictions of the tautomeric states of His¹² and His⁴⁸ and the conformational states of His⁴⁸ and His¹¹⁹ are in agreement with experiment. Based on the simulations of OMTKY3 and RNase A, the current work has demonstrated the capability of the CPHMD technique in revealing pH-coupled conformational dynamics of protein side chains.

INTRODUCTION

The stability and function of proteins are dependent on the environmental pH (1). Well-known examples of pH-dependent biological processes include fibril formation from one of 16 normally soluble and functional human amyloidogenic proteins such as amyloid β-peptides, transthyretin, and prion proteins (2,3), membrane insertion of diphtheria toxin (4) and influenza virus hemagglutinin (5), and proton gradient-driven ATP synthesis (6), as well as the catalytic pathway of dihydrofolate reductase (7). In a conventional molecular dynamics (MD) simulation the protonation state of the protein is preset and kept fixed according to the known pK_a values of the ionizable side chains. Two problems arise from the assumption of static protonation. First, because the pK_a value of an ionizable side chain is typically unknown in its protein environment one has to resort to the value of an isolated amino acid (model pK_a), which sometimes deviates significantly from the value in the protein. Second, the protonation/deprotonation of an ionizable side chain is a process that is coupled to the dynamics of the local environment. By artificially fixing the protonation state in a MD simulation, the dynamics of the ionization equilibrium is neglected, thereby precluding detailed understanding of the specific interactions that give rise to the pH-coupled biological phenomena.

The history of pH-coupled molecular dynamics is relatively short. A decade ago, Mertz and Pettitt (8) demonstrated a titration simulation of acetic acid using an open system Hamiltonian. Sham et al. (9) showed that the pK_a values of lysozyme can be accurately modeled using the protein dipoles Langevin dipoles model, which treats the protein relaxation in the microscopic framework of the linear response approximation. In more recent years, several simulation techniques that allow pH-coupled molecular dynamics have emerged. Most of these techniques are based on the combination of molecular dynamics (MD) and Monte Carlo (MC) sampling of protonation states, with the major differences being the solvent representation and the way the free energy change accompanying the switch of the protonation state is computed. In the methods of Baptista et al. (10,11) and Bürgi et al. (12), explicit solvent is used to generate the MD trajectory. While the method of Bürgi et al. (12) utilizes thermodynamic integration to determine the protonation free energy change of a single residue, the method of Baptista et al. (11) makes use of static pK_a calculations based on the implicit solvent Poisson-Boltzmann (PB) model. More recently, these hybrid MD/MC schemes were extended to implicit solvent simulations: Dlugosz and Antosiewicz (13) make use of the analytic continuum electrostatic and the PB models for generating the MD trajectory and evaluating the protonation free energy change respectively; Mongan et al. (14) use the Generalized-Born (GB) model throughout the simulation.

There are several issues that have to be dealt with in the hybrid MD/MC constant pH simulation schemes. First, the periodic abrupt switch in the protonation state introduces a discontinuity in energy and force, which may result in conformational and energetic instabilities. Second, since only one protonation site at an instantaneous conformation of the protein is randomly chosen during a MC step, sampling convergence with regard to protonation and conformational states may be slow for proteins containing many ionizable sites. Third, some issues remain relating to the determination of the free energy change accompanying the protonation state switch. In the methods of Baptista et al. (11) and Dlugosz and Antosiewicz (13), which use the instantaneous protein conformation for the evaluation of the free energy difference, a somewhat ad hoc protein dielectric constant has to be chosen to mediate the electrostatic interactions in the otherwise static protein configuration. On the other hand, in the method of Bürgi et al. (12), which employs a short run (tens of picoseconds) of free energy simulation such as thermodynamic integration, the increased computational cost associated with the large of number of MC steps has to be considered.

In contrast to the discrete methods, the methods of Börjesson and Hünenberger (15), and of Lee et al. (16) are based on simultaneous propagation of continuous titration and conformational degrees of freedom. Both approaches use linear combinations of the deprotonated and protonated states to model nonbonded interactions. Although the method of Börjesson and Hünenberger relies completely upon explicit solvent simulation and uses the λ-variable to represent the extent of protonation for each ionizable site (15), the method of Lee et al., which has its roots in the λ-dynamics method (17), utilizes the implicit GB solvent model (18) and attaches physical meaning only to the end points. To minimize the possible distortion due to the unphysical mixed states that are nonetheless necessary for the transition between the end-point states, an artificial titration barrier is utilized in the continuous pH molecular dynamics method (CPHMD) of Lee et al. (16), which serves to prolong the residency time of the end-point states. The combined advantage of a stable dynamics trajectory and low computational cost makes the CPHMD approach of Lee et al. particularly suitable and attractive as a means of exploring pH-dependent conformational processes in proteins.

One prerequisite for the application of the constant pH molecular dynamics method to pH-coupled protein dynamics is reasonable accuracy in the prediction of protonation states or pK_a values for ionizable side chains. Among the aforementioned methods, so far, only three have been tested on proteins. While two of them, the hybrid MD/MC methods of Bürgi et al. (12) and Mongan et al. (14) were tested only on hen egg white lysozyme, the CPHMD method of Lee et al. (16) was tested on four different proteins, including turkey ovomucoid third domain (OMTKY3), bovine pancreatic ribonuclease A (RNase A), bovine trypsin inhibitor, and hen egg white lysozyme. In this pilot study, the total average absolute error over all proteins was 1.6 pK units (16).

A quick survey of the computed pK_a values in the work of Lee et al. (16) reveals that the average absolute error is largest for the histidine groups (3.2 pK units), followed by the carboxyl (1.6 pK units) and amino groups (1.2 pK units). One obvious reason for the increased errors in predicting the pK_a of histidine is the simplistic treatment of proton isomerism, in which case the imidazole ring is split into two titration halves involving the ND1 and NE2 sites with an added penalty potential to prevent double deprotonation (16). This model will be referred to as the split model in the rest of the article. In a constant pH MD simulation, the split model gives rise to two problems. First, since the two titration halves have common atoms, proper atomic charge states cannot be assigned to the neutral histidine tautomers, HSE (protonated on NE2) and HSD (protonated on ND1). Second, the penalty function to eliminate double deprotonated histidine, Kλ₁λ₂, introduces an undesired biasing force.

In the present work, a new tautomeric state titration model, also referred to as the double-site model, is developed. This model allows simultaneous titration at two competing protonation sites, such as the NE2 and ND1 atoms in histidine. The new model utilizes an additional dynamic variable that is treated on an equal footing to the titration degrees of freedom to control the tautomer interconversion process. Besides histidine, which exhibits the true proton tautomerism in solution, carboxyl groups such as Asp, Glu, and the C-terminus can be considered as having two tautomeric protonation sites, since the exchange of two titrating oxygens due to rotation around the single bond is slow on the routine MD simulation timescale. In essence, our tautomeric state titration model is a two-dimensional λ-dynamics approach that can, in general, be extended to additional dimensions. For example, the titration of amino groups can be viewed as a tautomeric equilibrium among three states and can be dealt with by constructing a three-dimensional model. However, since most amino groups do not exhibit large pK_a shifts, as seen for example in hen egg white lysozyme, the necessity for the development of a more sophisticated model is questionable. In fact, as mentioned previously, the errors in the computed pK_a values for amino groups are the smallest in the existing CPHMD method of Lee et al. (16) Finally, it is worthwhile noting that although the two-dimensional λ-dynamics approach is applied to the coupled protonation and tautomeric interconversion equilibria in the present work, the approach is general and can be applied to other problems.

The CPHMD method is further extended in the present study to incorporate the newly developed GBSW implicit solvent model (19) because of the added capability of this method for simulations in a membrane environment (20) and for the greater computational efficiency (21) relative to the GBMV method (18) that was implemented in the original CPHMD code. Since the accuracy of the CPHMD simulations is intimately linked to conformational sampling and the underlying implicit solvent model, the applications of CPHMD will benefit from the improved sampling schemes as well as the solvent model.

The purpose of the present work is to extend and improve the existing CPHMD method developed by Lee et al. (16). In their work (16) it was noted that CPHMD simulations using the GBMV solvent model gave an overestimation of 0.3 pK units for the blocked aspartic acid. This has prompted us to examine the details of the titration simulations of model compounds aimed at understanding the convergence behavior and errors inherent to the CPHMD methodology. Other errors in the prediction of protein ionization equilibrium arising from the force field and implicit solvent model will be explored by revisiting two proteins: OMTKY3 and RNase A. Since the predictions of pK_a shifts in the carboxyl and histidine residues in these proteins proved particularly problematic in the previous work (16), they provide excellent test beds for the tautomeric state model as well as the GBSW solvent model.

The rest of the article is organized as follows. In the Theory section, following a brief review of the CPHMD methodology, the formalism of the two-dimensional λ-dynamics approach is outlined and discussed for two special cases where tautomerism manifests in either the protonated or the deprotonated state. In Methods, the derivations of model potential functions as well as the macroscopic pK_a values for the titration simulations involving histidine and carboxyl side chains are given. Force-field issues related to the construction of the protonation state models are discussed. The last subsection in Methods details the simulation protocol. In Results and Discussion, the convergence behavior and errors in the titration simulations of blocked aspartic acid and histidine are discussed. The pK_a values of OMTKY3 and RNase A obtained from the CPHMD simulations using the new model are analyzed and compared to those from the previous work of Lee et al. (16), from the static PB calculations and experimental data. The issues related to the force field and implicit solvation, as well as the dynamic coupling between protonation and the local conformation. The last section of the article draws conclusions and makes suggestions for future directions of research.

THEORY

Continuous constant pH molecular dynamics

To facilitate derivations and discussions of the new model, we briefly review the methodology of the continuous implicit solvent constant pH molecular dynamics (CPHMD) (16). In the CPHMD method, the protonation/deprotonation (titration) process at a protein titrating residue i is described by a set of continuous coordinates,

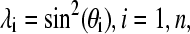(1)

the end points of which define the deprotonated (λ_i = 1) and protonated states (λ_i = 0). Thus, the CPHMD simulation is a special case of λ-dynamics (17), where the λ-variables define the titration coordinates.

In classical simulations, the deprotonation free energy of a protein side chain is obtained through modeling the difference between the free energy of deprotonating a side chain in the protein environment and that in solvent. Since the latter energy, namely, the deprotonation energy of a blocked amino acid (model compound) in solvent, is experimentally accessible, the deprotonation energy in the protein environment can be obtained as

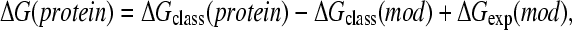(2)

where ΔG_exp(mod) is given as

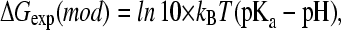(3)

and the pK_a value reflects the pH condition at which the populations of protonated and deprotonated states are equal.

Based on the above considerations, the total potential energy of the protein in the CPHMD simulation can be written as

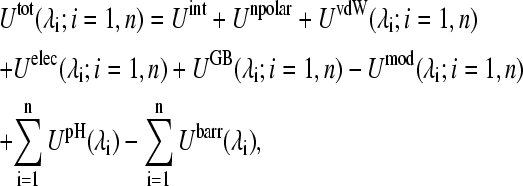(4)

where {λ_i;i = 1, n} is a set of titration coordinates for the n titrating residues as defined in Eq. 1. In Eq. 4, the two terms are the protonation-independent internal (bonded) energy and nonpolar solvation energy, and the rest are the protonation-dependent nonbonded and biasing potential energies.

The van der Waals energy for the interaction between the titrating proton i and another atom j is given by

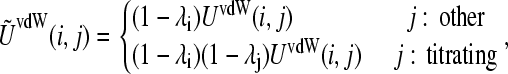(5)

where U^vdW(i, j) represents the protonation independent (full-strength) van der Waals interaction energy. The protonation dependence of the Coulomb and GB electrostatic energies is incorporated through the atomic partial charges on the titrating residue, which are linearly interpolated between the values in the deprotonated and protonated states,

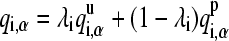(6)

where q_i,α represents the partial charge of atom α on residue i; and and 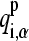are the charges in the deprotonated and protonated states, respectively.

The first biasing potential −U^mod in Eq. 4 originates from the term −ΔG_class(mod) in Eq. 2 and is a potential of mean force (PMF) along the λ-coordinate. Due to the nature of the nonbonded terms (Eq. 5 and Eq. 6), it is a quadratic function of the titration coordinate,

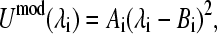(7)

and can be obtained via thermodynamic integration. The second biasing potential in Eq. 4 originates from the term ΔG_exp(mod) in Eq. 2 and models the pH-dependence of the deprotonation free energy. Thus,

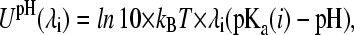(8)

where pK_a(i) is the pK_a value of the titrating group i.

The last term in Eq. 4 is called a barrier potential,

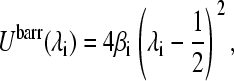(9)

where β_i is the barrier at the center of the titration coordinate. The barrier potential does not alter the energy difference between the end-point states (λ = 0 or λ = 1) but serves as an umbrella to prolong sampling time in the region of the end-point coordinates. This is necessary because the electrostatic and van der Waals interactions of the titrating residue associated with a mixed state (0 < λ < 1) are unphysical.

Two-dimensional λ-dynamics method

Tautomeric state model

As in most pK_a calculations, the existing CPHMD method assumes a particular protonating atom for residues that contain multiple titration sites, such as histidine and carboxyl groups. In what follows, a new model is introduced that removes this bias and treats the titration of the proton tautomers on an equal footing.

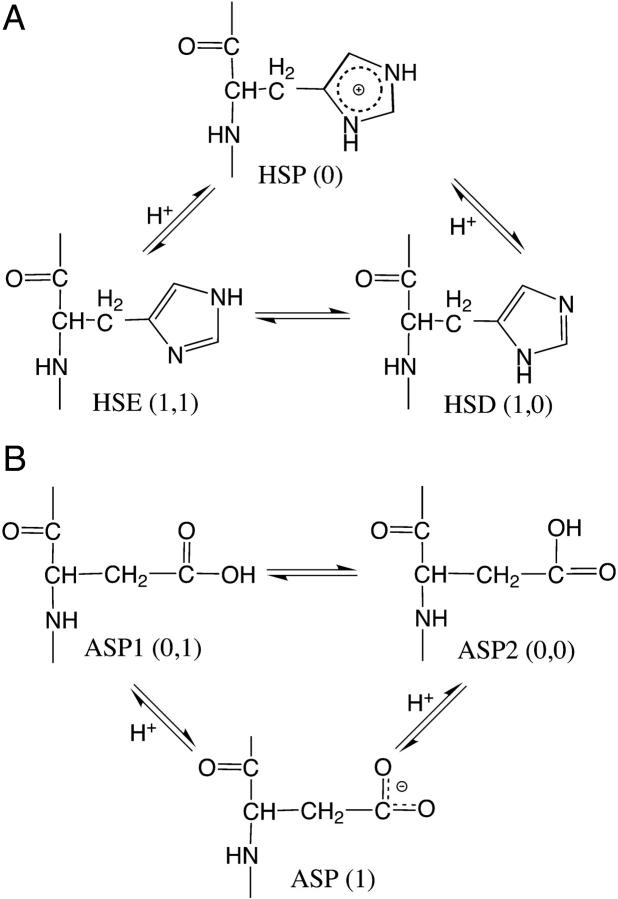
In the new model we assign an additional continuous coordinate x, which offers control of interconversion between the tautomeric states. This coordinate will be treated in the same manner as the titration coordinate λ. Thus, the titration of histidine involves interconversion among three states, which can be defined in terms of the titration and tautomeric coordinates as (0) for the doubly protonated state HSP; (1,1) for the NE2-protonated state HSE; and (1,0) for the ND1-protonated state HSD, where the first number in the parenthesis refers to the λ-value and the second the x value (Fig. 1 A). Notice that HSP can take on any x-value since its energy is degenerate with respect to x. Analogously, the three states in the titration of aspartic acid are defined as (1) for the deprotonated ASP; (0,1) for the OD1-protonated state ASPP1; and (0,0) for the OD2-protonated state ASPP2 (Fig. 1 B). Notice that ASP can take on any value of x.

FIGURE 1.

Acid-base and proton tautomeric equilibria of histidine (A) and aspartic acid (B).

The acid-base and proton tautomeric equilibria of histidine and aspartic acid are two special cases of two-dimensional λ-dynamics, where the two λ-driven processes are degenerate at one end point (either λ = 0 or λ = 1) and are coupled to each other via the x-coordinate at the other end point (either λ = 1 or λ = 0). Despite the formal identity of the two cases, somewhat different expressions have to be derived for the λ- and x-dependent potential energy functions (the second and third lines in Eq. 4). In our remaining discussions we will refer to both cases as the deprotonated (histidine) and protonated (aspartic acid) tautomerism.

Nonbonded interactions

Following the addition of the tautomeric state coordinate x, the atomic charge on a titrating group can be written as a linear combination of four charge states,

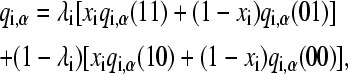(10)

where the values for the λ- and x-coordinates are given in parentheses. Since histidine has only one protonated state, q_i,α(01) = q_i,α(00). Analogously, for aspartic acid, q_i,α(11) = q_i,α(10). Notice that Eq. 6 can be recovered from Eq. 10 if the charge states of the tautomers are identical.

In the case of the deprotonated tautomerism (Fig. 1 A), the van der Waals energy for the interaction of titrating atom i and another atom j is given by

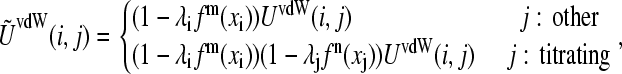(11)

where the superscripts m and n indicate the nature of the titrating atoms i and j, respectively. For example, in the titration of histidine, a value of 1 is associated with the titrating proton HE2 and 0 is associated with HD1. For a nontautomeric titrating proton, a value of −1 is assigned. Thus, the function f^m(x_i) can be written as

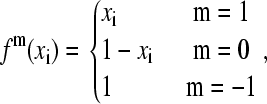(12)

where the function fⁿ(x_j) can be defined analogously. Notice that Eq. 5 can be recovered from Eq. 11 using the last definition of f^m(x_i), or fⁿ(x_i), in the absence of tautomerism.

In the case of the protonated tautomerism (Fig. 1 B), the van der Waals energy is given by

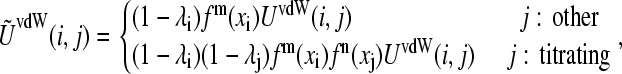(13)

where the function f^m(x_i) (or fⁿ(x_i)) m (or n) takes on the value of 1 for the titrating proton HD1, 0 for HD2, and −1 for a nontautomeric titrating proton. Eq. 5 can again be recovered from Eq. 13 in the absence of tautomerism.

Biasing potentials

In the presence of proton tautomerism, the pH-dependent potential function becomes

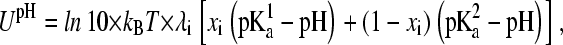(14)

where 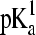and 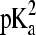refer to the microscopic pK_a values for the two titration sites. To suppress the population of mixed states in terms of x, a tautomer interconversion barrier potential in analogy to the titration barrier potential (Eq. 9) is applied to each coordinate x_i.

The functional form of the model potential in terms of the titration and tautomeric interconversion coordinates is determined by the functional forms of the Coulomb, GB electrostatic and van der Waals interaction energies. In the absence of tautomerism this leads to a quadratic function as mentioned earlier (Eq. 7). In the presence of proton tautomerism the coupling between λ and x results in a complex functional form for the model potential. However, since linear interpolation is used in the expressions for both the atomic partial charges and van der Waals interaction energy, the model potential function is expected to remain quadratic in either the λ- or x-variable.

Before attempting the derivation of the model potential function in the two-dimensional coordinate space (λ, x), it is instructive to consider the scenarios where either the titration or tautomeric interconversion coordinate is fixed at one of its end points. In the case of the deprotonated tautomerism, each process (or equilibrium) displayed in Fig. 1 A, is associated with a quadratic function. Since the energy of the protonated form, HSP, is independent of x, the potential function at HSP must be a constant. The following equations present the boundary conditions for the model potential function,

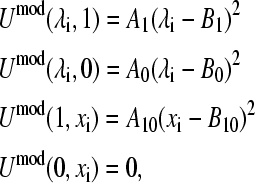(15)

where A₁, B₁, A₀, B₀, A₁₀, and B₁₀ are the parameters in the quadratic functions that describe the one-dimensional processes and are related to each other through the relationship

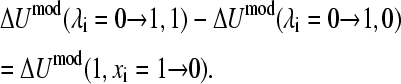(16)

In other words, the difference in the free energies of deprotonation for HSP→HSE and HSP→HSD is the same as the free energy of tautomer interconversion HSE→HSD. We will show later that the model potential parameters can be derived analytically by making use of the boundary conditions given in Eq. 15. It should be noted that the model potential function contains an arbitrary constant since the difference deprotonation energy (see Eq. 2) is the interesting quantity in this work. For the case of the protonated tautomerism, there exists an analogous set of equations that describes the one-dimensional conditions.

Since the model potential function is quadratic in either the λ- or x-variable, a general expression in the form of a bivariate polynomial containing eight parameters can be found:

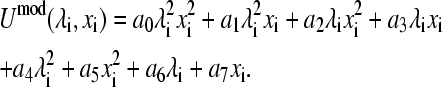(17)

In the case where tautomerism exists for one protonation form (either U^mod(0, x_i) = 0 or U^mod(1, x_i) = 0) there are, at most, six nonvanishing parameters in Eq. 17. One way to identify the nonzero terms is to follow the procedure below,

• Step 1, at fixed values of x, obtain parameters for the quadratic function of λ: f(λ;x) = A(x)[λ – B(x)]²;

• Step 2, fit the parameters A(x) and B(x) to the second-order polynomial: b₁x² + b₂x + b₃;

• Step 3, at fixed values of λ, obtain parameters for the quadratic function of x: f(x;λ) = A(λ)[x − B(λ)]²; and

• Step 4, fit the parameters A(λ) and B(λ) to the second-order polynomial: c₁λ² + c₂λ + c₃,

where some of the coefficients in the polynomial obtained in Steps 2 and 3 vanish. By matching the same order terms in f(λ;x) and f(x;λ) and utilizing the difference in the λ- and x-dependent polynomial forms (Steps 2 and 3), the nonzero terms in the general form of the model potential (Eq. 17) can be determined. A detailed derivation of the parameters in the model potential functions for the deprotonated (histidine) and protonated tautomeric (carboxylic acid) cases is given in the Supplementary Material.

METHODS

Macroscopic pK_a values from the tautomeric state model

In the CPHMD simulation, the fractional population of unprotonated states (unprotonated fraction) for a titrating residue is given as

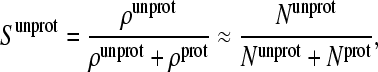(18)

where ρ^unprot and ρ^prot are the probabilities for the unprotonated and protonated states, which can be related to the number of times unprotonated (N^unprot) and protonated (N^prot) states are observed in the simulation, respectively.

Since bounded continuous coordinates are utilized for the propagation of protonation and tautomeric states, some cutoff values have to be used to define the pure protonation and tautomeric states. In this work we extend the convention employed previously by Lee et al. (16) to include the tautomeric states. Thus, the number of unprotonated and protonated states are defined as

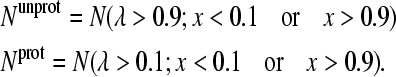(19)

Notice that the mixed tautomeric states (0.1 < x < 0.9) are discarded from the above definition, although the value of x is irrelevant for the doubly protonated state of histidine (Fig. 1 A) or the deprotonated carboxylate residue (Fig. 1 B). However, since the protonation states in the simulation are defined through some cutoff values, their energies do depend on x. Therefore, the mixed tautomeric states are not included in the statistics.

To obtain the pK_a value for a titrating residue, the unprotonated fractions at different pH were used to fit to the generalized form of the Henderson-Hasselbach equation,

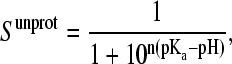(20)

where n is the Hill coefficient. The deviation of the value of n from unity reflects the degree of cooperativity (coupling) between groups that interact and ionize over the same pH range. In this work the Hill coefficient is included into the fitting procedure to account for the couplings between ionizable sites. It is noted, however, that the computed pK_a is only marginally affected by the value of n.

Given the equilibrium constants k₁ and k₂ for the microscopic deprotonation processes HSP → HSE, and HSP → HSD, respectively (Fig. 1 A), the equilibrium constant k for the macroscopic deprotonation of histidine is given as

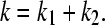(21)

Thus, by applying the definition of pK_a (pK_a = −log₁₀k, the macroscopic pK_a for the histidine titration can be related to the microscopic counterparts, pK₁ and pK₂ by

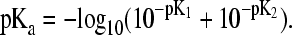(22)

Provided the reference microscopic value of 6.6 (pK₁) and 7.0 (pK₂) for the ND1- and NE2-titration in the blocked histidine, respectively, Eq. 22 leads to a macroscopic pK_a of 6.45.

Given the equilibrium constants k₁ and k₂ for the microscopic deprotonation processes of aspartic acid (Fig. 1 B), the equilibrium constant k for the macroscopic deprotonation can be written as

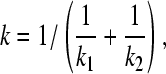(23)

which leads to the relation

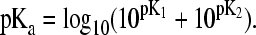(24)

Assuming a reference microscopic value 4.0 for both pK₁ and pK₂, Eq. 24 leads to a macroscopic pK_a of 4.3. Since the experimental macroscopic pK_a for the blocked aspartic acid is 4.0, a postcorrection is made (see later discussions).

Protonation state models

In the CPHMD method, the transition between protonation states of a titrating residue is modeled by linear attenuation of nonbonded energies while keeping the topology, bonded, and van der Waals parameters of the residue intact. Consequently, in a deprotonated state, the titrating hydrogen atom becomes a dummy atom with zero charge and has no van der Waals interaction with other atoms. This strategy is therefore similar to the single-topology scheme in free energy simulations.

The titration of histidine in the tautomeric state model is based on the topology and associated bonded as well as van der Waals parameters of the doubly protonated histidine (residue type HSP in CHARMM). The atomic charges of the three protonation states (Fig. 1 A) are identical to those in CHARMM type HSP, HSE, and HSD, respectively. In the intermediate or mixed states, the nonbonded interactions are computed by linear interpolation via the λ- and x-variables as described in the Theory section.

For the titrations of the carboxyl residue, a new CHARMM residue type is constructed based on carboxylic acid such that a second hydrogen atom is placed on the unprotonated oxygen. Let us consider aspartic acid. The titration of aspartic acid in the tautomeric state model is based on the topology, bonded and van der Waals parameters of the new hybrid residue, which will be referenced as ASDP. The force-field parameters of ASDP differ from those of aspartic acid (CHARMM type ASPP, protonated on OD2) in that the CG, OD1, and OD2 atoms are assigned with the corresponding bonded parameters of the deprotonated aspartate (CHARMM type ASP) whereas the titrating (dummy) hydrogens HD1 and HD2 are assigned with the bonded parameters of the aspartic acid (CHARMM type ASPP). From the hybrid residue ASDP, three protonation states are constructed: the deprotonated state ASP, with both dummy hydrogens uncharged and having no van der Waals interactions; two protonated states (ASP1 and ASP2), with either HD1 or HD2 charged and having van der Waals interactions. Notice that there is no interaction between the two dummy hydrogens due to the unphysical nature of the doubly protonated state, although both hydrogens are allowed to interact with other atoms in a mixed state.

One drawback of the dummy atom representation of the protonation states for the carboxyl residues is that the uncharged dummy hydrogen can lose the ability to gain charge once it is rotated to the anti position (16,14). A remedy used previously by Lee et al. (16) was to significantly lower the barrier to the rotation around the carboxylate bond such that the rotation back to the syn position is facilitated. A caveat is, however, that this can lead to nonnative hydrogen bonds as a result of stabilization of the unphysical out-of-plane conformations (16). The syn conformation is thermodynamically more favorable relative to the anti one by ∼2.8 kcal/mol, according to a solid-state NMR experiment (22). Quantum calculations and molecular dynamics simulations have shown a free energy difference of ∼1.6–1.9 kcal/mol (22,14). On the basis of these considerations, our solution is to kinetically disfavor the anti position by raising the C-O bond rotation barrier from 4.1 to 6.0 kcal/mol and placing the dummy carboxyl hydrogens at the syn positions at the beginning of the simulation.

Simulation protocol

All of the simulations described in this work were performed using the PHMD module with the all-atom CHARMM22 force field (24) for proteins including the dihedral cross term corrections (CMAP) (25) and the GBSW solvent model (20,19) in the CHARMM molecular dynamics program (26). The original PHMD module (16), in which the CPHMD method was implemented, was extended to allow tautomeric state titrations and to include pH-dependent solvation energy and force with the GBSW solvent model. The SHAKE algorithm was applied to hydrogen bonds and angles, such that a timestep of 2 fs could be used. A 22 Å distance truncation was applied to both the nonbonded and GB energy/force evaluations. All simulations utilized a Nosé-Hoover thermostat to ensure a canonical distribution of atomic velocities at a constant temperature of 298 K. For the GB calculations, a smoothing length of 0.6 Å at the dielectric boundary with 24 radial integration points up to 20 Å and 38 angular integration points were used. The nonpolar solvation energy was computed using the surface tension coefficient of 0.03 kcal mol⁻¹ Å⁻².

For the propagation of titration and tautomer interconversion coordinates, the velocities of λ and x were coupled to a three-mass (30, 50, and 70 amu) Nosé-Hoover chain (27,28) to ensure a canonical distribution at the target temperature of 298 K. Unless otherwise specified, the default initial velocity seed was used for the simulation. Model compounds used in this work were the blocked amino acids obtained by acetylating the N-terminus and amidating the C-terminus. To obtain the one-dimensional model potential functions, thermodynamic integrations based on 1-ns MD simulations (100 ps equilibration and 1 ns production) were performed at several fixed points along the titration or tautomer interconversion coordinates, as described previously (16). In single-site titration simulations, a titration barrier of 1.25 kcal mol⁻¹ was used (16). For double-site titrations, a titration barrier of 1.75 and a tautomer interconversion barrier of 2.75 kcal mol⁻¹ for the carboxyl groups and 2.5 kcal mol⁻¹ for histidines were applied, which in general keeps the fractional population of mixed titration and tautomeric states below 25% and 15%, respectively.

The microscopic reference pK_a values of 4.0, 4.4, and 3.8 were used for the Asp, Glu, and C-terminus carboxyl residues, respectively. This introduced a positive error of 0.3 units when both the carboxylate oxygens participated in the titration process (see Methods). Thus, we included a correction that accounts for this and other errors that occur in the titration simulations of model compounds in the reported pK_a values for the test proteins, OMTKY3 and RNase A (see the legends of Tables 3 and 5). For histidine, the microscopic reference values of 6.6 and 7.0 were used for the ND1- and NE2-titration, respectively. A correction that accounted for the error in the titration of blocked histidine was included in the reported pK_a values for the histidines in RNase A (see Table 5 legend). The reference pK_a value of 7.5 was used for the N-terminus amino group.

TABLE 3.

Computed pK_a values for OMTKY3 (see legend below)

Residue	Cryst.	NMR	OD1 (OD2)	GBMV	Static	Expt.
Asp7	2.8 (2.4)	3.2 (3.2)	4.0 (1.9)	4.5	2.9 (2.9)	<2.7
Glu10	3.1 (2.3)	2.6 (2.6)	2.5 (2.7)	5.1	3.4 (3.4)	4.2
Glu19	2.3 (2.1)	2.6 (2.5)	<0.0 (0.7)	2.7	3.2 (2.6)	3.2
Asp27	4.7 (4.7)	4.0 (3.9)	5.0 (4.6)	6.1	4.0 (3.6)	<2.3
Glu43	5.3 (5.5)	4.3 (4.6)	4.1 (4.5)	6.0	4.3 (4.4)	4.8
CT-Cys	1.3 (1.8)	1.0 (1.3)	0.9 (1.0)	4.6	2.7 (2.5)	<2.5
Avg. abs. error*	1.0 (1.2)	1.1 (1.0)	1.9 (1.5)	1.7	0.6 (0.6)	—

The pK_a values were obtained from 4-ns simulations of OMTKY3 at pH values 0, 1, 2, 3, 4, 5, and 6. An additional 200 ps was allotted for equilibration. Unless otherwise noted, the pK_a values obtained from 2-4 ns simulation time are listed in parentheses next to those from 0 to 2 ns. A value of 0.3 was added to all the pK_a values from the double-site simulations to correct the errors found in the model compound simulations (see Table 2). For the same reason, the computed pK_a values from the single-site titrations were corrected by adding 0.1 and 0.3, respectively (see Table 2). The double-site titrations were based on the crystal structure PDB:1PPF (44) (column Cryst.) or the first entry of the NMR structure ensemble PDB:1OMU (45) (column NMR). Column OD1 (OD2) refers to the 2-ns single-site titration at either OD1 or OD2, with the bonded parameters of the ionic aspartate. Column GBMV refers to the 1-ns single-site (OD2) simulations with the GBMV solvation model (16). Column Static refers to the static PB calculations of Forsyth et al. (46) and Antosiewicz et al. (in parentheses) (38) using the same crystal structure. Protein dielectric constant was set to 20 in these calculations. Column Expt. refers to the experimental data taken from Schaller and Robertson (47).

^*Average absolute deviations from experimental data. The upper limit is used when a range is given.

TABLE 5.

Calculated pK_a values for RNase A (see legend below)

Residue	This work	Lee	Static	Expt.
NT-Lys	7.2	6.6	7.0	7.6
Glu2	0.0	<−1.0	2.5	2.8
Glu9	2.6	5.8	4.1	4.0
His12	5.1	2.8	4.3	6.2
Asp14	3.1	3.5	2.0	2.0
Asp38	1.5	2.4	2.8	3.1
His48	6.3	7.7	6.5	6.0
Glu49	5.0	6.4	4.6	4.7
Asp53	3.8	4.5	3.6	3.9
Asp83	−0.9	7.4	2.1	3.5
Glu86	3.9	5.9	3.8	4.1
His105	7.3	10.8	6.2	6.7
Glu111	3.7	5.8	3.9	3.5
His119	5.7	7.5	6.5	6.1
Asp121	0.4	3.3	1.3	3.1
CT-Val	0.0	<−1.0	2.3	2.4
Avg. abs. error*	1.6	2.0	0.5
Avg. abs. error†	0.6	2.7	0.8
Abs. error‡	0.4	1.0	0.6

The pK_a values were obtained from 2-ns simulations of RNase A at a pH range between 0 and 8 with an increment of 1 using the crystal structure PDB:7RSA (39).To correct the errors found in the model compound simulations a value of 0.4 was subtracted from the computed pK_a values for His¹⁰⁵, and His¹¹⁹ whereas 0.1 was added to the computed pK_a values for His¹² and His⁴⁸ since they titrate via NE2 exclusively (see Table 1). For the same reason, the computed pK_a values were corrected by adding 0.3 units for all the carboxyl residues except for Asp⁵³, in which case 0.1 units was added to the computed value since it titrates via OD1 exclusively (see Table 2). Column Lee refers to the work of Lee et al. (16). Column Static refers to the static PB calculations of Antosiewicz et al. (38) using a protein dielectric constant of 20. Cited are the values averaged over the calculations which allow the protonation of histidine to occur at either NE2 or ND1 and with His¹¹⁹ being in the crystal conformation A. Column Expt. refers to the experimental data cited in the work of Antosiewicz et al. (38).

^*Average absolute error of the computed pK_a values for the carboxyl residues.

^†Average absolute error of the computed pK_a values for the histidine residues.

^‡Absolute error of the computed pK_a for NT-Lys.

Since the GBSW model was parameterized to closely mimic the solvation energies from the finite-difference Poisson method, the optimized radii for the latter method (29,30) were adopted to define the solvent-solute dielectric boundary in the present work with some small modifications to better match the experimental solvation free energies. Specifically, the solvation radii for the oxygen atom in carboxylate, Tyr, Ser, and Thr residues were adjusted by 0.1, −0.1, −0.14, and −0.14 Å, respectively.

Development of atomic radii for use with the GB model is a continuous effort. Previous radii parameterizations for the PB methods were targeted toward the experimental solvation energies of small molecules as well as the calculated interaction energy of small molecules containing charged side chains with explicit waters. However, this strategy is not ideal, for at least two reasons. First, the solvation treatment of small molecules is not entirely transferable to a protein environment. Second, reproducing the explicit solvent behavior using the TIP3P (32), or any other explicit water model carries along inherent problems of these models (33,34). Thus, current effort in the group is directed toward reoptimization of the existing PB radii by performing control GB simulations of model peptides and mini-proteins aimed at finding the balance among stability, foldability, and the underlying physical principles (31). Since the strength of the electrostatic interactions in a microscopic approach such as the current CPHMD method is sensitive to changes in solvation or desolvation energies, the accuracy of the constant pH simulations will greatly benefit from the improvement of the GB model.

In the current method, a fixed set of solvation radii was used throughout the titration simulations. This is a drawback, because the radii of ND1 and NE2 on histidine in the GBSW model vary according to the charge state. Although for the neutral state (HSD and HSE), the radius is 1.8 Å, it is 0.5 Å larger in the charged state (HSP). A solution would be to linearly interpolate the radius between these two states, which would, however, result in a deviation from the quadratic behavior in the model potential function. Thus, in the present work, we assumed a radius of 2.0 Å for ND1 and NE2 in the pH range, expanding one unit below and one unit above the reference pK_a value, and the default radii for the neutral or charged states under other pH conditions. Since the pK_a values of carboxyl groups in OMTKY3 and RNase A are a few units below that of the histidine, the error due to the fixed histidine radii approach is minor.

RESULTS AND DISCUSSION

Model compounds

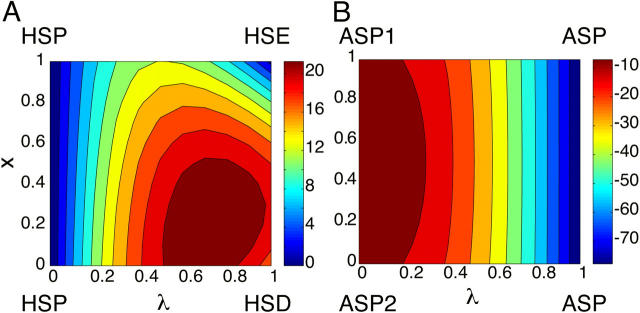
Fig. 2 shows the two-dimensional potential of mean force (PMF) maps for the blocked histidine and aspartic acid along the titration and tautomer interconversion coordinates. Notice that the PMF of the doubly protonated histidine HSP (Fig. 2, A λ = 0) and the deprotonated aspartate (Fig. 2, B, λ = 1) is constant. From the PMF map for histidine (Fig. 2, A), it is seen that the ND1-protonated form HSD (lower-right corner where λ = 0, x = 1) is higher in energy than the NE2-protonated form HSE (upper-right corner where λ = 0, x = 0). The barrier for HSP → HSD is higher and occurs later relative to that for HSP → HSE. From the PMF map for the aspartic acid (Fig. 2, B), it is seen that the OD1-protonated form ASP1 and OD2-protonated form ASP2 have almost identical energy. The barriers for ASP1 → ASP and ASP2 → ASP are very small (<5 kcal/mol, not visible in Fig. 2) and occur very early in the deprotonation process.

FIGURE 2.

Two-dimensional potential of mean force (PMF) map along the titration coordinate λ and tautomeric interconversion coordinate x for the blocked His (left) and Asp (right) residues. The color bars shown on the right indicate that the PMF increases from dark blue to dark red.

Blocked histidine

Table 1 summarizes the running pK_a values for the blocked histidine using the double- and single-site titration models. The pK_a values were obtained from the data collected from 2-ns time windows along five 10-ns trajectories that were initiated with random initial velocity seeds. Given the reference pK_a of 6.6 for the ND1 and 7.0 for the NE2 titration, the average running pK_a values in the first 2-ns simulations have a deviation of 0.4 and −0.2 pK units for the ND1- and NE2-titration, respectively. The associated standard deviation due to different initial velocity seeds is 0.45 and 0.27 pK units for the ND1- and NE2-titration, respectively. It is interesting to see that the error and standard deviation in the single-site titrations remain approximately constant over the entire 10 ns, suggesting the convergence of the protonation state sampling. The greater variation from the standard values and standard deviation in the ND1-titration simulations can be attributed to an inherent problem in the implicit solvent simulation of the charged histidine as discussed further below.

TABLE 1.

Computed running pK_a values for the blocked histidine from the double- and single-site titration simulations

	0–2 ns	2–4 ns	4–6 ns	6–8 ns	8–10 ns
1	6.8	6.4	7.1	6.8	6.6
2	6.4	7.0	6.6	6.7	6.4
3	6.8	6.5	6.8	6.7	6.8
4	6.9	6.7	6.8	6.6	6.7
5	7.3	7.3	7.3	7.1	6.6
Mean (std.)*	6.8 (0.32)	6.8 (0.37)	6.9 (0.28)	6.8 (0.19)	6.6 (0.15)
ND1†	7.0 (0.45)	7.0 (0.39)	7.0 (0.40)	7.0 (0.48)	7.0 (0.53)
NE2†	6.9 (0.27)	6.8 (0.18)	6.8 (0.19)	6.8 (0.21)	6.8 (0.21)

The pK_a values were obtained from 2-ns time windows with a total simulation time of 10 ns at pH values 6, 7, and 8. An additional 100 ps was allotted for equilibration. A random initial velocity seed was used for each simulation run.

^*Average and standard deviation of pK_a values obtained from five double-site titration simulations.

^†Average and standard deviations of pK_a values obtained from five single-site titration simulations.

Given the macroscopic pK_a value of 6.45 (see Methods), the error from the double-site titrations is ∼0.35 pK units in the 0–8-ns simulations and decreases to 0.15 in the last 2-ns simulations. The standard deviation from the double-site titrations is closer to that from the ND1-titrations in the first 4-ns simulations and decreases almost steadily to 0.15 pK units in the last 2-ns simulations. It is also interesting to observe that the average pK_a from the last 2-ns double-site titrations (6.6) coincides with that obtained by combining the pK_a values from the two tautomer titrations (7.0 and 6.8) using Eq. 22 from Methods, above. This suggests that with sufficient sampling of tautomeric states, the errors in the double-site titrations mainly originate from those in the single-site titrations, as will be seen in the titration simulations of blocked aspartic acid.

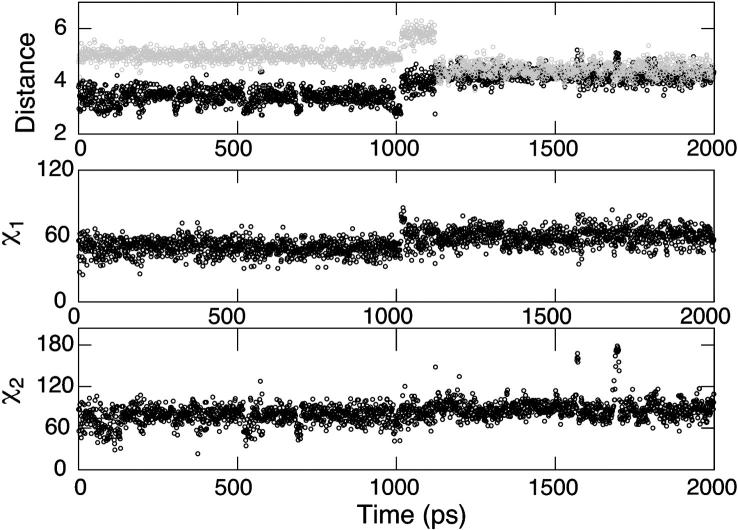
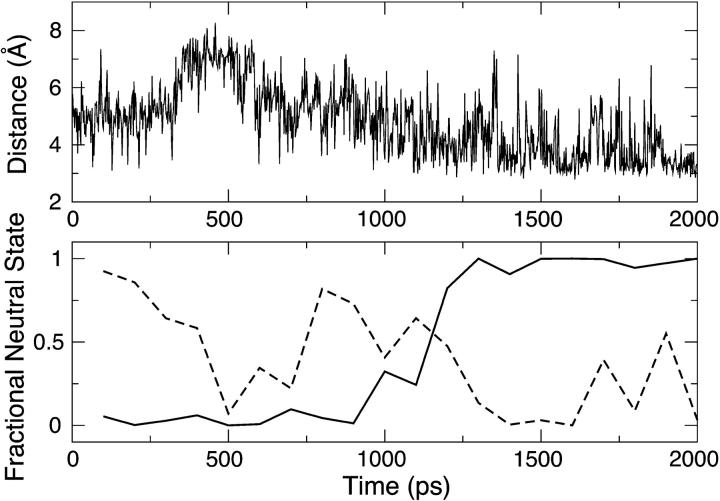
As mentioned in Methods, the difference between the solvation radii for ND1 and NE2 in the neutral and charged states of histidine is 0.5 Å. Since our approach uses a fixed set of radii for the λ-dependent GB energy and force, the protonation state whose assigned solvation radii are closer to the “true” values (as given in the PB radii set; see Refs. 28,29) may be artificially favored. For example, in the extreme case, if the true radius for the charged state HSP is used in the single-site titration simulations, the titrating nitrogen can become undersolvated resulting in a strong electrostatic attraction between the titrating proton and the partially negatively charged backbone carbonyl oxygen, which prevents the deprotonation to occur. Curiously, this has only occurred in titration simulations at the ND1 site. To better understand this bias, we performed a standard GBSW simulation of the blocked doubly protonated histidine. The top plot of Fig. 3 shows that up until 1 ns of MD simulation, the distance from the backbone oxygen to ND1 (solid) is ∼3.4 Å, which is >1 Å smaller than the distance to NE2 (shaded). At slightly after 1 ns, a conformational switch occurs, leading to the merge of the ND1-O and NE2-O distances. The middle plot of Fig. 3 shows a switch of the χ₁ dihedral angle from 50° to 59° at ∼1 ns. The bottom plot of Fig. 3 shows that the χ₂ dihedral angle remains approximately constant during the entire 2-ns simulation. Thus, the difference in the electrostatic environment between the ND1 and NE2 provides an explanation for the failure of titration at ND1. As the nitrogen radius for solvation is decreased to 2.0 Å, both the ND1-O and NE2-O distances increase but the former remains ∼1 Å smaller even after a conformational switch occurs at 1 ns (data not shown).

FIGURE 3.

2-ns standard GBSW simulation of the blocked doubly protonated histidine. The top plot shows the time series of the distance from the backbone carbonyl oxygen to ND1 (solid) and that to NE2 (shaded). The middle and bottom plots show the time series of the χ₁ and χ₂ angles, respectively.

In this work, we fix the solvation radii at 2.0 Å for both the neutral and charged states of histidine in the titration simulation. Also, we restrict the pH range for the titration to no more than 3 pK units, around the pH at which the protonation state is expected to change. A rigorous way to deal with the charge-state dependence of solvation radii is to introduce some mixing scheme, for example, a linear interpolation of radii with respect to λ. This is not implemented in the current version of the CPHMD module, because it would significantly complicate the derivation of an analytic form for the model potential function. As the CPHMD method becomes more elaborated, one can envision the inclusion of bonded parameters and solvation radii in the mixing scheme, in which case the derivation of the model potential function has to rely upon some numerical fitting scheme.

Blocked aspartic acid

Table 2 summarizes the running pK_a values for blocked aspartic acid in the double-site and single-site titration simulations. Given the target pK_a of 4.3 (see Methods), the double-site titrations lead to an underestimation of 0.5–0.6 pK units, with a standard deviation of 0.33 pK units in the first 2-ns simulation time. The magnitude of error and standard deviation decreases as the simulation continues. The last 2-ns gives an average error of −0.2 pK units with a standard deviation of 0.25.

TABLE 2.

Computed running pK_a values for the blocked aspartic acid from the double- and single-site titration simulations (see legend below)

	0–2 ns	2–4 ns	4–6 ns	6–8 ns	8–10 ns
1	3.9	3.5	4.2	4.3	4.3
2	3.4	3.5	4.1	4.0	4.2
3	3.7	3.7	3.7	3.9	3.7
4	4.3	4.5	4.7	4.2	4.3
5	3.8	3.1	3.4	3.8	4.0
Mean (std.)*	3.8 (0.33)	3.7 (0.52)	4.0 (0.50)	4.0 (0.21)	4.1 (0.25)
OD1†	3.9 (0.10)	4.0 (0.089)	4.0 (0.041)	4.0 (0.041)	4.0 (0.041)
OD2†	3.7 (0.12)	3.9 (0.055)	3.7 (0.045)	3.9 (0.083)	3.8 (0.083)
OD1‡	4.2 (0.31)	4.2 (0.28)	4.2 (0.25)	4.2 (0.23)	4.2 (0.13)
OD2‡	4.2 (0.34)	4.2 (0.28)	4.2 (0.31)	4.2 (0.23)	4.3 (0.23)

The pK_a values were obtained from 2-ns time windows with a total simulation length of 10 ns at pH values 3, 4, and 5. An additional 100 ps is allotted for equilibration. A random initial velocity seed was used for each run.

^*Average and standard deviation of pK_a values from five double-site titration simulations.

^†Average and standard deviation of pK_a values from five single-site titration simulations using the bonded parameters for the ionic aspartate (see text).

^‡Average and standard deviation of pK_a values from five single-site titration simulations using the bonded parameters for the neutral aspartic acid (see text).

Table 2 also shows results from two types of single-site simulations. First, simulations were conducted by keeping the topology and bonded parameters (of the ionic aspartate, see Methods, above) intact, while allowing only one carboxylate oxygen (OD1 or OD2) to titrate. For titrations at OD2 an average error of −0.3 pK units is observed for the first 2-ns simulations, the magnitude of which is reduced to 0.2 in the last 2-ns simulations. For titrations at OD1 there is an average error of −0.1 pK units in the first 2-ns simulations. The standard deviations in the single-site simulations are ∼0.1 pK units in the first 2-ns simulations and are smaller as the simulation progresses. A possible reason for the small underestimation of the pK_a value in the single-site titrations is a slight overstabilization of the ionic aspartate relative to the neutral aspartic acid due to insufficient relaxation of the peptide conformation in the latter state. In the titration simulation, the residency time of the end-point states is on the order of picoseconds (16), which is much smaller relative to the length of the thermodynamic integration simulations at discrete λ-values (typically 1 ns) that were used to determine the model potential function. Consequently, the employment of the bonded parameters of the ionic aspartate that have two C-O bonds with a formal bond order of 1.5 for both the ionic and neutral states in the case of insufficient sampling, can slightly favor the ionic state leading to a negative error in the predicted pK_a value.

If the above explanation were true, it would predict a positive error for single-site titrations using the bonded parameters of the neutral aspartic acid that has one single and one double C-O bond, as in the work of Lee et al. (16). This is indeed the case. The last two rows of Table 2 show a persistent overestimation by 0.2 pK units in the single-site titrations at OD1 or OD2 using the force-field parameters that are designed for aspartic acid. The same single-site model when used with the GBMV solvation method also gave a overestimation of 0.3 pK units in the predicted pK_a (16). Notice that the single-site titrations using the force-field parameters for the neutral species exhibit standard deviations twice those relative to using the parameters for the ionic species. Based on the above considerations and given the limitation of the current CPHMD methodology that allows only single topology, titration simulations of carboxyl group with the bonded parameters designed for the ionic species seems to be a better choice. It should be noted that the problem related to the force-field parameters does not exist in the titration simulations of histidine, since the latter has identical bonded parameters for both charge states in the CHARMM22 force field.

OMTKY3

Table 3 summarizes the computed pK_a values for turkey ovomucoid third domain (OMTKY3) from the double-site and single-site simulations and compares them with the results from experiment and other simulations. The double-site titration simulations with the crystal structure (column Cryst.) yield an average absolute error of 1.0 pK unit based on the first 2-ns simulations and 1.2 pK units based on the second 2-ns simulations. The double-site simulations with the NMR structure (column NMR) yield pK_a shifts (relative to the model compound reference values) of the same sign and the average absolute errors of similar magnitude. Thus we do not observe a strong initial structure dependence to the overall pK_a comparisons. The single-site OD1 and OD2 titrations with the crystal structure (column OD1 (OD2)) result in pK_a shifts of the same sign as from the double-site simulations, but much larger average absolute errors (1.9 and 1.5, respectively). As expected, the magnitude of these errors is similar to that from the single-site simulations with the GBMV solvent model (column GBMV). Compared to experimental data, the current simulations predict correct signs of pK_a shifts for all but one residue (Asp²⁷, see later discussions), whereas the GBMV simulations predict only one correct sign of the pK_a shift (Glu¹⁹). Finally, compared to the CPHMD simulations, the two sets of PB calculations employing a protein dielectric constant of 20 (column Static) based on the static crystal structure yield smaller average absolute errors (0.6 pK units).

To characterize the local electrostatic environment of titrating residues in OMTKY3, Table 4 summarizes the distances among titrating residues from the double-site simulations at three pH values and compares them with the distances measured in the crystal structure. These three pH values represent the conditions in which the specified residue is fully protonated (acidic), partially protonated, or fully deprotonated (basic). Below we will discuss the correlation between the pK_a value and the dominant electrostatic interactions involving the titrating residue as revealed by the simulations and the crystal structure data. In a related study, Li et al. (35) showed that pK_a values in OMTK3 could be reproduced using QM methods with minimal models including key interacting residues. It should be noted that since the crystal structure was obtained under basic (pH = 10) conditions, where all carboxyl groups were deprotonated, the measured distances between oppositely charged residues represent lower bounds to those measured at lower pH.

TABLE 4.

Distances between titrating residues and other charged residues in OMTKY3 (see legend below)

							Cryst.
Asp7	pH = 0		pH = 2		pH = 4
Glu10	11.0 (1.9)	6.4 (1.0)	7.2 (1.8)	6.6 (1.1)	7.6 (1.6)	6.8 (0.8)	6.7
Arg21	10.7 (1.3)	12.1 (0.9)	11.9 (2.1)	6.8 (3.0)	8.8 (1.5)	9.7 (1.3)	17.4
Lys34	6.3 (0.7)	7.1 (1.1)	6.6 (1.4)	5.3 (1.7)	4.0 (0.9)	3.8 (0.6)	5.0
Glu10	pH = 1		pH = 3		pH = 5
Asp7	7.3 (1.8)	6.8 (1.6)	8.3 (1.4)	6.7 (1.1)	8.5 (2.5)	6.5 (0.6)	6.7
Lys13	4.6 (0.9)	4.7 (0.9)	7.4 (2.2)	7.2 (2.6)	7.8 (2.4)	9.6 (1.2)	4.8
Arg21	12.5 (2.2)	11.1 (2.6)	7.3 (2.0)	5.1 (1.5)	6.8 (1.6)	5.8 (0.9)	18.2
Lys34	6.8 (1.5)	6.5 (1.8)	6.0 (2.7)	4.6 (1.6)	4.4 (1.9)	3.4 (0.3)	6.3
Glu19	pH = 1		pH = 2		pH = 4
Lys13	6.7 (1.0)	6.4 (1.4)	8.2 (1.9)	7.2 (2.0)	12.2 (1.6)	13.0 (1.4)	10.3
Arg21	9.7 (1.8)	6.9 (2.3)	9.2 (2.0)	7.9 (1.1)	4.5 (1.1)	4.2 (0.5)	8.6
Lys34	7.4 (1.7)	7.6 (1.7)	6.8 (1.8)	4.4 (1.3)	8.3 (1.6)	9.6 (1.2)	10.7
Asp27	pH = 2		pH = 4		pH = 6
Lys29	6.6 (0.7)	6.5 (1.1)	4.6 (1.1)	6.7 (1.1)	6.8 (1.7)	5.7 (1.7)	6.1
Tyr31	5.0 (0.7)	5.2 (0.9)	4.9 (0.8)	4.7 (0.6)	5.3 (1.0)	5.4 (1.1)	3.5
CT-Cys	pH = 0		pH = 2		pH = 3
His52	4.8 (0.6)	4.6 (0.6)	4.6 (0.6)	4.6 (0.6)	4.3 (0.6)	4.3 (0.6)	4.9
Lys55	9.0 (0.5)	9.1 (0.2)	8.9 (0.8)	8.5 (1.5)	8.8 (1.3)	9.2 (0.4)	7.9

Average and RMS fluctuations of distances (in Å) between the titrating and other charged residues in the first (0–2 ns, left column) and second half (2–4 ns, right column) of the simulations of OMTKY3 starting from the crystal structure PDB:1PPF (44), under three pH conditions. The pH values represent the conditions in which the specified residue is fully protonated (left), partially protonated (middle), and fully deprotonated (right). Only those distances smaller than 10 Å are shown. For Asp²⁷, Tyr³¹ is listed since it forms a hydrogen bond with Asp²⁷ in the crystal structure (see text). The residue-residue distance is defined as that to the carboxyl carbons, NE2 of histidine, NZ of lysines, and CZ of arginines. The column Cryst. refers to the distances measured in the crystal structure at pH 10.

Asp⁷ is a solvent-exposed residue that electrostatically interacts mainly with Glu¹⁰ and Lys³⁴. The positively charged Lys³⁴ provides stabilization for the ionic form of Asp⁷. The crystal structure (Table 4) shows that Asp⁷ is closer to Lys³⁴ (5 Å) than to Glu¹⁰, which explains the downfield pK_a shift of the experimental pK_a of Asp⁷ relative to the model compound value. Under acidic conditions (pH = 0, Asp⁷ is mainly neutral), Lys³⁴ is further away from Asp⁷ with the average distance of 6.3 Å and 7.1 Å in the first (0–2 ns) and second (2–4 ns) half of the simulation, respectively. With increasing pH, the Asp⁷-Lys³⁴ distance becomes smaller. Under neutral conditions (pH = 2), the Asp⁷-Lys³⁴ distance is 6.6 Å and 5.3 Å in the first and second half of the simulation, respectively. Under more basic conditions (pH = 4, Asp⁷ is mainly ionized), a salt bridge is formed between Asp⁷ and Lys³⁴: the average distance is 4.0 and 3.8 Å in the first and second half of the simulation, respectively. The lower pK_a value (pK_a = 2.4) of Asp⁷ in the second half of the simulation relative to that in the first half (pK_a = 2.8) is mainly due to the additional electrostatic attractions from Arg²¹, which moves on average ∼5 Å closer to Asp⁷ in the second half of the simulation. In contrast to the Asp⁷-Lys³⁴ distance, the Asp7-Arg²¹ distance becomes larger at pH 4.

The pK_a (2.8) for Asp⁷ obtained from the first 2-ns simulations using the double-site model is between the values computed using the OD1 (pK_a = 3.9) and OD2 (pK_a = 1.9) single-site model, and agrees well with the experimental value of 2.7 (Table 3). This is consistent with the reasonable agreement of the simulated major electrostatic interactions (Asp⁷ with Glu¹⁰ and Lys³⁴) under basic conditions with those from experiment (crystal structure).

The electrostatic environment of Glu10 is more complex, and includes the titratable groups Asp⁷, Lys¹³, Arg²¹, and Lys³⁴ (Table 4). In the crystal structure, Lys¹³ is the closest residue with the Lys¹³-Glu¹⁰ distance of 4.8 Å, followed by Lys³⁴, Asp⁷, and Tyr¹¹, that are >6 Å away. Arg²¹ is ∼18 Å from Glu¹⁰ in the crystal structure. In contrast, MD simulations under neutral to basic conditions show that Arg²¹ moves to be <7 Å away from Glu¹⁰ (Table 4).

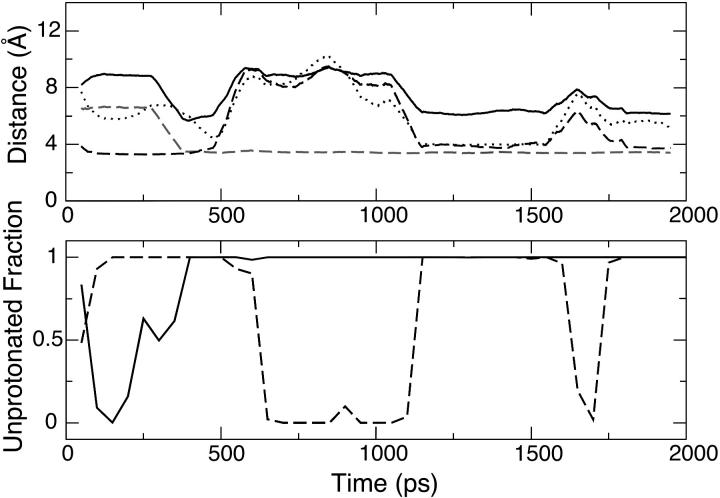
The top plot of Fig. 4 shows how the motion of Glu10 is correlated with that of Asp⁷, Lys³⁴, and Arg²¹ at pH 3, where Glu¹⁰ is partially deprotonated. At the beginning of the simulation, Lys³⁴ is in salt-bridge contact with Glu¹⁰ (dashed curve) and is ∼6.5 Å away from Asp⁷. Due to the attractive electrostatic force and the diminished mobility of Lys³⁴, Asp⁷ is driven closer to form a salt bridge with Lys³⁴ at ∼320 ps (shaded dashed curve), which also results in a sharp drop in the Asp⁷-Glu¹⁰ distance from 9 Å down to below 6 Å (solid curve). However, this local environment is not stable, due to the electrostatic repulsion between Asp⁷ and Glu¹⁰. At the same time, the electrostatic attraction between Arg²¹ and Glu¹⁰ facilitates the departure of Glu¹⁰ from Lys³⁴ and the formation of a loose salt-bridge contact between Glu¹⁰ and Arg²¹ at 450 ps (dotted curve), which then breaks off at 520 ps due to the motion of Glu¹⁰. The dynamics in the following period of time (until the end of the first half of the simulation), is dominated by the motion of Glu¹⁰, driven by the attraction from Lys³⁴ and Arg²¹. This continues at the beginning of the second half of the simulation and starting at ∼1.1 ns, Glu¹⁰ arrives at a position that allows it to form salt-bridge contacts with both Lys³⁴ and Arg²¹, although not as tight as the Lys³⁴-Asp⁷ salt bridge. The dynamics of the last part of the simulation (between 1.6 and 2 ns) is again characterized by the breaking and making of the electrostatic contacts of Glu¹⁰-Lys³⁴ and Glu¹⁰-Arg²¹.

FIGURE 4.

Coupling between Asp⁷ and Glu¹⁰ in a 2-ns simulation of OMTKY3 at pH 3. The top plot shows the time series of the running average distances between Asp⁷ and Glu¹⁰ (solid), Asp⁷ and Lys³⁴ (shaded dashed), Glu¹⁰ and Lys³⁴ (dashed), and Glu¹⁰ and Arg²¹ (dotted) computed from 100-ps time windows. The definitions of the residue-residue distances are given under Table 4. The bottom plot shows the running unprotonated fraction for Asp⁷ (solid) and Glu¹⁰ (dashed) computed from 100-ps time windows.

A comparison of the bottom plot of Fig. 4 with the top one shows a direct correlation between the unprotonated fraction of Asp⁷ (solid curve), that of Glu¹⁰ (dashed curve), and the existence of the salt bridge. Accordingly, Asp⁷ is protonated at the beginning of the simulation and becomes unprotonated once it forms and maintains the salt bridge with Lys³⁴. On the other hand, Glu¹⁰ is unprotonated at the beginning and becomes protonated upon its departure from both Lys³⁴ and Arg²¹. In the second half of the simulation it looses a proton again due to salt-bridge formation with Lys³⁴ and Arg²¹. Finally, the simultaneous loss of salt-bridge contacts between Glu¹⁰ and Lys³⁴ and between Glu¹⁰ and Arg²¹ is reflected in the plot as a dip in the curve of the unprotonated fraction. Fig. 4 also reveals that the salt-bridge formation in the second half of the simulation is the cause for the lowering of Glu¹⁰'s pK_a relative to the first half of the simulation, consistent with the observation for Asp⁷.

In contrast to the simulation, which reveals two on and off salt bridges (Glu¹⁰···Lys³⁴ and Glu¹⁰···Arg²¹), the crystal structure shows only one salt bridge (Glu¹⁰···Lys¹³). This is the reason for the negative difference (−1.1 pK units) in the computed pK_a for Glu¹⁰ relative to experiment. In the last 2-ns simulations, the simultaneous formation of the two salt bridges gives rise to a larger difference (−1.9 pK units) relative to the first 2-ns simulations (−1.1 pK units). The salt-bridge effects seem to be more pronounced in single-site titrations. As a result, the differences are larger: −1.8 for the OD1 and −1.5 pK units for the OD2 titrations. Interestingly, the PB calculation also gives an underestimation of 0.8 pK units.

In the crystal structure under basic conditions, Glu¹⁹ interacts with three positively charged groups (Lys¹³, Arg²¹, and Lys³⁴) at a distance over 8 Å (Table 4). However, in the simulation at pH >2, Glu¹⁹ forms a persistent salt bridge with Arg²¹, thereby preventing the protonation of Glu¹⁹. This is the reason for the negative difference of Glu¹⁹'s pK_a (−0.9 pK units) using the double-site simulations (Table 3) relative to experiment. The magnitude of the underestimation using the OD1 and OD2 titrations is ∼2 pK units larger.

The prediction of the pK_a for Asp²⁷ is most problematic, since it is partially sequestered from solvent and yet it is the most acidic residue in OMTKY3 according to experiment (Table 4). In the simulation at pH 4, Asp²⁷ is a hydrogen-bond acceptor to its backbone amide nitrogen and to that of Lys²⁹ with an occupancy of 20%. In addition, Asp²⁷ interacts with the hydroxyl oxygen of Tyr³¹ as both a hydrogen-bond acceptor and donor with an occupancy of 30%. In the first 2-ns, Asp²⁷ is >40% deprotonated due to the salt-bridge interaction with Lys²⁹ (Table 4). Although the mobility of Asp²⁷ is low, the fluctuation of the side-chain position of Lys²⁹ is large as seen from the >1 Å root-mean square (RMS) deviation of the Asp²⁷-Lys²⁹ distance. In the last 2-ns, Asp²⁷ loses the salt-bridge contact with Lys²⁹ and dominantly occupies the protonated state (Table 4). The convergence of the protonation state sampling for Asp²⁷ is incomplete, which can be seen from a large percentage of mixed states (∼36% in the first and 42% in the last 2-ns of simulation time).

The double-site titration model overestimates the pK_a for Asp²⁷ by 2.4 pK units, the largest error among all the residues in OMTKY3 (Table 3). Interestingly, Asp²⁷ shows the largest computational error in the static PB calculations as well, although to a lesser degree (overestimated by 1.7 and 1.3 pK units). As compared to the single-site model, the double-site model does not offer any advantage for the titration of Asp²⁷. One obvious reason for the large deviation from experiment is the aforementioned issue of incomplete sampling of protonation states. Conformational relaxation of buried residues in response to ionization requires much longer simulation time as demonstrated in a recent work by Simonson et al. (36). Another possible reason for the difference may be the overestimation of the desolvation effect due to undersolvation for the protonated aspartic acid relative to the charged aspartate, since the current GB model employs one atomic solvation radius for the both the neutral and charged forms.

Glu⁴³ does not have strong electrostatic interactions with other charged groups and has therefore a small experimental pK_a upshift of 0.4 units (Table 3). Although the OD1 and OD2 titrations give a downshift of 0.4 and a upshift of 0.1 pK units, respectively, the double-site model predicts an upshift of 0.9 units, consistent with the experimental values. The deviations from experiment are within statistical errors, as shown in the titration simulations for model compounds. Interestingly, the static PB calculation is unable to capture the sign of the experimental pK_a shift of Glu⁴³.

The local electrostatic environment around the α-carboxyl group CT-Cys includes two positively charged residues His⁵² and Lys⁵⁵ (Table 4). The pK_a downshift of CT-Cys is dominated by the interaction with His⁵², since the simulation data reveals the formation of a salt bridge between CT-Cys and His⁵² that does not exist in the crystal structure (Table 4). This explains why the double-site simulations result in a pK_a downshift that is 1.2-pK-units greater relative to experiment and the single-site titrations yield even larger errors.

RNase A

Bovine pancreatic ribonuclease A (RNase A) is an enzyme that catalyzes the transphosphorylation and hydrolysis reactions of RNAs (37). Table 5 summarizes the computed pK_a values from the double-site simulations with the GBSW solvation model (current model), in comparison with the split-model simulations (imidazole ring is split into two titration halves involving ND1 and NE2) with the GBMV solvation model (previous work) (16), and the PB static calculations (38), as well as experimental data. The current model gives an average absolute error of 0.6 pK units for the histidine groups, representing a significant improvement over the previous work using the split-model (2.5 pK units). In fact, the error from the current model is even smaller than that from the static PB calculations (0.8 pK units). It is noteworthy that results from the split-model simulations with the GBSW solvation model yield even larger differences (data not shown). The current model also gives smaller average absolute error (1.6 pK units) for the carboxyl groups relative to the previous work (2.0 pK units). For the N-terminus group, the current model yields a difference of 0.6 pK units, as compared to 1.0 pK unit from the previous work. Again, the current model predicts the correct sign for all pK_a shifts in RNase A, in contrast to the previous work that predicts the correct sign for only seven pK_a values (with a total of 17).

The protonation equilibria of active-site residues His¹² and His¹¹⁹ are responsible for the pH-dependent catalytic mechanism of RNase A. A traditional view is that His¹² and His¹¹⁹ act as general acid and base in RNA hydrolysis, respectively, whereas their roles are reversed in the transphosphorylation step (37). The crystal structure of the phosphate-free RNase A (PDB:7RSA, see Ref. 39; pH = 5.3), shows that His¹² is completely buried whereas His¹¹⁹ is partially buried in the protein interior. Thus, desolvation effects are expected to result in their pK_a downshifts. Distance measurements in the crystal structure reveal an electrostatic interaction between His¹² and His¹¹⁹ and a hydrogen bond between the NE2 of His¹¹⁹ and OD1 of Asp¹²¹ (Table 6).

TABLE 6.

Distances between histidine residues and other nearby residues in RNase A (see legend below)

				Cryst.
His12	pH = 4	pH = 5	pH = 7
r(NE2···ND1119)	4.3 (1.0)	4.8 (1.2)	3.9 (0.9)	6.3
His48	pH = 4	pH = 6	pH = 8
r(ND1···CG14)	3.8 (0.3)	4.1 (0.3)	7.1 (0.8)	4.3
r(ND1···O14)	3.3 (0.5)	3.7 (1.2)	4.1 (1.1)	3.3
His105	pH = 5	pH = 7	pH = 8
r(ND1···O75)	4.8 (0.7)	4.1 (0.9)	4.1 (1.0)	3.0
r(NE2···O76)	3.6 (0.6)	3.8 (0.6)	4.0 (0.6)	4.6
His119	pH = 4	pH = 5	pH = 8
r(NE2···OD1121)	4.0 (1.1)	5.3 (2.0)	7.1 (1.0)	1.9

Average and RMS fluctuations of the distances (in Å) between the histidine and other strongly interacting residues in the 2-ns simulations of RNase A starting from the crystal structure PDB:7RSA (38) under three pH conditions. The pH conditions are arranged such that the left and right ones give the fully protonated and deprotonated states, respectively, whereas the middle one gives partial protonation/deprotonation. The atoms used in the distance measurements are specified in parentheses, where the first atom refers to the underlined residue and the second one is indicated by the superscript. The column Cryst. refers to the distances measured in the crystal structure at pH 5.3.

The lower plot of Fig. 5 shows that His¹² is predominantly charged in the first half of the simulation (0–1 ns), and switches to be in the neutral state in the second half of the simulation (1–2 ns) under pH 5 conditions. On the other hand, the degree of deprotonation of His¹¹⁹ fluctuates at ∼0.5 in the first half of the simulation but becomes much smaller in the second half of the simulation. Fig. 5 also reveals that the degree of deprotonation on His¹² and His¹¹⁹ is correlated with the strength of the electrostatic interaction between them. As His¹² and His¹¹⁹ are >7 Å away from each other between 400 and 600 ps, the interaction is small, allowing both residues to be in the charged state at pH 5. As His¹¹⁹ moves closer to His¹² between 750 and 1000 ps, His¹¹⁹ starts to lose its proton more often. As the distance continues to shorten, the coupling between His¹² and His¹¹⁹ is so strong that only one residue (His¹¹⁹) is allowed to be charged to minimize the electrostatic repulsion. Thus, the strong coupling raises the pK_a of His¹¹⁹ and lowers that of His¹². The upper plot of Fig. 5 reveals that the fluctuation in the His¹²-His¹¹⁹ distance is linked to the change in the χ₂ dihedral angle of His¹¹⁹. In contrast, His¹² has a much lower mobility since it is buried and subject to steric hindrance from neighboring groups.

FIGURE 5.

Coupling between His¹² and His¹¹⁹ in a 2-ns simulation of RNase A at pH 5. The top plot shows the time series of the distance between NE2 of His¹² and ND1 of His¹¹⁹. The bottom plots shows the running fraction of neutral states for His¹² (solid) and His¹¹⁹ (dashed) computed from 100-ps time windows.

Another factor that affects the ionization equilibrium of His¹¹⁹ is its interaction with Asp¹²¹, which is a hydrogen-bond acceptor according to the crystal structure. In the simulation the hydrogen bond NE2-HE2¹¹⁹···OD1¹²¹ only exists under pH conditions below 5. At pH 5, His¹¹⁹ becomes partially deprotonated and the average distance between NE2¹¹⁹ and OD1¹²¹ is 5.3 Å (Table 6). The loss of the hydrogen-bonding interaction with Asp¹²¹ contributes to the stronger interaction between His¹¹⁹ and His¹², relative to that observed in the static crystal structure. This could arise from the fixed atomic solvation radii used in the current simulation. At pH 5, His¹¹⁹ in the charged state experiences less attraction from Asp¹²¹ due to the enhanced solvent screening as a result of the smaller solvation radius. On the other hand, the enhanced solvent screening decreases the unfavorable interaction between His¹¹⁹ and His¹². It should be noted, however, that the degree of the enhanced solvent screening is small, since both the NE2 and ND1 atoms are partially sequestered from solvent.

The interaction between His¹¹⁹ and His¹² is one reason for our underestimation of the pK_a for His¹². It may also be linked to the exaggerated desolvation effect, which can be again partially attributed to the fixed atomic solvation radii approximation. In this case, the neutral state is preferentially stabilized, as a result of a larger desolvation penalty for the charged state. It is interesting to see that the static PB calculation also gives a large underestimation for the pK_a of His¹².

The current simulations reveal that whereas the deprotonation process of His¹¹⁹ occurs via both ND1 and NE2 atoms, the deprotonation of His¹² occurs predominantly (>90%) at NE2 (data not shown). This is in agreement with a direct observation via the high-resolution x-ray diffraction of RNase A (sulfate bound) under different pH conditions (39) and is in support of the proposed mechanism, which suggests that the NE2 atom of His¹² exchanges a proton with the substrate (40). It is worthwhile emphasizing the importance of predicting the correct tautomeric state for the histidine titration. The PB calculation and the split-model simulation gave a significant underestimation of His¹²'s pK_a by 2.0 and 3.4 units, respectively.

His¹¹⁹ has two conformations due to the variation in the χ₁ dihedral, which are referred to as trans and gauche. In the above experimental study (40) both conformations were observed at the acid pH (pH = 5.2), whereas only the trans conformation was observed at the basic pH (pH = 8.8). The current simulations, however, show that the trans conformation exists exclusively in the pH range between 5 and 8. This is in line with the argument put forward by the authors that the coexistence of both conformations is made possible through hydrogen bonding with the sulfate ion whereas the trans conformation is favored in the ion-free environment due to its strong interaction with Asp¹²¹ (40).

His⁴⁸ is completely embedded in the protein interior and interacts with a nearby negatively charged embedded residue Asp¹⁴. Thus, the protonation equilibrium of His⁴⁸ is a result of the balance between the desolvation effect that favors the neutral state and the electrostatic interaction that favors the charged state. In fact, the experimental pK_a reveals only a small downshift. The simulation at pH 6 (partial deprotonation) shows that the charged state of His⁴⁸ is stabilized by a salt-bridge interaction with Asp¹⁴, as well as the hydrogen bond between HD1 of His⁴⁸ and the backbone carbonyl oxygen of Asp¹⁴ (Table 6). Thus, it appears that the ND1 atom is protected from deprotonation through its hydrogen bonding with Asp¹⁴. This is consistent with the observation made in the aforementioned experiment that the deprotonation of His⁴⁸ occurs via its NE2 atom (40). As His⁴⁸ becomes deprotonated, the current simulations show that the χ₂ dihedral angle changes from an average of −61° (pH = 6) to an average of −53° (pH = 8), in line with the experimental observation (40).

It is curious that His¹⁰⁵ exhibits an error of 0.6 units for its computed pK_a, although it is fully immersed in solvent and free of strong electrostatic interactions with other charged residues. A close examination of the MD trajectory at pH 7 (partial deprotonation) reveals occasional hydrogen-bonding contacts between its HD1 atom and the backbone carbonyl oxygen of Ser⁷⁵ with an occupancy of 24%, as well as between the HE2 atom and the backbone carbonyl oxygen of Tyr⁷⁶ with an occupancy of 13%, which do not exist in the crystal structure (Table 6). Consequently, the doubly protonated form of His¹⁰⁵ is stabilized resulting in an overestimation of its pK_a unit relative to experiment (Table 5).

From Table 5 it can be seen that the average absolute error of the computed pK_a values for RNase A is dominated by four groups, Glu², Asp⁸³, Asp¹²¹, and CT-Val. The pK_a downshifts for these groups are calculated to be too large by 2.8, 4.4, 2.7, and 2.4 units relative to the corresponding experimental values, respectively. Table 7 summarizes the computed distances between these and other nearby charged residues in comparison to the measured values. It should be noted that since the crystal structure was obtained at pH 5.3, where all carboxyl groups are deprotonated, the measured distances between the oppositely charged residues represent lower bounds to the distances measured at lower pH.

TABLE 7.

Distance between the carboxyl residues and other nearby charged residues in RNase A (see legend below)

		Cryst.
Glu2	pH = 0
r(CD···NZ7)	6.8 (1.3)	7.3
r(OE1···NH210)	3.5 (1.5)	2.8
r(OE2···NE10)	3.9 (1.6)	2.8
Asp38	pH = 2
r(CG···CZ10)	6.2 (2.8)	10.3
r(CG···NZ37)	7.9 (1.9)	4.1
r(CG···CZ39)	6.8 (1.3)	8.2
Asp83*	pH = 0
r(OD1···NE85)	2.9 (0.5)	6.6
r(OD2···NH285)	2.9 (0.2)	3.1
Asp121	pH = 0
r(OD1···N66)	3.8 (1.0)	3.7
r(OD2···N66)	3.8 (1.0)	2.8
r(OD1···NE2119)	4.5 (1.7)	2.9
CT-Val	pH = 0
r(OT2···NZ104)	4.3 (0.9)	4.7
r(OT1···N105)	2.9 (0.3)	5.0
r(N···O105)	2.8 (0.1)	2.9

Average and RMS fluctuations (in Å) between the carboxyl residues that exhibit large errors in the calculated pK_a values (>1.5 pK units) and other nearby charged residues in the 2-ns simulations of RNase A starting from the crystal structure PDB:7RSA (39) under a pH condition that gives partial protonation/deprotonation. The atoms used in the distance measurements are specified in parentheses, where the first atom refers to the underlined residue and the second one is indicated by the superscript. Column Cryst. refers to the distances measured in the crystal structure at pH 5.3.

^*Taken from the crystallographic conformation where Arg⁸⁵ is pointing toward Asp⁸³ (see text).

The protonation equilibria of Glu² and Asp³⁸ are coupled. Both the crystal structure and simulation at pH 0 show that the ionic form of Glu2 is stabilized through two charged hydrogen bonds to Arg¹⁰: OE1 with NH2 and OE2 with NE (Table 7). The simulation also reveals a slightly closer distance of Glu²-Lys⁷ relative to experiment. As pH is increased to 2, the simulation shows that whereas the double hydrogen bonds between Glu² and Arg¹⁰ are maintained, Asp³⁸ moves closer to Arg¹⁰ and forms a charged hydrogen bond to Arg¹⁰'s NH2 via its carboxylate oxygens alternately (Fig. 6 A). In contrast to the strong interaction between Asp³⁸ and Arg¹⁰ as revealed by simulation results, the crystal structure shows a salt bridge between Asp38 and Lys³⁷ (Table 7). Thus, it appears that the simulation overestimates the strength of the electrostatic interaction between a negatively charged residue and arginine.

FIGURE 6.

Snapshots from the 2-ns simulation of RNase A showing the salt-bridge and hydrogen-bond interactions involving Glu², Asp⁸³, Asp¹²¹, and CT-Val under pH conditions of 2, 0, 0, and 0, respectively.

The prediction of the pK_a for Asp⁸³ seems to be most problematic due to its interaction with Arg⁸⁵. The crystal structure shows that Arg⁸⁵ occupies two conformations with its amino groups either pointing toward or swinging away from the carboxyl group of Asp⁸³. In the former case, a salt bridge is formed between OD2 of Asp⁸³ and NH2 of Arg⁸⁵. However, independent of the starting conformation, the simulation leads to two charged hydrogen bonds between the carboxylate oxygens of Asp⁸³ and the hydrogens that are attached to the NE and NH2 atoms of Arg⁸⁵ (Fig. 6 B) within just a few hundreds of picoseconds.

The charged hydrogen bonding triad plays a major role in the protonation equilibria of Asp¹²¹ and CT-Val. The simulation at pH 0 shows that Asp¹²¹ is a hydrogen-bond acceptor to the backbone amide of Lys⁶⁶ via OD1 and to the NE2 atom of His¹¹⁹ via OD1 (Fig. 6 C). In contrast, the crystal structure shows only salt-bridge interactions between Asp¹²¹ and Lys⁶⁶ and between Asp¹²¹ and His¹¹⁹ (Table 7), although it has been suggested in other experimental work that the hydrogen bond between Asp¹²¹ and the backbone of Lys⁶⁶ was used to restrict the conformational entropy of the protein (41). Similarly, the simulation at pH 0 shows that CT-Val is a hydrogen-bond acceptor to the backbone amide of His¹⁰⁵ via OT1 that occasionally accepts a hydrogen bond from the NZ atom of Lys¹⁰⁴ (Fig. 6 D). Interestingly, the backbone amide of CT-Val is hydrogen bonded with the backbone carbonyl of His¹⁰⁵ as well (Fig. 6 D).

CONCLUDING REMARKS

In this work, we have presented a two-dimensional λ-dynamics approach to include proton tautomerism in continuous constant pH molecular dynamics (CPHMD) simulations. Consequently, a new tautomeric state model, also called the double-site titration model, is constructed for titration simulations involving histidine and carboxyl residues.

The double-site titration model combined with the GBSW solvation method was tested on blocked histidine and aspartic acid. Given sufficient sampling of tautomeric and protonation states, our calculations give good quantitative estimates of site-specific pK_a values. Sources of deviation in the titration simulations of blocked histidine and aspartic acid are the fixed-radii approximation, the use of the same bonded parameters for both the neutral and charged states, and sampling convergence of conformational variables. These issues represent areas of continuing improvement of such models.

The results of the CPHMD simulations using the double-site titration model and the GBSW solvation method are very encouraging and provide a significant improvement over the previous work. In contrast to the single-site model with the GBMV solvation, the new model predicts the right sign for all the pK_a shifts but one in the benchmark proteins. The new model offers a striking accuracy in the prediction of the protonation and tautomeric states of the histidine residues in RNase A.

However, our detailed analyses of the pH-dependent dynamics of the local electrostatic environment in OMTKY3 and RNase A point to potential areas for improvement of the underlying solvation model to ameliorate the undersolvation of salt bridges. This factor may account for the systematic underestimation of the pK_a values for carboxyl residues that interact with positively charged residues in solvent. The overstabilization of salt bridges in the context of continuum electrostatics is a known problem in the community of protein simulations. One remedy, as used in the work of Georgescu et al. (42), is to introduce some empirical function to dampen the ion-pair interactions. A straightforward but perhaps less pragmatic approach is to reoptimize the atomic solvation radii aiming for a balance among protein stability, foldability, and the underlying physical principles.

Conformational and protonation state sampling also influence the quantitative accuracy of calculated pK_a values, especially for coupled titrating residues such as His¹² and His¹¹⁹ in RNase A and buried residues such as Asp²⁷ in OMTKY3. The CPHMD approach will clearly benefit from the introduction of more efficient sampling techniques, such as replica-exchange MD (43). Our findings, nevertheless, clearly indicate that environmentally dependent factors, and their fluctuating character, mediate the protonation/deprotonation processes for such systems coupled to a pH bath.

One of our main goals in the development of the CPHMD technique is to model important pH-triggered conformational phenomena of proteins, such as the pH-dependent folding/unfolding, membrane insertion, ligand binding, and catalysis. Using OMTKY3 and RNase A, the current work has demonstrated in detail the capability of the CPHMD technique in revealing the pH-coupled conformational dynamics of protein side chains. Future work will include the development of more elaborate mixing schemes, which improve the representation of the λ-dependence in computing solvation energy, covalent interactions, and the addition of more complex sampling schemes.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.