Abstract
We investigate and then modify the hypothesis that a glutamate side chain acts as the fast gate in ClC-0 channels. We first create a putative open-state configuration of the prokaryotic ClC Cl− channel using its crystallographic structure as a basis. Then, retaining the same pore shape, the prokaryotic ClC channel is converted to ClC-0 by replacing all the nonconserved polar and charged residues. Using this open-state channel model, we carry out molecular dynamics simulations to study how the glutamate side chain can move between open and closed configurations. When the side chain extends toward the extracellular end of the channel, it presents an electrostatic barrier to Cl− conduction. However, external Cl− ions can push the side chain into a more central position where, pressed against the channel wall, it does not impede the motion of Cl− ions. Additionally, a proton from a low-pH external solution can neutralize the extended glutamate side chain, which also removes the barrier to conduction. Finally, we use Brownian dynamics simulations to demonstrate the influence of membrane potential and external Cl− concentration on channel open probability.
INTRODUCTION
Voltage-gated ClC Cl− channels are a family of anion channel present in every living cellular organism. ClC channels are selectively permeable to Cl− ions and perform a diverse range of functions. In skeletal muscle, they are known to help stabilize membrane potentials and control cellular excitability. In other situations, they help to regulate cell volumes and the acidification of intracellular vesicles (for recent reviews, see Jentsch et al. (1), Maduke et al. (2), Fahlke (3), and Jentsch et al. (4)). The most widely studied member of the family is ClC-0 from the Torpedo electroplax that was first discovered and characterized by Miller (5). Although a number of different ClC channel isoforms have been identified since then, the exact role of many of these channels is still largely unknown.
ClC channels form dimers with two independent pores and are known to have two distinct voltage-gating mechanisms. The “slow” or inactivation gate operates on both pores in the dimer simultaneously. Bursts of activity typically last 10–100 s before inactivation occurs (2). When active, channel currents fluctuate quickly between three conductance states corresponding to zero, one, or two open pores. This rapid modulation of currents is believed to be controlled by “fast” gates that act on individual pores, opening them upon depolarization (6). Furthermore, fast gating has been shown to be strongly facilitated by extracellular Cl−. As the extracellular concentration is increased, the open probability of the channel also increases. In contrast, intracellular Cl− has less effect on the channel gating properties, but high concentration decreases the closing rate of the fast gate (7). Substituting Cl− ions with other anions has shown that only permeant ions influence gating, and the anomalous mole fraction effect seen in channel currents in a mixture of permeating ions is also reproduced in the gating properties. Together these factors suggest that a permeating ion itself initiates channel gating (6,8) rather than other possibilities such as Cl− ions inducing gating by binding to an external site. Decreasing external pH also increases the open probability of ClC-0, but the effect is different from that of increased external Cl− (9). In the latter case, the curve for the open probability against membrane voltage shifts to the left without changing its minimum, whereas lower pH increases the minimal open probability without shifting the high-open-probability part of the curve.
Recently, new light was shed on the ClC channels and the mechanisms of gating by the publication of crystal structures of ClC proteins from Escherichia coli and Salmonella enterica (10,11). In these structures, a glutamate residue (Glu-148) blocks the middle of the likely conduction pathway. Dutzler et al. (10) showed that ClC-0 channels with mutations E148A, E148Q, or E148V do not exhibit fast gating behavior. They obtained x-ray crystal structures for the corresponding mutations of the E. coli ClC channel (ClC-0 and its mutants did not crystallize) and found that the neutral side chain of Gln-148 in the E148Q structure is stretched up the pore toward the extracellular vestibule, unlike the side chain of Glu-148. On this basis, Dutzler et al. (10) postulated that motion of the Glu-148 side chain between these positions is responsible for fast gating in ClC-0; the gate is closed when the side chain is in the middle of the pore and opens when the side chain moves toward the extracellular vestibule. Cohen and Schulten (12), among others, pointed out that this mechanism in particular does not explain how extracellular Cl− effects channel gating and facilitates the outward conduction of Cl− ions. However, Cohen and Schulten (12) accept this mechanism for the molecular dynamics (MD) study described in their study. In contrast, Bostik and Berkowitz (13) propose that protonation of the Glu-148 side chain, mediated by the local concentration of Cl−, opens the fast gate.
A further complication emerged when Accardi and Miller (14) demonstrated that the bacterial ClC protein that had been crystallized in fact appeared to act as a Cl−/H+ exchange transporter, unlike all other ClC proteins studied. Despite this, the bacterial ClC protein has significant sequence similarity with eukaryotic ClC proteins, and Accardi and Miller (14) support the idea that they share a very similar basic structure. Estévez et al. (15) studied inhibitor binding to prokaryotic and eukaryotic ClC channels and concluded that their structures are quite similar. Also, the similarity between pro- and eukaryotic channel protein structures has been demonstrated in at least one example by Law and Sansom (16). They created the structure of a bovine aquaporin by homology modeling based on a bacterial glyceroaquaporin x-ray structure and compared it to the actual aquaporin x-ray structure, finding great similarity. Together these results imply that it is at least plausible that the basic ClC-0 structure can be derived from the structure of the E. coli ClC.
Here we propose, and demonstrate with MD and electrostatic energy profiles, a slightly different mechanism of fast gating than that suggested by Dutzler et al. (10). We show that in the open state the Glu-148 side chain may be near the middle of the channel, but it is pushed back against the wall of the pore by Cl− ions passing through. The closed state occurs when the side chain is stretched up toward the extracellular vestibule, where its negative charge blocks Cl− ions from passing. This state can be caused by intracellular Cl− repelling the side chain from below. However, extracellular Cl− in the vestibule can drive the side chain back toward the middle of the channel, thus reopening the gate (or holding it open) for both inward and outward conduction. Additionally, low pH in the external vestibule can lead to protonation of the Glu-148 side chain, neutralizing its blocking charge and allowing Cl− to pass.
The proposed mechanism reverses the side-chain positions suggested by Dutzler et al. (10), but it accounts for all three essential aspects of fast gating: namely, i), the open probability of the channel is greater when the electrochemical gradient is driving Cl− ions through the channel from the extracellular side, ii), increasing concentration of Cl− on the extracellular side increases the open probability for outward conduction of Cl− ions, and iii), decreasing external pH increases the open probability. The proposed mechanism is also in accord with the observed lack of fast gating in the E148 neutral mutants.
Our approach to the study of ClC gating differs from the recent MD work of Cohen and Schulten (12) and Bostick and Berkowitz (13) in that we use a model of the open-pore ClC-0 channel rather than the S. enterica ClC (StClC) exchange transporter, and we simulate conduction events and the motion of the Glu-148 side chain, rather than finding a potential of mean force for ions in the pore. However, a problem faced when simulating conduction and gating with MD is that conduction events driven only by membrane potential and ion concentration require impossibly long simulation times, and therefore it is necessary to modify the behavior of the MD system. For example, Cl− ions are sometimes placed in preconduction positions when MD runs begin, and some of the Cl− ions can be held in certain positions while other Cl− ions, and the Glu-148 side chain, are free to move. Also, we use a simulation system based on the ClC-0 monomer only and use various constraints to prevent large changes in protein shape. Such compromises between speed and realism of the simulations imply that the evidence that we present for the proposed gating mechanism is not conclusive. Each of the procedures described below involves hundreds of picoseconds of simulation time (and tens or hundreds of hours of CPU time), but the real times for the events simulated are orders of magnitude longer. We support our MD results by showing energy profiles for a test Cl− ion that indicates why the proposed mechanism is energetically reasonable. Using Brownian dynamics, we also show how this gating mechanism can explain the concentration and voltage dependence of fast gating.
METHODS
Simulation system
The system used in our MD simulations, shown in Fig. 1, consists of i), the ClC-0 monomer, including all hydrogens, with its pore expanded to an open state as described below; ii), 920 TIP3 water molecules; and iii), up to four Cl− ions. The water molecules are retained within a radius 11.2 Å cylinder roughly aligned with the pore and terminated axially by periodic boundaries. The channel protein atoms (except for Glu-148, which is completely unconstrained) are held near their initial positions by harmonic constraints. Initially we used a constraint coefficient of 16 kT/Å2, but we also examined the effect of using weaker constraints (3.0 or 0.6 kT/Å2) in some studies described later. Thus, the pore-lining residues can respond to forces induced by the presence of ions, but the overall shape of the pore is retained. The MD system has been kept as small as possible by omitting the membrane and the water molecules that would surround it, but since the structural integrity of the protein is maintained by the constraints, the region of interest within the pore should be little affected (for purposes of this study) by this omission.
FIGURE 1.
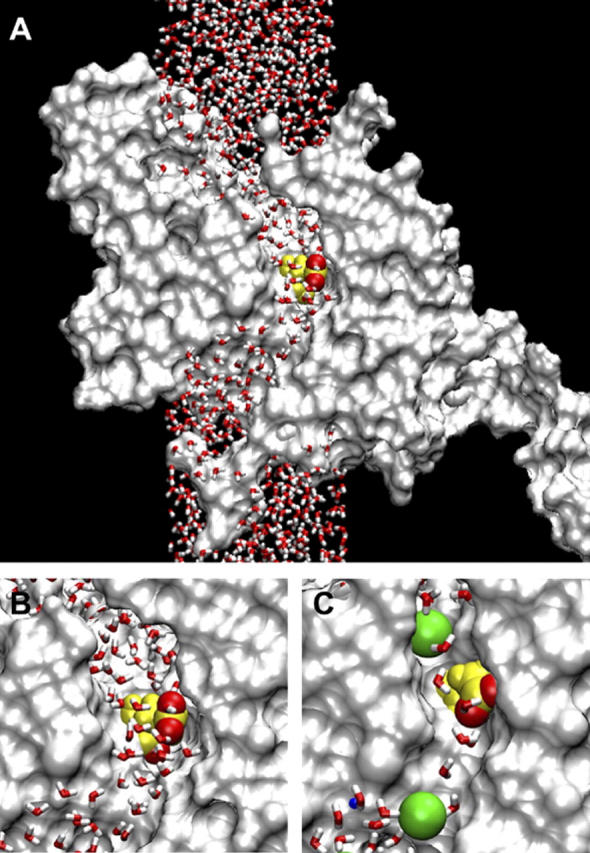
(A) The MD system with the ClC-0 monomer cross sectioned along the pore and represented by a solvent accessible surface. The water column extends to 90 Å total height. Glu-148 is highlighted at the center of the pore, with the two negatively charged oxygens of its side chain in red. (B) Detail view of the central region. (C) The same region in a model with a smaller minimum pore diameter (≈4 Å). Two Cl− ions are shown in green, radius 1.81 Å.
MD is carried out with the CHARMM (17) version c29b1 using the CHARMM27 force field (18). At times, certain ions are positioned with CHARMM MMFP spherical constraints (harmonic constraint to a specified point). In each series of ion positions, we generally used an MMFP coefficient of 25 or 50 kT/Å2 and changed the ion position by 0.5–1.0 Å after running MD 10–100 ps (see the upper line in Fig. 4, for example). The CHARMM Poisson-Boltzmann module, PBEQ, is used for the calculation of energy profiles for Cl− ions in the pore, and in this case a membrane of thickness 34 Å is included, along with bulk water. When calculating energy profiles, dielectric constants of 1.0 for protein and membrane, either 35 or 60 for water within the pore (−10 < z < 10), and 80 for the remainder of the system are used. The value of 60 within the pore matches the value used by our group for Brownian dynamics simulations although lower values (dependent on pore size, among other things) have been suggested elsewhere. As shown below (see Fig. 3), the choice of dielectric constant in the pore has little effect on our results. Since ClC-0 is a multi-ion channel, each energy profile is calculated with another Cl− ion at a fixed position in the pore below the test ion; this position was set at ∼8 Å below the Glu-148 side chain in cases when the test ion is likely to permeate or a similar distance below the highest point likely to be reached by the test ion in cases where it does not permeate.
FIGURE 4.
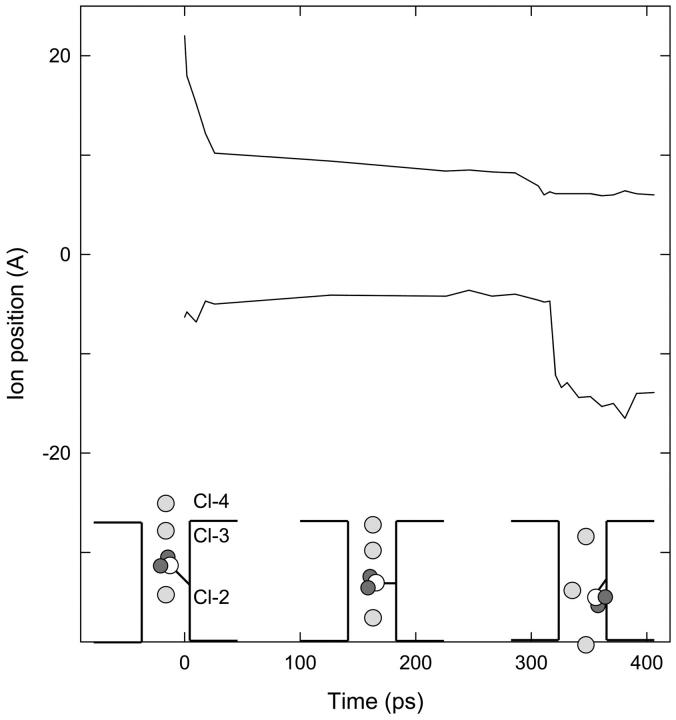
Fast gate opening to allow inward conduction. The upper curve shows the z position of Cl-4, and the lower curve shows the distance between this ion and Cl-3. Cl-4 is constrained near specified positions during the simulation, while the other ions and the Glu-148 side chain are free. Initial positions of ions and the side chain are sketched in the first inset. When Cl-4 is brought into the pore, the resulting configuration (middle inset) is relatively stable for ∼300 ps. But the side chain eventually retreats against the wall of the pore for a moment and Cl-3 slips past (right-hand inset).
FIGURE 3.
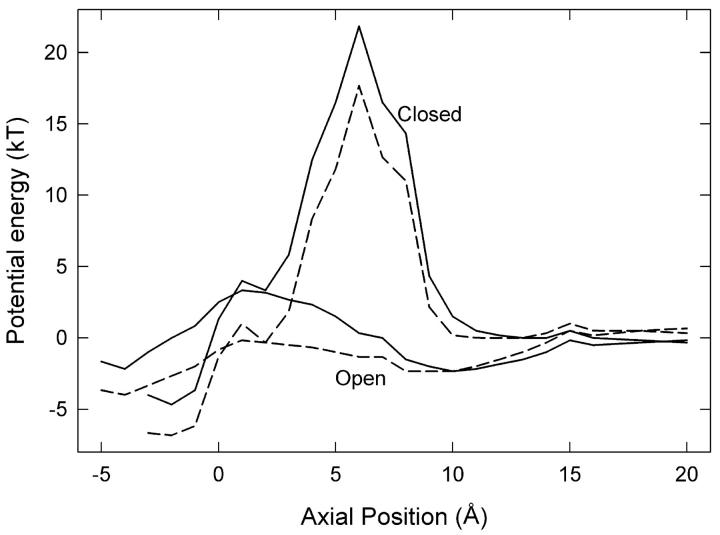
Energy profiles for a Cl− ion passing the channel gate. (Lower lines) The energy of the system is calculated as the ion moves through the pore with the Glu-148 side chain in the open position at z ≈ 1 Å (see Fig. 2 A) and a second Cl− ion fixed at z = −8 Å. (Upper lines) The side chain is in the closed configuration, stretched upward to z ≈ 5 Å (see Fig. 2 B), and a second Cl− ion is fixed at z = −6 Å. Dielectric constants of 35 (solid lines) and 60 (dashed lines) are used in the pore.
We base our opened ClC-0 protein structure on the recently crystallized ClC channel from E. coli (11) and construct a ClC-0 model as done successfully by Corry et al. (19,20). We assume that the structure of the ClC-0 protein is essentially the same as that of the bacterial protein as discussed in the introduction. We convert the bacterial ClC channel into ClC-0 using the primary sequence alignment of Dutzler et al. (11) and replace all nonconserved residues as done previously (19,20). In the crystal structure, no continuous pore exists through which ions can travel from one side of the membrane to the other. Since ClC-0 is a true channel rather than an exchange transporter, we create a continuous pore, using CHARMM to move atoms blocking the pore (including a few key residues Ser-107, Glu-148, and Tyr-445) by pushing the occluding atoms outward from the likely location of the pore with cylindrical repulsive forces as detailed by Corry et al. (19). Note that we use the residue numbering system from the E. coli sequence throughout this study. The diameter of the open pore was chosen to be ∼5 Å so that it could pass large permeant anions such as 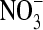 although the exact diameter was shown to have little influence on the conductance of the channel (19). Conduction properties of the ClC-0 model determined with Brownian dynamics (19) agree well with experiments in a range of conditions and yield some confidence in the model. The final structure is shown in Fig. 1. The pore follows a curved path through the protein and is wide enough that any cross section of the pore is likely to intersect three or more water molecules. The pore is roughly parallel to the z axis, and the z coordinate of the Cα of Glu-148 is 0.6 Å.
although the exact diameter was shown to have little influence on the conductance of the channel (19). Conduction properties of the ClC-0 model determined with Brownian dynamics (19) agree well with experiments in a range of conditions and yield some confidence in the model. The final structure is shown in Fig. 1. The pore follows a curved path through the protein and is wide enough that any cross section of the pore is likely to intersect three or more water molecules. The pore is roughly parallel to the z axis, and the z coordinate of the Cα of Glu-148 is 0.6 Å.
It is possible that the ClC-0 pore is more flexible than the rigid pores of the gramicidin channel or the KcsA K+ channel. Its resting diameter may be less than that necessary for larger anions to permeate (e.g., 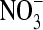 ). Therefore we repeated some of the simulations in a system with a smaller diameter pore (≈4 Å), just large enough for Cl− to pass. The two systems are compared in Fig. 1, B and C, the latter including two Cl− ions displayed at the Pauling radius of 1.81 Å. Not only is the pore narrower in Fig. 1 C, but also the water molecules are closer to single file.
). Therefore we repeated some of the simulations in a system with a smaller diameter pore (≈4 Å), just large enough for Cl− to pass. The two systems are compared in Fig. 1, B and C, the latter including two Cl− ions displayed at the Pauling radius of 1.81 Å. Not only is the pore narrower in Fig. 1 C, but also the water molecules are closer to single file.
Brownian dynamics
In Brownian dynamics simulations, we represent the protein and water as continuous dielectric media and follow the trajectory of ions in and around the pore. The ions experience random and frictional forces from the viscous water medium as well as electrostatic forces from interaction with other ions, the membrane potential, partial charges in the protein, and induced charges along any dielectric boundaries. In-house software was used to implement these simulations based on the Langevin equation, as described for ClC-0 by Corry et al. (19). Electrostatic forces are calculated using Poisson's equation with dielectric constants of 2 for the protein and membrane, 60 for water in the pore, and 80 for bulk water, and the diffusion coefficients of the ions are reduced to 50% of the bulk value in the pore.
RESULTS
MD simulations
After the initial expansion of the pore to an open state, the side chain of Glu-148 forms part of the wall of the pore at the center of the channel. When MD is carried out on the system without any ions, the side chain of Glu-148 drifts away from the wall of the pore, thereby placing its negatively charged tail within the pore, surrounded by the hydrogen atoms of several water molecules (Fig. 1, A and B). This position is very stable in the absence of ions. The bond between Cα and Cβ in Glu-148 points somewhat upward (toward the extracellular end of the pore), which makes it easier for the side chain to move upward rather than downward from this position.
Four Cl− ions were placed within the pore, two below and two above Glu-148, denoted Cl-1 to Cl-4, respectively. After 250 ps of MD in the wide pore with no added constraints, Cl-1, Cl-2, and Cl-3 remain within the pore located at z = −12, −5, and +8 Å, whereas Cl-4, the uppermost Cl− ion, slowly drifts farther upward.
Under a positive membrane potential, Cl− ions would be driven down into the pore. To simulate this we apply an electric field of 6 × 107 V/m to all atoms, corresponding to inward conduction of Cl− ions, but no significant inward motion of ions occurs within 500 ps of MD. To avoid having to simulate for excessive times, we therefore apply CHARMM MMFP constraints to Cl-4, gradually forcing it into the pore and using it to drive Cl-3 downward. In this way we can mimic the effect of a driving potential in a much shorter simulation. By the time Cl-4 reaches z = 6.5 Å, the Glu-148 side chain has retreated against the wall of the pore, and Cl-3 is passing by against the opposite wall of the pore, as shown in Fig. 2 A. Cl-1 and Cl-2 (not visible) are leaving the lower end of the pore by this stage. This procedure was repeated several times with minor variations in starting positions, and Cl-3 was always able to pass through the Glu-148 gate. Cl-4 and Cl-3 are ∼6 Å apart at this point, similar to the inter-ion distances in the simulations of Cohen and Schulten (12).
FIGURE 2.
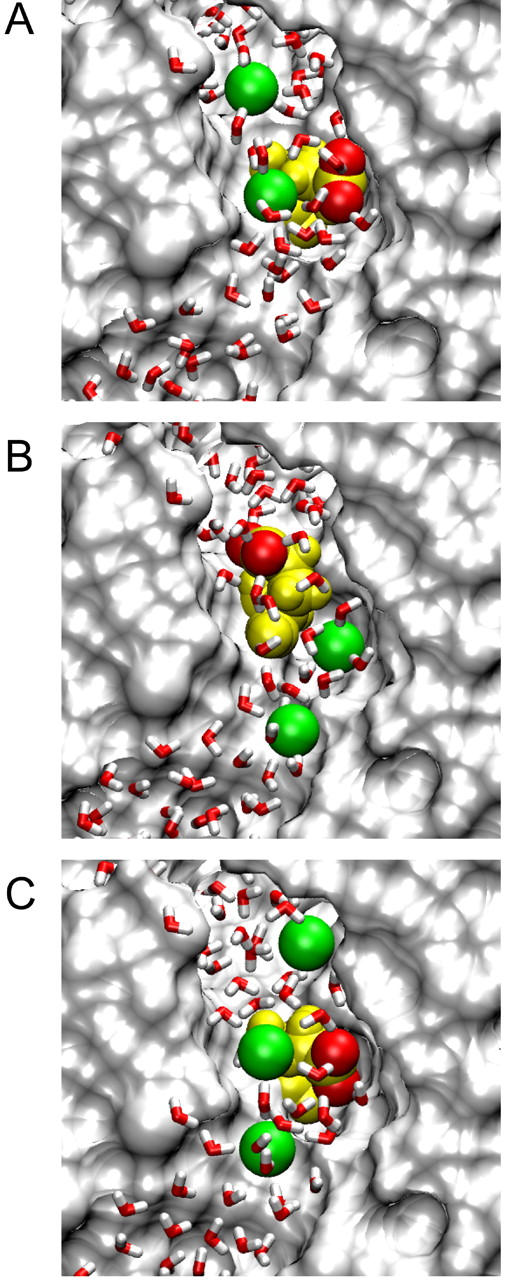
Positions of Cl− ions and the Glu-148 side chain during conduction attempts. Cl− ions are shown in green, Glu-148 in yellow with side-chain oxygens red; all atoms and ions are displayed at van der Waals radii. (A) Inward conduction: the lower Cl− ion (Cl-3) travels down past the Glu-148 side chain in its open configuration, while another ion (Cl-4) remains on the extracellular side of the gate. (B) During attempted outward conduction, the Glu-148 side chain has swung upward, blocking the pore. Ions Cl-2 (lower) and Cl-3 (upper) are shown. (C) For successful outward conduction, a third Cl− ion (Cl-3, uppermost) keeps the side chain in the open position while the middle Cl− ion (Cl-2) moves upward, influenced by Cl-1 (lowest). Cl-2 is about to replace Cl-3 (the “knock-on” effect).
We then calculate energy profiles seen by Cl-3 when the Glu-148 side chain is pushed against the wall as shown in Fig. 2 A. The two lower curves in Fig. 3 show the energy profiles encountered by a Cl− ion traversing the pore when the Glu-148 side chain is in this central position, with Cl-4 omitted. We used two different values of the dielectric constant in the pore, ɛp. The solid and dashed curves are obtained, respectively, with ɛp = 35 and ɛp = 60. These profiles are actually very conservative with respect to inward conduction because i), there are no Cl− ions in the pore above Cl-3, ii), Cl-2 is placed in the pore below the side chain at z = −8 Å, and iii), there is no applied membrane potential. Regardless of the assumed dielectric constant of the water in the pore, the Glu-148 side chain in this position (near z = 1) does not present much of a barrier to the movement of Cl− ions, despite its negative charge. A positive membrane potential or the presence of other Cl− ions farther up the pore will easily drive a Cl− ion down through the gate. Thus, we suggest that this position of the Glu-148 side chain represents an open configuration.
The energy profiles (lower curves in Fig. 3) also show that outward conduction would be possible, provided that the position of the Glu-148 side chain does not change. During one MD simulation, after Cl-3 had passed down through the gate and reached z = −6 Å, we reversed the membrane potential and brought Cl-2 gradually upward, which readily influenced Cl-3 to travel upward through the gate (the Glu-148 side chain did not move significantly in this case). However, the position of the side chain often does change in these circumstances. The usual result of trying to push a Cl− ion upward through the gate is shown in Fig. 2 B. Here the side chain of Glu-148 has rotated and extended up the pore, so that the negatively charged tail is at about z = 5 Å. We have forced Cl-2 up to z = −5 Å, but it cannot push Cl-3 above z = 0. Cl-3 occupies approximately the position previously held by the Glu-148 side-chain oxygens, i.e., the external binding site Sext (10). With the Glu-148 side chain in the upward position, the energy profiles seen by a Cl ion passing through the pore (with ɛp = 35 or ɛp = 60) are given by the two upper curves in Fig. 3. In this configuration, the tail of Glu-148 presents a barrier of order 20 kT centered around z = 6 Å, and therefore ion permeation is unlikely. In other words, the gate is firmly closed.
How can the gate be reopened for outward conduction? An event that promotes gate reopening is the approach of external Cl− ions above the Glu-148 tail. They tend to push the tail downward, which will in turn dislodge any Cl− ion sitting below it. Provided the side chain remains against the channel wall, conduction can then occur in either direction. However, as noted above, internal Cl− ions tend to force the side chain back to the closed configuration.
Before tackling the problem of outward conduction, we checked that the gate can be reopened by external Cl− ions to allow the inward conduction of ions. Fig. 4 tracks the progress of this simulation. Starting with the Glu-148 tail in the closed position (see Fig. 2 B) and Cl-2 at z = 0, we used Cl-4 to push Cl-3 downward from the outer end of the pore, as sketched in the first inset of Fig. 4. The upper curve in Fig. 4 shows the position of Cl-4 over time, and the lower curve shows the distance of Cl-3 below Cl-4. Initially we moved Cl-4 downward quite rapidly, which caused corresponding movement of Cl-3 and the Glu-148 tail. Cl-2 (unrestrained) began to move down toward the intracellular mouth of the pore. These positions (sketched in the middle inset of Fig. 4) remained fairly constant for ∼300 ps. Then, while Cl-4 was held at z = 6 Å, the Glu-148 tail momentarily retreated against the wall of the pore and Cl-3 rather suddenly passed through the gate, as sketched in the right-hand inset of the figure. This situation is similar to that already shown in Fig. 2 A. Hence, inward conduction of Cl− ions is straightforward, whether the gate is initially open or not, because external Cl− ions can readily open the channel.
Finally, we show that once the gate has been opened in this way, outward conduction of Cl− ions is also possible. For this to occur, however, an external Cl− ion must remain close to the Glu-148 tail to keep it in the open position. But if this ion is too close, it will prevent internal Cl− ions from passing through the gate. We postulate that there could be a “knock-on” effect, as Cl− ions passing through the gate dwell for some time just beyond it in an outer binding position. As an ion passes the Glu-148 side chain, it pushes the preceding ion out of the channel, occupies the outer binding position, and keeps the gate open. Such behavior is consistent with permeation characteristics observed in previous Brownian dynamics simulations (19,20).
We carried out an MD simulation in which we controlled the external Cl− positions to achieve the “knock-on” effect and saw two ions (Cl-3 and Cl-2) permeate outward through the gate. This simulation started with the gate open as above, and Cl-3 (unrestrained) was at z = −6 Å. Cl-2 was used to push Cl-3 gradually upward, whereas Cl-4 was placed initially at z = 5 Å and gradually raised to z = 8 Å. In the absence of Cl-4, the tail would usually rise and close the gate as shown earlier (Fig. 2 B), but in this case the Glu-148 tail remained clear of the pore and Cl-3 traveled upward through the gate. The simulation continued with each Cl− ion moved up one position: now Cl-2 was unrestrained, Cl-1 was repelling it from below, Cl-3 was restrained a few angstroms above the Glu-148 tail, and Cl-4 was free to leave. Again the Glu-148 tail did not swing up the pore, and Cl-2 passed through the gate (see Fig. 2 C). However, it must be noted that even though two Cl− ions in succession passed outward through the gate, the placement of the uppermost Cl− in Fig. 2 C is critical for successful conduction. A high concentration of external Cl− makes it more likely that Cl− ions will diffuse into the pore and open the gate or help to keep it open.
Protonation of Glu-148
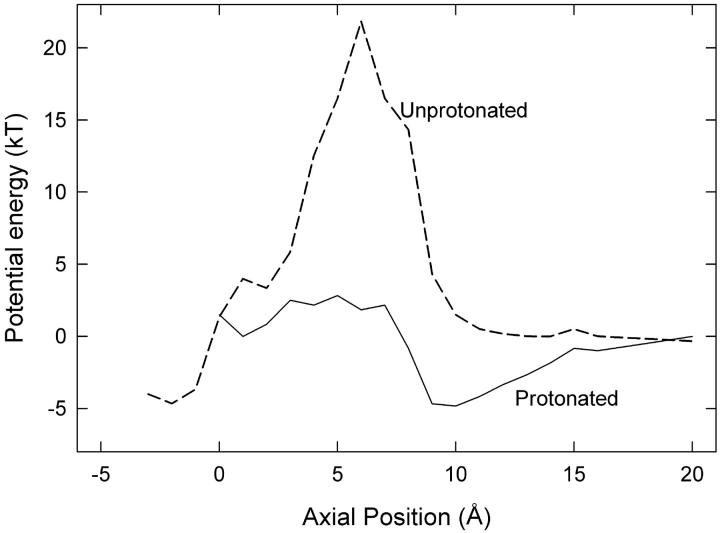
According to our proposals, the Glu-148 side chain is closest to the external solution when the gate is closed. Here the negatively charged side chain is exposed to external protons, which could neutralize it, removing the electrostatic energy barrier to permeation and thus open the gate. Therefore the open probability should increase with lower external pH, as found by Chen and Chen (9) and Dutzler et al. (10). The side-chain position of protonated Glu-148 would be similar to that of the neutral residue Gln-148 in the crystallized E148Q mutant, the ClC-0 equivalent of which does not exhibit fast gating (10). To examine the effect of protonation, we started MD simulations with the closed-gate configuration shown in Fig. 2 B and patched a proton onto the Glu-148 side chain. Then we gradually raised Cl-2 (the lower ion in Fig. 2 B) and found that Cl-3 readily slipped past the side chain into the external vestibule. This result is in clear contrast to the previous conduction attempts with unprotonated side chains. Hence protonation of Glu-148 is an alternative method of reopening the fast gate. The energy profile seen by Cl− ions in the pore with protonated Glu-148 is given in Fig. 5 where it is compared with the previous profile from Fig. 3 for the unprotonated case in the same position. The dielectric constant of the pore used to generate the profile is 35. Clearly protonation greatly reduces the energy barrier for outward conduction. The reduced barrier is roughly the same as when the unprotonated side chain is in the central position (Fig. 3). Protonation of the Glu-148 side chain would also facilitate the inwards conduction of chloride ions by reducing the energy barrier in this way although we have not focused on this case because the channel open probability is nearly independent of external pH for inwards conduction (9). Chen and Chen (9) emphasize that increasing the extracellular concentration of Cl− ions or of H+ increases the open probability of the channel via somewhat different mechanisms, which supports our suggestion here.
FIGURE 5.
Energy profiles for a Cl− ion when the Glu-148 side chain is extended toward the external vestibule, assuming dielectric constant of 35 for water in the pore. (Solid line) Protonated side chain, with a second Cl− ion at z = −3 Å. (Dashed line) unprotonated side chain, with a second ion at z = −6 Å (reproduced from Fig. 3).
Results with a narrower pore
To test how dependent our results are on the choice of initial open structure of the channel, the procedures detailed above were repeated for the narrow pore model shown in Fig. 1 C. However, with unchanged harmonic constraints on the protein, it was clear that even for the simplest case (inward conduction) the forces required to see ion permeation were much larger than for the wider pore. Therefore the protein constraints were relaxed by a factor of 5, to 3 kT/Å2, allowing greater flexibility in the shape and size of the pore in response to the movement of ions and water molecules. Inward conduction was then straightforward; outward conduction was blocked as before by the Glu-148 side chain moving up the pore; and external Cl− ions reopened the Glu-148 gate for inward conduction. The nearly single-file nature of the water column sometimes required water molecules to be pushed along the narrow pore, which rarely occurred in the wider pore. Outward conduction (facilitated by external Cl− ions) was more difficult under these conditions than in the original (wider) pore, but we found that removal of constraints on a few residues around the pore close to Glu-148 (i.e., Gly-146, Cys-354, and Gly-355) allowed Cl− ions to permeate outward as previously. Outward conduction with protonated Glu-148 was also difficult with the 3 kT/Å2 constraints, but conduction was readily achieved after a further reduction in the level of constraint to 0.6 kT/Å2.
These results show that the proposed gating mechanism is not an artifact of the particular pore size, nor of simulation details such as the constraints applied to the protein atoms. Indeed, the results suggest that a lower level of constraint on the protein would be favorable for the proposed gating mechanism. However, we have not attempted to optimize the level of constraint applied to the protein for a couple of reasons. First, some level of constraint is required because we only simulate one monomer, instead of a dimer in a lipid bilayer that would be intrinsically more stable. Second, to speed up conduction and gating events we apply additional forces to some of the ions, which creates larger than realistic forces on the surrounding protein atoms and is likely to cause significant local distortion of the protein in the absence of constraints.
Brownian dynamics simulations
In a series of experiments, Pusch et al. (6) showed that the open probability of the channel increased with extracellular Cl− concentration and increasing membrane potential. This is exactly what we would expect if the open probability is related to the time taken for external ions to enter the channel and approach the Glu-148 gate. We estimate this time by conducting Brownian dynamics simulations of the channel in its closed conformation, that is with the Glu-148 side chain upward and blocking the pore.
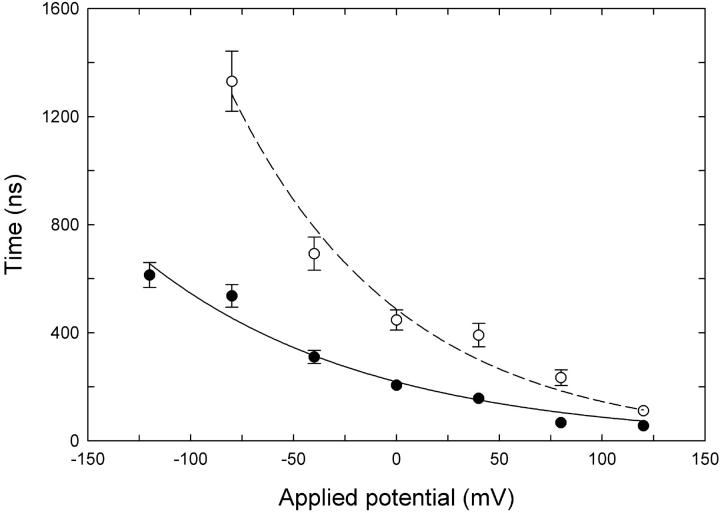
In MD runs, the glutamate side chain begins moving toward its open configuration if the Cl− ion comes within ∼7 Å of it. Therefore, in the Brownian dynamics simulations we timed how long it takes for an external Cl− ion to enter the pore and find its way to within 7 Å of the glutamate residue at a range of applied potentials and concentrations. The results of these simulations are shown in Fig. 6. It can be seen that the time it takes for an ion to approach the Glu-148 side chain decreases as the external Cl− concentration is increased. The approach time also decreases when a favorable membrane potential is applied.
FIGURE 6.
Mean approach times from Brownian dynamics simulations. The mean time for a Cl− ion to enter the outer vestibule and approach within 7 Å from the Glu-148 side chain (closed configuration) is plotted against membrane potential. External Cl− concentration is 150 mM (•) or 50 mM (○). Each data point represents the average of 32–48 separate runs. Error bars have a length of 1 ± SE and are not shown when they are smaller than the data points.
The results shown in Fig. 6 are not surprising, but they do help to demonstrate the means by which concentration and potential influence the open probability of the channel, consistent with the results from Pusch et al. (6). If the approach of an external Cl− ion to Glu-148 is required to open the channel, then the open probability will increase if external ions approach more quickly. However, the open probability is also likely to be dependent on the average time taken for the Glu-148 side chain to move to the open position once the external ion has approached. An ion residing in the region just above Glu-148 may not of itself be enough to open the channel; for example opening may only occur when the thermal motions of the Cl− and glutamate side chain are favorable, and in any case it will require a finite time. Thus we can expect that the probability of the channel opening with an ion near the gate is <1.0, which could be expressed in terms of an average time the ion has to be present before the gate opens (the dwell time). In other words, we can expect that the probability of the gate opening will depend on both an approach time and a dwell time for the external Cl− ions, with the dwell time becoming relatively more important as the approach time decreases. This makes it difficult to relate the approach time plotted in Fig. 6 directly to the open probability. The chance of the channel being open at any time also depends on the rate at which the gate closes again, which has not been considered here.
Other consequences of the proposed mechanism
Accardi and Pusch (21) studied the binding affinity of the p-chlorophenoxy-acetic acid (CPA) intracellular blocker of ClC-0 in relation to fast gating and point mutations and concluded that more than the simple movement of a side chain must be involved in fast gating. There is nothing in our proposal that rules out further movement of protein beyond the initial movement of the Glu-148 side chain. However, intracellular CPA penetrates the pore quite deeply (15), probably reaching Glu-148, which means that the position of the side chain could have a direct effect on CPA binding. Accardi and Pusch (21) found that CPA binds with much greater affinity when the channel is closed, corresponding (in our proposal) to the position of least obstruction by the side chain. They also found that point mutations near the intracellular mouth of the channel influence CPA binding much more when the channel is open, whereas the mutation T471S (ClC-0 numbering), deeper within the pore, has greatest effect when the channel is closed and is allowing the CPA blocker to penetrate farther.
Hence, reversing the open and closed positions of the Glu-148 side chain from the original Dutzler et al. (10) proposal as we are suggesting is consistent with these experimentally determined phenomena.
CONCLUSIONS
We have presented a possible fast gating mechanism in the ClC-0 Cl− channel. In agreement with the hypothesis of Dutzler et al. (10), we show that the side chain of the Glu-148 residue acts as the channel gate, but we suggest a somewhat different mechanism of operation. We find that when the Glu-148 side chain extends toward the external vestibule of the pore, it electrostatically prevents Cl− conduction, whereas, in the central position, the side chain tucks against the side of the pore and allows Cl− ions to pass. Furthermore, we show that Cl− ions on the external side of the Glu-148 residue can open the channel (when it is closed) by pushing the side chain inwards, and Cl− conduction can take place in both directions provided that an extracellular Cl− ion is present to hold the channel open. Additionally, low pH in the external vestibule can lead to protonation of the extended Glu-148 side chain, which removes the electrostatic barrier and also opens the channel for outward conduction. Protonation is a supplementary mechanism, however, and we differ from the Bostik and Berkowitz (13) hypothesis in saying that it is only significant under acid conditions. We have used Brownian dynamics to show how increases in the membrane potential and/or external Cl− concentration increase the probability of the channel being open.
Although our results suggest a plausible gating mechanism, they are not conclusive. We modeled our open ClC-0 structure on the crystal structure of the ClC protein from E. coli, and our results may be inaccurate if the native ClC-0 structure is significantly different from the model used here. Also, to be able to observe the process of channel opening and Cl− conduction within a reasonable time frame for MD simulations, we simplified the MD system and applied constraints to one or two Cl− ions. We used those ions to influence the motion of ions closer to the hypothesized channel gate, but it is possible that we have chosen unrealistic positions for the restrained ions. Despite these reservations, our proposed fast gating mechanism clarifies many experimental results that have been difficult to explain by other means.
Acknowledgments
The simulations were carried out on the Compaq AlphaServer SC at the APAC National Facility. Figs. 1 and 2 were created using the program VMD (22).
This work was supported by grants from the Australian Research Council, the National Health and Medical Research Council of Australia, and the Australian Partnership for Advanced Computing.
References
- 1.Jentsch, T. J., T. Friedrich, A. Schriever, and H. Yamada. 1999. The ClC chloride channel family. Pflugers Arch. 437:783–795. [DOI] [PubMed] [Google Scholar]
- 2.Maduke, M., C. Miller, and J. A. Mindell. 2000. A decade of ClC chloride channels: structure, mechanism, and many unsettled questions. Annu. Rev. Biophys. Biomol. Struct. 29:411–438. [DOI] [PubMed] [Google Scholar]
- 3.Fahlke, C. 2001. Ion permeation and selectivity in ClC-type chloride channels. Am. J. Physiol. Renal Physiol. 280:F748–F757. [DOI] [PubMed] [Google Scholar]
- 4.Jentsch, T. J., V. Stein, F. Weinreich, and A. A. Zdebik. 2002. Molecular structure and physiological function of chloride channels. Physiol. Rev. 82:503–568. [DOI] [PubMed] [Google Scholar]
- 5.Miller, C. 1982. Open-state substructure of single chloride channels from Torpedo electroplax. Phil. Trans. Roy. Soc. Lond. B. Biol. Sci. B299:401–411. [DOI] [PubMed] [Google Scholar]
- 6.Pusch, M., U. Ludewig, A. Rehfeldt, and T. J. Jentsch. 1995. Gating of the voltage-dependent chloride channel ClC-0 by the permeant anions. Nature. 373:527–531. [DOI] [PubMed] [Google Scholar]
- 7.Chen, T.-Y., M.-F. Chen, and C.-W. Lin. 2003. Electrostatic control and chloride regulation of the fast gating of ClC-0 chloride channels. J. Gen. Physiol. 122:641–651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen, T.-Y., and C. Miller. 1996. Nonequilibrium gating and voltage dependence of the ClC-0 Cl− channel. J. Gen. Physiol. 108:237–250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen, M.-F., and T.-Y. Chen. 2001. Different fast-gate regulation by external Cl− and H+ of the muscle-type ClC chloride channels. J. Gen. Physiol. 118:23–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dutzler, R., E. B. Campbell, and R. MacKinnon. 2003. Gating the selectivity filter in ClC chloride channels. Science. 300:108–112. [DOI] [PubMed] [Google Scholar]
- 11.Dutzler, R., E. B. Campbell, M. Cadene, B. T. Chait, and R. MacKinnon. 2002. X-ray structure of a ClC chloride channel at 3.0 Å reveals the molecular basis of anion selectivity. Nature. 415:287–294. [DOI] [PubMed] [Google Scholar]
- 12.Cohen, J., and K. Schulten. 2004. Mechanism of anionic conduction across ClC. Biophys. J. 86:836–845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bostik, D. L., and M. L. Berkowitz. 2004. Exterior site occupancy infers chloride induced proton gating in a prokaryotic homolog of the ClC chloride channel. Biophys. J. 87:1686–1696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Accardi, A., and C. Miller. 2004. Secondary active transport mediated by a prokaryotic homologue of ClC Cl− channels. Nature. 427:803–807. [DOI] [PubMed] [Google Scholar]
- 15.Estévez, R., B. C. Schroeder, A. Accardi, T. J. Jentsch, and M. Pusch. 2003. Conservation of chloride channel structure revealed by an inhibitor binding site in ClC-1. Neuron. 38:47–59. [DOI] [PubMed] [Google Scholar]
- 16.Law, R. J., and M. S. Sansom. 2004. Homology modelling and molecular dynamics simulations: comparative studies of human aquaporin-1. Eur. Biophys. J. 33:477–489. [DOI] [PubMed] [Google Scholar]
- 17.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- 18.MacKerell, A. D. Jr., D. Bashford, M. Bellot, R. L. Dunbrack Jr., J. D. Evanseck, M. J. Field, S. Fisher, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- 19.Corry, B., M. O'Mara, and S. H. Chung. 2004. Conduction mechanisms of chloride ions in CLC-type channels. Biophys. J. 86:846–860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Corry, B., M. O'Mara, and S. H. Chung. 2004. Permeation dynamics of chloride ions in ClC-0 and ClC-1 channels. Chem. Phys. Lett. 386:233–238. [Google Scholar]
- 21.Accardi, A., and M. Pusch. 2003. Conformational changes in the pore of ClC-0. J. Gen. Physiol. 122:277–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD—Visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]