Equilibrium and Kinetic Folding Pathways of a TIM Barrel with a Funneled Energy Landscape

Abstract

The role of native contact topology in the folding of a TIM barrel model based on the α-subunit of tryptophan synthase (αTS) from Salmonella typhimurium (Protein Data Bank structure 1BKS) was studied using both equilibrium and kinetic simulations. Equilibrium simulations of αTS reveal the population of two intermediate ensembles, I₁ and I₂, during unfolding/refolding at the folding temperature, T_f = 335 K. Equilibrium intermediate I₁ demonstrates discrete structure in regions α₀-β₆ whereas intermediate I₂ is a loose ensemble of states with N-terminal structure varying from at least β₁-β₃ (denoted I_2A) to α₀-β₄ at most (denoted I_2B). The structures of I₁ and I₂ match well with the two intermediate states detected in equilibrium folding experiments of Escherichia coli αTS. Kinetic folding simulations of αTS reveal the sequential population of four intermediate ensembles, I_120Q, I_200Q, I_300Q, and I_360Q, during refolding. Kinetic intermediates I_120Q, I_200Q, and I_300Q are highly similar to equilibrium αTS intermediates I_2A, I_2B, and I₁, respectively, consistent with kinetic experiments on αTS from E. coli. A small population (∼10%) of kinetic trajectories are trapped in the I_120Q intermediate ensemble and require a slow and complete unfolding step to properly refold. Both the on-pathway and off-pathway I_120Q intermediates show structure in β₁-β₃, which is also strikingly consistent with kinetic folding experiments of αTS. In the off-pathway intermediate I_120Q, helix α₂ is wrapped in a nonnative chiral arrangement around strand β₃, sterically preventing the subsequent folding step between β₃ and β₄. These results demonstrate the success of combining kinetic and equilibrium simulations of minimalist protein models to explore TIM barrel folding and the folding of other large proteins.

INTRODUCTION

Understanding the fundamental physics of protein folding is a goal of both experimentalists and theoreticians. Guided by landscape theory (1–8), an understanding of the fundamental principles of protein folding has recently advanced due to the development of small fast-folding peptide systems that are tractable to study by all-atom simulation and theory (9–16) and minimalist simulation models that can effectively sample the dynamics of larger protein systems (17–23). Although these research efforts are increasing our understanding of protein folding, many challenges remain.

Many recent studies have applied these minimalist models in molecular dynamics studies of the folding of intermediate length proteins (17,19–21). These studies have played a crucial step in validating landscape theory, because protein models with funneled energy landscapes show remarkable success in predicting experimentally determined structural and thermodynamic properties of protein folding pathways. However, it remains to be seen to what degree larger proteins will also obey the principle of minimal frustration. Furthermore, although minimalist models have proved highly advantageous in sampling smaller proteins, it is unclear as to how well they will sample folding states of larger proteins. It is necessary to use this basic same model in simulations to determine whether larger proteins can also be accurately described, thereby demonstrating that large proteins also have a low level of energetic frustration. Simulations of large proteins using minimalist molecular models will highlight some of the possible future challenges and computational shortcuts in all-atom simulations of large systems.

This study uses folding simulations of tryptophan synthase, a member of the TIM (triose phosphate isomerase) barrel structural family, to determine whether the energy landscape of this large protein is funneled as has been shown for smaller proteins (19,21,24). The TIM barrel is an excellent large protein structure to investigate with minimalist Go-models because it is the most ubiquitous protein family (10% of Protein Data Bank (PDB)). A fundamental understanding of TIM barrel folding could be applied to thousands of proteins across every genome.

Folding experiments of monomeric TIM barrels have been conducted on yeast (γTIM), rabbit muscle (rTIM), and Trypanosoma brucei (tbTIM) triose phosphate isomerase, the α-subunit of Escherichia coli tryptophan synthase (αTS), Sulfolobus solfataricus indole-3-glycerol phosphate synthase (sIGPS), E. coli indole-3-glycerol phosphate synthase (eIGPS), E. coli phosphoribosylanthranilate isomerase (PRAI), and rabbit muscle aldolase (25–43).

The stability and folding pathways of TIM barrel proteins have been the subject of discussion because the basic structure comprises repeating βα-units in a circular arrangement connecting the N- and C-termini, with the most common structure having eight βα-units. With respect to stability, it may appear that all eight units would be required for folding and activity because all eight strands are required to make contacts between the N- and C-terminal strands. However, truncation mutants of αTS have demonstrated that stable structure can exist in the N-terminal region of the protein without the C-terminal residues (40).

In addition, protein folding experiments have revealed that different TIM barrel proteins do not always fold in the same manner, although they typically fold in steps involving contiguous βα-units. Intermediates are typically observed in equilibrium unfolding experiments of most TIM barrels (26–28,31,32,35,39,43,44), with the possible exception of rTIM (36). Kinetic folding studies of all TIM barrels studied demonstrate multiphasic folding pathways and are consistent with folding intermediates (30–32,35,36,41,42).

Despite this common observation, the properties of folding intermediates, both equilibrium and kinetic, can be quite different between different TIM barrel proteins. The equilibrium folding pathway of the α-subunit of tryptophan synthase (αTS) from E. Coli involves an initial folding intermediate I₂ within regions α₀–α₄ (38,40) followed by an intermediate I₁ comprising regions α₀–β₆ + β₇ (37,40,45). The kinetic folding pathway of αTS shows early structure in regions α₀−β₆ + β₇ (30,45), as was found with intermediate I₁ in the equilibrium experiments. A similar equilibrium folding pathway was found in γTIM where initial folding initiates with intermediate I₂ comprising regions β₂−β₄ followed by an intermediate I₁ comprising regions α₁−β₆ (27). In contrast, no intermediates are observed in equilibrium unfolding of rTIM although an intermediate comprising the C-terminal regions β₅−α₈ is observed in kinetic refolding experiments (36). Also, a dialysis refolding experiment indicates that the folding pathway of rabbit muscle aldolase populates two intermediates with noncontinuous structural units α₀, β₄−β₈ (I₁) and α₀, β₄α₄, α₅, α₆β₇ (I₂) (34).

The fact that members of the TIM barrel structural family do not rigorously conserve their folding pathways suggests that overall fold is not sufficient to explain TIM barrel folding. Thus, the folding mechanism must be reflected in other subtler properties. One possible indicator of TIM barrel folding differences may be the slight differences in the contact topology due to different position and lengths of the α-helices and β-strands of each TIM barrel family member. Although contact topology certainly plays a role in folding, a possible additional determinant is differential energetic weighting from different amino acid types. Also, nonnative contacts, proline isomerization, and disulphide formation can play an important role in protein folding (42,46,47), although these phenomena are not explicitly included in models of this study for simplicity.

The primary question addressed in this work is whether the information provided from a contact map of the TIM barrel protein αTS is sufficient to accurately describe its folding pathway in a minimalist protein model, which would indicate that contact topology is the primary determinant of αTS folding (2,17,48). This would also support the hypothesis that the energy landscape of αTS is highly funneled to the native state. This work addresses this hypothesis using kinetic and thermodynamic simulations of minimalist model for αTS. Previous simulations of αTS without a funneled energy landscape also appear to successfully qualitatively capture the dominant intermediate in the αTS kinetic folding pathway (23). This previous study suggests that a non-Go-model can determine the TIM barrel folding pathways and ultimately discriminate the final native state. This study addresses whether energetically funneled Go-models can capture the experimentally determined equilibrium and kinetic pathway of αTS.

MATERIALS AND METHODS

Molecular dynamics

Molecular dynamics (MD) simulations were carried out using AMBER 6 software, compiled on a Linux platform, employing the sander_classic program as an integrator for initial energy minimization and subsequent molecular dynamics (49). The following describes the AMBER sander_classic molecular dynamics parameters used in this study. The specific parameter values are listed in parentheses. The time step was 0.001 ps (DT = 0.001). Translational and rotational motion was removed at the beginning of each run and every 1000 time steps thereafter (NTCM = 1, NSCM = 1000, NDFMIN = 0). Initial velocities were randomly selected (INIT = 3, IG = random). If the absolute value of the velocity of any atom exceeded 500 Å per time step, velocities are scaled such that the absolute value of the velocity of that atom = 500 Å per time step (VLIMIT = 500). Temperature was maintained with external bath using the method of Berendsen (50) with a coupling constant of 0.2 ps (NTT = 5, TAUTP = 0.2, TAUTS = 0.2). If the simulation temperature T_sim exceeds the average temperature T by >10 K, velocities are scaled such that T_sim = T. SHAKE was not used. Although no electrostatics were involved in the molecular dynamics, a default constant dielectric was used (IDIEL = 1) with a default delectric constant of 1 (DIELC = 1). The particle mesh Ewald method was not used (IEWALD = 0). During each integration step, interactions between all atom pairs were calculated and this contact pair list was updated only once at the beginning of the simulation (CUT = 9999, NSNB = 9999). No periodic boundary and pressure regulation were used (NTB = 0, NTP = 0). Structures and energies were saved every 1.5 ps (NTPR = 1500, NTWR = 1500, NTWX = 1500, NTWV = 1500, NTWE = 1500).

Go-model

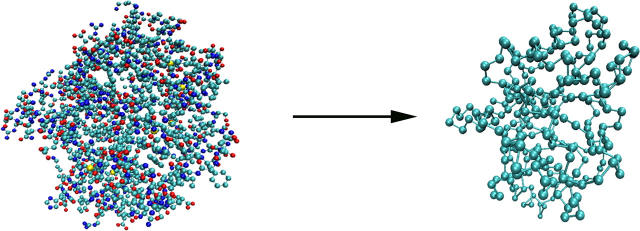
To model αTS, each amino acid in the α-subunit of Salmonella typhimurium tryptophan synthase is approximated with its single backbone C_α atom from the PDB file 1BKS, as shown in Fig. 1. All atoms not found in the α-subunit of tryptophan synthase were not included in the model. It should be noted that the model is based on the αTS structure from S. typhimurium and assumes that the structure of the α-subunit will be the same in the absence of the β-subunit. Ultimately, comparison is made between simulations and experiments on the isolated αTS subunit from E. coli (29–31,37–42,45,51). Nonetheless, it is logical to conclude that the isolated αTS structure and folding pathway of S. typhimurium will be similar to that of E. coli due to the nearly identical sequence conservation. For this reason, references to “αTS” apply to the α-subunit of tryptophan synthase of either S. typhimurium or E. coli, unless otherwise specified.

FIGURE 1.

Conversion of the PDB coordinates of 1BKS to a C_α model of αTS.

The overall potential energy for a given protein conformation is given by Eq. 1:

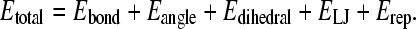(1)

Consistent with the original Go-model (52), the minimum energy of each energy term is obtained when the protein is in the native folded state.

For covalent bond distance terms,

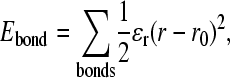(2)

where ɛ_r = 100 kcal mol⁻¹ Å⁻² is the bond energy, r is the bond distance in the simulation, and r₀ is the native C_αC_α bond distance in the reduced C_α PDB structure, summed over all bonds in the reduced C_α PDB structure. The minimum energy C_αC_α bond distance, r₀, in the disordered region of αTS (residues 178–191) is set to 3.81 Å.

For the bond angle term,

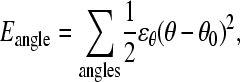(3)

where ɛ_θ = 20 kcal mol⁻¹ degree⁻² is the bond angle energy, θ is the bond angle in the simulation, and θ₀ is the C_αC_αC_α native bond angle in the reduced C_α PDB structure, summed over all bond angles in the reduced C_α PDB structure. The minimum energy C_αC_αC_α bond angle, θ₀, in the disordered region of αTS (residues 178–191) is set to 109.5°.

For dihedral energies,

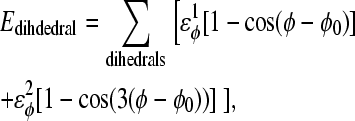(4)

where 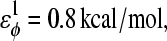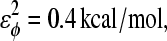φ is the dihedral angle in the simulation, and φ₀ is the C_αC_αC_αC_α native dihedral angle in the reduced C_α PDB structure, summed over all dihedral angles in the reduced C_α PDB structure. The energies of C_αC_αC_αC_α dihedrals in the disordered region of αTS (residues 178–191) are set to 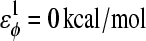and 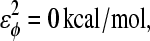effectively producing a flexible linker between αTS residues 177 and 192.

In the Go-model, two C_α atoms in a protein were selected as attractive if they are separated by four or more residues and are indicated to be in contact using contacts of structural units analysis (53). Each attractive C_α-C_α contact is described by an attractive Lennard-Jones potential

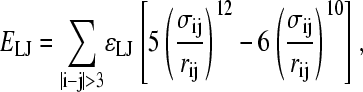(5)

where ɛ_LJ = 0.8 kcal/mol is the contact energy, σ_ij is the native distance between the two contact atoms, i and j, given from the crystal structure, and r_ij is the distance between the two contact atoms, i and j, determined for a given iteration of the simulation.

If any two atoms are not determined to be attractive or fall within three residues of each other (i,i + 3), then their interaction is defined by a repulsive term

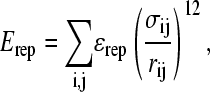(6)

where ɛ_rep = 0.8 kcal/mol is the repulsive energy, σ_ij is half the hard-sphere distance between two repulsive atoms i and j (1.9 Å), and r_ij is the distance between the two repulsive atoms, i and j, determined for a given iteration of the simulation.

The parameters used in the Go-model are shown in Table 1. These parameters were selected because they had produced an accurate folding temperature and stability of chymotrypsin inhibitor 2 in previous work (24).

TABLE 1.

Parameters of αTS Go-model

Parameter	Energy ɛ
Bonds	(kcal/mol)
CαCα	100
Angles	(kcal/mol)
CαCαCα	20
Dihedrals	(kcal/mol)
CαCαCαCα	0.8 ()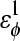
–	0.4 ()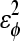
10–12 Contacts	(kcal/mol)
CαCα	0.8 (i,i + 4)

Thermodynamics

The initial structure used for MD studies of αTS was obtained from simulated annealing, using the 1BKS PDB coordinates as an initial structure (Fig. 1). For αTS, MD simulations were run for 420 ns at 330 K, 270 ns at 335 K, 1300 ns at 340 K, and 580 ns at 345 K. For each structure sampled throughout the simulations, the number of native contacts (Q) formed was calculated where each native contact was determined to be formed if it falls within 1.5 times the native distance. Thermodynamic quantities, such as free energy (G), energy (E), and entropy (S), are determined using all simulation temperatures simultaneously with the weighted histogram analysis method (WHAM) algorithm (54). Using WHAM, the potential mean force (PMF) is plotted versus the number of native contacts in the protein (Q) at a temperature, T, where a range of Q values are sampled using Eq. 7.

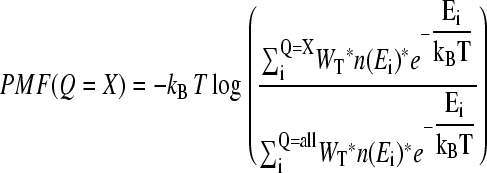(7)

In Eq. 7, k_B is the Boltzman constant, n(E_i) is the density of states in the simulation with the indicated value of Q, W_T is the WHAM-converged numerical weight for iterations in the trajectory with temperature T, Q = X denotes all simulation configurations with X native contacts, and Q = ALL denotes all simulation configurations. Although PMF is not a direct measure of free energy, differences in PMF are equivalent to the difference in free energy (ΔG). For example, the free-energy difference (ΔG_Q1Q2) between two discrete values of Q, i.e., folded Q₁ = 400 versus unfolded Q₂ = 25, can be calculated with Eq. 8:

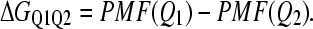(8)

Kinetics

For kinetic refolding simulations, 60 kinetic trajectories are collected to obtain statistically significant reaction rate measurements. The initial unfolded coordinates of each refolding trajectory are obtained from the final structure of a short simulation at 999 K of a randomly determined length (500–1500 ps) and random initial velocities, followed by 1 ns at 373 K and random initial velocities. For each refolding trajectory, these initial 373 K coordinates are subjected to 300 K and random initial velocities and followed for a minimum of 30 ns (30 × 10⁶ time steps). Although 30 ns was a sufficient number of computational steps to refold most αTS trajectories, trajectories that did not refold were simulated further until the native ensemble was reached. Kinetic modeling of the sequential αTS folding pathway in Fig. 9 B was performed with the KINSIM program (55).

FIGURE 9.

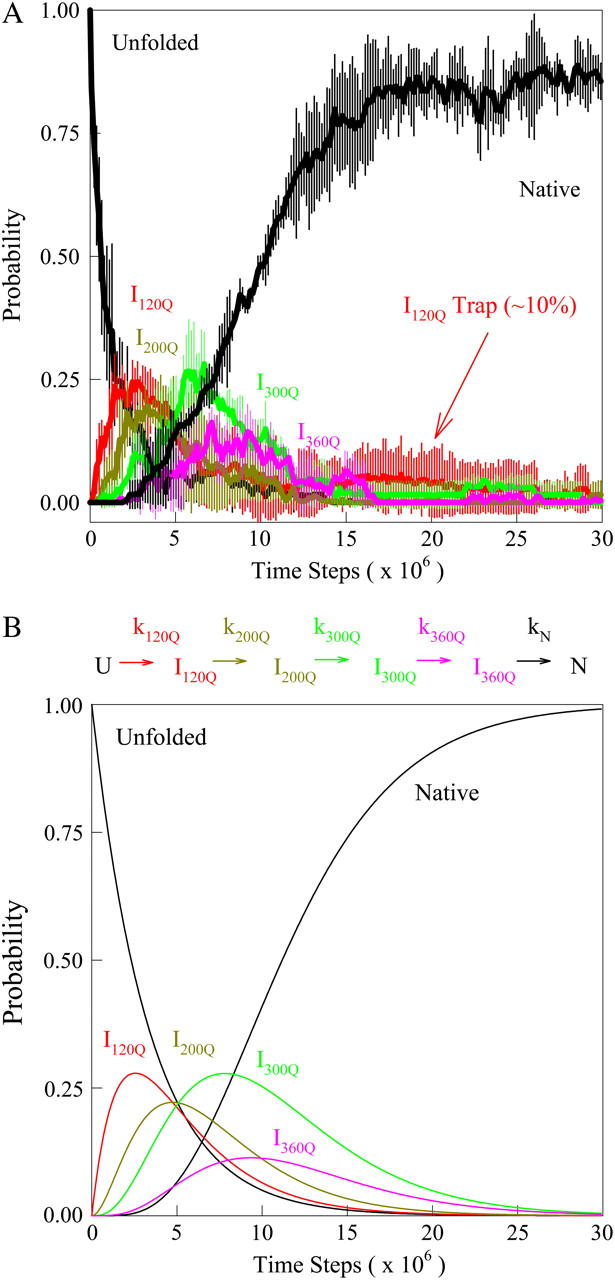
(A) The probability of populating unfolded, intermediate, and native ensembles at each time point during the simulation. Using the range of Q defined for each ensemble shown in Fig. 7, the probability of populating each ensemble is labeled and color coded for unfolded U (black), intermediate I_120Q (red), intermediate I_200Q (yellow), intermediate I_300Q (green), intermediate I_360Q (magenta), and native N (black). A long-lived trapped set of conformations in the I_120Q intermediate at long times is indicated with the red arrow labeled “I_120Q trap”. The probability was calculated separately for trajectory groups 1–20, 21–40, and 41–60. The global probability and standard deviation of the three separate probability calculations is shown with error bars at each time point (see Materials and Methods). (B) The populations of unfolded, intermediate, and native ensembles shown in Fig. 9 A are approximated using a 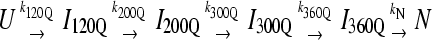kinetic model with irreversible rate constants k_120Q = 3 × 10⁻⁷, k_200Q = 5 × 10⁻⁷, k_300Q = 5 × 10⁻⁷, k_360Q = 3 × 10⁻⁷, and k_N = 7 × 10⁻⁷. Probabilities of each species are labeled and color coded as in Fig. 9 A, i.e., unfolded U (black line), intermediate I_120Q (red), intermediate I_200Q (yellow), intermediate I_300Q (green), intermediate I_360Q (magenta), and native N (black).

Statistical errors reported throughout the article are based on the following grouping of the kinetic trajectories. The 60 trajectories are divided into three groups of 20, i.e., trajectories 1–20, 21–40, 41–60. Properties of each group are averaged and these three separate averages are used to determine a global average. The reported standard deviation shown in Figs. 8 and 9 A, and Table 2, is the error of the three group averages.

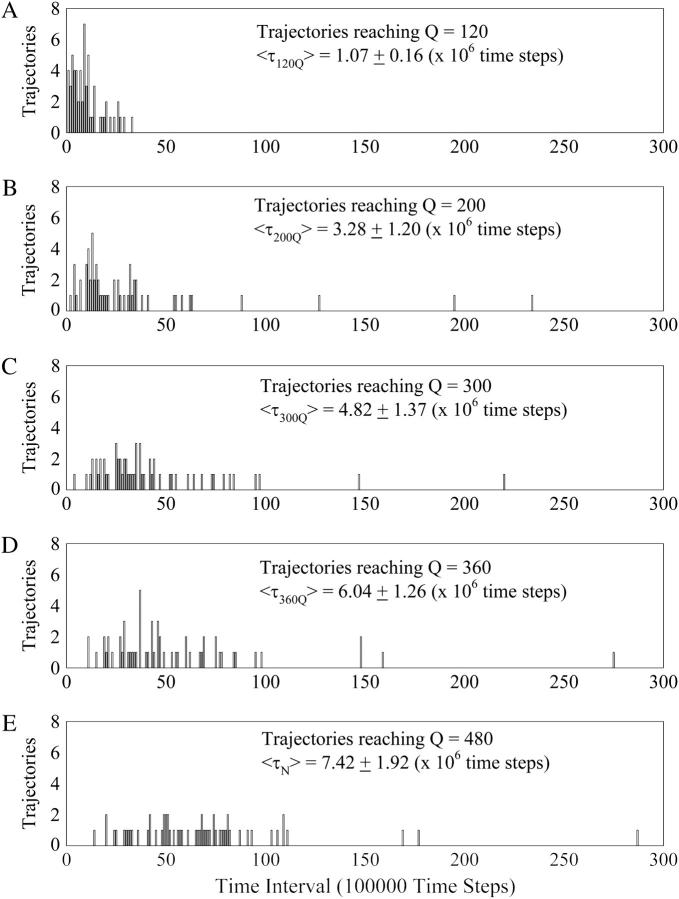
FIGURE 8.

The initial 3 × 10⁷ time steps of the kinetic trajectories are segregated into a histogram of 300 time intervals of 100,000 time steps. In Fig. 8, A–E, each of the 60 trajectories is “counted” in a time interval bin when it reaches Q = 120 (A), Q = 200 (B), Q = 300 (C), Q = 360 (D), and Q = 480 (E) native contacts, producing a histogram of folding times. To determine the folding time, the average folding time of trajectories 1–20, 21–40, and 41–60 were calculated separately. The global average, 〈τ〉, and standard deviation of the average folding time to reach each Q value is shown in Fig. 8, A–E (see Materials and Methods).

TABLE 2.

Average folding time (τ) and differences between folding times for kinetic trajectories reaching Q = 120, Q = 200, Q = 300, Q = 360, and native Q = 480

Average folding time 〈τ〉		Folding time difference
〈τ120Q〉	1.07 ± 0.16	〈τ120Q〉 − 0	1.07 ± 0.16
〈τ200Q〉	3.28 ± 1.20	〈τ200Q〉 − 〈τ120Q〉	2.21 ± 1.21
〈τ300Q〉	4.82 ± 1.37	〈τ300Q〉 − 〈τ200Q〉	1.54 ± 1.82
〈τ360Q〉	6.04 ± 1.26	〈τ360Q〉 − 〈τ300Q〉	1.22 ± 1.86
〈τN〉	7.42 ± 1.92	〈τN〉 − 〈τ360Q〉	1.38 ± 2.30

Errors are means ±SD.

RESULTS

Simulations of folding thermodynamics

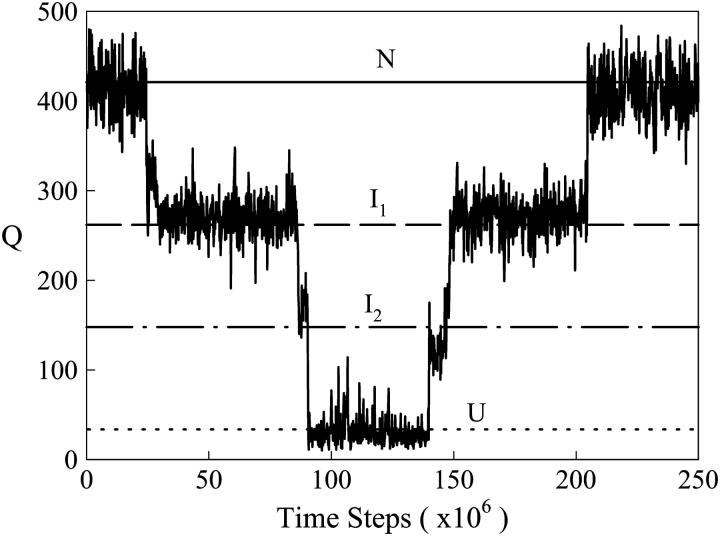
Fig. 1 shows a schematic for reduction of the PDB coordinates 1BKS to the C_α Go-model used for simulations in this study. Fig. 2 shows a representative region of an equilibrium αTS folding/unfolding trajectory this model at 330 K, plotting the number of native contacts, Q, as a function of simulation time steps. From Fig. 2, it is evident that the trajectory significantly samples two intermediate ensembles, I₁ and I₂, between the native ensemble, N, and the unfolded ensemble, U. Intermediates ensembles I₁, corresponding to Q ∼ 280, and I₂, corresponding to Q ∼ 150, are sampled in both the unfolding and refolding directions. It should also be noted that the αTS model parameters shown in Table 1 are calibrated to produce a simulation T_f near 335 K, consistent with the experimental T_f, as was shown for chymotrypsin inhibitor 2 in a previous study (24).

FIGURE 2.

The number of native contacts (Q) between 0 and 250 × 10⁶ time steps in an equilibrium simulation of αTS at T = 330 K. The simulation samples native N (solid line at Q ∼ 430), intermediate I₁ (dashed line at Q ∼ 280), intermediate I₂ (dotted-dashed line at Q ∼ 150), and unfolded U (dotted line at Q ∼ 25) ensembles.

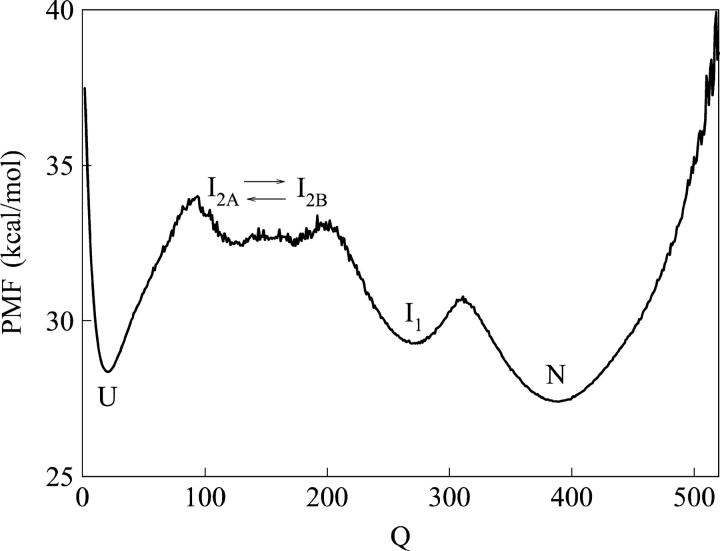
Through WHAM, the probability of Q values in the equilibrium αTS simulations is used to calculate the PMF of each value of Q sampled during the simulations using Eq. 7 (see Materials and Methods). Fig. 3 shows a plot of PMF versus Q determined at the folding temp, T_f = 335 K, and shows the relative free-energy differences between states sampled in the simulation. Fig. 3 shows free-energy minima for intermediate ensembles I₁, corresponding to Q ∼ 280, and I₂, corresponding to Q ∼ 150. However, Fig. 3 also shows that intermediate ensemble I₂ is actually a broad group of free-energy minima that consists of structures with different Q values. The least structured states are located in a free-energy minimum near Q ∼ 120, denoted I_2A in Fig. 3, and the most structured states are located in a free-energy minimum near Q ∼ 180, denoted I_2B in Fig. 3. It should be noted that error bars of the PMF are not shown due to the lack of repeating unfolding/refolding transitions in the αTS simulations. Although the Q values associated with αTS intermediate ensembles I₁, I_2A, and I_2B, are easily determined from Figs. 2 and 3, the free-energy differences between these intermediate ensembles remain questionable due to a lack of sampling the folding and unfolding transitions in the equilibrium simulation.

FIGURE 3.

A plot of potential mean force (PMF) versus native contacts (Q) at the αTS T_f = 335 K shows four free-energy minima at the native N (Q ∼ 430), intermediate I₁ (Q ∼ 280), intermediate I_2B (Q ∼ 180), intermediate I_2A (Q ∼ 120), and unfolded U (Q ∼ 25) ensembles. Intermediates I_2B and I_2A actually occupy the same ensemble intermediate (I₂) and are shown to interconvert (arrows).

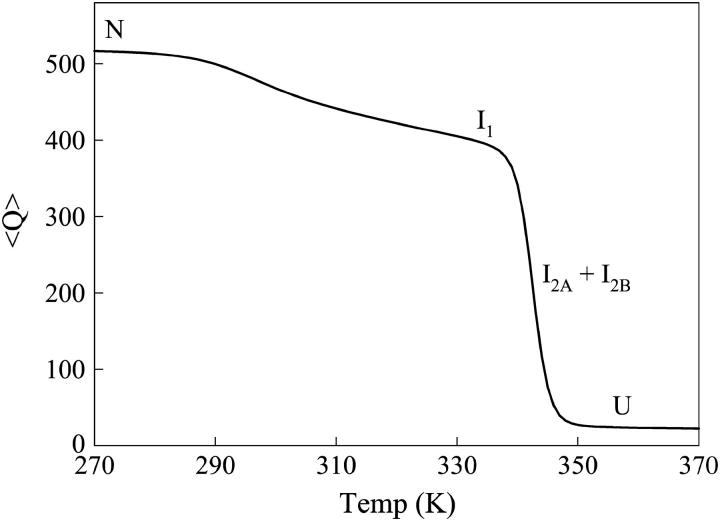
Fig. 4 shows the average value of Q, 〈Q〉, plotted as a function of simulation temperature. Two unfolding transitions can be clearly identified: 1), 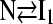near 310 K and 2), 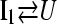at 345 K. Due to the low stability of I_2A and I_2B, transitions involving I_2A and I_2B are not discernable in Fig. 4. Also indicated in Fig. 4 are the temperature ranges at which each thermodynamic species U, I_2A + I_2B, I₁, and N, is maximally populated. The simulated titration in Fig. 4 is analogous to chemical or thermal denaturation of αTS in equilibrium experiments.

FIGURE 4.

The average value of Q, 〈Q〉, is plotted versus temperature (T) for αTS. Temperatures at which each equilibrium species is maximally populated are shown for native N, intermediate I₁, intermediate I₂ (I_2A + I_2B), or unfolded U ensembles.

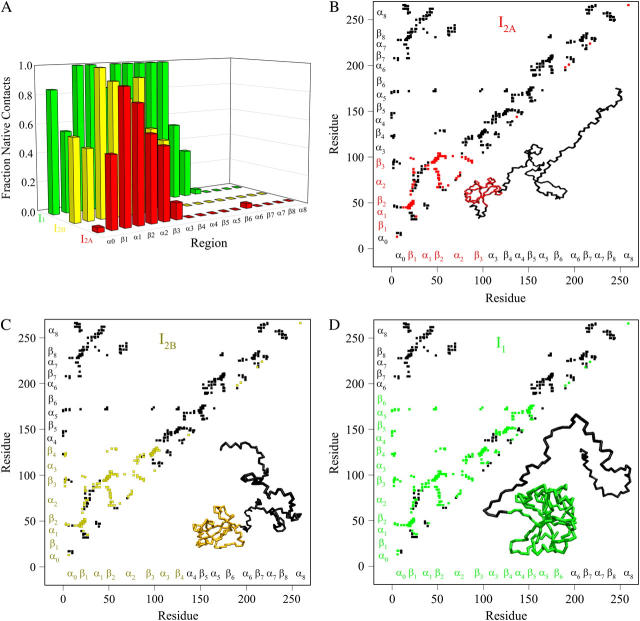
Fig. 5, A–D, shows the structure of the αTS equilibrium intermediate ensembles highlighted in Fig. 4. Fig. 5 A shows the fraction of total native contacts formed by each region of secondary structure in equilibrium αTS intermediate ensembles I_2A, I_2B, and I₁. If an arbitrary definition of 0.2 fraction of native contacts is used to define whether a given region is structured or unstructured, I_2A is structured in regions β₁–β₃, I_2B is structured in regions α₀–β₄, and I₁ is structured in regions α₀–β₆.

FIGURE 5.

Folded regions of αTS equilibrium intermediates. (A) Fraction of native contacts formed with probability >0.5 for intermediates I_2A (red bars), I_2B (yellow bars), and I₁ (green bars) in αTS equilibrium folding and unfolding simulations. (B) Contact map and representative MD structure for I_2A. Squares in the contact map indicating contacts populated >0.5 and regions in the I_2A structure with >0.2 fraction of native contacts folded are labeled in red. (C) Contact map and representative MD structure for I_2B. Squares in the contact map indicating contacts populated >0.5 and regions in the I_2B structure with >0.2 fraction of native contacts folded are labeled in yellow. (D) Contact map and representative MD structure for I₁. Squares in the contact map indicating contacts populated >0.5 and regions in the I₁ structure with >0.2 fraction of native contacts folded are labeled in green. In Fig. 5, B–D, squares in the contact maps indicating contacts populated <0.5 and regions of each MD structure with <0.2 fraction of native contacts folded are labeled in black. In Fig. 5, B–D, secondary structure elements of αTS are shown along each axis for reference with folded I_2A regions colored in red (Fig. 5 B), folded I_2B regions colored in yellow (Fig. 5 C), folded I₁ regions colored in green (Fig. 5 D), and unfolded regions colored in black.

A representative three-dimensional (3D) structure snapshot and a detailed map of native contacts formed in intermediate ensembles I_2A, I_2B, and I₁ is shown in Fig. 5, B–D, respectively. In Fig. 5, B–D, squares indicate a native contact as determined from the 1BKS structure with the two residues involved in the contact indicated on the x and y axes. A colored square indicates a native contact, which is formed with >0.5 probability in the intermediate ensemble whereas a black square indicates a native contact formed with <0.5 probability. For clarity, the folded secondary structure regions of I_2A (red), I_2B (yellow), and I₁ (green) are highlighted in color along the x and y axis. In addition, folded regions of I_2A (red), I_2B (yellow), and I₁ (green) are highlighted by colored portions of the chain in the shown 3D structure.

In Fig. 5 B, the folded β₁–β₃ regions of the intermediate I_2A ensemble conformations (110 < Q < 130) are indicated by red contact squares in the contact map and highlighted with red chain regions in the representative I_2A structure. In Fig. 5 C, the folded α₀–β₄ regions of the intermediate I_2B ensemble conformations (170 < Q < 190) are indicated by yellow contact squares in the contact map and highlighted with yellow chain regions in the representative I_2B structure. In Fig. 5 D, the folded α₀–β₆ regions of the intermediate I₁ ensemble conformations (270 < Q < 290) are indicated by green contact squares in the contact map and highlighted with green chain regions in the representative I₁ structure.

Simulations of refolding kinetics

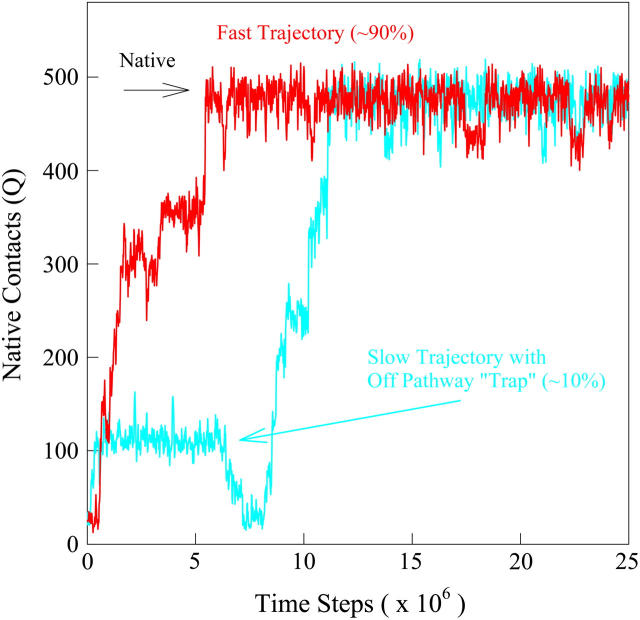
In addition to equilibrium simulations, 60 kinetic refolding simulation trajectories were run on αTS (see Materials and Methods) to explore the folding of αTS under kinetic conditions. Fig. 6 shows two sample “native contacts (Q) versus time” for a fast (red trace) and slow (blue trace) αTS trajectories. The red trajectory is representative of ∼90% of the trajectories and demonstrates progressive folding through a series of transient intermediates. The blue trajectory is representative of ∼10% of the trajectories, in which the trajectory is transiently “trapped” in an off-pathway intermediate that must unfold completely to refold correctly. With the exception of the off-pathway intermediate state, the intermediate structures sampled by both the red and blue trajectories during refolding appear qualitatively similar. The number of native contacts (Q) corresponding to the native state is indicated by the arrow labeled “Native” at Q = 480.

FIGURE 6.

The number of native contacts (Q) between 0 and 25 × 10⁶ time steps in a fast-folding (red) and slower-folding (blue) kinetic refolding trajectory of αTS at T = 300 K.

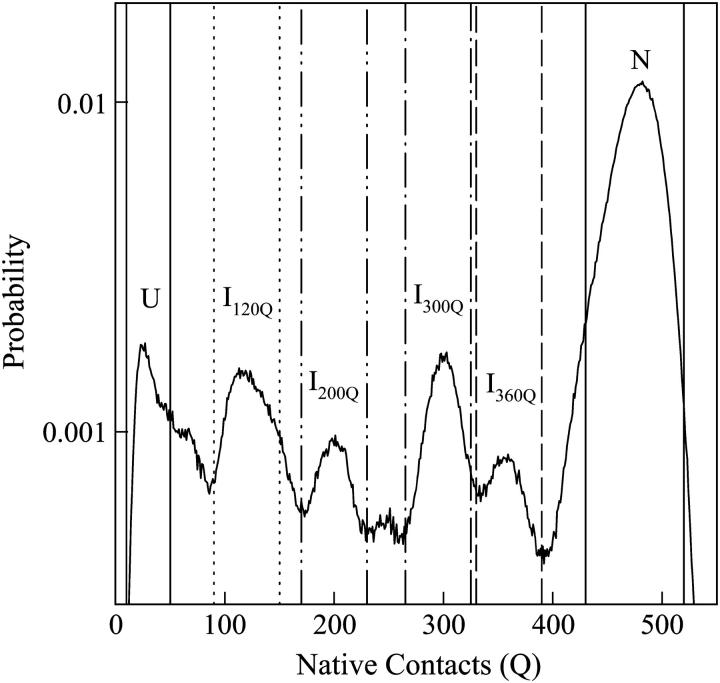
To characterize intermediates populated in kinetic refolding simulations of αTS, the probability sampling each value of Q within the first 30 ns (30 × 10⁶ time steps) of all 60 trajectories was calculated and shown in Fig. 7. The y axis of Fig. 7 indicates the probability of adopting a particular conformation with Q native contacts during refolding and is used to identify intermediates populated in refolding pathways. However, this probability cannot be directly related to the actual free energy of the states on these pathways because the probabilities are derived from kinetic, not equilibrium, trajectories. For example, determining the Q probabilities at increasing kinetic simulation lengths at 300 K will naturally increase the probability of sampling native conformations over other states, whereas this would not be observed in an equilibrium simulation at 335 K.

FIGURE 7.

The net probability of populating states with Q native contacts during the entirety of the first 30 × 10⁶ time steps of all 60 αTS kinetic refolding trajectories. High probability Q-regions are highlighted between colored lines for unfolded U (solid lines), intermediate I_120Q (dotted lines), intermediate I_200Q (double-dotted/dashed lines), intermediate I_300Q (single-dotted/dashed lines), intermediate I_360Q (dashed lines), and native N (solid lines).

From Fig. 7, four distinct kinetic intermediate ensembles are shown to populate significantly between refolding from the unfolded (Q ∼ 25) to the native (Q ∼ 480) ensemble in the 60 refolding trajectories of αTS and are located near Q values of 120 (I_120Q), 200 (I_200Q), 300 (I_300Q), and 360 (I_360Q). In Fig. 7, designated Q boundaries that define each intermediate ensemble are shown: unfolded U (10 < Q < 50, solid lines), I_120Q (95 < Q < 145, dotted lines), I_200Q (175 < Q < 225, double-dot/dashed lines), I_300Q (275 < Q < 325, single-dot/dashed lines), I_360Q (335 < Q < 385, dashed lines), and native N (440 < Q < 520, solid lines). Sampling of these intermediate ensembles can be qualitatively observed in the individual red and blue trajectories shown in Fig. 6.

For Fig. 8, A–E, the initial 3 × 10⁷ time steps of the kinetic trajectories are segregated into 300 time intervals of 100,000 time steps. In Fig. 8, A–E, each of the 60 trajectories is “counted” in a time interval bin when it reaches a set value of native contacts (Q) and the total count from all trajectories produces a histogram(56). Fig. 8 A shows a histogram of the time intervals in which the 60 trajectories reach Q = 120 (approximating I_120Q). Fig. 8 B shows a histogram of the time intervals in which the 60 trajectories reach Q = 200 (approximating I_200Q). Fig. 8 C shows a histogram of the time intervals in which the 60 trajectories reach Q = 300 (approximating I_300Q). Fig. 8 D shows a histogram of the time intervals in which the 60 trajectories reach Q = 360 (approximating I_360Q). Fig. 8 E shows a histogram of the time intervals in which the 60 trajectories reach Q = 480 (approximating Native). To determine the folding time, the average folding time of trajectories 1–20, 21–40, and 41–60 were calculated separately. The average 〈τ〉 and standard deviation of these three (1–20, 21–40, 41–60) averaged folding times is shown in Fig. 8, A–E, as well as in Table 2 (left column). Table 2 also shows the differences between the folding times between each set of two successive intermediate ensembles (right column). Table 2 indicates that the relative folding time difference between less structured folding ensembles is similar to more structured folding ensembles (right column), although the large relative error of the folding time differences precludes a detailed analysis.

A time-resolved description of αTS refolding is shown in Fig. 9 A. Using the Q boundary definitions shown in Fig. 7, the probability of adopting each particular ensemble at each simulation time step is determined from all 60 trajectories is indicated in Fig. 9 A: unfolded U (black line), I_120Q (red line), I_200Q (yellow line), I_300Q (green line), I_360Q (magenta line), and native N (black line). Two important observations of αTS refolding are evident in Fig. 9 A. First, the population increase of each folding ensemble is consistently faster for less structured ensembles and a notable “lag-phase” is observed for the formation of more structured ensembles (I_200Q, I_300Q, I_360Q, and N). This is consistent with a folding model where the intermediates shown in Fig. 7 are on-pathway and are each formed sequentially throughout the folding process. Second, ∼10% of the trajectories appear trapped in the I_120Q intermediate ensemble and require more time to refold. A representative trajectory involving one of these I_120Q trapped states is shown as a blue trace in Fig. 6.

In Fig. 9 A, it should be noted that the fraction of native structures does not equal 1 at 30 × 10⁶ time steps. This observation is due to the fact that three trajectories remain trapped in the I_120Q intermediate at this time and require further refolding time to fold completely. In addition, fluctuations in native contacts (Q) in the native ensemble at 300 K occasionally fall outside the range of Q used to define the native ensemble (440 < Q < 520). These fluctuations in Q can be observed in Fig. 6 after the red/blue trajectories have reached the native ensemble near Q ∼ 480.

To provide additional evidence for a sequential folding mechanism in simulations of αTS folding, a pathway involving four sequential intermediates is modeled using KINSIM (55) in Fig. 9 B and compared to Fig. 9 A. As shown in Fig. 9 B, the four kinetic intermediate ensembles observed in Fig. 7 are treated as discrete states in the following sequential kinetic model that assumes each folding step is irreversible:

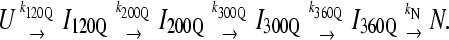In Fig. 9 B, rate constants k_120Q = 3 × 10⁻⁷, k_200Q = 5 × 10⁻⁷, k_300Q = 5 × 10⁻⁷, k_360Q = 3 × 10⁻⁷, and k_N = 7 × 10⁻⁷ produce transient intermediate populations in general agreement with the simulated intermediate populations in Fig. 9 A. In particular, the lag phase of intermediate ensemble formation in Fig. 9 A is well described using the simple sequential pathway kinetic model in Fig. 9 B.

Fig. 10, A–E, show the structure of the αTS kinetic intermediate ensembles highlighted in Fig. 7. Fig. 10 A shows the fraction of total native contacts formed by each region of secondary structure in kinetic αTS intermediate ensembles I_120Q, I_200Q, I_300Q, and I_360Q. If an arbitrary definition of 0.2 fraction of native contacts is used to define whether a given α-helix or β-strand region of αTS is structured or unstructured, I_120Q is structured in regions β₁, β₂–β₃, I_200Q is structured in regions α₀–β₄, I_300Q is structured in regions α₀–β₆, and I_360Q is structured in regions α₀–β₇.

FIGURE 10.

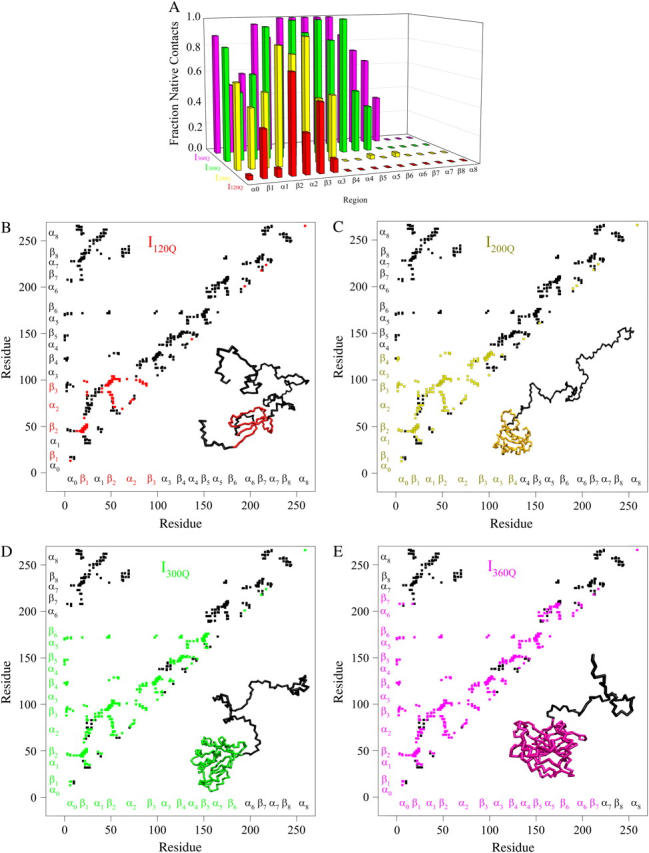
Folded regions of αTS kinetic intermediates. (A) Fraction of native contacts formed with probability >0.5 for intermediates I_120Q (red bars), I_200Q (yellow bars), I_300Q (green bars), and I_360Q (magenta bars) in αTS kinetic folding simulations. (B) Contact map and representative MD structure for I_120Q. Squares in the contact map indicating contacts populated >0.5 and regions in the I_120Q structure with >0.2 fraction of native contacts folded are labeled in red. (C) Contact map and representative MD structure for I_200Q. Squares in the contact map indicating contacts populated >0.5 and regions in the I_200Q structure with >0.2 fraction of native contacts folded are labeled in yellow. (D) Contact map and representative MD structure for I_300Q. Squares in the contact map indicating contacts populated >0.5 and regions in the I_300Q structure with >0.2 fraction of native contacts folded are labeled in green. (E) Contact map and representative MD structure for I_360Q. Squares in the contact map indicating contacts populated >0.5 and regions in the I_360Q structure with >0.2 fraction of native contacts folded are labeled in magenta. In Fig. 5, B–E, squares in the contact maps indicating contacts populated <0.5 and regions of each MD structure with <0.2 fraction of native contacts folded are labeled in black. In Fig. 5, B–E, secondary structure elements of αTS are shown along each axis for reference with folded I_120Q regions colored in red (Fig. 5 B), folded I_200Q regions colored in yellow (Fig. 5 C), folded I_300Q regions colored in green (Fig. 5 D), folded I_360Q regions colored in magenta (Fig. 5 E), and unfolded regions colored in black.

A representative 3D structure snapshot and a detailed map of native contacts formed in intermediate ensembles I_120Q, I_200Q, I_300Q, and I_360Q is shown in Fig. 10, B–E, respectively. In Fig. 10, B–E, squares indicate a native contact as determined from the 1BKS structure with the two residues involved in the contact indicated on the x and y axes. A colored square indicates a native contact, which is formed with >0.5 probability in the intermediate ensemble whereas a black square indicates a native contact formed with <0.5 probability. For clarity, the folded secondary structure regions of I_120Q (red), I_200Q (yellow), I_300Q (green), and I_360Q (magenta) are highlighted in color along the x and y axis. In addition, folded regions of I_120Q (red), I_200Q (yellow), I_300Q (green), and I_360Q (magenta) are highlighted by colored portions of the chain in the 3D structure.

In Fig. 10 B, the folded β₁, β₂–β₃ regions of the intermediate I_120Q ensemble conformations (95 < Q < 145) are indicated by red contact squares in the contact map and highlighted with red chain regions in the representative I_120Q structure. In Fig. 10 C, the folded α₀–β₄ regions of the intermediate I_200Q ensemble conformations (175 < Q < 225) are indicated by yellow contact squares in the contact map and highlighted with yellow chain regions in the representative I_200Q structure. In Fig. 10 D, the folded α₀–β₆ regions of the intermediate I_200Q ensemble conformations (275 < Q < 325) are indicated by green contact squares in the contact map and highlighted with green chain regions in the representative I_300Q structure. In Fig. 10 E, the folded α₀–β₇ regions of the intermediate I_360Q ensemble conformations (335 < Q < 385) are indicated by magenta contact squares in the contact map and highlighted with magenta chain regions in the representative I_360Q structure.

In Fig. 10 A, intermediates of higher Q value (for example, I_360Q) demonstrate a greater fraction of contacts formed in each α- or β-region than intermediates of lower Q values (for example, I_120Q). In Fig. 10, B–E, intermediates of higher Q value (for example, I_360Q) always contain contacts of the intermediates with lower Q values (for example, I_120Q), in addition to contacts consistent with further structure formation. These observations are highly consistent with a sequential single-pathway folding mechanism.

Simulations and analysis of on- and off-pathway refolding kinetics

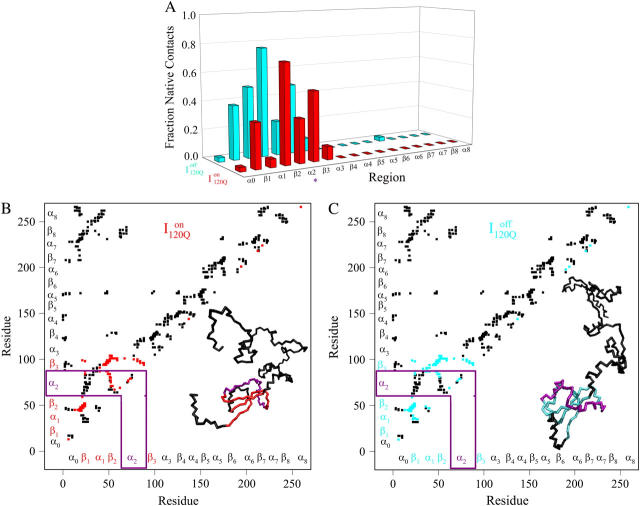
Conformations within the intermediate ensemble I_120Q appear to be responsible for productive fast folding to the native state (Fig. 6, red trajectory) as well as formation of a trapped state that delays proper folding (Fig. 6, blue trajectory). Therefore, it is important to compare the structures of the I_120Q ensemble found in the 54 fast-folding trajectories with structures of the I_120Q ensemble found in the six trapped slow-folding trajectories.

Fig. 11, A–C, highlight the structural differences between the fast-folding on-pathway ensemble conformations 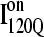observed in 54 trajectories (red) and trapped off-pathway ensemble conformations 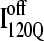observed in six trajectories (blue). Fig. 11 A shows the fraction of total native contacts formed by each region of secondary structure in kinetic αTS intermediate ensembles 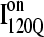and 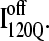If an arbitrary definition of 0.2 fraction native contacts is used to define whether a given α-helix or β-strand region of αTS is structured or unstructured, 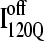is structured in regions β₁, β₂–β₃ and 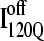is structured throughout regions β₁–β₃. Due to its significance to on- and off-pathway folding, the α₂ helix is denoted with a purple asterisk in Fig. 11 A.

FIGURE 11.

Folded regions of αTS kinetic on-pathway intermediate ensemble 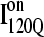(I_120Q from 54 trajectories) and off-pathway intermediate ensemble 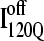(I_120Q from six trajectories). (A) Fraction of native contacts formed with probability >0.5 for intermediates 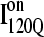(red bars) and 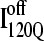(blue bars) in αTS kinetic folding simulations. (B) Contact map and representative MD structure for 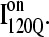Squares in the contact map indicating contacts populated >0.5 and regions in the 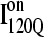structure with >0.2 fraction of native contacts folded are labeled in red. (C) Contact map and representative MD structure for 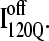Squares in the contact map indicating contacts populated >0.5 and regions in the I_200Q structure with >0.2 fraction of native contacts folded are labeled in blue. In Fig. 11, B and C, squares in the contact maps indicating contacts populated <0.5 and regions of each MD structure with <0.2 fraction of native contacts folded are labeled in black. In Fig. 5, B and C, secondary structure elements of αTS are shown along each axis for reference with folded 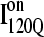regions colored in red (Fig. 5 B), folded 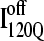regions colored in blue (Fig. 5 C), and unfolded regions colored in black.

A representative 3D structure snapshot and a detailed map of native contacts formed in intermediate ensembles 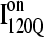and 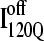are shown in Fig. 11, B and C, respectively. In Fig. 11, B and C, squares indicate a native contact as determined from the 1BKS structure with the two residues involved in the contact indicated on the x and y axes. In Fig. 11, B and C, a colored square indicates a native contact, which is formed with >0.5 probability in the intermediate ensemble whereas a black square indicates a native contact formed with <0.5 probability. For clarity, the folded secondary structure regions of 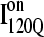(red) and 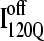(blue) are highlighted in color along the x and y axis. In addition, folded regions of 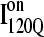(red) and 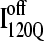(blue) are highlighted by colored portions of the chain in the 3D structure. 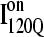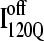Due to the significance of the α₂ helix in modulating on- and off-pathway folding, contacts between the α₂ helix and other folded regions of and are located within a purple boundary in the contact map and the portion of the 3D structure corresponding to the α₂ helix is also colored purple.

In Fig. 11 B, the folded β₁, β₂–β₃ regions of the intermediate 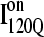ensemble conformations (95 < Q < 145 from 54 on-pathway trajectories) are indicated by red contact squares in the contact map and highlighted with red chain regions in the representative structure. In Fig. 11 C, the folded β₁–β₃ regions of the intermediate 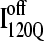ensemble conformations (95 < Q < 145 from six off-pathway trajectories) are indicated by blue contact squares in the contact map and highlighted with blue chain regions in the representative 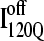structure.

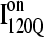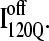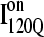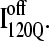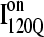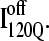In Fig. 11 A, it is interesting to note that contacts in α-helix α₁ are nearly absent in but largely present in In contrast, contacts in α-helix α₂ (indicated by purple asterisk) are slightly higher in than in In Fig. 11, B and C, it is observed which contacts explain these structural differences exist between and Comparing Fig. 11, B and C, one can observe that 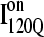lacks contacts formed between α₁ and α₂ and that 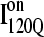lacks contacts formed between the C-terminus of β₂ and the N-terminus of α₂. Comparing the structures of 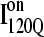and 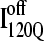in Fig. 11, B and C, it can be clearly observed that helix α₂, colored in purple, incorrectly wraps clockwise around strand β₃ in 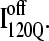This nonnative chiral arrangement of α₂ is stabilized by native contacts formed between the N-terminus of β₂ and the C-terminus of α₂. This nonnative 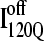conformation also places α₂ on the face of β₃ where the next strand, β₄, would dock in the subsequent intermediate ensemble I_200Q. The location of the α₂ helix in the 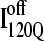conformation would sterically prevent stable assembly of β₃ and β₄, resulting in a dead-end folding intermediate.

If the 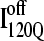conformation is a dead-end conformation, unfolding is required to correctly refold. To test whether 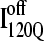conformations are dead ends, refolding kinetic simulations were conducted initiating with either an and 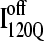conformation. For 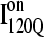conformations, five conformations with Q = 120 were randomly selected from six on-pathway trajectories (trajectories 6, 34, 45, 47, 57, and 59) as initial structures for refolding. For 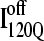conformations, five conformations with Q = 120 were randomly selected from the six off-pathway trajectories (trajectories 7, 35, 46, 48, 58, and 60) as initial structures for refolding. These structures are given random initial velocities and refolded at 300 K.

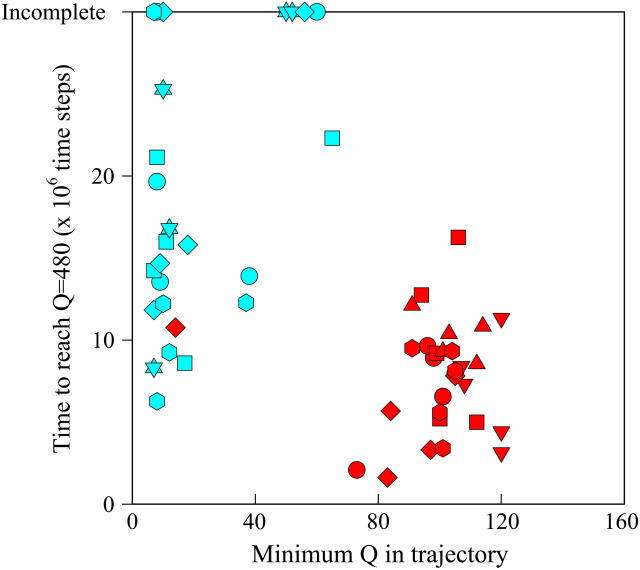
Fig. 12 shows the results of the 30 simulations initiating with either 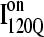(red symbols) or 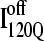(blue symbols) conformations. For each trajectory, Fig. 12 plots the minimum value of Q sampled on the x axis versus the folding time, the time to reach the native ensemble Q = 480, on the y axis. Symbol shapes indicate initial conformations obtained from trajectories 6,7 (circles), 34,35 (squares), 45,46 (triangles), 47,48 (inverted triangles), 57,58 (diamonds), and 59,60 (hexagons). If 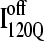is truly a dead-end structure, trajectories initiating from 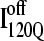should sample values of Q much lower than 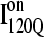before refolding, because they would have to unfold before correct refolding. Because unfolding is required before refolding, trajectories initiating from 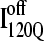would also be expected to take longer to properly refold.

FIGURE 12.

Time steps to reach native ensemble (Q = 480) and minimum value of Q sampled during simulations initiating with Q = 120 structures from 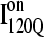(red symbols) and 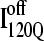(blue symbols) ensembles. Five different initial 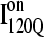configurations were obtained from trajectories 6 (circles), 34 (squares), 45 (triangles), 47 (inverted triangles), 57 (diamonds), and 59 (hexagons). Five different initial 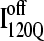configurations were obtained from trajectories 7 (circles), 35 (squares), 46 (triangles), 48 (inverted triangles), 58 (diamonds), and 60 (hexagons).

In Fig. 12, trajectories initiating from 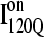and 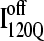clearly show significant differences and cluster in different regions of the plot. As expected, all 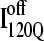trajectories sample lower values of Q (Q < 70) than all 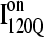trajectories (Q > 70), with one exception of an 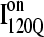trajectory that appears to unfold. This observation clearly shows that 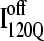conformations require a significant degree of unfolding before refolding. Although some 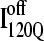trajectories refold to the native ensemble at times comparable to trajectories, the average refolding time is clearly slower for 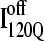trajectories. The fastest trajectories initiate from 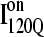conformations whereas the 14 slowest trajectories initiate from 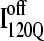conformations, with nine of these trajectories remaining unfolded at the end of the 30 × 10⁶ time steps (labeled “incomplete” on the y axis). There do not appear to be significant differences between values of different symbols of each 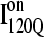(red) and 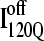(blue) trajectory subgroups, indicating that each structural subgroup is largely homogeneous with respect to folding.

DISCUSSION

Equilibrium simulations of αTS agree with experiments

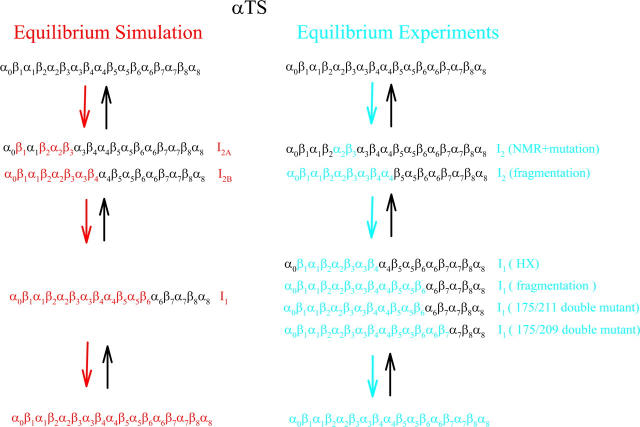
Figs. 2 and 3 indicate that equilibrium folding/unfolding of αTS at T_f = 335 K occurs with the population of two predominant intermediate ensembles, I₁ and I₂, in an apparently sequential process. Fig. 5, A–C, shows that structures within the intermediate I₂ ensemble (I_2A–I_2B) show contacts in the N-terminal region, although the I₂ structures occupy a broader distribution of Q values than I₁. The least structured of the I₂ ensemble (I_2A) shows native contacts in the β₁–β₃ regions whereas the most structured (I_2B) shows native contacts throughout the α₀–β₄ regions. Fig. 5, A and D, also shows that I₁ consists of a discrete ensemble of intermediate structures with native contacts in the N-terminal α₀–β₆ regions and the C-terminal region α₆–α₈ unstructured. Fig. 5, B–D, show that, within the folded region of each equilibrium intermediate ensemble (i.e., colored squares), both short-range and longer-range contacts are equally probable. Thus, even though unfolded regions still exist in these intermediates, the secondary (short-range) and tertiary (long-range) structure within the folded region of the αTS chain fold concomitantly. In Scheme 1, these results are compared to equilibrium experimental measurements on αTS.

SCHEME 1.

Comparison of equilibrium folding simulations and experiments for αTS.

Scheme 1 shows that αTS equilibrium folding simulations agree with αTS equilibrium folding experiments. The simulations produce two dominant free-energy minima, I₁ and I_2A + I_2B, in equilibrium folding, which agree well with the two intermediates identified from fits of experimental urea titrations (39). The simulation structure of intermediate I₁ (α₀–β₆) is highly similar to the structure of I₁ inferred from fragment stability experiments (α₀–β₆) (40), a Y175C/G211E double mutant perturbation study (α₀–β₆) (51), a Y175Q/L209V double mutant perturbation study (α₀–β₇) (45), although it is larger than I₁ structural regions exhibiting HX protection (β₁–β₄) (37).

In Scheme 1, conformations contributing to the free-energy minima between I_2A and I_2B also agree well with experimental studies probing the structure of intermediate I₂ (38,40). The earliest regions of folding in the simulation, denoted as intermediate I_2A, predict initial folding in the N-terminus (β₁–β₃), consistent with structured regions in I₂ measured with NMR and probed with changes in stability upon single-site mutagenesis (α₂, β₃) (38). The most structured of states in the I₂ intermediate ensemble in the simulations, denoted I_2B, indicate continuous structure in regions α₀–β₄. This finding is also consistent with fragmentation experiments that show that αTS fragments shorter than α₀–α₄ no longer fold (40). In addition, although HX experiments have not been able to detect HX protection under conditions where the I₂ intermediate is maximally populated, they do indicate an HX-resistant region of I₁ in regions β₁–β₄ that may reflect a stable core reflective of the I₂ structure (37). The consistency between the funneled energy model with these experiments supports the hypothesis that the energy landscape of αTS is highly funneled to the native state.

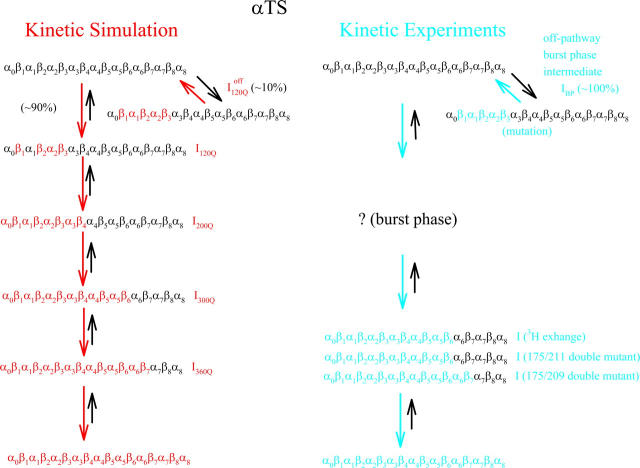
Kinetic simulations of αTS produce a sequential folding mechanism and folding intermediates consistent with experiments

Figs. 6, 7, 8, A–E, and 9 A indicate that kinetic folding of αTS at 300 K (∼0.9 T_f) occurs with the population of four predominant on-pathway intermediate ensembles (I_120Q, I_200Q, I_300Q, and I_360Q) and one off-pathway intermediate (denoted as 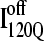) in a sequential process. Fig. 10 B shows that on-pathway I_120Q consists of initial structure formation in the N-terminal β₁, β₂–β₃ regions. Fig. 10 C shows that the subsequent intermediate, I_200Q, contains the same contacts as I_120Q, with additional contacts between regions α₀–β₄. Fig. 10 D shows that the next intermediate, I_300Q, contains the same contacts as I_200Q, with additional contacts between regions α₀–β₆. Fig. 10 E shows that the final intermediate, I_360Q, contains the same contacts as I_300Q, and with additional contacts between regions α₀–β₇.

For the αTS equilibrium simulations, an on-pathway sequential folding mechanism appears to be the case because both folding and unfolding events sample similar intermediate Q ensembles (Fig. 2). A sequential on-pathway folding mechanism is also consistent with 90% of αTS kinetic simulations and is supported by three observations. First, visual inspection of individual trajectories indicates sequential formation of the four intermediate ensembles during refolding (red trajectory shown in Fig. 6). Second, the increasing lag phase shown, respectively, for αTS intermediates I_200Q, I_300Q, I_360Q, and native state N in Fig. 9 A is consistent with the sequential pathway model shown in Fig. 9 B. Third, each successively more structured intermediate ensemble in Fig. 10, A–E, contains all the contacts of the previous intermediate ensemble. If these intermediates were each populated in a parallel pathway, this property might not be observed.

Scheme 2 shows that αTS kinetic folding simulations agree with the results of the αTS kinetic folding experiments conducted up to this point. Before comparison, it is important to note that the parallel pathways resulting from proline isomerization are not observed in the αTS kinetic refolding simulations (41,42). Although it is possible that proline isomerization could have been captured with this simple topological model of αTS, it is not surprising that isomerization was not observed in the simulations because proline isomerization was not specifically engineered into the model. Due to the complications of proline isomerization and a significant stopped flow signal within the dead time of mixing, a discrete number and structures of early αTS folding intermediates is difficult to determine (41,42). However, kinetic experiments of αTS suggest that at least one intermediate, with a structural ensemble similar to I₁ in equilibrium studies (α₀–β₇) is populated during kinetic refolding (30,41,42,45,51).

SCHEME 2.

Comparison of kinetic folding simulations and experiments for αTS.

Determining whether intermediates I_120Q, I_200Q, and I_300Q, populated in kinetic simulations, are also populated in kinetic experiments is difficult because early αTS refolding intermediates populate in the dead time of kinetic mixing. However, the structure of the final intermediate in simulations, I_360Q (α₀–β₇), can be compared to the final intermediate detected in experiments before native state formation. An early ³H exchange experiment revealed that this intermediate is significantly more protected in the N-terminal regions α₀–β₆ than the C-terminal regions α₆–α₈ (30). Furthermore, double mutant studies suggest that contacts between Y175 (β₆) and L209 (β₇) partially exist in the kinetic intermediate preceding native state formation (45), although contacts between Y175 (β₆) and G211 (β₇) were not detected for this intermediate in a similar study (51). The excellent structural agreement is found between simulation intermediate I_360Q and the structure inferred from kinetic experiments (α₀–β₇) is shown in Scheme 2.

The relative folding rates between on-pathway unfolded, intermediate, and native ensembles appear to be qualitatively similar throughout all the simulated kinetic trajectories. Table 2 shows quantitatively that differences between the average folding time do not vary significantly between different intermediate ensembles. For example, the folding time difference between the early intermediate ensembles, 〈τ_300Q〉 − 〈τ_200Q〉 = 1.54 × 10⁶, is similar to the final two species, 〈τ_N〉 − 〈τ_360Q〉 = 1.38 × 10⁶. This observation indicates that transition times throughout simulated αTS folding are similar. Furthermore, the simple kinetic model shown in Fig. 9 B produces similar intermediate populations during αTS refolding as observed from MD simulations in Fig. 9 A with similar rate constants for each kinetic step (k = 3–7 × 10⁻⁷ time steps⁻¹).

It should be noted that similar rates between different simulated αTS folding steps is not entirely consistent with different folding rates fitted in kinetic experimental data (k_UI ∼ 100 s⁻¹ and k_IN ∼ 10 s⁻¹) (41). One explanation for this discrepancy may be that the minimalist C_α model may not accurately capture the side-chain packing contribution to kinetic barrier heights at increasingly structured intermediate stages of αTS folding. Also, future mutational studies are needed to eliminate the off-pathway and proline isomerization steps to facilitate a direct rate measurement of k_UI and k_IN (42). Regardless of these rate discrepancies between simulations and experiments, the fact that the simulated intermediate populations (Fig. 9 A) are sufficiently modeled with a simple sequential kinetic model (Fig. 9 B) provides evidence for a predominantly sequential folding of αTS in the kinetic trajectories. The sequential nature of the on-pathway folding mechanism agrees qualitatively with experiments, neglecting proline isomerization (41).

Kinetic simulations capture the off-pathway intermediate observed in kinetic refolding experiments

Off-pathway intermediates have been shown in a number of theoretical (57), computational (8), and experimental (58,59) studies of protein folding. In αTS simulations, 10% of trajectories initially fold to a trapped intermediate, 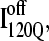which requires a relatively slow unfolding process to occur to properly refold through the productive sequential folding channel (blue trajectory shown in Fig. 6). Evidence for this trapped ensemble 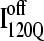is demonstrated by the persistent presence of 0.1 fraction of the I_120Q intermediate in Fig. 9 A and the resistance of this species to further folding. Although Fig. 11 A shows that the structures of on-pathway 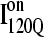and the off-pathway 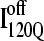both show contacts between β-strands β₁–β₃, there are very few helix α₁ contacts in 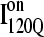and slightly fewer contacts between strand β₂ and helix α₂ in 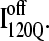A comparison of the structures of 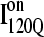(Fig. 11 B) and 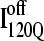(Fig. 11 C) reveals that, helix α₂, colored in purple, is wrapped in a nonnative clockwise chiral arrangement around β₃ in 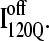Steric repulsion between α₂ and the next docking unit α₃β₄ prevents further folding unless an unfolding event would allow α₂ to disassemble and refold in the correct orientation. Fig. 12 confirms that 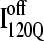conformations must at least partially unfold to correctly refold.

It is striking that the kinetic simulations in this study identify this off-pathway intermediate 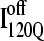because an off-pathway intermediate I_BP is also observed in kinetic experiments (41). Scheme 2 shows that the mechanism by which 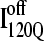is folded and slowly unfolded in simulations is similar to that proposed based on experimental kinetic studies of I_BP (41). Although kinetic simulations indicate that only a minor fraction (∼0.1) of the trajectories sample the off-pathway state, 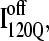experiments suggest that nearly all molecules should sample this off-pathway intermediate. Nonetheless, it is remarkable that the Go-model of αTS captures this off-pathway intermediate trap because the attractive contacts in the Go-model are determined solely from native contacts observed in the PDB structure 1BKS. Furthermore, perturbation of the stability of the off-pathway intermediate I_BP with single-site mutations provides evidence for structure of I_BP in regions β₁–β₃ (C. R. Matthews, University of Massachusetts Medical School, personal communication). This result is in excellent agreement with these simulations of the αTS Go-model, which demonstrate that the off-pathway kinetic intermediate, 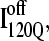also makes contacts between regions β₁–β₃ (Fig. 11 C).

The nature of the off-pathway trap 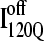is a nonnative chiral topology in the N-terminal bend of helix α₂ held in place by native contacts between the “ends” of the structural unit (N-terminus of β₂ and C-terminus of α₂) (Fig. 11 C). This topological arrangement prevents further assembly of αTS folding units beyond strand β₃ and requires breaking of at least 50 contacts to correctly refold (blue symbols in Fig. 12). Evidence for this structural hypothesis for 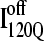formation involving the nonnative configuration of helix α₂ shown in Fig. 11 C may be determined in future mutational studies of αTS folding kinetics. In addition, future computational work will be aimed at developing an order parameter that is able to discern whether an intermediate conformation similar to I_120Q is folding competent (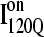) or less “foldable” than most unfolded conformations (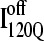). For this study, a complete equilibrium and kinetic analysis proved sufficient to identify the off-pathway intermediate conformation 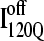using the Q order parameter.

The αTS folding pathway is robust between equilibrium and kinetic simulations

Comparison of the simulated αTS equilibrium folding pathway in Scheme 1 and simulated αTS kinetic folding pathway in Scheme 2 shows that αTS equilibrium and kinetic simulation pathways are highly similar. Despite the observation that the kinetic pathway appears to form four intermediate ensembles with an off-pathway intermediate and the equilibrium ensemble appears to form only two free-energy minima and no off-pathway intermediates, there are significant structural similarities between intermediates populated in these two pathways. Comparison of equilibrium and kinetic intermediates is based upon the whether α-helices and β-sheets are at least partially folded, as defined by whether a given α-helix or β-sheet has >0.2 fraction of native contacts formed with >0.5 probability (Figs. 5 A and 10 A).

First, the equilibrium intermediate I_2A (Fig. 5, A and B) shows folding throughout regions β₁–β₃, which is highly similar to kinetic intermediate I_120Q (Fig. 10, A and B), which is folded in four of these five structural regions (β₁, β₂, α₂, β₃). Second, the equilibrium intermediate I_2B (Fig. 5, A and C) shows folding throughout regions α₀–β₄, which is identical to folded regions of kinetic intermediate I_200Q (Fig. 10, A and C). Third, the equilibrium intermediate I₁ (Fig. 5, A and D) shows folding throughout regions α₀–β₆, which is identical to folded regions of kinetic intermediate I_300Q (Fig. 10, A and D). Although no equilibrium intermediate was identified that matched the structure of the kinetic intermediate I_360Q, I_360Q is the least-populated kinetic ensemble in Fig. 7 (T = 300 K) and may not be stable during equilibrium simulations at higher temperature (T = 335 K). Interestingly, I_360Q identifies β7 contacts consistent with those detected in both kinetic and equilibrium experiments using a double-mutant thermodynamic cycle (45). This agreement emphasizes the importance of using both kinetic and equilibrium simulations to explore protein folding pathways. In any case, the energy landscape of αTS appears to be extremely robust, such that the folding pathway is only minimally altered when αTS refolds and unfolds in reversible equilibrium at 335 K (T_f) (Fig. 2) or refolds irreversibly in kinetics at 300 K (0.9 T_f) (Fig. 6).

Comparison to previous TIM barrel simulations

It is also important to compare simulated αTS kinetics in this study with those in a previous kinetic simulation study of αTS (23). Certain energetic and entropic differences exist between the minimalist C_α Go-model in this study, in which the native state is defined as the lowest energy state, and the all-atom model of Godzik et al., which energetically biases local backbone atoms to the native dihedrals but permits nonnative long-range contacts with a Miyazawa-Jernigan weighted statistical potential (23). Also, this study uses off-lattice molecular dynamics whereas the previous all-atom study uses an on-lattice Monte-Carlo method.

Despite differences in the energy functions used, the results of this Go-model and the all-atom model are surprisingly consistent. First, both studies predict significant population of N-terminal kinetic intermediate ensembles, corresponding to I_300Q in this study (Fig. 10), which are also found in experiments (30,41,45,51). Second, both models appear to model the trapped off-pathway structures observed in experiments (41).

However, a few important differences do exist between this study and the all-atom study. First, this model predicts the earliest kinetic folding events in a region corresponding to residues 15–110 (intermediate ensemble I_120Q) whereas the all-atom study shows much of this area folding later than the neighboring contacts (23). Since equilibrium analysis has shown the I_120Q “contact cluster” to be metastable (intermediate I_2A and I_2B in Fig. 3), small differences in the on-lattice model may underweight the presence of the I_120Q ensemble. It is difficult to confirm the presence and structure of the putative I_120Q on-pathway kinetic intermediate with experiments because these intermediates would be expected to populate in the burst phase of stopped flow mixing and also copopulate with the unfolded ensemble (41).

Second, although both studies appear to capture off-pathway trapped states, significant differences exist as to the stability and structure of these off-pathway traps. In this study, the off-pathway intermediate, 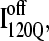is observed in 10% of the simulations and corresponds to N-terminal regions β₁–β₃. In the all-atom study, nearly half of the simulations appear trapped at the end of the run (native RMS > 8 Å) and appear to involve trapped structures involving both N- and C-terminal regions (50% N-terminal trap/50% C-terminal trap) (23). Recent mutational experiments support a trapped structure involving contacts between N-terminal regions β₁–β₃ and do not appear to involve C-terminal contacts (C. R. Matthews, University of Massachusetts Medical School, personal communication).

Regardless of these discrepancies, it is not surprising that differences are observed between the two models. These differences might be attributed to the fact that the previous lattice model uses explicit atoms and nonnative contacts whereas this C_α Go-model does not. Despite these differences, the intriguing similarity between the two models of αTS may help explain the ubiquitous occurrence of the TIM barrel fold across genomes. If the native fold and folding pathway, determined in this study using a native Go-model, can also be determined from simulations without a priori knowledge of native contacts (23), it is possible that the evolutionary selection process of protein structure also finds the TIM barrel fold a readily accessible motif. In terms of landscape theory, the TIM barrel appears to be a relatively uncomplicated fold with a low chain entropy penalty paid during folding. Alternatively, this fold could have evolved due to its functional versatility in the catalysis of metabolic reactions. Further studies of other members of the TIM barrel fold class will be necessary to address the degree to which small changes in the native topology of different TIM barrel proteins impact the folding of simple computational models, as well as real proteins.