Mechanically Unfolding the Small, Topologically Simple Protein L

Abstract

β-sheet proteins are generally more able to resist mechanical deformation than α-helical proteins. Experiments measuring the mechanical resistance of β-sheet proteins extended by their termini led to the hypothesis that parallel, directly hydrogen-bonded terminal β-strands provide the greatest mechanical strength. Here we test this hypothesis by measuring the mechanical properties of protein L, a domain with a topology predicted to be mechanically strong, but with no known mechanical function. A pentamer of this small, topologically simple protein is resistant to mechanical deformation over a wide range of extension rates. Molecular dynamics simulations show the energy landscape for protein L is highly restricted for mechanical unfolding and that this protein unfolds by the shearing apart of two structural units in a mechanism similar to that proposed for ubiquitin, which belongs to the same structural class as protein L, but unfolds at a significantly higher force. These data suggest that the mechanism of mechanical unfolding is conserved in proteins within the same fold family and demonstrate that although the topology and presence of a hydrogen-bonded clamp are of central importance in determining mechanical strength, hydrophobic interactions also play an important role in modulating the mechanical resistance of these similar proteins.

INTRODUCTION

Since the first report some eight years ago (1), single-molecule mechanical unfolding studies have been performed on many proteins of different size (2–4) and diverse topology (4–18). These data have shown that when mechanically extended via the N- and C-termini, proteins display a wide variety of mechanical behavior. Data available so far suggest that α-helical and mixed α/β proteins are less mechanically resistant than their all β-sheet counterparts. The type of secondary structure is thought to be a critical factor in determining mechanical resistance because the array of hydrogen bonds between adjacent β-strands in β-sheet proteins provides more stability against mechanical deformation than the hydrophobic contacts between helices in α-helical proteins (5). There also appears to be a correlation between the arrangement of β-strands within a protein (its topology) and mechanical resistance. Thus, although proteins with a classical immunoglobulin (Ig)-like fold, such as the I27 domain from titin and proteins of the related FNIII family, are usually highly mechanically resistant (12,13,19), other β-sheet proteins, such as the ferredoxin-like topology of C2A (a β-sandwich protein with an antiparallel β-sheet (6)), the β-sheet barrel of green fluorescent protein (4) and the barrel-sandwich hybrid topology of the lipoyl domain E2lip3 (15) are relatively mechanically labile. Furthermore, the geometry of the applied extension is also critical in defining mechanical resistance (3,15). Together, these results suggest that the type of secondary structural motif and its orientation relative to the applied extension geometry are strong determinants of mechanical resistance in proteins. Any protein with a topology that allows force to be applied parallel to the long axis of hydrogen-bonded adjacent β-strands should display mechanical resistance, irrespective of function.

The most mechanically stable arrangement of β-strands in proteins extended by their N- and C-termini (the most common orientation of the protein in experimental studies) are terminal strands that are parallel and directly hydrogen-bonded. However, although they are mechanically resistant, proteins with this arrangement of β-strands display a broad range of unfolding forces under similar extension rates that are difficult to rationalize (Table 1). To further test the hypothesis that the extension of parallel, directly hydrogen-bonded terminal β-strands correlates with high unfolding forces, and to identify and quantify the factors that modulate protein mechanical resistance, it is necessary to perform a systematic study of a large number of proteins, including those with very different folds as well as those with similar folds but different sequences. Such a database would facilitate the identification of other determinants of mechanical resistance in a similar manner to that used to determine the relationship between protein folding-rate constants and contact order in refolding experiments after chemical denaturation (20). Such correlations are difficult to identify for mechanical unfolding at this time, since 1), the database of information is too small (Table 1); 2), the proteins studied have been analyzed under different conditions by using polyproteins with different numbers of domains and different linker lengths; 3), of the 13 domains studied that have parallel terminal strands, only five have a fully elucidated three-dimensional structure (I1, I27, ¹⁰FNIII, ubiquitin, and ddFLN4) (Table 1); and 4), of these 13 protein domains, only ubiquitin does not belong to the Ig-like superfamily.

TABLE 1.

Mechanical unfolding properties of different protein domains studied to date by AFM

Protein	Construct	SCOP Class*	SCOP Fold*	Parallel terminal strands*	Force/pN (speed/nms−1)*	Reference
Calmodulin	(Cam)4	all α	EF Hand-like	No	<15 (600)	(6)
Spectrin	(R16)4	all α	Spectrin repeat-like	No	60 and 80 (3000)	(7)
Barnase	(I27)5(Ba)3	α+β	Microbial Ribonuclease	No	70 (300)	(8)
Ubiquitin	(Ub)9	α+β	β-grasp	Yes	203 (400)	(3)
Ubiquitin	(Ub)8	α+β	β-grasp	Yes	230 (1000)	(17)
GFP	(Ig)4GFP(Ig)4 or (DdFLN)3GFP(DdFLN)2	α+β	GFP-like	No	104 (3000)	(4)
C2A	(C2A)9	all β	Ferredoxin-like	No	60 (600)	(6)
E2lip3	(I27)4E2lip3	all β	Barrel-sandwich like	No	<15 (600)	(15)
FLN4	(I27–30)FLN4(I31–34)	all β	Immunoglobulin-like β-sandwich	Yes	63 and 53 (250–350)	(18)
1FNIII	(1FNIII-2FNIII)6	all β	Immunoglobulin-like β-sandwich	Yes	220 (600)	(13)
10FNIII	(10FNIII)8	all β	Immunoglobulin-like β-sandwich	Yes	75	(13)
12FNIII	(12FNIII-13FNIII)5	all β	Immunoglobulin-like β-sandwich	Yes	125	(13)
13FNIII	(I27-13FNIII)8	all β	Immunoglobulin-like β-sandwich	Yes	89	(13)
I1	(I27-I1)4	all β	Immunoglobulin-like β-sandwich	Yes	127 (600)	(64)
I4	(I4)8	all β	Immunoglobulin-like β-sandwich	Yes	171	(12)
I5	(I5)8	all β	Immunoglobulin-like β-sandwich	Yes	155	(12)
I27	(I27)8	all β	Immunoglobulin-like β-sandwich	Yes	180	(37)
I27	(I27)8	all β	Immunoglobulin-like β-sandwich	Yes	204	(12)
I28	(I28)8	all β	Immunoglobulin-like β-sandwich	Yes	257	(12)
I32	(I32)8	all β	Immunoglobulin-like β-sandwich	Yes	298	(12)
34	(I34)8	all β	Immunoglobulin-like β-sandwich	Yes	281	(12)

The proteins included here all consist of tandem arrays (the C-terminus of one domain is linked to the N-terminus of the next), which include no more than two different protein domains or are such that the protein under study was unambiguously assigned and was mechanically unfolded numerous times at a defined speed to obtain reliable estimates for the measured unfolding forces. The fold classification is taken from SCOP (34). FLN4 is reported to unfold via an intermediate, and both forces are included.

^*In heteropolymers, the data relates to the domain named in the first column.

Here we describe the mechanical unfolding properties of protein L, a protein not studied hitherto by mechanical means. We predicted, based entirely on its native structure, that this protein would show significant mechanical resistance despite the fact that the protein has no known mechanical function. We show that this small and topologically simple protein is remarkably mechanically resistant, reinforcing the view that extension of hydrogen-bonded parallel β-strands is key to defining mechanical strength. Moreover, by comparing the experimental data with molecular dynamics simulations, we show that protein L unfolds mechanically via a highly reproducible and unusually well defined pathway in a two-state transition. Finally, by comparing the mechanical unfolding properties of protein L and ubiquitin, which have identical topologies, we reveal the importance of the nature of side-chain packing in altering the mechanical unfolding properties of proteins.

MATERIALS AND METHODS

Construction of a pentameric polyprotein from protein L Y47W

The protein L domain used in this work consisted of residues 92–155 (2–64 using the sequence numbering from O'Neill et al. (21) used herein) of the B1 domain of protein L from Peptostreptococcus magnus (22) with the N-terminal addition of Ala-Met as residues 0 and 1. The protein also contains a Tyr-to-Trp mutation at position 47 as described previously (21).

Each protein L cassette was generated by PCR amplification using a modified pET15b vector as template. This vector encodes residues 0–64 of protein L and an N-terminal hexahistidine tag (21). Each cassette was amplified using different pairs of forward and reverse primers to incorporate a unique pair of restriction sites and to encode the linker amino acids at the DNA and protein levels, respectively. Each PCR product was purified, A-tailed, and ligated into a predigested pGEM-T vector as described previously (23). After sequence verification of each cassette, (protein L)₅ was constructed by sequential replacement of each I27 cassette in (C47S C63S I27)₅ (24) with its analogous protein L cassette. This yielded the following tandem array of five protein L domains: MHHHHHHSS(pL₁)GLVEARGG(pL₂)GLIEARGG(pL₃)GLSSARGG(pL₄) GLIERARGG(pL₅)CC. (protein L)₅ was transformed into the expression host Escherichia coli BLR[DE3] pLysS and (protein L)₅ was overexpressed and purified as described for (I27*)₅ (23). Protein purity and identity was verified by SDS-PAGE and ESI-MS: observed molecular mass 39,952 Da, expected molecular mass 39,952 Da. After purification, (protein L)₅ was dialyzed into Milli-Q water then stored as freeze-dried aliquots of 0.05 mg or 5 mg at −20°C until required.

Mechanical unfolding

All mechanical unfolding experiments were carried out using a Molecular Force Probe 1D (Asylum Research, Santa Barbara, CA) mounted with coated, unsharpened microlevers (MLCT-AUNM, Veeco, Cambridge, UK). The spring constants of the cantilevers were estimated under fluid using the thermal method (25) and found to be 43.4 ± 1.0 pN nm⁻¹. 0.05 mg (protein L)₅ was dissolved in 0.5 ml phosphate buffered saline (PBS), centrifuged at 13,000 rpm in a microfuge, and the supernatant retained. Before measurement, 40–60 μL of the protein solution was made up to 100 μL with PBS and applied directly onto a template-stripped gold surface mounted onto a microscope slide. Force-extension profiles were accumulated after thermal equilibration at a constant approach speed of 700 nm s⁻¹ and a retract speed that was varied between 40, 77, 140, 230, 400, 700, 1400, 2100, and 4000 nm s⁻¹. A full data set (45–275 unfolding events) was obtained for each extension rate in triplicate.

Analysis of mechanical unfolding data

The data were filtered using previously described criteria (26). The contour length was estimated by multiplying the number of amino acids within the fold (60) by the distance between two adjacent C_α atoms in a fully extended state (0.34–0.37 nm (17,27)), and subtracting the initial separation between the boundary amino acids (V4 and A63, 2.8 nm).

The instantaneous loading rate for each unfolding event was calculated by fitting a wormlike chain (WLC) model (28),

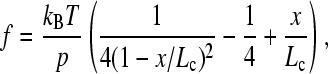(1)

to the rising edge of each sawtooth in a force-extension profile that had not been corrected to account for the movement of the tip. The measured force at unfolding was used to calculate the distance at which unfolding occurred (taken from the fit). Fit values for p, L_c, and x were inserted into a differentiation of the WLC equation

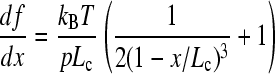(2)

and converted to loading rate by multiplication of the retraction speed at which the data was taken.

Data fitting: analytical approach

In analyzing the data, chemical kinetic theory was used to obtain the rate constant for unfolding (29,30). It is assumed that the thermal relaxation rate constant is faster than that for unfolding and the barrier separating the folded and unfolded states is sharp, so that the force dependence of the preexponential term can be neglected.

The applied force lowers the barrier in a linear manner; the energy required being fx_u at force f where x_u is a measure of the extent of the unfolding potential in the direction of pulling from its minimum to the barrier. The resulting expression for the rate constant at force f is

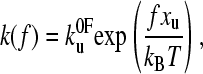(3)

where 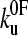is the thermal unfolding rate constant and f is the applied force at time t after starting the experiment. However, the rate constant is not measured directly but inferred from the distribution of unfolding forces. S(t) is the survival probability of one domain remaining folded at time t after starting to pull at time zero. If there are n identical domains then the probability is the product S₁(t), S₂(t)….S_n(t) and, if they are all equal to one another, the probability of all remaining folded becomes S(t)ⁿ. Experimentally the first one to unfold is measured; hence, if S(t)ⁿ is the chance that they all remain folded up to time t, then 1 − S(t)ⁿ is the chance that one has unfolded up to time t. S(t) is a cumulative distribution function and represents the chance of remaining folded from time t to infinity.

The chance that a domain will unfold between time t and t + dt, given that it has not failed up to time t, is the probability density function

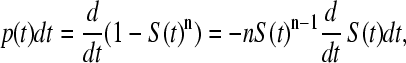(4)

and the most likely breakage is at the peak of this distribution. As the distribution is near to being symmetrical, the peak is close to the mean value.

S(t) is defined in terms of the rate constant k(t), and assuming that the breaking dominates refolding, then

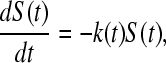(5)

and, by integrating, the equivalent equation for the probability is obtained:

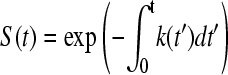(6)

It is convenient to change from time to force using the relationship 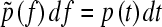as this is what is measured. As the protein has some compliance, the force generated by the protein, and therefore resisting extension, changes in some nonlinear way with the applied force. The interval dt is related to df by; 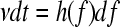, where h(f) is the compliance of the cantilever and protein, and v is the pulling speed, which is constant in the experiment. The probability of remaining folded at force f now becomes

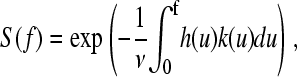(7)

and therefore the probability distribution for unfolding the n^th domain is

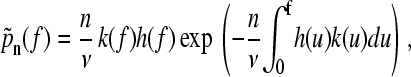(8)

from which the average unfolding force is 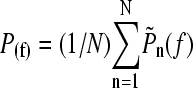. This result assumes that all unfolding events begin at zero force. This is a good approximation for mechanically stable proteins (low 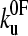), but leads to a minimum in the unfolding force for less mechanically stable (high 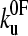) proteins. The maximum f* of the force distribution is calculated using

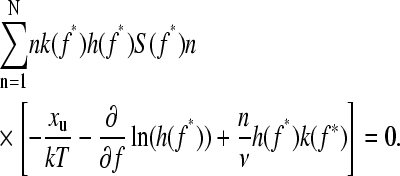(9)

This equation can only be solved numerically for f* at a given x_u and compliance. The number of domains folded at force f is n and, as the concatamer unfolds, n changes, as does h(f). The total compliance is given by

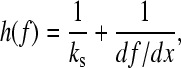(10)

where k_s is the force constant of the cantilever (typically 40 pN nm⁻¹) and df/dx is the “force constant” for the protein concatamer. To obtain this, a wormlike chain model of the force versus extension (Eq. 1) was used. The length L_c was calculated from the sequence and known extension of amino acids, and p is the persistence length taken to be 0.4 nm. Eq. 9 can be solved for f* to arbitrary precision, but solving to ±0.05 pN is sufficient for most practical purposes. In the calculation of the compliance, h (Eq. 10), we need to calculate df/dx. The extension at force f, x_f, is obtained by solving Eq. 1 for x. The solution to use is

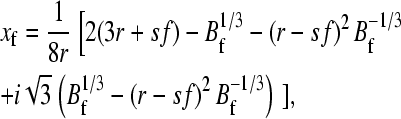where, for clarity, 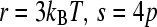, and

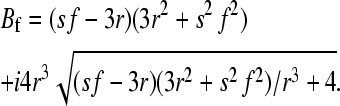The derivative dh/df is given by

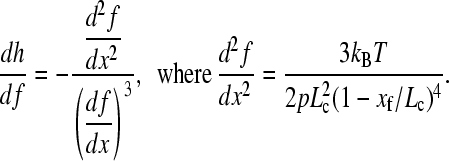The data were fitted by two methods. Using Eq. 8, all the force distributions were fitted simultaneously using a global nonlinear least-squares method to obtain x_u and 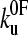. The best fit to the data was obtained by calculating the χ² statistic 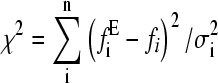, where 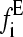is the experimental force f_i calculated at point i, and σ_i is the standard deviation of data points. This method was only partly satisfactory, as at very low pulling speeds an insufficient number of events on the low force side of the experimental distributions was present to allow satisfactory estimation of x_u and 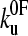. A second, more conventional method was tried in which the locus of points was determined around the minimum χ² where the value is larger by 1, by using Eq. 9 and varying x_u and 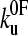over a wide range. This corresponds to a 68% confidence region. The function χ² (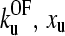) is approximately elliptical in the 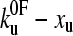plane, with the major axis having a negative gradient, and is shown in Fig. 3 b.

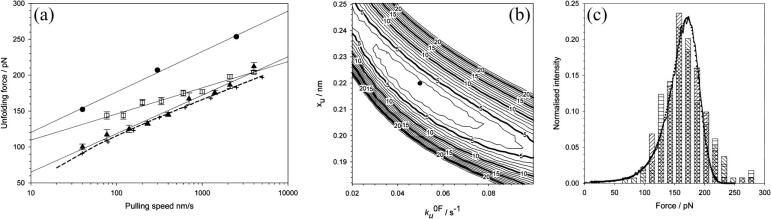
FIGURE 3.

(a) Speed dependence of the unfolding forces of (protein L)₅ (▴), (I27*)₅ (□), and (ubiquitin)₉ (•). Error bars, where shown, represent ±SE of triplicate data sets. Solid lines through each data set are a best fit to guide the eye. Data for I27 and ubiquitin taken from Brockwell et al. (23) and Carrion-Vazquez et al. (3), respectively. Fitting the data for protein L to an analytical solution (dashed line, see Materials and Methods) estimates that the height and the position of the unfolding barrier relative to the native state is smaller and shorter (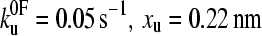) than that obtained for (I27*)₅ ( 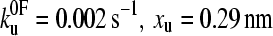(23)). Monte Carlo simulations, using the best fit parameters for protein L obtained above, give identical modal values (cross-hairs) to those predicted by the analytical model. (b) Error analysis of parameter pairs reveals degeneracy in the fit of 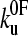and x_u to the observed experimental data for (protein L)₅. Contour lines link parameter pairs calculated to have equal χ² error. (c) The three experimental force frequency distributions at 1400 nm s⁻¹ are consistent with those predicted by the analytical model (dotted lines) and Monte Carlo simulation (solid black line) using the parameter pair marked by a solid circle in b.

Data fitting: Monte Carlo approach

Monte Carlo simulations were carried out using a two-state model for the unfolding rate constant in the presence of an applied force defined by Eq. 3. 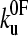(the unfolding rate constant in the absence of a force) and x_u (the distance to the transition state, assumed to be parallel to the stretch axis) were set from fitting the analytical model described above to the experimental data. Initially, all domains of the homopolymer were folded (N_f = 5) and placed in series with a cantilever of known spring constant. The cantilever was retracted at a constant rate and the force of the polymer calculated at each time interval from the WLC model (δ_t = 10⁻⁵ s, T = 297 K, p = 0.4 nm, L_f = 3.7 nm, L_u = 22.25 nm, L_linkers = 14.0 nm, k_s = 40 pN nm⁻¹). At each time step the probability of unfolding was calculated, 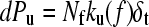, and compared with that of a random number (range 0–1). The time step δ_t was chosen so that dP_u ≪ 1. If unfolding occurred, the contour length of the homopolymer was increased by L_u − L_f, and the number of folded domains decreased by 1. The probability of refolding was assumed to be zero. This was continued until all domains unfolded and repeated 10,000 times for speeds 10–10,000 nm s⁻¹. Histograms of the unfolding force peaks were calculated (2-pN bins) from which the modal and average forces were found for a given rate.

Molecular dynamics simulations

Molecular dynamics simulations were performed using an all-atom model of the protein and an implicit model for the solvent (EEF1) (31). Implicit solvent models are sufficiently accurate and avoid artifacts due to the relaxation of the explicit solvent which might be slow relative to the fast conformational changes induced by the external force (32); moreover, the EEF1 implicit solvent is computationally efficient and allowed us to simulate cumulatively ∼1 μs. We used two alternative methods to force-unfold the protein and explored a broad range of unfolding timescales or forces. To gather sufficient statistics, we performed several independent simulations (at least 10) in each case. Starting configurations were generated by simulating, in native conditions, the structure of protein L (21) (PDB accession code 1HZ6).

Constant-velocity molecular dynamics (CVMD), also called steered molecular dynamics, is a nonequilibrium approach where, as in an atomic force microscopy (AFM) experiment, two atoms are pulled apart through a harmonic spring that moves at constant velocity. The force constant of the spring was set to 100 pN Å⁻¹ and constant velocities in the range 10⁶–10¹⁰ nm s⁻¹ were employed. Unfolding forces, as in the experiment, correspond to the maximum force in the force-extension profile.

Constant-force molecular dynamics (CFMD) are performed by adding an energy -fR_NC to the total energy of the system, where f is the applied force and R_NC is the separation between the N- and C-termini. Molecular dynamics simulations are then run from an initial (equilibrated) configuration in the presence of this force f. If the magnitude of the force is sufficiently large, the relaxation from a native initial conformation to an extended denatured state is observed. Constant forces in the range 300–700 pN were used. At 300 pN, no unfolding events were observed on a timescale of 100 ns, whereas at 400 pN all of the five simulations performed led to unfolding within 60 ns. Unfolding times (or inverse rates) were estimated by running a number of independent simulations for a maximum time of 100 ns. The average time to unfolding (τ) was estimated as described in Zagrovic and Pande (33).

All simulations where performed at 300 K with Langevin dynamics in low solvent viscosity conditions, imposing a holonomic constraint of the bonds involving hydrogen atoms and using a timestep of 2 fs.

Difference distance map

Distance maps were calculated using Perl. A distance matrix for a structure (1.6 Å total distance) before and after the force maximum was generated by calculating the nearest through-space distance between the side chain of each amino acid and every other residue in the protein. The difference distance map was then calculated by subtracting the later distance matrix from the earlier matrix.

RESULTS

Selection of a model protein

To investigate the determinants of mechanical resistance in proteins, we scanned the literature with the view of finding a domain predicted, de novo, to be mechanically stable. Such a domain had to fulfil a number of criteria: 1), it should have parallel and directly hydrogen-bonded terminal β-strands; 2), it must have a known high-resolution, three-dimensional structure; 3), it must be small and possess a simple topology; 4), it must not have an immunoglobulin-like or β-sandwich fold (using the SCOP classification (34)); 5), the thermodynamic stability of the protein must be sufficient to withstand concatenation; 6), it must not have been studied hitherto in mechanical terms; and 7), it must have no known mechanical function. Several protein domains meet these criteria, of which the smallest and simplest is the B1 domain of Protein L (herein referred to as protein L).

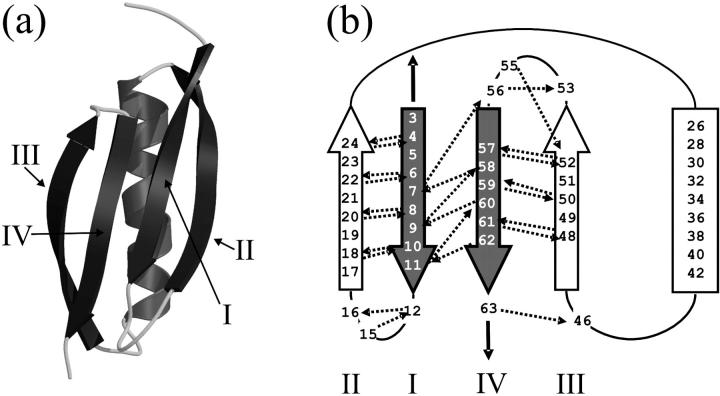
Protein L is naturally expressed in P. magnus as one of five homologous tandem domains that occur in the cell walls of 10% of isolates of this species (35). protein L is 62 amino acids in length and comprises a four-stranded β-sheet packed against a single α-helix (Fig. 1). The topology of this domain is such that the terminal β-strands (I and IV) are parallel with respect to each other and, importantly, form a hydrogen-bonded pair in the center of the four-stranded β-sheet. Mechanical deformation of this protein by extension of its N- and C-termini, therefore, should exert a shearing force on these strands, which, similarly to I27 (23,36,37) and other proteins from the Ig-like superfamily (13,18), is predicted to result in significant mechanical resistance. However, by contrast with Ig and Ig-like proteins, which resist extension parallel to their long axes as part of their function, protein L has no known mechanical function in vivo; the presence of tandem arrays of such proteins in the bacterial cell walls of pathogenic bacteria is thought to allow multisite binding (38) to a wide range of mammalian immunoglobulins (39) in a nonantigenic manner (35), facilitating wound colonization and evasion of the host's immune system.

FIGURE 1.

Three-dimensional structure and topology of protein L. (a) The structure of protein L showing the central α-helix packed against a four stranded β-sheet. The figure was generated using PDB file 1HZ6 (21), MolScript (65), and Raster3D (66). (b) Topology diagram of protein L. β-strands are shown as arrows and the helix as a rectangle. When extended in the geometry shown (black solid arrows), the parallel terminal β-strands (shaded arrows) are subjected to a shear force. Interstrand hydrogen bonds calculated to be ≤−0.5 kcal mol⁻¹ using DSSP (67) are shown as dashed arrows and point toward the acceptor. Strands are labeled I–IV in each representation.

protein L shows significant resistance to mechanical extension

To determine the mechanical properties of protein L, a polyprotein, (protein L)₅, was constructed by concatenation of the gene encoding the protein (see Materials and Methods). Such a procedure obviates problems associated with assigning each unfolding event to a specific domain and provides a highly characteristic “sawtooth” force-extension profile for mechanically resistant domains, from which the mechanical unfolding properties (unfolding force and distance) can be accurately determined (26). Each copy of protein L in the pentameric construct was separated by an 8- to 9-amino-acid linker containing one N-terminal and two C-terminal glycine residues to ensure that domain-domain interactions and steric effects were negligible.

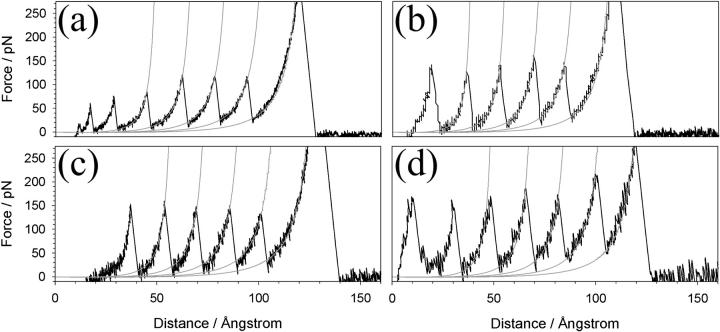
Sample force-extension unfolding profiles of (protein L)₅ are shown in Fig. 2. The data immediately show that this small and simple protein displays significant resistance to mechanical unfolding at all extension rates tested (average unfolding forces (±SE) 91 ± 3 pN and 205± 3 pN at 40 and 4000 nm s⁻¹, respectively). The distance between each unfolding event (interpeak distance) was extension rate-dependent, varying from 15.2 ± 0.3 to 16.9 ± 0.3 nm at extension rates of 40 and 2100 nm s⁻¹, respectively. This variation can be attributed to the dependence of the observed unfolding forces on the pulling speed: at lower pulling speeds the protein has longer to cross the barrier to unfolding than at higher speeds and so crosses a larger effective barrier at a smaller extension. Fitting the force-extension profile leading up to each unfolding event to a WLC model of polymer extension (28) allows the unfolding distance for each event at infinite force to be estimated. For protein L, this distance was found to be 18.8 ± 0.1 nm using a persistence length (p) of 0.4 nm. This is within the range of values of the calculated unfolding distance if each protein L domain fully unfolds at each unfolding event (17.6–19.4 nm, see Materials and Methods). The WLC model fits the rising portion of each unfolding event extremely well, suggesting that protein L unfolds in a two-state manner without the population of unfolding intermediates such as those reported for Ig domains from titin (12,40) and filamin (18), as well as for ¹⁰FNIII (41), GFP (4), and recently observed in constant force experiments on ubiquitin (42). Chemical denaturation methods (43,44) also suggest that monomeric protein L shows two-state folding/unfolding behavior under solution conditions very similar to those reported here. However, the intrinsic unfolding rate constant and unfolding pathways for mechanical and chemical unfolding are very different (see below).

FIGURE 2.

Force-extension profiles of (protein L)₅. Force-extension profiles shown were recorded at tip retraction rates of (a) 77, (b) 230, (c) 700, and (d) 2100 nm s⁻¹. The second to fifth peaks for each unfolding series, together with the final extension of the fully unfolded polymer, are fitted with a wormlike chain model (28) for polymer elasticity (shaded line) with p = 0.4 nm.

The barrier to protein L unfolding resists mechanical perturbation

The effect of force upon the strength of protein-protein and protein-ligand interactions has been studied extensively by both theoretical (29,45) and experimental approaches (46-48). Application of a force F applied at an angle θ tilts the energy landscape by -Fxcosθ, where the distance x is the molecular coordinate. By performing force spectroscopy experiments at different pulling speeds, basic features of the underlying energy landscape, including the depth and shape of the native well and the presence of other “hidden” barriers in the landscape can be inferred (48,49). To determine these mechanical unfolding parameters for (protein L)₅, the polyprotein was unfolded at a range of extension rates between 40 and 4000 nm s⁻¹. Each data set was obtained in triplicate and the unfolding forces and distances were measured as described previously (23,26). The number of events, hit-rate, mode unfolding force, unfolding distances, and estimated contour lengths for unfolding events in each protein L data set are shown in Table 2. Plotting the mode of the unfolding force for data pooled from the three replicate data sets acquired at each extension rate against the logarithm of extension rate (Fig. 3 a) resulted in a linear relationship (r² = 0.98). The speed dependence of the unfolding force of a previously studied pentamer of I27 ((I27*)₅, discussed by Brockwell et al. (23)) and data obtained from a nonameric construct of ubiquitin also linked between its N- and C-termini (3), are shown for comparison. Although all three proteins display significant mechanical resistance, protein L is the most mechanically labile. At 700 nm s⁻¹ protein L, I27, and ubiquitin unfold with forces of 152, 177, and 224 pN, respectively (calculated from the best-fit lines to the speed dependence of the unfolding force shown in Fig. 3 a). Interestingly, simulations comparing the mechanical resistances of NC-linked ubiquitin and protein G (a protein with an almost identical structure but only 16% sequence identity to protein L (38)) predicted both the rank order and magnitude of difference in the mechanical resistance of these proteins (50). However, direct comparison of the measured unfolding forces observed for different proteins are complicated by the effects of domain number (there are 5, 5, and 9 domains in the polymers of protein L, I27, and ubiquitin, respectively) and of construct compliance (24,51), which affects the rate at which force is loaded onto each domain (the loading rate). The compliance of each system varies since the chain length of each unfolded domain (64, 89, and 76 amino acids for protein L, I27, and ubiquitin, respectively), the linker length (8–9, 4–6, and 0 amino acids, respectively) and the cantilever stiffness (40–50 pN nm⁻¹) are different in each study. These effects are convoluted with the intrinsic unfolding rate constant and give rise to a characteristic unfolding force at a particular pulling speed. Hence, during the course of unfolding five covalently linked protein domains, the apparent mechanical strength of each domain varies in a complicated, but entirely predictable way (24).

TABLE 2.

Summary of unfolding statistics obtained for (protein L)₅ in phosphate-buffered saline at room temperature

Speed/nms−1	N*	Hit rate/%†	≥4 peaks/%‡	Mode Force/pN	Average (±SE)/pN	Mode interpeak distance (±SD)/nm	Average interpeak distance (±SE)/nm	Average ΔLc (±SE)/nm
40	116	18.6	78.6	86		15.6 (2.0)
40	55	5.7	60	92	91 (3)	14.7 (2.0)	15.2 (0.3)	N.D.
40	70	8.1	72	95		15.4 (1.7)
77	114	6.5	40	113		16.4 (1.5)
77	80	4.5	66.7	100	104 (4)	16.3 (1.4)	16.3 (0.1)	18.5 (0.1)
77	45	4	33.3	101		16.3 (1.6)
140	86	7.4	54.2	116		16.6 (1.8)
140	89	7.6	34.4	138	122 (8)	16.4 (1.3)	16.3 (0.3)	18.8 (0.2)
140	86	3.8	39.3	112		16 (1.9)
230	113	7.9	51.5	131		16.3 (3.2)
230	133	13.1	61.1	121	125 (3)	16.2 (1.7)	16.3 (0.2)	18.7 (0.1)
230	127	5.3	47.4	123		16.5 (1.5)
400	158	9.7	61.9	135		16.4 (1.5)
400	132	4.4	55.3	138	136 (1)	16.6 (1.6)	16.5 (0.1)	18.6 (0.1)
400	153	7.9	39.1	136		16.4 (1.6)
700	275	7.5	28.9	162		16.5 (1.6)
700	87	3.3	27.6	144	152 (5)	17.1 (1.4)	16.9 (0.2)	19.0 (0.1)
700	105	6.8	53.3	150		17.1 (1.6)
1400	131	8.1	60	167		16.6 (1.1)
1400	135	6.6	66.7	165	166 (1)	16.7 (1.7)	16.6 (0.1)	18.7 (0.1)
1400	113	5.1	47.1	167		16.6 (1.6)
2100	134	5.1	35.7	179		16.4 (1.4)
2100	107	3.4	48.3	175	179 (3)	17.3 (1.7)	16.9 (0.3)	19.0 (0.1)
2100	145	5.3	52.5	184		16.9 (1.4)
4000	104	9.6	31.4	208		16.9 (1.3)
4000	140	3.3	79.4	207	205 (3)	17.2 (2.1)	16.8 (0.2)	N.D.
4000	95	3	32.2	199		16.4 (1.1)

^*Number of unfolding events in data set.

^†Hit rate defined as percentage of the total number of force-extension profiles that remain after filtering data.

^‡Percentage of force-extension profiles after data filtering that contain four or more single protein L domain-unfolding events.

To estimate the parameters that characterize the basic features of the underlying unfolding landscape (the intrinsic unfolding rate constant at zero applied force 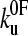and the distance to the unfolding transition state x_u), it is necessary to fit the speed dependence of the observed unfolding force to a model of the process (see Materials and Methods). This model contains the number of domains (folded or unfolded), the cantilever stiffness, and the length of linker regions, thus taking the effects of compliance and domain number on the loading rate into account. The fit of the analytical solution to the speed dependence of the unfolding forces for (protein L)₅ is shown in Fig. 3 a. Fitting the dependence of unfolding force on the logarithm of the extension rate in this manner results in large errors on 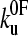and x_u (26,42,52), since many pairs of compensating values of 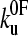and x_u fit the data equally well (as assessed by error analysis, see Fig. 3 b and Materials and Methods). Using this approach we estimate 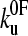and x_u to be 0.05 ± 0.03 s⁻¹ and 0.22 ± 0.02 nm, respectively. As a test of the analytical solution, these parameters were then used in a Monte Carlo simulation to calculate the expected dependence of the unfolding force on the logarithm of the extension rate. The resulting dependence is identical to that obtained both experimentally and fitted using the analytical model (Fig. 3 a). The shape of unfolding force-frequency histograms is also affected by the values of 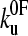and x_u (53). Comparison of the experimentally derived distributions with those predicted using either the analytical solution or the Monte Carlo method shows that the experimental force distributions are consistent with a two-state transition with 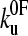of 0.05 s⁻¹ and x_u of 0.22 nm, respectively (Fig. 3 c). It has been noted previously (8,23) that proteins may traverse different energy barriers when unfolded by chemical and mechanical means. Such a comparison for protein L is complicated by deviations from linearity of the free-energy dependence on the denaturant concentration (44). Interestingly, the intrinsic unfolding rate constant at zero force ( 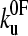= 0.05 s⁻¹) is faster than estimates for the intrinsic unfolding rate constant at zero denaturant concentration, which vary from 2 × 10⁻² to ∼4 × 10⁻⁴ s⁻¹ when estimated by different methods (43,44). This result is surprising as it suggests that under zero force the protein unfolds over a barrier that is higher in free energy than the mechanical unfolding barrier extrapolated to zero force. A similar observation has also been reported for the mechanical unfolding rate of ubiquitin measured by a force-clamp technique (42).

The loading rate dependence of the unfolding force reveals compliance effects

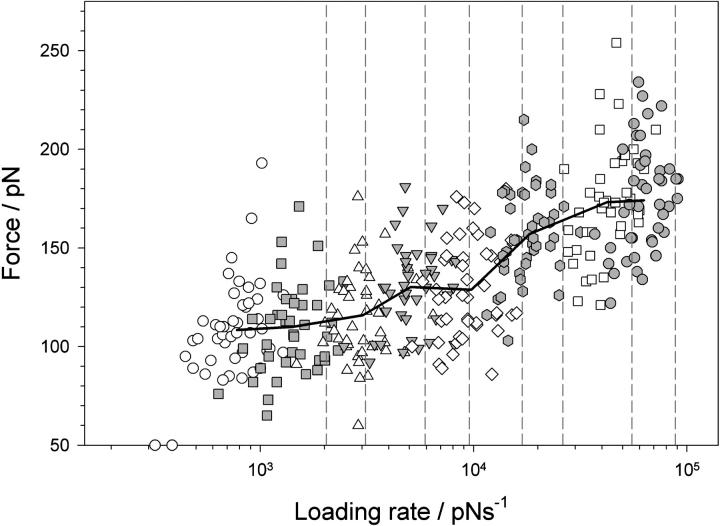
Mechanical unfolding experiments can be used to determine the intrinsic unfolding rate constant of a protein by a number of approaches, including modeling the linear relationship between the mode unfolding force versus the logarithm of the extension rate, or by fitting unfolding probability histograms in constant-force experiments (42,54). The latter has the advantage that the compliance effects outlined above do not complicate the analysis. The complex changes in polymer compliance as a function of the unfolding event can be demonstrated in constant-pulling speed experiments by measuring the instantaneous loading-rate dependence of the unfolding force. This can be determined by calculating the gradient of the rising edge of each force-extension sawtooth at the point of rupture and is distinct from the frequently used apparent loading rate, which is the product of extension rate and cantilever spring constant. To elucidate the relationship between unfolding force and instantaneous loading rate, nine force-extension profiles (∼45 unfolding events) at each extension rate were analyzed. The resulting loading rate dependence of the unfolding force is shown in Fig. 4. The difference in apparent and instantaneous loading rate can be seen by comparing the measured loading rates (symbols) with the apparent values (dashed lines). The differences in these parameters arise because each domain is not being extended directly from its mechanically resistant clamp through a rigid rod, but via compliant linkers consisting of folded proteins, unstructured polypeptide chains within and between each domain, and by the AFM cantilever. Each component has a characteristic elasticity that results in force being loaded onto the system at a significantly lower rate than that directly applied. The data also show that even though each domain is subjected to the same macroscopic extension rate, domains are microscopically extended over a wide range of loading rates since the compliance of the concatamer changes as each domain unfolds.

FIGURE 4.

Loading rate dependence of the unfolding force of (protein L)₅. The force at which a domain unfolds is plotted against the instantaneous loading rate at the unfolding point for each domain. Symbols show that the instantaneous loading rate differs significantly for domains extended at the same extension rate (open circles, 40 nm s⁻¹; shaded squares, 77 nm s⁻¹; open triangles, 140 nm s⁻¹; shaded upside-down triangles, 230 nm s⁻¹; open diamonds, 400 nm s⁻¹; shaded hexagons, 700 nm s⁻¹; open squares, 1400 nm s⁻¹; and shaded circles, 2100 nm s⁻¹). Solid black line joins points averaged in force and loading rate for each pulling speed. The apparent loading rate (dashed lines), calculated by multiplying the cantilever spring constant by the extension rate (40, 77, 140, 230, 400, 700, 1400, and 2100 nm s⁻¹) and measured loading rate for each retraction speed differ significantly since the protein polymer is more compliant than the cantilever.

Molecular dynamics simulations reveal a simple unfolding mechanism for protein L

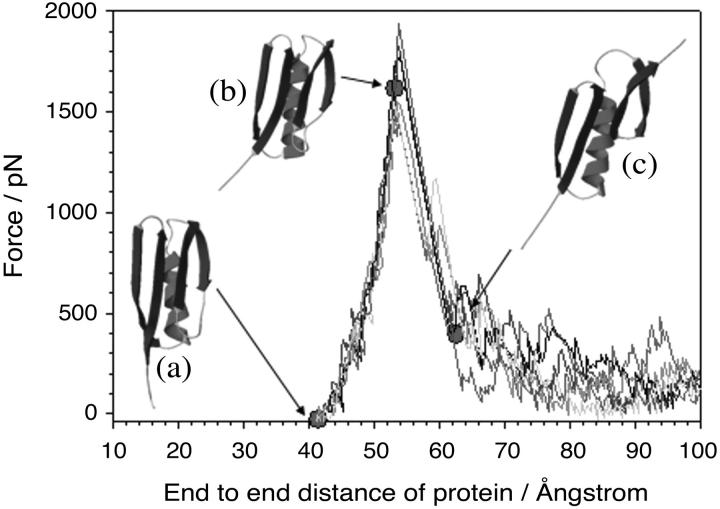
To gain insight into the structural origin of the mechanical resistance of protein L in atomistic detail, and specifically to test the hypothesis that the mechanical resistance of this domain arises from the hydrogen-bond clamp between the parallel N- and C-terminal β-strands, both constant-velocity (55) and constant-force (32) molecular dynamics simulations of the unfolding process were performed. Despite the limitations of such simulations, most notably the large difference in extension speeds between experiment (∼10¹–10⁴ nm s⁻¹) and simulation (10⁶–10¹¹ nm s⁻¹), the parity between the mechanism of mechanical unfolding determined by experiment and simulation has been demonstrated, at least for I27 (56). Unfolding trajectories of protein L using constant-velocity and constant-force simulations are shown in Figs. 5 and 6. Under constant-velocity extension (CVMD simulations) the force-extension profile of protein L is highly reproducible when several independent unfolding simulations are performed. All simulations show a clearly defined unfolding event in which force increases rapidly with a relatively small gain in extension (Fig. 5). Examination of the structures along the reaction coordinate suggests that protein L exhibits a brittle mechanical character. Thus, before the major unfolding event, the only structural change observed in the protein involves the reorientation of the N-terminal β-strand to align with the applied extension (compare structures a and b in Fig. 5). Rearrangement of the main-chain backbone in this manner results in the disruption of contacts between the N-terminal seven residues of β-strand I and the hydrophobic core. However, this rearrangement produces only a very small increase in length and so force is rapidly loaded onto the remainder of the protein. Unfolding occurs after an extension of 11 Å (or at an end-to-end length of 54 Å) as a single step and, as predicted, involves the rupture of contacts between the N- and C-terminal β-strands (structure c in Fig. 5). The position and width of the high-force portion of the trajectory and the reproducibility of the force-extension profile both at the same velocity (Fig. 5) and over a wide range of pulling speeds (10⁸–10¹¹ nm s⁻¹, data not shown) suggest that protein L unfolds via an unusually well-defined transition state that is represented by a narrow structural ensemble.

FIGURE 5.

Constant velocity molecular dynamics simulations of protein L unfolding reveal an unusually steep and narrow response to the extension of its termini. The production of very similar force-extension profiles at the same extension rate (shaded lines) suggests that protein L unfolds via a narrow bottleneck in the energy landscape. (Inset) Comparison of the initial structure (a) and structures before (b) and after (c) the force maximum (filled circles) shows that unfolding occurs when the C-terminal β-hairpin is pulled away from the rest of the structure. In this figure, simulations were carried out at 4 × 10⁹ nm s⁻¹. For clarity, every 40th data point has been plotted.

FIGURE 6.

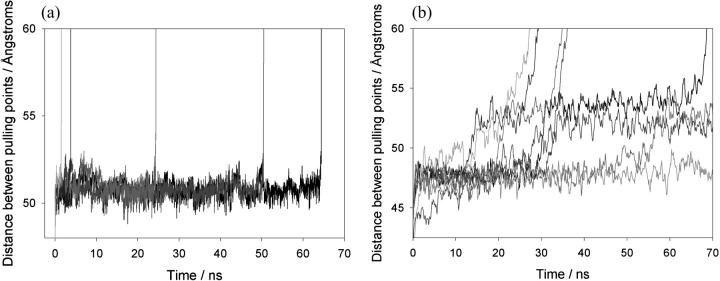
Constant force molecular dynamics simulations of protein L and I27. (a) Replicate simulations of extension of protein L at a constant force of 400 pN are shown and demonstrate that a metastable state very similar to the native state is populated before unfolding occurs in a two-state process. For clarity, every 500th data point is plotted. (b) Simulations of I27 unfolding at 400 pN show that this protein populates a metastable state for shorter periods and unfolds in a multistep manner.

The structural properties of the unfolding transition state can be shown more clearly by examining the unfolding behavior of protein L when subjected to molecular dynamics simulations using a constant applied force (CFMD) (Fig. 6 a). At a constant applied force of 400 pN, protein L initially extends to a metastable state with an end-to-end distance of ∼53 Å which is consistent with the high-force-resistant species observed at 54 Å in the CVMD simulations due to the alignment of β-strand I with the applied force vector. This species remains folded over nanosecond timescales (τ = 29 ± 6 ns, five simulations where τ is the average lifetime of the folded state under the applied force) before unfolding rapidly without the population of intermediates. Comparison of the unfolding trajectories of protein L with those of I27 obtained under identical conditions (Fig. 6 b) highlights the simplicity of the unfolding mechanism of protein L since, by contrast, I27 unfolds through a relatively broad transition-state ensemble and, in addition, populates unfolding intermediates in accord with previous results (37,40).

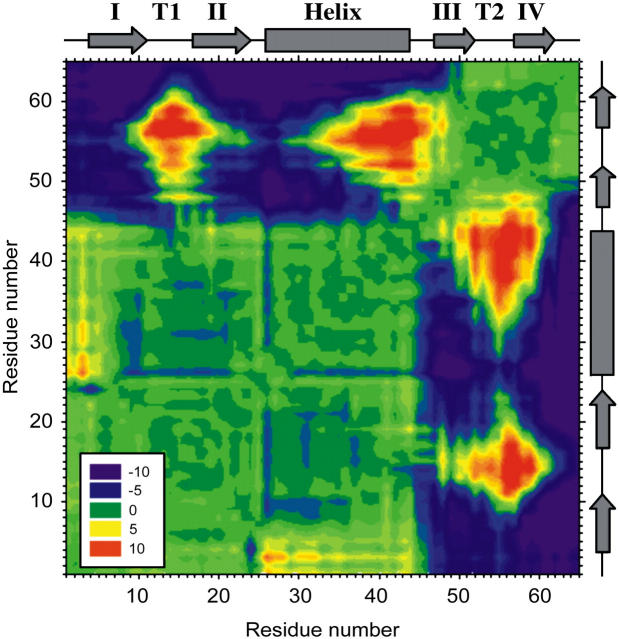
To identify and highlight the key contacts that are broken when the protein traverses the unfolding transition-state barrier, a distance difference map was constructed (Fig. 7 and Materials and Methods). The resulting diagram is striking, showing that protein L unfolds via two distinct structural units, one comprising β-strand I, turn 1, β-strand II, and the entire helix, and the second encompassing the second β-hairpin (β-strand III, turn 2, and β-strand IV). Although interresidue distances remain constant through the unfolding transition within these units (difference distance ≤5 Å, Fig. 7, green contours), the interresidue distance between residues spanning these structural units increases (5–10 Å, blue contours). The separation of these structural units, which occurs along an interface between the N- and C-terminal parallel β-strands, coincides with the reduction in force as the protein unfolds. The presence of a large energy barrier preventing the separation of these structural units is consistent with the hypothesis that shearing terminal parallel β-strands gives rise to mechanical strength. The postulated mechanical transition state described above is different from that elucidated for the denaturant-induced unfolding pathway, in which the transition state was found to be highly polarized with only the first β-hairpin containing nativelike structure, whereas the helix and second β-hairpin were fully unfolded (57).

FIGURE 7.

Contour plot showing the difference in distance between every pair of amino acids in protein L at a total extension (protein and cantilever) of 1.6 Å before and 1.6 Å after the mechanical unfolding event. Residue numbers (left-hand side and bottom) are shown opposite cartoons (right-hand side and top) depicting the type of secondary-structure element that each residue occupies in the native state (rectangle, α-helix; arrow, β-strand). Strands are labeled I–IV and turn 1 and turn 2 are shown as T1 and T2, respectively. Pairs of residues that move farther apart from each other during unfolding are colored purple to green (−10 to 0 Å); those that become closer to one another are shown green to red (0 to 10 Å).

DISCUSSION

Topology as a determinant of mechanical resistance

Protein L was selected to test the hypothesis that the arrangement of β-strands relative to the pulling direction correlates with mechanical resistance, as this protein has directly hydrogen-bonded, parallel terminal β-strands that are predicted to result in mechanical strength. The protein is also small and has a simple topology, and there is a wealth of knowledge about the mechanism of folding and unfolding of the protein after chemical denaturation (43,44,57). The high mechanical resistance of protein L observed at all extension rates tested experimentally (40–4000 nm s⁻¹) and at those simulated by CVMD (10⁶–10¹¹ nm s⁻¹) provides strong evidence that the topology of a protein (15,50,58–60), not its evolved function, is an important determinant of protein mechanical strength. This is in accord with previous experiments on non-force-bearing or non-force-responsive proteins (3,8,15).

The mechanical unfolding of protein L probes a single barrier

The pulling speed dependence of the unfolding force of protein L shows a constant gradient throughout the dynamic range of pulling speeds measured here. This behavior, seen for all proteins studied to date, contrasts markedly with that observed for the unbinding forces of protein-ligand interactions, which show that a series of previously undetectable sharp barriers along the reaction coordinate can become rate-limiting at different loading rates (45,46,48,61). Comparison of these data suggests, therefore, that the energy landscape for protein unfolding may be less rugged than that for protein-ligand interactions. In this situation, different barriers would become rate-limiting at different loading rates but are of such a similar height and position on the reaction coordinate that a switch in the transition state may be difficult to verify experimentally. More simply, however, mechanically unfolding proteins via their termini may dramatically reduce the possible choice of routes through which a protein can unfold. For mechanically resistant proteins this may result in a large barrier to unfolding that remains rate limiting over all of the pulling speeds currently accessible to the AFM. Such a conclusion is in accord with recent work on I27 (49), which suggests that a previously hidden outer barrier may become rate-limiting at pulling speeds slower than the dynamic range of current AFM instruments. The constant gradient of the speed-dependence plot and the simple two-state unfolding behavior of protein L presented here, however, imply that a single strong transition-state barrier may predominate for protein L over a very wide range of extension rates.

Modeling constant-velocity unfolding experiments accounts for the history effect

Protein mechanical unfolding experiments are usually, but not always (16), performed on polyproteins. Consequently, the resulting force-extension profiles are inherently more complex than those for protein-ligand unbinding events, as the mechanical properties of the polypeptide chain and unfolding probability of each domain change throughout the experiment. This history dependence of the unfolding force has recently been used to question the validity of using data derived from constant-velocity mechanical unfolding experiments to estimate the parameters 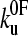and x_u (42). However, the statistics of a series of unfolding forces (i.e., the probability distribution) at different pulling speeds can be predicted, provided that the model used contains parameters that treat these history effects. Here we have used both analytical and Monte Carlo solutions to the two-state model to examine the unfolding of (protein L)₅ and demonstrate that the parameters 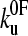and x_u determined by each approach are consistent with the experimental extension rate dependence of the unfolding force and the force frequency distributions.

Surprisingly, 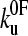was found to be significantly faster than even the upper estimate for the unfolding rate constant of monomeric protein L measured using chemical denaturation (43). At zero applied force or chemical denaturant, the protein is at equilibrium and the rate constant is determined by the height of the barrier encountered along each pathway, as may be represented by the Gibbs energy. Naively, one may expect the extrapolated rate constant for chemical unfolding to be faster than that for mechanical unfolding. Experimentally this is clearly not the case in protein L and ubiquitin (42). This effect may result from topography of the mechanical unfolding landscape, such that the mechanical unfolding rate constant is limited by an outer barrier in the energy landscape which is “hidden” at the loading rates used in this study (≥40 nm s⁻¹). Under zero applied force, this barrier, which is of higher energy than that of the chemical denaturant pathway, precludes unfolding via the mechanical pathway. At a certain pulling speed (<40 nm s⁻¹), the loading rate is such that this outer barrier, which is more strongly perturbed by force than the smaller, inner barrier, becomes substantially lowered in energy, such that mechanical unfolding occurs via the inner barrier, which is now rate-determining and of lower energy than the barrier to chemical denaturation. The extrapolation to zero force from high-pulling-rate experiments (>40 nm s⁻¹ for protein L) will then measure the protein unfolding over this barrier, and hence extrapolate to a rate constant larger than at zero force of denaturant. Alternatively, as pulling is a dynamic process, it is possible that the measured rate constant is not due to barrier height per se, but is limited by the dynamics of reaching a barrier. The protein produces friction on the reaction coordinate as it is pulled, because not only are residues moving one against another but also bonds are being stretched. These effects slow motion over the barrier and so the rate of approaching the barrier may become rate-limiting in the sense of Kramer's model of chemical kinetics in particular, or of diffusion-limited reactions in general. Additionally, one could have a transition state under applied force that can only be accessed by traversing a very narrow valley (in conformational space) of states that are rarely accessed under unforced unfolding conditions. The zero force limit of the subsequent forced unfolding rate 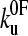could then be either higher or lower than in the unforced transition state, with the forced transition state stabilized against unforced unfolding because of the narrow and rarely accessed valley.

The role of long-range contacts in mechanical resistance

Despite the correlation between the mechanical strength of a protein and the presence of directly hydrogen-bonded terminal β-strands, it is evident that side-chain interactions also play an important role in determining a protein's mechanical character. For example, despite the presence of directly hydrogen-bonded terminal β-strands, proteins with similar topologies (Table 1) or those that differ by a single amino acid (16,56) can have very different mechanical properties. In this regard, it is interesting to compare the mechanical properties of protein L with those of ubiquitin, another model protein within the same fold family as protein L whose mechanical properties have also recently been characterized using both constant-speed (3,17) and constant-force (42) mechanical unfolding experiments. Despite both proteins being mechanically resistant, which is consistent with their similar topology, ubiquitin unfolds at a force ∼70 pN higher than that for protein L at all speeds measured, whereas x_u for both proteins is similar (0.22 for protein L (this work) and 0.23 (17) or 0.25 (3) nm for ubiquitin). Importantly, the difference in the mechanical properties of the two proteins cannot be simply attributed to the number of hydrogen bonds between the terminal strands of each protein, as ubiquitin possesses fewer hydrogen-bonded pairs in this region compared with protein L (five and six, respectively). This suggests that other features of the protein structure must be responsible for tailoring their mechanical properties.

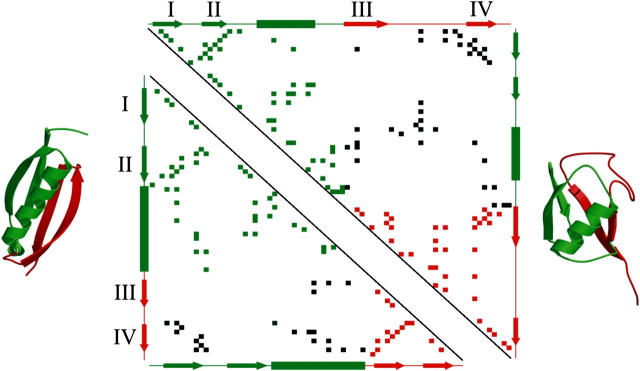
To obtain more insight into the possible role of side chains in the mechanical unfolding properties of protein L and ubiquitin, contact maps were constructed (Fig. 8) and the number and location of contacting residues in the native structure of the two proteins were compared. Residues in strands I and IV of both proteins make a similar number of contacts with the rest of the protein (65 and 59 contacts for protein L and ubiquitin, respectively), suggesting that the differences in mechanical resistance of these proteins are not related to the size of the hydrophobic core, but to contacts made between specific residues across the protein. Comparison of simulations of the unfolding processes of protein L and ubiquitin (42) suggests that these proteins unfold by a similar structural mechanism. The transition state to unfolding for both proteins involves the breaking of contacts between two well-defined structural units, one comprising β-strands I and II and the helix and the second involving the β-hairpin of strands III and IV. However, the number of long-range contacts that span the two unfolding units in protein L (22 contacts) is both significantly smaller and in fewer clusters than those for ubiquitin (38 contacts). A protein in which the side chains from each unit are enmeshed may have a higher mechanical resistance, as these residues must first be extracted, then pulled past other side chains to allow the protein to extend. Thus, although each protein has to be extended to a similar extent to reach the transition state to unfolding, in the case of ubiquitin a significantly greater force may be required to reach the transition point. Hence, protein mechanical stability does not only depend on the extension geometry relative to the topology, but also on the extent to which the domain is globally and cooperatively stabilized across the surfaces that are to be sheared. The interplay of sequence versus topological constraints in determining mechanical resistance is reminiscent of the effect that sequence plays in modulating the folding-rate constant in denaturant dilution experiments: the rate of folding in two-state proteins is largely determined by the contact order (20,62), but can be significantly altered by changing a single amino acid (63). Further experiments using protein L, its homologs, and other proteins with related folds, combined with site-directed mutagenesis studies, will now be needed to determine and quantify the balance of these effects in determining the mechanical stability of proteins. We have shown here that protein L is ideal for such a study, as the apparent simplicity of its unfolding trajectory provides an opportunity to elucidate the subtle complexities of unfolding proteins by force.

FIGURE 8.

Contact map of protein L (bottom left) and ubiquitin (top right). Side-chain contacts (nearest distance between atoms of two residues <5 Å, calculated by CSU software (68)) made by pairs of amino acids within structural unit 1 (β-hairpin 1 and the helix) or within structural unit 2 (β-hairpin 2) are shown by green and red squares, respectively. Contacts made between these structural units are shown in black. β-strands (labeled I to IV as in Fig. 1) and α-helices, predicted by DSSP (67), are shown as arrows and rectangles, respectively, alongside each contact map. The two structural units are colored green (unit 1) and red (unit 2) in each protein and are also shown superimposed onto the three-dimensional structure of protein L (left) and ubiquitin (right).