Magnetic Pulse Affects a Putative Magnetoreceptor Mechanism

Abstract

Clusters of superparamagnetic (SP) magnetite crystals have recently been identified in free nerve endings in the upper-beak skin of homing pigeons and are interpreted as being part of a putative magnetoreceptor system. Motivated by these findings, we developed a physical model that accurately predicts the dynamics of interacting SP clusters in a magnetic field. The main predictions are: 1), under a magnetic field, a group of SP clusters self-assembles into a chain-like structure that behaves like a compass needle under slowly rotating fields; 2), in a frequently changing field as encountered by a moving bird, a stacked chain is a structurally more stable configuration than a single chain; 3), chain-like structures of SP clusters disrupt under strong fields applied at oblique angles; and 4), reassemble on a timescale of hours to days (assuming a viscosity of the cell plasma η ∼ 1 P). Our results offer a novel mechanism for magnetic field perception and are in agreement with the response of birds observed after magnetic-pulse treatments, which have been conducted in the past to specifically test if ferrimagnetic material is involved in magnetoreception, but which have defied explanation so far. Our theoretical results are supported by experiments on a technical SP model system using a high-speed camera. We also offer new predictions that can be tested experimentally.

INTRODUCTION

To explain the biophysical basis of magnetic-field sensory perception, two different hypotheses have been offered, one invoking magnetically sensitive biochemical reactions (1,2), the other based on inclusions of biogenic magnetite (3,4). Being two competitive hypotheses based on different biophysical principles, neither is exclusive. As Block (5) points out, there may well be multiple solutions to a sensory problem, any one of which achieves the desired level of perfection. In that sense, it has been postulated from behavioral studies that both types of magnetoreceptor are realized in birds, albeit providing different magnetic information: a photoreceptor underlying magnetic compass orientation, and a magnetite-based magnetoreceptor for the navigational map system (6).

The magnetite hypothesis assumes that biogenic magnetite particles are connected to nervous structures. The elegance of this hypothesis lies in the simplicity of the postulated mechanism, which is analogous to a compass needle and already realized in nature in magnetotactic bacteria (7). Moreover, biogenic magnetite inclusions have been reported in a number of animal species (see Wiltschko and Wiltschko (6) for a reference). It is one thing to detect magnetite in animal tissue, and another to demonstrate its involvement in magnetoreception. One way of testing the magnetite hypothesis is to conduct behavioral experiments in animals using a brief but strong magnetic pulse (8). Because of its short duration (a few milliseconds), a magnetic-pulse treatment should, in principle, selectively affect ferrimagnetic material. Indeed, after treatment with a brief magnetic pulse of intensity 0.5 T, Australian silvereyes (Zosterops lateralis), deviated from their natural migratory direction either unimodally or bimodally by as much as 90°. A clear effect of the pulse was only observed for a few days after treatment, and the migrants returned to their normal migratory direction within one week (8–10). Similar results were obtained on different species of migratory birds (11–13). In homing pigeons an identical magnetic pulse induced deflections on the treated birds ranging from 1 to 60°. The direction and extent of the deflections depended in that case on the orientation of the treatment with respect to the head of the birds and a clear effect was only observed the first three days (14). Interestingly, in all cases only experienced birds were affected by the pulse, but not young, inexperienced birds, an observation that is in agreement with a magnetite-based system that provides positional information such as a navigational map (15).

The fact that migratory birds and homing pigeons display changes in their orientation behavior after a magnetic-pulse treatment may be taken as evidence of a magnetoreceptor system based on ferrimagnetic material. Traditionally, it has been postulated that magnetic particles similar to those found in magnetic bacteria, that is, magnetically blocked single-domain (SD) magnetite, may form the core of the animal magnetoreceptor (16). However, the observed behavioral responses after pulse treatments has defied explanation under this model (10). When interpreting results in physical terms, one needs to know how the magnetite particles are arranged in the tissue and the nature of the connection in the nervous system. A physical model can then be developed and predictions be made about the effects a magnetic pulse will have on the magnetic sense at the (sub)cellular level. It needs to be emphasized that the arrangement of the particles cannot be inferred from the behavioral response because behavior is a complex sum of neurophysiological processes, genetic disposition, individual experience, and motivation.

We therefore develop a physical model on the basis of detailed neurohistological findings: a structural candidate of a magnetoreceptor has recently been identified in somatosensory nerve terminals in the upper-beak skin of homing pigeons (17,18). The afferent dendritic terminals contain clusters of magnetite nanocrystals (grain size between 2 and 5 nm). The clusters are arranged in groups of 10–20 clusters in a chain-like configuration along the unmyelinated membrane of the terminal (18). The average size of the clusters is ∼1 μm (19). The close spacing between the clusters within a terminal implies that magnetic interactions between the clusters dominate the dynamics of the system and so magnetic interactions are likely to result in a mechanism sensitive enough to detect small changes in magnetic field intensity or direction (19).

Interestingly, the magnetite nanocrystals in the clusters have magnetic properties completely different to magnetically blocked (“stable”) SD particles of magnetite and appear to be superparamagnetic (SP) in character. These nanocrystals are, therefore, too small to serve as microscopic compass needles, and subject to constant buffeting by thermal fluctuations. This argument has been traditionally used against a magnetoreceptor involving SP particles. However, although the individual SP crystals cannot carry a stable magnetic remanence, a cluster of crystals does assume an induced magnetization in a magnetic field. Such a collective, statistical behavior is called superparamagnetism (20). Like a paramagnetic system, the SP collective loses its magnetization once the field is switched off. The prefix “super” refers to the fact that such a collective has a surprisingly large susceptibility; that is, even a magnetic field as weak as the geomagnetic field can induce a relatively large magnetization. That a magnetoreception mechanism based on SP magnetite is theoretically plausible has already been demonstrated (19,21,22). The model we present here focuses on the dynamics of a group of interacting SP clusters under a magnetic field. The model allows us to explain the observed effects in behavioral experiments and is supported by experiments on a SP model system using a high-speed camera.

THEORY

Our physical model is based on the well-understood physics of SP systems. In a uniform external magnetic field H₀, a cluster of SP particles is polarized and will have a macroscopic magnetic moment m. Assuming that the field inside a cluster is homogeneous, the free energy F of a group of N clusters is given by

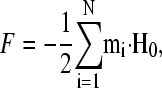(1)

where

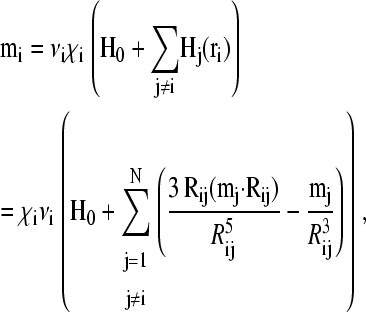(2)

is the magnetic moment of cluster i, ν_i denotes its volume, χ_i is its effective susceptibility, and H_j is the interaction field, that is, the magnetic field produced by cluster j situated at r_j acting on cluster i at r_i. R_ij is the distance vector joining the centers of cluster i and j. The effective susceptibility, χ_i depends on both the particle-size distribution and particle concentration in the cluster, and also includes corrections for both the demagnetizing field H_D = −N_D M and the Lorentz field H_L = 4 π M/3 (approximation for χ < 1), where M is the magnetization of the cluster and N_D its geometrical demagnetizing factor. For a spherical cluster, with N_D = 4 π/3, these corrections mutually annihilate each other and the effective susceptibility amounts to the microscopic susceptibility.

To calculate the free energy F for a particular configuration, m(r)_1…N from Eq. 1, a set of N linear equations Eq. 2 has to be solved first to find the magnetic moments m_1…N. Using an iterative approach, we substitute the zeroth-order expression 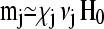for m_j on the right-hand side of Eq. 2 to obtain a first-order approximation, that is,

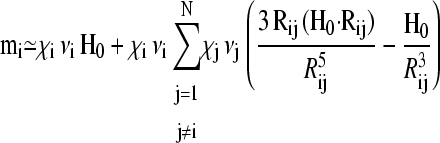(3)

Inserting Eq. 4 into Eq. 1 and omitting the constant term 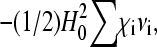we arrive at the following expression for the free energy F

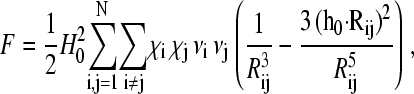(4)

with the unit vector h₀ = H₀/H₀. Now we are in a position to compute the trajectory of each SP cluster in a system of N clusters due to the magnetic interactions with the neighboring clusters. For our purpose, Eq. 4 can be further simplified: the SP clusters observed in the pigeon-beak skin were roughly similar in size (19) and so we concentrated on groups of similarly sized ferrofluid droplets in our model experiments (see below). Henceforth we consider a group of identical clusters (same radius R, volume ν = 4πR³/3, and microscopic susceptibility χ) constrained to move on a plane (imposed by experimental setup). Let (X_i, Y_i) be the Cartesian coordinates of the center of cluster i. Introducing the normalized coordinates x_i = X_i/R and y_i = Y_i/R and the dimensionless expression for the free energy 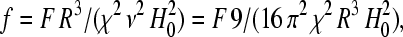Eq. 5 becomes

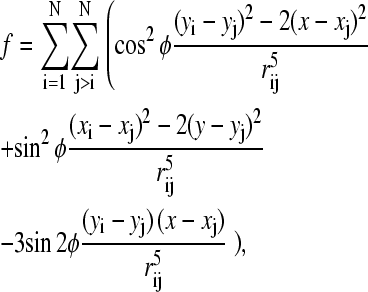(5)

where r_ij = R_ij/R. To prevent the clusters from overlapping each other (rigid-spheres approximation), we use the repulsive potential

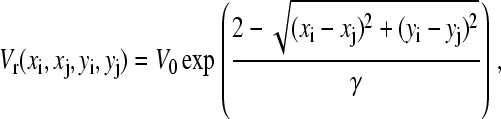(6)

where V₀ and 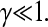To constrain the positions of the clusters within the dendrite, we include the potential

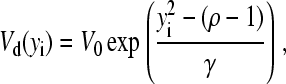(7)

where the axis of the dendrite defines the x-coordinate and ρ = R_d/R is the scaled radius of the dendrite.

To compute each trajectory r_1…N(t) in a system of N SP clusters interacting under a magnetic field, the following set of Stokes equations has to be solved:

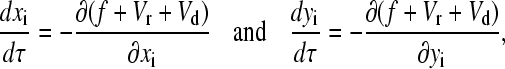(8)

where τ = t/t₀ denotes the dimensionless time, with

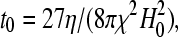(9)

where t₀ is the characteristic timescale, a measure of the time required to change the configuration of a group of SP clusters surrounded by a medium with a dynamic viscosity η, under a magnetic field H₀. The smaller the characteristic timescale, the faster the SP clusters in a group will be displaced from their positions by the magnetic interactions that arise among the clusters under a magnetic field. It is important to note that the characteristic time, t₀, does not depend on the size of the interacting SP clusters. We can therefore study the magnetic interactions between groups of relatively big SP clusters (such as the ferrofluid droplets of our model experiments) and later extrapolate the results to smaller SP clusters such as the ones found in the upper-beak skin of homing pigeons. Equations 5–8 enable us to trace the magnetostatically driven movements of every single SP cluster within a group of N clusters for a given configuration.

To illustrate the physical meaning of Eq. 5, we recast it in a more compact form,

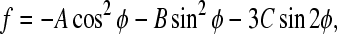(10)

where

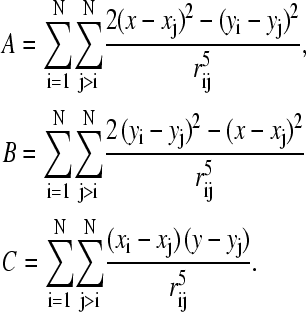(11)

The expression for the free energy (Eq. 10) is anisotropic with respect to the angle φ. If we choose the coordinate system in such a way that C = 0, the energy spectrum of the system shows a well-known uniaxial shape with a minimum value at φ = 0, i.e.,

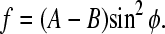(12)

This anisotropy produces a macroscopic torque

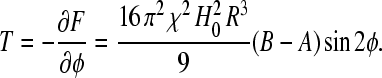(13)

A chain of clusters will therefore behave as an “axial” compass needle in a rotating magnetic field.

MODEL EXPERIMENTS WITH AN SP SYSTEM

To test our theoretical predictions, we conducted experiments on a model system. We used a magnetic fluid (ferrofluid EFH1 provided by FerroTec, Unterensingen, Germany), which is a colloidal suspension of magnetite nanoparticles with grain sizes between 5 and 10 nm. When brought into an aqueous environment, the suspension yields separate microdroplets between 10 and 50 μm in diameter. Microdroplets of ferrofluid can be considered technical analogs for the SP clusters found in the upper-beak skin of homing pigeons (21). Two different experiments were conducted:

1. We first studied the behavior of interacting ferrofluid microdroplets under weak magnetic fields (1–9 Oe). The magnetic field was applied in different directions for different arrangements of microdroplets, and the movement of the droplets was recorded with a video camera attached to the microscope. We then modeled the theoretical response of the initial configuration to a magnetic field using Eqs. 5–8.

2. We next studied the effect of a magnetic pulse. Ferrofluid microdroplets were placed under the microscope and a weak magnetic field was applied until chains and double chains of ∼10 droplets self-assembled. We chose this particular geometry because the SP clusters identified in the upper-beak skin of homing pigeons were found in chain-like arrangements of 10–20 clusters (18). A 0.5-T magnetic pulse was applied perpendicular to the long axis of the chains and the response of the system was recorded with a high-speed video camera. These results were later compared with the numerical results from our theoretical modeling, which also allowed us to estimate the time the system takes to recover its initial configuration.

RESULTS

Dynamics of SP clusters in a weak magnetic field

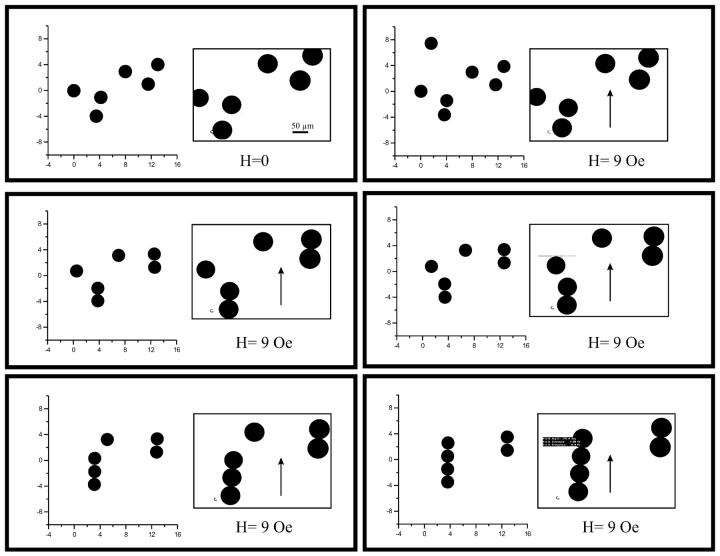
Fig. 1 shows the dynamics of ferrofluid droplets under a weak magnetic field (H₀ = 9 Oe) in comparison with the numerical simulation. It can be seen that our model realistically mimics the dynamics of a group of SP clusters. Our model also shows the strong tendency of SP clusters to self-organize into elongated macrostructures aligned with the magnetic field (i.e., single chains, double chains, etc.) as observed in the histological work (18). Wilhelm et al. (23) also reported the tendency of cellular endosomes containing an SP lumen to arrange into chaplets in a magnetic field. This is due to the dipole-dipole interactions that arise between neighboring clusters under the polarizing effect of an external magnetic field (19).

FIGURE 1.

Comparison between numerical simulations and experiments (insets) on magnetically interacting ferrofluid droplets, which self-assemble into a linear configuration under the influence of a magnetic field of 9 Oe (arrow). The scale bar represents 50 μm.

We therefore studied the dynamics of chain-like configurations of SP clusters in a magnetic field. According to our numerical simulations, if the chain is parallel to the field direction, it will hold together due to the dominating attractive forces; however, if the magnetic field is applied at oblique angles with respect to the chain axis, it will rotate into alignment with the axis of the field. Although this behavior, on a macroscopic scale, resembles that of a chain of magnetically stable SD particles as found in magnetotactic bacteria, the rotation of the chain is still performed by magnetostatically driven movement between adjacent clusters. The resulting torque (Eq. 13) is therefore referred to as pseudotorque. Interestingly, this pseudotorque only occurs if the angle between the long axis of the chain and the magnetic field direction does not exceed a critical value (45° for a single chain). Above this critical angle, repulsive interactions between adjacent clusters will arise and chain disruption occurs. This confirms earlier observations on ferrofluid microdroplets (19). The same response was observed in the case of an arrangement of SP clusters in which single chains are stacked above one another with an offset between layers. To illustrate this magnetic behavior we simulated the dynamics of chains of SP clusters in a rotating magnetic field (see online Supplementary Material; Double-ChainRotate.mov and Single-ChainRotate.mov). In such a scenario, the single chain proves mechanically less stable than a stacked arrangement of chains. We have also applied our numerical model to a situation in which chain-like structures of SP clusters are placed in a magnetic field that randomly changes its direction with respect to the chain axis. In that situation, a single chain of SP clusters is soon disrupted, whereas a stacked structure again shows a higher degree of stability in the same fluctuating magnetic field (see Supplementary Material; Double-ChainRandom.mov and Single-ChainRandom.mov). We also observed this behavior in the experiments on ferrofluid droplets (not shown).

From Eq. 9 we can also estimate the characteristic timescale for the magnetostatically driven motion of a chain of SP clusters under the Earth's magnetic field. For H₀ = 0.5 Oe, χ ∼ 0.1 (cgs), a value typical of ferrofluids based on magnetite, and η = 1 P the viscosity of the cellular cytoplasm, roughly 100 times that of water (24), the characteristic time is obtained as, t₀ ∼ 400 s. We note that the numerical value of χ is not certain as the magnetic susceptibility of the SP clusters in the pigeon has not yet been measured.

Dynamics of SP clusters in a strong pulsed field

When considering magnetite-based magnetoreception, a cellular structure analogous to a compass needle offers a simple yet effective transducer mechanism. The amount of torque in the case of a chain-like structure of SP clusters depends on the field direction and intensity (see Eq. 13), which are the magnetic field parameters used by birds for magnetic orientation and navigation (6).

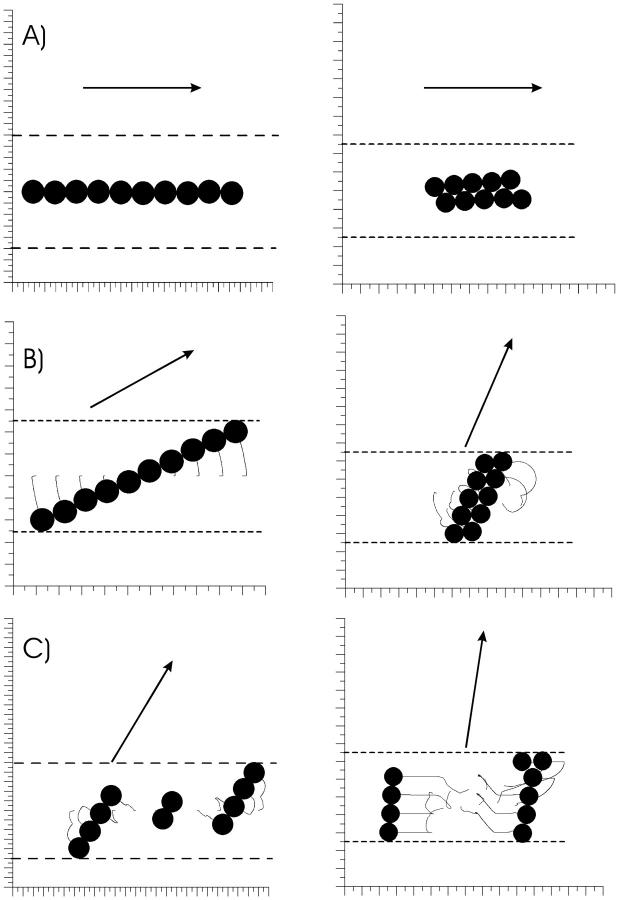
One way of testing whether the pseudotorque response underlies avian magnetoreception is by simulating the effect of a magnetic pulse on this putative magnetoreceptor mechanism and comparing our results with observed behavior of birds treated with a magnetic pulse. Fig. 2 A shows that a brief (1 ms) but strong pulse (0.5 T = 5000 Oe) applied exactly parallel to the chain's axis will cause no effect. When the pulse is applied at a small angle, the chain of droplets will behave as a mechanical unit and rotate into alignment with the field (Fig. 2 B). When applied at high oblique angles or perpendicular to the chain axis, the pulse will disrupt the chain into several subchains of varying lengths, which align into the axis of the pulse field (Fig. 2 C). Although the critical angle at which chain disruption occurs is φ ∼ 45° for the single chain, this value is φ ∼ 70° for the stacked chain. The value of the critical angle also varies with the number of clusters within the chains, with higher critical angles for smaller chains. It should be emphasized that the response of the chain of clusters depends on the axial direction, but not on the polarity of the pulsed field. As can be seen, according to our numerical model, a strong magnetic pulse will have the same effects on a chain-like arrangement of SP clusters as a weak constant field applied for a sufficiently long time.

FIGURE 2.

Numerical simulation of the effects of a brief magnetic pulse of strength 0.5 T applied for 2 ms to a single chain and a double chain of SP clusters. The trajectories of the clusters are represented by the gray wiggles. The dashed lines depict the membrane of the dendrite containing the clusters (ρ = 5). (A) A pulse applied parallel to the chain axis leaves the chain intact. (B) If applied at an oblique angle, the pulse torques the chain into alignment with the field. (C) This so-called pseudotorque response occurs only until a critical angle, whereas at higher angles the chain breaks up into subchains of variable sizes.

The experimental validation of our numerical simulations is shown in Fig. 3. For a single chain of ferrofluid microdroplets, the magnetic pulse leads to a disruption of the chain (the movie HighSpeedPulse.mov is provided as online Supplementary Material). The elongation of the droplets is only a transient feature and not the very reason why the chain breaks up. The disruption of the chain is caused by magnetostatic interactions between the particles, as can be seen from our numerical modeling. Similarly, a stacked arrangement is disrupted under the same pulse-field conditions.

FIGURE 3.

Experimental verification of the model (movie available as online Supplementary Material). (Top left) Initial configuration of the chain of ferrofluid droplets, aligned in a bias field of 1 Oe. (Top right and middle left) Application of a 0.5-T pulse for 2 ms perpendicular to the chain axis. The droplets elongate into the field direction and subsequently form pairs, thereby disrupting the chain configuration. (Middle right) Arrangement immediately after the pulse treatment and (bottom right) 25 ms thereafter.

DISCUSSION

Putative magnetoreceptor mechanism

The dynamics of chain-like structures of interacting SP clusters offer a novel mechanism for magnetic-field perception. The observed pseudotorque response is particularly interesting because it resembles the well-known mechanism for passive magnetotactic orientation displayed by magnetic bacteria. However, when discussing sensory transduction in general, one can postulate that the stimulus be converted into a receptor potential or nervous signal within a fraction of a second and, consequently, the characteristic timescale obtained for the dynamics of chains of SP clusters in cellular environments (t₀ ∼ 400 s) seems to stand in contradiction with that general tenet. The result of our analysis, therefore, has implications for the working principle of the putative receptor. Despite the tendency of a chain of SP clusters to align with the axial direction of the magnetic field, a group of SP clusters, arranged in a chain inside a terminal, will not track a relative change in the direction of the geomagnetic field on timescales of seconds to minutes. However, the mechanical torque exerted by the SP chain,

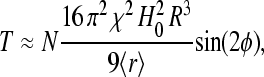(14)

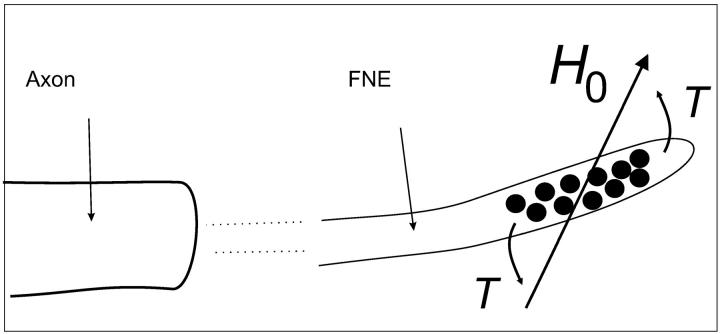
will be transferred immediately onto the bounding membrane (Fig. 4); in Eq. 14, 〈r〉 denotes the mean distance between two adjacent clusters, φ is the angle between the magnetic field and the chain axis. In other words, there is no macroscopic displacement of the SP clusters during the postulated magnetoreception process, yet there is a constant stress acting on the membrane of the free (unmyelinated) nerve endings. Because free nerve endings are mechanoreceptors, the stress due to the magnetomechanical torque can generate a nervous signal. We can conclude that a transducing mechanism in the form of chain-like structures of SP clusters is temporally stable, which is required for the animal to compare given parameters of the geomagnetic field at two different points to orient and navigate.

FIGURE 4.

Proposed mechanism of magnetic-field transduction. The clusters of SP magnetite are ensheathed by the membrane of the free nerve ending (FNE). Without the membrane, the chain of clusters would rotate into the field axis, therefore, the membrane experiences a bending torque T (Eq. 13). Because free nerve endings are sensitive to mechanic stimulation, the torque can be transduced into a nervous signal.

Furthermore, we note that the actual structure of the postulated transducer mechanism within a nervous terminal will be a result of two competing factors: i), the shape anisotropy of the structure, which will determine the amount of torque and hence, its theoretical suitability, and ii), the structural stability, which will determine its practical suitability as a sensory mechanism. In that sense, a group of N SP clusters arranged in a single chain shows a maximum shape anisotropy and hence induces a maximum torque, whereas it is easily disrupted under a fluctuating magnetic field. On the other hand, a stacked arrangement of the same number of clusters, has a smaller shape anisotropy and displays a smaller torque response, but is much more stable to any fluctuations of the ambient field. Although a loss in the amount of torque can be compensated by increasing the number of cellular receptors, the transducing mechanism needs to have a certain degree of structural stability for sensory purposes. Therefore, we consider a stacked structure of SP clusters the most efficient and likely configuration of the transducing mechanism. If this structural stability is indeed required for the functioning of the magnetoreceptor organ, then the observed effects of the magnetic pulse treatment on birds can be rationalized as follows.

Novel interpretation of behavioral results and suggestions for future experiments

The structural stability of the proposed transducer mechanism is lost when a strong magnetic pulse is applied at an angle perpendicular or largely oblique to the chain axis (Fig. 2). In this case, the original configuration of the SP clusters will dramatically change, impairing the transducer mechanism. We propose that the disruption of the chains and subsequent deterioration of the transduction mechanism is responsible for the behavioral response observed after a magnetic pulse treatment, as reported for migratory birds and homing pigeons.

Assuming that the magnetoreceptor system of these birds consists of a large number of cellular receptors in the form of stacked chains of SP clusters, the pulse treatment in Australian silvereyes and homing pigeons would have disrupted only a population of chains whose long axes were at angles larger than the critical angle for chain disruption with respect to the direction of the pulse (i.e., 70° for a double chain of N = 10 clusters), whereas chains oriented at lower angles would have been merely rotated by the magnetic pulse, the extent of rotation being dependent on the physical constraints of the cellular space; finally, dendrites aligned with the applied pulse would have remained unaffected (Fig. 2). That way, the magnetoreceptor system would only be partially damaged. Behavioral experiments (10,14) suggest that the pulse treatment did not entirely impair the magnetoreceptor system of the birds, but rather produced a partial impairment of the system, thus inducing the observed deflections instead of disorientation.

A possible explanation is that the cellular receptors form three different populations, each of which is calibrated to sense one particular component of the geomagnetic field. In order for this to work, the bird has to have developed an independent reference system, defined, for example, by the sun compass or the magnetic compass, which apparently are not affected by a pulse. In this case, the disruption of only one population of receptors would bias the sensory mechanism toward the other two components of the geomagnetic field, whereas the disruption of two of the three populations would produce a complete loss of the sensory mechanism. Because the x component of the geomagnetic field has a larger contribution to the horizontal intensity than the y component, it is expected that the disruption of the population of receptors sensitive to the x component will have more dramatic effects.

Nevertheless, in the study by Beason et al. (14) a group of homing pigeons was treated with a south-anterior pulse and another group with a south-left pulse (see Beason et al. (11) for a definition), that is, each group of birds was treated with a perpendicular field with respect to the other. Following the line of reasoning stated above, such a pulse treatment would have affected different populations of cellular receptors in the south-anterior and the south-left groups, and directional differences in the orientation response would be expected. Indeed, the two groups showed deflections with respect to the controls, although the deflections in the south-left group were greater (median 37°) than that of the south-anterior group (median 12°). When released from the same place, the direction of the deflection also differed from one group to the other. In the studies by Wiltschko et al. (9,10) all the birds were treated with the same pulse (south-anterior), and were deflected unimodally or bimodally roughly 90° with respect to the controls. This might indicate that a population of cell receptors sensitive to one of the horizontal components of the geomagnetic field was almost completely impaired, whereas the other remained almost unaffected, thus biasing the outcome signal.

That idea can be tested by treating the birds with two perpendicular pulses (i.e., a south-anterior pulse followed by a south-left pulse), in that way the two populations of cell receptors will be affected, because the chains not disrupted by the first pulse should be disrupted by the second. Such a treatment should yield more dramatic behavioral responses.

Chain recovery process

It has been reported (10,14) that the effects of a magnetic pulse treatment in birds are transient and last between 1 and 10 days. We have applied our numerical model to estimate the time required for a double chain of N = 10 clusters as shown in Fig. 2 A, disrupted by a perpendicular pulse field (90°), to recover the initial configuration under an Earth-strength magnetic field (H₀ = 0.5 Oe). Applying Eq. 9 we obtain a best-case estimate of some 15 h for the recovery time (between 150 and 200 dimensionless time steps). This timescale applies to the case where the dendrite containing the SP clusters remains oriented parallel to the magnetic field for the whole duration of the recovery process. In reality, however, a test bird will hop around in a rather erratic manner, which is equivalent to a magnetic field constantly changing in direction with respect to the bird's head. We therefore simulated the recovery process under a randomly changing magnetic field axis. It turns out that the recovery time is now much longer (between 2 and 3 days, or between 600 and 700 dimensionless time steps). This result is in good agreement with the recovery time observed in experiments on homing pigeons and Australian silvereyes. Interestingly, the diameter of the nerve terminal influences both the way a stacked chain breaks up and eventually recovers. When the inner radius of the dendrite, R_d, is decreased from 5 R to 2.1 R, the recovery is dramatically accelerated (by one order of magnitude) in a steady field applied parallel to the dendrite axis, albeit yielding a single chain instead of a stacked chain. This also holds for a steady magnetic field applied at a slightly oblique angle (up to 30°) with respect to the dendrite axis. At higher angles, however, the (linear) chain structure is not completely recovered and, instead, several subchains form. In the case of a fluctuating field, the original stacked configuration is indeed recovered, although the recovery process is sped up by some 50%. In terms of absolute time, this still translates into 1–2 days of recovery time. Thus, a fluctuating field (as realized by the bird hopping about in an erratic manner) is required to recover the stable double chain configuration. The simulations for the recovery process are provided as online material (Double-ChainRecoveryConstantField.mov and Double-ChainRecoveryRandomField.mov). It is important to mention that we here only consider physical forces driving the recovery process. Neural healing mechanisms may of course accelerate this process.

Effects of a biasing field

Wiltschko et al. (10) used a biasing field of 1 mT before the pulse treatment, in an attempt to align the magnetite system in a preferred direction, under the assumption that the magnetoreceptor mechanism consists of mobile, magnetically blocked SD magnetosome chains. Both test groups in Wiltschko et al. (10) were subjected to the same pulse treatment but to different bias fields; for one group the biasing field was parallel to the pulse direction (PAR-birds), whereas it was antiparallel for the other group (ANTI-birds). Although exposure for 5 s to the biasing field alone had no noticeable effect on the orientation behavior, the pulse treatment had the same effect on both PAR-birds and ANTI-birds.

From the calculations above, this biasing field would neither disrupt the chains of SP clusters nor effectively displace them in a preferred direction. Our model thus explains the absent effect of the biasing field on the orientation of the birds.

We further predict that the effects of a magnetic pulse are equivalent to those of a magnetic bias field applied for a sufficiently long time. We can estimate the time t_bias required for a given bias field H_bias to cause effects similar to a strong pulse. By applying Eq. 9, we obtain the following scaling relation

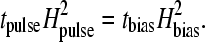(15)

From Eq. 15 it can be seen that a bias field of 10 mT applied for 5 s is needed to produce a behavioral response similar to that of the pulse-field treatment. It is possible that a pulsed field of lower intensity than those used in the behavioral experiments already causes chain disruption. We therefore suggest a behavioral experiment to determine the minimum pulse strength required to cause statistically significant misorientation. This way, the characteristic timescale of the receptor system can experimentally be determined. Finally, from Eq. 15 we can predict that a magnetic pulse of intensity H_pulse = 50 mT would cause no effect on the magnetoreceptor mechanism proposed here. Because a 50-mT pulse field should largely affect magnetically blocked SD magnetite, the absence of a behavioral response to the pulse would also argue strongly against the involvement of SD particles.

It is important to note that effects of the pulse treatment can be negated by blocking the ophthalmic branch of the trigeminal nerve (13). This observation further corroborates our conclusions because nervous terminals containing the SP clusters were identified as afferent endings of the (median) ophthalmic branch (18), which conveys the somatosensory input from the beak skin to the brain (25).

CONCLUSION

Based upon histological findings, we have developed and presented a physical model to simulate the dynamics of the putative magnetoreceptor in a magnetic field. According to our model, a stacked arrangement of chains of SP clusters is stable to magnetic-field fluctuations and shows a pseudotorque response that can potentially be used as a transducing mechanism of the geomagnetic field in the nervous system. We can also predict the effects of a magnetic pulse treatment on this putative magnetoreceptor mechanism. According to our model, a stacked arrangement of chains of SP clusters will: i), respond to the axis but not the polarity of the applied pulse; ii), disrupt under the action of a magnetic pulse perpendicular or at intermediate angles (φ > 70°) with respect to the axis of the chain; and iii), recover its original configuration under ambient field conditions within 2–3 days. These results are in agreement with behavioral experiments, namely i), the identical response of birds treated with antiparallel pulse fields; ii), the partial loss of magnetic orientation in birds subjected to a pulse; and iii), recovery times of the magnetoreceptor mechanism of up to 10 days.

Finally, a pulse affects the magnetic component of the navigational map, which relies on local geomagnetic field conditions and on the previous experience of each individuum. It is therefore impossible to explain in detail the effects of a pulse on orientation without knowledge of the local magnetic field conditions (intensity, direction, and gradients thereof). Likewise, the average deflection displayed by a group of birds may be deceptive by suggesting that all individuals were equally affected by the pulse. It may well be that some birds are more affected than others. Thus, we suggest that behavioral experiments should aim at monitoring the individual response of birds to magnetic field changes.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.