Local Compressibilities of Proteins: Comparison of Optical Experiments and Simulations for Horse Heart Cytochrome-c

Abstract

Spectroscopy with probe molecules yields local information on the environment of the probe. In this article we compare local compressibilities of cytochrome-c as obtained from molecular dynamics simulations with experimental results as obtained from spectroscopic measurements. The simulations show that the protein-core around the heme is much less compressible in a glycerol/water solvent than in pure water. The pocket is also much less compressible than the protein as a whole, although the compressibility of the water inside the rather incompressible protein-core is almost liquidlike. We show that the local compressibility values capture the collective correlations of local volume fluctuations with volume fluctuations in the surrounding protein-solvent system. The decoupling of the volume fluctuations of the core from the solvent shell explains the reduction of the heme-core-compressibility in glycerol/water solvent. This decoupling could be traced back to the suppression of the exchange between pocket-water and hydration-shell-water upon addition of glycerol as co-solvent.

INTRODUCTION

The compressibility of a protein is an important thermodynamic parameter: it is determined by the volume fluctuations, and hence, carries information about the flexibility. The flexibility, on the other hand, is itself an important quantity because it influences functional properties, such as, for instance, enzyme activities. Apart from that, the compressibility plays an important role in protein stability: many proteins are characterized by a rather broad temperature range where the compressibility is larger in the denatured state. This ensures that, above a certain pressure level, the volume of the denatured state falls below the volume of the native state, and as a consequence, the protein may eventually be forced to denature under high pressure (1–5). In some proteins, however, there may as well be a temperature range where the compressibility is lower in the denatured state. In this case, pressure stabilizes the protein. If so, there must necessarily exist a range (although a narrow one) in which both states have the same compressibility. Cytochrome-c, the protein on which we focus in this article, belongs to this category. This was explicitly shown by Dubins et al. (6). We note, however, that the thermodynamic quantities of a protein may strongly depend on the solvent.

As to the experimental determination of protein compressibilities by standard techniques, i.e., by measuring the density and sound velocity, the problem is that these techniques measure the compressibility of the solution (7–11). The value for the protein has to be extracted by varying the respective concentration. A major problem concerns the determination of the contribution from the hydration shell to the overall compressibility of the protein. Due to electrostriction the hydration shell may have a significant lower compressibility as compared to bulk water. It cannot be determined independently. However, there are well-established empirical rules that yield results with reasonable accuracy (8,9,11,12).

A direct way to measure local intrinsic compressibilities of proteins is provided by high-resolution optical spectroscopic techniques, such as, for instance, hole burning (13). Spectroscopic techniques rely on probe molecules. Hence, all information from such experiments on the environment of the probe, e.g., on the protein, is reflected in the interaction of the probe with its surroundings. The most relevant interactions, namely the dispersion and higher order electrostatic interactions, fall off with distance very quickly. Accordingly, the information retrieved from the spectrum reflects properties of the environment covering an area as determined by the averaged interaction radius. Hence, the compressibility as determined from spectroscopic experiments is the compressibility of a rather small volume around the probe with a typical radius of a few Å (14).

In this article we focus on microscopic aspects of protein compressibilities as revealed by constant pressure and temperature molecular dynamics (MD) simulations with explicit solvent models. Cytochrome-c (cyt-c) of horse heart is simulated in water and a glycerol/water mixture (3:2 v/v) typically used in spectroscopic experiments. In particular, we will show that the wealth of dynamic information from all around the protein and even from the hydration layer is reflected in the magnitude of the local compressibility, although it has only a local character. We further show that large compressibility variations may occur in the protein depending on the solvent used. A special feature in this context is that nearly liquidlike local areas with buried water molecules exist in the protein, despite the fact that the measured mean compressibility is quite low. Finally, we will show that some of the trends reflected in the simulations are also well reflected in the local compressibility as determined from optical experiments, although these experiments are low-temperature experiments.

Local compressibilities as determined by spectroscopic techniques

Basic aspects

Consider a probe molecule in a solvent. The respective solvent shift ν_s is defined as the difference between the absorption frequency ν and the so-called vacuum absorption frequency ν_vac, the frequency where the isolated probe would absorb. The value ν_s depends on the intermolecular distance as R⁻ⁿ, i.e., V^−n/3, where V is a spherical volume around the probe with radius R. Hence,

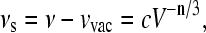(1)

with a proportionality constant c. If a pressure Δp is applied, ν_s changes. We call the respective change the pressure shift (s_p),

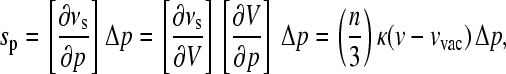(2)

where κ is the isothermal compressibility. Note that Eq. 1 holds also in the case where a proper averaging over the distances is taken into account. The proportionality between s_p and κ is a special feature of an R⁻ⁿ-interaction (13,15,16). By tuning the frequency ν through the inhomogeneous absorption band and measuring for each frequency the shift per pressure s_p/Δp, one obtains a straight line as a function of ν whose slope is given by (n/3)κ. For higher order electrostatic and dispersive interactions, n = 6. The value κ is the isothermal compressibility of that volume seen by the probe. Since these types of probe-solvent interactions are of a very short range, the system properties measured in this way, e.g., the compressibility, are local properties.

Interpretation of the parameters involved

The question arises whether the two parameters in Eq. 2 need some specific interpretation. The answer is: yes. For instance, ν_vac is not necessarily the absorption frequency of the probe in the gas phase. The reason is quite obvious: there are interactions of the probe with its environment which are not modified at the pressure level of our experiment (∼1 MPa). Hydrogen-bonding could serve as an example. Also a distortion of the molecules through the lattice or special molecular conformations or rigid structures provided by the environment, e.g., cage compounds, fall into this category. Then, ν_vac is the vacuum absorption frequency of a fictive probe comprising the probe plus all the interactions which are not modified by pressure. Clearly, this frequency may be quite different from the gas phase absorption frequency of a bare probe.

A similar fine-tuned interpretation is necessary for κ. The value κ is the compressibility of a nanoenvironment around the probe. Clearly, this nanoenvironment may be strongly influenced by the probe itself. For instance, a hydrophobic probe in a water-containing solvent will definitely have a different environment than a hydrophilic probe. Accordingly, different probes in the same solvent may lead to different κ-values in an optical experiment. However, as far as proteins are concerned, this specific feature of an optical pressure tuning experiment turns out to be an advantage. Since no artificial labeling is necessary, there is no probe-induced change.

Approximations involved

It should be mentioned that the spectroscopic determination of the compressibility is based on several approximations: first, the exponent n = 6 excludes contributions from dipole-dipole forces. However, the dipoles in the environment of the chromophore may point in many directions, so that the total contribution of the dipole forces to the pressure shift may be close to zero. Second, the simple model is based on the assumption that the pressure shift is proportional to the solvent shift. This assumption implies that it is only the density which is changed under pressure but not the local configuration of the residues around the chromophore. This is definitely not true because the spectral lines not only shift but broaden as well. The fact that broadening does occur tells us that pressure also induces conformational changes. In proteins, however, these changes are random but reversible at the pressure levels used; therefore they do not affect the average shift.

Finally, it should be stressed that the spectroscopic determination of the compressibility works best at low temperatures. There, the spectral selectivity is highest because the widths of the spectral lines come close to the natural line-widths. As a matter of fact, almost all experiments in this respect are done by using hole-burning techniques (16–18). Typical pressure levels in the experiments are of the order of 1 MPa. The respective displacements of the residues are extremely small, namely of the order of 10⁻² Å. Of course, compressibilities at low temperatures are expected to be smaller than at ambient temperatures. However, in densely packed systems like proteins or organic solids, the respective temperature dependence seems to be only marginal. As far as proteins are concerned, this seems to be true at least in a water/glycerol solvent, as is reflected in many experiments where data can be compared (14,18–20). The question is whether this apparent insensitivity of the compressibility against temperature variations has its origin in some systematic errors of the experimental procedures or in specific structural features of proteins. We argue that there is a physical reason: the thermal expansion of proteins is very small. For instance, the linear thermal expansion coefficient of Met-myoglobin is of the order of 100 × 10⁻⁶ K⁻¹ (21), meaning that the average distance between two arbitrarily chosen protein building blocks changes by ∼5% in a temperature interval of 300 K. This change is simply too small to induce significant changes in the curvature of the potentials of noncovalently bound pairs of blocks. Changes in the compressibility, however, can only be expected if the forces between the respective building blocks change. Along these lines of reasoning it can be understood why the temperature dependence of the compressibility may be small. In addition we are focusing on the trends rather than on absolute numbers. Hence, it seems to be justified to neglect possible changes of the compressibility with temperatures when comparing the results from simulations with the experiment.

Local compressibilities as determined by molecular dynamics simulations

The intrinsic compressibility of a solvated protein and the contributions of hydration and buried water to the compressibility can be derived directly from one molecular dynamics simulation evaluating volume fluctuations at ambient pressure and temperature (22,23). Yet, it has to be taken into account that the whole protein-solvent system in the simulation cell samples the distribution characteristic of the NPT ensemble (constant number N of atoms, constant pressure P, and constant temperature T). Therefore, the corresponding fluctuation relation reflects the coupling of the fluctuations of a specific local volume to the fluctuations of the total volume of the system (23). Using Voronoi volumes ensures additivity of the subsystem volumes, which is crucial for the determination of compressibilities from simulations.

To investigate local properties of the heme pocket, we divided the simulation system into four parts (compare Fig. 1): the heme pocket (H), protein atoms not belonging to the heme pocket (), the first solvation shell (S), and the region beyond the first shell (B). The heme pocket contains the chromophore and all protein heavy atoms (Hp) and water molecules (Hw) sharing at least one face of their Voronoi polyhedra with one chromophore atom (see Methods, below). Correspondingly, the first solvation shell is defined as those solvent molecules sharing at least one Voronoi face with one protein surface atom. For the glycerol/water solvent, the solvation layer is subdivided into water (Sw) and glycerol content (Sg). V_B is the volume of the solvent beyond the first shell. Thus, the system volume V is separated into the components

(3)

FIGURE 1.

Schematic representation of the volume components of the solvated cytochrome-c protein. Small circles represent water molecules; larger ellipses represent glycerol co-solvent molecules. Sw and Sg denote water and glycerol component of the first solvation layer in contact with the protein (dark region around the protein); B denotes the solvent beyond the first solvation shell. The heme chromophore and protein groups contacting the heme are denoted by Hp; water molecules coordinating the heme are denoted by Hw. Hp and Hw make up the heme pocket. The fraction of protein volume without the heme core Hp is denoted by

Accordingly, the total protein volume is For each of the components i (Hp, Hw, Sw, Sg, B), the isothermal compressibility κ_i can be obtained by averages of the statistical NPT ensemble (23):

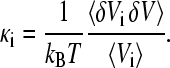(4)

The symbol δ stands for the deviation from the mean, e.g., δV_i = V_i − 〈V_i〉, k_B is the Boltzmann constant, and T is the absolute temperature. The symbol 〈…〉 stands for the average over the statistical ensemble. The mean compressibilities of combined regions can be calculated using the volume fractions, e.g., for the protein:

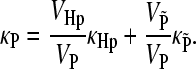Insertion of the total volume V allows for capturing the coupling of the volume fluctuation of component i to the volume fluctuations of any other part j ≠ i: 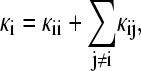with (5)

(5a)

and

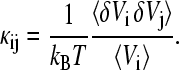(5b)

Each intrinsic compressibility value κ_i can be dissected into a contribution that captures the fluctuations of the local volume with variance (self-term), and contributions from volume fluctuations driven by fluctuations in other regions characterized by the covariance term 〈δV_i δV_j〉 which can be correlated or anticorrelated. The influence of the protein extends over several layers of solvent; therefore, the compressibility of the region outside the first solvent shell is not the true bulk value, but still contains contributions from volume fluctuations cross-correlated with the first solvation shell.

METHODS

Experimental

All experimental details have been described elsewhere (14).

Molecular dynamics simulations

The MD simulations were performed using the CHARMM program package (version c28b1, Ref. 24). Atomic interactions were modeled using the all-atom force field CHARMM22 for protein and heme (25), for glycerol (26) and the TIP3P water model (27). The modifications introduced by Prabhu et al. (28) were applied to connect the porphyrin covalently to Cys¹⁴ and Cys¹⁷ and hold the ligands (Met⁸⁰ and His¹⁸) bound to the heme iron (the heme chromophore is shown in Fig. 2). The starting structure for the protein was the high-resolution cyt-c structure from horse heart (29), PDB entry: 1hrc. The His residues were neutral with the hydrogens in the δ-position, all other titratable residues had their protonation state for neutral pH according to their aqueous pK_a values. The simulations were done at constant pressure and temperature (P = 0.1 MPa, T = 298 K).

FIGURE 2.

The heme chromophore in cytochrome-c. The rings of the porphyrin system are denoted by A, B, C, and D; the propionic side chains attached to rings A and D are denoted by prpA and prpD, respectively. The central metal atom in native cyt-c is Fe; in substituted cyt-c the central metal atom is Zn. Ligands to the central metal are His¹⁸ and Met⁸⁰. The heme group is covalently attached to the protein via thioether bonds from atoms CAB and CAC to Cys¹⁴ and Cys¹⁷, respectively.

To prepare the glycerol/water solvent box, we started from an equilibrated water box of side length 18.856 Å provided by CHARMM. To obtain the 3:2 v/v concentration we added glycerol molecules (αα-isomer, Ref. 30) at random positions and with random orientations. Water molecules overlapping within 1.6 Å were deleted. The final number ratio water/glycerol was 2.7:1 (85 water and 27 glycerol molecules) reproducing a density value (1.125 g/cm³) close to experiment (1.164 g/cm³, Ref. 31). Subsequently, the solvent box was equilibrated for 2 ns in the NVT ensemble, then continued for 2 ns in the NPT ensemble. The pre-equilibrated water and water/glycerol boxes, respectively, are used to build the cubic solvent boxes of side length L = 56 Å for the protein simulations. The protein (together with the 124 x-ray waters) was centered in the solvent box. All solvent molecules with any atom within 1.6 Å of the protein were deleted. Six chloride ions were added at random positions outside the ion exclusion radius to make the system neutral. The total number of solvent molecules was 4948 for the water simulation and 2030 water and 721 glycerol molecules for the water/glycerol simulation, respectively. In all simulations, the protein occupies 10% of the total volume of the simulation cell.

Periodic boundary conditions were imposed using the CRYSTAL facility in CHARMM. Constant temperature and pressure conditions were applied using extended system algorithms (32–34): Langevin piston collision frequency, 20 ps⁻¹; reference and bath temperature, 298 K; mass of the pressure piston, 500 amu; and mass (i.e., the parameter for the thermal inertia) of the thermal piston, 1000 kcal · ps². SHAKE (35) was used to constrain all covalent bond lengths to hydrogen atoms. A time step of 2 fs was applied for the numerical integration using the leapfrog algorithm. The long-range electrostatic interactions were treated with the particle-mesh Ewald method using a cubic grid of 64 points combined with a fourth-order B-spline interpolation (direct interaction cutoff 12 Å, Ewald parameter 0.36). A nonbonding pair list cutoff of 14 Å was used and the pair list was updated every 5–10 steps. A nonbonding cutoff of 12 Å and shifted forces were used in the calculation of the Lennard-Jones potentials.

The equilibration of the protein-solvent system was carried out in four steps: after rearrangement of the solvent around the fixed protein (500 ps), the protein was harmonically constrained by a mass weighted force constant (500 ps) and, finally, all constraints were cleared and the system was equilibrated for 1 ns in the NVT ensemble and additional 500 ps in the NPT ensemble. After equilibration, stable conformational states (root mean-square, i.e., RMS, deviation from the x-ray structure Cα-atoms were 1.25 Å for the water simulation and 1.19 Å for the water/glycerol simulation, respectively) and a constant amount of internal water was reached. The subsequent production runs of 1 ns in the NPT-ensemble were used for analysis, and structures were saved for analysis every 200 fs (5000 frames). During the production runs, the backbone RMS deviation from the starting structure did not exceed 1.1 Å (Table 1).

TABLE 1.

Structural and dynamical properties of cytochrome-c in two solvents

	Solvent: water	Solvent: glycerol/water (3:2 v/v)
Protein*
(a) RMSD Cα/Å	1.14 (0.23)	0.87 (0.11)
(b) RMSD SC/Å	1.89 (0.34)	1.35 (0.18)
(c) SASphob/Å2	1581 (44)	1486 (54)
(d) SASphil/Å2	4971 (136)	4896 (97)
Solvent†
(e) nw	4948	2030
(f) ng		721
(g) ρbulk/(g · cm−3)	0.992	1.125
Solvent shell‡
(h) nSw	673 (18)	321 (8)
(i) nSg		129 (5)
(j)	6.1 (1.7)/—	4.1 (1.5)/2.0 (1.4)
(k)	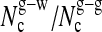	5.7 (1.9)/3.3 (1.3)
Heme pocket§
(l) nHp	142 (4)	140 (4)
(m) nHw	15 (2)	10 (2)
(n)	2.8 (0.6)/2.2 (0.6)	1.9 (0.4)/0.8 (0.3)

Values in parentheses are standard deviations.

^*Protein: (a) RMS deviations from the equilibrated structure and fluctuations of the C_α atoms; (b) RMS deviations from the equilibrated structure and fluctuations of the side-chain atoms; (c) solvent-accessible surface area (probe radius 1.6 Å) for hydrophobic residues; (d) solvent-accessible surface area (probe radius 1.6 Å) for hydrophilic residues.

^†Solvent: (e) number of water molecules; (f) number of glycerol molecules; and (g) bulk density.

^‡Solvent shell: (h) average number of water molecules; (i) average number of glycerol molecules; (j) average coordination number of a water molecule to water (w-w) or glycerol (w-g) molecules; and (k) average coordination number of a glycerol molecule to water (g-w) or glycerol (g-g) molecules.

^§Heme pocket: (l) average number of nonhydrogen protein atoms; (m) average number of water molecules; and (n) average coordination number between a water molecule in the heme pocket to other water molecule in the heme pocket (Hw-Hw) and water molecules in the solvent shell (Hw-Sw).

The solvent radial distribution function g(r) around the protein (perpendicular to the protein surface) was calculated by determining for each solvent molecule the closest distance r of the oxygen atoms from the protein atoms (including hydrogens). The ensemble average 〈ΔN(r)〉 of the number of molecules with a distance between r − Δr/2 and r + Δr/2 (Δr = 0.1 Å) was determined for distances 0 Å < r <13 Å. The distribution function was normalized to the bulk values: was determined in the region 10 Å < r < 13 Å.

The instantaneous coordination number N_c of each solvent molecules was obtained for configurations saved every 100 ps by counting all water (and glycerol) molecules within 3.5 Å from the water oxygen atom (all three glycerol oxygen atoms), which defines the first hydration shell of each molecule (36).

Volume calculations

The MD-generated configurations were used to calculate the Voronoi volumes for all heavy atoms of the system. The volume of any part of the system was obtained by adding the contributions from the constituent atoms. The calculation of the Voronoi polyhedra and the identification of atoms sharing a common face with the heme chromophore and with the atoms on the surface of the protein were carried out using the program package Code-Mbg (version 1.1) by Gerstein (37,38). The radius parameters for the glycerol molecule were taken from related compounds.

Statistical analysis of covariances

To calculate mean-square volume fluctuations 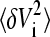and the associated covariance matrix C_ij = 〈δV_i δV_j〉 an extended statistical analysis is necessary (39,40). In the case of multimodal distributions of the volumes V_i—for instance, due to a nonconstant number of water molecules in the pocket—average, variance, and covariance are ill-defined. To obtain meaningful values for elements C of the covariance matrix we use a method discussed and applied by Maragliano et al. (40) for the calculation of the mean-square displacements of atomic positions. Instead of calculating time averages over the whole trajectory, the complete sequence of steps is broken up in N_B(L) blocks of length L (L · N_B = N_T, N_T = total number of frames saved for analysis). Time averages C_n (L) (n = 1,…, N_B) over each block n were calculated and the block average was obtained as

(6)

The proper choice of the block length L was determined in two steps: after the analysis of the statistical inefficiency s, we determined the suitable block length L > s with the χ-square test. Due to correlations persisting over a certain time, not all of the N_T stored data points are statistically independent. To consider the number of frames for which this correlation persists, we calculated, for a set of block lengths (L = 2, 4, 8, 10, 20, 40, 50, 100, 125, 200, 250, 500, 1000, 1250, 2500, and 5000 frames), the variances of the block averages σ²(〈C〉_B), and compared the respective values with the variance over the total run-time σ²(C). The fit of the quantity N_Bσ²(〈C〉_B)/σ²(C) versus 1/N_B (39) to a straight line leads to the statistical inefficiency s in the limes N_B → ∞. For the protein volume V_P, s = 10 was obtained in both simulations, and for the water simulation we found s = 10 (V_Hp, V_Hw), s = 25 (V_B), and s = 95 (V_Sw). For the water/glycerol simulation the values were s = 25 (V_Hp, V_Sw, V_B), s = 30 (V_Sg), and s = 95 (V_Hw). As a common value for all calculations, we used s_max = 100. In the second step, the distribution of the block averages C_n (L) for each L > s_max was assessed using the χ-square test (40,41). To do this, each distribution was binned and compared to a reference distribution given by the average value in each bin. The values of χ² for the distribution of block averages for each block length L was calculated.. For almost all of the variances we found the minimum of χ² for a block length L = 200 frames; in a few cases, the stability region extended over the range from L = 125 to L = 250 frames. As the value L = 200 is approximately in the center of this region, we used this block length in all calculations. From the block averages, we also obtained estimates for the errors of the mean values given by 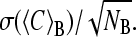The errors for the compressibilities given in Table 2 were calculated using error propagation.

TABLE 2.

Component volumes V_i and isothermal compressibilities κ_i of the protein-solvent system

	Solvent: water			Solvent: glycerol/water (3:2 v/v)
Component i	Vi/Å3	κi/Gpa−1	κexp/GPa−1	Vi/Å3	κi/GPa−1	κexp/GPa−1
Protein (P)	16,059 (17)	0.19 (0.01)		16,039 (16)	0.17 (0.01)
Heme pocket
Protein (Hp)	2853 (14)	0.15 (0.01)		2947 (14)	0.08 (0.02)	0.05*
Water (Hw)	434 (10)	0.46 (0.09)		274 (7)	0.37 (0.14)
1st solvation shell
Water (Sw)	18,837 (55)	0.19 (0.01)		8564 (36)	0.25 (0.03)
Glycerol (Sg)				16,552 (86)	0.35 (0.05)
Solvent (B)	130,770 (114)	0.49 (0.01)†	0.45‡	130,402 (121)	0.35 (0.01)†
		0.57 (0.01)§			0.40 (0.01)§
		0.61 (0.01)¶			0.68 (0.01)¶

Estimated errors of the mean values in parentheses (for details see text).

^*Experimental values from Lesch et al. (14).

^†Solvent beyond the first solvation shell.

^‡Experimental value from Lide et al. (31).

^§Solvent beyond the second solvation shell.

^¶Autocorrelated value (for details see text and Eq. 5a).

RESULTS AND DISCUSSION

MD simulations of cyt-c in two solvents, namely pure water and glycerol/water (3:2 v/v), at ambient pressure and temperature were carried out. Structural and dynamical details of the simulations can be found in Table 1. From the MD simulations we determined five compressibilities, namely the compressibility κ_P of the protein molecule averaged over all residues, the compressibility κ_S of the solvent shell around the protein (with components κ_Sw and κ_Sg for the water and glycerol compounds, respectively), the compressibility of the solvent κ_B (excluding the first solvation shell around the protein), the local compressibility κ_Hp of the heme-chromophore and the protein-core contacting it, and the local compressibility κ_Hw of the water molecules coordinating the heme. The respective numbers are listed in Table 2. Fig. 1 gives an overview over the individual parts of the simulation system. In the following we compare the respective numbers for cyt-c in the two solvents. In addition, for the solution with glycerol as a co-solvent, we compare the local compressibility κ_Hp with the value obtained from spectroscopic experiments (Fig. 6) that measure the compressibility within a range of ∼4–5 Å around the chromophore (14).

FIGURE 6.

Absorption spectrum of Zn-cytochrome-c at 4 K. The dotted line shows the part of the vibrational band that is subtracted to get the (0,0) transition. In the long wavelength band, pressure-tuning hole-burning experiments were performed. The respective values of the shift per pressure are shown. The slope of the fit line determines the compressibility. The wavenumber where s_p vanishes is the so-called vacuum absorption wavenumber ν_vac.

Cytochrome-c in pure water

Due to its definition, the heme pocket comprises not only the respective atoms of the protein-core and associated water but the respective voids as well. It amounts to ∼20% of the total protein volume. The maximum distance to a heme atom is 4.5 Å. Seventy-five percent of the protein groups contacting the heme are hydrophobic. On average, 15 water molecules are coordinating the heme, most of them are located in the hydrophobic region near the side chains of the porphyrin rings B and D (Fig. 2). This means that the water molecules of the pocket are in a cavity with weak hydrogen-bonding capacity. Two-to-three water molecules and two charged groups are located near the propionic acid side chains of the heme. Note that eight of these 15 pocket waters are already found in the x-ray structure (two waters near the propionic acid on ring A, #125 and #129, and six, #129, #165, #119, #112, #128, and #182, in contact with porphyrin rings and side chains). The average lifetime of heme-water contacts is 10 ps. Each of the water molecules in the pocket coordinates, on average, to 2.8 cavity waters and to 2.1 waters in the hydration shell (Table 1). The total coordination, therefore, is not different from the situation found in the hydration shell. The layer of surface-bound water molecules has a volume comparable to the protein volume (Table 2) and contains ∼13% of the total number of water molecules in the cell. Exchange between cavity and hydration shell is possible via a pathway built by the rather flexible Ω₁ (residues 20–35) and Ω₂ (residues 36–48) loops.

Table 2 summarizes the calculated volumes and associated isothermal compressibilities of the simulation system. First, we compare the simulation values, κ_B, for the isothermal compressibility of the solvent (without the first solvent shell) with the experimental value for the bulk solvent. For water under normal pressure, this value is 0.45 GPa⁻¹ (31). From the simulation we obtain a value of 0.49 GPa⁻¹, which increases to 0.57 GPa⁻¹ if we exclude, in addition to the first shell, the second shell around the protein. This increase is a clear indication that the influence of the proteins extends beyond the first solvation shell. The value of 0.57 GPa⁻¹ is near the autocorrelation value of 0.61 GPa⁻¹ (Fig. 3), which represents the isothermal compressibility of bulk water for the TIP3P water model (22,23). The deviation from the experimental value has been traced back to deficiencies of this model (22). For the protein as a whole, we find an isothermal compressibility of κ_P = 0.19 GPa⁻¹. This value is of the same order as calculated (23) for BPTI and lysozyme, but higher than the value calculated by Dadarlat and Post (22) for these proteins. The hydration shell is by more than a factor-of-2 less compressible than bulk water. This reduction in the compressibility is larger than the 20–24% reduction found for BPTI and lysozyme (23). Presumably, the high polar surface area of cyt-c (75%, Table 1) favors an increased electrostrictive reduction of the volume fluctuation of water near the surface. An outstanding result of the simulations concerns the local intrinsic compressibility parameters of the heme pocket (κ_Hp and κ_Hw). A straightforward expectation is that the compressibility of this region would be high due to internal voids as a consequence of packing defects. We find that this is true for the water molecules in the pocket which are nearly as compressible as bulk water. However, the respective portion of the protein scaffold is highly incompressible.

FIGURE 3.

Contributions to the intrinsic compressibilities of components of the protein-solvent system: (a) Cytochrome-c in pure water solvent; (b) Cytochrome-c in glycerol/water (3:2 v/v) solvent. The compressibility values in the rectangular boxes refer to self-terms (Eq. 5a) representing the local fluctuations of the site volumes, i.e., the values connecting different parts of the system represent compressibility contributions due to cross-correlations of volume fluctuations (note that κ_ij ≠ κ_ji, Eq. 5b).

These results can be understood in terms of the coupling of the local volume fluctuations of a given site to other parts of the protein-solvent system. With the help of the fluctuation formulae (Eqs. 5a and 5b) it is possible to separate the compressibility of a local volume V_i into an autocorrelation term κ_ii and into cross-correlation terms κ_ij. The importance of cross-correlations for the volume fluctuations for the water simulation can be seen from Fig. 3 a. The variances of the fluctuations of the protein-core in the heme pocket and the rest of the protein are quite different, with the pocket atoms showing the larger variability—in agreement with the expectations mentioned above. However, the two parts of cyt-c differ largely in the cross-correlation terms. The larger variance of the local volume fluctuations of the Hp site is partially compensated by anticorrelated fluctuations of the surrounding protein Positively correlated fluctuations of the hydration shell Sw contribute approximately the same amount of +0.07 GPa⁻¹ to κ_P and κ_Hp. This shows that the hydration shell drives not only fluctuations on the protein surface but in the protein interior, where the heme is located. This coupling to the interior is mediated by the water drop (Hw) in the heme pocket (see below). Altogether, the simulations show that the protein-core around the heme (Hp) is less compressible than the overall protein by ∼25%.

The most prominent example for the importance of collective correlations is the water in the heme pocket (Hw). The total compressibility value results from a remarkable cancellation of contributions (Fig. 3 a). Taking into account the variance of the local volume V_Hw only, a large compressibility self-term of 1.34 GPa⁻¹ results. However, exchange of water between the pocket and the hydration shell drives anticorrelated volume fluctuations and leads to a reduction of the compressibility value by 1.19 GPa⁻¹. It is the additional coupling of the internal water to the protein and to the solvent beyond the first solvation shell B—mediated via the hydration shell Sw—which brings the compressibility of the pocket water (0.46 GPa⁻¹) into the range of bulk water. The analysis reveals also that the low compressibility of the hydration shell Sw is a result of anticorrelated volume fluctuations in bulk and hydration shell, which cannot be compensated by the positively correlated fluctuation of the much more rigid protein volume.

Cytochrome-c in water with glycerol as a co-solvent

It is well known that glycerol as a co-solvent may have a significant influence on structural and dynamical properties of proteins and, therefore, on their compressibility. According to observations, the protein becomes less compressible. For instance, it was found (42) that a 30% (v/v) glycerol/water mixture reduces the compressibility by ∼1/3 as compared to pure water. The magnitude of the reduction depends on the glycerol concentration. This behavior is interpreted in terms of a loss of protein internal water, so-called lubricant water, induced by the co-solvent. According to this interpretation, the co-solvent induces a kind of negative osmotic pressure that sucks the water out of the protein. This loss leads to a collapse of the protein-internal voids and, concomitantly, to an increased intramolecular binding and suppressed dynamics (43). The combined effect shows up in a reduced compressibility.

Additionally, the co-solvent molecules affect the water structure and, therefore, the stability of the protein. Glycerol molecules penetrate into the solvent shell as a result of the balance among several interactions (44):

1. Repulsion from nonpolar groups and backbone amid groups.

2. Attraction from polar regions of the protein.

3. Attraction between water and glycerol.

Preferential binding of water or glycerol in the solvation layer around the protein is an expression of the difference between the interaction of the two solvent components with the protein. It was found (44) that for glycerol concentrations of 10–40% the co-solvent is excluded from the surface, whereas preferential binding of the co-solvent occurs around a glycerol concentration of 70%.

For a glycerol concentration of 60% (v/v) as used in the simulation, we find a preferential binding of glycerol in the hydration shell. The volume fraction V_Sg/(V_Sw+V_Sg) (compare Table 2) of glycerol increased to 65% as compared to 60% in bulk, this indicates an 8% higher occupancy in the shell as compared to a random occupation (45). The radial distribution functions (g(r), Fig. 4) show a similar organization pattern of water and glycerol. Glycerol replaces water molecules and forms hydrogen-bonds with the protein surface. This result is in agreement with Raman measurements of amide modes in lysozyme (46). Yet, the water structure is not destroyed as indicated by the average total coordination numbers (Table 1), which are similar to those found for pure water. The preferential interaction of glycerol molecules is clearly shown by the per-molecule average of noncovalent interaction energies. One glycerol molecule has an average attractive interaction to the protein of −8.0 kcal/mol; the interaction to other solvent molecules in the shell is −4.3 kcal/mol. One water molecule in the shell has an attractive interaction to the protein of −4.3 kcal/ mol, whereas the interaction to other solvent molecules is larger, at −7.1 kcal/mol. For comparison: one hydration water molecule in the case of pure water solvent has approximately equal attractive interactions to the protein (−3.6 kcal/mol) and to other water molecules (−4.8 kcal/mol). The average coordination numbers (Table 1) show that glycerol fits very well into the hydrogen-bond network around the protein. For each shell water, approximately two coordination sites are replaced by glycerol molecules, leaving the overall coordination constant. Each glycerol molecule has approximately two waters coordinating each hydroxyl function of the co-solvent molecule.

FIGURE 4.

Solvent-protein radial distribution function around cytochrome-c in pure water solvent (a) and in glycerol/water (3:2 v/v) solvent (b) as a function of the distance between the solvent oxygen atoms and the nearest protein atoms including hydrogen atoms.

Glycerol does not only lead to a dehydration of the protein surface, but also to a partial dehydration of the internal cavity around the heme: the average number of buried water molecules is reduced from 15 to 10 (Table 1) with a concomitant decrease of the volume V_Hw by 37% and a reduction of the average coordination of pocket water molecules (Table 2). However, the protein-core around the heme does not collapse. Due to the reduction of the level of hydration, glycerol induces a suppression of protein dynamics, as is, for instance, evident from the lower root mean-square fluctuations (Table 1). The exchange of pocket water with shell water is drastically slowed down, as reflected by the increased lifetime of heme-water contacts to 60 ps as compared to 10 ps in pure water solvent.

The presence of glycerol as a co-solvent in the aqueous medium decreases the hydrophobicity of the protein surface, as seen by the 6% reduction of hydrophobic surface area (Table 1). The protein adopts a more compact and a more spherical form with smaller surface area. Surface hydrophobic groups prefer to migrate into the interior of the protein to avoid contact with the solvent. This trend develops extremely in the region of the Ω₁ and Ω₂ loops. The resulting partial closing of the pathway for pocket water is presumably responsible for the reduced exchange. On the other hand, the total volume remains constant (Table 2, Fig. 5). However, the response of the residue volumes to the addition of glycerol as co-solvent is striking and quite heterogeneous (Fig. 5).

FIGURE 5.

Relative volume change for the residues of cytochrome-c upon addition of 60% (v/v) of glycerol to the water solution. The volumes were calculated for the equilibrated structures in the two solvents using the Voronoi technique. The residue on position 105 represents the heme chromophore.

Glycerol was also reported to be a structural effector of myoglobin (47). It was demonstrated that glycerol alters the heme pocket region of the protein and influences its functionality. Furthermore, conformational changes involving the loop region were reported. These drastic changes in structure and dynamics of the protein and the solvent shell are reflected in the volume fluctuations responsible for the compressibilities. Just as in the case of the H₂O-solvent, the structuring influence of the protein extends over several layers of solvent, as is reflected in the differences of the calculated compressibilities of the solvent for the three cases, namely excluding the first solvation shell only (0.35 GPa⁻¹), excluding the first two solvation shells (0.40 GPa⁻¹), and the autocorrelated value (0.68 GPa⁻¹; compare Table 2 and Fig. 3). Unfortunately, no experimental value for the isothermal compressibility of a 60% (v/v) glycerol/water solvent at ambient pressure and temperature is available. In addition, a reference calculation for a bulk glycerol/water solvent is still missing. Despite the partial dehydration, the heme pocket still contains a highly compressible water droplet. Although the respective compressibility κ_Hw is 20% lower than the corresponding value in pure water solvent, it is still a factor-of-2 higher than the mean compressibility of the protein. On the other hand, the protein core around the heme chromophore becomes dramatically stiffer if glycerol is present as a co-solvent: the respective compressibility κ_Hp decreases by a factor of 2 as compared to the overall compressibility κ_P of the protein. The two components of the solvation shell show different intrinsic compressibilities. Compared to the pure water, the compressibility of the water in the binary solvent does not drastically increase and is still a factor-of-2 lower than bulk water—consistent with the finding that the water structure around the protein is conserved. The glycerol component of the mixed solvent has a higher compressibility, presumably due to larger voids and packing defects around the bulky molecules. In contrast to water, glycerol does not seem to experience a significant electrostriction by the protein surface residues. The compressibility of the total solvent layer is 0.33 GPa⁻¹ (calculated from the individual contribution and the corresponding volume fractions given in Table 2) and is, therefore, only marginally different from the value for the solvent beyond the first solvation shell.

The suppression of protein dynamics due to the presence of the co-solvent is clearly reflected in the reduction of localized volume fluctuations and their cross-correlations (Fig. 3 b). On the other hand, the cross-term connecting the fluctuations in the hydration layer Sw with the protein is conserved and a contribution of the same magnitude and sign adds from the glycerol component Sg. For the glycerol/water solvent, in contrast to pure water, the solvation shell is no longer able to drive fluctuations in the protein-core around the heme. This missing contribution (+0.07 GPa⁻¹ in water) leads to the observed drastic reduction of the compressibility κ_Hp. We interpreted these driven fluctuations to be mediated by the exchange between pocket water and hydration water. The consistency of this assumption is proven by the concomitant drastically reduced anticorrelation of volume fluctuations in these two parts of the system. Again, the water component in the heme pocket has the most complex interaction pattern. Due to the fact that the fluctuations of the volume fractions Sw and Sg associated with the water and glycerol molecules in the solvent shell are anticorrelated, they add cross-terms of opposite sign to κ_Hw. This anticorrelation also mediates the contribution of the bulk volume fluctuations to κ_Hw. The fluctuations of the local volume associated with the water component Sw in the solvent shell is comparable to the respective value of a pure water shell, consistent with the conserved water structure around the protein surface as already indicated by the distribution function and the coordination pattern. Anticorrelated volume fluctuations of Sg and B bring κ_Sw to a range comparable to the value found for a pure water solvent shell. The volume fraction Sg of glycerol molecules in the solvation shell shows the largest fluctuation of all analyzed components. This is indicative of large voids, packing defects, and the absence of electrostriction. Volume expansions of Sg are balanced by volume reductions in the B and Sw components. This anticorrelation results in the low value of κ_Sg.

Comparison with spectroscopic experiments

Simulations make it possible to gain microscopic information on local properties of a complex system, e.g., on local compressibilities, on local electric fields, on local dielectric constants or local inhomogeneities of any system parameter, associated with any volume around any structural center of interest. From the local properties the respective spatial fluctuations and their correlations as well as the bulk properties can be determined. However, most experimental techniques cannot probe local properties. Local properties can be measured only via spectroscopic techniques that exploit the short interaction range of molecular probes.

Recently, we determined experimentally the size of the interaction volume of a chromophore with its environment (14). The protein was a modified cytochrome-c, where the native heme group was replaced by the respective Zn-derivative. The latter served as the probe. We found that the average interaction radius is rather small, namely ∼5 Å. It just comprises the heme pocket and the adjacent residues. Accordingly, the compressibility of the protein, as determined from hole-burning experiments, is the compressibility of the volume around the chromophore covering distances of ∼4–5 Å. We determined this compressibility in a glycerol/water glass (3:2 v/v) by burning many holes into the absorption of Zn-cyt-c and exploiting Eq. 2. The value we found is rather low, namely of the order of 0.05 GPa⁻¹, which is a factor-of-3 lower than the mean compressibility of the protein κ_P as determined by the simulations (Table 2). Experimental values for the mean compressibility of cyt-c in glycerol/water glass are not available, but our simulation value (κ_P = 0.19 GPa⁻¹) fits quite well into the order-of-magnitude values reported for the isothermal compressibilities of globular proteins (0.14 ± 0.03 GPa⁻¹, Ref. 48). Experimental estimates vary in a rather large range, most probably because the influence from the hydration effect is hard to estimate. In addition, most experimental results refer to adiabatic compressibilities—which are smaller, anyway, than isothermal compressibilities. Apart from that, our simulation results refer to Fe(II)-cyt-c. However, a variety of experiments indicate that the Zn-substitution does not change the protein structure in the vicinity of the heme (49) or the reactivity (50), or the splitting of the Q-band of the chromophore (51).

The results of our simulations for the local compressibility of the protein-core around the heme chromophore κ_Hp = 0.08 GPa⁻¹ are in reasonable agreement with the experimental value (Fig. 6, κ_Hp = 0.05 GPa⁻¹, Ref. 14). We want to stress that the result of our experiments on the core compressibility is totally unexpected and most surprising, because it is the core volume that contains most of the voids of the protein. Hence, this volume constitutes a rather soft part of the total volume of the protein, and, consequently, a higher compressibility is expected. The simulations, however, reflect the correct trend with respect to the experiment. In line with the observation, the 5 Å protein-core is quite stiff when the solution contains glycerol as a co-solvent. On the other hand, water in the cavity has nearly the high compressibility of liquid water. Similar arguments for the distribution of the local compressibilities in proteins were already given by Priev et al. (42).

The role of collective correlation functions

The simulations revealed the extreme importance of correlations between volume fluctuations for understanding local compressibilities. The local properties of various sites, like compressibilities or dielectric constants (52,53), capture not only the localized fluctuations but the coupling of the local property (volume or polarization, respectively) to the properties of the surroundings as well. The significance of these cross-correlation terms κ_ij (Eq. 5b) results from the fact that they can be positive as well as negative quantities that can obtain magnitudes comparable to the variances. The simulations show that rather long-range coupling (e.g., between bulk and cavity water or between heme pocket and hydration shell) does occur. The results for the self-terms, showing a higher variance of the fluctuations of the local volumes of the protein-core around the heme as compared to the overall protein, fit very well with the expectations mentioned above, but the final compressibility values contain a great deal of contributions from volume fluctuations driven by the surrounding. Neglect of the coupling between the volume fluctuations of the protein and the hydration shell leads to a 40% lower mean compressibility of the protein. This may explain the lower compressibility values from simulations reported, e.g., for BPTI by Dadarlat and Post (22), as compared to the values using the correlated fluctuation formula (23).

As a consequence, the protein's local compressibilities are very sensitive to the behavior of the solvent. Despite the fact that they have local character, they reflect a wealth of dynamic information from all around the protein and even from the hydration layer and the bulk solvent. The strong coupling of the dynamics of the protein to the dynamics of the solvent—as revealed here in the volume fluctuations of local sites in the protein—is a common feature of solvated proteins. It was shown (46,53,54) that the slaving of protein motions to bulk-solvent and hydration-shell fluctuations is essential for the functionality of the proteins.

The dissection of the correlation pattern is a valuable analysis tool. This analysis revealed the origin of the reduced local compressibility of the protein-core around the heme chromophore upon addition of glycerol as co-solvent. The reduction could be traced back to the reduced exchange of water molecules between heme pocket and hydration shell, thus indicating a strong coupling of the hydration of the nonpolar cavity to the solvent in pure H₂O-solvent. As an indirect consequence, volume fluctuations of the protein-core driven by fluctuations of the hydration water are lost. These strong correlations also limit the ability of these regions to respond separately to applied perturbations, e.g., external pressure fields.

Apparent compressibilities

Finally, we want to consider the close correlation between experimental and calculated compressibility values an encouraging result, because in all experiments on protein compressibilities absolute numbers are hard to compare: in combined densimetry and sound velocity experiments, it is the problem that hydration shell effects can only be estimated and local fluctuations cannot be determined. Moreover, the solvent itself as well as the pH have a large influence. With the theoretical method applied, it is possible to calculate apparent isothermal compressibilities (κ_a) from intrinsic contributions of protein (P), solvent shell (S), and the solvent beyond the first solvation shell (B) (23):

(7)

These values can be directly compared with the experimental values from sound velocity measurements. (Note, however, that sound velocity experiments measure adiabatic compressibilities which can, in some cases, be significantly different from isothermal compressibilities. To convert one quantity into the other, the specific heat and the thermal expansion has to be known.) For the two solvents used in the simulation, we find the κ_a = −0.16 GPa⁻¹ for cyt-c in water and κ_a = +0.13 GPa⁻¹ for cyt-c in glycerol/water (3:2 v/v). Due to the close similarity of the compressibilities of the solvent shell and solvent outside the first shell in the glycerol/water mixture, the experimental values in this solvent should be close to the intrinsic value. So, comparison of the trends, e.g., between spectroscopic and sound velocity experiments or between various types of experiments and simulations (e.g., by varying the solvent as done here), are more important, and it is gratifying to see that in the present case the simulations correctly reflect the trend of the optical experiments on core compressibilities of proteins.

SUMMARIZING CONCLUSION

We have shown that different solvents may have a significant influence on intrinsic protein compressibilities, mainly due to long-range correlated volume fluctuations. Glycerol as a co-solvent stiffens the protein, especially the inner core around the heme chromophore, where the effect is really dramatic. Compressibilities as determined from spectroscopic experiments reflect the trend of the simulations. These findings render a great deal of confidence to the respective numbers as determined from optical experiments and open new perspectives. For instance, instead of chromophores as local probes, aromatic amino acids, e.g., tyrosine, can be used (20). If the protein contains several tyrosines, it is possible to measure local compressibilities in various regions of the protein. In favorite cases, these quantities can be determined separately for each tyrosine from the experiment and the accompanying simulations. This opens new insights on local properties as well as on the level of accuracy of the simulations and the experiment.