Sedimentation Velocity Analysis of Heterogeneous Protein-Protein Interactions: Sedimentation Coefficient Distributions c(s) and Asymptotic Boundary Profiles from Gilbert-Jenkins Theory

Abstract

Interacting proteins in rapid association equilibrium exhibit coupled migration under the influence of an external force. In sedimentation, two-component systems can exhibit bimodal boundaries, consisting of the undisturbed sedimentation of a fraction of the population of one component, and the coupled sedimentation of a mixture of both free and complex species in the reaction boundary. For the theoretical limit of diffusion-free sedimentation after infinite time, the shapes of the reaction boundaries and the sedimentation velocity gradients have been predicted by Gilbert and Jenkins. We compare these asymptotic gradients with sedimentation coefficient distributions, c(s), extracted from experimental sedimentation profiles by direct modeling with superpositions of Lamm equation solutions. The overall shapes are qualitatively consistent and the amplitudes and weight-average s-values of the different boundary components are quantitatively in good agreement. We propose that the concentration dependence of the area and weight-average s-value of the c(s) peaks can be modeled by isotherms based on Gilbert-Jenkins theory, providing a robust approach to exploit the bimodal structure of the reaction boundary for the analysis of experimental data. This can significantly improve the estimates for the determination of binding constants and hydrodynamic parameters of the complexes.

INTRODUCTION

When an external force is applied to solutions of macromolecular components that interact on a timescale much faster than the experiment, the resulting migration of the macromolecular species is coupled. The concentration profiles of the free and bound components will evolve with velocities that are characteristic for the interacting system, are intermediate between those that would be observed for stable free and bound species, and are dependent on the initial composition and the equilibrium constant. The observation and analysis of the coupled migration of interacting proteins has a long history in sedimentation velocity, electrophoresis, and gel permeation chromatography. In the 1950s, Gilbert and Jenkins developed a theoretical description of migration experiments for the limiting case of rapid reactions and negligible diffusion (1). In this theory, sedimentation velocity gradients (asymptotic boundary profiles or Schlieren patterns) can be calculated for proteins in self-association equilibria (2) and for multicomponent mixtures with heterogeneous protein-protein interactions (3). A more general framework for the interactions with arbitrary attractive or repulsive forces was subsequently described by Nichol and Ogston (4).

The Gilbert-Jenkins theory (GJT) has had a profound impact upon the understanding of migration experiments of interacting systems. For the sedimentation of two-component solutions, it predicts the existence of two boundaries: the undisturbed sedimentation of the free species of one of the components, and the reaction boundary exhibiting the coupled sedimentation of a mixture of complex and free forms of both components. The undisturbed boundary sediments with a single sedimentation coefficient, whereas the reaction boundary extends over a range of sedimentation coefficients that correspond to different ratios of free and complex species. The amplitude of each boundary, as well as the asymptotic shape of the reaction boundary can be calculated (3). The predicted features have been experimentally verified (5). They have been used as qualitative guides in the interpretation of experimental boundaries and for the quantitative analysis of transport experiments (6,7). In analytical ultracentrifugation, however, in comparison to the frequent use of weight-average sedimentation coefficients for the determination of association constants (8–10), apparently only relatively few applications have made quantitative use of the boundary structure, for example, the amplitudes and s-values predicted by GJT (see, e.g., Singer et al. and others (11–13)). This may be partially due to the numerical complexity of the calculations at the time, and/or the difficulty in precise determination of the boundary amplitudes and shapes in the presence of diffusion, as described, for example, in Palmer and Neet (14).

Subsequently, much interest has been devoted to the numerical solution of Lamm equations, the partial-differential equations of sedimentation, including chemical reaction kinetics as well as diffusion terms (6,15–22), and similar approaches have recently been implemented for the fitting of experimental sedimentation experiments (23–26). However, although this approach is very powerful, these models may not always be suitable in practice because they imply a detailed interpretation of the shape of the sedimentation boundary, which is exquisitely sensitive to any heterogeneity of the sample, such as impurities or microheterogeneity (26–29). Therefore, the more robust analysis of the concentration dependence of weight-average sedimentation coefficients continues to be of practical importance (for examples of applications, see Frigon and Timasheff and others (31–38); for methodological analyses, see Correia (39) and Schuck (24)). The weight-average s-value of the sedimenting mixture is based solely on mass balance considerations and is completely independent of the boundary shape. This study is focused on the question of how one can extract more robust information from sedimentation experiments beyond the overall mass balance, by exploiting the characteristic bimodal shapes of the boundaries for the quantitative analysis of heterogeneous protein interactions.

Recently, we have introduced a method for the computation of diffusion-deconvoluted sedimentation coefficient distributions c(s) from noisy experimental sedimentation data (40,41). It is based on the direct modeling of the sedimentation data with superpositions of Lamm equation solutions for noninteracting species, and is combined with maximum entropy regularization to result in the simplest distribution consistent with the experimental sedimentation data. The diffusion is approximated by means of a hydrodynamic scale relationship of sedimentation and diffusion and is based on a weight-average frictional ratio of the sedimenting macromolecules, extracted from the experimental data. This approximation takes advantage both of the weak shape dependence of the frictional ratio, and the lower size dependence of diffusion relative to sedimentation. Many applications have verified the high resolution and sensitivity of the resulting c(s) distributions (42). Although the interpretation of c(s) is straightforward for mixtures of noninteracting proteins, interacting systems show concentration-dependent peak positions and areas (29), as can be expected from GJT. For interacting systems, we have previously shown that the integration of c(s) over all peaks of the interacting system allows a rigorous determination of the weight-average s-value of the system, that is essentially independent of the kinetics of the interaction (24). In the accompanying article, we have described the shapes of c(s) distributions obtained at different reaction rate constants, and characterized the transition from c(s) resolving slowly interacting sedimenting species to c(s) representing the sedimentation/reaction boundaries of rapidly interacting systems. One goal of the present work is to provide a more general theoretical framework for the latter case of rapid interactions, that will allow a quantitative analysis of the c(s) peaks, utilize the deconvolution of diffusion, and exploit the structure of the underlying sedimentation boundaries of rapidly reacting systems.

For the limiting case where one component is small and exhibits a vanishing concentration gradient, it was shown that the reaction boundary can be described by a single diffusion coefficient (26,43,44). This suggests that the deconvolution of diffusion in the c(s) distribution may approximate diffusion-free reaction boundaries. In this study, we systematically compare the results from c(s) with the asymptotic velocity gradients, dc/dv, predicted by GJT. Despite the approximations in the deconvolution of diffusion in c(s), and the neglect of radial geometry and radial-dependent force in the theory for dc/dv, we find good qualitative and quantitative agreement. This supports the use of isotherms characterizing the reaction boundary based on GJT for the more detailed data analysis of c(s) profiles for rapidly interacting systems. As a practical consequence of this, we examined in this work how the isotherms derived from the concentration dependence of the signal-average fast boundary component and the signal amplitudes of the reaction and undisturbed boundary components can be used for estimating equilibrium binding constants and the sedimentation coefficients of the complex from experimental data.

THEORY

Gilbert-Jenkins theory for asymptotic diffusion-free reaction boundaries

We recapitulate the theory described by Gilbert and Jenkins (3) for the reaction of proteins A and B forming a reversible complex AB. In a solution with rectangular geometry and radial-independent force, the Lamm equations can be written as

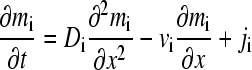(1)

where m_i for i = 1, 2, and 3 denotes the local molar concentration m_A, m_B, and m_AB of species A, B, and AB, respectively, and D and v are the species diffusion coefficients and linear velocities (with v in units of Svedbergs). The reaction fluxes j_i follow mass conservation with j_A = j_B = −j_AB = j, and it is assumed that all species are in instantaneous equilibrium following the mass action law 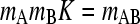(with the equilibrium association constant K). A change of variables from spatial and time coordinates x and t to the velocity v = x/t and the inverse time w = 1/t is used to transform Eq. 1 into

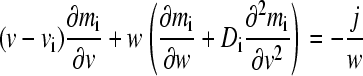(2)

In the limit of infinite time (w → 0) the asymptotic equation system

(3)

can be derived, which can be solved for m_A(v), m_B(v), and m_AB (v). This limit corresponds to the asymptotic boundary shape when diffusion and reequilibration have become negligible due to the differential transport (3). For Eq. 3, Gilbert and Jenkins have given analytical solutions (1,3), but a numerical algorithm was later described for more general reactions (45). After determining m_A(v), m_B(v), and m_AB (v), the asymptotic Schlieren patterns dc/dv can be predicted (with c here denoting the total signal taking into account each species' individual signal contribution, i.e., dc/dv = ɛ_A dm_A/dv + ɛ_B dm_B/dv + (ɛ_A + ɛ_B)dm_AB/dv), as well as the signal amplitudes of the undisturbed boundary, c_slow, and the reaction boundary, c_fast, respectively. Similarly, the asymptotic Schlieren patterns of each component in molar units, dm_A,tot/dv = dm_A/dv + dm_AB/dv) and dm_B,tot/dv (= dm_B/dv + dm_AB/dv) can be predicted. For the quantitative analysis the signal-average sedimentation coefficient of the reaction boundary can be calculated as

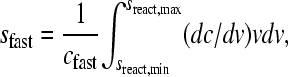(4)

where s_react,min and s_react,max denote the predicted range of s-values of the reaction boundary.

It will be of interest to compare this value of s_fast with the overall weight-average sedimentation coefficient, s_w, which can be predicted from the initial composition of the mixture of A and B in equilibrium and at rest, before the application of the external force. Under these conditions, the well-known application of mass action law and mass conservation gives

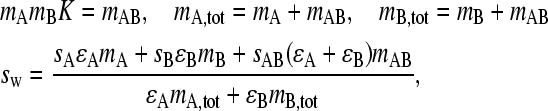(5)

(with ɛ denoting each species' extinction coefficient).

We have implemented these calculations in the software SEDPHAT for modeling isotherms of s_fast (), as well as the concentration dependence of the signal amplitudes of the slow and fast boundary components, c_slow and c_fast, respectively. From the analysis of these isotherms, binding constants as well as an s-value of the complex can be determined by nonlinear regression.

Sedimentation coefficient distributions c(s)

The signal a(r,t) from the sedimentation process of an unknown mixture is approximated as a superposition

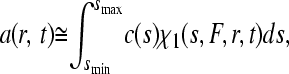(6)

where c(s) denotes the differential sedimentation coefficient distribution in units of the observed signal (40); χ₁(s,F,r,t) denotes the solution of the Lamm equation (46) in the absence of a reaction, at unit concentration and with sedimentation coefficient s and a hydrodynamic frictional ratio F = (f/f₀) that scales the diffusion coefficients to the sedimentation coefficients

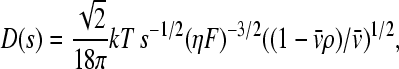(7)

(with η and ρ the solvent viscosity and density, respectively, and 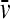the partial-specific volume of the macromolecules). F is adjusted in nonlinear regression (41), and the c(s) distribution is calculated using maximum entropy regularization (47) and F-statistics. For details, see Dam and Schuck (29). Unless noted otherwise, the c(s) distribution was calculated with F and the meniscus position optimized by nonlinear regression, and with regularization at P = 0.7.

Integration of the c(s) distribution can be used to determine the overall weight-average s-value, s_w

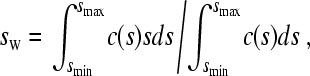(8)

which is consistent with the definition of s_w from mass balance considerations, and is independent of boundary shape (24). Data comprising the complete sedimentation process were included in the determination of s_w by Eq. 8, which provides the most precise estimate of s_w (24). If the integration limits are replaced with the range of s-values s_react,min and s_react,max, identified to reflect only the fast reaction boundary component, experimental values of s_fast corresponding to Eq. 4 can be obtained. Similarly, the area of the c(s) peaks corresponding to the amplitude of the fast boundary component, c_fast, can be calculated. The expressions for s_fast and c_fast take the form

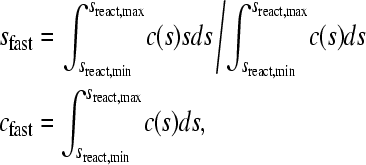(9)

and an analogous integration leads to the amplitude of the slow boundary component c_slow.

Equation 6 can be extended to multicomponent sedimentation coefficient distributions c_k(s), which can be calculated from globally modeling multiple signals λ as

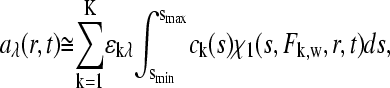(10)

provided that each component k contributes in a characteristic way to the signal λ according to a predetermined extinction coefficient (or molar signal increment) matrix ɛ_kλ (48).

The c(s) and c_k(s) distributions are implemented in the software SEDFIT and SEDPHAT, available free of charge from the authors and described at www.analyticalultracentrifugation.com. It should be noted that this c(s) distribution is not identical to that calculated with the software ULTRASCAN, due to the absence of regularization in the latter (version 7.1). Also, it is fundamentally different from the “histogram envelope plot” of the van-Holde-Weischet distribution, which may have a similar appearance as the familiar differential sedimentation coefficient distributions, in particular, after application of the postfitting smoothing operation by Gaussians that was proposed recently by Demeler and van Holde (52). However, the latter does not have a rigorous theoretical foundation and does not deconvolute diffusion except for single species or mixtures with visibly separating sedimentation boundaries (41).

RESULTS

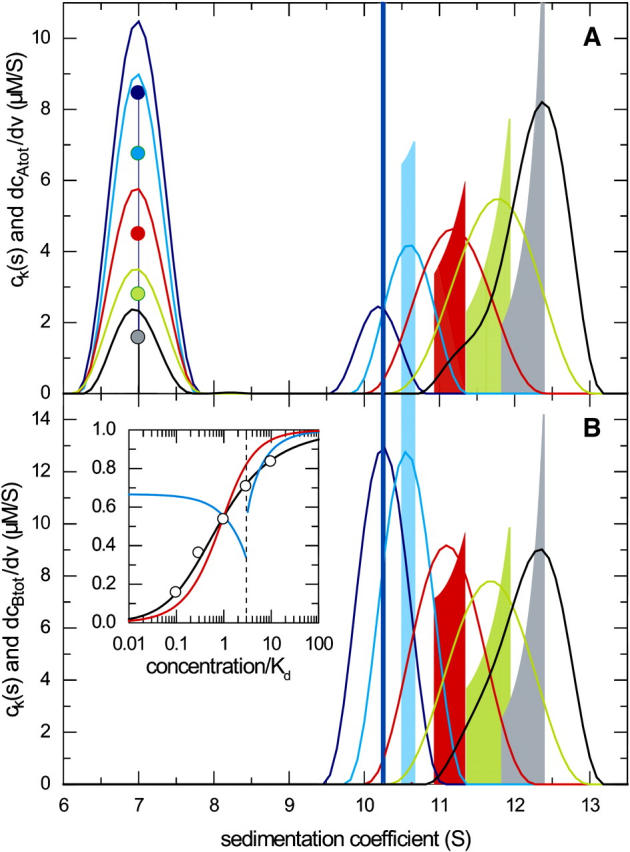
To compare the shapes of the asymptotic reaction boundaries dc/dv with the results of c(s) analysis, sedimentation profiles were simulated for a reacting system A + B ↔ AB using Lamm equation solutions incorporating the reaction terms (Eq. 1) for a reaction in instantaneous local equilibrium at all times. The algorithm implemented in SEDPHAT was used (26) with parameters mimicking a conventional sedimentation velocity experiment with a 10 mm solution column at 50,000 rpm of a 100 kDa, 7 S protein A reacting with a 200 kDa, 10 S protein B, forming a 13 S complex. Simulated loading concentrations were chosen as equimolar 0.1-, 0.3-, 1-, 3-, and 10-fold the equilibrium dissociation constant K_D (assumed 10 μM), and 0.005 fringes of normally distributed noise was added. (Normally distributed noise, appropriate for fringe data (49), of this magnitude was also added to all following simulated sedimentation profiles in this article, to obtain realistic broadening of the c(s) profiles from the regularization.) Under these conditions, two boundary components can be readily discerned—the undisturbed boundary and the reaction boundary—as predicted by Gilbert and Jenkins (1). The corresponding c(s) traces (Fig. 1 A, solid lines) show two peaks, corresponding to the undisturbed boundary of free A, and the reaction boundary (composed of a mixture of free A, free B, and the complex AB). The data show the typical features of a concentration-dependent fast boundary component, with the peak s-value being significantly below the s-value of the complex even at concentrations of 10-fold K_D. In comparison, the shapes of the solid bars depict the asymptotic reaction boundaries dc/dv from GJT. The peak positions of dc/dv were found consistent with those of c(s), and the amplitudes of the undisturbed boundary and the reaction boundary in dc/dv were consistent with the peak areas of c(s). The peak width of dc/dv was not well represented in c(s), which can be expected due to the regularization generating the broadest peaks consistent with the raw data. This effect can be easily discerned at the lowest concentration, where the signal/noise ratio is limiting. At the higher concentrations, the smoother appearance of c(s) can be expected to reflect the imperfections of diffusional deconvolution. As shown below, the assumption of a linear geometry in the GJT does not contribute significantly to the differences between c(s) and dc/dv.

FIGURE 1.

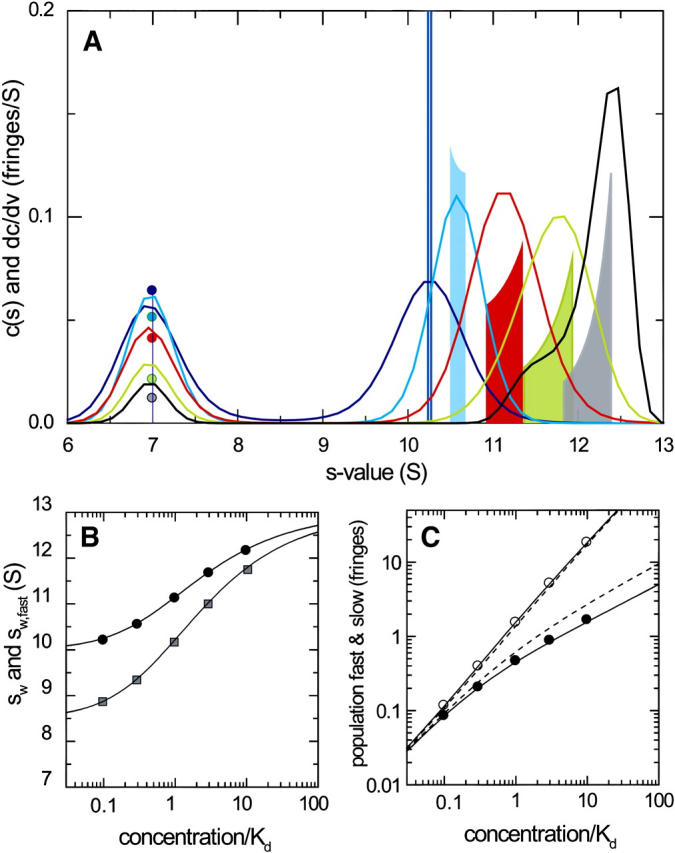
Sedimentation boundary analysis of a reacting system A + B ↔ AB at a series of equimolar total concentrations. Theoretical sedimentation data were calculated by solving the Lamm equation for a 100-kDa, 7-S component A, and a 200-kDa, 10-S component B forming a 13-S complex in instantaneous local equilibrium, with 0.005 fringes normally distributed noise added. (A) Sedimentation coefficient distributions c(s) from the best-fit model of the simulated sedimentation data (solid lines) are shown at concentrations of 0.1-fold K_D (dark blue), 0.3-fold K_D (light blue), K_D (red), threefold K_D (green), and 10-fold K_D (gray), in units of fringes/S. The shapes of the asymptotic reaction boundaries dc/dv calculated for the same parameters are shown as solid bars, with the corresponding infinitely sharp undisturbed boundary indicated as solid circles (shown in fringe units). For clarity, both the c(s) and the dc/dv distributions were normalized to the same loading concentrations, and the reaction boundary of dc/dv was reduced fivefold in scale. (B) Isotherms of the signal-average s-value of the reaction boundary, s_fast, as derived from integration of the fast c(s) peak only (black circles), and s_w of the total sedimenting system derived from integration of the complete c(s) distribution (gray squares). The solid lines are the theoretically expected isotherms from GJT (Eq. 4) and the composition following mass action law for the system at rest (Eq. 5), respectively. (C) Signal amplitudes c_fast (○) and c_slow (•) of the two boundary components determined by integration of the c(s) peaks, and corresponding isotherms determined by GJT (solid lines). The short-dashed lines indicate the isotherms for the population of free A and (free B+AB) calculated by mass action law.

A more quantitative comparison is possible by calculating the signal-average s-value of the reaction boundary, s_fast (Fig. 1 B, solid circles), as well as the amplitudes of the undisturbed boundary, c_slow (Fig. 1 C, solid circles), and the reaction boundary, c_fast (open circles), determined from integration of the slow and fast peaks of the c(s) profiles, respectively (Eq. 9). The concentration dependence of these values forms an isotherm that can be compared with the theoretical isotherm determined from the analogous integration of the dc/dv boundaries predicted by GJT (Eq. 4). In Fig. 1, B and C, the solid lines represent the GJT isotherms based on the parameter values underlying the simulations. The comparison with the c(s)-derived data (solid and open circles) shows excellent agreement. As predicted by Gilbert and Jenkins, the signal amplitudes of the fast and slow boundary components do not correspond to the populations of free and bound species calculated by the mass action law for the initial composition of the system before migration (short-dashed lines in Fig. 1 C), due to the coexistence of free A and B in the reaction boundary.

Although the curves shown in Fig. 1, B and C, do not involve fitting of any parameter, these isotherm models based on GJT were implemented in SEDPHAT for nonlinear regression of experimental data extracted from c(s) analysis for estimating the s-value of the complex and the binding constant. The concentration dependence of s_fast, c_slow, and c_fast can be analyzed globally and jointly with the weight-average s-values, s_w (shaded squares in Fig. 1 B). In this configuration of equimolar loading concentrations, the global analysis of all four data sets essentially halves the error estimates of the binding constant, as compared to the analysis of s_w alone

Clearly, the shapes of the sedimentation boundaries will depend on total loading concentrations of both A and B (c_A,tot and c_B,tot, respectively). Therefore, the value of s_fast(c_A,tot, c_B,tot) forms a two-dimensional isotherm and it is of interest to explore its shape. Fig. 2 shows the shape of the isotherm of s_fast(c_A,tot, c_B,tot) as predicted by GJT for the parameters used in Fig. 1, in comparison with the well-known isotherm s_w(c_A,tot, c_B,tot). For a data analysis, in practice, any combination of loading concentrations can be used that permits sampling the isotherm surface in several points sufficient to characterize its shape. Solely to systematically explore the properties of s_fast(c_A,tot, c_B,tot) in this work, we examine the relationship between GJT and c(s) for combinations of loading concentrations that follow three lines: the diagonal (equimolar dilution series corresponding to Fig. 1; see black lines in Fig. 2), a line of constant c_B,tot (titration with the smaller species; red lines in Fig. 2), and a line of constant c_A,tot (titration with the larger species; magenta lines in Fig. 2). These series of loading concentrations also highlight the properties of c(s) distributions for different variations of loading concentrations in different regimes. However, it should be noted that this does not imply constraints in the different experimental designs in practice, which may be chosen differently, for example, to accommodate practical limitations in the amounts of material. (Also, the implementation in SEDPHAT does not require following any particular experimental design.)

FIGURE 2.

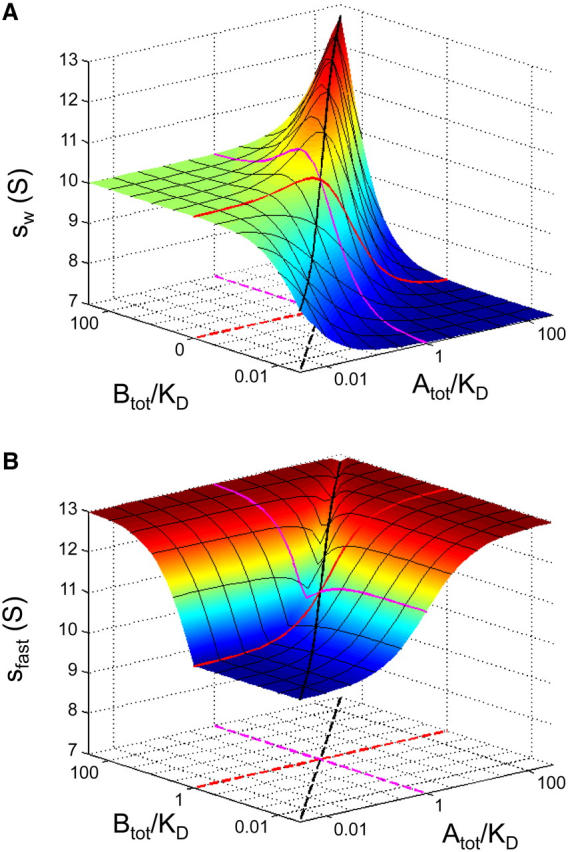
Isotherms of the theoretical concentration dependence of the weight-average sedimentation coefficient, s_w (A), and of the reaction boundary, s_fast (B). Sedimentation and interaction parameters are the same as those in Fig. 1. s_w(c_A,tot,c_B,tot) was calculated on the basis of the mass action law for the composition of the system at rest (Eq. 5), and s_fast(c_A,tot,c_B,tot) was calculated from GJT (Eq. 4). The lines indicate the configurations used to explore the sedimentation behavior of this system. They correspond to one-dimensional isotherms for the equimolar dilution series shown in Fig. 1 (black lines), the titration of a constant concentration of larger species with variable concentrations of the smaller species shown in Fig. 3 (red lines), and the titration of a constant concentration of the smaller species with variable concentrations of the larger species shown in Fig. 4 (magenta lines). Any experimental configuration of data points sampling the shape of the isotherms will be sufficient for the estimation of s_AB and K_D.

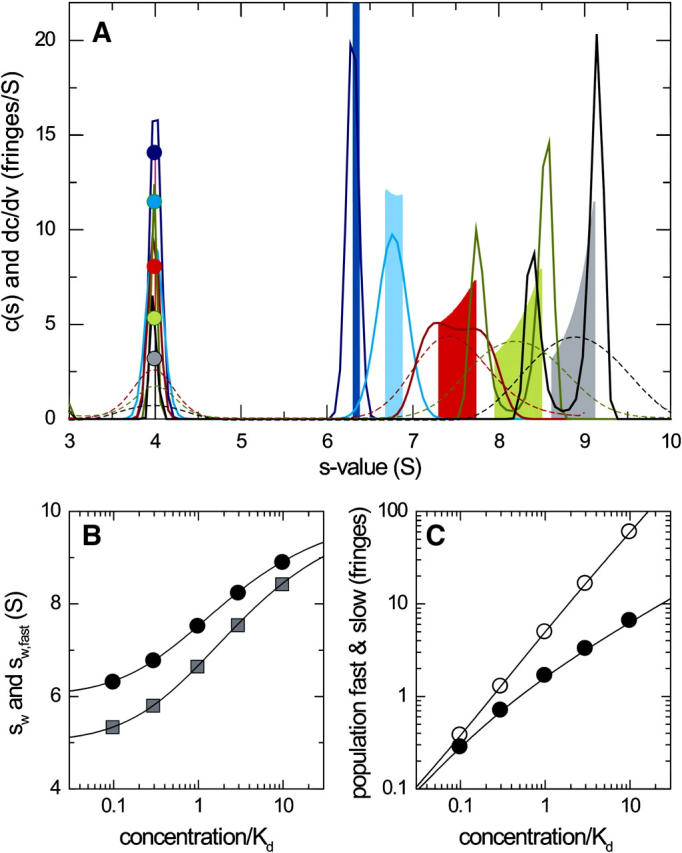
Next, we examined the c(s) and dc/dv traces for a titration of a constant loading concentration of the larger 10-S component (c_B,tot = K_D) with varying concentrations of the smaller 7-S component (with c_A,tot ranging from 0.1-fold K_D to 10-fold K_D), under otherwise identical conditions. Fig. 3 A shows the c(s) curves shifting in the peak position of the reaction boundary, starting at slightly above 10 S at the lowest concentration of A, and increasing monotonically with increasing loading concentrations of A. This again mimics the behavior of the asymptotic boundary shapes, and we find excellent quantitative agreement with regard to s_fast (Fig. 3 B) as well as the signal amplitudes c_slow and c_fast of the boundary components (Fig. 3 C). Here, the amplitude of the fast boundary does not change very much because the constant concentration of B is limiting the complex formation.

FIGURE 3.

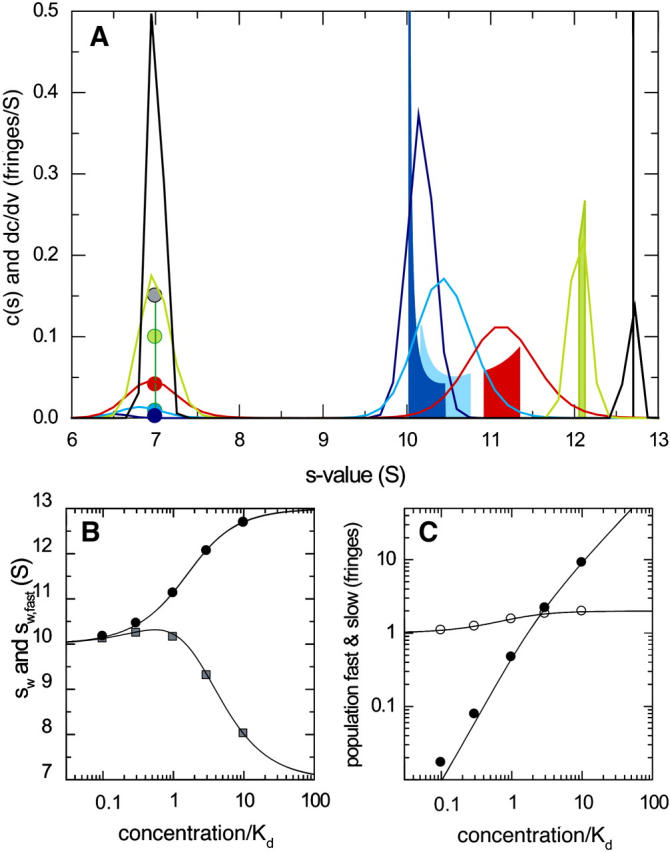
Sedimentation boundary analysis of a reacting system A + B ↔ AB at a constant concentration of the larger species B, in a titration series with the smaller species A. Sedimentation parameters were the same as those in Fig. 1, with sedimentation coefficients of 7 S and 10 S for the species A and B, respectively, forming a 13-S complex. (A) Sedimentation coefficient distributions c(s) from the best-fit model of the simulated sedimentation data (solid lines) are shown at concentrations of 0.1-fold K_D (dark blue), 0.3-fold K_D (light blue), K_D (red), threefold K_D (green), and 10-fold K_D (gray), in units of fringes/S. The presentation is analogous to Fig. 1. (B) Isotherms of s_fast as derived from integration of the fast c(s) peak (black circles), and s_w from integration of the complete c(s) distribution (gray squares). The solid lines are the theoretically expected isotherms for s_fast from GJT (Eq. 4) and for s_w from mass action law at rest (Eq. 5), respectively. (C) Signal amplitudes c_fast (○) and c_slow (•) as determined by integration of the c(s) peaks, and corresponding isotherms determined by GJT (solid lines).

In contrast to the equimolar configuration shown in Fig. 1, the titration series appears to have a significant advantage for determining the s-value of the complex. At the highest concentrations of 10-fold K_D, the peak s-value is 12.7 S, significantly closer to that of the complex species at 13 S. The isotherm of s_fast shows a qualitatively different behavior than the isotherm of the weight-average s-value, s_w, of the whole system (Fig. 3 B): s_w has a shallow maximum and then decreases due to excess A, whereas s_fast increases throughout, approaching the complex s-value, because the excess of A sediments largely in the undisturbed boundary. This highlights the advantage of exploiting the hydrodynamic separation of boundary components, as opposed to restricting the analysis to the overall mass balance reflected in s_w. If the complete set of four isotherms shown in Fig. 3, B and C, is used in nonlinear regression to estimate the complex s-value and binding constants, an error analysis based on the covariance matrix shows a 4.8-fold reduction of the error for s_AB and 2.7-fold reduction of the error of log₁₀(K_D) as compared to the analysis of s_w alone.

The reverse titration of a constant loading concentration of the smaller 7-S component (c_A,tot = K_D) with an increasing concentration of the larger 10-S component is shown in Fig. 4. Qualitatively different effects are observed, in that the reaction boundary, even at the lowest concentration of B, is well in between the s-value of free B and that of the complex. This is due to the fact that a substantial fraction of total B is already present in the complex form. Although the asymptotic boundaries are sharp at low concentrations of B, the c(s) distribution is broad due to the limited signal/noise ratio at the low concentrations. Adding more B shifts the s-value of the reaction boundary toward free B, which is a result of the limited (constant) concentration of A available for complex formation, and correspondingly the fraction of free A decreases. Importantly, at a certain concentration where B is sufficiently in excess over A, all of A will participate in the reaction boundary, and the excess of species B will constitute the undisturbed boundary (gray and green circles in Fig. 4 A). The transition point under the conditions of Fig. 4 is at approximately threefold K_D. The transition point was found to depend on the s-values of A and B, and also on the stoichiometry of the interaction. For concentrations exactly at the transition point, the undisturbed boundary vanishes and the two-component mixture sediments in a single boundary. Slightly above the transition point, the asymptotic boundary is very broad, which is well reflected by c(s) (green curve). At a much higher excess of B, a sharp peak in both dc/dv and c(s) is observed closer to the complex s-value. It is important to note that, initially at low concentration of B, the position of the c(s) peaks as well as those of dc/dv do not change very much with increasing concentrations of B until the transition point is passed.

FIGURE 4.

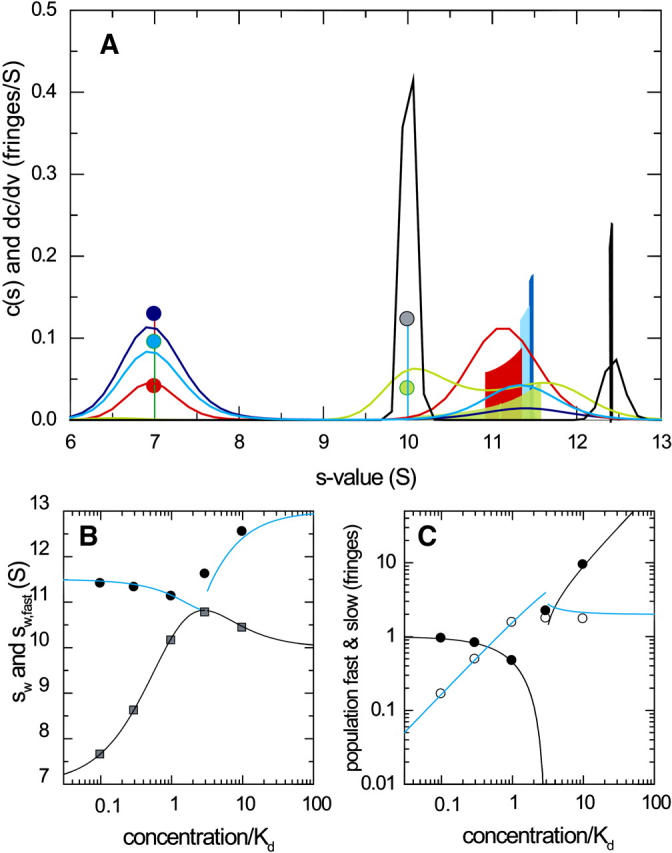
Sedimentation boundary analysis of a reacting system A + B ↔ AB at a constant concentration of the smaller species A (7 S), in a titration series with the larger species B (10 S). Sedimentation parameters and labels are the same as those described in Fig. 3. For clarity, the isotherms of s_fast and c_fast are shown in blue in panels B and C.

The isotherms of s_fast, c_slow, and c_fast determined by integration of c(s) are in reasonable quantitative agreement with the predictions of dc/dv, reflecting the transition of the undisturbed boundary. A small deviation of the theoretical and c(s)-derived value of s_fast can be discerned in Fig. 4 B, which is due to the difficulty in distinguishing the undisturbed boundary from the reaction boundary close to and slightly above the transition point (green circle and bar in Fig. 4 A). In the analysis of experimental data, this data point close to the transition point should be excluded from the isotherms (it can be included in the isotherm of s_w, for which the ambiguity of the boundary interpretation is irrelevant (24)). The global analysis of the remaining isotherms provides three- to fourfold reduced error estimates when compared to the analysis of s_w alone.

The asymptotic boundaries obtained with GJT are derived under the assumption of a rectangular cell geometry and at infinite time. To test how well this limiting case does describe sedimentation boundaries in the absence of diffusion in sector-shaped cells, we have simulated the sedimentation of particles with very small diffusion coefficients. Because the finite element Lamm equation solution is numerically unstable at a value of D = 0, simulations were performed in a series of sequentially 10-fold lower diffusion coefficients (Fig. 5). Except for some minor oscillations at values of D < 10⁻¹⁵ m²/s, the boundary profiles (transformed to apparent sedimentation coefficient distributions g*(s) with the ls-g*(s) method) approached a limiting value. This was examined for the case of equimolar loading concentration corresponding to the red trace in Fig. 1 A, and the broader distribution shown in the green trace of Fig. 4 A at conditions close to the transition point. In both cases, when the ls-g*(s) distributions are compared to the dc/dv traces of GJT, only minor differences are visible, primarily the lack of the sharp peak appearing at the maximum of dc/dv. Closer inspection revealed a slight overestimation of the s-values in GJT, which is reflected in an s_fast value exceeding that of the limiting ls-g*(s) trace by ∼0.26%. If this is attributed to the lack of radial dilution in the rectangular geometry of GJT, corrections can be applied using the approximation for the effective time-average radial dilution during the sedimentation (Eq. 8 in (24)). The basis for calculating the radial dilution was taken as the s-value of the undisturbed boundary for component A and the s-value of the reaction boundary for component B. This reduced the deviation between s_fast values between GJT and the limiting s-values from solving the Lamm partial-differential equations (PDE) to 0.05%.

FIGURE 5.

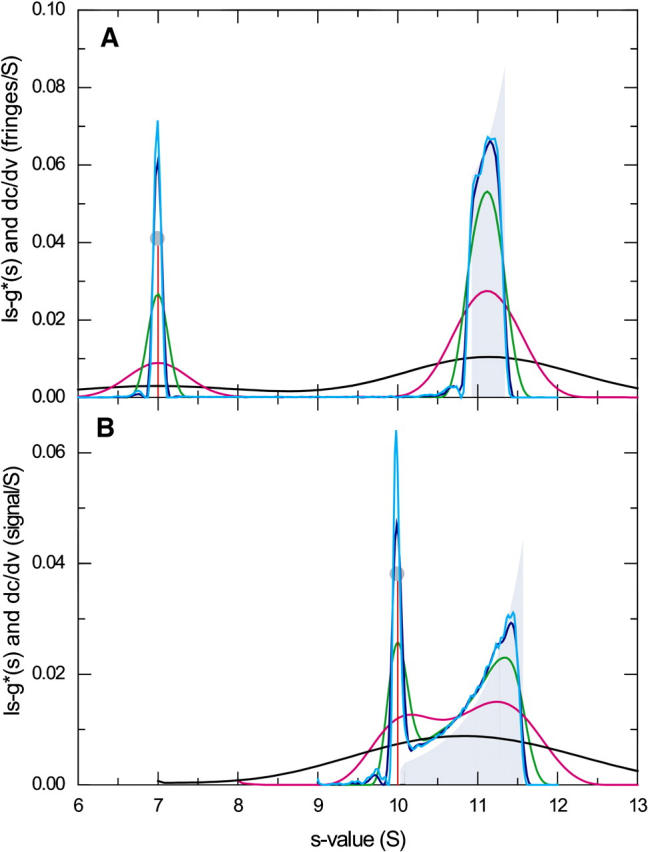
A comparison of the boundary shapes predicted by GJT for rectangular cells at infinite time with Lamm equation solutions of sedimenting, reacting particles in the limit of very small diffusion coefficients. Lamm equations were solved for the same parameters as shown in Figs. 1 and 4, respectively, with the diffusion coefficient reduced by a factor 10⁴ (cyan), 10³ (blue), 100 (green), 10 (magenta), and unreduced (black), using the algorithm for a semiinfinite solution column (26). The simulated sedimentation profiles were transformed into sedimentation coefficient distributions using the ls − g*(s) method (50). For comparison, the profiles dc/dv are shown as gray bars and circles for the reaction and undisturbed boundary, respectively. The profiles were normalized to the same area. (A) Simulation under the same conditions as in Fig. 1, with equimolar loading concentration of A and B equal to K_D. (B) The same conditions as in Fig. 4 with a threefold molar excess of B over A.

So far, the comparison of c(s) and dc/dv has been made for relatively large proteins, where, under most conditions, the undisturbed and the reaction boundaries are clearly visible in the raw data. A very stringent test for the performance of c(s) for the deconvolution of diffusion from the reaction boundaries is its application to small molecules, where the appearance of the experimental concentration profiles allows the visual discernment of only a single, diffusionally broadened boundary. This case was examined in a simulation equivalent to that shown above (in the equimolar case), but with a 2.5 S species A and a 3.5 S species B forming a 5 S complex with 1:1 stoichiometry. The dashed lines in Fig. 6 A show the g*(s) profiles, calculated as ls-g*(s) (50), which verifies that the raw sedimentation profiles appear as only a single broad boundary. In contrast, the c(s) curves resolve the undisturbed and the reaction boundaries, except for the lowest concentration where the signal/noise ratio is the limiting factor. The agreement between the peak positions of c(s) and dc/dv is good. However, an indication of too strong deconvolution is observed at the highest concentration in the form of a small secondary peak of the reaction boundary (black line at ∼4 S). Nevertheless, the isotherms of s_fast, c_slow, and c_fast are in excellent agreement (Fig. 6, B and C). (The data points for the lowest concentration were omitted due to the lack of resolution.) In this case, only a ∼1.5-fold improvement of the global isotherm analysis was found when compared to the analysis of s_w alone.

FIGURE 6.

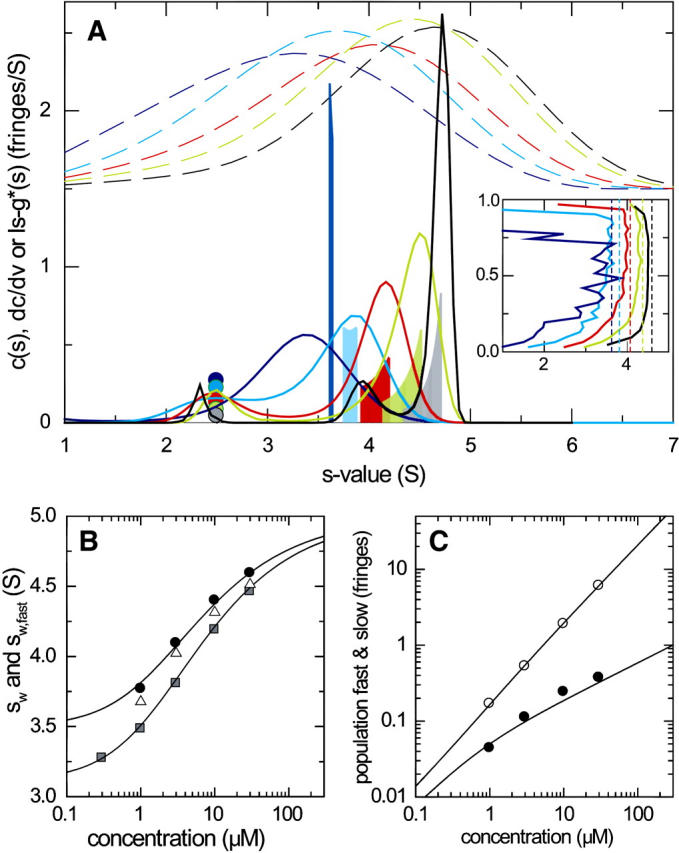
Comparison of c(s) and the asymptotic boundary shape dc/dv for small species. Sedimentation conditions were analogous to those shown in Fig. 1, but simulating the interaction of a protein of 25-kDa, 2.5-S binding to a 40-kDa, 3.5-S species forming a 5-S complex with a equilibrium dissociation constant K_D = 3 μM, and a dissociation rate constant k_off = 0.01/s, studied at 50,000 rpm. Interference optical detection was assumed, with noise level of 0.005 fringes. Concentrations were equimolar at 0.1-fold K_D (dark blue), 0.3-fold K_D (light blue), K_D (red), threefold K_D (green), and 10-fold K_D (gray). The presentation of the results is as indicated in Fig. 1. The dashed lines in panel A are g*(s) distributions obtained from ls − g*(s) analysis of the simulated sedimentation profiles. The inset in panel A shows the integral sedimentation coefficient distributions G(s) from van Holde-Weischet analysis (41) (solid lines), and the expected s_fast (short-dashed vertical lines). Panel B presents the isotherms of s_fast (solid circles) and s_w (shaded squares) from c(s) and the theoretical expectation (solid lines). Also included for comparison are the maximum s-values of the G(s) distribution from van Holde-Weischet analysis (open triangles). Panel C presents the signal amplitudes c_fast (○) and c_slow (•) of the boundary components, respectively.

An alternative sedimentation velocity analysis approach is the extrapolation method by van Holde and Weischet to determine integral sedimentation coefficient distributions G(s) (51), which, to some extent, can unravel the effects of diffusion from sedimentation. The inset in Fig. 6 A shows G(s) distributions calculated on the basis of the least-squares algorithm described in Schuck et al. (41). In the absence of smoothing of the data, which may introduce bias in the subsequent analysis, the extrapolation of the high boundary fractions has the property of being very sensitive to noise and results in too small s-values. This is a limitation inherent in the extrapolation method requiring to locate the boundary fraction. This is particularly difficult at low signal/noise ratio and for regions of the sedimentation profiles with small gradient. Clearly, the integral sedimentation coefficient distributions would allow the correct diagnosis of the presence of the interaction, but would not permit a quantitative analysis. As described previously for the study of noninteracting mixtures, the van Holde-Weischet method cannot deconvolute diffusion from species that do not exhibit clearly separating boundaries (i.e., when the rms displacement from diffusion is smaller than the distance between boundary midpoints), and instead produces sloping G(s) profiles with intermediate s-values (41). This is due to the property of the inverse error function, on which the extrapolation is theoretically based, not being linear in its parameters. This problem is not addressed by the additional layer of extrapolation recently proposed (52). In theory, the average position of G(s) also does not lend itself to the analysis of weight-average sedimentation coefficients, as no rigorous relationship to mass conservation considerations are known (24). Similarly, in this case, no undisturbed boundary can be discerned, except for the presence of slower-sedimenting boundary contributions indicated by G(s) sloping to lower s-values. Further, even the maximum s-values of the G(s) distributions do not approach those expected for the fast boundary component (open triangles in Fig. 6 B).

The last aspect studied on the analysis of a 1:1 reaction of the type A + B ↔ AB was the performance of the multicomponent c_k(s) analysis from global multisignal analysis of the sedimentation profiles. For the conditions of Fig. 1, assuming equimolar concentrations, we simulated sedimentation profiles at two signals with twofold different extinction coefficients for A and B at both signals. As shown previously, the multicomponent c_k(s) analysis permits the determination of the separate sedimentation coefficient distributions of components A and B, and the determination of the molar ratio of the complexes formed (48). The component c_k(s) distributions are in excellent agreement with the composition of the asymptotic boundary, calculated as component boundaries dm_A,tot/dv and dm_B,tot/dv predicted via GJT (Fig. 7). If the ratio of the concentrations of A and B in the reaction boundary is calculated for this instantaneous reaction, equimolar concentrations 10-fold higher than K_D are required to achieve an 85% average saturation of the complex in the reaction boundary (inset in Fig. 7 B). However, if the concentration of B is lower (for example, c_B,tot = K_D), a concentration of A at c_A,tot = 10 K_D leads to a significantly higher saturation of the reaction boundary (95% for c_B,tot = K_D).

FIGURE 7.

Multicomponent c_k(s) analysis compared with the components of the asymptotic reaction boundary dm_A,tot/dv and dm_B,tot/dv predicted by GJT. Sedimentation parameters were the same as those given in Fig. 1, and Lamm equation solutions were calculated simulating two signals, each with twofold different extinction coefficients for component A and B, respectively. Loading concentrations were equimolar at 0.1-fold K_D (dark blue), 0.3-fold K_D (light blue), K_D (red), threefold K_D (green), and 10-fold K_D (gray). The presentation is analogous to that of Fig. 1, with the scaled c_k(s) distributions obtained for component A in panel A, and the c_k(s) distribution obtained for component B in panel B. The inset in panel B shows the molar ratio of the components A/B as calculated from integrating the reaction boundary peak of the respective c_k(s) distributions (circles), and the theoretically expected molar ratio of the reaction boundary from GJT (black line). For comparison, the theoretical isotherm of the molar ratio in the reaction boundary for the titration of constant concentration of B with increasing concentrations of A (analogous to that of Fig. 3) is shown in red, and the reverse titration of constant A with increasing B (analogous to that of Fig. 4) is shown in blue.

The motivation for examining the application of the c(s) analysis to the analysis of reaction boundaries was the observation that the reaction boundary sediments approximately with a single s- and D-value, which was predicted from the “constant bath” approximation. Interestingly, it has been shown that this also holds for reactions with stoichiometry >1:1 (43,44,53). Therefore, we also examined the application of c(s) to the analysis of sedimentation profiles from a two-site reaction A + 2B ↔ AB + B ↔ ABB. As before, we first generated sedimentation profiles by solving the Lamm equation with explicit reaction terms for a two-site reaction. The sedimentation profiles were calculated for an instantaneous reaction between molecule A (100 kDa, 6 S) with two identical noncooperative sites for a smaller ligand molecule B (50 kDa, 4 S), resulting in 8-S and 10-S complexes. The comparison of the c(s) analyses at different concentrations with the asymptotic boundaries for this reaction is shown in Fig. 8. Similar to the case of the reaction with 1:1 stoichiometry, the peaks of c(s) provide a good approximation of the undisturbed boundary and the reaction boundary predicted from GJT. Interestingly, here the broader sedimentation boundaries at concentrations >K_D,1 (the macroscopic binding constant of the first site) result in a double peak structure of c(s) (Fig. 8 A, black and green solid line). This appears to be caused by an overcompensation of diffusion. However, if the frictional ratio in the c(s) modeling is fixed to 1.3, broader structures consistent with dc/dv appear (short-dashed lines in Fig. 8 A). Independent of the frictional ratio value, the integral over the c(s) peaks of the reaction boundary (taken over the double peak structure) does reflect the correct weight-average s-value and amplitude of the reaction boundary, as shown in Fig. 8, B and C. (It should be noted that the double peak structure in Fig. 8 A can be easily distinguished from the peaks of a slow reaction A + B ↔ AB, which would also be expected to produce a total of three peaks, but with all peaks at constant position.) In comparison with the analysis of the overall weight-average s-value alone, the error analysis for the global isotherm model indicates an improvement in the statistical precision of the s-value of the 1:1 and 2:1 complexes by a factor of 100 and 5, respectively, and an improvement in the value of the binding constant by a factor of 50.

FIGURE 8.

Comparison of c(s) and dc/dv for the sedimentation of a two-site reaction A + 2B ↔ AB + B ↔ ABB with equivalent noncooperative sites. Sedimentation profiles were calculated on the basis of Lamm equation solutions with explicit reaction terms for instantaneous local equilibrium. The parameters were based on a molecule A (100 kDa, 6 S) with two identical noncooperative sites available for binding of a smaller ligand molecule B (50 kDa, 4 S), resulting in 8-S and 10-S complexes. Simulated concentrations were for A: 0.1-fold K_D,1 (dark blue), 0.3-fold K_D,1 (light blue), K_D,1 (red), threefold K_D,1 (green), and 10-fold K_D,1 (gray), and B in twofold molar excess of A, respectively. (A) Sedimentation coefficient distributions c(s) (solid lines, in units of fringes/S) for P = 0.9, and asymptotic reaction boundaries dc/dv calculated for the same parameters (solid bars, in units of fringes/S), with the corresponding undisturbed boundary indicated as solid circles (shown in fringe units). For comparison, the short-dashed lines indicate c(s) profiles calculated for the three highest concentrations with a frictional ratio fixed at 1.3. (B) Isotherms of s_fast, as derived from integration of the fast c(s) peak only (black circles), and s_w of the total sedimenting system derived from integration of the complete c(s) distribution (gray squares). The solid lines are the theoretically expected isotherms for s_fast from GJT (Eq. 4) and for s_w from mass action law at rest (Eq. 5), respectively. (C) Signal amplitudes c_fast (○) and c_slow (•) determined by integration of the c(s) peaks of the boundary components, and corresponding isotherms determined by GJT (solid lines).

A more stringent test for the GJT-based analysis of c(s) curves is a 2:1 reaction of smaller molecules, where the deconvolution of diffusion will be significantly more important. To examine a configuration with even broader reaction boundaries, we have simulated a 2:1 system where the bivalent species A is smaller than the ligand B. Further, we assume a titration series of constant concentration of A with an increasing concentration of B, which exhibits a switch in the species of the undisturbed boundary and the corresponding broadening of the reaction boundary (compare Fig. 4). Such sedimentation profiles were simulated with Lamm equation solutions for a receptor A (31 kDa, 2.66 S) with two indistinguishable and noncooperative sites for binding of a larger ligand B (45 kDa, 3.56 S), forming 4.96 S and 6.11 S complexes in instantaneous local equilibrium. The macroscopic K_D for site I (K_D,1) underlying the simulations is 1.7 μM. As shown in Fig. 9, dc/dv exhibits extremely broad reaction boundaries close to the transition point (black and blue bars in Fig. 9 A), similar to the situation encountered in Fig. 4 (green bar). Also, as in Fig. 4, at concentrations lower than the transition point the peak positions of neither c(s) nor dc/dv change very much with increasing concentration of B.

FIGURE 9.

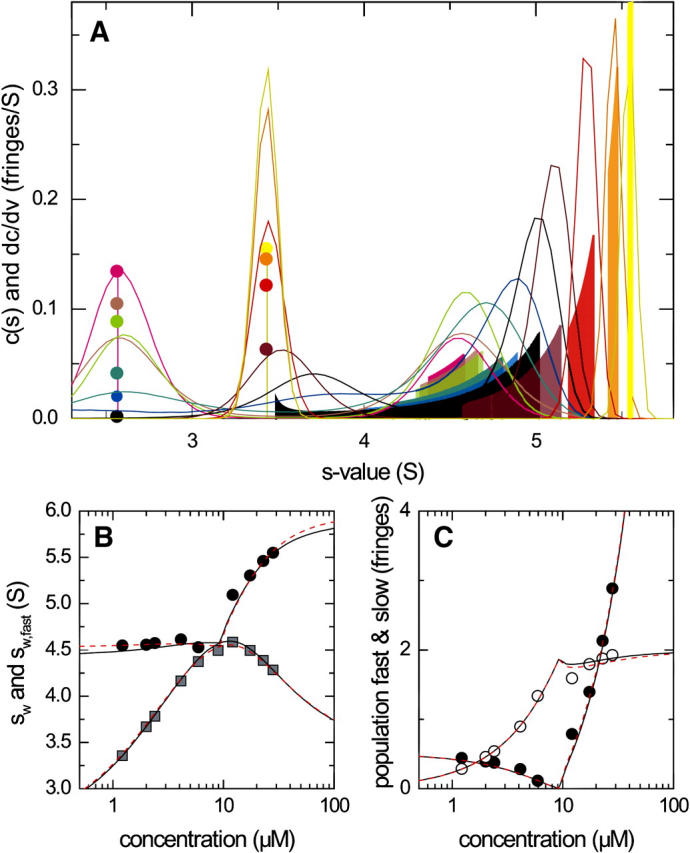
Comparison of c(s) and dc/dv for the sedimentation of a two-site reaction A + 2B ↔ AB + B ↔ ABB for small molecules. Sedimentation profiles were calculated as Lamm equation solutions with explicit reaction terms. The parameters were based on a molecule A (31 kDa, 2.66 S) with two identical noncooperative sites for binding of a smaller ligand molecule B (45 kDa, 3.56 S), resulting in 4.96- and 6.11-S complexes. An instantaneous reaction was assumed. Simulated concentrations were at constant 4.96 μM for A, and 1.24 (magenta), 2.05 (light gray), 2.44 (light green), 4.20 (light blue), 6.04 (blue), 9.14 (black), 12.4 (violet), 17.7 (red), 23.3 (orange), 28.7 (yellow) μM for B, respectively, with equivalent noninteracting sites with the macroscopic binding constant of site one of K_D,1 = 1.7 μM. (A) Sedimentation coefficient distributions c(s) based on a fit with optimized meniscus position, optimized f/f₀, and with the regularization scaled to P = 0.9 (solid lines, normalized, in units of fringes/S), and asymptotic reaction boundaries dc/dv calculated for the same parameters (solid bars, in units of fringes/S), with the corresponding undisturbed boundary indicated as solid circles (shown in fringe units). (B) Isotherms of s_fast, as derived from integration of the fast c(s) peak (black circles), and s_w of the total sedimenting system derived from integration of the complete c(s) distribution (gray squares). The black solid lines are the theoretically expected isotherms for s_fast from GJT (Eq. 4) and for s_w from mass action law at rest (Eq. 5), respectively; the red short-dashed lines are the corresponding best-fit isotherms, resulting in s-values for the complexes of 5.23 and 6.20 S, respectively, and a binding constant K_D,1 of 2.4 μM. (C) Signal amplitudes c_fast (○) and c_slow (•) determined by integration of the c(s) peaks, and corresponding isotherms expected by GJT (solid lines) and from the best fit of GJT isotherms (red short-dashed lines).

Overall, good agreement of c(s) with dc/dv is observed. Without additional knowledge, the width of the boundaries close to the transition point (black bar extending from 3.5 to 5 S) may result in a misinterpretation of the c(s) peak at 3.8 S (black line) as representing the new undisturbed boundary, shifted slightly to higher s-values. However, it may be possible to recognize, either from the superposition of c(s) traces at different concentrations, or by comparison with the expected s-value of the free ligand, that the 3.8- and 5-S peaks jointly reflect the reaction boundary. In any case, the trace in question was excluded from the GJT isotherm analysis shown in panels B and C. (It should be noted that in the alternative titration series in the design of Figs. 1 and 3, there is no transition, and therefore no ambiguity about this point.) The global fit resulted in parameter estimates for the s-values of the 1:1 and 2:1 complexes of 5.23 and 6.20 S, and a binding constant of 2.4 μM for K_D,1 (short-dashed red lines). As can be expected, the s-value of the 1:1 intermediate is the most difficult to determine from the sedimentation data. Nevertheless, using the weight-average s-values and the GJT isotherms jointly reduced the error estimates by factors of 10 (s_AB), 50 (s_ABB), and 20 (K_D), respectively, as compared to the analysis of s_w alone.

Because, in practice, it may not be known if the reaction rate of a given system of interacting proteins can be considered infinitely fast on the timescale of sedimentation, we have studied the effect of finite reaction rate constants. Fig. 10 shows the isotherms of a simulated sedimentation system equivalent to Fig. 9, except for having a finite rate of chemical reaction with an off-rate constant of 2.5 × 10⁻³/s. To make the analysis of the GJT isotherms realistic, the s-value of the fast boundary component at the transition point is not included. The effect of the finite reaction rate can be observed, for example, in the higher s-value of the reaction boundary (Fig. 10 A, circles compared to black solid line), and an underestimation of the signal amplitude of the reaction boundary (Fig. 10 B, open circles) combined with an overestimation of the signal of the undisturbed boundary (Fig. 10 B, solid circles). This can be understood considering that the finite reaction will lead to a longer persistence of the complex during sedimentation and lower concentrations of free species cosedimenting in the reaction boundary. If these deviations are ignored (because the reaction kinetics may not be known) the parameters derived from a fit of the GJT isotherms are K_D,1 = 2.3 μM, s_AB = 4.84 S, and s_ABB = 6.14 S, as compared to the values underlying the simulations of K_D,1 = 1.7 μM, s_AB = 4.53 S, and s_ABB = 6.08 S, respectively. The largest error appears in the s-value of the reaction intermediate, the 1:1 complex. Despite the deviations of the parameter estimates, the GJT isotherms still permit unequivocal assignment of the reaction scheme. The best fit with an impostor 1:1 interaction model is depicted in Fig. 10 as blue lines. It leads to sevenfold higher rms errors for the fit. Qualitatively similar results were observed with slower reactions with k_off < 10⁻³/s (data not shown).

FIGURE 10.

The effect of finite reaction kinetics on the isotherm analysis. Sedimentation profiles were simulated using the Lamm equation solution for the same conditions as presented in Fig. 9, but with a finite reaction rate characterized by a chemical off-rate constant of 2.5 × 10⁻³/s. Panel A shows the isotherms of s_fast (circles) and s_w (squares), respectively, as determined from integration of c(s) of the simulated data (symbols), and predicted from GJT and initial composition (black lines). The red lines indicate the best-fit isotherms with a 2:1 model (short-dashed and long-dashed lines for s_fast and s_w, respectively), the blue lines the best-fit isotherms from an impostor single-site model. Panel B shows the signal amplitudes c_fast (○) and c_slow (•) determined by integration of the c(s) peaks, and corresponding isotherms expected by GJT (solid lines) and from best fit of GJT isotherms (red lines) and from an impostor single-site model (short-dashed and long-dashed lines for c_fast and c_slow, respectively).

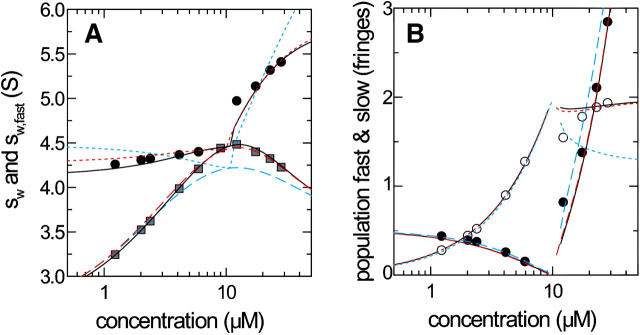
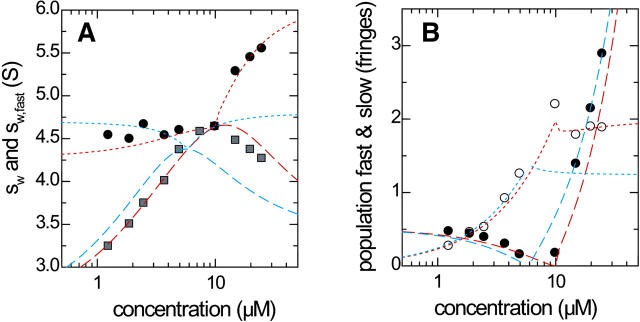
Finally, we applied the GJT-based analysis of the c(s) traces to the experimental data of a natural killer cell receptor Ly49C (31 kDa) interacting with a MHC molecule H-2Kb (45 kDa) sedimenting at 50,000 rpm (35). This interaction was previously shown to have a 2:1 stoichiometry with equivalent sites (35), and the experimental parameters and best-fit sedimentation parameters from Lamm equation modeling (26) are equivalent to those simulated in Fig. 10. The additional aspects of analyzing real experimental data were the appearance of c(s) peaks of small and very large species, most likely traces of impurities or degradation products. Further, occasionally multiple small peak structures appeared in the s-range of the free species, in addition to the main peak of the undisturbed boundary. As a practical approach to arrive at c_slow, we integrated the c(s) regions of the free species, as determined in the experiments with each component alone. Data sets where the reaction boundary could not be distinguished well from the undisturbed boundary were excluded from the GJT analysis, but included in the isotherm of s_w. Similarly, for data sets where the undisturbed boundary could not be satisfactorily assigned, the corresponding data point was excluded from the GJT isotherm analysis, but included in the s_w isotherm.

The s-values and amplitudes of the boundary components are shown in Fig. 11. Clearly, the quality of fit is not as good as that of the theoretical data set in Fig. 10. It was not possible to fit for the s-value of the transient 1:1 complex, as the parameter converged to unreasonably high values (5.8 S for the correct two-site model, and 7.5 S for the impostor single-site model). Therefore, this value was constrained to the sedimentation coefficient predicted using the program HYDRO (54) on the basis of the crystallographic structure (35). The best-fit estimates were 1.2 μM for the macroscopic K_D,1 of site 1, and 6.08 S for the sedimentation coefficient of the 2:1 complex (Fig. 11, red long-dashed lines), close to the results obtained from Lamm equation modeling (26). Further, qualitatively different isotherms were found with the best-fit parameters of the incorrect 1:1 interaction model (Fig. 11, blue short-dashed lines). Possible fractions of incompetent material in the loading mixtures were not considered in the fit.

FIGURE 11.

Analysis of experimental data from the sedimentation of a natural killer cell receptor Ly49C (31 kDa) interacting with a MHC molecules H-2Kb (45 kDa) sedimenting at 50,000 rpm (35). The experimental parameters and best-fit sedimentation parameters from Lamm equation modeling (26) are equivalent to those simulated in Fig. 10. Panel A shows s_fast (circles) and s_w (squares), respectively, as determined from integration of c(s) (symbols). The red lines indicate the best-fit GJT isotherms with a 2:1 model, the blue lines the best-fit isotherms from an impostor single-site model.

DISCUSSION

The quantitative analysis of the reaction-diffusion-sedimentation process in sedimentation velocity analytical ultracentrifugation studies can be approached by different strategies. Since it has become possible recently to rapidly solve the partial-differential equations governing sedimentation (the Lamm PDE), the global nonlinear regression of sedimentation profiles obtained at a series of different loading concentrations has become practical. In theory, this appears to be the most rigorous approach, but it depends on kinetic, thermodynamic, and hydrodynamic parameters that may not always be easily unraveled from experimental data (26). In practice, it can frequently be difficult to establish sufficiently well-defined experimental conditions, e.g., with regard to sample purity and microhomogeneity, to allow a complete and detailed model of the data with satisfying fit quality and unambiguous interpretation of the experiment. While it is a known strength of sedimentation velocity that it is sensitive to, and frequently can hydrodynamically resolve, even trace amounts of smaller and larger species in solution, this may in some cases also become a disadvantage for the robust analysis of reacting systems.

A popular and generally much more robust approach is the interpretation of the weight-average sedimentation coefficient as a function of loading concentration (8,31–38). The analysis of this isotherm does not depend on the reaction kinetics (except for a small influence caused by radial dilution), and permits a rigorous thermodynamic analysis of the interaction without requiring detailed interpretation of the shape of the sedimentation profiles, as long as a good empirical description of the sedimentation boundary can be found for the implicit mass conservation considerations (24). Although the isotherm analysis is well conditioned only if a large concentration range can be covered or if the sedimentation coefficients of the complexes are known, it is computationally considerably simpler and may serve to discriminate between alternative models for different reaction schemes. A practical advantage is that the weight-average s-values can be obtained by integration of the differential sedimentation coefficient distributions, which, in particular in conjunction with the c(s) analysis, may allow excluding from the analysis any sedimenting species not participating in the interaction of interest (24). So far, an open question has been how more information can be extracted from the structure of the sedimentation coefficient distributions, and in particular, how the details of the peak structure of the c(s) distribution can be interpreted for the interacting systems, other than representing the overall weight-average s-value. We have addressed this problem in this article and have proposed a new analytical approach for interacting systems that does not require the full Lamm equation modeling but nevertheless takes advantage of the structure of the sedimentation boundary.

Beyond the rigorous detailed description of the sedimentation with the Lamm PDE and the rigorous mass balance analysis in the form of analyzing the weight-average s-values, only approximate descriptions of the reaction-diffusion-sedimentation process are known. For reactions that can be considered essentially instantaneous on the timescale of sedimentation, Gilbert and Jenkins have described the characteristic shapes of asymptotic sedimentation boundaries obtained at infinite time (i.e., in the absence of diffusion), in a rectangular cell geometry, and with constant force (1,3). For two-component mixtures, the GJT predicts the presence of an undisturbed boundary component sedimenting with the s-values of one free species, and the velocity profile of the reaction boundary. This work has been very influential in the development and understanding of transport experiments of reacting systems. Although the asymptotic boundaries can, in principle, be experimentally determined by differential sedimentation approaches (45), this experimental technique has been dormant, as well as the quantitative use of GJT for data analysis.

In preparation for the quantitative use of GJT, in this work we have examined the influence of the assumption of rectangular geometry on the asymptotic boundary profiles, with the use of Lamm equation solutions of reacting particles in the limiting case of negligible diffusion. Our results show that the cell geometry has only small effects on the shape of dc/dv and on the weight-average s-value of the reaction boundary. A small overestimation of the s-value in GJT can be attributed to the effect of radial dilution, as discussed for self-associating systems in (24). Although this deviation is small and perhaps negligible in most cases, corrections can be applied by considering the time-averaged radial dilution introduced previously (24). As expected, the limiting case of infinite time in GJT corresponded to the limiting case of negligible diffusion at finite time.

A theory for a different special case of the reaction/diffusion/sedimentation process was described initially by Krauss and co-workers (43) and reintroduced by Urbanke and colleagues (20,44). It treats the sedimentation process of a reactive system in the presence of diffusion, at finite times, and in sector-shaped solution columns under the influence of a radial-dependent force, but assuming the concentration gradient of one free species A to vanish in the reaction boundary, such that a larger species B and the complexes AB sediment in a “constant bath” of the smaller species. Although this situation cannot be physically realized strictly, it is conceived as a special case for the interaction of small ligands with larger proteins. In the accompanying article, we have shown that it provides a useful and robust description also for proteins differing in size by only twofold (26). An important result of the “constant bath” approximation is that the reaction boundary (B+C) can be described by a single sedimentation s* and diffusion coefficient D*, a prediction that was shown to yield an excellent description of the sedimentation process (26). In this framework, the deconvolution of diffusion achieved in the c(s) analysis of reacting systems can be understood. Further, it can be argued that the finite gradients of the first free species A (which are originally neglected in the “constant bath” approach) will lead to a variation of the fractional occupation of the second species (C/(B+C)), which results in a dispersion of the sedimentation velocity of the reacting mixture that is represented in the shape and finite width of the c(s) profiles. To the extent that the effective diffusion D* of the reactive system does not vary greatly within the range of composition of the reaction boundary (compare Fig. 3 in (26)), and as long as the dispersion of the sedimentation velocity is not too large, the error in the deconvolution of diffusion based on a hydrodynamic scaling law of c(s) (D* ∼ s*^−1/2), as opposed to a composition-dependent value of D*, should remain small. To study if this approximation captures the essential qualitative and quantitative features of the sedimentation process, we solved the Lamm PDE for different configurations, and systematically compared the results of the c(s) analysis with the asymptotic boundaries of the GJT, thus testing the hypothesis that c(s) can be regarded as an approximation of the diffusion-free sedimentation coefficient distributions of the reacting system.

Despite the different theoretical framework and the different approximations made in the GJT (constant force, linear geometry, infinite time) and this c(s) interpretation (diffusion of the reaction boundary proceeds with D* ∼ s*^−1/2), very good agreement was observed overall, after making allowance for the fact that a finite signal/noise ratio does not permit sharp features in the sedimentation coefficient distributions to be resolved. This was true for both the conventional c(s) profiles as well as for the multicomponent c_k(s) distributions from global multisignal analysis (48). Deviations were found mainly for data with low signal/noise ratios, where the maximum entropy regularization employed in the c(s) approach is known to cause broadening and merging of adjacent peaks, as well as for configurations generating very broad reaction boundaries, such as those where the undisturbed boundary vanishes. These situations can be easily identified when considering a series of experiments at different loading concentrations. Some overcompensation of diffusion was observed for the two-site binding model, which could be identified by a drop in the apparent weight-average frictional coefficient obtained in the c(s) model, and could be eliminated by constraining this parameter. Further, some differences were observed in the two-site interaction of small molecules. It is unclear if the latter are a result of incorrect deconvolution of the diffusion, or simply a result of the boundaries not being sufficiently developed under these conditions to resemble the limit of infinite time assumed in the GJT. In any case, these deviations did not affect the excellent consistency of the amplitude of the undisturbed and both the amplitude and s-value of the reaction boundary from integration of c(s) with the predictions of GJT.

Therefore, we propose to use the isotherms of the amplitudes of both the undisturbed and the reaction boundary, as well as the average s-value of the reaction boundary as an analytical tool. This makes quantitative use of the bimodal shape of the reaction boundary of interacting two-component mixtures, thereby significantly improving the determination of the equilibrium constant of the interaction as well as the sedimentation coefficient (and therefore the hydrodynamic shape) of the complex. These isotherms are more generally applicable than the isotherms of the effective s-value of the “constant bath” theory, which we have examined previously (26), and additionally permit the interpretation of the boundary amplitudes (peak areas in c(s)). The new isotherms based on GJT modeled to the integrals of c(s) regions were found to be not very sensitive to deviations in the underlying assumption of an infinitely fast reaction. In fact, even a reaction that is very slow on the timescale of sedimentation appeared to provide satisfactory results (data not shown). Similarly, the isotherm analysis is not very sensitive to imperfect knowledge of the loading concentrations as would be encountered in the analysis of experimental data. Like the analysis of the overall weight-average s-values, it has the advantage that trace contaminations of material not participating in the reaction can be easily excluded from consideration. In the implementation in SEDPHAT, the global analysis of the isotherms of the overall weight-average sedimentation coefficients and that of the amplitudes and s-values of the reaction boundaries can be performed jointly, thus maximizing the information extracted from the experiment. Data points from experiments where the undisturbed and the reaction boundary components cannot be easily discerned can be excluded from the GJT-based isotherms.

We have systematically explored different regimes of loading concentrations that lead to qualitatively different behavior. Interestingly, at concentrations below K_D, the titration of a smaller species at constant concentration with increasing concentration of the larger species can lead to c(s) and dc/dv traces with very little change in peak position, potentially mimicking the concentration-independent peak positions of interacting mixtures with slow kinetics. Although the difference should be apparent from the lack of a third peak for the free larger species, and from the different s-value of the reaction boundary as compared to the s-value of the individual species, this highlights the importance of conducting experiments over a sufficient range of concentrations, including concentrations both significantly higher and lower than K_D. Another interesting feature of this titration design is the appearance of a transition point of the undisturbed boundary and a characteristic shape of the s_fast isotherm dependent on the reaction scheme.

Loading configurations with the concentration of the smaller component greater than K_D and in significant excess of the larger component, enable the closest approximation of the complex s-value by the reaction boundary, as well as the best approximation of the molar ratio for multicomponent c_k(s) analysis (55). Under these conditions, the s-value of the reaction boundary allows a significantly better representation of the s-value of the complex than is obtained from the weight-average s-value.

Regarding the analysis of the concentration dependence of the boundary amplitudes, it is well known that the undisturbed boundary does not accurately reflect the free concentration of the smaller species in the loading mixture. Although the contribution may be small, some free species of both components are always comigrating in the reaction boundary, and it is significant in this regard that the transition point of the GJT isotherms of Figs. 4 and 7 does not occur at equimolar loading concentration of the components. These effects are considered in the “population isotherms” model of the SEDPHAT software based on GJT, assuming a fast reaction on the timescale of sedimentation.

Beyond the original development and direct application of GJT (11,12,14), other approaches have been proposed to take advantage of boundary structure beyond the determination of the weight-average s_w. Correia suggested the use of higher averages, for example, z-averages and z + 1 averages as determined from integration of the apparent sedimentation coefficient distributions g(s*) derived from the dc/dt transformation (39). These averages were used previously to deduce qualitatively the presence of self-association (56), but the theoretical concept for their quantitative analysis was developed on the basis of s_z as a derivative s_z = d(cs_w)/dc of the isotherm s_w(c), with the values of s_w(c) being the experimentally determined quantities (57,58), and thus not reflecting on the boundary shapes. However, with regard to the moments of g(s*), it is unclear how the effects of diffusion could be taken into account, short of calculating full Lamm PDE solutions to derive s_z. The GJT-based isotherm analysis introduced in this work may also provide an alternative approach for the robust analysis of g*(s) distributions. Although the deconvolution of diffusion in c(s) is a key for the theoretical link between GJT and the analysis of the boundary structure via the experimentally determined sedimentation coefficient distributions, in many cases the boundary components may be discerned even from g*(s) traces (from either the least-squares method ls-g*(s) (50) or using the dc/dt transformation (59)), and the corresponding s_fast, c_fast, and c_slow values may be determined by integration. It could be envisioned that they be modeled with GJT-based isotherm presented here. On the other hand, it is not apparent to us that this would provide any advantage over the c(s)-based approach, as this would sacrifice resolution, could utilize only a fraction of the raw sedimentation data, and potentially introduce bias (60).

For self-associating systems, a different approach was suggested by Winzor and colleagues (13,61). It consists of the approximate elimination of diffusion contributions to the sedimentation boundary by extrapolation of boundary divisions to infinite time on an inverse timescale, similar to the van Holde-Weischet extrapolation (51). The resulting sedimentation coefficient distribution was interpreted in the framework of asymptotic boundaries of the GJT (13). This approach clearly displayed the presence of the self-association and the dispersion of the sedimentation coefficients in the reaction boundary. A limitation of this approximation is that unraveling the diffusion through extrapolation to infinite time is successful only for single species or where multiple species show clearly separating sedimentation boundaries (41). It is not clear that this approach is sufficiently well defined for reaction boundaries to permit quantitative modeling. Krauss and co-workers have taken diffusion into account more rigorously for heterogeneous interactions of a macromolecule with a small ligand (43). They have introduced the “constant bath” approximation of the Lamm equation, which allows making full use of the average s-value of the reaction boundaries (26,43,44). As described in the accompanying article (26), the isotherm of s_fast(c) from the “constant bath” approximation is virtually identical to that of GJT, and can be extended to take advantage of diffusional deconvolution of c(s), but it is restricted to the experimental configurations for which the “constant bath” approximation holds. Thus, to fully exploit the structure of the reaction boundary as an analytical tool in addition to the weight-average s-value, we suggest that the combination of diffusional deconvolution of c(s) in combination with the general and rigorous theoretical framework of GJT could be advantageous.

In summary, we have compared the sedimentation coefficient distributions c(s) and the asymptotic boundary profiles dc/dv from GJT, and found very good qualitative and quantitative agreement. Although both approaches are based on different approximations of the Lamm PDE, their consistency can be understood on the basis of the “constant bath” approximation (26,43), and is supported by systematic computer simulations using the full Lamm PDE (26). This view provides a new approach for obtaining robust information from experimental sedimentation velocity data of protein-protein interactions by exploiting quantitatively the bimodal structure of the reaction boundary. Although we have examined reactions with 1:1 and 2:1 stoichiometry, employing the same strategy, this approach may be extended to the analysis of experimental data from other reaction schemes, if the full solution of the Lamm PDE can be used to demonstrate the consistency of GJT and c(s).