An Empirical Extremum Principle for the Hill Coefficient in Ligand-Protein Interactions Showing Negative Cooperativity

Abstract

The Hill coefficient (n_H) is a central parameter in the study of ligand-protein interactions, which measures the degree of cooperativity between subunits that bind the ligand in multisubunit proteins. The most common usage of n_H is as an estimate of the minimal number of interacting binding sites in positively cooperating systems. In the present study, a statistical interpretation of n_H for a generalized system of multiple identical binding sites is developed. This interpretation is then applied to the derivation of an empirical extremum principle for n_H in negatively cooperating systems of identical binding sites, which can be used for the estimation of the minimal number of interacting sites in such systems.

INTRODUCTION

Dating back to the studies by Hill (1) on oxygen binding to hemoglobin, the phenomenon of cooperative binding of small molecule ligands to multimeric proteins has held a special role in the understanding of physiological regulation of protein and enzyme function. For systems exhibiting positive cooperativity, it has been demonstrated that the Hill coefficient, n_H, places a lower limit for the number of interacting sites on the protein (2,3). Comprehensive theoretical studies of various models of cooperative and allosteric systems have been published, as well as more generalized treatises. In particular, J. Wyman and various colleagues have contributed much to the analysis of the binding curves of cooperative systems (4–6). Such analyses are based on the general partition function dictated by the Adair equation, and show that n_H is related to the variance of the binding number (the average occupancy of the protein taken over the whole ensemble). These studies proved mathematically that n_H is a lower limit on the number of interacting sites, in positively cooperating systems (3). This extremum principle is highly useful in that it allows experimentalists to estimate the minimum number of binding sites on the protein and to compare this result with direct physical measurements. Negative cooperativity, a phenomenon in which binding at one site interferes with binding to additional, identical sites on the protein, is less well understood (7–11). Specifically an extremum principle is unknown for such systems, and there is no method to estimate the minimal number of interacting binding sites. Indeed, under the assumptions of the Koshland-Nemethy-Filmer model, the minimal theoretical value of n_H is 0. However, n_H is inherently an empirical entity, and the experimental conditions impose additional constraints on its values. The identification of an empirical lower limit for n_H is an important issue since one of the main stumbling blocks in the identification of negatively cooperating systems is the fact that a mixture of nonidentical binding sites will also yield an n_H value <1, and unless comprehensive additional studies are undertaken to prove that the binding sites are a priori identical, it is not possible to identify a system as a negatively cooperating system using only the fact that n_H < 1 (12). Here, I have extended previous analyses by demonstrating that n_H can be described wholly in statistical terms as the ratio of the variance of the binding number to the variance of the binding number in a reference system consisting of an identical number of noninteracting binding sites. This additional generalization allows the derivation of an analogous extremum principle for systems with negative cooperative interactions between binding sites, showing that the minimum empirical value of n_H in a negatively cooperating system of N identical binding sites is 1/N, assuming that one uses the empirical saturation point as the absolute saturation point, without reference to the theoretical saturation capacity of the system. Since such a restriction does not hold for a system of N independent nonidentical binding sites, this finding provides an additional tool for distinguishing bona fide negative cooperativity from a mixture of binding sites.

THEORY

Consider a macromolecule P, which contains N identical sites for ligand L. We define the general (macroscopic) formation constants K_n for the n^th ligated species of the macromolecule as

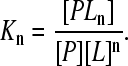(1)

The generalized Adair equation becomes

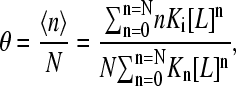(2)

where θ denotes the fractional occupancy and 〈n〉 is the average binding number. As shown by others (2), the slope of the Hill plot for this scheme is

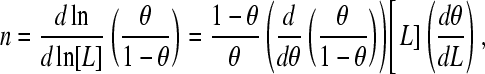(3)

which simplifies to (2,4)

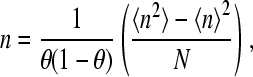(4)

where 〈n²〉–〈n〉² is the variance of the binding number (2). I now wish to point out that the term Nθ(1 − θ) is simply the variance of the binomial distribution case where the probability of a site to be bound by the ligand is θ and the probability for a site to be unoccupied is 1 − θ. This is the case for a noncooperative protein with the same fractional saturation at the same ligand concentration. Therefore the slope of the Hill plot for a generalized Adair equation can be written as

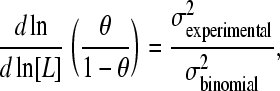(5)

where σ is the standard deviation of the binding number. This interpretation of the Hill plot holds for all values of θ. Since the Hill coefficient is defined as the slope of the Hill plot at 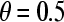, we can write for n_H that

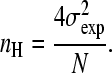(6)

One can readily verify that this equation will reduce to N in the extremum case of infinite positive cooperativity; in this case, the only observable forms of the protein are the unligated and the fully ligated species. Thus, at a saturation of 0.5 the standard deviation of the occupancy will be equal toN/2, and we can write

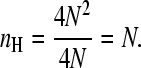(7)

Derivation of an empirical extremum principle for a negatively cooperating system of N identical binding sites

In contrast with the extremum case for positive cooperativity, in which no intermediately ligated species can be observed, I wish to define an empirical extremum scenario for negative cooperativity as a system with N identical binding sites where the first ligand binds with a finite dissociation constant, but subsequent bindings show an infinitely large dissociation constant. The experimental binding isotherm will reach an asymptote in which one ligand is bound. Subsequently, the observed (as opposed to the theoretical) maximal binding number is 1 and the standard deviation at the apparent fractional occupancy of 0.5, will be 0.5. By substituting these values into Eq. 6, we find for the slope of the Hill plot at θ_app = 0.5 that

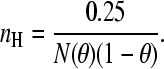(8)

The minimal value of 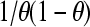is 4: this can be readily derived by setting the derivative with respect to θ to 0 and identifying the value of θ at the extremum as 0.5. Hence the actual value of Nθ(1 − θ) (Eq. 4) will not exceed N/4, and the slope of the Hill plot at the experimentally determined half-saturation point cannot be <1/N, and we can write

(9)

It is important to stress that this analysis is predicated on the fact that N (or more precisely, b_max, which equals N[P], where [P] is the protein concentration) is not explicitly known to the experimentalist; we assume that the experimentalist chooses the half-saturation point empirically according to standard curve-fitting procedures, at the concentration that yields one-half the extrapolated saturation value. If one uses the true value of N to define the half-saturation point (e.g., 2 in a tetramer) instead of the empirical saturation point, one is not able to derive this relationship, and the theoretical limit of n_H becomes 0, as predicted by simple Koshland-Nemethy-Filmer models with infinite interaction between sites (13). A more general approach to this issue is to point out that a minimal variance would require the protein to be in one of two binding states; inclusion of additional binding states would increase the variance. Since the half-saturation point would be between the two binding states, and neglecting other binding states, one arrives again at a binomial two-state distribution. Since the minimal Δn between any two states is 1, we arrive at the same 0.25 value for the minimal variance of a binding curve for a homogeneous population of sites at half-saturation.

Distinguishing negative cooperativity from a mixture of binding sites

One of the problematic aspects of negative cooperativity is that a Hill coefficient less than unity can be observed with a heterogeneous mixture of binding sites, without assuming interactions between the sites. If we can demonstrate that a mixture of sites can empirically reach arbitrarily small values of n_H, this will add a tool for distinguishing the two cases.

One may derive an expression for the average fractional saturation of a mixture of N monomer classes with different dissociation constants K_i, as

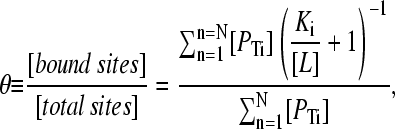(10)

where [P_Ti] denotes the total concentration of protein species i, K_i is the dissociation constant for the i^th protein species with the ligand L, 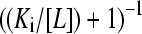is the fractional saturation of the i^th species (or θ_i), and the summation runs over N protein species. This expression may be simplified by the introduction of the statistical weight α_i, such that

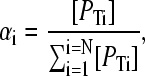(11)

and therefore

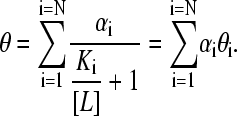(12)

We can write for the slope of the Hill plot, from Eq. 3,

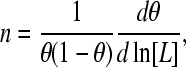(13)

and differentiating Eq. 12 with respect to ln[L], we obtain

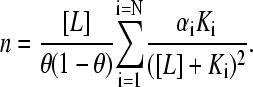(14)

Note that in this case N is the number of species, and is not linked to properties of the individual protein molecules. Therefore, the slope cannot have a lower limit that is related to the number of subunits. An extremum situation for a mixture, analogous to that derived above for an N-mer of equivalent binding sites, occurs when one of the species (species 1 for the sake of discussion) has a much smaller dissociation constant than the rest such that there exists a range of [L] in the experimental isotherm where K₁ ≪ [L] ≪ K_i holds, for all i ≠ 1. This implies that species 1 is saturated under conditions where binding of the ligand to other species is negligible. As before, the experimentalist observes only the K₁ isotherm, and higher terms in the summation are negligible at the half-saturation point of the K₁ species. In this case, Eq. 14 reduces to

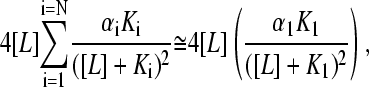(15)

since all θ_i ≅ 0 for i > 1. As the experimentalist has chosen the halfway point of the K₁ isotherm as the halfway point of the whole titration, one may also approximate [L] ≈ K₁, and the expression for the slope of the Hill plot at the experimental half-saturation point is then further simplified as

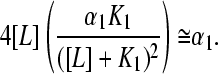(16)

This treatment yields an arbitrarily small value of n_H for a mixture, since there are no a priori minimal value constraints on α_i that depend on molecular properties of the binding species.

Examples of n_H values for known proteins and enzymes with negative cooperativity

To verify the relevance of these derivations, one may survey recent literature and compare n_H values of characterized enzymes (Table 1). Of the 11 enzymes listed in Table 1 with negative cooperativity, and which have a known subunit composition, none have an n_H value of <1/N. In addition, it should be noted that higher oligomerization states are able to reach lower n_H values, as predicted from the derivation described above.

TABLE 1.

N and n_H values for documented protein-ligand and enzyme-substrate interactions showing negative cooperativity

Enzyme	Binding sites/subunits	N	nH	Reference
Adenylosuccinate synthase	Dimer	2	0.8	(16)
Human glutathione synthetase	Dimer	2	0.75	(17)
V-ATPase	Hexamer	6	0.16 ±0.03	(18)
NAD-dependent glutamate dehydrogenase	Tetramer	4	0.3	(19)
UDP-GlcNAc 2-epimerase	Hexamer	6	0.45	(20)
Glyceraldehyde-3-phosphate dehydrogenase	Tetramer	4	0.64	(21)
Glutathione-S-transferase P1-1	Dimer	2	0.65 (5°C)	(22)
Metabotropic glutamate receptor	Dimer	2	0.55	(23)
Aspartate kinase	Dimer	2	0.7	(24)
Deoxycytidine kinase	Dimer	2	0.6	(25)
ATP citrate lyase	Tetramer	4	0.45	(26)

DISCUSSION

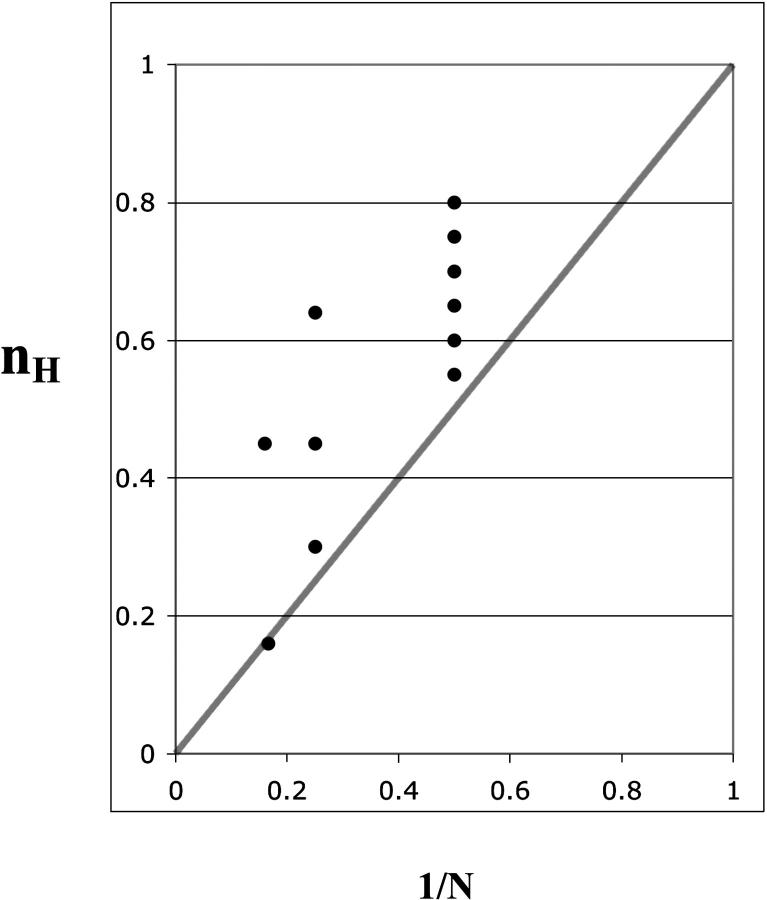
The extremum principle derived in this presentation is an empirically useful relationship that complements the well-known mathematical limit to the Hill coefficient at positive cooperativity. The experimentally derived values for known cases of negative cooperativity in which quaternary structures have been determined are in striking agreement to the central prediction, which limits n_H to values >1/N in cases of true negative cooperativity. In Fig. 1, we observe a series of parallel vertical arrays of data points, each defining a line that represents a given N. In the dataset of Fig. 1, I have represented N = 2, 4, and 6, as described in Table 1. One can observe that there are six dimers in the data set, three tetramers, and two hexamers. Despite the paucity of higher oligomerization states, it is evident that as N increases, the data points reach lower values of n_H, and in addition reach values closer to the theoretical limit of 1/N. In particular, the experimental value for V-ATPase (0.16 ± 0.03) is within experimental error of the limit (0.16666…). These results are in agreement with the predictions of the 1/N rule. This relationship can therefore be used as a rule of thumb for gauging the degree of coupling between sites. A particularly instructive case, which has been omitted from Table 1, is that of dopamine β-mono-oxygenase. This is a tetrameric enzyme, which shows negative cooperativity with respect to ascorbate. The measured n_H was found to be 0.15–0.30, and showed batch-dependent variability (14). Subsequently, it was shown that the protein exists as a mixture of dimers and tetramers, which have different kinetic parameters (15). Although both forms of the enzyme show negative cooperativity, the difference in kinetic parameters between the two forms creates a mixture of catalytic sites which leads, in some preparations, to a lower than expected value of n_H. This demonstrates a practical application of the 1/N rule—that the observation of n_H values <0.25 for a tetramer indeed correlates with the existence of a mixture of binding sites.

FIGURE 1.

Graphic representation of n_H versus 1/N for the interactions documented in Table 1. The diagonal line indicates the 1/N limiting value for n_H.