Main Phase Transitions in Supported Lipid Single-Bilayer

Abstract

We have studied the phase transitions of a phospholipidic single-bilayer supported on a mica substrate by real-time temperature-controlled atomic force microscopy. We show the existence of two phase transitions in this bilayer that we attribute to two gel (L_β)/fluid (L_α) transitions, corresponding to the independent melting of each leaflet of the bilayer. The ratio of each phase with temperature and the large broadening of the transitions' widths have been interpreted through a basic thermodynamic framework in which the surface tension varies during the transitions. The experimental data can be fit with such a model using known thermodynamic parameters.

INTRODUCTION

In addition to their crucial importance in the biological and medical fields, phospholipidic biomembranes have received great interest recently for their applications in nano- and microtechnology. Supported on a solid substrate, these membranes enable the biofunctionalization of inorganic solids or polymeric materials (1,2). Because these membranes are highly electrically resistant, and ordered, they can be used for biosensor technologies based on electrical and optical detections. Indeed, they provide a perfect matrix for embedding natural or artificial ion channels or for incorporating receptors for target/receptors detection such as bodies/antibodies detection. In the past few years, large amount of work has been reported on the properties of phosphatidylcholine (PC) with different structures: monolayer, single- or multibilayers, free-standing or supported on a substrate (3–9). One of the most interesting properties of these lipids relies on their ability to realize phase transitions between different states with changes in temperature. The main transition is a gel/fluid transition attributed to the melting of the lipids' carbon chain. This transition is of great interest, since, in the fluid state, the supported lipids provide a lateral fluidity to the system in the plane of the substrate. In addition to this main transition, many of these studies have reported the presence of other gel/gel transitions at lower temperature.

The presence of these transitions depends on the lipid type chosen for the study as well as on its structure (7,10,11). Although these phase transitions have been studied for different lipids by many techniques (12–14), the study of supported bilayers has seen a renewal in the last 10 years with the use of atomic force microscopy (AFM), which offers a direct observation of the surface. Many articles report the observation of the main gel/fluid transition for monotype lipid or lipid mixtures by AFM, but few works present data obtained in real-time by AFM with a temperature-controlled system. Among these studies, Tokumasu et al. (12) and Feng Xie et al. (14) have studied the gel/fluid phase transition of single-bilayers of 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) on mica. In contrast to a free-standing bilayer (FSB) for which the main transition is sharp (the transition width is lower than 1°C; see Ref. 13) and occurs at 23.7°C (7), they show that the transition in the supported bilayer is much broader (8°C) and shifted to ∼28°C (12). Tokumasu et al. (12) explain this large transition width through a finite-size-limited first-order transition model in which the diameter of intrinsic domains is 4.2 nm, whereas Feng Xie et al. (14) interpret this behavior in the framework of a classic van't Hoff transition.

In this work, we also present a temperature-controlled AFM study of DMPC single-bilayers supported on a mica substrate. Although our results are similar to those of Tokumasu et al. (12) and Feng Xie et al. (14), sharing features such as the transition width and the temperature shift, our interpretation differs drastically. We model these properties with a basic thermodynamic framework without the use of more elaborated theory as has been done previously. In contrast to vesicles, the transition in supported layers occurs at nearly constant surface area. Simply taking into account this fact, we show that the expected temperature transition width corresponds to the observed temperature width measured by AFM. In addition, we show the existence of two independent transitions on a supported single-bilayer that we attribute to the independent melting of each leaflet of the bilayer.

MATERIALS AND METHODS

Sample preparation

DMPC (Avanti Polar Lipids, Birmingham, AL) was used without further purification. Multilamellar vesicles were obtained by dispersing 10 mg/ml of DMPC in 10 mM NaCl. The dispersion was then sonicated for 30 min to obtain large unilamellar vesicles. Small unilamellar vesicles were subsequently obtained by extrusion using an extruder with a polycarbonate filter pore size of 100 nm (Avestin, Ottawa, Canada). Because we consider that lipid is conserved during extrusion, a final vesicle solution of 1 mg/ml is obtained by diluting the extrusion product in 10 mM NaCl.

Muscovite mica disks (JBG-Metafix, Montdidier, France) are used as substrates. Bilayers are obtained by the fusion of DMPC vesicles onto the mica substrate. Before each lipid adsorption, the mica samples are cleaved and set in our liquid cell with 200 μl of 10 mM NaCl solution. The subsequent addition of 200 μl DMPC vesicles solution (at 1 mg/ml, 10 mM NaCl) at room temperature (22–23°C, just below the FSB transition temperature) followed by an active stirring leads to the formation of a single-bilayer over the substrate, with a surface coverage of 95–98%. Before the AFM experiments, the liquid cell is rinsed many times with 10 mM NaCl solution to remove the excess DMPC vesicles without drying the sample.

Temperature-controlled atomic force microscopy

The heating and cooling system consists of a Peltier element located directly below the sample. The liquid cell is placed on top of the sample. The temperature is monitored by a homemade thermocouple of type K maintained directly on top of the sample. The measured temperature is a relative temperature with respect to the room temperature, which is monitored separately with a thermometer. This experimental setup allows us to follow the lipid bilayer under the AFM from 5°C to 65°C in a real-time continuous acquisition. All imaging was carried out in liquid tapping mode using a stand-alone AFM from NT-MDT (Zelenograd, Moscow, Russia).

Image acquisition and processing

Images were taken at a scan rate of 1 Hz while the sample was continuously heated under the AFM at 0.1°C/min. All the AFM data were converted to JPEG files. To estimate the percentage of each phase and holes, we used the color range selection function of the software Photoshop (Adobe Systems, San Jose, CA). The percentage of each phase and hole were obtained by counting the pixels of the corresponding range of color.

RESULTS AND DISCUSSION

Self-limited single-bilayer formation of supported DMPC on mica

Supported bilayers are obtained by the fusion of vesicles onto the mica substrate. The formation of either single- or multibilayers depends on the lipid type and on the salinity of the solution. In 10 mM MgCl₂ or isopropanol (15), for example, DMPC is known to form multibilayers. In Fig. 1, a–d, we have followed the formation of the layer starting from few islands on the mica surface to a nearly complete bilayer (between each image, 2.5 μl of DMPC were stirred in). Further addition of lipids (Fig. 1 e) did not change the surface, and there are no indications of an extra bilayer formation on top of the first one. Moreover, the cross-section shown in Fig. 1 f (taken along the line in Fig. 1 b) indicates a height of ∼4.5 nm, which is in agreement with the height of a typical DMPC bilayer (4). These results show that in 10 mM NaCl the vesicle fusion is self-limited after the first bilayer formation. This point will be important later for the interpretation of the data. In the following, supported bilayers on mica were obtained as described previously.

FIGURE 1.

AFM images (8 × 2.5 μm) of the lipid bilayer formation in 10⁻² M NaCl. Between each image, 2.5 μl of DMPC at 10 mg/ml has been added and stirred in the solution. The vesicle fusion is self-limited after the first bilayer.

Phase transitions

The data reported in this article have been obtained from three different samples. Each of these samples presents the same features with, however, few differences in the transition temperatures as later shown. The values of the transition temperatures indicated below are the average of the temperatures obtained on the three different samples. A set of data is reported in Fig. 2 for temperatures in the range 26–43.6°C (since the sample is heated continuously, the temperature indicated on each image corresponds to the temperature in the middle of the image). At 26°C, the bilayer is nearly complete with the presence of small black areas. The measured height contrast between those black areas and the rest of the surface is ∼4.5 nm, and it corresponds to the thickness of a DMPC bilayer. They are attributed to holes in the bilayer. As the temperature increases, small islands appear on the surface (see Fig. 2). Such islands have already been observed by AFM and have been attributed to different phases where the lower phase (darker contrast) corresponds to a fluid phase whereas the upper one (lighter contrast) is gel (6,12,14). This contrast arises from the height difference of the lipids in the fluid and the gel states as well as from differences in the viscoelasticity of the two phases (16,17). Starting from the gel phase at room temperature (22–23°C), the fluid phase begins to appear at an average temperature of 27°C (between 26 and 27.5°C, depending on the sample) and the fluid/gel phase ratio increases slowly with temperature to 1 at an average temperature of 33°C (between 32 and 35°C; see Fig. 2). Simultaneously, holes present in the layer at the beginning of the experiment close during the transition (transition 1). So far, these data are similar to the ones obtained by Tokumasu et al. (12) and Feng Xie et al. (14). Before further describing the experiment, note that at a heating rate of 0.1°C/min, the bilayer seems to be at equilibrium. That is, if we stop the heating at a given temperature and take several images of the same location for an hour we do not see any evolution. As seen in Fig. 2, heating to higher temperature leads to the observation of a second transition sharing similar features with transition 1. This transition (transition 2) starts and ends at average temperatures of 39.5°C (between 36 and 42.5°C) and 44.5°C (between 42 and 47°C). To ensure that these transitions are not issued from metastable states, we have checked their reversibility. Repeated heating and cooling always show the presence of the two transitions excluding metastable states. Fig. 3 shows transition 1 and the holes' evolution with both increasing and decreasing temperatures. Although reversible, both transitions 1 and 2 show the presence of a 1–2°C hysteresis when cooling the sample with respect to the transition temperature when heating. Another feature of the first transition is the reversibility of the closing and opening of the holes. Holes that close when heating the sample reopen when cooling.

FIGURE 2.

AFM images (3 × 3 μm) of transitions 1 and 2 of the DMPC supported single-bilayer at different temperatures. The darkest areas are holes in the bilayer. The sample is continuously heated under the AFM tip at a rate of 0.1°C/min. The temperature indicated in each image corresponds to the temperature in the middle of the image.

FIGURE 3.

Experimental curves of transition 1 (open triangles) and evolution of holes (solid triangles) at increasing and decreasing temperatures.

Our data shows for the first time the presence of two transitions, or three phases, on a supported single-bilayer. Prior to this work, the presence of more than one transition has only been observed on supported lipid multibilayers or FSBs (6,7,10,18,19,20). These transitions are commonly attributed to the presence of many gel phases such as L_c subgel, L_β gel, 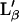gel, and P_β ripple. One may therefore think that transition 1 observed in our experiment is a gel/gel transition whereas transition 2 would be the main gel/fluid transition. However, we exclude the presence of a gel/gel transition. Indeed, one could consider two cases. The first one is a planar (L_c subgel, L_β gel, ) to ripple gel (P_β, ) transition. Because our high resolution AFM images show neither the modulations created by the lipids (9) nor the crystallographic orientation of the domains expected in the ripple phase (6,20), we exclude this possibility. The other possibility would be a transition between two different planar gel phases. We think that the relatively large height contrast (0.4–0.7 nm) observed with AFM during transition 1 cannot originate from the low difference in structural and viscosity properties between the two involved phases. Instead, we propose that the origin of the two transitions arises from the fusion at different temperatures of each leaflet of the bilayer. The same height difference observed in AFM between the two phases involved in both transitions concurs with this assumption. Indeed, the two leaflets of the bilayer are not equivalent; one is at the lipid/substrate interface (inner leaflet), whereas the other one (outer leaflet) is at the lipid/solution interface. Therefore, only the inner leaflet can significantly interact with the substrate. From this viewpoint, the two leaflets of the bilayer are expected to have different transition temperatures, and the two observed transitions are both expected to be fluid/gel transitions. This interpretation is supported by previous differential scanning calorimetric experiments on supported DPPC bilayers on mica where two transitions above the main transition temperature of vesicles were observed (21). Because ripple phases are excluded, we suppose the gel phase of both leaflets to be in the 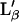state (7), whereas their fluid phase is in the L_α state.

In comparison with the gel/fluid transition temperature observed for free standing DMPC vesicles (23.7°C; see Ref. 7), the transition in the supported bilayer occurs at higher temperature. The beginning of the transition is shifted by 2–3.5°C and the end of the transition is shifted by 8–11°C with respect to the main transition temperature of vesicles. Such shifts in transition temperature have been reported in previous studies between FSB and DMPC-supported bilayers on mica (12,14). We could attribute this phenomenon to the substrate interaction with the first layer that would limit the membrane fluctuations. Although this limitation should induce a transition temperature shift, we believe the effect is weak compared to the one induced by the difference of surface tension between an FSB and a bilayer supported on a substrate. Another major difference in the behavior of FSB and supported DMPC bilayers is the transition widths (FSB have transition widths much smaller than 1°C). The large widths observed for a supported bilayer have been interpreted through a finite-size-limited first-order transition model or in a van't Hoff theory framework (12,14). In the following section, we calculate the transition width simply taking into account that the transition in supported layers does not occur at constant tension as in the case of vesicles. We will show that this difference is sufficient to explain the large temperature width of the transition.

Model

In a free-standing bilayer, the variation in molecular area during the transition is at least 12% (depending on the initial gel phase; see Ref. 7). To spread on the surface during the transition, the supported-bilayer needs a lipid-free area either on the surface or to leave the substrate. We have excluded the latter possibility. In our case the variation of surface corresponding to the filling of the holes in the surface is ∼2%. Compared to the variation of molecular area in the FSB, this limited surface variation implies the tension in the bilayer changes in the transition to maintain a constant average molecular area in the layer. Therefore, in contrast with FSB in solution for which the transitions occur at constant tension and variable surface, the transition in the supported single-bilayer occurs at variable surface tension and nearly constant surface. During the transition, the equilibrium temperatures at different gel/fluid ratios correspond to melting temperatures at different surface tensions. In a basic model of constant surface transition, the ratio of each phase, the temperature, and the surface tension can be easily related to the parameters measured for a transition at constant tension. The shift in surface tension and the shift in melting temperature, with respect to those of an FSB, are related by the Clausius-Clapeyron equation

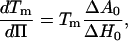(1)

where Π is the surface tension and T_m is the transition temperature of the vesicle. Its value is 23.7°C (7) for DMPC. The values ΔH₀ and ΔA₀ are, respectively, the melting enthalpy and variations in the molecular area between the gel and the fluid phases during a transition at constant tension. For small variations in transition temperature, this leads to

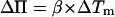(2)

with 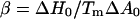(see Ref. 22).

At a given temperature T during the transition, if one assumes the gel-to-fluid phases ratio to be at equilibrium, Eq. 2 allows the evaluation of the tension shift in the supported layer ΔΠ with respect to the tension of a vesicle with ΔT_m = T − T_m. Obviously, the surface tension shift originates from the surface's inability to expand during the transition. This means that the fluid phase is compressed compared to the fluid phase of an FSB. For a given phase, the variation in molecular area is related to the variation in tension and the variation in temperature by

(3)

where κ is the bilayer compressibility, K is the thermal expansion coefficient, and A is the molecular area. Equation 3, written for the gel or the fluid phase, and Eq. 2 give

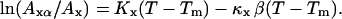(4)

Depending on whether we consider the fluid or the gel phase, A_x is either the gel molecular area (A_g) or the fluid molecular area (A_f) of an FSB near its transition temperature, and A_xα is the molecular area of the considered phase for a supported bilayer during the transition at the considered temperature T (A_fα and A_gα are the molecular areas of, respectively, the fluid and the gel phase corresponding to a fluid phase ratio α). With Eq. 4 one can evaluate the relative molecular area of each phase during the transition of the supported layer with respect to the molecular area of the corresponding phases in an FSB at T_m.

We now consider the transition starting from a gelled supported layer with the same molecular area as in an FSB. This transition occurs at constant surface and constant matter. These assumptions lead to

(5)

where α is the ratio of the fluid phase, and A_fα and A_gα are the molecular areas in, respectively, the fluid and the gel phases for a given α. With Eqs. 4 and 5, a relationship between the ratio of one phase and the temperature can be easily established as

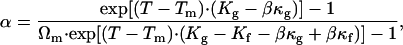(6)

with Ω_m = A_g/A_f corresponding to the molecular area ratio between the fluid and the gel states for the FSB at T_m. This relation is plotted on Fig. 4.

FIGURE 4.

Calculated curve of the percentage of gel phase versus temperature. In this calculation we consider a simple transition at constant surface and constant matter.

For κ_f, κ_g, K_f, and K_g, we have chosen typical values found in the literature for bilayers: for the L_α phase, κ_f ∼ 6.9 m²/J (13), K_f = 5 10⁻³ K⁻¹ (23); and for the gel planar phase 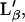κ_g∼1.1 m²/J (13), K_g = 6.5 10⁻⁴ K⁻¹ (23). For ΔH₀ and ΔA₀, different values can be found in the literature leading to a large dispersion of β (between 1.5 10⁻³ Jm⁻² K⁻¹ and 2.7 10⁻³ Jm⁻² K⁻¹) (13,24). We have chosen a value determined from experimental measurements on a Langmuir monolayer of DPPG (25) (β = 2.16 10⁻³ Jm⁻² K⁻¹ for a bilayer). The value of Ω_m was taken from the literature for the 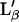-L_α transition (7) (Ω_m = 0.88). It is important to notice that whereas the value of β doubles if we consider a bilayer instead of a leaflet, the value of κ is halved. As K is the same for both the leaflet and the bilayer, Eqs. 4 and 6, written with values for the bilayer, remains valid for a single leaflet (and vice versa). Thus, the calculation can be applied to model a bilayer transition or an independent single leaflet transition (this assumes a weak coupling between leaflets). Fig. 4 shows that the transition is accompanied by a large temperature width. Thus, although this constant surface transition model does not fit our data, we believe the large temperature width observed in AFM experiments must be attributed to a nearly constant surface transition. To improve the agreement with our data, we must consider other factors. First, hole-closing is observed during the transition leading to a small variation in the layer surface. Second, even though the supported layer is obtained from gelled vesicles fusion, the lipid density of the layer after vesicles fusion may differ from the density in the vesicles. These considerations replace Eq. 5 with

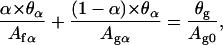(7)

where A_g0 is the molecular area of the lipids at the beginning of the transition (α = 0). The values θ_α and θ_g are the bilayer surface coverages for, respectively, a given α, and at the beginning of the transition. Assuming a linear closing of the holes with α gives

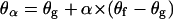(8)

where θ_f is the final coverage of the leaflet. From Eqs. 4, 7, and 8 we obtain

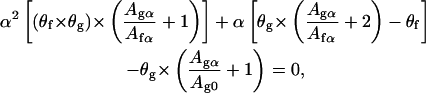(9)

where A_gα/A_fα is deduced from Eq. 4 and equals

(10)

Resolving Eq. 9 leads to a relationship between the ratio of the fluid phase (α) or the gel phase (1–α) and the temperature T. In the following we describe how the different equation parameters are chosen or calculated.

The coverages at the beginning and at the end of the transition, θ_g and θ_f, are obtained from the experimental AFM results. Their ratio θ_g/θ_f is related to the closing of holes. For the first transition, the variation in coverage of the leaflet is equal to twice the apparent variation in surface coverage. Indeed, during transition 1, the thermal expansion of the leaflet in the state is expected to be very low since it is still gel. Therefore the closing of the hole implies the transfer of molecules from the transiting leaflet to the gelled one. In this case, the variation in coverage of the transiting leaflet corresponds roughly to the double of the holes closing measured by AFM (∼2%). From our AFM images this leads to θ_g/θ_f = 0.96. For the second transition, the closing of holes is negligible and we choose θ_g/θ_f = 1. The values A_gα/A_g0 can be written as (A_gα/A_g) × (A_g/A_g0). From Eq. 4, one can evaluate the area compression (Γ = A_g/A_g0) of each leaflet with respect to the FSB at the beginning of their transition. These compressions are responsible for the temperature shift at the beginning of the melting with respect to the melting temperature of an FSB. For the first transiting leaflet and second transiting leaflet, the compressions found are, respectively, 0.5% and 2.6%. For the same values of κ_f, κ_g, K_f, K_g, and Ω_m used previously and with Γ = 1.005 corresponding to the 0.5% of compression of the first transiting leaflet, the solution of Eq. 9 is plotted on Fig. 5 with an experimental curve resulting from the average of the three different measurements. Fairly good agreements are found between the experimental and calculated curves. The same calculation has been applied for the second transition. With 2.6% of compression for the second transiting leaflet with respect to the FSB, the transition width cannot be fit with the same parameters as used for the first transiting leaflet. To fit the data, we have slightly lowered the compressibility of the fluid phase to 5.78 m²/J instead of 6.9 m²/J for the first transiting leaflet layer. This decrease in compressibility is probably due to a higher density of lipids in the leaflet than in the other one.

FIGURE 5.

Experimental and modeled curves of the two transitions. The experimental curves are the average of three different measurements.

So far, the value of Ω_m, the relative variation in molecular area in an FSB, has been taken from the literature. However, Ω_m can be estimated from our model. Writing Eq. 4 for the gel phase at the beginning of the transition (at T_g) and the fluid phase at the end of the transition (at T_f) and considering the conservation of matter during the transition (θ_g/A_g0 = θ_f/A_f1, where A_g0 and A_f1 are the molecular areas at the beginning and at the end of the transition, respectively) leads to

(11)

Using our experimental values for the first transition, T_g = 27°C and T_f = 33°C, Eq. 11 gives a variation in lipid molecular area variation between the fluid and the gel phases in an FSB of 12% (Ω_m = 0.88). This value is in good agreement with previous measurements obtained for the 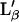-L_α transition (7).

Melting temperature of the leaflets

For the first time, AFM experiment demonstrates two main phase transitions on a supported DMPC single-bilayer. Our calculation shows the features of these transitions are in agreement with the constant surface melting of two DMPC leaflets having different densities. An obvious difference between the two leaflets is their non-equivalent environment. The inner leaflet is at the lipid/substrate interface whereas the outer one is at the lipid/solution interface. Considering the outer leaflet, its environment is quite similar to that of an FSB. We expect its melting temperature to be the closest to that of an FSB. Thus we attribute the first transition to the outer leaflet melting. We think the interaction of the inner leaflet lipids with the mica substrate is strong enough to modify the density in the inner leaflet. The density of lipids in the inner leaflet is related to the adsorption energy of lipids on the substrate. On one hand, the gain of energy due to the adsorption of lipids on the substrate tends to increase the density of lipids in the inner leaflet relative to the outer one. On the other hand, this increase raises the energy in the leaflet due to the repulsive interactions between the lipids. A higher density of lipids in the inner leaflet with respect to the outer leaflet can then be expected at equilibrium. The higher the adsorption energy, the higher the density in the inner leaflet will be. The large melting temperature difference observed infers large adsorption energy of DMPC on mica. This is consistent with the high negative surface charge of mica, which most likely presents a high affinity for the positive DMPC terminal amine group. The observation of different melting temperatures indicates that the coupling between the two leaflets is weak in agreement with previous studies (26,27).

Considering simply that the transition occurs at nearly constant surface and nonconstant tension, we have been able to model the observed transition widths using parameters found in the literature. In this model, we have not considered the line tensions at either the phase boundaries or the holes' edges (28). This could explain the small differences observed between the model and the experimental data. Moreover, we have assumed a linear closing of the holes, which is not always verified, leading to narrow transition widths. Depending on this transition width, one may wonder whether a van't Hoff formalism would become valid again.

CONCLUSIONS

A van't Hoff formalism in a constant tension transition framework, usually used to describe FSB melting (29), has been recently applied to describe the melting temperature widths of supported single-bilayers (12,14). However, no experimental data shows that transitions of supported bilayers occur at constant surface tension. On the contrary, our findings show that a nearly constant surface transition framework describes the large transition temperature widths observed for a supported lipid single-bilayer on mica. This underlines that the van't Hoff formalism that is usually used to describe transitions of supported layers is not likely to be suitable, especially for supported single-bilayers strongly interacting with the substrate. One must note that, to maintain a transition at constant surface tension even at low layer/substrate interaction, some of the layer needs to leave the substrate surface due to the lipid expansion during the transition. In the case where the layer/substrate interaction is high, this phenomenon does not happen due to a too-great cost in energy. For low substrate layer interaction, it could be that some of the layer leaves the substrate surface, but this would not necessarily imply a transition at constant surface tension. In this case we can expect a very low variation of surface tension leading to narrow transition widths, and one may wonder whether a van't Hoff formalism would become suitable again to interpret larger transitions widths than that induced by the small variation of surface tension.

We have also demonstrated two transitions arising from the independent melting of each leaflet at different temperatures. The shifts in temperature with respect to the FSB are attributed to different leaflet compressions induced by the adsorption of the lipids on the mica substrate. These findings are crucial since fluidity is a major feature required for technological applications.