Interactions of Cholesterol with Lipid Membranes and Cyclodextrin Characterized by Calorimetry

Abstract

Interactions of cholesterol (cho) with different lipids are commonly believed to play a key role in the formation of functional domains in membranes. We introduce a novel approach to characterize cho-lipid interactions by isothermal titration calorimetry. Cho is solubilized in the aqueous phase by reversible complexation with methyl-β-cyclodextrin (cyd). Uptake of cho into the membrane is measured upon a series of injections of lipid vesicles into a cyd/cho solution. As an independent assay, cho release from membranes is measured upon titrating lipid/cho mixed vesicles into a cyd solution. The most consistent fit to the data is obtained with a mole fraction (rather than mole ratio) partition coefficient and considering a cho/cyd stoichiometry of 1:2. The results are discussed in terms of contributions from 1), the transfer of cho from cyd into a hypothetical, ideally mixed membrane and 2), from nonideal interactions with POPC. The latter are exothermic but opposed by a strong loss in entropy, in agreement with cho-induced acyl chain ordering and membrane condensation. They are accompanied by a positive heat capacity change which cannot be interpreted in terms of the hydrophobic effect, suggesting that additive-induced chain ordering itself increases the heat capacity. The new assays have a great potential for a better understanding of sterol-lipid interactions and yield suggestions how to optimize cho extraction from membranes.

INTRODUCTION

There is evidence that membrane constituents do not move freely and do not distribute homogeneously over cell membranes, a fact that has enormous consequences for biological functions such as signaling and others. The raft hypothesis (1–4) explains functional inhomogeneities or domains in terms of a spontaneous demixing of membrane lipids forming different local pseudo-phases. The recent view combines the concept of functional domains (lipid rafts) with those of liquid-ordered phases in model membranes and detergent-resistant membranes (DRM). A major link between these originally unrelated models is cholesterol (cho). Application of the detergent Triton X-100 at 4°C to cell membranes solubilizes part of the lipids and proteins into small micelles but leaves cho-rich DRMs behind that are large enough to be separated by centrifugation (5,6). In model membranes, large amounts of cholesterol induce the formation of coexisting domains (7) that are described as a phase separation between liquid-ordered and liquid-disordered phases (8–10). These findings have tempted many researchers to take it for granted that lipid rafts are functional, liquid-ordered domains that can be isolated from cell membranes by cold Triton. However, recent studies have suggested that DRMs may be substantially different from functional domains in vivo (rafts) (3,11,12).

An assay for studying functions of cho is based on the effects of removing cho from cells (or model membranes) by means of cyclodextrin (cyd). Cyd is a ring-shaped molecule consisting of glucose units (seven units for β-cyd), which is well soluble in water but contains a hydrophobic cavity that binds (and thus solubilizes) small hydrophobic molecules including cho. Many biological studies have utilized this phenomenon on a semi-empirical basis for extracting cho from cells or (re-)supplying it to them (e.g., 13,14). The interpretation of such experiments is, however, complicated by the fact that cho has multiple biochemical and biophysical effects in cells and that cyd interacts also with other membrane constituents, including phospholipids.

Our study pursues two major goals. First, we establish an optimized model describing the partitioning of cho between a cyd solution and a membrane phase and show its importance for avoiding artifacts in cho extraction assays. Second, we are using cyd as a tool to investigate the key thermodynamic parameters of nonideal interactions between cho and phospholipid in the membrane.

Much insight in the membrane effects of cho has been gained from scanning calorimetry and other studies of the phase behavior of lipid-cho mixtures (7,15–17). A classical approach to the problem of cho-lipid affinities has been based on measuring the equilibrium distribution of cho between two fractions of vesicles with different lipid composition (18). This technique may, however, suffer from problems due to slow kinetics of cho transfer and difficulties to separate the two vesicle fractions from each other. One sophisticated solution to this problem was described by Huster et al. (19), who measured differences in cho-lipid affinities within the same membrane in terms of the NMR cross-relaxation rates between cho and different lipids. NMR served also to determine differential affinities of cho to different lipids expressed in terms of tie lines in ternary phase diagrams (20). Other authors solved the problem of slow cho exchange kinetics between different lipid vesicles by cyd. Steck and co-workers (21) used cyd-extraction kinetics to provide additional evidence for a fast transbilayer flip-flop of cho in the red cell membrane. Leventis and Silvius (22) showed that small amounts of cyd act as a potent catalyst for cho exchange so that, for example, 1 mM cyd speeds up the intervesicle transfer of cho by a factor of ∼60. Hence, cho can become equilibrated between different glycerolipid vesicles within a few minutes. Given the almost exclusive catalytic role of cyd in this approach, interactions between cyd and cho need not be quantified (see also Silvius' general review (23)). Niu and Litman (24) pointed out that problems in separating the two fractions of vesicles can be avoided by studying the different vesicles in separate experiments. They used cyd not as a catalyst but as a means to solubilize substantial amounts of cho. Then, the partitioning of cho between vesicles and cyd (as a common reference state) was measured and quantified in terms of a mole-ratio partition coefficient. Assuming implicitly a 1:1 stoichiometry of cho-cyd complexes, they obtained, e.g., a partition coefficient of 6.7 for cho between cyd and POPC at 37°C. The partitioning of cho between two different lipid membranes is then derived as the ratio between the two lipid-cyd partition coefficients.

Here we establish similar assays measuring the partitioning of cho between cyd and lipid vesicles using isothermal titration calorimetry (ITC). The major advantage of this technique is that it yields the affinity of cho for a lipid species as well as the enthalpic and entropic contribution to the cho-lipid interaction—shedding light on the generalized forces governing mixing or demixing in cho-lipid membranes. Furthermore, it is fast and straightforward and does not require the use of labeled compounds. Two protocols are introduced, analogously to the ITC uptake and release protocols for membrane-water partitioning of soluble compounds (25). The cho-uptake protocol is based on a titration of lipid vesicles into a solution of cyd and cyd-cho complexes. After each injection, some cho is transferred into the membrane. For the cho-release protocol, mixed lipid-cho vesicles are injected into a cyd solution so that part of the membrane-bound cho is extracted by cyd. The data are evaluated in terms of four alternative models, comparing mole-ratio with mole-fraction partition coefficients and allowing for different stoichiometries of the cho·cyd complex. The study gives rise to a comprehensive thermodynamic understanding of the system and to rules to be considered upon application of cyd to membranes. The new protocols can now be applied to vesicles of other lipids.

THEORY

The affinity of a hydrophobic or amphiphilic molecule to insert into a membrane in a nonspecific manner is usually described in terms of a membrane-water partition coefficient. The formation of a complex of two compounds is quantified by a binding constant given by the mass action law. The distribution of cho between cyd complexes and membranes must therefore be modeled by a combination of the two formalisms. Such a combined model is derived making use of the fact that both partitioning and complex formation contain cho in aqueous solution as a common reference state. The fact that this cho concentration in water, 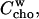is extremely small and cannot be determined experimentally is no problem, since it does not show up in the final equation relating membrane-bound and cyd-complexed cho with one another.

Membrane-water partitioning

There are many different definitions of membrane-water partition coefficients used in the literature. This is due to the fact that the application of Nernst's partitioning law (26) for dilute solutions in two macroscopically separate phases (such as octanol/water) can only approximately be applied to substantial contents of additives in microheterogeneous systems such as vesicle suspensions.

The mole fraction partition coefficient, 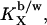between bilayer and water (b/w) is constant if the additive mixes ideally with the host lipid (27),

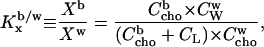(1)

with X^b and C_cho denoting mole fractions and molar concentrations, respectively, of cho in bilayers (superscript b) and water (w) and X^w the mole fraction of cholesterol in aqueous solution (note that 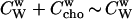). The concentration of a dilute aqueous solution is generally 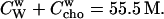The phospholipid concentration is C_L and all lipids are assumed to be in the bilayer.

Many amphiphilic compounds partitioning into membranes can be well described assuming a constant mole ratio partition coefficient, 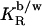(28–30),

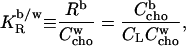(2)

based on the cho/lipid mole ratio within the membrane, R^b. A constant 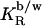corresponds to a characteristic nonideal mixing represented by a decreasing :

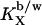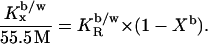(3)

Systems with a mole fraction partition coefficient that is constant or even increases with X^b should not be treated assuming a constant mole ratio partition coefficient.

Stoichiometric binding of cho to cyd

For the binding process of cho to cyd, we may write

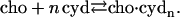(4)

The equilibrium constant K^cyd/w is given by the mass action law,

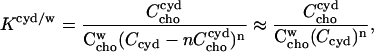(5)

where 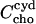stands for the concentration of cho bound to cyd which is equal to the concentration of cho·cyd_n complexes (assuming that each complex contains one cho molecule), n is the stoichiometry of the complex, and C_cyd is the total cyd concentration. The approximation in the last part of Eq. 5 applies to the case of negligible saturation of the cyd, 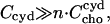which is generally fulfilled in our experiments.

Membrane-cyd partitioning of cho

Relating either Eq. 1 or Eq. 2 with Eq. 5 eliminates 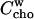and yields the bilayer/cyd mole fraction partition coefficient,

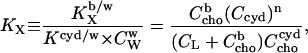(6)

and the mole ratio partition coefficient,

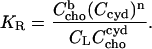(7)

Assuming n = 1, Eq. 7 becomes equivalent to the model used by Niu and Litman (24). Substituting 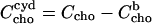we may solve Eqs. 6 and 7 for the membrane-bound cholesterol concentration,

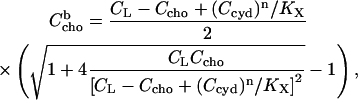(8)

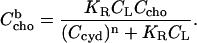(9)

MATERIALS AND METHODS

Substances and sample preparation

1-Palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) was purchased from Avanti Polar Lipids (Alabaster, AL) and cholesterol (cho) and randomly methylated β-cyclodextrin (cyd) were from Fluka (Buchs, Switzerland). Mixtures of POPC and cho were prepared by addition of cho to the dry lipid powder, resuspension in chloroform/methanol, and consecutive drying under a gentle stream of nitrogen. The sample was then held under vacuum for at least 12 h for further drying. The composition of the sample was checked by weighing the dry material before and after an addition. The dry lipid mixtures were suspended in 100 mM NaCl, 10 mM Tris buffer at pH 7.4 by gentle vortexing to reach a POPC concentration of 10 mM. After five consecutive freeze-thaw cycles, large unilamellar vesicles were prepared by 10 extrusion runs through a Nucleopore polycarbonate filter with a pore diameter of ∼100 nm in a Lipex extruder (Northern Lipids, Vancouver, Canada). Extrusion was performed at 50°C. Our results imply in agreement with the literature (31,32) that cho flip-flop between the outer and inner lipid leaflet is fast (a few minutes or less), so that cho is homogeneously distributed over the membrane. Samples containing 50 mol % cho have been reported to be subject to artifacts arising from a separation of the dry substances leading to a heterogeneous distribution of cho between the vesicles (33). For homogenization, we have therefore sonicated these samples before freeze-thawing (restoring the multilamellar state) and extrusion. Large unilamellar vesicles were stored in the dark under nitrogen and used for a week at maximum.

ITC measurements

ITC experiments were performed on a VP ITC calorimeter from MicroCal (Northampton, MA) (34,35). The calorimeter performs a series of injections from a computer-controlled, 300-μL injection syringe into the calorimeter cell (1.4 mL). The temperature of the cell is kept constant by a power compensation feedback. Each injection leads to a peak of the power of the compensation heater, which is integrated to obtain the heat response of the system.

Both uptake and release assays are based on a titration of lipid vesicles (10 mM POPC) into a solution of cyd (2.5–10 mM). Cholesterol is either included in the titrant (release assay) or in the initial cell content (uptake assay). The cho/cyd ratio was always below 1:20 so that free cyd was in large excess and saturation with cho remained negligible. Mixing after each injection leads to an equilibration of cho between membranes and cyd which, in turn, gives rise to the heat signal.

All solutions were degassed before filling to avoid air bubbles. The typical sequence of injections was 1 × 1 μL, 3 × 5 μL, and ∼10 × 10 μL. The first injection is subject to larger errors, therefore its volume is chosen very small and its heat is not taken into account upon curve fitting. The three 5-μL injections are performed to increase the resolution in the beginning of the titration, where the heats are largest and vary strongly from one to another.

After each injection, the heat power of reaction was recorded for a sufficient time to ensure that the signal returns to the baseline level. Depending on the kinetics of cho exchange between membrane and cyd, waiting times ranged between 10 min (in particular at 50°C) and 1 h (25°C) giving rise to a total time of ∼2–14 h per titration.

The primary data analysis was performed using Origin for ITC (MicroCal) provided with the instrument. Integration of the power peaks after each injection (see Fig. 1, top) from a manually adjusted baseline yields the differential heat response of the system to the injection. These data are normalized with respect to the number of moles of lipid injected. The results of a blank run, i.e., titration of pure lipid into a cyd solution for both protocols, were subtracted from each data set of cho partitioning. The resulting corrected, normalized heats were exported into an Excel spreadsheet for curve fitting.

FIGURE 1.

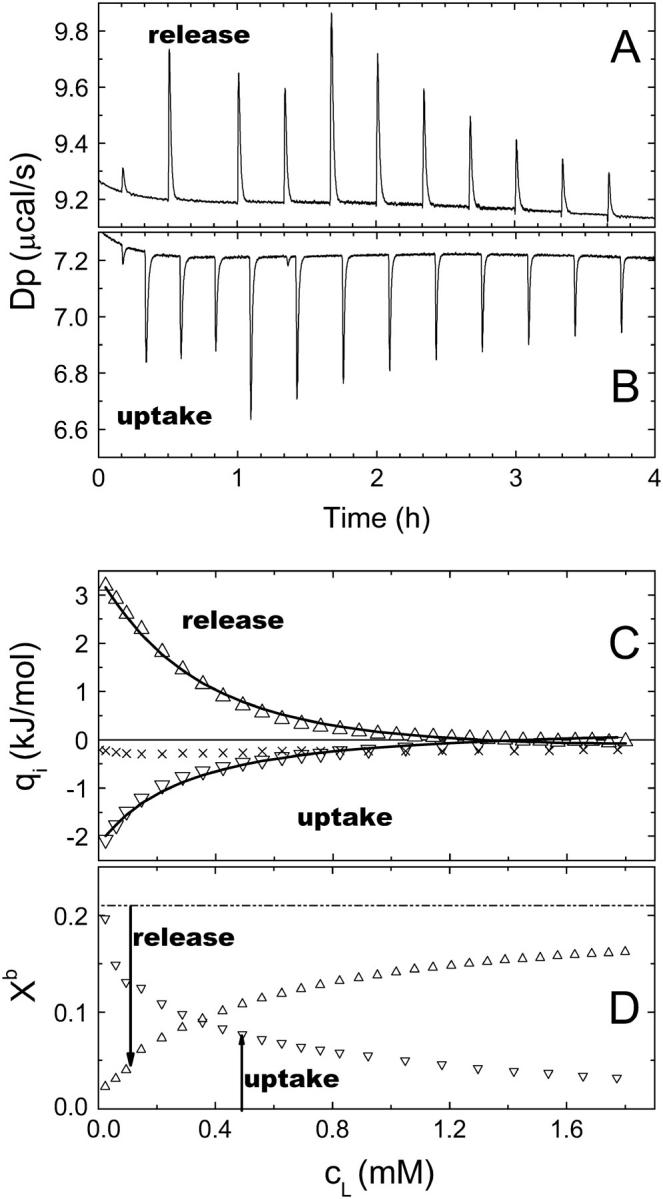
Data of cho uptake and cho release experiments at 37°C, 5 mM cyd. (A) Detail of the raw data of a release experiment, showing the compensation heat power versus time t. The injection volumes are 1 × 1 μL, 3 × 5 μL, and others 10 μL, respectively. (B) Detail of raw data of an uptake experiment (analogous to A). (C) Integrated, normalized heats of uptake (▿) and release (▵) after subtraction of the blank (×). The fit curves correspond to a global fit (setup and fit parameters given in the text). (D) Average X^b in the cell during the experiments (symbols as in C) calculated using K_X obtained in C. X^b in the syringe is 0.21 (release) and 0 (uptake).

Curve fitting

The data were evaluated using a Microsoft Excel spreadsheet (Microsoft, Seattle, WA) in a stepwise mode. The spreadsheet contains information about the experimental setup (initial concentrations in the cell and syringe and injection volumes). It calculates the concentration of all components, cho, cyd, and lipid after each injection in the cell assuming that injection of a volume of ΔV_i changes each concentration by

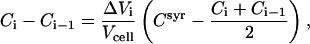(10)

where C^syr, C_i, and C_i−1 denote concentrations of the respective compound in the syringe, after and before the i^th injection, respectively. The equation takes into account the addition of compound from the syringe (if C^syr ≠ 0) and the displacement of ΔV_i of cell content (average concentration (C_i + C_i−1)/2) out of the completely filled cell. Eq. 10 is based on the assumption that overflown material is no longer in contact with the cell content as recommended by the manufacturer. Solving Eq. 10 for C_i yields

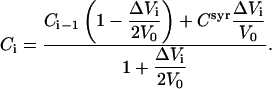(11)

Based on arbitrarily chosen initial values for K (either K_R or K_X), the table also calculates the corresponding concentration of membrane-bound cho after the i^th injection, 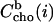(Eqs. 8 or 9), and the corresponding mole fraction of cho in the membrane, X^b(i). The difference between 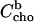after and before a given injection, 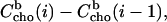results from several effects:

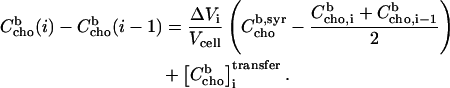(12)

First, membrane-bound cho is added from the syringe (only for the release protocol) and flows over from the cell content. This contribution, which does not give rise to any heat, is calculated analogously to Eq. 10 replacing the total concentrations C^syr, C_i, and C_i−1 by the membrane-bound ones. Second, the re-equilibration in the cell after disturbing the equilibrium by the injection leads to a transfer of cho from cyd into the membrane or vice versa; the corresponding contribution 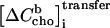is the source of the measured heat.

The absolute heat measured after the i^th injection, q_i, is linearly related to the mole number of transferred cho, which is obtained from 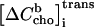by multiplication with the cell volume, V_cell, and the molar enthalpy of transfer, ΔH:

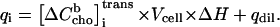(13)

Note that both ΔH and 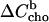are generally defined for the membrane uptake of cho from cyd. The fact that the sign of the heat, q_i, is different for cho release is considered by 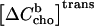becoming negative. Since q_i should correspond to experimental data after subtraction of a blank that covers most heats of dilution and other unwanted heat effects, the remaining dilution heat q_dil should be very small. However, tests have shown that the precision of the fit parameters is improved by allowing for a small constant q_dil to account for imperfections of the blank or of the model (36).

Eq. 13 could be used for fitting data, but we prefer using heats that are normalized with respect to the mole number of injected lipid, Q_i, yielding (V_cell cancels out)

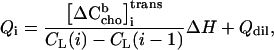(14)

where Q_dil also becomes a value given per mole of lipid injected. Eq. 14 is used to fit K, ΔH, and Q_dil by the Excel solver tool to the experimental data.

RESULTS

Uptake and release experiments at 37°C

Fig. 1 shows part of the raw data (Fig. 1 A) and normalized differential heats (Fig. 1 C) of a release experiment titrating 10 mM POPC including 19 mol % (2.3 mM) cho into the calorimeter cell loaded with 5 mM cyd. After each injection, part of the cho located in the injected vesicles is extracted by cyd, giving rise to an endothermic heat of transfer. The steps in the peak heights (Fig. 1 A) are due to different injection volumes and vanish upon normalization (Fig. 1 B). The values of Q_i (Δ) are obtained after subtraction of those measured in a blank run, injecting cho-free 10 mM POPC into 5 mM cyd. These blank heats presented as the symbol “×” are small and almost constant. Larger, more variable blanks are obtained for experiments utilizing 7.5 mM and in particular 10 mM cyd.

Fig. 1 B shows raw data of an uptake experiment injecting 10 mM POPC vesicles into a mixture of 5 mM cyd and 90 μM cho. The injected lipid vesicles take up part of the cho from cho·cyd_n complexes. As the reverse transfer of the cho release, the accompanying heats must of course be exothermic. The blank is the same as for the release.

The fit curves in Fig. 1 are obtained by a global fit of both uptake and release data using Eq. 14 and correspond to K_X = (37 ± 7) mM, n = 2 (set), ΔH = −(16 ± 2) kJ/mol, and small constant heats of dilution Q_dil(uptake) = 0.2 kJ/mol and Q_dil(release) = −0.16 kJ/mol. The uncertainties are estimated maximum errors. The fit is good, showing that the data are consistent and that the system reaches equilibrium after each injection. Comparing data of many experiments, the data of independent uptake, independent release, and global fits agree often within experimental error. In some cases, there seems to be a trend of independent uptake fits to overestimate K and yield a ΔH that is somewhat less exothermic than obtained by global and release fits. Separate fits of the two curves in Fig. 1 yield, for example, K_X = 41 mM (release) and 49 mM (uptake), and ΔH = −16 kJ/mol (release) and −11 kJ/mol (uptake).

A global evaluation of the same data based on Eq. 8 and n set to 1 yields similarly good fit curves with K_R = 7, ΔH = −17 kJ/mol, q_dil(uptake) = 0.2 kJ/mol, and q_dil(release) = −0.5 kJ/mol. The value of K_R agrees with the literature (6.7, as published by Niu and Litman (24)) and ΔH is in line with the result of the model described above. The data could also be fitted by the models based on K_X, n = 1 and on K_R, n = 2 (results not shown). The selection of the best model requires a variety of data sets measured under different conditions (see below).

Using K_X determined by the fit one can calculate the membrane composition in the calorimeter cell during the titration (Fig. 1 D). In the beginning of the release assay, the membrane-bound cho (X^b = 0.21 in the syringe) is almost fully extracted, but at the end, the injections cause only a reduction to X^b ∼0.15. Therefore the heat of titration decreases in the course of the titration. In the beginning of the uptake assay, all cho is already in the cell but there is very little POPC yet so that X^b is maximum, ∼0.2. In the course of the titration, the membrane-bound cho distributes over more vesicles and X^b decreases.

The effect of the cyclodextrin concentration

Cholesterol uptake experiments injecting POPC vesicles into cyd-cho solutions were performed at varying cyd concentrations. Technical constraints limit the applicable cyd concentration in our assays to the range from 2.5 mM through 10 mM. The lower limit is determined by the sensitivity of the calorimeter, because the cho/cyd ratio was always kept below 1:20 (mol/mol) and at least 30–50 μM cho are required to obtain a sufficient signal/noise ratio.

The maximum applicable cyd concentration of ∼10 mM is determined by the requirement to keep factors other than cholesterol transfer negligible. Blank experiments titrating POPC into cyd solutions excluding cho showed small, almost constant heats at cyd concentrations of up to 5 mM but increasing, variable signals at higher cyd concentrations. These blank heats were always subtracted from the experimental data of cholesterol uptake and release experiments, but at >10 mM cyd they were no longer small compared to the experimental signal, thus adding substantial experimental error. The origin of these heat effects at C_cyd > 10 mM probably relate to the binding of PC to cyd (24,37), possible minute impurities of the cyd, heats of dilution of the cyd solution by the injection, and others.

The dilution of cyd in the cell by the injection could be avoided (only in the uptake protocol) by including cyd in the syringe. However, a test titrating a POPC dispersion including 7.5 mM cyd into 7.5 mM cyd showed similar heats like the usual blank, injecting cyd-free POPC into 7.5 mM cyd. Test experiments titrating POPC/cyd into cyd/cho yielded consistent but somewhat less reproducible results for K and ΔH, possibly due to vesicle changes caused by long-term incubation with cyd. We therefore decided to use cyd-free titrants.

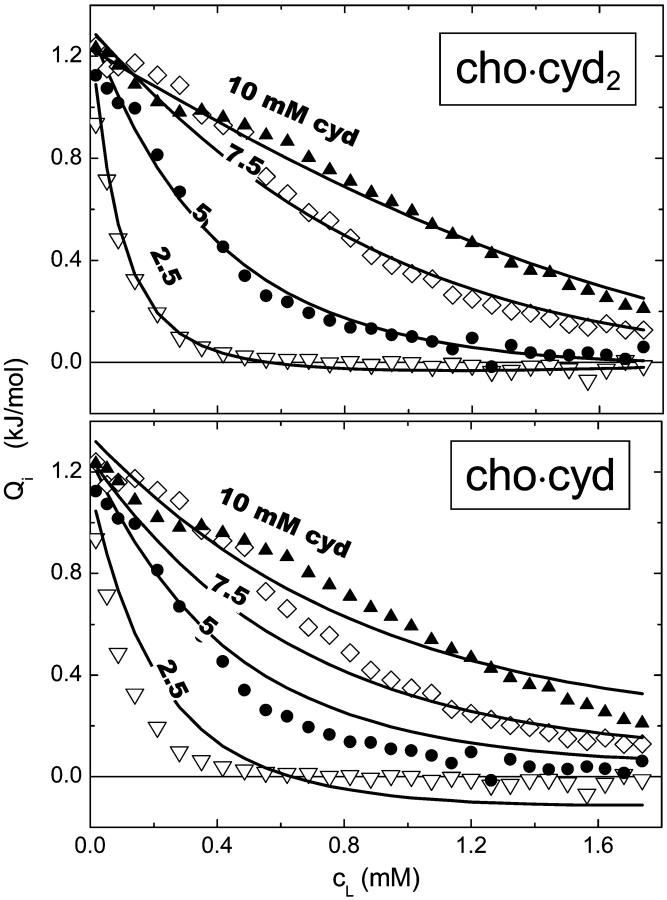
Apart from these technical limits for the cyd concentration, the interaction parameters determined by the fit procedure should not depend on the experimental cyd concentration if the model is correct. Both panels of Fig. 2 show the same results of release experiments injecting vesicles including 21 mol % of cho into cyd solutions of 2.5, 5, 7.5, and 10 mM at 50°C. The upper panel shows curves of a good global fit of all data sets based on a stoichiometry of n = 2, K_X = 32 mM, ΔH = −5.0 kJ/mol and individual, small Q_dil values ranging from −0.1 to 0.01 kJ/mol. Global fits as shown in Fig. 2 allow also for an additional, free fit of the stoichiometry, yielding values of n = 2.0 ± 0.2 for several data sets. The bottom panel illustrates the best fit that is possible with n set to 1; there is no doubt that the assumption of exclusive cho·cyd (1:1) complexes is inconsistent with these data. Analogous measurements at X^b = 0.1 and 0.3 yield the same result (not shown).

FIGURE 2.

A stoichiometry of cho·cyd₂ (n = 2) agrees with the data much better than cho-cyd. The data represent release experiments injecting vesicles of 10 mM POPC, 21 mol % cho, into cyd solutions of 2.5 mM (▿), 5 mM (•), 7.5 mM (⋄), and 10 mM (▴) at 50°C (same in both panels). The fit curves in the top panel are obtained by a global fit assuming a stoichiometry of cho·cyd₂ (n = 2) (parameters given in text), those in the bottom panel illustrate the best fit possible assuming n = 1.

The effect of the cholesterol content in the membrane

The cholesterol content in the membrane specified in terms of the mole fraction, X^b, varies during a titration. If cho mixes nonideally with POPC, K and ΔH are a function of X^b. This appears to be in conflict with our model, which is based on constant values of K and ΔH. However, previous membrane partitioning studies of surfactants and peptides have shown that ITC data are usually not very sensitive to composition-dependent variations of K or ΔH (36). Instead, it was found that the formal application of an ideal model (K and ΔH constant) to a nonideal system yields rather good fits with parameters corresponding to an effective membrane composition, X^b, in the beginning of the titration. For example, the shape of the curves in Fig. 1 C is mainly determined by injections inducing changes in X^b from ∼0.2 to ∼0 (release) or vice versa (uptake) (Fig. 1 D). The results of both experiments correspond, thus, to an effective X^b of ∼0.2. It should be noted that a global fit of uptake and release data with substantially different effective X^b would be less consistent.

The fact that X^b changes only moderately during an experiment and the results can be approximately associated with one effective X^b makes the data rather insensitive to composition-dependent phenomena and makes it virtually impossible to derive information regarding nonideal effects from a single run. Imagine, for example, a formation of POPC₂·cho complexes of relatively high affinity. Most cho molecules up to X^b ∼0.33 (and practically all up to X^b = 0.2) would form such complexes so that ΔH and K_X in the experiments shown in Fig. 1 would be constant and provide no clue of complex formation.

Instead of refining the model for evaluating single ITC curves, we have to compare the results of different experiments with different effective X^b if we want to shed light on nonideal, composition-dependent phenomena. We have therefore performed series of uptake and release experiments at varying cho concentrations and evaluated the data using the ideal model. For release experiments, it is straightforward to assign the effective X^b to the known cho content in the titrant. For uptake experiments, we calculated X^b (C_L→0) as an estimate (upper limit) of the effective X^b using the K_X value obtained by the fit. For global fits of uptake and release data, we chose data sets with a similar effective X^b. A plot of the results as a function of the effective membrane composition is shown in Fig. 3.

FIGURE 3.

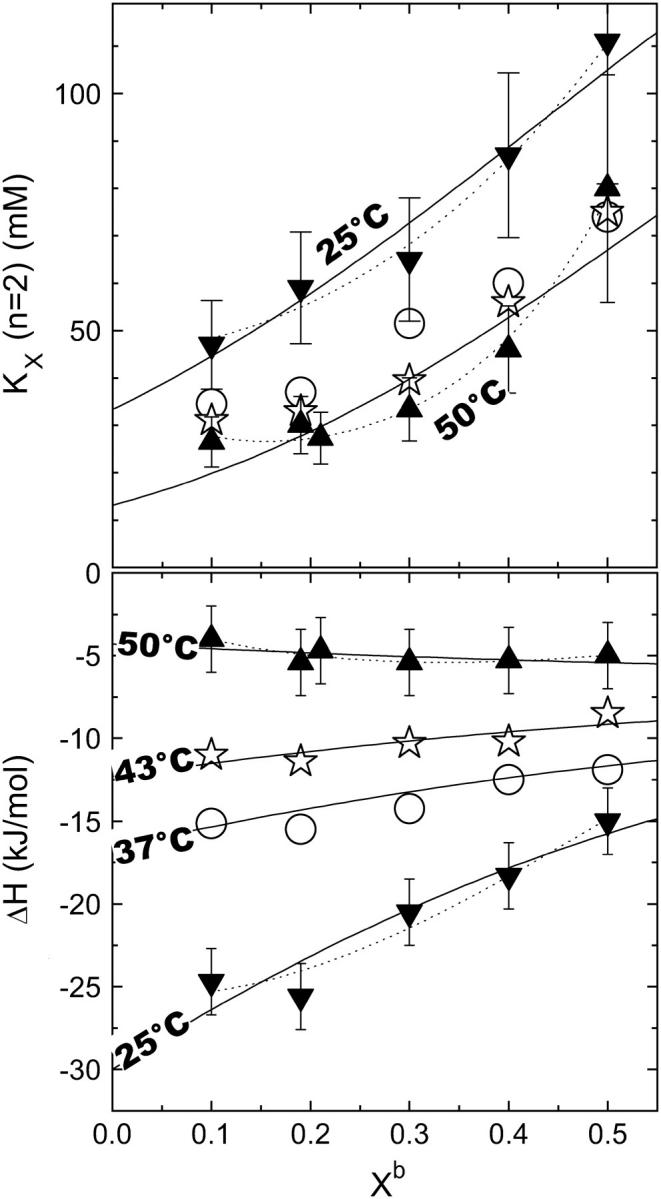
The cyclodextrin-membrane partition coefficient, K_X (top) and the molar enthalpy change of transfer, ΔH (bottom) as a function of the effective cholesterol content in the membrane, X^b (see text for definition). The data correspond to experiments at different temperatures as indicated in the plot. Estimated maximum errors are generally 20% for K_X and ±2 kJ/mol for ΔH, some error bars are omitted for clarity. The lines correspond to best fits according to Eqs. 19 and 18 considering only pairwise (solid) and also multibody (dotted) interactions, respectively (see Discussion).

For effective X^b ≤ 0.3, the composition-dependent variation of the data is smaller than the estimated maximum errors of ±20% for K_X and ±2 kJ/mol for ΔH, indicating that deviations from ideal mixing are relatively small. For higher cho contents, nonideal mixing effects become significant at least for K_X (increasing with X^b) and ΔH (25°C) (becoming less exothermic with increasing X^b).

Temperature dependency

Results obtained at different temperatures are included in Fig. 3.

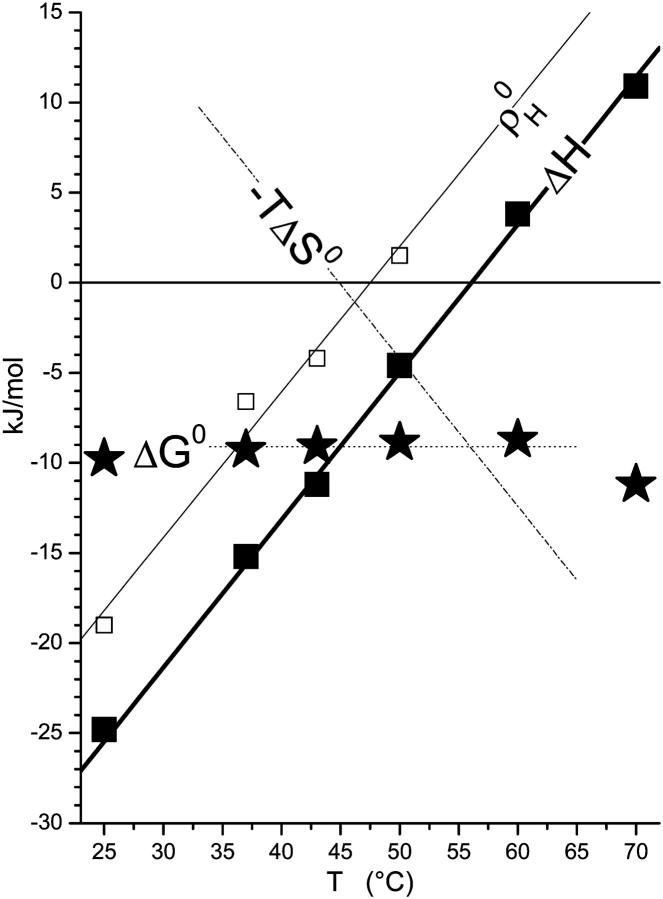
Fig. 4 shows the corresponding thermodynamic potentials of transfer of cho from cho·cyd₂ complexes into POPC-cho vesicles as a function of temperature. The enthalpy changes, ΔH, were measured directly in the calorimeter; the points displayed in Fig. 4 refer to small cho contents in the membrane (X^b = 0.1–0.2). The changes in the standard Gibbs free energy, ΔG⁰, were calculated from K_X according to

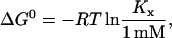(15)

where R is the ideal gas constant and T the absolute temperature. The standard state of all compounds used to derive an activity-based, dimensionless value of K was chosen a 1-mM solution at the given temperature. Referring all activities to 1 M, all values of ΔG⁰ would be larger by ∼7 RT. A linear regression of ΔH(T) yields a positive heat capacity change of ΔC_P = (0.8 ± 0.1) kJ/(mol K) and a temperature of vanishing ΔH of 56°C. Above 56°C, the transfer of cho into the membrane becomes endothermic. The ΔG⁰ data could, in the frame of the experimental uncertainty, be well described by a temperature-independent value of ΔG⁰ = (−9.1 ± 0.2) kJ/mol (at least, within 37–50°C). From these fit lines, the entropic contribution to ΔG⁰, −TΔS⁰, was calculated according to

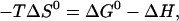(16)

assuming the enthalpy of transfer to be virtually independent of concentrations so that ΔH = ΔH⁰. Fig. 4 also includes enthalpic nonideality parameters which are discussed in Nonideal Mixing of POPC and Cho, in the next section.

FIGURE 4.

The standard Gibbs free energy, ΔG⁰ (★), and enthalpy, ΔH (▪), of transfer of cho from cho·cyd₂ complexes into POPC membranes as a function of temperature. The average ΔG⁰ (dotted line) and linear fit of ΔH (thick solid line, slope ΔC_P = 0.8 kJ/(mol K)) correspond to an entropic contribution of −TΔS illustrated by the dash-dotted line. The enthalpic nonideality parameter, 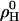(□), exhibits the same slope as a function of T as ΔH (see Nonideal Mixing of POPC and Cho, in text).

DISCUSSION

Distinguishing between effects of cyd-to-membrane transfer and nonideal mixing in the membrane

One of our goals is to discuss the thermodynamic phenomena that govern the mixing or demixing behavior in lipid-cho membranes. To this end, we have to distinguish two contributions to, e.g., ΔH:

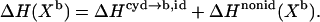(17)

The first, ΔH^cyd→b,id, corresponds to the transfer of cho from cyd complexes into a hypothetical ideally mixed membrane; it is by definition independent of the membrane composition X^b. The second, ΔH^nonid(X^b) arises from specific, nonideal interactions between cho and POPC within the bilayer. Generally, ΔH^nonid = 0 for pure phases which would allow for a direct measurement of ΔH^cyd→b,id = ΔH(X^b→1). However, since pure cho forms no fluid bilayers, we have to compute ΔH^nonid using a model describing the composition-dependence of ΔH at lower X^b. The limited X^b-range and precision of the data do, unfortunately, not warrant a complex model. We have chosen a statistical model (see next section for a discussion of other possible concepts) with one or two nonideality parameters, yielding for the enthalpy (38,39),

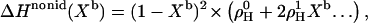(18)

and, taking into account Eq. 15, for K_X,

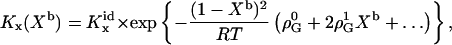(19)

where 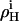and 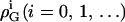denote nonideality parameters of the enthalpy and of the free energy of mixing, respectively. For 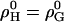and vanishing higher order terms, ρⁱ(i > 0) = 0, these equations correspond to the model of regular solutions, describing nonideality in terms of pairwise interactions. For lipid bilayers, we have to consider 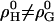since the entropy is not governed by the arrangement of the molecules alone (which is assumed to be random), but includes major contributions from intramolecular degrees of freedom. Higher order terms in 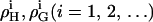account for nonpairwise, multibody interactions of cooperative units of i + 2 molecules. It should be noted that such multibody interactions are equivalent to stoichiometric complexes of i + 2 molecules (i.e., lipid·cho₂, and lipid₂·cho in our case) provided the association constant of the complex is weak.

Fitting Eqs. 18 and 19 to the data (curves in Fig. 3) allows us to approximately split the enthalpy and K_X value of transfer to nonideal membranes into contributions from transfer into hypothetical, ideally mixed membranes (see The effect of acyl chain order on heat capacity, below) and from nonideal mixing of POPC and cho (see below).

Nonideal mixing of POPC and cho

The hypothesis that biological membranes contain lipid rafts, functional domains that are formed by a spontaneous demixing of different lipids in the presence of cholesterol, has led to an enormous interest in the nonideal mixing behavior of cho with phospholipids. In the case of ideal mixing of cho and POPC, the partition coefficients K_X and enthalpies of uptake, ΔH, should be independent of the membrane composition, X^b. Nonideal systems may either show a tendency 1), to demix into different domains if cho-rich environments are favorable; 2), to arrange into superlattices if cho-rich environments are unfavorable; or 3), to form stoichiometric complexes.

Radhakrishnan and McConnell (40) have found that saturated lipids can form stoichiometric complexes with cho, whereas unsaturated lipids do not. Indeed, our data show no evidence for the formation of high-affinity, cholesterol-rich complexes which should give rise to a drop in K_X at a stoichiometric composition X^b ≤ 0.5 (41,42). Superlattice formation should also give rise to rather sudden drops of K_X at specific X^b (43,44), which are not observed here. A real phase separation into coexisting liquid-ordered and liquid-disordered phases as reported by de Almeida et al. (45) should be represented by jumps of ΔH at the boundaries but constant ΔH in between. This general behavior was explained in detail for the example of membrane-micelle coexistence (39,46) and would apply (qualitatively) analogously to an liquid-ordered/liquid-disordered coexistence. The value K_X(X^b) should increase within the coexistence range, since cho affinity would be higher in the liquid-ordered, than in the liquid-disordered, phase. Again, we do not find evidence for such behavior.

Our data show the thermodynamic behavior as discussed for cho-induced chain ordering in a largely randomly mixed membrane. Fitting K_X(X^b) excluding higher order terms (all ρⁱ = 0 for i > 0) is, within experimental error, compatible with the data but systematic deviations remain (solid lines in Fig. 3). These fits suggest pairwise interactions that are somewhat unfavorable by 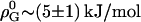at all temperatures investigated. This means that each molecule in a mixture containing 30% cho has, on average, an increased free energy of ∼1 kJ/mol as a result of unfavorable POPC-cho interactions (excess free energy; see Heerklotz et al. (39)). Hence, the cost of nonideal mixing is less than, but on the same order of magnitude as, the gain due to the entropy of ideal mixing, 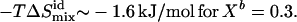At room temperature, the nonideal interaction is highly exothermic 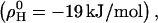suggesting that the unfavorable Gibbs free energy is dominated by a large loss in intramolecular entropy. The nonideal interaction causes a strong increase in heat capacity by 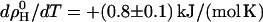(see open square in Fig. 4). The precision and particularly the limited composition range of the data in Fig. 3 do not strictly justify a fit with more adjustable parameters but we have, nevertheless, repeated the fits allowing also for 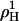and 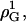respectively (dotted lines in Fig. 3). These fits yield substantial values for 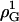(4 and 13 kJ/mol at 25 and 50°C, respectively), suggesting slightly unfavorable POPC₂·cho units but two- to threefold more unfavorable POPC·cho₂ units.

The nonideal behavior observed here (unfavorable but exothermic) has been described to accompany the chain-ordering, membrane condensing effect of cho, since tighter packing and increased order cost entropy but improve enthalpically favorable interactions and conformations. The cooperative, multibody character of this interaction is also illustrated by the umbrella model (31). This suggests that cholesterol intercalates between lipids without occupying much space in the headgroup region, so that it is screened from water by the headgroups like under an umbrella. The thermodynamic pattern (unfavorable but exothermic) has also been described for the transfer of cho from gel to fluid bilayers, which is also accompanied by chain ordering (47).

The effect of acyl chain order on heat capacity

A surprising result is the positive heat capacity change. A generally accepted rule relates a positive ΔC_P to either an increase in water-exposed hydrophobic surface area or to a dehydration of polar groups (48). The intercalation of cho between lipids should, however, reduce the exposure of hydrophobic groups to water (umbrella) and allow for a better hydration of the surrounding lipid headgroups (since the polar group of cho needs very little space). This paradox suggests the hypothesis that the ordering of the lipid chains itself causes a strong increase in heat capacity. This is surprising, taking into account that lipid melting, which is accompanied by a dramatic change in chain order, has virtually no ΔC_P (15,49). However, melting is a complex process including many phenomena which are different from gradual changes in order in a fluid membrane. This hypothesis also provides an explanation for the negative 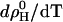(50) and anomalously negative values of ΔC_P observed for the membrane uptake of membrane-disordering compounds such as detergents (50,51) and alcohols (52), which could not be explained in terms of the hydrophobic effect alone.

The transfer of cho from cyd into hypothetical, ideally mixed membranes

The fit parameter ΔH^cyd→b,id excludes specific cho-POPC interactions and allows us to interpret the dissociation of the cho·cyd₂ complex and the transfer of cho to a state corresponding to a hypothetic ideally mixed membrane. The standard free energy gain of ∼−(12 ± 1) kJ/mol is essentially of enthalpic nature (ΔH^cyd→b,id ∼ −(11 ± 2) kJ/mol) at 25°C. The entropy change (−TΔS⁰ = −(1 ± 3) kJ/mol) and the heat capacity change d[ΔH^cyd→b,id]/dT = −(0.1 ± 0.1) kJ/(mol K) are negligible. This means that the transfer of cho between cyd and the membrane is neither promoted nor opposed by the hydrophobic effect. One has, however, to keep in mind that the hydrophobic surface of cyd is fully exposed to water in the absence of cho whereas the membrane anneals after removal of cho and does not expose a free hydrophobic binding site to water. Hence, the screening of cho from water must be better in the membrane to compensate for the accessible hydrophobic surface of free cyd.

The cho·cyd₂ complex

The binding of cho to cyd is governed by the hydrophobic effect as discussed in the previous section. That means that cho covers most of the hydrophobic surface area of cyd and vice versa, thus avoiding its exposure to water. Given the molecular dimensions, two stacked cyd molecules seem to be required to largely screen a cho molecule from water, taking into account that a cho molecule is ∼18 Å long, whereas the cavity of cyd is only ∼8 Å long.

The section on the effect of the cyclodextrin concentration has indeed provided strong evidence that the cho-cyd interaction can be described much better in terms of the formation of a cho-cyd₂ than cho·cyd complex. The comparison of these two most simple cases does, of course, not exclude more complex behavior such as sequential binding leading to a coexistence of cho·cyd, cho·cyd₂, and maybe even cho·cyd₃ complexes, but cho·cyd₂ seems at least to be the dominating species.

The idea that more than one cyd molecule binds one cho is further supported by our observation that a stock solution of 100 mM cyd, 10 mM cho is stable, but dilution to 10 mM cyd, 1 mM cho leads to precipitation. This is very likely due to the formation of aggregates of free cho which are formed when the free cho concentration, 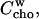supersedes the solubility limit. The mass action law (Eq. 5) yields (replacing :

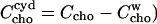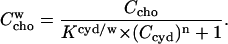(20)

Let us consider Eq. 20 for the case that both C_Cho and C_Cyd are reduced by the same factor upon dilution. If n = 1, dilution decreases 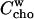or leaves it unchanged (if K^cyd/w · C_cyd ≫ 1). An increase in 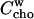upon dilution, as suggested by the precipitation, implies a higher stoichiometry, n > 1.

Pointing out that a model based on K_X and n = 2 is clearly superior, we note that the conclusions drawn by Niu and Litman (24) working with K_R and n = 1 are not questioned. They have related cho affinities for different lipids to each other that were measured at identical cyd and cho concentrations. Errors appear only if one used their K-values for calculating the cyd-membrane distribution at a different cyd concentration.

The application of cyd to the selective extraction of cho from membranes

Extraction of cho from cell and model membranes by cyd has become a widely used approach to study the function of cho. Our results imply that the cyd concentration used for this purpose must be carefully chosen. Our model parameters (K, n) allow calculating the fraction of cho that remains membrane-bound, 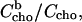at a given cyd concentration. We calculated curves showing this fraction assuming membranes of 1 and 0.1 mM POPC + cho (30 mol % cho) as shown in Fig. 5.

FIGURE 5.

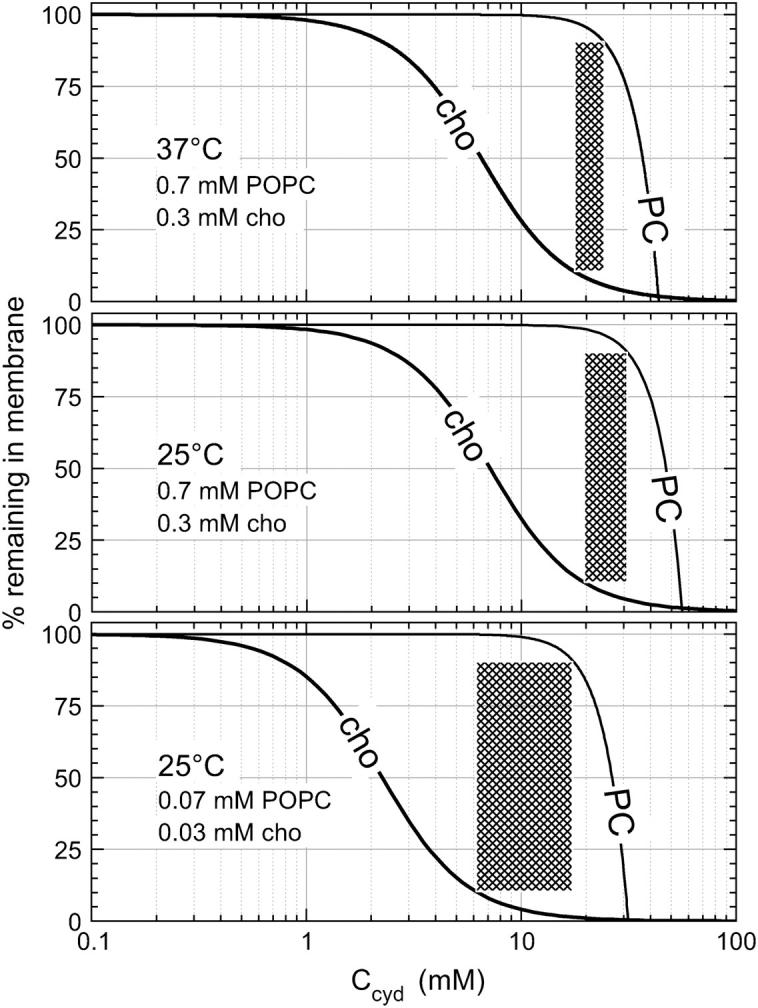
Retention of cho and POPC in membranes as a function of the cyd concentration at different cho and POPC concentrations and temperatures as indicated in the plot. The curves for cho are calculated on the basis of n = 2, K_X ∼60 mM (25°C) and 50 mM (37°C), and those for PC are based on Eq. 21 with K = 192 M⁻³ (37°C) and 71 M⁻³ (25°C) derived from Anderson et al. (37). The cross-hatched areas indicate the range where >90% of the cho, but <10% of the POPC, are extracted.

For comparison, we simulated the retention of POPC in these membranes, 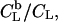in the same range of cyd concentrations on the basis of the results of Anderson et al. (37). These authors established a model for PC binding to cyd, which implies a membrane-retained fraction of lipid as

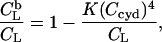(21)

with a temperature-dependent K yielding, by interpolation, a value of 192 M⁻³ at 37°C.

Let us, at first, consider a sample of 0.3 mM cho, 0.7 mM POPC (top panel of Fig. 5). At a cyd concentration of 1 mM, the removal of molecules from the membrane is negligible as discussed already by Leventis and Silvius (22). A cyd concentration of 5 mM extracts 40%, and one of 10 mM removes ∼75% of the cho from the membrane, without binding significant amounts of phospholipid. The range where ≥90% of cho but ≤10% of POPC are extracted (cross-hatched in Fig. 5, top) is quite narrow, ∼18–24 mM cyd. At 40 mM cyd, most of the membrane is destroyed by cyd.

Our calculations suggest two strategies for broadening the applicable range in cyd concentrations in which a substantial extraction of cho is reached without removal of lipid. These are dilution of the membrane system and lower extraction temperature. For example, a 10-fold dilution and extraction at 25°C increases the cross-hatched range to 6–18 mM cyd (Fig. 5, bottom).

Fig. 5 cannot, of course, specify an optimum cyd concentration window that would be applicable to all membrane systems. For example, preliminary data suggest that sphingomyelin seems to be more susceptible to extraction by cyd but to attenuate the extraction of cho. Hence, the available window of cyd concentrations for selective removal of cho would become even narrower. The discussion of Fig. 5 illustrates, at least, the problem of optimizing the cyd concentration, and provides typical concentrations and optimization strategies that may also be worth trying when biological membranes are concerned.

Another technically important problem is how much time is needed for cho extraction from or cho loading into membranes. We could show that both cho extraction from membranes and cho loading into membranes (of POPC) equilibrate largely within <1 h at 25°C and within a few minutes at 50°C. The observation that the same state is reached by both uptake and release is a strict criterion for equilibration, confirming the suggestion from Niu and Litman (24), who found that no further uptake is detectable after ∼1 h.

CONCLUSIONS

1. Isothermal titration calorimetry is an excellent new technique to study the interaction of cho with lipid membranes in detail.

2. Cho exhibits a nonideal interaction with POPC which is exothermic but entropically unfavorable and accompanied by a positive heat capacity change. This nonideal behavior corresponds to the well-known membrane-ordering effect of cho.

3. An anomalous increase in heat capacity accompanying the nonideal interaction gives rise to the hypothesis that additive-induced membrane ordering yields a positive, and disordering a negative, contribution to ΔC_P. Hence, heat capacities of additive partitioning into membranes may deviate markedly from the otherwise well-established rule relating ΔC_P to changes in water-exposed surface area.

4. Complexes of cho with cyd have a dominant stoichiometry of cho·cyd₂.

5. There is only a very narrow window of cyd concentrations that allow for a substantial extraction of cho from membranes without destroying the membrane. At least for POPC, this window becomes broader upon dilution of the membrane dispersion and at lower temperature.