The Nonequilibrium Phase and Glass Transition Behavior of β-Lactoglobulin

Abstract

Concentrated solutions of bovine β-lactoglobulin were studied using osmotic stress and rheological techniques. At pH 6.0 and 8.0, the osmotic pressure was largely independent of NaCl concentration and could be described by a hard sphere equation of state. At pH 5.1, close to the isoelectric point, the osmotic pressure was lower at the lower NaCl concentrations (0 mM, 100 mM) and was fitted by an adhesive hard sphere model. Liquid-liquid phase separation was observed at pH 5.1 at ionic strengths of 13 mM and below. Comparison of the liquid-liquid and literature solid-liquid coexistence curves showed these solutions to be supersaturated and the phase separation to be nonequilibrium in nature. In steady shear, the zero shear viscosity of concentrated solutions at pH 5.1 was observed at shear rates above 50 s⁻¹. With increasing concentration, the solution viscosity showed a progressive increase, a behavior interpreted as the approach to a colloidlike glass transition at ∼60% w/w. In oscillatory shear experiments, the storage modulus crossed the loss modulus at concentrations of 54% w/w, an indication of the approaching glass transition. Comparison of the viscous behavior with predictions from the Krieger-Dougherty equation indicates the hydrodynamic size of the protein decreases with increasing concentration, resulting in a slower approach to the glass transition than a hard sphere system.

INTRODUCTION

Recent advances in the theory of concentrated particulate dispersions have lead to the prediction of nonequilibrium states such as repulsive and attractive glasses (1), transient gels, and also to equilibrium cluster phases (2). The occurrence of such states depends upon the range and strength of the attractive and repulsive forces acting between the particles. Experimentally these states have been principally observed in colloidal systems although it has been shown that there are strong analogies between the behavior of colloidal and concentrated globular protein solutions (2). In model colloidal systems the particles are generally spherical although they may have a limited polydispersity, and the system prepared so as to have well-defined interparticle forces. On the other hand, globular proteins are generally nonspherical and there remain uncertainties in the prediction of interparticle forces. Part of this uncertainty arises as a result of the polyampholyte characteristics of the protein. Although the protein globule may carry a zero net charge, its surface charge distribution is heterogeneous and the net charge reflects the balance between positive and negative charges. This results in an orientation-dependent interparticle force and the possibility of dipolar interactions. In the experimental situation, although the protein particle is expected to be monodisperse, in practice a limited aggregation is often observed.

For colloidal systems with a dominant repulsive interaction, the viscosity of a suspension progressively increases with increasing volume fraction, φ, of particles (3,4). At high volume fractions there is a sufficient slowing of particle dynamics such that liquidlike configurations cannot be explored over practical timescales (5,6). For small applied stresses, the material has the solidlike characteristics of a glass with the particles forming jammed structures that are stress bearing. For a random packing of noninteracting monodisperse hard spheres, these structures may form at volume fractions in the vicinity of 0.6 with a random close packing limit, φ_c, of ≈0.644 (7,8). These structures result from repulsive excluded volume interactions. As short-ranged attractive interactions between particles are introduced (9), the attraction first “melts” the glass and then leads to the formation of a qualitatively different glassy state. With increasing attraction, three dimensional particle networks, with solidlike characteristics (colloidal gels), form at significantly lower particle volume fractions (10). Recent research has emphasized the similarities between jammed structures which form with increasing volume fraction of particles and those, more open structures which form as a result of an increasing attractive interaction between particles (9). A further aspect of nonequilibrium behavior exhibited by solutions of proteins with short-ranged attractive interactions is metastable liquid-liquid separation (11,12). The metastability is with respect to solid-liquid coexistence, that is, the solutions are supersaturated. In contrast to the glasses and networks, these are relatively low viscosity liquid states.

Earlier research (13) examined the colloidal glass transition behavior of a globular protein (bovine serum albumin) where there was a net repulsion between the protein globules. This article examines the rheological behavior of concentrated aqueous solutions of the globular protein β-lactoglobulin (BLG) as the colloidal glass transition is approached. The strength of the interparticle attraction is controlled through varying pH and ionic strength and the interparticle interaction probed through the determination of the osmotic pressure as a function of composition.

MATERIALS AND METHODS

Materials

BLG was obtained from Sigma-Aldrich (Poole, UK) (L0130) and is a mixture of genetic variants A and B. A polyethylene glycol fraction (PEG 20—average molecular mass of 20 kDa) and silicone oil (200/500 cs) were obtained from VWR (Poole, UK). Spectro/Por dialysis tubing, molecular mass cutoff 8 kDa, was a regenerated cellulose obtained from Spectrum Laboratories, NBS Biologicals (Huntingdon, UK). All other chemicals were Analar grade.

Mass spectrometry

The BLG preparation was examined by liquid chromatography-mass spectroscopy using reverse phase chromatography with on-line electrospray-ionization mass spectrometry (MicroMass, Cary, NC) as described previously (14). The preparation contained approximately equal amounts of BLG A (mass 18365) and BLG B (mass 18278). Small amounts (∼10% w/w) of lactosylated BLG (masses 18690, 18603) were also present in the preparation.

Photon correlation spectroscopy

The apparatus employed was an ALV/SP-86 spectrogoniometer (ALV, Langen, Germany) equipped with a Coherent (Ely, UK) Radiation Innova 100-10 vis Argon Ion laser operating at 0.5 W and a wavelength of 514 nm. BLG (6 g/L) was dissolved in 0.03 M NaCl and adjusted to the required pH with dilute NaOH. The aqueous solutions were filtered through a 0.22 μm Millipore (Billerica, MA) filter into a quartz cuvette and maintained at 25°C. The scattered light intensity was monitored using an ALV/PM-15 ODSIII detection system at a fixed scattering angle of 90°. After amplification and discrimination, signals were directed to an ALV/5000E Multiple Tau Digital Correlator and time-intensity correlation functions recorded, typically for 600 s duration. Size distribution functions were computed using the appropriate Windows-based ALV software, which incorporated regularized inverse Laplace transform and ALV-CONTIN packages. Additional analysis was undertaken using Origin V6 (Microcal, Studio City, CA) proprietary software.

Osmotic stress technique

The dependence of the osmotic pressure of BLG solutions on protein concentration, pH, and added NaCl concentration was determined using an osmotic stress technique. Two ml of a buffered BLG solution was dialyzed against buffered PEG solutions of known osmotic pressure (15,16) at 20°C for 24 h. After dialysis the dialysis tube was removed from the PEG solution and the BLG concentration determined by spectrophotometry. Under certain conditions either limited aggregation, as evidenced by turbidity, or the formation of two distinct liquid phases was observed. The amount of aggregated material, or the composition of the coexisting phases, was measured by centrifuging the samples for 5 min at 4000 g, removal of the upper phase, and determination of protein content of the aggregates or the concentration in each coexisting phase using spectrophotometry.

Modeling of osmotic pressure

The adhesive hard sphere (AHS) model is capable of describing the phase diagram and osmotic pressure of globular proteins taking account of excluded volume and short-ranged attractive contributions to the interparticle potential. Approximate analytic solutions are available for the pressure, Π (17–19)

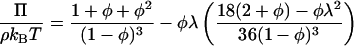(1)

and

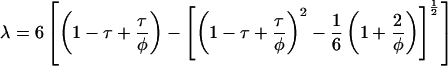(2)

where φ is the hard sphere volume fraction of the protein solution, ρ the protein number density, k_B Boltzmann's constant, and T absolute temperature. The dimensionless parameter τ is a measure of the strength of the attraction or the adhesiveness (stickiness) of the potential which is represented as an infinitely narrow deep well at the particle surface. An infinite value of τ corresponds to negligible attraction, i.e., hard sphere behavior, and a value tending to zero to infinite adhesiveness. In practice the hard sphere osmotic pressure characteristic is realized for τ > 100, and only the first term on the right hand side of Eq. 1 need be retained. For τ ≤ 0.113 the AHS model predicts liquid-liquid phase separation (20) which is metastable with respect to solid-liquid coexistence (21).

Rheological measurements

The rheology of BLG solutions at 20°C was determined using a Rheometrics (Ithaca, NY) ARES-LS2 rheometer with parallel plate geometry. The lower platen consisted of a Peltier temperature control surface. The upper platen was of ceramic (diameter, 25 mm or 50 mm). The minimum torque limit was 2 × 10⁻⁶ Nm. The BLG solutions were prepared using the osmotic stress technique. The sample was transferred directly from the dialysis bag onto the lower platen, and upper platen lowered until the sample filled the gap (typical gap was 0.3 mm). The visible sample surface was then coated in silicone oil (200/500 cs) to prevent water loss. The normal force was constantly monitored, while manually adjusting the gap, and not allowed to exceed 0.2 N. The normal force had relaxed to <0.05 N before testing commenced. Dynamic tests were performed over the frequency range 0.02–30 Hz and constant shear rate measurements (clockwise and counterclockwise) from 0.005 to 500 s⁻¹. The viscoelastic behavior was measured as a function of applied strain, γ, at a fixed oscillatory frequency of 1 Hz to determine the region of linear viscoelasticity. The frequency-dependent response was then examined at a γ within this region.

RESULTS AND DISCUSSION

Photon correlation spectroscopy

Photon correlation spectroscopy was used to characterize the dilute solution behavior of the BLG preparation through the determination of a translational diffusion coefficient, D_t. For a particle in solution subject to Brownian motion, the translational diffusion coefficient is related to the measured intensity correlation function g(2)(τ) by the expression (22)

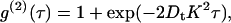(3)

where K, the scattering vector, is given by

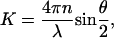(4)

where n is the refractive index of the solution, θ, the scattering angle, and λ the wavelength of light.

The conformation and association behavior of BLG are pH dependent (23,24). The monomeric unit has a molecular mass of 18.3 kDa. At pH ≥3.5 there is significant protein dimerization. This monomer-dimer equilibrium is dependent on ionic strength and protein concentration. At lower pHs an increase in ionic strength screens the electrostatic repulsion of positive charges on the monomer and stabilizes the dimer (25,26). At pH 4.6, the dimers may further aggregate to form an octamer, a structure observed predominantly at subambient temperatures (27,28). At pH 7.5 the protein conformation undergoes a reversible transition which leads to a swelling of the monomeric unit (29,30). At higher pHs there is the potential for a time-dependent irreversible aggregation.

The effective hydrodynamic radius, R_h, of BLG was obtained from the Stokes-Einstein relation

(5)

where η is the solvent viscosity. Fig. 1 shows a compilation of experimental values of the hydrodynamic radius, R_h, as a function of pH for BLG in aqueous solution obtained from this and previous studies (25,31–34). Only broad comparisons can be made as the studies were carried out at different ionic strengths and different protein concentrations. At low pHs (2.0–3.0) the calculated value of R_h, obtained by extrapolation of the diffusion coefficients to zero concentration, is ∼2.2 ± 0.1 nm, reflecting the hydrodynamic size of the monomeric unit and its associated electrolyte cloud (25,31). At pHs in the vicinity of neutrality (pH 6.0–8.0) the calculated values of R_h range from 2.6 to 4.9 nm. This range of values in part reflects the equilibrium between monomer and dimer. If the dimer is modeled as two touching spheres (31), the ratio of the R_h of dimer and monomer is ∼1.33 giving an estimated R_h of the dimer of 2.93 nm.

FIGURE 1.

Hydrodynamic radius of BLG as a function of pH. This study (•, ○); Takata et al. (34) (▪, □); Aymard et al. (25) (◂); Baldini et al. (31) (▸); Beretta et al. (32) (▴); Le Bon et al. (33) (♦). Open symbols represent second slower diffusive process, where reported, attributed to aggregated/associated BLG (34).

In this study at pH 7.9, the measured value of D_t for a 0.6% w/w BLG solution in 30 mM NaCl was 7.5 × 10⁻¹¹ m²s⁻¹, in agreement with previous measurements carried out under similar conditions and concentration (33). As the pH was reduced below 7.9, or increased above 10, the presence of a second slower diffusive process in the autocorrelation function was observed, which was attributed to a very limited aggregation/association of BLG (34). At pHs in the vicinity of the isoelectric point (pH 5.1), the calculated R_h of both the protein in solution and its aggregate increased in size and was correlated to the phase separation/precipitation of BLG from aqueous solution at these concentrations and ionic strength (34).

Osmotic stress and nonequilibrium phase diagram

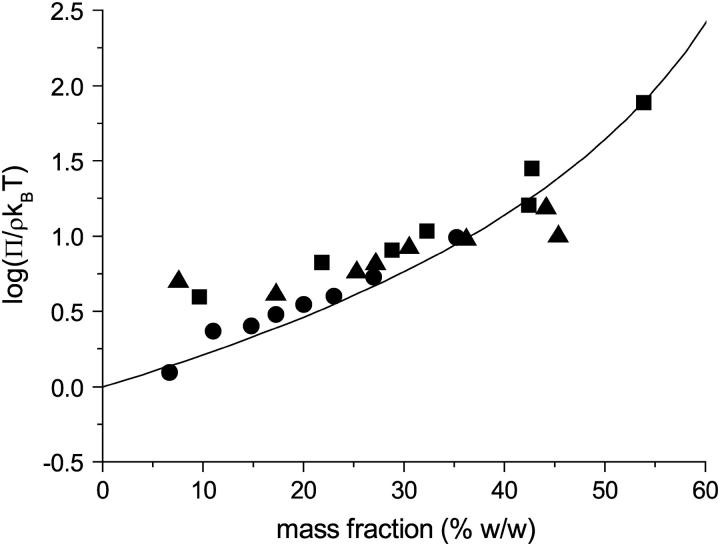
In Figs. 2–4, the osmotic pressure determined using the osmotic stress technique is plotted as the dimensionless compressibility factor, Π/ρk_BT, as a function of protein mass fraction for pH 8.0, 6.0, and 5.1 (10 mM buffer) and NaCl concentrations of 0 mM, 100 mM, and 1 M. To calculate the protein number density, the dimer molecular mass of 36.6 kDa and a protein specific volume of 0.75 ml g⁻¹ (35) were assumed. At pH 8.0 the osmotic pressure is independent of ionic strength and increases monotonically with protein mass fraction. At this pH (and pH 6.0) the osmotically stressed solutions were single phase with no visible turbidity. Also plotted in Fig. 2 is the osmotic pressure calculated using an approximate hard sphere equation of state (only the first term on the right hand side of Eq. 1 is used) assuming the apparent specific volume of the protein phase to be 1.12 ml g⁻¹. The ability of this model to fit the data indicates that the protein-protein interactions under these conditions are predominantly repulsive. At this pH the protein has a net negative charge, the dimer carrying a charge of −17e (36), where e is the protonic charge; and so the apparent specific volume would be expected to have a contribution from net repulsive electric double layer interactions in addition to the excluded volume of the hydrated protein itself. The insensitivity of the osmotic pressure to salt concentration indicates that the Donnan effect is apparently making little contribution to the overall osmotic pressure (37,38). Qualitatively similar osmotic behavior is observed at pH 6.0 (Fig. 3). At this pH, the osmotic pressure is weakly dependent upon salt concentration, increasing at high salt concentrations. The theoretical equation of state does not describe the experimental results as well as at pHs 8.0 (hard spheres, Fig. 2) or 5.1 (AHS, Fig. 4). The discrepancy at the lower concentrations (mass fraction ∼7–16% w/w) could be decreased if the assumed molecular weight (MW) were reduced from the dimer MW to the monomer MW. However, the photo correlation spectroscopy results at pH 6.0 do not support this explanation (Fig. 1).

FIGURE 2.

Dimensionless osmotic compressibility of BLG at pH 8.0 (10 mM buffer) as a function of mass fraction and NaCl concentration: 0 mM (▪); 100 mM (•); 1 M (▴). Solid line is the equation of state for hard spheres calculated assuming an apparent protein specific volume of 1.12 ml g⁻¹.

FIGURE 3.

Dimensionless osmotic compressibility of BLG at pH 6.0 (10 mM buffer) as a function of mass fraction and NaCl concentration: 0 mM (▪); 100 mM (•); 1 M (▴). Solid line is the equation of state for hard spheres calculated assuming an apparent protein specific volume of 1.12 ml g⁻¹.

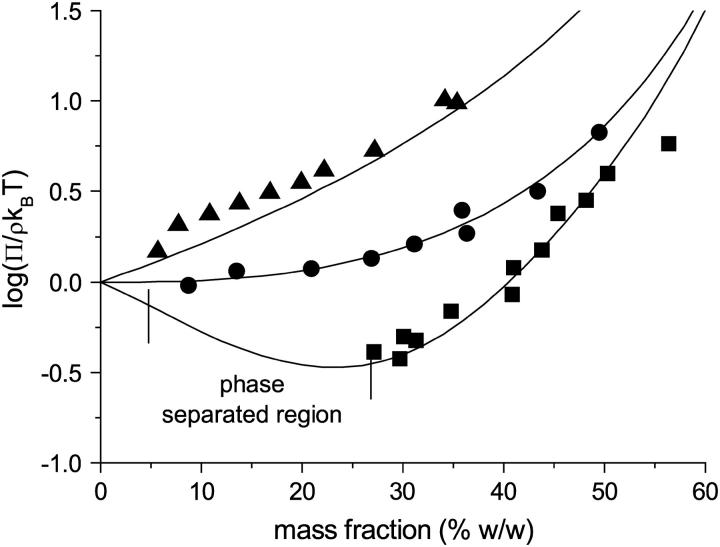
FIGURE 4.

Dimensionless osmotic compressibility of BLG at pH 5.1 (10 mM buffer) as a function of mass fraction and NaCl concentration: 0 mM (▪); 100 mM (•); 1 M (▴). Solid lines are the equation of state for AHSs calculated assuming apparent protein specific volume of 1.12 ml g⁻¹ and stickiness parameters of 0.11 (NaCl concentration, 0 mM); 0.24 (100 mM); and 1000 (1 M). With a stickiness parameter of 1000 the 1M NaCl line is essentially that for hard spheres.

At pH 5.1, close to the isoelectric point, the osmotic pressure was significantly lower at lower ionic strengths (Fig. 4), the compressibility factor being ≤1 for mass fractions up to ∼40% w/w. Whereas at 100 mM NaCl a limited aggregation occurred (this amounted to <15% of the protein), for the 10 mM buffer without added NaCl a liquid-liquid phase separation was observed for mass fractions below 27% w/w. Fig. 5 shows the coexisting phases for a solution which contained 15% w/w BLG overall. Mass spectrometry showed that there was no significant fractionation of BLG A and BLG B in either the aggregation or the phase separation. No extensive crystallization was observed under the conditions and timescales of our experiments. At this pH the ability of the AHS model to describe the osmotic behavior was examined, holding the apparent protein specific volume constant at 1.12 ml g⁻¹ and varying the stickiness parameter. At the highest salt concentration (1 M) the magnitude of the stickiness parameter (τ ∼ 1000) was indicative of a system with negligible stickiness, that is, the interactions could be modeled simply using an excluded volume hard sphere model. At the two lower ionic strengths, the osmotic data could be modeled with stickiness parameters, τ, of 0.24 (100 mM NaCl) and 0.11 (10 mM buffer alone). As the ionic strength is lowered there are increasingly strong short-ranged attractive interparticle interactions. The observation of liquid-liquid phase separation in the solution with no added NaCl and a stickiness parameter of 0.11 is the predicted behavior for a system of AHSs under these conditions (18,20).

FIGURE 5.

15% w/w BLG solution in 10 mM pH 5.1 acetate buffer showing phase separation.

The dependence of the phase behavior on ionic strength at pH 5.1 was examined more extensively, resulting in the nonequilibrium phase diagram shown in Fig. 6. At 20°C the solution has a critical point at ionic strengths of ∼13 mM and becomes increasingly subcritical as the ionic strength is lowered. In addition to the homogeneous liquid phases, the conditions under which limited aggregation occurred are also noted. Aggregation occurs at the protein concentrations at which phase separation occurs (<30% w/w) but at higher ionic strengths 20 mM < I < 200 mM. At higher ionic strengths (≥400 mM) and protein concentrations (≥30% w/w), only transparent single phase solutions are found.

FIGURE 6.

Nonequilibrium phase diagram of BLG at pH 5.1 as a function of ionic strength showing liquid phase (▴); liquid phase + limited aggregation (•); liquid-liquid coexistence (▪ and short dashed line); liquid-glass transition (▾ and long dashed line); solid-liquid coexistence (Grönwall (41)) (□ and solid line). Lines are only an aid to the eye.

The observed phase behavior is consistent with literature measurements of both the second virial coefficient (39,40) and the solid-liquid coexistence line (41). The second virial coefficient is negative in this pH region, indicative of there being short-ranged attractive forces. Piazza and Iacopini's light scattering study using BLG A (39) showed a minimum in the second virial coefficient at pH 4.2, which was found to be related to a transient clustering rather than phase separation. However, at pH 5.0 the virial coefficient remained negative as also found by Schaink and Smit (40) using membrane osmometry (mixed BLG A and B) at pH 5.2. The ionic strength dependence of the solid-liquid coexistence line for BLG at pH 5.1 as measured by Grönwall (41) is plotted in Fig. 6. This shows that liquid-liquid separation occurs in a region of the phase diagram which is metastable with respect to solid-liquid phase separation. This is a common behavior of protein phase diagrams and of particles with short-ranged attractive interparticle forces, e.g., AHSs (11,12). What is more unusual is the salting-in behavior which affects both the solid-liquid and the liquid-liquid coexistence lines. At pH 5.1 BLG is close to its isoelectric point and so, in terms of electrostatic interactions, those depending upon the charge heterogeneity rather than the net charge will tend to dominate. Early measurements (42) showed BLG has a dipole moment of a sufficient magnitude to generate significant attractive dipole-dipole interactions which are predicted to be screened by increasing ionic strength at the concentrations relevant to this study (40,43).

Results of osmotic squeezing at pH 3.6 were affected by an aggregation process which led to poor reproducibility particularly at low NaCl concentration. The overall effect of pH on the osmotic compressibility at 1 M NaCl is shown in Fig. 7. Whereas the results at pH 5.1, close to the isoelectric point, and pH 6.0 and 8.0, when the protein carries a net negative charge, can be described by hard sphere behavior those at pH 3.6 when the protein has a high net positive charge (dimer > +36e) are lower, indicating the presence of attractive forces and aggregation processes under these conditions.

FIGURE 7.

Effect of pH on the dimensionless osmotic compressibility of BLG as a function of mass fraction at a NaCl concentration on 1 M. pH: 3.6 (▪); 5.1 (•); 6.0 (▴); 8.0 (▾). Solid line is hard sphere equation of state calculated assuming an apparent protein specific volume of 1.12 ml g⁻¹.

Rheology

We have previously proposed that the rheology of globular protein solutions may be usefully compared to the rheology of colloidal suspensions (13). The rheology of polymer latex and microgel suspensions has been the subject of extensive investigation (4,44–47), with the viscosity showing a characteristic dependence on particle volume fraction. When the viscous behavior is examined as a function of shear rate, suspensions of intermediate volume fraction (0.2–0.5) show two Newtonian plateaus separated by a shear thinning region (48). For hard sphere suspensions the low shear viscosity, η₀, includes contributions from hydrodynamic forces associated with minimally perturbed equilibrium structures, whereas for the high shear viscosity, η_∞, the structure is substantially perturbed. For noninteracting particles, the shear stress, σ, at which the viscosity is intermediate between η₀ and η_∞, is of the order of

(6)

where a is the particle radius (4,48). For a particle the size of the BLG dimer, the calculated value of σ is ∼50 kPa. Shear stresses in excess of this are required to overcome diffusion driven equilibria. Given the comparatively low viscosity of the system, this relates to a shear rate in excess of 10³ s⁻¹.

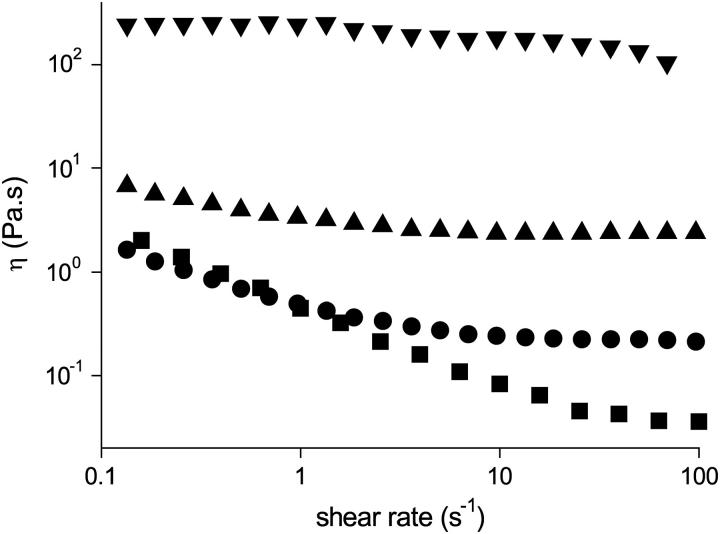
Fig. 8 shows a plot of shear viscosity versus shear rate for BLG solutions in the concentration range 23–52% w/w at pH 5.1 in 10.0 mM acetate buffer containing 1 M NaCl at 20°C. At the lower concentrations, Newtonian behavior was observed at shear rates, 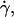in the range 10–100 s⁻¹. As the associated shear stress was ≪50 kPa, we ascribe this behavior to being equivalent to the η₀ of hard sphere colloidal suspensions. Below the short Newtonian plateau, the viscosity increases with decreasing shear rate. These observations are consistent with reports of the solidlike behavior of relatively dilute globular protein solutions (0.1–10% w/w) with strong shear thinning behavior being observed with increasing shear rate (49–51) and the storage modulus, G′, being larger than the loss modulus (49–53), G″. One proposed explanation for this behavior is that at low concentrations, a lattice type structure is formed. An alternative explanation is that in this concentration range, the presence of an interfacial layer of protein has a marked influence on the observed rheology. The interfacial layer can form both at an air/water (54–57) and an immiscible liquid/water interface (58,59). In a study (60) of the interfacial rheology of BLG, it was found that the protein formed a gellike elastic layer at the interface. The addition of the surfactant Tween 20 to the subphase abolished the shear elasticity as a consequence of the disruption of the adsorbed layer (60).

FIGURE 8.

Shear-rate dependence of the viscosity of BLG solutions in 10 mM pH 5.1 acetate buffer containing 1 M NaCl for mass fractions: 23.0% w/w (▪); 27.0% w/w (•); 45% w/w (▴); 52% w/w (▾).

From the Newtonian region, η₀ of the protein solution was obtained and the relative viscosity, η_r,0 = η₀/η_s, calculated where η_s is the solvent viscosity assumed to be 1.0 mPas. Fig. 9 shows the dependence of η_r,0 on BLG concentration at pH 5.1 in 10 mM acetate buffer and in this buffer containing 100 mM and 1.0 M NaCl. η_r,0 increases with increasing mass fraction of protein. At a fixed mass fraction, the solution viscosity of BLG in 100 mM and 1.0 M NaCl at pH 5.1 is similar but is higher at the lower ionic strength.

FIGURE 9.

Effect of mass fraction and NaCl concentration on the relative zero shear viscosity of BLG solutions at pH 5.1. NaCl concentration: 0 mM (▪); 100 mM (•); 1.0 M (▴). Equation 6 also plotted with ν = 3.6 and φ_max = 0.71 and apparent protein specific volume 1.47 ml g⁻¹ (solid line) and 1.12 ml g⁻¹ (dashed line).

For suspensions of spherical particles the dependence of relative viscosity, η_r, on volume fraction, φ, is given to a first approximation by Berli and Quemada (61)

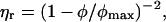(7)

where φ_max is the maximum packing fraction, which is 0.63 ± 0.02 at low shear and 0.70 ± 0.02 at high shear (4). In experimental studies on essentially monodisperse hard sphere suspensions, the value of φ_max, required to fit the dependence of η_r on φ (based on measurements of η₀ and various forms of Eq. 7), ranged from 0.58 to 0.64. The observed variability is in part dependent on polydispersity and its effect on packing and in part dependent on uncertainties in the volume fraction (62). By rescaling the volume fraction, it was possible to obtain a master curve of published data. For particles which have a diffuse outer layer, φ may be replaced by an effective volume fraction (61), φ_eff, which may be calculated from a hydrodynamic size determined from measurements of the viscosity of dilute suspensions. Particle deformability may also influence the observed viscous behavior with the increase in η_r with φ being less pronounced at the higher volume fractions (45). Deformability has a major effect on the relative high shear viscosity, η_r,∞, and a much weaker effect for the relative zero shear viscosity, η_r,0. Weak attractive interactions between particles are expected to primarily affect η_r,0.

Solutions of globular proteins are particulate suspensions. Ideally, the suspensions are monodisperse although in practice there is often a limited amount of aggregated material present. An important additional factor which should be considered is their shape. Although globular proteins may be approximated to spherical particles, they are usually asymmetric. An alternative expression to Eq. 7 which allows for the effects of particle asymmetry through a parameter, v, is given by

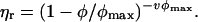(8)

This is the Krieger-Dougherty equation, where v for hard spheres is expected to be 2.5 (3,63). Particle asymmetry also has an impact on the maximum packing fraction (64). For example, it has recently been shown that the simulated packing of ellipsoidal particles showed a dependence on aspect ratio and can approach a packing, φ_max, of ∼0.74. The “bare” BLG dimer may be approximated to a prolate ellipsoid with a length of 6.9 nm and a width of 3.6 nm (24). For prolate ellipsoids of this aspect ratio, the maximum packing fraction is ∼0.71 (64). The value of v estimated from measurements of the reduced viscosity of dilute solutions of BLG as a function of concentration or from the known dimensions of the dimer is in the range 3.6–4.5 (35). Based on the R_h of the monomer of 2.2 nm, a specific volume of 1.47 ml g⁻¹ was used to convert protein mass to volume. A specific volume of protein of 0.75 ml g⁻¹ was then used to obtain the mass of water in the hydrodynamic domain of the protein, and from this the volume fraction of protein at known mass fractions was estimated. The predicted dependence of η_r on mass fraction for particles with a v of 3.6 and a φ_max of ∼0.71 is plotted in Fig. 9. At the higher ionic strengths, and at mass fractions in the vicinity of 30% w/w (φ ∼0.5), there is some correspondence between the measured and expected values of η_r,0. With increasing mass fraction, the expected increase in η_r,0 with φ is less than expected. The origin of this difference arises from the estimation of φ from mass fraction. Using a specific volume of 1.47 ml g⁻¹, obtained from the R_h of the BLG monomer in dilute solution, leads to values of φ for the more concentrated solutions which are above the expected φ_max or, using the reverse of the above conversion, a mass fraction of 43.1% w/w. Although this value of specific volume is required to approximate the viscous behavior at intermediate protein concentrations, the specific volume used for approximating the concentration-dependent osmotic pressure (1.12 ml g⁻¹) gives better agreement at higher protein concentrations (Fig. 9).

It is well accepted that water in the vicinity of the protein globule contributes toward its hydrodynamic behavior, particularly in dilute solution (65,66). Bead-modeling methodologies are available which allow the calculation of hydrodynamic quantities from the detailed atomic-level structure (65). For a range of proteins, a typical value of the thickness of the hydration layer is ∼0.15 nm. For small globular proteins, such as BLG, the volume of this layer is comparable to the volume of the dry protein. The viscous behavior of globular protein solutions will therefore be strongly influenced by the characteristics of this hydration layer. Information on the dynamics of protein hydration may be obtained from ¹⁷O magnetic relaxation dispersion measurements, which indicate that water molecules at protein surfaces are highly mobile (66,67). A recent dynamic hydration model has established a link between protein hydrodynamics and hydration dynamics, more particularly the effect of hydration dynamics on rotational and translational diffusion (66). The observed concentration-dependent behavior suggests that the influence of this hydration layer on viscosity decreases with increasing concentration.

For the BLG solutions containing 1 M NaCl at pH 5.1, the osmotic pressure data indicate that the dominant interaction between the protein particles is repulsive. In the solutions containing 100 mM NaCl and 10 mM acetate buffer alone, this interaction becomes increasingly attractive at short range. For colloidal systems, the initial effects of attraction, particularly at high volume fractions, is a reduction in viscosity as the initial clustering of particles increases the free volume available for structural rearrangement (1). With increasing attraction there is the potential to form particle networks or gels (68–70). In the case here, the effect of the weak attraction between the BLG particles is an increase in η_r,0 at a fixed φ.

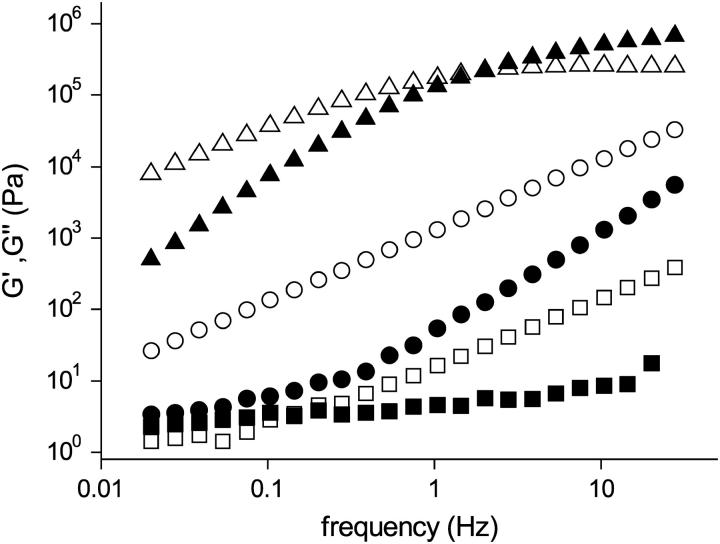
At high BLG concentrations, the marked increase in η_r,0 with increasing φ and the consequent slowing of structural rearrangement indicates the onset of solidlike behavior. The viscoelastic behavior of BLG solutions in 1.0 M NaCl at pH 5.1 in the concentration range 45–54% w/w was determined by oscillatory rheometry. At small strains, γ < 0.01, both G′ and G″ were independent of γ. The frequency dependence of G′(ω) and G″(ω) is shown in Fig. 10 for 45%, 52%, and 54% w/w BLG solutions. For the concentrations 45% and 52% w/w, G″ > G′ over the frequency range examined of 0.02–30 Hz, a viscous liquid-like response. For the 54% w/w solution, G′ crosses G″ at ∼2 Hz, a transition to an elastic solidlike response. This crossover indicates the approach of a dynamic transition which can be compared to the colloidal glass transition (5,70). For particles such as BLG in 1.0 M NaCl where the dominant interaction is repulsive, the glasslike transition is primarily influenced by particle crowding (5,70). In this case the particle motions become constrained in cages and the particles can no longer diffuse freely. The dominant elasticity results from distortions in the average particle configurations and is thought to be entropic in nature (70). In addition to the divergence of viscosity (Fig. 9), the change in viscoelasticity is a further indication of the onset of a glass transition with increasing BLG concentration.

FIGURE 10.

Frequency sweep of the complex shear modulus of concentrated BLG solutions at pH 5.1 with 1.0 M NaCl for mass fractions: 45% w/w (▪,□); 52% w/w (•,○); 54% w/w (▴,▵). The storage modulus, G′, and loss modulus, G″, are the solid and open symbols, respectively.

Recent studies have indicated that there is a qualitatively different glass transition at high volume fractions for particles which have a weak attraction (1). With increasing particle attraction, solidlike behavior may be obtained through the formation of particle networks within which the solvent is dispersed. We did not observe either of these phenomena in our experiments. At pH 5.1 the osmotic pressure measurements indicate there are short-ranged attractive interactions at low ionic strength, but these result in liquid-liquid phase separation which is apparently unhindered by any kinetic arrest. In the range in which we were able to measure these systems, the dynamic shear moduli show the system to be predominantly liquidlike. Theoretically the occurrence of particle gel formation is linked with percolation although this is a necessary rather than a sufficient condition for gelation to occur (21). For AHS both approximate analytic (71) and recent machine calculations (20) indicate that to a very large extent the metastable liquid-liquid coexistence curve lies below the percolation line, and so particle gel formation rather than liquid-liquid separation is predicted. Calculations (21) show that if a longer ranged attraction is added on to the AHS model, although the percolation line does not move, the effective stickiness varies such that the liquid-liquid coexistence line is no longer below the percolation line, a potential explanation for the absence of particle gelation.

GENERAL DISCUSSION

The compositions at which the relative viscosity (Fig. 9) diverges provide an indication of the position of the liquid-glass transition. For the sample with no added NaCl, the divergence occurs at a mass fraction of ∼52% w/w, increasing to 56% w/w at 1M NaCl. These points and the liquid-glass transition boundary have been added to the nonequilibrium phase diagram (Fig. 6). The liquid-liquid coexistence region and glass transition are well separated, and so the two processes will not affect one another. As we discussed previously (13), the behavior in this study is relevant to globular proteins subjected to osmotic stress in biological situations. Cytoplasmic concentrations relevant to macromolecular crowding are typically up to 40% v/v (72). If the cytoplasm is dehydrated as, for example, in the desiccation of a seed, the results indicate that when the concentration of globular proteins exceeds 60% w/w this component will vitrify. This will arrest diffusion at the protein globule length scale. However, flexible polymers and lower molecular weight components typically vitrify at much lower water contents (<20% w/w). Conversely, in a germinating seed the hydration of vitrifed storage proteins will be a necessary step to mobilize them and make them available for use.