Global Rigid Body Modeling of Macromolecular Complexes against Small-Angle Scattering Data

Abstract

New methods to automatically build models of macromolecular complexes from high-resolution structures or homology models of their subunits or domains against x-ray or neutron small-angle scattering data are presented. Depending on the complexity of the object, different approaches are employed for the global search of the optimum configuration of subunits fitting the experimental data. An exhaustive grid search is used for hetero- and homodimeric particles and for symmetric oligomers formed by identical subunits. For the assemblies or multidomain proteins containing more then one subunit/domain per asymmetric unit, heuristic algorithms based on simulated annealing are used. Fast computational algorithms based on spherical harmonics representation of scattering amplitudes are employed. The methods allow one to construct interconnected models without steric clashes, to account for the particle symmetry and to incorporate information from other methods, on distances between specific residues or nucleotides. For multidomain proteins, addition of missing linkers between the domains is possible. Simultaneous fitting of multiple scattering patterns from subcomplexes or deletion mutants is incorporated. The efficiency of the methods is illustrated by their application to complexes of different types in several simulated and practical examples. Limitations and possible ambiguity of rigid body modeling are discussed and simplified docking criteria are provided to rank multiple models. The methods described are implemented in publicly available computer programs running on major hardware platforms.

INTRODUCTION

The challenge of the postgenomic era, when large numbers of genome sequences have become available, has led to large-scale macromolecular structure determination projects using x-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy aiming at structure determination of individual proteins or their domains (1). Although this atomic information is extremely valuable, it is also limited, as increasing evidence indicates that proteins function in the context of the cell not as individual entities but in complex with other macromolecules. Consequently, the focus of modern structural genomics is rapidly shifting toward the study of macromolecular complexes (2,3). These macromolecular assemblies are difficult to study by high-resolution methods due to their large size, inherent structural flexibility, and often transient nature. Since in many cases the structures of individual components are available, models of complexes can be built by rigid body assembly of the components based on experimental information from lower resolution methods. Thus, cryo-electron microscopy (cryo-EM) reconstructions provide a framework for docking the high-resolution models into the shapes of macromolecular complexes. This approach leads in many cases to excellent results (2), but application of cryo-EM is usually limited to large macromolecular aggregates (starting from a few hundred kDa).

Small-angle scattering (SAS) (4,5) is a universal low-resolution method to study native particles in solution and to analyze structural changes in response to variations of external conditions. SAS needs monodisperse solutions of purified macromolecules, but, normally, does not require special sample preparation. Similarly to cryo-EM, the scattering of x rays and neutrons yields information about the overall shape of the macromolecule, and, thanks to the recent progress in the analysis methods, particle shapes can be reconstructed from the SAS data ab initio (6–11). Although the three-dimensional cryo-EM images typically provide more detailed shapes then the ab initio SAS reconstructions, the latter experiments (especially for x rays) and data analysis are much faster, and SAS is applicable to a broader range of conditions and sizes (from a few kDa to hundreds MDa).

SAS, also being a powerful tool for rigid body modeling, employs a different strategy from that of EM. In the latter case, the high-resolution models of the individual subunits are usually docked into the envelope of the complex obtained after three-dimensional image reconstruction. In contrast, the SAS modeling is data-driven, i.e., the spatial arrangement of the subunits is sought by a direct fitting of available experimental scattering data from the complex. Several approaches were proposed to speed up this computationally demanding search. In the method in Wall et al. (12), the subunits are first represented by triaxial ellipsoids to find an approximate arrangement followed by docking of the atomic models. In the constrained fit procedure (13,14), the high-resolution models are represented by bead assemblies and thousands of possible bead models are screened, also accounting for other results, from ultracentrifugation. Another set of modeling tools operates directly on atomic models using spherical harmonics to accurately compute the scattering from individual domains (15,16). Algorithms for rapid computation of the scattering from the complex (17) are coupled with three-dimensional visualization programs (18,19) for interactive fitting of the experimental data by manipulating the subunits on the computer display. A local automated refinement using an exhaustive search in the vicinity of the current configuration is also possible. In all the rigid body analysis approaches, the use of information from other methods is extremely valuable to build sound structural models. This can be, e.g., information about contacting residues from mutagenesis studies, distance constraints from Fourier transform infrared (20), data on surface complementarity and energy minimization (21), or residual dipolar coupling NMR data reducing the rotational degrees of freedom during the modeling (22).

We have developed a new set of methods for global rigid body modeling based on the fast spherical harmonics algorithms (15–19). In the present program suite, either exhaustive or heuristic algorithms are employed for rigid body modeling of complex particles based on the SAS data. The methods cover different types of macromolecular complexes, allow one to account for the particle symmetry, to include information about the intersubunit contacts, to simultaneously fit multiple scattering patterns, and to add missing linkers or domains. The approaches and programs presented are applicable for the modeling of both x-ray and neutron scattering data. The efficiency of the methods is illustrated by simulated and practical examples, limitations and ambiguity of the rigid body modeling technique are discussed, and additional criteria for the choice of the best solution are presented.

THEORY

Rigid body modeling technique

Let us assume that a complex consists of K subunits with known structure. The scattering amplitude from each subunit in a reference position is denoted as C^(k)(s), where s is the scattering vector in reciprocal space, s = 4π sin(θ)/λ, 2θ is the scattering angle, and λ is the wavelength. The idea of modeling is to find the spatial arrangement of the subunits, scattering from which would best fit the experimental scattering from the entire complex. The subunits are moved and rotated as rigid bodies, which changes their scattering amplitudes. The scattering intensity I(s) of the entire complex is expressed as (23)

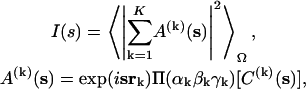(1)

where A^(k)(s) denotes the scattering amplitude of the k^th rigid body at the given position, 〈…〉_Ω stands for the spherical average in reciprocal space, and Π(α_kβ_kγ_k) is the rotational operator (24). The modified scattering amplitudes A^(k)(s) of each body depend in the general case on six parameters, the vector of the shift r_k, and the Euler rotation angles α_k, β_k, and γ_k. The use of spherical harmonics for the multipole expansion of the scattering amplitudes allows a convenient analytical representation of the scattering intensity in the form of

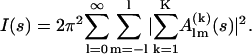(2)

Here, the complex functions 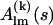are the partial scattering amplitudes of the k^th rigid body, which depend on its scattering amplitudes, 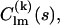in reference position and orientation and on the six rotational and translational parameters. The reference amplitudes 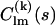can be calculated from the high-resolution structures using the programs CRYSOL (15) for x rays or CRYSON (16) for neutrons. The analytical relationship between 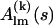and 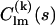is described elsewhere (25).

Biological macromolecules and their complexes often contain equivalent subunits forming symmetric structures. The presence of symmetry can significantly reduce the number of non-zero terms in Eq. 2. Thus, for symmetric particles having point groups P_n and 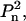it can be assumed without loss of generality that the n-fold axis coincides with the z axis, and that the twofold axis (in the case of 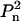symmetry) coincides with the y axis, which leads to the specific selection rules for the spherical harmonics. In this case, summation in Eq. 2 runs only over symmetry-independent rigid bodies in the ensemble, and only over m equal to zero or multiples of n; and, moreover, in the case of 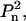terms of order l0 with odd l, as well as all imaginary parts, vanish.

The goodness-of-fit provided by a given arrangement of bodies to the experimental data I_exp(s) is measured by the discrepancy

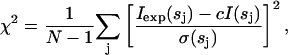(3)

where N is the number of experimental points, c is a scaling factor, and σ(s_j) is the experimental error at the momentum transfer s_j.

To construct physically sound models, the target function E = χ² + Σα_iP_i can be employed, where the penalty terms α_iP_i formulate the requirements of interconnectivity and absence of overlaps and also permit to incorporate additional information from other methods if available (e.g., interresidue distances). The penalty weights α_i are selected to ensure the significance of the given penalty in each particular case and yield 10–50% contribution to the function at the end of the minimization.

The choice of the global minimization method depends on the number of adjustable parameters describing the complex, which in turn depends on the particle symmetry and on the available constraints. In the general case of an asymmetric complex, this number is equal to 6K–6 (the position and orientation of each rigid body is given by six spatial parameters, and the reduction by six is due to arbitrary orientation and position of the center of the ensemble). Fewer parameters are required when the symmetry is taken into account: in particular, 6K/n–2 for P_n symmetry and 3K/n for 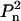symmetry.

Given the limited conformational space, for hetero- and homodimeric particles and for symmetric oligomers formed by identical subunits it should be possible to perform an exhaustive grid search of the best configuration in reasonable computing time. For macromolecular assemblies consisting of more than two distinct subunits, heuristic algorithms have to be applied for the global minimization. In the present article, four algorithms are described for global rigid body modeling depending on the type of the system (hetero- and homodimers, higher oligomers, multisubunit complexes, and multidomain proteins).

Fast modeling of homo- and heterodimers

A fast simplified algorithm can be designed for the modeling of globular homo- or heterodimeric structures whereby one monomer is rolled on the surface of the other. For this, the shapes of the two monomers are represented by angular envelope functions F(ω), where ω is the solid angle in real space. These envelopes can be generated by the programs CRYSOL (15) or CRYSON (16) on a quasiuniform angular grid (17) (Fig. 1 A) on the surface of a sphere. A sequence of Fibonacci numbers for the evaluation the values of polar angles defining the sampling directions (the greater the order of the Fibonacci grid, the greater the number of directions generated).

FIGURE 1.

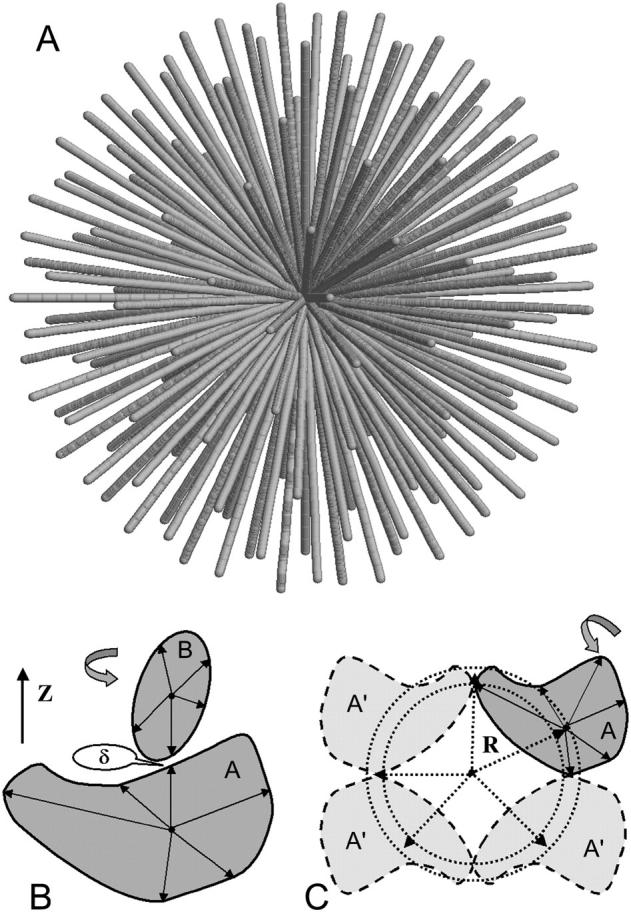
A quasiuniform grid of angular directions generated for 11th Fibonacci number (145 directions) (A) and the schemes of the two grid-search modeling approaches: DIMFOM modeling of heterodimers (B) and GLOBSYMM modeling of symmetric oligomers (C).

Starting from both monomers centered at the origin, the first monomer is rotated to bring the j^th direction of Fibonacci grid ω_j to the z axis, and the other is rotated to bring the i^th direction of its Fibonacci grid ω_i antiparallel to the z axis. In the case of homodimers with twofold symmetry axis, only the j = i case is taken to ensure the symmetric arrangement of monomers. Finally, the second monomer is shifted along the z axis by F⁽¹⁾(ω_j) + F⁽²⁾(ω_i) + δ and rotated about this axis by an angle 0 < ψ < 2π with a discrete angular step (Fig. 1 B). The offset δ ∼ 0.3 nm between envelopes ensures a reasonable contact between the surfaces of monomers and diminishes the probability of steric clashes. Using this algorithm, the second body is always shifted along the z axis, which significantly speeds up the computations (25).

The approach is implemented in the computer program DIMFOM, which makes a search over all ω_j, ω_i (with i = j in the case of symmetric homodimers) and discrete rotations of the second subunit, in order to find the arrangement best fitting the experimental data. Although this approach is limited by the low resolution of the envelope function and generates dimeric structures that contact each other approximately along the line connecting their centers, it is useful for rapid modeling of complexes consisting of globular domains.

A brute-force modeling of symmetric oligomers

Symmetric assemblies of identical monomers (homodimers, trimers, etc.) can be constructed by appropriate positioning of the monomer and generation of the symmetry mates. The entire structure is thus described by six parameters—shift of the monomer by r = (r, ψ, φ) and rotation by α, β, and γ. Moreover, the scattering intensity computation using Eq. 2 is accelerated in the presence of symmetry thanks to the selection rules as described above. The limited number of parameters and rapid computation of the intensity make it possible to employ an exhaustive grid search procedure to minimize discrepancy in Eq. 3.

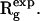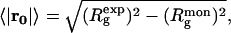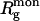The general scheme of the procedure is displayed in Fig. 1 C. The spatial and angular grids for the search of the position and orientation of the monomer are generated as follows. The magnitude of the shift vector r is constrained by the experimental value of the radius of gyration of the entire oligomer The average value of the shift from the origin is where is the radius of gyration of the monomer.3 Moreover, for the symmetry P_n (z is n-fold axis), it is sufficient to consider only displacements along the x axis. The global search of four (for P_n) or six (for 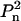) positional parameters is performed over the allowed range of r (by default from 0.95r₀ to 1.05r₀), whereby the angular parameters ψ, φ of the shift are taken from a Fibonacci grid. The Euler angles triplets are also selected to yield discrete rotations about the axes matching the generated Fibonacci grid directions (the orders of the grids for rotations and translations may differ from each other).

To avoid the oligomeric structures with loose contacts between the monomers and those with steric clashes, the generated models of protein complexes are rapidly checked using the coordinates of C_α atoms. The two criteria (cross- and contact-criteria) are introduced as follows. In the given configuration of the oligomer a sphere is drawn with the radius of r = 0.76 nm around each C_α atom of the first monomer and all C_α atoms belonging to the symmetry mates are identified inside the sphere. For each such C_α–C_α pair, the distance d is computed. If d < 0.38 nm, the pair contributes to the overall cross-value as (1/d − 1/0.38). If 0.38 < d < 0.76, a contact value 1/d is assigned to the pair of monomers containing these C_αs. The threshold value of d = 0.38 nm, being the distance between two subsequent C_αs in a polypeptide chain, is also a good estimate of an average residue radius. Inspection of the high-resolution models of multisubunit proteins indicates that the residues, where the C_α atoms separated by more than two dimensions, are unlikely to contact each other. The two monomers are assumed to be in contact if their total contact value is larger than 2.5 nm⁻¹ (which corresponds to at least one pair with d < 0.4 nm or to the existence of more than one pair). The overall cross-value is then normalized to the total number of monomers and the overall connectivity of the oligomer is computed from the contacts between individual monomers. Disconnected structures and those with the average cross-value exceeding the threshold of 50 nm⁻¹ are discarded without calculating the scattering intensity, to speed up the minimization procedure; otherwise, the overall cross-value is added as a penalty P_cross to the target function. For nucleic acids, a similar criterion is computed using the coordinates of P atoms.

If the information about distances between specific residues in the oligomer is available (e.g., from mutagenesis studies or fluorescence labeling), it can be used as a further restraint. For each such pair of residues, the expected C_α–C_α distance d_k0 is specified and a penalty term with a quasispring potential is computed as

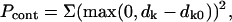(4)

where d_k is the actual distance in the given configuration. Again, coordinates of P atoms can be used to account for the distance restraints for nucleic acids.

The above exhaustive search algorithm of the quaternary structure of symmetric oligomers is implemented in a computer program GLOBSYMM. The target function to be minimized has the form

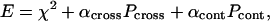(5)

where α_cross and α_cont are the weights of the corresponding penalties.

During the run the program keeps a list of 20 best solutions, which are grouped after the minimization is finished. All solutions within the group differ from the best model of this group with RMSD less than the threshold specified by the user (the default value is 20% of the experimental radius of gyration). The overall best model is saved onto a Protein Data Bank (PDB) file; the parameters of the representative solutions of each group are stored in the log-file and can be retrieved by GLOBSYMM to generate these models.

Quaternary structure determination of multisubunit complexes

The above exhaustive search methods are hardly applicable for complexes containing several symmetrically unrelated subunits. The conformational space to be explored would have been too large, leading to a prohibitively long computation time for the brute-force calculations. A feasible alternative to the exhaustive search methods is simulated annealing (SA) (26), a technique used for global minimization of multivariant functions in different fields, and, in particular, for ab initio small-angle x-ray scattering (SAXS) data analysis (10,11,27).

The main aim of SA is to perform random modifications of the system (i.e., in our case, of the current subunits arrangement) by always moving to configurations, which decrease the scoring function E but occasionally also to those increasing E. The probability of accepting the latter moves decreases in the course of the minimization (the system is cooled). At the beginning, the temperature is high and the changes are almost random, whereas at the end a configuration with (nearly) minimum E is reached. Further details of the SA protocol in its faster quenching version applied here are described elsewhere (28,29).

The minimization procedure starts from an arbitrary initial assembly of K subunits, e.g., from their arrangement in a tentative model of the complex or just from all subunits centered at the origin in their reference orientations. It is possible to fix selected subunits at their starting positions and orientations to preserve known substructures. The scattering amplitudes of the subunits 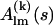are computed and the scattering intensity of the complex is calculated using Eq. 2. A single modification of the assembly is done by rotation of a randomly selected subunit by an arbitrary angle φ < φ_max about a rotation axis (selected from the Fibonacci grid) followed by a random shift r < r_max along an arbitrary direction. At each step only one subunit is moved/rotated, and it is sufficient to recompute only the amplitudes of this subunit in Eq. 2, which significantly speeds up the calculation of the scattering intensity.

In some cases, not only the experimental scattering pattern of the entire macromolecular complex but also those measured from its partial constructs (substructures) are available. Assuming the same arrangement of subunits in the substructure(s) and in the complex, all the data sets can be fitted simultaneously. The scattering curves of the substructures are computed from the appropriate subsets taken from the entire assembly. The use of multiple scattering data sets, similarly to the contrast variation technique in neutron scattering, permits one to increase the experimental information content and thus to obtain more reliable results.

The SA protocol is employed in the program SASREF to construct an interconnected ensemble of subunits without steric clashes, providing the possibility of fitting a single or multiple data set(s) by minimizing the target function:

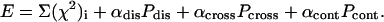(6)

Here, the sum runs over the discrepancies to the available data sets. The penalty P_dis = ln (K/K_G) ensures interconnectivity of the model, where K_G is the number of subunits in the longest interconnected subset (graph) found in their current arrangement and P_cross requires the absence of overlaps between subunits. The contact criteria between subunits to find the longest interconnected graph and the crossover penalty P_cross and the contacts term P_cont have the same form as in the brute-force modeling of symmetric oligomers described in the previous section. The later term permits us to incorporate information about distances between residues or nucleotides similar to Eq. 4. Additionally, ranges of residues (nucleotides) can be specified that are expected to be in the contact, and the program selects the minimum distance between the two groups to verify the contact criterion.

For symmetric particles with K subunits in the asymmetric unit, appropriate symmetry mates are generated to build the model of the entire complex. In this case, only the symmetry-independent part is modified during SA, whereas the rest is generated by appropriate symmetry operations.

Rigid body modeling coupled with addition of missing fragments

Very often in practical applications the high-resolution models of the subunits are only partially available, and the structure(s) of some fragments remain unknown. This could be the case for multisubunit assemblies but also for multidomain proteins consisting of globular domains linked by flexible loops. The high-resolution structures or homology models may be available for the individual domains but usually not for the linkers. In this case, a combined rigid-body and ab initio modeling approach can be employed to determine the overall structure of the entire assembly against the x-ray scattering data. The idea is to simultaneously find optimal positions and orientations of the domains/subunits moved as rigid bodies and probable conformations of the flexible linkers attached to the appropriate terminal residues of the domains. These linkers are represented as interconnected chains composed of dummy residues (DR). In the DR representation, a loop or protein fragment with unknown structure is substituted by a flexible chain of interconnected residues with spacing 0.38 nm. Each DR has a form-factor equal to that of an average residue in water and the x-ray scattering amplitude from such a chain is readily computed as described in Svergun et al. (11) and Petoukhov et al. (27). Accounting for the scattering from the DR-represented portions, Eq. 2 takes the form of

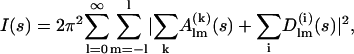(7)

where 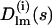are the partial amplitudes of DRs comprising the linkers.

As in the above modeling of multisubunit complexes, SA is employed for global minimization. The initial DR linkers are planar zig-zaglike polylines connecting the appropriate residues between the domains. A single modification of the system is performed by a random rotation of the part of the structure between two randomly selected DRs about the axis connecting these DRs, or alternatively, a single DR is selected dividing the entire chain into two parts and the smaller part is rotated by a random angle about a random axis drawn through this DR.

Multiple scattering data sets from partial constructs (e.g., deletion mutants), if available, can be fitted simultaneously. The target function has the form

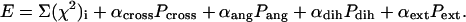(8)

Here, penalty P_cross requires absence of overlaps between the domains and the DR linkers; P_ang and P_dih penalties to ensure proper distribution of bond and dihedral angles, respectively, in the flexible DR chains (27); and P_ext is introduced to avoid a too-extended conformation of the DR loops by restraining their radii of gyration, as

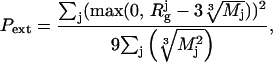(9)

where 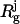is the radius of gyration of the j^th fragment consisting of M_j DRs, the value 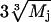being an R_g estimate of a globular protein containing M_j amino acids, and the sum runs over all the DR loops. The connectivity restraint, P_dis, used for the multisubunit complexes, is not required here—since the model is always interconnected, thanks to the DR linkers connecting the domains.

The above algorithm to reconstruct domain structure and missing fragments against single or multiple scattering data set(s) from partial constructs is implemented in the program BUNCH. The program is primarily oriented toward single chain proteins or symmetric assemblies containing one polypeptide chain per asymmetric part. BUNCH can, in principle, also be used for the modeling of macromolecular complexes consisting of several subunits, when not all the structures of the subunits are known. In this case, not only can missing loops within one single subunit be reconstructed, but also the shape(s) of the missing subunit(s) can be restored. As the linkers are usually heavily hydrated, a possibility is added in BUNCH to increase up to 50% the partial amplitudes of the DRs representing the missing loops, which allows one to take the bound water into account. It should, of course, be kept in mind that the configuration of the loops provided by BUNCH reflects an average conformation of (often flexible) loops, and can effectively serve as an indicator of the volume occupied by the loops, and not as a representation of their actual tertiary structure.

Scattering experiments, data processing, and analysis

The experimental SAXS data sets from the protein solutions used for testing the methods on practical examples were collected, following standard procedures on the X33 camera (30–32) of the European Molecular Biology Laboratory on the storage ring DORIS III (DESY, Hamburg, Germany) except for the data from hemocyanin solutions collected on the D24 station at LURE (Orsay-Paris, France) (33). The sample preparation, data processing, and analysis are described in detail elsewhere (27,34–37).

Computer programs and testing

The programs GLOBSYMM, DIMFOM, SASREF, and BUNCH run on IBM PC-compatible machines under Windows 9x/NT/2000/XP, Linux, and Mac OSX, as well as on major Unix platforms. The main features and possible applications of the four algorithms are summarized in Table 1. All the programs (except DIMFOM) are able to take into account particle symmetry by generating symmetry mates for the rigid bodies (and DR residues) in the asymmetric part (point groups P2–P6 and P222–P62 are currently supported). The programs were tested on simulated examples to adjust the parameters of the minimization procedures, in particular the weights of the penalty terms. The optimum parameters found are used in all the programs as default values. Both SA programs have two modes of operation: the user mode, using minimum input and the default values of the minimization parameters; and the expert mode, where these values may be modified.

TABLE 1.

Comparison of algorithms for global rigid body modeling

	DIMFOM	GLOBSYMM	SASREF	BUNCH
Objects	Homo- and heterodimers	Symmetric oligomers with one monomer per asymmetric part	Macromolecular complexes	Multidomain proteins; complexes of subunits with missing fragments
Multiple data sets fitting	No	No	Yes	Yes
Maximum number of independent rigid bodies	2	1	10	10
Symmetry	P1, P2	P2–P6, P222–P62	P1–P6, P222–P62	P1–P6, P222–P62
Minimization method	Rolling on the surface	Global grid search	Simulated annealing	Simulated annealing
Constraints	Symmetry, interconnectivity	Symmetry, interconnectivity	Symmetry	Symmetry, interconnectivity
Restraints	—	Steric clashes, pair contacts	Interconnectivity, steric clashes, pair contacts	Compactness, steric clashes, and bond/dihedral angles in DR loops
Number of target function evaluations/CPU, min	4000/0.5	15,000/3	1.2 × 105/50	3 × 105/80

RESULTS

Validation of the techniques against simulated data

The proposed methods were first tested against synthetic model examples. Theoretical scattering patterns were generated from known complexes taken from PDB (38), and these complexes were broken into subunits. The x-ray scattering amplitudes from the subunits were computed using CRYSOL and the structure of the complex was restored by fitting its scattering pattern by one of the above programs. Below we present a synthetic example of a protein-RNA complex to demonstrate that the methods are applicable not only to protein complexes.

The complex was constructed using crystallographic coordinates of two proximal monomers of glutamil-tRNA synthetase (GTS) complexed with tRNA (PDB entry 1g59; see Ref. 39). The entire crystallographic dimer (in Fig. 2 A, top row) has the molecular weight of 156 kDa and contains 468 amino acids and 75 bases per monomer. The two monomers are related by a twofold symmetry axis. First, the scattering curve of the dimeric complex was computed and randomized to yield a constant relative error of 3% in each data point (Fig. 2 B). Generation of other types of error distributions did not influence significantly the results of the modeling. The resulting curve was fitted with the P₂ symmetry constraint using the structure of the GTS-tRNA monomer as a single rigid body. The reconstructions were made independently by three programs (DIMFOM, GLOBSYMM, and SASREF) all yielding good fits (not shown) to the simulated data with χ = 1.39, 1.12, and 0.93, respectively. The reconstructed models demonstrate the same arrangement of monomers as the correct dimer, with the RMSD between the atomic coordinates of the simulated complex and the rigid body models of ∼0.2 nm. Typical parameters for the grid search methods used in the simulated and practical examples below were Fibonacci grid with 145 angular directions, the rotational sampling of 10°, and, if required, spatial step 0.1 nm. For the SA techniques, up to 10,000–20,000 function evaluation per temperature were made and the temperature was decreased with a factor 0.9 (maximum 100 temperature steps). The numbers of target function evaluations and CPU times required for running this test example on a 2.2-GHz Pentium PC machine are given in Table 1.

FIGURE 2.

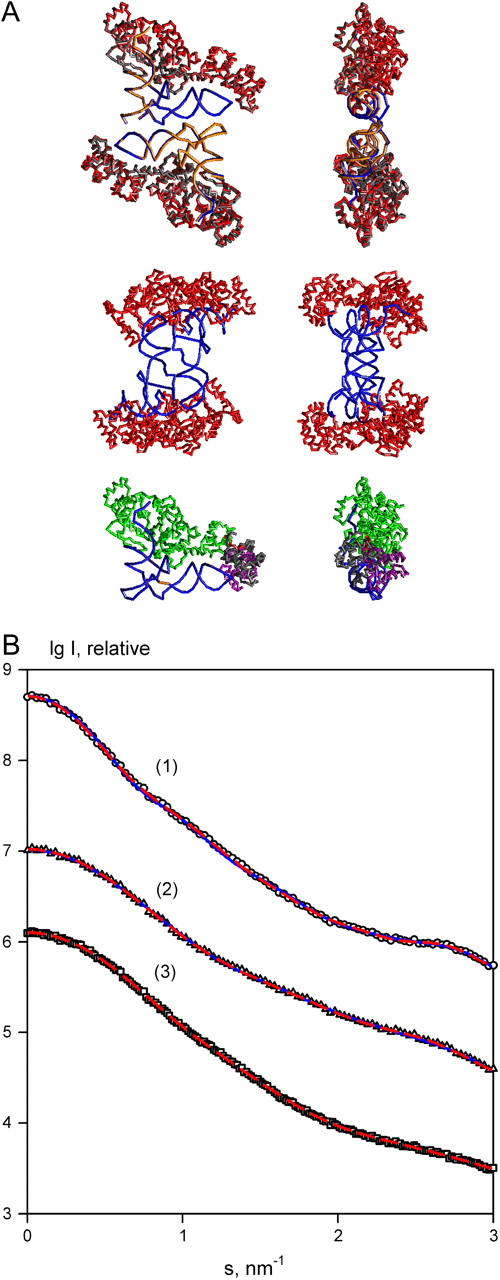
Validation of the rigid body modeling techniques on a simulated tRNA-GTS complex. (A) Models of the complex. (Top row) Initial model of the dimer (orange and gray) superimposed with the model reconstructed by SASREF using the distance restraint as described in the text. The restored model fits the curves of the dimeric tRNA and the entire complex using one tRNA (in blue) and one GTS monomer (in red) in the asymmetric part. (Middle row) An incorrect arrangement obtained by SASREF without the distance restraint. (Bottom row) Superposition of the model of monomeric GTS-tRNA complex built by BUNCH with the initial monomer. Fixed domain of GTS, DR linker, and the moving domain are shown in green, red, and magenta, respectively. The right panel is rotated by 90° about the vertical axis. (B) Scattering patterns of the dimeric complex, 1; dimeric tRNA, 2; and monomeric complex, 3. The simulated data are denoted by open circles, triangles, and squares; the fits obtained by SASREF with contacts restraint and by BUNCH are displayed as red dashed lines; and those from the in the middle model as blue solid lines.

To further explore the capabilities of SASREF, the GTS-tRNA monomer was split to protein and nucleic acid parts and the program was run to simultaneously fit the two simulated scattering curves of the entire complex and of the dimeric tRNA (the latter computed in the same way as described above for the complex) while adjusting the arrangement of the two rigid bodies in the asymmetric part (GTS monomer and tRNA monomer). At this more complicated level of modeling, ambiguous reconstructions were obtained with different configurations of RNA and protein parts, all yielding good fits to both scattering curves. An example of such ambiguity is presented in Fig. 2 A (middle row), displaying a configuration that fits the data of tRNA and of the complex with χ = 1.01 and 1.39, respectively (Fig. 2 B). The ambiguity can be resolved by using the distance constraints. In particular, proximity of U513 with Pro⁵⁰³ and of A573 with Gly¹²¹ permits us to obtain an unambiguous result within RMSD = 0.1 nm to the initial structure. The accuracy of the position and orientation of the monomer was characterized by the shift of its center-of-mass δr relative to the initial position, and by a rotation angle ω, respectively. The latter parameter was calculated by finding the rotation matrix bringing the monomer to its initial position, which can always by represented as a rotation by an angle ω around an axis. As the direction of the axis depends on the overall orientation of the entire complex, the magnitude of the rotation ω is the most specific parameter describing the change of the monomer orientation. The final model provides δr = 0.02 nm and ω = 2° (Fig. 2 A) and yields χ = 0.94 and 0.92 to the data sets (Fig. 2 B) of tRNA and of the complex, respectively. The parameters δr and ω are also listed below together with the RMSD, to characterize the quality of the obtained solutions.

The monomer of the GTS-tRNA complex was used to test the program BUNCH. It was assumed that GTS consists of two domains (Met¹–Phe³⁷³ and Glu³⁸¹–Ala⁴⁶⁸) connected by a seven-residues' linker of unknown structure and that the structures of the first domain in complex with tRNA and of the second domain are known. The task was to build the model of the entire monomeric complex which fits the simulated scattering curve from the monomeric GTS-tRNA (curve 3 in Fig. 2 B). BUNCH was employed to find the position and orientation of the second domain and the conformation of the linker, given the fixed tRNA and first domain part. Multiple reconstructions were performed, and the position of the second domain was in all cases correctly found, although not always with precise orientation. A typical model reconstructed by BUNCH (in Fig. 2 A) yields an overall RMSD = 0.58 nm to the correct GTS-tRNA monomer and χ = 0.95 to the simulated scattering curve (Fig. 2 B).

Rigid body modeling against experimental scattering data

After validation on simulated examples, the methods were employed to reconstruct quaternary structures of several macromolecular complexes with known and unknown crystal structures from the experimental data. We have selected objects from already published studies, most of which (except for the hemocyanin study) were user projects at the X33 beamline of the EMBL, Hamburg Outstation. For some of the projects, interactive rigid body modeling has already been performed earlier, and it was also interesting to compare the results of the new methods with the previously published data.

For all the cases, the x-ray scattering amplitudes from the individual subunits were computed by CRYSOL using default parameters (Van der Waals' excluded volume and the hydration layer 10% denser than the bulk water). This could in principle lead to an overestimate of the hydration layer contribution on the contact interfaces between the subunits, not accessible to the solvent. As the hydration layer effect as such is relatively small compared to the contribution of the macromolecule itself, these overestimates do not significantly influence the results. To verify this, CRYSOL was used to compute the scattering patterns from the obtained final models of the complexes, and the fits to the experimental data were practically the same as those given by the rigid body refinement methods.

Location of two small subdomains of the Escherichia coli F₁ ATPase

The extrinsic F₁ complex of the membrane-integrated ATP synthase of Escherichia coli (∼380 kDa) contains five subunits in the stoichiometry α₃β₃γδɛ (40,41). The experimental scattering pattern of E. coli F₁ ATPase (in Fig. 3 A, right panel) is neatly fitted by the theoretical curve calculated from the crystallographic model of F₁ ATPase from bovine heart mitochondria (PDB entry 1e79; see Ref. 42). For testing this crystal structure was represented as a heterodimer formed by the large (α₃β₃γ) and small (δɛ) substructures as two monomers and the program DIMFOM was run to build the full complex by rolling the δɛ-part on the surface of α₃β₃γ part. The reconstruction in Fig. 3 A (left panel) yields a good fit to the experimental data of the E. coli F₁ ATPase with χ = 1.2 (Fig. 3 A, right panel). Building this model took ∼30 min CPU time on a 2.2 GHz Pentium PC. Although the orientation of the δɛ-part is different from that in the crystallographic model (ω = 180°, i.e., the δɛ-subunit appears flipped around its long axis), the position of the substructure was found correctly (δr = 0.73 nm) and the overall shape of the protein was also retained (overall RMSD between the two models in Fig. 3 A is 0.62 nm). In the earlier model (34) constructed interactively the ɛ-subunit was also located at the bottom of F₁ but at a somewhat different position which can be explained by the fact that the structure of the γ-subunit protruding to the bottom stalk was only partially available at that time.

FIGURE 3.

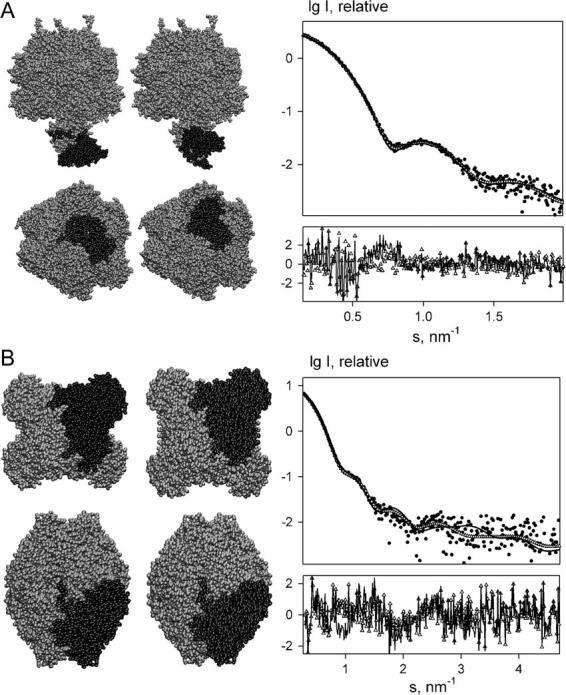
Results of grid-search rigid body modeling of F₁ ATPase using DIMFOM (A) and of tetrameric ZmPDC using GLOBSYMM (B). (Left panel) Structural models. The crystal structures and the results of the modeling are shown on the left and the right columns, respectively. The δɛ substructure of F₁ ATPase and the monomer of ZmPDC are displayed in dark shading. The bottom views in A and B are rotated by 90° about the horizontal axis. (Right panel) Scattering curves. Dots denote experimental data; open triangles and solid lines are, respectively, theoretical scattering curves computed from crystal structures and fits from the rigid body models. The corresponding reduced residuals of the fits, i.e., individual terms in Eq. 3, are given in the insets.

Quaternary structure of tetrameric pyruvate decarboxylase from Zymomonas mobilis

Pyruvate decarboxylase from the recombinant wild-type of Zymomonas mobilis (ZmPDC) (43) consists of four identical subunits with molecular mass of ∼60 kDa, which form a symmetric (point group P222) homotetramer (PDB entry 1zpd; see Ref. 43). Solution scattering studies demonstrated that this enzyme has the same quaternary structure in the crystal and in solution (35), and the protein is an interesting test example for a brute-force modeling. The quaternary structure of the tetrameric enzyme was restored from the experimental scattering pattern in Fig. 3 B (right panel) by GLOBSYMM starting from an arbitrarily positioned crystallographic monomer and assuming a P222 symmetry. The best model reconstructed in several runs of the program with different order of Fibonacci grids fits the experimental data with χ = 0.96 (Fig. 3 B, right panel) and yields the RMSD of ∼0.6 nm from the atomic coordinates of crystal structure (δr = 0.45 nm and ω = 10° in terms of the monomer position and orientation). A typical GLOBSYMM run (145 Fibonacci directions for both rotation and positioning) required ∼15 min on a 2.2-GHz PC. The comparison of the reconstructed model with the crystallographic tetramer is given in Fig. 3 B (left panel). This example was also used to test the additional criteria for ranking of the solutions (see below).

Arrangement of functional units in proteolytic fragments of the Rapana venosa hemocyanin (Hc)

Hc from Rapana venosa is a giant oxygen-binding protein (with MM of a few MDa) built from the functional units of MM = 50 KDa. The two experimental scattering curves (Fig. 4 A, left panel) from 100- and 150-kDa proteolytic fragments of Rapana Hc (36) containing two and three functional units, respectively, were employed for rigid body modeling of these fragments. Assuming that the two first functional units have the same mutual arrangement in 100 and 150 kDa fragments, both scattering data sets were fitted simultaneously using the crystal structure of the functional unit of Octopus Hc (PDB entry 1js8; see Ref. 44), which has 50% sequence identity (66% similarity) with the one from Rapana Hc. The program SASREF performed restrained rigid body modeling of the Hc proteolytic fragments against the two data sets requiring a single chain connectivity of the entire model. To fulfill the latter requirement, the distance between the C- and N-termini of the adjacent functional units was restrained not to exceed 1 nm. The resulting model shown in Fig. 4 A (right panel) demonstrates linear arrangement of the functional units in agreement with the results of the earlier study of low-resolution structure of Rapana Hc proteolytic fragments (36). The entire model and the subset of its first two units yield the fits with χ = 3.3 and 1.2 to the scattering data from 150- and 100-kDa fragments, respectively (Fig. 4 A, left panel). Interestingly, the small systematic deviations between the calculated and experimental data of a 150-kDa construct (curve 1) were also observed in the previous study (36) and they may indicate slight polydispersity or flexibility of the 150-KDa proteolytic fragments. A typical SASREF run required <4 h on a 2.2-GHz PC.

FIGURE 4.

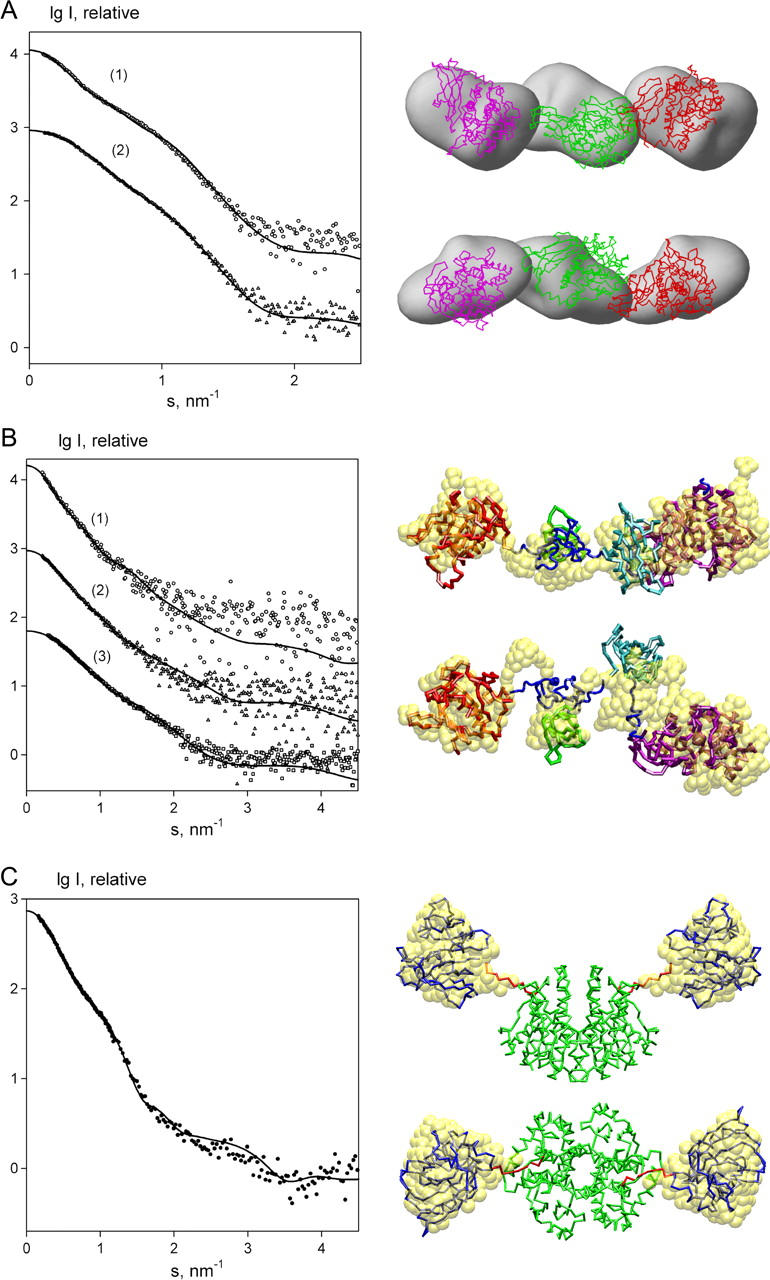
Results of rigid body modeling of Hc (A), BTK (B), and GST-DHFR (C) using simulated annealing. (Left panel) X-ray scattering patterns. The experimental data in A–C are displayed as symbols, and the fits from the reconstructed models are shown as solid lines. In A, 1 and 2 stands for 150- and 100-kDa constructs, respectively; in B, the full-length BTK, PH–SH3–SH2, and SH3–SH2 constructs are denoted as 1, 2, and 3. (Right panel) Structural models. (A) Assembly of Hc structural units reconstructed from the SAXS data of 100- and 150-kDa fragments by SASREF. A low-resolution model previously reconstructed using envelope functions (36) is displayed in gray. The first, second, and the third subunits are displayed as red, green, and magenta C_α-traces, respectively. (B) Domain structure of BTK restored by simultaneous multiple data sets fitting using BUNCH. PH, SH3, SH2, kinase domain, and flexible DR linkers are shown in red, green, cyan, magenta, and blue, respectively. The earlier published model obtained by subsequent fitting (37) is displayed as yellow beads. (C) Dimeric GST-DHFR fusion protein. Crystallographic GST dimer is displayed in green, the two DHFR monomers and the linkers positioned by BUNCH using P2 symmetry are shown in blue and red. Yellow beads represent the two DHFR domains of the fusion protein reconstructed ab initio in the previous work (27). The bottom views in A–C are rotated by 90° about the horizontal axis.

Domain structure of Bruton tyrosine kinase (BTK)

BTK consists of four rigid domains with known high-resolution structures (PH, SH3, SH2, and kinase domain) connected by linkers of unknown conformations. The SAXS patterns of the full-length BTK and its deletion mutants containing PH–SH3–SH2 and SH3–SH2 domains are presented in Fig. 4 B (left panel). In the earlier study (37), conformation of the full length BTK in solution was determined by subsequent fitting of the scattering data. The rigid body modeling started from the smaller construct (SH3–SH2) followed by the addition of other two domains one by one. The missing linkers were then added to the fixed arrangement of the four domains. In the present article, BTK conformation was reconstructed by simultaneous fitting of the three data sets from the two deletion mutants and from the full-length protein by the program BUNCH. A typical result presented in Fig. 4 B (right panel) displays an extended conformation of the full-length protein with weak interdomain interactions. This finding correlates with the previous results also demonstrating nearly linear domains arrangement. All the scattering data were neatly fitted as shown in Fig. 4 B (left panel), where SH3–SH2, PH–SH3–SH2 portions and the full-length model yield χ-values of 0.70, 0.48, and 0.91 to the appropriate experimental curves. A typical BUNCH run required ∼12 h on a 2.2-GHz PC.

Structural characterization of GST-DHFR fusion protein

The GST-DHFR fusion protein consists of Schistosoma japonicum glutathione S-transferase (GST, MM = 26 kDa) and E. coli dihydrofolate reductase (DHFR, MM = 17 kDa) connected by a 10-residues' linker. It was shown (27) that GST-DHFR is dimeric in solution and its dimerization interface is compatible with the crystallographic GST dimer possessing the twofold symmetry axis. The experimental scattering pattern of GST-DHFR is shown in Fig. 4 C (left panel). The program BUNCH was employed to build the dimeric fusion protein accounting for the P2 symmetry from the high-resolution models of GST (PDB entry 1gta; see Ref. 45) and DHFR (1ra9; see Ref. 46) connected by the linker represented by 10 DRs. The GST monomer was fixed at the position yielding the proper dimerization interface. The search procedure was refining the position of the DHFR subdomain and the conformation of the DR chain representing the linker in the symmetry independent part. The resulting model yields a good fit to the experimental data of the fusion protein with χ = 0.97 and is also consistent with the earlier model where the entire DHFR portion of the fusion protein was reconstructed ab initio using dummy residues approach (the compatibility of the two models is demonstrated in Fig. 4 C, right panel). A typical BUNCH run required <2 h on a 2.2-GHz PC.

Ranking of the rigid body models using simplified docking criteria

As seen from the above examples, rigid body modeling may yield multiple solutions providing (nearly) the same fits to the experimental data. The requirements of interconnectivity, non-overlapping and information on distances between specific residues do reduce the ambiguity of model building but in some cases additional criteria may be indispensable. For multisubunit complexes, such criteria may be obtained by the analysis of the intersubunit interfaces.

Various approaches to analyze protein-protein interfaces have been developed largely utilizing a combination of energetics and shape complementarity. Analysis of the interaction sites using surface patches (47) uses solvation potential, residue interface propensity, hydrophobicity, planarity, protrusion and accessible surface area as parameters to rank the interfaces. Empirical scoring functions for structure-based binding affinity prediction (48) accounts for van der Waals interaction, hydrogen bonding, deformation penalty, and hydrophobic effect. Amino acid compositions and sizes of the recognition sites of protein-protein complexes were analyzed in Chakrabarti and Janin (49) and Lo Conte et al. (50). The soft-docking algorithm (51) performs a complex type-dependent filtering of candidate binding modes on the basis of geometric matching, hydrophobicity and electrostatic complementarity. The method (52) employs a low-resolution rigid body Monte Carlo search followed by simultaneous optimization of backbone displacement and side chain conformations for the docking. The pairwise shape complementarity scoring function maximizing the total number of atom pairs between the receptor and the ligand within the distance cutoff is developed (53) and can be optimized together with disolvation free energy and electrostatics (54). Approaches for filtering and selection of structural models based on combining docking with biochemical and biophysical information (i.e., NMR data) are developed (55,56).

Most of the above methods are very useful for building and refining energetically sound detailed models, and the calculation of these criteria is usually computationally intensive. Given the low resolution of the SAXS method, our aim was to devise simple and fast methods estimating the quality of the intersubunit contacts, which could also be used as restraints during the rigid body modeling. The quality assessment is done using C_α-only representation of the molecules and considers the two aspects: shape complementarity and amino acid composition at the interface. Another potential aspect, charge complementarity, heavily relies on all-atom representation of the surfaces for accurate electrostatic energy calculations and would be rather inaccurate in C_α-only representation.

The shape complementarity criterion is formulated in terms of maximization of the total number of contacts N_cnt between distinct subunits made by pairs of their C_αs. It is assumed that two residues belonging to different subunits in a complex compose a pair if the distance between their C_α atoms does not exceed the average threshold of r_cnt = 0.7 nm. This criterion is not residue-specific and is applicable to rank subunit arrangements without steric clashes only, as overlapping subunits would obviously yield higher number of the pairs.

As the interactions between the residues are the major driving force for protein-protein interface formation, a simplified residue-specific criterion was also introduced. The high-resolution structures of more than 80 protein complexes of different types (protein-inhibitor, antibody-antigen, homodimers, etc.) downloaded from the PDB were analyzed to get the average contact frequency between pairs of residues using the same threshold r_cnt for assignment of a contacts to two residues. The average histogram of frequency distribution h_ex of 210 (= 20 × (20 + 1)/2) possible residue pairs should thus give information about which residues are more and less likely to be involved in the interface formation. For polar residues, the average frequency of observing a pair of oppositely charged residues was twice that for the residues having the same charge. This indicates that such a histogram, which is effectively a simplified version of residue-level potentials or an interface propensity table (47,49,50,57), also bears information about the charge complementarity.

Given a model of the complex, a histogram of its interface h_obs can be computed and the correlation coefficient (CC) between h_obs and h_ex can be used to assess the quality of the interface. The value CC is computed using the standard formula of

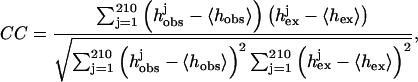(10)

where

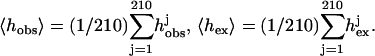The CC value ranges between 1 and −1 and, on average, the higher the value, the better the interface.

The criteria were tested on several examples, in particular on the family of the best solutions of ZmPDC quaternary structure restored by GLOBSYMM. As this program allows for having minor overlaps between the monomers only histogram correlations were computed. The crystal structure of ZmPDC and the best model from GLOBSYMM (in Fig. 5 A, left panel, first and second rows) yield CC = 0.25 and 0.23, respectively. These values are higher than those calculated from most of other models top-ranked by GLOBSYMM. There is however a model yielding an even higher CC = 0.28 but a poorer fit to the experimental data than that from the two above models. Interestingly, this latter model (Fig. 5 A, left panel, third row) displays a correct arrangement of monomers within the dimer and, moreover, the architecture of the entire tetramer, which is very similar to that of a homologous PDC from yeast (PDB entry 1pvd; see Ref. 58). Fig. 5 A (left panel, bottom row) displays a model with an incorrect oligomerization interface, which yields a poorer docking criterion (CC = 0.18), though its fit to the experimental data is nearly as good as that of the best model (Fig. 5 A, right panel, magenta curve).

FIGURE 5.

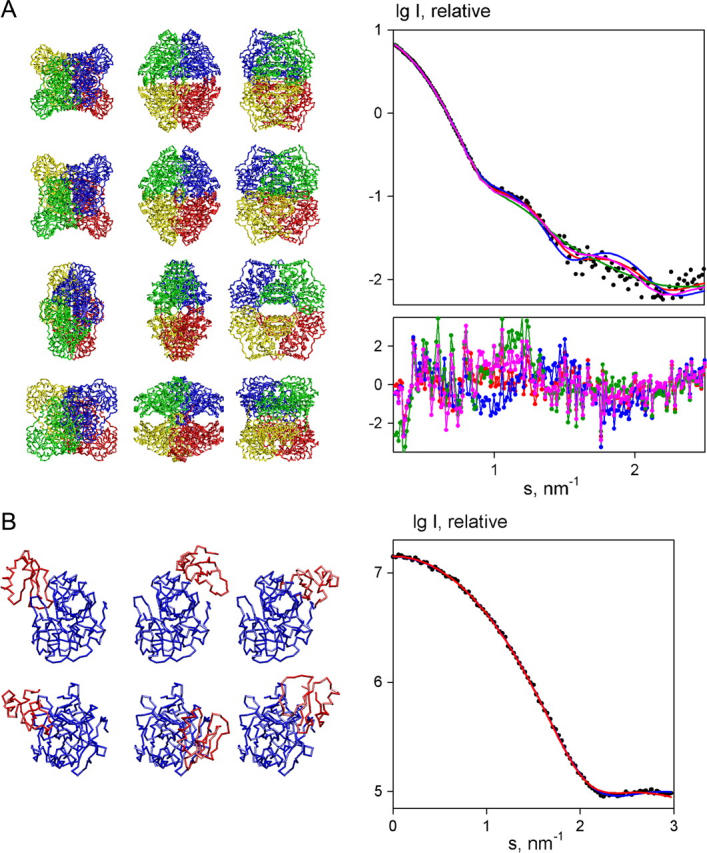
Screening of the multiple models provided by rigid body refinement methods. (A) Models of ZmPDC generated by GLOBSYMM. (Left panel, first row) Crystal structure of ZmPDC; (second row) the best GLOBSYMM model; (third row) the model with the highest CC; and (fourth row) the model with a poor correlation criterion. The four subunits of ZmPDC are shown in different colors, the models in middle column are rotated by 90° about the horizontal axis, those in right column are further rotated by 90° about the vertical axis. (Right panel) Experimental data (black dots) from ZmPDC and the fits from the above models (plotted as red, blue, green, and magenta lines, respectively). The reduced residuals are given in the inset using the same colors. (B) Modeling of chymotrypsin-eglin complex using SASREF. (Left panel, left column) Crystallographic model of the complex; (middle column) the model with N_cnt = 31 and CC = 0.40; and (right column) the model with N_cnt = 40 and CC = 0.31. Chromatin and eglin molecules are displayed in blue and red, respectively. Bottom view is rotated by 90° about the horizontal axis. (Right panel) Simulated data of the complex (dots), and fits from SASREF models in the middle and the right columns (blue and red solid lines, respectively).

The above example demonstrates the usefulness of the simplified docking criteria and similar results were also obtained in other tests. One must however be aware of limitations of such criteria, illustrated by the example below. A simulated scattering curve from the complex of bovine α-chymotrypsin with eglin C (PDB entry 1acb; see Ref. 59) displayed in Fig. 5 B was computed in the same way as described for GTS-tRNA. This curve was used for the modeling based on the structures of α-chymotrypsin (chain E) and eglin (chain I) as two rigid bodies. Multiple reconstructions were performed by SASREF, and the variety of solutions without steric clashes yielding good fits to the simulated data (in Fig. 5 B, right panel) were screened to find those having maximum number of contacts between the subunits and yielding the highest correlation coefficients. The two best models according to the docking criteria (Fig. 5 B, left panel, middle and right column) have the parameters N_cnt = 31 and 40 and CC = 0.40 and 0.31, respectively, which are apparently better than those of the crystallographic complex (N_cnt = 34 and CC = 0.19). Though the overall shapes of the SASREF models are similar to the crystallographic one, the relative orientation of the subunits in both models is different from that of the crystallographic complex (both yield RMSD = 1.2 nm). Admittedly, the arrangement of the two proteins in the crystallographic complex, where the contact is established via an extended loop Pro⁴²–Arg⁴⁸ of eglin, cannot be considered a typical intersubunit interface. Nevertheless, this example demonstrates the possibility of getting false-positives when using the simplified docking criteria. It is worth noting that addition of a distance constraint requiring proximity of Trp²¹⁵ of chymotrypsin with Thr⁴⁴ of eglin allows SASREF to obtain a unique solution with the eglin position shifted by δr = 0.22 nm and rotated by ω = 13° and within the RMSD = 0.1 nm from the crystal structure.

In test calculations on other simulated and practical examples, the use of simplified docking criteria did provide additional information for the selection of the correct model. Still, to avoid biasing the minimization algorithms toward the false positives it was decided not to include the N_cnt and CC criteria into the goal function at this stage but rather to compute and list these parameters for the best selected models. The algorithms rapidly computing the simplified docking criteria are also available as standalone programs for the screening of multiple models.

CONCLUSIONS

A versatile set of tools presented here allows one to rapidly construct rigid body models of macromolecular complexes with minimum user intervention while maximizing the information content in the scattering data (multiple curves fitting) and adding information from other sources (symmetry, distance restraints, docking criteria). With recent instrumental and methodical advances, rigid body refinement against SAS data indeed became a powerful method to study complexes, allowing, in many cases, unique results to be obtained. Given the limited resolution of SAS data, one should, however, bear in mind that the models constructed by rigid body refinement, although built from high-resolution domains, are still low-resolution models. In particular, one should bear in mind that obtaining a configuration of subunits corresponding to an enanthiomorphous structure is always possible. Potential limitations of the technique and the possibility of obtaining multiple solutions compatible with the experimental data are presented here as a word of caution in using the rigid body refinement methods. In some cases, multiple runs of the programs and ranking of the models according to their biological relevance are indispensable for the cross-validation of the results.

Most of the methods presented here can be used for the analysis of x-ray and neutron scattering data from complexes of proteins, nucleic acids, and other biological macromolecules. The programs DIMFOM, GLOBSYM, and SASREF require precomputed x-ray or neutron scattering amplitudes from the domains/subunits, which can be done by the programs CRYSOL or CRYSON, respectively. The power of specific deuteration of contrast variation in neutron scattering can thus be fully exploited. The only exception is the program BUNCH, which explicitly utilizes the x-ray form factor of a dummy residue to compute the scattering from missing loops and can thus only be used for the x-ray data.

Regarding the relation between the brute-force and the heuristic methods, there are advantages and shortcomings in both of them. In default operation modes, the brute-force methods are faster, but in principle they may miss the global minimum because of the finite grid sampling. A combination of the two approaches is possible, where the heuristic method is started in the refinement mode (i.e., at a low temperature) from the solution obtained by a brute-force method. Of course, the applicability of the latter methods is limited to one subunit per asymmetric unit, whereas the heuristic algorithms can handle more complex systems.

The programs described in the present article can be downloaded as precompiled executables for all major computer platforms (from http://www.embl-hamburg.de/ExternalInfo/Research/Sax/software.html). These rigid body analysis programs have been made available to the biological community as beta-versions some time ago, and valuable feedback from the users has already been received. We have also used these beta-versions in several experimental projects (60–62), where they did provide a significant advantage over the earlier rigid body modeling methods. The present versions of the programs include numerous modifications and improvements from the beta-testing phase.