Three-Dimensional Characterization of Tethered Microspheres by Total Internal Reflection Fluorescence Microscopy

Abstract

Tethered particle microscopy is a powerful tool to study the dynamics of DNA molecules and DNA-protein complexes in single-molecule experiments. We demonstrate that stroboscopic total internal reflection microscopy can be used to characterize the three-dimensional spatiotemporal motion of DNA-tethered particles. By calculating characteristic measures such as symmetry and time constants of the motion, well-formed tethers can be distinguished from defective ones for which the motion is dominated by aberrant surface effects. This improves the reliability of measurements on tether dynamics. For instance, in observations of protein-mediated DNA looping, loop formation is distinguished from adsorption and other nonspecific events.

INTRODUCTION

Tethered particle microscopy (TPM) experiments track the motion of a microsphere that is tethered to a surface by a DNA fragment or other biopolymer (1–3). TPM techniques are very powerful assays that yield insight into the dynamics of a single biomolecule and its interactions with the surrounding environment. However, accurate interpretation of TPM experiments conducted with conventional microscopy has generally been limited by incomplete characterization of the microsphere-tether system. In this article, we demonstrate how total internal reflection fluorescence (TIRF) microscopy with stroboscopic illumination can be used to enhance the capabilities of TPM experiments involving tethers whose contour length is less than a micron.

TPM experiments typically derive information from the thermal motion of the tethered microsphere. For instance, the range of Brownian motion can be used to infer the lengths of DNA tethers (1,4). In addition, temporal changes in the Brownian motion can be used to monitor dynamic changes in tether length over time. This enables measurements of the rate of protein-mediated looping (5) and the processivity of RNA polymerase (4). An analysis of the Brownian motion can also be used to assess changes in tether elasticity, such as it occurs when ssDNA is hybridized into dsDNA (6).

The complications in the analysis and interpretation of TPM experiments arise from a number of different sources. First, many TPM experiments suffer from incomplete information about the particle trajectory. Although TPM experiments typically track the x-y position of the microsphere as projected onto the image plane, TPM setups are typically unable to measure out-of-plane displacements (i.e., displacement parallel to the central axis of the microscope objective). Second, TPM data are often gathered at standard video rates. This limits the temporal resolution of the particle trajectory and can create artifacts due to motion of the microsphere during a single exposure interval (7). Third, the preparation of tethered particle samples is nontrivial and often produces malformed tethers. These imperfections can be caused by a number of factors including nonspecific adsorption of parts of the tethering polymer to the coverslip or microsphere surfaces, polydispersity in size and shape of the attached colloidal particles, inhomogeneous surface charge, and multiple tether attachments.

The difficulties associated with inhomogeneous samples have been documented for a number of recent TPM experiments. For instance, Zocchi explains how nonspecific sticking, multiple tether attachments, damaged contact areas, and surface roughness complicate data analysis for TPM measurements on the force needed to rupture a biotin-streptavidin bond (8). Ultimately, only 9 of 25 measurements were judged to be acceptable. Subsequent investigations of DNA hybridization continued to suffer from nonspecific adsorption (6). Likewise, while calibrating DNA tether lengths for detection of Holliday junction unfolding, Pouget et al. report that ∼40% of tethered microspheres exhibit some irregularity (1). Furthermore, Vanzi et al. report that their TPM measurements of protein synthesis by ribosomes were complicated by sample heterogeneity and by RNA tethers that exhibited asymmetric motion (3).

In the Methods section, we present an experimental approach that mitigates the aforementioned complications of traditional TPM experiments. In contrast to typical TPM experiments that use bright-field, differential interference contrast, or epi-fluorescence video microscopy to trace the position of the tethered particle in the imaging plane, we make this measurement by exciting tethered fluorescent microspheres with an evanescent field that is generated by reflecting light off the glass-sample interface. The amplitude of the evanescent field decays exponentially with distance from the interface and therefore the out-of-plane displacement can be determined from the intensity of the fluorescent emission. Other experiments have measured out-of-plane position of microspheres by evanescent field scattering (8,9). However, our technique exploits the combined high resolution, selective imaging, and out-of-plane measurements that accompany TIRF imaging in TPM studies. Furthermore, by utilizing stroboscopic illumination, we reduce photobleaching and particle tracking error due to microsphere motion during a single exposure. Lastly, our fast charge-coupled device (CCD) camera enables three-dimensional particle tracking with temporal resolution in excess of the intrinsic relaxation time of typical DNA-microsphere complexes.

Our image acquisition and data analysis algorithms allow us to calculate motion, symmetry, and time constant statistics for each tethered microsphere. The Results section describes how these statistics are used to characterize the motion of legitimate DNA-tethered microspheres and their malformed counterparts. Based on our observations, we offer quantitative selection criteria for distinguishing well-behaved tethers from improperly formed ones and we demonstrate how these criteria improve the reproducibility of TPM motion measurements. We also demonstrate how dynamic changes in tether length can be monitored and how our three-dimensional tracking can be used to distinguish between DNA adsorption and protein-mediated DNA loop formation. In the Discussion section, we focus on how our methodological improvements provide improved physical insight into tethered particle motion, thereby providing TPM with even greater promise as a quantitative tool for molecular biophysics.

METHODS

Optics

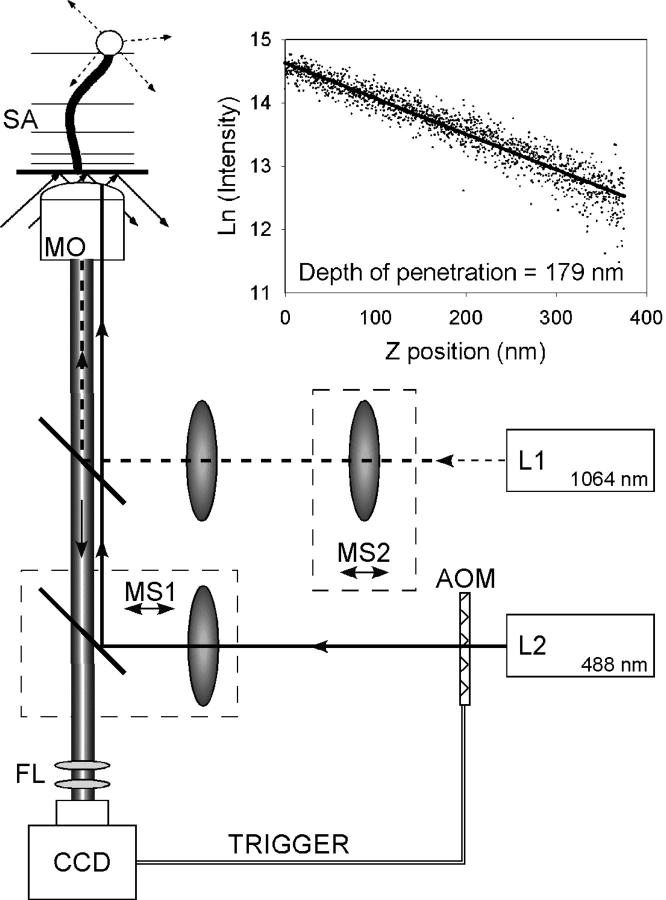
We assembled our microscope optics and sample stage on a floating table (Newport Corp., Irvine, CA). Mechanical stability of the sample stage was assured by mounting it to three steel posts of 1-inch diameter. The light beam for the evanescent excitation field originates from an Ar⁺/Kr⁺ laser operating at 488 nm. Key elements in the beam path include an acousto-optic modulator (AOM, IntraAction, Bellwood, IL), a 5× beam expander, a focusing lens, a dichroic mirror, a TIRF microscope objective (Olympus (Melville, NY) 1.45 NA, oil immersion), and a motorized sample stage (Fig. 1). The microscope objective is inverted, and no prism is used. Hence, the sample mounting area is freely accessible. Samples are secured to the stage by stiff springs.

FIGURE 1.

Experimental setup consists of a TIRF microscope with integrated optical tweezers. The sample, a DNA-tethered fluorescent microsphere, is illuminated by a 488 nm Ar⁺/Kr⁺ laser beam (L2) and imaged onto a CCD camera. A trigger from the CCD camera pulses the excitation light. A Nd:YAG laser (L1) creates a moveable optical trap within the sample, which is used to calibrate the intensity profile of the evanescent field (inset). MS, moveable stage; MO, microscope objective; SA, sample; and FL, emission filter.

The evanescent field excites tethered fluorescent microspheres within a flow cell. The consequent emission passes through the dichroic mirror and an emission filter onto a CCD camera (Photometrics (Tucson, AZ) Cascade 650). The AOM produces stroboscopic illumination of the sample by deflecting the laser light in synchrony with the exposure of the CCD camera. At a frame rate of 100 Hz, we typically used an illumination duty cycle of 7%. Frame rates are usually in the 30–100 Hz range but can exceed 350 Hz. As measured with a diffraction grating, each CCD pixel corresponds to 91 nm × 91 nm in the sample plane (scaling error is <1%).

To obtain an illuminated spot with a uniform angle of incidence at the glass-sample interface, the excitation beam is focused on the back focal plane of the microscope objective. The focusing lens and the dichroic mirror immediately downstream are jointly mounted on a translation stage (MS1, Fig. 1) that moves perpendicular to the axis of the objective. This allows continuous adjustment of the penetration depth of the evanescent field.

To calibrate the evanescent field and enable future micromanipulation experiments, a separate optical tweezing beam from a 1064 nm Nd:YAG laser is introduced into the objective via a second dichroic mirror. A gimbaled mirror and a movable lens (MS2, Fig. 1) allow three-dimensional localization of the trap. To determine the penetration depth of the evanescent field, a 1-micron diameter microsphere is optically trapped and translated to and from the glass-water interface by using MS2 to adjust the location of the trap focus. The resulting change in intensity is then plotted against the known depth of the trap within the sample (Fig. 1, inset). In general, the penetration depth was determined to be 200 nm with an alignment-dependent variation of 30%.

Sample preparation

To make flow cells, coverslips are cleaned in a solution of anhydrous sulfuric acid and 30% hydrogen peroxide in a 3:1 ratio for ∼5 min and then thoroughly rinsed with flowing deionized water. The clean glass coverslips are then mounted onto a glass microscope slide using double-sided adhesive tape or melted parafilm as a spacer. The gap between the two glass surfaces defines a space for tethering microspheres in an aqueous environment. Buffer exchange is achieved via Tygon tubing attachments to inlet and outlet holes drilled in the glass slide.

Our best samples are obtained with the following protocol: First, the interior surfaces of the flow cell are coated with digoxigenin binding sites by flowing in a solution of 20 ug/mL anti-digoxigenin (polyclonal from sheep, Roche, Indianapolis, IN) in PBS (pH = 7.4) and incubating for 25 min. The sample is then flushed with 15 or more volumes of blocking buffer (10 mM Tris, 200 mM NaCl, pH 7.4, 0.1 mg/ml alpha casein, 0.1 mM EDTA, 0.2 mM DTT, 5% DMSO, 70 mM cysteamine). The cysteamine is thought to reduce microsphere adsorption, possibly by preventing unwanted cross-linking caused by photo-induced reactive oxygen species (10). Meanwhile, DNA constructs are prepared that can bind to anti-digoxigenin at one end and a biotin-coated surface on the other end. This is accomplished via PCR amplification in which one primer is labeled with biotin and the other with digoxigenin. After the blocking buffer has incubated for an hour, 10 pM of the dual-labeled DNA constructs are introduced into the flow cell for an additional hour of incubation. Then the flow cell is flushed with 10 volumes of wash buffer (same as blocking buffer but without DMSO or DTT). For the final reaction, streptavidin-coated, fluorescent, latex beads (Bangs Laboratories (Fishers, IN) 480/520 nm or Molecular Probes (Eugene, OR) 505/515 nm; diameters used range from 200 nm to 1 μm) are washed according to manufacturer's instruction and introduced into the flow cell at a concentration of ∼100 pM in wash buffer. After the microspheres are allowed to bind to the tethered DNA for 25 min, the flow cell is flushed with 10 volumes of blocking buffer and immediately mounted on the microscope stage for observation.

Lac Repressor (LacR) protein was prepared by overexpressing the protein in Escherichia coli, strain BKN, with pGlnKpLacI plasmid (11,12). The crude lysate is treated with protease inhibitors, centrifuged, and subjected to ammonium sulfate precipitation (50% saturation). The pellet is dialyzed overnight at 4°C to 80 mM KCl, 50 mM Tris-Cl (pH 7.4), 10% glycerol, and .05% v/v Tween-20 (13). Then, heparin-sepharose affinity chromatography is performed with a KCl step gradient, (LacR elutes at 350 mM). The LacR is ≈70–80% pure, as estimated by SDS-PAGE and Coomassie staining.

Image acquisition and analysis

Movies of fluorescent-tethered particles are digitally recorded using Winspec software (Roper Scientific, Tucson, AZ). Image analysis is done with in-house MATLAB code (available upon request) and is similar to established routines (14). Since each movie may contain more than one bead, a registration algorithm is applied to each movie to identify distinct microspheres. Before analyzing each microsphere individually, a list of initial microsphere centroid positions passes through two filters. The first filter eliminates all candidate microspheres whose area is unreasonably small or large (possibly due to sample contamination or microsphere aggregation). The second round of filtering requires that each candidate microsphere be a minimum distance from every other microsphere and from the boundary of the image frame. This second filter ensures that the image signals analyzed are not distorted by boundary effects or the overlapping signal of a neighboring microsphere. The microspheres that pass the two sets of filters are considered “analyzable”. For these microspheres, a region of interest (ROI) is specified that is centered on the estimated anchor point of its associated tether.

After establishing a set of ROIs for the analyzable microspheres, a time series for the three-dimensional coordinates of each microsphere is computed as follows. First, a threshold value is chosen that consistently differentiates image signal from background noise. Then for each frame of each analyzable ROI, a contiguous group of above-threshold pixels is identified as the microsphere signal. The average background is then subtracted and the in-plane position of the microsphere, 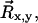is calculated by determining the center of intensity. In mathematical terms,

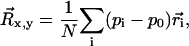where the sum is over the N pixels constituting the microsphere signal, 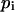is the intensity of the ith pixel, 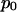is the background signal, and 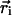is the displacement vector for the ith pixel. The calculation of in-plane position is analogous to a center of mass calculation. Because the microsphere signal spreads across a number of pixels, the image is effectively oversampled and subpixel resolution is obtained. Out-of-plane position, z, is determined by computing the logarithm of the cumulative background-adjusted intensity value of the microsphere signal and scaling by the penetration depth of the evanescent field. Quantitatively,

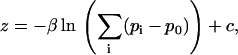where β represents the penetration depth and is an additive constant (typically set so that the frame of maximum intensity has zero displacement). Since out-of-plane displacements scale with relative changes in intensity rather than absolute intensity, the out-of-plane resolution is a function of the penetration depth and not the microsphere diameter. To correct for slow-scale sample drift and photobleaching, we apply a high-pass filter to the three-dimensional traces of microsphere displacement. Specifically, the moving average, which is a measure of the slow-scale variation, is subtracted from the raw signal so that only the high-frequency component remains. The high-frequency component retains the essential characteristics of Brownian Motion and any abrupt intramolecular changes. The moving average is typically taken over a 2-s window. Importantly, this is much larger than the intrinsic relaxation time of submicron sized DNA tethers.

To test the effectiveness of our filter, we considered the average correlation coefficient for seven microspheres in the same field of view. Before applying the filter, the average correlations were .05 and .27 for the two orthogonal in-plane axes and .09 for the out-of-plane axis (a value of 1 corresponds to perfect correlation). After applying the moving average filter, the correlation coefficient dropped under .04 for all three dimensions, demonstrating that the simple filter effectively removes error due to systematic drift. An alternative approach to removing noise due to global motion artifacts is to use an immobile microsphere in the field of view as a reference point. Then for every frame a differential measurement is made of the position of the tethered microsphere relative to the immobile one. However, subtracting the motion of an immobile microsphere has the danger of contributing to measurement noise, especially because it is difficult to ascertain whether a microsphere is truly immobile. Furthermore, the moving average filter is a better method of correction for photobleaching than differential measurements because different microspheres are likely to have different rates of photobleaching.

To estimate the noise in the centroid determination algorithm, we determined the time series for the distance between a pair of apparently immobile microspheres. We then calculated the standard deviation of this differential measurement. Taking the average over four independent pairs, we found the standard deviation of our differential measurement was 4 nm for the in-plane dimensions and 5 nm for out-of-plane displacement. We consider these numbers to be the upper limit of our algorithm's precision.

Microsphere statistics

We quantify the range of motion by calculating the root mean square of the filtered displacement for each dimension. We also compute time constants for each dimension by fitting a monoexponential decay curve to the autocorrelation of the position signal. Last, we calculate a symmetry statistic for the in-plane position scatter. For this computation, we first construct the covariance matrix for the in-plane displacement,

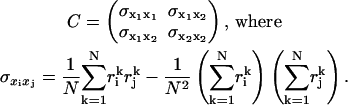Here N is the number of frames and 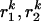are the in-plane coordinates of the microsphere for frame k. If 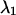and 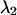represent the maximum and minimum eigenvalues of 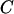respectively, then the symmetry statistic is given by

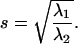The symmetry statistic represents the ratio of major axis to minor axis of an ellipsoidal representation of the scatter plot and has an ideal value of one (i.e., tether motion should be radially symmetric). If the symmetry statistic is applied to the intensity distribution of individual microsphere images, the statistic can also be useful for assaying the physical integrity of microspheres by ensuring that they are sufficiently round and that their fluorophore density is reasonably uniform.

RESULTS

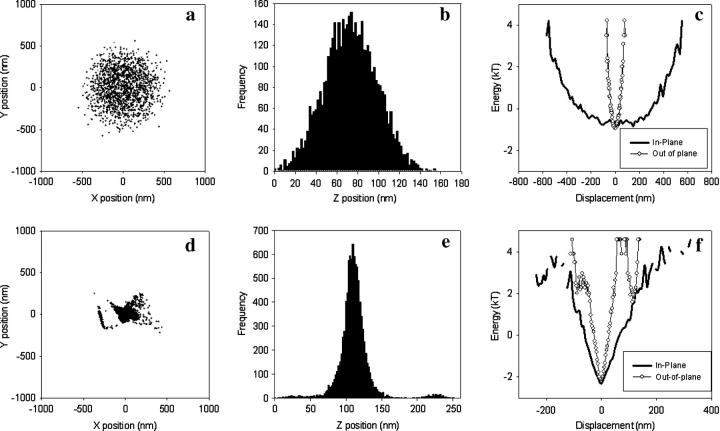
Using our stroboscopic, prismless TIRF setup, we acquired video data of fluorescent microspheres attached to a flat glass surface via a DNA tether. Fig. 2, a–c, represents the motion of a 560 nm diameter microsphere attached to a 1.6 kbp DNA tether. Characteristic measures for the motion of the tethered microsphere include in-plane and out-of-plane displacement distributions and in-plane symmetry. As described in more detail below, these measures can be used to distinguish well-formed DNA tethers from their malformed counterparts.

FIGURE 2.

Characterization of tethers. (a–c) Data for a well-formed tether. (a) Scatter plot for the in-plane position. (b) Histogram of the out-of-plane displacement. (c) Energy profiles for in-plane and out-of-plane motion. The in-plane profile is the average of the energy profiles for two orthogonal in-plane axes. Tether length = 1.6 kbp. In-plane symmetry = 1.02 (see text for definition of symmetry statistic). (d–f) Data for a microsphere with “tetherlike” behavior in a sample containing no DNA. The plots are analogous to panels a–c. For both the well-formed and malformed tether, the microsphere diameter = 560 nm.

Fig. 2 a shows a scatter plot of the centroid position for a “well–behaved” tether. The in-plane symmetry, defined as the ratio between major and minor axis of the in-plane position distribution, is 1.02. The almost unitary value of the symmetry statistic indicates that the motion for this tether is radially symmetric. Thus, the motion of this microsphere is unlikely to be complicated by multiple tether attachments or other artifacts of sample preparation. The root mean square of the displacement in each direction provides a measure of the amplitude of motion. For this microsphere, the motion along each of the two axes of the scatter plot is 210 nm. Fig. 2 b shows a histogram of the out-of-plane displacement which has a root mean square value of 25 nm. To ascertain our ability to resolve motion, we imaged microspheres that were rigidly adhered to the coverslip. Averaged over three microspheres, the root mean square motion for immobile microspheres was 8–9 nm for the two orthogonal in-plane motion coordinates and 10 nm for out-of-plane motion. (Note that these motion measurements are different than the root mean square differential values used to ascertain the precision of the particle tracking algorithm as described in the Methods section.) This nonzero apparent motion of an immobilized microsphere is a combination of optical noise, the finite precision of our image analysis algorithm, and true motion of the microsphere due to compliance of its attachment or drift. Since these error contributions are independent of the true motion of a properly tethered microsphere, at most they contribute in quadrature to the measured variance of a tethered particle's displacement. Thus, after correcting for the 10 nm out-of-plane noise error, the 25 nm observed out-of-plane motion of the tether in Fig. 2 b represents a true out-of-plane motion of ∼23 nm.

Fig. 2 c plots the in-plane and out-of-plane free energy profiles for a tethered microsphere. The free energy is computed by applying Boltzmann statistics to the position distributions seen in Fig. 2, a and b. Due to radial symmetry, the in-plane plot represents the energy profile along an arbitrary in-plane axis. Although there is an inherent asymmetry in the state-space of out-of-plane displacement, the associated energy profile is quite symmetric. A quadratic fit to the energy profile gives a nominal spring constant of .095 pN/μm for the in-plane axes and 6.6 pN/μm for the out-of-plane axis. (Statistics from 18 well-behaved tethers yield an average in-plane spring constant of .10 ± .01 pN/μm and out-of-plane spring constant of 3.5 ± 4.4 pN/μm.)

Fig. 2, d–f, shows data for a tether that was formed in the absence of DNA (i.e., in a sample for which no tethers should form). In contrast to the well-behaved tether, the malformed tether shows marked asymmetry of motion with an in-plane symmetry statistic of 1.57.

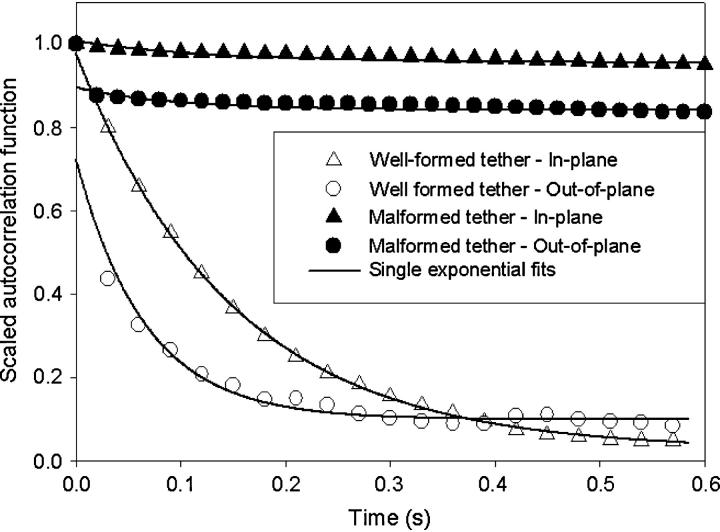
In addition to characterizing the static properties of tethered microsphere, we can monitor temporal dynamics. Fig. 3 plots the time-autocorrelation function for the motion of the two tethers considered in Fig. 2. As expected for a particle in a harmonic potential, the autocorrelation for the well-behaved tether decays monoexponentially. The time constants of the decay are 150 ms for motion along an in-plane axis and 65 ms for out-of-plane motion. Meanwhile, the autocorrelation functions of the malformed tether significantly deviate from a monoexponential decay and suggest that a simple analysis based on the Brownian motion of a particle attached to a Hookean spring is not applicable.

FIGURE 3.

Position autocorrelation functions for the microsphere data shown in Fig. 2. For the well-formed tether, monoexponential fits yield a time constant of 148 and 66 ms for the in-plane and out-of-plane motion, respectively.

Although the velocity of the microsphere varies over time, a meaningful amplitude that allows us to estimate how much the microsphere moves during a single exposure is the ratio of the time constant to the root mean square of the displacement. For the tether in Fig. 2, a–c, this velocity is 1.4 nm/ms. If we imaged with continuous exposure at video frame rate (60 Hz), the microsphere could travel well over 20 nm per frame. Subsequent inability to observe the microsphere when it is at the extremes of its potential well would tend to artificially reduce the spread in the ensemble of displacements (7). In contrast, over the course of a single exposure, we would like the microsphere to move significantly less than our computational resolution (5 nm). Our stroboscopic illumination takes care of this constraint. Since our typical illumination time is .5 ms, the microsphere is expected to travel <1 nm per exposure.

Malformed tethers are not the only type of abnormality that can distort analysis of TPM experiments. Another complication that can occur during data acquisition is adsorption. This can happen in a few different ways—the tether can adsorb to the glass surface, the tether can adsorb to the microsphere, or the microsphere can stick directly to the glass surface. The occurrence and classification of adsorption events can be determined by monitoring unexpected decreases in the motion. Adsorption of the tether to the glass surface occurs when the motion decreases in conjunction with an observed displacement of the anchor point as determined by the center of the in-plane motion. In contrast, the adsorption of the tether to the microsphere is characterized by a decrease in motion with no shift in the anchor point. Microsphere-surface adsorption occurs when the motion decreases to the point where the position data become indistinguishable from that obtained from immobile microspheres.

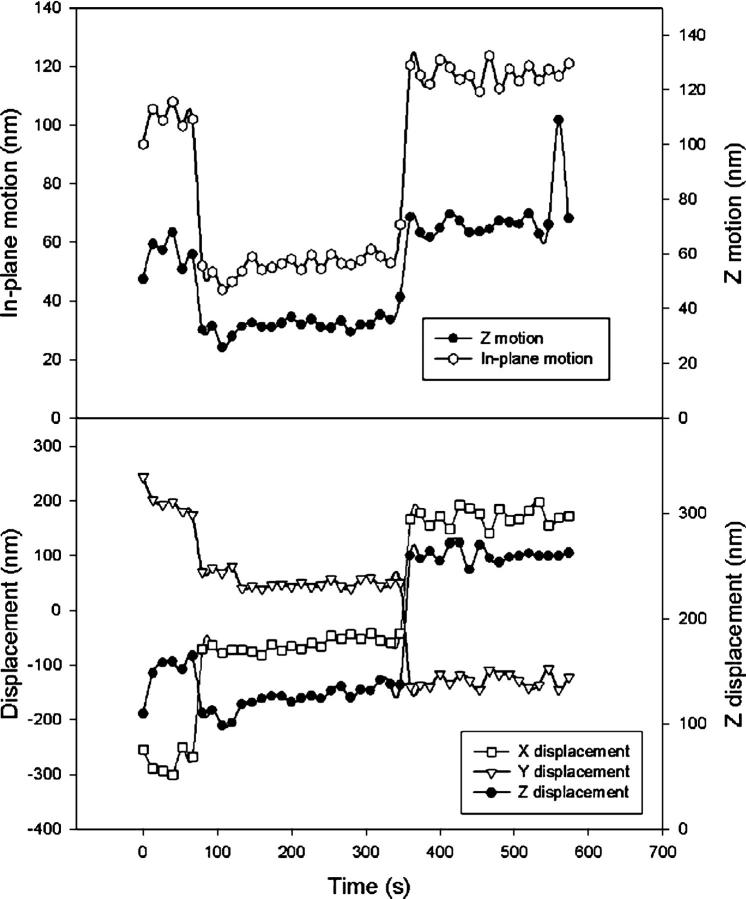
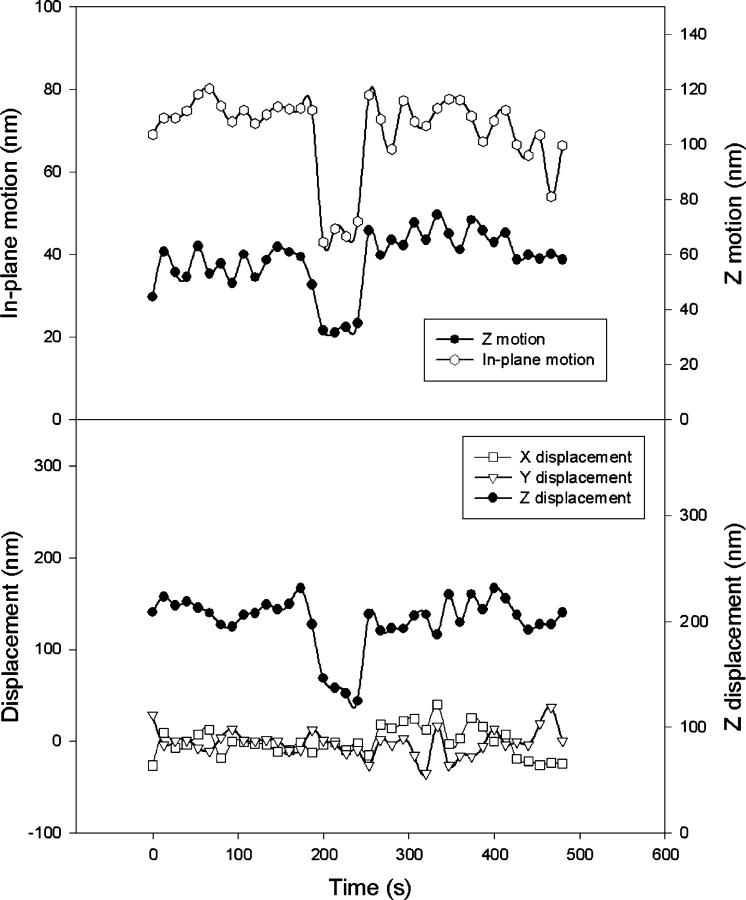
Fig. 4 illustrates the type of data expected of transient adsorption of DNA to the glass surface. To produce this figure, the position trace for a tethered microsphere was divided into intervals of 200 frames each (corresponding to 6.7 s). Then motion statistics for each “200 frame window” were computed. Fig. 4 top shows how the windowed in-plane and out-of-plane motion varies over time. Fig. 4 top can be divided into three distinct phases of constant motion. In the first and third phase, the in-plane motion stays above 90 nm. For the middle interval, the in-plane motion is always under 60 nm. Meanwhile, the out-of-plane motion is always above 50 nm for the flanking intervals and under 40 nm for the middle interval. The correlated decrease in the in-plane and out-of-plane motion indicates a transition at 75 s with a recovery of motion at 345 s. Fig. 4 bottom helps to elucidate the nature of these transitions. For each dimension, Fig. 4 bottom plots the displacement of the microsphere averaged over each 6.7 s window. Fig. 4 bottom shows discrete jumps in the displacement in conjunction with the observed transitions of Fig. 4 top. At 75 and 345 s, the averaged in-plane displacement shifts by over 250 nm. The large shift in the out-of-plane displacement suggests a change in the tether's anchor point as may occur during adsorption and desorption of DNA onto the glass surface. Another finding that is consistent with adsorption and desorption of DNA is that the plot of out-of-plane displacement shows the microsphere moves closer to the coverslip surface when the motion decreases and away from the surface when the motion recovers. The displacement transitions seen in Fig. 4 bottom cannot be due to mechanical instability of the microscope. This is because the changes in motion seen in Fig. 4 top imply an alteration in the structural properties of the tethered microsphere system.

FIGURE 4.

Transient adsorption. (Top) Time series of motion. Each data point represents the motion calculated from 200 frames of data (6.7 s). The in-plane motion is defined as the mean of the root mean square displacement along two orthogonal in-plane axes. The z-motion is the root mean square of the displacement of the microsphere relative to the coverslip. A distinct transition is seen at t = 75 s, suggesting a shortening of the effective tether length with a recovery of motion at t = 345 s. (Bottom) Time series of average displacement for each dimension (corrected for linear drift). Again, each point is representative of a 6.7 s window. Distinct shifts of the in-plane (x-y) displacement at t = 75 s and t = 345 suggest a change in the tether anchor point. Microsphere diameter = 200 nm, tether length = 1.1 kbp.

To obtain clean statistics and avoid artifacts in TPM analysis, it is important to identify well-behaved tethers and exclude malformed ones. Figs. 2–4 illustrate some of the features that can be used to distinguish well-behaved tethers from improper ones. The figures motivate the creation of selection criteria for choosing which tethered microspheres warrant inclusion in quantitative TPM analysis. In particular, a key feature that can be used to identify malformed tethers is radial symmetry of the in-plane motion and corresponding energy profile. An in-plane position symmetry requirement eliminates the analysis of many nonspecific tethers that may arise from aberrant electrostatic interactions or other anomalies of sample preparation. Because extra anchor points will likely impose nonradial mechanical constraints, the in-plane position symmetry can also be used to identify multiply tethered microspheres.

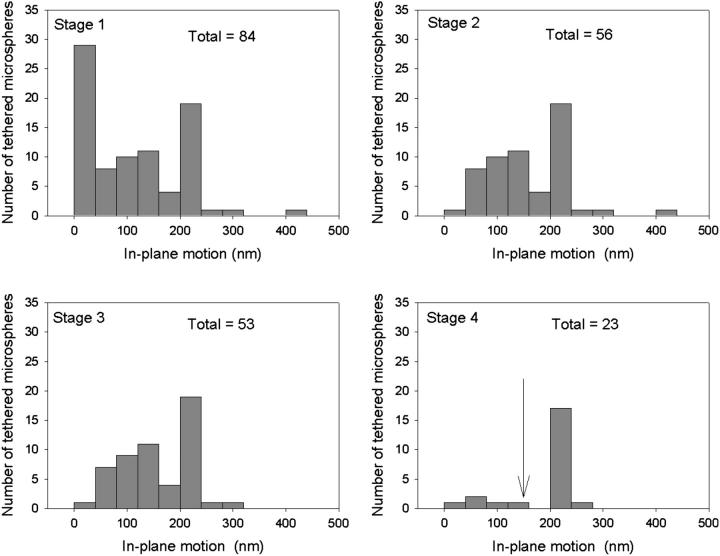
Fig. 5 shows how the application of selection criteria improves the reproducibility of TPM measurements. Fig. 5 Stage 1 contains a histogram of the in-plane motion measurements for 84 nominally identical tethered microspheres. Fig. 5 Stage 2 excludes immobile beads by showing a histogram of the 56 microspheres in Fig. 5 Stage 1 that pass a minimum in-plane motion requirement of 10 nm. The 53 microspheres in the Fig. 5 Stage 3 histogram satisfy an additional steady motion requirement, which specifies that the in-plane motion calculated from the last 1000 frames of data acquisition must be within 20% of the in-plane motion calculated from all frames. This criterion selects against adsorption events and identifies tethers that break apart during observation. Finally, Fig. 5 Stage 4 contains a histogram of the 23 microspheres that also satisfy our requirement that the in-plane motion symmetry criteria is <1.2. The mean and standard deviation of the motion measurements for all the microspheres in Fig. 5 Stage 1 is 96 and 87 nm, respectively, whereas the corresponding numbers for the microspheres in Fig. 5 Stage 4 is 170 and 62 nm. The increasingly narrow distribution of successive histograms shows that our application of selection criteria improves the reproducibility of TPM measurements by excluding the analysis of improper tethers. One can also impose a more stringent length constraint that considers the tether's contour length. For instance, requiring that the in-plane motion be at least 60% of the motion predicted from a wormlike chain model for the tether (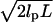 where l_p is the persistence length of DNA and L is the contour length of the tether) eliminates the five microspheres in Fig. 5 Stage 4 with the smallest motion. The resulting distribution has a distinct peak at 200 nm with a width of 11 nm. Presumably, this narrow peak corresponds to unconstrained full-length DNA tethers, whereas the five microspheres in Fig. 5 Stage 4 with in-plane motions <150 nm arise from tethers for which partial adsorption of DNA occurred before the start of data acquisition.

FIGURE 5.

Effectiveness of selection criteria. (Stage 1) Histogram of the in-plane motion for a collection of tethers that are nominally 1.6 kbp in length. The in-plane motion is defined as in Fig. 3. (Stage 2–4) Histograms for the tethers in Stage 1 that pass successive selection criteria. Stage 2 criterion: the in-plane motion must exceed 10 nm (immobile bead filter). Stage 3 criterion: the in-plane motion of the last 1000 frames must be within 20% of the calculated motion for all frames (adsorption filter). Stage 4 criterion: the in-plane symmetry statistic that measures the ratio of the axes in an ellipsoidal representation of the scatter plot must be <1.2 (malformed tether filter). The arrow in the stage 4 histogram indicates the motion corresponding to 60% of the nominal end-to-end length of the tether (144 nm) that can be used as an additional threshold requirement. Note that as the selection criteria are applied, the distribution of in-plane motion narrows. Microsphere diameter = 560 nm, imaging time = 20–80 s per bead.

The goal of many TPM experiments is to monitor dynamic changes in tether length such as those due to specific DNA-protein interactions. As a final application of our three-dimensional characterization of tethered microspheres, we monitored dynamic changes in tether length caused by DNA looping. Looping is initiated by the introduction of LacR in an experiment similar to the one reported by Finzi and Gelles (5). The DNA tethers for this experiment contain two binding sites for LacR. DNA looping occurs when LacR binds simultaneously to both sites, thereby shortening the effective length of the tether. This, in turn, decreases the Brownian motion and out-of-plane position of the attached microsphere. A transition that obeys these looping criteria is shown in Fig. 6, which plots motion statistics and average displacement for successive 6.7 s intervals. As in Fig. 4 top, the motion remains reasonably constant for three intervals, separated by two distinct transitions. At 190 s, a sharp decrease in motion likely indicates the onset of loop formation. At 240 s, the motion recovers to its original value as would be expected of a loop that breaks open. Consistent with our image of looping, Fig. 6 bottom shows that as the motion decreases, the average height of the tether also decreases. The fundamental difference between Fig. 6 and Fig. 4 is evidenced in the plots of the in-plane displacement. Whereas Fig. 4 bottom shows a shift in the apparent anchor point of the tether, Fig. 6 bottom shows no abrupt change. This suggests that the process observed in Fig. 6 is one that is internal to the tether, a finding that again reinforces the likelihood of a DNA looping event. The absence of an anchor point shift provides a criterion to distinguish looping transitions from nonspecific transient adsorption events. This should improve the accuracy of future kinetic measurements of single-molecule loop formation.

FIGURE 6.

Looping Transition: (Top) Time series of in-plane and out-of-plane motion for windows of 6.7 s (as in Fig. 3). Formation of a LacR-mediated DNA loop decreases the effective tether length and thereby decreases the motion as evidenced with the transition seen at t = 190 s with recovery at t = 240 s. (Bottom) Time series of average displacement for each dimension (again using 6.7 s windows and corrected for linear drift). In contrast to Fig. 3, there are no distinct shifts in the in-plane displacement and therefore no change in the anchor point. This indicates that the transitions seen in the top panel are internal to the tether and do not involve the coverslip surface, a finding that is consistent with DNA looping. Microsphere diameter = 560 nm, tether length = 1.5 kbp.

DISCUSSION

By providing a method to monitor three-dimensional displacement, our TPM technique extends the characterization of tethered particle behavior. The sensitivity of TIRF microscopy ensures that our TPM experiments can be conducted with nanometer spatial resolution. Furthermore, stroboscopic illumination in conjunction with a moving average correction minimizes photobleaching artifacts and improves tracking resolution, even in the presence of slow-drift noise. This allows accurate testing of tethered particle theory such as Qian and Elson's application of the Rousse model. In this model, a series of beads and springs without intrasegment hydrodynamic coupling are used to emulate the tether-microsphere system (2). Subsequent advances include Segall and Phillip's consideration of nontrivial surface-microsphere excluded volume effects (15). In addition, Barsky et al. have conducted hybrid simulations that combine coarse grain models with molecular dynamics simulations (16). Continued theoretical developments in conjunction with experimental validation will provide the basis for the interpretation of increasingly complex TPM measurements.

To motivate the need for further theoretical development, we compare our experimental measurements with the classic Gaussian chain model for DNA (17). This model is often used to describe the Brownian motion of tethered particles and the response to applied force. However, it ignores excluded volume effects and other interactions arising from contact between the microsphere, the tethering DNA, and the anchoring surface. According to the Gaussian chain model, the theoretical value for the spring constant is 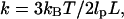where 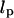is the persistence length of DNA (53 nm) (18) and L is the length of the tether. By this formula, the spring constant for the 1.6 kbp tether observed in Fig. 2, a–c, is expected to be .21 pN/μm, in contrast to our measured values of .1 pN/μm for the in-plane spring constant. The discrepancy between the calculated and measured spring constant is in part due to the microsphere's ability to pivot around the tether-attachment point. This pivot adds an extra degree of freedom that increases the motion of the microsphere beyond the end-to-end motion of the tether itself. The extra contribution to the motion implies that the measured in-plane spring constant is smaller than the intrinsic spring constant of the tether.

A discrepancy between the measured in-plane and out-of-plane spring constant is expected due to the anisotropy of the tethered microsphere geometry. For the case in which the microsphere diameter is comparable to the tether's contour length, the flow cell surface limits the degree to which the microsphere can rotate. This limitation implies that the out-of-plane motion is not amplified by the presence of the microsphere. Furthermore, Segall and Phillips report that the inability of the microsphere to penetrate the anchoring surface imposes an effective force on the DNA tether of ∼80 fN (15). Differentiating the force-extension relationship for the wormlike chain model of DNA (18) and evaluating the result for a 1.6 kbp strand subjected to 80 fN of tension suggests that the out-of-plane spring constant should be .57 pN/μm. In addition, electrostatic interactions may occur between the microsphere and surface as described by a Derjaguin-Landau-Verweg-Overbeek potential (19,20). Indeed, we observe that the shape and width of the out-of-plane potential changes as the ionic strength is reduced (data not shown). However, the Debye screening length for our 200 mM NaCl sample buffer is .7 nm (19). Given the short distance for which an electrostatic field becomes screened, it appears unlikely that electrostatic effects have a significant effect on our measurements. Further investigation is needed to reconcile our measured out-of-plane spring constants (3.5 ± 4.4 pN/μm) with theory.

The energy profile of a microsphere is determined by the ensemble of displacements and contains no information about dynamics. In contrast, the time constant associated with the monoexponential decay of the position autocorrelation (Fig. 3) holds useful information about the tethered microsphere's hydrodynamic environment. From a theoretical standpoint, for a particle in a quadratic potential the time constant is given by the ratio of the friction coefficient to the spring constant (17). Using the spring constant values obtained from Fig. 2 cand Stoke's formula for the friction coefficient of a microsphere, this yields a time constant of 45 ms for in-plane motion and .8 ms for out-of-plane motion. This contrasts with the 150 ms in-plane time constant and 65 ms out-of-plane time constant found in Fig. 2 c. However, Qian and Elson's Rousse model of DNA tethers suggests there is an additional contribution to the time constant equal to 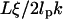(2), where ξ is the frictional coefficient per persistence length of DNA (10⁻⁹ Ns/m according to Lin and Schurr (21)). For our 1600 bp tether, this adds 24 ms to the theoretical time constants for each dimension. With this adjustment, there is greater agreement between the measured and predicted values for the time constants, particularly in the out-of-plane dimension. Another correction to the time constant can be made due to hydrodynamic coupling between the surface and the microsphere (22). Future measurements should help to clarify how tethered microsphere architecture affects the hydrodynamics and associated time constants of TPM experiments.

As discussed above, for a well-formed DNA tether we expect the in-plane microsphere motion to be radially symmetric and the time-autocorrelation functions to show a smooth monoexponential decay. In contrast, the data of Fig. 2, d–f, obtained from a microsphere exhibiting tetherlike motion in a sample containing no DNA, demonstrate that TPM analysis may be compounded by nonspecific effects. Based upon analysis of the out-of-plane energy profiles and force-induced disruption of nonspecific tethers, Zocchi et al. have deduced that these tethers originate from a loose polymer strand emanating from the microsphere (8,23). Our complete three-dimensional characterization of the motion has provided additional insight into the physical properties of these tethers. In particular, we have found that these nonspecific tethers often exhibit marked asymmetry in the in-plane motion and associated energy profiles (Fig. 2, d–f). We have also found that these tethers exhibit a large variation in energy landscapes that are sensitive to ionic conditions (data not shown) and that the root mean square displacements often exceed 100 nm. These findings are inconsistent with the notion of a single polystyrene strand attachment being responsible for their behavior and suggest that other factors may play a role. In particular, the stability of these tethers may by due to a more substantial irregularity of the microsphere surface or electrostatic pockets of interaction between the glass and microsphere (24). In the latter case, surface roughness can contribute to the degree of microsphere-surface interaction (8,25). Electrostatic interactions may also be the cause of transient adsorption events such as the one seen in Fig. 4.

Our new insight into the physics of tethers has lead to improvements in sample preparation and data analysis. However, because of the complications due to electrostatic interactions, multiply tethered microspheres, microsphere aggregates, and other sample preparation artifacts, we cannot expect to create a sample that is free of malformed tethers and adsorption. Rather, our in-depth analysis motivates a set of selection criteria that can be uniformly applied to a set of TPM data. The realization that sample artifacts can produce tetherlike motion of microspheres in the absence of a tethering polymer further underscores why TPM analysis must account for these abnormalities.

TPM experimentalists have reported careful consideration of their data in the context of known sample artifacts (1,8). However, it is often unclear whether selection criteria are applied in a systematic manner. The value of our selection procedure is demonstrated in Fig. 5, which shows a reduction in the spread of in-plane motion measurements as successive selection criteria are systematically applied to a large set of data. Of particular interest is the value of our in-plane symmetry statistic, which significantly narrows the distribution of motion measurements (compare Fig. 5, C and D) even though its calculation is independent of the specific value for the in-plane motion.

Although it is common to discover that a given microsphere fails multiple selection criteria, in our measurements the different selection criteria exhibit a high degree of independence. If there were strong correlation then the last selection criteria (i.e., symmetry requirement) would not have eliminated 57% of the remaining tethers. The independence of selection criteria is reasonable because there is no inherent rationale for correlation between them—the first checks for immobile microspheres, the second for adsorption events, and the last for multiply attached tethers and other motion artifacts. Since the selection criteria are easy to implement, are based on physical grounds, and are fairly independent of each other, we believe that all three of them should be used to ascertain the integrity of unconstrained tethers. Although we have used the selection criteria primarily to ascertain whether an individual data set is consistent with the expected behavior of a well-formed tether, the criteria may also be used as global standards to assay the quality of a particular sample preparation protocol.

By expanding the repertoire of available measurements, our combination of TIRF and TPM techniques provides new opportunities for characterizing the dynamics of single biomolecules. The observation of protein-mediated DNA looping (Fig. 6) provides an illustrative example. When compared to Finzi and Gelles' original measurements of single-molecule looping (5), our analysis capabilities provide two advantages. The first is that we can employ a more sensitive and specific test for detecting looping transitions. The increased sensitivity is due to our ability to track the displacement of all three dimensions of a tethered microsphere with high temporal resolution. Thus, an apparent change in the mechanical properties of a tether can be verified by observing correlated transitions in all three dimensions. The improved specificity arises because the variety of measurable quantities can be used to validate the authenticity of an observed transition. For instance, transient adsorption (Fig. 4) can be distinguished from data that are indicative of DNA looping (Fig. 6) by assaying for a shift in the tether's anchor point on the coverslip surface. The careful monitoring of apparent anchor position is a feature that would be beneficial in the analysis of other TPM experiments whose analysis can be distorted by nonspecific adsorption. Nevertheless, care must be taken to use adequate controls because certain events such as transient adsorption of tethers onto the microsphere surface are not detectable with this method.

The second advantage of our technique for observing DNA looping is that we can measure additional characteristics of DNA looping besides the transition rate. For instance, the combined use of in-plane and out-of-plane measurements may improve the accuracy with which decreases in effective tether length can be measured. This improved accuracy would enable the estimation of the degree of kinking that looping proteins induce in the DNA external to the loop and thus provide important, hard to obtain structural information about DNA-protein conformation in an aqueous environment (26).

CONCLUSION

We have shown that TIRF microscopy with synchronous stroboscopic illumination can be used to characterize the three-dimensional spatiotemporal dynamics of surface-tethered particles. By measuring root mean square displacements, symmetry, and time constants, we have been able to distinguish properly formed DNA tethers from their malformed counterparts. Using quantitative measures as a screen, we eliminate the analysis of tethered particles that are corrupted by erratic surface interactions or nonspecific adsorption and thereby significantly narrow the heterogeneity of TPM measurements. This enables the use of TPM as a more quantitative tool for investigations of the dynamics of DNA tethers and DNA-protein interactions. We demonstrated the utility of this approach by observing protein-mediated DNA looping in a typical TPM experiment and showed that loop formation events can be distinguished from surface adsorption events. We conclude that three-dimensional spatiotemporal tracking by TIRF microscopy adds unique new quantitative capabilities to TPM.