Optical Measurement of Surface Tension in a Miniaturized Air-Liquid Interface and its Application in Lung Physiology

Abstract

We have previously shown that lamellar body-like particles, the form in which pulmonary surfactant is secreted, spontaneously disintegrate when they contact an air-liquid interface, eventually creating an interfacial film. Here, we combined these studies with a new technique enabling the simultaneous and non-invasive measurement of surface tension (γ). This method is a refinement of the pendant-drop principle. A sapphire cone with a 300-μm aperture keeps the experimental fluid by virtue of surface coherence in a fixed and nearly planar position above the objective of an inverted microscope. The radius of curvature of the fluid meniscus is related to γ and determines the pattern of light back-reflection upon epi-illumination. This method, which we name “inverted interface”, has several novel aspects, in particular its microscopic dimensions. When using lamellar body-like particles freshly released by alveolar type II cells, we found that their conversion at the interface resulted in γ-reduction close to 30 mN/m. After a fast initial decay, γ-decrease proceeded slowly and in proportion to single particle conversions. These conversions ceased with time whereas γ decreased further, probably due to reorganization of the already deposited material. The present investigation indicates that surface film formation by adsorption of large surfactant aggregates is an important mechanism by which γ is reduced in the lung.

INTRODUCTION

Pulmonary surfactant is a mixture of phospholipids and proteins that covers the air-liquid interface in the lung. The importance of this surface coat is best demonstrated in the premature infant lung, where deficiency of this material causes alveolar collapse with life-threatening consequences unless cured by surfactant administration strategies (1,2). In mature lungs, surfactant is released by alveolar type II cells as μm-sized, globular complexes (lamellar bodylike particles; LBPs), which undergo a transformation process to finally create a surface film that lowers γ close to 0 mN/m at end-expiratory lung volumes (3–5). However, the mechanisms promoting transformation of these compact particles into surface-active components is still poorly understood (6).

Previously, we demonstrated that freshly released LBPs are stable particles but transform spontaneously and rapidly (<1 s) when they contact the air-liquid interface (7). These transformations stopped when the surface was already occupied by previously deposited material or when γ of the experimental fluid was low. From these observations, we concluded that γ is the force that drives LBP-disintegration, and that LBPs are able by themselves to reduce γ to a certain extent. However, these conclusions were indirect, as we were not able to measure LBP transformation and γ simultaneously.

In this article, we present a sensitive and noninvasive method to measure γ of a miniaturized inverted air-liquid interface in combination with fluorescence imaging microscopy. It is based on the analysis of light reflection at a fluid meniscus whose radius of curvature is related to its surface tension. This method is highly suited to studying dynamic surface phenomena at μm-scaled dimensions, e.g., transformation and adsorption of single LBPs that reach the interface spontaneously by sedimentation. To our knowledge, this method of γ-measurement is one of the most sensitive reported as the required quantity of LBPs is extremely low.

Our results showed that LBPs, released by rat alveolar type II cells, dispersed when reaching a clean air-liquid interface, and that this process entailed a reduction of γ in relation to the number of transformed LBPs. These transformation events gradually ceased with time, supporting a self-regulated process driven and controlled by surface forces. We conclude that ∼35 mN/m is close to the γ-equilibrium of spontaneously adsorbing LBPs, and that further reduction of γ < 30 mN/m may be caused by the slow rearrangement of the surface-associated material. However, additional mechanisms may be required to attain the low γ-values that have been found in the lung. The inverted interface should be a suitable approach to study, in more detail, the adsorption of particulate surfactant in relation to surface film formation.

METHODS AND RESULTS

Design of the inverted interface

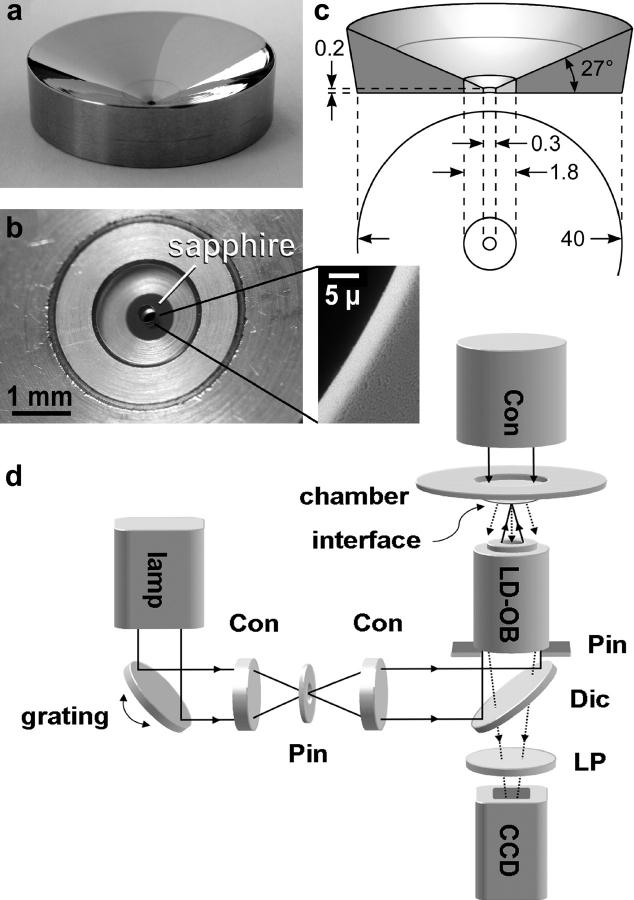
The chamber confining the interface has been improved further as compared to its initial introduction (7). It is made of polished stainless steel in its upper part, and synthetic sapphire in its lower part (Fig. 1, a–c). Sapphire was used because it meets all quality criteria comparable to those for glass. In addition, it has an extremely smooth surface finish over all its parts, which is difficult to realize in glass due to grinding or etching procedures. Furthermore, these cones are readily available in various sizes with sharply edged and perfect circular apertures (Ø ± 0.1%; Comadur, Switzerland). Perfect aperture circularity is necessary to obtain an axisymmetric liquid curvature. Likewise, contact angle problems are minimized when the edge of the aperture is close to 90°. Furthermore, the hydrophobic character of this material (8) is useful as the fluids are stably kept within the aperture plane. Since a minimally domed surface is necessary for γ-measurements as described below, a force is required to counteract γ. This is best achieved by a constant hydrostatic pressure exerted by the fluid itself. To accommodate the fluid (∼0.5–5 ml), we designed the embodiment of the aperture with a conical shape that served several additional purposes: First, contact angle problems and capillary effects on the upper fluid surface are reduced, or abolished, when it is flat over an extended region perpendicular to the lower aperture. Second, small volume changes are tolerable as they change fluid height to a minimal extent only. Third, the cone might help to concentrate sedimenting LBPs onto the small interface. Fourth, inspection of the interface by transmission illumination, phase contrast imaging, or the introduction of patch pipettes or other manipulating devices as well as substitution of fluid components (e.g., by superfusion of the interface), are substantially facilitated. Before all experiments, the chamber was cleaned with water and acetone in an ultrasonic cleaner, flushed with distilled water, and dried with sterile air.

FIGURE 1.

Design of the inverted interface and sketch of the optical setup. (a) Photography of the chamber. (b) Chamber bottom with the sapphire and its central aperture. (Enlarged: electron microscopy of edge.) (c) Schematic drawing of overall dimensions (not in scale; units = mm). (d) Illumination pathway used for combined epifluorescence and reflection measurements. The inverted interface is denoted as a fluid-filled pinhole only. Con = condenser, Pin = pinhole, LD-OB = long distance objective, Dic = dichroic beam splitter, and LP = longpass filter.

Design of the setup

The inverted interface is mounted on the stage of an inverted microscope (Zeiss 100, Carl Zeiss, Oberkochen, Germany) (Fig. 1 d). At the lower aperture, liquid in the chamber formed an interface with the air below, inspectable by air objectives. We used a 20× Plan-Neofluar, N.A. 0.5, throughout all experiments to image the aperture on the CCD completely, or a 40× LD-Achroplan, N.A. 0.6 (both Zeiss), for higher resolution visual inspections. Light from a polychromatic source (Xenon arc lamp) is reflected by a diffraction grating (Jobin-Yvon, Longjumeau, France) into the rear port of the microscope. The grating is mounted on a precision scanner to allow selection of desired wavelengths. After passing a condenser, light was focused on a field stop, and directed by a second condenser to a dichroic beam splitter (515 nm) into the objective and the interface. The scanner allowed us to quickly change between 470 and 550 nm—the wavelengths used to monitor FM 1-43 fluorescence and reflected light, respectively. The field stop reduced the amount of light passing peripheral sections of the transparent sapphire, thus minimizing the amount of scattered light and undesired reflections at the inner walls of the cone. In addition, the field stop was useful, since it allowed us to focus on a structureless surface (e.g., when using high magnifications in combination with large interface apertures), and to align the inverted interface to the optical path. A second diaphragm (Ø 5 mm), inserted into the rear aperture of the objective, reduced the spatial angle of the outgoing light cone, and thus increased the sensitivity with respect to curvature discrimination while reducing out-of-focus distortions. Reflected or fluorescent light was collected, after passing a longpass filter (535 nm), by a cooled CCD camera (Imago-SVGA, Till Photonics, Germany). It was operated at an image acquisition rate of 1 Hz with a symmetrical binning factor of 2. Control of illumination and image analysis was performed by Tillvision (Till Photonics). The microscope setup was placed in a dark and temperature-stabilized room (25 ± 1°C). It was shielded by various means to minimize air turbulences and contamination by air-borne material.

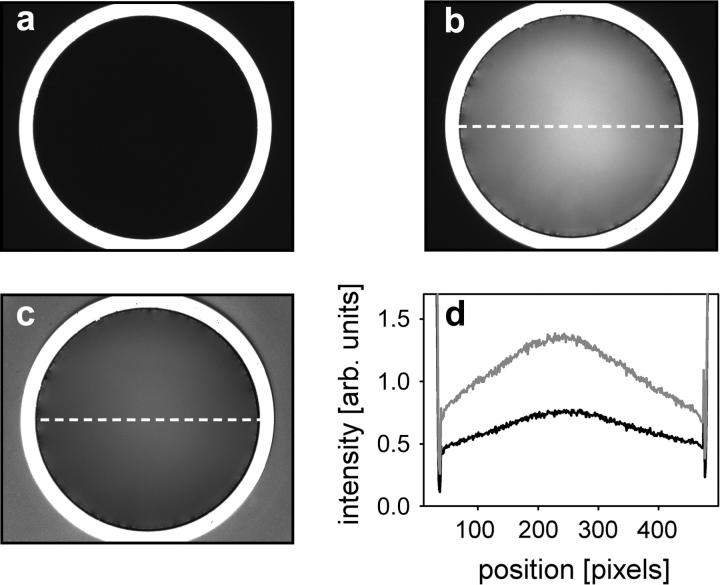
Inspection of the inverted interface

The aperture of the sapphire cone, illuminated by 550 nm, was aligned with respect to the field stop, and the objective focused to its flat bottom (Fig. 2 a). Thus, the distance of the objective with respect to the aperture was held constant during the experiments. In principle, the objective could be focused to the interface directly, as soon as the chamber had been filled with water. This, however, is difficult unless the interface contains detectable structures. Furthermore, when γ changes (see below), the focus has to be adjusted continuously, introducing an additional source of error. Thus, after initial focus adjustment to the aperture bottom, the cone was filled with water, and a series of images has been captured. They showed an axisymmetric intensity distribution as depicted in Fig. 2 b. Since this could also be the result of uneven illumination, we compensated for this possibility by shading correction. This was performed by standardizing pixel intensities to those obtained from images of flat, polished microscopic slides according to

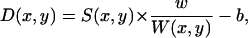(1)

where D is destination and S the source image, W the white reference image, and w the mean grayscale of the white and b the mean grayscale of the black reference image, respectively. From corrected images (Fig. 2 c), an intensity profile, i.e., the pixel intensities along a line across the interface, was calculated (Fig. 2 d). The intensity distribution along this line then characterizes different angular orientations of the fluid interface; bright pixels denote a flat section, and darker ones an oblique section, giving the impression of an axisymmetric, spherically domed profile.

FIGURE 2.

Microscopic views of the inverted interface. (a) Appearance of the aperture in the reflected light modus under dry conditions. Field of view is limited by a circular field stop (outer black region). The bright rim is due to light back-reflection from the bottom of the sapphire cone. (b) Same view when chamber was filled with water. Light was back-reflected from the interface at varying intensities. (c) Same picture as in b, corrected for uneven illumination by shading correction. (d) Pixel intensity profiles, calculated along the line shown in b and c, for original (shading) and shading-corrected images (solid line).

Principle of measurement

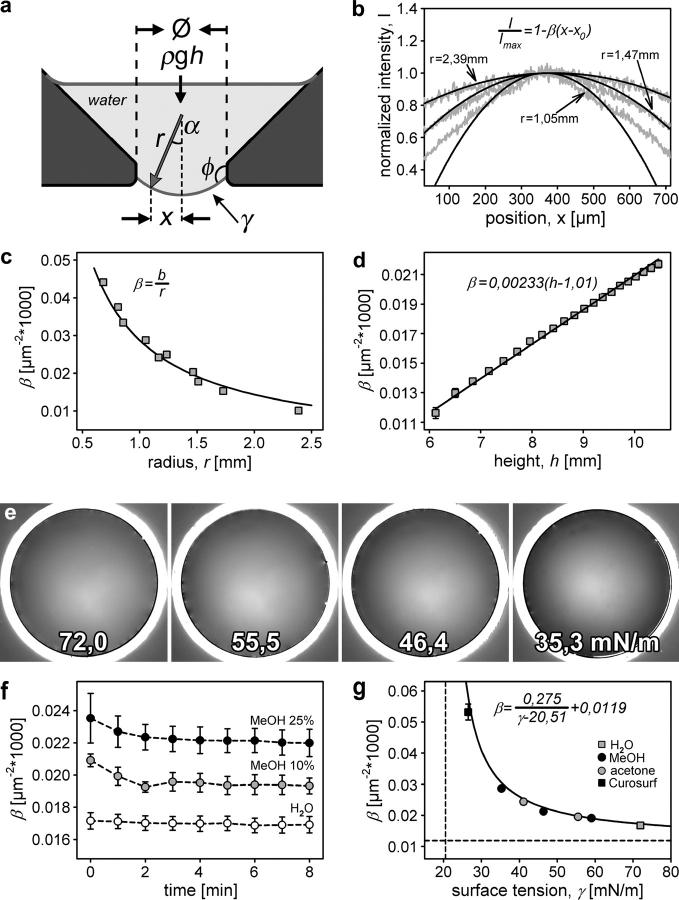
To analyze the observation in Fig. 2 d in more detail, three effects have to be considered. The first one, shown in Fig. 3 a, is based on the feature of a pendant water surface to adopt a convex shape, with a local radius of curvature r depending on the hydrostatic pressure p = ρgh (ρ and h being the density and the filling height of the liquid, respectively; and g = 9.81 m/s²), and on γ, as

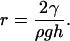(2)

This equals the Laplace equation describing the radius of curvature of a small drop of liquid if the hydrostatic pressure is substituted by the γ-induced pressure within the liquid drop. Therefore, the image in Fig. 2 c is likely the result of a curved liquid surface, and by measuring its radius it should be possible to determine γ, provided that the nature of the liquid and its filling height are known.

FIGURE 3.

Determinants of surface curvature and γ-calibration. (a) Principal determinants of surface curvature of a given fluid. (Ø, aperture diameter, ρgh, hydrostatic pressure of the fluid, γ, surface tension, r, local radius of curvature, α, local angle of the surface tangential plane, x, radial coordinate from apex of curvature, and Φ, contact angle.) (b) Line profiles (shading) obtained from pendant drops of indicated radii and fit (solid lines) by the indicated parabolic function demonstrating the feasibility of curvature discrimination by back-reflected light. (c) The β-coefficient obtained from b as a function of curvature radius r (b = fit parameter). (d) The β-coefficient is linearly related to incremental increase in fluid height in the chamber (n = 3). (e) Examples of shading-corrected images obtained at defined γ. Surface tension was adjusted by solutions of methanol/acetone in water. (f) Time-dependent change in the β-coefficient of three solutions used in g. Values for calibration were chosen after reaching a stable recording. (g) Experimentally measured β-coefficients plotted as a function of γ (n = 3). The model (solid line) is a hyperbolic function, its asymptotes (offset parameters) are indicated by the dashed lines. Note that error bars are smaller than symbols.

The second effect is due to the fact that light of intensity I(x), specularly reflected from a small area of the surface at a position x (x is a radial coordinate measured from the center of the surface; Fig. 3 a), and collected by the microscope's objective with its limited N.A., depends on the angle α(x) = arcsin(x/r) of the incident light with respect to the optical axis, since this angle determines the direction into which the light is reflected. This was tested by imaging pendant drops of water positioned by a micromanipulator above the objective (the water contained a light-absorbing dye to reduce unspecific light reflections). As shown (Fig. 3 b), the back-reflected light has a maximum in the center falling off smoothly approaching the periphery. It turns out that the one-dimensional intensity profile along the radial coordinate x in the region of the center of the drop (x = 0) can be approximated by a parabolic shape,

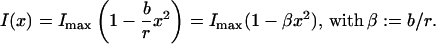(3)

The curvature of the parabola is proportional to the curvature of the drop (i.e., ∼br⁻¹), with a constant scaling factor b, which depends on the optical parameters of the setup and which has to be calibrated. Thus, a fit of the radial light intensity profile should result in a parabola with a curvature parameter β, depending reciprocally on the radius of curvature of the convex surface. This was tested by pendant drops of water as described before, adjusted to defined sizes by a precision nanoliter pump (Fig. 3 b; radius of drop meniscus was determined from photographs taken with a side-positioned camera). The intensity of back-reflected light was normalized to the maximum in the respective image center, I_max. The normalized profiles were fit in their central region by parabolas (indicated in the Fig. 3), and β was obtained as a fitting coefficient. To test the relation of Eq. 3, β is plotted in Fig. 3 c as a function of curvature radius r. The expected reciprocal dependency of the β-coefficient from the radius of curvature was thus verified (fitting curve β = b/r as indicated in Fig. 3, with b = 2.87 × 10⁴ μm⁻¹). The data show that the imaged light intensity distribution obtained by reflection from a curved surface can be approximated in its center by a parabola, whose curvature, characterized by the β-coefficient, is a direct and reliable measure of surface curvature of both solid (not shown) and liquid materials.

The third effect to be considered is the contact angle (Φ) formed between any fluid and solid matter (Fig. 3 a). A fluid of given surface tension γ will adopt a different radius of curvature r depending on the surface properties of the material used. Conversely, at a given surface property, any decrease in γ would decrease Φ (9), probably forcing the fluid meniscus into a less convex shape than predicted by Eq. 2. Practically, this results in an offset of the measured γ (see below) as compared to its value expected from Eq. 2. However, when using fluids with a γ lower than that of pure water, we were able to detect a minute creeping of these fluids (in the range of a few μm) in contact with the wall. This small wetting effect is sufficient to increase the curvature of the fluid meniscus as the edge of our aperture is not infinitely sharp (Fig. 1 b).

Calibration

To obtain γ from the fitted curvature parameters β we substituted r from Eq. 2 into Eq. 3. One finally obtains for the measured β the relation

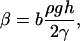(4)

where b is the previously calibrated parameter of the setup, depending mainly on the used N.A. of the microscope objective. The dependencies expressed by Eq. 4 were tested in Fig. 3 d, where the β-coefficient was plotted as a function of the height of the fluid. One obviously obtains a linear dependency of β from the fluid height, which is expected by Eq. 4 and confirms the validity of our assumptions. Furthermore, according to Eq. 4, the measured β-coefficient should depend reciprocally on γ. To test this, we used standard dilutions of methanol and acetone in water for which accurate surface tension values are reported: H₂O 71.97; MeOH 10% 59.04, 25% 46.38, 50% 35.31; acetone 5% 55.50, 20% 41.10; % = v/v, γ = mN/m, and T = 20–25°C (10). For each defined solution, a series of images was captured and analyzed as described below. As shown (Fig. 3 e), fluids with different γ yielded different grayscale distributions in shading corrected images. To compensate for resulting differences in fluid density, corresponding volumes (3–4.185 ml) were applied to keep the hydrostatic pressure constant. Below ∼30 mN/m, these solutions were no longer retained by the aperture and started to leak-through immediately. However, leakage occurred only with pure solutions but not with surfactant-containing samples, which are well retained even below that value. Differences in viscosity or the presence of insoluble surface films are likely important factors for their enhanced adherence. Therefore, we used a commercial surfactant (Curosurf; Nycomed, Linz, Austria) to extend our range of calibration toward a lower γ. The value for a static surface tension (= γ_abs) of Curosurf (3 mg/ml ∼26.5 mN/m; see Ref. 11), was taken as a reference because dynamic values (γ_min, γ_max) are not comparable with our measurements. As mentioned before, solutions with low γ tend to wet the aperture to a slightly higher extent, resulting in a time-dependent change in the measured β-coefficient. In Fig. 3 f, this effect is exemplarily shown for three standard solutions used. Obviously, this wetting phenomenon is a slow process taking several minutes. Therefore, the β-coefficients used to calibrate the system were noted after reaching stable values, and were plotted as a function of the corresponding γ (Fig. 3 g). The observed dependency is in accordance with the expected reciprocal behavior (β ∼ 1/γ ; a fitting curve is sketched). It is a hyperbolic function where the asymptotes represent the limitations of our system. In particular, the horizontal one takes into account that the surface seems to have a small offset curvature even at an infinite γ, which can be due to a slightly inhomogeneous surface illumination or boundary (contact angle) effects. The vertical asymptote indicates that γ-measurements are not feasible below ∼20 mN/m. Both theoretical limitations confine our measurements to within the indicated range of experimental values, with the highest sensitivity between ∼60 and 30 mN/m.

Image analysis

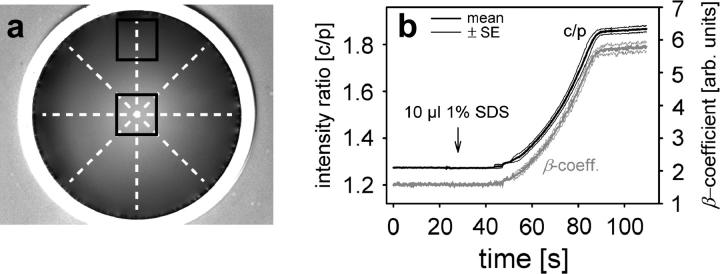
All image analyses were performed as follows. Four line scans, displaced at 0°, 45°, 90°, and 135° and crossing each other at the center of shading corrected images, were constructed (Fig. 4 a). They yielded a mean β-value, intended to further minimize imperfect alignments and spatial deviations from axisymmetry. As shown, measurements were restricted to a portion of ±138 μm from the apex. Within that region, the fluid meniscus should be least affected by incomplete wetting of the aperture plane, evidenced by a peripheral rim of dark spots in this contrast-enhanced picture. This potential problem most likely arises from small surface imperfections of the cone material and could not be avoided.

FIGURE 4.

Image analysis. (a) Construction of four lines across the interface used for the calculation of a mean β-coefficient. As shown, the line profiles were restricted to ±138 μm from apex. For a continuous and convenient on-line analysis, light reflection could also be characterized by an intensity ratio calculation (center/periphery ratio, c/p) using two spaced regions of interest (dark rectangles). (b) At constant fluid height, the apparent surface curvature (β-coefficient and c/p ratio) remained constant. Addition of a small amount of synthetic surfactant (sodium dodecyl sulfate) lead to significant changes in both parameters (n = 5; β-coefficient was not calibrated in this example).

As further shown in Fig. 4, surface curvature can also be characterized by a simple center/periphery intensity ratio calculation. This method, using two rectangular regions of interest, is convenient when a continuous on-line registration of a rapidly changing surface curvature is required. For example, when we applied a small amount of sodium dodecyl sulfate (an anionic surfactant), on top of the fluid-filled cone at the indicated time, the change in the on-line acquired center/periphery ratio compared well with that of the off-line calculated β-coefficient (Fig. 4 b). Although this alternative method was not used for quantitative measurements, it should demonstrate the principal feasibility to obtain fast and time-dependent estimations of γ-changes.

Combined surface tension and fluorescence measurements

Combined γ- and fluorescence measurements were made by alternately switching between 470- and 550-nm light exposures. Our protocol (Tillvision) was set to obtain fluorescent (470 nm) images every second and reflected (550 nm) light every 30 s. In addition, to obtain a maximum of fluorescence information, we focused on the interface directly when using 470 nm, and refocused to the aperture plane for reflected light. This was done by a fixed focus stop, allowing us to perform this adjustment within 1 s. To visualize LBPs, we used the styryl dye FM 1-43 (Molecular Probes, Eugene, OR) as described (12). Before the experiments, we tested whether it interferes with γ-measurements. At high concentrations, FM 1-43 has a considerable surface activity itself. Thus, we used this dye at 0.2 μM, and no effect was detectable when measured by the inverted interface or by the vertical pull method (γ = 71.8 ± 0.14 mN/m; n = 3; see Ref. 7). However, at this low concentration, labeling of LBPs was reduced as well.

Analysis of LBP transformations

Freshly released LBPs were harvested from filtered AT II cell supernatants as described in detail in our previous publication (7). These supernatants contained 150 mM NaCl, 5 mM KCl, 1 mM MgCl₂, 2 mM CaCl₂, 0.05 mM NaH₂PO₄, and 5 mM glucose, supplemented with 0.1 mg/ml streptomycin, 100 U/ml penicillin, and the secretagogues MgATP (100 μM) and phorbol 12-myristate 13-acetate (100 nM), pH 7.4 at 25°C. The experiments with LBPs were started by replacing 0.5 ml of a total 3-ml experimental solution (150 mM NaCl, 5 mM KCl, 1 mM MgCl₂, 2 mM CaCl₂, 0.05 mM NaH₂PO₄, and 0.2 μM FM 1-43; pH 7.4 at 25°C) with that of LBP suspension on top of the fluid-filled cone. LBP-interface interactions were analyzed off-line using the stored image sequences comprising 900 single high-resolution images per experiment. By repeated backward and forward scrolling of image sequences, the amount of stably incorporating and transforming LBPs could be counted. Transforming LBPs were judged as a sudden (<1 s) disappearance of fluorescent spots, as exemplified in Fig. 5 a and outlined in more detail previously (7).

FIGURE 5.

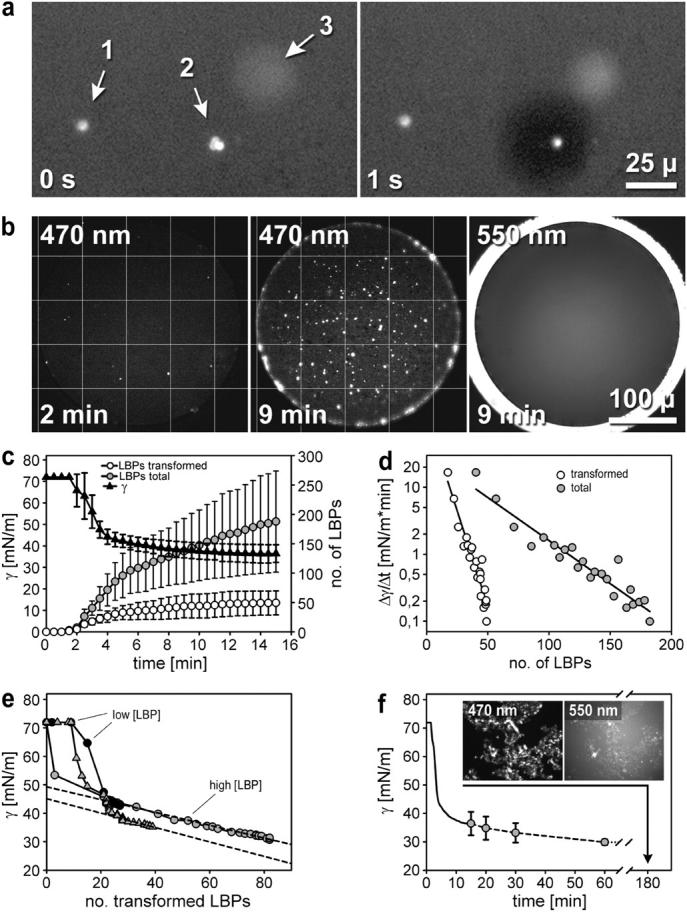
Combined fluorescence and reflection measurements of LBP-interactions at the interface. (a) Examples of LBP-interface interactions. Arrow 1 is a stably surface-associated, FM 1-43 labeled LBP that did not transform; arrow 2 is a group (three) of LBPs with subsequent (<1 s) transformation from distinct spherical spots into an expanded surface area (dark region), one of them remaining surface-associated; and arrow 3 is the out-of-focus signal of one (or more) LBP(s) in the process of surface approach. Total LBPs comprise the amount of transformed and stably incorporating particles. Images (40× LD-Achroplan) were contrast-enhanced for clarity. (b) With ongoing LBP-sedimentation, an increasing number of fluorescent spots was visible at the interface (20× Plan-Neofluar; measurements correspond to data in c). Note that in the middle image, focus was adjusted to the central portion of the interface. In the (simultaneous) reflection mode (550 nm; focus adjustment to the field stop), no interference with surface-associated material could be observed. (c) Number of total arriving (total) and transforming LBPs (transformed) in relation to the change in γ over time (LBP-count and γ were measured simultaneously). The prominent scatter is due to different LBP concentrations used (n = 3). (d) Rate of γ-decrease (log scale; Δt = 30 s) versus cumulative amount of transformed and total LBPs. (e) Plots of single experiments corresponding to c. The γ-data were expressed with respect to the cumulative amount of transformed LBPs, suggesting a nearly linear relationship between single transformations and γ after reaching ∼45 mN/m or ∼20 LBPs, respectively. (f) The γ-measurements shown in c (solid line) extended for 60 min (dashed line) and inspection of the interface after 3 h (inset), showing aggregated structures in both fluorescence (470 nm) and reflection (550 nm) channels.

LBP transformations and surface tension

Added LBPs approached the focal plane, i.e., the air-liquid interface, due to ongoing sedimentation (which is equal to the sedimentable fraction of the added LBP-suspension). After surface contact, they rapidly transformed by spreading into expanded structures, indicating an immediate adsorption process and insertion of particle components into the interface (Fig. 5 a). However, the incidence of LBP transformations progressively declined despite ongoing LBP sedimentation. These accumulating LBPs maintained a compact appearance and became surface-associated, but did not spread (Fig. 5, b and c). Thus, the sedimentable amount of LBPs comprises two populations—those that stably incorporate into the interface and those that rapidly disorganize. Appearance and transformation of LBPs was accompanied by a decrease in γ which seemed to level off during 15 min of observation (Fig. 5 c). The similarity in the time course of γ-decrease and LBP-transformations suggest that both processes are interrelated. Thus, we analyzed the time-dependent rate of γ-decrease in relation to both the total sedimentable and the transforming LBPs (Fig. 5 d). As shown, the kinetics of γ-decay relate with a logarithmic function to the cumulative amount of transformation events (i.e., particle adsorption). However, there was still an obvious, though much less pronounced, dependency of γ-decay on the amount of total sedimentable LBPs. This is certainly due to the fact that transformed LBPs are included here. In addition, it might be explained by the presence of a soluble, surface-active material other than that of an LBP. We cannot exclude the contribution of any such material, which inevitably will form out of LBPs during our sample preparations.

To estimate such contribution, we analyzed the decrease in γ with respect to the amount of transformed LBPs in all experiments separately. Furthermore, the sedimentable fraction was intended to be different between each preparation. As shown (Fig. 5 e), transformation of the first ∼20 LBPs did not reveal any common characteristic between the single measurements. The initial drop in γ, therefore, seems to have no quantitative relation to single particle conversions, and most likely is caused by a rapidly adsorbing soluble material. However, despite the considerable difference in their total number, ∼20 LBPs reduce γ in all three experiments to the same extent (45–40 mN/m). Furthermore, after passing this surface tension value, and/or exceeding that amount of LBPs, γ-decrease followed in proportion to the transformation of single LBPs. This analysis reveals different behaviors of LBP-transformations if the interface is clean or occupied by previously transformed surface active material.

The above results suggest that γ-decrease is not complete. Therefore, we prolonged our measurements over time (Fig. 5 f). They show that γ fell continuously, reaching values <30 mN/m after 60 min. Interestingly, these low γ-values would not have been measurable in our setup with pure fluids for the reasons described above. It indicates that LBPs already formed a surface coat with adherence and/or viscous properties different than those of other fluids. In addition, γ-decrease approached to, but probably did not fully reach, a final value. Thus, we speculate that γ-equilibrium of spontaneously transforming LBPs is <30 mN/m, corresponding with the results obtained with a comparable source of native surfactant (13). Finally, all measurements converged at ∼30 mN/m (29.9, mean ± 1.02 SE), despite the considerable difference in the sedimentable fraction. We speculate that a slow reorganization of already surface-deposited material is taking place, resulting in a low γ independent on the initial rate of LBP-transformations. Indeed, between ∼20 and 60 min, the interface becomes increasingly covered by amorphous material interspersed with distinct structures. These in fact originated from aggregated LBPs, and were observed by fluorescence and reflection mode likewise (Fig. 5 f, inset). However, the development of these structures made single-particle counting difficult, so we restricted their measurements to within 0–15 min.

DISCUSSION

There is an abundance of methods measuring the γ of liquid-gas interfaces. However, in pulmonary physiology, the Wilhelmy surface balance (14), the pulsating bubble surfactometer (15), and the captive bubble technique (16,17) are among the most widely used, and contributed enormously to our present understanding of surfactant functions (18). In this article, we introduce a new implementation of the pendant-drop principle, which we call the inverted interface, and emphasize its use in specific areas of surfactant research and related fields. It is a sensitive, contactless, and noninvasive technique that operates at microscopic dimensions. The air-liquid interface is in a stationary equilibrium and remains within the microscopic field during the experimental protocols. This allows extended high-resolution imaging of the interfacial processes, which is not always feasible in systems using macroscopic surface areas, e.g., modified Langmuir troughs (19). Of particular importance is that LBPs reach the interface directly and rapidly by sedimentation. Thus, stirring is not a prerequisite as in other systems to minimize the mass transfer resistance in the case of random particle migrations. Finally, the LBP requirement to perform γ-measurements is actually, by orders-of-magnitude, lower than that of other systems.

Except for contact-angle measurements, only a few optically based methods were used to determine the curvature of a fluid meniscus directly, either from pendant drops (seldomly used in pulmonary surfactant research, e.g., by Park et al., Ref. 20), from fluids within a micropipette (21), by measuring the different angles at which two spaced light beams are reflected (patent GB 1447262), or by measuring the intensity of transmitted or reflected light in microtiter plates (22). These methods, however, are not suited to analyze structural dynamics at an air-liquid interface. An implementation of microscopy on very small air-liquid interfaces was reported earlier (23). When combined with atomic force microscopy (24), such a system could allow us to simultaneously determine surface tensions. However, this method is not yet established. In comparison, the method described here measures the configuration of a liquid surface upon epi-illumination, assessing the overall intensity of the back-reflected light by simple microscopy. The air-liquid interface is stably formed within a small (300-μm Ø) aperture at the bottom of a cone, exposing an area of only 0.07 mm² to direct optical measurements by any kind of inverted microscope. At a given fluid volume within the cone, the radius of curvature of the fluid meniscus is related to its γ. Assuming perfect aperture circularity and aperture wetting, interfacial physics predict a nearly spherical and minimally domed surface area at a high liquid surface tension, with decreasing radius of curvature when γ is reduced. In search for a least slow and invasive method to determine this, we analyzed the light reflection at the liquid interface. Applications of fluids with defined γ revealed a nonlinear dependency of apparent surface curvature on γ, which, however, is predicted by our physical model and could be used as a calibration curve.

However, our system has limitations:

1. It does not allow us to dynamically compress and expand the surface as have others (25), and experiments are confined to determine a static surface tension only (= γ-adsorption; see Ref. 11).

2. At very low surface tensions (∼35 mN/m), pure liquids are not retained in the aperture but leak through. In principle, measurements in a low γ-range would require smaller apertures than we used here. However, 300-μm Ø was still very suited for our purposes, in particular because surfactant-containing fluids behave differently and were kept in place despite a γ < 30 mN/m (Fig. 3 g).

3. In a high γ-range (>70 mN/m), the system is still precise (Fig. 3, f and g), but we faced an increasing loss in accuracy. Solutions with different composition (e.g., salt-containing solutions) but almost the same tension, showed different characteristics with respect to capillary effects and/or contact angles. The resulting imperfect wetting of the aperture plane (tested directly by analyzing the projection of grids onto the liquid surface; not shown) interfered with the radius-dependent light back-reflection and lead to miscalculation of our fitting parameters. It is clear that perfect wetting of the aperture plane is critical, but cannot be forced by direct manipulation. Therefore, we had to accept that our system is not suitable to give reliable values above that of water, which was out of interest in any case for the present investigation.

4. We noted that pure solutions, e.g., methanol (Fig. 3 f), or Triton X-100 (not shown), may not stabilize immediately. The time required for that stabilization has to be taken into account when fast dynamic processes have to be investigated.

5. Since visualization of surface curvature is critically depending on the specificity of the optical instruments used, an empirical calibration will always be necessary.

6. Surface structures can disturb the images obtained in the reflection mode and interfere with line-scan analysis (Fig. 5 f).

When the system was tested with isolated LBPs, we found that their incorporation at the interface is paralleled by a decrease in γ, reaching values close to ∼35 mN/m after a 15-min protocol, and declined further to <30 mN/m after 1 h. These values are in the range of other studies using a comparable source of pulmonary surfactant (isolated lamellar bodies; see Ref. 13), as well as common surfactant preparations studied under static conditions (25). Therefore, we conclude that LBPs released by stimulated cells contain surface-active material able to decrease γ to within a physiological range. We further conclude that our method yields appropriate results with respect to surface tension determinations. For this reason, we dispensed with verifying the obtained γ-values by established methods. These measurements would have imposed a considerable manipulation (e.g., expansion and compression) of the spontaneously created interface without the possibility for us to relate γ to the number of transformed LBPs. We also assume that, in our system, γ could change on the upper and lower surfaces independently, since the LBPs sediment in one direction only. Finally, and importantly, we do not know a method sensitive enough to measure the interfacial effects of the small amounts of LBPs released by cultured cells.

The minimum equilibrium surface tension of fluid phospholipid monolayers is ∼25 mN/m (26), and this value is generally considered as the minimum γ-equilibrium of a well-functioning pulmonary surfactant in the absence of area compression (27). Important determinants thereof are the chemical composition, temperature, the amount of surface-active material, and probably its structural organization at and beneath the air-liquid interface. The slightly higher value (∼30 mN/m) as found by our investigation cannot be fully explained on the basis of the present data because it likely reflects a combination of more than one of these parameters: An experimental temperature (25°C) lower than used elsewhere; an extremely low and probably limiting amount of phospholipids and surfactant-associated proteins; and a slow decline in γ, which may reflect an ongoing adsorption/reorganization process that is not finally terminated after completion of our measurements. Further investigations will certainly be necessary to address these questions in more detail.

The fraction of transforming LBPs with respect to all LBPs reaching the interface decreased with time and almost ceased when γ approached ∼35 mN/m (Fig. 5 c). This denotes that LBPs arriving at reduced γ preferably accumulate at the interface without apparent structural change. This is in agreement with previous findings that LBPs do not transform when γ was kept <40 mN/m (7). It has been suggested that a high γ is the direct force causing LBP disintegration, which comes to a final halt when cohesive and tensile forces acting on these particles come to equilibrium. In line with this assumption, the present data (Fig. 5 c) show that LBP transformations commenced and leveled off with a similar time course than the change in γ. However, it is not readily intelligible why this process should be progressive (decreasing rates) instead of abrupt (complete transformation of all particles until γ is reduced). In addition, the different behavior of LBPs might also be due to differences in their phospholipid/protein compositions and/or to variation in their internal structure, as well as to their orientation when they contact the air-liquid interface. In light of their known pleomorphic nature (28), this is a likely explanation. Alternatively, the composition of a surface coat is inhomogeneous. In that case, LBPs could either transform or stably associate, depending on the particular phase condition prevailing at the specific site of contact. To this end, structure/function relations of LBPs, though highly desired, are still far from being understood.

The kinetics of surface tension decay was related to the cumulative amount of transformed LBPs (Fig. 5 d). This is consistent with the view that the process of LBP transformation finally delivers surface-active components which adsorb into the air-liquid interface. The logarithmic dependency of Δγ/Δt on adsorption is in accordance with reports using surfactant preparations of different origin (29). In our experiments, it also shows that late arriving and adsorbing LBPs contribute, to a lesser extent, to γ-reduction than LBPs contacting a still clean interface (Fig. 5, d and e). Three reasons appear plausible to explain this observation:

1. Heavier LBPs, approaching the interface earlier, could have higher γ-reducing abilities than lighter particles contacting the interface later. This is in agreement with earlier findings that LBPs have different sedimentation properties and surface activities (30).

2. Earlier transforming LBPs could modify the interface and thereby decrease the ability of late LBPs to reduce γ despite their transformation.

3. A soluble surface-seeking material other than LBPs is present in our samples. This is not unlikely, since, according to our findings, LBPs disintegrate whenever an interface (or solid surface) is present (7), probably releasing fluid-phase components during sampling and preparation.

This obvious contribution is seen by a lack of clear correlation to γ-reduction among the three experiments within the first ∼2 min of measurements (corresponding to ∼20 LBP transformations, or γ-decrease to ∼45 mN/m; Fig. 5 e). However, after that initial phase, the relation between LBP transformation and γ became linear, indicating that γ-reduction is most likely a direct consequence of regulated LBP transformation and/or conversion into other surface structures.

The present investigation is the first to demonstrate that γ-reduction is related to the conversion of single freshly released LBPs at an air-water interface. Simultaneous measurements of γ and LBP conversion were possible with a newly developed inverted interface, allowing the direct visual analysis of both parameters in a noninvasive way. An intriguing outcome of this study is that a fraction of LBPs adsorb immediately, whereas another fraction remain surface-associated. It remains to be determined which mechanisms are responsible for further degradation and/or reorganization of LBPs into other functional units.