Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2005 May 20;89(2):1389–1397. doi: 10.1529/biophysj.105.060723

Computational Model for Cell Migration in Three-Dimensional Matrices

Muhammad H Zaman *,†, Roger D Kamm †,‡, Paul Matsudaira *,†,§, Douglas A Lauffenburger †,§
PMCID: PMC1366623  PMID: 15908579

Abstract

Although computational models for cell migration on two-dimensional (2D) substrata have described how various molecular and cellular properties and physiochemical processes are integrated to accomplish cell locomotion, the same issues, along with certain new ones, might contribute differently to a model for migration within three-dimensional (3D) matrices. To address this more complicated situation, we have developed a computational model for cell migration in 3D matrices using a force-based dynamics approach. This model determines an overall locomotion velocity vector, comprising speed and direction, for individual cells based on internally generated forces transmitted into external traction forces and considering a timescale during which multiple attachment and detachment events are integrated. Key parameters characterize cell and matrix properties, including cell/matrix adhesion and mechanical and steric properties of the matrix; critical underlying molecular properties are incorporated explicitly or implicitly. Model predictions agree well with experimental results for the limiting case of migration on 2D substrata as well as with recent experiments in 3D natural tissues and synthetic gels. Certain predicted features such as biphasic behavior of speed with density of matrix ligands for 3D migration are qualitatively similar to their 2D counterparts, but new effects generally absent in 2D systems, such as effects due to matrix sterics and mechanics, are now predicted to arise in many 3D situations. As one particular sample manifestation of these effects, the optimal levels of cell receptor expression and matrix ligand density yielding maximal migration are dependent on matrix mechanical compliance.

INTRODUCTION

Cell migration plays a critical role in many physiological systems. Among many diverse examples that could be cited, migration of fibroblasts and vascular endothelial cells is essential for wound healing (1), metastatic tumor cells migrate from the tumor mass to the circulatory system (2), and active cell motility is crucial for embryonic development (3). An accurate understanding of cell migration and motility requires an understanding of not only of the chemical and biological basis for the migration of cells at the cellular or tissue level, but also of the mechanical basis and force generation in cells responsible for cell migration (4–9). However, most of our current knowledge of cell motility and migration comes from in vitro studies carried out on two-dimensional (2D) substrates (10). These studies have helped us understand the very basic mechanisms by which cells migrate, interact with the substrate, and change their speed or direction over time on 2D surfaces.

When surrounded by an extracellular matrix (ECM), the cells experience a different environment than when they are attached to a 2D surface (11,12). In vitro studies carried out in 2D may induce an artificial apical-based cell polarity that may not exist in vivo (13). The dense fibers in a 3D matrices can block any movement in the absence of matrix-degrading enzymes (matrix metalloproteinases, or MMPs). In addition, the ability of the cells to move in a 3D ECM will also depend upon the viscosity and stiffness of the ECM (7,14). Therefore, to fully understand the underlying mechanisms by which cells migrate in vivo, it is necessary to study the movement of cells in 3D environments. Indeed, literature describing experimental studies in 3D matrices has begun to grow substantially in the past few years (5,10,11,15–18).

In addition to state-of-the art experiments, mathematical models and theoretical studies have also improved our understanding of cell migration behavior (19–23). Models and computational predictions are useful as they not only connect the experimental results to first principles, but also describe the behavior of the systems as a function of a single variable, a scenario often unattainable with the current experimental techniques. In addition, mathematical models are useful in identifying certain key parameters that play a central role in defining the overall behavior of the system, and thus lead to new and more informative experiments.

In this article, we present a model that makes qualitative predictions about the migration of cells in 3D matrices. The model describes a new approach to cell migration by addressing the motility in discrete time steps rather than describing the motility as a continuous process. Our model takes into account the basic aspects of cell migration, namely force generation, polarity, and adhesion of the protein ligands in the ECM (such as fibronectin and laminin) to integrins (receptors on the cell surface). These aspects are expressed during the three major phases in cell migration (24): cell protrusion and attachment of the leading edge, cell contraction by myosin motors inserting between actin bundles, and detachment of the adhesions at the trailing edge of the cell. Our model takes into account the protrusion phase as well as the forces responsible for traction and contraction. Small protrusions of the leading edge that are often balanced by corresponding retractions result in a very small protrusive force, and hence do not result in significant motility (25,26). Our model uses a time-averaged protrusive force that is strong enough to result in migration. Our approach predicts the time-averaged behavior of individual cells in a protrusion, adhesion, and detachment cycle and is not designed to calculate the short-timescale dynamics of the leading edge (27). The model also incorporates parameters such as the mechanical stiffness of the ECM collagen fibers, viscosity of the ECM, and the forces due to attachment of the cell to the matrix.

Based on these factors, the model predicts central features of cell migration as characterized in terms of experimentally measurable quantities such as velocity of the cell. These predictions provide a framework to experimentalists for designing experiments that will elucidate the key aspects of cell migration in 3D matrices.

MODEL FORMULATION

The model is designed to predict cell migration as a function of time by calculating the forces acting on the centroid at each time step (Δt). Our approach is designed to track the key parameters required for migration at individual time steps. Furthermore, averaging over several runs and a large number of time steps represents the averaged behavior of many cells. The model focuses on the basic underlying processes involved in cell locomotion, such as asymmetry of the cell, traction, and force generation. In addition, we address aspects such as the stiffness of the matrix and the effect of ligand density on the overall migration rate. Thus, the model is neither cell-centric nor matrix-centric, but simultaneously focuses on both the cell and the matrix as the cell moves in 3D.

The total force, represented as a vector, is used to calculate the velocity and position of the cell at each point, assuming a net force balance. The time step (Δt) in our simulation is equal to the time taken by the leading edge to produce stable protrusions, adhere to the ligands in the matrix, and move in the direction of protrusion. For our simulations, each time step is equal to 600s, which is approximately the time required to complete one migration cycle in many fibroblasts, epithelial cells, etc. As parts of protrusion, adhesion, and traction often overlap, it would be artificial to assign individual timescales for protrusion, adhesion, traction, and detachment. Our approach therefore assumes that the time step is large enough for the entire cycle of protrusions, adhesion, and detachment of the rear end to take place. Since the time step used in our simulations is much longer than the timescale of dynamics at the leading edge, events such as periodic lamellopodial contractions or the formation of actin waves (27) cannot be addressed by our model.

The total force is divided into traction forces (Ftrac) due to the traction of the front and the rear of the cell, forces due to cell protrusion in the 3D matrix, and the resistive forces resulting from the viscous drag experienced by the cell due to the viscoelastic nature of the ECM.

The traction force comprises at least two opposing components, namely Ftrac-f and Ftrac-b, to account for the traction force in the forward and the backward direction.

The two components of traction force can be mathematically represented as

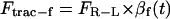graphic file with name M1.gif (1a)

and

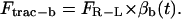graphic file with name M2.gif (1b)

Thus, the traction force at the front and the rear depend upon the force per ligand-receptor complex (FR-L), which is a function of the Young's modulus, Emod, of the surrounding medium. The force per ligand-receptor complex is assumed to vary directly with Emod up to a certain value of Emod (1 Mpa for our purposes) and then saturates with further increase in Emod. Thus,

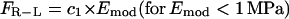graphic file with name M3.gif (2a)

and

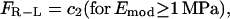graphic file with name M4.gif (2b)

where c1 is a constant of proportionality (units of area) and c2 is the saturation value of the force for Emod ≥ 1 MPa. In other words, for a system where Emod approaches infinity, force per receptor-ligand complex would only approach the saturation value. In our simulation, we assume the saturation force per ligand-receptor complex to be equal to 1 pN (19). To account for the possibility of different numbers of receptors at the front and the back of the cell, and/or difference in binding strength of these receptors to the ligand, we introduce β(t), which we term “adhesivity”, a dimensionless parameter measuring the binding strength of the receptors to the ligands in the ECM. βf is defined as

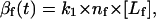graphic file with name M5.gif (3a)

where nf is the total number of available receptors on the front part of the cell, [Lf] is the concentration of the ligands at the leading edge of the cell in the ECM (in M), and k1 is the binding constant for the binding of integrins at the front end of the cell to the ligands in the ECM (in M−1). Similarly,

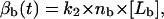graphic file with name M6.gif (3b)

where nb is the total number of available receptors on the rear part of the cell, and k2 is the binding constant for the binding of integrins at the rear end of the cell to the ligands in the ECM (in M−1). For our model we assume that as the cell polarizes, integrins are distributed asymmetrically on the cell surface, i.e., nf > nb. Also, k1 may be ≥k2 depending upon the cell type. For our model we assume k1 = k2.

The ligand density in the extracellular matrix can be altered by matrix metalloproteinases produced by the migrating cells or other tissue-resident cells. At the same time, all these cell types can also synthesize new matrix components with associated adhesion receptor ligands. The dynamics of these competing processes may be important for modulation of migration through the matrix. In this first incarnation of a 3D model, we will neglect these processes (or, equivalently for this purpose, assume that they are in steady-state balance). We are intending to relax this simplification in future versions of the model. Additionally, we will assume here that the ligand density is spatially uniform throughout the matrix; this restriction can likewise be relaxed, to permit analysis of haptotactic migration in future studies.

The model addresses the relationship between steric resistance and adhesivity for a migrating cell. Our approach assumes that ligand density is proportional to steric hindrance, and that at very high ligand concentration the matrix is too dense for the cells to migrate.

The final category of forces is comprised of a protrusion force, namely Fprotrusion, and the resistive force, Fdrag, arising from viscous resistance to movement. Proportional to the cell movement speed, the drag force is given by

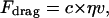graphic file with name M7.gif (4)

where η is the effective viscosity of the viscoelastic medium (considered a constant throughout the matrix) and v is the velocity. The constant c depends on the shape of the cell; for a spherical cell in an infinitely viscous medium, c = 6π × cell radius. In a Maxwell solid, the force necessary to deform the matrix would depend on the rate of deformation and, hence, the velocity. Although this represents a crude approximation to the much more complicated reality, we introduce it here simply to imply a velocity-dependent opposing force associated with the viscoelastic character of the surrounding matrix. The viscosity, η, therefore is representative of the viscous resistance of the matrix material. In the ideal case of a spherical cell moving through a Newtonian, viscous medium, c = 6π × cell radius. It is of interest to note that if the cell were migrating through a pure elastic medium, the force required to deform the matrix as the cell migrates would be independent of velocity. Hence, a more realistic representation of the opposing force would be the summation of two contributions, one that depends on cell velocity and one independent of it.

Fprotrusion arises from actin polymerization and cell/matrix attachments at the new site of lamellipod protrusion. This force is distinct from the cytoskeletal contractile force transmitted to the matrix. This force is generated by actin polymerization and the order of magnitude estimate of Fprotrusion is determined from previous experimental studies (28,29). The direction of Fprotrusion is chosen randomly at each time step. The protrusion force in our model is, in fact, a time-averaged value of positive protrusive forces over Δt. In other words, small unstable protrusions that are often balanced by corresponding retractions are not taken into account (25–27). Only stable protrusions that result in attachment of the leading edge to the matrix, with no corresponding retractions during the time interval Δt, are considered. Thus, our model incorporates protrusions above a certain threshold, and very small and reversible protrusions that do not lead to migration are ignored.

The total force acting on the cell is therefore given by

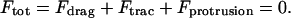graphic file with name M8.gif (5)

Our model uses Eq. 5 to calculate the cell velocity within its movement enviroment for each simulation cycle, or time step. In each cycle, the cell protrudes in a particular direction with Fprotrusion, makes attachments based upon the k1, k2, nf, and nb, and experiences resistive forces due to viscoelastic resistance. The cell/substratum traction force is proportional to Emod of the ECM. Asymmetric polarization of a cell permits the number of receptors available at the front and the back, and/or their strength of attachment to matrix ligands, to be disparate, which can result in a difference between the disruption force per receptor-ligand bond in the front and the disruption force per bond at the rear end. This difference in the load per bond can yield preferential bond breakage at the rear, and as the bonds at the trailing edge detach one by one, the load per bond would increase further till all bonds break and the rear end detaches. Our model does not explicitly follow the kinetics of the bond disruption, but instead integrates these kinds of subcellular events through each time step. Thus, we assume that if and when a threshold of asymmetry exists in the disparity between the disruption force per bond for any given time step, then detachment at the rear will occur in that cycle. If this threshold is not reached for a given time step, so that the disparity between disruption force per bond at the front and the rear is sufficiently small, then rear detachment does not occur during that cycle and hence there is no net translocation in that time step. The net velocity of movement for a time step is calculated using Eq. 5. Our model assumes a sufficiently large time step, during which the cell extends a lamellipodium, experiences a force due to the contraction of the actin network, and may (or may not) detach its rear end.

Computations are performed using Mathematica 4.1 software (Wolfram Research, Champaign, IL), and the total force on the cell is calculated at each time step. Ten thousand simulations of 300 time steps each (to simulate ∼48 h of migration) were carried out on an Intel PIV cluster. The initial location of the cell in the ECM and the protrusion vectors were determined using a random number generator. Due to the nature of the equations governing our model, we did not experience any singularities and although the simulations showed variance at short timescales (first 10–20 time steps) over longer timescales the simulations showed convergence.

Model parameter estimates are offered in Table 1. The model is designed to make qualitative predictions for different experimentally measurable parameters and is not meant to make precisely quantitative predictions at this point.

TABLE 1.

Order of magnitude estimate of the parameters used in the model

[M] 10−10 M (33,34)
k1= k2 108 M−1 (35,36)
[L0] 10−5 M (37)
N 105 receptors/cell (35,36,38)
Young's modulus of collagen 100 kPa (39)
Cell length 50 μm (40)
Cell width 10 μm (40)
Viscosity (η) 103 poise (35,36,38)
Ligand density 103 mol/μm3 (38)
Open in a new tab

RESULTS

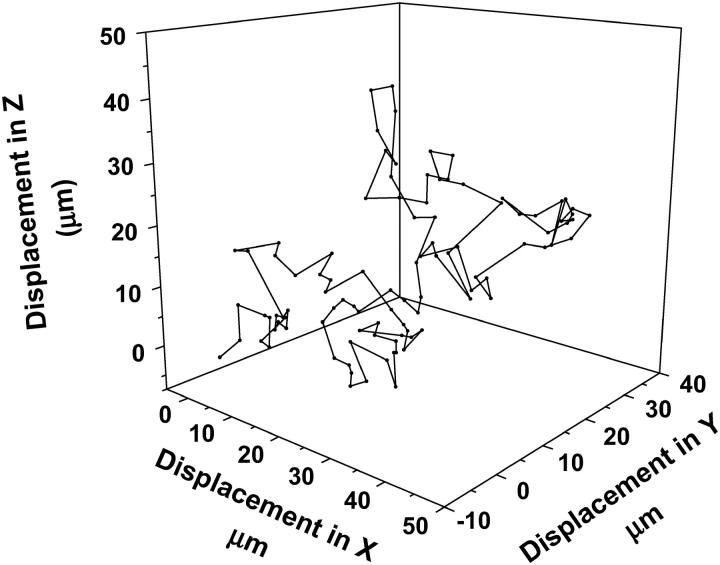
The computational model developed above predicts that the cells display a random walklike behavior as they move through a 3D matrix. In Fig. 1, the raw displacement data for cells moving in 3D is plotted for each time step. This behavior is similar to the observed and predicted behavior of cell migration in 2D and 3D matrices. (5,30).

FIGURE 1.

FIGURE 1

Open in a new tab

Random walk in 3D. The model predicts that the migration of cells in a three-dimensional matrix is similar to a random walk in three dimensions. The raw (displacement) data for a cell moving in three dimensions is shown in the figure.

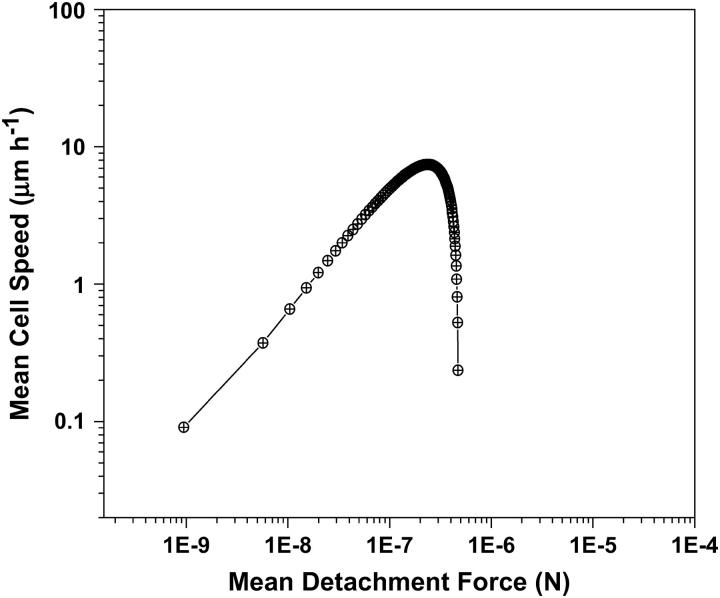
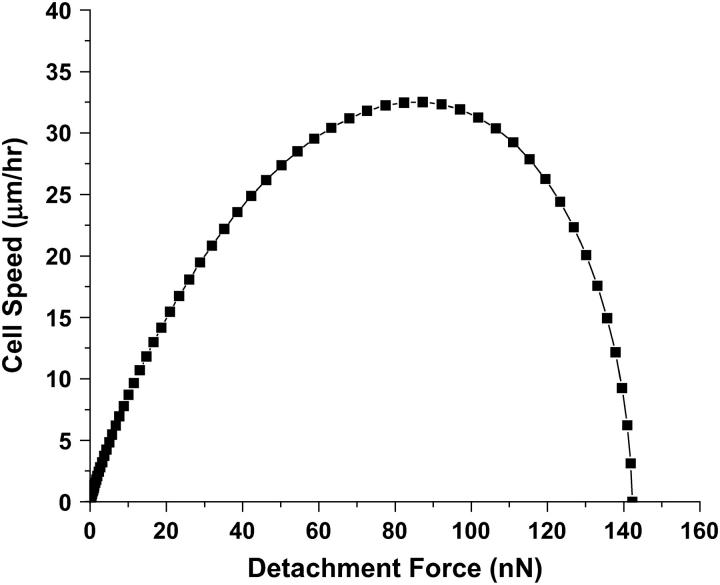
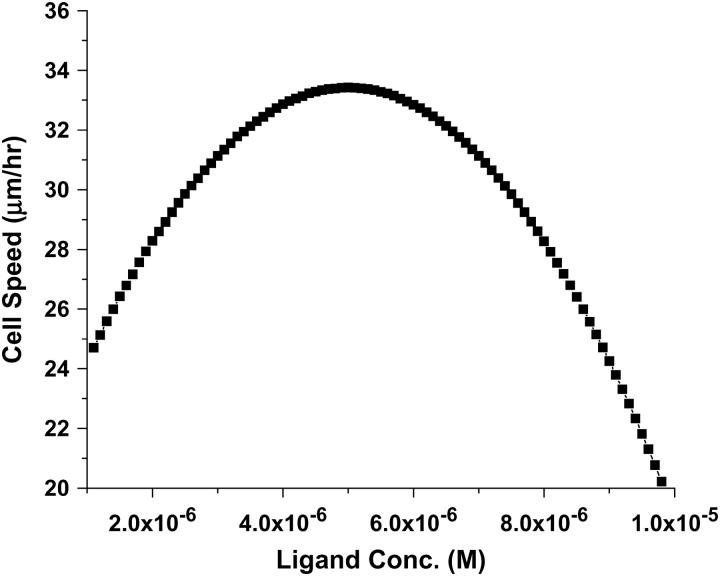
To test the accuracy of our model, we compared predictions of our new computational model for cell migration within 3D matrices against earlier available experimental data for migration on 2D substrata as a simple limiting case. Here, cell migration speed is determined as a function of ligand concentration on the surface (over which the cell crawls) or a function of mean detachment force (the traction force at the rear end of the cell) (31,32). We compare the results with the available data for the movement of cells on a flat surface by including the receptor matrix interactions only in x and y dimensions in our model. We also ignore the steric resistance of the matrix that is negligible in 2D migration experiments. In the 2D case, there was no matrix resistance and a uniform ligand density. The predicted results for 2D surfaces are shown in Fig. 2. The model makes a fairly accurate prediction in capturing the overall features of the experimental result. The biphasic behavior, first postulated by DiMilla et al. (19) and later confirmed experimentally (32), is qualitatively captured by this model. At low values of mean detachment force, there is little difference in the forward and rear traction forces, which result in smaller velocities. Very high detachment forces correspond to very high adhesivity, therefore blocking any internal contraction of the cell. This results in negligible movement on the 2D surface.

FIGURE 2.

FIGURE 2

Open in a new tab

Force-velocity curves for cells on a 2D substrate. Results are obtained using a 2D version of the model presented in text, ignoring steric resistance and assuming receptor-ligand interaction on a flat 2D surface. The value for βf is varied between 0 and 1 and the magnitude of Fprotrusion is varied between 100 pN and 100 μN (28,29). The value of nf = 0.9 × N. This behavior of cell speed as a function of mean detachment force is very similar to results obtained through experiments of cell migration on 2D surfaces (32).

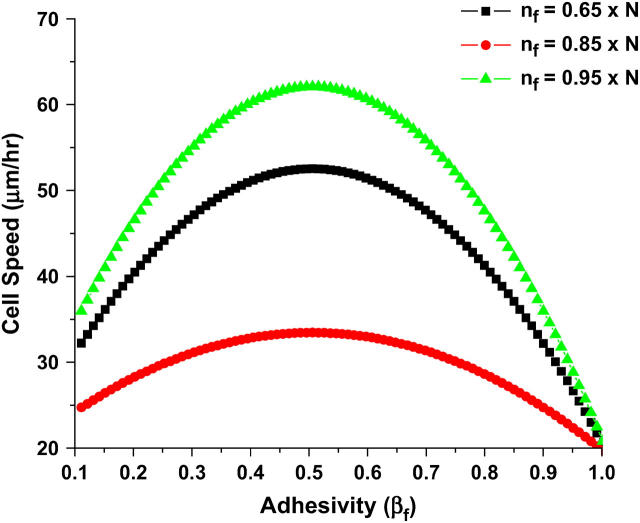
In a 3D ECM, cell speed as a function of adhesivity at the front of the cell, βf (Fig. 3) is predicted to display a biphasic behavior. This more complicated model includes the presence of a third dimension in the forces acting on the cell and includes a steric resistance to migration as well as random attachment of the cell to the 3D matrix.

FIGURE 3.

FIGURE 3

Open in a new tab

Cell speed as a function of receptor-ligand adhesivity at the front of the cell. The biphasic behavior suggests that at extremes of adhesivity the cell shows very little motility. The maximum speed is obtained at an intermediate adhesivity and increases with the increase in the degree of asymmetry of the cell. The number of receptors is the same as given in Table 1. The value of βf is normalized so that the maximum adhesivity for the parameters listed in Table 1 is 1. The figure is a summation over many individual simulations, and each point represents the averaged behavior in an ensemble of simulations with a given value of βf.

Low adhesivity corresponds to either a very small number of ligands present in the cell environment or a poor ligand-receptor interaction. The resulting traction forces are therefore low and consequently result in negligible velocities. On the other hand, at high adhesivity, steric resistance of the matrix obstructs the movement of the cell. Similar to its 2D counterpart, the maximum velocity is also observed when the ratio nb/nf (ψ)→0. Thus, maximum velocity is observed for cells with the highest degree of asymmetry.

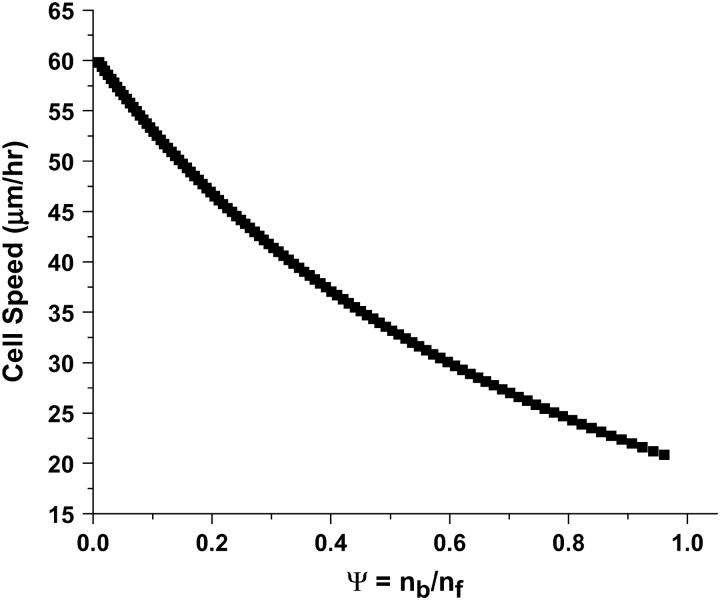
The effect of asymmetry on the overall speed of the cell is illustrated in Fig. 4, where ψ is plotted against cell speed for fixed values of adhesivity and ligand density.

FIGURE 4.

FIGURE 4

Open in a new tab

Cell speed as a function of asymmetry of the cell. The speed of the cell decreases as ψ increases. The ligand density used is equal to the one reported in Table 1.

The net detachment force is responsible for the net movement of the cell. Fig. 5 shows the cell speed as a function of the net detachment force. A biphasic behavior, similar to that of its 2D counterpart, is observed. At low detachment force, the cell doesn't move due to too much adhesion and steric resistance, whereas at very high detachment force, not enough ligands are present for the cell receptors to bind. The maximum velocity is obtained when ψ→0 (data not shown).

FIGURE 5.

FIGURE 5

Open in a new tab

Cell speed as a function of mean detachment force. A biphasic relationship suggests that no net cell migration is observed when either there is no protrusion, or the very small individual protrusions are balanced by retractions, such that the time-averaged protrusive force is very small, and the cell is unable to move due to very strong bonds at the front and the rear of the cell.

The number of ligands available for the cell to bind affects the overall velocity of the cell. As the number of ligands increases from zero to some finite value, the cell starts to move; however, a maximum value [L] implies maximum adhesivity and a biophysical hindrance to cell migration. This feature of cell motility is shown in Fig. 6, where the cell speed is plotted as a function of [L], the total number of available ligands in ECM.

FIGURE 6.

FIGURE 6

Open in a new tab

Cell speed as a function of the number of available ligands. The cell speed varies with the number of available ligands, first increasing with an increase in the total number of available ligands and then decreasing as further increase in the number corresponds to steric hindrance to the cell movement.

The cell speed varies as a function of the number of available receptors (which in turn affects the adhesivity), ligand density, and matrix properties such as matrix mechanical properties and matrix stiffness. Fig. 7 A shows a 3D plot where the cell speed is plotted simultaneously as a function of matrix stiffness and number of available receptors. Although a high receptor number results in high speeds, change in matrix stiffness results in a biphasic behavior in speed. Lower values of stiffness correspond to low traction forces and low net speeds, whereas at higher stiffness the cells generate higher traction and are unable to detach successfully and the mean detachment forces are low. Similarly, Fig. 7 B shows a 3D plot where the cell speed is plotted simultaneously as a function of matrix stiffness and matrix ligand density. Similar to Fig. 7 A, the highest speeds correspond to intermediate matrix stiffness, but unlike Fig. 7 A, now the highest speeds correspond to intermediate ligand density (as opposed to high receptor number in Fig. 7 A). This is because very high ligand densities correspond to higher steric obstructions. This result is also in agreement with experimental observations, as in the case of many biological substrates (e.g., matrigel and collagen I gels) where high ligand density corresponds to increased steric resistance and results in low overall migration. These plots also underline the complexity of migration where multiple factors affect the overall migration behavior, and varying one factor (such as matrix stiffness) also affects other variables such as sterics, traction forces, etc.

FIGURE 7.

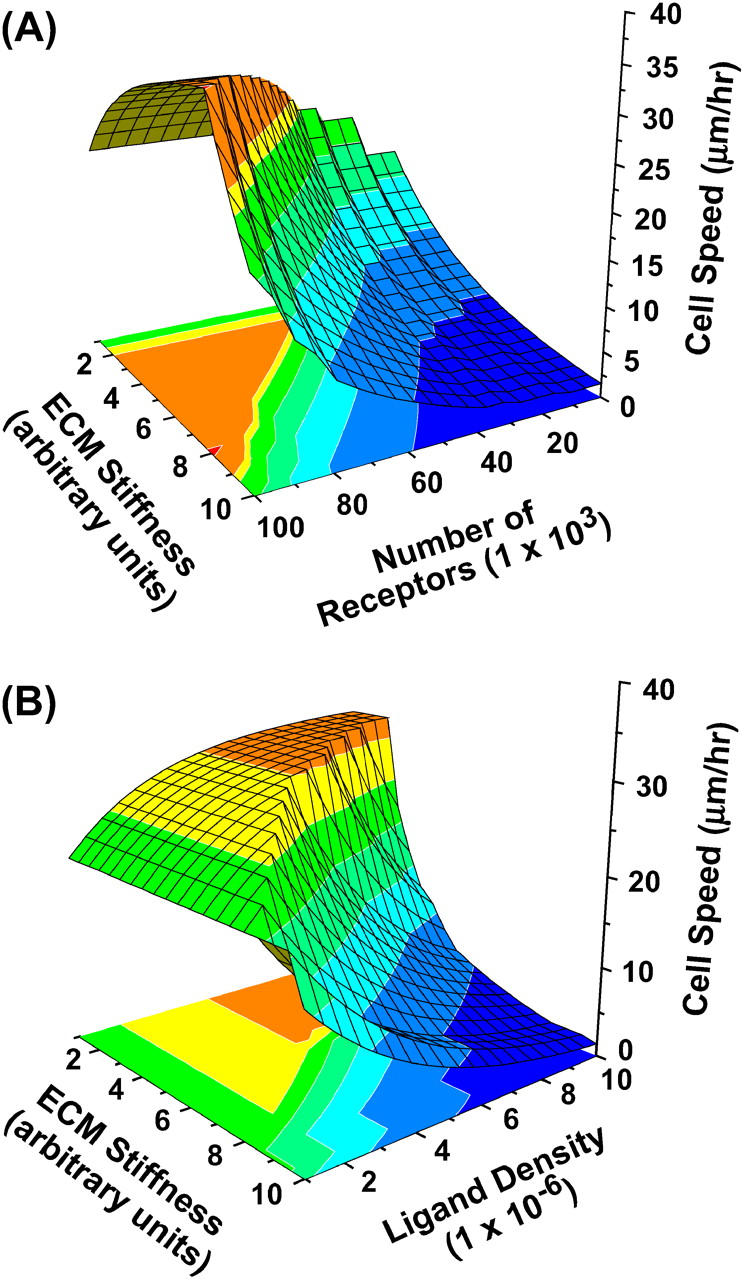
FIGURE 7

Open in a new tab

3D plot of cell speed as a function of matrix stiffness, ligand density, and available receptors. (A) The cell speed is plotted simultaneously as a function of matrix stiffness (varying by one order of magnitude in arbitrary units) and number of available receptors (varying by two orders of magnitude). The highest speed occurs at maximum receptors and intermediate stiffness. Lower stiffness values correspond to lower traction and lower speeds, whereas at very high stiffness the traction forces are high and the cells are unable to detach. (B) The cell speed is plotted simultaneously as a function of matrix stiffness and number of available ligands. The maximum speed occurs at intermediate stiffness and intermediate ligand concentration. Higher ligand concentrations correspond to steric resistance, whereas very low ligand concentrations correspond to negligible traction.

DISCUSSION

We have described a new computational model to address the migration of cells in 3D matrices. Our approach is based on calculation of total force on the centroid at discrete time steps. This approach is fundamentally different from the continuum models describing the migration of cells on 2D surfaces as a continuous process. This approach thus allows us to monitor the migration of the cell at each individual time point. Our model incorporates the stable protrusions of the leading edge, biophysical resistance of the matrix, and the stiffness of the fibers in the ECM. Thus, our model focuses on both the cell and the matrix simultaneously and presents a balance between cell-centric and matrix-centered approaches.

We predict a biphasic behavior of cell speed with adhesivity in 3D matrices, similar to the observed and predicted behaviors in 2D substrates. The biphasic behavior suggests that maximum speed is obtained at intermediate values of adhesivity, and that at extreme values the cells show little or no motility. A bimodal behavior is also seen for cell migration velocity as a function of cell traction. We also predict that the cell speed increases with an increase in the stiffness of the fibers in the ECM. The overall speed is a function of the degree of asymmetry existing between the lamellopod (front of the cell) and the uropod (rear of the cell), and increases as the asymmetry increases. The model predicts that cell speed is also sensitive to the number of ligands in the ECM. The results described above are not meant to make a quantitative prediction about cell speed as a function of different parameters, but are meant to predict the qualitative behavior of cells migrating in 3D matrices. Nonetheless, since most of the parameter values used in our model (Table 1) are taken from experiments conducted on fibroblasts, our predicted values will have a stronger resemblance with 3D experiments on fibroblasts than with experiments on faster moving cells (e.g., macrophages).

A comparison of the results predicted by our model with the experimentally determined 2D motility results shows a great deal of similarity as well as a few differences. The biphasic behavior present in essentially all the velocity plots is similar to the predicted and experimentally determined results of cell motility on 2D substrates. The increase in the overall velocity with increase in the asymmetry of the cell is also similar to the behavior of the cell on a flat surface. However, we believe that these similarities will be qualitative, and the overall velocity will be different for cells moving on a flat surface versus the cells moving through 3D matrices. The models of motility on 2D substrates do not take into account the biophysical resistance of the matrix. The nature of the ECM, adhesions in all three dimensions, and viscoelastic resistance to migration play a key role in the motility of the cell through 3D matrices. These factors not only increase or decrease the velocity by several orders of magnitude, but can also stop the cells from moving altogether.

Recently, several successful efforts have been made to understand the migration of cells in 3D matrices. These efforts have focused on understanding the role of MMPs in degrading the matrix, the use of microfabrication technology to understand the effect of adhesion, and the nature of the 3D networks and the use of gel compaction experiments to study the effect of traction on migration of fibroblasts.

Lutolf et al. used synthetic hydrogels to mimic the native ECM and observed that invasion of these 3D networks depended upon the degradation kinetics of MMPs (17). They also demonstrated that the cell invasion rate depended upon the concentration of ligands in their engineered ECM. They observed a biphasic behavior for cell invasion rate as a function of the ligand concentration in the ECM. Our prediction (Fig. 6) agrees with their finding as we observe that the cell motility shows a bimodal nature with an increase in the ligand concentration. A higher number of ligands corresponds to a dense matrix that resists the movement of the cell, whereas fewer ligands results in lack of adhesion required for traction and movement.

In microfabricated devices, Saltzman and co-workers demonstrated that the motility of the neutrophils depended upon cell adhesivity in 3D networks (18). They observed that migration speed on strongly adhesive surfaces such as unpatterned quartz was much slower (∼10-fold) than 2D surfaces with intermediate adhesivity (such as collagen-coated quartz surfaces). The authors noticed a biphasic behavior of cell motility as a function of adhesivity in 3D gels and networks. Our results show good agreement with these findings, as the negligible velocities are predicted for very high or very low adhesivity (Fig. 3).

In a recent study comprising experimental and theoretical findings, Shreiber et al. reported the migration and traction of a population of rat dermal fibroblasts and human foreskin fibroblasts within 3D biopolymer gels (5). They observed that rat dermal fibroblasts exhibited a biphasic relationship between traction and migration, a result similar to our findings in Fig. 5. For human foreskin fibroblasts, however, they could not conclude whether or not there was any biphasic relationship, probably due to the lack of any high-traction state of the cells. Fig. 5 shows the cell speed as a function of net detachment force, which depends upon adhesivity β in our model, reaches a maximum for intermediate values of the overall traction force, and at lower and high values of traction force approaches zero.

Although the exact magnitude of the cell speed in 3D networks and gels varies with the cell type, the overall behavior observed in these experiments shows very good agreement with the findings of our model.

Despite the ability of our model to capture the essential features of migration of cells in 3D matrices, and the qualitative agreement of our results with recent experimental findings, the model has several limitations. First, we can only model the ECM implicitly and cannot address the effect of cell movement on ECM. Our model also addresses only the ensemble-averaged operation of migrating cells as a function of matrix properties, and does not address the complex nanoscale molecular dynamics at the leading and trailing edges, occurring at much faster timescales; among these would be included the periodic extension and contraction of the leading edge that occurs at a very fast (∼10- to 20-s) timescale, as well as the disruption of individual receptor-ligand bonds at either end. Due to cell-level asymmetry in the number of receptors, and/or their strength of interaction with the cytoskeleton and ECM at the front and the back, the disruption force per bond at the front and rear can be disparate, which can lead to individual bonds breaking at the rear end, resulting in further increasing the load per bond until all bonds at the rear are ruptured. Our model assumes that if and when a threshold degree of this asymmetry is reached in any movement cycle, the attachments at the cell rear will break preferentially to permit net forward movement during that time step. Our model therefore implicitly integrates the dynamics of bond breakage across a time step instead of explicitly addressing a change in load per bond as the bonds break one by one, but the net effect comprises the same biophysical reasoning.

In addition, our model gives no information about the change in the shape of the cell as it moves. It has been recently reported that due to steric resistance of the matrix, the cell might change its morphology to move through the matrix and might be able to crawl through the ECM to a certain extent even when MMP activity is blocked (11,15). A detailed description of chemical basis of contraction due to the actin network is also not addressed in our model. Such aspects of cell migration are beyond the scope of our model at this moment. Additionally, our model combines the resistive forces due to the viscosity of the ECM and the elastic resistance force into one “viscoelastic” drag term. Though this assumption works well as a first approximation, however, a more sophisticated model will address these two resistive forces separately. Finally, we do not deal with dynamic changes in the ECM that are likely to arise from cell-mediated production and/or degradation. These changes could include loss of ligands for binding by cell adhesion receptors or gain of receptor-binding domains arising from exposure of cryptic sites, both potentially due to proteolytic enzyme activities. At the same time, protease activities may alter mechanical properties of the matrix, perhaps decreasing steric hindrance or increasing mechanical compliance. Taken together, the next outcome for cell migration of these protease-mediated effects may be complicated and time-varying. We are currently working on an extension of our model to incorporate these mechanisms. However, despite all these limitations and perhaps others as well, we believe that our model presents a novel and useful approach to addressing many questions related to cell migration in 3D matrices.

The model presented here is designed to predict cell migration as a function of experimentally measurable parameters. Experiments such as 3D tracking of fluorescent beads in ECM-like matrices will provide useful information about the cells' ability to pull on the ECM fibers. This can be achieved by measuring the displacement of individual beads due to cellular pulling on the matrix as a function of time. Tracking of cell centroid with varying collagen concentrations in ECM-like matrices will test the predicted biphasic behavior of cell migration as a function of the number of available ligands. Comparison of such results with cell migration trends in matrices comprised of stiffer (or floppier) fibers will shed some light on migration as a function of stiffness of the ECM. Alternatively, the changes in collagen structure can be induced thermally or chemically, and migration trends as a function of such changes will also provide useful information on cell motility as a function of parameters such as the Young's modulus in our model. Inhibition of MMPs in cells that do not change their morphology significantly will determine whether all motility is associated with the creation of holes in the ECM or whether the cells are able to move even in the absence of MMPs, as has been shown for certain types of cells (15). Migration of cells in several gels with a varying number of ligands available will provide information about the cell migration as a function of adhesivity β.

We hope that the information obtained using the computational model described here will be used to design experiments that measure the velocity of the cell as a function of the matrix stiffness, concentration of ligands in the matrix, and the rate of matrix proteolysis. Such nontrivial experiments will not only validate or disprove the predictions of models such as ours, but also will identify the key parameters responsible for cell motility in vivo.

Acknowledgments

We thank members of our group for numerous enlightening discussions. This work was supported by National Institutes of Health grant R01-GM 57418 (P.T.M.), National Science Foundation grant NIRT 0304128 (P.T.M.), the National Institute of General Medical Sciences Cell Migration Consortium Computational Modeling Initiative (D.A.L.), National Cancer Institute Integrative Cancer Biology Program (D.A.L.; grant No. 1-P50-CA112967-01), and National Institutes of Health grant P01-HL064858) (R.D.K.). M.H.Z. gratefully acknowledges the support of Sokol Foundation.

References

  • 1.Martin, P., and S. M. Parkhurst. 2004. Parallels between tissue repair and embryo morphogenesis. Development. 131:3021–3034. [DOI] [PubMed] [Google Scholar]
  • 2.Condeelis, J., and J. E. Segall. 2003. Intravital imaging of cell movement in tumours. Nat. Rev. Cancer. 3:921–930. [DOI] [PubMed] [Google Scholar]
  • 3.Knecht, A. K., and M. Bronner-Fraser. 2002. Induction of the neural crest: a multigene process. Nat. Rev. Genet. 3:453–461. [DOI] [PubMed] [Google Scholar]
  • 4.Dickinson, R. B., L. Caro, and D. L. Purich. 2004. Force generation by cytoskeletal filament end-tracking proteins. Biophys. J. 87:2838–2854. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Shreiber, D. I., V. H. Barocas, and R. T. Tranquillo. 2003. Temporal variations in cell migration and traction during fibroblast-mediated gel compaction. Biophys. J. 84:4102–4114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Galbraith, C. G., and M. P. Sheetz. 1999. Keratocytes pull with similar forces on their dorsal and ventral surfaces. J. Cell Biol. 147:1313–1324. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Munevar, S., Y. L. Wang, and M. Dembo. 2001. Distinct roles of frontal and rear cell-substrate adhesions in fibroblast migration. Mol. Biol. Cell. 12:3947–3954. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Wakatsuki, T., B. Schwab, N. C. Thompson, and E. L. Elson. 2001. Effects of cytochalasin D and latrunculin B on mechanical properties of cells. J. Cell Sci. 114:1025–1036. [DOI] [PubMed] [Google Scholar]
  • 9.Wakatsuki, T., M. S. Kolodney, G. I. Zahalak, and E. L. Elson. 2000. Cell mechanics studied by a reconstituted model tissue. Biophys. J. 79:2353–2368. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Cukierman, E., R. Pankov, D. R. Stevens, and K. M. Yamada. 2001. Taking cell-matrix adhesions to the third dimension. Science. 294:1708–1712. [DOI] [PubMed] [Google Scholar]
  • 11.Friedl, P., and E. B. Brocker. 2000. The biology of cell locomotion within three-dimensional extracellular matrix. Cell. Mol. Life Sci. 57:41–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Boudreau, N., and M. J. Bissell. 1998. Extracellular matrix signaling: integration of form and function in normal and malignant cells. Curr. Opin. Cell Biol. 10:640–646. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Klein, C. E., D. Dressel, T. Steinmayer, C. Mauch, B. Eckes, T. Krieg, R. B. Bankert, and L. Weber. 1991. Integrin α2β1 is upregulated in fibroblasts and highly aggressive melanoma cells in three-dimensional collagen lattices and mediates the reorganization of collagen I fibrils. J. Cell Biol. 115:1427–1436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Lo, C. M., H. B. Wang, M. Dembo, and Y. L. Wang. 2000. Cell movement is guided by the rigidity of the substrate. Biophys. J. 79:144–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Wolf, K., I. Mazo, H. Leung, K. Engelke, U. H. von Andrian, E. I. Deryugina, A. Y. Strongin, E. B. Brocker, and P. Friedl. 2003. Compensation mechanism in tumor cell migration: mesenchymal-amoeboid transition after blocking of pericellular proteolysis. J. Cell Biol. 160:267–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Cukierman, E., R. Pankov, and K. M. Yamada. 2002. Cell interactions with three-dimensional matrices. Curr. Opin. Cell Biol. 14:633–639. [DOI] [PubMed] [Google Scholar]
  • 17.Lutolf, M. P., J. L. Lauer-Fields, H. G. Schmoekel, A. T. Metters, F. E. Weber, G. B. Fields, and J. A. Hubbell. 2003. Synthetic matrix metalloproteinase-sensitive hydrogels for the conduction of tissue regeneration: engineering cell-invasion characteristics. Proc. Natl. Acad. Sci. USA. 100:5413–5418. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Tan, J., H. Shen, and W. M. Saltzman. 2001. Micron-scale positioning of features influences the rate of polymorphonuclear leukocyte migration. Biophys. J. 81:2569–2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.DiMilla, P. A., K. Barbee, and D. A. Lauffenburger. 1991. Mathematical model for the effects of adhesion and mechanics on cell migration speed. Biophys. J. 60:15–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Dickinson, R. B., and R. T. Tranquillo. 1993. A stochastic model for adhesion-mediated cell random motility and haptotaxis. J. Math. Biol. 31:563–600. [DOI] [PubMed] [Google Scholar]
  • 21.Tranquillo, R. T., and W. Alt. 1996. Stochastic model of receptor-mediated cytomechanics and dynamic morphology of leukocytes. J. Math. Biol. 34:361–412. [DOI] [PubMed] [Google Scholar]
  • 22.Gracheva, M. E., and H. G. Othmer. 2004. A continuum model of motility in ameboid cells. Bull. Math. Biol. 66:167–193. [DOI] [PubMed] [Google Scholar]
  • 23.Rubinstein, B., Jacobson, K. and Mogilner, A. 2005. Multiscale two-dimensional modeling of a motile simple-shaped cell. SIAM J. Multiscale Model. Simul. 3:413–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Lauffenberger, D. A., and A. F. Horwitz. 1996. Cell migration: a physically integrated molecular process. Cell. 84:359–369. [DOI] [PubMed] [Google Scholar]
  • 25.Krause, M., J. E. Bear, J. J. Loureiro, and F. B. Gertler. 2002. The Ena/VASP enigma. J. Cell Sci. 115:4721–4726. [DOI] [PubMed] [Google Scholar]
  • 26.Bear, J. E., T. M. Svitkina, M. Krause, D. A. Schafer, J. J. Loureiro, G. A. Strasser, I. V. Maly, O. Y. Chaga, J. A. Cooper, G. G. Borisy, and F. B. Gertler. 2002. Antagonism between Ena/VASP proteins and actin filament capping regulates fibroblast motility. Cell. 109:509–521. [DOI] [PubMed] [Google Scholar]
  • 27.Giannone, G., B. J. Dubin-Thaler, H. G. Dobereiner, N. Kieffer, A. R. Bresnick, and M. P. Sheetz. 2004. Periodic lamellipodial contractions correlate with rearward actin waves. Cell. 116:431–443. [DOI] [PubMed] [Google Scholar]
  • 28.Harris, A. K., P. Wild, and D. Stopak. 1980. Silicone rubber substrata: a new wrinkle in the study of cell locomotion. Science. 208:177–179. [DOI] [PubMed] [Google Scholar]
  • 29.James, D. W., and J. F. Taylor. 1969. The stress developed by sheets of chick fibroblasts in vitro. Exp. Cell Res. 54:107–110. [DOI] [PubMed] [Google Scholar]
  • 30.Tranquillo, R. T., D. A. Lauffenburger, and S. H. Zigmond. 1988. A stochastic model for leukocyte random motility and chemotaxis based on receptor binding fluctuations. J. Cell Biol. 106:303–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Maheshwari, G., A. Wells, L. G. Griffith, and D. A. Lauffenburger. 1999. Biophysical integration of effects of epidermal growth factor and fibronectin on fibroblast migration. Biophys. J. 76:2814–2823. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Palecek, S. P., J. C. Loftus, M. H. Ginsberg, D. A. Lauffenburger, and A. F. Horwitz. 1997. Integrin-ligand binding properties govern cell migration speed through cell-substratum adhesiveness. Nature. 385:537–540. [DOI] [PubMed] [Google Scholar]
  • 33.Yebra, M., G. C. Parry, S. Stromblad, N. Mackman, S. Rosenberg, B. M. Mueller, and D. A. Cheresh. 1996. Requirement of receptor-bound urokinase-type plasminogen activator for integrin αvβ5-directed cell migration. J. Biol. Chem. 271:29393–29399. [DOI] [PubMed] [Google Scholar]
  • 34.Homandberg, G. A., F. Hui, C. Wen, C. Purple, K. Bewsey, H. Koepp, K. Huch, and A. Harris. 1997. Fibronectin-fragment-induced cartilage chondrolysis is associated with release of catabolic cytokines. Biochem. J. 321:751–757. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Akiyama, S. K., and K. M. Yamada. 1985. The interaction of plasma fibronectin with fibroblastic cells in suspension. J. Biol. Chem. 260:4492–4500. [PubMed] [Google Scholar]
  • 36.Akiyama, S. K., E. Hasegawa, T. Hasegawa, and K. M. Yamada. 1985. The interaction of fibronectin fragments with fibroblastic cells. J. Biol. Chem. 260:13256–13260. [PubMed] [Google Scholar]
  • 37.Berry, H., and V. Larreta-Garde. 1999. Oscillatory behavior of a simple kinetic model for proteolysis during cell invasion. Biophys. J. 77:655–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Goodman, S. L., G. Risse, and K. von der Mark. 1989. The E8 subfragment of laminin promotes locomotion of myoblasts over extracellular matrix. J. Cell Biol. 109:799–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Wainwright, S. A., W. D. Biggs, J. D. Currey, and J. M. Gosline. 1976. Mechanical Design in Organisms. Princeton University Press, Princeton, NJ.
  • 40.Trinkaus, J. P. 1984. Cells Into Organs. The Forces That Shape the Embryo. Prentice Hall, Englewood Cliffs, NJ.

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES