Effect of Urea on Peptide Conformation in Water: Molecular Dynamics and Experimental Characterization

Abstract

Molecular dynamics simulations of a ribonuclease A C-peptide analog and a sequence variant were performed in water at 277 and 300 K and in 8 M urea to clarify the molecular denaturation mechanism induced by urea and the early events in protein unfolding. Spectroscopic characterization of the peptides showed that the C-peptide analog had a high α-helical content, which was not the case for the variant. In the simulations, interdependent side-chain interactions were responsible for the high stability of the α-helical C-peptide analog in the different solvents. The other peptide displayed α-helical unwinding that propagated cooperatively toward the N-terminal. The conformations sampled by the peptides depended on their sequence and on the solvent. The ability of water molecules to form hydrogen bonds to the peptide as well as the hydrogen bond lifetimes increased in the presence of urea, whereas water mobility was reduced near the peptide. Urea accumulated in excess around the peptide, to which it formed long-lived hydrogen bonds. The unfolding mechanisms induced by thermal denaturation and by urea are of a different nature, with urea-aqueous solutions providing a better peptide solvation than pure water. Our results suggest that the effect of urea on the chemical denaturation process involves both the direct and indirect mechanisms.

INTRODUCTION

Unfolding is a common approach, used by experimentalists and theoreticians alike, to map protein folding pathways (1). Experimentally, urea and guanidinium chloride are widely used as denaturant agents, but it is still not clear by which molecular mechanism they denature proteins. It is well known that the solubility of most protein side chains and backbone increases with denaturant concentration (2). Urea is very soluble in water, and high concentrations of denaturant are often required to observe denaturation (3). The denatured state is stabilized by the denaturant upon a higher exposure to the solvent compared to the native state (4). It has been shown that the free energy of transfer of hydrocarbons from water to denaturant aqueous solution is approximately linear with the denaturant concentration (4,5) and that the constant of proportionality correlates with the amount of protein surface exposed to solvent upon unfolding (6). Furthermore calorimetric studies demonstrated that both the enthalpy and entropy of transfer from water to urea water solution are linear functions of the urea concentration (7), supporting the use of the linear extrapolation method for the interpretation of the experimental data from urea denaturation studies.

Urea's molecular action mechanism

Two concepts have guided the investigation of the effect of urea in denaturation during the last 40 years (8). The first is the so-called indirect mechanism in which urea acts indirectly, altering the structure of the solvent, which in turn weakens the hydrophobic effect. The second is the direct mechanism, which proposes that the polypeptide is solvated by both urea and water (9).

The indirect mechanism described by Frank and Franks (10) considers urea as a “water-structure breaker” that disturbs the ability of water to maintain tetrahedral hydrogen bonding. This idea remains controversial, and several groups have rejected this concept (3,7,11–17). However, it has also been argued that the hydrogen bonds formed by water in the solvation shell around urea are more bent than in bulk water (18). Also, molecular dynamics (MD) simulations indicate that both water and urea dynamics are stiffened in the presence of urea (19), and Bennion et al. suggest a weakening of the water structure (20).

In turn, the direct mechanism comprises two aspects: The interaction of urea with apolar solutes and the interaction of urea with polar solutes mainly via hydrogen bonding. The urea-apolar interaction has principally an entropic character. The hydrophobic effect is weakened due to the displacement of ∼4 water molecules by the larger urea molecule from the apolar solvation shell. In this situation the released waters will regain entropy (7,9,13,14). In addition, solute size seems to be a very important factor in the free energy of transfer and free energy of cavity formation (16,21,22), a factor that can explain the anomalous hydrophobic effect experienced by a pair of methane molecules when immersed in urea aqueous solution (3). The cosolvent size is also important since cavity formation is more favorable in the presence of large cosolvents, and even more so if they also have lower hydrogen bond donor/acceptor density than water (9,13). The reason is intimately related to the balance between the loss of orientational freedom suffered by the solvent and the attempt to maintain hydrogen bonds when a solute or cosolvent molecule is introduced in the system.

With respect to the interaction of urea with polar solutes, solvation enhancement is attributed to the more favorable hydrogen bond formation between the peptide amide units and urea than with water (23) because urea itself is a soluble amide. It has also been suggested that urea induces an “outside-in” denaturation process of electrostatic character by adhering on the surface of charged residues, leading to a repulsion between residues. The result of the repulsion is an opening to water into the protein interior that will provoke the unfolding. This explains the need of high urea concentration to achieve denaturation (3,24).

The C-peptide

Two peptide fragments from the α-helical N-terminus of bovine ribonuclease A, the C-peptide (residues 1–13) and the S-peptide (residues 1–19), have attracted much attention because unlike a majority of peptide sequences, they present a significant α-helical structure in water when they are isolated from the rest of the ribonuclease molecule at low temperature (25) and low pH (26–30). The stability of the isolated C-peptide α-helix in water suggested the possibility of helices being autonomous folding units: the sequence itself carries enough information to fold properly. When this was discovered in the 1970s, the helix-coil theory postulated the impossibility of formation of stable short α-helices in water environments. This finding together with the extensive work performed in alanine-based peptides and host-guest polymers (31) encouraged further experimental and statistical studies on α-helices, trying to establish the rules for α-helical stability (32–34). The results indicate a similar helical formation mechanism for proteins and peptides and revealed the importance of other factors such as specific side chain-side chain interactions, helical capping, helix-dipole interactions, as well as the dependence of the α-helical propensities on the location inside the helix. These and other factors were later included in different modified Lifson-Roig based helix-coil models (see Doig (35) for a review).

Diverse experiments show that the stability of the C-peptide and S-peptide α-helices depends on both temperature and pH. The α-helical content decreases with increasing temperature, which indicates that α-helical formation is enthalpically driven (25). The main source of stability is the side-chain interaction between the residues Glu^2--Arg¹⁰⁺ (36–39) and the interaction between the aromatic rings Phe⁸-His¹²⁺ (40,41). Both are pH dependent. The protonation of His¹² has been shown to increase the helix stability (37,42–44). These two specific side-chain interactions are also present in the intact protein (45,46). Other interactions that influence the α-helical stability are the complementary electrostatic interactions between charged groups located close to the C- and N-termini and the helix dipole (28,32,36).

Although the exact molecular mechanism by which urea induces protein unfolding in urea aqueous solution is unclear, the most widely spread theory for protein denaturation by urea is the direct mechanism, which consists of a combination of a mainly entropic hydrophobic contribution and a polar contribution (7,14,20). However, alternative mechanisms have been suggested which are a mixture between the direct and indirect mechanism (20,47). Even though the atomistic description of MD simulations may provide invaluable information for a better understanding of this complicated process, only a few MD simulations of proteins in explicit urea aqueous solution have been reported (20,47–50). Two reasons are that achieving full unfolding in the simulation timescale is difficult and that the most successful simulations use relatively high temperature.

To shed light on the structural denaturation mechanism of the C-peptide α-helix by urea, we have performed several MD simulations on two C-peptide analogs in both water and 8 M urea aqueous solution. Additionally we have characterized experimentally the solution conformation of the peptides studied in conditions used for the simulations. One peptide was designed to maximize helicity and the other, having the same composition but a different sequence, was designed to minimize helical formation. Since peptides encompass the main features of protein secondary structure formation and are computationally more tractable than large proteins, the study of how they are affected by the presence of urea molecules can help clarify the mechanism of solute denaturation and even contribute to our understanding of early events of protein folding.

METHODS

Peptide design, synthesis, and characterization

Two tridecapeptide sequences were designed based on the C-peptide of bovine ribonuclease A (H₂N-KETAAAKFERQH-hSer(lactone)) (25). The first peptide, (Cpep⁺) (Succ-AETAAAKFLRNHA-NH₂), contains three substitutions included to increase inherent helicity, stability, and ease of synthesis (E9L and Q11N) and preserve the length of the original peptide (hSer(lactone)13A). Additionally, the N- and C-terminal amino acids were succinylated and amidated, respectively, to prevent the unfavorable interaction of ionized amino and carboxyl groups with the helix dipole. A second peptide, (Mut⁺), contained an amino acid composition (complete with terminal modifications) identical to Cpep⁺ but with a sequence chosen to minimize inherent helicity and sequence identity to the first peptide (Succ-AKERAFTANAHLA-NH₂).

Both peptides were synthesized starting from a p-methylbenzhydrylamine-resin, purified, and characterized essentially as described previously (51). Before deprotection and cleavage, the peptides were succinylated at the N-terminus using succinic anhydride in dimethylformamide containing an equivalent of diisopropylethylamine. Circular dichroism (CD) spectra were recorded using an Aviv 202SF spectrapolarimeter (Aviv Instruments). Peptide concentrations were determined by quantitative amino acid composition (52). ¹H, ¹³C, and ¹⁵N nuclear magnetic resonance assignments were obtained at natural isotopic abundance (5 mM peptide, pH 4.5, and 277 K) using standard techniques as described previously (53). Random coil chemical shifts were taken from Wishart and Sykes (54).

Peptide setup for the MD simulations

Simulations were performed on the two previously mentioned peptides and in another two, Cpep⁰ and Mut⁰, with the same sequence as Cpep⁺ and Mut⁺, respectively, but with standard 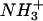and COO⁻ termini. To reproduce low pH conditions consistent with the experimentally observed maximal helicity, the His imidazole was protonated in Cpep⁺ (His¹²) and Mut⁺ (His¹¹), and in all simulations the Glu carboxyl was ionized due to the experimentally observed salt bridge between this residue and the Arg¹⁰ residue in the wild-type C-peptide (28,36,38,39). This choice of protonation states corresponds to a pH of ∼5.5, according to the experimental titrations (See Results).

Since experimentally Cpep+ displays significant helical structure, the initial coordinates of Cpep⁺ were built from the coordinates of the first structure of the ribonuclease A C-peptide solved by NMR (55). Although the Mut⁺ peptide did not show significant helical structure in CD experiments, the initial backbone coordinates were the same as those of the Cpep⁺. Initial coordinates for Cpep⁰ and Mut⁰ were built as ideal α-helices in the CHARMM program (56).

MD simulation protocol

The CHARMM (56) program with the all-atom parameter set (57) was used in all energy minimizations and all MD simulations. An atom-based force-shift method for the long-range electrostatic interactions with the relative dielectric constant equal to 1.0, which is known to produce accurate and stable simulations (58), as well as an atom-based shifting function for the van der Waals interactions was used to truncate the nonbonded interactions. The truncation cutoff was at 12 Å in all cases, and the nonbonded list was generated to 14 Å, with updates as soon as any atom had moved >1 Å. SHAKE was applied to all covalent bonds involving hydrogens (59). The leap-frog algorithm was used in all simulations with a 2 fs integration time step, and the coordinates were saved every 5 ps for analysis and every 0.2 ps for the calculation of the rotational diffusion correlation function. Periodic boundary conditions were used in the energy minimization and the MD simulations. The model of water used was the modified TIP3P model (60,61), whereas the urea parameters were obtained in analogy to the Asn side chain. The urea partial charges were −0.502 (O), +0.142 (C), −0.569 (N), +0.416 (H_cis), and +0.333 (H_trans). These charges were obtained to fit the potentials for urea-water systems of Åstrand et al. (62,63) (A. Caballero-Herrera and L. Nilsson, unpublished).

The 8 M urea aqueous solution box for Cpep⁺ and Mut⁺ was prepared by randomly distributing 206 urea molecules in a (35.0 Å)³ box and then immersing them in an equilibrated (35.0 Å)³ box of water molecules. All water molecules overlapping with the urea molecules were removed. The 8 M urea (35.0 Å)³ box contained 199 urea molecules and 876 water molecules, corresponding to 0.755 grams of denaturant per gram of water, which is the experimental value (64). The box was minimized at 1000 steps of steepest-descent (SD) minimization followed by 1000 steps of adopted basis Newton-Raphson (ABNR) minimization. The peptides were then immersed in the box, and the water and urea molecules overlapping with the peptide molecule were deleted. To keep the right urea concentration, the criterion for overlapping was a distance smaller than 1.8 Å between any urea atom and any of the peptide atoms and smaller than 2.0 Å between any water atom and any atom of the peptide. Then, the water molecule with lowest oxygen electrostatic energy was removed and substituted by one chloride ion to neutralize the system. A few additional water molecules were removed to get a final system formed by the peptide (Cpep⁺ or Mut⁺) 843 water molecules, 191 urea molecules, and 1 chloride ion. This system was then minimized by 1000 cycles of SD minimization followed by 1000 cycles of ABNR minimization. An MD simulation run of 30 ps at constant pressure at reference pressure of 1 atm and at 298 K was then performed to get the right size of the system. During the last 10 ps of these constant pressure simulations, the side of the boxes remained constant with oscillations bellow 0.2 Å. Constant pressure was maintained by using the Langevin piston method (65) with collision frequency γ = 20 ps⁻¹, piston mass = 400 amu, and the piston coupled to a temperature bath at 300 K. The final stable sizes of the boxes were (34.2 Å)³ for both peptides. Thereafter followed an equilibration period of 100 ps. The MD simulation had a duration of 12 ns. The temperature was constrained to be 298 K ± 10 K by scaling the velocity.

For the simulations of Cpep⁺ and Mut⁺ peptide in water, the peptides were immersed in a (35.0 Å)³ cubic box of water molecules and the overlapping waters were deleted. The systems were formed by Cpep⁺ and 1364 water molecules and the Mut⁺ peptide and 1352 water molecules. Both systems were then minimized by 500 steps of SD minimization and thereafter by 1000 steps of ABNR minimization. The systems were gradually heated in a 100 ps period from 50 K to 277 K, for the water at 277 K simulations and from 50 to 300 K for the water simulations at 300 K. An equilibration period followed, and MD simulations of 10 ns at 277 K and 300 K (±10 K), respectively, were performed.

The 8 M urea rectangular box for the nonprotonated peptides was built up in a similar way starting with a 37 × 34 × 29 ų box containing 960 water molecules and 165 urea molecules. The system was minimized by 500 steps of SD minimization followed by 500 steps of ABNR minimization. Then the peptides (Cpep⁰ or Mut⁰) were introduced in the box, and the water and urea molecules overlapping with the peptide were deleted. The final systems contained 152 urea and 731 water molecules or 154 urea and 741 water molecules for Cpep⁰ and Mut⁰, respectively, for a urea/water ratio of 0.69 (w/w), which is slightly lower than the experimental value for an 8 M urea solution. For the water simulations the Cpep⁰ and Mut⁰ peptides were immersed in a 37 × 34 × 29 ų rectangular water box finally containing 1140 and 1142 water molecules, respectively. All these systems were then subjected to a global minimization of 500 SD steps followed by 1000 ABNR steps, afterwards to gradual minimization consisting of 50 ABNR steps of minimization with harmonic constraints on all the peptide atoms with a force constant of 10 kcal × mol⁻¹ × Å⁻², followed by 50 steps of ABNR minimization steps with the harmonic force constant reduced to half and only applied to the backbone heavy atoms. Finally the harmonic constraints were completely turned off during the last 100 steps of ABNR minimization. Each simulation was initialized with a 100 ps heating period from 50 K to 300 K followed by 100 ps of equilibration. The length of the simulations was 10 ns, and the temperature constrained to 300 K ± 10 K by scaling the velocity.

Analysis procedures

RMSD

The backbone pair-wise root mean square deviation (RMSD) matrix plots were built up calculating the backbone RMSD, after least-squares superpositioning of the backbone atoms, between all pairs of conformations at 5 ps intervals.

A probe sphere of radius 1.4 Å was used to calculate the accessible surface area (ASA) (66).

Hydrogen bonds

Hydrogen bonds and their lifetimes were calculated along the simulations using either a 2.4 Å or a 1.8 Å cutoff on the hydrogen-acceptor distance.

The histograms of the number and lifetimes of peptide-water/urea hydrogen bonds were normalized by the time of the simulation as well as by the number of water and urea molecules, respectively, in the simulation. The cutoff used for the hydrogen bond was 2.4 Å. The data were split into the number of hydrogen bonds that water/urea oxygens or hydrogens formed with the peptide backbone or with the peptide side chains.

Solvation number

The solvation number is the number of solvent molecules contained in the hydration shell around the peptide, or around a part of it, within a solvation radius (r_solv.) Two different r_solv, 3.5 Å (20) and 2.4 Å, have been used for analyzing the data. The former is an estimation of the minimum radius that can be chosen to ensure the enclosure of the centers of all molecules that can be in contact with the peptide; the second (r_solv = 2.4 Å) was used to relate the number of solvent molecules around the peptides and the number of hydrogen bonds that they made with the peptide (hydrogen bond cutoff = 2.4 Å). The solvation number around the polar atoms and apolar atoms was also calculated.

Rotational diffusion correlation function

Second order dipole rotational correlation times, τ, were computed for water molecules with the oxygen atom within 3.5 Å around the Cpep⁺ in the water at 277 K and in 8 M urea simulations by fitting an exponential, exp{−t/τ}, to the correlation function:

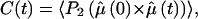where the P₂ is the second order Legendre polynomial, 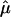is the unit vector along the water dipole, and 〈 … 〉 denotes averaging over the trajectory.

These correlations decay very fast. The coordinates for analysis were sampled every 0.2 ps, and only the last 2 ns of the trajectories were used in the analysis.

RESULTS

Experimental characterization of peptides

Peptides Cpep⁺ and Mut⁺ were readily soluble in water and displayed no signs of aggregation at concentrations up to 10 mM as both the far-ultraviolet (UV) CD spectra and ¹H NMR line widths were concentration independent for conditions tested (10 ≥ pH ≥ 2 and 278 K ≤ T ≤ 308 K, data not shown). The CD spectra of peptide Cpep⁺ show a double minimum (208 and 222 nm) and maximum (190 nm) characteristic of significant helical content, which increases with decreasing temperature (Fig. 1 a). An isodichroic point is observed near 203 nm, which is consistent with a two-state helix-disorder (random coil) transition (67). The spectra of peptide Mut⁺ shows a strong minimum at 200 nm characteristic of a disordered conformation and displays essentially no temperature dependence. It is noteworthy that the spectra of peptide Mut⁺ also go through the isodichroic point defined in spectra of peptide Cpep⁺. Given this, the conformations of peptide Mut⁺ can be seen as consistent with conformations allowed in the two states exhibited by peptide Cpep⁺. For comparison, peptides Cpep⁺ and Mut⁺ have an estimated helical content of 38% and 7% helix content (41) at 298 K pH 4.5 calculated for all 13 amino acids. Under similar conditions, the C-peptide of ribonuclease A has ∼2% helix content (41). At 278 K, peptides Cpep⁺ and Mut⁺ had 61% and 9% helix content, respectively, and that of the C-peptide, ∼21% (41). In 8 M urea, both peptides have CD spectra largely characteristic of disordered structures (Fig. 1 a) and are not sensitive to temperature. It could not be determined if they too would pass through the isodichroic point as the absorbance of the 8 M urea solution precluded measurements below 210 nm.

FIGURE 1.

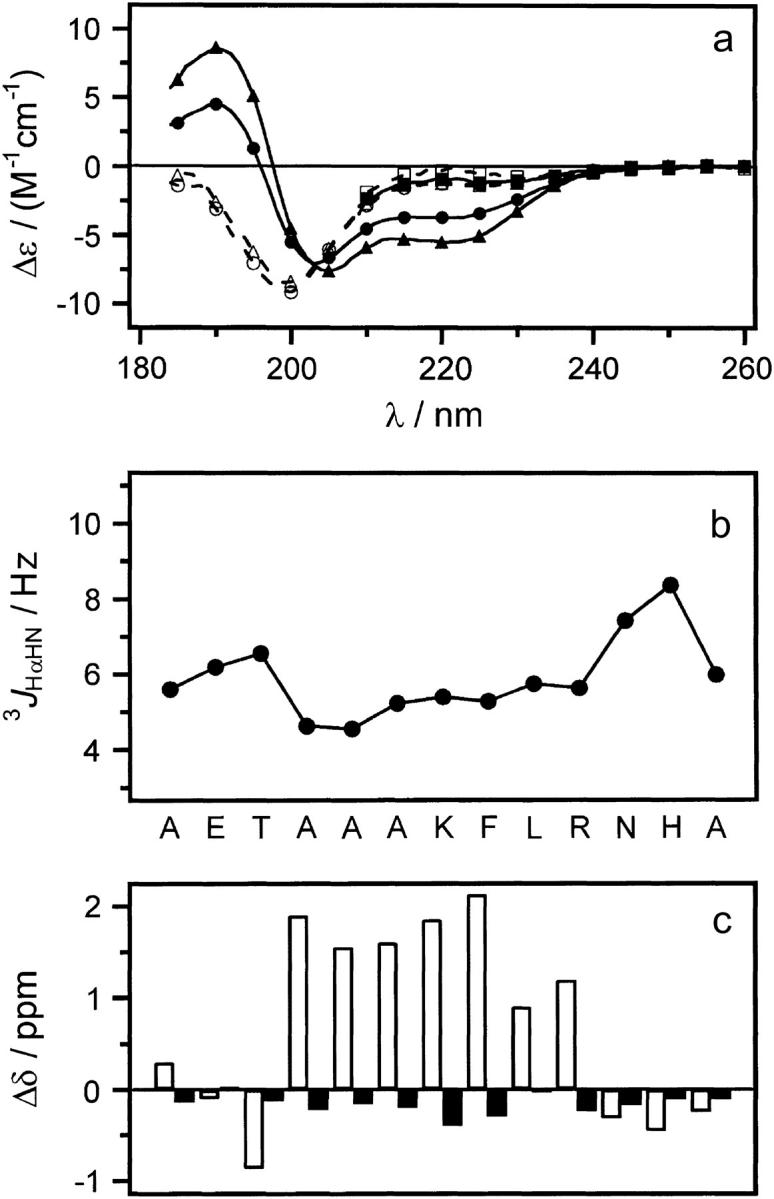
Experimental data for peptides Cpep⁺ and Mut⁺. (a) Far-UV CD spectra of peptides: Cpep⁺ (•) and Mut⁺ (○) in water, 298 K; Cpep⁺ (▴) and Mut⁺ (▵) water, 278 K; and Cpep⁺ (▪) and Mut⁺ (□) 8 M urea 298 K. (b) Scalar coupling constants ³J_HNHα (pH 4.6, 277 K) plotted versus the amino acid sequence of peptide Cpep⁺. (c) Differences (Δδ) between the observed chemical shifts for peptide Cpep⁺ and the corresponding random coil values for ¹H_α (black) and ¹³C_α (white) nuclei.

Complete ¹H, ¹³C, and ¹⁵N nuclear magnetic resonance assignments were obtained for peptide Cpep⁺ at natural isotopic abundance (pH 4.5 and 277 K). Unfortunately, only incomplete assignments could be obtained for peptide Mut⁺ due to poor chemical shift dispersion leading to severe overlap in spectra recorded under these conditions. Scalar coupling constants ³J_HNHα were measured for residues 1–13 in peptide Cpep⁺. Residues 4–10 have values <6 Hz with significantly increased values for the three N- and three C-terminal residues. This is evidence that residues 4–10, but not residues 1–3 and 11–13, populate helical conformations significantly on the NMR timescale.

NMR chemical shifts are commonly used to assign polypeptide secondary structure (68). This method is based on the difference (Δδ) between the observed chemical shift and the random coil value experimentally determined for that particular amino acid type in an unfolded conformation. Helical conformation has been shown to correlate with downfield shifts for ¹H_α and upfield shifts for ¹³C_α nuclei (68), whereas the opposite is true for an extended, strandlike conformation. When applied to the data for peptide Cpep⁺ (Fig. 1 c), one indeed observes negative values of Δδ for ¹H_α and positive values of Δδ for ¹³C_α calculated for residues 4–10, indicating a significant helical conformation.

To determine the ionization state for the peptide Cpep⁺, a pH titration of ¹H_N chemical shifts (2 ≤ pH ≤ 10) yielded data (not shown) that fit well to an independent two-site ionization model using nonlinear regression (Igor Pro, Wavemetrics, Lake Oswego, OR). Average values of 4.36 ± 0.08 and 6.51 ± 0.05 were obtained and are attributed to Glu² and His¹², respectively.

MD overall characterization of peptide conformations

Inspection of the time evolution of the backbone RMSD (Fig. S1 in Supplementary Material) revealed striking differences between the peptides. The Cpep⁺ backbone remained practically unchanged along all three simulations, with an RMSD average below 2 Å, and in water at 277 K below 1 Å. However Cpep⁰ began to gradually unfold, from the first picoseconds of the 8 M urea simulation and after 2 ns in water at 300 K, reaching values up to 3.5 Å; the backbone RMSD values were somewhat higher in the 8 M urea simulation. A very similar behavior was observed for Mut⁰ but with a faster initial RMSD rise and higher final values. In contrast with the previous cases the Mut⁺ unfolding was characterized by an abrupt change of its backbone RMSD (Fig. S1) at the very beginning of the simulation in water at 300 K and after ∼3 ns in the other two simulations, followed by a stable period. The backbone RMSD values of the simulation in water at 277 K were lower than those of the rest of simulations, and during the last nanosecond of simulation in 8 M urea a further backbone RMSD rise was observed, reaching values up to 4.2 Å.

Structural backbone similarities between the sampled conformations during the simulations were analyzed using pair-wise RMSD matrix plots (Fig. S2). The Cpep⁺ displayed a very high correlation between the different structures that it sampled in each of its three simulations (Fig. S2, a, a′, and a″). Only in the water simulation at 300 K was there some evidence of a different cluster of similar structures during the last 2 ns of the simulation compared with the rest of the structures. The Cpep⁰ had very different behavior and passed across two major different clusters of similar structures in the water simulation and across three slightly more heterogeneous clusters in the 8 M urea simulation (Fig. S2, b and b′). The Mut⁺ peptide sampled two clusters of similar structures in all its three simulations (Fig. S2, c, c′, and c″); in water at 277 K and 300 K the clusters were well defined and delimited, in particular the second cluster at 300 K; however, for the 8 M urea simulation the distinction between the two clusters was less clear. On the other hand, Mut⁰ showed, as in the case of Cpep⁰, a more unstructured backbone (Fig. S2, d and d′). At the end of the water simulation, the backbone reached one structure clearly different from the rest of the previously sampled conformations. In the 8 M urea simulation, however, there was no abrupt change between clusters of structures.

Average solvent ASA per peptide atom was quite similar for the four peptides (from 7.4 Ų for Cpep⁺ to 7.5 Ų for Mut⁺ in the water simulations at 277 K), with a slight increase observed in the water simulations at 300 K (from 7.5 Ų for Cpep⁺ to 8.1 Ų to Mut⁰) and in 8 M urea (7.5 Ų for Cpep⁺ to 8.4 Ų for Mut⁰).

Backbone hydrogen bonds and helical structure

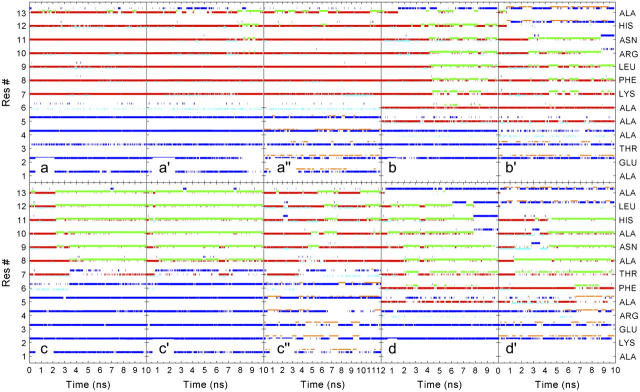
The α-helical content (i, i + 4 hydrogen bonds) as well as the π- and 3₁₀-helical content (i, i + 5 and i, i + 3 hydrogen bonds respectively) were monitored along the trajectory (Fig. 2). In general, each peptide displayed similar characteristics in the different simulations but with a stronger urea influence for the less stable peptides. The seven initial α-helical hydrogen bonds formed by Cpep⁺ were maintained during the entire simulation in water at 277 K (Fig. 2 a). Only the two closest to the C-terminus were partially disrupted and in particular the Phe⁸ carbonyl switched temporarily its α-helical hydrogen bond to a π-helical hydrogen bond. 3₁₀-helical hydrogen bond formation was also observed for all the residues but Phe⁸. The difference when the peptide was simulated in water at 300 K concerned the C-terminus half of the helix (Fig. 2 a′). The most C-terminus α-helical hydrogen bond practically disappeared, and on this occasion the π-helical hydrogen bond accepted by Phe⁸ carbonyl lasted up to the end of the simulation and propagated two residues toward the N-terminus. In the 8 M urea simulation, the Cpep⁺ intrabackbone hydrogen bond pattern features were analogous to the previous case but with lower π-helical hydrogen bond formation and propagation (Fig. 2 a″).

FIGURE 2.

Time evolution of backbone amide hydrogen bonds. Hydrogen bonds are denoted by colored dots: red, α-helical (amide i, carbonyl i − 4); green, π-helical (amide i, carbonyl i − 5); cyan 3₁₀-helical (amide i, carbonyl i – 3); blue, amide-water; orange, amide-urea. (a) Cpep⁺ simulation in water at 277 K, (a′) Cpep⁺ simulation in water at 300 K, (a″) Cpep⁺ simulation 8 M urea, (b) Cpep⁰ simulation in water at 300 K, (b′) Cpep⁰ simulation 8 M urea, (c) Mut⁺ simulation in water at 277 K, (c′) Mut⁺ simulation in water at 300 K, (c″) Mut⁺ simulation 8 M urea, (d) Mut⁰ simulation in water at 300 K, and (d′) Mut⁰ simulation 8 M urea.

The nine α-helical hydrogen bonds of the starting ideal α-helical Cpep⁰ were not maintained during the two simulations (Fig. 2, b and b′). Unwinding started from the C-terminus propagating toward the N-terminus (Fig. 2 b). Disappearance of α-helical hydrogen bonds was correlated with the appearance of π-helical hydrogen bonds with a further propagation toward the N-terminus. At approximately the middle of the water simulation, all residues that still retained helical structure participated in π-helical hydrogen bonds, most of which remained until the end of the simulation. In the 8 M urea simulation, the intrabackbone hydrogen bond pattern of the Cpep⁰ was largely similar to the water simulation; although the two α-helical hydrogen bonds closest to the C-terminus disappeared completely after 2 ns of simulation followed much later by the next two, π-helical hydrogen bonds vanished also (Fig. 2 b′). The final structure contained only five intrabackbone hydrogen bonds, three α- and two π-helical. Formation of a short-lived 3₁₀-helical hydrogen bond was also observed in both simulations.

In both water simulations, the Mut⁺ peptide rapidly lost its seven initial α-helical hydrogen bonds (Fig. 2, c and c′), converting into π-helical hydrogen bonds in a cooperative manner from the C-terminus toward the N-terminus, and on some occasions coexisting with them. The unfolding process of the Mut⁺ backbone in the 8 M urea simulation was slower and to some extent different than in the water simulations (Fig. 2 c′). In general the majority of the α-helical hydrogen bonds were maintained most of the time in this simulation, but in this case disruption of α-helical hydrogen bonds took place in the middle of the helix and at the N-terminus before than at the C-terminus, with π-helical hydrogen bond propagation from the N- toward the C-terminus. The most N-terminus α-helical hydrogen bonds disappeared at the end of the simulation. The Mut⁰ backbone very quickly lost its α-helical hydrogen bonds beginning from its C-terminus and propagating toward the N-terminus (Fig. 2, d and d′). In water as well as in urea the α-helical hydrogen bonds were lost completely or were turned into π-helical hydrogen bonds, which for some residues also disappeared after a while. However, in 8 M urea, disruption of α-helical hydrogen bonds did begin not only at the C-terminus but also at the middle of the helix (Fig. 2 d′). In general, formation of a 3₁₀-helical hydrogen bond was rare and less frequent than for the Cpep⁺ and Cpep⁰ simulations, but for Mut⁺ and Mut⁰ there was an appreciable higher content of 3₁₀-helical hydrogen bonds in 8 M urea than in water.

Side-chain interactions

Cpep⁺

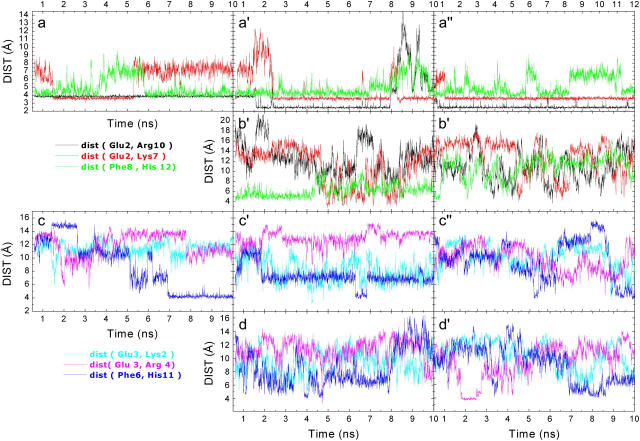
The Glu²⁻ … Arg¹⁰⁺ salt bridge in the Cpep⁺ simulations comprised two normally simultaneous hydrogen bonds with Arg¹⁰. In water at 277 K these interactions were present 99% of the simulation time (Table 1); the interaction between Glu² and Arg¹⁰ was achieved by the hydrogen bonds between the Arg¹⁰ hydrogens Hɛ and one of the Hη and the two oxygens of Glu², Oɛ₁, and Oɛ₂ (Figs. 3 a and 4 a), which allowed close contact between the concerned side chains. These two hydrogen bonds were also present at the beginning of the other two Cpep⁺ simulations, but after 1.5 ns in the water simulation at 300 K and ∼0.5 ns in the 8 M urea simulation, the two hydrogen bonds were instead formed by the two Hη hydrogens of Arg¹⁰ and the two Oɛ₁ and Oɛ₂ oxygens of Glu² (Fig. 4 c). These two hydrogen bonds persisted ∼63% of the simulation time in the Cpep⁺ simulation in water at 300 K and disappeared 2 ns before the end of the simulation although finally one of them was recovered. In 8 M urea, the Glu² side chain formed two hydrogen bonds with the Arg¹⁰ side chain 93% of the time.

TABLE 1.

Occurrence (%) of specific intrahelical hydrogen bonds

		WAT 277 K	WAT 300 K	Urea 8 M
Cpep+	Ala1(Succ O)-Ala1(HN)	7	20	5
	Ala1(Succ O)-Lys7(Hζ)	-	12	-
	Glu2(Oɛ)-Glu2(HN)	-	13	-
	Glu2(Oɛ)-Lys7(Hζ)	33	40	41
	Glu2(Oɛ)-Arg10(Hη11)	99	15	93
	Glu2(Oɛ)-Arg10(Hη12)	-	63	18
	Glu2(Oɛ)-Arg10(Hη21)	-	4	-
	Glu2(Oɛ)-Arg10(Hη22)	-	62	97
	Glu2(Oɛ)-Arg10(Hɛ)	99	14	-
	Thr3(Oγ1)-Thr3(HN)	18	15	14
	Thr3(Oγ1)-Ala6(HN)	39	29	30
	Lys7(O)-Asn11(Hδ21)	-	13	22
	Phe8(O)-His12(Hδ1)	23	4	1
	Leu9(O)-Ala13(Amide HT2)	46	39	52
	Arg10-Asn11(Oδ1)	-	2	17
	Arg10(O)-Ala13(Amide HT2)	21	7	13
	Asn11(Oδ1)-His12(Hδ1)	45	-	-
	Asn11(Oδ1)-His12(HN)	17	-	-
	His12(O)-Ala13(Amide HT2)	-	5	4
Cpep0	Ala1(O)-Ala(Std N-term HT)		4	3
	Glu2(Oɛ)-Glu2(HN)		7	-
	Thr3(Oγ1)-Thr3(HN)		21	18
	Ala6(O)-Asn11(Hδ22)		12	18
	Lys7(O)-Asn11(Hδ22)		21	6
	Arg10(Hɛ)-Asn11(Oδ1)		5	7
	Arg10(Hη)-Asn11(Oδ1)		3	4
	Ala13(St Cterm OT)-Ala13(HN)		3	3
Mut+	Ala1(Succ O)-Arg4(Hɛ/Hη)	6	6	4
	Ala1(O)-Arg4(Hɛ)	-	14	1
	Glu3(Oɛ)-Arg4(HN)	12	-	19
	Glu3(Oɛ1/Oɛ2)-Thr7(Hγ1)	1/4	22/21	24/11
	Glu3(O)-Thr7(Hγ1)	9	12	20
	Phe6(O)-His11(Hδ1)	-	4	2
	Arg4(HN)-Thr7(Oγ1)	-	-	4
	Arg4(O)-Asn9(Hδ)	11	17	0
	Thr7(HN)-Thr7(Oγ1)	7	7	17
	Thr7(Oγ1)-Ala8(HN)	-	-	8
	Ala8(O) -Ala13((Amide HT2)	-	3	-
	Asn9(O)-Ala13(Amide HT2)	65	60	47
	Ala10(O)-Ala13(Amide HT2)	10	4	18
	Leu12(O)-Ala13(Amide HT2)	2	4	3
Mut0	Ala1(O)-Ala1(St N-term HT)		3	3
	Lys2(O)-Thr7(Hγ1)		9	14
	Glu3(Oɛ)-Arg4(Hɛ/Hη12)		-	9/7
	Glu3(Oɛ)-Thr7(Hγ1)		6	11
	Arg4(Hɛ/Hη)-Asn9(Oδ1)		3/3	0/1
	Arg4(O)-Asn9(Hδ)		20	25
	Phe6(O)-His11(Hδ1)		8	4
	Thr7(HN)-Thr7(Oγ1)		7	19
	Thr7(O)-His11(Hδ1)		1	3
	Asn9(Hδ22)-Ala13(Std C-term OT)		3	-
	Ala13(HN)-Ala13(Std C-term OT)		4	6

FIGURE 3.

Salt bridges and Phe-His distances. (a) Cpep⁺ simulation in water at 277 K, (a′) Cpep⁺ simulation in water at 300 K, (a″) Cpep⁺ simulation 8 M urea, (b) Cpep⁰ simulation in water at 300 K, (b′) Cpep⁰ simulation 8 M urea, (c) Mut⁺ simulation in water at 277 K, (c′) Mut⁺ simulation in water at 300 K, (c″) Mut⁺ simulation 8 M urea, (d) Mut⁰ simulation in water at 300 K, (d′) Mut⁰ simulation 8 M urea. The distance (Glu, Arg) is the distance between the center of mass of the Glu Oɛ¹ and Oɛ² atoms and the center of mass of the Arg Hη¹¹, Hη¹², Hη²¹, and Hη²² atoms. The distance (Glu, Lys) is the distance between the center of mass of the Glu Oɛ¹ and Oɛ² atoms and the Lys Hζ¹, Hζ², and Hζ³ atoms. The distance (Phe, His) is the distance between the centers of mass of the two rings.

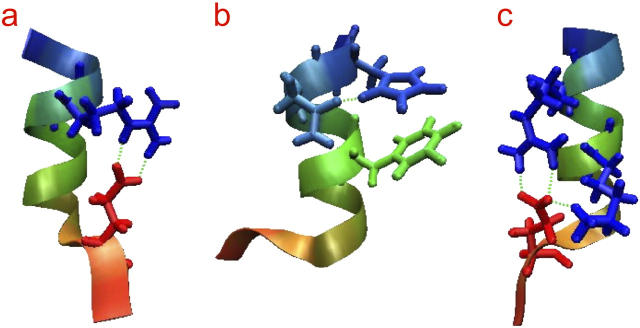
FIGURE 4.

Structural snapshots from the Cpep⁺ simulations. (a) Hydrogen bonds Glu²(Oɛ¹)-Arg¹⁰(Hɛ) and Glu²(Oɛ²)-Arg¹⁰(Hη) in water at 277 K. (b) Hydrogen bond between Asn¹¹(Oδ1)-His¹²(Hδ) in water at 277 K. (c) Hydrogen bonds Glu²(Oɛ¹)-Arg¹⁰(Hη¹²) and Glu²(Oɛ²)-Arg¹⁰(Hη²²) occurring simultaneously with the hydrogen bond Glu²(Oɛ²)-Lys⁷(Hζ) in water at 300 K. The color of the peptide changes from red at the N-terminus to blue at the C-terminus. This and following molecular images were created with the VMD program (89).

Another commonly formed interaction in all the three simulations of Cpep⁺ was the hydrogen bond between the side chains of Glu² and Lys⁷ (Figs. 3, a, a′, and a″, and 4 b), which correlated with the formation of the hydrogen bond between the Lys⁷ O and the Asn¹¹ Hδ side chain. The interaction between Asn¹¹ Oδ and His¹² Hδ1 was observed in the water at 277 K simulation only when the two previously mentioned interactions were not formed (data not shown). Thus, the Glu²-Lys⁷ interaction indirectly precludes the hydrogen bond between the side chains of Asn¹¹ and His¹². The Glu² Oɛ - Lys⁷ Hζ hydrogen bond was only displayed during 33% of the water simulation at 277 K but was present most of the time in the other two simulations (Fig. 4 c). The hydrogen bond between the Asn¹¹ Oδ and His¹² Hδ was only present in the water at 277 K simulation and formed only once the hydrogen bond between the Glu² Oɛ and Lys⁷ Hζ broke. From this point up to the end of the simulation, the Phe⁸ O competed with the Asn¹¹ Oδ for making a hydrogen bond with the His¹² Hδ; however, the hydrogen bond between the Asn¹¹ Oδ and His¹² Hδ had a higher occurrence. In water at 300 K, the Glu² Oɛ and Lys⁷ Hζ hydrogen bond survived until 8 ns and ∼0.5 ns later the Glu² Oɛ - Arg¹⁰ Hη hydrogen bond broke as well, although this hydrogen bond was recovered ∼1 ns later (Fig. 3 a′). When the Lys⁷ side chain recovered the contact with Glu², it only formed one hydrogen bond but at the same time it also made a hydrogen bond to the succinylated N-terminus, an interaction that was not observed in the other two simulations.

The ring-ring interaction between His¹² and Phe⁸ was found in all three simulations (Fig. 3, a, a′, and a″). It disappeared for ∼2.5 ns in the middle of the 277 K water simulation and similarly after 8 ns in the 300 K water simulation. However, in the 8 M urea simulation the interaction disappeared at different periods during the simulation, getting completely lost 3 ns before the end of the simulation. In the 300 K water simulation, partial unwinding was observed at the C-terminus. This was related with the noninteraction between His¹² and either the Phe⁸ residue or Asn¹¹ side chain (Fig. 3 a′). On the contrary, in the 8 M urea simulation, unwinding was not observed, one of the reasons being that the hydrogen bond between the Asn¹¹ and Arg¹⁰ side chains during large periods shielded the last α-helical turn from exposure to the solvent although this was not sufficient to promote the aromatic interaction between the His¹² and Phe⁸ residues (Fig. 3 a″). There was a clear correlation between the disruption of the interaction and the formation of π-helical hydrogen bonds.

In addition, hydrogen bonds between the N- and C-termini and the closest residues of the peptide (Table 1) were commonly formed in the three simulations of Cpep⁺. The amidated C-terminus frequently formed hydrogen bonds with the carbonyl oxygens of Arg¹⁰ and Leu⁹ in water at 277 K and in 8 M urea, which probably helped in preserving the last α-helical turn closest to the C-terminus, hindering unwinding in these simulations. However, the higher thermal energy of the system in the water at 300 K simulation also influenced the two termini of the peptide that became much more flexible here, causing during some periods the loss/creation of hydrogen bonds between the N- and C-termini and some inner residues with further implications for the helix stability.

Finally, the two hydrogen bonds that the Thr³ Oγ made with its own HN and with the Ala⁶ HN, probably assisting in fixing the first α-helical turn of the peptide, were observed all the time in all three simulations.

Cpep⁰

The peptide did not achieve any of the most significant interactions between side chain-side chain or side chain-backbone interactions displayed by Cpep⁺ (Fig. 3, b and b′, Table 1). In general, the hydrogen bonds formed between the side chains or side chain-backbone had a very low frequency and very short duration. Only the hydrogen bonds Thr³ Oγ -Thr³ HN in both simulations, the Lys⁷ O-Asn¹¹ Hδ hydrogen bond in the water simulation, and the Ala⁶ O-Asn¹¹ Hδ hydrogen bond in the 8 M urea simulation were established ∼20% of the simulation time, mainly occurring intermittently at different periods of the simulations. The His¹²-Phe⁸ ring-ring interaction was only present at the beginning of the simulations, and analogously to Cpep⁺, the interaction disappeared as soon as the first π-helical bond was formed. In general, the C- and N-termini of the peptide did not display significant hydrogen bonding with the closest residues in any of the simulations.

Mut⁺ and Mut⁰

The side chains of the Mut peptide formed few hydrogen bonds that could help in maintaining the α-helical structure (Table 1 and Fig. 3). The interactions between charged side chains were rare and also did not contribute to preserving the helical structure and instead interacted more often with other residues. In particular, in the Mut⁺ simulations in water at 300 K and in 8 M urea, and less frequently in water at 277 K, the Thr⁷ Hγ side chain formed numerous hydrogen bonds with the Glu³ Oɛ and O. In turn, the Arg⁴ Hɛ and Hη formed hydrogen bonds with the Ala¹ O in the Mut⁺ simulations, especially in the 300 K water simulation. Apparently the interaction between the Phe⁶ and His¹¹ (Table 1 and Fig. 3) as well as the other commonly found hydrogen bond between the Asn⁹ Hδ and the Arg⁴ O were the two interactions that could assist in maintaining helical structure, but π-helical, since they appeared uniquely when the peptides had a high π-helical content. Analogously to the Cpep⁺ simulations, the amidated C-terminus of the Mut⁺ peptide formed frequent hydrogen bonds with the Asn⁹ O and Ala¹⁰ O. Hydrogen bonds with the succinylated N-terminus were rare. Similarly to the Cpep⁰ simulations, the standard C- and N-termini of Mut⁰ formed very infrequent hydrogen bonds with the closest residues.

Solvent interactions

Peptide-solvent hydrogen bonds

At the beginning of all simulations the backbone amide hydrogens involved in α-helical hydrogen bonds were inaccessible to water or urea (Fig. 2). Once the simulations proceeded and the α-helical hydrogen bonds were disrupted, solvent penetration was observed. In general the backbone amide hydrogens closest to both ends of the initial α-helices were more prone to bind solvent. On the contrary, in all simulations most of the carbonyl oxygens were accessible to solvent and most of the time had water or urea molecules attached to them. At the ends of the helices, double or even triple hydrogen bonds were persistently found between one backbone carbonyl and one or more solvent molecules.

Peptide-water

Considering all simulations, there were on average between 25 and 32 peptide-water hydrogen bonds (≤2.4 Å) with water acting as donor and between 13 and 18 hydrogen bonds with water acting as acceptor (Table 2). The lowest and highest number of hydrogen bonds were found for Cpep⁺ and Mut⁺, respectively. The ratio between the number of peptide carbonyl oxygen-water hydrogen bonds and peptide amide-water hydrogen bonds was ∼2:1, which is slightly lower than the ratio (3:1) observed in a group of globular proteins (69). The higher frequency of hydrogen bond formation to backbone carbonyl groups compared with backbone amides has been attributed to a) the capability of the backbone carbonyl oxygen to form bifurcated hydrogen bonds, and not the backbone amides; b) in the helices to the tilt-out of the backbone carbonyl groups and tilt-in of the amide groups; and c) the general less solvent accessibility of backbone amides groups than the backbone carbonyl groups (69). When adding urea, the number of peptide-water hydrogen bonds increased for all peptides. On the contrary, increasing the temperature of the system did not induce a discernible increase of water-peptide hydrogen bond formation for Cpep⁺ and Mut⁺.

TABLE 2.

Average number of peptide backbone-solvent hydrogen bonds with 1.8 Å and 2.4 Å hydrogen bond cutoffs

	WHPO* 2.4 Å	WOPH 2.4 Å	UHPO 2.4 Å	UOPH 2.4 Å	WHPO 1.8 Å	WOPH 1.8 Å	UHPO 1.8 Å	UOPH 1.8 Å
Cpep+ 277 K	25.3	12.8			8.5	2.3
Mut+ 277 K	30.1	16.3			10.4	2.8
Cpep+ 300 K	25.4	12.8			7.9	2.1
Cpep0 300 K	25.7	15.7			8.4	3.1
Mut+ 300 K	29.0	15.7			9.6	2.5
Mut0 300 K	26.8	16.5			8.6	3.1
Cpep+ 8 M	28.7	14.7	7.7	3.5	9.1	2.3	1.7	0.9
Cpep0 8 M	26.0	17.1	9.3	5.1	8.3	3.4	2.3	1.4
Mut+ 8 M	32.2	17.4	9.7	4.8	10.9	2.8	2.1	1.1
Mut0 8 M	28.6	17.7	7.6	4.8	9.4	3.4	1.7	1.3

^*W, U, and P denote water, urea, and peptide, respectively; subscripts O and H denote acceptor and donor functions.

The increase of the number short hydrogen bonds (≤1.8 Å), when adding urea, was not as marked as with standard cutoff (2.4 Å). The number of short hydrogen bonds was a little higher for simulations with urea than those with water and decreased when increasing the temperature of the simulation. However, the ratio of short to standard average number of hydrogen bonds was slightly lower in the 8 M urea simulations than in the water simulations. In all cases the ratio of short to standard average number of hydrogen bonds with water acting as donor was higher than when water acted as acceptor.

The number of peptide-water hydrogen bonds per snapshot accepted by the peptide followed a normal distribution for each trajectory (Supplementary Material, Fig. S3, and Table S1). In all cases, for the 2.4 Å cutoff, the standard deviation (SD) of the distribution increased slightly for simulations in water at 300 K (SD = 0.0018–0.0021) compared to those in water at 277 K (SD = 0.0016–0.0018), but with urea as cosolvent the increase was substantial (SD = 0.0036–0.0046). For the 1.8 Å cutoff, the SD decreased slightly for simulations in water at 300 K while the same trend was observed with urea, although in this case the SDs were in general lower in all simulations.

Peptide-urea

As for the case of peptide-water, the urea molecules made about twice as many hydrogen bonds to the peptide backbone carbonyl oxygens as to the backbone amides. Although in this case, at most only nine backbone carbonyl-urea hydrogen bonds on average were present, representing 6% of the urea molecules. The two peptides that had most urea interactions were Cpep⁰ and Mut⁺. The ratio of short (≤1.8 Å) to standard (≤2.4 Å) hydrogen bonds was quite similar (∼25%) for backbone carbonyls and amides. Consequently urea oxygen and hydrogen had comparable facility to bind closely (≤1.8 Å) to the protein. Moreover, if a peptide forms a hydrogen bond with a urea oxygen, the probability that this hydrogen bond will be short is higher than if the peptide binds water instead.

Lifetime of the peptide-solvent hydrogen bonds

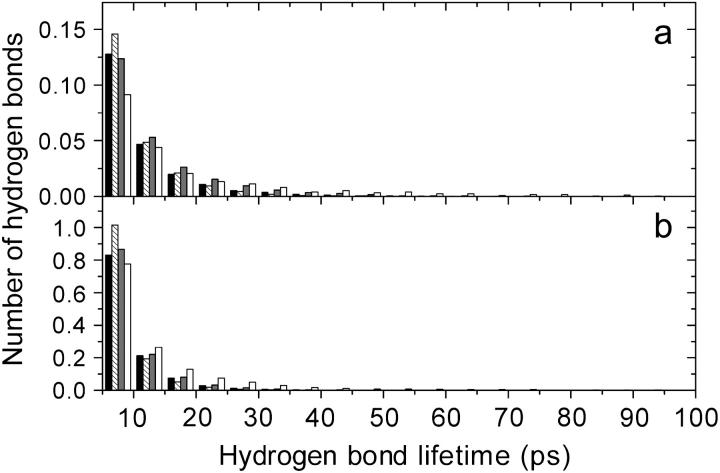
Water bound to the peptide mainly through forming hydrogen bonds with the peptide backbone carbonyls, whereas the peptide backbone amides formed approximately half of the number of hydrogen bonds that the backbone carbonyls formed with water (Table 2). The majority of the hydrogen bonds between peptide carbonyl and water had a very brief lifetime, ∼7.5 ps (Fig. 5 b). The water simulations at 300 K were those where the brief hydrogen bonds between peptide carbonyl and water were the most abundant, whereas urea did not influence these hydrogen bonds so much.

FIGURE 5.

Cpep⁺ backbone-solvent hydrogen bond lifetime distributions. The histograms are normalized by the simulation time as well as by the number of solvent (water or urea) molecules in the simulations. (a) Backbone amide-solvent hydrogen bonds. (b) Backbone carbonyl-solvent. Peptide backbone, water hydrogen bonds in water at 277 K (black), in water at 300 K (striped), in the 8 M urea simulation (shaded), and peptide backbone—urea hydrogen bonds in the 8 M urea (white). The lifetime axis is truncated at 100 ps, but there are several backbone-urea hydrogen bonds with lifetimes longer than 100 ps.

On the contrary, the hydrogen bonds that the peptide backbone amides formed with water (mean lifetimes between 9.5 and 13.6 ps; Table 3 and Fig. 5 a) had longer lifetimes than with the backbone carbonyls and even the hydrogen bonds with 40–45 ps lifetime had statistical importance here. Still, the backbone amide-water hydrogen bonds had the shortest lifetimes in the 300 K water simulations. For all peptides there was a clear difference between the backbone amide-water hydrogen bonds in pure water and in 8 M urea, particularly between the water simulations at 300 K and 8 M urea. In general, the mean lifetimes were ∼2 ps longer in the 8 M urea simulations. The mean lifetimes were 8.5–10.8 ps in water at 300 K and 10.2–13.6 ps in 8 M urea (Table 3).

TABLE 3.

Peptide backbone-solvent hydrogen bond mean lifetimes (ps)

	PH-WO*	PO-WH	PH-UO	PO-UH
Cpep+ 277 K	9.5	7.5
Cpep+ 300 K	8.5	6.6
Cpep+ 8 M	11.4	7.6	16.7	12.0
Cpep0 300 K	8.7	6.9
Cpep0 8 M	10.2	7.7	22.5	11.2
Mut+ 277 K	13.4	7.3
Mut+ 300 K	10.8	6.4
Mut+ 8 M	13.6	7.6	21.3	11.6
Mut0 300 K	9.6	6.8
Mut0 8 M	11.3	7.5	19.2	11.0

^*W, U, and P denote water, urea, and peptide, respectively; subscripts O and H denote acceptor and donor functions.

The peptide side chains formed only slightly more hydrogen bonds with solvent hydrogens than with oxygens and with very similar lifetimes (data not shown) although in general, the hydrogen bonds that the peptide side chains accepted from the solvent had longer lifetimes (mean lifetimes from 8.3 ps for the Cpep⁰ in the water simulation to 11.2 ps for Mut⁺ in the 8 M urea simulation) than the hydrogen bonds with the backbone amides. On the other hand, the peptide formed more long-lived hydrogen bonds with urea than with water (Table 3 and Fig. 5), in particular the hydrogen bonds that urea accepted from the peptide had an average 50%–100% longer lifetimes than those accepted by water. In many cases the urea molecules formed hydrogen bonds to the backbone with lifetimes longer than 70 ps, whereas the water molecules formed such long hydrogen bonds very rarely and almost exclusively in the 8 M urea simulations. In fact, in the Cpep⁺ simulation, urea formed several hydrogen bonds to the backbone amides with lifetimes ∼100 ps and to the backbone carbonyl ∼200 ps. Even longer lived hydrogen bonds between urea and the peptide side chain were observed (up to 425 ps in the case of the Cpep⁺). Also, in several cases urea molecules made simultaneous bonds to different residues in the peptide, in particular with the side chains. Some of these bridges were present 50%–60% of the simulation, with individual urea molecules occupying the same bridging position for as much as 240 ps. Moreover, side chain-urea-backbone bridges were also formed during a relatively long time (the Glu² backbone amide was bridged by urea to its own side chain 8% of the Cpep⁺ simulation).

Solvation number

Appreciable differences were found between simulations in pure water and 8 M urea solutions (Table 4). In pure water, both at 277 K and 300 K, ∼60% of the water molecules within the 2.4 Å solvation shell made hydrogen bonds with some peptide oxygen, whereas when urea was present as cosolvent, ∼90% of the first shell water molecules made hydrogen bonds with some peptide oxygen. With respect to the hydrogen bonds between water oxygen and peptide, the number of hydrogen bonds per water molecule within the shell was ∼0.9 in pure water and 1.4 in the urea simulations, that is, in presence of urea all the water oxygens within the hydration shell made at least one hydrogen bond to the peptide and 40% of them formed bifurcated hydrogen bonds. The number of urea-peptide hydrogen bonds per urea molecule in the first solvation shell (Table 4) was ∼0.8 for hydrogen bonds to backbone carbonyls. This quantity increased for the backbone amide-urea hydrogen bonds (∼1.0 hydrogen bond/urea molecule).

TABLE 4.

Solvation number and number of hydrogen bonds

	Nsol* WHPO	NHB†WHPO	NHB/Nsol‡WHPO	Nsol*WOPH	NHB†WOPH	NHB/Nsol‡WOPH	Nsol*UHPO	NHB†UHPO	NHB/Nsol‡UHPO	Nsol*UOPH	NHB†UOPH	NHB/Nsol‡UOPH
Cpep+ 277 K	43.4	25.3	58.4	14.9	12.8	86.1
Mut+ 277 K	48.4	30.1	62.1	17.5	16.3	93.2
Cpep+ 300 K	43.8	25.4	57.9	14.9	12.8	85.9
Cpep0 300 K	44.1	25.7	58.2	16.5	15.7	95.5
Mut+ 300 K	47.3	29.0	61.4	17.2	15.7	91.3
Mut0 300 K	46.0	26.8	58.2	17.1	16.5	96.9
Cpep+ 8 M	31.9	28.7	89.8	10.7	14.7	137.8	9.46	7.70	81.4	3.69	3.52	95.4
Cpep0 8 M	29.2	26.0	89.3	11.4	17.1	150.1	9.89	9.33	94.4	4.68	5.12	109.4
Mut+ 8 M	34.6	32.2	93.0	12.4	17.4	140.8	11.14	9.73	87.3	4.87	4.82	99.0
Mut0 8 M	31.8	28.6	90.0	11.8	17.7	149.5	8.54	7.58	88.8	4.23	4.80	113.4

^*Number of water or urea (W or U) hydrogen or oxygen atoms (H or O) within 2.4 Å of the peptide (P) oxygen (O) or hydrogen atoms.

^†Number of hydrogen bonds formed by solvent (W or U) atoms (O or H) and the peptide with a 2.4 Å hydrogen bond cutoff.

^‡Fraction (%) of solvent atoms (H or O) within 2.4 Å of the peptide (P) oxygen or hydrogen (O or H) atoms that donate (accept) hydrogen bonds to the peptide.

For simulations in pure water the peptide solvation shell (r_solv = 3.5 Å) contained on average between 121 (Cpep⁰) and 132 (Mut⁺) water molecules, whereas for simulations in urea the number of water molecules decreased to between 80 (Cpep⁰) and 94 (Mut⁺), but in this case the hydration shell contained on average between 25 (Cpep⁰) and 30 (Mut⁺) urea molecules as well (Table 5).

TABLE 5.

Solvation number around different parts of the peptide

	Water PEPT*	Urea PEPT*	Water POL†	Urea POL†	Water NPOL‡	Urea NPOL‡	U/W§ PEPT*	U/W§ POL†	U/W§ NPOL†	U/W§ TOT	Δ¶PEP*	Δ¶POL†	Δ¶NPOL†
Cpep+ 277 K	127.3		68.8		115.9
Mut+ 277 K	132.9		80.7		114.8
Cpep+ 300 K	127.4		70.2		114.5
Cpep0 300 K	121.5		72.7		105.5
Mut+ 300 K	129.6		77.7		112.4
Mut0 300 K	126.2		75.6		110.1
Cpep+ 8 M	90.0	25.4	49.1	15.9	82.5	23.6	0.28	0.32	0.29	0.23	24	43	26
Cpep0 8 M	80.0	24.9	47.5	17.7	70.0	21.9	0.31	0.37	0.31	0.21	49	79	50
Mut+ 8 M	94.8	29.7	56.1	20.4	82.4	26.0	0.31	0.36	0.32	0.23	38	60	39
Mut0 8 M	86.4	22.8	50.9	15.8	75.7	20.2	0.26	0.31	0.27	0.21	27	49	28

^*Number of solvent molecules within 3.5 Å of the whole peptide.

^†Number of solvent molecules within 3.5 Å of the polar peptide atoms.

^‡Number of solvent molecules within 3.5 Å of the apolar peptide atoms.

^§Denotes the ratio of urea to water molecules.

^¶Increment in % of the fraction U/W respect to the bulk (U/W TOT).

To detect differences between the solvent around the peptide and in the bulk in the 8 M urea-aqueous solution, the mean number of urea molecules per water molecule was calculated (Table 5). Although in bulk solvent there was ∼0.22 urea molecules per water molecule, this ratio increased to 0.24 for Cpep⁺, 0.49 for Cpep⁰, 0.38 for Mut⁺, and 0.27 for Mut⁰ in the hydration shell (r_solv = 3.5 Å), demonstrating that urea accumulated in excess around the peptide (Fig. 6). This effect was more pronounced around the polar atoms of the peptide, where the ratios were between 0.43 (Cpep⁺) and 0.79 (Cpep⁰).

FIGURE 6.

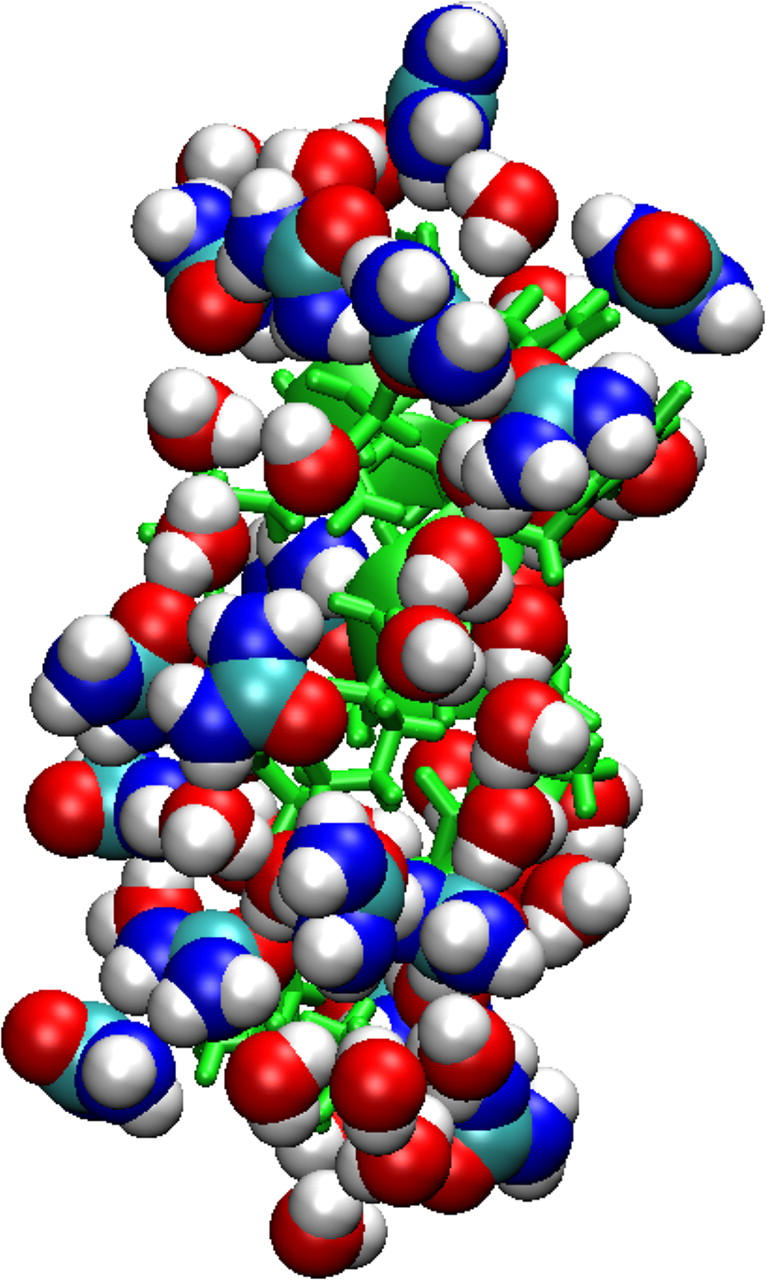
Urea accumulates in excess at the protein surface. Typical snapshot of the Cpep⁺ simulation in urea. A solvent molecule is included in the shell if any of its atoms are located within 2.4 Å of the protein.

The correlation time obtained from the second order rotational diffusion correlation functions was 2.2 ps for the water molecules around the peptide in the simulation of the Cpep⁺ in water at 277 K. This correlation time increased 35% in the 8 M urea simulation.

DISCUSSION

Side-chain interactions were responsible for the high stability of the Cpep⁺ as was also found in the case of the ribonuclease C-peptide (70). Furthermore, these α-helical stabilizing side-chain interactions were correlated and interdependent. The simulations revealed that the Cpep⁺ in water was the most conformationally stable peptide. At 277 K, its backbone RMSD was always below 2 Å (calculated with reference to the start conformation), indicating that the conformational features of the backbone were largely intact throughout the simulation. In contrast, the other peptides immersed in the different solvents lost at least part of their helical structure. This mirrors largely the experimental behavior of the peptides in the respective solvents. At 278 K, both CD and NMR experimental data provide direct evidence for a highly α-helical conformation for peptide Cpep⁺ and highly disordered conformation for peptide Mut⁺. Based on both the NMR chemical shifts and ³J_HNHα scalar coupling constants, the helical conformation in Cpep⁺ is confined largely to residues 4–10 with residues 1–3 and 11–13 displaying clear indications of conformational variability. This very different conformational behavior, despite identical amino acid compositions, underscores the influence of the amino acid sequence (specific side-chain interactions) in determining helix content.

The conformations that the peptides sampled during the simulations depended mainly on their specific sequence but also on the effect of the solvent. In particular, the Glu²⁻… Arg¹⁰⁺ salt bridge formed in the Cpep⁺ was of vital importance for maintaining the α-helical structure of this peptide. The hydrogen bonds formed between the side chains of these two residues acted as a clip stabilizing other side-chain interactions at the other face of the helix such as the interactions between His¹² and the Phe⁸ or Asn¹¹ side chains that in conjunction with the salt bridge maintained the backbone α-helical structure in the Cpep⁺ simulation in water at 277 K. It was also important how the two hydrogen bonds between the Glu² and Arg¹⁰ side chains were established; indeed in Cpep⁺ in water at 277 K, the hydrogen bonds were formed by the Hɛ and one of the Hη hydrogens of Arg¹⁰, instead of with the two Hη hydrogens as in the simulations in water at 300 K and in 8 M urea, where helical unwinding at the C-terminus was observed. The hydrogen bonds formed in the 277 K water simulation kept the Arg¹⁰ closer bound to Glu², restraining the peptide backbone structure, whereas in the other simulations the Glu² side chain had the possibility to bind simultaneously the Lys⁷ side chain, thus hindering the interaction between Asn¹¹ and His¹² and eventually breaking the interaction with Arg¹⁰. The hydrogen bond between the Asn¹¹ and His¹² side chains, which was only displayed in the water at 277 K simulation, corresponds to a similar hydrogen bond in the native protein (55) between the Gln¹¹ and His¹² side chains. In the Cpep⁰, Mut⁺, and Mut⁰ simulations, the peptide side chains scarcely formed hydrogen bonds that could maintain the α-helical structure.

Unwinding of the α-helix was achieved in all the simulations of all peptides except for the Cpep⁺ simulation in water at 277 K, and it is likely that complete denaturation would be achieved in longer simulations. However there is some discrepancy about the timescale of α-helix formation/unfolding with further implications in the protein folding models. Laser T-jump studies suggest fast formation (nanosecond) (71), whereas stopped-flow CD proposes a millisecond timescale (72). MD simulations of Ala- and Gly-based pentapeptides also show very fast helix nucleation times (0.1–1 ns) (73) although from a Zimm-Bragg based model for helix-coil transition and results from free energy simulations a dramatic dependence of both folding and unfolding times (≤100 ns) on the length of the polypeptide has been pointed out (74). The loss of α-helical hydrogen bonds lead to partial α-helical unwinding, in most cases starting from the C-terminus and propagating toward the N-terminus, as has been observed in earlier studies of α-helix denaturation (75,76).

In our simulations the loss of α-helical hydrogen bonds was related to the rupture of some relevant side-chain interactions and solvent penetration and in general led to π-helical hydrogen bond formation with a further cooperative propagation of the disruption, in most cases, toward the N-terminus. The Lifson-Roig helix coil theory states a high penalty for formation of π-helical segments from a coil, according to the experimental observation of the low amount of π-helix found in nature. However, in analogy to the helix-coil theory formalism of Rohl and Doig for conversion between 3₁₀/α-helical segments (77), it could be possible that transitions between α- to π-helical hydrogen bonds or vice versa will have a low penalty allowing such transitions. Even though π-helical formation has been observed in different MD simulations (78–82), it has been suggested that this is a force field artifact (83); in our simulations π-helix formation is mainly related to peptide instability, and in the case where the peptide is highly stable (Cpep⁺ simulation in water at 277 K) π-helical hydrogen bonds were rarely found (Fig. 2).

Behavior of the solvent around the peptide

The two peptides with most urea in the first solvation shell (Cpep⁰ and Mut⁺) were also those in which the peptides have the highest total averaged ASA. Protection of the backbone amide hydrogens of the C-terminus half (residues 6–12) from the solvent was observed for the Cpep⁺ helix in water as well as in urea, whereas for the rest of the peptides, principally Mut⁺ and Mut⁰, a higher number of the backbone amide hydrogens were accessible to the solvent. The solvent penetration of the backbone amides was related with subtle changes in the intrahelical hydrogen bonding pattern. On the contrary, the backbone carbonyl oxygens of all simulations were accessible to the solvent and most of the time had at least one solvent molecule attached to them. When the backbone was exposed to the solvent, water always preceded urea in solvating these groups. Furthermore, in the Cpep⁺ simulations the fraction of solvent molecules in the first solvation shell (r_solv = 2.4 Å) forming hydrogen bonds to the peptide was lower than for all the other peptides, as if the stability of the helix depends on its ability to avoid too many hydrogen bonds with the solvent.

The effect of urea was remarkable: the number of peptide-water hydrogen bonds increased substantially when urea was present as cosolvent, although in these simulations there were fewer water molecules in the boxes. In particular, the number of peptide carbonyl-water hydrogen bonds increased ∼13%. In addition, the duration of the backbone amide hydrogen-water oxygen bonds increased too, as well as the dipole rotational correlation times of the water molecules within the solvation shell around the peptide. The water molecules get restricted, losing mobility, and the hydrogen bonds last longer than with pure water. Magnetic relaxation dispersion measurements of the urea-induced denaturation of intestinal fatty acid-binding protein (I-FABP) observe a much more retarded rotation of water in the denatured state than for a fully solvated polypeptide (84). Although the peptide-urea hydrogen bond lifetimes that we observe are longer than in the peptide-water case, they are still limited to below 425 ps. We do not find any urea-binding sites with ns lifetimes as has been reported for I-FABP (84), indicating a difference between proteins and peptides in this respect. However, the ratio of short (≤1.8 Å) to long (≤2.4 Å) peptide-water hydrogen bonds generally decreased in the 8 M urea simulations. A previous simulations has observed a drop in the number of short water-water hydrogen bonds, suggesting a weakening of the water structure (20).

The enhanced ability of water molecules to form hydrogen bonds with the peptide in the 8 M urea simulations was also obvious when the water molecules accepted hydrogen bonds from the peptide. Indeed, when a water molecule in an 8 M urea simulation got close to the peptide it always accepted at least one hydrogen bond from it. Furthermore, 40% of the water oxygens of the solvation shell (r_solv = 2.4 Å) formed bifurcated hydrogen bonds to the peptide. It can be pointed out that in general for such bifurcated hydrogen bonds the donor-acceptor distances cannot be very short, if the donor of both hydrogens is not the same atom, but still they can have relatively long lifetimes. Also most of the water hydrogens in the 2.4 Å solvation shell of the 8 M urea simulations formed hydrogens bond with the peptide (∼90%), whereas in pure water it was <60%.

Most of the urea molecules (80–90%) of the first solvation shell participate in hydrogen bonds with the polar groups of the peptide, as seen in an 8 M urea solution MD simulation of barnase (48). In several cases urea molecules bridged different parts of the peptide with very long residence times, indicating a very favorable urea-peptide interaction. The lifetimes of the hydrogen bonds that the peptide backbone formed with urea were longer than with water in agreement with experimental and MD results (20,85), in particular the increment was more pronounced when urea accepted hydrogen bonds from the peptide, which is consistent with the MD simulations of Klimov et al. (86). Moreover urea accumulated in excess around the peptide, which has also been seen in other MD simulations (20,47,48) especially around the polar groups. Similarly, an excess of guanidine hydrochloride molecules in the protein surface has been observed (87). It has been shown that the water molecules with long residence times associated with myoglobin are those located in cavities or clefts and that the local geometry of the protein surface is the main determinant of water mobility (88). Since there is an excess of urea molecules in the solvation shell around the peptide and urea interacts very favorably with the peptide with very long residence times, the water molecules in the shell get trapped between the urea molecules and the peptide, thus leading to reduced mobility (Fig. 7).

FIGURE 7.

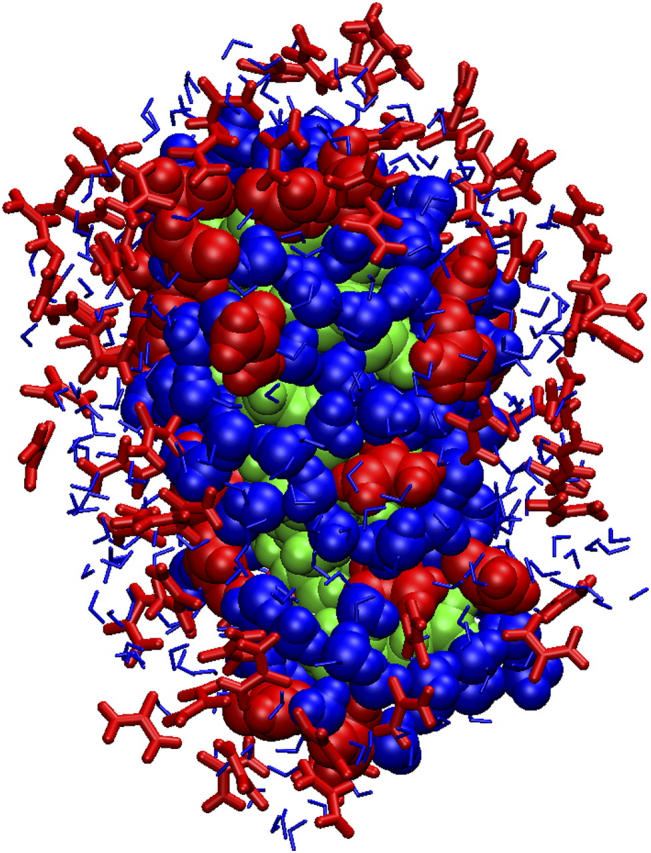
Water entrapment. Water molecules become trapped between urea molecules and the peptide at different positions in this snapshot of the Cpep⁺ simulation in 8 M urea. The solvation shell is 4 Å around the peptide. The peptide is green, and urea and water molecules are red and blue, respectively.

When increasing the temperature of the simulation the amount of peptide-water hydrogen bonds remained similar or slightly increased and as expected shortened the hydrogen bonds' lifetime between water and peptide (mean lifetimes <10 ps). On the contrary, the peptide flexibility increased and the ends of the helix could form hydrogen bonds with the other residues that destabilized the initial α-helical structure of the peptide. In consequence, these results suggest that the unfolding mechanisms induced by thermal denaturation and by urea are of a different nature.

Our results, which concern the behavior of water and urea near the peptide, suggest that urea acts indirectly in the denaturation process, decreasing water mobility around the peptide, increasing the ability to form peptide water hydrogen bonds with longer lifetimes, and also directly by giving urea molecules access to the polar groups of the peptide, thus providing a better peptide solvation than pure water.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.