Abstract
The static fluid mosaic model of biological membranes has been progressively complemented by a dynamic membrane model that includes phospholipid reordering in domains that are proposed to extend from nanometers to microns. Kinetic models for lipolytic enzymes have only been developed for homogeneous lipid phases. In this work, we develop a generalization of the well-known surface dilution kinetic theory to cases where, in a same lipid phase, both domain and nondomain phases coexist. Our model also allows understanding the changes in enzymatic activity due to a decrease of free substrate concentration when domains are induced by peptides. This lipid reordering and domain dynamics can affect the activity of lipolytic enzymes, and can provide a simple explanation for how basic peptides, with a strong direct interaction with acidic phospholipids (such as β-amyloid peptide), may cause a complex modulation of the activities of many important enzymes in lipid signaling pathways.
INTRODUCTION
The reactions catalyzed by lipid metabolic enzymes are part of many cellular processes. The knowledge about their mechanisms can contribute to the understanding of regulation and signaling phenomena in cells. Among the lipid phosphatases, the enzymes of the phospholipase C family (PLC) (1) are key players involved in lipid signaling pathways in all cells. These enzymes, with reaction products affecting both intracellular levels of free calcium ([Ca+2]i) and protein phosphorylation (2,3) can regulate secretion, transport, metabolism, and gene transcription and translation. To make kinetic measurements, and because phospholipases react best in a lipid-water interface, different experimental systems have been developed using phospholipid vesicles, phospholipid and detergent-mixed micelles or phospholipid monolayers. As a first step in the catalytic process, the soluble enzyme would bind to the lipid phase, allowing many catalytic cycles with the substrate in that phase before the enzyme detaches from the interface and returns to the solution.
A model, based on the theory known as surface dilution kinetics (4), has been proposed to interpret the kinetic measurements of phospholipases. This theory can estimate the main enzyme kinetic parameters considering the change in the enzyme reaction rate due to the change in the substrate concentration in the lipid phase (“surface dilution”). Similar to most enzyme kinetic models, this theory applies the mass action law and the steady-state assumption for enzyme intermediaries. When a molecule involved in some elementary kinetic step is dissolved in the water phase, the calculations consider its concentration in that phase. In the case of a molecule dissolved in the lipid phase, the calculations consider its mole fraction in the lipid phase. As a result of this theory and validated by many kinetic experiments, a mechanism common to several lipid-metabolizing enzymes has been proposed. This mechanism proposes two binding steps of the enzyme: a first binding step to the lipid phase and a second binding step to the substrate. Depending on how the soluble enzyme binds to the lipid phase there are two possible models for this mechanism. When the enzyme binds specifically to the phospholipid substrate, the model is called phospholipid binding model (Fig. 1 A). When the enzyme binds to any lipid phase region, the model is called surface binding model (Fig. 1 B). The following are the kinetic equations derived for the phospholipid binding model (Eq. 1) and the surface binding model (Eq. 2) (4,5):
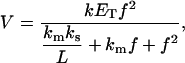 |
(1) |
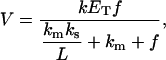 |
(2) |
where V is the rate of product formation (mol/(vol time)), f is the mole fraction of the substrate (dimensionless), k is the catalytic time constant (time−1), 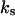 is the dissociation constant (mol/vol),
is the dissociation constant (mol/vol), 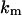 is the constant (dimensionless),
is the constant (dimensionless), 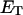 is the total enzyme concentration (mol/vol), and L is the total lipid concentration (mol/vol).
is the total enzyme concentration (mol/vol), and L is the total lipid concentration (mol/vol).
FIGURE 1.
(A) Phospholipid binding model. In this model the enzyme binds specifically to the phospholipid substrate. (B) Surface binding model. In this model the enzyme binds to any lipid phase region.
Thus far, the kinetic models that have been described in the literature only consider homogeneous lipid phases. However, it is known that phospholipids can reorder in lateral domains (see reviews (6,7)). These domains can arise from the interaction between the same phospholipid molecules, or from the interactions between phospholipids and the cytoskeleton or charged soluble molecules. Related to this last situation, a very interesting case is the molecular induction of acidic phospholipid domains that are important for metabolism and signaling. For example, phosphatidylinositol 4,5-biphosphate (PIP2) and phosphatidylserine (PS), can be reordered in lateral domains because of the direct interactions with ions such as Ca2+, basic molecules such as spermine (a tetravalent ligand), the protein myristoylated alanine-rich C kinase substrate (MARCKS), or pentalysine (Lys-5), one of the first five amino acid residues of bovine MARCKS (8). Glaser et al. (8) have suggested that a peptide induction of PIP2 (the substrate of PLC) domains could induce a reduction of the PLC activity, affecting the path of phosphoinositide signaling. A similar idea has been proposed by Zhou et al. (9) in relation to an eventual phosphatidyl inositol reordering induced by Ca2+ that could explain the reduction by this ion of the hydrolytic activity of PLC-γ1 on this substrate. In contrast to these artificial lipid binary membrane systems where formation of microdomains has been studied, the structure and dynamics of lipid microdomains in biological membranes are expected to be widely diverse and influenced by a scaffolding of cell proteins (10).
The explanations given in the literature related to the effects of substrate enriched domain formation on enzyme activities in lipid phases have not been systematically developed in a mathematical formulation. Furthermore, we think that they appear somewhat contradictory. Thus, in the works cited above, it was suggested that, to explain a decrease in PLC activity caused by formation of PIP2 or phosphatidylinositol (PI) domains, the enzyme could be exposed to less substrate outside these domains and therefore the total enzyme activity would be diminished. In contradiction with this suggestion, the high increase of PLCβ activity obtained with moderated increases in the mole fraction of PIP2, has been attributed to the formation of enriched substrate domains into which the enzyme could also be included (11). Hence, it is not clear whether the formation of domains enriched in a phospholipid substrate produce an increase or a decrease of the total enzymatic activity, considering that the activity can arise from both inside or outside these domains (e.g., Fig. 2). Therefore, we wish to propose a comprehensive quantitative model that explicitly takes into account all the enzyme substrate interactions in the different phospholipid phases.
FIGURE 2.
Effects of phospholipid domains on enzyme activity. (A) Homogeneous substrate distribution. (B) Biphasic substrate distribution. In panel B, two phases can be distinguished: the domain phase that corresponds to the lipid phase with the largest substrate mole fraction and the nondomain phase that corresponds to the surface with low substrate mole fraction. •, phospholipid substrate; ○, nonreactive lipid;  , enzyme.
, enzyme.
THEORETICAL FRAMEWORK
Our analysis of lipase activities in membranes assumes that in each possible lipid phase structure (micelle, liposome, or monolayer), all lipids in the lipid-water interface expose the same area to the aqueous phase. Hence, the surface of the lipid phase is proportional to the amount of lipid molecules.
To understand how the substrate lateral reordering can affect the enzyme kinetics, we developed here a generalization of the two-step model of enzyme binding to a lipid phase, allowing for a condition where the substrate can be distributed in two coexisting lateral phases. In this case, and as it has been done in homogenous interfaces (4), we apply the kinetics surface dilution theory to the surface binding model and to the phospholipid binding model.
We define the redistribution effect as the kinetic change obtained by going from a homogeneous substrate distribution (Eqs. 1 and 2) to a heterogenous substrate distribution (domain formation). When the domain has been induced by soluble peptides (e.g., basic peptides such as Lys-5) that are located in the lipid-water interface interacting directly with the phospholipid substrate (i.e., acidic phospholipid such as PIP2), in addition to the redistribution effect, we expect a competitive effect. This effect would be due to the fact that there is less free substrate that can bind to the enzyme, i.e., the domain-inducing peptide would compete with the enzyme for the substrate. In this work, we propose that the superposition of both the redistribution and competitive effects can explain some results reported in the literature. We will not consider the inhibitory effect caused by the substrate dilution due to the protein insertion in the bilayer. In this respect, we consider that the number of enzyme molecules bound to the lipid phase is much smaller than the number of phospholipid substrate molecules, and that the peptide that induces the phospholipid domain either would not penetrate the lipid phase or its interface concentration can be considered negligible.
Thus, in the following work we have made a theoretical analysis within the framework of the phospholipid binding model and the surface binding model in relation to the effect of phospholipid substrate domain formation. To simplify the reading of this work, we have set aside in Appendix I (“Lipid phase model with domain formation”) the theoretical analysis, mathematical derivations, and calculations for the phospholipid binding model, the surface binding model, and the competitive effects of the domain-inducing peptide. Similarly, we present in Appendix II the derivations for substrate binding to the domain-inducing peptide.
DISCUSSION
In this work we have theoretically studied the effect of losing membrane homogeneity on the kinetics of two binding models for enzymes acting on a lipid phase (Appendixes I and II). In the nonhomogenous model we assumed that the substrate reordered itself in two phases with different mole fractions. The derived kinetic equations for the biphasic membrane model give rise to the known homogenous kinetic model equations when the phases tend to homogeneity.
In this model we have shown that going from a homogeneous to a biphasic membrane can produce a change in total enzymatic activity, depending on the characteristics of enzyme binding to the lipid phase. This effect on enzyme activity, named, by us, reordering effect, exist only for the phospholipid binding model, but not for the surface binding model, and it consists of an increase of the total enzymatic activity. This result is due to the fact that substrate reordering in the lipid phase is associated with the redistribution of the enzyme in the same phase. Analysis of the two enzyme kinetic models studied here showed that formation of domains induces an increase in the enzyme fraction bound to the domain phase and a decrease of the enzyme fraction bound to the nondomain phase (Eqs. 28 and 33, Appendix I).
For the phospholipid binding model, the increase of the enzyme bound to the domain phase is enough to obtain a global increase of enzyme bound to all the lipid phases (Eq. 29, Appendix I). The increase of the enzyme concentration in the lipid phase, in the phospholipid binding model, will determine that the binding to the substrate in the domain effectively occurs in an enzyme-enriched environment, facilitating the catalytic step. Thus, in this case, the rise of the enzymatic activity in the domain overcomes the fall of the enzymatic activity in the nondomain, giving as a result that the total activity is increased (Fig. 3). A similar conclusion can be obtained from Eq. 27 (Appendix I). We conclude that to obtain an increase in the total enzyme activity it is enough to increase at least one of the two domain variables (area or substrate mole fraction), as long as the other variable would not decrease.
FIGURE 3.
Effect of substrate distribution in lateral domains on total enzyme activity. (A) Total rate of product formation in the lipid phase as a function of the domain phase variables  (substrate mole fraction) and a (total area fraction). These variables can only have values that fulfill the following condition:
(substrate mole fraction) and a (total area fraction). These variables can only have values that fulfill the following condition: 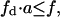 because of the conservation and equivalence of lipid areas (Eq. 7). (B) Projection of the surface shown in panel A on the plane
because of the conservation and equivalence of lipid areas (Eq. 7). (B) Projection of the surface shown in panel A on the plane 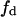 vs. a, employing a chromatic scale to denote the V-values. V-values were normalized to the rate of product formation in the homogeneous lipid phase. In Fig. 3, A and B, the border lines with
vs. a, employing a chromatic scale to denote the V-values. V-values were normalized to the rate of product formation in the homogeneous lipid phase. In Fig. 3, A and B, the border lines with 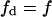 or
or 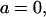 correspond to V=1; f = 0.01, L = 200 μM. The values for the kinetic parameters used in the calculations correspond to those of the enzyme PLCβ acting on PIP2 in Triton X-100 micelles (13): km = 0.13, ks = 170 μM.
correspond to V=1; f = 0.01, L = 200 μM. The values for the kinetic parameters used in the calculations correspond to those of the enzyme PLCβ acting on PIP2 in Triton X-100 micelles (13): km = 0.13, ks = 170 μM.
In contrast, the surface binding model predicts that the total enzyme bound to the lipid phase does not change when the enzyme becomes redistributed due to domain formation (Eq. 34, Appendix I). The increase in enzyme activity in the domain phase is cancelled out with the decrease in enzyme activity in the nondomain phase. Therefore, the formation of domains does not cause a change in the total enzyme activity.
The previous predictions for the phospholipid binding model can be contrasted with reported data in the literature. Thus, the PLCβ kinetic data obtained employing micelles have been fitted to the phospholipid binding model using Hill coefficients (12–14). However, the same type of kinetic equation did not fit experiments in monolayers that showed large increases in enzyme activity after small increases in the PIP2 fraction (11). The analysis of pressure versus area isotherm of the monolayers with different concentrations of PS and PIP2 suggested a nonhomogeneous distribution of the lipids. As a consequence it was proposed that the PIP2 molecules get together into enriched lateral domains because it should favor the PLCβ activity. This hypothesis is in agreement with the effect of substrate redistribution predicted here for the phospholipid binding model. Another interesting result is the rise in the PLC (δ1 and δ3) activity obtained after addition of polyamines or basic proteins such as spermine, protamine, histone, and melittin (15). Considering that many of these basic molecules can induce formation of acidic phospholipid domains in membranes, this rise of enzyme activity can also be explained from our phospholipid binding kinetic model with biphasic distribution.
In our nonhomogeneous surface binding model, when a phospholipid domain-inducing peptide competes with the enzyme for the substrate, its competitive effect always diminishes the enzymatic activity (Eq. 37, Appendix I) (This conclusion was based on the reasonable assumption that the substrate is in equilibrium with the peptide, and that the peptide in the lipid phase does not penetrate into the bilayer). In the phospholipid binding model, the decrease in enzyme activity due to this competitive effect opposed the rise in activity due to substrate redistribution, producing a maximum activity for some domains, and an acute declination for others (Fig. 4). As this reasoning predicts, a decrease in activity was observed in PLCβ experiments that used vesicles with acidic phospholipid domains induced by the basic molecules Lys-5, spermine, and MARCKS (151–175) (8).
FIGURE 4.
Effect of substrate reordering in lateral domains on total enzyme activity in the presence of a basic phospholipid binding peptide. (A) Total rate of product formation in the lipid phase as a function of the domain phase variables 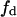 (substrate mole fraction) and a (total area fraction), for conditions that fulfill
(substrate mole fraction) and a (total area fraction), for conditions that fulfill 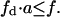 (B) Projection of the surface shown in panel A on the plane
(B) Projection of the surface shown in panel A on the plane 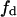 vs. a, employing a chromatic scale to denote the V-values. V was normalized for the product rate formation in a lipid homogeneous phase in the absence of domain-inducing peptide. In Fig. 4, A and B, the border lines with components
vs. a, employing a chromatic scale to denote the V-values. V was normalized for the product rate formation in a lipid homogeneous phase in the absence of domain-inducing peptide. In Fig. 4, A and B, the border lines with components 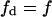 or a = 0, correspond to V = 0.9998. In the calculations shown in this figure we assumed that the enzyme PLCβ acted on PIP2 (valence 3), in the presence of the basic peptide pentalysine (CP = 1 mM, effective valence 5, KP = 0.1 M−1); f, L, km, and ks have the same values as in Fig. 3.
or a = 0, correspond to V = 0.9998. In the calculations shown in this figure we assumed that the enzyme PLCβ acted on PIP2 (valence 3), in the presence of the basic peptide pentalysine (CP = 1 mM, effective valence 5, KP = 0.1 M−1); f, L, km, and ks have the same values as in Fig. 3.
Validity of the theory and proposed experiments
To validate our proposed kinetic models, besides the kinetic measurements, it is important to determine the ratios of enzyme bound to the two phases and the mole fraction of the substrate as described in Eqs. 28 and 33 (Appendix I). Furthermore, measurements of the total enzyme bound to the lipid phase can be contrasted with Eqs. 29 and 34 (Appendix I) to distinguish between the two previously mentioned kinetic models. This would allow distinguishing the phospholipid binding model, which predicts changes in total membrane enzyme upon domain formation, from the surface binding model, that predicts constant total membrane enzyme upon domain formation. It is important to underline that these equations have been deduced for a certain range of substrate concentration in the lipid phase. Outside this range, approximation of equality between the kinetic parameters of the domain and nondomain phases would not be correct.
In our lipid biphasic model, we do not consider effects due to the border of the phases. This condition, although a simplification, gives amplitude to the model because the domain can be represented as a single total continuous domain, resulting from the sum of all the individual domains, as long as they have the same substrate mole fraction. Thus, besides accounting for the enzyme kinetics of a lipid phase system with domain subphases, our results can also be extended to a micelle or liposome system composed of a mixture of two types of micelles or liposomes with homogeneous lipid phases, but each one with a different substrate mole fraction. In this mixture of liposomes or micelles with different substrate concentrations, the total lipid surface of the micelles or liposomes with the larger substrate mole fraction could be equivalent to the domain phase. The rest of the lipid surface, belonging to the micelles or liposomes with smaller substrate mole fraction, would be equivalent to the nondomain phase. Such experimental design could contrast directly our kinetic predictions.
Theory projections
The projection of our results to a mixed micelle (or liposome) system, such as the one previously described, could explain part of the cooperativity reported in in vitro experiments for some phospholipid binding enzymes. As discussed above, heterogeneity of the substrate mole fraction in different individual micelles (or liposomes) would make such a system analogous to a lipid phase with multiple domains. Thus, our phospholipid binding model would predict an increase in the enzyme activity in a heterogeneous (concentration) micelle population, compared to a homogeneous micelle population. This increase could be erroneously interpreted as cooperativity.
It is known that proteins with strong phospholipid affinities can induce phospholipid domains (16). Then, it is possible that many complex metabolic effects of these types of proteins can be explained in a simple manner considering a phospholipid binding model and as a result of the balance between the competitive effects of the enzyme and protein for the substrate and the effect of substrate redistribution into enriched domains that can increase enzyme activity. As an example of a complex metabolic response in which a protein with strong lipid interaction is able to activate or inhibit different membrane enzymes (sometimes depending on the protein concentration), we have a family of β-amyloid peptides, involved in Alzheimer's disease. Some of these peptides have contradictory effects on the activities of phospholipases A2, D, and C (17–25). It is important to highlight that all the mentioned enzymes behave according to the surface dilution kinetic theory in in vitro experiments with micelles (4,26). We think that these apparently contradictory results allow postulating that the complex pattern of metabolic effects induced by β-amyloid peptides could derive from their phospholipid binding properties—particularly when it has been demonstrated that the toxicity of the β-amyloid peptides is mediated by electrostatic interactions with the cell membranes (27) and specifically with acidic phospholipids, especially with PI and PIP2 (28), and that the acidic phospholipids favor its aggregation in the membrane (29,30).
We believe that the heterogeneities of substrate distribution in membranes must be included in kinetic models of lipid metabolizing enzymes. We have demonstrated that a kinetic theory generalization to a heterogeneous system allows us to explain complex peptide effects on membrane enzymes that otherwise might seem contradictory.
Acknowledgments
We thank Prof. Arthur Sherman for fruitful discussions.This work was supported by FONDECYT 2990111 and FONDECYT 1000691.
APPENDIX I: LIPID PHASE MODEL WITH DOMAIN FORMATION
Let's have a lipid phase of area 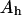 with its lipid components distributed homogeneously and with a phospholipid substrate S present at a mole fraction f. We will define this interface as being homogeneous. Let's have now a reordering of S to a two-phase medium: the domain phase (of area
with its lipid components distributed homogeneously and with a phospholipid substrate S present at a mole fraction f. We will define this interface as being homogeneous. Let's have now a reordering of S to a two-phase medium: the domain phase (of area 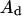 and molar fraction
and molar fraction 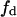 of S) and the nondomain phase (of area
of S) and the nondomain phase (of area 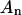 and mole fraction
and mole fraction 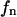 of S, with
of S, with  ). We assume the conservation relation for the interface areas,
). We assume the conservation relation for the interface areas,
 |
(3) |
The cross-sectional area of any lipid molecule and in any phase is assumed as constant. From this condition, a relation of the total phospholipid S area conservation in the interface can be concluded to be:
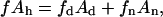 |
(4) |
with
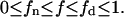 |
(5) |
The fraction of the total lipid area that is occupied by the domain phase is given by
 |
(6) |
From this definition and Eqs. 3 and 4, the following dimensionless relation can be obtained
 |
(7) |
From which we can obtain
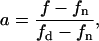 |
(8) |
and
 |
(9) |
Thus, the biphasic lateral lipid distribution can be completely determined with only two of three variables 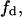 fn and a. We will see below that in our model, this relation implies that these two variables are sufficient to determine the total enzyme activity, V (the sum of the enzyme activities in both phases).
fn and a. We will see below that in our model, this relation implies that these two variables are sufficient to determine the total enzyme activity, V (the sum of the enzyme activities in both phases).
We show later in our analysis that we can ignore the border effects in the phases. In particular, when we study the peptide-phospholipid interaction, we assume that the average distance between the lipid surface and its counterion (known as Debye length, ≈10 Å in a univalent salt solution, 0.1 M) is much shorter than the average diameter of the domain and nondomain phases.
The kinetic models
Model I: the phospholipid binding kinetic model for a lipid phase with domain formation
Scheme 1 represents the enzyme-phospholipid binding kinetics. The upper sequence represents the binding kinetics in the domain phase, and the lower sequence represents the binding kinetics in the nondomain phase. We will use the apostrophe (') to indicate the species and quantities in the nondomain phase. Both sequences are similar to the model represented in Fig. 1 A. As shown, the same enzyme species (E) in solution binds to both phases. Rigorously speaking, the enzyme participating in the reaction is the enzyme that is at the layer closer to the lipid phase. However, similarly to previous applications of the surface dilution kinetic theory (4) we will assume homogeneity and continuity of the boundary layer and bulk phase and use the molar concentration of the enzyme dissolved in aqueous solution.
SCHEME 1.
Phospholipid binding kinetic model for a lipid phase with domain formation.
As usually done in the kinetic theory of surface dilution, we will apply the mass action law for each elementary step in the reaction. Because the first step of the reaction derives from a three-dimensional collision, the species involved participate according to their concentrations in the bulk aqueous solution. For S, its concentration can be obtained multiplying its mole fraction in the lipid phase by the total lipid concentration in the bulk aqueous solution. Once the enzyme is bound to the lipid phase, the reaction remains confined to two dimensions. Due to this constraint, in subsequent reaction steps the species dissolved in the lipid phase participate according to their mole fractions. In our model, we disregard border effects in both phases in the kinetic derivations. From here on, we will assume that the enzyme molecules bound to the lipid phase are fewer than the phospholipid molecules in that phase (i.e., 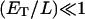 ). This assumption allows setting the total substrate molecules equal to the initial substrate molecules (initial velocity condition) and disregard the enzyme perturbation on the conservation of the lipid area.
). This assumption allows setting the total substrate molecules equal to the initial substrate molecules (initial velocity condition) and disregard the enzyme perturbation on the conservation of the lipid area.
Definitions are: [E] is the molar concentration of aqueous enzyme solution. 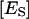 and
and 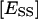 are the molar concentrations of ES and ESS in the domain phase.
are the molar concentrations of ES and ESS in the domain phase. 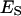 and
and 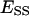 are the mole fractions of ES and ESS in the domain phase.
are the mole fractions of ES and ESS in the domain phase. 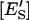 and
and 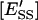 are the molar concentrations of E′S and E′SS in the nondomain phase.
are the molar concentrations of E′S and E′SS in the nondomain phase. 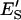 and
and 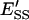 are the mole fractions of E′S and E′SS in the nondomain phase.
are the mole fractions of E′S and E′SS in the nondomain phase. 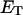 is the total enzyme molar concentration. [P] is the total product molar concentration from the enzymatic reaction. L is the total aqueous lipid molar concentration.
is the total enzyme molar concentration. [P] is the total product molar concentration from the enzymatic reaction. L is the total aqueous lipid molar concentration.
Note that La and 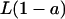 are the lipid molar concentrations for the domain and nondomain phases, respectively. Thus, the conservation equation for the total enzyme concentration,
are the lipid molar concentrations for the domain and nondomain phases, respectively. Thus, the conservation equation for the total enzyme concentration, 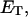 is given by
is given by
 |
(10) |
The total product reaction is generated by the catalytic activity of both phases. Thus, the reaction velocity V is
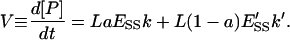 |
(11) |
The rest of the differential equations that determine the changes in the intermediaries are:
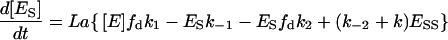 |
(12) |
 |
(13) |
 |
(14) |
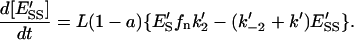 |
(15) |
If we assume steady state for the enzyme intermediaries:
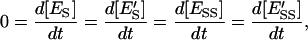 |
(16) |
defining:
 |
(17) |
and from Eqs. 10 to 15, we obtain the general relation for the initial velocity for this enzymatic model:
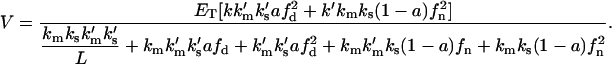 |
(18) |
Up to this point we have assumed that the kinetic parameters from both phases can be different. However, in a homogenous model, the experimental determinations of these parameters are carried out in a defined range of substrate mole fraction (0–0.3, for PIP2 concentration (31)). In this concentration range the enzyme activity measurements agrees with the predictions of the surface dilution kinetic theory, and only one set of kinetic parameters are needed to describe the velocity versus substrate concentration relation. As long as the concentrations in the domain and nondomain phases remain within this range (the range where the kinetic parameters were determined in a homogenous model), we believe that it is reasonable to assume only one set of kinetic parameters for both phases. Hence, assuming equality of kinetic parameters between domain and nondomain, we obtain
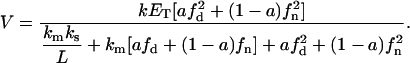 |
(19) |
Assuming the same values for the surface area of each lipid and conservation of the total area of the lipid phase (Eq. 7), we obtain a more simple expression for V:
 |
(20) |
with
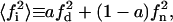 |
(21) |
where 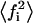 is the average of the square of the substrate mole fraction weighted by the phase area. The symmetry between the upper and lower parts of Scheme 1 (domain and nondomain phases) is not obvious in Eqs. 19 and 20. However, using the change of variable shown in Eq. 21 as defined in Eq. 8, results in the following expression:
is the average of the square of the substrate mole fraction weighted by the phase area. The symmetry between the upper and lower parts of Scheme 1 (domain and nondomain phases) is not obvious in Eqs. 19 and 20. However, using the change of variable shown in Eq. 21 as defined in Eq. 8, results in the following expression: 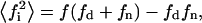 which is symmetrical with respect to the domain and nondomain mole fractions. An alternative way of expressing the velocity equation, as a function of only the variables in the domain phase,
which is symmetrical with respect to the domain and nondomain mole fractions. An alternative way of expressing the velocity equation, as a function of only the variables in the domain phase, 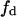 and a, can be obtained from substitution of Eq. 9 in Eq. 21:
and a, can be obtained from substitution of Eq. 9 in Eq. 21:
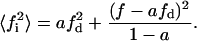 |
(22) |
As a control in our calculus, when the domain phase tends to occupy the area of the total phase or when both phases tend to the same mole fraction, we can see that the equation for V tends to the known equation for a lipid homogeneous phase (Eq. 1):
 |
(23) |
In Eq. 20, we can see that V depends hyperbolically on 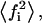 that have minimal and maximal values equal to
that have minimal and maximal values equal to 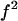 and f, respectively. Thus, we can deduce for V a minimal,
and f, respectively. Thus, we can deduce for V a minimal,  and a maximal value,
and a maximal value, 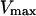 :
:
 |
(24) |
(We can see that 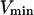 corresponds to V for a lipid homogeneous phase (Eq. 1))
corresponds to V for a lipid homogeneous phase (Eq. 1))
 |
(25) |
From Eqs. 20 and 22, it can be demonstrated that
 |
(26) |
Furthermore, if 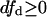 and da ≥ 0, then:
and da ≥ 0, then:
 |
(27) |
For this reason the total enzyme activity increases when the recruit of S to the domain increases, due to an increase of the domain mole fraction (fd) or extension of the domain (a).
Considering all of the above, we can conclude that the surface generated for the points (fd, a, V) that satisfy Eq. 20, should be similar to that shown in Fig. 3. This figure was estimated using the kinetic parameters values determined for PLCβ in vitro using PIP2 as substrate in Triton X-100 micelles (13). These authors showed that this enzyme obeys the phospholipid binding model. To account for some grade of cooperativity in the isoenzymes of the PLC family, other authors have employed Hill coefficients (12–14). For the sake of simplicity, our calculations do not include Hill coefficients. However, as shown in the Discussion, some degree of apparent cooperativity can be predicted from the phospholipid binding model applied to a heterogeneous substrate distribution.
Enzyme bound to the lipid phase in the phospholipid binding model
As done before, we will set the same kinetic parameters for the domain and nondomain phases. Similarly, we will assume that the surface area for each lipid and the conservation of the total area of the lipid phase are invariant (Eq. 7). From Eqs. 10 and 12–17 it can be deduced that the domain/nondomain ratio for membrane-bound enzyme can be expressed as:
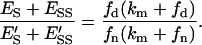 |
(28) |
Furthermore, the molar concentration of total enzyme bound to the lipid phase, 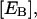 is
is
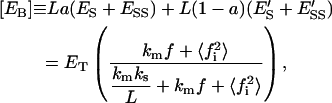 |
(29) |
where 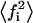 has the same meaning as defined in Eq. 21. From the inequalities shown in Eq. 5 it can be said that
has the same meaning as defined in Eq. 21. From the inequalities shown in Eq. 5 it can be said that 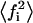 has a minimum equal to
has a minimum equal to 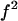 and a maximum equal to f.
and a maximum equal to f.
Model II: surface binding kinetic model for lipid phases with domain formation
Scheme 2 represents the kinetics of binding of the enzyme to the lipid phase. The upper sequence represents the kinetics of surface binding to the domain. The lower sequence of the scheme is similar to the upper sequence, except that it occurs in the nondomain phase. Both sequences are similar to the model shown in Fig. 1 B. The considerations related to the nomenclature and theoretical model are similar to those used in the model shown in Scheme 1. To simplify the theoretical derivations we will consider that, in this case, the binding of the enzyme to the membrane is to any location on the surface. This implies that the rate of binding would be proportional to the total lipid molar concentration instead of being proportional to the molar concentration of S (the substrate). This means that in the previous calculation we must change 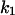 and
and 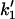 for
for 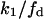 and
and 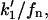 respectively, to obtain the kinetic equation that correspond to the surface binding model. (This result is equivalent to replace, in Eq. 18,
respectively, to obtain the kinetic equation that correspond to the surface binding model. (This result is equivalent to replace, in Eq. 18, 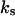 and
and 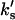 for
for 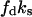 and
and 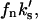 respectively):
respectively):
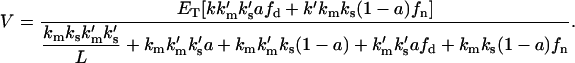 |
(30) |
SCHEME 2.
Surface binding kinetic model for lipid phases with domain formation.
As previously done, assuming equality between domain and nondomain parameters:
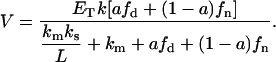 |
(31) |
From this equation and assuming the same value of surface area for each lipid and the conservation of the total area of the lipid phase (Eq. 7), it follows that
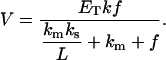 |
(32) |
This result coincides with the homogeneous case (Eq. 2), indicating that the domain formation does not affect the total enzyme kinetics for this model.
Enzyme bound to the lipid phase in the surface binding model
Considering the difference between the surface binding model and the phospholipid binding model, the calculations for the surface binding model can be performed by replacing 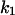 and
and 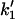 for
for 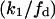 and
and 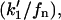 respectively, in the previously shown calculations for the phospholipid binding model. Thus, it can be deduced that the ratio of enzyme bound to the domain phase with respect to the nondomain phase will be given by:
respectively, in the previously shown calculations for the phospholipid binding model. Thus, it can be deduced that the ratio of enzyme bound to the domain phase with respect to the nondomain phase will be given by:
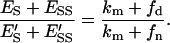 |
(33) |
Similarly, the molar concentration of the total enzyme bound to the lipid phase, 
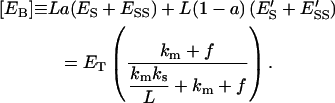 |
(34) |
The kinetic effects of peptide induction of phospholipid domains
We will analyze now the effects on the kinetics of a lipolytic enzyme due to peptide-induced domain formation. To start, we will assume that the peptide that induces the domain binds with a 1:1 stoichiometry to the substrate phospholipid molecule (32). As previously assumed in the mass balance expression, we will not consider the effects on substrate concentration of the substrate transformations to product or intermediaries of the enzymatic reaction. In this case, we will consider three substrate molar concentrations for each phase 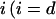 for the domain phase and
for the domain phase and 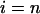 for the nondomain phase): the free substrate mole fraction (
for the nondomain phase): the free substrate mole fraction (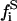 ), the P bound substrate mole fraction (
), the P bound substrate mole fraction (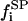 ), and the total initial substrate mole fraction (
), and the total initial substrate mole fraction (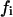 ). Giving
). Giving
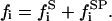 |
(35) |
We assume that the domain-inducing peptide is in equilibrium with the phospholipid substrate, obeying a Langmuir isotherm, and we defined 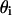 as the S fraction that is bound to P in the i phase, with an intrinsic binding constant (see Appendix II for
as the S fraction that is bound to P in the i phase, with an intrinsic binding constant (see Appendix II for 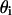 calculation).
calculation).
In the deduction of the expression for the enzyme activity rate, the kinetic equations will be similar to the previous derivation in kinetic models I and II, except that here we will consider that not all the substrate is available for binding to the enzyme. The free substrate that will be available for binding to the enzyme can be expressed, in accordance with Eq. 35 and the 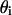 definition, as
definition, as 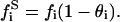
According to these considerations, and carrying out derivations similar to those used for kinetic models I and II, the following results can be obtained (assuming, as before, equality between the domain and nondomain kinetics parameters):
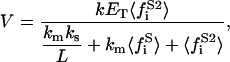 |
(36) |
for the phospholipid binding model, and
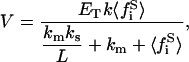 |
(37) |
for the surface binding model. With
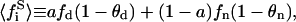 |
(38) |
being 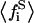 the average of the substrate mole fractions not bound to P, weighted by the phase area, and
the average of the substrate mole fractions not bound to P, weighted by the phase area, and
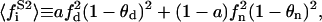 |
(39) |
being 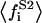 the average of the substrate square mole fraction not bound to P, weighted by the phase area.
the average of the substrate square mole fraction not bound to P, weighted by the phase area.
Assuming similar cross-sectional areas in all classes of lipid and assuming also that the domain-inducing peptide does not penetrate the membrane, it can be said, similarly to sections I and II, that 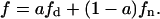 This expression allows diminishing in one degree of freedom the kinetic expressions. In Fig. 4 we made a numerical calculation employing in Eq. 36 the same value for the kinetics parameters of the enzyme PLCβ, acting on PIP2 as substrate, employed in Fig. 3. As the PIP2 domain-inducing peptide we chose Lys-5 (pentalysine) (Appendix II). We can see a maximum for some function domains, with acute declination for others.
This expression allows diminishing in one degree of freedom the kinetic expressions. In Fig. 4 we made a numerical calculation employing in Eq. 36 the same value for the kinetics parameters of the enzyme PLCβ, acting on PIP2 as substrate, employed in Fig. 3. As the PIP2 domain-inducing peptide we chose Lys-5 (pentalysine) (Appendix II). We can see a maximum for some function domains, with acute declination for others.
In the case of the surface binding model (Scheme 2), in Eq. 37, we see that V is an increasing function with respect to the 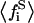 variable. Because the peptide substrate binding will always diminish the average free substrate fraction
variable. Because the peptide substrate binding will always diminish the average free substrate fraction 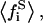 the total enzymatic activity (V) will also diminish, accordingly. If the stoichiometry of lipid binding to the peptide were larger than one (as Kim et al. describes (33)), the trapping (binding) of substrates by the peptide would be incremented in both the surface and phospholipid binding model. This would imply that the enzyme activity in Fig. 4 would decrease more dramatically at low substrate mole fractions.
the total enzymatic activity (V) will also diminish, accordingly. If the stoichiometry of lipid binding to the peptide were larger than one (as Kim et al. describes (33)), the trapping (binding) of substrates by the peptide would be incremented in both the surface and phospholipid binding model. This would imply that the enzyme activity in Fig. 4 would decrease more dramatically at low substrate mole fractions.
APPENDIX II: CALCULATION OF SUBSTRATE BINDING TO THE DOMAIN-INDUCING PEPTIDE
Calculation of the substrate fraction that is bound to peptide in the i phase (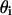 ):
):
We assume that the domain-inducing peptide is in equilibrium with the phospholipid substrate, obeying a Langmuir isotherm
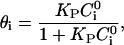 |
(40) |
in which 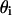 is the fraction of S that is bound to P in the i phase, with an intrinsic binding constant,
is the fraction of S that is bound to P in the i phase, with an intrinsic binding constant, 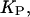 and with a peptide concentration in the water phase near the surface of the lipid phase,
and with a peptide concentration in the water phase near the surface of the lipid phase, 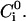 The value of this concentration is determined by the electrochemical equilibrium according to a Boltzmann-like relationship that includes the membrane potential in the i phase,
The value of this concentration is determined by the electrochemical equilibrium according to a Boltzmann-like relationship that includes the membrane potential in the i phase, 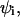 and the peptide concentration,
and the peptide concentration, 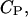 in the bulk solution:
in the bulk solution:
 |
(41) |
To calculate the membrane potential, we employed the Gouy-Chapman-Stern theory similarly to the canonical approaches made by Denisov et al. analysis (32):
In a lipid phase (d or n), the surface charges are the result of the homogeneous distribution of the lipid-water interface molecules. In our calculation, we assume that the substrate phospholipid is the only charged lipid in the lipid phase. We will assume that the rest of the membrane where the substrate is included is formed by neutral molecules, such as phosphatidylcholine or Triton X-100. The other charged molecules on the interface will be the domain-inducing peptides bound to the substrate. For simplicity, we do not consider the univalent counterion bound to the lipid substrate (34).
The solution contains a univalent electrolyte, with concentration
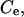 and the ionic multivalent peptide (with trace concentration
and the ionic multivalent peptide (with trace concentration 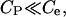 valence
valence 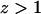 ) that are treated employing a mean-field theory.
) that are treated employing a mean-field theory.The electrostatic potential on the surface of a phase (i) is described by the Gouy equation (34):
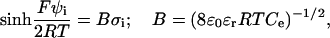 |
(42) |
being 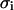 the surface charge density, F the Faraday constant, R the gas constant, T the temperature,
the surface charge density, F the Faraday constant, R the gas constant, T the temperature, 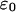 the permittivity of free space, and
the permittivity of free space, and 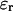 is the dielectric constant of the solution.
is the dielectric constant of the solution.
The charge in the i-phase for the 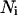 lipid mol will be
lipid mol will be 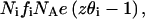 where
where 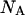 is the Avogadro's number and e is the elemental charge (positive). This charge is homogeneously distributed in an area
is the Avogadro's number and e is the elemental charge (positive). This charge is homogeneously distributed in an area  being
being 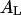 the transverse area of a lipid molecule. Thus, we have that the surface charge density for the i-phase is:
the transverse area of a lipid molecule. Thus, we have that the surface charge density for the i-phase is:
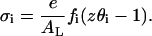 |
(43) |
From Eqs. 40 to 43, 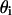 can be calculated numerically.
can be calculated numerically.
In Fig. 4 we chose Lys-5 (pentalysine) as the PIP2 domain-inducing peptide, for several reasons: a), the parameters for application of the Gouy-Chapman-Stern theory are available from the experimental and theoretical work of Denisov et al. (32). These authors used Lys-5 as an acidic phospholipid domain-inducing peptide, binding with a 1:1 stoichiometry to PIP2. b), The interaction between this peptide and charged bilayers has been studied by Murray et al. (35), and using also the solid-state NMR technique. It is known that they induce anionic phospholipid domains of a size larger than 0.1 μm, with a half-life larger than 100 ms (16). And, finally, c), it has been demonstrated that the Lys-5 adsorption to phospholipid vesicles is mainly due to electrostatic interactions, and is not related to the membrane penetration (36). Thus, we can consider that the peptide interaction does not perturb the conservation of the lipid phase area. However, although the peptide binding is not localized, we employed a localized binding model (Langmuir isotherm) to simplify our calculations. This simplification does not affect qualitatively our conclusions.
Abbreviations used (definition of symbols in the equations): 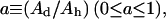 the fraction of the total lipid area that is occupied by the domain phase;
the fraction of the total lipid area that is occupied by the domain phase; 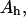 area of total lipid phase with its lipid components distributed homogeneously; Ai, area of the i phase;
area of total lipid phase with its lipid components distributed homogeneously; Ai, area of the i phase; 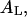 transverse area of a lipid molecule;
transverse area of a lipid molecule; 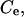 univalent electrolyte concentration;
univalent electrolyte concentration; 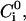 peptide concentration in the water phase near the surface of the lipid phase;
peptide concentration in the water phase near the surface of the lipid phase; 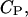 peptide concentration in the bulk solution; e, elemental charge (positive); [E], molar concentration of aqueous enzyme solution;
peptide concentration in the bulk solution; e, elemental charge (positive); [E], molar concentration of aqueous enzyme solution; 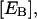 molar concentration of total enzyme bound to the lipid phase;
molar concentration of total enzyme bound to the lipid phase; 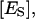 molar concentration of ES in the domain phase;
molar concentration of ES in the domain phase; 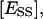 molar concentration of ESS in the domain phase;
molar concentration of ESS in the domain phase; 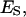 mole fraction of ES in the domain phase;
mole fraction of ES in the domain phase; 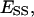 mole fraction of ESS in the domain phase;
mole fraction of ESS in the domain phase; 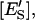 molar concentration of E′S in the nondomain phase;
molar concentration of E′S in the nondomain phase; 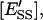 molar concentration of E′SS in the nondomain phase;
molar concentration of E′SS in the nondomain phase; 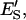 mole fraction of E′S in the nondomain phase;
mole fraction of E′S in the nondomain phase; 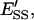 mole fraction of E′SS in the nondomain phase;
mole fraction of E′SS in the nondomain phase; 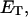 total enzyme concentration; f mole fraction of substrate S in a homogeneous interface of area Ah;
total enzyme concentration; f mole fraction of substrate S in a homogeneous interface of area Ah; 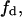 substrate (S) mole fraction in the domain phase;
substrate (S) mole fraction in the domain phase; 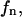 substrate mole fraction in the nondomain phase;
substrate mole fraction in the nondomain phase; 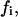 total initial substrate mole fraction in the i phase;
total initial substrate mole fraction in the i phase; 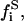 free substrate mole fraction in i phase;
free substrate mole fraction in i phase; 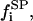 peptide (P) bound substrate mole fraction in i phase;
peptide (P) bound substrate mole fraction in i phase; 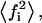 average of the square of the substrate mole fraction weighted by the phase area;
average of the square of the substrate mole fraction weighted by the phase area; 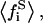 average of the substrate mole fraction not bound to the peptide, weighted by the phase area, in the i phase;
average of the substrate mole fraction not bound to the peptide, weighted by the phase area, in the i phase; 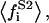 average of the substrate square mole fraction not bound to the peptide, weighted by the phase area, in the i phase; F, Faraday constant; i corresponding to the phase i (i = d for the domain phase and i = n for the nondomain phase);
average of the substrate square mole fraction not bound to the peptide, weighted by the phase area, in the i phase; F, Faraday constant; i corresponding to the phase i (i = d for the domain phase and i = n for the nondomain phase); 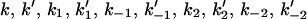 (each of these individual kinetic constants defined as shown in Schemes 1 and 2);
(each of these individual kinetic constants defined as shown in Schemes 1 and 2); 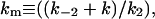 interfacial Michaelis constant in the domain phase (dimensionless);
interfacial Michaelis constant in the domain phase (dimensionless); 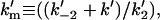 interfacial Michaelis constant in the nondomain phase (dimensionless);
interfacial Michaelis constant in the nondomain phase (dimensionless); 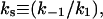 dissociation constant in the domain phase (mol/vol);
dissociation constant in the domain phase (mol/vol); 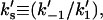 dissociation constant in the nondomain phase (mol/vol);
dissociation constant in the nondomain phase (mol/vol); 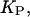 intrinsic binding constant of substrate binding to a peptide (vol/mol); L, total lipid concentration;
intrinsic binding constant of substrate binding to a peptide (vol/mol); L, total lipid concentration; 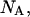 Avogadro's number;
Avogadro's number; 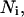 mol of lipids in the i phase; [P], total product molar concentration from the enzymatic reaction (mol/vol); R, gas constant; T, temperature (°K); V, total rate of product formation (mol/(vol time)); z, valence of the ionic multivalent peptide; Greek symbols: ɛ0, permittivity of free space; ɛr, dielectric constant of the solution;
mol of lipids in the i phase; [P], total product molar concentration from the enzymatic reaction (mol/vol); R, gas constant; T, temperature (°K); V, total rate of product formation (mol/(vol time)); z, valence of the ionic multivalent peptide; Greek symbols: ɛ0, permittivity of free space; ɛr, dielectric constant of the solution; 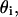 substrate fraction that is bound to the peptide in the i phase;
substrate fraction that is bound to the peptide in the i phase; 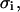 surface charge density in i phase;
surface charge density in i phase; 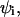 membrane potential in the i phase.
membrane potential in the i phase.
References
- 1.Hurley, J. H., and J. A. Grobler. 1997. Protein kinase C and phospholipase C: bilayer interactions and regulation. Curr. Opin. Struct. Biol. 7:557–565. [DOI] [PubMed] [Google Scholar]
- 2.Berridge, M. J. 1993. Inositol triphosphate and calcium signaling. Nature. 361:315–325. [DOI] [PubMed] [Google Scholar]
- 3.Clapham, D. E. 1995. Calcium signalling. Cell. 80:259–268. [DOI] [PubMed] [Google Scholar]
- 4.Carman, G. M., R. A. Deems, and E. A. Dennis. 1995. Lipid signaling enzymes and surface dilution kinetics. J. Biol. Chem. 270:18711–18714. [DOI] [PubMed] [Google Scholar]
- 5.Hendrickson, H. S., and E. A. Dennis. 1984. Kinetic analysis of the dual phospholipid model for phospholipase A2 action. J. Biol. Chem. 259:5734–5739. [PubMed] [Google Scholar]
- 6.Edidin, M. 1997. Lipid microdomains in cell surface membranes. Curr. Opin. Struct. Biol. 7:528–532. [DOI] [PubMed] [Google Scholar]
- 7.Mouritsen, O. G., and K. Jφrgensen. 1997. Small-scale lipid-membrane structure: simulation versus experiment. Curr. Opin. Struct. Biol. 7:518–527. [DOI] [PubMed] [Google Scholar]
- 8.Glaser, M., S. Wanaski, C. A. Buser, V. Bogulavsky, W. Rashidzada, A. Morris, M. Rebecci, S. Scarlata, L. Runnels, G. D. Prestwich, J. Chen, A. Aderem, et al. 1996. Myristoylated alanine-rich C kinase substrate (MARCKS) produces reversible inhibition of phospholipase C by sequestering phosphatidylinositol 4,5-biphosphate in lateral domains. J. Biol. Chem. 271:26187–26193. [DOI] [PubMed] [Google Scholar]
- 9.Zhou, C., D. Horstman, G. Carpenter, and M. F. Roberts. 1999. Action of phosphatidylinositol-specific phospholipase Cγ1 on soluble and micellar substrates. J. Biol. Chem. 274:2786–2793. [DOI] [PubMed] [Google Scholar]
- 10.Harder, T. 2003. Formation of functional cell membrane domains: the interplay of lipid- and protein-mediated interactions. Philos. Trans. R. Soc. Lond. B Biol. Sci. 358:863–868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.James, S. R., A. Paterson, T. K. Harden, R. A. Demel, and C. P. Downes. 1997. Dependence of the activity of phospholipase Cβ on surface pressure and surface composition in phospholipid monolayers and its implications for their regulation. Biochemistry. 36:848–855. [DOI] [PubMed] [Google Scholar]
- 12.Hernández, S. M., C. De Los Santos, J. A. Muñoz, and V. M. Loyola. 1999. Kinetic analysis of phospholipase C from Catharanthus roseus transformed roots using different assays. Plant Physiol. 120:1075–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.James, S. R., A. Paterson, T. K. Harden, and C. P. Downes. 1995. Kinetic analysis of phospholipase Cβ isoforms using phospholipid-detergent mixed micelles. evidence for interfacial catalysis involving distinct micelle binding and catalytic steps. J. Biol. Chem. 270:11872–11881. [DOI] [PubMed] [Google Scholar]
- 14.Jones, G. A., and G. Carpenter. 1993. The regulation of phospholipase C-γ1 by phosphatidic acid. Assessment of kinetic parameters. J. Biol. Chem. 268:20845–20850. [PubMed] [Google Scholar]
- 15.Matecki, A. 1997. Expression, purification and kinetic properties of human recombinant phospholipase C delta 3. Acta Biochim. Pol. 44:221–229. [PubMed] [Google Scholar]
- 16.Watts, A. 1998. Solid-state NMR approaches for studying the interaction of peptides and proteins with membranes. Biochim. Biophys. Acta. 1376:297–318. [DOI] [PubMed] [Google Scholar]
- 17.Ishikawa, H., H. Ozawa, T. Saito, N. Takahata, and H. Takemura. 1998. Calcium mobilization evoked by amyloid beta-protein involves inositol 1,4,5-triphosphate production in human platelets. Life Sci. 62:705–713. [DOI] [PubMed] [Google Scholar]
- 18.Singh, I. N., D. G. McCartney, and J. N. Kanfer. 1995. Amyloid beta protein (25–35) stimulation of phospholipases A, C, and D activities of LA-N-2 cells. FEBS Lett. 365:125–128. [DOI] [PubMed] [Google Scholar]
- 19.Singh, I. N., K. Sato, A. Takashima, and J. N. Kanfer. 1997. Activation of LA-N-2 cell phospholipases by single alanine substitution analogs of amyloid beta peptide (25–35). FEBS Lett. 405:65–67. [DOI] [PubMed] [Google Scholar]
- 20.Singh, I. N., G. Sorrentino, and J. N. Kanfer. 1997. Amyloid beta protein (25–35) stimulation of phospholipase C in LA-N-2 cells. J. Neurochem. 69:252–258. [DOI] [PubMed] [Google Scholar]
- 21.Singh, I. N., G. Sorrentino, D. S. Sitar, and J. N. Kanfer. 1998. (−)Nicotine inhibits the activations of phospholipases A2 and D by amyloid beta peptide. Brain Res. 800:275–281. [DOI] [PubMed] [Google Scholar]
- 22.Strosznajder, J., A. Zambrzycka, M. D. Kacprzak, and R. P. Strosznajder. 1999. Amyloid beta peptide 25–35 modulates hydrolysis of phosphoinositides by membrane phospholipase(s) C of adult brain cortex. J. Mol. Neurosci. 12:101–109. [DOI] [PubMed] [Google Scholar]
- 23.Strosznajder, J., A. Zambrzycka, M. D. Kacprzak, D. Copczuk, and R. P. Strosznajder. 1999. Alteration of phosphoinositide degradation by cytosolic and membrane-bound phospholipases after forebrain ischemia-reperfusion in gerbil: effects of amyloid beta peptide. Neurochem. Res. 24:1277–1284. [DOI] [PubMed] [Google Scholar]
- 24.Wallace, M. A. 1994. Effects of Alzheimer's disease-related beta amyloid protein fragments on enzymes metabolizing phosphoinositides in brain. Biochim. Biophys. Acta. 1227:183–187. [DOI] [PubMed] [Google Scholar]
- 25.Zambrzycka, A., R. P. Strosznajder, and J. B. Strosznajder. 2000. Aggregated beta amyloid peptide 1–40 decreases Ca2+- and cholinergic receptor-mediated phosphoinositide degradation by alteration of membrane and cytosolic phospholipase C in brain cortex. Neurochem. Res. 25:189–196. [DOI] [PubMed] [Google Scholar]
- 26.Chalifa Caspi, V., Y. Eli, and M. Liscovitch. 1998. Kinetic analysis in mixed micelles of partially purified rat brain phospholipase D activity and its activation by phosphatidylinositol 4,5-bisphosphate. Neurochem. Res. 23:589–599. [DOI] [PubMed] [Google Scholar]
- 27.Hertel, C., E. Terzi, N. Hauser, R. Jakob-Rφtne, J. Seelig, and J. A. Kemp. 1997. Inhibition of the electrostatic interaction between β-amyloid peptide and membranes prevents β-amyloid-induced toxicity. Proc. Natl. Acad. Sci. USA. 94:9412–9416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.McLaurin, J., and A. Chakrabartty. 1997. Characterization of the interactions of Alzheimer β-amyloid peptides with phospholipid membranes. Eur. J. Biochem. 245:355–363. [DOI] [PubMed] [Google Scholar]
- 29.Seelig, J., R. Lehrmann, and E. Terzi. 1995. Domain formation induced by lipid-ion and lipid-peptide interactions. Mol. Membr. Biol. 12:51–57. [DOI] [PubMed] [Google Scholar]
- 30.Martínez-Senac, M. del M., J. Villalaín, and J. C. Gómez-Fernández. 1999. Structure of the Alzheimer β-amyloid peptide (25–35) and its interaction with negatively charged phospholipid vesicles. Eur. J. Biochem. 265:744–753. [DOI] [PubMed] [Google Scholar]
- 31.Robson, R., and E. Dennis. 1983. Micelles of nonionic detergents and mixed micelles with phospholipids. Acc. Chem. Res. 16:251–258. [Google Scholar]
- 32.Denisov, G., S. Wanaski, P. Luan, M. Glaser, and S. McLaughlin. 1998. Binding of basic peptides to membranes produces lateral domains enriched in the acidic lipids phosphatidylserine and phosphatidylinositol 4,5-biphosphate: an electrostatic model and experimental results. Biophys. J. 74:731–744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kim, J., M. Mosior, L. A. Chung, H. Wu, and S. McLaughlin. 1991. Binding of peptides with basic residues to membranes containing acidic phospholipids. Biophys. J. 60:135–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.McLaughlin, S. 1989. The electrostatic properties of membranes. Annu. Rev. Biophys. Biophys. Chem. 18:113–136. [DOI] [PubMed] [Google Scholar]
- 35.Murray, D., N. Ben-Tal, B. Honig, and S. McLaughlin. 1997. Electrostatic interaction of myristoylated proteins with membranes: simple physics, complicated biology. Structure. 5:985–989. [DOI] [PubMed] [Google Scholar]
- 36.Ben-Tal, N., B. Horing, R. M. Peitzsch, G. Denisov, and S. McLaughlin. 1996. Binding of small basic peptides to membranes containing acidic lipids: theoretical models and experimental results. Biophys. J. 71:561–575. [DOI] [PMC free article] [PubMed] [Google Scholar]








