DNA Overstretching Transition: Ionic Strength Effects

Abstract

As double-stranded DNA is stretched to its B-form contour length, models of polymer elasticity can describe the dramatic increase in measured force. When the molecule is stretched beyond the contour length, it further shows a highly cooperative overstretching transition. We have developed a theoretical description for this transition by coupling the two-state model and the elasticity theory proposed earlier by others. Furthermore, we have extended this model to account for monovalent salt effects on elastic moduli during the transition. We find that this theoretical description is in very good agreement with recent measurements for the salt dependence of the overstretching transition, allowing us to gain insight into the mechanisms that govern the transition. In double-stranded DNA, the effective length per unit charge varies with salt in agreement with the Manning and Poisson-Boltzmann models for thin polyelectrolyte rods, whereas the other model parameters describing structural features have barely any salt dependence. The results thus suggest that the electrostatic component of force-induced overstretching is mediated mesoscopically via elasticity.

INTRODUCTION

A variety of biologically important processes involving the key molecules of life such as DNA and proteins are accompanied by structural transitions in these molecules (1). Thanks to the recent development of single-molecule manipulation techniques (2–5), the intriguing aspects of these transitions and related implications for biomolecular function can nowadays be studied in quantitative detail.

DNA, in particular, has recently been subject to thorough experimental and theoretical investigations by many groups, with a view to understanding the elastic properties of DNA and its stability against force-induced overstretching (2,6–9). These studies all focus on how double-stranded B-DNA is stretched and bent, and how, at some critical force of ∼70 pN, it will give way to an elongated partner, here for simplicity denoted S-DNA. Perhaps surprisingly, the molecular origin of the overstretching transition is still somewhat unclear. Here, for reasons that will be explained later, we shall take the view that S-DNA is denatured or melted into a defective helix with bubbles of single strands (9), rather than a stretched ladderlike structure as advocated (implicitly or explicitly) by Clausen-Schaumann et al. (2) and Ahsan et al. (10).

The nature of force-induced denaturation on DNA puts severe constraints on theoretical modeling: the passage from B-DNA to S-DNA involves mesoscopic elastic deformations as well as more localized processes, notably breaking of basepairs. A reasonable overstretching and denaturation model must, therefore, contain two distinct, but coupled, sets of state variables for elasticity and breaking of basepairs, respectively. Models along those lines, with particular views of the denaturation process, have been proposed by Ahsan et al. (10), and (implicitly) by Rouzina and co-workers (7–9). These models both are appealing and have been able to describe some of the key features of the overstretching transition. Yet, they are incomplete in some respects. Although Rouzina and co-workers do offer comments on the cooperative nature of the denaturation process, their otherwise very careful and far-reaching analysis assumes that denaturation is a straightforward first-order phase transition with an associated Clausius-Clapeyron equation. However, a transformation of that kind is not allowed for in intrinsically one-dimensional systems such as DNA. Ahsan et al. (10), in turn, propose a faithful (Ising-type) model of denaturation and couple it, in an elegant way, to the mesoscopic elastic deformations. Yet, the model used to describe elasticity in this case is perhaps too approximative as it assumes the elastic parameters of B-DNA and S-DNA to be similar. In comparison, the approach proposed by Podgornik et al. (11) seems to be highly promising for this purpose.

A related issue is that the existing models of the B-to-S transition have ignored the salt dependence of this transformation or described that in a manner that invites a number of questions. First of all, one wonders if the electrostatic component of the B-to-S transition is a manifestation of effects already included in the mesoscopic elasticity, or whether other (local or global) effects are involved. Based on ideas by Manning (12,13), the data fitting and analysis by Wenner et al. (9), supports the latter view, yet the mesoscopic elasticity model proposed by Podgornik et al. (11) does not rule out the possibility of merely including the contribution to denaturation of electrostatics through the elastic parameters. Second, one can ask how well the data conform to the much-invoked Manning condensation theory (13). Rouzina and Bloomfield have discussed that approach in the context of thermotropic properties of DNA (14), and irrespective of the detailed correctness of the Manning theory (15), it would be worthwhile to shed further light on the Manning approach.

This study will address the above questions theoretically on the basis of a hybrid model that combines the Ising-model approach of Ahsan et al. (10) and the elasticity theory by Podgornik et al. (11). A detailed analysis of the hybrid model allows us to compute force-extension curves that depend on (phenomenological) electrostatic, Ising, and elastic parameters, and that fit experimental data very well. By fitting elastic parameters well away from the overstretching plateau, i.e., for small extensions (pure double-stranded (ds) elasticity) and for very large extensions (pure single-stranded (ss) elasticity), roughly as in Wenner et al. (9), we can focus on the salt dependence of the remaining Ising and structural parameters by fitting close to the overstretching plateau. Thorough fitting to the experimental data (9) reveals that there is one key parameter that is strongly salt-concentration dependent: the effective length per unit charge a. In double-stranded DNA, we find that a varies with salt in surprisingly detailed agreement with the Manning condensation theory, i.e., from ∼0.67 nm at low 10 mM (monovalent) salt, to 0.17 nm at 1000 mM salt. Furthermore, the fitting reveals that the other Ising and structural constants have barely any salt dependence. These results suggest that the electrostatic component of force-induced overstretching is mediated mesoscopically via elasticity.

The organization of this article is as follows. In “DNA elasticity” we outline essential theory of DNA elasticity needed later in the article, and in “Overstretching transition” we present the model used to describe the overstretching transition. The model proposed here is confronted and compared with experiments in “Comparison with experiments”, and a discussion of our results ends this article in “Discussion and summary”. Finally, details of calculations are given in the Appendix.

DNA ELASTICITY

Consider a polymer chain of contour length L. After allowing the chain to thermally equilibrate we can measure the force f required to maintain the end-to-end distance at a fixed value x. The resulting force-extension (f-x) curve is then the equation of state for the chain under study.

The elastic properties of the standard B-form DNA can be modeled very conveniently by a simple theory known as the worm-like chain (WLC), borrowed from studies of stiff polymers (16). Let us first consider a case without charge effects. The leading parameter associated with the theory is the elastic bending modulus K_C. At small force f, bends are removed from DNA and the double strand acts as an entropic spring. This portion of the force-extension curve in the limit of small f is well described by the WLC model and is dominated by polymer flexibility expressed in terms of the bending rigidity K_C. In the opposite limit of large force the end-to-end distance approaches molecular contour length and subsequently the force-extension curve begins to rise quickly. At these large forces, DNA can be extended slightly beyond its contour length, which is accounted for by the elastic stretching modulus λ. The stretching modulus takes into account the energy involved in stretching the chain by a certain amount.

Although the above picture is a very convenient one, it does not account for the role of electrostatics. After all, DNA is strongly charged due to the phosphate groups, and the influence of charges can be considerable regarding the elastic properties of DNA. Thus, to account for the charged nature of DNA, the theoretical model has to include also an electrostatic potential between charged monomers. It turns out that the effect of electrostatic interaction can be included by tuning of elastic parameters K_C and λ. An appropriate way to demonstrate this matter is to consider DNA in an aqueous solvent with monovalent salt ions. If the salt concentration is high, then to a good approximation the electrostatic interaction is described by the screened Debye–Hückel potential, which reads in continuum limit as

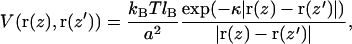(1)

where l_B is the Bjerrum length defined by

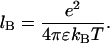(2)

Here a is the effective separation between the charges after counterion condensation has taken place and κ is the inverse Debye length. Furthermore, z and z′ are the coordinates that parameterize the polymer along its contour length. It has been shown (9) that in the limit of large external force the force-extension relation reads as

(3)

where 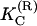and λ^(R) are renormalized elastic moduli. Their dependencies on the parameters in electrostatic potential are given by the following relations

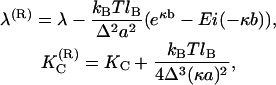(4)

where K_C and λ are the bare values of elastic parameters corresponding to a limit of infinite concentration of salt. The Ei(x) is the standard exponential integral function and Δ is the local stretching parameter introduced as

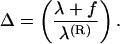(5)

In classical elasticity theory the bending rigidity and stretching modulus of a thin rod made of homogeneous, elastic continuum should be proportional to each other (17). However, here the situation is different. From relations Eq. 4 it is clear that a decreasing salt concentration leads to an increase in the bending modulus, while the stretching modulus is decreased. These effects were explained qualitatively in Podgornik et al. (11): the change in the bending modulus is related to the fact that the effective interaction between distant segments along DNA is repulsive, thus the interactions oppose bending and give rise to higher bending modulus. The stretching modulus, in turn, is proportional to the second derivative of the interaction potential with respect to the polymer curve coordinate. This, in turn, implies that if the chain is charged, then the Debye-Hückel repulsion will locally stretch the segment length. As this length becomes longer, the profile of the interaction energy at the minimum becomes less steep, and its second derivative thus smaller. Therefore, a stronger electrostatic repulsion leads to a smaller value of the stretching modulus.

Clearly Eq. 3 can be inverted to give the required force as a function of the relative elongation x/L. However, we can straightforwardly calculate the free energy G_el(f, L) of the chain related to the external force by

(6)

which is the condition of mechanical equilibrium in a fixed force ensemble. This can be easily integrated to give

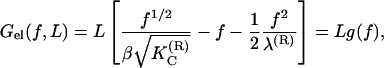(7)

where β = 1/k_BT. Equation 7 provides the elastic free energy of a charged semiflexible chain under external force f. This expression for the free energy can be taken as a starting point when a model for the DNA overstretching transition is developed in “Overstretching transition”.

OVERSTRETCHING TRANSITION

Two-state model

It has been shown in many experiments (9,3,18–21) that when a double-stranded DNA is stretched beyond its B-form contour length, it shows a highly cooperative overstretching transition. It seems that the DNA molecule abruptly increases its length by a factor between 1.5 and 2 when the external force f exceeds a threshold in the range of 60–70 pN. This phenomena is recapitulated in Fig. 1. At this point the DNA molecule suddenly extends with little additional force. After this point, the force again rises rapidly with a slope that depends on the stretching rate (9,22).

FIGURE 1.

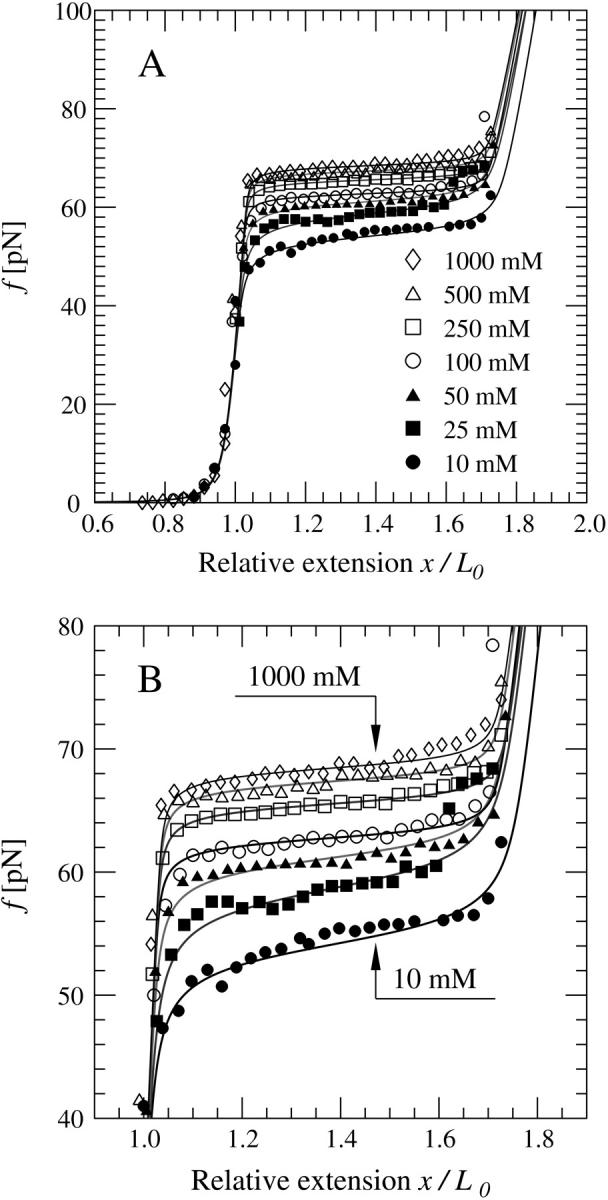
Room temperature force-extension curves for a single dsDNA molecule in different salt concentrations. The solid lines correspond to theoretical curves calculated using the global coupling theory developed in this work. Experimental data are by Wenner et al. (9). (A) Data over all regimes showing the complete force-extension curves. (B) The same data showing only the overstretching portion.

To describe this transition, Cluzel et al. proposed a model of an overstretched DNA as a new double-stranded form of DNA, referred to as S-DNA (6). According to this model, if the ends of the molecule are allowed to rotate freely under traction, then the structure of S-DNA is ladderlike and can be considered as an unwound double helix. This unwinding leads to an elongation of S-DNA compared to B-DNA. Two main facts supporting this model are that DNA does not break at the end of the overstretching transition, and that a cross-linked DNA exhibits an overstretching transition somewhat similar to unmodified DNA. Although the model describing S-DNA did predict an overstretching transition, the predicted transition was less cooperative and occurred at a higher force than that observed experimentally (18,19).

Rouzina and Bloomfield and Williams et al. (7,8,20,21) approached the issue from a different perspective and proposed that the overstretching transition is a force-induced melting transition. In this model, the basepairs holding the two DNA strands together break as DNA unwinds during the transition. However, DNA does not break at the end of the overstretching transition because some bases remain paired or unmelted. To test the force-induced melting model, Williams et al. (20,21) measured the DNA overstretching as a function of pH and temperature. The resulting parameters describing these dependences—the heat capacity of DNA upon melting and the entropy of DNA upon melting at the melting temperature—were in good agreement with measurements (20,21). Finally, they also measured the monovalent salt dependence of DNA overstretching and showed that the DNA strands must remain close together during the transition (9).

It is remarkable that the salt-dependence data obtained through experiments are consistent with both the S-DNA and force-induced melting models (7,21). Then the question is how to find a simple and general elastic model able to describe the overstretching transition and reveal the mechanism that governs this process.

Cluzel et al. approached this problem as follows. They proposed a two-state model (or Bragg-Zimm model) coupled to external traction (6). In the model, the B and S sections are separated by narrow borders (“junctions”), which are energetically unfavorable. The higher the junction energy, the more the B-to-S transformation becomes cooperative. Although the model produced a good fit to their force-extension curves in the region of the B-to-S transformation, one should note that this model does not include the elastic properties of the chain and thus fails in the low force regime. Moreover, it further does not account for the role of salt.

Later, Ahsan et al. proposed a two-state WLC, which is a combination of the two-state model and the WLC (10). This approach is highly appealing, because the pure WLC and the pure two-state model are limiting cases of this two-state WLC, and the new force-extension curve reduces to Eq. 3 in the limiting case of small force, where the entropic part of the free energy due to the bending elasticity dominates. Thus, we consider this approach to be a highly suitable starting point for our purposes, where we aim to design a model for the salt dependence of the DNA overstretching transition.

To define the two-state model more precisely, we divide the DNA chain into a sequence of short segments of length a₀ such that every segment can be said to be either in the B or S state, σ_i. The state of a “B segment” is denoted by spin up (↑) and σ_i = +1, whereas that of a “S segment” by spin down (↓) and σ_i = −1. The easiest possible description of this kind of system is provided by a nearest-neighbor one-dimensional Ising model, in which the energy spectrum takes on four different values: ΔE(↑↑), ΔE(↑↓), ΔE(↓↑), Δ(↓↓), depending on the state of two neighboring segments. Assuming a symmetric spectrum around the middle level ΔE(↑↓) = ΔE(↓↑), this spectrum can be parameterized by two quantities, J and H, as

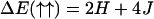(8)

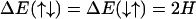(9)

(10)

The Hamiltonian for this kind of nearest-neighbor Ising model can be written as

(11)

The quantities H and J describing the internal degrees of freedom of DNA must be determined either by molecular modeling or by taking them as fitting parameters to be determined by comparison with experiments. Physically, 2H can be identified as the zero-tension free-energy difference per segment between the B and S states. The parameter J measures the correlation energy between adjacent segments, and by analogy to the Ising model we can interpret exp(−4J/k_BT) as a measure of the degree of cooperativity. Next an additional parameter δ is included in this model, describing the fractional elongation of the S state over the B state. Although one assumes here that the elastic bending energies of the S and B states are identical, it will be shown later that relaxing this constraint makes it possible to include the description of force-induced melting transition into the picture. Finally, the global coupling between the internal structure and chain conformation is provided by the constraint:

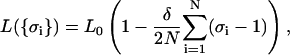(12)

with L₀ being the length of the chain in the pure B phase, 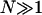the number of the segments, and a₀ = L₀/N the segment length. Thus, we see that the chain length L has become a statistical variable whose expectation value has to be determined over the canonical distribution of energy states.

From Eqs. 11 and 7 we can write the total effective Hamiltonian as

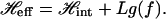(13)

By using this simple description of the tension-induced B-to-S conversion, it is possible to analytically obtain a new force-extension relationship. The derivation is shown elsewhere (10), and the result is

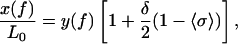(14)

where the thermodynamic average of the state variable is given by

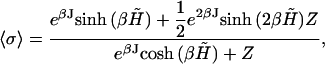(15)

with

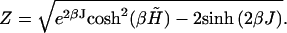(16)

Furthermore, the equation of state y(f) = x/L as derived by Ahsan et al. (10) is given by Eq. 3 using the bare values of elastic parameters. Finally, the renormalized external field 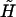is given by

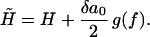(17)

Ahsan et al. (10) applied their model to the experimental data by Cluzel et al. over the whole force-extension curve (6) and found good agreement except for relative extensions of ∼1. The remarkable agreement in this case lends considerable support to this model and encourages one to ask whether it could describe the salt dependence as well.

Thus, using the force-extension relation Eq. 14 of the combined model of Ahsan et al. (10), but with the equation of state for the self-interacting WLC according to Eq. 3 (11), we tried to fit this description to the experimental data of Wenner and Williams (9) for different salt concentrations. The salt dependence was included in the elastic moduli according to Eq. 4, whereas H, J, and δ were given fixed values assumed in the study of Ahsan et al. (10), J = 1.25, H = 1.75, and δ = 0.78. Furthermore, the segment length was taken to be a₀ = 0.34 nm corresponding to one basepair, following again the assumption made by Ahsan et al. Therefore, the additional piece of information used here, compared to Ahsan et al. (10), is the salt dependence of elastic moduli. By plotting the resulting theoretical curves against experimental results we readily found that this kind of description cannot adequately describe the equation of state of the polymer chain for all values of salt concentration (data not shown). More precisely, the above model for the force-extension relation cannot reproduce the change in the overstretching force according to the experiments of Wenner and Williams (9), as salt concentration is varied.

One can speculate that the above approach failed because the elastic energies of the B and S segments were treated as equal. This idea is supported by experiments. It has been shown that the force required to stretch the chain rises again after the plateau in the force-extension curve, with a slope that depends on pulling rate. The rise continues up to ∼140 pN, where the f-x curve of double-stranded DNA (dsDNA) then matches that of single-stranded DNA (ssDNA) (23). Because it is well known that the elastic moduli of ssDNA differ significantly from those of dsDNA (24), one is tempted to conclude that models where elastic parameters along DNA are treated as constants are not adequate. Rather, it would be justified to aim for a full description of the force-extension curve through a model in which the elastic parameters are allowed to change along DNA, including their salt dependence. In the following section we develop a formalism in which this view has been accounted for.

Coupling of elastic moduli in two-state model

The reasons for the failure of Eq. 14 at interpreting the salt-dependent experimental data are not difficult to identify, if we analyze qualitatively the physics that is associated with the salt-dependent, force-induced overstretching of a DNA molecule. The internal B-to-S structural change, which underlies the DNA overstretching, has several consequences. It results in an inhomogeneity in the elastic properties along the molecule; it also generates an inhomogeneous charge distribution; moreover it leads to a reduced average charge density. The first two aspects are not included in the two-state WLC model described by Eq. 7 at all.

As an improvement on that model, we propose a model of our own. In our model, an internal structural state of the DNA molecule is described by segments in so-called B-state, or double-stranded state and segments in so-called S-state, or the denatured state. We model the segments in the S-state as two slightly separated, but parallel strands still coupled together electrostatically, in the sense that they interact electrostatically in a way similar to segments in the B-state. In other words, we do not make distinction between an overstretched DNA molecule and one that is fully in the denatured state. This assumption is consistent with the experimental finding (9,23), that the behavior of a DNA molecule stretched beyond the overstretching plateau is close to that of an ssDNA molecule.

We then construct the following ansatz for the effective free energy associated with an internal structural state of a WLC under a constant force:

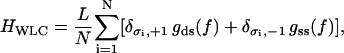(18)

where Kronecker symbols 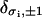have their usual mathematical meaning. Here g_ds(f) and g_ss(f) are free-energy densities corresponding to a pure B-state (double-stranded state) and a pure S-state (denatured state) DNA molecule, respectively. They have the same functional dependence on the applied force f as that described in Eq. 7, but involve different renormalized elastic moduli, corresponding to the B-state and the S-state DNA, respectively. The renormalized ds-state and ss-state moduli have the same functional dependences on their respective “bare” values, which are described explicitly in Eq. 4, and a single, effective charge separation a enters the renormalization. The only difference lies in the different values of the “bare” elastic moduli. This distinction between g_ds(f) and g_ss(f), and their linearly combined contribution to the total internal free energy, thus, form a simple description of the inhomogeneity in the elastic properties of an overstretched DNA molecule, incorporating one of the important aspects mentioned above. This simple description has, however, its limitation in that it assumes that the contribution to the total interaction energy from the ds-segments is independent of that from the ss-segments. Clearly, this assumption neglects the long-range effects of electrostatic interactions that must be there necessarily due to the inhomogeneities both in the charge distribution and in the elastic properties.

Our model ansatz provides a simple, minimal remedy for the limitation of the linear-combination model description of the elastic properties. This point can be made clear if we reexpress the total free energy—the sum of Eqs. 11 and 18—associated with an internal state in terms of the internal state variables, σ_i's. With very little algebra, we arrive at the following explicit form:

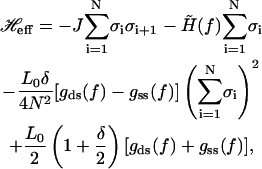(19)

where the effective external field 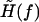is given by

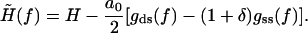(20)

It is easy to see that the second line in Eq. 19 indeed describes a global, or long-range, coupling between the internal state variables, σ_i's.

We may argue further for the explicit form of our ansatz. This ansatz assigns the WLC free energy the property that it is an extensive function of the chain length. It also reduces to the two right limit cases corresponding to a pure B-state chain and a pure S-state chain. Within the framework of an Ising model, the global coupling is the simplest form possible for the pairwise, long-range coupling between different states. Of course, these arguments do not prove, in a fundamental sense, the validity of our ansatz. However, a quantitatively good and physically meaningful fitting between our theoretical prediction and the experimental data will provide the strongest argument, at the level of effective theories, for the effectiveness of our model. As we will describe later, such a fitting is achieved.

Another remark on the ansatz formulated in Eq. 18 is necessary. The ansatz implies that we treat each segment of length L/N as if it were a flexible polymer, because Eq. 4 was derived for long WLCs. In a general case of a DNA molecule consisting of very short stretches of one type of segments or the other, this assumption is less justified. However, it works correctly in the two limit cases of a pure B-state and a pure S-state DNA molecule. Furthermore, if the force-induced denaturing is sufficiently cooperative, then long enough stretches of the same type of segments will appear to justify the assumption. What is long enough, is clearly determined by the persistence length of both dsDNA and ssDNA. We have checked that for the parameters we have considered, the coherence lengths of both the B-state and S-state domains are reasonably large. We discuss this issue in more detail in “Comparison with experiments”.

Theoretically calculated force-extension relation

Given the effective “Hamiltonian” associated with a single internal structural state of the DNA molecule, Eq. 19, we can now perform the statistical ensemble average over all possible internal states to evaluate the partition function and calculate the force-extension relation. The presence of the global coupling term prevents a straightforward evaluation of the partition function, but the calculation can be facilitated by the so-called Hubbard-Stratonovich transformation. We relegate the presentation of the detailed calculation to the Appendix, and only quote the final expression of the force-extension relation, which is in fact exact in the thermodynamic limit,

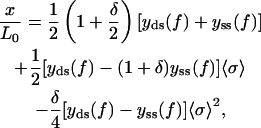(21)

where the average state variable 〈σ〉 and the renormalized external field 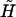are defined in the Appendix. Furthermore, we can take advantage of the condition of mechanical equilibrium y_ds(f) = −∂g_ds/∂f, as given by Eqs. 3 and 6, and y_ss(f) is defined correspondingly. These are just the force-extension curves given by Eq. 3, but with the elastic parameters replaced by appropriate ones for the ds-state and the overstretched state, respectively.

From Eq. 21 it is easy to see that the f-x curve reduces to pure dsDNA in the limit 〈σ〉 = +1 and to pure overstretched DNA in the limit 〈σ〉 = −1. This means that we have coupled the change in the elastic parameters with the overstretching transition in a nontrivial way that gives the correct limiting behavior. Furthermore, electrostatic effects are incorporated in this formulation through renormalized elastic moduli as discussed in “DNA elasticity”. Using the final interpolation formula for the force-extension curve, Eq. 21, we may now compare our theory with experiments.

COMPARISON WITH EXPERIMENTS

Overall comparison

In principle, the fitting involves two effective charge separations, one for the B- and one for the S-state. It turns out that numerically only one of them can be fitted accurately, namely the charge separation a in the S-state. The salt dependence of the fitting parameters J, H, a, and δ are determined by a nonlinear least-squares fitting method using all the data measured by Wenner and Williams (9). This set of experimental data was chosen for comparison because, to our knowledge, it is the most comprehensive one in terms of the salt dependence of the overstretching transition.

The redundancy in the fitting involving many adjustable parameters is reduced by first fitting the bare elastic parameters well away from the overstretching plateau, i.e., for small extensions (pure double-stranded elasticity) and for very large extensions (pure single-stranded elasticity), roughly as in Wenner et al. (9). The salt-dependent part of the elastic constants is assumed to be given by Eq. 4. The remaining part of the fitting involves a highly nonlinear fitting function, as given by Eq. 21. The salt dependence of the remaining adjustable Ising structural and electrostatic parameters are adjusted close to the overstretching plateau in an almost unique fashion. Overall, we found that it was not possible to prepare two equally good fits with different sets of values for the structural and electrostatic parameters. The results are hence optimal in the sense that we found no other distinctly different solutions with comparable fitting properties.

In the double-stranded or B-state we used the bare values given by Wenner et al. in the 1-M case (9), i.e., λ_ds = 1256 pN and K_ds/k_BT = 46 nm. In the single-stranded state we fixed the bare values of elastic moduli to be such that our theoretical force-extension curve interpolates between the experimental results for dsDNA and the ssDNA f-x curve to minimize the error (23). These bare values are given by λ_ss = 920 pN and K_ss/k_BT = 0.75 nm. It is worth noting that the bare value of persistence length is the same as that obtained by Smith et al. in the 150-mM case (24). This is consistent with our fitting, because numerically we found that the renormalized values of the bending rigidity in the S-state almost coincide with the bare values. This is clearly consistent also with elasticity theory; for large forces the f-x curve is dominated by the stretching modulus, and bending rigidity gives only minor contribution. On the other hand, it is really the changes of stretching moduli in S-state compared to B-state, that give the correct slope for f-x curve in the overstretching regime.

The parameter values corresponding to the optimal fitting are given in Table 1. Based on these values, as depicted in Fig. 1, the theoretical model developed in this work describes the experimental data of Wenner et al. (9) notably well for all salt concentrations. The only case where minor deviations between the theory and experimental data appear is the regime after the transition. In this regime for x/L₀ > 1.6, our fitting procedure tries to optimize the agreement between the theory and the ssDNA f-x curve for values f > 140 pN (23). However, the part of the force-extension curve between 70 and 140 pN has been shown to be rate dependent (22), which implies that this regime is not well defined and quantitative details should be taken with caution.

TABLE 1.

DNA elasticity parameters comprising the results of a nonlinear fit for the parameters J, H, a, and δ with different salt concentrations in a [Na⁺] buffer

[Na+] (mM)	a (nm)	H (kBT)	J (kBT)	δ
1000	0.170 ± 0.003	1.32 ± 0.01	1.75 ± 0.10	0.77 ± 0.01
500	0.225 ± 0.003	1.32 ± 0.01	1.75 ± 0.10	0.77 ± 0.01
250	0.300 ± 0.003	1.32 ± 0.02	1.75 ± 0.10	0.78 ± 0.01
100	0.355 ± 0.003	1.32 ± 0.02	1.75 ± 0.20	0.75 ± 0.02
50	0.440 ± 0.004	1.32 ± 0.02	1.45 ± 0.30	0.74 ± 0.02
25	0.540 ± 0.004	1.32 ± 0.03	1.25 ± 0.20	0.74 ± 0.02
10	0.670 ± 0.005	1.32 ± 0.03	1.25 ± 0.20	0.75 ± 0.03

Having found that this theory describes experimental data very well, let us discuss the conclusions we can draw based on this work. The numerical fitting was done using the force-extension relation, Eq. 21, letting all the parameters vary as a function of salt. Additionally, the elastic moduli were treated as salt dependent according to Eq. 4. The main conclusion of the numerical study is that the whole force-extension curve can be fitted only if the salt dependence of the effective charge separation a is taken into account. Importantly, we further find from Table 1 that a interpolates between the structural length a₀ of 0.17 nm at high salt (no effect of electrostatics) and the Bjerrum length l_B of 0.74 nm in water in the no-salt limit (strong electrostatic coupling). These results are consistent with the Manning and Poisson-Boltzmann theories for thin polyelectrolyte rods (13,25). We discuss the significance of these findings below.

All the other parameters remained by and large constant, as can be seen from Table 1. For low salt concentrations, also interaction strength parameter J varies slightly. However, this is mainly due to the fact that the elasticity theory of Podgornik et al. breaks down in the zero-salt limit (11). To be more specific, the effective potential between monomers described by the linearized Debye-Hückel theory, Eq. 1, is valid only in the limit of high salt where effects due to electrostatic interactions are not very prominent. It is therefore not surprising that in the opposite limit of low salt concentrations one finds deviations caused by nonlinearities. Nevertheless, they demonstrate the buildup of long-range effects that could be incorporated in this theory, if needed: instead of a nearest-neighbor interaction only, it might be reasonable to complement the model by next-nearest neighbor and higher-order interactions that could in part account for the effects at low salt concentrations. However, we feel that this is beyond the scope of this work.

To characterize the cooperativity of the B-to-S transition, we can use a similar analysis as introduced already by Rouzina and Bloomfield (7). Due to the one-dimensional nature of the B-to-S transition, one can define an average size of both B-type, k_ds, and S-type, k_ss, clusters, for any point on the f-x curve along the transition. This gives the average number of basepairs in both types of regions as a function of force f.

To justify our free-energy ansatz Eq. 18, we have to guarantee that the average sizes of both B- and S-domains are larger or of the order of the persistence length. To this end, we use the formulas given in Rouzina and Bloomfied (7) to calculate the average sizes of the B- and S-clusters. At the transition midpoint, i.e., 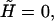the average number of basepairs in both type of domains is roughly 30. For S-DNA the persistence length is only ∼1.5 bp, which clearly satisfies the requirement set above. Obviously, 30 correlated basepairs is smaller than the number of basepairs per persistence length in B-DNA, which is of the order of 150. However, it should be noted that the number of correlated basepairs changes very rapidly with force. Thus, at the regions where the second derivative of the f-x curve changes sign (turning points), the number of basepairs already exceeds the critical value 150. For the 1-M case we found average numbers k_ss = k_ds ≈ 180 bp, and for the 10-mM case k_ss = k_ds ≈ 300 bp, at the turning points. Interestingly, all the parameters in our model are mostly determined by the curvature of the f-x curve at these turning points.

Salt dependence of overstretching force

As we can see from Fig. 1, the increase in the overstretching force is correctly reproduced by the interpolation formula Eq. 21. This seems to rule out the need for any logarithmic corrections in the free energy to explain the change in reference state used by other groups (7–9). To better understand the changes that take place during DNA overstretching, we can use our analytical results to predict the explicit (Na⁺) dependence of the overstretching force. A good estimate of the overstretching force may be given by the force value, at which the renormalized external field 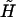changes sign from positive to negative. Mathematically, this is defined by the following equation:

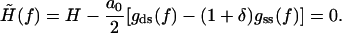(22)

Thus, for all values of salt concentration we have an estimate for the overstretching force. Clearly, for low ionic strengths this equation agrees with the logarithmic form given by Wenner et al. (9). In the regime of high salt concentrations, our model achieves more than that used by Wenner et al. (9). Their model, which is based on the polyelectrolyte theory, turns out to be inadequate for predicting the salt dependence in this regime. In contrast, our model can be linearized with respect to the limit of infinite salt concentration, κa ≳ 1 and thereby gives the leading contribution to the overstretching force, which arises from a high, but finite, salt concentration. The “limit” or “bare” value of the overstretching force is easily estimated from Eq. 22 by setting the elastic moduli to their bare values and by using for the Ising and structural parameters the numerical values given in Table 1. It turns out to be 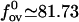pN. This value may be taken as a theoretical upper bound for the overstretching force. For a high, but finite, salt concentration, linearization of Eq. 22 by an expansion to the first order in deviations δλ and δK_C immediately yields the leading-order contribution to the force, which reads as,

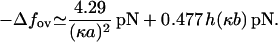(23)

Combining the bare part of the overstretching force with the salt-dependent part we get

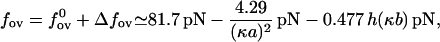(24)

where h(x) is defined by h(x) = e^x −Ei(−x). Equation 24 provides a reasonably good approximation for the overstretching force with salt concentrations higher than 100 mM.

DISCUSSION AND SUMMARY

This article has dealt with the salt dependence of the force-induced B-to-S transition of DNA, with a focus on two major questions, namely: i), whether the electrostatic component of the B-to-S transition is a manifestation of effects already accounted for in the mesoscopic elasticity, or whether other (local or global) effects are involved; and ii), how well the data analyzed conform to the much-invoked Manning condensation theory (13).

To address these questions theoretically, we have developed a model that combines the Bragg-Zimm or Ising model approach used by Ahsan et al. (10) and the elasticity theory by Podgornik et al. (11,26). Furthermore, we have extended the model to account for effects of electrostatics (salt) on structural and Ising parameters.

In the model developed here, S-DNA is thought of as two parallel, slightly separated but electrostatically coupled (8) strands with fundamental electrostatic interactions largely similar to those in B-DNA. The main difference between B-DNA and S-DNA lies in the elastic parameters.

In addition, we have introduced a global coupling (Eq. 18) between single- and double-stranded segments of an elastically stretched DNA molecule. This coupling should be seen as a minimal, effective description of the generic long-range nature of the complex electrostatic interactions present in the system.

Based on the theoretical model, we have predicted the force-extension relation (or curve) as a function of the relevant parameters, which in turn depend on the salt concentration. We have then fitted the theoretical prediction with the available experimental data, and from the fitting determined the numerical values of the model parameters as functions of the salt concentrations. We recapitulate here the most important results obtained from the fitting:

1. Both the coupling of the elastic moduli to the B-to-S structural change and the global coupling introduced and described in Eq. 18 are necessary for successful fitting over the whole range of force and extension that has been investigated.

2. The fitting between the theoretical prediction and the experimental data works remarkably well for all of the salt concentrations investigated. Moreover, the fitting reveals that the parameter that is most sensitive to the salt concentration is the effective length of charge separation. As shown in Table 1, the salt dependence of this length varies in agreement with the Poisson-Boltzmann and Manning condensation theories for thin rods, i.e., from ∼0.67 nm at low 1 mM (monovalent) salt, to 0.17 nm at 1000 mM salt. These results show that the fit between our model prediction and the experimental data is not only of good numerical quality, but is also physically meaningful.

3. Within the range of validity of the theory, corresponding roughly to salt concentrations exceeding physiological salt concentrations (100 mM for monovalent salt), the Ising structural constants J and H have no salt-dependent electrostatic components.

Based on these results, we may draw the conclusion that our model is successful in interpreting the experimental data, despite its crudeness. On the one hand, this success is not surprising. It is obvious, from a qualitative point of view, that electrostatic effects must imply long-range coupling between the charges distributed along a DNA molecule immersed in an ionic solution and that they must renormalize the elastic parameters of the molecule. These two features have been included in our model. On the other hand, the same success is less than obvious. The internal B-to-S structural change, which underlies the force-induced overstretching of the DNA molecule, changes the physical properties of the DNA molecule in several respects. First, the elastic properties become inhomogeneous along the length of the molecule. Secondly, the charge distribution also becomes inhomogeneous. Finally, the average structural charge separation is increased. It is not clear exactly how these two types of inhomogeneities manifest themselves in the electrostatic interactions, or in other words, how the free energy should be expressed as the functionals of the inhomogeneities, and what role the average charge density plays in the total free energy. Our model proposes a very simple effective approach to this complex problem: 1), it recognizes the inhomogeneity in the elastic properties of the overstretched DNA molecule by assigning different “bare” elastic moduli to the B-segments and the S-segments; 2), it follows the philosophy of the Manning theory by assuming pairwise, salt-screened Debye-Hückel interactions between charge distributed along the molecule; 3), it assumes that the electrostatic interactions make their influence primarily through the renormalization of the elastic moduli (11); 4), it makes the simplification that the inhomogeneity in the charge distribution does not affect the renormalization of the elastic moduli, in other words, an average effective charge separation appears in the renormalized elastic moduli; and 5), it assumes a minimal description of the long-range effects that must arise from the inhomogeneity in the elastic properties as well as the charge-distribution inhomogeneity. The good fit between our theory and the experimental data suggests that this simple effective approach may have captured in a nontrivial way the most essential aspects of the complex electrostatic interactions.

Two notes of caution are, however, called for. First, in view of several fitting parameters in our model, the support provided here for the Manning and Poisson-Boltzmann theories of counterion organization near thin polyelectrolyte rods (13,25), is somewhat indirect. Our model cannot fully establish the detailed correctness of those models. However, these theoretical models provide a framework for interpreting our fitting parameters and for gauging the quality of our fitting procedure. Second, it must be borne in mind that the Manning theory has limited predictive powers: it does not give a simple, explicit expression for the salt dependence of the effective charge separation, which interpolates between the chemical separation at large salt concentrations (no effect of electrostatics) and the Bjerrum length of 7.4 Å in water in the no-salt limit (strong electrostatic coupling). Furthermore, there are limitations to be imposed in any successful application of the Manning theory to further questions of interest (15,25). For example, it is likely that colligative properties of B-DNA (15,27) cannot be understood straightforwardly on the basis of the Manning theory, except in infinite dilution. Nevertheless, our results indicate that the Manning theory provides one reasonable framework among other ones for analyzing problems in biopolymer electrostatics.

APPENDIX: TWO-STATE MODEL WITH GLOBAL COUPLING

The two-state model described in the text for the internal structure of the chain is mathematically identical to the one-dimensional Ising model, as described by Ahsan et al. (10). The Hamiltonian for this kind of the nearest-neighbor Ising model can be written as

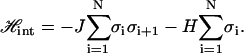(A1)

Here, σ_i = +1 for a B segment, σ_i = −1 for an S segment, and i = 1, 2, …, N runs over the N segments of the chain. The quantities J and H describing the internal degrees of freedom of DNA must be determined either by molecular modeling or taking them as fitting parameters to be determined by comparison with experiments.

Next 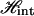must be complemented by the elastic energy of WLC. In the original model of Cluzel et al. (6), it was assumed that the B-state and the S-state have identical elastic moduli. We can immediately find this free energy, which is related to the condition of mechanical equilibrium in the fixed-force ensemble as follows

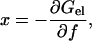(A2)

where we can use the explicit force-extension relation for the end-to-end distance of the polymer, x, obtained by Podgornik et al. (11). It is easy to show that the free energy can be written as

(A3)

The effective Hamiltonian is a sum of the Ising Hamiltonian 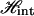and the elastic free energy F_el. The final force-extension relation (Eq. 14) can then be straightforwardly derived by following the footnotes of Ahsan et. al (10).

If we now want to relax the assumption of constant elastic moduli for both states, we need to replace Eq. A3 by a new one, which reduces to the pure B-state WLC free energy and to the pure S-state free energy in the limits σ_i = +1 and σ_i = −1 for all i = 1, 2, …, respectively. Using this idea we construct an ansatz for the WLC free energy in the fixed-force ensemble according to Eq. 18

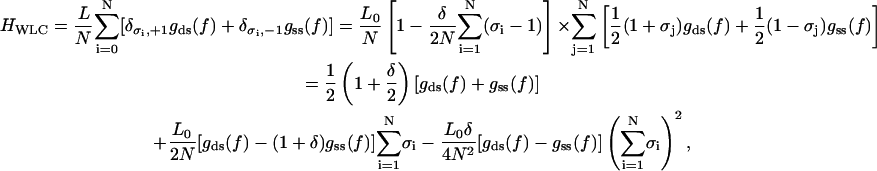(A4)

where we have used a shorthand notation for elastic free energies in the B- and S-states discussed in the text. Summing the Ising Hamiltonian together with the WLC part (Eq. A4) one ends up with the effective Hamiltonian

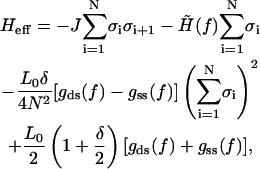(A5)

where the effective external field 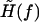is now slightly modified from Eq. 17 as

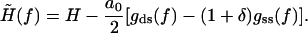(A6)

Thus, the partition function can be written as a trace over spin variables

(A7)

where β = 1/k_BT. The Hamiltonian in the partition function is quite similar to one used to derive the force-extension relation Eq. 14, but with a difference that now a global quadratic term prevents the exact evaluation of the configurational sum. To do further progress, we replace the global term by a continuous fluctuating field. The price to be paid from this trick is that instead of a tedious summation over discrete spin variables one has to carry out a continuous integral over the fluctuating field. Now we formulate explicitly this trick often called the Hubbard-Stratonovich transformation (28). We replace the quadratic term in Eq. A7 by the following Gaussian integral

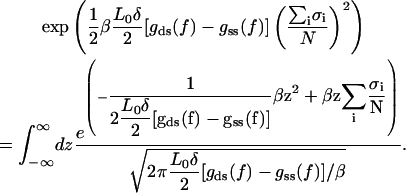(A8)

This transformation enables us to recast the partition function into the form similar to the one-dimensional Ising model as

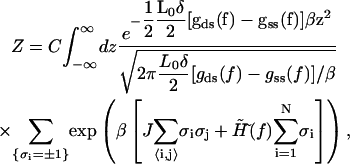(A9)

where a new external field 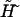and a constant factor C are defined as

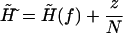(A10)

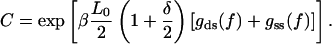(A11)

Now the trace over the configurational degrees of freedom {σ_i} produces

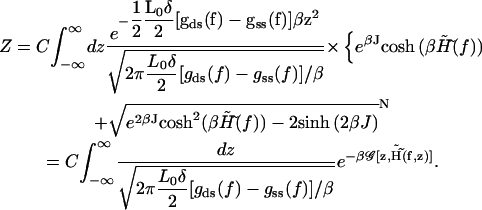(A12)

In the last row a definition of a new effective free energy is used

(A13)

The final integral over the variable z cannot be evaluated exactly, but one can find the value of z that minimizes the effective free energy 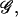namely the saddle point of 𝒢 with respect to z. Furthermore, 𝒢 can be expanded to the second order in z around the saddle point as

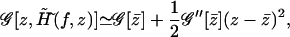(A14)

where the mean-field property of the point is exploited to get rid of the first-order term. This integral can be carried out trivially due to its Gaussian nature

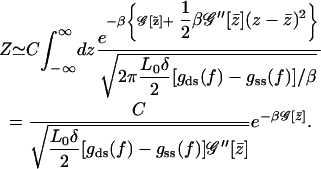(A15)

To simplify the above result further one has to calculate 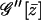explicitly. Actually this cannot be done because the form of the saddle-point equation is too complicated. However, it can be written in a more tractable form as

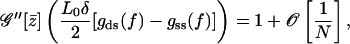(A16)

which shows that in the thermodynamic limit the denominator of the partition function truncated to second order becomes constant. Furthermore, it can easily be shown that the higher-order terms in the expansion of 𝒢 around the mean field give rise to even higher order terms in 1/N, thus vanishing in the limit 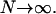Next the calculation of the free energy for the two-state model with global spin-spin coupling is performed as

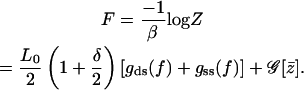(A17)

The final goal, the force-extension relation for the combined model, can be calculated using the condition of mechanical equilibrium in the fixed-force ensemble according to Eq. A2

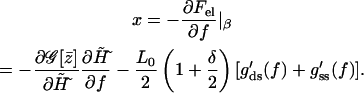(A18)

Here one should notice that in the thermodynamic limit 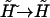for fixed 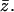Thus, the previous equilibrium condition can be written as

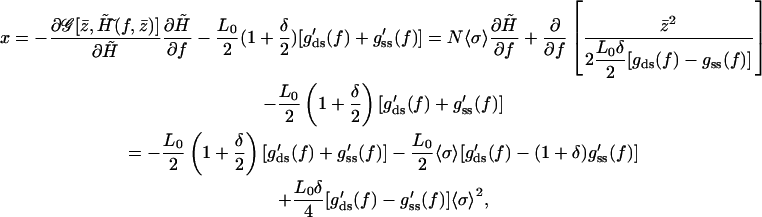(A19)

where we have defined the average spin according to Eq. 15, but now 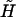is given by Eq. A6. The second term in the spin arising from the derivative of 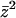term with respect to 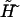in the free energy vanishes in the thermodynamic limit as 1/N. Further simplification for the equation of state can be done by noticing that according to Eqs. 3 and 7 g′(f) = −y(f) for both double-stranded and single-stranded chains. Thus, we arrive at Eq. 21

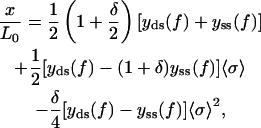(A20)

which is quite similar to Eq. 14, but now a mixture of double-stranded and single-stranded force-extension relations appears in the final equation of state. This means that we have coupled the different elastic moduli together in a highly nontrivial way, which reduces to the correct model at both limits of the overstretching transition.