Potentials of Mean Force for the Interaction of Blocked Alanine Dipeptide Molecules in Water and Gas Phase from MD Simulations

Abstract

We calculate potentials of mean force (PMFs) for the intermolecular interaction of two blocked alanine dipeptide (AcAlaNHMe) molecules in water and gas phase at two temperatures, 278 and 300 K, from all-atom molecular dynamics simulations. Simple models based on buried solvent accessible surface and one-dimensional potentials derived from distance-based radial distribution functions are not capable of expressing the short- and long-range complexity of the solute-solute interactions in water. Instead, radial and angular variations in the PMFs are observed with the two-dimensional potentials. The strength of the interactions for specific relative orientations of the molecules in the two-dimensional PMFs is more than double that observed in the one-dimensional PMFs. The populations of specific blocked alanine dipeptide conformations in water, such as α_R and PPII, vary with temperature, and most significantly, with the distance between the centers of mass. A preference for helical conformations is observed at close encounter between molecules.

INTRODUCTION

Mapping intermolecular interaction between solutes in dilute aqueous solution has a great impact in understanding complex biological phenomena such as protein-protein association, protein ligand recognition, protein-membrane association, and the protein folding problem. Studies of peptide–solvent and peptide-peptide interactions in water have potential in identifying essential elements involved in early protein folding events and weakly bound, transient multienzyme complex formation for which structural studies that use experimental techniques such as x-ray crystallography are almost impossible (1). These studies have become even more relevant with the discovery of naturally unfolded or intrinsically unstructured proteins (IUPs) (2). IUPs perform well-defined, key functions in DNA/RNA-protein interactions, such as inhibitors and scavengers, and facilitators of complex formation in activators/coactivators of DNA transcription (3). Quantifying peptide-peptide interactions in water is relevant for understanding IUPs because these proteins are unfolded in solution and might fold only upon binding to other proteins or DNA/RNA.

Solute-solute interaction in solution has been extensively studied before through a range of techniques from colloidal approaches to all-atom simulations. Fundamental forces that control the solution behavior of biologically important molecules have been considered in light of the Derjaguin-Landau-Verwey-Overbeek (DLVO) theory, or by taking into account molecular solvation and the hydrophobic effect. The DLVO description of intermolecular interactions, although successful in describing protein crystallization, protein aggregation rates, and binding kinetics (4), fails to predict specific intermolecular interactions. The lack of structure, such as geometry, flexibility, and chain connectivity, makes it difficult to extrapolate the results from spherical solutes to specific solute-solute interaction in biomolecular systems. It has been recently recognized that taking into account protein flexibility, via molecular dynamics simulations, for example, can enhance the predictive power of the computational drug design methods (5).

In this work, we study in detail the intermolecular interactions in a model system of two blocked alanine dipeptide (bAdp) molecules in water and gas phase from long molecular dynamics (MD) simulations. The use of all-atom simulations and low peptide concentration (large number of water molecules) allows for an accurate description of solvation effects and quantitative comparison between simulation and experiment. The blocked (or capped) alanine dipeptide–N-acetyl-l-alanine-N′-methylamide (AcAlaNHMe) has long been regarded as a prototype for protein backbone dihedral angles (6,7), and has served as a standard test case for models of peptide solvation (8–15).

The conformational flexibility of the bAdp molecule (Fig. 1, A and B) has been used as prototype for protein backbone conformations and to calibrate energy functions describing torsional angles. It is most usually represented by a Ramachandran plot (16) or a map of allowed torsional angles—a (Φ,Ψ) map. The Ψ angle, sometimes referred to as the “folding coordinate”, is generally used as a reporter of the molecular conformation in solution where the distribution of the Φ angle cannot discriminate well between molecular conformations.

FIGURE 1.

(A) Snapshot of the simulated system: two bAdp molecules, bAdp1 and bAdp2, separated by several layers of water molecules (water molecules not shown). In the notation of bAdp atoms, the atoms at the left of the C_α atoms are denominated by their chemical symbol followed by an “L”, and those on the right of C_α have an “R” attached to their chemical symbol. Atoms CL, NL, CA, CRP, and NL are explicitly labeled in the figure, as well as the dihedral angles Φ and Ψ. CA is identical to Cα. Fig. 1 (B) Snapshot of the simulated system: two bAdp molecules interacting at short distance; e₁ and e₂ are the end-to-end vectors of the molecules. The two blocking methyl groups of C_L and C_R as well as the central C_α carbon atoms of the alanine amino acid are labeled in the picture.

Early characterization of the free energy surface of the alanine dipeptide molecule produced a so-called “derivation diagram” for a single bAdp molecule in gas phase based on a hard sphere model (17), and indicated three significant allowed regions for the (Φ,Ψ) pairs represented in a Ramachandran plot: a), a large region in the (−Φ,Ψ) quadrant corresponding to the β-sheet, PPII, and 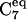conformations, an region in the (−Φ,−Ψ) quadrant containing the right-handed α-helical conformations, and a small region in the (Φ,Ψ) region, 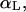containing the left-handed α-helical conformations. In gas phase, there is a fourth region that is populated, in the fourth quadrant (Φ,−Ψ) region, the so-called 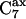conformers. The empirical energy surface of the dipeptide in the gas phase differs from the observed distribution of (Φ,Ψ) angles in proteins. Conformational energy calculations for single alanine dipeptide molecules in gas phase (18,19) reproduce qualitatively the expected conformational distribution in most respects.

The full free energy surface for bAdP-bAdP molecular interaction, is calculated here at two different temperatures, T₁ = 278 K and T₂ = 300 K from all-atom simulations of two bAdp molecules in water—TIP3P model and gas phase. The backbone conformational equilibria and conformational changes of the molecules due to intermolecular interactions are mapped as a function of intermolecular distance and temperature. We calculate the one-dimensional (1D) potentials of mean force (PMFs) from radial distribution functions (RDFs) and two-dimensional (2D) PMFs from radial-angular distribution functions and discuss their significance for understanding biomolecular interaction. The article is organized as follows: the Methods section presents a short theoretical description of the free energy—potential of mean force calculation for the solute-solute interaction in water and the MD simulation protocol. This section is followed by the Results section, which presents and discusses the results of the analysis of the MD trajectories: the changes in the (Φ,Ψ) maps in gas phase and solution, the temperature effects on the conformational equilibria, the analysis of the solvent accessible surface of the two molecules as a function of the distance between the molecules, and an analysis of the molecular dipole moments and their mutual orientations in gas phase and solution. The Results section is capped with an analysis of the change in conformational populations as a function of the intermolecular distance, and finally, a comparison between the 1D and 2D PMFs. We show that the 1D PMFs are not capable of expressing the complexity of the free energy surface for the bAdp-bAdp interaction in water and that the conformational populations of the molecules are dependent on the intermolecular distance, the α-type conformations being promoted at close intermolecular interaction. Size and sampling effects on determining the 2D PMFs are briefly discussed in the last subsection of the Results section. In the Conclusions section we discuss the significance of our results for understanding early events in protein folding, the complexity of the free energy surface of interaction between two small peptides, and the adequacy of using low-dimensional PMFs for describing these interactions.

METHODS

Computation of the potential of mean force

Consider a simple model of two solute molecules of type A solvated in water at infinite dilution. The radial distribution function of A particles around a central A particle, g_AA(r→;ρ_W;T), will allow to estimate the Gibbs free energy change (or PMF) for bringing two A particles from infinite separation to the separation 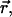in water at density ρ_w, and temperature T:

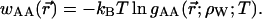(1)

The free energy surface of the bAdp-bAdp molecular interaction, 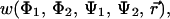is calculated from all-atoms MD simulations with CHARMM (20) at constant P (P = 1 atm) and T (T₁ = 278 K and T₂ = 300 K). Two box-centered bAdp molecules initially situated at a distance of 8.25 Å between their centers of mass, are solvated in equilibrated cubic boxes of 2100 (64,000 ų) and 1000 (30,000 ų) water molecules (TIP3P model) by removing the water molecules that overlap with the solutes. Preequilibration runs (100 ps) allow for the rearrangement of the water molecules around the fixed bAdp molecules. Next, the systems are preequilibrated with no constraints for another 1000 ps before starting the production run. RDFs are calculated as functions of the distance between the centers of mass, 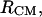and the distance between the central Carbon atom positions, 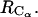The PMFs determined here are from simulations in the large boxes of 64,000 ų in volume. The small box simulations are used to probe the short distance range more extensively.

Simulation protocol

Periodic boundary conditions are imposed using the CRYSTAL facility in CHARMM. Constant temperature and pressure conditions (NPT ensemble) have been applied using the Nose-Hoover method of coupling to a heat bath (21,22) and extended system algorithms for controlling the pressure of the system (23), with coupling constants of 5 ps for both pressure and temperature. Covalent bonds involving hydrogen atoms were constrained with the SHAKE algorithm (24) to allow for a time step of 2 fs. A nonbonded cutoff of 12 Å and shifted forces were used in the calculation of Lennard-Jones potentials. The nonbond pair lists are updated using a heuristic test (i.e., whenever necessary): every time the energy of the system is calculated, the program also computes the distance each atom moved since the nonbonded list was last updated. If any of these distances is larger than a given number (1 Å, in this case), the nonbonded list is updated. With this option and for this specific system, the nonbonded lists are updated at 8–15-step intervals. The electrostatic forces and energies are calculated using the particle-mesh Ewald method (25,26) with a charge grid spacing of 0.7 Å and direct sum tolerance of 4 × 10⁻⁶ for interpolation. Structures for analysis are saved every 0.1 ps. The simulations were carried out on a 16-node, Pentium IV, 2 GHz, Linux Beowulf cluster. For T = 278 K, the average molecular density is 〈ρ〉 = 1.608 Å⁻³ (〈ρ〉 = 9 10⁻³ g/cm³) and the average length of the simulation box is 〈L〉 = 39.6 Å. For T = 300 K, 〈ρ〉 = 1.57807 Å⁻³ and 〈L〉 = 39.9 Å. We also run simulations in smaller boxes of average length 〈L〉 = 30 Å and density 〈ρ〉 = 1.91 10⁻² g/cm³, at both temperatures, to sample more extensively the short intermolecular distance range. The gas phase simulations were carried out using the same periodic boundary conditions described for the solvated systems, and the same molecular densities. The simulations performed for this study, including the number of molecules, phase type (gas or liquid), length of the simulations (in nanoseconds), temperature, and box shapes and dimensions are presented in Table 1 (does not include the equilibration of the pure water boxes).

TABLE 1.

Performed MD simulations

Simulation/phase	Time(ns)	Temp (K)	No. water molecules	Box type	〈L〉*/axis (Å)
1 bAdp/gas	20	300	0	Octahedron	35
1 bAdp/gas	20	278	0	Octahedron	34
2 bAdp/gas	30	300	0	Cubic	39.92
2 bAdp/gas	30	278	0	Cubic	39.71
1 bAdp/liquid	20	300	1099	Octahedron	35.08
1 bAdp/liquid	20	278	1099	Octahedron	34.55
2 bAdp/ liquid	30	300	2122	Cubic	39.87
2 bAdp/ liquid	50	278	2120	Cubic	39.62
2 bAdp/ liquid	30	300	990	Cubic	31.0
2 bAdp/ liquid	60†	278	990	Cubic	30.82
2 bAdp/ liquid	60‡	278	990	Cubic	30.82

^*〈〉 denotes a time average.

^†Simulations were carried out on a 16-node, Pentium IV, 2 GHz, Linux Beowulf cluster.

^‡Different initial conditions, simulations performed on a dual AMD Athlon computer.

Molecular conformations of the bAdp molecule in gas phase and solution are defined by the magnitude of the dihedral angles Φ and Ψ formed by the CL-NL-CA-CRP atoms, and NL-CA-CRP-NR, respectively. The configurational space corresponding to the 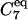state is centered at Φ = −80 and Ψ = 70. The definitions for 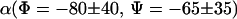and PPII are similar to those in Garcia (27). The basin of the β-type conformation is situated at (−150,160). In Fig. 1 A, bAdp2 is in a typical α-conformation and bAdp1 is in a more stretched (almost PPII) conformation and in Fig. 1 B both molecules are in PPII-like conformations. Experimental NMR data show that the basin corresponding to the α-conformation is located at (Φ,Ψ) = (−80,−30) and that of the PPII conformation at (Φ,Ψ) = (−80,150) (28). The sets of (Φ₁,Ψ₁) and (Φ₂,Ψ₂) angles are determining the conformations of the molecules in the two-molecule system (Fig. 1 A). Table 2 summarizes the definitions for the conformations of the bAdp molecules discussed throughout this work.

TABLE 2.

Conformational definitions

Dihedral angle/atoms	α-type	α-restricted	PPII type	PPII restricted	β
Φ CL/NL/CA/CRP	−80 ± 40	−80 ± 40	−80 ± 40	−80 ± 40	−150 ± 20
Ψ NL/CA/CRP/NR	−65 ± 45	−60 ± 35	30 < Ψ < −120	>30	>60

RESULTS AND DISCUSSION

Φ-Ψ maps in gas phase and solution

The energy landscape of the individual alanine dipeptide molecules in gas phase consists of two deep and broad basins in the second quadrant of the Ramachandran plot and a shallow basin in the α-region of the Φ-Ψ map at both 278 (Fig. 2 A) and 300 K (Fig. 2 B). The upper, elongated basin in the second quadrant of the Ramachandran plot corresponds to the PPII and β-type conformations with the maximum at PPII, and the lower basin corresponds to (Φ = −80,Ψ = 70)-type conformations. The α-region is sparsely populated at both temperatures. A comparison between the Φ-Ψ maps at 278 and 300 K reveals the fact that the α-region is less populated at 300 than 278 K. The dominance of the conformation in gas phase is in good agreement with prior geometry optimizations (6) and recent experimental results from torsion-rotation interactions (29) that predict the 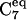conformation as the lowest energy form in the gas phase. This conformation exhibits an intramolecular H-bond.

FIGURE 2.

(A–C) Ramachandran log plots of the conformational space sampled by the bAdp molecules in gas phase at 278 and 300 K. Panels A and B are represented as 10 contour plots between 0 and 3.5 and are the result of two-molecule simulations and panel C is the result of a one-molecule simulation at 300 K in a simple Φ-Ψ plot.

Fig. 2 C represents the Φ-Ψ map of the conformational space of a single bAdp molecule in gas phase at 300 K. It is evident from this figure that the PPII region is not as well populated as the β-region, contrary to the results of the two-molecule simulation at the same temperature (Fig. 2 B). This result indicates that the conformational populations of the molecule are influenced by the presence of the second molecule in the system. In this case, the net result is that PPII becomes more populated than β in the presence of intermolecular interactions in gas phase, as suggested by a comparison between Fig. 2, A and B (two-molecule simulation) on one hand, and Fig. 2 C (one-molecule simulation) on the other hand.

The energy landscape of the two bAdp molecules in water (Fig. 3) is qualitatively very different from the corresponding energy landscape in gas phase (Fig. 2). It is composed of two basins, roughly equally populated—one of PPII character in the upper second quadrant and one in the α-region (third quadrant) of the Ramachandran plot. The system rarely samples the conformations; these conformations are not stable in water. The large jumps in conformational space between conformations sampled in solution, especially in the Ψ angles, between the PPII and α-type conformations, coupled with broad basins for both conformations, indicate that the bAdp molecules are more flexible in water than in gas phase.

FIGURE 3.

Normalized Ramachandran plot for the conformational space sampled by two bAdp molecules at 300 K in water: 14 contours between 0 and 0.18. The definitions for 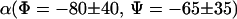and PPII are similar to those in Garcia (27). The β-type region is centered around (−150,160).

Our results are in agreement with experimental results from NMR dipolar coupling experiments obtained by Weisshaar and co-workers, and recent ¹³C NMR structure determination, which concluded that an almost equal mixture of rapidly interconverting PPII and α_R structures is more likely in water (28,30). A predominant PPII conformation is likely in nonhydrogen bonding environments, solids, and crystals (28). It has been proposed that the PPII conformation is stable in water because it maximizes the probability for peptide-water cooperative hydrogen binding, whereas the α_R geometry is stable primarily because of its large dipole moment (30).

In the system of two bAdp molecules, the conformational population of each single molecule can be described by the sampled 2D map, (Φ,Ψ). To describe the conformational space available to the two-molecule system, a four-dimensional conformational space, 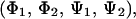is needed. In these simulations, the Φ-angle distribution is approximately the same for the two main conformations, α and PPII (Fig. 3). A small asymmetry in the Φ-angle distribution toward large and negative Φ-angles is due to the presence of a small amount of β-type conformations (<5–6% of the whole population). The distributions for one- and two-molecule simulations are similar at 278 and 300 K, with wider basins and a slight increase in β-type conformations at higher temperatures. The same variation of conformational population with temperature has been observed by other workers for single-molecule simulations (31).

The main goal of this work is to understand the interaction between two alanine dipeptide molecules in water. Therefore, we focus our conformational analysis on the two major conformations present in solution, α and PPII. In the two-molecule system, there are four possible states for the system: one in which both molecules adopt α-type conformations, a second one in which bAdp1 is in an α-conformation and bAdp2 is in a PPII conformation, a third one in which bAdp1 takes on a PPII conformation and bAdp2 is in an α-conformation, and finally, a fourth state in which both molecules adopt PPII conformations: α-α, α-PPII, PPII-α, and PPII-PPII. The “simultaneous” conformational space sampled by the two bAdp molecules is well described in a 2D space, 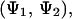because of the previously stated inability of the Φ-angle to discriminate between the states in solution. The map at 278 K that illustrates the four possible combinations of states and their relative populations is presented in Fig. 4, as a contour plot (A) and a histogram (B). Fig. 4 clearly shows that all four possible states of the two molecules in solution are well sampled during the simulations.

FIGURE 4.

(A and B) Simultaneous conformational space sampled by the two-bAdp-molecule system as a contour plot (A) and as a histogram (B).

Temperature and box size effects on the conformations and relative populations of the blocked alanine dipeptide molecules

The conformations and relative populations of the alanine dipeptide molecules are sensitive to temperature. In Fig. 5 we show differences between the normalized Ramachandran plots of the two-molecule simulations at 278 and 300 K (Fig. 5 A), the difference between the normalized Ramachandran plots of the two-molecule simulations in the small box (SB, 1000 water molecules) and the large box (LB, 2100 water molecules) simulations (Fig. 5 B), and the difference between the normalized Ramachandran plots of the two-molecule and one-molecule systems at 278 K (Fig. 5 C). Even small differences in the conformational populations can be observed with the difference plots. An increase in the populations of PPII and β-type conformations at higher temperatures becomes evident in the upper left corner of the plot in Fig. 5 A. The 300-K distribution is wider and this contributes to a relative decrease of populations in the center of the basins of both α and PPII populations.

FIGURE 5.

(A–C) Contour plots of the differences between the normalized Ramachandran plots of the conformational space sampled. Twelve contour plots between −0.02 and 0.02. (A) The difference between the two-molecule simulations at 278 and 300 K in the large box; (B) the difference between the two-molecule simulations in the small (SB) and large box (LB) at 300 K; (C) the difference in conformational populations between the two-molecule and one-molecule simulations at 278 K.

The net effect of more sampling in the short intermolecular distance range (the two-molecule simulation in the smaller box) at 300 K is shown in Fig. 5 B: the α-region is more populated and there is a displacement of the PPII position toward lower Φ and Ψ. In Fig. 5 C we represent the difference plots of the conformational spaces sampled in the single bAdp and multiple (two) bAdp simulations at 278 K. When only one molecule is present in the system, the population of PPII conformations is larger than the PPII population in the two-molecule simulation, whereas the α-region is more populated in the two-molecule simulation.

Hydrophobic effect: solvent-accessible surface areas

The hydrophobic interactions are usually considered to be proportional to the apolar solvent-accessible surface area (SASA) of the molecules. We have proceeded to analyze the distributions of SASA in our model system by calculating the individual molecular SASA and the contact or buried SASA upon molecular association. There is little difference between the distributions of solvent-accessible surface areas of the two molecules at 278 and 300 K. The mean surface area exposed to the water by each molecule is 375 Ų with a mean ± SD 9 Ų. If fully solvated, a bAdp molecule interacts on average with 38 ± 1 water molecules (supposing each water molecule occupies 10 Ų of the peptide solvent-accessible surface area). Molecular SASA is calculated here using CHARMM with a probe radius of 1.4 Å.

The total surface area can be divided into polar (NH and CO groups) and apolar components (methyl hydrogens and carbons, and C_α and C_β atoms together with their hydrogens). The average total apolar surface area of each molecule is 280 Ų and the average polar surface area is 95 Ų; one-fourth of the total surface is polar and three-fourths are apolar. There is practically no difference between the apolar and polar surface areas of the two possible conformations, α and PPII (the difference between the positions of the maxima in the corresponding distributions is 5–6 Ų). This suggests that the hydrophobic effect does not play a significant role in the transition from one molecular conformation to the other for the single molecule or in determining the conformation of a single bAdp molecule. Our observation is similar to the result obtained by Thirumalai and co-workers (32) who investigated the equilibrium dynamics of a single valine dipeptide in water.

When two bAdp molecules interact in solution, the total solute SASA exposed to the solvent varies with the distance between the molecules. The total SASA is smaller than the sum of the SASA of the two individual molecules starting with distances between the centers of mass as large as 14 Š(Fig. 6). For short distances, the total solvent-accessible surface area of the two molecules is reduced by as much as 31%, or 232 Ų, from a combined total of 750 Ų surface area of the two molecules at large distances. This is equivalent to a release of 23 water molecules from the direct contact with bAdp molecules to the bulk water. It is interesting to note that the distribution of buried surface areas is narrow for short distances and becomes wider at large separations between the centers of mass (Fig. 6). This is a consequence of the increasing number of mutual orientations available to the molecules as they move further apart.

FIGURE 6.

Buried solvent accessible surface area (SASA): total (black), polar (light gray), and apolar (dark gray) as a function of the intermolecular distance, R_CM.

We have established earlier that the hydrophobic effect does not play a role in the selection of single-molecule conformations of bAdp in water, but it might be the dominant factor in the intermolecular interactions. The buried surface area contribution to the free energy of molecular association, the hydrophobic contribution to solvation, is usually expressed as a function of the change in the two-molecule system SASA upon molecular association, 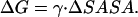For the calculation of 1D PMF derived from the buried surface area equation shown above, we used the average of the total buried SASA values from Fig. 6, 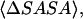calculated for each corresponding distance between the centers of mass. Typical association energies in protein-protein complexes are in the range of 5–20 kcal mol⁻¹. For protein-protein interaction, γ is between 16 and 25 cal mol⁻¹ Å⁻² (33,34). This range of γ-values is appropriate for “lock and key” type, rigid body interactions. The bAdp-bAdp interaction potential derived from the average buried SASA as a function of distance between the molecules (see Fig. 9, the curve with squares) was calculated using a value of γ of 5 cal mol⁻¹ Å⁻², approximately four times smaller than the average value reported by Chothia. At the 1D PMF minimum situated at 5.8 Å, the total buried area varies between 120 and 180 Ų, therefore ΔG(SASA) varies between 0.6 and 0.9 kcal mol⁻¹. The percentage of average apolar surface contribution to the total buried SASA increases as the two molecules are coming in closer contact. To what extent this is a sign of the hydrophobic character of the interaction is hard to tell at this point.

FIGURE 9.

1D PMFs at 278 K derived from radial distribution functions 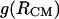(circles) and 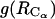(diamonds). The 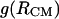curve with square symbols represents the PMF derived from the average apolar SASA area buried by molecules at respective 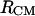separations.

Electrostatic interaction

It is valuable to understand the role of electrostatics in the interaction between two solute molecules in water, and the water-solute interaction in a polar system where both solute and solvent molecules have large dipole moments. The bAdp molecules are neutral molecules, but they have quite large dipole moments, two or three times larger than the dipole moment of a water molecule, depending on the conformation. We are exploring whether the molecular dipole moment plays a role in the intermolecular interaction.

Molecular dipole moments prove to be good discriminators between the possible conformations of the peptide, in good agreement with the definitions from the (Φ,Ψ) maps. In the α-like conformation, the two peptide dipoles are oriented parallel to each other rendering a large total dipole moment. The PPII-like conformation is characterized by antiparallel orientation of the peptide dipoles, resulting in a lower total dipole moment. A characteristic distribution of dipole moments in gas phase and in solution is presented in Fig. 7. There are two distinctive maxima in the solution dipole moment distribution indicative of a bimodal distribution (the solid and dotted-line curves in Fig. 7). The lower peak, at 4.75 Debye (mean ± SD 1.35) corresponds to PPII-like conformations and the higher peak at 7.93 Debye (mean ± SD 0.5) corresponds to α-like conformations. The dipole difference between the two conformations is a little larger than the dipole of a single water molecule (2.8 Debye). The dipole moment distribution in gas phase (the curve with circles in Fig. 7) is very different from the solution distribution and reflects the different conformational space sampled by the molecules in gas phase: the conformation characteristic to the gas phase conformational space (see Fig. 2, A and B) has a characteristic dipole close in magnitude to that of a water molecule; the maximum is at 3 Debye. The elongated tail of the gas phase distribution is due to contributions from the PPII conformations and, to a lesser extent, contributions from the α-type conformations.

FIGURE 7.

Molecular dipole moment distributions in gas phase (circles) and solution at 278 K (solid line) and 300 K (dotted line).

Close interaction promotes α-helix formation

To assess the effect of the local (micro) environment on the behavior of the molecules in solution, we calculate the variation in the populations of α, PPII, and β-conformations with the distance between the centers of mass. For this calculation, we use a stricter definition of α, β, and PPII conformations, to coincide with the definitions of Garcia (27), for easier comparison with the results presented in that work. The results are presented in Fig. 8, A and B. At large 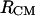distances, the composition of the population distributions reproduces well the population distribution of the central amino acid in the alanine polypeptide studied by Garcia (27) (Fig. 3, in above-cited article): 45.2% at 278 K and 40% at 300 K for the α-type conformation, and 25% at 278 K and 28% at 300 K for the PPII conformation. At large separation distances (>14 Å), we observe a decrease in the α-type population with increasing temperature and an increase in the PPII population from 278 to 300 K. These trends are also observed in the work of Garcia (27). The β-type conformations are <5% for both temperatures, with a slight increase (∼1%) at 300 K.

FIGURE 8.

(A) Population content as a function of intermolecular distance; α-helix populations at 278 K (circles) and 300 K (diamonds) and PPII populations at 278 K (squares) and 300 K (triangles). The definitions for and PPII 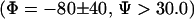are similar to those in Garcia (27). The two lower curves correspond to the populations of β-type conformations at 300 K (dotted curve) and 278 K (dot-dashed curve). (B) Variation of conformational populations with the intermolecular distance in the two-bAdp-molecule simulation from the two 60-ns independent simulations in the small box (L_box ∼ 30 Å) at 278 K and P = 1 atm. The top curve represents the variation of the α-population (circles) from 2,400,000 data points with the distance between the centers of mass, 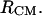The middle curve represents the variation of the PPII population (squares) and the bottom curve represents the variation of the β-population (diamonds), respectively.

The most interesting aspect of Fig. 8 A is that the population distribution of conformations adopted by the blocked alanine dipeptide is significantly dependent on the intermolecular distance between the centers of mass. In fact, at 300 K and distances <14 Å, the population of α-type conformations is strongly influenced by the presence of the second molecule in the system. We observe a large increase in the α-type population between 4.4 and 6 Å, with a maximum of 57% at an 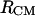of 4.9 Å. A significant increase of 6% is also noted between 8.5 and 14 Å. The change in the conformational populations with the distance between the centers of mass is very long ranged (up to 16 Å) and is in direct response to the change in local environmental conditions, represented by both (change in) water networks and the second bAdp molecule. These variations in the populations of representative conformations of the bAdp molecule are intrinsically related to the complexity of the PMF surface. It has been well established that polyalanine adopts mostly α-helical conformations in organic media (35,36). To probe the variation of conformational populations with intermolecular distance more extensively, we have performed two independent 60-ns simulations of the solvated bAdp molecules in the smaller box (Table 1, last two rows). The data in Fig. 8 B are derived from the combined two 60-ns simulations for a total of 2,400,000 snapshots of the bAdp molecules in the small box (30 Å) simulations at 278 K. Even though the conformational space sampled in the small box simulations is different from that of the large box (see our discussion in the last subsection of this section), we observe the same effect: an increase in the population of α-type conformations at distances <9 Å, from 41 to 49%. The propensity of this conformation at short distances is shown by the top curve in Fig. 8 B (curve with circles), which represents the variation of α-type population with the distance between the centers of mass in the small box. Fig. 8 B also shows a depletion of 10–15% in the PPII population at distances <6 Å (the middle curve with squares).

The observation that α-helix conformations are promoted at close molecular encounter could in fact be related to the partially “organic” (micro) environment that the two molecules provide for each other. It has been recently shown that a moderately hydrophobic environment, such as the interior of the GroEL cavity upon complexion with ATP and GroES, is sufficient to accelerate the folding of a frustrated protein by more than one order of magnitude (37). Our result could provide a partial explanation of the mechanism involved in the accelerated folding of the frustrated protein.

One-dimensional PMFs for bAdp-bAdp interactions in water

We have determined the pair RDFs of the distance between the centers of mass and the distance between the central 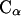atoms of the two molecules, 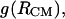and 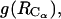respectively. The 1D PMFs, calculated using 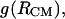and according to Eq. 1, are represented in Fig. 9 (curve with circles and curve with diamonds, respectively). A comparison between the PMFs derived from the RDFs of 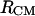and 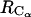(Fig. 9) reveals details that are not easy to reconcile. The shoulder at 4.7 Å in the PMF derived from the RDF of 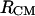is not observed in the PMF derived from the RDF of 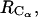whereas both exhibit a shallow minimum at 14–15 Å.

A potential of mean force based on a model that calculates the total desolvation energy from the total average buried SASA between the two molecules (Fig. 9), 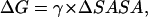whereγ = 5 cal mol⁻¹ Å⁻², is also shown in the figure (squares). The PMFs derived from SASA can match well the 1D PMFs derived from RDFs in the mid-range distance of 7–11 Å. They cannot reproduce well either the short- or long-range interactions.

The 1D PMFs at 278 and 300 K represented in Fig. 10, have common features, such as two minima, for distances <10 Å. The first and deeper minimum of −1.6 k_BT in the 278 K PMF (diamonds) is situated at 5.3 Å separation of the C_α atoms, and the second minimum of −0.82 k_BT is at 7.7 Å. In the 300 K PMF (the curve with circles in Fig. 10) the first minimum of −0.93 k_BT is at 5.45 Å and the second minimum of −0.66 k_BT is at 7.5 Å. The first two minima in the PMFs could partially reflect the nonspherical shapes of the molecules. Two quantities are relevant in trying to understand the significance of the 1D PMFs: the average end-to-end distance between the terminal methyl carbons and the radius of gyration of the bAdp molecule. The average end-to-end distance between the terminal methyl carbons of each molecule is 6.48 Å (with a mean ± SD 0.46 Å). The radius of gyration of the molecules in solution is represented by a bimodal distribution with two well-defined picks at 2.8 and 2.91 Å, corresponding to the two main conformations of the molecules. If we think of the bAdp molecules as having an ellipsoidal shape, the first minimum at 5.3 Å could correspond to the interaction of the two molecules in close contact along the short axes. The second minimum at 7.5 Å could be a combination of attractive forces due to close contact along the longer molecular axes and a solvent separated minimum effect, where the molecules are separated by one layer of water molecules. Longer range attractive forces are manifested in the lower temperature potential.

FIGURE 10.

1D PMFs derived from RDFs of 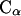atoms at two temperatures: 278 K (diamonds) and 300 K (circles).

The 1D PMFs presented here in Figs. 9 and 10 are projections of the complex free energy surface of bAdp-bAdp interaction in water on the chosen coordinates: the separation between the centers of mass and the distance between the C_α atoms of the two molecules. For example, represented in Fig. 9, is qualitatively and quantitatively different from 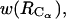in that 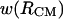exhibits a shoulder at 4.7 Å and an almost inexistent second minimum. One can only guess at this point that the shoulder at 4.7 Å is indicative of an improbable but favorable intermolecular interaction such as a hydrogen bond formation. This possibility is illustrated in Figs. 1 B and 11 A, which show possible intermolecular H-bond formation between a carbonyl group in one molecule and an NH group in the other molecule. Further investigation is necessary to verify this hypothesis. In conclusion, 1D PMFs are limited in conveying the complexity of interactions even between two relatively simple molecules such as the blocked alanine dipeptides in water.

FIGURE 11.

(A) A snapshot of the bAdp-bAdp interaction at short distances, with a possible (transient) H-bond formation between the molecules and hydrophobic interaction between two pairs of methyl groups: the blocking left and right groups and the two alanine methyl groups. (B) Representative conformations and mutual orientations of the two alanine dipeptide molecules at short center of mass distances; according to the 2D potentials of mean force coupled to the preference for α-type conformations at short distances, this particular intermolecular orientation with the end-to-end vectors at 180° is one of the most favorable for the bAdp-bAdp interaction in water.

Two-dimensional PMFs for bAdp-bAdp interactions in water

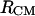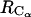The 1D PMFs reflect the average overall relative intermolecular orientations for a given or distance. A better understanding of the bAdp-bAdp intermolecular interactions is afforded by the introduction of an additional degree of freedom that is related to the relative orientation of the molecules. Here, we are choosing the angle θ between the end-to-end vectors of the two molecules as our second variable or degree of freedom. The end-to-end vector is defined as the vector distance between the positions of the carbon atoms of the blocking methyl groups (Figs. 1 B and 11 A), e→_end-to-end = r→_CL−r→_CR. We concentrate our 2D PMF analysis on the longest simulation of 50 ns in the 40-Å cubic box at 278 K (row 8 of Table 1).

At large distances between the molecules, molecular tumbling averages out any orientational dependence of the interaction, but at shorter separations the relative orientation of the molecules and perhaps the geometry of the local water network are essential in determining the magnitude of the attraction. The 2D PMFs show a pronounced variation in the magnitude of the interaction with the relative intermolecular orientation (Fig. 12). A clear preference for antiparallel (180°) end-to-end vector orientation is noted at short-range interaction, between 4 and 7 Å separation of the centers of mass. The deepest minimum of −3.6 k_BT is at 4.6 Å. This interaction is three times stronger than the interaction reported by the 1D PMF derived from the RDFs of intermolecular distances (black line with circles in Fig. 9).

FIGURE 12.

Contour plot of the 2D PMF of the bAdp-bAdp interaction as a function of the distance between the centers of mass between 3 and 15 Å and the angle θ between the end-to-end vectors, e₁ and e₂. Eight contour plots are shown here between 0 and −2.0 k_BT. The 2D PMF is derived from 50-ns simulations in a cubic box of 2200 water molecules with a side length L of 40 Å.

In Fig. 11, A and B, we show some representative conformations and mutual orientations of the two bAdp molecules in close contact. In Fig. 11 B, both molecules are in α-like conformations, which we have shown previously to be favored at close encounter (Fig. 8, A and B). The end-to-end vectors are oriented at 180° (antiparallel) and the dipole moments are oriented at small angles. There are two methyl-methyl group interactions: the 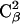methyl of bAdp2 interacts with the methyl group of 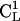and the 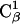methyl group interacts with the methyl group. According to the 2D PMF, intermolecular orientations such as this one are responsible for the most favorable interactions between the molecules.

The preference for the 180°-antiparallel orientation of the end-to-end vectors is clearly shown in Fig. 13. A pronounced change in the histogram of the cosine of the angle between the end-to-end vectors, θ, is shown for 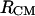distances between 4 and 7 Å (dotted histogram) as compared with the all distance histogram (solid histogram).

FIGURE 13.

Histogram of the cosine angle between intermolecular end-to-end vectors for all centers of mass distances (solid line) and for distances between 4 and 7 Å (dotted line).

Another second variable that measures the relative orientation between molecules and can be easily calculated from MD trajectories is the angle between the molecular dipoles. The results from the 50-ns MD simulation in the large box indicate that the molecular dipole moments prefer to orient more or less parallel to each other (θ is between 0 and 50°) at close molecular encounter. The parallel orientation of the dipole moments in solution is opposite to their orientation in the gas phase. In the gas phase, the short-range intermolecular interaction of the two alanine dipeptide molecules seems to be driven by the dipole-dipole interaction because the molecular dipoles tend to orient antiparallel (results not shown but available by request). Calculations of the 1D PMFs between the two alanine dipeptide molecules in gas phase show a very strong intermolecular attraction of −6 k_BT at 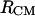= 4.15 Å. This interaction is four times stronger than the 1D intermolecular interaction in solution. The parallel orientation of the molecular dipoles in solution may be indicative of the fact that the intermolecular dipole-dipole interaction is not the driving force for bAdp-bAdp attraction in solution. Instead, the formation of the transient molecular “dimer” in solution may be driven by a combination of factors such as the hydrophobic effect, solute hydration, and intermolecular electrostatic interaction with water. At short distance, the molecules tend to adopt an α-helical conformation, which has the higher dipole moment (Figs. 8 and 7), and then orient their dipoles parallel to each other as if to optimize the interaction of the formed transient “dimer” with the significant dipoles of the polar solvent.

Sampling and size effects in determining the 2D PMFs for bAdp-bAdp interactions in water

To address the issue of conformational sampling in the short distance range between molecules, we have performed two independent 60-ns simulations of two bAdp molecules in a “small box” of 990 molecules with a total volume of 29,271 ± 214 ų, at 278 K and constant pressure of 1 atm (rows 11 and 12 in Table 1). Each 60-ns simulation took 4 months of computer time, as compared to 18 months of computer time necessary for the 50-ns simulations in the box of 2120 water molecules and a volume of 64,000 ų (row 8 in Table 1) on one node of a Linux Beowulf cluster. These simulations were performed with different starting initial conditions, with the molecules at distances of 20 and 8 Å apart, respectively. The 2D PMFs calculated from the two 60-ns small box simulations are qualitatively and quantitatively different from the 2D PMFs calculated from the larger box, but consistent with each other. The calculated errors for the 1D PMFs are 10–20% in the short distance range (4–8 Å). These results indicate that 60-ns simulations seem to be sufficient to sample the small box conformational space even at short distance range. The 2D PMFs calculated from the two 60-ns simulations exhibit most favorable interactions that are half of those calculated from the large box simulations and the minima at both parallel and antiparallel orientations of the end-to-end vectors at short distance are equally populated. The differences in the 2D PMFs between the larger and smaller boxes have two sources: one is related to the possibility that sampling is insufficient in the short distance range in the large simulation box and the other is related to the small size of the simulation box that confines the molecules and thus limits their diffusion and independent molecular tumbling. Separating the size and sampling effects in determining the PMFs for the interaction between two molecules is a very difficult task.

CONCLUSIONS

Our study indicates that the conformations adopted by the blocked alanine dipeptide molecules in water are dependent on the distance between the molecules. Close intermolecular interaction promotes α-helix formation. To the best of our knowledge, this is the first time when an intermolecular distance-dependent conformational population has been observed. This result could provide a new perspective on the events involved in early protein folding and an insight into the mechanism involved in the accelerated folding of frustrated proteins, such as GroEL cavity upon complexion with ATP and GroES (37). The variation of the α-helical populations with the distance between the two molecules and its dependence on solvation, may indicate that helical propensities of amino acids are not intrinsic properties; they are functions of the detailed chemical environment being modulated not only by the solvent environment, but also by the surrounding solutes and cosolutes. This is an extension to conclusions of previous studies on solvent effects on the energy landscapes and folding kinetics of polyalanine (38).

In order for two molecules to attract, they must find favorable relative orientations by rotational diffusion. We have shown here that the interactions even between small molecules, such as the blocked alanine dipeptide molecules, are strongly dependent on their mutual orientation. When favorable mutual orientations are sampled, the interactions between solutes are much stronger than those apparent from the 1D PMFs or a solvent accessible area model.

The 2D PMFs between two bAdp molecules calculated using radial and angular pair distribution functions show a complex interaction that tends to maximize the hydrophobic interaction between the molecules and optimize the solute-water interaction for the “bound” conformations of the transient “dimer,” by aligning the molecular dipoles parallel, such as to maintain a strong electrostatic interaction with water. The projection of the PMFs onto a low-dimensional subspace such as the distance between the centers of mass, does not resolve the complexity of the intermolecular interactions or their partitioning between hydrophobic and others.

We find that the short-range intermolecular interaction of two blocked alanine dipeptide molecules in gas phase might be driven by the dipole-dipole interaction because the dipoles tend to orient antiparallel to each other. By contrast, in solution, at short center of mass distances, the bAdp molecular dipoles orient parallel to each other. This behavior represents a drastic change from the gas phase case and indicates that the intermolecular dipolar interaction is no longer the driving force in the bAdp-bAdp interaction in water. Instead, a combination of the hydrophobic effect, solute hydration, and electrostatic interaction with water could be the driving force for intermolecular interaction at short distances in water. The change in the orientation of molecular dipoles between the gas phase and solvated systems is an indication that implicit solvent models that calculate the solvation free energy as a sum over group contributions may have to take into account the variation in the molecular environment in solution with the distance between molecules.

There is a standing debate in the literature on whether implicit solvent models can appropriately take into account the role of water in the protein folding mechanisms (39). It has been argued, based on MD simulations of protein folding, that it is possible for an implicit solvent model to reproduce explicit solvent results because water equilibration is fast relative to that of protein conformational rearrangements. Our results, especially the finding that the α-helical conformations are more favored upon molecular association, add a new dimension to this debate. The explicit role of the solvent in determining the specific radial and angular variations shown here in the PMFs as well as a comparison with implicit solvent predictions will be investigated in future work. The hydrophobic effect was shown to be dependent on the molecular size (40). We have shown here that even for small molecules, the flexibility of the molecules and the specific intermolecular orientations play a significant role in the intermolecular interactions.

Ideally, the PMFs should be determined from simulations in very large boxes (to mimic “infinite dilution”) but this is practically impossible because of the prohibitive amount of computer time required for all atom MD simulations. However, the calculation of the PMFs from finite-time, finite-box-size systems is useful for determining features of the intermolecular interactions, such as the variation of conformational population with the distance between the molecules, that might be overlooked when this interaction is determined from implicit solvent models only. Ultimately, a careful combination of all-atom MD simulations and implicit solvent might be the best method for calculating PMFs especially for large systems such as protein-protein complexes.