Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2005 Jun 10;89(3):1455–1463. doi: 10.1529/biophysj.104.058495

Exploring Global Motions and Correlations in the Ribosome

Joanna Trylska *,†, Valentina Tozzini *,‡, J Andrew McCammon *,§
PMCID: PMC1366652  PMID: 15951386

Abstract

We studied slower global coupled motions of the ribosome with half a microsecond of coarse-grained molecular dynamics. A low-resolution anharmonic network model that allows for the evolution of tertiary structure and long-scale sampling was developed and parameterized. Most importantly, we find that functionally important movements of L7/L12 and L1 lateral stalks are anticorrelated. Other principal directions of motions include widening of the tRNA cleft and the rotation of the small subunit which occurs as one block and is in phase with the movement of L1 stalk. The effect of the dynamical correlation pattern on the elongation process is discussed. Small fluctuations of the 3′ tRNA termini and anticodon nucleotides show tight alignment of substrates for the reaction. Our model provides an efficient and reliable way to study the dynamics of large biomolecular systems composed of both proteins and nucleic acids.

INTRODUCTION

Ribosomes, assemblies of proteins, and ribosomal RNA (rRNA), consist of two subunits, small and large, which in bacteria are denoted 30S and 50S, respectively. The 30S subunit contains 21 proteins (S1, S2, etc.), one ∼1500-nucleotide-long 16S rRNA chain, and binds mRNA. The 50S subunit is composed of over 30 proteins (L1, L2, etc.), 23S rRNA (∼2900 nucleotides), and 5S rRNA (120 nucleotides). There are three tRNA binding sites situated across both subunits, A, P and E, standing for Aminoacyl, Peptidyl, and Exit. The peptide bond synthesis occurs between the aminoacyl and peptidyl ends of A- and P-site tRNAs. After the reaction, tRNAs must cooperatively translocate to their new positions (P and E) with the advance of mRNA by exactly one codon. The E-site tRNA is then ready to leave the ribosome, a new tRNA may bind in the A-site, and the cycle may be repeated.

Translation, apart from being accurate, with errors occurring only every 104 bases, is extremely fast (10–20 amino acids per second in Escherichia coli in vivo) (1). Such speed must be accompanied by large structural rearrangements, and, indeed, the ribosome has been proven to be a dynamic machine (2–10). These conformational changes are functionally important to assure correct frame reading and translocation of tRNAs. For instance, by means of cryo-electron microscopy (cryo-EM) it was predicted that translocation involves a significant movement of the L1 stalk of the large subunit (9,11). Flexibility of the L7/L12 stalk was also observed (12,13). Ribosomal motions are controlled by various factors (e.g., elongation factor G, i.e., EF-G) binding during different stages of translation. Cryo-EM studies have shown that the ribosome undergoes a ratchetlike rotation of the small subunit upon binding of EF-G (6). A recent kinetic model suggests that GTP hydrolysis drives and accelerates these large conformational rearrangements (14). Although translocation also occurs without GTP hydrolysis (15), it is 50–100-fold slower. A whole factor-free translation, even though extremely slow, was observed under certain conditions in vitro (16–18). Global functional mobility is, therefore, an intrinsic property of the ribosome which is only accelerated by GTP hydrolysis. However, how these motions and rearrangements of the ribosomal parts take place and, more importantly, how they are correlated with each other is not yet clear, and further studies of ribosomal dynamics are required.

Up to this date, theoretical studies of the large-scale motions of the ribosome were performed by means of normal mode analysis, which assumes harmonic motions (8,10) and does not allow us to study transitions among stable states or dissociation of bonds. The system in Gaussian network models or elastic network models is described by a network of beads; all beads that are less than a certain distance apart are connected by harmonic elastic springs (19,20). The spring constant is usually similar for all the interacting centers. Therefore, these models assume harmonicity of motions and since the movements may be predicted only around a local minimum, no dissociation of pseudobonds is possible. Such simulations are extremely biased toward a starting configuration. In this work, we developed a coarse-grained model for the ribosome that both accounts for the anharmonic motions and allows for the breakage and formation of connections in the system. We built and parameterized a force field for a low-resolution representation of proteins and RNA, and applied it in molecular dynamics (MD) simulations. Parameterization is only structure-specific in the local regions keeping the local nonbonded order, and for all other parts it is general and allows for large-scale conformational changes. Apart from investigating the conformational freedom, we analyzed the correlations of movements among the ribosomal parts, and proposed their role in the translocation process. In addition, MD simulations enabled us to reach timescales that are not available for all-atom simulations with explicit solvent. In the model, amino acids and RNA nucleotides are represented as single interacting beads that bear a radius and mass, and are centered on the positions of the carbon Cα and phosphorus P atoms. The formula for the effective potential energy (more accurately, a potential of mean force) is composed of typical classical force-field energy terms, including the bonded and nonbonded interactions. The nonbonded potentials are represented by an anharmonic Morse function. The parameterization of the force field is based on the radial distribution function derived from the crystal structure. Boltzmann inversion (21) is applied to these distributions and analytical functions are fitted to obtain the initial parameters for the interactions. However, the average crystal field has an overall compression effect and, therefore, structure-derived parameters are known to be too compressed when compared with theoretical distributions obtained without taking into account the crystal packing and thermal motion (e.g., see (22)). Hence, to avoid bias toward the starting structure and to validate the force field, the parameters were adjusted in the course of test MD simulations to obtain final parameters that allow for configurational flexibility with the amplitudes of global motions that are in accord with experimental cryo-EM data (e.g., see (4) and (6)).

The developed model and the parameterization are described in Methods. In Results, we describe four 500-ns MD simulations. Functionally important principal directions include rotation of the small subunit in phase with the L1 stalk, widening of the tRNA cleft, and, most importantly, a counterphase movement of the distant L7/L12 and L1 stalks. A link to the elongation process is discussed. Small fluctuations of the 3′ tRNA termini and anticodon nucleotides are shown and confirm tight alignment of the substrates for the reaction. Conclusions follow.

METHODS

A coarse-grained model of the ribosome

Our methodology is based on one-bead models proposed originally for studies of proteins (23–26). We extend the model so that not only amino acids but also nucleotides are represented as single spherical beads centered on the positions of phosphorus P and carbon Cα atoms. For the proteins, the model was tested before in the coarse-grained studies of the flap opening in HIV-1 protease (V. Tozzini and J. A. McCammon, unpublished results).

To account for the interactions among the beads, we define a force field that includes the energy terms

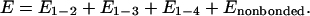graphic file with name M1.gif (1)

The first three bonded terms account for the pseudo-bond, pseudo-angle, and pseudo-dihedral interactions between the two, three, and four successive beads in each chain, respectively. We use the harmonic potential to describe these interactions, 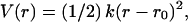Inline graphic where r0 is the equilibrium distance taken from the starting structure, and the force constant k depends on the type of bead and pseudo-bond, pseudo-angle, and pseudo-dihedral interaction. The use of the Morse potential to describe the bonded types of interactions does not change the results of our simulations; therefore, we chose to parameterize the harmonic potential in this case.

However, we use two Morse potential formulas for the nonbonded energy term Enonbonded of Eq. 1. One is applied within a certain cutoff (Rcut) and is structure-specific,

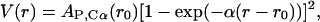graphic file with name M3.gif (2)

where the equilibrium distance r0 is taken from the starting geometry, and AP,Cα, is an analytical formula that depends on the bead type. The interactions outside Rcut are not structure-dependent and are defined with similar Eq. 2, but r0 depends only on the bead type and not on the starting configuration. In the latter case, AP,Cα is an analytical formula that is different for the P···P, Cα···Cα, and P···Cα interactions. AP,Cα is an exponentially decreasing function (see Table 1) that accounts for assigning weaker parameters to interactions with higher equilibrium distances.

TABLE 1.

Parameters and functions used for the P and Cα beads in the coarse-grained model of the ribosome

Parameter Cα beads P beads
k1–2 50.0 3.0
k1–3 5.0 2.5
k1–4 1.5 0.5
ksec — 1.0
α 0.707 0.707
Radius (r0/2) 4.75 8.8
A(r) 4 × exp(−r/2.8) 2 × exp(−r/6.0)
Open in a new tab

Force constants are in units of kcal/mol and distance is in Å.

The secondary structure of rRNA must be known from the crystal structure and is accounted for with a harmonic potential Inline graphic with the equilibrium distance taken from the starting configuration.

Parameterization of the force field

The initial parameters were based on the statistical analysis and were derived from the radial distribution function of the starting geometry by applying the Boltzmann inversion (21). If a variable q describes a degree of freedom in the system, then P(q), the probability distribution associated with this degree of freedom, is related to the potential of mean force, W(q), by the equation

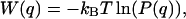graphic file with name M5.gif (3)

where kB is the Boltzmann constant and T temperature. The value W(q) coincides with the potential energy V(q) associated with the variable q only in case of a single degree of freedom. Otherwise, it is often used as an approximation to the potential energy in the so-called knowledge-based force fields (e.g., see Refs. 28–30).

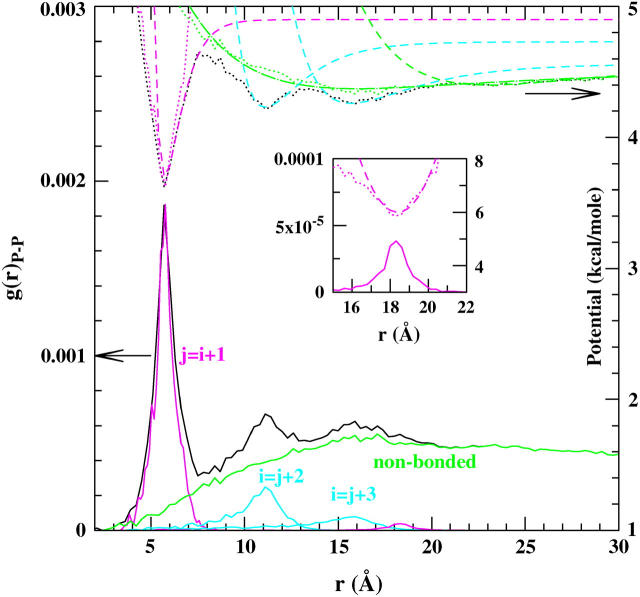
For the ribosome model, the pair distribution functions, g(r), are analyzed and the corresponding potentials are extracted and parameterized. The g(r) distribution for the P–P pairs in the starting configuration of the ribosome is shown in Fig. 1. The corresponding potential (dotted lines) was obtained by Boltzmann inversion. To include all the secondary structure interactions, the cutoff in the anharmonic network model, in case of P beads, was set to Rcut = 20 Å.

FIGURE 1.

FIGURE 1

Open in a new tab

Plot shows the g(r) distribution for the P–P pairs in the 70S ribosome structure (black solid line). The corresponding (r) is shown as a black dotted line. The structural interactions for g(r) were extracted: the first neighbor and paired-bases distributions are shown in magenta, whereas the interactions between second and third neighbors along the chain (corresponding to angle and dihedral interactions) are shown as cyan solid lines and the Morse potential as cyan dashed lines. The nonbonded interactions, after subtracting the structural interactions, are shown as a green solid line with a corresponding Boltzmann inversion shown as a green dotted line. The green long-dashed line shows the fitted Morse potential. The potential used outside the cutoff is shown as green dashed line. The inset shows the radial distribution and the respective potential for the paired bases in the secondary structure. The normalization of g(r) and the additive constant for the potential energy are arbitrary.

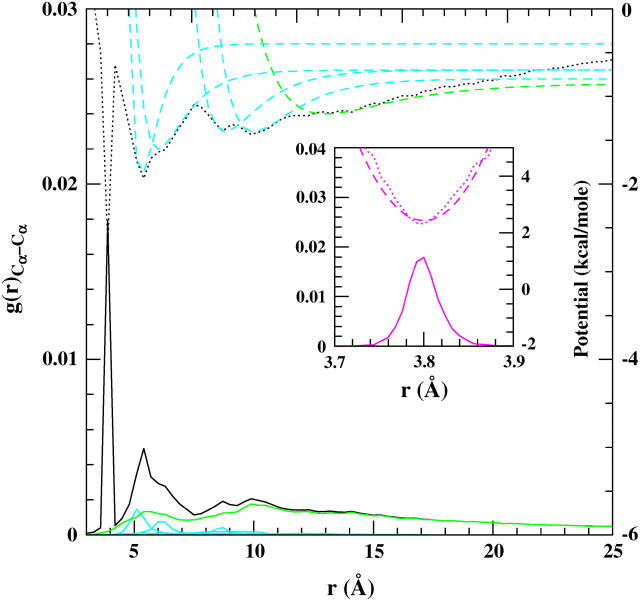
The above procedure was applied to the Cα–Cα distribution function. It can be seen in Fig. 2 that the overall picture is much more complex. However, the distribution of subsequent amino acids is very well peaked at 3.8 Å, and the corresponding potential is conveniently parameterized as a harmonic one (see inset of Fig. 2). In contrast to the rRNA case, the distribution of the second, third, and following neighbors along the chain does not diminish completely until a very large cutoff. This happens due to the long-range correlations of the β-sheets along the protein chain. However, by setting the cutoff value, Rcut, in the anharmonic network model to 12 Å, one already includes all the most important interactions for both the α-helices and β-sheets, as well as additional secondary interactions peaked at 10 Å. Within this approach the four main interactions within Rcut (cyan dashed lines in Fig. 2) can be modeled with the harmonic or Morse potential, and nonbonded interactions (green dashed lines) with the Morse potential function to account for greater flexibility and evolution of the tertiary structure.

FIGURE 2.

FIGURE 2

Open in a new tab

Plot shows the g(r) distribution for the Cα–Cα pairs in the 70S ribosome structure (black solid line). The corresponding (r) is shown as a black dotted line. For g(r) the structural interactions were extracted (cyan solid lines) with the corresponding fitted Morse potentials (cyan dashed lines). The nonbonded interactions, after subtracting the structural interactions, are shown as a green solid line. Green dashed line shows the fitted Morse potential outside the cutoff. The inset shows the g(r) distribution for subsequent amino acids, the Boltzmann inversion and the corresponding fitted harmonic potential. The normalization of g(r) and the additive constant of the potential energy are arbitrary.

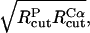To obtain the parameters for the Cα–P beads, we use the so-called “geometric averaging” (e.g., the Inline graphic is set to Inline graphic which leads to a value of 15.5 Å).

Some of the initial parameters for the P and Cα beads that were derived based on the radial distribution functions obtained from crystallographic data and presented in Figs. 1 and 2 were too strongly biased toward the starting structure. This is due to many reasons, e.g., crystal compression forces (22) and the use of a noninteracting ideal gas reference state for Boltzmann inversion, whereas molecules are finite systems composed of interacting particles (31,32). Therefore, many test MD simulations were performed and some of the parameters were iteratively refitted (21) in the course of the simulation to avoid this strong bias and to allow the model to be flexible enough to describe large fluctuations in conformational dynamics. The final parameters applied in MD simulations are shown in Table 1. For the Cα beads the initial parameters were derived based on the crystal structure of the 70S ribosome and a set of structures for the HIV-1 protease, and were subject to detailed analysis in the earlier work (V. Tozzini and J. A. McCammon, unpublished results). For the P beads, the radial distribution function of the ribosomal RNA was the initial data set for the parameterization. In this work, we do not study protein folding or binding, but conformational dynamics; therefore, our set of parameters should account for the flexibility well enough. The parameter set obtained for the P beads is similar in range to that developed by Malhotra et al. for the RNA refinement protocol (33) and for the MD study of the assembly of the 30S subunit (34).

Molecular dynamics simulations

The 70S ribosome structure, obtained to a resolution of 5.5 Å, was taken from the Protein Data Bank (PDB) (35). It contains only the positions of P and Cα atoms. We modeled some of the missing positions of Cα beads inside the protein chains. The PDB structure included three tRNA chains but in two MD simulations we kept just the A- and P-site tRNAs, because during translocation only two tRNAs are bound at a time. The other two simulations were carried out without tRNA molecules. MD simulations were performed with the DL_POLY package (36). The system was gradually heated from 10 K to 300 K in a 2-ns simulation. During the thermalization process, the L9 protein chain, whose initial PDB location points in the direction away from the ribosome, attached itself to the system with its C-terminal end in proximity to proteins L2 and S6. This position is in accord with the one modeled by Tama et al. (8) based on a cryo-EM map (6). The equilibration involved a 10-ns simulation. To account for the coupling with a thermal bath, two thermostats were applied: Nose-Hoover (37) and Berendsen (38). The dynamical properties of the ribosome did not depend on the coupling used. To account for the stochastic collisions with the solvent, we also implemented a Langevin-type bath (39) into DL_POLY (36) and tested it with our model. The general global motions of the ribosome are similar; however, this approach will be described in a future study. The applied time step was 50 fs, but the energy is stable up to a timestep of 100 fs. Four 0.5-μs production runs were analyzed. The energy and the secondary structure are stable over that length of time. The cutoff value for all the nonbonded interactions (outside Rcut) was set to 40 Å.

The average root mean-square deviation (RMSD) from the equilibrated structure for all beads is 2.7 ± 0.2 Å for simulations with A- and P-site tRNA and 3.7 ± 0.2 Å for the free ribosome. Cα beads have higher RMSDs because proteins are wrapped around the RNA chains. Our result is in accord with the average experimental temperature factors shown in the PDB structures of the large and small subunits, indicating that Cα atoms are more mobile than P atoms.

Simulations were carried out on the Linux cluster at the Center for Theoretical Biological Physics using 16 2.8-GHz Xeon processors with 2-GB RAM each. One-nanosecond simulation takes between 1 and 1.4 h depending on the applied cutoff for the nonbonded interactions. The principal component analysis (PCA) (40), extracting the most important directions of motions, was performed with the GROMACS package (41) and visualized with the Essential Dynamics Software (42) incorporated into VMD (43). Overall translation and rotation were removed by fitting to a reference structure. The first 10 eigenvectors do not resemble cosines. PCA convergence was checked by analyzing different ranges of trajectory. Principal directions of motions are invariant to the details of the force-field parameters. The spectral analysis was performed for trajectories representing individual principal components. The trajectories were projected onto 10 essential principal directions with the Essential Dynamics Software (42). (For details of the spectral analysis, see Refs. 44–46.) To obtain the density of states, the Fourier transform of the velocity autocorrelation function was calculated for frames from 200-ns trajectories due to the need of frequent storage of the atomic positions.

RESULTS AND DISCUSSION

Global motions and correlations

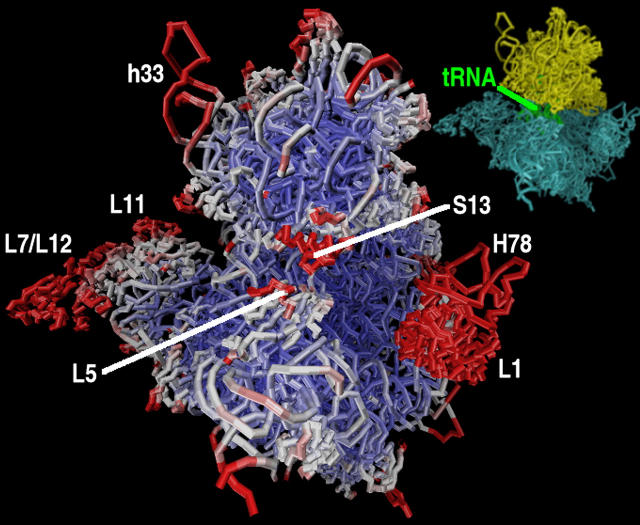
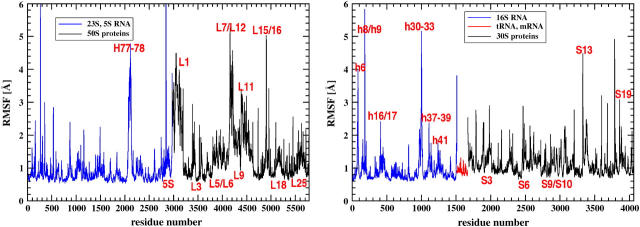
In this work we analyze the results of four 500-ns MD simulations of the 70S bacterial ribosome, and we see similar motions and correlation patterns in all the trajectories. Simulations point to two flexible fragments in the large subunit. One is the L7/L12 stalk with the stalk base, consisting of the L7/L12 dimer and protein L11 with helices H42–H44 forming an RNA portion of the base. The other one is the L1 stalk, composed of the L1 protein and helices H76–H78 of the 23S rRNA. They are situated on the opposite ends of the large subunit and the tRNA path (Fig. 3), and are over 200 Å apart. It was shown that these lateral stalks play a crucial role in proper functioning of the ribosome. Four copies of L7/L12 are present in the ribosome; they are organized as two dimers, and are required for the binding of translational factors. The removal of the whole L7/L12 stalk in E. coli reduces the rate of translation by an order of magnitude (47); at least one dimer is needed to retain activity (48,49). Note that 70S ribosome PDB structure (35) contains only one dimer of L7/L12. Ribosomes that lack the L1 protein have a reduced rate of protein synthesis (50). Moreover, the configuration of the L1 stalk is different in the T. thermophilus 70S structure (35) in comparison with the separate 50S subunit from D. radiodurans (51); in the latter it is tilted by 30°. It has been proposed that the release of tRNA through its exit path requires the movement of the L1 stalk because the stalk interacts with the E-site tRNA (8,10,11,35). Fig. 4 reports the root mean-square fluctuations (RMSF) from the average structure. Indeed, the segments that fluctuate the most include the L7/L12 and L1 lateral stalks.

FIGURE 3.

FIGURE 3

Open in a new tab

Ribosome structure colored according to the average temperature factors derived from a 500-ns molecular dynamics simulation. The scale is from red, which shows the highest fluctuations, through white to blue showing the smallest movements. The inset shows the relative position of the small subunit (yellow) with respect to the large subunit (cyan).

FIGURE 4.

FIGURE 4

Open in a new tab

Root mean-square fluctuations of ribosomal fragments. Single peaks correspond to termini.

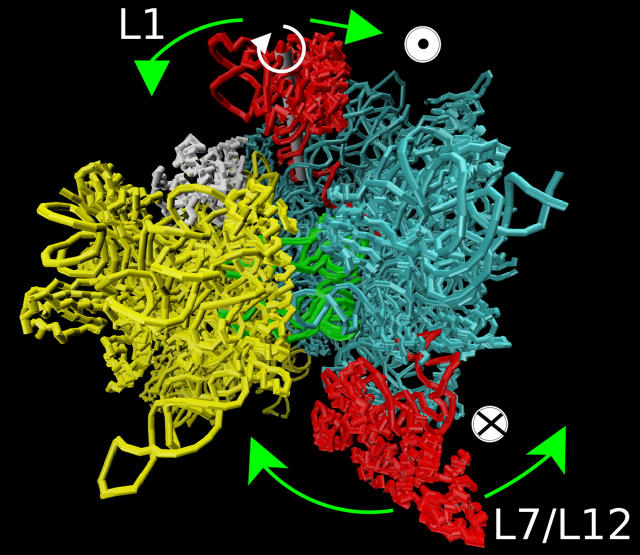
Principal component analysis (40) (PCA) gives essential degrees of freedom that may be relevant for ribosome function and enables description of low-frequency collective motions. Fig. 5 shows the principal directions of movements that involve L1 and L7/L12 stalks. For L1 these include closing over E-tRNA binding site toward the middle of intersubunit space, rotation around the axis of helix H76, and side movement toward the 30S subunit in the direction of proteins S7 and S11. Most importantly, this latter movement, coupled with a slight rotation around helix 76, is anticorrelated with the side movement of L7/L12 stalk toward the 30S subunit. Fig. 6 shows the dynamical correlation pattern for residues representing, among others, the lateral stalks, and confirms their anticorrelated movement (L1 protein with helix H77–H78 and L7/L12 stalk with L11 forming its base show negative correlations). It was shown that mutation of S7 or S11 protein disrupts dynamics and function of the ribosome (52); therefore, it suggests that this side movement of L1, anticorrelated with the L7/L12 stalk, may be biologically relevant. S7 and S11 are on the E-tRNA exit path, and the side motion of the L1 stalk is supposedly blocking and unblocking the ability of the E-tRNA to leave the ribosome.

FIGURE 5.

FIGURE 5

Open in a new tab

Principal directions of movements for the L7/L12 and L1 stalks. Green arrows show the anticorrelated direction of movement (see Supplementary Movie in Supplementary Material). (Colors: 30S in yellow; 50S in cyan; tRNA in green; and S7 and S11 in white. The axis of rotation of L1 is shown in gray.) The symbols ⊙ and ⊗ show the movement out of and into the plane of the figure, respectively.

FIGURE 6.

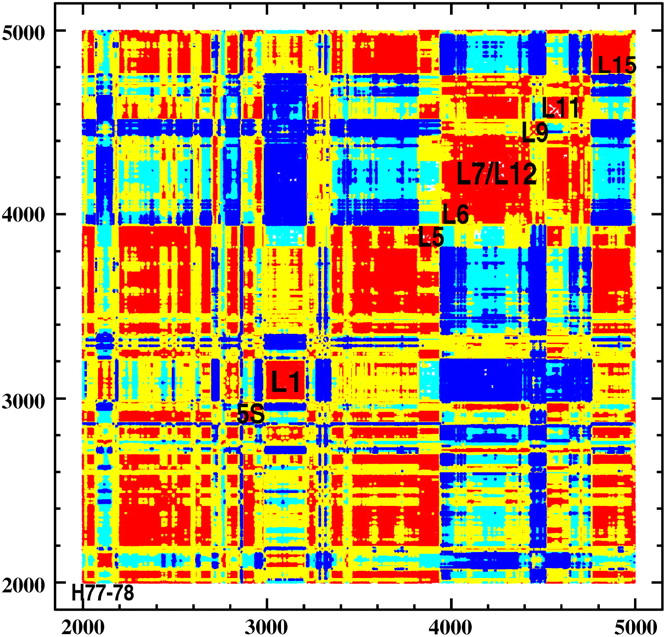
FIGURE 6

Open in a new tab

Dynamical correlation pattern showing the anticorrelated movement of L1 and L7/L12 stalks (see also Supplementary Movie in Supplementary Material). (Correlation scale and coloring: −1 < r < −0.7 = blue; −0.7 < r < −0.1 = cyan; 0.1 < r < 0.7 = yellow; and 0.7 < r < 1.0 = red.)

Other interesting interdependencies derived from the correlation plot point to L5, whose movement is positively correlated with 23S RNA helices H81–H88 and also with 5S RNA. L5 protein and 5S RNA are closely situated and cover the tRNA binding site from the side of the 50S subunit. The movement of L6 protein is also anticorrelated with the movement of L7/L12 stalk because L6 is in proximity to L11 stalk base. The motion of L15 protein is negatively correlated with the motion of L6. These two proteins are situated at the opposite sides of the large subunit; L15 is on the L1 side and L6 on the L7/L12 side. Therefore, they also participate in the counterphase stalk movement. Other interdependencies (data not shown) include the protein L16, which moves in phase with 5S RNA. L16 protein lies close to tRNA and contacts 5S RNA. Also, L16 and H69 are key factors influencing the precise positioning of tRNA within the peptidyl transferase center. The protein L18, which contacts 5S RNA, moves in phase with it. The helix h41 of 16S RNA moves in phase with proteins S9 and S10, which lie on both sides of this helix.

PCA, RMSF, and dynamical correlation matrix analysis indicate that the large subunit shows more internal correlated motions and local rearrangements than the small one. The 30S subunit moves as a whole uniform and compact segment, and does not have as many distinguishable, highly mobile parts as the 50S subunit. On average, the two subunits show an anticorrelated rotational movement. This is in accord with the observation that the entire small subunit rotates by ∼6° upon binding of EF-G (4,6). In our MD simulation we do not steer the rotation, and we do not simulate the EF-G-GTP binding, but the ratchetlike rotation is still seen as one of the principal components of the 30S subunit movement.

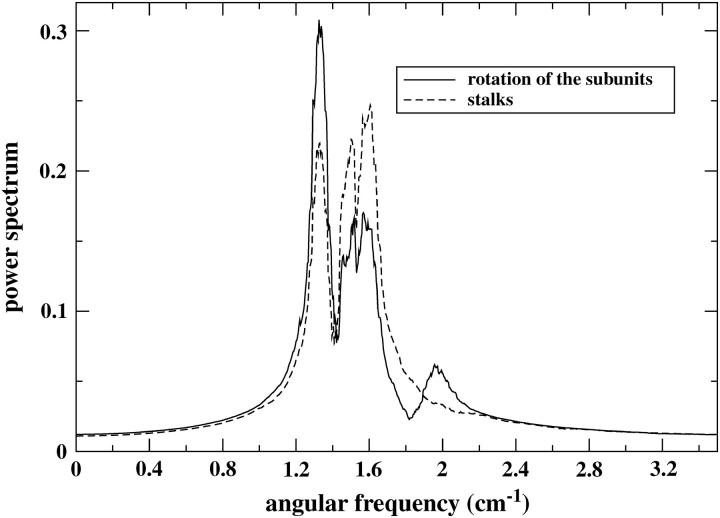
To analyze the timescale of the low-frequency anharmonic collective motions of the collections of proteins and RNA in the ribosome, we performed the spectral analysis. To assign proper frequencies to certain collective movements, such analysis was carried out not only for the original trajectory but for the individual essential modes. For the trajectories representing the principal modes—most importantly, the rotation of the subunits and anticorrelated movement of stalks—we calculated the Fourier transform of the velocity autocorrelation function (44–46). Fig. 7 shows the power spectrum obtained from those two PCA-derived trajectories representing the movement of stalks and the 30S subunit rotation. The ratchetlike rotation and the stalk movement are in the angular frequency number range of 1.3 and 1.6 cm−1, corresponding to the period of 160 and 130 ps, respectively. One may see that these two modes are quasiharmonic and that the movement of the subunits and the stalks are coupled with each other and cannot be treated separately. The internal vibrations in small globular proteins below the wavenumber 50 cm−1 are likely to be anharmonic and to show the main contributions to mean-square displacements (e.g., see (53)). We study the intermolecular vibrations of collections of proteins and RNA, therefore, they are likely to occur at much lower frequencies. For these very low-frequency modes, all atoms move in a concerted manner and the ribosome behaves like a continuous body. However, one must bear in mind that, similar to normal mode analyis, we do not account for solvent effects explicitly, and as a result these motions may be partially damped by viscous solvent (54,55). On the other hand, the ratchetlike rotation upon EF-G binding was observed as a functional movement by cryo-EM studies (6). Even though the model in the current stage does not include explicit solvent and the solvent environment is included only implicitly in the potential forms, we observe these functional motions. The effect of the friction constant in the Langevin equation for these modes will be the topic of the next study.

FIGURE 7.

FIGURE 7

Open in a new tab

Power spectrum for two principal modes representing the rotation of ribosomal subunits and the anticorrelated movement of L1 and L7/L12 stalks derived from a sample 200-ns MD simulation.

Counterphase movement of stalks in the elongation stage

One possible scenario of events in the elongation stage emerging from the principal movements of the ribosome and, most importantly, from the counterphase movement of the stalks, may be as follows:

  1. We start in a pre-translocational state with the A-, P-, tRNAs, and mRNA occupying their binding sites. Upon binding of EF-G-GTP, regions interacting with this factor from both subunits move toward each other; this includes an inward movement of the L7/L12 stalk (12). The movement of L7/L12 dimer toward the intersubunit space, coupled with its slight rotation, is one of the principal motions extracted from MD, and is in accord with recent NMR data (13). L7/L12 is a long segment whose movement helps accommodate the incoming EF-G in the binding site or allows it to dissociate from the ribosome. We have previously shown that the base of the stalk displays a positive electrostatic potential patch, and the domains G and V of EF-G that bind to the base are negatively charged (56).

  2. With the GTP hydrolysis and deacylated P-site, the counterclockwise, ratchetlike motion of the subunits takes place (6,8,10). This rotation is coupled with the backward and outward movement of the L7/L12 stalk (the movement of the 30S shows negative correlation with the motion of the L7/L12 stalk) and a side and forward movement of L1 stalk (Fig. 5). This corroborates the recent experimental observation that the rotation of the 30S is coupled with the movement of the L1 stalk (9) and is in accord with the correlations derived from our simulations.

  3. Coupled with the rotation of the 30S subunit and widening of the tRNA cleft, and following the EF-G-dependent GTP hydrolysis, the translocation of tRNAs takes place, and mRNA chain advances by one codon. It was proposed that EF-G actively pushes and displaces the A-site tRNA (57,58). The L1 stalk is positioned toward the intersubunit space, and its movement, in phase with the 30S subunit, confirms that it may interact with the intermediate P/E tRNA translocation state in which the peptidyl end of P-tRNA reaches the E-site in the large subunit. In our earlier electrostatic studies, we observed a positive potential patch associated with protein L1, meaning that there is an attraction toward the intersubunit space between the P- or E-site tRNA and the L1 stalk (56).

  4. The small subunit rotates back to its original position, whereas EF-G is released, and the L7/L12 stalk moves back to its neutral position. Reverse rotation of the 30S subunit is coupled with the reverse movement of the L1 stalk to its neutral position, possibly giving room for the E-site tRNA to properly and fully accommodate in the E-tRNA pocket. The posttranslocational state is achieved.

  5. After translocation, elongation factor Tu with the new A-site tRNA must bind to the ribosome. After the positive decoding process, the L7/L12 moves toward intersubunit space to help accommodate the new A-tRNA. Binding of the A-tRNA releases the E-site tRNA meaning that L1 has to move aside, making way and possibly helping the E-site tRNA to exit.

Tight alignment of tRNA termini

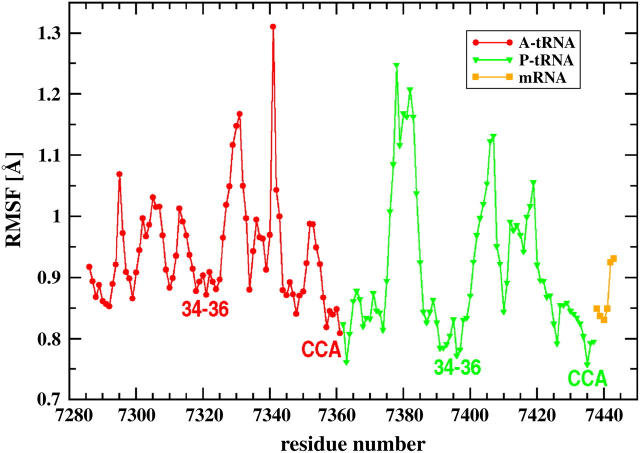
The ribosome accelerates peptide bond synthesis by the order of 107. It is believed that one reason for this is tight binding of amino acids that are carried by tRNAs at their 3′ termini. RMSFs of tRNAs presented in Fig. 8 show that 3′ termini are the least fluctuating parts. Other tRNA parts that are restrained are the residues 34–36, which form the anticodon nucleotides. The fixation of these fragments aids accurate frame-reading. The whole acceptor stem of both tRNAs also shows relatively small fluctuations. Moreover, Fig. 8 shows that the A-site tRNA has slightly more freedom than the P-site tRNA. The tRNA loops are more mobile, but overall their fluctuations are smaller than in other fragments of the ribosome (compare with Fig. 4). Therefore, the ribosome assures tight binding of the CCA-3′ ends and anticodons while, at the same time, allowing for some mobility of the other parts of tRNAs. This fact may have important implications for the translocation during which tRNAs must gain some degree of freedom. It has been shown that the movement of acceptor stems of A- and P-tRNAs with respect to the large subunit was spontaneous (59). Higher mobility of the D- and T-stems may initiate such spontaneous movement of the A- and P-site tRNA termini located in the 50S subunit toward its P- and E-site's large subunit binding sites. The average RMSF of the intermolecular B1b bridge (35) formed between proteins S13 and L5, which are in close contact with the P-site tRNA, is 4.5 Å. Even though these proteins are mobile (Fig. 4), the CCA-3′ ends and anticodons of tRNAs are still fixed. We observe an outward movement of S13 and L5, widening the tRNA cleft, which is probably an additional factor allowing for translocation.

FIGURE 8.

FIGURE 8

Open in a new tab

Root mean-square fluctuations of the A- and P-site tRNAs and mRNA chain derived from a sample 200-ns MD simulation. Anticodon and CCA-3′ termini are annotated.

CONCLUSIONS

A low-resolution model for the ribosome was developed and applied in MD simulations. It corroborates experimentally observed motions but also points to correlations among various ribosomal segments. The motions of the lateral stalks, L1 and L7/L12 of the large subunit, revealed fluctuations of these segments up to 15 Å. Moreover, we showed that side movement of these stalks is negatively correlated. Such counterphase motion of distal fragments suggests evidence for a link between their movement and ribosome function. In addition, this fact has important implications for understanding the process of translocation, because these stalks are situated at the opposite ends of the tRNA path. The large subunit displays much internal motion, whereas the small subunit moves as a uniform and compact block. Principal directions of motions indicate the rotation of the 30S subunit relative to the 50S, which is in accord with the ratchetlike movement observed experimentally and shown by normal mode analysis (6,8,10). The dynamical correlation matrix derived from the MD trajectory also shows that the small and large subunit motions occur on average in counterphase. The only part of the large subunit that moves in phase with the small subunit is the L1 stalk. This observation is in accord with recent cryo-EM studies, showing that the rotation of the small subunit is accompanied by the movement of L1 stalk (9). Both the CCA-3′ ends and the anticodon bases show the smallest fluctuations in the A- and P-tRNA molecules. This observation aids proof that the ribosome enforces a tight alignment of substrates in the binding site, and in this way accelerates the peptide synthesis. MD simulations with our coarse-grained model are fast and the accessible simulation time is of the order of hundreds of nanoseconds. With the knowledge of the secondary structure of RNA or DNA, the model may be easily applied in studies of other large biologically important systems.

SUPPLEMENTARY MATERIAL

A supplementary movie of the counterphase movement of the L1 and L7/L12 stalks accompanies this article. This online supplement can be found by visiting BJ Online at http://www.biophysj.org.

Supplementary Material

[supplemental]
biophysj_104.058495_index.html (649B, html)

Acknowledgments

We thank Donald Hamelberg and Justin Gullingsrud for all their help and Qizhi Cui for useful discussions. The figures were prepared with VMD (43), SMONGO, GIMP, and XMGRACE.

This project is supported in parts by National Institutes of Health (GM31749 for J.A.M.), National Science Foundation (MCB-0071429 for J.A.M.), Howard Hughes Medical Institute, W. M. Keck Foundation, San Diego Supercomputer Center, National Biomedical Computation Resource, Center for Theoretical Biological Physics, and Accelrys. J.T. was also supported by the Polish State Committee for Scientific Research (115/E-343/BST-993/ICM/2004 and 115/E-343/ICM/BST-1076/2005) and by European CoE MAMBA (QLRI-CT-2002-90383).

References

  • 1.Rodnina, M. V., and W. Wintermeyer. 1998. Form follows function: structure of an elongation factor G-ribosome complex. Proc. Natl. Acad. Sci. USA. 95:7237–7239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Wilson, K. S., and H. F. Noller. 1998. Molecular movement inside the translational engine. Cell. 92:337–349. [DOI] [PubMed] [Google Scholar]
  • 3.Gabashvili, I. S., R. K. Agrawal, R. Grassucci, C. L. Squires, A. E. Dahlberg, and J. Frank. 1999. Major rearrangements in the 70S ribosomal 3D structure caused by a conformational switch in 16S ribosomal RNA. EMBO J. 18:6501–6507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Agrawal, R. K., A. B. Heagle, P. Penczek, R. A. Grassucci, and J. Frank. 1999. EF-G-dependent GTP hydrolysis induces translocation accompanied by large conformational changes in the 70S ribosome. Nat. Struct. Biol. 6:643–647. [DOI] [PubMed] [Google Scholar]
  • 5.Stark, H., M. V. Rodnina, H. J. Wieden, M. van Heel, and W. Wintermeyer. 1998. Large-scale movement of elongation factor G and extensive conformational change of the ribosome during translocation. Proc. Natl. Acad. Sci. USA. 95:7237–7239. [DOI] [PubMed] [Google Scholar]
  • 6.Frank, J., and R. K. Agrawal. 2000. A ratchet-like inter-subunit reorganization of the ribosome during translocation. Nature. 406:318–322. [DOI] [PubMed] [Google Scholar]
  • 7.Ogle, J. M., F. V. Murphy IV, M. J. Tarry, and V. Ramakrishnan. 2002. Selection of tRNA by the ribosome requires a transition from an open to a closed form. Cell. 111:721–732. [DOI] [PubMed] [Google Scholar]
  • 8.Tama, F., M. Valle, J. Frank, and C. L. Brooks III. 2003. Dynamic reorganization of the functionally active ribosome explored by normal mode analysis and cryo-electron microscopy. Proc. Natl. Acad. Sci. USA. 100:9319–9323. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Valle, M., A. Zavialov, J. Sengupta, U. Rawat, M. Ehrenberg, and J. Frank. 2003. Locking and unlocking of ribosomal motions. Cell. 114:123–134. [DOI] [PubMed] [Google Scholar]
  • 10.Wang, Y., A. J. Rader, I. Bahar, and R. L. Jernigan. 2004. Global ribosome motions revealed with elastic network model. J. Struct. Biol. 147:302–314. [DOI] [PubMed] [Google Scholar]
  • 11.Gomez-Lorenzo, M. G., C. M. T. Spahn, R. K. Agrawal, R. A. Grassucci, P. Penczek, K. Chakraburtty, J. P. G. Ballesta, J. L. Lavandera, J. F. Garcia-Bustos, and J. Frank. 2000. Three-dimensional cryo-electron microscopy localization of EF2 in the Saccharomyces cerevisiae 80S ribosome at 17.5 Ångstrom resolution. EMBO J. 19:2710–2718. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Agrawal, R. K., J. Linde, J. Sengupta, K. H. Nierhaus, and J. Frank. 2001. Localization of L11 protein on the ribosome and elucidation of its involvement in EF-G-dependent translocation. J. Mol. Biol. 311:777–787. [DOI] [PubMed] [Google Scholar]
  • 13.Bocharov, E. V., A. G. Sobol, K. V. Pavlov, D. M. Korzhnev, V. A. Jaravine, A. T. Gudkov, and A. S. Arseniev. 2004. From structure and dynamics of protein L7/L12 to molecular switching in ribosome. J. Biol. Chem. 279:17697–17706. [DOI] [PubMed] [Google Scholar]
  • 14.Savelsbergh, V., I. Katunin, D. Mohr, F. Peske, M. V. Rodnina, and W. Wintermeyer. 2003. An elongation factor G-induced ribosome rearrangement precedes tRNA-mRNA translocation. Mol. Cell. 11:1517–1523. [DOI] [PubMed] [Google Scholar]
  • 15.Rodnina, M. V., A. Savelsbergh, V. I. Katunin, and W. Wintermeyer. 1997. Hydrolysis of GTP by elongation factor G drives tRNA movement on the ribosome. Nature. 385:37–41. [DOI] [PubMed] [Google Scholar]
  • 16.Pestka, S. 1969. Studies on the formation of transfer ribonucleic acid-ribosome complexes. VI. Oligopeptide synthesis and translocation on ribosomes in the presence and absence of soluble transfer factors. J. Biol. Chem. 244:1533–1539. [PubMed] [Google Scholar]
  • 17.Gavrilova, L. P., O. E. Kostiashkina, V. E. Koteliansky, N. M. Rutkevitch, and A. S. Spirin. 1976. Factor-free (non-enzymic) and factor-dependent systems of translation of polyuridylic acid by Escherichia coli ribosomes. J. Mol. Biol. 101:537–552. [DOI] [PubMed] [Google Scholar]
  • 18.Southworth, D. R., J. L. Brunelle, and R. Green. 2002. EFG-independent translocation of the mRNA: tRNA complex is promoted by modification of the ribosome with thiol-specific reagents. J. Mol. Biol. 324:611–623. [DOI] [PubMed] [Google Scholar]
  • 19.Tirion, M. 1996. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 77:1905–1908. [DOI] [PubMed] [Google Scholar]
  • 20.Haliloglu, T., I. Bahar, and B. Erman. 1997. Gaussian dynamics of folded proteins. Phys. Rev. Lett. 79:3090–3093. [Google Scholar]
  • 21.Reith, D., M. Pütz, and F. Müller-Plathe. 2003. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 24:1624–1636. [DOI] [PubMed] [Google Scholar]
  • 22.Lesyng, B., G. A. Jeffrey, and H. Maluszynska. 1988. A model for the hydrogen-bond-length probability distributions in the crystal structures of small molecule components of the nucleic acids. Acta Crystallogr. B. 44:193–198. [DOI] [PubMed] [Google Scholar]
  • 23.Levitt, M., and A. Warshel. 1975. Computer simulation of protein folding. Nature. 253:694–698. [DOI] [PubMed] [Google Scholar]
  • 24.McCammon, J. A., S. H. Northrup, M. Karplus, and R. M. Levy. 1980. Helix-coil transitions in a simple polypeptide model. Biopolymers. 19:2033–2045. [Google Scholar]
  • 25.Go, N., and H. Abe. 1981. Noninteracting local-structure model of folding and unfolding transition in globular proteins. I. formulation. Biopolymers. 20:991–1011. [DOI] [PubMed] [Google Scholar]
  • 26.Bahar, I., M. Kaplan, and R. L. Jernigan. 1997. Short-range conformational energies, secondary structure propensities, and recognition of correct sequence-structure matches. Proteins. 29:292–308. [DOI] [PubMed] [Google Scholar]
  • 27.Reference deleted in proof.
  • 28.Sippl, M. J. 1995. Knowledge-based potentials for proteins. Curr. Opin. Struct. Biol. 5:229–235. [DOI] [PubMed] [Google Scholar]
  • 29.Sippl, M. J. 1996. Helmholtz free energy of peptide hydrogen bonds in proteins. J. Mol. Biol. 260:644–648. [DOI] [PubMed] [Google Scholar]
  • 30.Bahar, I., and R. L. Jernigan. 1997. Inter-residue potentials in globular proteins and the dominance of highly specific hydrophilic interactions at close separation. J. Mol. Biol. 266:195–214. [DOI] [PubMed] [Google Scholar]
  • 31.Sippl, M. J. 1990. Calculation of conformational ensembles from potentials of mean force—an approach to the knowledge-based prediction of local structures in globular proteins. J. Mol. Biol. 213:859–883. [DOI] [PubMed] [Google Scholar]
  • 32.Zhou, H. Y., and Y. Q. Zhou. 2002. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci. 11:2714–2726. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Malhotra, A., R. K.-Z. Tan, and S. C. Harvey. 1994. Modeling large RNAs and ribonucleoprotein particles using molecular mechanics techniques. Biophys. J. 66:1777–1795. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Cui, Q., and D. A. Case. 2005. Low-resolution modeling of the ribosome assembly of the 30S subunit by molecular dynamics simulations. 229th American Chemical Society National Meeting and Exposition, San Diego, March 13–17.
  • 35.Yusupov, M. M., G. Z. Yusupova, A. Baucom, K. Lieberman, T. N. Earnest, J. H. D. Cate, and H. F. Noller. 2001. Crystal structure of the ribosome at 5.5 Å resolution. Science. 292:883–896. [DOI] [PubMed] [Google Scholar]
  • 36.Smith, W., and T. R. Forester. 1996. DL_POLY_2.0: A general-purpose parallel molecular dynamics simulation package. J. Mol. Graph. 14:136–141. [DOI] [PubMed] [Google Scholar]
  • 37.Hoover, W. G. 1985. Canonical dynamics—equilibrium phase-space distributions. Phys. Rev. A. 31:1695. [DOI] [PubMed] [Google Scholar]
  • 38.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. Dinola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
  • 39.Loncharich, R. J., B. R. Brooks, and R. W. Pastor. 1992. Langevin dynamics of peptides: the frictional dependence of isomerization rates of n-acetylalanyl-n-methylamide. Biopolymers. 32:523–535. [DOI] [PubMed] [Google Scholar]
  • 40.Amadei, A., A. B. M. Linssen, and H. J. C. Berendsen. 1993. Essential dynamics of proteins. Proteins Struct. Funct. Genet. 17:412–425. [DOI] [PubMed] [Google Scholar]
  • 41.Lindahl, E., B. Hess, and D. van der Spoel. 2001. GROMACS 3.0: a package for molecular simulation and trajectory. J. Mol. Model. (Online). 7:306–317. [Google Scholar]
  • 42.Mongan, J. 2004. Interactive essential dynamics. J. Comput. Aided Mol. Design. 18:433–436. [DOI] [PubMed] [Google Scholar]
  • 43.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD—visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
  • 44.Kitao, A., F. Hirata, and N. Go. 1991. The effects of solvent on the conformation and the collective motions of protein—normal mode analysis and molecular-dynamics simulations of melittin in water and in vacuum. Chem. Phys. 158:447–472. [Google Scholar]
  • 45.Furois-Corbin, S., J. C. Smith, and G. R. Kneller. 1993. Picosecond timescale rigid-helix and side-chain motions in deoxymyoglobin. Proteins Struct. Funct. Genet. 16:141–154. [DOI] [PubMed] [Google Scholar]
  • 46.Hayward, S., A. Kitao, and N. Go. 1994. Harmonic and anharmonic aspects in the dynamics of BPTI: a normal mode analysis and principal component analysis. Protein Sci. 3:936–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Pettersson, I., and C. G. Kurland. 1980. Ribosomal protein L7–L12 is required for optimal translation. Proc. Natl. Acad. Sci. USA. 77:4007–4010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Oleinikov, A. V., G. G. Jokhadze, and R. R. Traut. 1998. A single-headed dimer of Escherichia coli ribosomal protein L7/L12 supports protein synthesis. Proc. Natl. Acad. Sci. USA. 95:4215–4218. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Griaznova, O., and R. R. Traut. 2000. Deletion of C-terminal residues of Escherichia coli ribosomal protein l10 causes the loss of binding of one L7/L12 dimer: Ribosomes with one L7/L12 dimer are active. Biochemistry. 39:4075–4081. [DOI] [PubMed] [Google Scholar]
  • 50.Subramanian, A. R., and E. R. Dabbs. 1980. Functional studies on ribosomes lacking protein L1 from mutant Escherichia coli. Eur. J. Biochem. 112:425–430. [DOI] [PubMed] [Google Scholar]
  • 51.Harms, J., F. Schluenzen, R. Zarivach, A. Bashan, S. Gat, I. Agmon, H. Bartels, F. Franceschi, and A. Yonath. 2001. High resolution structure of the large ribosomal subunit from a mesophilic eubacterium. Cell. 107:679–688. [DOI] [PubMed] [Google Scholar]
  • 52.Robert, F., and L. Brakier-Gingras. 2003. A functional interaction between ribosomal proteins S7 and S11 within bacterial ribosome. J. Biol. Chem. 278:44913–44920. [DOI] [PubMed] [Google Scholar]
  • 53.Go, N., T. Noguti, and T. Nishikawa. 1983. Dynamics of a small globular protein in terms of low-frequency vibrational modes. Proc. Natl. Acad. Sci. USA. 80:3696–3700. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Smith, J., S. Cusack, B. Tidor, and M. Karplus. 1990. Inelastic neutron scattering analysis of low-frequency motions in proteins: harmonic and damped harmonic models of bovine pancreatic trypsin inhibitor. J. Chem. Phys. 93:2974–2990. [Google Scholar]
  • 55.Hayward, S., A. Kitao, F. Hirata, and N. Go. 1993. Effect of solvent on collective motions in globular protein. J. Mol. Biol. 234:1207–1217. [DOI] [PubMed] [Google Scholar]
  • 56.Trylska, J., R. Konecny, F. Tama, C. L. Brooks III, and J. A. McCammon. 2004. Ribosome motions modulate electrostatic properties. Biopolymers. 74:423–431. [DOI] [PubMed] [Google Scholar]
  • 57.Agrawal, R. K., P. Penczek, R. A. Grassucci, and J. Frank. 1998. Visualization of elongation factor G on the Escherichia coli 70S ribosome: the mechanism of translocation. Cell Biol. 95:6134–6138. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 58.VanLoock, M. S., R. K. Agrawal, I. S. Gabashvili, L. Qi, J. Frank, and S. C. Harvey. 2000. Movement of the decoding region of the 16S ribosomal RNA accompanies tRNA translocation. J. Mol. Biol. 304:507–515. [DOI] [PubMed] [Google Scholar]
  • 59.Moazed, D., and H. F. Noller. 1989. Intermediate states in the movement of transfer tRNA in the ribosome. Nature. 342:142–148. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[supplemental]
biophysj_104.058495_index.html (649B, html)
Download video file (391.8KB, mov)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES