Pathways and Timescales of Primary Charge Separation in the Photosystem II Reaction Center as Revealed by a Simultaneous Fit of Time-Resolved Fluorescence and Transient Absorption

Abstract

We model the dynamics of energy transfer and primary charge separation in isolated photosystem II (PSII) reaction centers. Different exciton models with specific site energies of the six core pigments and two peripheral chlorophylls (Chls) in combination with different charge transfer schemes have been compared using a simultaneous fit of the absorption, linear dichroism, circular dichroism, steady-state fluorescence, transient absorption upon different excitation wavelengths, and time-resolved fluorescence. To obtain a quantitative fit of the data we use the modified Redfield theory, with the experimental spectral density including coupling to low-frequency phonons and 48 high-frequency vibrations. The best fit has been obtained with a model implying that the final charge separation occurs via an intermediate state with charge separation within the special pair (RP₁). This state is weakly dipole-allowed, due to mixing with the exciton states, and can be populated directly or via 100-fs energy transfer from the core-pigments. The RP₁ and next two radical pairs with the electron transfer to the accessory Chl (RP₂) and to the pheophytin (RP₃) are characterized by increased electron-phonon coupling and energetic disorder. In the RP₃ state, the hole is delocalized within the special pair, with a predominant localization at the inactive-branch Chl. The intrinsic time constants of electron transfer between the three radical pairs vary from subpicoseconds to several picoseconds (depending on the realization of the disorder). The equilibration between RP₁ and RP₂ is reached within 5 ps at room temperature. During the 5–100-ps period the equilibrated core pigments and radical pairs RP₁ and RP₂ are slowly populated from peripheral chlorophylls and depopulated due to the formation of the third radical pair, RP₃. The effective time constant of the RP₃ formation is 7.5 ps. The calculated dynamics of the pheophytin absorption at 545 nm displays an instantaneous bleach (30% of the total amplitude) followed by a slow increase of the bleaching amplitude with time constants of 15 and 12 ps for blue (662 nm) and red (695 nm) excitation, respectively.

INTRODUCTION

Photosystem II (PSII) is one of the two photosystems that performs the initial reaction in oxygenic photosynthesis: primary charge separation in the D1/D2/Cytb₅₅₉ reaction center (RC) (1–4). According to the x-ray structure (5–7), the PSII-RC comprises eight chlorins and two carotenes, all of which participate in the energy transfer and/or electron transfer processes. Four chlorophyll (Chl) and two pheophytin (Phe) molecules are arranged in two branches D1 and D2 in the central part of the complex. The D1 branch is known to be active in charge separation (2). Two Chls are bound at the periphery of the complex at distances of ∼24 Å from the core pigments. The biophysical processes in this complex including energy transfer and primary steps of charge separation have been studied by nonlinear spectroscopic techniques, such as visible pump-probe (8–16), visible pump-IR probe (M.-L. Groot, N. P. Pawlowicz, L. J. G. W. van Wilderen, J. Breton, I. H. M. van Stokkum, and R. van Grondelle, unpublished results), time-resolved fluorescence (16,17), photon echo (18), hole-burning (19,20), and Stark spectroscopy (21).

Room temperature pump-probe studies performed by Klug and co-workers (8–11) showed transient absorption (TA) spectra with a negative peak at 681 nm (assigned to the bleaching of P680 and Phe Q_y absorption bands), a negative peak at 545 nm (assigned to the bleaching of Phe Q_x absorption), and a positive band at 460 nm (assigned to the Phe anion absorption). Kinetics in the 660–695-nm region gave 100-fs, 3-ps, and 21–27-ps components reflecting energy transfers and dynamics of the bleaching associated with the radical-pairs formation. The 100-fs component changes its sign upon tuning the excitation from 665 to 695 nm, thus suggesting fast downhill and uphill transfers between the excited states at the blue and red side of the band (8). The slower 3-ps component reflects the decay of excited states due to the primary charge transfer step. The 21-ps component was assigned to Phe⁻ formation, since it was found to be the dominant component in the 545- and 460-nm kinetics upon 695-nm excitation (9,11). Decay of the stimulated emission sideband at 730 nm occurs with the same 21-ps time constant as well as the growth of the radical pair absorption in this region (11). Tuning the excitation to 665 nm slows this component down to 27 ps (10), which was attributed to a slow energy transfer from peripheral Chls absorbing near 670 nm.

Slow picosecond dynamics in the Phe anion band and Phe Q_x band bleach was also observed by Wasielewski and co-workers (15), who reported time constants of 7 and 48 ps at 460 nm and 9 and 54 ps at 545 nm upon long-wavelength excitation. These authors also found a large instantaneous bleach at 545 nm, which they fully attributed to singlet-excited Phe. These time constants differ from the 21 ps observed earlier (9–11). Similar time constants for charge separation have been obtained by Holzwarth with co-workers using time-resolved fluorescence (FL) (17) and pump-probe (12) studies. Both techniques gave visible (i.e., apparent) rates of charge separation of ∼100–150 ns⁻¹ corresponding to time constants of 7–10 ps. At cryogenic temperatures, time constants of 5 ps (22) and 3 ps (23) were found at 545 nm.

Groot et al. (14) have measured a 400-fs component of the TA kinetics and attributed it to the formation of the intermediate state of low dipole strength that has charge-transfer character and lies below the excited states. The second 20-ps component was assigned to charge separation dynamics limited by slow energy transfer.

Modeling of the PSII-RC was performed using the so-called multimer model (24–26), where the transition energies of the six core pigments (P_D1, P_D2, Chl_D1, Chl_D2, Phe_D1, and Phe_D2) were taken to be equal, giving rise to delocalized states. Dynamics was calculated with the Redfield theory (weak exciton-phonon coupling). Magic-angle TA and anisotropy decays calculated for short time delays (0–1.5 ps) upon 694-nm excitation were in good agreement with the measured data (25). Kinetics of charge separation in the 0–200-ps range was modeled by including the coupling of the excited states to the radical pairs (26). No attempt was made to model the nonlinear responses at different probe wavelengths.

The multimer model with equal transition energies for all six core-pigments was used (in combination with Redfield theory) to model the photon echo at 1.3 K (18) and pump-probe spectra at 77 K (27). From the photon echo modeling it has been proposed that, at least at low temperatures, the accessory Chl on the active branch Chl_D1 acts as primary electron donor and that the 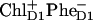pair occurs first, followed by electron transfer from P_D1 to Chl_D1 and 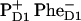formation (18).

An adaptation of the multimer model was also proposed (28), which implies that Phe_D2 in the inactive branch D2 is 100 cm⁻¹ blue-shifted with respect to the other pigments (the so-called pentamer model). The blue-shift of Phe_D2 was, however, not confirmed by chemical exchange of this pigment (29).

Renger and co-workers (30) extracted the site energies from a fit of the 5 K linear spectra (absorption, i.e., OD; linear dichroism, i.e., LD; circular dichroism, i.e., CD, fluorescence, i.e., FL) and temperature dependence of OD in the 6–277 K range using the modified Redfield theory. These site energies were verified by calculations of the absorption difference spectra for RCs with: 1), modified Phe_D2; 2), modified Phe_D1 and Phe_D2; 3), reduced Phe_D1; 4), absorption of the RC-5 complexes that lack one of the peripheral Chls; and 5), triplet minus singlet (T-S) spectra at 10 K and 277 K, assuming a thermal distribution of the triplet state between P_D1 and Chl_D1. The thus-obtained site energies differ from those of the multimer model. The accessory Chl_D1 was suggested to be the redmost pigment which acts as the primary donor, in agreement with results obtained from site-specific mutagenesis on the ligands for P_D1 and P_D2 (31), thereby supporting the original suggestion by van Brederode et al. (32) and van Brederode and van Grondelle (33).

The assignment of the final radical pair state as 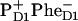(i.e., with the hole localized at the active-branch Chl of the special pair) implies that the P_D1 is reduced by tyrosine residue D1-161(Y_Z), which oxidizes the Mn cluster (2,31,34).

Recently, room temperature transient absorption and time-resolved fluorescence have been measured for PSII RC complexes purified from spinach (16). In this article we model this data using the modified Redfield theory. We put forward a model of energy transfer and charge separation in the RC based on simultaneous fits of OD, LD, CD, steady-state FL spectra, TA kinetics upon different excitation wavelengths, and FL kinetics. The model suggests that charge separation occurs through an intermediate state with charge separation within the special pair P_D1–P_D2 as the primary event. The mixing of this state with the exciton states of the core-pigments results in a charge-transfer intermediate that lies below the pure exciton states, has significant dipole strength, and which can be reached via fast energy transfer from the core-pigments. The time constants for the next charge separation steps strongly depend on the realization of the disorder. Knowledge of the key microscopic parameters of the model adjusted from a quantitative fit of the data allows us to explore the pathways and timescales of the energy and electron transfer. The proposed model is compared with alternative exciton models and charge-separation schemes.

THE MODEL

We consider an isolated PSII-RC complex consisting of eight pigments, arranged in the D1 and D2 subunits with pseudo-C2 symmetry, i.e., two chlorophylls of the special pair P, two accessory chlorophylls, two pheophytins, and two additional chlorophylls (denoted as Chlz). We will number them as: 1, P_D1; 2, P_D2; 3, Chl_D1; 4, Chl_D2; 5, Phe_D1; 6, Phe_D2; 7, Chlz_D1; and 8, Chlz_D2, where the active branch corresponds to the D1 subunit. The primary steps of charge separation are accounted for by considering a sequence of two radical pairs (RP₁ and RP₂) or of three radical pairs (RP₁, RP₂, and RP₃). Thus, the excited-state manifold consists of electronically excited sites 1–8 and radical pair states, i.e., 9-RP₁, 10-RP₂, and 11-RP₃.

The one-exciton Hamiltonian includes unperturbed site energies E_nn of the excited (n = 1–8) and charge-transfer (n = 9–11) states as diagonal elements and off-diagonal interaction energies M_nm. The interaction energies between the excited states (n, m = 1–8) have been obtained from the structural data (6), file 1IZL in the Protein Data Bank, http://www.rcsb.org/pdb) in the dipole-dipole approximation, assuming a dipole strength of 18 and 10 D² for the Q_y-transitions of Chl and Phe, respectively.

Generally, the dipoles of the Q_y-transitions of Chl and Phe can form some angle with the N_B–N_D axis. In our modeling the value of this angle necessary to obtain a good fit is no more than 5–6°. The first radical pair is coupled to the electronically excited sites 1, 2, or 3 (depending on the model; see below), the corresponding energies are M₉₁, M₉₂, or M₉₃. Couplings between radical pairs are M_10,9 and M_11,10 (other interactions are neglected for simplicity). The couplings involving radical pair states are not known and should be determined from the fit of the data together with the site energies.

The two-exciton Hamiltonian is constructed on the basis of double-excited states S₁(n)–S₁(m) of molecular pairs n–m, and double-excited monomeric states S₂. The ratio of the transition dipoles for the S₁–S₂ and S₀–S₁ transitions in the Chl monomer is taken to be 0.5, and the S₁–S₂ transition energy is blue-shifted by 150 cm⁻¹ with respect to the S₀–S₁ transition energy. In the radical pair state n⁺m⁻ the S₀–S₁(n) and S₀–S₁(m) transitions are forbidden, giving rise to a bleaching of the exciton states with contributions of the n^th and m^th pigments. We do not consider the absorption of the radical pairs, i.e., dipole moments of the n⁺m⁻ → (n⁺m⁻)* transitions are supposed to be negligible. We also do not include the electrochromic shifts of the site energies due to radical-pairs formation.

The site inhomogeneity (diagonal disorder) is 120 cm⁻¹ (full-width at half-maximum, i.e., FWHM of a Gaussian distribution) for the excited states and 350 cm⁻¹ for the charge-transfer states. This threefold increase in static disorder reflects the stronger coupling of charge-transfer states to slow nuclear motions and conformations of the surrounding. Diagonalization of the one- and two-exciton Hamiltonian for each realization of the disorder gives us energies and eigenfunctions of the N = 11 one-exciton eigenstates (including a mixing of purely exciton and charge-transfer states) and N(N+1)/2 = 66 two-exciton eigenstates. Then the linear and third-order nonlinear spectral responses can be calculated using the expressions from Appendices A–D. The exciton relaxation and charge-transfer dynamics are described by the modified Redfield theory.

The electron-phonon spectral density C(ω) (Eq. D2) includes an overdamped Brownian oscillator with the parameters λ₀, γ₀, and 48 high-frequency modes with frequencies ω_j, couplings λ_j = S_jω_j (where S_j is the Huang-Rhys factor of j^th mode), and damping constants γ_j (which are taken to be small, i.e., γ_j = 3 cm⁻¹). Parameters of the low-frequency part (as determined from the simultaneous fit of linear spectra) are λ₀ = 35 cm⁻¹ and γ₀ = 40 cm⁻¹. Parameters of the high-frequency vibrations (from 97 to 1673 cm⁻¹) were taken from the fluorescence line narrowing (FLN) data (35), and further scaled and adjusted from the fit of the 6 K OD, LD, CD, and FL spectra. The adjusted parameters of the high-frequency modes are listed in Table 1.

TABLE 1.

Frequencies ω_j, cm⁻¹, and Huang-Rhys factors S_j for nuclear modes j = 1−48 (∑ S_j = 0.75)

ωj	Sj	ωj	Sj	ωj	Sj	ωj	Sj
97	0.0371	604	0.0034	1143	0.0303	1354	0.0057
138	0.0455	700	0.005	1181	0.0179	1382	0.0067
213	0.0606	722	0.0074	1190	0.0084	1439	0.0067
260	0.0539	742	0.0269	1208	0.0121	1487	0.0074
298	0.0488	752	0.0219	1216	0.0111	1524	0.0067
342	0.0438	795	0.0077	1235	0.0034	1537	0.0222
388	0.0202	916	0.0286	1252	0.0051	1553	0.0091
425	0.0168	986	0.0162	1260	0.0064	1573	0.0044
518	0.0303	995	0.0293	1286	0.0047	1580	0.0044
546	0.0030	1052	0.0131	1304	0.0057	1612	0.0044
573	0.0094	1069	0.0064	1322	0.0202	1645	0.0034
585	0.0034	1110	0.0192	1338	0.0037	1673	0.0010

The v_n and w_n factors (Appendix C) which determine possible site-to-site variation of exciton-phonon couplings (λ₀ and λ_j) are taken to be equal for all electronically excited states, i.e., v_n = w_n = 1 for n = 1–8. To account for a stronger coupling of radical pairs to phonons and vibrations we use v_n = w_n = 1.5 for n = 9–11.

The total reorganization energy in the site representation (given by Eq. D2) is λ = 598 cm⁻¹. Below (see Table 2) we use the site energies that do not include a reorganization shift. Diagonalization of the Hamiltonian containing the thus-determined site energies gives the energies corresponding to the first moment of the absorption of the k^th exciton state ω_k. The zero-phonon line (which determines the main absorption peak of the k^th component) will be red-shifted from ω_k due to reorganization effects. The value of this shift in the exciton representation is equal to v_nλ multiplied by the participation ratio (PR) of the k^th state (Eq. D3). The PR value for our models lies in the range 0.4–0.75 (see below), thus the reorganization shift for the pure exciton states (with v_n = 1) is expected to be 240–450 cm⁻¹, where more localized states display a larger red-shift. For the charge transfer states (characterized by a stronger coupling to fast nuclear motions) this shift is even bigger. Such large reorganization shifts are determined mostly by coupling to high-frequency modes (note that low-frequency phonons are responsible for a reorganization energy of λ₀ = 35 cm⁻¹, which is only a small part of the total reorganization energy λ = 598 cm⁻¹). This coupling to high-frequency modes manifests itself as an intense vibrational wing in the absorption and fluorescence spectra (see below). Due to this wing the first moment of the spectral line (for the k^th exciton component) differs significantly from the position of a relatively narrow low-frequency peak (for the same component).

TABLE 2.

Unperturbed transition energies of the pigments n = 1–8 for different exciton models of RC (Models A–D); transition energies are given in cm⁻¹, and do not include the reorganization energy shift

n	1	2	3	4	5	6	7	8
Pigment	PD1	PD2	ChlD1	ChlD2	PheD1	PheD2	ChlzD1	ChlzD2
Model A	15,130	15,165	15,095	15,110	15,175	15,280	15,435	15,430
Model B	15,110	15,425	15,090	15,330	15,190	15,290	15,420	15,470
Model C	15,210	15,210	15,019	15,233	15,091	15,151	15,461	15,438
Model D	15,300	15,105	15,030	15,130	15,100	15,100	15,425	15,420

Extraction of the parameters

The unperturbed site energies of the excited states (n = 1–8) have been determined from the linear OD/LD/CD/FL spectra fit based on evolutionary algorithm. (The site inhomogeneity value and parameters of the spectral density necessary to explain the experimental lineshapes have been adjusted from the fit as well). An evolutionary-strategy-based search for the best fit allows us to find several models with different site energies. These models have been further checked by fitting the TA and FL kinetics. The TA/FL fit allowed an adjustment of other parameters, i.e., parameters of the double-excited and radical-pair states.

The S₁–S₂ transition energies and oscillator strengths of the Chl and Phe have been adjusted from the fit of the TA spectral shape. Variation of these parameters changes the relative intensities and positions of the negative bleaching and positive excited-state absorption bands. The scaling factor of the S₁–S₂ transition dipole and the corresponding shift of the transition energy (with respect to the S₀–S₁ transition) were taken to be the same for the Chl and Phe monomers.

The couplings and energies of the radical-pair states can be determined by modeling the time evolution of the TA and FL dynamics in different timescales (from subpicosecond to picosecond and 10–100-ps regions). Simultaneous fit of the fast TA decay and long-lived FL requires a radical-pair sequence with specific energies and couplings producing an effective (fast) charge transfer, together with the channels of back transfers to the emitting excited states. We also have found that a quantitative fit of the data is impossible without increasing the energetic disorder of the radical pairs.

RESULTS

Exciton models

We have found that a simultaneous fit of OD, LD, CD, and FL spectra can be obtained in many different ways, i.e., using different sets of the site energies. In Table 2 we show a few possible configurations with different energies of the pigments n = 1–8. Notice that the site energies given in Table 2 do not include the reorganization energy shift due to strong coupling to phonons and vibrational modes.

Model A is the multimer model: the redmost pigments 1–4 (i.e., P_D1, P_D2, Chl_D1, and Chl_D2) are almost isoenergetic, resulting in strong exciton coupling. The lowest exciton state is super-radiant, being delocalized over pigments 1–4 with some coherent admixture of pigments 5 and 6. Notice that Phe_D2 in the inactive branch D2 is blue-shifted, so that this configuration resembles an adaptation of the multimer model, i.e., the pentamer model (28).

Model B can be denoted as the asymmetric multimer model: the exciton states are delocalized over the pigments 1-3-5 of the D1 branch, which are red-shifted with respect to the pigments 2-4-6 of the D2 branch.

Model C is characterized by a symmetric special pair with isoenergetic P_D1 and P_D2 shifted to the blue. The redmost pigment is the accessory Chl of the active branch (Chl_D1), which is a good candidate for the primary electron donor (31). Model C is close to the model recently proposed by Renger with co-workers (30).

Model D is similar to Model C but with an asymmetric special pair. The lowest exciton state is delocalized over pigments 2 and 3 (P_D2 and Chl_D1 with a bigger contribution of Chl_D1), pigment 1 (P_D1) is blue-shifted, pigments 4, 5, and 6 (Chl_D2 and Phes) are red-shifted, 7 and 8 (extra-Chlzs) are on the blue. Notice that the Models C and D agree with the suggestion of Diner et al. (31) that P_D1 absorbs more to the blue than the redmost Chl_D1.

The Models A–D allow a simultaneous fit of the room-temperature OD, LD, CD, and FL spectra with the site energies given in Table 2. The OD, LD, CD, and FL spectra at 6 K can be explained with the same models, but in this case a little adjustment of the site energies (within 1–3 nm) is needed for some of the pigments.

Radical pair states

To describe the charge-separation dynamics, we have to include coupling between the exciton states and the charge-transfer states with lower energies. Due to this coupling the lowest exciton states become mixed with the highest radical-pair states. As a result, the higher radical pair will become dipole-allowed, borrowing some dipole strength from the excited-state manifold. In its turn, the mixing with charge-transfer states increases the exciton-phonon coupling for the lowest exciton states.

The simplest schemes (proposed in the literature) imply a sequence of two radical-pair states RP₁→RP₂:

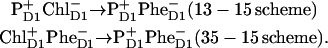The first scenario is possible for Models A and B, where the primary donor P_D1 contributes significantly to the lowest excited state. The second scheme is better for Models C and D, where the third pigment (Chl_D1) is redmost. But this scheme is also suitable for Model B, where pigments 1 and 3 contribute equally to the lowest state. In the multimer model (Model A) the relative contribution of Chl_D1 to the lowest state is lower, but still significant, so that the second scheme (or some superposition of the 13–15 and 35–15 pathways) can work. Both schemes also agree with the suggestion (31) that, after long time, the cation resides preferentially on P_D1.

These schemes allow us to obtain a qualitative explanation of the TA and time-resolved FL (including the correct time constants and the signs of the main kinetic components), but no quantitative fit can be obtained (it is difficult to reproduce the amplitudes of the main kinetic components). However, a fit is possible by using 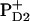instead of 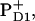i.e., using 23-25 and 35-25 sequences. Both schemes allow a quantitative fit of the kinetics (in the Q_y region of Chls and Phes), at least for Model B. The 23-25 scheme is in agreement with the kinetics in the Q_x band of Phe (measured by Klug with co-workers; see Refs. 9 and 11, and Wasielewski with co-workers; see Ref. 15), whereas the 35-25 scheme predicts much faster kinetics of the Phe Q_x bleaching. In both schemes there is electron or hole transfer between the sites 2 and 3. Most probably such a transfer occurs via the intermediate site 1. This can be explicitly taken into account in modified schemes with a sequence of three radical pairs, RP₁→RP₂→RP₃:

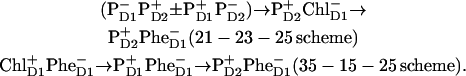In the first scheme, it is supposed that the lowest exciton state of the special pair is mixed with the superposition of charge transfer states (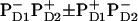). The lowest state of this superposition (with some contribution of 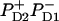) acts as a donor for the next radical pair 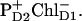In the second scheme the final state also could be a superposition like (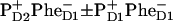), but the data can only be reproduced with a predominant localization of the hole at P_D2.

In the following sections we will discuss in detail the Model B with the 21-23-25 charge-transfer sequence, which allows the best fit of the kinetics. Then we will compare it with the results obtained with Model B and the 35-15-25 scheme. Finally we will show some results for the multimer Model A, which is quantitatively not as good as Model B. The Models C and D gave no fit to the observed FL and TA kinetics even at a qualitative level.

Asymmetric multimer model (electron transfer from special pair)

In this section we discuss the results obtained with Model B and the 21-23-25 charge-transfer sequence. The site energies of the eight pigments are given in Table 2. The energies of radical pairs (counted from (E₁₁ + E₂₂)/2 are ΔE_RP1 = −100 cm⁻¹, ΔE_RP2 = −340 cm⁻¹, and ΔE_RP3 = −480 cm⁻¹. These energies do not include a reorganization shift. The interaction energies determined from the fit are M₉₁ = M₉₂ = 50 cm⁻¹, M_10,9 = 70 cm⁻¹, and M_11,10 = 30 cm⁻¹. These values are close to the interaction energies in the bacterial RC. Thus, the coupling between the primary donor and the first radical pair is 20–50 cm⁻¹ according to molecular dynamics (36), path integral simulation (37), and Redfield theory modeling of the coherent electron-vibrational dynamics (38). The coupling between the first and second radical pair is 80–135 cm⁻¹ (36,37).

Linear spectra

The fit of the linear spectra is shown in Fig. 1. The main peaks in the OD near 675 nm and the FL at 680 nm are determined by the main Q_y transitions coupled to low-frequency phonons. The broad absorption at 620 nm and the FL shoulder with a maximum at 740 nm are determined by high-frequency vibrations (in our modeling we neglect the Q_x transitions that may contribute to the absorption near 630 nm). Notice that the experimental CD spectra of PSII-RCs are nonconservative with intense positive peaks both in the visible and the Soret bands (39). To improve the fit of the CD we assume a monomeric CD contribution proportional to the linear absorption. In Fig. 1 the amplitude of this monomeric CD is 20% of the excitonic CD maximum. The calculated red wing of the OD spectrum is more intense than the experimental one due to the fact that the tails of higher exciton states are broadened due to ultrafast relaxation. This is a well-known lineshape artifact of the Redfield theory (40,41), appearing due to the exponential relaxation term (see Eq. D1) which determines a Lorentzian lineshape with broad wings. A more realistic lineshape should probably be closer to a Gaussian profile (at least in the red edge of the absorption band). For example, using the Redfield theory it is impossible to correctly explain the polarization of fluorescence of LH1/LH2 complexes (due to off-resonance excitation of higher exciton states even upon excitation at the very red edge), but it can be done by assuming a Gaussian lineshape for the exciton states (with the same FWHMs) (41). On the other hand, this Redfield theory artifact typically has a minor effect on isotropic TA and FL kinetics.

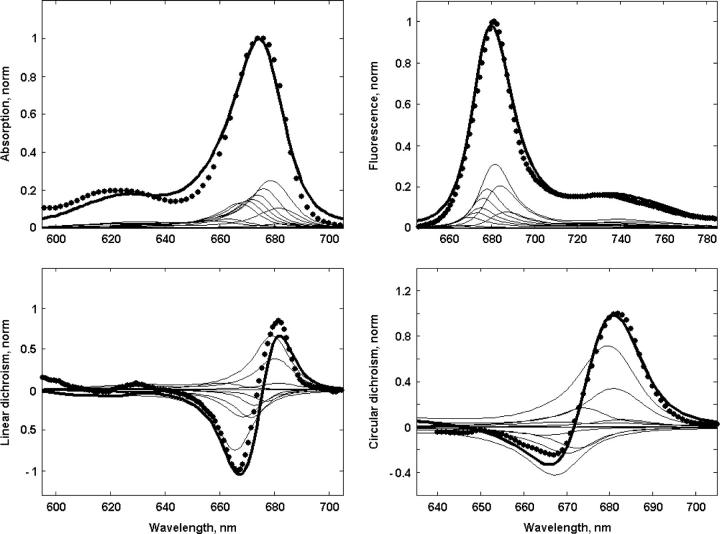
FIGURE 1.

Fit of the linear spectra (OD, LD, CD, and steady-state FL) at room temperature. Experimental OD and steady-state FL data measured in Andrizhiyevskaya et al. (16) and LD and CD states (E. G. Andrizhiyevskaya, unpublished results) are shown by points, a calculation according to Model B, assuming the 21-23-25 charge separation scheme, is shown by solid lines. Thin lines correspond to the exciton components of the overall spectra.

Participation ratio

The PR for the 11 exciton states calculated for 4000 realizations of the disorder are shown in Fig. 2 (bottom frame). Depending on the realization of the disorder the exciton states of the six core pigments (between 650 and 680 nm) are delocalized over 1.3–3 sites. The states determined by the monomeric Chlzs (with PR close to unity) are clearly distinguishable between 665 and 675 nm. The three lowest states below 680 nm (with PR from 0.5 to 1) are determined by radical pairs mixed with exciton states and mixed with each other. Each radical pair state is treated as one site, so the PR = 0.5 below 700 nm implies a delocalization of the charge-separated state over two radical pairs, i.e., RP₂ and RP₃. Below 715 nm we find the localized RP₃ state. Averaging over realizations gives delocalization over 1.5–2 sites (without including the Chlz states) in the main absorption band between 660 and 685 nm (Fig. 1, top frame).

FIGURE 2.

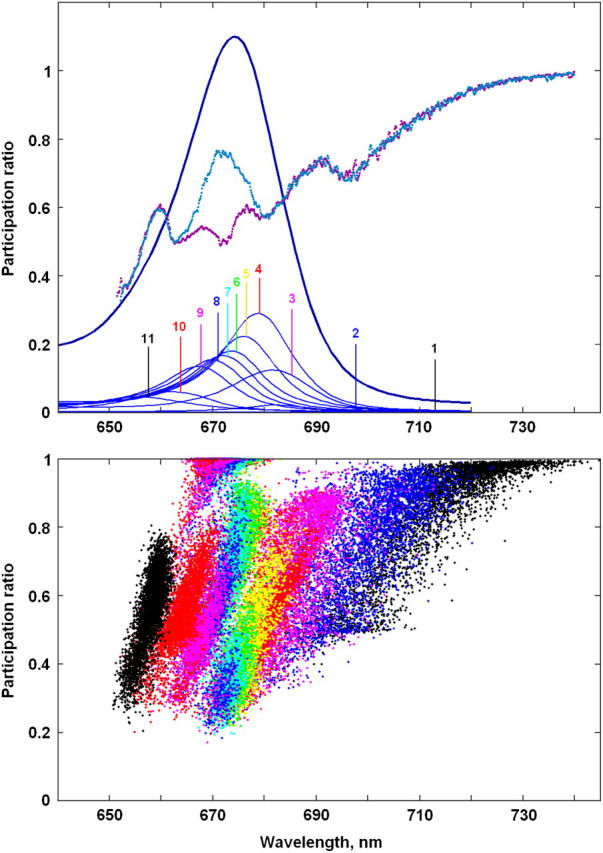
Participation ratio (PR) of the exciton states for Model B. (Top frame) OD spectrum with the exciton components (the same as in Fig. 1) together with the PR as a function of the wavelengths corresponding to the zero-phonon lines (ZPL) of the exciton states. Bars 1–11 show the averaged positions of ZPLs for the exciton states from k = 1 to k = 11. Blue and magenta curves show PR averaged over disorder with (blue) and without (magenta) including the states localized at peripheral Chlzs. (Bottom frame) PR as a function of ZPL shown for 4000 realizations of the disorder. Each realization is presented by 11 points (shown by different colors) corresponding to a PR for the exciton states k = 1–11. Colors of the exciton states correspond to the colors of the bars in the top frame.

Density matrix for exciton states

The origin of the exciton states can be unraveled by the density matrix averaged over disorder for each exciton state as shown in Fig. 3. The three lowest states k = 1, 2, and 3 are determined by the sites 11, 10, and 9—i.e., RP₃, RP₂, and RP₁, respectively. Off-diagonal density matrix elements within the (9–11) × (9–11) area reflect coherent coupling between radical pairs. In the k = 3 state there are coherences between the highest radical pair (the ninth site) and pigments 2 and 3. Due to this coherent mixing the charge-transfer state k = 3 borrows significant dipole strength from the excited states (see Figs. 1 and 2).

FIGURE 3.

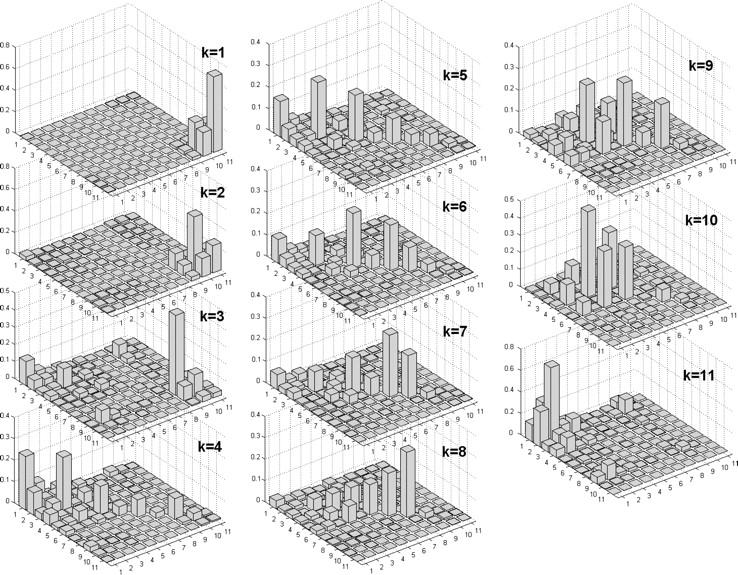
Density matrix for the exciton states from k = 1 to k = 11 averaged over disorder. Bars show the density matrix elements (n,m) in the site representation. Numbers of the sites correspond to the eight pigments and three radical pairs in the following order: 1, P_D1; 2, P_D2; 3, Chl_D1; 4, Chl_D2; 5, Phe_D1; 6, Phe_D2; 7, Chlz_D1; 8, Chlz_D2; 9, RP₁; 10, RP₂; and 11, RP₃. Data corresponds to Model B with 21-23-25 charge separation scheme.

In the lowest exciton state (k = 4) the pigments 1 and 3 are most populated with some population of pigments 5, 7, and the first radical pair. See diagonal elements (1,1), (3,3), (5,5), (7,7), and (9,9). There is coherence within the D1 branch, i.e., (1,3), (3,5); the D2 branch (2,4), (4,6); the special pair (1,2); and between the special-pair and the accessory Chls—i.e., the (2,3) and (1,4) elements. Thus, k = 4 is the lowest level of the 1-2-3-4-5-6 multimer with a predominant localization of the excitation on the D1 pigments 1, 3, 5 and with some coherent admixture of RP₁. A partial charge transfer character of the lowest exciton states was suggested by Frese et al. (21), who observed unconventional features in the Stark spectra at the red wing of the PSII-RC Q_y absorption band.

The structure of the next three states (k = 5, 6, and 7) is similar to that of the k = 4 state with increasingly more population on sites 3 and 5 and less population on site 1. Notice that the coherences between sites 1, 3, and 5 are relatively small for all the states from k = 4 to k = 7. It means that the delocalization over the core pigments of the D1 branch is not completely coherent, thus containing a noncoherent mixture of states with a predominant localization around sites 1, 3, or 5 depending on the realization of the disorder.

The states from k = 8 to k = 11 contain more contribution from the D2 pigments. Levels k = 9 and 10 are coherently delocalized between pigments 4 and 6. Level k = 11 is the higher exciton state of the special pair with a predominant population of P_D2.

Pigments 7 and 8 (peripheral Chlzs) participate in the states from k = 4 to k = 10 with a maximum contribution to k = 7 and k = 8, but there is no coherence between them and any of the other sites. Such a completely noncoherent mixture means that in different realizations each of the states k = 4–10 can be multimeric (delocalized over the core pigments without presence of Chlzs) or monomeric with localization at Chlzs.

Transient absorption

The fit of the TA kinetics upon 662- and 695-nm excitation is shown in Figs. 4 and 5 together with the population dynamics in the site representation.

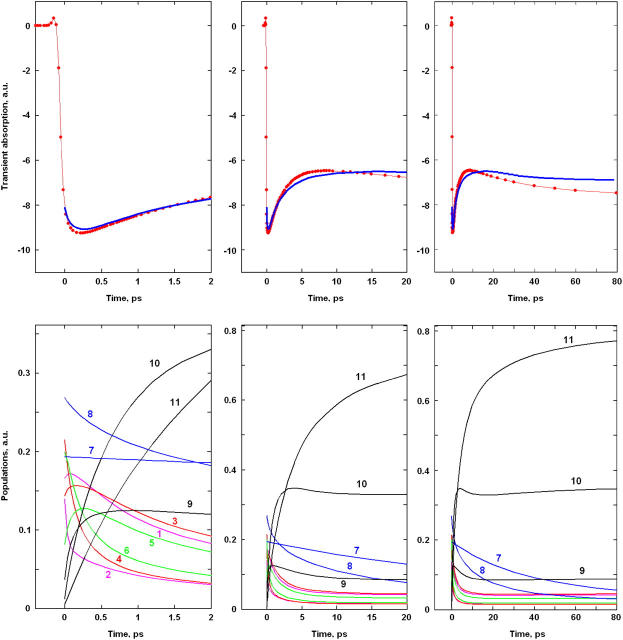
FIGURE 4.

Kinetics of transient absorption (TA) at 680 nm upon 662 nm excitation and population dynamics in the site representation for Model B with 21-23-25 charge separation scheme. (Top frames) Measured TA kinetics (red points connected by thin lines; data taken from Ref. 16) and calculated ones (blue lines) for time delays from 0 to 2 ps (left) 20 ps (middle), and 80 ps (right). (Bottom frames) Populations of the sites 1–11 (numbered as in Fig. 3) calculated for the same timescales as shown in the top frames.

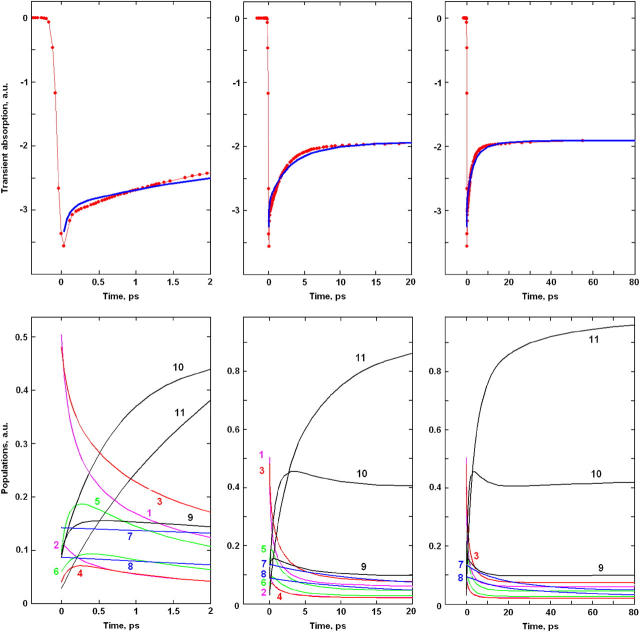
FIGURE 5.

The same as in Fig. 4, but for 695-nm excitation.

Upon 662-nm excitation (Fig. 4) we have the predominant excitation of pigments 2, 4, and 6 from the D2 subunit (which are blue-shifted), followed by their fast depopulation during a few hundred femtoseconds. This fast decay is mirrored by a fast rise of excited state population on the red-shifted pigments 1, 3, and 5 of the D1 subunit. After 500 fs, the largest part of the excitation density is concentrated on pigments 1, 3, and 5. It is interesting, however, that pigment 1 is more populated initially (at time zero) than pigment 2 because the higher exciton level of the special pair 1–2 (with a larger contribution of P_D2) is only weakly allowed (see Figs. 2 and 3). That is why, even at short-wavelength excitation, this level is less populated than the lower exciton levels of the complex with a significant contribution of P_D1.

The fast exciton relaxation results in a quick population of the first radical pair, which is strongly mixed with the core pigments. The fastest component of ∼100 fs is determined by the coupling of RP₁ with P_D2 (see the 0–2-ps frame of Fig. 4, where a very fast decay of site 2 is mirrored by a rise of site 9). The coupling of RP₁ with P_D1 gives slower transfer rates. The intrinsic rates are strongly dependent on the realization of the disorder. For different realizations the time constant of P_D1 →RP₁ transfer varies from subpicoseconds to several picoseconds. The intrinsic rates of the next charge-separation steps RP₁→RP₂ and RP₂ →RP₃ are of the same order. This large spread of values is connected with the big disorder (which is comparable or even larger than the splitting between the unperturbed energies of the radical pairs). The effective rates (shown in Figs. 4 and 5) reflect a complicated interplay of forward and back transfers averaged over disorder. Superposition of many forward and back transfer pathways results in the occurrence of slow components (up to 10–30 ps) in the overall equilibration dynamics. This slow dynamics is superimposed with the even slower transfers from the peripheral Chlzs (pigments 7 and 8) with time constants of 10–100 ps.

Thus we have several timescales of overall equilibration. First, the 0–0.5-ps range, which corresponds to equilibration within the core pigments, including formation of the first radical pair (see left frames in Fig. 4). During the second, 0.5–5-ps scale the equilibrated core-pigments are depopulated and equilibration between them and the first two radical pairs RP₁ and RP₂ is reached (middle frames in Fig. 4). During the third, 5–100-ps period, the equilibrated core pigments and two radical pairs are slowly populated from Chlzs and depopulated due to the formation of the third radical pair, RP₃ (right frames in Fig. 4).

Note that the first radical pair in our model, i.e., the state k = 3 that is mixed with the excited states and populated within 500 fs, resembles the intermediate state suggested earlier by Groot et al. (14). Thus, the 400-fs component observed in TA kinetics was attributed to the formation of an intermediate state that 1), has low dipole strength, 2), has charge-transfer character, and 3), lies below the excited states (14). The state k = 3 in our model has exactly the same features as characteristics 1–3, but the dynamics of its population is more multiphasic, including fast pathways of ∼100 fs together with the slower ones.

Upon long-wavelength, 695-nm excitation (Fig. 5), we have the predominant excitation of red-shifted pigments 1, 3, and 5 of the D1 subunit. The most populated are pigments 1 and 3, but after 500 fs the excitation is almost uniformly distributed among 1, 3, and 5. Uphill relaxation also increases the population of D2 pigments 4 and 6 (the population of pigment 2 is initially high due to the strong exciton coupling with pigment 1). Inversion of the initial conditions upon tuning the excitation to the red changes the direction of energy transfer (from D2→D1 to D1→D2, i.e., from downhill to uphill) and leads to an inversion of the TA dynamics during the 0–0.5-ps time region. This feature, observed in earlier experiments (8) and in a recent study (16), is well reproduced by the model (compare left top frames of Figs. 4 and 5).

The dynamics after 0.5 ps is not much different from the case of 662-nm excitation. The only difference is associated with the different initial excitation of extra-Chlzs (which affects the slow dynamics during 10–100 ps). Upon short-wavelength 662-nm excitation, the decay of initially excited peripheral Chlzs increases the bleaching at 680 nm between 10 and 100 ps. This feature is absent upon long-wavelength excitation, when Chlzs are almost non-populated, and so their decay has not as pronounced an effect on the slow dynamics in the 10–100-ps range.

Time-resolved fluorescence

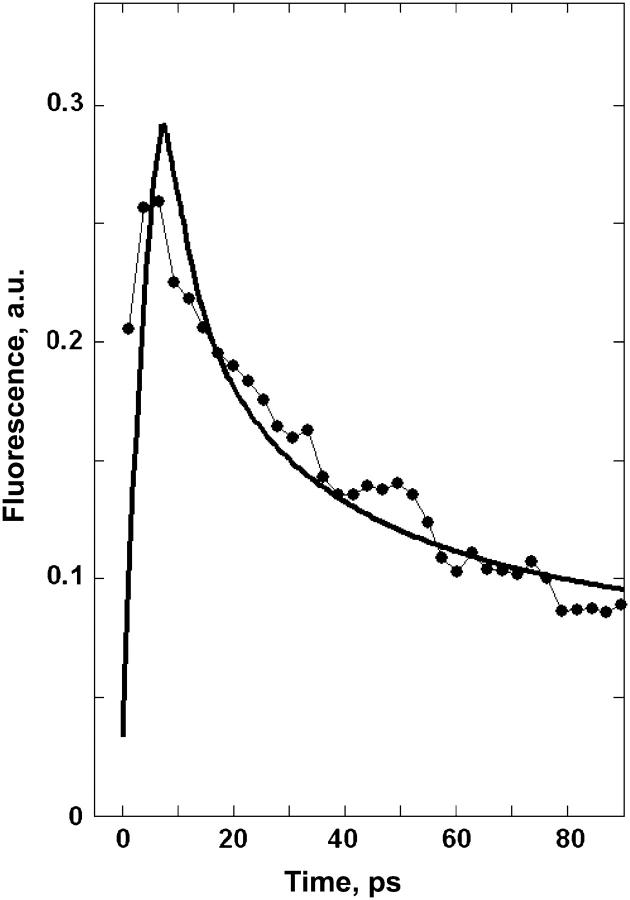
The fit of FL kinetics in shown in Fig. 6. It is important that the long-lived fluorescence suggests a reversible charge transfer. We have found that the TA kinetics can be explained in terms of irreversible charge separation, i.e., supposing slower transfer to low-lying radical pair states without significant back transfer to the core pigments. This is possible because TA is mainly sensitive to bleaching of pigments participating in radical pairs and does not depend on the energy of the radical pair states, which are dark states (in the case of a large energy difference between the RP states and the excited states). In contrast, FL is determined by the excited-state populations that decay very fast in the irreversible scheme. To explain the FL decay with time constants of 40–80 ps and even longer, we have to reduce the energy separation between the radical pairs and the excited states. In such a scheme the intrinsic times of charge separation can be very short (subpicoseconds to a few picoseconds), but due to efficient back transfers we have a long-lived equilibration process.

FIGURE 6.

Fluorescence kinetics measured at 680 nm with 6-ps resolution upon 665-nm excitation (points connected by thin lines; data taken from Ref. 16) and calculated with the same model as in Figs. 4 and 5 (solid line).

Furthermore, a simultaneous fit of the fast TA decay (in the 0–20-ps timescale) and the slower 40–80-ps FL decay is impossible without introducing a big energetic disorder for the charge-separated states (up to 350 cm⁻¹). This is the case for all the models that we tried. In the case of a low disorder, the FL decay becomes too fast. Reduction of the energy difference between the RP and the excited states results in slower FL decay (making it closer to the measured one), but in this case the TA dynamics (in the 0–20-ps timescale) becomes too slow. Moreover, the FL kinetics in the case of a low disorder has a pronounced bi-exponential character, with a fast decay during 0–20 ps followed by a slow decay with the 60–100-ps time constant (in contrast with the almost mono-exponential decay of the measured FL in the 0–100-ps time interval).

Alternative charge-separation pathways

Now we wish to compare alternative charge-separation schemes. In particular we have found that the asymmetric multimer model (Model B, described in the previous section) allows a reasonable fit of the data (linear spectra, TA kinetics upon different excitation wavelengths, and FL kinetics) using the 35-15-25 charge-transfer sequence. At short time, the exciton equilibration is almost the same as for the 21-23-25 scheme discussed above. The only difference is connected with the faster decay of the site 3, which is connected to the formation of the first radical pair 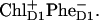Remember that when charge separation starts from the special pair, pigment 1 decays faster than pigment 3 for both excitation wavelengths (see the dynamics during the 0–2-ps time interval shown in Figs. 4 and 5). The dynamics of the further steps of charge separation is quite similar in both schemes. The final state is the same, i.e., 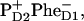thus giving the same spectrum of the bleaching. The intermediate states for the two schemes include different combinations of the pigments 1, 2, 3, and 5. But all these pigments are coherently and noncoherently mixed in levels k = 4–6, thus giving strongly overlapping (and hardly distinguishable) bleaching components. Although the 21-23-25 scheme gave a better fit of the data we still conclude that it is difficult to distinguish between the two pathways using pump-probe data in the Q_y absorption region (at least at room temperature).

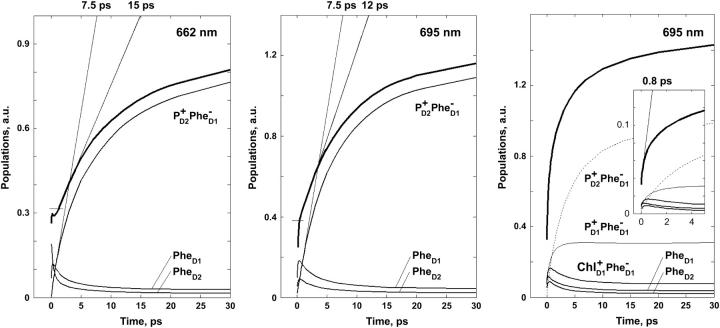
On the other hand, the two schemes predict very different dynamics of the Phe absorption bleaching and Phe anion formation. For the 21-23-25 scheme the Phe bleaching appears due to excitation of pigments 5 and 6, and due to the 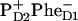radical pair formation. Thus, the bleaching amplitude is given by the sum of populations of the sites 5, 6, and 11. In Fig. 7 we show populations of these sites upon 662- and 695-nm excitation. Formation of the anion band is given by the formation of the 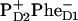state, which occurs in both cases with a time-constant of ∼7.5 ps. The effective Phe absorption bleaching displays time constants of 15 and 12 ps for the blue and red excitations, respectively. We remind that, according to the measured bleaching of the Phe Q_x band at 545 nm, Klug and co-workers (9,11) estimated these time constants as 27 and 21 ps. Wasielewski and co-authors (15) reported the Phe anion band formation (at 460 nm) and Phe bleaching (at 545 nm) upon red-side excitation with the time constants of 7 and 9 ps. This is close to our 7.5- and 12-ps values. Notice that experimental kinetics at 545 nm showed instantaneous bleaching of ∼40% from the total bleaching amplitude (15). In the model the instantaneous bleaching due to the initial excitation of the two Phe pigments is ∼30%. This instantaneous bleaching is followed by the slow dynamics due to charge separation (as shown in Fig. 7).

FIGURE 7.

Dynamics of the Phe bleaching and 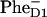formation calculated according to Model B with different charge-separation schemes. (Left frame) Populations of Phe_D1, Phe_D2, and radical pair 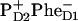are shown for the 21-23-25 scheme upon 662-nm excitation, together with the sum of these kinetics (giving the Phe bleaching). Horizontal bar shows the amplitude of the instantaneous bleaching. (Middle frame) The same as in left frame, but for 695-nm excitation. (Right frame) Populations of two Phes and of three radical pairs involving 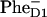are shown for the 35-15-25 scheme with 695-nm excitation, together with the sum of these kinetics (giving the Phe bleaching for this scheme).

In contrast, the 35-15-25 scheme predicts very fast Phe dynamics, because Phe is involved in all three radical pairs. It means that the bleaching kinetics is given by the sum of populations of the 5, 6, 9, 10, and 11 sites (see Fig. 7, right frame). The dynamics of the first two radical pairs is rather fast, including subpicosecond components. According to our modeling, more than half of the Phe bleaching develops with a time constant of ∼0.8 ps. Thus, the model with accessory Chl as a primary donor is in contradiction with the available pump-probe data in the 545- and 460-nm region (15).

Multimer model

Finally we will briefly discuss the results obtained with a traditional multimer model (18,24,25,26) with equal or almost equal energies of the core pigments. Any changes in the exciton structure of the model should, in principle, influence the fast components of the dynamics during 0–0.5 ps. We have seen that this fast TA component is determined by a combined action of many relaxation channels (including the fastest one of ∼100 fs superimposed with slower components). It is important that this component that changes its sign when tuning the excitation from blue to the red. An asymmetric model can reproduce this feature at a quantitative level. Due to the D1–D2 asymmetry a blue or red pump pulse allows the selective excitation of either the D2 or the D1 pigments. Subsequent equilibration within the D1–D2 core produces a fast TA component with different sign. Upon blue excitation we got a fast increase of the D1 branch bleaching at 680 nm due to D2–D1 relaxation (Fig. 4, 0–2 ps frame). Red excitation results in uphill dynamics within D1 and from D1 to D2 with a fast decrease in D1 bleaching at 680 nm (Fig. 5, 0–2-ps frame).

In the multimer model (Model A) there is 1), a strongly coupled core-cluster giving a super-radiant exciton level on the red side, and 2), blue-shifted peripheral Chlz pigments. Blue excitation results in the excitation of the peripheral sites and some (weaker) excitation of the coherent superposition of core pigments. There is no fast transfer from blue Chlz pigments, and there is no significant redistribution of excited state population within the core pigments either (see Fig. 8, left frame). As a result, the fast component of TA is almost absent. Exciton relaxation within the core-cluster, including fast transfer to the first radical pair, does not significantly change the bleaching amplitude during the subpicosecond time-interval. The calculated amplitude of the TA decay during 0–5 ps (reflecting the transfer from the core pigments and RP₁ to the radical pairs RP₂ and RP₃) is also less than in the experiment (due to the weak initial excitation of the core pigments in the multimer model).

FIGURE 8.

Site populations and density matrix for the multimer Model A. Population kinetics are shown upon 662- and 695-nm excitation (colors of the sites are the same as in Figs. 4 and 5). The density matrix (with the same representation as in Fig. 3) is shown for the k = 10 and k = 4 states, which are initially most populated upon 662- and 695-nm excitation, respectively.

Upon red excitation, we mostly excite the core-cluster. Because core-pigments participate nonuniformly in the lowest states, there is some equilibration dynamics during 0–0.5 ps (see Fig. 8, right frame) with a decrease in the special pair (pigments 1 and 2) and accessory Chls (pigments 3 and 4) populations. This results in a decrease of the 680-nm bleaching, in qualitative agreement with the experiments, but the amplitude of this decrease is always much less than the measured one.

Altogether, we got a quantitative fit for Model B and a qualitatively correct picture for the multimer Model A. Models C and D gave no fit, even at a qualitative level. For these models the sign of the fast TA component is opposite to the experiment both for blue and red excitation. In the Models A and B the excitation of the long-wavelength states gives rise to larger TA values (due to the specific exciton structure of the lowest states and due to the large bleaching of the special pair in the first radical pair state). Thus, the downhill exciton relaxation increases the bleaching. The Models C and D have a different structure of the excited and charge-transfer states. In particular, the first radical pair is characterized by smaller bleaching values, giving rise to a lower bleaching at the red side. Correspondingly, a downhill relaxation reduces the bleaching amplitude, thus changing the sign of the fast component.

Note that the TA modeling is done in the doorway-window representation (Appendix A), by neglecting a coherent artifact due to pump-probe overlap. The latter has a duration of ∼√2τ, where τ is the pulse duration (40). Thus, for τ = 100 fs (16) the pulse overlap is important from −70 fs to +70 fs delays. Such an artifact can contribute, for example, to the amplitude of the sharp bleaching near 0-fs delay at 695-nm excitation TA, but cannot affect the TA kinetics for larger delays. Note that, in this respect, the Models C and D give a wrong sign of the overall relaxation dynamics during at least 500 fs.

DISCUSSION AND CONCLUSIONS

The simultaneous fit of linear spectra and nonlinear kinetics allowed us to test various exciton models for the PSII RC and to unravel the pathways and timescales of excited state relaxation and primary charge separation.

The first features that occur in the subpicosecond region (below 500 fs) are exciton relaxation, dephasing, and migration within the core-RC, i.e., pigments 1–6. The fastest components (up to 100 fs) correspond to relaxation from the blue- to red-shifted exciton states, including the lowest states with pronounced charge-transfer character due to their mixing with the first radical pair. These fast components result in excitation-wavelength-dependent TA kinetics during 0–0.5 ps. This fast TA dynamics is extremely sensitive to the model of the RC. First of all, to the choice of the site energies of the core pigments, which is a good test for the exciton models that can be proposed? We found that simultaneous fit of OD, LD, CD, and steady-state FL spectra allows multiple solutions. Many of them, however, fail to explain the shape of the TA dynamics during 0–500 fs upon different excitation conditions, and should therefore be ruled out. Thus, only Model B survived from the models listed in Table 2. In Model B, fast relaxation occurs between two groups of states determined by pigments 1-3-5 (D1-branch) and 2-4-6 (D2-branch), respectively. We did not model the anisotropy dynamics, but it appears that the 400-fs anisotropy decay upon red-side excitation (25) is connected with a dephasing between the exciton states, within the 1-3-5 group superimposed with migration within the D1 branch.

After 0.5–1 ps, the excited core-pigments are almost completely equilibrated. Their total population decreases due to transfer to the charge-transfer states, but their relative populations during this process are not changing. There is no significant redistribution between these pigments. If we switch off the coupling to the radical pairs, then the excited-state populations will be constant after 0.5 ps. Thus, the decay of the excited states after 0.5 ps and within ∼5 ps reflects the formation of the second radical pair (the first one, strongly mixed with the exciton states, is populated during the exciton relaxation, i.e., during the 0–0.5-ps period). By formation we mean that the population of the second radical pair reaches its quasi-equilibrium with the core-pigments and the first radical pair (so that the equilibrium of sites 1–6 and 9–10 is reached).

After 5 ps, we have the slow transfers between three groups, i.e.: 1), sites 1–6 and 9–10 acting as one equilibrated subsystem; 2), a third radical pair, i.e., site 11; and 3), peripheral pigments 7 and 8. Transfer from group 1 to group 2 occurs with 7.5-ps effective time constant, i.e., a visible time constant averaged over forward and back transfers with intrinsic pairwise constants ranging from subpicosecond to 2–3 ps. Transfer from group 3 to groups 1 and 2 has time constants within the 10–100-ps range (the spread is due to the disordered character of the system).

The TA kinetics in the Q_y transition region (together with time-dependent FL of the corresponding excited states) associated with charge separation between 0.5 ps and 100 ps can be reproduced using different radical pair sequences. These different schemes give approximately the same time-constants for the first, second, and third pair formation. But the assignment of the radical pairs in these models is different. For example, in the 21-23-25 scheme the appears in the third charge-separation step and thus must have a 7.5-ps rising time. In contrast, in the 35-15-25 scheme, a fast subpicosecond dynamics is expected for the formation, which already occurs in the first step. To distinguish between the two schemes some technique is needed sensitive to the Phe anion population (for example, IR excited-state spectroscopy, or visible pump-probe in the Phe anion absorption or Q_x bleaching region). At the moment such measurements have led to controversial results. Thus, the TA kinetics at 460 and 545 nm suggested slow 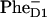formation (7 ps) and Phe Q_x bleaching (9 ps), close to 7.5 ps and 12 ps in our 21-23-25 model with the special pair as a primary donor. On the other hand, recent infrared data gave evidence for a 0.6–0.8 ps 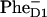dynamics (M.-L. Groot, N. P. Pawlowicz, L. J. G. W. van Wilderen, J. Breton, I. H. M. van Stokkum, and R. van Grondelle, unpublished results), which is in agreement with the 0.8 ps predicted by our 35-15-25 model where the electron transfer occurs from accessory Chl.

Other types of experiments that could lead to a better understanding of the exciton structure, energy transfers, and primary charge-separation reactions in PSII include: TA pump-probe spectroscopy with improved spectral and temporal resolution at room and low temperatures, steady-state OD/LD/CD/FL, Stark spectroscopy on site-specific mutants with changed site energies of certain core-RC chlorophylls, and other methods. It is also useful to compare the exciton model of RC with the absorption difference spectra corresponding to modified/reduced Phe, removed Chlz (RC-5 complex), and triplet formation (T-S spectrum) (as was done recently by Renger and co-workers; see Ref. 30). Here we restrict to discussion of how the main features of the Phe-modified, RC-5, and T-S spectra are reproduced by our working Model B and Models A, C, and D.

In all the models (Models A, B, C, and D) we got peripheral Chlzs with zero-phonon line (ZPL) distribution peaked near 670 nm (the ZPL distribution of the Chlzs with high PR values in the 665–675-nm region is shown in Fig. 2). The absorption maximum of the monomeric states is 2–3-nm blue-shifted from the ZPL position. Thus, removing of one of the Chlzs results in bleaching in the 665–670-nm region is in agreement with the experiment (42).

According to our preliminary studies, the shape of the T-S spectra with the main bleaching near 680 nm (29) can be reproduced, supposing a delocalization of the triplet state between P_D1 and Chl_D1 with predominant population of P_D1 (for Model B at room temperature). Note that experimental studies (31,46,47) suggested a distribution of the triplet state between P_D1 and Chl_D1 at high temperatures; however, with predominant localization at Chl_D1 (the feature that agrees with Models C and D), it is difficult to explain with Model B.

In Model B the Phe_D2 contributes to the exciton states k = 7–10 (Fig. 3) absorbing in the 664–676-nm region (as shown in Fig. 2) with the maximal contribution to the k = 9 state peaked at 667 nm. The Phe_D1 contributes to the states k = 4–8 with absorption maximums in the 672–680-nm region. The difference spectrum with reduced or modified Phe_D2 has the main bleaching at 667–670 nm (depending on small variation of the site energies around the values given by Model B). Very similar results can be obtained with the Model A (with the same energies of Phe_D1 and Phe_D2). Both models (A and B) are in agreement with the experiment of Jankowiak et al. (28) giving bleaching at 668 nm. Note that this experiment is in contradiction with the exchange (Phe_D2-modified) experiment (29) that showed bleaching at 679 nm. The latter can be better explained by the Models C and D with more red-shifted Phe_D1 and Phe_D2.

A new result of our model is that, in the radical-pair state RP₃, the hole is delocalized within the special pair with a predominant localization at the 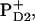at least in isolated PSII reaction centers. We note, however, that this delocalization may be different in isolated PSII reaction centers and in intact, oxygen-evolving PSII core complexes. In intact PSII, the redox active tyrosine on the D2 branch (Tyr¹⁶⁰, or Y_D) is usually oxidized, whereas in isolated PSII reaction centers illumination does not result in the oxidation of Y_D (43). The positive charge near this molecule may influence the charge distribution between the special-pair molecules. In intact PSII there is convincing evidence that (at long times) the hole is localized predominantly on 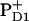(2,31), implying a hole localization near the Mn-cluster.

APPENDIX A: DOORWAY-WINDOW REPRESENTATION OF PUMP-PROBE

We use a doorway-window representation (44,45) for the sequential two-color pump-probe scheme. The excited-state dynamics is described with the modified Redfield theory (45). The modified version in its present form (45) neglects 1), the coherences between one-exciton states; 2), population relaxation during the pump/probe pulse; and 3), transfers of ground- to one-exciton coherences and one- to two-exciton coherences. In the basis of one- and two-exciton eigenstates the transient absorption (TA) can be expressed as a sum of the photobleaching (PB), stimulated emission (SE), and excited-state absorption (ESA),

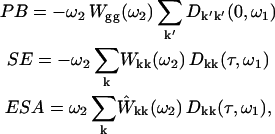(A1)

where ω₁ and ω₂ are pump and probe frequencies, τ is the pump-probe delay, and g and k denote the ground and one-exciton states, respectively (an average over the static disorder is implied in Eq. A1). In the sequential pump-probe experiment the pump pulse creates a superposition of electronic states in the one-exciton manifold with the doorway amplitudes D_kk(0,ω₁), together with the hole in the ground state given by −∑_kD_kk(0,ω₁). The evolutions of the excited-state wavepacket due to exciton relaxation/migration during pump-probe delay is given by D_kk(τ,ω₁). The ground-state hole is time-independent because one-exciton relaxation does not change the number of excitations, i.e., −∑_kD_kk(τ,ω₁) = const. The absorption of a weak probe is determined by the overlap of the doorway and window wavepackets (Eq. A1). The initial doorway amplitude D_kk(0,ω₁), and the window amplitudes W_kk(ω₂), Ŵ_kk(ω₂), and W_gg(ω₂) are given by

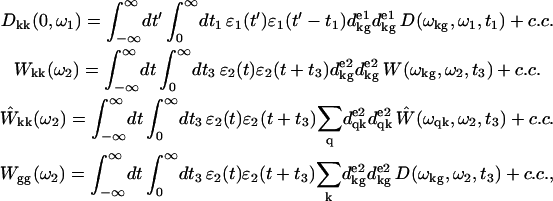(A2)

where ɛ₁ and ɛ₂ are the envelopes of the pump and probe pulses (they are taken to be real). Here we use indices g, k, and q for ground, one-, and two-exciton states, respectively. Transition dipoles d_kg and d_qk correspond to g→k and k→q transitions, with the transition frequencies ω_kg and ω_qk, respectively. Transition frequencies ω_ab = ω_a − ω_b are given by the difference of frequencies of the a- and b-eigenstates. Superscripts e1/e2 denote projection of the transition dipoles to the polarization vectors of the pump/probe pulses. D, W, and Ŵ are the lineshape functions describing a dephasing during the electronic coherence periods t₁ and t₃. They correspond to ground-state absorption, excited-state emission, and excited-state absorption, respectively. Note that the window amplitude W_gg(ω₂) depends on the D-function being determined by the ground-state absorption. Integration over t and t′ can be done analytically if one specifies the pulse shape. For example, supposing Gaussian pulses 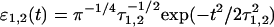with FWHM of 1.66τ_1,2, we get

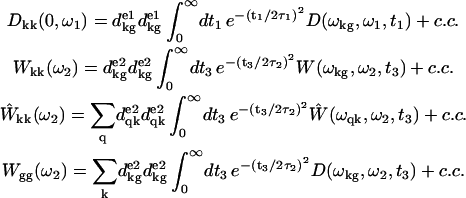(A3)

In modified Redfield theory, the lineshape functions are

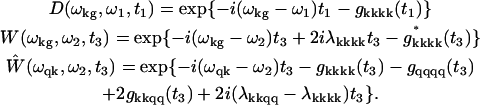(A4)

The line-broadening g-functions and reorganization energy values λ in these expressions appear due to strong diagonal exciton-phonon coupling. They are connected with the spectral density of electron-phonon coupling in the eigenstate representation C_abcd(ω),

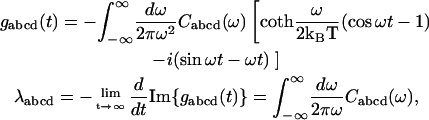(A5)

where a, b, c, and d indices denote k- or q-values numbering the states from one- or two-exciton manifolds. Transition frequencies in Eq. A4 correspond to the first moment of the absorption lines. They are determined by the eigenvalues of the exciton Hamiltonian, i.e., ω_k and ω_q, which do not include a reorganization energy shift. In the presence of strong phonon coupling the thus-determined transition frequencies are different from the frequencies of the zero-phonon transitions.

The time evolution of the initially created doorway packet is given by

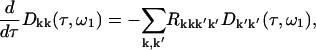(A6)

with the initial conditions given by the first of Eqs. A2 or A3. Here R is the relaxation tensor calculated according to the modified Redfield approach.

The expression for a time-dependent fluorescence (FL) is formally equivalent to a formula for SE (Eq. A1), but instead of probe-pulse envelope some instrument response function should be used.

APPENDIX B: MODIFIED REDFIELD TENSOR

The modified Redfield tensor corresponding to the one-exciton population transfers is (45)

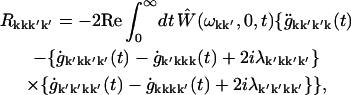(B1)

where g- and λ-functions are connected with the spectral density of electron-phonon coupling in the eigenstate representation C_{kk′k″k″′}(ω).

APPENDIX C: UNCORRELATED DIAGONAL DYNAMIC DISORDER

The matrix of spectral densities in the eigenstate representation (for example, C_{kk′k″k″′}(Ω) needed to evaluate the relaxation tensor in Eq. B1 or the more general form C_abcd(Ω) in Eqs. A4 and A5 containing two-exciton states) can be expressed through the site-representation spectral density C_{nn′n″n″′}(ω). To do it we first specify the exciton-phonon Hamiltonian in the site representation as

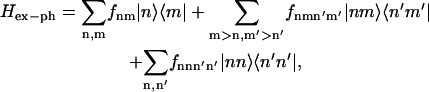(C1)

where the first and second sums account for a bath-induced relaxation in the one- and two-exciton manifolds of an aggregate made of two-level molecules. The third term appears in the case of three-level molecules and reflects a contribution of doubly excited states. We neglected terms like |g〉·〈n|,|g〉·|nm|, and |n〉·〈nm|, which are responsible for radiationless decay of one- and two-exciton states, and |n〉·〈nn|, which is responsible for singlet-singlet annihilation. We further suppose a diagonal disorder, i.e., f_nm = δ_nmf_n, f_nmn′m′ = δ_nn′δ_mm′(f_n + f_m), and f_nnn′n′ = δ_nn′f_nn without intersite correlations, i.e., 〈f_nf_n′〉 = δ_nn′v_n and 〈f_nnf_n′n′〉 = δ_nn′w_n. This model implies that each molecule has its own independent bath. We also neglect correlation between singly and doubly excited states of one molecule 〈f_nnf_n〉, which means that S₁ and S₂ also have independent coupling to the bath. This is a stronger assumption, because the dynamic disorder of different electronic states within one molecule is more correlated than the disorder acting on different molecules. Notice, however, that generalization to the case of more complicated disorder is straightforward: it will lead to additional terms in the Redfield tensor that we reject here for simplicity.

For this model the spectral density in the site representation is C_{nn′n″n″′}(Ω) .2= δ_nn′δ_n′n″δ_n″n″′v_nC(ω) or w_nC(ω) for double-excited states. Here v_n (or w_n) is a dimensionless factor that reflects possible site-to-site variation of exciton-phonon coupling (when n corresponds to electronically excited states) and changing of coupling for charge-transfer states (when n corresponds to radical-pair coupled to one-exciton manifold). A transformation to the eigenstate representation is given by

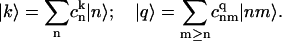(C2)

In the model of uncorrelated diagonal disorder, the g-matrices are connected with the g-function

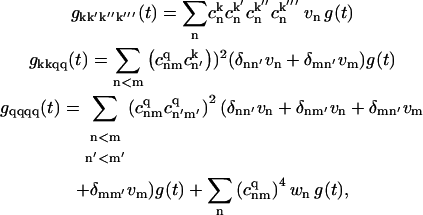(C3)

and the same equations connect the λ-matrices with the λ-value, where

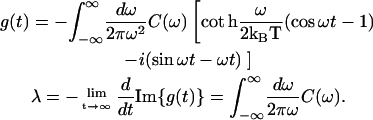(C4)

APPENDIX D: LINEAR SPECTRA

The absorption (OD), circular dichroism (CD), linear dichroism (LD), and steady-state nonselective fluorescence (FL) spectra are given by

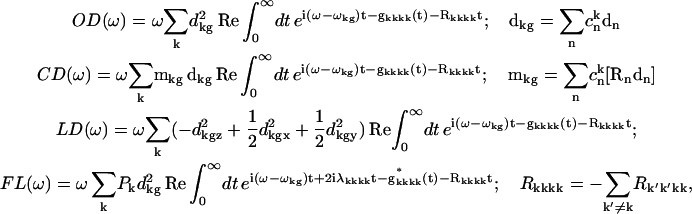(D1)

where P_k denotes the steady-state population of the k^th state, d_kg is transition dipole, and m_kg is rotational moment of the k^th exciton state (expressed through a transition dipole d_n and radius-vector R_n of the n^th molecule), d_kgz denotes projection to the z axis which is normal to the membrane planes, and d_kgx and d_kgy are the in-plane components. We have introduced into the expressions in Eq. D1 a relaxation-induced broadening of the exciton states given by their inverse lifetimes, i.e., R_kkkk. The expressions in Eq. D1 give homogeneous lineshapes. In the presence of static disorder (for example, site inhomogeneity) the homogeneous OD, LD, and FL profiles should be averaged over a random distribution of the site energies that will perturb energies and eigenfunctions of the exciton states. To construct the spectral density profile we use the sum of an overdamped Brownian oscillator and resonance contributions due to high-frequency modes,

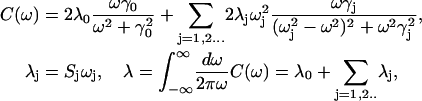(D2)

where 2λ is the Stokes shift, and S_j is the Huang-Rhys factor of the j^th vibrational mode. Parameters of vibrational modes can be taken from the low-temperature FL line-narrowing data (or from molecular dynamics simulation) and then adjusted from the fit of the linear spectra at different temperatures using the expressions in Eq. D1. The thus-determined g-function can then be used for simulation of nonlinear responses (see Appendices A–C). Notice that according to Eq. C3,

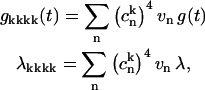(D3)

i.e., line-broadening functions and reorganization energies in the exciton representation (g_kkkk and λ_kkkk) are smaller than in the site representation (v_ng and v_nλ) by a factor of 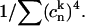The latter is known as the inverse participation ratio, which is equal to a delocalization length of individual exciton states.