How Noise and Coupling Induce Bursting Action Potentials in Pancreatic β-Cells

Abstract

Unlike isolated β-cells, which usually produce continuous spikes or fast and irregular bursts, electrically coupled β-cells are apt to exhibit robust bursting action potentials. We consider the noise induced by thermal fluctuations as well as that by channel-gating stochasticity and examine its effects on the action potential behavior of the β-cell model. It is observed numerically that such noise in general helps single cells to produce a variety of electrical activities. In addition, we also probe coupling via gap junctions between neighboring cells, with heterogeneity induced by noise, to find that it enhances regular bursts.

INTRODUCTION

Bursting action potentials, which are characterized by rapid firing interspersed with quiescent periods in pancreatic β-cells, play a central role in the secretion of insulin, the hormone for glucose homeostasis. It has been reported that isolated β-cells actually show continuous spikes or fast and irregular bursts (1–3), whereas β-cells in a cluster or in an intact islet produce regular bursting action potentials (4–7). As for the correlations between the electrical activity on the cell membrane and insulin secretion (8), the robust bursts appear more effective in maintaining glucose homeostasis than continuous spikes, since coupled β-cells can control insulin release better than isolated β-cells (9–11). However, the question as to whether bursting is an endogenous property of individual β-cells or of a cluster still remains to be answered, which has attracted a number of investigations. Among proposed explanations is the channel-sharing hypothesis, which postulates that current fluctuations arising from channel-gating stochasticity prevent single cells, originally capable of bursting, from bursting, but when they are electrically coupled, the perturbing effects are shared by neighbors and the regular bursting is recovered (12–14). In contrast to this hypothesis of negative effects of noise, recent research (15–19) has established that noise can play a constructive role in many biological systems including β-cell bursting (20). The heterogeneity hypothesis, providing another explanation, was also postulated by the same group. According to it, when heterogeneous cells, each of which produces continuous spikes or bursts depending upon such cell parameters as the size, channel density, etc., are coupled, those cells in the cluster exhibit more pronounced bursts. This gives a useful insight into the functioning of heterogeneous cell populations (21).

In this study, we expand the concept of heterogeneity and probe how such general heterogeneity enhances bursting. It is proposed that noise induces heterogeneity in otherwise homogeneous individual β-cells, which in turn assists the β-cells to produce robust bursts when they are coupled. Existing studies have mostly focused on the synchronizing role of coupling (22,23); the slow dynamics, which has a period ∼10–60 s, is synchronized successfully between adjacent cells. In contrast, we focus here on the fact that rapid firing in the active phase of bursting is asynchronous between neighbors (24) and these fluctuating currents through the gap junction act like noise, enhancing the robust bursting action potential. It is also presented that various action potentials of single β-cells are embodied with optimal noise induced by thermal fluctuations or by ionic channel-gating stochasticity. In particular, noise occasionally stimulates itself to produce fast bursts in a single cell.

There are four sections in this article: In the second section the mathematical model for β-cells is introduced and the simulation method is described. The third section is devoted to the effects of random noise in currents and of voltage-dependent noise in single cells; and the fourth section examines how coupling between cells influences the electrical activity of a cell. Finally, main results are summarized and discussed in the last section.

MODEL AND METHODS

Mathematical model for a β-cell

Because the Hodgkin-Huxley model (25) describes the electrical activity on the cell membrane with ion channels, a few mathematical models for β-cells, based on the electrophysiological data (26–28) of the ion channels in β-cells, have been proposed. Although there are simple models using two-dimensional maps (29–31), we consider the Sherman model, which allows direct physical interpretation (20,32).

The model is described by the current balance equation between capacitive and ionic currents,

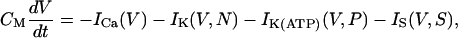(1)

where C_M and V denote the membrane capacitance and the membrane potential, respectively. The activation variable N and the slow variable S are governed by

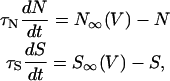(2)

with appropriate relaxation times τ_N and τ_S, which are taken to be constants for simplicity. The fraction P of open K(ATP) channels may also be regarded as a constant for the moment (see Eq. 11). Ionic currents here are fast voltage-dependent L-type Ca²⁺ current I_Ca, delayed-rectifier K⁺ current I_K, ATP-blockable K⁺ current I_K(ATP), and very slow inhibitory potassium current I_S:

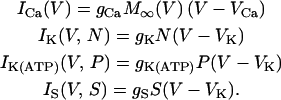(3)

The values I_Ca and I_K are responsible for generating action potentials; I_Ca is assumed to respond instantaneously to a change in the membrane potential, whereas I_K is governed by the dynamics of the activation variable N via Eq. 2. The value I_K(ATP) is the background current with voltage-independent conductance g_K(ATP); this determines the plateau fraction, i.e., the ratio of the active phase duration to the burst period. For example, as g_K(ATP) decreases under high glucose concentration, there are only active phases without silent phases. The value I_S is a phenomenological current representing slow dynamics in the bursting action potential. This model thus assumes that single β-cells originally contain the slow dynamics, which works just under the appropriate condition. Biological candidates for such slow dynamics include slow free Ca²⁺ dynamics (33) and ATP metabolism (34). Finally, M_∞, N_∞, and S_∞ of the voltage-dependent activation are defined to be

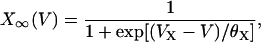(4)

where X denotes M, N, or S.

This set of coupled nonlinear differential equations in Eqs. 1–3 has been analyzed in detail (35,36). There it is noted that S responds on a much slower timescale than V and N because τ_S has the timescale of several seconds compared with the millisecond timescale in firing. Then S is regarded simply as a parameter, and the dynamics of the fast subsystem on the two-dimensional phase space of V and N is analyzed. Furthermore, after eliminating one degree of freedom by substituting N_∞ to N, the whole behavior of this model may be analyzed approximately with fast variable V and slow variable S.

Numerical details

Integration of differential equations including noise demands some caution, and is commonly achieved via the Euler method. For better efficiency, we employ the Euler method for integrating the noise term, combined with the second-order Runge-Kutta method for other terms. To be concrete, we consider the one-variable problem

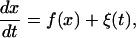(5)

where f(x(t)) is a (nonlinear) function of x, the variable of concern, and ξ(t) is the white noise with zero mean and δ-function correlations

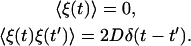(6)

Taking the time step of size Δt, we obtain from the equation of motion the value of x at time t + Δt:

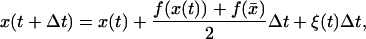(7)

where 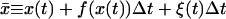(37). Although there is no guarantee that this algorithm should converge in general, it works fine here since the noise term does not depend on the variable x (38).

The white noise ξ of variance D is produced by the Gaussian random numbers with the variance σ² determined by

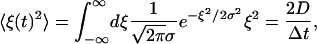(8)

where the Dirac delta function has been represented by Δt⁻¹ within the numerical accuracy. We thus have the relation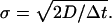

In our simulations, we take Δt = 1 ms, which turns out to be small enough, and integrate the set of equations for current balance. This gives the time evolution of the action potential, from which the power spectrum is computed through the use of the fast Fourier-transform technique.

RESULTS AND DISCUSSION

Noise effects

Before explaining the coupling effects, we first probe the role of noise, either the usual (additive) random noise or the (multiplicative) voltage-dependent one. Comparison of the effects of such noise helps us to better understand the coupling effects.

Random noise

Among many kinds of noise on the cell membrane, the simplest case is the random noise, which may come from thermal fluctuations (see below). When such random current fluctuations are present on the membrane, the current balance equation in Eq. 1 is generalized to

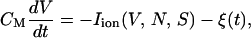(9)

where I_ion represents all the ionic currents on the right-hand side in Eq. 1, and the noise current ξ(t) satisfies Eq. 6 with the variance denoted by D_ξ.

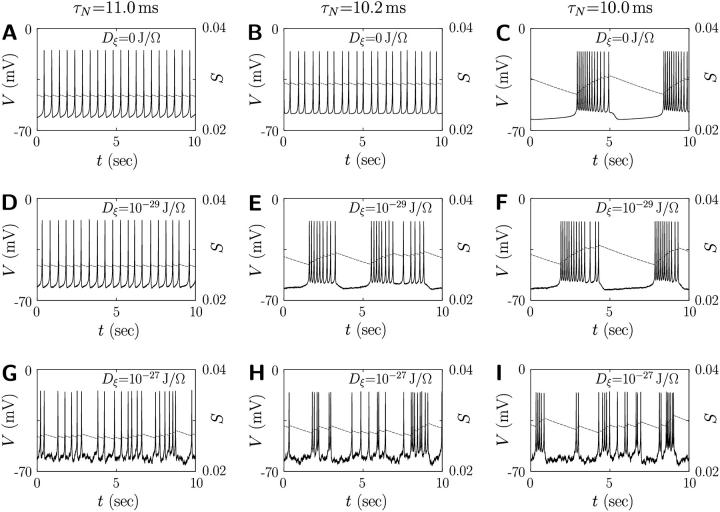
Fig. 1 exhibits the solution of the set of coupled differential equations in Eqs. 2 and 9 under various strengths of the random noise. It is observed that single β-cells produce various electrical activities according to the value of τ_N in Eq. 2, which lies in the narrow range 4–11 ms, depending on the membrane potential (27). When the time constant τ_N of delayed-rectifier K⁺ channel activity exceeds 11.0 ms, the β-cell produces regular spiking action potentials in Fig. 1 A, whereas for τ_N below 10.0 ms, faster repolarization does not allow enough time for the slow variable S to decrease, yielding bursting action potentials (see Fig. 1 C). In the intermediate regime of τ_N = 10.2 ms, Fig. 1 B shows that spiking action potentials are generated but the bursting property is resident. As an appropriate amount of noise comes into play, in particular, the regular spikes in Fig. 1, A and B and bursts in C, change into fast bursts in E, irregular spikes in G, or irregular bursts in H and I.

FIGURE 1.

Action potential V and slow channel activity S in single β-cells at the noise level D_ξ = 0, 10⁻²⁹, and 10⁻²⁷ J/Ω under several values of time constant τ_N of delayed-rectifier K⁺ channel activity N. All simulations have been performed under the standard parameter values in Table 1 except τ_N, the values of which are given above.

To explain these phenomena, we note two thresholds of the slow variable S: One is the upper threshold above which the membrane potential is falling into the resting potential; the other is the lower threshold above which the membrane potential begins to fire. At the moment that fluctuations take negative values, they may assist the repolarizing membrane potential to remain above the lower threshold before the membrane repolarizes completely and then, depolarizes slowly to the lower threshold. This induces occasionally consecutive firing in Fig. 1 G or even fast bursts in Fig. 1 E for the β-cell in the critical parameter range, i.e., τ_N = 10.2 ms. Such consecutive firing raises the average membrane potential for a while, compared with the case of regular spikes. Hence the value of S_∞ becomes large, and consequently S grows with the delay represented by the time constant τ_S. When it goes over the upper threshold, the membrane potential returns to the resting potential. At the same time, S_∞ now becomes small and S reduces to the lower threshold. During this period of S varying from the upper threshold to the lower one, the membrane potential stays in the silent phase. When S comes to the lower threshold, the membrane potential starts to depolarize and fire. Repetition of these processes simply constitutes the fast bursts. As the noise level is raised further, the slow variable S may start to increase before it reaches the lower threshold, assisted by the fluctuations taking negative values. Similarly it may start to decrease before it reaches the upper threshold due to positive fluctuations. In consequence, irregular bursts in Fig. 1, H and I, can thus be induced. When fluctuations become sufficiently strong and dominant, such a role of noise, turning on the slow dynamics of S, is concealed and the membrane potential appears noisy. Here it is notable that under optimal fluctuations, there exists the critical parameter range in which the difference between the upper and lower thresholds is small and the dramatic effect of fast bursts is produced; similar results were obtained in a recent study (12).

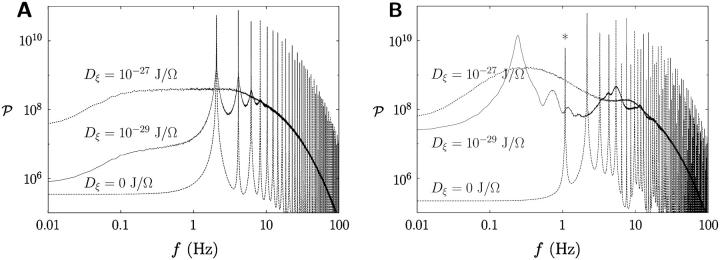
It is revealing to examine the power spectra of the obtained action potentials, computed through the use of the fast Fourier transform technique for various noise levels and displayed in Fig. 2. In particular, Fig. 2 B manifests that the regular spiking action potential of frequency 2 Hz in the absence of noise has changed into fast bursts containing oscillations of 0.2 Hz and 5 Hz at moderate noise levels.

FIGURE 2.

Power spectra of the action potentials for the random noise levels in Fig. 1. The time constant τ_N of the activation variable N is (A) 11.0 ms and (B) 10.2 ms. Observed in the power spectra are main peaks together with their harmonics. The peak at 1 Hz, indicated by the asterisk in B, reflects the tendency to form dimerization of spikes. Each power spectrum has been obtained from the average over 1000 samples, each having a time sequence of 132 s.

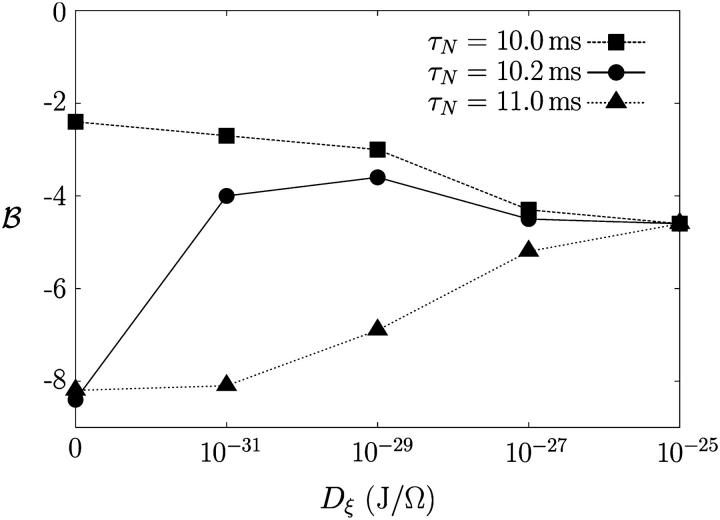
To characterize the positive/negative role of noise in bursting, we define the bursting tendency according to ℬ ≡ log[𝒫(f_B)/𝒫(0)], where 𝒫(f_B) is the power spectrum at the bursting frequency f_B and 𝒫(0) is the background intensity at 0 Hz. Fig. 3 shows the behavior of the bursting tendency ℬ with the noise level, manifesting the noise effects on bursting.

FIGURE 3.

Bursting tendency ℬ of β-cells versus the noise level for several values of τ_N, corresponding to different firing patterns in the absence of noise.

Finally, one may ask whether thermal fluctuations known to generate white noise are enough to induce the fast bursts, irregular bursts or spikes, observed in our simulations. In simulations, the variance D_ξ is taken in the range 10⁻²⁹ J/Ω ∼10⁻²⁷ J/Ω. In reality, noise currents due to thermal fluctuations can be estimated via the fluctuation-dissipation theorem: D_ξ = k_BT/R. This gives D_ξ ∼10⁻²⁹ J/Ω when R is taken to be a few gigaOhms (GΩ) or less. Accordingly, thermal fluctuations alone may not be enough to induce irregular spikes or bursts. Nevertheless, it appears possible that thermal fluctuations actually expedite the emergence of fast bursts when the cell lies in the critical parameter regime.

Voltage-dependent noise

As another simple type of noise, one can consider the voltage-dependent fluctuations, which are closely related to the channel-gating stochasticity (see below). In the presence of such multiplicative noise, the current balance condition in Eq. 1 takes the form

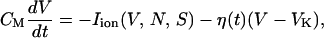(10)

where I_ion also represents all the ionic currents in Eq. 1, and η(t) is the Gaussian white noise, again satisfying Eq. 6 with variance D_η. Solving numerically the coupled differential equations given by Eqs. 2 and 10 at various noise levels with τ_N set equal to 11 ms, we obtain the results, which are illustrated in Fig. 4. Note the overall similarity to the case of random (additive) noise shown in Fig. 1, D and G.

FIGURE 4.

Action potential V and slow channel activity S in single β-cells at two values of the voltage-dependent noise. Again parameter values in Table 1 have been used.

When the voltage-dependent noise stimulates the cell membrane, irregular spikes arise, similarly to the case of random noise, if its amplitude multiplied by the voltage difference (V − V_K) is comparable to the amplitude of random noise. In fact, voltage-dependent noise may be regarded simply as the noise weighted more in the active phase of the membrane potential than in the silent phase. When taking negative values, therefore, fluctuations boost firing more effectively in the active phase and contribute less to the erratic evolution of the resting potential in the silent phase.

Such voltage-dependent (multiplicative) noise may arise from ion channel-gating stochasticity, since currents through channels depend upon the membrane potential difference. If the number of channels is sufficiently large, the channel stochasticity can be described by a Langevin equation (39–41). Specifically, the stochasticity of K(ATP) channels has been considered (20). In the expression for the ATP-dependent K⁺ current, I_K(ATP) = g_K(ATP)P(V − V_K), the opening ratio P, which is no more constant, evolves according to

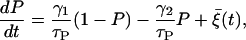(11)

where γ₁/τ_P and γ₂/τ_P represent the rates for a closed channel to switch to the open state and vice versa, respectively. Note that γ₁ and γ₂ thus determine the equilibrium ratio between the open state and the closed one. Fluctuations in the opening ratio are described by the Gaussian white noise 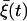satisfying Eq. 6 with the variance

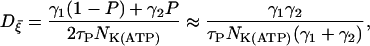(12)

where N_K(ATP) is the total number of ATP-dependent K⁺ channels in a β-cell (40).

Solving Eq. 11, we obtain that P fluctuates around the equilibrium value P₀, taken to be 0.5 in our simulations: 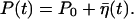Here 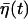is colored noise, characterized by the variance

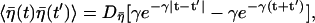(13)

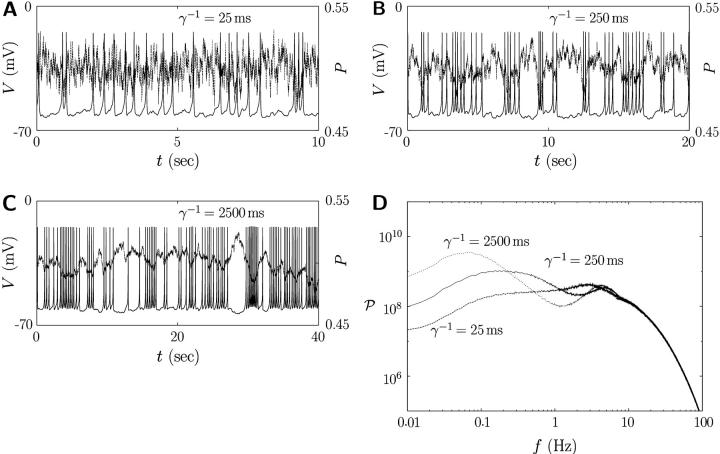
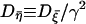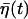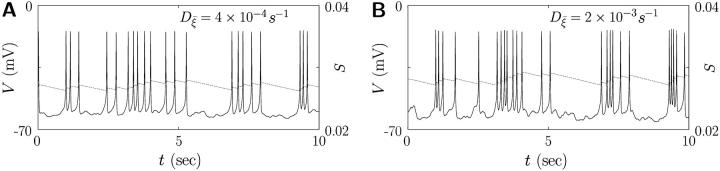
with γ ≡ (γ₁ + γ₂)/τ_p and (see Appendix for details). Note that the firing timescale is comparable to the correlation time γ⁻¹ of the noise (see Fig. 5). Consequently this colored noise is more effective to induce several consecutive firings, which resemble irregular burst, than the white noise. In particular, the modules of several spikes are observed to become longer as the correlation time γ⁻¹ is increased. Fig. 6 shows the behaviors in the presence of the channel-gating noise 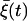for two different channel numbers. In this case of multiplicative colored noise, modules of spikes arise more efficiently than in the case of multiplicative white noise shown in Fig. 4. Further, it is also found that stronger gating fluctuations from fewer channels (N_K(ATP) = 500) in Fig. 6 B give rise to modules of more rapid spikes, compared with the case N_K(ATP) = 2500 in Fig. 6 A.

FIGURE 5.

Correlations between the action potential and multiplicative colored noise due to channel-gating stochasticity. The correlation time γ⁻¹ is taken to be (A) 25 ms, (B) 250 ms, and (C) 2500 ms. Note that each figure has a different timescale. Their corresponding power spectra are shown in D. Parameter values in Table 1 have been used except τ_P.

FIGURE 6.

Action potential V and slow channel activity S in single β-cells at two values of the channel-gating stochasticity: A and B correspond to the channel number N_K(ATP) = 2500 and 500, respectively. Note that Fig. 5 B, and panel A, from this figure, represent the same sample path, but with different variables plotted. Other parameter values have been taken from Table 1.

Similar results can be obtained with fluctuations in the Ca²⁺ channels and in the delayed-rectifier K⁺ channels although they act somewhat differently from the fluctuations in the ATP-blockable K⁺ channels (data not shown).

It is thus concluded that noise generates diverse firing patterns in single β-cells. In a real (physiological) islet, however, β-cells are not isolated but coupled with each other, making it desirable to consider coupled β-cells and to investigate effects of noise together with those of coupling. This will be the subject of the next section.

Coupling effects

We consider two cells coupled with each other via a gap junction. With the coupling incorporated, Eq. 1 is extended to the coupled equations, as

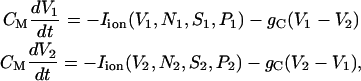(14)

where the subscripts 1 and 2 are the cell indices, I_ion again denotes all the ionic currents, and g_C is the coupling conductance. Note that the heterogeneity between both cells is accommodated in the K(ATP) channel opening ratio P. Namely, the noise associated with channel-gating stochasticity induces continuously heterogeneity between the cells.

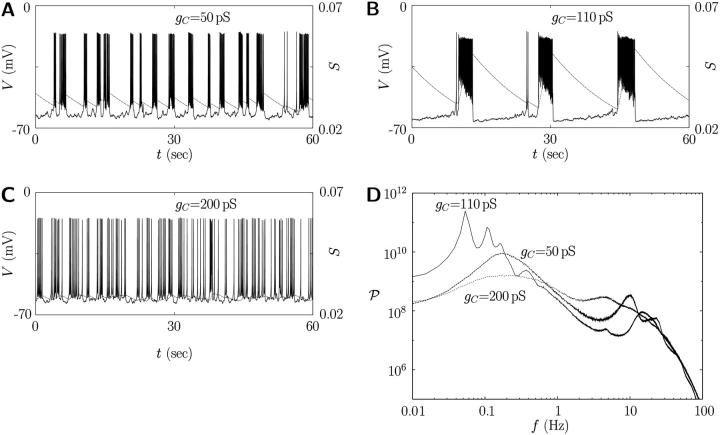
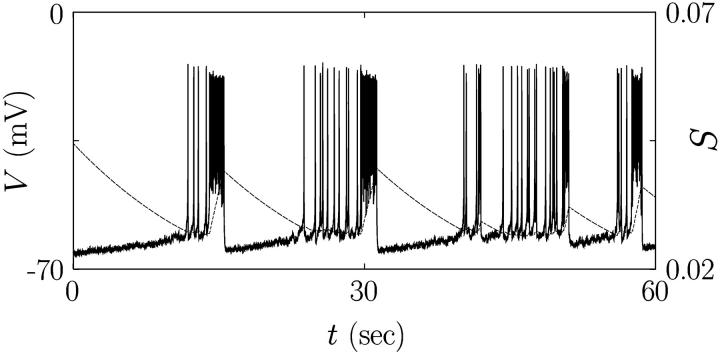
We thus have eight coupled differential equations, which consist of Eqs. 2 and 11 for each cell and Eq. 14, for eight variables (V, N, S, and P for each cell). Integration of these coupled equations yields the results displayed in Fig. 7, for the channel-gating noise of variance 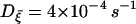given by Eq. 12 and for three values of the coupling conductance: g_C = 50 pS, 110 pS, and 200 pS. Revealed is the optimal coupling strength for longer bursting periods: Although weak coupling is not enough to couple individual cells and to generate consecutive firing, too strong coupling tends to make the cluster behave as a single large cell (22). Robust bursts emerge as a consequence of the competition between heterogeneity and coupling (23). On the one hand, the coupling term in Eq. 14 helps the two cells to act synchronously; on the other hand, it also plays the role of stimulating noise, which acts strongly on the two cells with asynchronous phases. The perfect asynchrony results from the harmony of coupling to be similar and heterogeneity to be different (see Fig. 8). Namely, the coupling currents between asynchronous neighboring cells give rise to consecutive firing; this in turn increases the upper threshold of the slow variable S above which firing disappears. As S grows up toward the increased upper threshold, it takes longer to reduce down to the lower threshold. This larger rising and falling divides more clearly the active and silent phases in the membrane potential, and accordingly induces robust bursting action potentials with periods longer than 20 s. Note that in the absence of coupling we have not been able to observe bursting periods longer than 10 s (see Figs. 1–6) (Parameter values different from those in Table 1 may yield bursting periods somewhat longer than 10 s even in a single cell. In this case, the coupling gives rise to robust bursting of even longer periods—say, 30 s—still demonstrating its crucial role in generating regular bursts.) In the two-cell model here the optimal value of the coupling conductance is observed to be g_C = 110 pS. As the number of cells is increased, however, more heterogeneity is introduced, which should be matched by stronger coupling to generate robust bursts with longer periods. Although the detailed investigation is beyond our computing capacity, we have performed multi-cell simulations, which indeed confirms such an increase of the optimal coupling conductance. For example, the optimal conductance in the system of 1000 cells turns out to be 100–300 pS (data not shown), which coincides with experimental results of the gap junctional conductance (42).

FIGURE 7.

Action potential V and slow channel activity S in the presence of coupling via the gap junction of conductance g_C = (A) 50 pS, (B) 110 pS, and (C) 200 pS. Heterogeneity has been induced by channel-gating stochasticity of variance 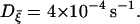The corresponding power spectra are shown in D. Parameter values in Table 1 have been used except g_C.

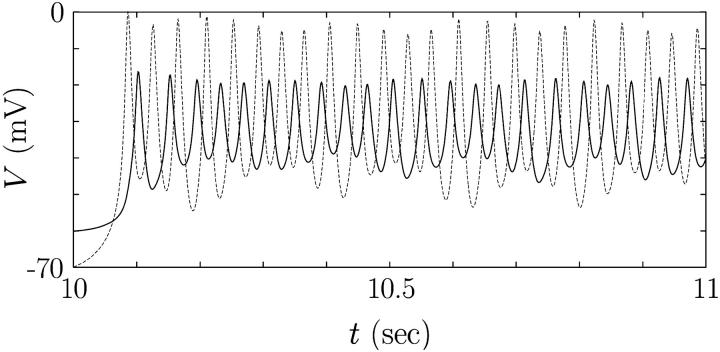
FIGURE 8.

Enlarged view of the interval between 10 s and 11 s in Fig. 7 B, disclosing the detailed behavior of the two membrane potentials V₁ (solid line) and V₂ (dashed line).

TABLE 1.

Standard parameter values

CM = 6.3 pF	gCa = 3000 pS
gK = 4000 pS	gK(ATP) = 1000 pS
gS = 3000 pS	gC = 110 pS
VCa = 25 mV	VK = −75 mV
VM = −20 mV	θM = 12 mV
VN = −17 mV	θN = 5.6 mV
VS = −22 mV	θS = 8.0 mV
τN = 1.1 × 10−2 s	τS = 20 s
τP = 0.50 s	NK(ATP) = 2500
γ1 = 1	γ2 = 1

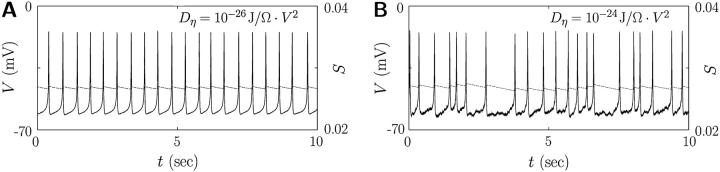
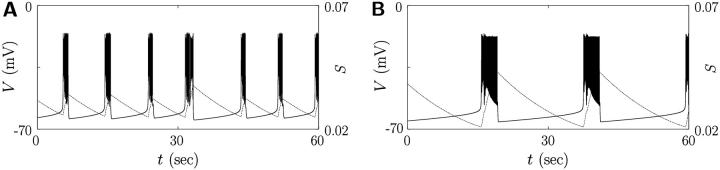
These features of the coupled cells do not change much in the presence of the voltage-dependent noise instead of the channel-gating noise, except that the channel-gating noise is more efficient for robust bursting than the voltage-dependent one, as shown in Fig. 9 for D_η = 10⁻²⁴ J/Ω · V² and 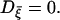Note also that the coupled cells depicted in Figs. 7 and 9 do not burst in the absence of noise-induced heterogeneity.

FIGURE 9.

Bursting action potential induced by cell coupling via the gap junction of conductance g_C = 110 pS under the voltage-dependent noise of strength D_η = 10⁻²⁴ J/Ω · V². Parameter values in Table 1 have been used.

Recall that in the emergence of robust bursts, the asynchrony from the heterogeneity induced by noise plays an important role, which has also been addressed in a very recent study (43). Similar to such noise-induced heterogeneity, the cell-to-cell heterogeneity associated with variations of the cell parameters among the cells is also expected to work for robust bursts (21). To check this, we allowed variations of the membrane capacitance C_M related to the cell size as well as of the channel conductance g_K(ATP) and examined the resulting behavior: Shown in Fig. 10, A and B, are bursts generated in the case of 20% variation of C_M (5.0 pF, 6.3 pF) and in the case of 10% variation of g_K(ATP) (1000 pS, 1100 pS), respectively. Specifically, a spiking cell (with C_M = 6.3 pF) is coupled with a bursting cell (with C_M = 5.0 pF) in Fig. 10 A, which results in both cells bursting synchronously with a longer bursting period than that of a single cell (5.0 pF). In Fig. 10 B, on the other hand, two spiking cells (with g_K(ATP) = 1000 pS and 1100 pS) are coupled with each other, and both are bursting. Therefore heterogeneity is, in general, important for bursting in coupled cells, no matter whether it is cell-to-cell heterogeneity or induced by noise.

FIGURE 10.

Bursting action potential induced by cell coupling, with the cell-to-cell heterogeneity due to variations of the membrane capacitance C_M and of the ATP-blockable K⁺ channel conductance g_K(ATP): (A) 20% variation of C_M (5.0 pF, 6.3 pF); and (B) 10% variation of g_K(ATP) (1000 pS, 1100 pS). Other parameter values have been taken from Table 1.

CONCLUSIONS

We have probed whether noise and coupling serve as an appropriate stimulus for inducing the bursting action potential in pancreatic β-cells, and found that they effectively call into action the inherent slow dynamics in individual cells. Fast bursts, irregular spikes, or bursts in single β-cells have been observed as the results of the noise effects. In particular, the emergence of regular bursts assisted by an appropriate amount of noise [see Figs. 1 E and 2 B] is reminiscent of coherence resonance (15–19). In view of physiology, the consecutive firing induced by fluctuations gives rise to relative depolarization for a while, which is followed by the activation of the slow potassium channel lasting until the slow variable reaches the upper threshold. At this time the slow K⁺ channel opens fully, and the outflux of cytosolic potassium ions gets very large, thus hindering depolarization. Accordingly, the membrane potential is compelled to stay in the silent phase, and the slow K⁺ channel in turn starts to be inactivated. In consequence, the membrane can become depolarized as the outflux of K⁺ ions reduces. Finally, firing occurs again, and consecutive firing also happens by the help of appropriate stimulation. As candidates for the stimulus, both the (additive) random noise coming from fluctuating currents and the (multiplicative) voltage-dependent noise from the channel-gating stochasticity have been considered.

In particular, coupling between cells has turned out essential for attaining regular bursts with longer periods compared with the fast bursts. The coupling term, proportional to the potential difference between two cells, operates in a similar manner to the voltage-dependent noise: It increases with the potential difference and thus becomes large for the cells in active phases, stimulating the cells like noise. On the other hand, it is small for perfectly synchronized cells in silent phases. The coupling also increases the upper threshold of S and induces robust regular bursts.

In the analysis, the heterogeneity has been found to play an important role in inducing strong fluctuations during active phases, which may cause robust bursts. Namely, bursting in general results from the interplay of coupling and heterogeneity. This allows us to interpret the fact that large cell clusters (up to the critical size) show more regular bursts (20,22): Assuming a cubic islet, we have considered β-cells arranged into an L³ cube, under free boundary conditions. Adopting physiological gap junction conductance, g_C = 200 pS (42), we have found that the bursting period and duration first increases with the size L but tends to saturate beyond L = 5 (data not shown). Such saturation behavior may be explained as follows: Via the coupling through gap junctions, the number of nearest neighbors in the three-dimensional space is limited, e.g., to six or so; this suggests that the cluster above some critical size can get no more advantage of the heterogeneity from neighboring cells through given coupling strength.

The Langerhans islet, however, consists of several endocrine cells in addition to β-cells. Other endocrine cells in an islet have been studied recently (44,45), and it will be of interest to study the coupling effects between originally different α-, β-, and δ-cells, coupled via hormones or neurotransmitters (46). This might give a clue to understanding the size of a Langerhans islet in the pancreas, which is left for further study.

APPENDIX

Equation 11 can be solved to give the time evolution of the opening ratio P:

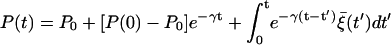with P₀ ≡ γ₁/(γ₁ + γ₂) and γ ≡ (γ₁ + γ₂)/τ_p, where P(0) is the initial value of P. After sufficiently long time, we thus have P fluctuating around the equilibrium ratio P₀: 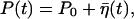where the noise 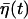is given by

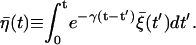From the above definition of the noise 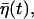it is straightforward to derive its characteristics as

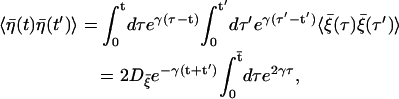where we have used the relation 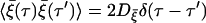and 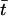denotes the smaller one between t and t′. We thus obtain the correlations of the noise 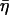at different times

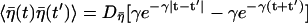with 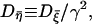which manifests the colored nature.