Direct Measurement of Osmotic Pressure of Glycosaminoglycan Solutions by Membrane Osmometry at Room Temperature

Abstract

Articular cartilage is a hydrated soft tissue composed of negatively charged proteoglycans fixed within a collagen matrix. This charge gradient causes the tissue to imbibe water and swell, creating a net osmotic pressure that enhances the tissue's ability to bear load. In this study we designed and utilized an apparatus for directly measuring the osmotic pressure of chondroitin sulfate, the primary glycosaminoglycan found in articular cartilage, in solution with varying bathing ionic strength (0.015 M, 0.15 M, 0.5 M, 1 M, and 2 M NaCl) at room temperature. The osmotic pressure (π) was found to increase nonlinearly with increasing chondroitin sulfate concentration and decreasing NaCl ionic bath environment. Above 1 M NaCl, π changes negligibly with further increases in salt concentration, suggesting that Donnan osmotic pressure is negligible above this threshold, and the resulting pressure is attributed to configurational entropy. Results of the current study were also used to estimate the contribution of osmotic pressure to the stiffness of cartilage based on theoretical and experimental considerations. Our findings indicate that the osmotic pressure resulting from configurational entropy is much smaller in cartilage (based on an earlier study on bovine articular cartilage) than in free solution. The rate of change of osmotic pressure with compressive strain is found to contribute approximately one-third of the compressive modulus (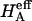) of cartilage (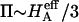), with the balance contributed by the intrinsic structural modulus of the solid matrix (i.e., 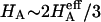). A strong dependence of this intrinsic modulus on salt concentration was found; therefore, it appears that proteoglycans contribute structurally to the magnitude of 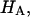in a manner independent of osmotic pressure.

INTRODUCTION

Articular cartilage is a resilient bearing material capable of withstanding loads reaching several times of body weight. The major constituents of cartilage are water (60–85% by wet weight), type II collagen (15–22% by wet weight.), and proteoglycans (5–10% by wet weight). Proteoglycans consist of a protein core with covalently bonded glycosaminoglycan (GAG) side chains. Aggrecan is the most abundant proteoglycan in cartilage (4–7% by wet weight), and its GAG residues consist primarily of keratan sulfate and chondroitin sulfate (CS) chains, which are mostly sulfated at either the 4- (CS-4) or 6-position (CS-6) of the galactosamine residues. In the presence of water, the collagen network traps the proteoglycans and limits the pore size of the extracellular matrix to 2–10 nm (1,2).

The selective behavior of the extracellular matrix to the penetration of various solutes is regulated by interaction of the collagen network with the proteoglycans and water. The immobilized sulfate and carboxyl groups in CS and keratan sulfate become charged in solution and contribute to a net negative charge in the tissue, relative to the surrounding fluid. This negative fixed charge density (FCD) ranges from 0.05 to 0.35 mEq/ml H₂O (1,3) in healthy articular cartilage. The fixed negative charges are situated close together within the collagen network and experience like-charge repulsion (4); however, the presence of mobile electrolytes neutralize the fixed negative charge groups. To maintain an electroneutral environment within the tissue, an unbalanced distribution of mobile ions (primarily Na⁺ and Cl⁻) will exist and contribute to a net osmotic pressure in the tissue (1,5). This osmotic pressure causes cartilage to swell, acting as a prestress, and enhances the tissue's ability to bear load (6–8). Various experimental and theoretical studies have measured or estimated this swelling pressure to vary from 0.02 to 0.2 MPa (1,7,9).

From theoretical considerations, the osmotic modulus is the contribution of osmotic pressure to the compressive stiffness of cartilage, and derives from the rate of change of this pressure with compressive strain (5,10,11). Because the osmotic pressure of cartilage is dependent upon the fixed charge density of its proteoglycans, and because the relationship between fixed charge density and compressive strain is given from basic kinematic considerations, it is thus possible in principle to directly estimate the contribution of the osmotic pressure to the stiffness of cartilage from experimental measurements of its variation with FCD.

Previous studies have investigated the osmotic pressure induced by CS in solution through the use of equilibrium dialysis (3,7,12) or sedimentation equilibrium (13). These data have been mostly obtained through indirect chemical equilibration measurements, where the osmotic pressure of GAGs is measured relative to that of uncharged macromolecules such as polyethylene glycol (PEG) (3). This indirect technique is sensitive to the nonlinear behavior of PEG at different temperatures, as it has been shown that its osmotic pressure responses at 4°C and 25°C are not linearly related, contrary to Raoult's Law (3,7,12). Therefore, the first objective of this study was to design an apparatus for directly measuring the osmotic pressure of chondroitin sulfate solutions. These measurements were performed at room temperature, where the osmotic pressure data can be interpreted in the context of existing data on cartilage mechanical properties, often measured at room temperature as well. The second objective was to estimate the contribution of osmotic pressure to the stiffness of cartilage, based on theoretical and experimental considerations.

MATERIALS AND METHODS

Direct membrane osmometer

A custom-designed stainless steel cylindrical device (∅ 2.5- × 4.5-cm long) was used to measure the osmotic pressure of polymer solutions (Fig. 1). The direct membrane osmometer (DMO) device consists of a centrally located fluid chamber (∅ 0.8- × 2.5-cm deep) with a ∅ 0.85-mm port at the bottom. A piezoresistive microchip pressure transducer (NPC 1210-100G; Lucas Novasensor, Fremont, CA) with a range of 0–0.69 MPa is bonded to the bottom of the chamber, with the ports of the pressure transducer and chamber aligned. The voltage output of the transducer was recorded in 10-s intervals with a data acquisition card and Labview software (National Instruments, Austin, TX).

FIGURE 1.

Direct membrane osmometer. (a) Side view of the stainless steel cylindrical device with microchip pressure transducer. (b) Polymeric solutions are injected into the fluid chamber, and the resulting pressure is measured at the pressure port. Ion and fluid exchange occurs through the buffer portal located in the lid of the device. Dialysis membrane and stainless steel wire-mesh backing for the membrane are not shown.

In each trial, 1 ml of a polymer solution was injected into the fluid chamber using a syringe and needle. A magnetic microstir bar (Fisher Scientific, Leicestershire, UK) was placed in the fluid chamber with its long axis parallel to the bottom of the chamber. A piece of dialysis membrane (molecular weight cutoff = 1 kDa, ∅ 2.2 cm; Spectrum Laboratories, Rancho Dominguez, CA) was wetted with an NaCl solution, corresponding to the same concentration as the bath ionic concentration, and was laid down on the polymer solution meniscus while ensuring that air bubbles were not trapped in the fluid chamber. A stainless steel wire mesh (McMaster-Carr, Type 316 SS woven wire cloth, no. 9319T575) was laid on top of the membrane to prevent it from bulging when pressurized, and the lid of the device was tightened against an O-ring seal. The DMO was then inverted and placed in a 200-ml bath of NaCl at 25°C leaving the device standing on its three pegs. This setup allowed the bathing solution to penetrate into the chamber via the buffer portal, flowing perpendicular to the membrane/mesh (Fig. 1). Another magnetic stir bar was placed in the buffer bath and the entire setup was placed on a magnetic stir plate. The resulting pressure inside the chamber was measured as a function of time until it did not change significantly, which indicated that equilibrium was reached.

Polymer solutions

To validate the DMO, the osmotic pressure of polyethylene glycol (20 kDa) (Fluka, Buchs, Switzerland) was measured at concentrations of 50, 100, 150, and 200 mg/ml (n = 4 for each concentration) in 0.15 M NaCl at 25°C. The osmotic pressure of chondroitin sulfate-C (CS-C, Sigma, St. Louis, MO; 89.6% chondroitin-6-sulfate (CS-6) + 10.3% chondroitin-4-sulfate (CS-4) from shark cartilage) solutions was measured over a range of macromolecular concentrations (50–200 mg/ml, n = 6–8 at each concentration). Measurements of CS-C pressure were conducted in the presence of varying NaCl buffers (0.015, 0.15, 0.5, 1, or 2 M), where 0.15 M NaCl was considered physiological. Chondroitin sulfate-A (CS-A, Sigma), which is comprised of 61% CS-4 and 39% CS-6 isoforms from bovine trachea, was also tested at 0.15 and 2 M NaCl. During each solution preparation, the lyophilized polymer was dissolved in 5 ml of NaCl solution corresponding to the same ionic concentration as the external bath, and vortexed for 1 h to ensure maximal solubility. The GAG content was estimated from the mass of CS and the final volume of the solution, while taking into account the water content of the powder as reported by the supplier (6.62 ± 1.67%, Sigma).

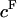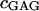The fixed charge density () was calculated as where is the mass of GAG per volume of water, and 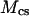is the molecular weight of a monomeric subunit (i.e., 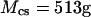per CS disaccharide) (9). The valence, 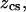represents the number of charges per monomeric subunit, and is calculated from a weighted average of the constituent oligosaccharide found in each isoform of CS ( 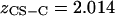and 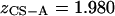charges per CS disaccharide) (14).

Theoretical analysis

Under equilibrium conditions in the DMO, the osmotic pressure difference between the polymer solution of concentration 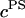in equilibrium with the NaCl bath of concentration 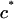can be represented as a polynomial expansion in integral powers of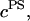

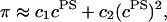(1)

where 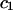and 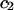are virial coefficients that depend on 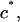to be determined experimentally from measurements of π with varying polymer concentrations.

In a one-dimensional analysis of cartilage under equilibrium conditions in a NaCl bath, the total stress σ in cartilage is equal to the superposition of the osmotic pressure difference between the interstitial fluid and external salt solution, π, and the elastic stress in the solid matrix,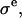

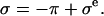(2)

The negative sign in front of π reflects the convention that pressures are positive in compression whereas stresses are negative, and all variables are treated as scalars in this one-dimensional analysis. By analogy to Eq. 1, the osmotic pressure resulting from the proteoglycans can be represented as a polynomial expansion in integral powers of their effective fixed-charge density,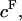

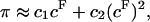(3)

where 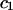and 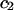similarly depend on 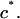(More generally, if cartilage is equilibrated against a solution of a polymer that cannot permeate into the tissue, then

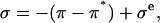(4)

where 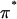is the osmotic pressure of the polymer solution against a saline bath; both π and 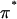may vary with the NaCl concentration.)

In confined compression, under small strains, the effective aggregate modulus of the tissue is given by the rate of change of total stress with applied strain ɛ,

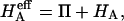(5)

where 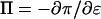is the osmotic modulus, representing the contribution from the rate of change of osmotic pressure with strain, and 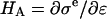is the contribution from the intrinsic stiffness of the solid matrix of cartilage (10). For small deformations, the fixed charge density varies with strain according to

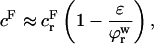(6)

where 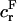and 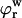are, respectively, the FCD and water volume fraction of the tissue in a reference state of zero strain (5). (Lai et al. (5) propose that such a reference state can be achieved experimentally in an unloaded state and hypertonic conditions, under the premise that 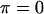under these conditions. However, in our recent study on bovine cartilage (15), we showed that π is not necessarily negligible in 2 M NaCl, leaving the tissue in a swollen state; nevertheless, the reference state of 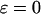could be achieved experimentally by applying a compressive stress that exactly counteracted the osmotic pressure π.) In these expressions the fixed charge density is evaluated as the ratio of charge per volume of total water in the tissue. It follows from Eqs. 3 and 6 that

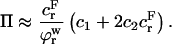(7)

Statistical analysis

Statistical analysis was performed on all experimental results using two-way ANOVA for fixed charge density and bathing concentration dependence. Tukey's HSD post hoc test was applied, with p < 0.05 considered statistically significant.

RESULTS

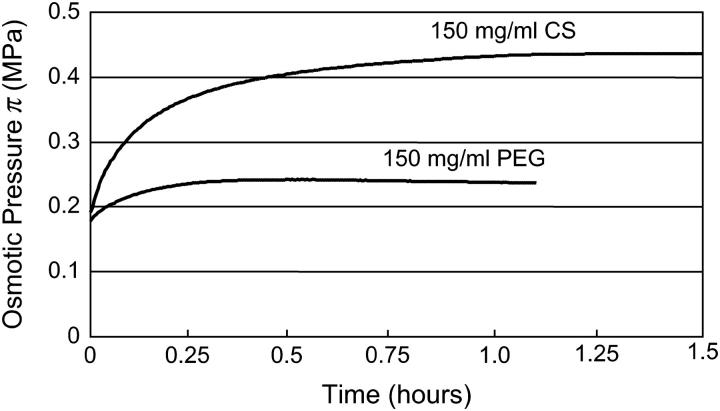
All pressure measurements represent gauge pressure relative to atmospheric levels. Upon tightening of the device lid, the pressure rapidly increased to a nonzero tightening pressure in <10 s. Once placed in the bathing solution, the pressure increased nonlinearly as a result of water transport across the membrane, reaching equilibrium within 1–3 h, depending on concentration. This rate of transport is likely a function of the dialysis membrane permeability, and pressure chamber and transducer impedance. Typical time-dependent curves for one of the tested concentrations (150 mg/ml) of PEG and CS in 0.15 M are shown in Fig. 2. Only equilibrium osmotic pressure results were used in subsequent analyses.

FIGURE 2.

Typical pressure response as a function of time for representative CS and PEG solutions (150 mg/ml).

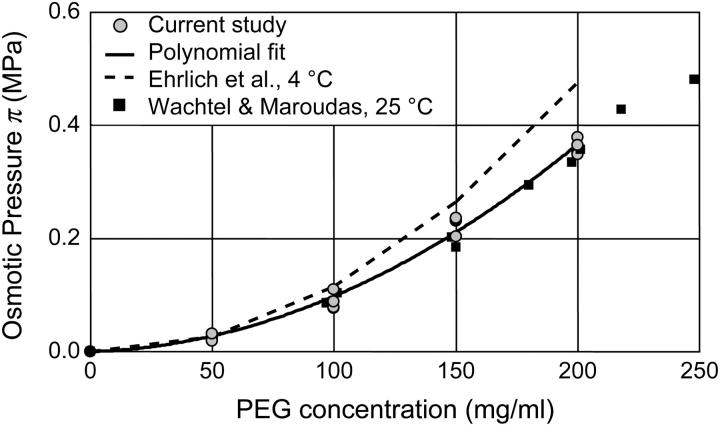
The osmotic pressure response of polyethylene glycol as a function of concentration is shown in Fig. 3. The repeated measure of pressure within each concentration group showed minimal variability (mean deviation = 9.6 × 10⁻³ MPa). The osmotic pressure increased nonlinearly with increasing concentration in 0.15 M NaCl at 25°C. A virial expansion of the osmotic pressure yielded 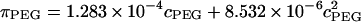( 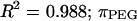in units of MPa and 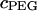in units of mg/ml) (Fig. 3).

FIGURE 3.

Osmotic pressure of 20 kDa PEG solutions as a function of concentration. Current study (25°C) with corresponding polynomial fit; Wachtel and Maroudas (16) pressure measured at 25°C; Ehrlich et al. (12) pressure measured at 4°C.

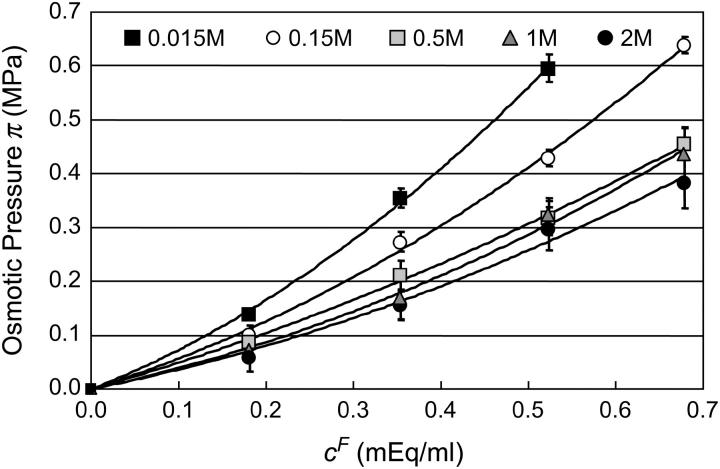
The osmotic pressure of CS-C solutions increased nonlinearly with increasing concentration, and thus fixed charge density (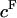), in the presence of all bathing solutions (Fig. 4). The increase in CS-C pressure with increasing 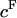was also modulated by the concentration of the bathing solution. Osmotic pressure was greatest in 0.015 M NaCl and decreased nonlinearly with increasing salt concentration to 1 M NaCl. As the concentration of the bath increased from 1 M to 2 M NaCl, no significant decrease was noted in the measured osmotic pressure (p > 0.8; Fig. 4). Under the most hypotonic conditions (0.015 M NaCl), a maximum pressure of ∼0.6 MPa was attained at the nominal concentration of 150 mg/ml. Therefore, pressure measurements of 200 mg/ml of CS could not be carried out in 0.015 M NaCl due to the upper limit of the pressure transducer operating range. Quadratic curve fits of the CS-C osmotic pressure (π) versus fixed charge density (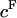) in each bathing concentration, in the form of Eq. 3, are plotted in Fig. 4. All curve fits showed excellent agreement with experimental results (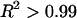), and the resulting virial coefficients are presented in Table 1.

FIGURE 4.

Equilibrium osmotic pressure of CS-C solutions measured using the DMO as a function of fixed charge density (25°C), in various NaCl concentrations. Solid lines indicate the corresponding virial expansion polynomial fits.

TABLE 1.

Virial coefficient (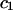 and ) for CS-C solutions in equilibrium with NaCl solutions of various concentrations, at 25°C, from fitting the data of Fig. 4

NaCl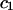
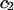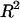0.015 M	0.628 ± 0.051	0.986 ± 0.11	0.999
0.15 M	0.500 ± 0.053	0.645 ± 0.091	0.997
0.5 M	0.460 ± 0.032	0.306 ± 0.056	0.999
1 M	0.342 ± 0.060	0.462 ± 0.010	0.996
2 M	0.381 ± 0.078	0.241 ± 0.013	0.981

See Eq. 3; π is given in units of MPa and c^F in units of mEq/ml (mean ± SE).

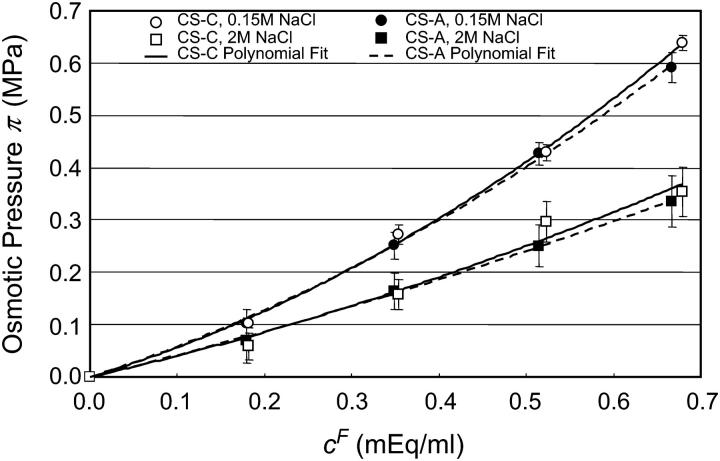
The osmotic pressure of CS-A solutions was measured at the physiological (0.15 M NaCl) and most hypertonic (2 M NaCl) bath concentrations. The osmotic pressure of CS-A increased nonlinearly with increasing fixed charge density, and decreased with increasing NaCl bath concentration (Fig. 5). Moreover, the osmotic pressure response of CS-A was indistinguishable from that measured for CS-C at both 0.15 and 2 M (Fig. 5). A linear regression comparing the response of CS-C versus CS-A confirmed this linearity with a near unity-regression coefficient β (0.15 M NaCl, β = 0.999, R² = 0.999; 2 M NaCl, β = 1.083, R² = 0.998).

FIGURE 5.

Osmotic pressure of CS-A solutions measured at 0.15 and 2 M NaCl. The corresponding CS-C data points are plotted for comparison between the two mixtures of isoforms. Solid lines indicate the corresponding polynomial fits.

DISCUSSION

The objectives of this study were to directly measure the osmotic pressure of chondroitin sulfate solutions in the presence of varying NaCl concentrations, and use these results to estimate the contribution of osmotic pressure to the effective aggregate modulus of cartilage. These measurements were performed at room temperature, where the osmotic pressure and modulus can be interpreted in the context of existing data on cartilage mechanical properties, often measured at room temperature as well.

Osmotic pressure measurements of PEG, a neutral macromolecule in solution, were performed at room temperature using the DMO to validate the custom-built device and technique. A comparison to the calibration of Wachtel and Maroudas (16), performed at 25°C using a specially adapted stirred ultrafiltration cell, revealed excellent agreement (R² = 0.97) with this study (Fig. 3).

Furthermore, measurements of CS-C osmotic pressure at 25°C were nearly identical (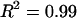) to the osmotic pressure of CS-A at both 0.15 and 2 M NaCl, suggesting that there is no significant difference between these two sources of chondroitin sulfate with regard to osmotic pressure (Fig. 5). This finding allows direct comparison of our more extensive CS-C results with previous studies examining the osmotic pressure of CS-A (3,12). With respect to human articular cartilage, it should be noted that that articular cartilage comprises mostly CS-6 (93.3%), which more closely mimics the compositional content of CS-C from shark cartilage (89.6% CS-6 versus 10.3% CS-4) than CS-A isolated from bovine tracheal cartilage (58.4% CS-6 versus 40.1% CS-4) (14).

The results of this study are in qualitative agreement with the study of Ehrlich et al., which examined the osmotic pressure of CS-A (12). Both studies demonstrate that the osmotic pressure (π) of CS solutions increases quadratically with increasing fixed-charge density, and decreases with increasing NaCl concentration, with no further change in π observed above 1 M NaCl. However, quantitatively, our measured pressures exceed those of Ehrlich et al. at 0.5, 1.0, and 2 M NaCl, whereas theirs are greater at 0.015 and 0.15 M NaCl (12). Their measurements were conducted at 4°C, which may account for these differences, albeit on the assumption that temperature dependence varies nonlinearly with NaCl concentration. A more likely explanation appears to be the difference in the measurement methodology. The indirect approach adopted by these authors was to equilibrate CS solutions placed in dialysis sacs against PEG solutions of known concentrations, and deduce the osmotic pressure of the CS solutions from the calibrated PEG osmotic pressure, under the condition that the sacs do not become turgid.

The equilibrium osmotic pressure of concentrated glycosaminoglycan solutions is comprised of both electrostatic and nonelectrostatic contributions. The electrostatic component, representing the interaction between the negatively charged groups, has been previously described in the context of Donnan pressure (1,5) or through microstructural modeling of the GAG molecules (17,18). The nonelectrostatic contribution represents the configurational and mixing entropy of the GAG chains in solution (3,12,19). Polymeric GAG chains in solution can assume a number of configurations that contribute to their entropy; furthermore, the presence of a polymeric GAG molecule in solution excludes other molecules from occupying that same space, resulting in an excluded volume effect (19–21). A previous study by Kovach (19) has reviewed these effects by incorporating a lattice model of GAG chains into a statistical thermodynamics analysis. Accordingly,

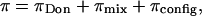(8)

where the contribution from mixing entropy was found to be negligible compared to the contribution from configurational entropy, i.e., 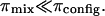From Donnan law it is known that the electrostatic contribution to the osmotic pressure is dependent on electrolyte concentration (i.e., NaCl concentration). At high NaCl concentrations, the presence of excess salt ions in solution shields the electrostatic repulsion of GAG chains, thus resulting in a decrease of 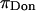toward zero as the NaCl concentration increases toward infinity. From the observation that no significant decrease was measured in π between 1.0 and 2.0 M NaCl (Fig. 4), it is reasonable to conclude, as also reported by Ehrlich et al. (12), that the Donnan charge contribution becomes negligible at these higher concentrations. Thus, the measured osmotic pressure at 2 M, 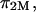is dominated by configurational entropy, i.e., 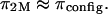However, our experimental results for 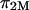(e.g., 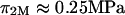at 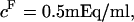25°C), as well as those of Ehrlich et al. ( 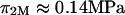at 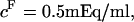4°C), exceed significantly the theoretical estimation of 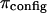in the analysis of Kovach ( 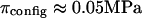at 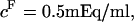25°C) (12,19). This suggests that theoretical models of entropic contributions may be useful for qualitatively interpreting experimental results under hypertonic NaCl conditions, but are not yet sufficiently accurate. In the analyses of Kovach (19) and Ehrlich et al. (12), it was further assumed that 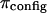is independent of the NaCl bath concentration, so that the electrostatic contribution to osmotic pressure at any NaCl concentration could be estimated from 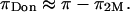In fact, Ehrlich et al. (12) fitted their experimental results of 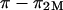to a Poisson-Boltzmann equation using a rod-in-cell model for GAGs, which they used to explain their observed deviations from ideal Donnan law (where the osmotic and activity coefficients are taken to be unity).

The results of the current study also deviate from ideal Donnan law, whether or not 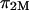is subtracted from π. However, we interpret our results in a different context. Under hypotonic NaCl concentrations when charge-shielding effects are small, the charge-to-charge repulsion of GAG chains in a polymer contribute to stiffening of the molecule, reducing its ability to bend and twist. In contrast, under hypertonic salt concentrations where charge-to-charge repulsion is negligible, the flexibility of the molecule is much greater (22). Consequently, the number of molecular configurations that can be assumed by these GAG chains, and the resulting entropic pressure (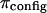), are significantly affected by NaCl concentration, with the implication that 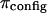decreases with decreasing salt concentration. 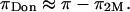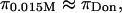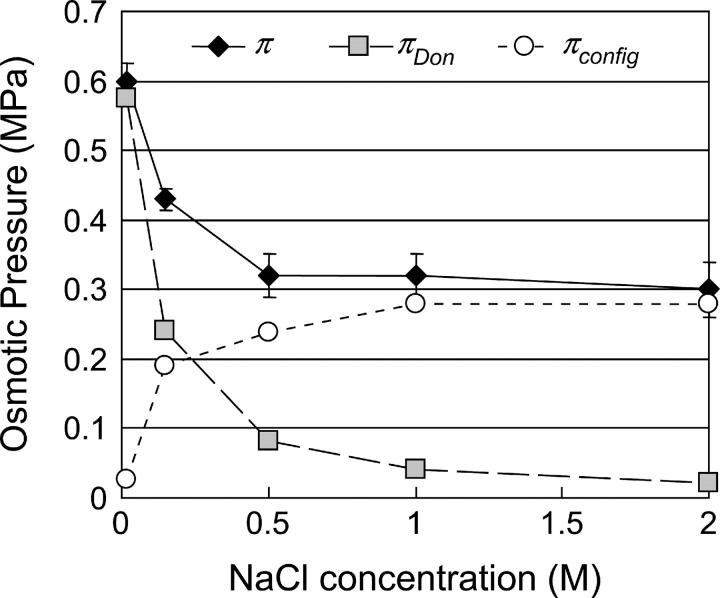This argument implies that the electrostatic contribution to osmotic pressure cannot be estimated reliably from On the contrary, the implication is that the measured osmotic pressure is dominated by electrostatic contributions in the limit of hypotonic conditions, and by configurational entropy under hypertonic conditions, 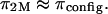A breakdown of our experimental measurements of π versus NaCl concentration into hypothetical contributions from 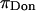and 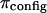is illustrated in Fig. 6, indicating that 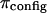is not constant and reflecting our assumption about the limiting conditions under hypertonic and hypotonic salt concentrations.

FIGURE 6.

Osmotic pressure π measured in CS-C solutions of 150 mg/ml, at various NaCl concentrations. The breakdown of 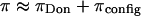into its contributing components is hypothetical and illustrates the possibility that the contribution from configurational entropy decreases with decreasing salt concentration.

We carry this argument one step further, by considering the number of configurations that can be assumed by the GAG chains of proteoglycan molecules in cartilage. Because proteoglycans are constrained within the collagen matrix, they cannot assume as many configurations as in free solution. Hence, we expect the entropic contribution to the osmotic pressure of proteoglycans in situ to be smaller than measured in free solution. To our knowledge, only two studies have attempted to report direct measurements of the osmotic pressure of proteoglycans within articular cartilage (6,15).

In the study by Maroudas and Bannon (6), cartilage samples were equilibrated against PEG solutions of known osmotic pressure, resulting in tissue compression; from the measurement of the proteoglycan fixed charged density in the compressed state a relationship was derived between π and 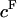in cartilage. This analysis assumed that the compressive stress supported by the cartilage collagen matrix was negligible, to equate the applied PEG osmotic pressure to the osmotic pressure π of the proteoglycans (i.e., 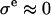in the notation of Eq. 4 so that 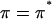under the free-swelling state 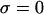). These authors concluded that the osmotic pressure of proteoglycans inside cartilage could be predicted from the osmotic pressure of proteoglycans in solution, as long as the fixed charge density within cartilage was calculated relative to the extrafibrillar water content (because intrafibrillar water is not accessible to the proteoglycans).

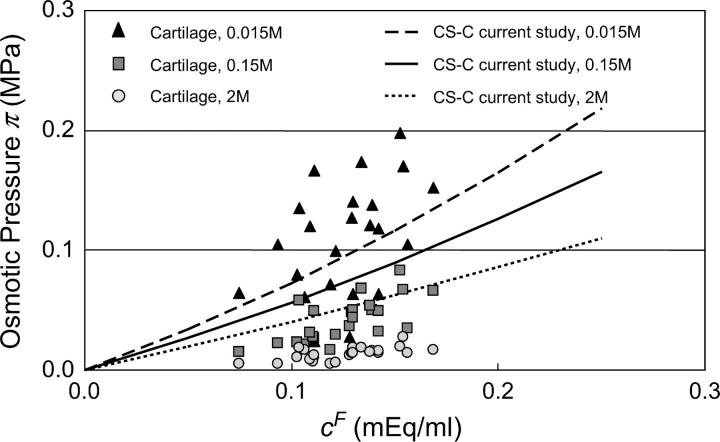
In our recent study (15), mechanical loading was used to estimate the osmotic pressure within cartilage. Using a microscope-mounted loading device and optical strain measurements, the stress-strain response of cubic bovine cartilage specimens was measured at small strain increments, in 0.015, 0.15, and 2 M NaCl. The stress-strain response was found to vary nonlinearly when the applied strain was smaller than the free-swelling strain of the tissue matrix. When the applied strain exceeded the swelling strain the response became linear, suggesting that the collagen matrix was no longer in tension. The osmotic pressure could then be deduced from the magnitude of the applied stress required to overcome the tensile swelling strain; the results from that study are plotted together with the current measurements of CS osmotic pressure at the three salt concentrations (Fig. 7). From these results, it is apparent that the osmotic pressure of proteoglycans inside cartilage is smaller than that of CS in solution at 0.15 and 2 M. These findings support our hypothesis that the constraints imposed by the collagen matrix on the proteoglycan molecules reduce the configurational entropy of the PGs, and that the contribution of configurational entropy to the osmotic pressure of PGs inside cartilage is much smaller than in solution. Therefore, the osmotic pressure of PGs in cartilage is attributed mostly, though not exclusively, to electrostatic interactions. Moreover, the reasonably good agreement between the osmotic pressure of PGs in cartilage and that of CS solutions at 0.015 M NaCl (Fig. 7) further supports our hypothesis that the osmotic pressure of GAGs (and PGs) is dominated by electrostatic interactions under hypotonic salt concentrations (Fig. 6).

FIGURE 7.

Osmotic pressure of proteoglycans in bovine articular cartilage at 25°C, in 0.015, 0.15, and 2 M NaCl from the study of Chahine et al. (15), with comparison to CS solutions from this study.

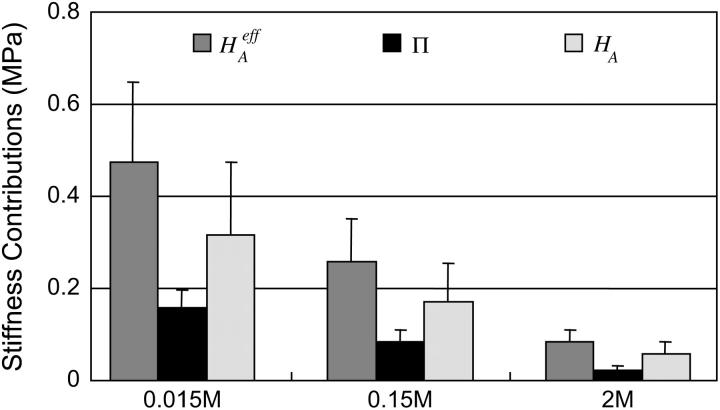
To estimate the contribution of proteoglycan osmotic pressure to the compressive stiffness of cartilage, the quadratic polynomial relation of Eq. 3 is fitted to the in situ measurements of π versus 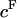from our earlier study on bovine articular cartilage (Fig. 7), producing the virial coefficients shown in Table 2. From these fits, the value of the osmotic modulus, Π, is evaluated using Eq. 7 with 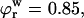based on measurements of water content for these specimens. From experimental measurements of Young's modulus 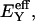and with the assumption that 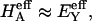the value of 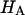is estimated from Eq. 5. Plots of 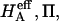and 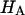at 0.015, 0.15, and 2.0 M NaCl (Fig. 8) demonstrate that all three quantities decrease significantly with increasing salt concentration. The decrease of Π with increasing salt concentration is expected from Donnan theory. However, 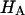has generally been assumed not to depend on salt concentration in previous theoretical analyses (5,10), on the assumption that it represents an intrinsic property of the collagen matrix of cartilage. In fact, in our recent study (10), we showed from theory that the assumption that 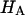is independent of salt concentration implies that the tensile and shear moduli of cartilage are insensitive to changes in the ionic environment of the tissue. However, experimental data suggest that the tensile modulus does indeed vary with salt concentration (11,23) and the shear modulus is very sensitive to the proteoglycan content of cartilage (24). Both of these outcomes are consistent with the current finding that the “intrinsic” modulus 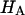is in fact dependent on both the proteoglycan content and NaCl concentration.

TABLE 2.

Virial coefficient (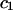 and 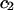) for osmotic pressure of proteoglycans in bovine articular cartilage at equilibrium with NaCl solutions of various concentrations, at 25°C, from fitting the bovine cartilage data of Fig. 7

NaCl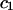
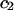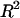0.015 M	0.619 ± 0.46	1.774 ± 3.4	0.209
0.15 M	0.095 ± 0.14	1.855 ± 1.1	0.463
2 M	0.055 ± 0.046	0.417 ± 0.34	0.407

See Eq. 3; π is given in units of MPa and 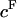in units of mEq/ml; mean ± SE).

FIGURE 8.

Compressive aggregate modulus, 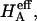of bovine articular cartilage and osmotic modulus (Π, obtained from Eq. 7 using the virial coefficients of Table 2) and intrinsic modulus of the solid matrix ().

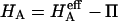A simple explanation for this observation is an extension of our earlier discussion of CS solutions. Proteoglycans exhibit a structural stiffness that derives from two related contributions: first, the intrinsic stiffness of their component atoms and molecules, which occupy a finite volume; and second, the additional stiffness imparted by charge-to-charge repulsion of the GAG chains. This is very well supported by the recent atomic force microscopy studies of aggrecan-aggrecan interactions by Dean et al., who report force-distance relationships in solutions of varying NaCl concentrations (25). 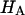is a measure of the combined structural stiffness of proteoglycans and the collagen matrix in which they are enmeshed. As we argued earlier with regard to CS solutions, the stiffness of polymeric GAG chains will increase under hypotonic salt concentrations due to charge-to-charge repulsion, which explains the increase of 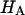with decreasing NaCl concentration.

Of particular interest is the observation that the contribution of Π to 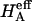(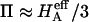) is significantly smaller than that of 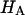(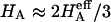) at all concentrations. This means that the structural contribution of the proteoglycan-collagen matrix to the stiffness of cartilage (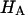) is more significant than the contribution stemming from the change in osmotic pressure with strain (Π). Both mechanisms are directly dependent on the proteoglycan content, which emphasizes the dominant contribution of this macromolecule to the compressive stiffness of cartilage. In fact, a comparison of 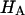at 2 M with 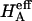at 0.15 M suggests that the contribution of the charge-independent intrinsic structural stiffness of the collagen-proteoglycan matrix to the compressive modulus under physiological conditions is no greater than ∼23%. In a broad sense, this supports the existing dogma in the cartilage literature about the mechanical role of proteoglycans, with a notable distinction: the conventional assumption has been that the stiffness of cartilage contributed by proteoglycans stems exclusively from their osmotic pressure (hence exclusively from Π in our current notation). Yet the results for 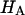and Π presented in Fig. 8, which derive from one of only two studies to have measured π as a function of fixed-charge density in cartilage (Fig. 7), suggest that there are indeed two significant contributions to 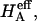both of which depend on proteoglycan content and salt concentration, with the structural contribution dominating ().

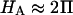There is a conceptual similarity between the current study and that of Eisenberg and Grodzinsky (26) who modeled the confined compression stress in cartilage as 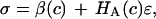where c is the salt concentration and 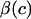is a “chemical stress”. Clearly these authors recognized that the aggregate modulus of cartilage can indeed be a function of salt concentration, and they performed experimental measurements on bovine articular cartilage and corneal stroma from which they deduced the functions 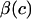and 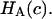In our study, 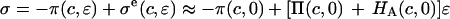to a first-order approximation in the strain (15), which shows that their 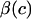is equivalent to the osmotic pressure π at zero strain, 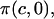and their 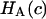is equivalent to our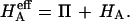

In conclusion, this study finds that the osmotic pressure of CS-C and CS-A solutions measured at 25°C increases with increasing CS concentration and decreasing NaCl ionic bath environment. Above 1 M NaCl the osmotic pressure changes negligibly with further increases in salt concentration, suggesting that Donnan osmotic pressure is negligible above this threshold. The substantial osmotic pressure observed at 1 and 2 M NaCl is attributed to configurational entropy. This entropic pressure is much smaller in articular cartilage than in free solution. Thus, the osmotic pressure in articular cartilage is attributed mostly, though not exclusively, to electrostatic effects. By estimating the rate of change of this pressure with increasing fixed-charge density (and thus increasing compressive strain), osmotic pressure is found to contribute approximately one-third of the compressive modulus of cartilage, with the balance contributed by the intrinsic structural stiffness of the collagen-proteoglycan matrix. Because of the strong dependence of this intrinsic structural modulus on salt concentration, it appears that proteoglycans contribute significantly to its magnitude, in a manner independent of osmotic pressure.