Light-Scattering Studies of Protein Solutions: Role of Hydration in Weak Protein-Protein Interactions

Abstract

We model the hydration contribution to short-range electrostatic/dispersion protein interactions embodied in the osmotic second virial coefficient, B₂, by adopting a quasi-chemical description in which water molecules associated with the protein are identified through explicit molecular dynamics simulations. These water molecules reduce the surface complementarity of highly favorable short-range interactions, and therefore can play an important role in mediating protein-protein interactions. Here we examine this quasi-chemical view of hydration by predicting the interaction part of B₂ and comparing our results with those derived from light-scattering measurements of B₂ for staphylococcal nuclease, lysozyme, and chymotrypsinogen at 25°C as a function of solution pH and ionic strength. We find that short-range protein interactions are influenced by water molecules strongly associated with a relatively small fraction of the protein surface. However, the effect of these strongly associated water molecules on the surface complementarity of short-range protein interactions is significant, and must be taken into account for an accurate description of B₂. We also observe remarkably similar hydration behavior for these proteins despite substantial differences in their three-dimensional structures and spatial charge distributions, suggesting a general characterization of protein hydration.

INTRODUCTION

Early efforts to describe the osmotic second virial coefficient, B₂, for protein solutions involved applications of standard colloidal models with the proteins represented by idealized geometries, such as spheres or ellipsoids (1–4). These models were then fit to experimental data by balancing contributions from electrostatic and dispersion interactions using the relative magnitude of the two contributions as an adjustable parameter. More sophisticated treatments (1,5,6) included permanent and induced dipole moment interactions and charge fluctuation interactions. Despite reasonable quantitative agreement with observed trends in protein solution behavior, the physically unrealistic parameters that were derived by data fitting, such as those for the Hamaker constant, remained worrisome (1–3,6,7). Reasons cited for the unrealistic parameter values included the inherent approximations made in applying simple geometries to represent protein shape, and the inability to account for more complex effects, such as those arising from solvation (8). Nevertheless, characterizations of protein-protein interactions based on simple interaction potentials and idealized geometries have provided the basis for generalized phase diagrams of broad classes of proteins (9,10).

In light of these earlier efforts, it is remarkable that the importance of molecular shape and charge complementarity in governing protein solution thermodynamics was appreciated as early as the 1940, at a time when no protein crystal structures were available (11). Molecular descriptions of protein-protein interactions have, however, received little attention until only recently. Neal et al. (12) used more realistic molecular thermodynamic models of protein solutions in accounting for both protein shape and charge heterogeneity to reveal the decisive role played by highly complementary protein-protein orientations. Specifically, they showed that attractive electrostatics coupled with geometric complementarity could explain the ionic strength-dependence observed in B₂ measurements for chymotrypsinogen solutions as a function of pH. A similar approach was developed by Elcock and McCammon (13), who accounted for protein structure in a more elaborate model for electrostatic interactions to describe the pH-dependence of B₂.

A molecular thermodynamic model of protein solutions in which the configurational complementarity of protein-protein interactions plays a central role naturally leads to a consideration of the molecular nature of protein hydration. The view of hydration obtained from small-angle scattering experiments (14), high resolution crystal structures (15), and molecular simulations (16,17) is of a primary hydration layer around the protein that is ∼3 Å thick and has a density 10–20% higher than bulk water density. A primitive treatment of protein hydration considers the excluded volume effect of this primary hydration layer on protein-protein interactions, which is captured in calculating B₂ by effectively increasing the excluded volume of the protein (18). However, simply accounting for protein shape in estimating the excluded volume contribution to B₂ for globular proteins gives rise to a contribution that is greater than that for the sphere of equivalent volume (19). The magnitude of this difference is roughly equivalent to adding a uniform hydration layer 3 Å thick, which suggests that incorporating a uniform “hydration” layer as an additional excluded volume contribution merely corrects for simplifying the protein geometry. Moreover, surface roughness at the atomic level, in addition to protein shape, can impact the excluded volume contribution to B₂, and therefore, a dense hydration layer of uniform thickness and adjustable scattering length density may also account for the side-chain packing efficiency of amino acids at the protein-water interface (14). A more detailed treatment of protein hydration considers the underlying local hydration structure (20,21). In this view, there is a spatial distribution of hydration sites at the protein-water interface characterized by the interactions of water molecules with the local environment. Averaging local densities at these specific hydration sites over the primary hydration layer gives a density higher than that of bulk water. More importantly, though, a spatially heterogeneous distribution of hydration sites can alter the configurational complementarity of protein-protein interactions in the ensemble of highly favorable configurations that dominate B₂ calculations.

In a recent publication (22), we presented an analysis of osmotic second virial coefficients obtained by light-scattering from protein solutions. Two principal contributions to B₂ were identified: 1), the (ideal) Donnan contribution, which accounts for electroneutrality in a multicomponent solution of (poly)electrolytes; and 2), a contribution due to protein-protein interactions in the limit of infinite dilution. Distinguishing these separate contributions allowed us to model the interaction part of B₂ by molecular computations. In comparing our model predictions with measurements of B₂ for lysozyme, we found that long-range electrostatic interactions dominate the interaction part of B₂ at low ionic strength; however, short-range electrostatic/dispersion interactions with specific hydration are essential for an accurate description of B₂ derived from experiment. Specific hydration is accounted for in the model by adopting a quasi-chemical description in which we consider an ensemble of explicit water molecules that are taken to be strongly associated with the protein. The effect of including specific hydration is to reduce short-range attractive dispersion interactions by attenuating a number of highly complementary protein-protein configurations.

Here, we analyze the role of specific hydration in more detail. The criterion used in our treatment to identify strongly associated water molecules from molecular dynamics simulations is examined, and a more general characterization of hydration behavior for small globular proteins is undertaken in the context of this quasi-chemical description of hydration. We also report new results for B₂ obtained by light-scattering from staphylococcal nuclease solutions, and compare our model predictions for staphylococcal nuclease (SN), lysozyme (LYS), and chymotrypsinogen (CGA) to our experimental data as well as data reported in a previous study (6). An analysis of the interaction part of B₂ reveals differences in the solution thermodynamic behavior for CGA relative to SN and LYS that highlights the importance of evaluating the individual contributions to B₂.

THEORY

In this section, we briefly review our analysis of light-scattering from protein solutions and describe the model for protein-protein interactions as background for developing a thermodynamic treatment of specific hydration. Details of this analysis and the theoretical basis for our model are given elsewhere (22).

The starting point of our analysis is Stockmayer's expression for the turbidity of a solution due solely to the composition fluctuations (23), which requires partial derivatives of chemical potentials with respect to the molar concentrations of the solution components. We consider a solution consisting of a protein component, added salt component, and solvent (water), where a component is defined to be electrically neutral, although each electroneutral component may consist of charged constituents (24). The solvent is denoted by 0, the salt component by 1, and the protein component by 2. For simplicity, the added salt is assumed to be NaCl, and the protein, P, carries a positive charge z. Therefore, the protein component is PCl_z. The concentrations of free HO⁻ and H⁺ ions in solution are taken to be negligible in comparison (compare with Ref. 24). The resulting expression for turbidity, τ, is

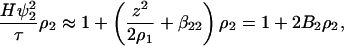(1)

where ρ_i is the molar concentration of component i, ψ₂ = ∂n/∂ρ₂ is the derivative of the refractive index of the solution with respect to the protein concentration, H is an optical constant, and the coefficient B₂ is identified as the osmotic second virial coefficient. The two contributions comprising B₂ are the so-called Donnan term, z²/2ρ₁, and

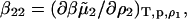(2)

the nonideal contribution due to protein-protein interactions and the target of our molecular modeling efforts. Here 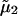is the excess chemical potential of the protein component, and β = 1/kT with kT the thermal energy. In this analysis, we have neglected partial derivatives of 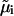with respect to ρ₁, which represent nonideal contributions arising from preferential partitioning of the salt ions in the vicinity of protein molecules that become important at high protein charge and/or high ionic strength (25). Also, for the protein concentrations and ionic strengths considered here ρ₁ ≫ ρ₂, and we have made the physically reasonable assumption that ψ₂ ≫ ψ₁ (24).

We adopt the Debye-Hückel model of protein-protein interactions in the limit of large protein-protein separations, which is taken as the protein surfaces separated by more than a Debye length, or r > (a + κ⁻¹), where a is the nominal diameter of the protein, and κ is given by the usual expression,

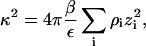(3)

where ε is the solution dielectric constant. In the limit ρ₂ → 0, κ² is proportional to ρ₁, the ionic strength of the solution due to the added salt. Recognizing that the Donnan contribution is recovered from the Debye-Hückel model, we obtain the expression for the long-range contribution to β₂₂,

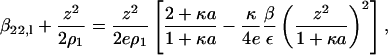(4)

where e is the base of the natural logarithm. The additional subscript l emphasizes that this contribution corresponds to just the long-range part of β₂₂.

For protein-protein interactions at separations between a and (a + κ⁻¹), we express the shape and orientation dependence of the potential of mean force (PMF) between protein molecules in solution explicitly, and write

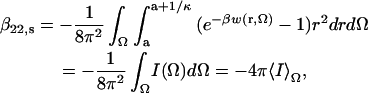(5)

for the short-range contribution to β₂₂. Here Ω is a collective variable for all Euler and polar angles describing the relative orientation of the two protein molecules, and w(r, Ω) is the PMF in that orientation as a function of separation, r. The term I(Ω) represents the contribution to β_22,s of the particular orientation, Ω.

Our final expression for β₂₂ is

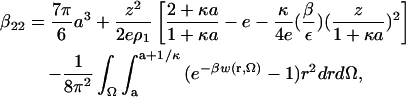(6)

where the first term on the right-hand side is the protein-excluded volume plus an approximation to the small contribution due to the protein-solvent PMF. The electrostatic contributions embodied in w(r, Ω) are calculated using an earlier model (12), as described in Asthagiri et al. (22). Dispersion interactions are modeled using a hybrid Lennard-Jones/Lifshitz-Hamaker approach also described earlier (26). The configurational integral in Eq. 6 is estimated by Monte Carlo sampling of the configurational space (27). A total of 10⁴ configurations were generated for each calculation.

HYDRATION THERMODYNAMICS

Although the hybrid Lennard-Jones/Lifshitz-Hamaker approach captures the essential features of surface complementarity in intermolecular interactions, the effect of strongly associated water molecules is lost. In the quasi-chemical description of hydration (28), it is natural to view these water molecules as part of the protein. The solution thermodynamics is then described in terms of quasi-components comprised of the protein and associated water molecules immersed in a statistical field due to the exterior medium. Here, we identify strongly associated water molecules through explicit molecular dynamics (MD) simulations and retain the statistical description for the remainder.

We implement this quasi-chemical view of hydration as follows. First, a grid is constructed to fill a proximal volume around the protein such that each grid point defines a cubic volume 1 Å on a side. This proximal volume is taken to be within 3.5 Å of the heavy atoms comprising the protein surface. Selected grid points are then identified to represent those water molecules that are strongly associated with the protein. The selection of these grid points depends on the interaction of a water molecule with its local environment at each grid point relative to bulk water, which is expressed in terms of a chemical equilibrium constant for water association with the protein at that grid point, or equivalently,

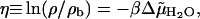(7)

where 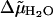is the difference in the excess chemical potential of water at the grid point and in bulk water, and ρ/ρ_b is the corresponding ratio of water densities. Eq. 7 provides the thermodynamic framework for selecting grid points to represent strongly associated water molecules based on MD simulations that supply the required densities. Grid points with η > 0 have, on average, water densities higher than the bulk density, and therefore are identified as locations for water molecules that associate with the protein. Our criterion for strong association is η > 2, which corresponds to a free energy of association that is more favorable than dissolution in bulk water by at least 2 kT. For SN, only 212 out of a total of 11,690 proximal grid points were observed to have η > 2.0. The observed numbers of proximal grid points with η > 2.0 for LYS and CGA were 135 out of 7855 and 267 out of 12,672, respectively. In each case, we assume that all grid points satisfying the criterion η > 2.0 are equivalent in terms of their respective affinities for water molecules, and as such, water molecules are retained at all of them in our model. However, we account for overpopulating the grid points with water molecules by decreasing the TIP3P Lennard-Jones ε-parameter for water molecules placed at these grid points by a factor of 3, which corresponds to the observation that there are roughly three times as many grid points as there are water molecules in the primary hydration layer that satisfy the criterion η > 2.0.

SN coordinates used in the simulation were obtained from the NMR-minimized average structure (29) (PDB ID: 1JOO). The NMR structure was preferred over the crystal structure (PDB ID: 1STN) because the latter has a total of 13 residues missing from loop regions at the C-and N-termini. Differences between the two structures other than these loop regions are minimal considering the thermal motion of the protein in water. The root mean-square deviation between corresponding α-carbons in the NMR and crystal structures is 2.3 Å compared to a root mean-square deviation of 1.7 Å in α-carbon positions computed from MD simulation (30).

SN was solvated by inserting the NMR structure into a cubic box 62 Å on a side containing 8000 TIP3P water molecules (31), and removing water molecules within 4 Å of the heavy atoms of the protein. A total of 6822 water molecules remained in the final system. The protein atoms were held fixed throughout the simulation since the model for β₂₂ is based on a rigid protein structure. The system was initially relaxed by executing 20,000 steps of a steepest-descent minimization cycle. All simulations were carried out at 298 K and 1 bar using NAMD (32) with the CHARMM27 force field (33). The system temperature was held constant by applying the Langevin dynamics method to all nonhydrogen atoms with a damping coefficient of 1 ps⁻¹. The system pressure was maintained using a Nosé-Hoover Langevin piston (34) with a period of 200 fs and a decay of 100 fs. Periodic boundary conditions were imposed and electrostatic interactions were determined using the particle-mesh Ewald method (35) with a real-space cutoff of 12 Å. The same cutoff was used for nonbonded nonelectrostatic interactions. Water geometry was constrained by the SHAKE algorithm (36). Equilibration was carried out for 200 ps, followed by a production run of 2 ns with a time step of 2 fs. Water configurations were saved every 0.1 ps for further analysis.

MATERIALS AND METHODS

Wild-type SN was expressed and purified to ≥98% as determined by SDS-PAGE following the procedure of Shortle and Meeker (37). SN was flash-frozen in liquid nitrogen and stored at −80°C. For each experiment, fresh SN was thawed and centrifuged for at least 30 min to remove any misfolded/denatured protein and aggregates. SN solutions for the static light-scattering (SLS) measurements were prepared by either dialyzing extensively against the desired solution or by successive dilutions using Amicon Ultra Centrifugal Filter Tubes with 5000-MW cutoff (Amicon Plastics, Houston, TX).

NaCl (S9888, Sigma-Aldrich, St. Louis, MO) was used to adjust the ionic strength of the protein solutions. Buffer salts—sodium acetate (3470-01, J.T. Baker, Paris, KY), bis-Tris (156663, Sigma-Aldrich), and Tris (T-1503, Sigma-Aldrich)—were used to stabilize the pH at values of 5.0, 6.5, and 8.0, respectively. The pH was restricted to a maximum value of 8.0 to avoid SN aggregation near its pI (∼10). The solution pH was measured using a Mettler Toledo MP220 pH meter (Mettler-Toledo AB, Stockholm, Sweden) and was adjusted by addition of small quantities of 0.1–0.5 M HCl (9535-33, J.T. Baker) and NaOH (3722-01, J.T. Baker). All SLS samples were prepared with filtered deionized water obtained from a Barnstead NANOpure UV water filter system (Barnstead International, Dubuque, IA). The buffer solutions were filtered with Whatman 20-nm inorganic filters (Whatman PLC, Brentford, UK) and were used to prepare stock solutions of SN at ∼10 mg/ml and various solution conditions. The protein samples were filtered with Amicon Ultrafree MC centrifugal filter devices (Millipore, Billerica, MA) with 100-nm pore size before taking measurements. All glassware was first treated with detergent, stored overnight in HELLMAMEX II alkaline cleaning solution, and then washed thoroughly with filtered and deionized water, shortly before an experiment.

SLS data were collected at an angle of 90° on a Malvern 4700C system (Malvern Instruments, Malvern, Worcestershire, UK) equipped with a Lexel 95 Ar-ion laser (Lexel, Palo Alto, CA) operating at a wavelength of 488 nm, and a Malvern MULTI8 computing correlator (7032 CN). Toluene (TX 0735-6, EMD Chemicals, Gibbstown, NJ) was used as an index matching fluid in the glass container that held the sample cell. This container was also periodically cleaned with isopropyl alcohol during the course of the study to avoid dust affecting the measurements. A NesLab RTE-210 water bath (NesLab Instruments, Portsmouth, NH) was used to control the temperature at 25 ± 0.1°C by circulating water through the metal casing that encloses the glass container assembly. Benzene (HPLC grade; 27079, Sigma-Aldrich) was used as a calibration solvent to obtain the excess Rayleigh ratio of protein solutions.

In the SLS experiment, the Rayleigh ratio, R_θ, rather than turbidity, is usually measured. The Rayleigh ratio is related to the turbidity by R_θ = 3/8π × τ(1 + cos² θ). Also, it is customary to use units of (g/vol) for the protein concentration. In such cases, ρ₂ = c₂/M_w, with c₂ in g/vol and M_w the molecular weight of the protein. With these units, Eq. 1 becomes

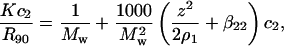(8)

where K = 4π²n²(ψ₂)²/λ⁴N_A is an optical constant, λ is the wavelength of incident light, N_A is Avogadro's number, and R₉₀ is the excess Rayleigh ratio of the protein solution at θ = 90°. A plot of the left side of Eq. 8 as a function of the protein concentration, c₂, gives 1/M_w as the intercept and 2B₂ as the slope, where units of B₂ are mol ml/g². R₉₀ for each sample was calculated by calibration with benzene during an experiment as

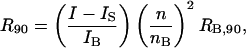(9)

where I, I_S, and I_B are the scattered intensities at 90° for the protein sample, pure solvent, and benzene, respectively. The value n_B is the refractive index of benzene and R_B,90 is the absolute Rayleigh ratio of benzene at 90°, taken to be 38.6 × 10⁻⁶ cm⁻¹ (6,38). A value of ψ₂ = 0.2 ml/g was found to best fit the light-scattering data for SN. This value lies within the narrow range reported for other globular proteins, such as chymotrypsinogen, lysozyme, and bovine serum albumin at λ = 488 nm (6,39). R = R₉₀ is implied in the discussion below.

RESULTS AND DISCUSSION

Light-scattering measurements of B₂

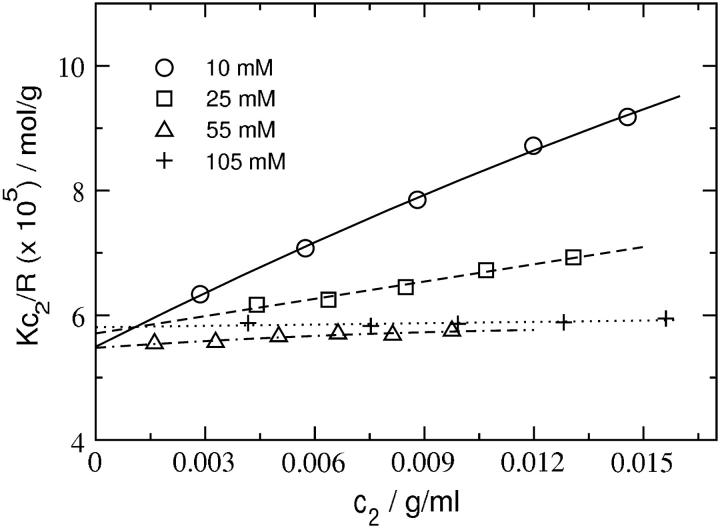
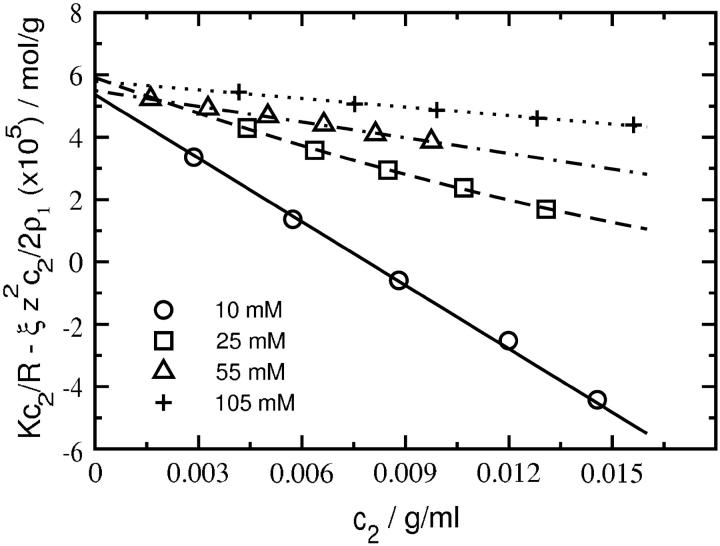
Fig. 1 shows plots of Kc₂/R as a function of SN concentration for several ionic strengths at pH 8.0. The same plots are shown in Fig. 2 with Kc₂/R adjusted for the Donnan contribution, 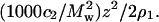The data in Fig. 2 are fit to quadratic functions of c₂ and limiting slopes are obtained by taking the derivative at c₂ = 0. The values of β₂₂ derived from these slopes are given in Table 1. The weight-averaged molecular mass obtained from the intercepts is 17.6 ± 0.4 kDa, which is slightly greater than the molecular mass calculated from the amino-acid sequence of SN, 16.8 kDa. This result indicates the presence of higher molecular weight aggregates of SN in solution. Assuming these aggregates are SN dimers, we estimate ∼4.8% dimers by weight in solution, which is consistent with 1H NMR measurements (40) that find a small fraction of SN in dimers at the protein concentrations studied here. In comparison, our earlier light-scattering measurements for LYS (22) yielded within experimental uncertainties a single intercept corresponding to a molecular weight that was identical to the value calculated based on amino-acid sequence.

FIGURE 1.

SLS plots for staphylococcal nuclease (compare with Eq. 8) at pH 8.0 and various ionic strength conditions. Lines represent quadratic fits to the data.

FIGURE 2.

SLS plots for staphylococcal nuclease at pH 8.0 and various ionic strengths adjusted for the Donnan contribution, 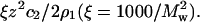The curves are quadratic fits to the data; β₂₂ is obtained from the slope in the limit c₂ = 0.

TABLE 1.

SLS results for staphylococcal nuclease

pH	z	I	2B2	z2/2ρ1	β22
5.0	14	0.010	152.1	347.2	−195.1
5.0		0.030	38.1	115.7	−77.6
5.0		0.060	12.7	57.9	−45.2
5.0		0.110	8.5	31.6	−23.0
6.5	9	0.010	40.4	143.5	−103.1
6.5		0.025	13.7	57.4	−43.7
6.5		0.055	6.6	26.1	−19.5
6.5		0.105	2.1	13.5	−11.7
8.0	7.9	0.010	37.2	110.6	−73.4
8.0		0.025	10.4	44.2	−33.8
8.0		0.055	3.3	20.1	−16.8
8.0		0.105	1.1	10.5	−9.4

B₂ × 10⁴ and the contributing terms are given in units of mol ml/g² as is customary. I is the ionic strength (including buffer) in moles/liter. The value z is the charge carried by SN calculated using intrinsic pK_a values.

Table 1 summarizes the SLS results for SN at all solvent conditions. The values of 2B₂ obtained directly from the limiting slope of Kc₂/R as a function of c₂ match those calculated as the sum of z²/2ρ₁ and β₂₂. Therefore, only the latter values are reported in this table. We observe that B₂ is positive at all values of pH and decreases with ionic strength, consistent with the notion that repulsive electrostatic interactions are progressively screened with increasing ionic strength. We also find that β₂₂ is negative at all values of pH, implying attractive nonideal protein-protein interactions, and becomes progressively less negative with ionic strength. Similar behavior was noted in our earlier light-scattering study of LYS solutions (22). The physical interpretation of this result, i.e.,

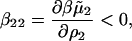(10)

is that adding protein in the limit ρ₂ → 0 increases the ionic strength of the solution, which reduces the free energy of charging the distinguished protein molecule. The effect is to screen the long-range electrostatic interactions that dominate β₂₂ at low ionic strength.

Modeling protein-protein interactions

The results for β₂₂ and the contributing terms for SN are given in Table 2. Calculated values of β₂₂ as a function of solution pH and ionic strength are also compared with those derived from our SLS experiments. We find that the agreement is reasonable and the correct ionic strength dependence is recovered. Moreover, the solution thermodynamic behavior is qualitatively similar to that reported earlier in our light-scattering study of protein-protein interactions in LYS solutions (22). Specifically, β₂₂ is large and negative at low ionic strength and becomes progressively less negative with increasing ionic strength. In addition, the contribution to β₂₂ from β_22,l dominates, particularly at low ionic strength, and as such, determines the ionic strength-dependence of β₂₂. Lastly, the contribution from β_22,s is positive at low ionic strength, but decreases with ionic strength and eventually becomes slightly negative at high ionic strength. These results, combined with those from our earlier study of LYS (22), show the dominance of long-range electrostatic interactions at low ionic strength as well as the importance of short-range electrostatic/dispersion interactions for an accurate description of these protein-protein interactions.

TABLE 2.

Modeling results for staphylococcal nuclease

pH	z	I	β22,s + 7πa3/6	β22,l	β22,calc	β22,exp
5.0	14	0.010	35.5	−263.6	−228.1	−195.1
5.0		0.030	22.7	−88.8	−66.1	−77.6
5.0		0.060	12.0	−43.7	−31.7	−45.1
6.5	9	0.010	24.2	−84.9	−60.7	−103.1
6.5		0.025	10.1	−35.5	−25.4	−43.7
6.5		0.055	0.2	−16.5	−16.3	−19.5
8.0	7.9	0.010	18.6	−62.4	−43.8	−73.4
8.0		0.025	5.9	−26.3	−20.4	−33.8
8.0		0.055	−1.5	−12.3	−13.8	−16.8

β₂₂ × 10⁴ and contributing terms are given in units of mol ml/g². I is the ionic strength (including buffer) in moles/liter. The value z is charge on the protein calculated using intrinsic pK_a values. The sphere diameter for electrostatics calculations, Eq. 5, is 40.0 Å. The contribution from 7πa³/6 is 7.2 × 10⁻⁴ mol ml/g².

Interestingly, our model of protein-protein interactions for CGA solutions at pH 7.0 shows distinctly different behavior. The results for β₂₂ and contributing terms are given in Table 3. Again, comparing the calculated β₂₂ with values derived from experiment, we find reasonable agreement and the correct ionic strength-dependence. In this case, however, the positive Donnan contribution approximately offsets the negative contribution from β_22,l at all ionic strengths, such that β₂₂ is determined predominantly by β_22,s. Moreover, β_22,s is negative at low ionic strength and becomes progressively less negative with increasing ionic strength in contrast to the behavior for LYS and SN. Indeed, we found several CGA-CGA orientations for which local charge effects at contact give rise to short-range attractive electrostatic interactions. It should also be noted that CGA has a net charge of only 4.2 at pH 7.0, approximately half that of LYS or SN at the same pH, which is expected to enhance effects due to its local charge distribution.

TABLE 3.

Modeling results for chymotrypsinogen at pH 7.0 and charge, z = 4.2. β₂₂ × 10⁴ and contributing terms are given in units of mol ml/g²

I	β22,s + 7πa3/6	β22,l	β22,calc	2B2	z2/2ρ1	β22,exp
0.008	−28.5	−8.4	−36.9	−17.6	16.8	−34.4
0.080	−8.3	−1.0	−9.3	−13.4	1.7	−15.1
0.160	−3.1	−0.5	−3.6	−9.4	0.8	−10.2

Experimental data from Velev et al. (6). The sphere diameter for the electrostatics calculations, Eq. 5, is 46.2 Å. The contribution from 7πa³/6 is 3.4 × 10⁻⁴ mol ml/g².

Role of specific hydration

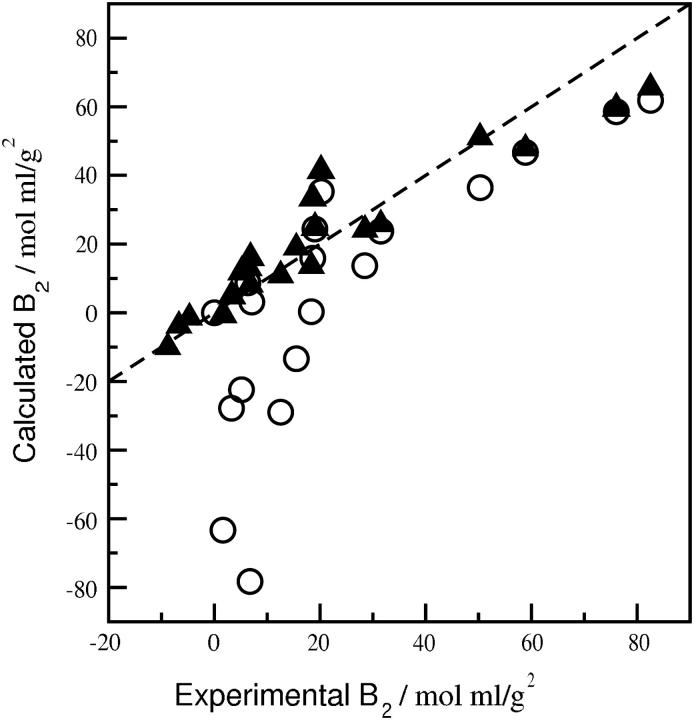
Fig. 3 compares β₂₂ derived from the SLS experiments to values calculated for SN, LYS, and CGA with and without specific hydration, where the same ensemble of configurations was used in both cases. When specific hydration is considered (Fig. 3 A), a linear fit of the data gives a slope ∼1.0 with a correlation coefficient of 0.93 and an intercept near zero. Scatter in the data is noticeably larger, however, when specific hydration is not taken into account (Fig. 3 B); the correlation coefficient in this case is 0.49. The intercept of ∼60 mol ml/g² also indicates that removing strongly associated water molecules produces highly complementary configurations resulting in a large negative β₂₂. The β₂₂ calculations are also more sensitive to specific hydration at high ionic strength, where short-range dispersion interactions become more important. The net effect is to enhance the influence of strongly associated water molecules in altering the steric complementarity of these interactions, which leads to the nonzero intercept in Fig. 3 B. Conversely, the influence of specific hydration on β_22,s is diminished at low ionic strength, where long-range electrostatic repulsion dominates in the β₂₂ calculations. The impact of specific hydration directly on the calculation of osmotic second virial coefficients is shown in Fig. 4, where B₂ for the three proteins calculated with and without specific hydration is compared to experiment. The largest deviations are observed for slightly negative experimental values of B₂, which have significance for protein crystallization (41). In this case, B₂ calculated with specific hydration is in good agreement with experiment, whereas the values calculated without specific hydration are more negative by several orders of magnitude.

FIGURE 3.

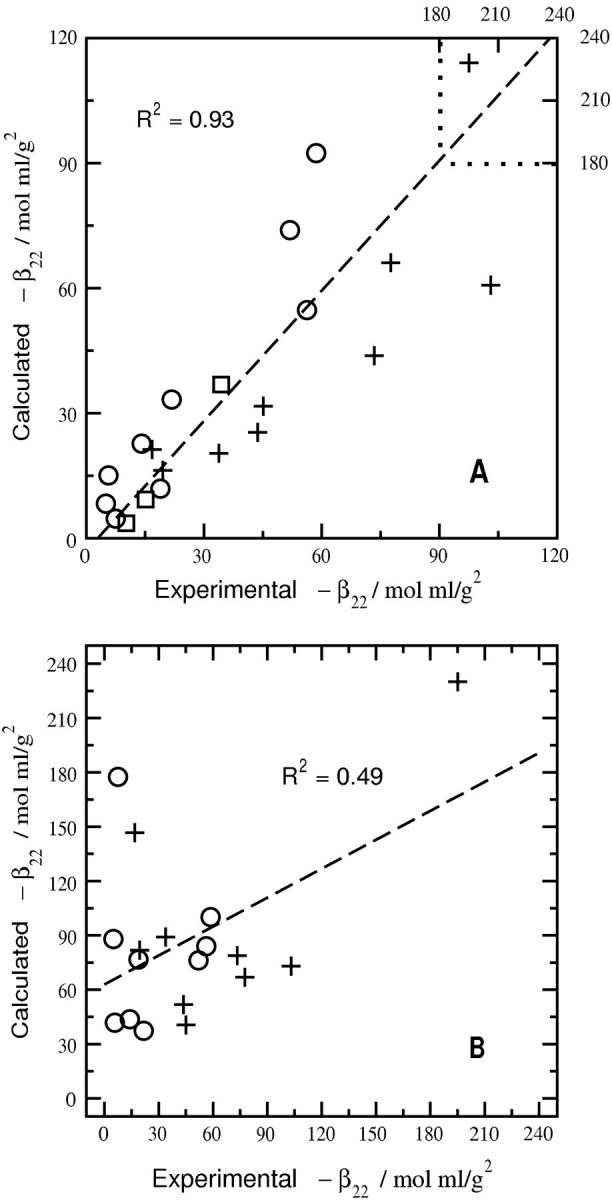
Comparison of experimental and calculated values of β₂₂ for three globular proteins with (A) and without (B) bound waters of hydration. Circles, pluses, and squares represent points for LYS, SN, and CGA, respectively. In B the calculated values of β₂₂ for CGA are on the order of ∼−10³, and therefore, are not shown. The dashed line in A is a linear fit of all the points. The dashed line in B is a linear fit of the points for SN and LYS.

FIGURE 4.

Comparison of experimental and calculated values of B₂ for LYS, SN, and CGA with (solid triangles) and without (open circles) specific hydration. The dashed line is a linear fit of the points with specific hydration and gives a correlation coefficient of 0.94. For experimental values of B₂ less than zero, B₂ calculated without specific hydration is several orders of magnitude more negative than the experimental value, and therefore is not shown.

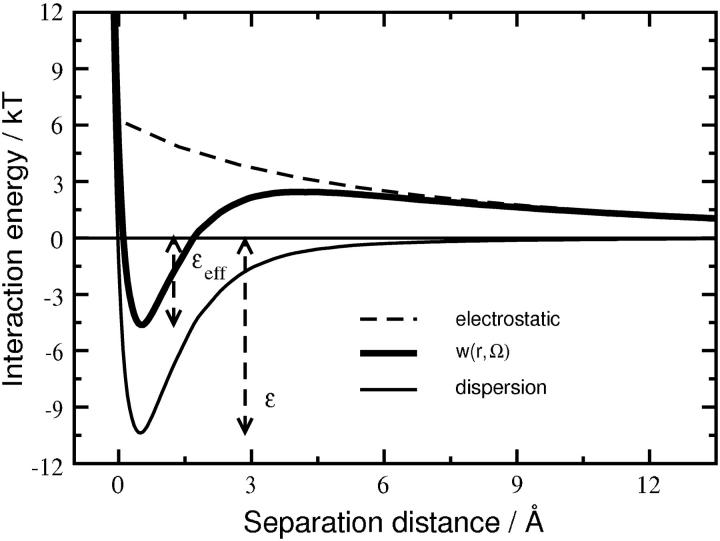
Although both electrostatic and dispersion interactions contribute to the protein-protein PMF used to calculate β_22,s, the distinguishing feature of this PMF is the short-range nature of the dispersion interactions relative to electrostatic interactions. Fig. 5 shows both interactions calculated as a function of separation distance for a pair of SN molecules in a single, representative orientation at pH 8.0 and I = 0.05 M. The dispersion interactions are characterized by an attractive well and a strong repulsion at contact due to the protein-excluded volume. These interactions are clearly short-ranged, and become negligible for separations >∼6 Å. In contrast, electrostatic interactions—repulsive for this specific orientation—are still significant (∼1 kT) at a separation of 13.6 Å or one Debye length. They also vary much more slowly with protein-protein separation, and as a result, simply shift up or down the well-depth for dispersion interactions. We take this shifted or effective well-depth, ε_eff, divided by kT, as a characteristic parameter for describing the short-range interactions embodied in β_22,s.

FIGURE 5.

Typical profile for PMF, w(r, Ω), at pH 8.0 and I = 0.05 M, between a pair of SN molecules in a given orientation, Ω, as a function of separation distance between them. Profiles for dispersion and electrostatic interaction components of the PMF are also shown. Separation distance is normalized to a value of zero where dispersion interaction energy changes sign. The value ε(Ω) is the dispersion interaction-energy well-depth. Note that the range of dispersion interactions is much shorter than that of the electrostatic interactions, and the role of repulsive electrostatic interactions in this orientation is effectively to reduce the short-range well-depth from ε → ε_eff.

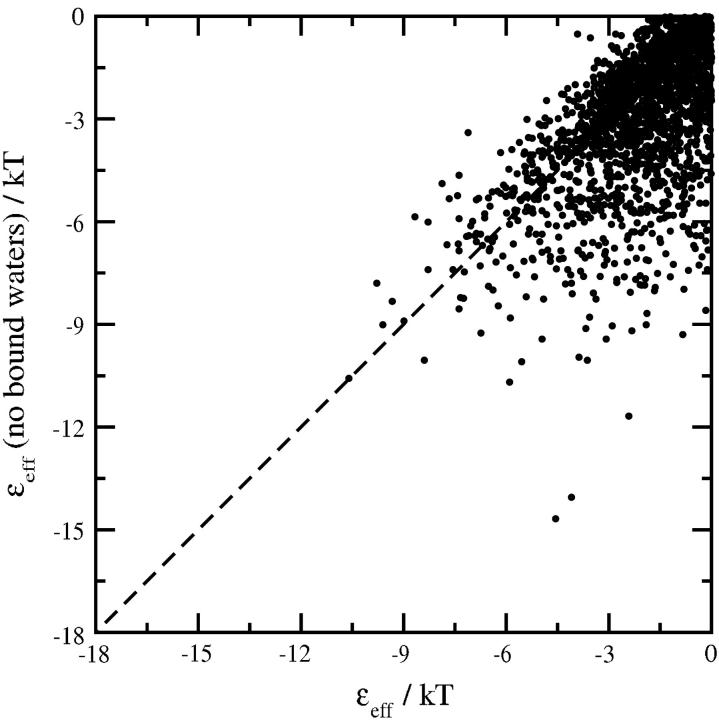
Fig. 6 compares ε_eff/kT calculated with and without specific hydration for the same ensemble of SN-SN orientations. Each point in the figure represents one orientation; only those orientations with ε_eff/kT < 0 are shown. The addition of electrostatic interactions to the dispersion interactions substantially reduces the overall number of favorable protein-protein orientations—i.e., orientations with ε_eff < 0—such that the number of orientations corresponding to short-range repulsion increases substantially at these solution conditions. Nonetheless, there is a clear bias to more shallow (less attractive) well-depths for those orientations with ε_eff < 0 when specific hydration is taken into account. The net effect is to preferentially exclude the most attractive SN-SN orientations from contributing favorably to β_22,s when strongly associated water molecules are considered, which leads to an order-of-magnitude decrease in the negative value of β_22,calc from −146.7 × 10⁻⁴ to −13.8 × 10⁻⁴ mol ml/g², in good agreement with the experimental value of −16.8 × 10⁻⁴ mol ml/g² at pH 8.0 and I = 0.05 M (see Table 2).

FIGURE 6.

Comparison of ε_eff/kT at pH 8.0 and I = 0.05 M for a pair of SN molecules in the same ensemble of protein-protein orientations with and without strongly associated waters of hydration. The calculations were carried out for an ensemble of 10⁴ SN-SN orientations; only those orientations with ε_eff/kT < 0 are shown. The addition of strongly associated waters to SN molecules precludes the most attractive orientations from contributing favorably toward β_22,s, leading to a net increase in β_22,calc from −146.7 × 10⁻⁴ to −13.8 × 10⁻⁴ mol ml/g² (see Table 2).

It should also be noted that the observed discrepancies between the calculated and experimental values of β₂₂ (Fig. 3 B) cannot be resolved by adjusting the protein-excluded volume to account for steric interactions that arise from a dense hydration layer. Although the additional excluded volume makes a positive contribution to β_22,calc, the increase is much too small to improve agreement significantly with the experimental values of β₂₂. For example, a uniform layer of water 3 Å thick around a protein with a nominal diameter of 40 Å increases the excluded volume contribution to β_22,calc from 5 × 10⁻⁴ to only 7.6 × 10⁻⁴ mol ml/g². The impact of this contribution is minimal compared to treating specific hydration in terms of its impact on the steric complementarity of short-range protein-protein interactions.

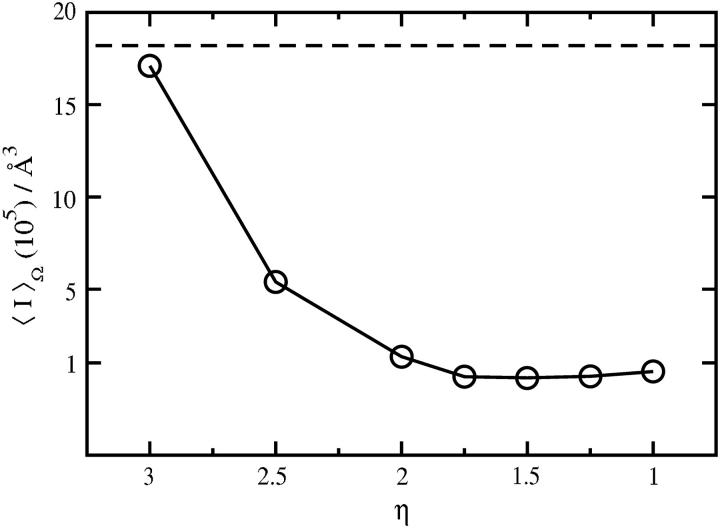
Specific hydration in Fig. 3 is characterized by an ensemble of water molecules that we consider to be strongly associated with these proteins, where the criterion for strong association is η > 2.0. Here we examine the sensitivity of our results to this value of η. Our approach is to calculate β_22,s, or equivalently 〈I〉_Ω in Eq. 5, as a function of η for dispersion interactions alone. The results for SN are shown in Fig. 7. Decreasing η relaxes the criterion for strong association, and thus corresponds to a larger number of water molecules in the ensemble of strongly associated water molecules. Conversely, increasing η reduces the number of strongly associated water molecules, with η ∼3.0 giving 〈I〉_Ω for the protein with no associated waters. Fig. 7 shows that 〈I〉_Ω decreases by an order of magnitude as η is decreased from 3.0 to 2.0, but changes very little for η < 2.0. Thus, η = 2.0 defines a lower bound on the number of water molecules that must be considered to obtain the full effect of water association on short-range interactions. Including a larger number of more weakly associated water molecules in our treatment of specific hydration would have only a minimal effect on the β_22,s calculations.

FIGURE 7.

〈I〉_Ω as a function of η = ln(ρ/ρ_b). The dashed horizontal line represents 〈I〉_Ω obtained using the SN molecule with no waters strongly associated to it.

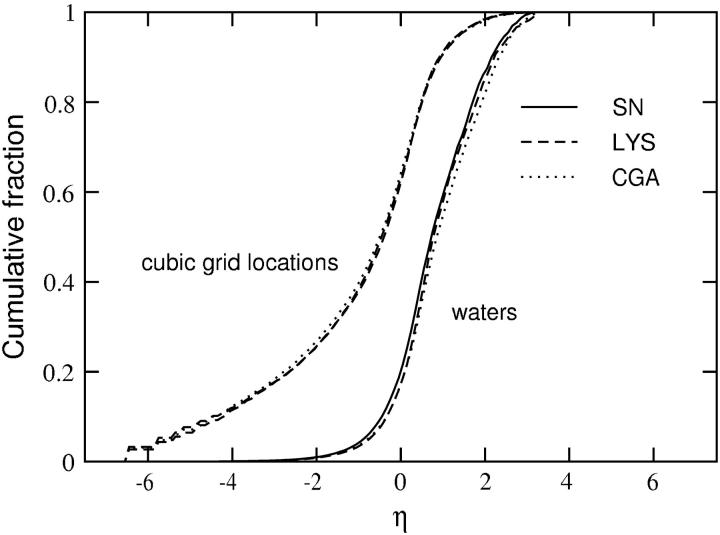
We also calculated the η distributions for water molecules in the first hydration shell of SN, LYS, and CGA, where η for a particular water molecule is defined by η for the nearest grid point. Fig. 8 shows cumulative fractions of both the first-shell water molecules and the grid points as a function of their assigned η-value for all three proteins. Only those grid points actually occupied by a water molecule during the simulation are included. The most striking observation is that these profiles virtually superimpose despite substantial differences in the three-dimensional structures and spatial charge distributions for these proteins. As expected, the more strongly associated water molecules are also more localized. For example, 60% of the first-shell water molecules have η ≤ 1.0 and occupy nearly 90% of the grid points, whereas the remaining 40% of the water molecules with η > 1.0 occupy only ∼10% of the grid points. Moreover, the strongly associated water molecules (η > 2.0), which account for ∼15% of the total number in the first hydration layer, occupy fewer than 2% of the grid points. The remarkable similarity in hydration behavior for these proteins suggests a universal character to protein hydration when described in terms of the η distribution of first-shell water molecules, consistent with the observation that the fractional compositions of nonpolar, polar, and charged surface regions are similar among diverse proteins (21,42). The results in Fig. 7, on the other hand, indicate that short-range protein interactions are influenced by the specific hydration of only a relatively small fraction of the protein surface; evidently, what differentiates the effect of specific hydration on protein-protein interactions is the variation in the spatial distributions of strongly associated water molecules on the surfaces of these proteins.

FIGURE 8.

The cumulative fraction of cubic grid points (dashed) and water molecules (solid) present in the first hydration shell of the protein, as a function of η = ln(ρ/ρ_bulk). Data are shown for three proteins, staphylococcal nuclease (SN), lysozyme (LYS), and chymotrypsinogen (CGA).

CONCLUSIONS

The quasi-chemical description of protein hydration adopted here highlights the important role played by explicit water molecules in mediating weak protein-protein interactions through their local interactions with specific, solvent-accessible regions on the protein surface. Although the thermodynamic affinities that reflect these local interactions have remarkably similar distributions for the three proteins we studied, a key finding of this study is that protein hydration is distinguished by the spatial heterogeneity of strongly associated water molecules on the protein surface and its impact on the surface complementarity of short-range protein-protein interactions. For the three proteins we studied here, strongly associated water molecules identified in molecular dynamics simulations account for ∼15% of the total number of water molecules in the primary hydration layer, they are highly localized, and the effect of including them in calculating the interaction part of B₂ is to reduce short-range attractive dispersion interactions by eliminating a number of highly complementary protein-protein contact configurations. Our results lead to the generalization of a finding made specifically in our previous study of B₂ measured by light-scattering from lysozyme solutions; i.e., this treatment of specific hydration is essential for an accurate description of protein-protein interactions embodied in B₂. In contrast, hydration models that consider an effective excluded volume contribution due to a dense hydration layer around the protein cannot resolve discrepancies between our model predictions and experimental data.

Finally, our analysis of protein-protein interactions for staphylococcal nuclease, lysozyme, and chymotrypsinogen as a function of solution pH and ionic strength indicates that differences in the solution thermodynamic behavior and the correlation between B₂ and short-range electrostatic/dispersion interactions that were found to be unique to chymotrypsinogen at certain solution conditions are based on compensating contributions from the Donnan term and long-range electrostatic interactions. This analysis emphasizes the importance of distinguishing the Donnan contribution to B₂, thereby allowing us to interpret the interaction part of B₂ using molecular computations.