Comparison of the Light-Harvesting Networks of Plant and Cyanobacterial Photosystem I

Abstract

With the availability of structural models for photosystem I (PSI) in cyanobacteria and plants it is possible to compare the excitation transfer networks in this ubiquitous photosystem from two domains of life separated by over one billion years of divergent evolution, thus providing an insight into the physical constraints that shape the networks' evolution. Structure-based modeling methods are used to examine the excitation transfer kinetics of the plant PSI-LHCI supercomplex. For this purpose an effective Hamiltonian is constructed that combines an existing cyanobacterial model for structurally conserved chlorophylls with spectral information for chlorophylls in the Lhca subunits. The plant PSI excitation migration network thus characterized is compared to its cyanobacterial counterpart investigated earlier. In agreement with observations, an average excitation transfer lifetime of ∼49 ps is computed for the plant PSI-LHCI supercomplex with a corresponding quantum yield of 95%. The sensitivity of the results to chlorophyll site energy assignments is discussed. Lhca subunits are efficiently coupled to the PSI core via gap chlorophylls. In contrast to the chlorophylls in the vicinity of the reaction center, previously shown to optimize the quantum yield of the excitation transfer process, the orientational ordering of peripheral chlorophylls does not show such optimality. The finding suggests that after close packing of chlorophylls was achieved, constraints other than efficiency of the overall excitation transfer process precluded further evolution of pigment ordering.

INTRODUCTION

The evolution of a biological network over geological timescales is shaped by its dynamics over timescales of cell growth and physiological function. A hierarchy of physical constraints on the dynamics of a biological network determines its organization and evolution. However, there are two major challenges in relating network organization and function to network evolution. First, accidental events play a major role during evolution. Thus, any model of network evolution has to be stochastic rather than deterministic. Second, empirical data regarding the state of a biological network during different stages of evolution are hard to obtain. In this regard, light-harvesting complexes and their associated excitation transfer networks provide a unique opportunity, where the geometry of a biological network and a detailed quantum mechanical description of its dynamics can be compared for closely related species. In this article, the excitation transfer network of the membrane protein-pigment complex photosystem I (PSI) in plants (Pisum sativum var. Alaska) (1,2) (PDB accession codes 1QZV and 1YO9, respectively) is examined in detail and results are compared to those of earlier studies (3,4) on PSI from cyanobacteria (Synechococcus elongatus) (5) (PDB accession code 1JB0). Since chloroplasts in plants have evolved through endosymbiosis of cyanobacteria over a billion years ago (6,7), the present study constitutes a necessary step in determining the forces that shape the evolution of the excitation transfer network of PSI.

PSI, together with photosystem II (PSII), is one of two major reaction center complexes utilized by oxygenic photosynthetic organisms, such as cyanobacteria, green algae, or higher plants (8–11). PSII uses the electronic excitation energy resulting from absorption of a photon for removing electrons from water, releasing oxygen and H⁺. The electrons removed by PSII are delivered to PSI, which in a subsequent light-driven electron transfer via ferrodoxin and ferrodoxin-NADP-reductase reduces NADP⁺ to NAPDH. During electron transfer an electrochemical gradient is formed across the membrane which is subsequently utilized by the enzyme ATP-Synthase for ATP synthesis. ATP and NADPH are later used for fixing carbon dioxide to produce sugars and all cell compounds. This mechanism, by which incident light energy is stored in progressively more stable forms, is the main source of energy for most of the biosphere (12,13).

PSI consists of a reaction center and electron transfer chain surrounded by a pigment antenna array held together by a protein scaffold (see Figs. 1 and 2). Recently solved crystal structures for PSI in cyanobacteria (5) as well as higher plants (1) provide insight into the geometry and function of the respective pigment networks, thus permitting a comparison between these two related domains of life. The two pigment networks are compared in Fig. 1. The chlorophyll a binding core of PSI complexes from cyanobacteria and plants are seen to display great structural similarity, with differences appearing mostly in outlying protein subunits. Specifically, the PSI subunits PsaG and PsaH are present only in plants but not in cyanobacteria, whereas the subunits PsaX and PsaM are found only in cyanobacteria but not in plants. Furthermore, subunit PsaL displays important structural differences between plants and cyanobacteria.

FIGURE 1.

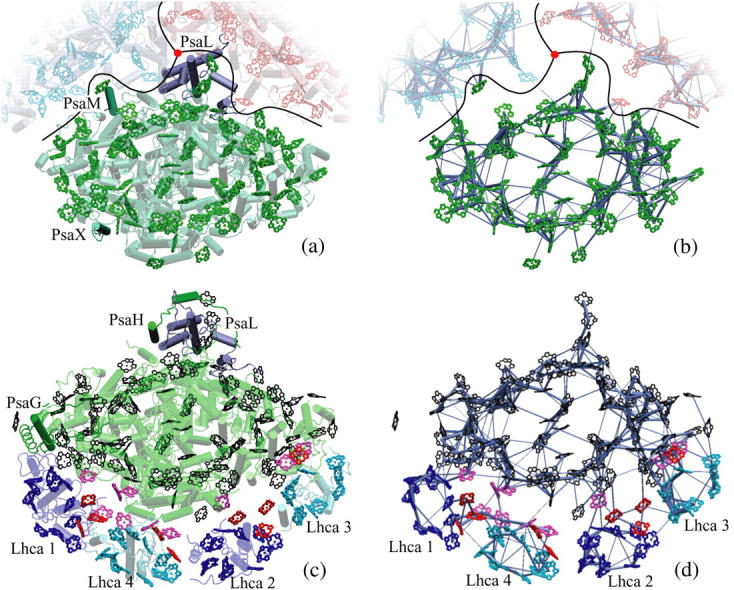
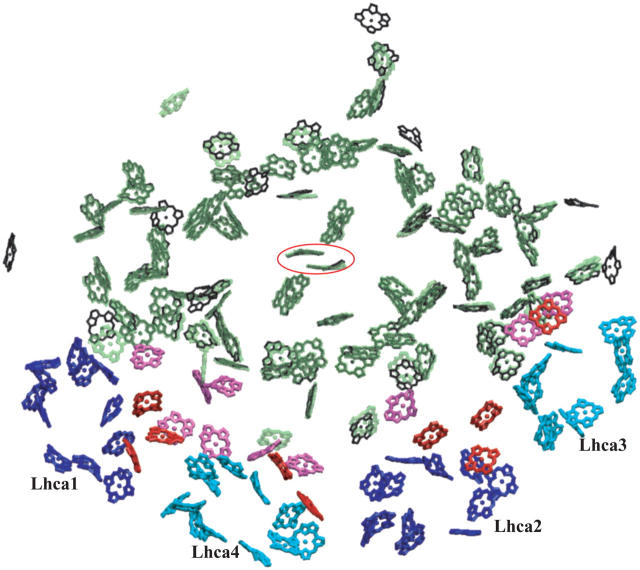
Comparison of cyanobacterial and plant PSI structures and corresponding excitation transfer networks. (a) Top view of cyanobacterial PSI (5). The relative positions of two additional PSI monomers (in blue and red) in a trimer as well as the trimer axis (red disk) are indicated. Subunits PsaM and PsaX, which are unique to cyanobacteria, and the subunit PsaL, located near the trimer axis, are highlighted. (b) Excitation transfer pathways in the chlorophyll network of cyanobacterial PSI. The thickness of a bond between two pigments is proportional to log(t) + c, where c is a constant and t is the transfer rate between pigments. The highest of the forward and backward transfer rates is chosen. A lower cutoff of 0.22 ps⁻¹ is introduced on transfer rates for displaying only the strongest connections. (c) Top view of the plant PSI-LHCI supercomplex (1,2). Subunits PsaG and PsaH, which are unique to plants, are highlighted, along with subunit PsaL. Lhca subunits and their associated chlorophylls are represented in blue (Lhca 1 and 2) and cyan (Lhca 3 and 4). (See Fig. 2 for the labeling of various chlorophyll groups for plant PSI.) Determination of chlorophyll orientations is explained in detail in Jolley et al. (2). (d) Excitation transfer pathways in the chlorophyll network of the plant PSI-LHCI supercomplex. The same cutoff as the one in b is used for comparison. The network shown corresponds to the model in column C of Table 1. (Figure made with VMD; see (77).)

FIGURE 2.

Chlorophyll clusters of PSI. (Green, transparent) cyanobacterial PSI chlorophylls; (black) plant PSI core chlorophylls; and (pink) plant PSI “gap chlorophylls” situated between core chlorophylls and Lhca chlorophylls. (Blue and cyan) Chlorophylls associated with plant Lhca subunits 1, 4, 2, and 3, alternatingly; and (red) plant Lhca “linker chlorophylls” (see (1) for a detailed discussion of plant PSI-LHCI chlorophyll clusters). Eighty-one of the original 96 chlorophylls in cyanobacterial photosystem I have a corresponding chromophore in the plant system located within 1 Å. The special pair chlorophylls, where charge separation is initiated, are indicated by a surrounding red ellipse. For simplicity chlorophylls are represented only by their chlorine rings. Some Lhca chlorophylls are shown as porphyrins since their orientations were not determined unambiguously in the structural model (2). (Figure made with VMD; see (77).)

These differences in outer subunits facilitate two major variations in terms of the supramolecular organization of the PSI complex in cyanobacteria and plants. First, PSI in cyanobacteria is known to form trimers under certain physiological conditions, whereas plant PSI is never observed in a trimeric form (4,14,15). The subunits PsaM and PsaL are responsible for trimer formation and stabilization in cyanobacteria (5). The absence of the PsaM subunit, the structural changes of the PsaL subunit, and the presence of the PsaH subunit prevents trimer formation in plant PSI. As a second major organizational difference between cyanobacteria and plants, plant PSI typically forms a supercomplex consisting of the core complex and an external antenna array comprised of four peripheral chlorophyll a/b binding LHCI complexes (1,16), named Lhca1-Lhca4 after their encoding genes. The PsaG subunit found in plant PSI provides an anchoring point for Lhca subunits as seen in Fig. 1. The attachment of peripheral light-harvesting complexes to PSI is dynamic as plants and algae contain up to nine different genes for Lhca proteins. For example, the presence of a new type of Lhca subunit, Lhca5, that might replace Lhca4 in high light conditions, was recently reported (17,18).

A further difference in the supramolecular organization of the PSI complex between plants and cyanobacteria is revealed under iron-stress conditions, where cyanobacteria develop a ring of iron-stress induced (isiA) subunits surrounding a trimeric PSI core, nearly doubling the light-harvesting cross-section of the core complex (19–22). No isiA rings are found to be associated with plants or algae. There is a superficial similarity between the way Lhca subunits accompany a PSI core in plants and algae and the presence of isiA rings around cyanobacterial PSI. However, the coupling of the PSI core to Lhca subunits was reported to be weaker in algae than the coupling to the isiA ring in cyanobacteria (23,24).

One means by which the plant photosynthetic apparatus adapts to changing light conditions is the mechanism of state transitions (25–27). When excess light energy is delivered preferentially to PSI, more LHCII external antenna complexes associate with PSII, directing more energy to it. This is known as state I. Conversely, in state II, PSII receives more light energy and consequently more LHCI and even LHCII antenna complexes associate with PSI to balance the energy distribution. Therefore, PSI in state II has significantly more chlorophylls associated with it than in state I. The exact composition of Lhca subunits accompanying plant PSI probably depends on growth conditions (16). The crystal structure (1) (1QZV) and the atomic structural model (2) (1YO9) for plant PSI used in the present study represent the state I form of PSI.

PSI shares structural similarities also with PSII (28,29) suggesting a common evolutionary origin (7). However, the center of the PSII core is more devoid of pigments than PSI, probably as a protective measure against the high oxidative potential of PSII and the process of photodamage, resulting in a lower quantum yield in PSII as compared to PSI.

It was suggested that the evolution of PSI was initiated over 3.5 billion years ago through the formation of a homodimeric reaction center that later evolved into a heterodimeric reaction center via gene duplication, which became a precursor to PSI (7,30). The differences in organization of PSI complexes in plants, cyanobacteria, and algae should reflect the habitat these species have evolved in. It is likely that the common ancestor to both plant and cyanobacterial PSI was a monomeric PSI with fully developed core antenna without PsaM, PsaX, or any of the plant specific subunits present, and without any accompanying peripheral antenna complexes. Trimeric PSI is likely a new invention of cyanobacteria to adapt to lower light intensities at a time when cyanobacteria had to compete with plants and algae for light (7,9). Later, plants have developed the LHCI and LHCII complexes and cyanobacteria have then developed the phycobilisome antenna, which allows them to capture green light for both photosystems and gives them an advantage over the plants. The purple bacterial light-harvesting apparatus was suggested to be an ancestor of most photosynthetic systems (31), but the evidence is not conclusive (32).

Structural information on PSI, in particular information on the geometry of the chlorophyll array, permits the construction of microscopic models for the excitation transfer network (3,4,33–39). Once the location and orientation of pigments are determined, excitation transfer rates between pigments are described well by Förster theory (40–42). An alternative description relevant for strong couplings and fast timescales is given by Redfield theory (43,44).

The excitation transfer pathways along the pigment antenna array of a light-harvesting complex naturally define a network, where the nodes are given by the pigments, P_i, and the edges are characterized by the excitation transfer rates, T_ij, between pigments P_i and P_j. The size for such an excitation transfer network can range from hundreds of pigments for PSI in plants or cyanobacteria to thousands for a comprehensive model for the purple bacterial photosynthetic unit consisting of dozens of pigment-protein complexes (45–49). The transfer rate matrix with elements T_ij, in general, is not symmetric. It is also uniformly nonzero, though the T_ij values decrease rapidly with increasing distance between pigments. It is natural to visualize an excitation migration network with a cutoff on excitation transfer rates as done for cyanobacterial and plant PSI in Fig. 1, b and d, respectively.

A wide variety of complex networks can be found among biological systems (50). Unlike, for example, a protein-protein interaction network, the topology of an excitation transfer network bears the implications of a spatial structure in three dimensions and is not described well by the tools of random graph theory or scale-free networks. In general, topology of excitation transfer networks and the constraints that shape their evolution has not been studied at the same level of methodological detail as for other complex biological networks. However, the excitation transfer network of a light-harvesting complex for which an atomic structural model exists can be modeled in microscopic detail rarely enjoyed by other networks in biology. This permits not only the computation of the relevant kinetic parameters such as average excitation lifetime and overall quantum efficiency to a reasonable accuracy, but also the construction of stochastic models with which robustness (error tolerance) and optimality (high relative fitness) of the network can be probed computationally by comparing a given pigment network geometry with alternative geometries (3,4,38,39,51,52).

A detailed model for the evolution of an excitation transfer network might be rather elusive, but PSI provides a unique opportunity in the form of the availability of structures from two structurally closely related, yet evolutionarily distant species. The detailed description of the excitation transfer process in plant PSI presented below is derived from a computational atomic model of plant PSI (2), which, in turn, is based on the 4.4 Å crystal structure of the PSI-LHCI supercomplex (1). This structural model utilizes the 2.5 Å cyanobacterial PSI structure (5) for side-chain identification in the conserved subunits as well as the 2.72 Å LHCII structure (53) for insight into the structure of LHCI subunits, revealing the orientations of chlorophylls. A comparison of the light-harvesting functions in plant and cyanobacterial PSI complexes is presented below based on the respective structures.

The organization of this article is as follows. The next section introduces for the description of excitation migration a hybrid effective Hamiltonian for plant PSI that is based on a detailed cyanobacterial model and on new structural data for plant PSI. The resulting excitation transfer kinetics in plant PSI is compared to the kinetics established earlier for cyanobacterial PSI. The light-harvesting role and interconnectivity of Lhca subunits as well as the role of gap and linker chlorophylls in facilitating connectivity is investigated. The question of the optimality of the pigment network geometry is discussed in the context of the non-conserved chlorophylls found only in plant PSI. The last section contains our concluding remarks.

MODEL

A model for light-harvesting networks can be formulated concisely in terms of an effective Hamiltonian with diagonal elements denoting the Q_y excitation energies of individual chlorophylls (site energies) and off-diagonal elements denoting electronic couplings between chlorophylls. In the following we define first the plant PSI Hamiltonian in relation to the architecture of cyanobacterial PSI. The precise site energies, in principle, are unknown and could pose a problem were it not for the fact that the proper function of the light-harvesting network requires a high degree of insensitivity to actual site energy values as demanded by the robustness of the system under the effects of thermal disorder. This issue and the ensuing choices of site energies adopted in this study are discussed next. Finally, we provide a brief summary of the equations that permit one to calculate lifetime and quantum yield from the effective Hamiltonian.

Hybrid effective Hamiltonian for the PSI-LHCI supercomplex

In this section, an effective Hamiltonian for the chlorophyll network of the plant PSI-LHCI supercomplex is constructed to model the excitation transfer dynamics. The atomic structural model (2) for the plant PSI-LHCI supercomplex is used for this purpose. A similar effective Hamiltonian for cyanobacterial PSI reported previously (3,4) was shown to satisfactorily reproduce the observed excitation transfer kinetics (10,11) (see Table 1). The aforementioned cyanobacterial effective Hamiltonian used full Coulomb couplings between chlorophyll pairs, taking into account higher multipole contributions, as well as utilizing chlorophyll site energies reported in Damjanović et al. (38).

TABLE 1.

Average excitation lifetime and quantum yield for various models

	Cyanobacterial PSI		Plant PSI-LHCI supercomplex
Model	A*	B†	C‡	D§	E¶	F‖	G**
τ (ps)	31.9	32.7	49.4	51.1	51.7	52.0	60.0
Quantum yield	0.968	0.967	0.950	0.983	0.995	0.948	0.939

^*A, Monomeric cyanobacterial PSI described by an effective Hamiltonian with full Coulomb couplings for chlorophyll interactions (4).

^†B, Monomeric cyanobacterial PSI with a hybrid effective Hamiltonian (see text).

^‡C, Plant PSI with a hybrid effective Hamiltonian with spectroscopically derived site energies for Lhca chlorophylls (see Table 2). Column C values corresponding to the refined hybrid effective Hamiltonian discussed in the text are highlighted.

^§D, Same as C, but with a dissipation rate k_diss = (3 ns)⁻¹. (Models A, B, C, F, and G all employ a uniform dissipation rate of k_diss = (1 ns)⁻¹.)

^¶E, Same as C, but with k_diss = (10 ns)⁻¹.

^‖F, Plant PSI with a hybrid effective Hamiltonian with a uniform site energy assignment of 678.8 nm (same as PSI core average) for all non-conserved chlorophylls, including gap, Lhca, and linker chlorophylls.

^**G, Plant PSI with a hybrid effective Hamiltonian with a random distribution of site energies for non-conserved chlorophylls (ensemble average over 400 configurations).

Following Şener et al. (3,4) and Hu et al. (54), an effective Hamiltonian for the PSI chlorophyll network using chlorophyll Q_y-excited states as a basis set is formally defined through

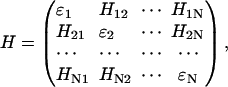(1)

where N = 96 for monomeric cyanobacterial PSI (5) and N = 167 for the plant PSI-LHCI supercomplex (1,2) investigated here. The diagonal elements ε_i are the chlorophyll site energies, and off-diagonal elements H_ij denote the couplings between chlorophylls.

A challenge in the construction of an effective Hamiltonian for plant PSI is the lack of needed resolution in the available structure data for an accurate computation of site energies ε_i as was performed for the cyanobacterial system (38). Since the geometry of the core chlorophyll network is highly conserved between cyanobacteria and plants, one can utilize information available for the cyanobacterial system in the construction of an effective Hamiltonian for plants. A total of 81 of the 96 original chlorophylls in cyanobacterial PSI have corresponding chromophores within 1 Å in the plant PSI structure (see Fig. 2), which, henceforth, shall be denoted “conserved chlorophylls”. With the currently available resolution it is not possible to compute chlorophyll site energies from first principles for plant PSI. However, the atomic model (2) shows that the immediate surroundings of the conserved chlorophylls (such as the ligand to the central Mg²⁺ ion of the chlorine ring system) are well conserved. Therefore, the reported site energies (38) for the cyanobacterial structure will be used below for conserved chlorophylls in the plant structure. It must be kept in mind that these site energy assignments are tentative since a higher resolution structure is needed for a more accurate determination of site energies. Assignment of site energies for non-conserved chlorophylls is discussed in the next subsection. The effect of alternative site energy assignments on excitation transfer kinetics will also be discussed below.

It was shown earlier (3,38) that a lack of accurate site energy data precludes a satisfactory description of excitation migration at low temperature due to the inability to correctly account for spectral resonance between neighboring pigments. However, at room temperature thermal broadening of pigment lineshapes makes it possible to maintain spectral overlap between chlorophylls, thus making it possible for even rudimentary site energy assignments based on spectral observations to account for a satisfactory approximation of global excitation transfer dynamics. This is because the dispersion of site energies, as determined by quantum chemistry computations (38), is seen to be comparable in magnitude to the fluctuations of site energies under thermal disorder (3,55). The robustness of the pigment network, necessary for proper resonant excitation transfer under thermal fluctuations, requires the network to function without fine tuning of chlorophyll site energies.

A notable characteristic of PSI complexes that a detailed effective Hamiltonian formulation is expected to account for is the presence of so-called red chlorophyll forms, which absorb at wavelengths longer than the primary electron donor. It was suggested that red chlorophylls not only extend the total absorption profile of the light-harvesting complex, but also have a considerable effect on excitation transfer kinetics (24,36,56,57). The plant PSI-LHCI supercomplex has two red chlorophyll pools, one associated with the core, as found in cyanobacteria, and another one associated with Lhca subunits (57). Earlier studies of cyanobacterial PSI revealed that even with a higher resolution structure enabling a first principles computation of chlorophyll site energies, it is not possible to accurately account for the nature of the red chlorophyll band (38). This problem remains relevant for the plant PSI-LHCI supercomplex as well, where even less is known about chlorophyll site energies. Thus, the true nature of red chlorophylls and their spatial assignments remain a limiting factor for the quality of any excitation transfer model for PSI in any species.

Once a given set of site energy assignments is decided upon, a hybrid effective Hamiltonian for the plant PSI-LHCI supercomplex can be constructed by taking a subblock of the monomeric cyanobacterial Hamiltonian (4) corresponding to conserved chlorophylls and combining it with couplings involving non-conserved chlorophylls computed in the transition dipole-transition dipole approximation. In plant PSI, non-conserved chlorophylls include all gap, Lhca, and linker chlorophylls. Thus, the effective Hamiltonian in Eq. 1 can be formally written in a hybrid form as

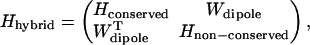(2)

where H_conserved is an 81 × 81 matrix corresponding to the conserved block in the cyanobacterial Hamiltonian and W_dipole as well as the off-diagonal entries of H_{non-conserved} are couplings involving non-conserved chlorophylls, which are computed in the dipolar approximation according to the expression

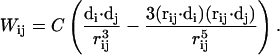(3)

Here d_i denotes the unit vector along the Q_y transition-dipole moment of chlorophyll i as given by the vector connecting the N_B and N_D atoms on the chlorine ring of the chlorophyll, and C = 116,000 ų cm⁻¹ is chosen uniformly for all chlorophyll pairs. All off-diagonal elements of H_conserved in Eq. 2 are computed in a full-Coulomb model that includes higher multipole contributions as outlined in the Appendix of Şener et al. (3).

Site energy assignments for chlorophylls

In the present model the site energies for the conserved chlorophylls are taken from the corresponding assignments in their cyanobacterial counterparts (38). Since these values were determined up to an arbitrary vertical offset, their average has been set to 678.8 nm to correctly reproduce the average of the absorption spectrum for the plant PSI core (in the following, site energies are denoted by their corresponding wavelengths).

Spectral information about the PSI-LHCI supercomplex can be used to refine site energy assignments for non-conserved chlorophylls beyond just the assignment of a uniform value. However, caution must be exercised, since an attempt to assign all chlorophyll site energies based on spectral information alone is difficult (37,38). Therefore we limit the extent of spectra-based assignments to uniform values for specific chlorophyll pools, but monitor the sensitivity of the resulting model to the assignment.

Various site energy assignments for non-conserved chlorophylls with increasing levels of sophistication were examined in this study (see Table 1). The simplest such model is one in which all non-conserved chlorophylls—including all Lhca, linker, and gap chlorophylls (see Fig. 2)—are assigned the same uniform value. This model contains only a single parameter for describing non-conserved chlorophyll site energies, namely the average of the PSI-LHCI spectrum (see Column F in Table 1). A slightly more involved model assumes an ensemble of randomly generated site energies for non-conserved chlorophylls. These random site energy assignments are taken from a Gaussian distribution that approximates the computed cyanobacterial site energy values (38). Therefore, the random site energy model contains two parameters describing the center and the width of the site energy distribution. Excitation transfer kinetics of the random site energy model need to be evaluated in the form of an ensemble average (see Column G in Table 1). Finally, we consider a model that utilizes currently available structural and spectral information about Lhca subunits for assigning different site energies to various chlorophyll pools according to their type (a or b). Since chlorophyll a/b assignments are not known in detail, this model is to be regarded as tentative (see Column C in Table 1 and Table 2). This last model is explained in detail in the remainder of this section. The comparison of average excitation lifetimes and quantum yields (defined in the next subsection) for these models is presented in Table 1, together with similar results for cyanobacterial PSI.

TABLE 2.

Tentative site energy assignments for Lhca chlorophylls

	Chlorophyll a	Chlorophyll b	Tentative chlorophyll b sites
Lhca1	677.6	646.5	1017, 1026, 1031
Lhca2	678.6	646.9	1017, 1021, 1026, 1031, 1033
Lhca3	676.4	647.3	1031, 1032, 1033
Lhca4	676.2	646.9	1017, 1021, 1026, 1031, 1032, 1033
PSI core avg.	678.8	—	—

Energies are reported in corresponding wavelengths in nm. A uniform site energy value as stated in the table was assigned to all chlorophylls of a given type (a or b) within a given chain (i.e., Lhca1, Lhca2, Lhca3, and Lhca4), including the associated linker chlorophylls, with the exception of four specific chlorophylls; chlorophylls 1015 and 1025 in chains 3 and 4 are assigned a site energy of 695 nm rather than the stated uniform value for the other chlorophyll a units of the same chains. All Lhca chlorophylls are assumed to be chlorophyll a with the exception of the ones denoted in the table to be tentatively assigned to be chlorophyll b (see text). As a point of reference, the average site energy value for PSI core chlorophylls taken from the cyanobacterial model (38) is set to 678.8 nm. The site energy for non-conserved chlorophylls of the PSI core, including the gap chlorophylls, is also set to this uniform value. The values in this table were used for the results in Column C of Table 1.

The spectra-based site energy assignment used in this study is based mainly on mutation analysis studies (58–60). The chlorophyll a and chlorophyll b pools in Lhca subunits are tentatively identified based on a comparison with the LHCII structure (53). All chlorophylls of the same type (a or b) within a given Lhca subunit are assigned the same energy value, except four specific chlorophylls in Lhca3 and Lhca4 subunits, which are considered to be red forms. The linker chlorophylls (see Fig. 2), which provide connections between individual Lhca subunits and have no counterparts in LHCII, were considered of chlorophyll b type. The reason for this assignment is that the Lhca1-Lhca4 heterodimer coordinates more chlorophyll b than the monomers Lhca1 and Lhca4 do (61), and that the native preparation of LHCI coordinates less chlorophyll b than expected, i.e., some of the linker chlorophylls might have been lost during purification (62). The site energies for the chlorophylls in the Lhca complexes and in the PSI core were chosen as the first-order central moment of the room temperature absorption spectrum of the individual complexes. The chlorophyll a average site energy was placed in the 660–750-nm region and the chlorophyll b average site energy in the 630–660-nm region. The resulting site energy assignments and chlorophyll a/b occupancies for Lhca subunits are shown in Table 2.

It had been demonstrated previously that the red forms in both Lhca3 and Lhca4 originate from an excitonic interaction involving chlorophyll a's at sites 1015 and 1025. The low energy absorption band of the system was found at 708 nm and the high energy band at 683 nm. The two chlorophyll a's were suggested to be isoenergetic (60,63). On this basis, a site energy value of 695 nm for these two chlorophylls is employed in the present model. This value already contains the contribution of the displacement energy (12), which cannot be separately calculated in the context of the current model.

Unfortunately, much less is known about the spectral characteristics of the non-conserved chlorophylls that are not part of the Lhca band. These most notably include the so-called gap chlorophylls that provide a connection between the Lhca subunits and the PSI core having no counterparts in cyanobacterial PSI (see Fig. 2). Due to this lack of information, all PSI core associated non-conserved chlorophylls, including the gap chlorophylls, are assigned the same uniform site energy value of 678.8 nm—namely, the average of the PSI core.

From the effective Hamiltonian to excitation transfer dynamics

In this subsection, the hybrid effective Hamiltonian in Eq. 2 is used to describe the excitation transfer dynamics for plant PSI. In the case of excitation transfer in cyanobacterial PSI reported earlier (3,4), such description yielded an average excitation lifetime of ∼30 ps (see column A of Table 1), in good agreement with observed lifetimes of 20–40 ps (10,11). A summary of the theory of excitation transfer is presented below, with the reader being referred to earlier reports (3,4) for a more detailed account of the methodology used.

The transfer rate T_ij between pigments P_i and P_j, i ≠ j, according to Förster theory (3,4,40–42), is expressed in terms of the elements H_ij, ε_i, and ε_j of the Hamiltonian in Eq. 1,

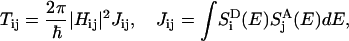(4)

where J_ij is a spectral overlap between donor emission spectrum 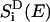and acceptor absorption spectrum 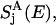approximated as Gaussians with a width of 160 cm⁻¹ centered around ε_i − S and ε_j, respectively, where S = 240 cm⁻¹ is the room-temperature Stokes shift (64). The diagonal matrix elements T_ij, i = j, in Eq. 4 are set to zero.

Following Ritz et al. (42) and Şener et al. (4), the average excitation lifetime τ and the overall quantum yield Q, i.e., the probability of electron transfer per absorbed photon, can be given in terms of the transfer rate matrix in Eq. 4 as

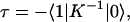(5)

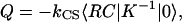(6)

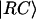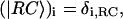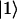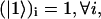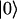where k_CS = 1 ps⁻¹ is the charge separation rate at the reaction center (4,65–67), is defined through where δ_{i, RC} equals one for i = 1 (one of the special pair chlorophylls, ec-A1, i.e., residue 1011, is responsible for charge separation; see (4,68–70)) and is zero otherwise; the vector is given by and by 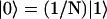. (The vector |0〉 denotes a uniform initial probability distribution). The matrix K in Eqs. 5 and 6 is related to the transfer matrix T through the relation

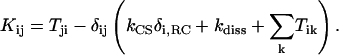(7)

Here k_diss = (1 ns)⁻¹ denotes a dissipation constant assumed to be uniform for all chlorophylls. The average excitation lifetime and quantum yield for various PSI models are given in Table 1.

The use of a hybrid effective Hamiltonian that mixes full-Coulomb couplings for the conserved chlorophylls with the dipolar approximation for couplings involving non-conserved chlorophylls raises a question on the effects of this approximation on kinetic properties of excitation transfer such as lifetime and quantum yield. To examine these effects, a hybrid effective Hamiltonian for cyanobacterial PSI was constructed as a control by replacing the full-Coulomb couplings reported in Şener et al. (3,4) for the non-conserved chlorophylls in monomeric cyanobacterial PSI by dipolar couplings. A total of 15 cyanobacterial chlorophylls have no corresponding match in plant PSI within 1 Å and, therefore, are regarded as non-conserved. As seen in columns A and B of Table 1, the approximate, through dipolar couplings yields no discernible effect on the quantum yield and excitation lifetime of the system. The reason for this insensitivity is that all 15 non-conserved cyanobacterial chlorophylls are in the peripheral region of the complex where their particular arrangement has little effect on the efficiency of the excitation transfer process (3,39,52).

RESULTS

In the following we present the key results of our analysis. We first discuss the dependence of the PSI-LHCI supercomplex excitation lifetime and quantum yield on site energies. Presenting three schematic scenarios, we argue that the quantum yield is purposefully insensitive to the choice of site energies. We then describe how the absorbed excitation migrating through the supercomplex repeatedly approaches the reaction center, every time getting a chance to initiate electron transfer and, if not successful, going through new rounds of excitation migration (sojourns) before reapproaching to the reaction center. We then describe the transfer of excitation among the main PSI-LHCI clusters, in particular, the transfer from the Lhca subunits into the PSI core, which is greatly facilitated by the presence of gap chlorophylls. We finally argue that the geometries of the Lhca subunit chlorophylls are optimized simply for increasing the overall photon absorption, not for speeding up transfer to the PSI core.

Excitation lifetime and quantum yield for plant PSI

The kinetic quantities for the plant PSI-LHCI supercomplex computed for the hybrid effective Hamiltonian with spectrally informed site energy assignments discussed in the previous section is given in column C of Table 1. The computed average excitation lifetime of 49.4 ps is in agreement with observations (57,71,72), in particular, with the average lifetime of 47 ps recently reported for Arabidopsis thaliana (57). A more detailed analysis of the wavelength dependence of excitation lifetime would require accurate site energy assignments that are currently unavailable.

The computed quantum yield for the aforementioned model is 0.950. The overall quantum yield of PSI in both plants and cyanobacteria is known to be nearly unity. It is important to emphasize that the computed quantum yield depends sensitively on the particular value assumed for the dissipation rate k_diss which is not known with great accuracy. Following Şener et al. (3) and Yang et al. (39), a value of k_diss = (1 ns)⁻¹ was used throughout this article in the computation of excitation transfer kinetics. The effect of smaller dissipation rates on quantum yield and excitation lifetime are shown in columns D and E of Table 1. Although the excitation lifetime undergoes only minor changes with decreasing dissipation rate, the corresponding quantum yield quickly approaches unity, attaining a value of 0.995 for k_diss = (10 ns)⁻¹. This suggests the possibility of an overall overestimation of k_diss also in similar calculations reported earlier (3,4,39,42).

To address the uncertainty regarding site energy assignments discussed earlier, the sensitivity of the aforementioned model to the choice of non-conserved chlorophyll site energy assignments is examined. We consider first a flat site energy distribution for non-conserved chlorophylls. The excitation lifetime and quantum yield for plant PSI corresponding to a hybrid Hamiltonian with a uniform site energy of 678.8 nm for all non-conserved chlorophylls, including gap, Lhca, and linker chlorophylls, is given in column F of Table 1. The resulting average excitation lifetime is 52 ps. Despite an enhanced spectral overlap between peripheral chlorophylls resulting from a uniform site energy assignment, the choice of a uniform site energy does not result in a faster transfer compared to the primary model in column C of Table 1, because the relative blueness of the Lhca subunits with respect to the PSI core is not taken into account in a uniform site energy assignment.

We consider second an ensemble of random site energy configurations for non-conserved chlorophylls. The ensemble average over 400 configurations with randomly distributed site energies for non-conserved chlorophylls is presented in column G. The random site energies are drawn from a Gaussian distribution approximating the site energies computed for cyanobacterial PSI in Damjanović et al. (38), adjusted for a mean value of 678.8 nm. The computed average lifetime in this case is 60 ps.

The results are reminiscent of their cyanobacterial counterparts reported in Şener et al. (3), reinforcing the idea that an exact tuning of chlorophyll site energies is not necessary for efficient light-harvesting at physiological temperatures. The uniformly high quantum yields given in Table 1 also indicate an efficient coupling of the outer lying Lhca subunits to the PSI core, as was suggested in Melkozernov et al. (24). This will be discussed further below.

Sojourns of excitation in cyanobacteria and plants

The electronic excitation delivered to the reaction center from peripheral chlorophylls does not always result in an immediate charge separation. There is a significant chance that the excitation escapes from the reaction center back to the periphery and subsequently returns to the reaction center for another chance at charge separation. A method, the sojourn expansion (3,4), expands the average excitation lifetime τ in terms of repeated escape events:

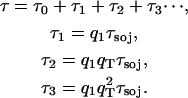(8)

Here the first usage time τ₀ denotes the average excitation lifetime without any escape events. τ₀ corresponds to the lifetime τ in the limit where the charge separation rate k_CS in Eq. 7 is infinite. The sojourn time τ_soj is the average time for an excitation that escaped from the reaction center to return to the reaction center. The escape probabilities q₁ and q_T correspond to a uniform initial state, and an initial state after immediate escape from the reaction center, respectively. Naturally, q₁ and q_T have similar values and become identical in the dissipationless limit.

A comparison of sojourn expansion coefficients for cyanobacterial and plant PSI chlorophyll networks is presented in Table 3. Expectedly, the first usage time τ₀ corresponding to the first delivery of the excitation to the reaction center goes up significantly from 19.2 ps in cyanobacteria to 30.1 ps in plants, as the diffusion of excitation takes a longer time in the enlarged chlorophyll network. Similarly, the sojourn time τ_soj after an escape is longer for the plant system due to the increased size of the chlorophyll network. The escape probabilities q₁ and q_T are nearly identical across the two models. This is because identical coupling and site energy values were used in both models for the core chlorophylls, all of which are structurally conserved.

TABLE 3.

Comparison of sojourn expansion coefficients for cyanobacterial and plant PSI

	τ (ps)	τ0 (ps)	τsoj (ps)	q1	qT
Cyano	32.7	19.2	7.73	0.630	0.638
Plant	49.4	30.1	11.0	0.620	0.633

Cyanobacterial values (first row) correspond to column B of Table 1 whereas plant values (second row) correspond to column C of Table 1. (See text for an explanation of quantities.)

Connectivity of the PSI-LHCI chlorophyll clusters

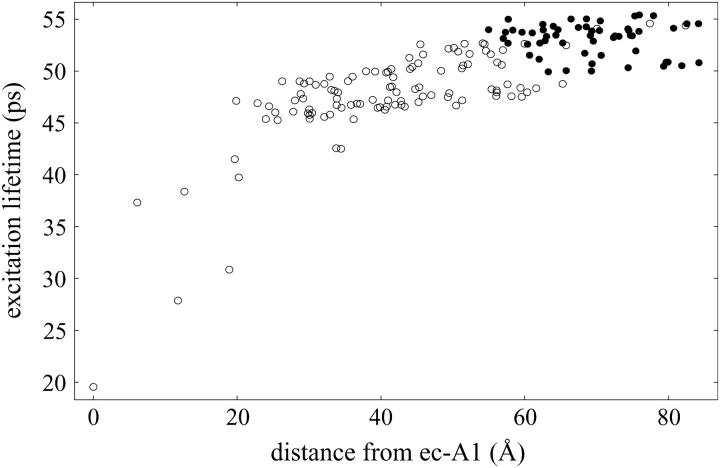
The excitation transfer pathways in Fig. 1 d suggest a close integration of the Lhca chlorophyll network with the PSI core. As proposed in Ben-Shem et al. (1), gap chlorophylls provide an efficient connection between the outer and inner chlorophyll clusters. A further indication of this connection is the dependence of the average excitation lifetime on the initially excited chlorophyll, as shown in Fig. 3. The difference between mean excitation lifetimes over the PSI core (including gap) and Lhca (including linker) chlorophyll clusters is only 5.4 ps, i.e., only ∼10% of the 50 ps overall mean lifetime. An efficient coupling between the Lhca subunits and the core has already been reported in Melkozernov et al. (24). For Arabidopsis the observed lifetime of 47 ps was reported to contain two distinct components of 20 ps and 82 ps, tentatively associated with the PSI core and the Lhca subunits, respectively (57). If the Arabidopsis PSI structure is similar to pea (1), then Fig. 3 suggests that these two distinct time constants cannot be associated with a spatial decomposition involving Lhca subunits. It is possible that the longer component is associated with a red chlorophyll pool which, in the current context, cannot be taken into account satisfactorily.

FIGURE 3.

Average excitation lifetime as a function of the distance of the starting chlorophyll from the reaction center chlorophyll ec-A1. Open circles represent PSI core and gap chlorophylls, whereas solid circles represent Lhca and linker chlorophylls. Excitation lifetimes for outer chlorophylls are seen to be not much longer than those for core chlorophylls, indicating an efficient coupling of Lhca subunits to the core. The mean lifetime averaged over all Lhca subunits (including linker chlorophylls) is 53.1 ps and 47.6 ps when averaged over the PSI core (including gap chlorophylls). The overall average excitation lifetime of the PSI-LHCI supercomplex is 49.4 ps. (See column C of Table 1.)

To probe the subunit connectivity in the plant PSI-LHCI supercomplex, the total rates of excitation transfer between chlorophylls of different subunits were computed following the method for computing excitation transfer rates between two pigment clusters suggested in Ritz et al. (42). Based on the assumption that the donor excited states are populated according to the Boltzmann distribution, the total rate of excitation transfer between the excited states of a donor pigment cluster D and an acceptor pigment cluster A is

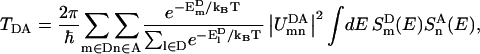(9)

where 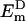and are eigenvalues of Hamiltonian H_D for the donor pigment cluster D, defined as the corresponding subblock of the effective Hamiltonian in Eq. 1. The coupling term 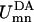in Eq. 9 between the m^th excited state of the donor pigment cluster D and n^th excited state of the acceptor pigment cluster A is

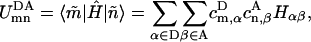(10)

where H_αβ are matrix elements of the effective Hamiltonian in Eq. 1 that couple donor and acceptor pigments, an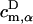d and 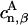are coefficients of the eigenfunctions for donor and acceptor Hamiltonians H_D and H_A, respectively. Forward and backward transfer rates, in general, are different from each other. Underlying Eqs. 9 and 10 is the assumption that excitation in the cluster is coherently shared, which neglects dynamic disorder (73). A more realistic description would be rather complex (see (73)), and would likely not deviate substantially from the description underlying Eqs. 9 and 10.

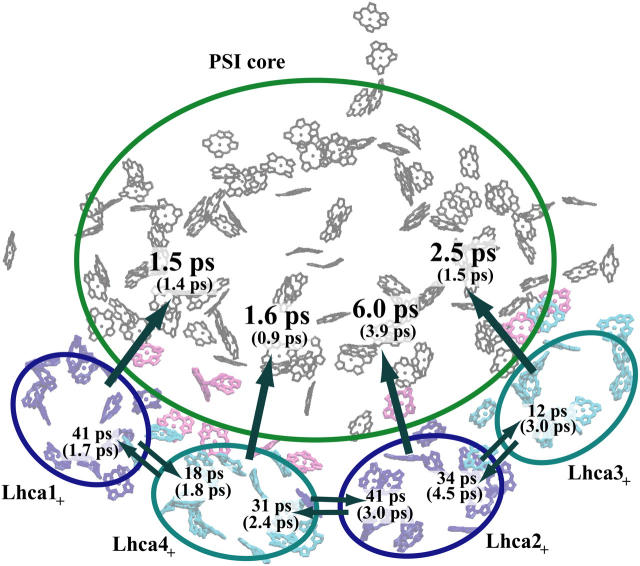
The resulting rates for excitation transfer from Lhca subunits to the PSI core are presented in Fig. 4. Since it is difficult to distinguish excitation transfer events originating from any of the Lhca chlorophylls and the neighboring linker chlorophylls, the chlorophylls of the PSI-LHCI supercomplex are divided in Fig. 4 into five clusters, one for each of the four Lhca subunits and one for the PSI core. The Lhca chlorophyll clusters include the linker chlorophylls associated with the same Lhca subunit and the PSI core chlorophyll cluster includes the gap chlorophylls that link the Lhca subunits to the core (see Fig. 1). Fig. 4 illustrates that excitation is transferred rapidly (within a few picoseconds) from Lhca subunits to the PSI core. The collective transfer rate from all Lhca subunits to the PSI core (including gap chlorophylls) is 2.1 ps. These results are found to be largely insensitive to site energy assignments. However, computed inter-Lhca transfer rates exhibit a higher degree of sensitivity to site energy assignments, thus rendering it impossible to arrive at a conclusive estimate.

FIGURE 4.

Transfer times (reciprocal of transfer rates) between the Lhca subunits and the PSI core. The subscript “+” of the Lhca subunits indicates that the neighboring linker chlorophylls belonging to the same chain are included with a given subunit. A Boltzmann equilibrium of donor states is assumed before transfer (see text). The first number corresponds to a spectrally refined hybrid Hamiltonian (model C in Table 1), whereas the second number (in parentheses) corresponds to a uniform site energy distribution for non-conserved chlorophylls (model F in Table 1). We conclude that inter-Lhca transfer rates cannot be assigned reliably due to the parameter sensitivity of these values on site energy assignments. The collective transfer time from all Lhca subunits to the PSI core (including gap chlorophylls) is 2.1 ps (becoming 1.5 ps in the uniform site energy model). The transfer time from the chlorophyll-b forms to the chlorophyll-a pool of Lhca subunits, computed similarly (according to model C in Table 1), is 288 fs.

An excitation of any chlorophyll b is expected to rapidly transfer to the chlorophyll a pool of the Lhca subunits before migration to the PSI core. Indeed, the computed excitation transfer time from the chlorophyll b pool to the chlorophyll a pool is only 288 fs, the rapid transfer being a consequence of the energy difference between chlorophyll b and a forms.

It was suggested in Ben-Shem et al. (1) that the gap chlorophylls play a key role in connecting the Lhca subunits to the PSI core. To probe this role, transfer rates from the Lhca cluster to the PSI core without gap chlorophylls were computed. In the absence of gap chlorophylls, the collective Lhca-core transfer time indeed increases from 2.1 ps to 10.5 ps.

A similar question pertains to the role of linker chlorophylls. They may only be extra antennae increasing the total absorption cross-section or, alternatively, they may have an important role in connecting the Lhca subunits with each other. It is difficult to resolve this question within the framework of the present model. All linker chlorophylls are assumed to be of chlorophyll b type and due to their respective high relative energy they provide poor connections between neighboring Lhca subunits. We suggest that the main role of linker chlorophylls is increasing the total absorption cross-section of the complex rather than facilitating Lhca subunit connectivity, which is probably not necessary for the light-harvesting function of the PSI-LHCI supercomplex.

Are peripheral chlorophyll geometries optimal?

A comparison of cyanobacterial (5) and plant (1,2) PSI chlorophyll networks in Figs. 1 and 2 reveals a high degree of conservation of the core chlorophyll network. In the light of divergent evolution (6) between cyanobacteria and plants, this conservation raises the question as to whether the PSI core chlorophyll network exhibits an evolutionary advantage over alternative geometries. The quantum yield of the pigment network will be considered below as a crude measure of fitness. In this section, the optimality of the geometry of peripheral chlorophyll groups that are unique to plant PSI, namely Lhca, linker, and gap chlorophylls, will be examined.

In an earlier study (3) it was reported that the excitation transfer pathways in cyanobacterial PSI display signs of robustness and optimality when quantum yield is taken as a measure of fitness. Robustness manifests itself as an error tolerance against various perturbations of the pigment network, such as removal of chlorophylls, fluctuations of chlorophyll site energies in the presence of thermal disorder, or fluctuations of chlorophyll orientations. It was seen that the quantum yield of the chlorophyll network of cyanobacterial PSI remained high under all these perturbations and this high quantum yield was seen to result largely from a separation of timescales between dissipation and excitation transfer. Furthermore, a comparison of the original chlorophyll network with an ensemble of randomly generated chlorophyll orientations revealed a notably higher quantum yield for the original geometry as compared to alternative geometries. Similar results regarding the robustness and optimality of the PSI chlorophyll network were reported in Yang et al. (39) and Vasil'ev and Bruce (52). In particular, it was suggested that the optimality of the network arises to a large degree from the configuration of the six reaction center chlorophylls (39) and from the geometry of a few chlorophylls bridging the reaction center to the periphery (52).

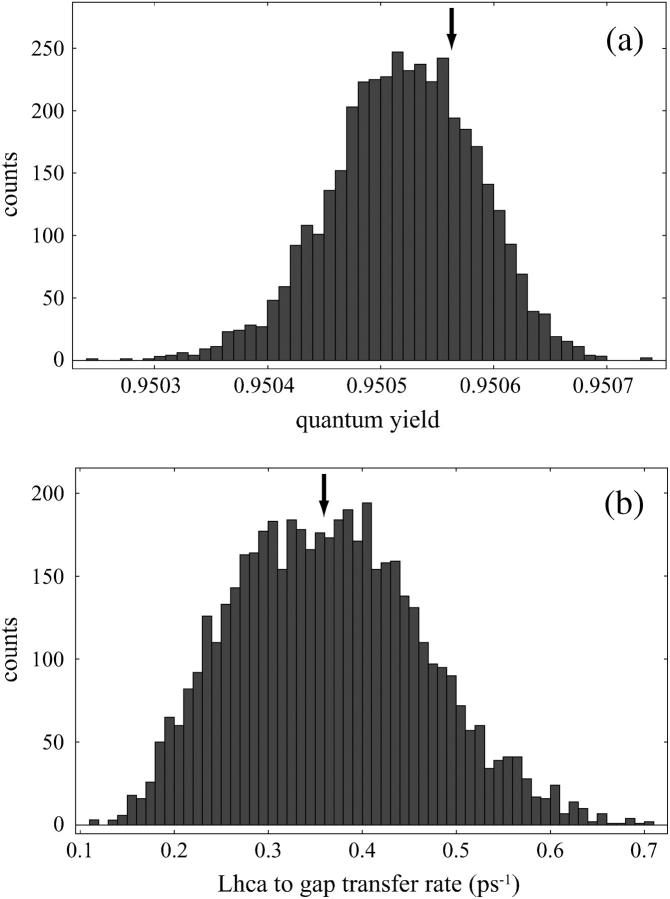
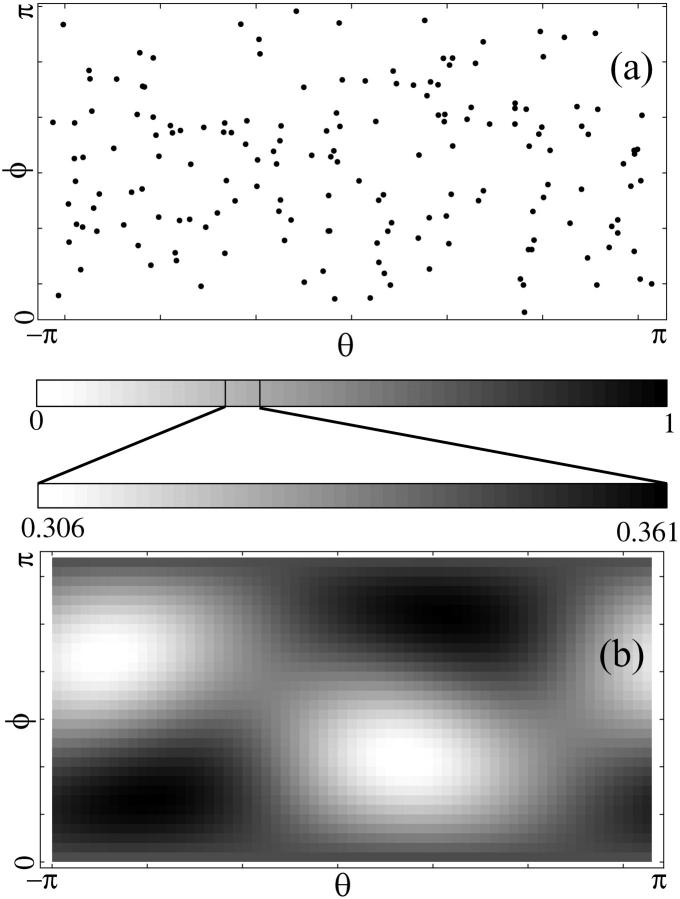
A test of optimality for the geometry of the chlorophylls in the peripheral Lhca subunits is shown in Fig. 5 a. Quantum yields were computed for an ensemble of chlorophyll geometries generated by random reorientation of the chlorophylls of Lhca1 and Lhca4 subunits without modifying the rest of the network. It is seen that the quantum yield changes only by a very small amount across this ensemble and that the quantum yield of the original configuration lies nearly in the middle of the histogram thus generated. A similar result is seen for the effect of gap chlorophyll geometry on quantum yield (not shown).

FIGURE 5.

Probing incremental optimality of peripheral chlorophylls. (a) The histogram shows quantum yields within an ensemble of 4000 configurations where the chlorophylls of the Lhca1 and Lhca4 subunits are randomly reoriented. The vertical arrow denotes the quantum yield corresponding to the original geometry. It is seen that the overall quantum yield depends only minutely on the Lhca chlorophyll geometry and within that variation the original configuration shows no signs of optimality. A variation of gap chlorophyll geometries reveals a similar result regarding their effect on quantum yield (not shown). (b) The histogram shows the transfer rate from all Lhca chlorophylls to gap chlorophylls within an ensemble of 5000 configurations where the 10 gap chlorophylls are randomly reoriented. The vertical arrow denotes the transfer rate corresponding to the original geometry. It is seen that within the given model, gap chlorophyll orientations do not optimize rapid delivery from Lhca subunits even though their presence is essential for efficient coupling to the PSI core.

In the previous subsection it was reported that the presence of gap chlorophylls greatly enhances the excitation transfer rates from the outer Lhca subunits to the PSI core. This raises the question as to whether it is only the position or also the orientation of gap chlorophylls that facilitates efficient excitation transfer. Fig. 5 b shows that the original geometry of gap chlorophylls does not facilitate the highest transfer rates from the Lhca subunits when compared with an ensemble of alternative gap chlorophyll orientations. This result is reminiscent of a similar lack of orientational optimization of the inter-monomer boundary chlorophylls in the trimeric cyanobacterial PSI for facilitating the fastest cross-monomer excitation transfer (4).

As a further probe of chlorophyll orientation effects, the dependence of the quantum yield on the polarization of the incident light was investigated. Fig. 6 a shows the distributions of chlorophyll transition dipole moments over the unit sphere for all the chlorophylls of the plant PSI-LHCI supercomplex. The distribution is found to be very uniform, and as a result the average polarization overlap of an incident photon with the transition dipole moments of the pigments is fairly uniform, too, as shown in Fig. 6 b. In fact, polarization overlaps shown are consistent with those expected for a uniform random distribution of chlorophyll transition dipole moments over the unit sphere.

FIGURE 6.

Polarization dependence of quantum yield. (a) Distribution of chlorophyll transition dipole moments over the unit sphere. (b) Average of directional overlaps between the polarization of incident light and the transition dipole moments of chlorophylls represented on an expanded scale. Absorption probability of an incident photon is proportional to this directional overlap. (On a linear scale where white corresponds to zero overlap and black corresponds to perfect alignment, the averages shown in b become indistinguishable across the graph. Therefore, the scale is expanded in b as shown.) These results are consistent with a uniform random distribution of chlorophyll orientations over the unit sphere, suggesting the absence of a specific arrangement of the distribution of orientations of the chlorophyll aggregate beyond that of a random collection.

The results reported in this section collectively indicate that the close packing of chlorophylls, rather than their orientations, has been optimized during the evolution of PSI, especially for the peripheral chlorophyll clusters.

DISCUSSION

We have used structure-based modeling methods to construct the excitation transfer network of the plant PSI-LHCI supercomplex based on a hybrid effective Hamiltonian and compared it to the cyanobacterial system. Efficient coupling of the peripheral Lhca subunits to the PSI core is observed with gap chlorophylls facilitating the rapid transfer of excitation.

The high degree of conservation between cyanobacterial and plant antenna systems raises the question of how far their particular chlorophyll arrangements optimize light-harvesting. Earlier structure-based studies (3,39) revealed a sign of optimization in chlorophyll network geometries, interpreted as a notably higher quantum yield, with respect to alternative chlorophyll orientations. However, later studies (4,51,52) suggested that this orientational optimality arises mostly from a small number of pigments near the reaction center whereas outer chlorophyll orientations are apparently selected without regard to maximizing the quantum yield. Similarly, Lhca and gap chlorophyll orientations do not seem to be optimized for the absolute highest quantum yield, i.e., for the most rapid transfer of excitation from the peripheral chlorophylls to the PSI core. It must be noted, however, that orientations of gap, linker, and Lhca chlorophylls as given in Jolley et al. (2) are not known with high accuracy. A more definitive resolution of the degree of optimization of peripheral chlorophyll orientations will require a higher resolution structure. Also, results of the previous section show that the presence of gap chlorophylls is essential for efficient excitation transfer to the core, even if their orientations do not display further optimization.

In light of the observation that orientational optimization is limited to a small number of central chlorophylls, the near exact conservation of the orientation of more than 80 chlorophylls in the PSI core is very puzzling. It is unlikely that the constraints on the excitation transfer process alone are sufficient to explain this high degree of conservation. The transfer of excitation to the reaction center is not the efficiency limiting step of the overall energy transformation process. Issues other than excitation transfer, such as ligation of chlorophylls, electron transfer, photoprotection of chlorophylls by carotenoids, spectral composition of pigments, and the requirements of assembly, and possibly repair (but see (74)), which reports cells to undergo apoptosis, rather than engage in repair from singlet oxygen damage), are likely to play determining roles in shaping the evolution of a light-harvesting system (75). The apparent lack of optimality of the geometry of the peripheral chlorophyll network suggests then that the aforementioned issues display a higher priority for the fitness of the system than the excitation transfer process.

It is yet to be determined conclusively whether minute changes (on the order of a percent or less) in the efficiency of one cellular process, such as light absorption and subsequent excitation transfer, play a determining role in shaping the evolution of an organism. On the one hand, the daily survival of an organism requires a degree of robustness against changing conditions. This is manifested, for example, in the insensitivity of the quantum yield to the site energy composition of the pigment network. This insensitivity is essential for surviving the effects of thermal disorder which causes pigment site energies to fluctuate considerably. In fact, the width of the heterogeneity of site energies of PSI chlorophylls is comparable in magnitude to kT at 300°K (38). On the other hand, chlorophyll site energies of PSI display a sign of optimality in the form of a small, but notable, difference in quantum yield when compared with random site energy assignments (39). A similar result is also revealed in Table 1 (columns C versus G). This suggests that a difference in efficiency which maybe insignificant for the daily survival of a single organism may, in fact, be of great significance when integrated over several generations for the survival of the species competing in a habitat with other species.

Unfortunately, no quantitative models exist for the rate of evolution of a pigment network. For example, what is the diffusion constant, in terms of Ų per million years, of an average pigment position within a light-harvesting complex during its evolution? What is the rate, in terms of events per million year, for the addition or removal of a pigment to an existing light-harvesting complex? What is the rate with which entire new pigment-protein clusters are added—an evolutionary strategy suggested in Kjaerulff et al. (76) for subunit PsaG arising via gene duplication of subunit PsaK in a chloroplast progenitor?

Quantitative stochastic models for the evolution of a biological network would require close scrutiny of the effect of physical processes determining network kinetics on the hierarchy of constraints shaping network evolution. Combining structural information and its implications on the physics of network dynamics across multiple related species is necessary before any quantitatively relevant evolutionary model can be constructed. Excitation transfer networks of light-harvesting complexes present natural candidates for such studies, due to the ability to accurately relate the structural information regarding pigment geometry to the biophysics of the light-harvesting process. Our present study, in comparing the excitation transfer networks of cyanobacterial and plant PSI, constitutes a necessary step toward a comprehensive model of pigment network evolution.