Lamellipodial Contractions during Crawling and Spreading

Abstract

Most eukaryotic cells can crawl over surfaces. In general, this motility requires three distinct actions: polymerization at the leading edge, adhesion to the substrate, and retraction at the rear. Recent experiments with mouse embryonic fibroblasts showed that during spreading and crawling the lamellipodium undergoes periodic contractions that are substrate-dependent. Here I show that a simple model incorporating stick-slip adhesion and a simplified mechanism for the generation of contractile forces is sufficient to explain periodic lamellipodial contractions. This model also explains why treatment of cells with latrunculin modifies the period of these contractions. In addition, by coupling a diffusing chemical species that can bind actin, such as myosin light-chain kinase, with the contractile model leads to periodic rows and waves in the chemical species, similar to what is observed in experiments. This model provides a novel and simple explanation for the generation of contractile waves during cell spreading and crawling that is only dependent on stick-slip adhesion and the generation of contractile force and suggests new experiments to test this mechanism.

INTRODUCTION

Fibroblasts crawl during wound healing; neutrophils track down pathogens; and metastatic cancer cells invade distant parts of the body. The crawling of these cells through the extracellular environment entails at least three separate physical processes: 1), cytoskeletal extension at the front of the cell; 2), adhesion to the substrate at the cell front and release at the rear; and 3), pulling up the rear of the cell body (1–3). Of these three processes, the most studied has been the polymerization-driven advance of the leading edge, which occurs in the foremost region of the cell called the lamellipodium. Polymerization and addition of new actin filaments at the leading edge of the cell drives extension through either a polymerization ratchet mechanism (4,5) or swelling (6–8). In vitro experiments have revealed the minimal components required to reconstitute this process as well as suggesting useful models for how the more complex cellular system works (9–11).

In the lamellipodium, a cohort of actin nucleation and depolymerization proteins drives assembly at the front and disassembly at the rear, leading to a lamellipodium with a relatively constant length and constant actin gradient (9,12). At the membrane, protein complexes such as Arp2/3, N-WASP, Ena/VASP family proteins, and Scar/WAVE serve to increase actin filament nucleation and polymerization, whereas back from-the-edge disassembly is mediated by ADF/cofilin and possibly gelsolin (13,14).

Transmembrane proteins, such as integrins, anchor cells to the substrate (15–17). An individual integrin bond is able to withstand 10–30 pN (18,19), and, as there are hundreds of integrins per square micron of adhesion, cell adhesions can withstand up to a few nN of force per square micron (20–24). However, more recently, it has been observed that at the leading edge of keratocytes, small forces on the order of a few pN per square micron are able to peel the front of the cell from the substrate (S. Bohnet, R. Ananthakrishnan, A. Mogilner, J. J. Meister, and A. B. Verkhovsky, unpublished).

The mechanism by which force is generated to drive translocation of the cell body is still debated. Originally, this force was attributed to an actomyosin system similar to muscle (26,27). However, Myosin II-null Dictyostelium discoideum cells are still capable of translocation (28,29). Mogilner and Oster suggested that the depolymerization of an actin meshwork could generate a contractile force to pull up the cell rear (30) and, more recently, a gel model for depolymerization-induced retraction has been shown to agree quantitatively with in vitro experiments with nematode sperm extracts (31).

Although much is known about the individual biochemical players in cell motility, a detailed understanding of the biochemical regulation and the mechanical and dynamical processes underlying crawling and spreading are still lacking. Through close inspection of the leading-edge motions of crawling and spreading mouse embryonic fibroblasts using TIRF and DIC microscopy, Sheetz's group discovered that the lamellipodium undergoes periodic contractions that are substrate-dependent (12). Although periodic contractions were observed on substrates coated with 10 μg/mL fibronectin, steady advance without contraction occurred on polylysine-coated slides and random contractions were observed on silanized coverslips (12). The periodic contractions left periodic rows of matrix-bound β3-integrin and paxillin while generating waves of rearward-moving actin-bound α-actinin and myosin light-chain kinase (12). In addition, the period of the contraction is dependent on the width of the lamellipod, as shown by addition of low concentrations of latrunculin A (12).

In this article, I propose a simple model for the generation of lamellipodial contractile waves during cell spreading and crawling. This model assumes that the actin network generates steady contractile force and that adhesion to the substrate can only produce a finite amount of force. The combination of these two features leads to periodic contractions at the front of the cell that are consistent with experimental observations. In addition, coupling the periodically contracting actin network with a reaction/diffusion/advection model for actin-binding proteins, such as β3-integrin or myosin light-chain kinase, produces periodic waves of actin-binding protein concentration that then form rows at the rear of the lamellipod. This is also in agreement with experiments. Finally, this mechanism suggests new experiments that can test the proposed model.

THE STICK-SLIP MODEL FOR CONTRACTILE WAVE GENERATION

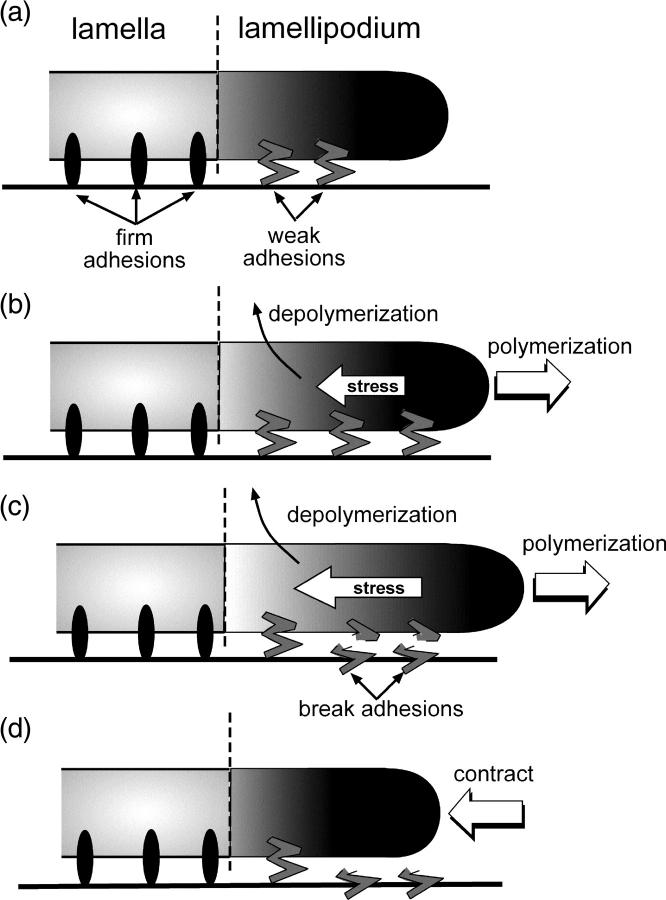
Analysis of migrating newt lung epithelial cells and potoroo kidney epithelial cells using quantitative fluorescent speckle microscopy has shown that migrating cells possess two distinct actin networks, the lamellipodium and the lamella (32). The lamellipodium is the foremost part of the crawling cell and is ∼1–3 μm in width. The lamella lies directly behind, and possibly slightly underneath, the lamellipodium (32). Focal adhesions typically form only in the lamellar region of the cell (32). Consistent with these findings, I model the cell as two distinct regions with the lamellipodium directly in front, yet attached to the lamella (Fig. 1 a). The lamella is characterized by firm adhesion to the substrate, whereas the lamellipodium is adhered through weak adhesions (Fig. 1 a).

FIGURE 1.

Schematic of the model. (a) The migrating cell is composed of two regions, the lamellipodium and the lamella. The lamellipodium is weakly attached to the substrate and directly in front of the lamella, which is attached to the substrate through firm adhesions. (b) Polymerization at the front of the cell pushes the leading edge forward, whereas depolymerization of the network induces contractile stress in the lamellipod. (c) When sufficient stress has been generated, the weak adhesions can break (d), leading to contraction of the leading edge.

Both cellular actin networks are composed of cross-linked and entangled actin filaments surrounded by cytosolic fluid, i.e., a gel-like material. Nucleation and polymerization of new actin at or near the membrane pushes the leading-edge forward (Fig. 1 b). A number of recent models have used the physics of gels to describe the dynamics of the cytoskeleton in crawling cells (see, for example, Refs. 8, 33, and 34). A model for how depolymerization of a gel can produce contractile forces in crawling nematode sperm quantitatively matches experimental data from in vitro experiments with cell extracts (31). However, it is not clear what generates contractile force in lamellipodia of actin-based cells. Although an actomyosin system is often proposed, transfecting fish keratocytes with ML7 (a potent inhibitor of myosin II) leads to increased retrograde flow of the actin network (35). Therefore, I chose to model contractile stress generation in the lamellipod using a depolymerization model.

In this model, the ratio of filamentous actin volume to total volume is defined as the volume fraction, φ. An equilibrium volume fraction, φ₀, is determined by the equilibrium between four forces: 1), the entropic tendency for the gel filaments to diffuse outwards; 2), the “counterion pressure” that tends to inflate the gel; 3), the entropic elasticity of the gel filaments that tends to resist expansion; and 4), the attractive interactions between the filaments that also tend to hold the gel together (for a more complete description, see Refs. 33 and 36). The stress, σ, in the gel can be directly related to φ. For simplicity, I chose a linear stress,

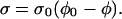(1)

Depolymerization of the gel at rate γ decreases φ and, therefore, contractile stress is generated that tends to drive the gel back to its equilibrium volume fraction (Fig. 1 b). The force generated by this stress is f = ∇ · σ. As the drag force on the polymer is much larger than inertia, the velocity of the polymer, v, is assumed to be proportional to f, through the drag coefficient ζ. The dynamics that drive the change in volume fraction are derived in the Appendix. Although we have made a specific choice that depolymerization generates contractile force, the dynamic model for how stress is generated for this model is similar to a simplified model for stress generation arising from the action of molecular motors, such as myosin (see the Appendix).

As depolymerization progresses, the stress builds in the lamellipod (Fig. 1 c). When sufficient stress is generated, the adhesions break (Fig. 1 c) and the lamellipod contracts and slides with respect to the substrate (Fig. 1 d). This type of adhesion process, which is generically called stick/slip adhesion, is similar to the behavior of a block on a table when the static coefficient of friction is larger than the kinetic coefficient of friction (37,38). This type of adhesion has been suggested previously in a model for the crawling of nematode sperm (39). To implement this mechanism, we define the critical force at which the adhesions break as f_cr = ζV_slip. Therefore, if v < V_slip, v = 0. When f > ζV_slip, v = f/ζ, and the lamellipod slides. At slow velocities, we imagine that weak adhesions have time to reform and, at v = V_stick, the lamellipod is able to stick to the substrate again, at which point v = 0 again. The v remains zero until it exceeds V_slip, and the process repeats (for a detailed description of the mathematical model, see the Appendix). This adhesion model leads to cycles of extension and contraction.

RESULTS

Experiments suggest that the adhesion to the substrate is a major factor in the production of periodic contractions. On slides coated with polylysine, which should provide strong cell adhesion, steady advance of the lamellipod was observed (12). On silanized coverslips, where adhesion is weak, random, large amplitude contractions occurred (12). However, periodic lamellipodial contractions were consistently observed on fibronectin-coated substrates. To test whether this model produces periodic contractions of the leading edge, the cytoskeletal dynamic equations (A1–A8) were integrated using an explicit time method and a finite difference discretization. To reduce the number of free parameters in the model, the equations were non-dimensionalized using the initial width of the lamellipod, L₀, and the gel relaxation time, 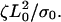The remaining dimensionless parameters are described in Table 1. As little is known about the magnitude of the force required to break the weak adhesions in the lamellipod, I varied the slipping velocity, leaving all other parameters fixed. For large values of the slipping force, the stress is never sufficient to break the adhesions and the leading edge steadily advances (Fig. 2 a, solid line). For smaller values of this force, periodic contractions of the lamellipod occur (Fig. 2 a, dashed and dotted lines). As the slipping force decreases, the amplitude of the contractions gets smaller as does the period of the contractions.

TABLE 1.

Symbol	Definition	Value
L/L0	Ratio of the lamellipodial width to the initial width.	0.2–1
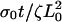	Dimensionless time.	N/A
σ0Vslip/ζL0	Dimensionless slipping velocity.	0.1–0.4
σ0Vf/ζL0	Dimensionless polymerization velocity.	0.1–0.4
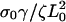	Dimensionless decay rate.	0.05–0.2
φ0	Equilibrium volume fraction.	0.1

FIGURE 2.

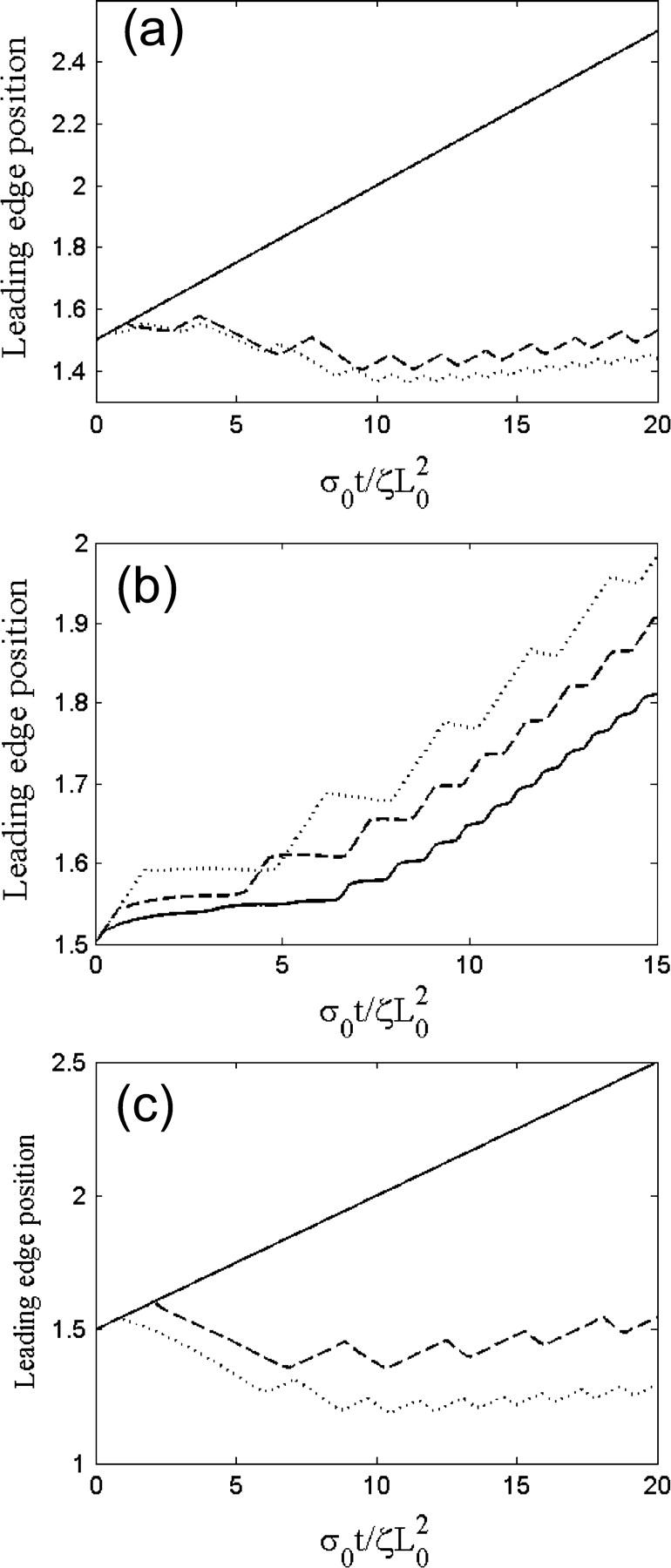
Leading-edge position in arbitrary units as a function of time for three different values of (a) the slipping force, V_slip: σ₀V_slip/ζL₀ = 0.4 (solid), σ₀V_slip/ζL₀ = 0.3 (dashed), and σ₀V_slip/ζL₀ = 0.2 (dotted), with 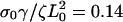and σ₀V_f/ζL₀ = 0.1; (b) the ratio of the polymerization velocity, V_f, to the slipping velocity, V_slip: V_f/V_slip = 1.75 (solid), V_f/V_slip = 1.0 (dashed), and V_f/V_slip = 0.78 (dotted), with 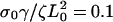and V_slip: σ₀V_f/ζL₀ = 0.14; and (c) the decay rate γ: 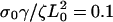(solid), 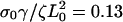(dashed), and 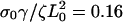(dotted), with σ₀V_slip/ζL₀ = 0.32 and σ₀V_f/ζL₀ = 0.1.

The shape of the leading-edge position versus time is strongly dependent on the relative magnitude of the polymerization velocity to the slipping velocity. Fig. 2 b shows the profile of the leading edge in time for three different values of the polymerization velocity, V_f, with constant slipping velocity. For large polymerization velocities, the leading edge keeps advancing even though the lamellipod is slipping. Therefore, the leading edge profile is wavy, but always increasing (Fig. 2 b, solid line). When the polymerization velocity is roughly equivalent to the slipping velocity, contraction of the network occurs at approximately the same speed as advance. Therefore, periodic contractions of the lamellipod produce a leading-edge profile that is roughly flat during contraction (Fig. 2 b, dashed line). Decreasing the ratio V_f/V_slip increases the period between contractions and the size of the advance step. When V_f/V_slip < 1, contractions are faster than the advance due to polymerization, and, therefore, periodic contractions produce a leading-edge profile that advances and retreats (Fig. 2 b, dotted line).

Experiments showed that addition of low concentrations of latrunculin A reduced the size of the lamellipod and decreased the periodic contraction period (12). The action of latrunculin A at these concentrations increases the depolymerization of the actin network by sequestering G-actin monomers. In this model, we can simulate this process by increasing the depolymerization rate, γ. At low values of γ, stress is generated slowly and never becomes large enough to rip the leading edge from the substrate. The solid line in Fig. 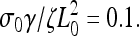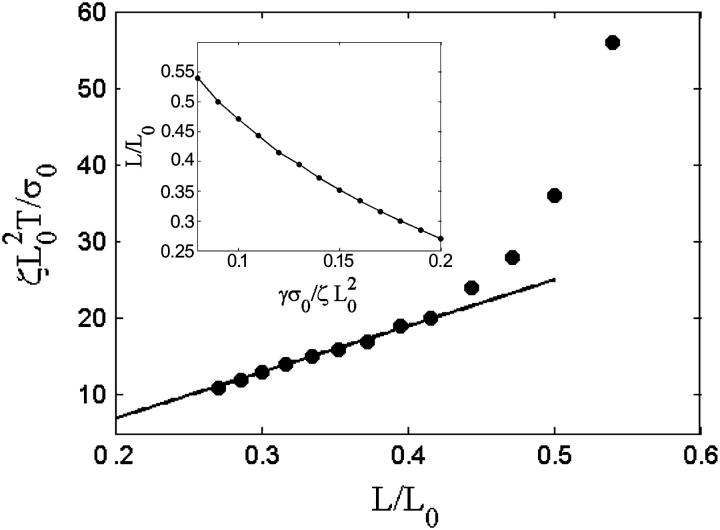2 c, shows the steady advance of the leading edge for a decay rate of Increasing this rate to 0.13, however, creates sufficient stress to break the weak adhesions. The leading edge begins moving forward at the same steady rate as was observed initially with 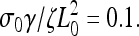Then, sufficient force is generated, the adhesions break, and the lamellipod contracts (Fig. 2 c, dashed line). Then the contraction relieves the stress and advance of the lamellipod resumes. Repeating this process leads to periodic contractions. Increasing the depolymerization rate further generates stress more quickly, and therefore both the contraction period and amplitude are smaller (Fig. 2 c, dotted line). Furthermore, it was observed that the width of the lamellipod decreased with increase in the depolymerization rate (Fig. 3, inset). In agreement with the experimental finding that the contraction period was linear with the width of the lamellipod, comparison of the period of the contractions with the lamellipodial width was linear up to a point at which width the period diverged (Fig. 3). This divergence is due to the fact that at low depolymerization rates, the stress is never sufficient to induce contractions. Therefore, the period is effectively infinite at a finite lamellipodial width.

FIGURE 3.

Effect of increased depolymerization on the lamellipod. Plot of contraction period, T, versus the lamellipodial width, L/L₀. For smaller widths, the period is linearly proportional to the width (solid line shows linear fit). (Inset) Dependence of lamellipodial width on the decay rate, γ.

As mentioned previously, fluorescently labeled actin-binding proteins, such as myosin light chain kinase, exhibit periodic rearward traveling waves during periodic lamellipodial contractions. In addition, β3-integrin and paxillin form periodic rows at the back of the lamellipod. To explore the dynamics of chemical binding to the cytoskeleton during lamellipodial advance and contraction, I propose a simplified kinetic model for the dynamics of actin-binding proteins. I assume that the cytosol contains a well-mixed, constant concentration of free actin-binding protein. Protein binds to the cytoskeleton with a rate constant, k_on, and an off-rate, k_off. Once bound to the cytoskeleton, the protein is transported with velocity v. Therefore, the dynamics for the actin binding protein concentration, C, is

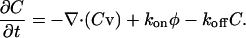(2)

Solution of these equations using k_on = 4.0 and k_off = 0.32 produces both rearward traveling waves and periodic rows (Fig. 4, b and c). During advance, depolymerization reduces the actin concentration leading to less binding of the protein. During contraction, the dependence of the on-rate on the volume fraction leads to more binding during a contraction phase, which intensifies the rearward flux over the situation of constant bound concentration advecting with the retrograde cytoskeletal velocity. As the firm lamellar adhesions advance, the variation in the actin concentration gets “locked in” producing periodic rows of bound actin-binding proteins (Fig. 4, a and c). In the simulations, the dynamics of the actin-binding protein concentration are “turned off” in the lamella to emphasize the development of these periodic rows (Fig. 4 c).

FIGURE 4.

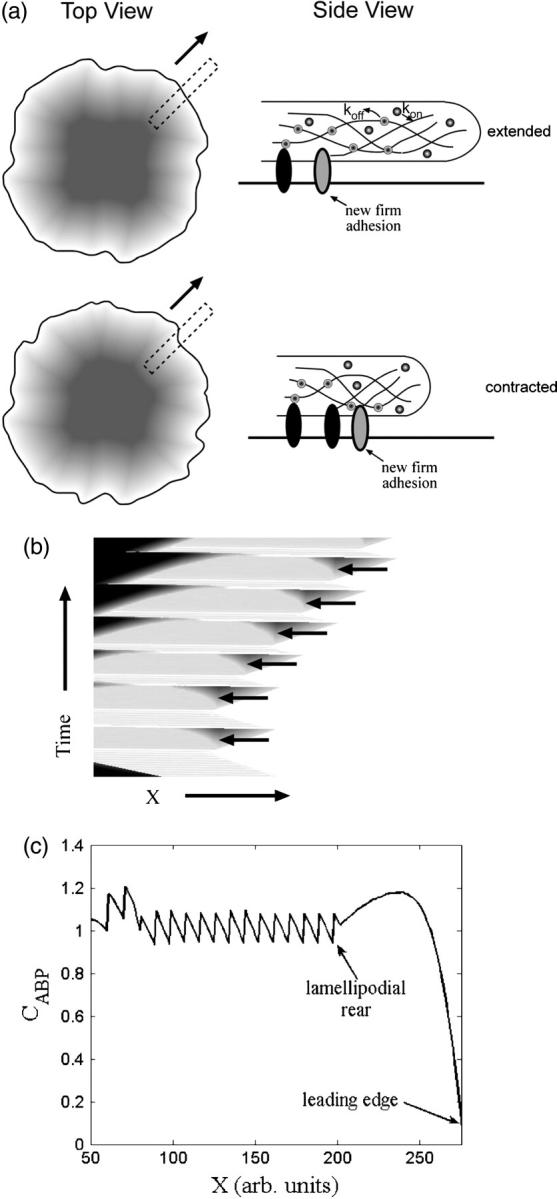
Contractions produce rearward traveling periodic waves and rows in the concentration of actin-binding proteins at the rear of the lamellipod. (a) Schematic showing how contractions and advance of the lamellar adhesions “lock in” periodic variations in the concentration. The top view shows a spreading cell at two times. The dotted rectangles represent a slice of the cell used to generate a kymograph. The side view shows the actin-binding protein concentration inside the cell during a contraction. (b) Kymograph of the concentration of actin-binding proteins obtained from stacking the one-dimensional simulation results of the solution to Eq. 2 with 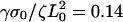and σ₀V_slip/ζL₀ = 0.32 showing rearward traveling waves in the concentration (solid arrowheads). (c) Concentration of actin-binding protein as a function of position in the lamellipod. The periodic waves produce rows of high concentration at the rear of the lamellipod.

DISCUSSION

Here I have shown that a simple model incorporating stick/slip adhesion with a contractile stress-generating mechanism that is proportional to the concentration of actin can produce periodic lamellipodial contractions. This model reproduces a number of qualitative similarities to results that are observed experimentally: 1), periodic contractions are strongly dependent on the substrate; 2), increasing the actin depolymerization rate through addition of latrunculin A leads to a shorter lamellipod with the contraction period linearly proportional to the lamellipod width; and 3), coupling the dynamics of actin binding proteins to this model leads to rearward traveling waves and periodic rows of actin binding protein at the rear of the lamellipod. Furthermore, consistent with this model, the leading-edge position retracts less steeply than is observed in the absence of latrunculin A (see Fig. 6 b in Ref. 12). The primary component of the model that leads to periodic contraction is the stick/slip mechanism for adhesion in the lamellipod. As the experiments on lamellipodial contractions used surfaces that can stimulate different signaling behavior, the difference between contractions on fibronectin and polylysine could also be due to differences in signaling on these substrates. In addition, I have assumed that the adhesive force in the lamellipod is constant. However, integrin clustering is dynamic and adhesion may be greater at the posterior region of the lamellipodium. If this is the case, then there will be quantitative differences in the model results, but, overall the mechanism will behave qualitatively similar.

Though it was assumed that the stress was generated by depolymerization of the actin network, this assumption is not necessary for the production of these contractile waves; however, it is sufficient. The connection of the depolymerization model for stress generation to experiments with latrunculin A is strongly suggestive that this mechanism may play a role in generating contractile stress in actin-based cells as has been previously proposed for crawling nematode sperm (31).

This model assumes that the lamella only provides rigid resistance against the contractions of the lamellipodium. In real cells, however, the actin bundles in the lamella are weakly coupled to the actin network of the lamellipodium. Therefore, this assumption may be an oversimplification and contractions in the lamellipodium may influence or be influenced by processes occurring in the lamella. As the mechanical coupling between these two regions is unclear, this model does not make any predictions about the dynamical coupling between the lamellipod and the lamella.

The role of myosin II in crawling cells is unclear. Myosin is often considered to play a role in generating contractile force. Based on this assumption, one would expect that inhibition of myosin II using ML7 would alter the periodic lamellipodial contractions, and, indeed, treatment of cells with ML7 leads to periods of fast protrusion followed by the cessation of edge activity as opposed to periodic contractions (12); however, myosin II is present exclusively in the lamellar region of the cell (32) and therefore generating contraction in the lamellipodium would require coordinated coupling between the lamella and lamellipodium. Recent experiments, though, suggest alternative mechanisms by which this could occur. In fish keratocytes, treatment with ML7 has been shown to lead to larger retrograde flow of the actin network at the leading edge, in contrast to the smaller retrograde flow that would be expected if myosin II was generating contractile force (35). If ML7 affects adhesion between the cytoskeleton and the substrate as is proposed in Jurado et al. (35), then addition of ML7 would be predicted to reduce the slipping force between the cytoskeleton and the substrate, altering the periodic contractions. If, instead, myosin II acts like an actin cross-linker, the action of myosin would tend to stiffen the cytoskeleton, thereby reducing the affect of the contractile stress. Then, if ML7 acts to inhibit crosslinking, the cytoskeletal network would tend to be weakened, leading to larger contraction and retrograde flow.

This model suggests a number of new experiments that can test its validity. First, as the mechanism proposed here does not require any features specific to mouse embryonic fibroblasts, periodic lamellipodial contractions should be possible in many other motile cells. Second, as predicted by Fig. 2 b, the shape of the leading-edge position versus time should be strongly dependent on the slipping force. By increasing or decreasing the adhesive force by coating the substrate with different concentrations of fibronectin or polylysine, one can test whether or not kymographs of the leading edge are consistent with the model. Decreasing the adhesion should increase the ratio of the polymerization velocity to the slipping velocity, thereby increasing the frequency and reducing the degree of contraction.

APPENDIX A: VOLUME FRACTION DYNAMICS

In this Appendix, I derive a simple model for the dynamics of the cytoskeletal network in the lamellipod. As the cytoskeleton is a network of polymer surrounded by fluid, a complete description of the dynamics requires accounting for both the motion of the polymer and the solvent. The equations that describe this two-phase system have been derived previously (33,40). A simplified version of these equations that preserves some of the main qualitative features can be obtained by assuming that the fluid phase is relatively stationary, and therefore, only consider the polymer network dynamics (41,42). Therefore, the drag force on the fluid is ζv, which is balanced by the polymer stress force,

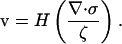(A1)

The function H(y) enforces the stick/slip adhesion:

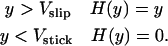(A2)

For V_stick < y < V_slip, if y was stuck on the previous time step, then it remains stuck. Otherwise, H(y) = y.

The position of material points, X, in the polymer network are found from

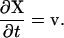(A3)

The polymer also is depolymerized at a rate, γ. A continuity equation defines how the polymer volume fraction, φ, changes due to this velocity and depolymerization,

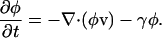(A4)

If we assume a one-dimensional lamellipod and use Eq. 1, then

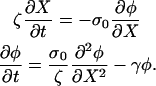(A5)

At the leading-edge (X = f), polymerization of the network drives the cell forward, therefore,

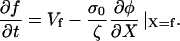(A6)

In the absence of external forces, σ(f) = 0, so φ(f) = φ₀.

At the juncture between the lamella and the lamellipod (X = r), we assume that the lamella steadily advances at the rate of polymerization. Therefore,

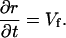(A7)

If the lamellipod to lamella transition is defined by the establishment of firm adhesions, then we expect that v(r) = 0, which requires that

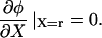(A8)

To further enforce the assumption of firm adhesion in the lamella, we demand that v = 0 for all X < r, and, for simplicity, we do not solve the equations in this region.

APPENDIX B: COMPARISON OF A SIMPLE MODEL FOR DEPOLYMERIZATION-INDUCED STRESS TO A MODEL FOR MOLECULAR MOTOR-INDUCED STRESS

In this Appendix, I show that the simple depolymerization model developed here generates stress in the cytoskeletal network in a similar manner to what would be expected from a simple model for the stress induced by the action of molecular motors, such as myosin. Using Eqs. 1 and A5, the time-rate of change for the stress from the depolymerization model is

. (B1)

If, we assume that myosin can also bind to the actin network and generate a force proportional to the concentration of bound myosin, m, then

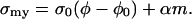(B2)

The binding of myosin to the actin depends on the concentration of actin. In addition, once bound, the myosin is advected with the polymer. Therefore,

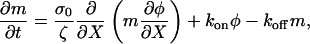(B3)

where k_on is the binding rate and k_off is the release rate.

For this model, the time-rate of change of σ is

, (B4)

where we have ignored the polymer decay term, γ. Since both Eqs. B1 and B4 produce stress at a rate proportional to the volume fraction, both models are similar in the way in which stress is generated. Therefore, though the dynamics may not be quantitatively the same, the mechanism for stress generation (which drives the contraction) should behave qualitatively similar.