A Kinetic and Stochastic Analysis of Crossbridge-Type Stepping Mechanisms in Rotary Molecular Motors

Abstract

The bacterial flagellar motor is generally supposed to be a stepping mechanism. The main evidence for this is based on a fluctuation analysis of experiments with tethered bacteria in which rotation frequency was varied by applying an external torque: the variance in time taken for a fixed number of revolutions was found to be essentially proportional to the inverse square of the frequency. This behavior was shown to characterize a Poissonian stepper. Here we present a rigorous kinetic and stochastic analysis of elastic crossbridge stepping in tethered bacteria. We demonstrate that Poissonian stepping is a virtually unachievable limit. To the extent that a system may approach Poissonian stepping it cannot be influenced by an externally applied torque; stepping mechanisms capable of being so influenced are necessarily non-Poissonian and exhibit an approximately inverse cubic dependence. This conclusion applies whatever the torsional characteristics of the tether may be, and contrary to claims, no perceptible relaxation of the tether following each step is found. Furthermore, the inverse square dependence is a necessary but not sufficient condition for Poissonian stepping, since a nonstepping mechanism, which closely reproduces most experimental data, also fulfills this condition. Hence the inference that crossbridge-type stepping occurs is not justified.

INTRODUCTION

It is commonly considered that both the proton-driven bacterial flagellar motor and the proton-translocating ATP synthase are stepping motors (1–3). Although stepping has been directly observed on the ATP synthase with different preparations (4–6), it has only been indirectly inferred in the case of the flagellar motor. Samuel and Berg (7) carried out a fluctuation analysis of the motor rotation and interpreted the results in terms of a Poissonian stepping model. Here we show that this model is incompatible with the experimental procedure used, namely imposing a variable external torque on tethered cells to obtain different rotational frequencies. We further show that the results of the fluctuation analysis can be satisfactorily reproduced by a nonstepping model (8).

The model considered by Samuel and Berg (7) comprises a single, and thus rate-limiting, biochemical step linked to an elementary angular step φ of some unspecified element around the periphery of the rotor (see Fig. 1), which results in an equal increment in rotation angle Δθ. Thus the Poissonian distribution of the biochemical events is directly translated into a Poissonian distribution of steps in rotation angle. The authors showed theoretically that the variance in the time taken for n revolutions at a given rotational frequency f is

(1)

where A = n/k with k denoting the number of elementary steps per revolution. Since their variance measurements obtained by imposing a variable external torque on tethered Escherichia coli cells conformed with Eq. 1 (see Fig. 5, case 1), they concluded that the observations were consistent with a Poissonian stepping mechanism using ∼400 steps per revolution.

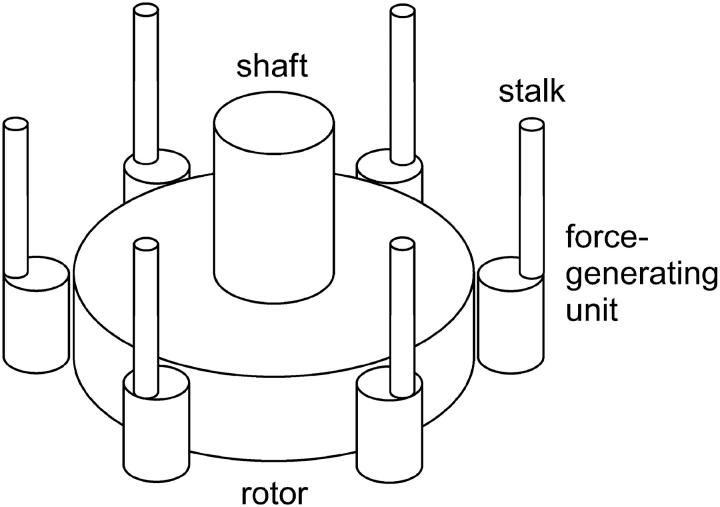
FIGURE 1.

Schematic diagram of the bacterial flagellar motor. The flagellar filament is attached by means of a hook to the shaft, which passes through a bushing in the cell wall (not shown, see Ref. 3). The force-generating units (MotA/MotB subunits), arrayed around the rotor (M and C rings), are permanently fixed to the cell wall by means of the stalks. In the case of the stepping model they are reversibly bound to specific attachment points on the peripheral surface of the rotor (not shown). From time to time one of the units steps to an adjacent attachment point. In so doing the stalk of the unit is elastically deformed, giving rise to a change in the torque exerted on the rotor. The rate constants governing the stepping depend on the driving force for the rotation (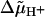) and the elastic energy associated with the deformation.

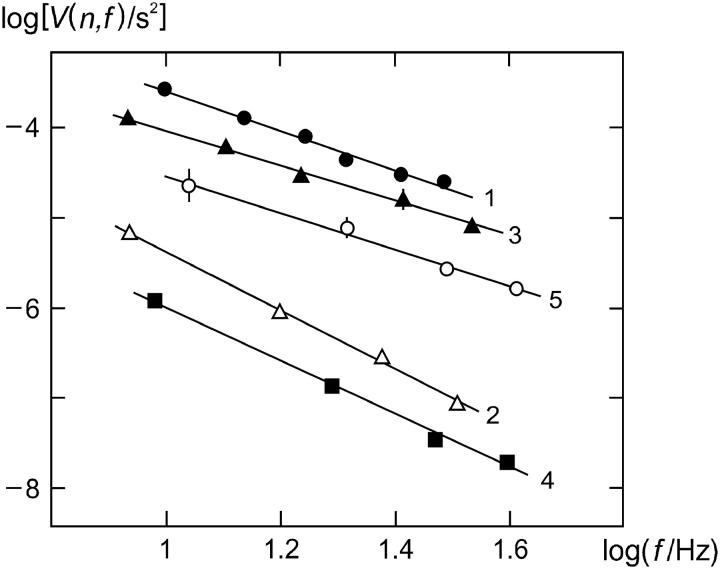
FIGURE 5.

Analysis of V(n,f), the variance in time for n revolutions at rotational frequency f, according to the relation log[V(n,f)] = log A − m log f ; where applicable the average number of elementary steps per revolution 〈k〉 is given (see text). (case 1) Experimental data (Ref. 7), m = 2.22 ± 0.14, 〈k〉 = 414 ± 36; (case 2) bidirectional stepping model, m = 3.28 ± 0.12; (case 3) unidirectional stepping model (α₀ varied), m = 1.96 ± 0.08, 〈k〉 = 207 ± 26; (case 4) model of Ryu et al. (1), m = 3.00 ± 0.15; and (case 5) electrostatic model, m = 2.06 ± 0.14. Parameter values as follows: case 2, λ = 0.5, α₀ = 200 s⁻¹; case 3, λ = 0, σ = 23.9 nN nm/rad², α₀/s⁻¹ = 500, 750, 1000, 1500, and 2000 (T_ex not used); case 4, λ = 0, u = 5, α₀ = 1.23 × 10⁵ s⁻¹, for other details see Ryu et al. (1); case 5, u = 11, for other details, see Walz and Caplan (8). Except where stated, u = 8, σ = 0.8 nN nm/rad², k_χ = 0.4 nN nm/rad², φ = 2π/50, D_b = 0.256 rad²/s, d = 20, 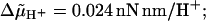T_ex/(nN nm rad⁻¹) = 0, 1, 2, 3; n = 10; and temperature, 22°C. For graphical reasons, curves 2–5 are vertically displaced by −0.8, −0.7, 0, and −0.5 units, respectively. Standard deviations are shown by vertical bars where they exceed the size of the symbols.

In the model of Samuel and Berg an increment Δθ can only occur if the unspecified element mentioned above is elastic. For Δθ to equal φ, the rate of relaxation of this elastic element has to be high enough to allow the relaxation to be essentially completed before the next elementary step takes place. Moreover, the effect of an externally applied torque T_ex is not taken into account, but it is implicitly assumed that changing T_ex yields different frequencies f. To clarify this issue we have analyzed a stepping model in which explicit consideration is given to the relaxation of the stepping units and that of a tether, as well as to the effect of T_ex.

ANALYSIS AND SIMULATIONS

Stepping model

The scheme in Fig. 1 shows the salient features of our elastic stepping model, whereas the notation used is defined in Fig. 2. Consider u units, each of which is bound to one of r equally spaced attachment points on the rotor. At a given time t, this brings about an angular displacement ξ_j(t) of the j^th unit from its rest position,

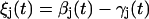(2)

(see Fig. 2). This unit then exerts a torque

(3)

on the rotor and simultaneously a torque −T_j(t) on the cell body, where σ is an elasticity coefficient reflecting the deformation of the stalk. The total torque T_el exerted by all units is

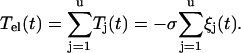(4)

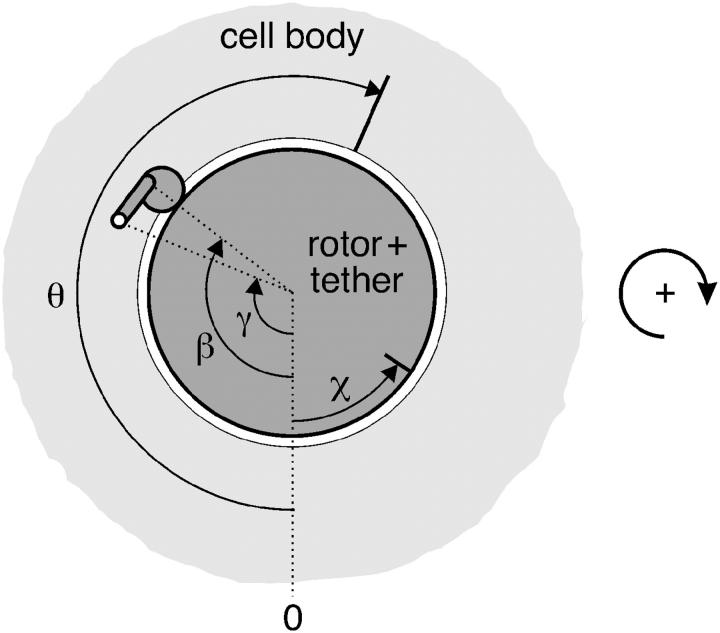
FIGURE 2.

Projection of the motor in a cell which is tethered to a support, viewed from the side of the tethering filament (i.e., from the top in Fig. 1). The dotted line marked “zero” is the reference point on the support with respect to which angles are measured (positive sense indicated on the right, corresponding to the clockwise direction of rotation of the cell body in nonreversing strains). The elastically deformed stalk of one of the units is shown whose attachment points on the rotor and the cell body are represented by the angles β and γ, respectively (subscripts j for j^th unit omitted for clarity). Note that θ is the rotation angle of the cell, whereas χ is the torsion angle of the tether (usually negative, as shown).

The rotation rate of the cell body dθ/dt as a result of T_el and a constant externally applied torque T_ex is

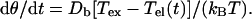(5)

Here D_b denotes the rotational diffusion coefficient of the cell body, k_B is Boltzmann's constant, and T the absolute temperature. The torsion rate of the tether dχ/dt as a result of T_el is

(6)

where k_χ is the torsional spring constant of the tether (9) and D_r is, in effect, a rotational diffusion coefficient of the rotor plus tether.

The evolution of θ and χ in time arises from the stepping of one of the units to an adjacent attachment point at a time-point t_i and the subsequent relaxation of the displacements ξ_j during the time-interval Δt_i = t_i+1 − t_i (see Appendix for a detailed derivation). The intervals Δt_i are determined by the rate constants

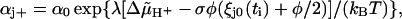(7a)

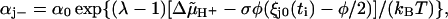(7b)

describing the stepping of the j^th unit, where α_j+ and α_j− pertain to a step by +φ and −φ, respectively, and φ = 2π/r is the angle between adjacent attachment points (see Appendix). The coefficient λ reflects the position of the transition state in the step, 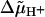is the electrochemical potential difference for protons driving the rotation, and ξ_j0(t_i) denotes the displacement just before the stepping of the unit.

Trajectories θ(t) and χ(t) were obtained by Monte Carlo simulation, taking into account exclusion of attachment points due to steric hindrance (see Appendix), and the rotational frequency f was determined as the slope of a linear regression to θ(t). The trajectories θ(t) were evaluated according to the procedure of Samuel and Berg (7), and the variances were fitted to the relation

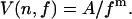(8)

For a Poissonian stepper, m = 2 (see Eq. 1); moreover, k = 〈t_n〉²/[nV(n,f)] at any value of f, where t_n is the time taken for n revolutions (7), and an average value 〈k〉 can then be calculated.

Poissonian versus Non-Poissonian behavior

With physically reasonable parameters, which yield the correct frequencies for the actual 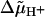value used (8), our stepping model winds up the tether to an average steady-state angle χ_ss such that its restoring torque k_χχ_ss balances the average elastic torque 〈T_el〉 (see Fig. 3 B and Eq. 6). The corresponding frequency f = 2π [dθ/dt]_ss is determined by T_ex − 〈T_el〉 and D_b (Eq. 5), i.e., f can be varied by an externally applied torque T_ex, which includes stalling the motor (Fig. 3 A). The variance analysis of this case yields a value of m above 3 (Fig. 5, case 2), which is to be expected since a single rate-limiting step does not occur. Depending on T_ex, between 0.7% and 7% of all steps are “back steps”, i.e., pertain to −φ. Two relaxation times, with their associated exponential functions, appear in the equations of the model (Eqs. 20). Simulations were performed of the time courses of the incremental changes θ′(t′) and χ′(t′) (see Appendix, Eqs. 9) and the average displacement 〈ξ〉(t′) = 〈ξ〉(t_i) + χ′(t′) − θ′(t′) (Eqs. 12, 18, and 20) in the intervals 0 ≤ t′ ≤ Δt_i. These revealed that the two relaxation times, τ₊ and τ₋ (Eq. 22), govern the relaxation of the displacements ξ_j and the torsion of the tether, respectively. Hence, the extent of relaxation during the time intervals Δt_i is indicated by the values of the functions g_±(t′) (Eq. 21) at t′ = Δt_i. These functions are bounded by the limits 0 and 1 corresponding to zero and complete relaxation, respectively. It is evident from Fig. 4, A and B, that the relaxation of the displacements ξ_j is rarely complete, while that of the tether is only marginal. Interestingly, we do find m close to 2 with u = 1 (a single stepping unit, not shown), but 〈k〉 = 1540 ± 150 — although in this particular case, k should be equal to 50, and back-stepping ranges between 11% and 32%.

FIGURE 3.

Trajectories of rotation angle θ (A, C) and torsion angle χ (B, D), calculated as described in the Appendix. Parameter values: u = 8 and r = 50 (10), φ = 2π/50 (7.2°), D_b = 0.256 rad²/s, corresponding to a frictional drag coefficient 2π k_BT/D_b = 0.1 nN nm rad⁻¹ Hz⁻¹ (8), d = 20, k_χ = 0.4 nN nm/rad² (9), 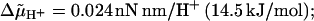T_ex /(nN nm rad⁻¹) = 0 (a), 1.5 (b), −1.53 (c); temperature, 22°C; sampling time, 5 ms; bidirectional stepping model, σ = 0.8 nN nm/rad², α₀ = 200 s⁻¹, λ = 0.5 (A, B); unidirectional stepping model, σ = 23.9 nN nm/rad², α₀ = 500 s⁻¹, λ = 0 (C, D). The relaxation time (ms) for χ (t) in B and the frequency f (Hz) at steady state in A are 13.6 ± 0.7 and 8.7 ± 0.3 (a), 10.2 ± 1.1 and 19.9 ± 0.4 (b), 17.2 ± 0.4 and 0.002 ± 0.2 (c), respectively. The corresponding values for D and C are 41.1 ± 1.6 and 8.6 ± 0.4 (a), 44.4 ± 2.3 and 8.5 ± 0.4 (b), and 42.4 ± 0.6 and 8.8 ± 0.4 (c), respectively.

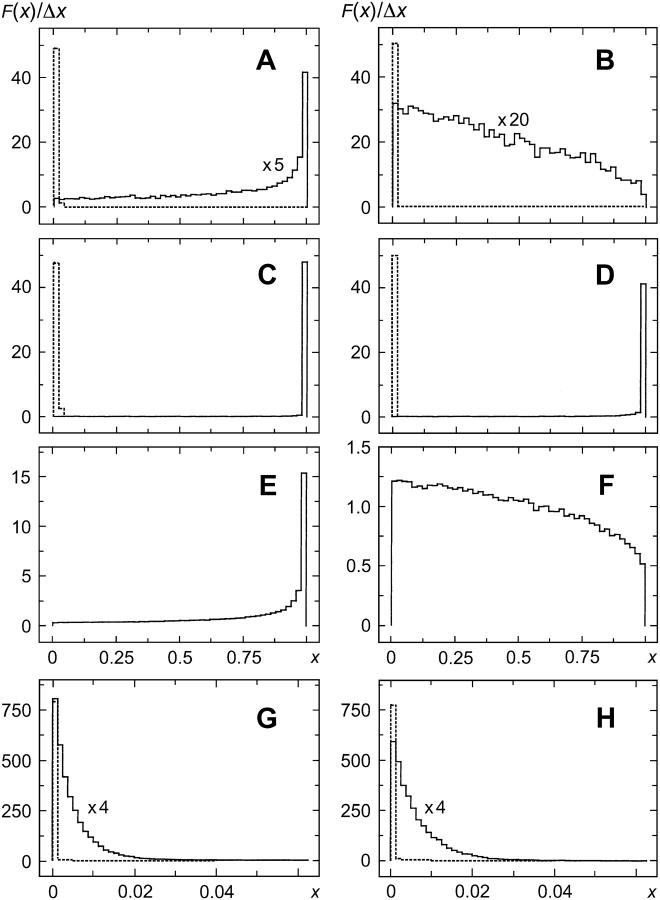
FIGURE 4.

Partition functions (histograms) for values of g_± (Eq. 22) and g (Eq. 27) at the end of the time intervals Δt_i. F(x) denotes the normalized frequency with which values of the variable x were found in the interval from x to x + Δx, x represents g₊(Δt_i) (solid line), g₋(Δt_i) (dotted line) in A–D, G, and H, or g(Δt_i) in E and F; Δx = 0.02 (A–F) and 0.00125 (G, H). For graphical reasons F(x) for g₊(Δt_i) in A, B, G, and H is multiplied by a factor as indicated. Bidirectional stepping model with T_ex = 0 (A) and 3 nN nm/rad (B); unidirectional stepping model with α₀ = 500 s⁻¹ (C, E) and 2000 s⁻¹ (D, F) for d = 20 (elastic tether, C and D) and d = 0 (stiff tether, E and F); model of Ryu et al. (1) with T_ex = 0 (G) and 40 nN nm/rad (H), in this case F(x) ≡ 0 for x > 0.0625. Other parameter values are given in the legends to Figs. 3 and 5. The relaxation times τ₊ (μs) and τ₋ (ms) are 113 and 44.4 (A, B); 3.96 and 42.1 (C, D); and 175 and 45.8 (G, H), respectively, whereas τ_b = 87.4 μs (E, F). The mean values of the time intervals Δt_i (μs) obtained from the simulations are 242 ± 252 (A), 76 ± 79 (B), 286 ± 284 (C), 73 ± 75 (D), 291 ± 297 (E), 73 ± 74 (F), 0.82 ± 0.86 (G), and 1.08 ± 1.11 (H); note that the standard deviations are close to the mean values as required for a Poisson distribution.

Unidirectional stepping should be possible when λ is set to 0, i.e., α_j+ = α₀ (Eq. 7a), and the elasticity coefficient σ of the stalks is increased until the usually negative term commencing with σ in Eq. 7b becomes large enough to satisfy the condition α_j− → 0. Simulations with increasing values of σ revealed that back-steps persist (and even increase in frequency) until a critical value of 22.8 nN nm/rad² is reached. Upon further increase of σ there is an increasing incidence of steps for which the quantity ξ_j0(t_i) − φ/2 is positive (i.e., α_j− → ∞), and α_j− for these steps has to be set to 0 to eliminate very large and physically meaningless values of α_j−. The critical value of σ causes τ_b and thus τ₊ (Eqs. 17 and 22) to be so small that g₊(Δt_i) is larger than 0.94 (see Fig. 4, C and D), i.e., relaxation of the displacements ξ_j during the time intervals Δt_i is essentially complete. On the other hand, a (Eq. 16) and thus q (Eq. 23) approach unity, which in turn causes τ₋ (Eq. 22) to be so large that g₋(Δt_i) ≤ 0.04, i.e., the tether still does not relax to an appreciable extent. Such a unidirectional stepper, however, is insensitive to an externally applied torque T_ex (see Fig. 3 C), and its frequency f is solely determined by α₀. Hence, the only possible means of changing f is by direct alteration of α₀, which would require changing the temperature rather than imposing an external torque. A simulation of this case indeed yields a value of m close to 2 (Fig. 5, case 3), but the value of 〈k〉 is ∼200 instead of 400 as predicted by Samuel and Berg (10). This arises from the exclusion of steps due to steric hindrance. If this condition is released, m ≈ 2 and 〈k〉 ≈ 400 are obtained (not shown), but almost all α_j− values tend to infinity and have to be eliminated. Moreover, a crossing-over of units occurs, and the displacements attain unrealistically high values of up to 12π.

Ryu et al. (1) have proposed a stepping model in which each step comprises three substeps covering 5%, 90%, and 5% of the step interval, respectively, with a corresponding subdivision of 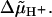This model is sensitive to T_ex despite the condition λ = 0 for the rate constants of all substeps, but Monte Carlo simulations performed with this model yield again an m value of 3 (Fig. 5, case 4).

Nonstepping model

We have shown (8) that an entirely different model based on electrostatic interactions, in which no attachment points are present and hence no stepping occurs, reproduces the results of a wide variety of different studies, providing two proton channels are assigned to each force-generating unit; biochemical evidence that this is probably the case has since been presented (11,12). The simulations with this model were previously carried out using a deterministic (kinetic) methodology. We have reexamined this model using Monte Carlo simulations (13) and including Brownian motion, thus making fluctuation analysis possible. The results are not only fully in agreement with our earlier simulations, but yield a value of m close to 2 for the simulation of the Samuel and Berg study (7) (Fig. 5, case 5).

DISCUSSION

The stepping model proposed by Ryu et al. (1) incorporates three states per step in which the units are always bound to the attachment points (high duty ratio). It is purely phenomenological, since no mechanistic explanation is provided as to how the transport of protons through the channel of a unit causes its release from an attachment point and its movement to the adjacent point. Moreover, proton movement is described in terms of 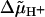instead of explicitly in terms of proton concentrations and a membrane potential (8,14). The value of the intrinsic rate constant α₀ necessary for the simulation of the experimental results gives rise to time intervals Δt_i, which are at least two orders-of-magnitude smaller than the relaxation times τ₊ and τ₋. Hence g_±(Δt_i) ≤ 0.04 (Fig. 4, G and H), i.e., there is very little relaxation of the displacements ξ_j as well as of the tether, and the term σφ (ξ_j0(t_i) − φ /2) in Eq. 7b is rather small. As a consequence, despite the setting of λ = 0, considerable “back stepping” occurs (49% and 34% for T_ex = 0 and 40 nN nm rad⁻¹, respectively). In addition, as already noticed by Ryu et al. (1), the model is rather insensitive to the value of σ if chosen in a physically reasonable range, which can be estimated from the elastic parameters of actin filaments (15,16). It is therefore not surprising that this model cannot reproduce the experimentally observed inverse second-power dependence of variance on frequency.

For reasons of consistency we have adopted the approach of Ryu et al. (1) when designing our stepping model. This model can be considered to be a simplified version of the three-state model in which binding, release, and transfer of protons in a channel all take place in one step. Although this simplification reduces the number of possible transitions by a factor of 3, a rate-limiting step still does not appear if physically reasonable parameter values are used. Such a step can only occur if λ is set to zero and the stalks are assumed to be extremely stiff. This, however, eliminates the dependence on 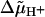since α_j+ = α₀ (Eq. 7a) and back steps whose rate constants α_j− depend on 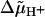are excluded. On the other hand, for the intrinsic stepping expressed by the rate constant α₀, the considerable elastic work involved in the movement of a unit between attachment points (see Eq. 30) would have to be covered by thermal energy, which is already highly unlikely at the critical value of σ and is even less feasible as σ becomes larger. We also find that the presence of T_ex does not alter the rotational frequency f (Fig. 3 C, and additional simulations with T_ex up to 200 nN nm rad⁻¹), in clear contradiction to what was found experimentally (7,17). Moreover, the unidirectional stepping model cannot reproduce the experimentally observed proportionality between f and the number of units (10). Simulations with u = 4 and 1 yield frequencies which are, respectively, 8% and 17% larger than those for u = 8. The corresponding m values are still close to 2, whereas the 〈k〉 values decrease to ∼140 and 60, respectively. Hence it appears that the model used by Samuel and Berg (7) to explain the observed inverse second-power dependence of variance on frequency is neither physically feasible nor able to reproduce experimental results.

The rotational mobility of the rotor plus tether expressed by the parameter D_r plays only a minor role. Simulations performed with different values of D_r up to the limit of 1280 rad² s⁻¹, which corresponds to a frictional drag coefficient 2π k_BT/D_r = 2 × 10⁻⁵ nN nm rad⁻¹ Hz⁻¹ as estimated by Berg (3) for a freely movable rotor in a lipid phase, revealed that D_r merely affects the time required for the system to reach the steady state, whereas the characteristics outlined above are not altered. In particular, the model with the large value of σ required for unidirectional stepping remains insensitive to an externally applied torque T_ex even for the largest value of D_r. In fact, the rather stiff elements in this model firmly connect the cell body to the rotor plus tether, which makes them behave as one rigid body. As a consequence, in contrast to the case of the less rigid stalks, T_ex (which acts on the cell body) has no effect on the rotational frequency but manifests itself entirely in an altered average steady-state tether angle χ_ss (Fig. 3 D) at which the restoring torque k_χ χ_ss is balanced by the average elastic torque 〈T_el〉 and T_ex. Thus it would seem that the picture envisaged by Berg (3,18) for a stepping motor cannot hold true. In that picture the stepping of a unit first predominantly winds up the more mobile tether, which subsequently relaxes, thus carrying the cell body forward. However, this postulated relaxation of the tether is imperceptibly small in our simulations (see Fig. 4).

A rigid tether is obtained if D_r is set to zero, and Eq. 20 is then replaced by Eq. 26 (see Appendix). Simulations and variance analyses under this condition yield essentially the same results as with an elastic tether. The m values are slightly decreased by ∼0.2 for the model of Ryu et al. (1) and our stepping model with λ = 0.5 (i.e., bidirectional) and σ = 0.8 nN nm/rad². They remain at ∼2 for our model with λ = 0 (i.e., unidirectional) and σ ≥ 22.8 nN nm/rad². However, the function g(Δt_i) in Eq. 27, which is analogous to g₊(Δt_i) in Eq. 20, adopts all possible values in the interval from 0 to 1 with variable frequencies depending on the value of α₀ (Fig. 4, E and F). This indicates that relaxation of the displacements ξ_j during the time intervals Δt_i is mostly incomplete under these circumstances, but this criterion seems not to be crucial for m to attain a value close to 2.

Brownian motion was excluded from the simulations with the stepping models in order not to blur the stepping behavior. Including Brownian motion has little effect on the model of Ryu et al. (1) and our model with λ = 0 and σ ≥ 22.8 nN nm/rad², but decreases m by ∼0.4 if λ = 0.5 and σ = 0.8 nN nm/rad². It should be mentioned that Brownian motion in a broken motor yields, for all models, m ≈ 3 (not shown), as is experimentally observed.

The experimental finding that the motor in de-energized cells appears to be “locked” (9) may be considered as evidence for a motor with units always bound to attachment points. However, simulations with the stepping models as well as with our electrostatic model at 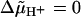did not show any locking of the motor. But we can reproduce this phenomenon if we assume closure of proton channels upon de-energization, in analogy to the closure of channels in a sodium ion-driven motor (11). Hence it is not the type of interaction between rotor and stator (binding of units or electrostatic interaction) but the restricted proton movement that causes the locking of the motor.

In conclusion, the inverse second-power dependence of variance on frequency (Eq. 1) is not a suitable criterion for stepping; in fact a nonstepping mechanism can comply with this criterion, whereas a stepping mechanism in many cases does not. Hence there is no evidence for the notion (1,3,7) that the flagellar motor operates in a stepwise mode with units that are virtually always engaged (high duty ratio).

APPENDIX A

Motor rotation due to stepping of units and relaxation of elastic elements as well as elastic tether

Let θ′ and χ′ denote the advancement of θ and χ during the relaxation period Δt_i = t_i+1 − t_i, respectively, such that

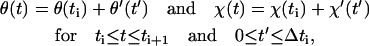(9)

where

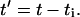(10)

Since all units are attached to the rotor and the cell body during this period, i.e., a duty ratio of 1 (see Ref. 1),

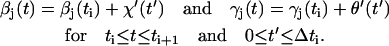(11)

Hence by means of Eq. 2,

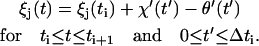(12)

Recalling that ξ_j0(t_i) denotes displacements just before the stepping of the k^th unit occurs, it follows that

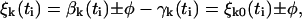(13a)

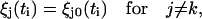(13b)

where φ = 2π/r. Note that steps of +φ and −φ give rise to positive and negative contributions to the displacement, respectively. Inserting Eqs. 4, 9, 10, 12, and 13 into Eqs. 5 and 6 yields

(14a)

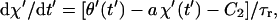(14b)

with the abbreviations

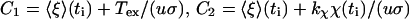(15)

and

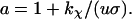(16)

Here τ_b and τ_r are scaling factors denoting, respectively, characteristic rotation times of the cell body and the rotor plus tether, and are defined as

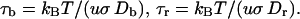(17)

The quantity 〈ξ〉(t_i) is the average displacement just after the k^th unit has stepped,

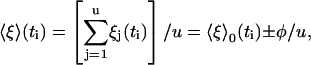(18)

where

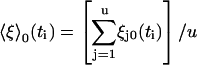(19)

is the average displacement just before stepping of the unit. The solutions to Eqs. 14 satisfying the boundary conditions θ′(0) = χ′(0) = 0 are found to be

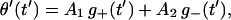(20a)

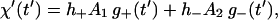(20b)

where

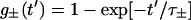(21)

and the relaxation times τ_± are defined as

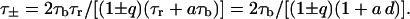(22)

The quantities d, q, and h_± are abbreviations that read

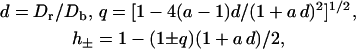(23)

and the constants A₁ and A₂ are given by

(24a)

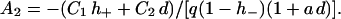(24b)

Since the ξ_j values reached at the end of the i^th time interval Δt_i are the ξ_j0values of the next interval starting at t_i+1, it follows from Eq. 12 that

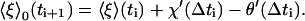(25)

Special case D_r → 0

This case corresponds to a rigid or motionless tether. Here d → 0, q → 1, h₊ → 0, h₋ → 1 (Eq. 23), τ₊ → τ_b (Eq. 22), and A₁ = C₁ (Eq. 24a). The term A₂ g₋(t′) can be shown, by L‘Hopital’s rule, to go identically to zero in this limit. Hence

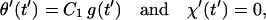(26)

where

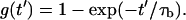(27)

Kinetics

Following Ryu et al. (1) the rate constants α_j+ and α_j− describing the stepping of the j^th unit are assumed to be determined by an intrinsic rate constant α₀ and a Boltzmann factor which comprises the difference in free energy ΔG_j± associated with the step and a coefficient λ reflecting the position of the transition state in the step,

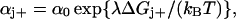(28a)

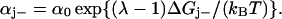(28b)

ΔG_j± is composed of two terms, the free energy which powers the rotation, i.e., 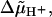and the difference in elastic energy ΔG_j,el between the initial and the final state of the step in the direction that gives rise to a positive contribution to T_el. The elastic energy can be determined by integrating the relation

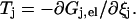(29)

Hence by means of Eq. 3, and with the boundary condition G_j,el = 0 for ξ_j = 0,

(30)

Since the displacements ξ_j0(t_i) and ξ_j(t_i) represent the initial and final states of a step by +φ, but the final and initial states of a step by −φ, the difference in free energy becomes (see Eq. 30)

(31)

Inserting Eqs. 13a (with k = j) and 31 into Eqs. 28 then yields Eqs. 7.

Monte Carlo simulations

For the Monte Carlo simulation (13) it is convenient to renumber the rate constants as

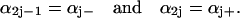(32)

The order of the renumbered rate constants is not crucial. An alternative numbering yielding the same results is α_j = α_j− and α_{u+ j} = α_j+. The time interval Δt_i at the time point t_i is then given by

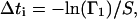(33)

whereas the index k satisfying the condition

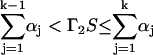(34)

determines which unit steps, and in which direction. In Eqs. 33 and 34 the quantities Γ₁ and Γ₂ are random numbers drawn from a unit-interval uniform distribution, and S denotes the sum over all rate constants:

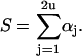(35)

Since binding of two units to the same attachment point should be excluded for steric reasons, a bookkeeping of occupied attachment points is performed, and the rate constant of a step which would end in an occupied attachment point is set to zero.

Trajectories θ(t) and χ(t) can then be calculated by means of Eqs. 7, 9, and 15–25, starting from the initial conditions t₀ = θ (t₀) = χ(t₀) = 〈ξ〉₀(t₀) = 0.

APPENDIX B: GLOSSARY

a

Dimensionless quantity defined by Eq. 16.

D_b

Rotational diffusion coefficient of cell body.

D_r

Rotational diffusion coefficient of rotor plus tether.

d, q, h₊, h₋

Dimensionless quantities defined by Eqs. 23.

F(x)

Normalized frequency with which values of x occur in the interval x to x + Δx.

f

Rotational frequency.

g₊, g₋, g

Exponential functions associated with τ₊, τ₋, and τ_b, respectively (Eqs. 21 and 27).

k

Number of elementary steps per revolution.

k_B

Boltzmann's constant.

k_χ

Torsional spring constant of tether.

m

Exponent of f in expression for V: for a Poissonian stepper m = 2.

n

Number of revolutions.

r

Number of attachment points.

T

Absolute temperature.

T_el

Total torque exerted by all elastic units.

T_ex

Externally applied torque.

T_j

Torque exerted by j^th unit on rotor.

t

Time.

u

Number of stepping units.

V

Variance in time taken for n revolutions at rotational frequency f.

α_j+, α_j−

Rate constants specifying the stepping of the j^th unit.

α₀

Intrinsic rate constant.

β

Angle specifying attachment point of stepping unit to rotor.

Γ₁, Γ₂

Random numbers drawn from a unit-interval uniform distribution.

γ

Angle specifying attachment point of stepping unit to cell body.

ΔG_j+, ΔG_j−

Free energy differences associated with the j^th step.

ΔG_j,el

Elastic energy difference between initial and final state of the j^th step.

Δt_i

Time interval between steps at time points t_i and t_i+1.

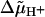
Electrochemical potential difference for protons driving rotation.

θ

Rotation angle of cell.

λ

Coefficient reflecting the position of the transition state in a step.

ξ

Angular displacement of a stepping unit from its rest position.

σ

Elasticity coefficient of stepping unit.

τ_b, τ_r

Characteristic rotation times of cell body and rotor plus tether, respectively.

τ₊, τ₋

Relaxation times governing unit displacements and tether torsion, respectively.

φ

Elementary angular step.

χ

Torsion angle of tether.

χ_ss

Average steady-state torsion angle of tether.

′

Denotes an incremental change between steps (e.g., θ′).