Influence of the Long-Chain/Short-Chain Amphiphile Ratio on Lateral Diffusion of PEG-Lipid in Magnetically Aligned Lipid Bilayers as Measured via Pulsed-Field-Gradient NMR

Abstract

Lateral diffusion measurements of polyethylene glycol(PEG)-lipid incorporated into magnetically aligned lipid bilayers, composed of dimyristoyl phosphatidylcholine (DMPC) plus dihexanoyl phosphatidylcholine (DHPC) plus 1 mol % (relative to DMPC) dimyristoyl phosphatidylethanolamine-n-[methoxy(polyethylene glycol)-2000] (DMPE-PEG 2000), were performed using stimulated-echo pulsed-field-gradient proton (¹H) nuclear magnetic resonance spectroscopy. The DMPE-PEG 2000 (1 mol %, 35°C) lateral diffusion coefficient D varied directly with the mole fraction of DMPC, X_DMPC = q/(1+q) where q = DMPC/DHPC molar ratio, decreasing progressively from D = 1.65 × 10⁻¹¹ m² s⁻¹ at q ≈ 4.7 to D = 0.65 × 10⁻¹¹ m² s⁻¹ at q ≈ 2.5. Possible sources of this dependence, including orientational disorder, obstruction, and PEG-lipid sequestration, were simulated using, respectively, a diffusion-in-a-cone model, percolation theory, and a two-phase PEG distribution model. Orientational disorder alone was not capable of reproducing the observations, but in combination with either obstruction or PEG-lipid two-phase distribution models did so satisfactorily. A combination of all three models yielded the most reasonable fit to the observed dependence of lateral diffusion on q. These same effects would be expected to influence lateral diffusion of any bilayer-associating species in such systems.

INTRODUCTION

Lateral diffusion of bilayer membrane components is fundamental to membrane function, and lateral diffusion measurements provide a valuable perspective on membrane structure and lateral organization (1–5). The most widely and successfully employed technique for determining membrane lateral diffusion coefficients involves fluorescence-recovery-after-photobleaching (FRAP) measurements on fluorophore-tagged membrane-bound diffusants (2,3).

To avoid FRAP's requirement for an attached fluorophore with its attendant synthetic challenges and concerns regarding perturbation, nuclear magnetic resonance techniques have been developed for measuring lateral diffusion coefficients in bilayer membranes. One such technique, described recently, uses pulsed-field-gradient (PFG) nuclear magnetic resonance (NMR) spectroscopy to measure membrane lateral diffusion coefficients in magnetically aligned lipid bilayers (6). In PFG NMR a pulsed linear gradient of magnetic field is imposed across the sample such that the nuclear spin resonance frequency becomes transiently position dependent (7). The experiment is arranged such that refocusing of the nuclear-spin magnetization in an echo-type sequence decreases with increasing translational diffusion in the direction of the applied field gradient. The PFG NMR method is well established in studies of molecular diffusion in both isotropic and anisotropic media (for reviews, see 8–11), and has been applied to study lateral diffusion in lipid bilayers either under magic-angle spinning conditions (12), or macroscopically aligned between glass slides oriented at the magic-angle (13,14), both of which situations produce narrow resonance lines.

Bicelles, or bilayered micelles, also yield narrow NMR resonances by virtue of their tendency to spontaneously align in magnetic fields. They consist of mixtures of long chain and short chain amphiphiles which self-assemble such that the long-chain amphiphiles form a planar lipid bilayer whereas the short-chain amphiphiles segregate to regions of high curvature at the edges of the bilayer (for reviews, see 15–17). When placed in a magnetic field, bicelles composed of mixtures of dimyristoyl phosphatidylcholine (DMPC) with dihexanoyl phosphatidylcholine (DHPC), first introduced by Sanders and Schwonek (18), spontaneously align such that the normal to the plane of the lipid bilayer is oriented perpendicular to the direction of the magnetic field (19). It has been demonstrated that PFG ¹H NMR on magnetically aligned bicelles, in the case of a magnetic field gradient oriented perpendicular to the direction of bicellar alignment, directly measures lateral diffusion within the plane of the bicelle's lipid bilayer (6).

Despite their wide popularity in NMR studies, critical details of bicelle morphology remain controversial. The classical view holds that bicelles consist of planar disks having DMPC sequestered to the planar bilayer disk body with DHPC sequestered to the highly-curved disk edges (15). Although there is general agreement that this disk morphology pertains at temperatures below the DMPC phase-transition temperature and at low lipid concentrations and low DMPC/DHPC ratios, where the bicelles are small and free to tumble isotropically, at higher lipid concentrations and/or higher DMPC/DHPC ratios small-angle neutron scattering (SANS) studies indicate a conversion to a morphology consisting of DMPC-rich continuous bilayer lamellae perforated by toroidal holes lined with DHPC (20,21). This view has received support from fluorescence-resonance-energy-transfer studies (22), but remains controversial (23,24).

PFG NMR lateral diffusion measurements of bicelle-incorporated polyethylene glycol (PEG)-lipids indicate that, for DMPC/DHPC = 4.5 bicelles, PEG-lipids experience unrestricted lateral diffusion over diffusion distances on the order of microns, a finding that supports the perforated lamellae model rather than the disk model of bicelle morphology (6). PEG-lipids are added to bicelles to enhance bicelle stability by virtue of steric stabilization (25). They consist of a hydrophobic anchoring group, such as dimyristoyl phosphatidylethanolamine (DMPE), to which a PEG group is covalently attached through the lipid's polar headgroup. The water-soluble PEG becomes effectively grafted to the lipid bilayer surface through its DMPE hydrophobic anchor. Lateral diffusion of PEG-lipid is particularly facile to measure using PFG ¹H NMR because the PEG headgroup is highly mobile and provides a narrow NMR resonance.

The ratio of long-chain to short-chain amphiphiles in the bicelle mixture is a critical determinant of bicelle morphology. To date, its influence on lateral diffusion within bicelles has not been investigated, but one anticipates several possible mechanisms through which such influence might be exerted. In particular, if there is a morphological change from a perforated lamellar to a discoidal phase, then lateral diffusion will become restricted by the dimensions of the disks. Further, regardless of the morphological phase, bicelle orientational order decreases with decreasing DMPC/DHPC ratio (15), an effect likely to decrease the apparent lateral diffusion coefficient. Moreover, any DHPC-rich toroidal perforations, the number and/or size of which depend on the DMPC/DHPC ratio, will act as obstructions to lateral diffusion. Finally, PEG-lipids partition between highly curved and planar regions of bicelles (26–28), where their diffusion properties should differ markedly—resulting in an altered PEG-lipid lateral diffusion with increasing DHPC content.

Ultimately, it is desired to develop bicelles as a general platform for lateral diffusion measurements of not just PEG-lipid, but any amphiphilic membrane-associating species whether protein, or lipid, or drug. Consequently, we have undertaken PFG ¹H NMR measurements of the lateral diffusion of PEG-lipids in magnetically aligned DMPC plus DHPC bicelles as a function of the ratio q = DMPC/DHPC to examine the influence of this critical parameter, to better understand bicelle morphology, and to potentiate measurements on a wider range of diffusants.

EXPERIMENTAL MATERIALS

1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC), 1,2-dihexanoyl-sn-glycero-3-phosphocholine (DHPC), and 1,2-dimyristoyl-sn-glycero-3-phosphoethanolamine-n-methoxy(polyethylene glycol)-2000 (DMPE-PEG 2000) were purchased from Avanti Polar Lipids (Alabaster, AL). All other biochemicals and reagents were purchased from Sigma-Aldrich (Oakville, ON).

Sample preparation

Bicelles were prepared to consist of either 15 wt % or 25 wt % lipid in aqueous 150 mM NaCl + 50 mM Tris-HCl, ph 7.4, in D₂O, as described previously (29,30). The ratio q, being the proportion of long-to-short chain amphiphiles (DMPC/DHPC), was varied between ∼q = 2.4 and q = 4.7, with the exact value in any one sample being determined via ³¹P NMR spectroscopy. DMPE-PEG 2000 was included in all bicelle preparations at the level of 1 mol % relative to DMPC.

NMR spectroscopy

All NMR spectra were recorded on a Chemagnetics (Fort Collins, CO) CMX300 NMR spectrometer using a magnetic resonance imaging/spectroscopy probe (Doty Scientific, Columbia, SC) equipped with actively shielded gradient coils and dual radio-frequency channels in addition to the lock channel. Note that the various NMR spectra of the magnetically aligned samples investigated here consist of relatively narrow resonances spread over relatively narrow spectral ranges and, as such, may be acquired under conditions usual to solution-state NMR spectroscopy. Details regarding the spectral referencing, acquisition, and processing conditions for ²H, ³¹P, and ¹H NMR spectra are provided elsewhere (6). All spectra were recorded at a sample temperature of 35°C ± 0.5°C.

¹H NMR diffusion measurements were performed using the pulsed-field gradient (PFG) stimulated-echo (STE) procedure (31), with phase cycling of the radio frequency pulses to remove unwanted echoes (32), and a train of gradient pulses to equalize eddy current effects (33), as described previously (6). The gradient strength (typically 250 G cm⁻¹) was calibrated from the known diffusion coefficient of HDO at 25°C (34).

RESULTS AND DISCUSSION

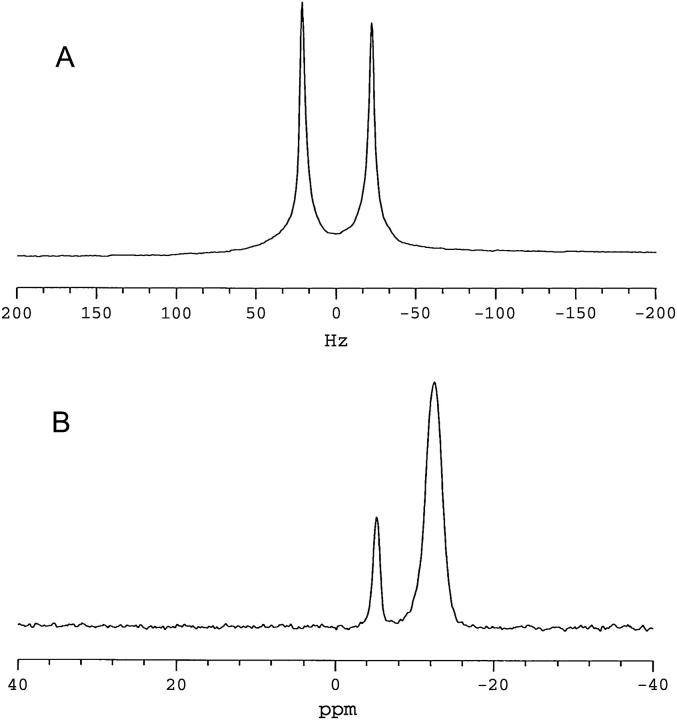
The STE PFG NMR method for bilayer lateral diffusion measurements relies on spontaneous magnetic orientation to produce macroscopically aligned bilayers. To demonstrate that such macroscopic alignment has been achieved, Fig. 1 shows ²H NMR (Fig. 1 A) and ³¹P NMR spectra (Fig. 1 B) of 25 wt % lipid magnetically aligned DMPC/DHPC (q = 4.7) bilayers containing 1 mol % DMPE-PEG 2000, all obtained at 35°C.

FIGURE 1.

NMR spectra (35°C) of magnetically aligned bilayers: DMPC/DHPC (q = 4.7, 25 wt % lipid) + 1 mol % DMPE-PEG 2000. (A) ²H NMR spectrum of HDO. The residual quadrupolar splitting of 44 Hz indicates magnetic alignment of bilayers. (B) ³¹P NMR spectrum showing resonances from DMPC (−12.45 ppm) and DHPC (−5.33 ppm), DMPC/DHPC intensity ratio of 4.7 ± 0.2. The position of the DMPC resonance is indicative of bilayers aligned with their normal to the plane of the bilayer oriented perpendicular to the direction of the magnetic field. The resonance from 1 mol % DMPE-PEG 2000 is not resolved.

Spectrum A is a ²H NMR spectrum of HDO and exhibits a quadrupolar splitting equal, here, to 44 Hz, in agreement with previous reports (19,35,36). The residual quadrupolar splitting arises from fast exchange of HDO between bulk water and oriented water bound at the surface of magnetically aligned lipid bilayers.

Spectrum B in Fig. 1 is a ³¹P NMR spectrum of the same magnetically aligned bilayers and shows two narrow well-resolved resonances. The more intense upfield resonance occurs at −12.45 ppm (referenced to 85% H₃PO₄), a frequency indicative of liquid-crystalline DMPC contained within a magnetically aligned bilayer oriented with its bilayer normal perpendicular to the direction of the magnetic field (15). The second resonance occurs at −5.33 ppm and has an integrated intensity of ∼1/(4.7 ± 0.2) relative to that at −12.45 ppm, indicating that it arises from DHPC. (The signal/noise ratios of the DMPC and DHPC resonances were 60 and 30, respectively, equating to a 5% error in the determination of q through this method.) The smaller residual chemical shift anisotropy of DHPC relative to DMPC is a consequence of the former's tendency to segregate into regions of high local curvature. The ³¹P NMR spectra confirm, therefore, that magnetic alignment of the bilayers has been achieved, and that the alignment of the bilayer normal is perpendicular to the magnetic field direction. The ³¹P NMR resonance due to 1 mol % DMPE-PEG 2000 is too small to discern in such spectra.

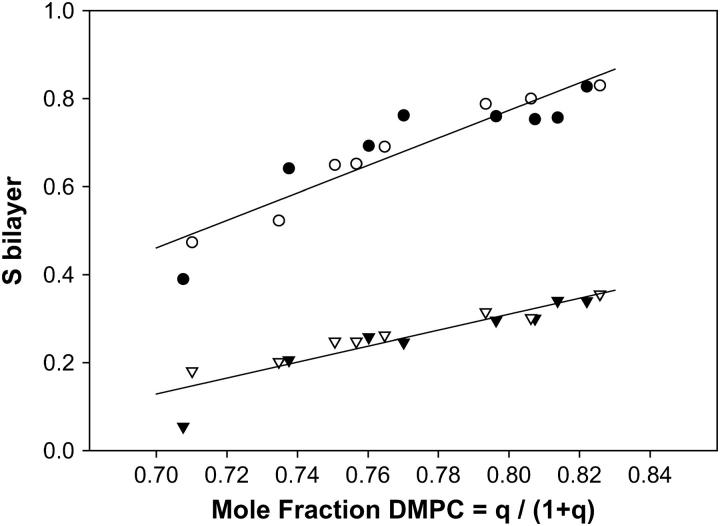
Fig. 2 illustrates the effects of varying q on the ³¹P NMR residual chemical shift anisotropy of DMPC and DHPC, where we convert to the less commonly used but more transparent variable of the mole fraction of DMPC, X_DMPC = q/(1 + q). There is a general trend toward lower values of these anisotropic quantities with decreasing X_DMPC, as expected given that q scales the system order. For the case of chemical shift anisotropy one may quantify the order parameter S_bilayer as described by Sanders et al. (15),

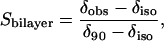(1)

where δ_obs is the observed ³¹P NMR chemical shift of the perpendicular aligned bilayers relative to the isotropic chemical shift δ_iso, whereas δ₉₀ is the chemical shift of the 90°, i.e., upfield, shoulder in the ³¹P NMR powder spectrum of corresponding nonoriented bilayers. S_bilayer, then, quantifies the degree to which the instantaneous symmetry axis of the bilayers deviates from the idealized average orientation of 90° relative to the magnetic field direction. The ³¹P NMR data for DMPC and DHPC are expressed in this fashion in Fig. 2, and confirm the trend toward decreasing bilayer order with increasing DHPC, in accord, both qualitatively and quantitatively, with earlier observations (15). Within the limits of the scatter of the data, the relationship between S_bilayer and X_DMPC is approximately linear. No consistent difference was discernible between samples containing 15 wt % and 25 wt % lipid.

FIGURE 2.

Bilayer orientational order as a function of the mole fraction of DMPC. S_bilayer was calculated from the ³¹P NMR chemical shift as per Eq. 1 in the text. The mole fraction of DMPC was calculated using X_DMPC = q/(1+q) where q was derived from the relative integrated intensities of the ³¹P NMR resonances of DMPC versus DHPC. Circles, DMPC; triangles, DHPC. Open symbols, 25 wt % lipid; solid symbols, 15 wt % lipid. The straight lines show linear regression fits to the combined 15 and 25 wt % lipid data. For DMPC the regression line has slope 3.13, intercept −1.73, and r² 0.87. For DHPC the regression line has slope 1.81, intercept −1.14, and r² 0.86.

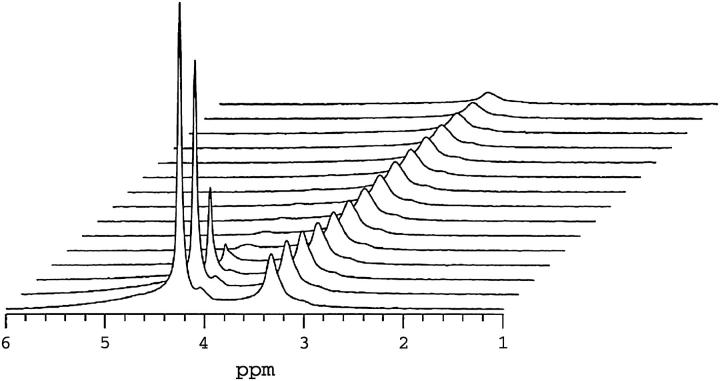
Fig. 3 shows a series of ¹H NMR spectra from q = 4.7 (25 wt % lipid, 35°C) mixtures containing 1 mol % DMPE-PEG 2000 as a function of increasing gradient-pulse duration δ in the stimulated-echo (STE) pulsed-field-gradient (PFG) NMR pulse sequence (31), employed here for measurement of lateral diffusion coefficients. The two dominant resonances are those of HDO (4.2 ppm) and the overlapping resonances of the DHPC choline methyl protons (3.2 ppm) and the PEG ethylene oxide protons (3.3 ppm). The rationale for this assignment has been described previously (6). The broad ¹H NMR resonances expected from the acyl chain, glycerol backbone, or headgroup protons of DMPC (37,38), all of which experience significant residual homonuclear dipolar interactions, are largely absent with an echo delay time of 10 ms due to rapid transverse relaxation. The PEG headgroup and the DHPC choline methyls, in contrast, experience nearly isotropic motional freedom due to, respectively, rapid rotational isomerization within the ethylene oxides of the PEG headgroup and rapid exchange of DHPC on and off the bilayers. Thus, these resonances are ideally narrow for our STE PFG NMR lateral diffusion measurements.

FIGURE 3.

¹H NMR spectra (35°C) of magnetically aligned DMPC/DHPC (q = 4.7, 25 wt % lipid) + 1 mol % DMPE-PEG 2000 bilayers as a function of the field-gradient-pulse duration δ in the STE PFG NMR sequence. The two major resonances are assigned to HDO (4.2 ppm) and overlapping DPME-PEG 2000 ethoxy and DHPC choline methyl protons (3.3 ppm). Other lipid resonances are not visible due to their short transverse relaxation times relative to the spin-echo delay (10 ms) used in the acquisition of this spectrum. The gradient-pulse amplitude was 250 G cm⁻¹, whereas τ₂ equaled 10 ms and τ₁ equaled 200 ms. Gradient pulse durations were, from front to back in units of ms, 0.1, 0.25, 0.50, 0.75, 1.0, 1.25, 1.5, 1.75, 2.0 2.5, 3.0, 3.5, 4.0, 5.0, and 6.0. The water resonance at 4.2 ppm decays rapidly due to water's fast diffusion. The combined DHPC choline methyl and DMPE-PEG 2000 headgroup resonance at 3.3 ppm decays far more slowly, as expected for bilayer intercalated species.

In STE PFG NMR diffusion measurements, center-of-mass diffusion causes the intensity of the stimulated echo to decay according to Eq. 2,

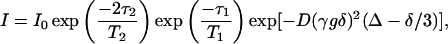(2)

where D is the isotropic diffusion coefficient, γ is the relevant magnetogyric ratio, g is the gradient pulse amplitude, δ is the gradient pulse duration, Δ = τ₁ + τ₂ is the experimental diffusion time, and T₁ and T₂ are the longitudinal and transverse relaxation times, respectively. The gradient pulses are applied during the interpulse delays τ₂ to encode and then decode a given diffusing species according to its chemical shift and any change of position along the gradient direction. During the interpulse delay τ₁, the nuclear spin magnetization is stored along the z-direction so that, for situations where T₁ > T₂, the experimentally accessible diffusion time Δ = τ₁+τ₂ is limited by T₁ rather than T₂. In this way the STE PFG NMR sequence may permit the use of longer diffusion times, thereby facilitating diffusion measurements for cases of slower diffusion, or lower gradient strengths, or lower γ nuclei. Experimentally, either the gradient-pulse amplitude, or its duration, or the diffusion time, is incremented progressively and the diffusion coefficient is extracted from the slope in a plot of Ln(I/I₀) versus (γgδ)²(Δ−δ/3).

The series of ¹H NMR spectra shown in Fig. 3 were acquired as a function of increasing gradient-pulse duration δ with a gradient strength of 250 G cm⁻¹, whereas τ₁ = 200 ms and τ₂ = 10 ms. Of the two dominant resonances, the HDO resonance intensity decays almost immediately to invisibility with increasing δ, due to water's rapid diffusion and the particular choices of gradient strength and delays τ₁ and τ₂. Using Eq. 2 to fit the decay of the proton resonance of HDO in this sample yields a water diffusion coefficient equal to 1.6 × 10⁻⁹ m² s⁻¹. This is roughly a factor-of-two slower water diffusion in oriented bilayers relative to bulk water at the same temperature (34), the difference being attributed to the large fraction of bilayer surface-bound water in fast exchange with the bulk. Since in our measurements the field gradient was applied in a single direction only, perpendicular to the bilayer normal of the aligned bilayers, it is not possible to observe the anisotropy of water diffusion known to occur in macroscopically oriented bilayers in general (39) and in magnetically aligned bicelles in particular (40,41).

In Fig. 3 the combined [DHPC choline methyl + PEG headgroup] resonance decays far more slowly than that of the water, as expected for lipids constrained to diffuse laterally within a bilayer. Importantly, the particular choices of diffusion time Δ = 210 ms and gradient strength g = 250 G cm⁻¹ produce a substantial decay of the resonance intensity over an accessible range of gradient-pulse durations δ, sufficient to measure reliably the lipid's lateral diffusion coefficient.

Lateral diffusion in membranes is inherently anisotropic, so that for field gradients applied solely along the laboratory z-direction, as is the case here, only the D_zz element of the diffusion tensor is measured (7). After transforming into a molecular frame defined with respect to the lipid bilayer, only two independent diffusion tensor elements persist: specifically, D_|| and D⊥ representing, respectively, diffusion parallel and perpendicular to the bilayer normal (13,42). Thus, D⊥ corresponds to lateral diffusion within the bilayer. For the case of macroscopically aligned lipid bilayers in the presence of a field gradient applied parallel to the direction of the main magnetic field, g_z, the measured diffusion coefficient becomes

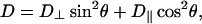(3)

where θ is the polar angle between the bilayer normal and the direction of the applied field gradient.

It is reasonable to assume that diffusion parallel to the bilayer normal is orders-of-magnitude slower than diffusion perpendicular to the bilayer normal, i.e., lateral diffusion, so the second term in Eq. 3 may be ignored. For spontaneously magnetically aligned DMPC/DHPC bilayers, the bilayer normal is oriented at 90° relative to the magnetic field direction. Hence for a perfectly aligned bilayer sample, i.e., having an infinitely narrow mosaic spread of alignments, the apparent diffusion coefficient measured in our STE PFG NMR experiment is directly equal to the lateral diffusion coefficient within the bilayer.

For the case of well-resolved resonances, knowledge of T₁ or T₂ is not essential to diffusion coefficient measurements via the STE PFG NMR technique since typically both τ₁ and τ₂ are constant in any one measurement series. For the case of overlapping or poorly-resolved resonances, however, the echo intensity in the STE PFG NMR experiment is a sum of contributions, and knowledge of the individual T₁ and T₂ relaxation times is a prerequisite to extracting the individual diffusion coefficients from the overall intensity decay.

Table 1 lists values of T₁ and T₂ measured for the combined [DMPE-PEG 2000 headgroup + DHPC choline methyl] resonance in magnetically aligned bilayers at 35°C. The overlapping DHPC choline methyl and PEG resonances have individual T₁ and T₂ relaxation times that are too similar to permit a resolution of their individual contributions to either T₁ inversion recoveries or T₂ spin-echo intensity decays. Hence, a weighted average value of T₁ and T₂ is reported. In all cases T₁ > T₂ by at least an order of magnitude, confirming that the STE PFG NMR sequence is an optimal choice for diffusion measurements in these cases. Although there is significant scatter across the range of sample compositions, in general both T₁ and T₂ are shorter for the 25 wt % lipid than for the 15 wt % lipid samples. Although no consistent dependence of T₁ on q is evident, it appears that lower values of q yield somewhat longer values of T₂.

TABLE 1.

¹H NMR Longitudinal (T₁) and transverse (T₂) relaxation times for combined [DMPE-PEG 2000 headgroup + DHPC choline methyl] resonance in magnetically aligned bilayers at 35°C

				T2¶ (ms)
q = DMPC/DPHC*	XDHPC†	XPEG‡	T1§ (ms)	PEG	DHPC
15 wt % lipid
2.4	0.60	0.40	733	41	15
3.2	0.54	0.46	734	31	23
2.8	0.57	0.43	731	25	15
3.4	0.53	0.47	850	33	29
3.9	0.50	0.50	773	34	27
4.2	0.49	0.51	791	31	28
4.4	0.48	0.52	763	25	20
4.6	0.47	0.53	668	21	21
25 wt % lipid
2.5	0.59	0.41	668	27	10
2.8	0.57	0.43	684	24	11
3.1	0.55	0.45	707	19	11
3.0	0.55	0.45	687	18	12
3.3	0.54	0.46	716	18	11
3.8	0.51	0.49	695	15	11
4.2	0.49	0.51	695	14	10
4.7	0.47	0.53	680	14	13

^*Determined from the relative integrated intensities of the respective ³¹P NMR resonances.

^†The fractional contribution of the nine DHPC choline methyl protons relative to the 1 mol % DMPE-PEG 2000 headgroup protons for the experimentally determined q.

^‡The fractional contribution of the 1 mol % DMPE-PEG 2000 headgroup protons, based on four protons per 45 ethylene oxide units per DMPE-PEG 2000, relative to the DHPC choline methyl protons at the experimentally determined q.

^§The intensities of the combined [DHPC choline methyls + DMPE-PEG 2000 headgroup] proton resonance in the inversion-recovery experiment could not be resolved into separate contributions and were fit as a single exponential having the indicated T₁.

^¶The intensities of the combined [DHPC choline methyls + DMPE-PEG 2000 headgroup] proton resonance in the spin-echo experiment could not be resolved into separately decaying contributions and were fit to a single exponential having the indicated PEG T₂. However, in fitting the diffusion decays according to Eq. 4, better fits were obtained by adjusting the DHPC T₂ to the shorter value indicated in the table.

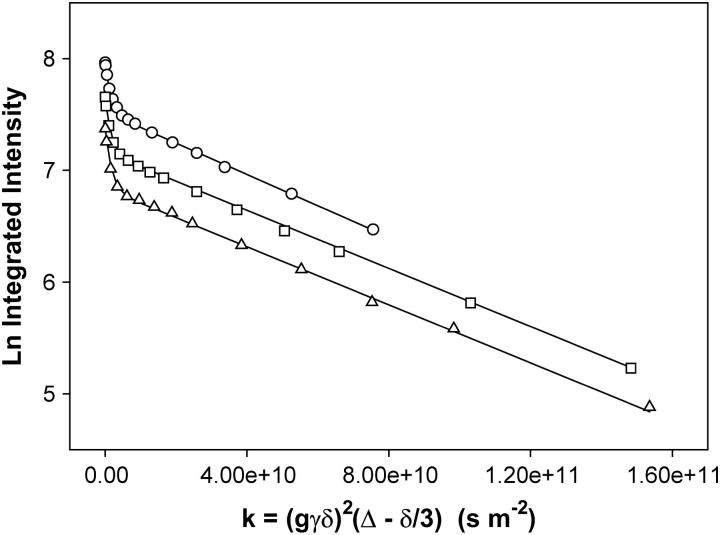
The diffusion coefficient is derived from a plot of Ln (I/I₀) versus (γgδ)²(Δ−δ/3) as shown in Fig. 4. For a population undergoing unrestricted center-of-mass diffusion characterized by a single uniform diffusion coefficient, such a plot should be linear with a slope proportional to the diffusion coefficient. This is clearly not the case for the combined [DHPC choline quaternary methyl + PEG headgroup] resonance. As reported previously (6), the best description of the observed diffusion decay assumes a superposition of decays from two diffusing species, one being DHPC and the other being DMPE-PEG 2000, according to Eq. 4,

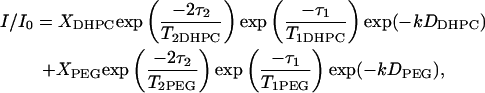(4)

where k = [(γgδ)²(Δ−δ/3)], and X_DHPC = 1−X_PEG is the fractional intensity contributed initially by the DHPC choline quaternary methyl protons, and D_DHPC and D_PEG are the diffusion coefficients of DHPC and DMPE-PEG 2000, respectively. In fitting diffusion data of the type shown in Fig. 4 to Eq. 4, it is assumed that all of the DHPC choline quaternary methyl and the PEG headgroup protons are initially NMR-visible, with intensities modulated by their respective T₁ and T₂ relaxation times. Optimal fits were obtained when T_{2 DHPC} was permitted to vary somewhat, while T_{2 PEG} was held fixed at the value listed in Table 1. Values of T_{2 DHPC} yielding optimal fits were generally somewhat shorter, as listed in Table 1. D_DHPC values were always ∼7.0 × 10⁻¹⁰ m² s⁻¹, in agreement with previous measurements for q = 4.5 bilayers at 25 wt % lipid in water and 35°C (6). The particular choice of T_{2 DHPC} and D_DHPC, in fact, has only a marginal influence on the remaining fitting quantity, D_PEG, since this is determined primarily from the slope of the intensity decay at larger k-values where the intensity contributed by DHPC is minimal due to its faster diffusion. Specifically, for q = 4.7 bilayers containing 1 wt % DMPE-PEG 2000 at 25 wt % lipid and 35°C, D_PEG is found to equal 1.40 × 10⁻¹¹ m² s⁻¹ in the case Δ = 210 ms, which lies in the range expected for a diacyl phospholipid diffusing laterally within the plane of a liquid-crystalline lipid bilayer (3).

FIGURE 4.

Normalized stimulated-echo intensity decays from STE PFG ¹H NMR spectra (35°C) of magnetically aligned DMPC/DHPC (q = 4.7, 25 wt % lipid) bilayers + 1 mol % DMPE-PEG 2000. Gradient amplitude = 250 G cm⁻¹. Circles, Δ = 210 ms; squares, Δ = 410 ms; and triangles, Δ = 610 ms. Lines of best fit using Eq. 4 are shown with D_DHPC = 7.0 × 10⁻¹⁰ m² s⁻¹, values of X_DHPC, X_PEG, T₁, and T₂ as per Table 1, and D = 1.40 × 10⁻¹¹ m² s⁻¹ at Δ = 210 ms, whereas D = 1.3 × 10⁻¹¹ m² s⁻¹ at both Δ = 410 ms and Δ = 610 ms.

The series of three STE PFG NMR intensity decays in Fig. 4 were obtained for the combined [DHPC choline quaternary methyl + DMPE-PEG 2000 headgroup] resonance for three different values of the diffusion time Δ = τ₁ + τ₂ wherein τ₂ was held constant at 10 ms while τ₁ was altered progressively from 200 to 400 to 600 ms. The intensity decay is progressively greater with increasing Δ due to the combined effects of T₁ relaxation and longer diffusion time. The curves of best fit shown in the figure were obtained using Eq. 4, employing the known values of X_PEG and X_DHPC, values of T₁ and T₂ for the DHPC choline methyl and the DMPE-PEG 2000 headgroup protons as per Table 1, allowing D_DHPC to equal 7.0 × 10⁻¹⁰ m² s⁻¹, and inputting D_PEG as the parameter of fit for the three different diffusion times. It is found that with increasing diffusion time Δ, the observed DMPE-PEG 2000 diffusion coefficient decreased only slightly from 1.40 × 10⁻¹¹ m² s⁻¹ at Δ = 210 ms, to 1.3 × 10⁻¹¹ m² s⁻¹ at both Δ = 410 ms and Δ = 610 ms. All three diffusion coefficients fall within the range expected for liquid-crystalline lipids (3).

For all values of q investigated here, the DMPE-PEG 2000 diffusive decays in plots of the type shown in Fig. 4 were linear with increasing δ and the DMPE-PEG 2000 diffusion coefficient was nearly independent of the diffusion time Δ. This indicates that over the range 2.4 < q < 4.7 investigated here, these mixtures retain a perforated lamellar morphology, because the planar regions of this phase form a continuous phase permitting unrestricted lateral diffusion over large distances. Specifically, for two-dimensional diffusion, the root-mean-square (RMS) lateral diffusion distance is calculated according to Eq. 5,

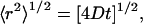(5)

where D is the diffusion coefficient and t = Δ is the characteristic experimental diffusion time. For DMPE-PEG 2000 in magnetically aligned bilayers, where typically D = 1.60 × 10⁻¹¹ m² s⁻¹ and for Δ = 615 ms, the RMS diffusion distance of DMPE-PEG 2000 equals 6.27 μm. The radius of an ideal discoidal bicelle may be calculated for a given q (43) and equals 300 Å for the case q = 4.5, decreasing progressively with decreasing q. Since the experimental RMS lateral diffusion distance far exceeds the size of a single discoidal bicelle, and no evidence of restricted diffusion is apparent (restricted diffusion would produce a flattening of the diffusive decays in Fig. 4 at larger values of k), our results demonstrate that the perforated lamellar phase is maintained over this range of q, temperature, and wt % lipid. Note that this morphology is not unique to DMPC/DHPC mixtures. Perforated, or defective, lamellar phases in fact have been observed in a number of different amphiphilic self-assemblies, and can be shown to align in magnetic fields (Ref. 44 and references therein).

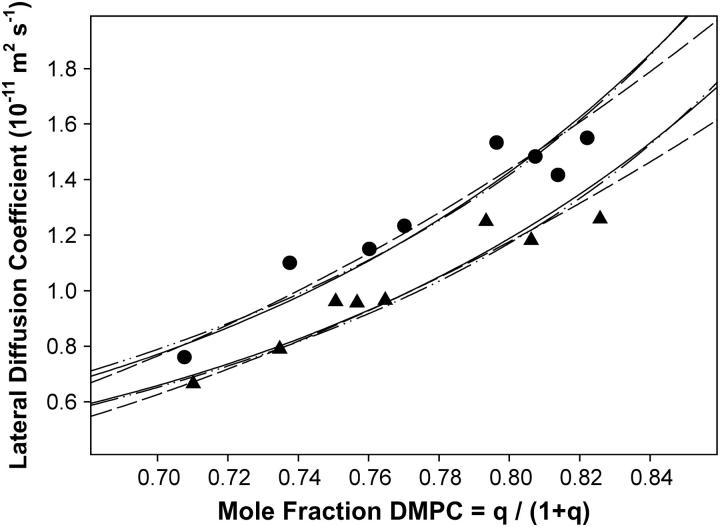
Fig. 5 compares the DMPE-PEG 2000 diffusion coefficients derived from STE PFG ¹H NMR intensity decays for magnetically aligned bicelles at both 15 wt % and 25 wt % lipid, as a function of the mole fraction of DMPC, X_DMPC. There is evidently a progressive decrease in diffusion coefficient with decreasing DMPC content (increasing DHPC). The diffusion coefficients at 25 wt % lipid were consistently smaller than those at 15 wt % lipid.

FIGURE 5.

The STE PFG ¹H NMR derived lateral diffusion coefficient of DMPE-PEG 2000 in DMPC/DHPC magnetically aligned bilayers (35°C) as a function of the mole fraction of DMPC. Values plotted are the mean of diffusion coefficients obtained at Δ = 210, 410, and 610 ms. Triangles, 25 wt % lipid; and circles, 15 wt % lipid. The solid curves are fits to the diffusion data obtained using a combination of orientational disorder, obstruction, and two-phase PEG distribution models as described in the text: order × obstruction, dashed line; order × two-phase, dashed-dotted-dotted line; and order × obstruction × two-phase, solid line.

If there is no morphological change from the perforated lamellar phase over the range of q investigated here, then other sources of the influence of the bilayer DMPC/DHPC ratio q on the lateral diffusion coefficient of DMPE-PEG 2000 in magnetically aligned bilayers as measured by STE PFG ¹H NMR need to be examined. Several likely possibilities can be envisioned. First, since decreasing the ratio q also decreases the bilayer orientational ordering (15), it may be that D is linked to S_bilayer. Second, assuming the perforated lamellar phase applies, decreasing q must increase the surface coverage of toroidal holes, thereby progressively obstructing lateral diffusion. Third, PEG-lipid may distribute between curved and planar regions of the bicelle (26–28), and may experience different lateral diffusion behavior in each, the effect obviously scaling proportionately with q. The focus of the remainder of this article will be to address which, if any, of these possibilities appears reasonable.

Bilayer orientational order and lateral diffusion

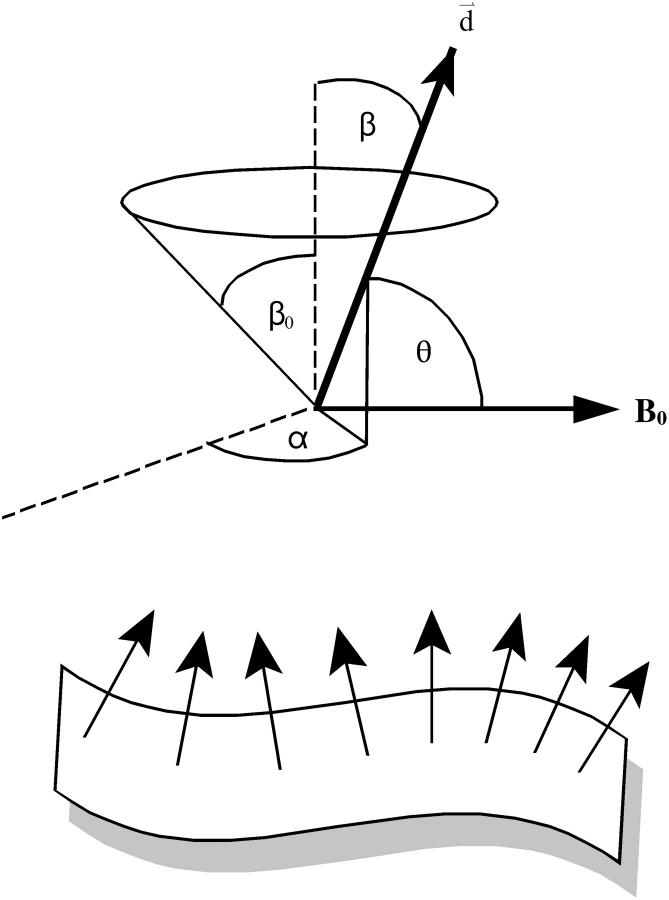
To address the relationship between the apparent diffusion coefficient, D_app, and the magnetically aligned bilayer's orientational order, S_bilayer, we invoke the diffusion-in-a-cone model (45–47) to describe fluctuations of the bilayer normal with respect to the magnetic field direction. We assume that such fluctuations occur in addition to those usually undergone by lipids in bilayer membranes as proposed by Sanders et al. (15) in their definition of S_bilayer. Such motions might consist of collective local fluctuations or undulations occurring with a rate that is fast relative to the measurement time. Hence, the sin²θ term in Eq. 3 must be replaced with its time- and ensemble-average value 〈sin²θ〉 as per Eq. 6,

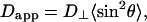(6)

where θ is the angle between the bilayer normal and the direction of the magnetic field gradient. The diffusion-in-a-cone model as applied here assumes that the normal to the bilayer wobbles freely within a cone described by the cone semiangle β₀ and that the wobble is axially symmetric with respect to the azimuthal angle α as illustrated in Fig. 6. The orientational order parameter S_bilayer is then related to the cone semiangle β₀ as per Eq. 7 (45–47),

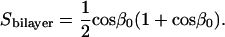(7)

To calculate 〈sin²θ〉 we invoke ergodicity (time-average = number-average over ensemble), and assuming, further, a random distribution of bilayer normal vectors within the cone, we integrate over all values of θ, where cosθ = sinβ sinα for the geometry in Fig. 6, resulting in Eq. 8,

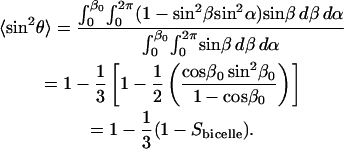(8)

From Fig. 2, over the range 0.7 < X_DMPC < 0.8 (i.e., 2.4 < q < 4.7), S_bilayer decreases from ∼0.80 to 0.40. Eq. 8 predicts, however, a decrease in the apparent diffusion coefficient on the order of only 14% over the same range of X_DMPC. Clearly the decrease in bilayer order alone is not sufficient to entirely explain the >50% reduction in the apparent diffusion coefficient of DMPE-PEG 2000 over the same range.

FIGURE 6.

The diffusion-in-a-cone model as applicable to lateral diffusion measurements in magnetically aligned bilayers using STE PFG NMR measurements. Collective fluctuations of the bilayer normal d modulate the angle θ so that the ensemble- and time-average of 〈sin²θ〉 enters Eq. 6. The normal is considered to diffuse freely in a cone of half-angle β₀, with its instantaneous orientation defined in terms of the polar-angle β and the azimuthal-angle α.

A further refinement of the diffusion-in-a-cone model is to assume a Gaussian distribution about the preferred orientation such that the order parameter is equated to the standard deviation of the Gaussian (45,48). Invoking such a Gaussian distribution, in fact, leads to predicted values of 〈sin²θ〉 equally, or even more weakly, dependent on S_bilayer than those predicted by the constant distribution implicit in Eq. 8.

Toroidal obstruction and lateral diffusion

The DHPC-rich toroidal holes perforating the DMPC-rich lamellae should constitute obstructions to free diffusion. Obstruction effects increase in proportion to the surface area occluded by the obstruction, so that apparent diffusion should decrease with decreasing q-value, in qualitative agreement with our observations. To place this on a more quantitative footing we invoke the theoretical expression, Eq. 9, obtained by Van Beijeren and Kutner (49) for obstructed diffusion (where the relative diffusion coefficient D*(c,γ) = D(c,γ)/D(0) involves the diffusion coefficient D(c,γ) at a concentration c of obstacles of relative mobility γ, and D(0) is the diffusion coefficient in the absence of obstacles),

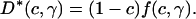(9)

The correlation factor f(c,γ) is

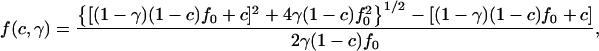(10)

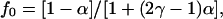(11)

where c is the area fraction of obstacles, γ is the ratio of the mobility of the observed diffusant relative to the obstacles, and α is a constant that depends on the lattice (e.g., square, triangular, or honeycomb).

Saxton (50) compared the results of Monte Carlo simulations of lateral diffusion with the behavior predicted by the theoretical expression of Van Beijeren and Kutner (49) and found generally good agreement. One exception was the situation in which the obstacles were completely immobile, where theory imperfectly predicted the percolation threshold. Another was at high surface coverage of obstacles, where generally there were small but significant discrepancies between theory and Monte Carlo simulation. For our purposes it is important to note that the Monte Carlo simulations of Saxton (50) indicate only a very weak dependence of the obstruction effect on the size of the obstacle, in contrast to the strong effect of the area fraction of obstacles.

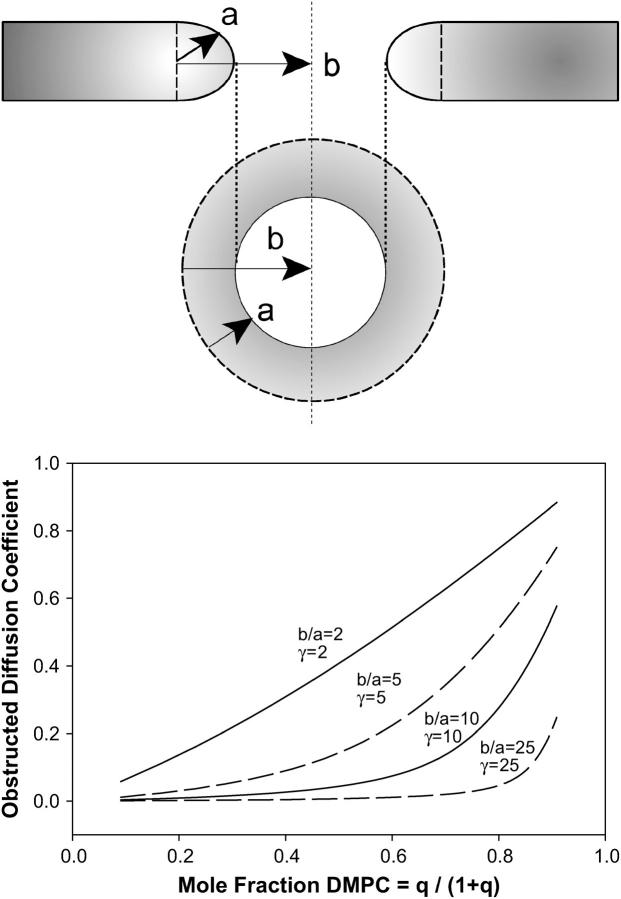
To estimate the surface area fraction of toroidal holes c at a given q-value we assume first an idealized toroid as shown in Fig. 7. It is assumed further that DMPC occupies solely the planar regions whereas DHPC segregates exclusively to the curved edges. This annulus of DHPC has a radial thickness a, whereas the toroidal hole itself has a radius b. Assuming a uniform size of toroidal holes, the fractional surface area obstructed by toroids is

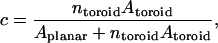(12)

where n_toroid is the number of toroidal obstructions, and A_toroid = πb² (b ≥ a for all cases) is the surface area obstructed by each such toroid. The surface area of the inner toroidal annulus occupied by DHPC is

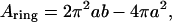(13)

so that the number of DHPC per toroid becomes

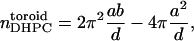(14)

where d is the surface area occupied per DHPC, leading readily to the number of such toroids,

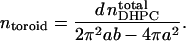(15)

The planar area occupied by DMPC is simply the product of the number of DMPC and the area per DMPC. It is assumed that both DMPC and DHPC occupy identical surface areas d, since the phosphocholine headgroup is common to both. Substituting into Eq. 12, the fractional obstructed surface area becomes, simply,

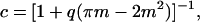(16)

where m = a/b.

FIGURE 7.

Obstruction effects for the perforated lamellae model of bicelle morphology and the predicted effects on PEG-lipid lateral diffusion. The perforated lamellae model posits the presence of DHPC-rich toroidal holes perforating the DMPC-rich bilayer lamella. In the schematic at the top, the toroidal holes are modeled in terms of an annulus of DHPC with radial dimension a and overall radius b, thereby permitting an evaluation of their fractional surface coverage as described in the text, in turn permitting an estimate of obstruction effects on lateral diffusion for a given mole fraction of DMPC and a particular mobility γ of the PEG-lipid relative to the toroidal hole. The graph shows the predicted apparent decrease in PEG-lipid lateral diffusion from such an obstruction model for various dimensions and mobilities of the toroidal holes as a function of the mole fraction of DMPC. Note that only relatively small, mobile holes yield lateral diffusion coefficients near those observed experimentally.

Calculation of the obstructed lateral diffusion coefficient D*(c,γ) requires an estimate of the size ratio m = a/b, where b is the radius of the toroidal holes, plus some estimate of the relative mobility γ of the tracer, i.e., DMPE-PEG 2000, versus the obstructions, i.e., the toroidal holes. Fig. 7 shows the predictions of this obstruction model for the lateral diffusion coefficient as a function of the mole fraction of DMPC for various sizes and mobilities of the toroidal obstructions. As expected, lateral diffusion decreases with increasing number of DHPC-rich toroidal holes, even when these are relatively small (b/a = 2) and mobile (γ = 2). The effect grows profoundly with increasing toroidal size and/or decreasing mobility. Thus, qualitatively, the obstruction model yields the desired dependence of lateral diffusion on the mole fraction of DMPC.

Quantitatively, provided that orientational disorder effects are included as per Eq. 8, the obstruction model provides a reasonable fit to both the 15 and 25 wt % lipid lateral diffusion data for the case b/a = 5 and γ = 15, using a value of D(0) equal to 3.3 × 10⁻¹¹ m² s⁻¹ for 15 wt % and 2.7 × 10⁻¹¹ m² s⁻¹ for 25 wt% lipid, as shown via the dashed line in Fig. 5. The generally accepted hydrodynamic theory of Saffman and Delbrück (51) indicates only a weak logarithmic decrease in lateral diffusion with an increasing radius of diffusant. For instance, large membrane proteins such as the acetylcholine receptor, rhodopsin, and ATPase diffuse only approximately a factor of 2–3 times more slowly than DMPC (1). This suggests that γ = 15 represents unreasonably immobile toroidal holes. As for the size of the toroidal holes, we are not aware of any measurements of their dimension. However, the lateral diffusion coefficients measured here for DMPE PEG 2000 at higher values of q lie very close to those reported for 100% DMPC at comparable temperatures (52), indicating that obstruction effects are minimal at such q-values. This precludes the presence of large holes, since their obstruction effects already would be pronounced in the region X_DMPC ≈ 0.8, and indicates that b/a = 5 is an acceptable choice for the size of the toroidal holes.

Two-phase PEG distribution model and lateral diffusion

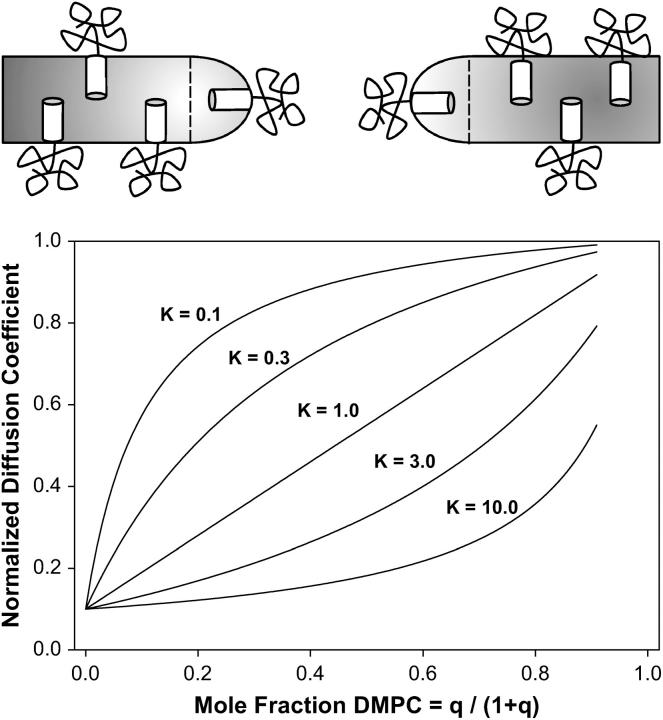
Recent reports (26–28,53) strongly suggest that PEG-lipids accumulate in regions of high curvature, such as the annulus of lipids forming the toroidal holes of the perforated lamellae assumed to exist under the conditions pertinent to our DMPC/DHPC mixtures, as shown schematically in Fig. 8. Since lateral diffusion of any PEG-lipid contained within such a region would be restricted to that of the toroidal hole itself, this suggests that another explanation for the experimentally observed decrease in lateral diffusion of PEG-lipid with increasing mole fraction of DHPC is that PEG-lipid is in fast exchange between planar and highly curved regions of the bicelle assemblies. Slow exchange is precluded by the lack of any experimentally observed nonlinearity of diffusive decay of the PEG-lipid ¹H NMR signal (once DHPC diffusion is accounted for) or dependence on the diffusion time over the range 200 ms < Δ < 600 ms.

FIGURE 8.

The two-phase PEG-lipid distribution model and its predicted effects on PEG-lipid lateral diffusion. PEG-lipid is considered to partition between planar and highly curved regions of the bilayers, as shown schematically at the top. Exchange between the two phases is fast on the NMR experimental diffusion timescale, whereas the partitioning is characterized by a partition constant K. Apparent diffusion along the direction of the applied field gradient (z-direction) is slow within the highly curved region because of geometric effects on sin²θ. The graph shows the predicted apparent decrease in PEG-lipid lateral diffusion from such a two-phase PEG-distribution model for various values of the partition constant K, assuming that diffusion within the highly curved regions is a factor-of-10 slower than in the planar regions. Note that only values of K on the order of unity yield lateral diffusion coefficients near those observed experimentally.

In the case of fast exchange between two phases, the apparent diffusion coefficient equals

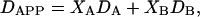(17)

where X_i and D_i represent, respectively, the mole fraction and lateral diffusion coefficient of PEG-lipid in a particular phase (8). For a partition function K = [B]/[A] describing the relative preference for one phase over another, the mole fraction in either phase equals

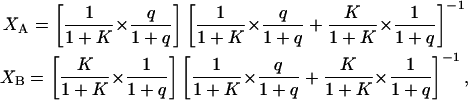(18)

where q = DMPC/DHPC, and phase A is equated with DMPC and phase B with DHPC.

Fig. 8 illustrates the apparent diffusion coefficient predicted by the two-phase PEG distribution model as a function of the mole fraction of DMPC for various values of the partition function K, assuming a 10-fold slower lateral diffusion within the DHPC-rich toroidal holes relative to the DMPC-rich planar regions. Again, the behavior is similar qualitatively to that observed experimentally. Quantitatively, for both 15 and 25 wt % lipid data, only situations with K very large (e.g., 20, indicative of PEG-lipid heavily favoring the DHPC-rich phase) and D_B very slow (e.g., 0.0001 × D_A, indicative of virtually no diffusion of PEG-lipid within the DHPC-rich phase) reproduced the steep dependence of lateral diffusion on X_DMPC, as shown by the dashed-dotted line in Fig. 5, even when in combination with orientational order effects as per Eq. 8. Moreover, it was necessary to assume values of D(0) equal to 9.2 × 10⁻¹¹ m² s⁻¹ for 15 wt % and 7.6 × 10⁻¹¹ m² s⁻¹ for 25 wt % lipid to achieve these fits. These, of course, are unreasonably high relative to literature values (52).

Combined orientational disorder, obstruction, and two-phase model

The three effects discussed here—orientational disorder, toroidal obstruction, and two-phase PEG distribution—should act in concert to influence the observed dependence of PEG-lipid lateral diffusion on X_DMPC in aligned bilayers. To predict their combined effects, the apparent diffusion coefficient in Eq. 17 is assumed to be an average over diffusion within two phases, where within the DMPC-rich planar region the diffusion coefficient of the PEG-lipid is reduced by obstruction, as predicted via Eqs. 9–16, and is scaled by orientational disorder effects, as per Eqs. 6–8. Such a combined model yields good fits to both the 15 and 25 wt % lipid diffusion data, as shown by the solid lines of fit in Fig. 5, using b/a = 4, γ = 4, K = 4, and DB = 0.25 for both, with values of the unperturbed diffusion coefficient D(0) equal to 4.9 × 10⁻¹¹ m² s⁻¹ for 15 wt % lipid and 4.0 × 10⁻¹¹ m² s⁻¹ for 25 wt % lipid. These fitting parameters appear more physically reasonable than those obtained using the obstruction or distribution models alone.

CONCLUSIONS

Lateral diffusion of PEG-lipid in aligned bilayers is influenced by the ratio q of long-chain/short-chain amphiphiles composing the self-assembly. Smaller q equates to slower apparent lateral diffusion. Modeling indicates that this effect can be attributed to a combination of orientational disorder, obstruction by toroidal perforations, and the distribution of PEG-lipid between planar and highly curved phases. These same effects could be expected to influence the observed lateral diffusion of any bilayer-associating species, and unless caution were exercised might confound the analysis of other influences on lateral diffusion such as the presence of cholesterol, proteins, etc. Because the diffusive decays of our stimulated-echo amplitudes are strictly linear and virtually independent of the diffusion time it is not possible for us to differentiate definitively between the obstruction and the two-phase models. For instance, only near the percolation threshold will obstruction effects lead to a diffusion-time-dependent diffusion coefficient (50). But bicelles convert to an isotropic phase at q ≲ 2, so the experiment cannot be performed. However, if the diffusion time can be shortened sufficiently that there is effectively slow exchange of PEG-lipid between the planar and the curved phases, then it may be possible to demonstrate directly the effects of the two-phase PEG-lipid distribution of lateral diffusion.