Behavior of Tn3 Resolvase in Solution and Its Interaction with res

Abstract

The solution properties of Tn3 resolvase (Tn3R) were studied by sedimentation equilibrium, sedimentation velocity analytical ultracentrifugation, and small-angle neutron scattering. Tn3R was found to be in a monomer-dimer self-association equilibrium, with a dissociation constant of 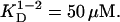Sedimentation velocity and small-angle neutron scattering data are consistent with a solution structure of dimeric Tn3R similar to that of γδ resolvase in a co-crystal structure, but with the DNA-binding domains in a more extended conformation. The solution conformations of sites I, II, and III were studied with small angle x-ray scattering and modeled using rigid-body and ab initio techniques. The structures of these sites do not show any distortion, at low resolution, from B-DNA. The equilibrium binding properties of Tn3R to the individual binding sites in res were investigated by employing fluorescence anisotropy measurements. It was found that site II and site III have the highest affinity for Tn3R, followed by site I. Finally, the affinity of Tn3R for nonspecific DNA was assayed by competition experiments.

INTRODUCTION

Tn3 is the prototype of a family of closely related mobile genetic elements referred to as the class II or Tn3 family of transposons (1). Tn3-family transposons almost always encode a transposase and a site-specific recombinase. The transposase generates, from the donor replicon (containing a copy of the transposon) and the target DNA, a transposition intermediate referred to as a cointegrate, which contains two copies of the transposon. The site-specific recombinase (resolvase) is responsible for the excision of the donor replicon and one copy of the transposon from the cointegrate, leaving behind a simple transposon insertion in the target sequence. res is a specific DNA sequence located in the 170-bp intergenic region between the tnpA (transposase) and tnpR (resolvase) genes of Tn3. These genes are divergently transcribed from promoters within res. In Tn3 transposition, the resolution of the cointegrate is achieved by a serine recombinase, Tn3 resolvase (Tn3R).

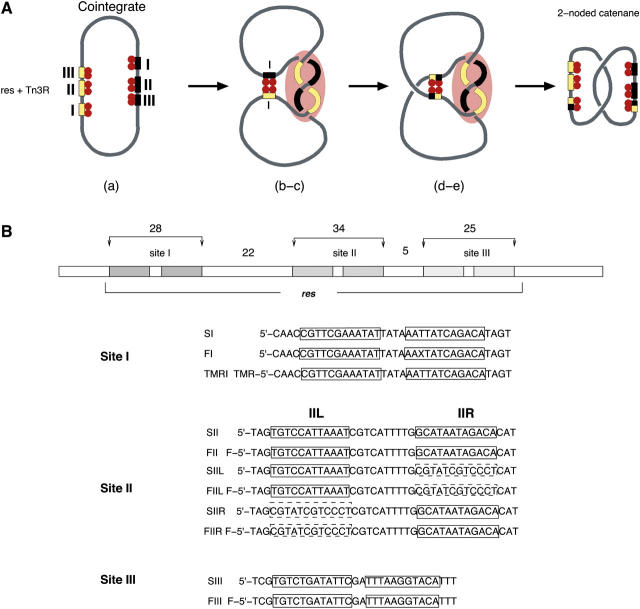
Tn3R belongs to a family of serine recombinases which also includes the γδ, Tn21 and Tn501 resolvases, and the DNA invertases Gin and Hin (2). Tn3R and γδ resolvase (γδR) have 82% identity at the amino acid level, and are regarded in this study as being structurally identical. In vitro, Tn3R is able to resolve supercoiled plasmids containing directly repeated 114-bp res sites (analogous to a cointegrate; see above) into two smaller circular plasmids, each of them with a single res site. Each res site is composed of three individual binding sites for resolvase (see Fig. 1 A). The reaction can be subdivided into five steps (see Fig. 1 A):

1. Resolvase subunits bind to the two res sites present in a DNA plasmid, forming two res-Tn3R complexes.

2. The res-Tn3R complexes come together.

3. A synaptic complex (synapse) composed of two intertwined res sites and 12 Tn3R subunits is formed.

4. The DNA strands at sites I and I′ are cleaved and exchanged (the prime being assigned to the second copy of the res site in the plasmid).

5. Finally, the strands are rejoined in their new arrangement. The recombination product is a (−2) catenane.

FIGURE 1.

Resolution of the cointegrate by Tn3 resolvase and the res site. (A) Resolution of the cointegrate by Tn3R. Tn3R binds two res sites in direct repeat orientation. The Tn3R bound res sites come together and form a synapse, which is resolved into a two-noded catenane by strand exchange. The relative positioning of the protein subunits and the DNA path shown in this scheme are only hypothetical. (B) DNA sequences of the sites used in this study. F and TMR refer to fluorescein and tetra-methylrhodamine, respectively. X refers to a fluorescein-dT-modified base. The sequences of the bottom strands were designed to be complementary to the top strands, so as to obtain a final double-stranded DNA fragment with blunt ends. The left-hand boxes in site II correspond to a wild-type site II sequence (SII, FII, SIIL, FIIL, solid line) or to a random sequence (SIIR, FIIR, dashed line). Similarly, the right-hand boxes correspond to wild-type site II sequence (SII, FII, SIIR, FIIR, solid line) or to the same random sequence as employed for SIIL (SIIR, FIIR, dashed line).

The Tn3 res site contains three individual subsites, each of which binds a resolvase dimer. Each subsite is made up of inverted copies of an imperfectly conserved common 12-bp recognition sequence, separated by short spacers of slightly different sizes (4 bp in site I, 10 bp in site II, and 1 bp in site III). The strand exchange reaction has been shown to occur at the center of subsite I (Fig. 1 B; 3). The distances between the three binding sites vary (22 bp between sites I and II, and 5 bp between sites II and III). The synapse, a complex formed by Tn3 resolvase and two res sites before strand cleavage and exchange, comprises two parts. One part, which includes a binding site I from each res and four resolvase subunits, is primarily responsible for catalysis (crossover-site synapse, i.e., the X-synapse) . A second “accessory” part includes binding sites II and III of each res along with a further eight resolvase subunits, and is implicated in the regulation of activity (1). Structural information regarding the architecture of the X-synapse has been reported recently (4). Several models for the architecture of the accessory part of the synapse have been proposed (5–8), but no direct structural information confirming or refuting these models has been reported so far.

In gel-binding assays, γδ resolvase has been shown to form three separable protein-DNA complexes with γδ res, implying the binding of one, two, or three γδ resolvase dimers (7). Under similar conditions, Tn3R was found to form six complexes, corresponding to the binding of individual monomers of Tn3R (9,10). The unusual differences between the sequences of the individual sites in res were proposed to trigger structural differences in the way in which Tn3R binds to them (6,10). These different binding modes may arise from protein conformational flexibility or DNA distortion near the centers of the binding sites. The DNA bending caused by the binding of Tn3R to sites I, II, and III has also been suggested to vary for each site. In the case of site I, a γδ resolvase-site I co-crystal structure (11) showed that the DNA is kinked by 60° toward the major groove. Gel retardation studies on γδ resolvase have suggested that the bend at sites II and III is even more pronounced (1). DNase cleavage and cyclization studies with γδ resolvase have shown that the bend in site II is directed toward the minor groove (1). Blake et al. (10) showed that monomeric Tn3R binds to site II in a two-step process. One monomer was found to bind to the left end of site II, followed by the cooperative binding of a second monomer to the right end of site II. In contrast, γδ resolvase was found to bind to site II as a dimer. The authors also reported that the Tn3R-site II protein-DNA complex was structurally asymmetric, and that this asymmetry was functionally essential. The differences in the binding of Tn3R to sites I, II, and III and to their half-sites may be important in defining the distinct roles of resolvase at these sites (catalysis at site I and architectural at sites II/III), in the synchronization of the assembly of the synapse, and, possibly, in the regulation of transcription of transposase/resolvase genes (1).

In this article, the oligomerization behavior and solution conformation of Tn3R are studied using sedimentation equilibrium (SE) and sedimentation velocity (SV) analytical ultracentrifugation, and small angle neutron scattering (SANS). In addition, the solution conformations of sites I, II, and III were studied with small angle x-ray scattering (SAXS) and modeled using rigid-body and ab initio techniques. Finally, the equilibrium properties of binding of Tn3R to res sites I, II, III and nonspecific DNA are investigated in solution using steady-state fluorescence anisotropy.

MATERIALS AND METHODS

Tn3R preparation

Wild-type Tn3 resolvase (Tn3R) was purified by a procedure based on that described previously (12). Purity was assayed by SDS-polyacrylamide gel electrophoresis (13). Tn3R stock concentrations were estimated using SDS-polyacrylamide gel electrophoresis, by comparison to a reference sample whose concentration was determined by amino-acid analysis (10). The molecular mass of the Tn3R monomer was deduced from sequence composition to be 20,600 g/mol.

Oligonucleotide synthesis and purification

The sequences of the oligonucleotides employed in this study are as shown in Fig. 1 B. Oligonucleotides were purchased (Sigma-Genosys, Haverhill, UK or MWG-Biotechnology, Ebersberg, Germany; HPLC-purified) and resuspended in TE buffer (10 mM Tris-HCl, pH 8.4, 0.1 mM EDTA). Modified sites I, II, and III (TMRI, FII, and FIII; Fig. 1 B) were labeled with fluorescein or tetramethylrhodamine at their 5′ ends. The fluorescein-labeled site I (FI, Fig. 1 B) had a fluorescein-modified dT residue at position 23. Oligonucleotide solutions were added to 1 volume of formamide buffer (80% v/v formamide, 100 mM EDTA, pH 8.0), heated at 95°C for 10 min, and purified by denaturing polyacrylamide gel electrophoresis (13). The bands were visualized by placing the gel on a phosphorescent screen and reflecting UV light from a handheld UV lamp, to avoid the use of chromophoric markers which would have had to be removed later in the purification process. DNA bands were excised, crushed in 1 ml of TE buffer in a light-tight Nunc tube (Camlab, Cambridge, UK), and finally incubated at 30°C overnight on a rotating wheel mixer. The supernatant was loaded into a 0.22-μm cellulose acetate filter (Spin-X, Costar, High Wycombe, Buckinghamshire, UK) to remove excess polyacrylamide. The flowthrough was then concentrated using a Speedy-Vac evaporator, and the buffer was exchanged for TE buffer with a G25 spin-column (Amersham, Buckinghamshire, UK). Complementary oligonucleotides were annealed by mixing equal molar amounts in TES50 (TE buffer plus 50 mM NaCl), and heated to 95°C for 10 min, followed by slow cooling to room temperature. The oligonucleotides used for scattering studies were purified by size-exclusion chromatography, using two Superose 12 columns in series (Amersham).

Plasmid DNA was purified by the CsCl gradient ultracentrifugation method (13). pMM1 was derived from pUC18 (14) and contains two res sites separated by a kanamycin resistance gene. pCO1 was derived from pMTL23 (15) and contains a res site I in the polylinker region. pUC71K is identical to pUC4K (16). (The full sequences of all the plasmids are available on request from W.M.S.)

Fluorescence anisotropy methods and binding data analysis

Steady-state fluorescence anisotropy (FA) measurements were used to monitor the changes in the ligand (DNA) that accompany protein binding. Fluorescence anisotropy measurements were taken with a ThermoSpectronic Series-2 luminescence spectroscope (Aminco-Bowman, Urbana, IL). Fluorescently labeled oligonucleotide solutions were initially prepared at concentrations ranging from 20 to 50 nM, in buffer TES50. Tn3R was added from a stock at ≈50 μM. The temperature was regulated using a temperature-controlled water bath (Haake, Karlsruhe, Germany). FA signals from fluorescein and tetramethylrhodamine were measured by setting the excitation wavelength at 494 or 530 nm, and the emission wavelength at 518 or 550 nm, respectively. A titration was performed by adding aliquots of Tn3R to a solution containing the labeled acceptor (DNA fragment), followed by thorough mixing. After each titration event, the FA signal was left to stabilize for at least 10 min, to be certain both that the equilibrium temperature was reached and that the binding process was fully completed. The quartz cuvette employed for the assays was thoroughly washed with methanol and 4 M NaCl after each use. The observed FA signal (f_obs) was normalized as 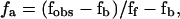where f_b is the FA of the acceptor when no ligand is present, and f_f is the FA signal when the acceptor sites are saturated.

In the case of having more than one binding site, the concentration of free ligand (C_S) can be written in terms of the total concentration of ligand (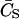), the fractional saturation (f_a), and the number of binding sites (p) as

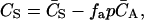(1)

where 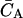is the total concentration of acceptor, which only varies during the titration due to dilution effects. Following standard practices (17), the binding data (see Figs. 6 A and 7) were expressed as the fractional saturation f_a versus the free ligand concentration C_S. Binding curves were analyzed using either a single binding-site equation or the Hill equation. The former can be expressed as

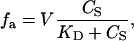(2)

where V is a constant, and K_D is the dissociation constant. For p occupancy-dependent but equivalent binding sites, cooperativity can be quantified by using the Hill equation, which can be written as

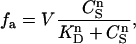(3)

where n, and K_D are parameters of the fit. The term n is the Hill constant, a direct measure of cooperativity. At the upper limit, n is equal to the number of binding sites. The cooperativity is positive for n > 1 and negative for n < 1. There is no cooperativity for n = 1.

FIGURE 6.

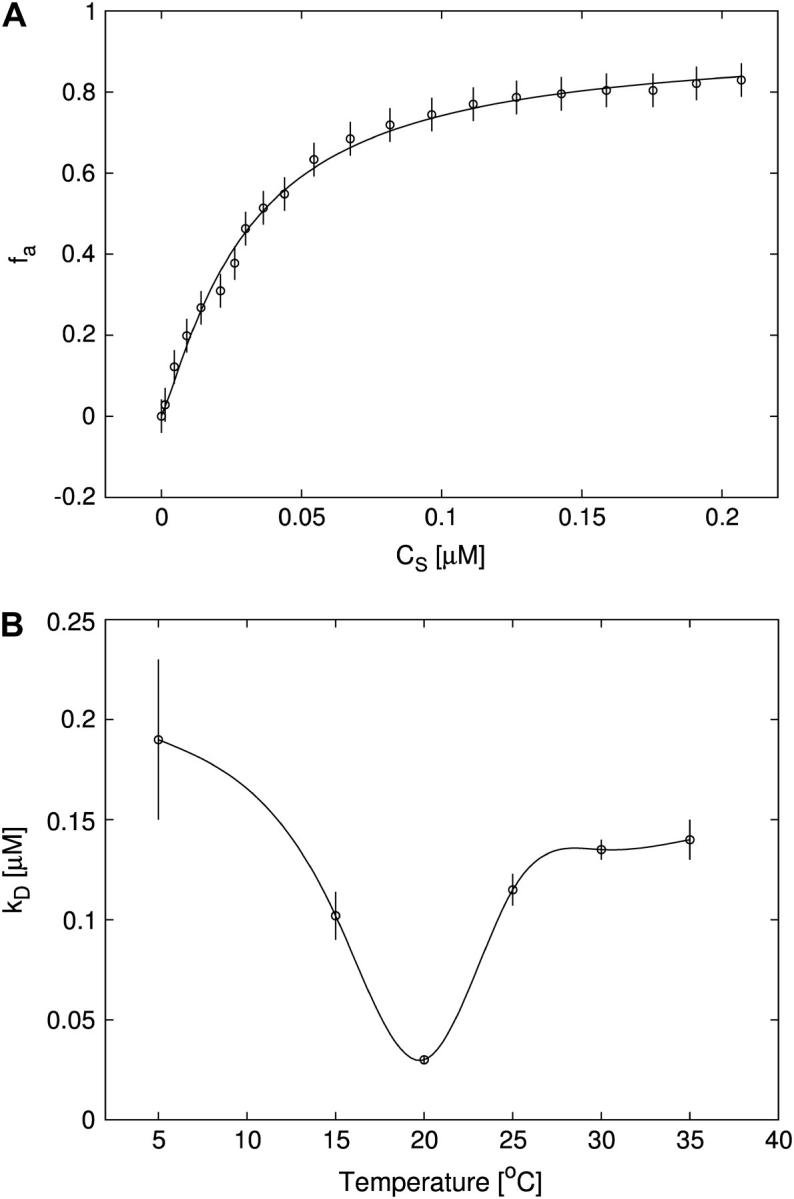
(A) Titration of FI (≈30 nM) with Tn3R at 20°C (open circles) and Hill model best fit (solid curve), with 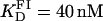and n = 1.2. The value f_a represents the binding function and C_S the free Tn3R concentration (see Materials and Methods). (B) Temperature dependence of the dissociation binding constant for the binding of Tn3R to FI in solution, as observed with FA measurements. 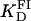and n were calculated by fitting a Hill model to the binding curves produced at different temperatures (data not shown). Solid lines represent spline approximations, and serve as a guide to the eye.

FIGURE 7.

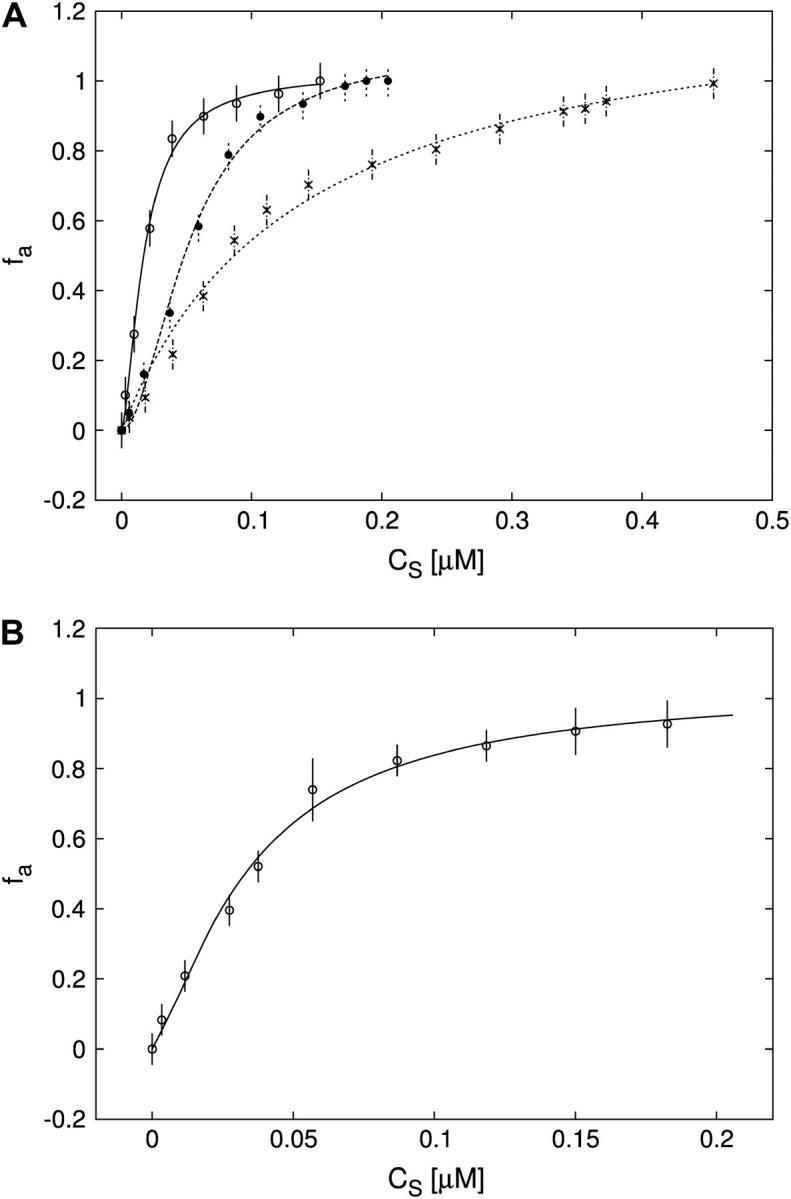
(A) Titration of FII (open circles), FIIL (solid circles), and FIIR (crosses) with Tn3R at 20°C. Binding data were fitted with a Hill model (FII and FIIL) or a one-species model (FIIR), resulting in 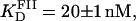n = 1.5 (solid line), 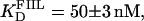n = 1.7 (dashed line), and 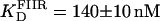(dotted line). (B) Titration of FIII (open circles) with Tn3R at 20°C. Binding data were fitted with a Hill model, resulting in 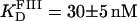with n = 1.4 (solid line).

Competition experiments with plasmid DNA

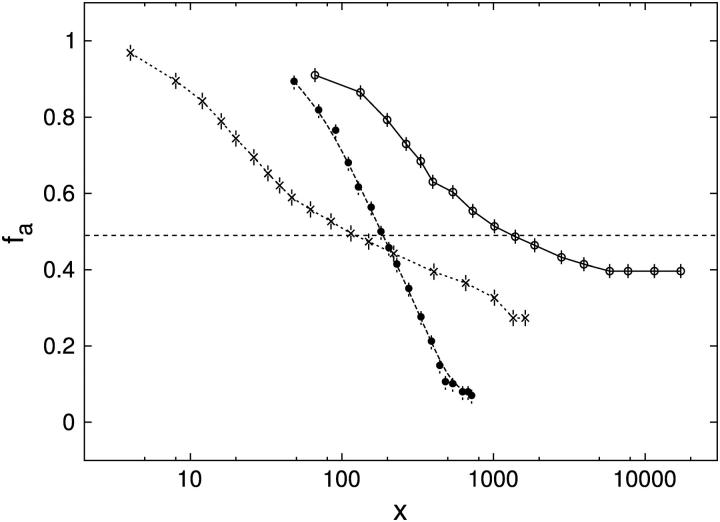
Competition experiments were performed to assess the specificity of binding of Tn3R to nonspecific sites in closed supercoiled DNA (plasmid DNA). Tn3R was added to a solution of fluorescein-labeled site I (FI) until half-saturation of the FA signal was achieved. This solution was further titrated with three different plasmids: pUC71K, a 3900-bp plasmid with no Tn3R binding site; pCO1, a 2530-bp plasmid with only one binding site for Tn3R (binding site I); and pMM1, a 4600-bp plasmid with six binding sites for Tn3R (two complete res sites). The FA signal was monitored as the solution was titrated with competitor DNA (Fig. 8 B). The molar ratio of nonspecific binding sites in the plasmid DNA to the total number of specific binding sites (x) was calculated as 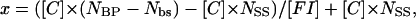where [C] and N_BP are the molar concentration and number of basepairs of the plasmid DNA, N_bs is the number of basepairs in the Tn3R binding site, [FI] is the molar concentration of FI, and N_SS is the number of specific binding sites in the plasmid DNA. For pUC71K, x represents the ratio of nonspecific binding sites in pUC71K to specific binding sites in the fluorescently labeled FI.

FIGURE 8.

Competition experiments determining the specificities of binding of Tn3R to plasmid DNA containing specific and nonspecific sites, by using pUC71K (no binding sites for Tn3R; open circles, solid curve, x₅₀ = 1000), pCO1 (one copy of binding site I; crosses, dashed curve, x₅₀ = 100), and pMM1 (two complete res sites, i.e., six Tn3R binding sites; solid circles, dashed curve, x₅₀ = 200). The value x is defined in the text.

Small angle neutron and x-ray scattering

Small angle neutron scattering (SANS) data were obtained on beamline D11, at the Institut Laue-Langevin (Grenoble, France). Experiments were performed at 4°C, at a protein concentration of 300 μM, in buffer TES1000 (20 mM Tris-HCl , pH 8.4, 0.1 mM EDTA, 1 M NaCl, 100% D₂O). Tn3R was first prepared in H₂O buffer and then transferred to the D₂O-based buffer by extensive dialysis. On D11, low-s data (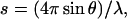 where 2θ is the scattering angle and λ is the neutron wavelength) were obtained with λ = 8 Å and the two-dimensional detector located 5 m from the sample, whereas λ = 5 Å and a sample/detector distance of 2 m were used at higher s-values. The overall s-range measured was 0.01 < s < 0.15 1/Å. Data collection times were of the order of 8 h per sample or buffer. Raw datasets were analyzed as in Ghosh et al. (18).

The SAXS datasets were obtained on beamline 2.1 at the Synchrotron Radiation Source (SRS, Daresbury, UK). The camera lengths used in SRS were: 2 m to cover an s-range of 0.05 < s < 0.38 1/Å, and 4.5 m for 0.014 < s < 0.17 1/Å. The detector was calibrated using samples of wet rat tail collagen and silver behenate. The experimental data were collected and averaged as 30 × 60 s-frames. The data were then normalized to the intensity of the incident beam, and corrected for the detector response by using the computer program XOTOKO (19). DNA SAXS curves were measured at different sample concentrations (ranging from 350 to 30 μM) and were corrected for interparticle interaction effects.

The scattering of the buffer was subtracted, and the difference curves were then scaled for concentration using the computer program PRIMUS (20). The final scattering curve was obtained by merging the low-angle region of the low concentration curve with the high-angle region of the high concentration measurement (using PRIMUS), to correct for interparticle interaction effects in the low-angle region of the high concentration data. The particle maximum dimension (D_MAX) and the particle distance distribution function (p(r)) were obtained by using the indirect Fourier transform program GNOM (21). The radii of gyration (R_g) were determined by using both the Guinier approximation (22) and GNOM.

Rigid-body and ab initio modeling of scattering data

The structural models for dimeric and monomeric Tn3R (Tn3R-dim, Tn3R-mon) were constructed by using coordinates extracted from the co-crystal structure of the γδ-site I complex (Protein Data Bank, i.e., PDB, code1gdt, see Ref. 11; see also Tn3R-dim in Fig. 3 B). Two other models for the conformation of dimeric and monomeric Tn3R (Tn3R-ext and Tn3R-ext-mon) in solution were generated by extracting the protein component of 1gdt and extending the DNA-binding domains so that they would have a more expanded conformation by opening the hinges linking the α-helices (see Tn3R-ext in Fig. 3 C). The degree of opening was similar for both models. The 36-bp B-DNA fragments with the sequence of SI (Fig. 1 B) and different kink angles (DNA₀, DNA₃₀, DNA₄₀, DNA₅₀, DNA₆₀, and DNA₉₀) were built by using the computer program NAB (23) with a similar procedure to that employed by Strater et al. (24). The kink angle ψ was defined as the angle between the DNA helical axes on either side of the kink (see Fig. 4 B, inset).

FIGURE 3.

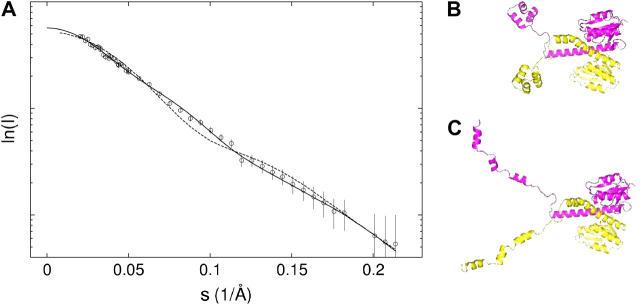
SANS data for Tn3R in solution. (A) Experimental (circles) and simulated (dashed and solid lines) SANS curves (see text for more details). (B–C) Structural models for dimeric Tn3R in solution were generated by using the protein component of the co-crystal structure 1gdt (dashed line, panel B11) and a modified version in which the DNA-binding domains of Tn3R were extended in an open conformation (see Materials and Methods; solid line, Tn3R-ext, panel C).

FIGURE 4.

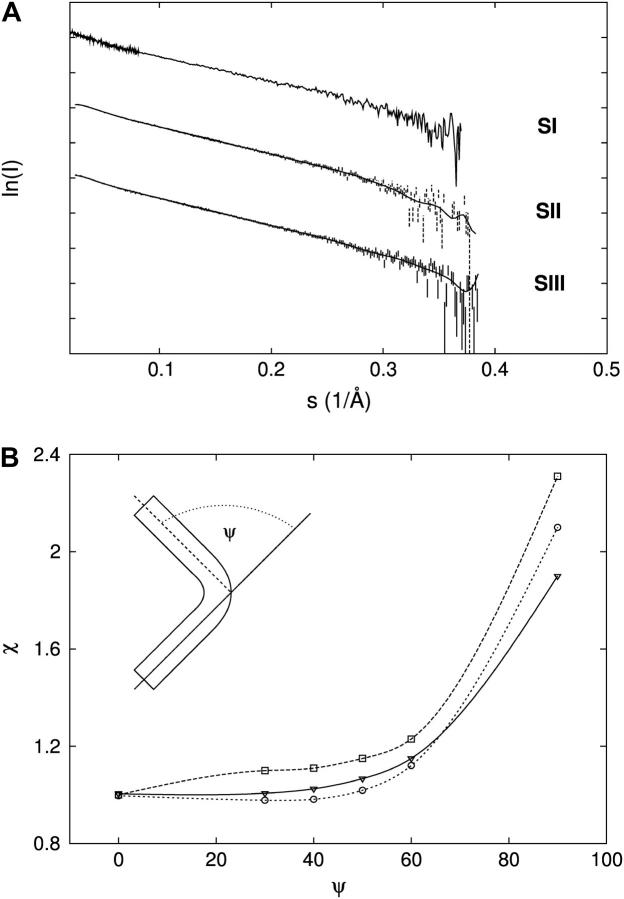
SAXS data for sites I, II, and III. (A) SAXS data for sites I, II, and III (SI, SII, and SIII, respectively). SAXS curves have been shifted on the y axis for clarity. (B) Rigid-body modeling results shown as a plot of the χ of the fit of each DNA structural model (DNA_ψ, see Materials and Methods) as a function of the kink angle ψ when fitted to the experimental datasets from sites I (down triangles), II (open squares), and III (open circles).

The scattering profiles of all structural models produced were calculated by using either CRYSOL or CRYSON (x rays and neutrons, respectively; see Refs. 25 and 26). Treatment of hydration is as described by Svergun et al. (25). For DNA models, the maximum excluded volume allowed was increased to 40 nm³ to allow for higher hydration (compared with protein). The χ-value produced when fitting the scattering intensity of the models (I(s_i)) to the experimental data (I_e(s_i)) was calculated by 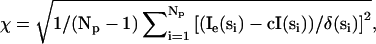where N_p is the number of experimental points, δ(s_i) are the experimental errors, and c is a scale factor (more details are in Ref. 25).

Ab initio shape restoration techniques have proved to be successful in reconstructing the solution conformation of rigid macromolecules of simple topologies (27). Various ab initio reconstruction algorithms exist (28–33). In this article, we have employed DAMMIN (32), a well-established ab initio reconstruction method. DAMMIN was run in batch mode on Intel Linux workstations, using default answers, in slow mode and without imposing any symmetry restriction. The analysis of the reconstructions was based on the methodology described by Volkov et al. (34). At least 10 different runs were performed for each reconstructed macromolecule. The final reconstructions were superimposed onto the reference reconstruction (randomly chosen from the ensemble of reconstructions provided that the reconstruction process was stable, i.e., different runs produce similar reconstructions) using the computer program SUPCOMB (35). Two independent reconstructions were considered as similar when the normalized spatial discrepancy was ≤1 (34). The consensus reconstruction was obtained by averaging similar reconstructions using the computer programs DAMAVER and DAMFILT (35).

Sedimentation velocity and hydrodynamic modeling

Sedimentation velocity experiments were performed using a Beckman-Coulter (Palo Alto, CA) Optima XL-I analytical ultracentrifuge and an AN-60 Ti rotor. The experiments were carried out at 4°C in TES1000 buffer at a rotor speed of 50,000 rpm. A series of 40 scans, 6-min apart, was obtained for each sample, using absorbance optics in continuous mode with a 0.003-cm radial step size and three averages. Experiments were carried out at a Tn3R concentration of 250 μM. The samples (380 μl) were loaded into double-sector centerpieces. Sedimentation profiles were analyzed with the computer program SEDFIT (36), which allows the user to subtract radial and time-independent noise, and to directly model boundary profiles as a continuous distribution of discrete noninteracting species (c(s) analysis). The sedimentation coefficients were also evaluated by using the finite element method to find the sedimentation coefficient that best fitted the Lamm equations (also using SEDFIT). In both cases, the systematic noise deconvolution model was employed (36). Due to nonideality effects stemming from the pronounced asymmetry of the dimer, the value of the molecular mass obtained from the single species Lamm equation model fit (≈33,000 g/mol), which reflects the boundary spreading, does not agree with the predicted mass of a Tn3R dimer (41,200 g/mol). For this reason, when fitting the SV data with a one-species Lamm equation model, the mass conservation model was not employed. The experimental sedimentation coefficient is later compared to those obtained computationally from low-resolution structural models of Tn3R in solution.

Buffer densities were measured by using a density/specific gravity meter (Model DA-510, Integrated Scientific, Rotherham, UK). The viscosity of the buffer was calculated from buffer composition using the computer program SEDNTERP (37). The program HYDROPRO (38) was employed to calculate the hydrodynamic parameters of the high-resolution models of the protein. HYDROPRO computes the hydrodynamic properties of rigid particles from their atomic structure (specified in a PDB format file).

Sedimentation equilibrium

Sedimentation equilibrium (SE) experiments were carried out in a Beckman (Palo Alto, CA) Optima XL-I analytical ultracentrifuge, using absorption and interference optics in separate runs. The experiments were performed in TES1000 buffer at 4°C and at rotor speeds of 16,000, 23,000, and 33,000 rpm. Scans were obtained at each speed until satisfactory overlay of traces separated by 4 h was obtained, indicating attainment of equilibrium. Five samples of Tn3R at concentrations of between 25 and 270 μM were loaded into six-channel Yphantis-type centerpieces. Data were the average of three scans obtained in continuous mode with a 0.003-cm radial step size over the radial range 5.8–7.2 cm. The partial specific volume of Tn3R (0.764 ml g⁻¹) was calculated using the program SEDNTERP (37). The SE data were analyzed by global modeling using the computer program SEDPHAT (39) (http://www.analyticalultracentrifugation.com/sedphat/).

RESULTS AND ANALYSIS

Oligomerization state and conformation of Tn3R in solution

The solution behavior of Tn3R was investigated by sedimentation equilibrium (SE) and sedimentation velocity (SV) analytical ultracentrifugation.

Five Tn3R concentrations, ranging from 270 to 25 μM, and three rotor speeds were utilized for the SE experiment. Both absorbance and interference optics were used, yielding identical results. A global fit of the 15 datasets was performed using a series of possible models, namely those of a one-species, monomer-dimer equilibrium (1-2 model), and a monomer-dimer-tetramer equilibrium (1-2-4 model) (40). The model that best globally represented the experimental datasets was the 1-2 model, with 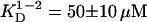(monomer-dimer dissociation constant). The 1-2-4 model fitted the data as well as the 1-2 model but the predicted total concentration of tetramer, even at the highest concentrations, was negligible (<1%). A typical and representative fit to the SE data with a one-species and a 1-2 model are shown in Fig. 2 B. The 1-2 model produces a considerably better fit to the data, with smaller and more randomly distributed residuals (Fig. 2 A). From the dissociation constant obtained from the fit by a 1-2 model, it was possible to calculate the relative distribution of each species assuming monomer-dimer self-association equilibrium. At the highest Tn3R concentration (270 μM), dimeric Tn3R would be expected to represent >80% (in terms of mass) of the species present. At the concentrations used for binding experiments (<1 μM), however, Tn3R would be expected to be >95% monomeric.

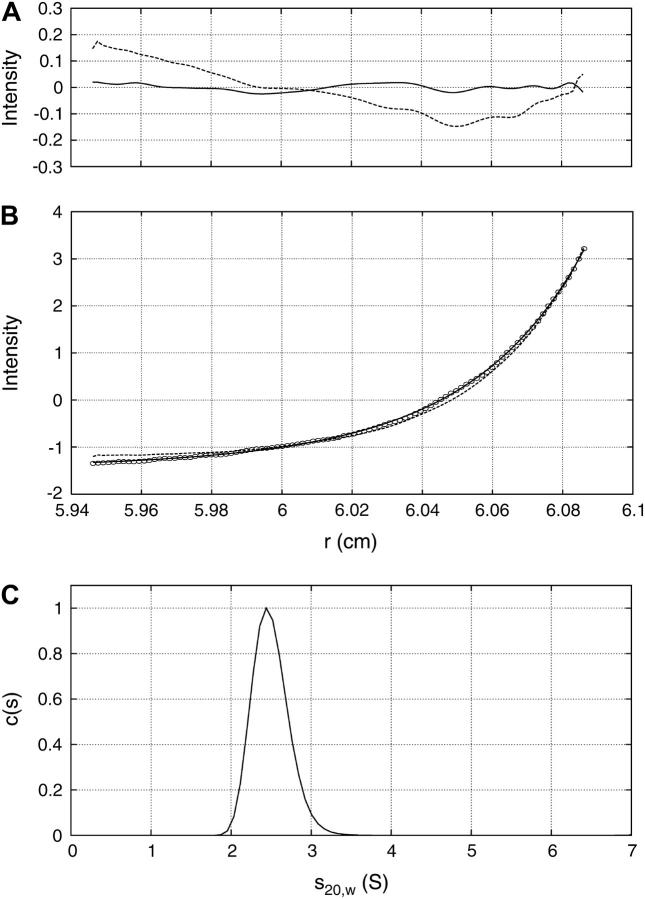
FIGURE 2.

Experimental sedimentation equilibrium and velocity data for Tn3R. (A) Residuals of the fits. (B) A representative experimental SE profile (interference optics) for Tn3R at 33,000 rpm (open circles) with a fit produced by a 1-2 model (solid line) and a one-species model (dashed line). (C) Size distribution c(s) profile from SV data analyzed with SEDFIT (36) for Tn3R.

To confirm these findings, SV experiments were performed. At a Tn3R concentration of 25 μM, the sample behaved as a single species according to c(s) analysis (Fig. 2 C), with an apparent sedimentation coefficient of s_{w, 20} = 2.3 ± 0.1 S. The SV data were also fitted with a one-species noninteracting model by using the finite element method implemented in SEDFIT (36). In this case, the resulting true sedimentation coefficient was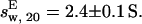

The computer program HYDROPRO (38) was employed to simulate the sedimentation coefficient of a monomer and a dimer of γδ resolvase, using coordinates extracted from the co-crystal structure of the γδ-site I complex (PDB code 1gdt;11; see also Materials and Methods and Fig. 3 B). Tn3R-mon and Tn3R-dim were expected to represent the structures of monomeric and dimeric Tn3R in solution, at least for the catalytic domains. 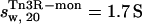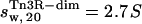The values of the simulated sedimentation coefficients for Tn3R-mon and Tn3R-dim were and (with a hydration of 0.4 and 0.36 g water/g protein, respectively). When no DNA is present, the DNA-binding domains of Tn3R are expected to be highly flexible and partially disordered in solution (41,42), thus decreasing the observed sedimentation coefficient. Further models for the conformation of monomeric and dimeric Tn3R (Tn3R-ext-mon and Tn3R-ext, respectively) in solution were generated by opening the hinges linking the α-helices in the DNA-binding domains (Materials and Methods; see Tn3R-ext in Fig. 3 C). These models were based on the work by Pan et al. (42), who studied the secondary and tertiary structural changes of the DNA-binding domain of γδR in solution by NMR spectroscopy. In that study it was found that, in the absence of NaCl, the tertiary structure of the DNA-binding domains of γδR is significantly destabilized, with changes in the secondary structure that were localized near the hinge regions between the helices. The sedimentation coefficients of Tn3R-ext and Tn3R-ext-mon were simulated as above, resulting in 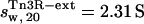and 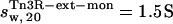(with a hydration of 0.45 and 0.4 g water/g protein, respectively). The simulated sedimentation coefficient of Tn3R-ext agrees well with the experimentally determined sedimentation coefficient (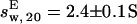), confirming that Tn3R is essentially dimeric at concentrations higher than 250 μM, and suggesting that the DNA-binding domains of Tn3R in solution are rather elongated.

SANS experiments were performed on Tn3R in solution, at a concentration of 300 μM (Fig. 3 A, circles). The radius of gyration (R_g) of Tn3R was firstly estimated by using the Guinier approximation to be 34.7 ± 2 Å. The particle distance distribution function (p(r)) was calculated by using the computer program GNOM (21). The R_g obtained from the p(r) function (using GNOM) is 35 ± 1.3 Å, in agreement with that from the Guinier analysis. The structure of dimeric Tn3R was modeled using the protein content of 1gdt, as described above (Materials and Methods and Fig. 3 B). The SANS scattering curve from this model was simulated by using CRYSON (26), producing a reasonable agreement with the experimentally obtained SANS curve (χ = 1.38, Fig. 3 A, dashed line; R_g = 30.1 Å). This agreement was further improved by using Tn3R-ext (see Materials and Methods; Fig. 3 C; and fit of the model to the data in Fig. 3 A, solid line, χ = 1.14, R_g = 35.7 Å). These findings support the SV data in that Tn3R appears to be dimeric in solution at high concentrations. In addition, they are, in general terms, consistent with the crystal conformation of a γδ resolvase dimer in a complex with DNA (1gdt; see Ref. 11), and with the solution NMR structure of the catalytic domain of γδ resolvase (43). Finally, they are consistent with the proposal put forward by Rice et al. (41), that the DNA-binding domains of resolvase would be expected to be highly flexible and partially disordered in solution. An elongated conformation of the DNA-binding domains produces an improved fit to the SANS data, but because of the low resolution of the SV and SANS data presented, other possible structural alterations cannot be excluded.

Rigid-body and ab initio modeling of sites I, II, and III

The low-resolution structures of sites I, II, and III (SI, SII, and SIII, Fig. 1 B) were investigated with SAXS since their conformations in solution could be responsible for the different binding modes of Tn3R. Scattering curves of SI, SII, and SIII were obtained in TES50 buffer (see Fig. 4 A) at beamline 2.1 of the SRS (Daresbury, UK). The radii of gyration (R_g values) of SI, SII, and SIII were firstly estimated by using the Guinier approximation to be 31.6 ± 1, 31.8 ± 1, and 31.3 ± 1 Å, respectively. The p(r) functions were obtained from the scattering data by using GNOM (21) (data not shown). The D_MAX of SI, SII, and SIII obtained from the p(r) functions were 124 ± 2, 123 ± 1, and 124 ± 2 Å, respectively, whereas the R_g values were 35 ± 2, 33.1 ± 2, and 35.4 ± 2 Å, larger than those from the Guinier analysis.

The structures of six kinked DNA fragments mimicking the possible conformations of sites I, II, and III were constructed as described in Materials and Methods (Fig. 4 B, inset). SAXS profiles were simulated from these models and fitted to the experimental datasets by using CRYSOL (25). The plots of χ versus the kink angle ψ (Fig. 4 B) show that the best model representing the SAXS data for all three sites is DNA₀; so, according to these experiments, the DNA sites SI, SII, and SIII are straight.

The computer program DAMMIN (32) was employed to restore ab initio models for SI, SII, and SIII from the experimental SAXS datasets. The reconstruction processes were stable, in that the normalized spatial discrepancy values were smaller than 1 for all reconstructions (see Materials and Methods). The R_g values from the consensus models of SI, SII, and SIII were 34.5, 33.7, and 34.6 Å, respectively, in agreement with those obtained from the experimental p(r) functions. The three consensus reconstructions represent straight cylinderlike structures (see Fig. 5). From this analysis, one can conclude that sites I, II, and III are not kinked, in agreement with the rigid-body analysis.

FIGURE 5.

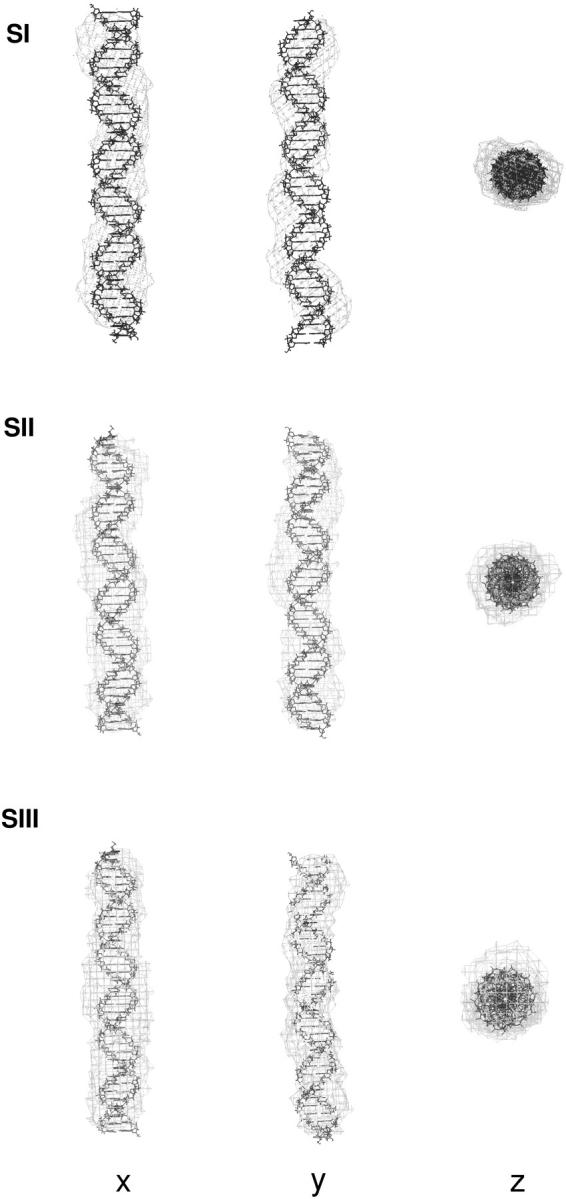
Three orthogonal views of the ab initio consensus shape restorations of sites I, II, and III. DNA atomic resolution models with ψ = 0° (DNA₀, see Materials and Methods) are shown as lines whereas ab initio consensus reconstructions are shown as shell models.

Binding to site I

To investigate the equilibrium binding of Tn3R to site I in solution, the fluorescence anisotropy of a fluorescein-labeled site I (FI, see Fig. 1 B) was monitored as the Tn3R concentration was increased. The total fluorescence intensity was also monitored as FI was titrated, but there was no systematic change with Tn3R concentration (data not shown). From this, it was concluded that the quantum yield of FI does not change upon complex formation.

A series of titrations of FI was performed at different temperatures, ranging from 5 to 35°C. The resulting binding curves were analyzed by using the Hill model (see Materials and Methods). At 20°C, the equilibrium dissociation binding constant (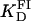) was 40 ± 5 nM, and there were signs of weak cooperativity in the binding process (n = 1.2 ± 0.1, Fig. 6 A). As the temperature increased or decreased from 20°C, the dissociation binding constant increased, suggesting a decrease in the binding affinity (Fig. 6 B). The degree of cooperativity (n) also varied with temperature, having its maximum (1.8) at ∼25°C (data not shown). All subsequent experiments were performed at a fixed temperature of 20°C.

The influence of the buffer conditions on the binding of site I to Tn3R was investigated. Tn3R was added to a solution containing FI at 20 nM until the fluorescence anisotropy (FA) signal increased to approximately half its saturation value. This solution was titrated with NaCl, and the FA signal was monitored as a function of NaCl concentration. From an initial concentration of 50 mM, the FA signal monotonically decreased with NaCl concentration, with half the amount of initial Tn3R-FI complex at ≈220 mM NaCl (data not shown). A similar experiment showed a sharp decrease in the amount of Tn3R-FI complex as a function of MgCl₂ concentration, with half the amount of initial Tn3R-FI complex at ≈20 mM MgCl₂ (data not shown). To rule out a possible change in the FA of FI due to the interaction of fluorescein with the added ions, the experiments were repeated under the same conditions but without protein. No change in the FA signal was observed (data not shown). Moreover, similar experiments using tetramethylrhodamine-site I (TMRI) as acceptor produced identical results (data not shown). These data are in agreement with the hypothesis that ionic interactions are important in the binding of Tn3R to site I.

Binding to site II

A similar approach to that employed to measure the equilibrium binding constant of site I was employed for site II. A fluorescein-site II DNA fragment (FII) was synthesized and purified as described in Materials and Methods. Titrations of FII with Tn3R were performed under conditions identical to those used with FI (Fig. 7 A, open circles). A fit of the binding data with a Hill model produced a dissociation binding constant of 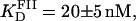with n = 1.5 ± 0.1, suggesting a moderate cooperativity between binding sites IIL and IIR in site II (see Fig. 1 B).

The interaction of Tn3R with site II is highly asymmetric (10). To confirm this, two additional fluorescein-labeled DNA fragments were synthesized. FIIL had the wild-type sequence of the left end of site II and a random sequence replacing its right end. Similarly, FIIR had the wild-type sequence of the right end of site II and a random sequence replacing its left end side (Fig. 1 B). FIIL and FIIR were titrated with Tn3R as before (Fig. 7 A, solid circles and crosses, respectively). FIIL shows a much higher affinity for Tn3R than FIIR. The FIIL binding data were fitted with a Hill model, resulting in 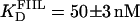and n = 1.7 ± 0.1 (Fig. 7 A, dashed line). This apparent cooperativity suggests that the predominant species is a dimer bound to FIIL, which could be accounted for by a first protein subunit binding specifically to the left end of FIIL and a second subunit binding nonspecifically to the right end. In the case of γδR, a protein dimer binding to a DNA fragment containing only the left-end common recognition sequence of site II was reported by Blake et al. (10). This peculiarity was attributed in that study to the presence of interactions between the protein subunits and not between the second subunit and the DNA. The FIIR binding data were fitted with a one-binding-site model, with 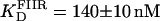(Fig. 7 A, dotted line). These results show that the binding of Tn3R to site IIL is approximately three times stronger than to site IIR.

Binding to site III

Binding to site III was studied in a similar fashion. A fluorescein-site III DNA fragment (FIII, see Fig. 1 B) was synthesized and purified as described above. Titrations of FIII with Tn3R were performed under conditions identical to those used with FI. A fit of the binding data with a Hill model produced a dissociation binding constant of 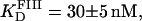with n = 1.4 ± 0.1 (see Fig. 7 B).

Binding of Tn3R to nonspecific DNA

Competition experiments were performed to assess the affinity of binding of Tn3R to nonspecific sites in closed supercoiled DNA (plasmid DNA, see Materials and Methods). The FA signal emitted by FI was monitored as the solution was titrated with pUC71K, pCOI, and pMM1 (see Fig. 8 B). When a plasmid containing no specific binding site for Tn3R is employed (pUC71K, N_SS = 0), the FA signal drops to half its original value when x ≈ 1000 (this defines x₅₀; see Fig. 8 B, solid line). By assuming standard equilibrium binding relations, one can deduce that the dissociation binding constant of Tn3R to nonspecific binding sites is K_NS ≈ 4 μM. On the other hand, the existence of specific Tn3R binding sites in the plasmid DNA reduced this number to approximately x₅₀ ≈ 100 (Fig. 8 B, dashed lines). At x₅₀, for pMM1 and pCO1 the concentration of specific binding sites in plasmid DNA is much lower than that in labeled sites (FI). For pCO1 and pMM1, assuming that the specific binding sites in these plasmids have the same affinity for Tn3R as for FI, one can deduce in this case that the dissociation binding constant of Tn3R to nonspecific binding sites for plasmid DNA containing specific binding sites is 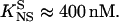These findings imply unexpectedly that when a plasmid DNA contains binding sites specific for Tn3R, the affinity of the nonspecific binding sites is enhanced by approximately 10-fold (see Discussion, below).

DISCUSSION

We have explored the behavior of Tn3R in solution and its interaction with the different binding sites in res.

Sedimentation equilibrium analytical ultracentrifugation was employed to study Tn3R oligomerization in solution. The protein is in a monomer-dimer self-association equilibrium, with a dissociation constant of 50 μM. Accordingly, the protein is mostly dimeric at high concentrations (>200 μM) and monomeric at low concentrations (<10 μM).

Data from SV and SANS experiments are consistent with Tn3R being dimeric at high concentrations. The solution conformation of dimeric Tn3R was modeled from the crystallographic and NMR high-resolution structures of the catalytic domains of γδ resolvase (44, 43) and a γδ resolvase-DNA co-crystal structure (1gdt; see Ref. 11). SV and SANS experiments were, in general terms, in agreement with this model. A second model for dimeric Tn3R in solution was built by modifying the torsion angles at the hinges between the three α-helices comprising the DNA-binding domains so that the domains would adopt a rather extended conformation. The existence of disordered conformations of the DNA-binding domains of resolvase have been previously proposed by Rice et al. (41), and shown to exist at low NaCl concentration by NMR spectroscopy (42). The sedimentation coefficient and SANS profile simulated from this new model improved the fits to both SV and SANS experimental datasets. Other models, where the degree of opening of the hinges between the α-helices in the DNA-binding domains was modified to different extents, were produced. The data simulated from these models fitted the experimental datasets equally well (data not shown). The experiments presented in this article are therefore consistent with an extension of the DNA-binding domains with respect to their structures in 1gdt but are not of high enough resolution to clearly define their final configurations. The DNA-binding domains of Tn3R could represent yet another instance of an intrinsically disordered protein domain that adopts a folded structure upon binding to its biological target (induced folding). This type of disorder-to-order transition is recognized as a mechanism that provides high specificity coupled with low affinity (45), and the possibility of binding various different targets by structural adaptation of the binding surfaces (46,47). This feature could be related to the ability of Tn3R to adopt different configurations at binding sites with very different sequences, such as those in res.

Fluorescence anisotropy was employed to study the binding of resolvase to the three binding sites in res, namely sites I, II, and III. It was shown that the highest affinity of Tn3R for site I is at 20°C, resulting in a dissociation binding constant of 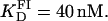At this temperature, there was only a weak degree of cooperativity (n ∼1.2) so that, in practical terms, the binding of protein monomers to the two binding sites in site I can be considered as independent events. Previous gel-shift assays revealed a high cooperativity of binding of Tn3R to site I (9,48). This conclusion was reached from the observation that, in such experiments, the site I-Tn3R dimer complex is much more abundant, except at low Tn3R concentration, than site I-Tn3 monomer complexes. However, gel-shift assays can artifactually destabilize some of the complexes in a mixture, and thus might not reflect their real equilibrium concentrations in solution. In addition, those experiments were performed under different experimental conditions, with longer DNA fragments at much lower concentration, and in the presence of “carrier” DNA.

The concentration of cations in the buffer (Na⁺ or Mg²⁺) was shown to greatly affect the binding of Tn3R to site I (data not shown), indicating the existence of an electrostatic component in the interaction.

The equilibrium binding of Tn3R to site II in solution was investigated in a similar fashion. Tn3R was shown to have very different affinities for the two monomer-binding half-sites of site II. The binding of Tn3R to site IIL was shown to be at least three times stronger than to site IIR. These results agree well with those reported by Blake et al. (10), who reported different affinities for IIL and IIR from gel-shift assay data. The authors hypothesized that the higher affinity of Tn3R for site IIL might be related to its need to assemble at res in an organized manner, to prepare the complex for its role in the recombination reaction.

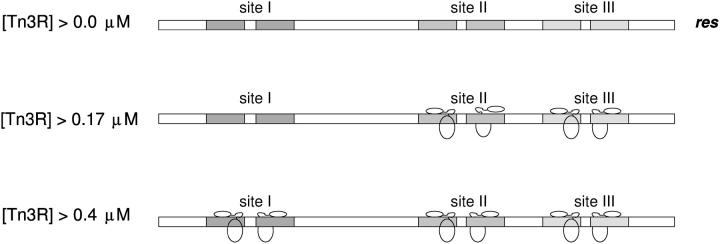
The affinity of binding of Tn3R to site III was shown to be very similar as to site II, but higher than that to site I. Based on this result, assuming binding saturation when the protein concentration is 10 × K_D, it is possible to design a simplified model for the occupancy of the sites in res at different Tn3R concentrations (Fig. 9). According to this model, at the lowest concentration Tn3R is mainly bound to site III and site II. Because of the high cooperativity of binding of site II, both sites IIL and IIR are occupied at this first stage. At higher concentrations, site I also becomes occupied. In a recent structural model for the architecture of the synapse (8), it has been proposed that the resolvase monomer bound to site IIR is at the center of the accessory sites synapse. The possibility that distortions in the structures of binding sites I, II, and III could account for the different binding modes of Tn3R was investigated in this study by analyzing the low-resolution conformations of sites I, II, and III by SAXS. From rigid-body and ab initio modeling of the experimental scattering data, it was concluded that the DNA fragments containing the binding sites are straight B-DNA; and thus the different modes in which Tn3R binds to sites I, II, and III are entirely due to sequence specific protein-DNA interactions. Tn3R might have weaker affinity for certain subsites in res to allow for structural rearrangements during the assembly or function of the synapse. These different binding modes of Tn3R to sites I, II, and III might also be associated with the role of res as a regulatory sequence for the transcription of the Tn3R and Tn3 transposase genes.

FIGURE 9.

Model for the equilibrium binding of Tn3R to the different binding sites in res. Binding site saturation is assumed at a protein concentration 10-times higher than the corresponding dissociation binding constant.

Finally, the affinity of binding of Tn3R to nonspecific supercoiled DNA was assayed. It was found that the dissociation binding constant of Tn3R to nonspecific binding sites, in a plasmid that does not contain specific Tn3R binding sites, is ∼4 μM. Hence, in genomic DNA, a monomer of Tn3R would be expected to be bound in equilibrium to a region of 100 nonspecific basepairs for each monomer bound to a specific binding site. When plasmid DNA containing binding sites specific for Tn3R was employed, the affinity of nonspecific binding sites apparently increased 10-fold. Two possible mechanisms could account for this curious difference. Tn3R monomers could self-oligomerize at the specific binding sites in plasmid DNA, thus increasing the apparent observed affinity of nonspecific sites. Alternatively, the specific binding sites could function as nucleation or landing sites for Tn3R, thus indirectly increasing the observed specificity of nonspecific sites. It is not clear whether this effect is observed for any other site-specific DNA-binding proteins. More experiments, beyond the scope of this study, would be required to elucidate the causes of this effect.