Incomplete Ion Dissociation Underlies the Weakened Attraction between DNA Helices at High Spermidine Concentrations

Abstract

We have investigated the salt sensitivity of the hexagonal-to-cholesteric phase transition of spermidine-condensed DNA. This transition precedes the resolubilization of precipitated DNA that occurs at high spermidine concentration. The sensitivity of the critical spermidine concentration at the transition point to the anion species and the NaCl concentration indicates that ion pairing of this trivalent ion underlies this unusual transition. Osmotic pressure measurements of spermidine salt solutions are consistent with this interpretation. Spermidine salts are not fully dissociated at higher concentrations. The competition for DNA binding among the fully charged trivalent ion and the lesser charged complex species at higher concentrations significantly weakens attraction between DNA helices in the condensed state. This is contrary to the suggestion that the binding of spermidine at higher concentrations causes DNA overcharging and consequent electrostatic repulsion.

INTRODUCTION

The compaction of DNA by multivalent ions has been studied now for many years (1–11). Several DNA delivery systems used for gene therapy have taken advantage of the tight packaging of DNA by multivalent ions (12–17). DNA will spontaneously precipitate as the concentration of these multivalent ions reaches a critical value that is dependent on the concentrations of other salts and solutes present. It is commonly presumed that these multivalent ions mediate either attractive electrostatic (6,7,18–23) or hydration (5–7,24,25) forces between helices. A peculiar feature of the precipitation phase diagram is that DNA is resolubilized at even higher concentrations of the nominally trivalent ion spermidine (∼100 mM) or the nominally tetravalent ion spermine (∼150 mM) in the absence of salt (8,26–29). This effect has been attributed to an overcharging of DNA (19,21,30–32), i.e., counterion binding is sufficiently favorable that more ions can be bound than are necessary to neutralize DNA charge. Overcharging would result in repulsive forces between helices and resolubilization. This interpretation implicitly assumes that these multivalent ions are completely dissociated at high concentrations. Many multivalent ions, however, are known to form ion pairs with surprisingly small dissociation constants. The trivalent cation cobalt hexamine 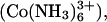for example, is widely used to condense DNA. The dissociation constant for the divalent ion-paired complex Co(NH₃)₆Cl²⁺, however, has been reported as 32 mM at 25°C from conductance measurements (33) and 13 mM at 25°C and a constant 54 mM ionic strength from spectroscopic measurements (34). A dissociation constant of 20 mM would mean that at a nominal Co(NH₃)₆Cl₃ concentration of only 8 mM, equal concentrations of +3 and +2 ions would already be present in solution. Since DNA precipitation depends on counterion valence, incomplete salt dissociation can account for the observed resolubilization without the need to invoke overcharging.

The distance between helices in the condensed phase can be conveniently measured using x-ray scattering. Before SpdCl₃ concentrations sufficiently high for dissolution are reached, an abrupt change in interaxial spacing of ∼30 Å to ∼32 Å is observed (27,28) that has been attributed to a columnar hexagonal to cholesteric packing transition. The 32 Å reflection is substantially broader than the 30 Å one. We have examined this transition in more detail.

A key difference between the overcharging and incomplete ion dissociation mechanisms is in the role of anions. Overcharging should not depend on the identity of the anion; ion-pairing, however, will naturally strongly depend on the specific nature of the associating anion. With Cl⁻ anion, we find the hexagonal to cholesteric transition occurs at ∼70 mM spermidine concentration. In contrast, the transition occurs at ∼30 mM spermidine with 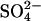anions and at ∼125 mM with acetate anions (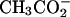). The osmotic coefficients of these spermidine salts at 100 mM are significantly smaller than observed for LaCl₃ or CrCl₃ and are comparable to that measured for Co(NH₃)₆Cl₃ also at 100 mM. These results indicate that the spermidine salts are not fully dissociated at these concentrations. Furthermore, the osmotic coefficients of the 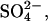Cl⁻, and OAc⁻ salts of spermidine correlate with their concentrations at the hexagonal-cholesteric transition midpoint.

We have also measured the interdependence of SpdCl₃ and NaCl concentrations at the transition point. The observed slope, d ln[Spd_total]/d ln[Cl_total], at small NaCl concentrations is the opposite sign from that predicted by an overcharging mechanism. We crudely estimate that the dissociation constant of SpdCl²⁺ is ∼150 mM from the ratio of concentrations of Spd³⁺ and an analogous diamine putrescine²⁺ at the transition midpoint. From the dependence of spermidine concentration at the transition midpoint on the osmotic pressure of a polyethylene glycol (PEG) solution acting on the condensed DNA array, we estimate that ∼10% of the bound Spd³⁺ is displaced by SpdCl²⁺ across the transition.

The available evidence supports the incomplete ion dissociation mechanism as opposed to DNA overcharging as the underlying cause of the hexagonal to cholesteric transition and, subsequently, the resolubilization. The dependences of the spacing between DNA helices on spermine and Cobalt hexamine concentrations show different behaviors from SpdCl₃, but are still rationalized by ion-pairing.

METHODS AND MATERIALS

Materials

High-molecular-weight chicken blood DNA was prepared as described previously (35). Polyethylene glycol (average molecular weight is 8000), spermidine·3HCl, spermine·4HCl, and spermidine base were purchased from Fluka (micro-select grade; Fluka Chemical, Buchs, Switzerland). Co(NH₃)₆Cl₃, LaCl₃, and CrCl₃ were purchased from Aldrich Chemical (Milwaukee, WI). All chemicals were used without further purification.

Sample preparation

Precipitated DNA samples for x-ray scattering were prepared in several ways. Concentrated (∼0.1 M) SpdCl₃, SpmCl₄, or Co(NH₃)₆Cl₃ was added to 200 μl of 1.35 mg/ml chicken erythrocyte DNA (∼2 mM bp) in 10 mM TrisCl (pH 7.5) in steps of 0.4 mM. The samples were thoroughly mixed before adding more condensing ions. Precipitation with spermidine and cobalt hexamine occurs at the 1.6 mM step and with spermine at 1.2 mM. Alternatively, condensing ions were added to DNA in a single aliquot to a final concentration of 4 mM, or DNA was ethanol-precipitated in 0.3 M NaAcetate. The fibrous samples were centrifuged and the DNA pellets transferred to salt solutions of condensing ions (1–1.5 ml) in screw cap microtubes. Samples were equilibrated for at least several days with occasional vigorous mixing before transferring to fresh solutions. Samples were considered equilibrated after 1–2 weeks of incubation. No change in the x-ray scattering pattern is observed after 6 months' storage. X-ray scattering profiles did not depend on the method used to prepare the initial DNA pellet.

X-ray scattering

An Enraf-Nonius Service Corporation (Bohemia, NY) fixed-copper-anode Diffractis 601 x-ray generator equipped with double focusing mirrors (Charles Supper, Natick, MA) was used for x-ray scattering. DNA samples were sealed with a small amount of equilibrating solution in the sample cell, and then mounted into a temperature-controlled holder at 20°C as described in Mudd et al. (36). The sample-to-film distance was ∼16 cm. The scattered x rays pass through a helium-filled Plexiglas cylinder with Mylar windows to minimize background scattering. Diffraction patterns were recorded by direct exposure of Fujifilm BAS image plates and digitized with a Fujifilm BAS 2500 scanner (Fuji, Tokyo, Japan). The images were analyzed using the FIT2D (A.P. Hammersley, European Synchrotron Radiation Facility, Grenoble, France) and SigmaPlot 8.0 (SPSS, Chicago, IL). The sample-to-image plate distance was calibrated using powdered p-bromobenzoic acid. Mean pixel intensities between scattering radii r − 0.05 mm and r + 0.05 mm averaged over all angles of the powder pattern diffraction, 〈I(r)〉, were used to calculate integrated radial intensity profiles, 2πr〈I(r)〉. The sharp, intense ring corresponds to interaxial Bragg diffraction from DNA helices packed in a hexagonal array.

Osmotic pressure

Osmotic pressures of the spermidine salts, Co(NH₃)₆Cl₃, LaCl₃, and CrCl₃ solutions were measured directly using a Vapro Vapor Pressure Osmometer (Model 5520, Wescor, Logan, UT) operating at room temperature.

RESULTS

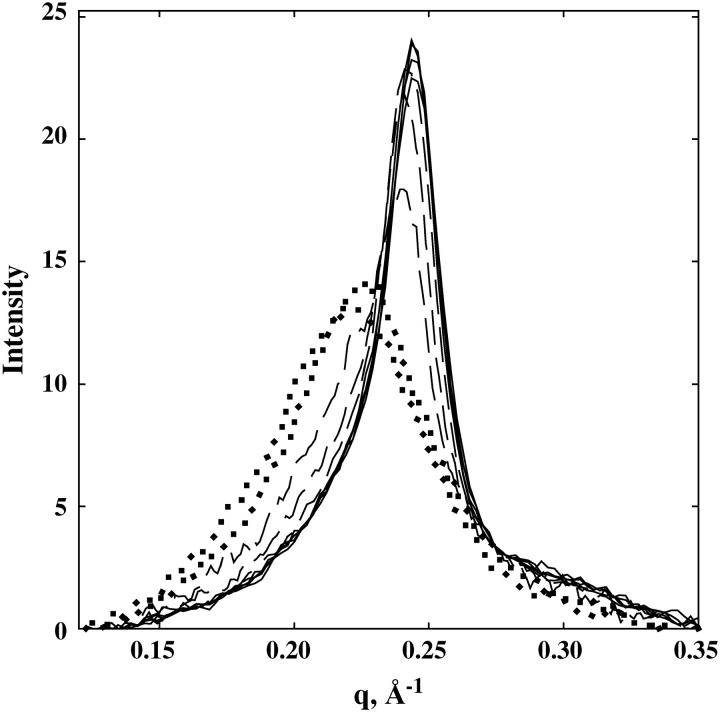
Fig. 1 shows the DNA interaxial scattering profiles for a set of SpdCl₃ concentrations between 0.5 and 100 mM in 10 mM TrisCl (pH 7.5). Between 0.5 and 20 mM, there is very little change in the scattering profile. The interaxial spacing remains 29.7 ± 0.1 Å. At 40 and 60 mM SpdCl₃, a small shoulder on the scattering peak appears at low q-values. This shoulder is quite pronounced at 70 mM. At 80 and 100 mM SpdCl₃, there is again a single scattering peak that is much broader and at lower q-values. The peak at 80 mM corresponds to an interaxial spacing for hexagonal packing of 32 Å. The peak position continues to shift to lower q-values (larger interaxial spacings) and to become broader as the SpdCl₃ concentration is increased even further. The DNA pellet disappears at ∼130 mM SpdCl₃.

FIGURE 1.

Scattering intensity profiles are shown for different SpdCl₃ concentrations. The area under the scattering curve for each concentration is normalized to 1. In terms of the Bragg spacing between helices, D_Br, the scattering parameter q = 2π/D_Br. There is virtually no difference in scattering profiles for 0.5, 2, 10, and 20 mM SpdCl3 (solid lines). At 40, 60, and 70 mM SpdCl₃ (dashed lines), a scattering shoulder at lower q-values is increasingly apparent. At 80 and 100 mM SpdCl₃ (dotted lines), the scattering profile is again symmetric, but with a much broader width and larger spacing than at lower SpdCl₃ concentrations. All samples also contained 10 mM TrisCl (pH 7.5) and were equilibrated at 20°C.

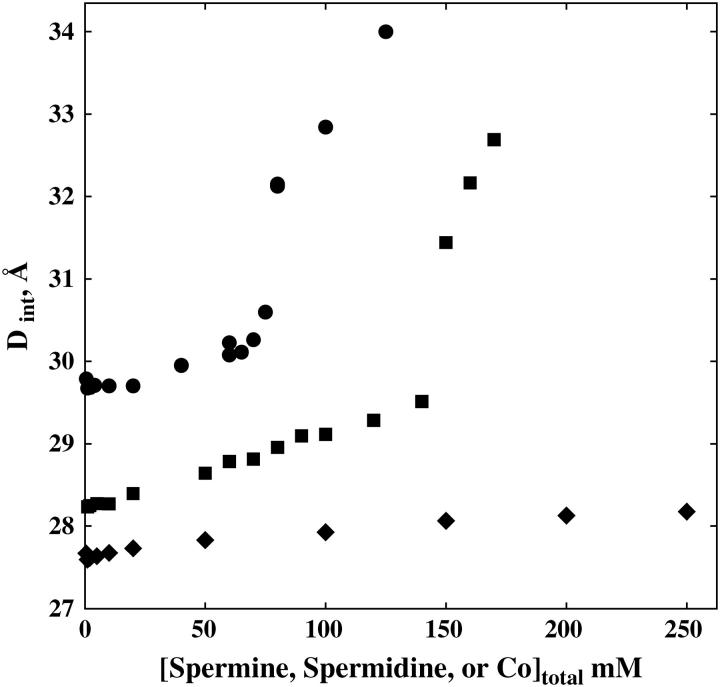
Fig. 2 shows the dependence of the interaxial spacing D_int determined from the peak position on SpdCl₃ concentration in 10 mM TrisCl (pH 7.5). An abrupt transition occurs at ∼70 mM SpdCl₃. This data is consistent with the reported results of Pelta et al. (28), who report only observing the hexagonal phase at SpdCl₃ concentrations below ∼40 mM in the absence of NaCl, a coexistence of hexagonal and cholesteric packing between 40 and 70 mM SpdCl₃, and a transition to a cholesteric phase at 70 mM SpdCl₃. The change in spacings seen at 40 and 60 mM SpdCl₃ may reflect the slight contribution of the cholesteric phase to the overall intensity. The data was not sufficiently precise to justify a fit to two Gaussian scattering peaks. The scattering profiles between 40 and 75 mM SpdCl₃, however, can be fit reasonably well with linear combinations of the profiles at 20 and 80 mM SpdCl₃. The transition is substantially reversible. Starting from DNA samples in the cholesteric region and lowering the SpdCl₃ concentration shows the transition at ∼65 mM, rather than ∼70 mM seen with the forward titration.

FIGURE 2.

The spacing between helices is shown as a function of condensing ion concentration for spermidineCl₃ (•), spermineCl₄ (▪), and Co(NH₃)₆Cl₃ (♦). Bragg spacings between helices were determined from quadratic fits to scattering profile peaks as seen in Fig. 1. Local hexagonal packing was assumed in calculating interaxial distances from Bragg spacings, D_int = 2D_Br/√3. Both SpdCl₃ and SpmCl₄ condensed DNA show abrupt changes in spacing at well-defined ion concentrations. The peak profiles on either side of the critical concentration are consistent with a hexagonal-to-cholesteric transition. Co(NH₃)₆Cl₃ condensed DNA does not show this transition through 250 mM. All samples contained 10 mM TrisCl (pH 7.5) and were equilibrated at 20°C.

Pelta et al. (28), however, report a transition from the cholesteric to an isotropic phase at ∼80 mM SpdCl₃; and we see this transition at 130 mM. The difference in DNA length may account for this variation. We have used high-molecular-weight chicken erythrocyte DNA, whereas Pelta et al. (28) used 145 bp nucleosomal DNA. The hexagonal-cholesteric transition seen for SpdCl₃ is unchanged in 10 mM Tris-Acetate buffer (pH 5.5). The titration of charged spermidine amine groups is not responsible. Similarly, the transition is unchanged between 5 and 20°C.

Fig. 2 also shows the dependence of D_int on spermine (SpmCl₄) concentration in the presence of 10 mM TrisCl (pH 7.5). Between 0.5 and 10 mM, D_int is 28.25 ± 0.05 Å. The spacing increases almost linearly between 10 and 120 mM SpmCl₄ to 29.3 Å without any change in the shape of the scattering profile, i.e., no additional shoulder as with SpdCl₃ appears (data not shown). At 140 mM SpmCl₄, a shoulder does appear on the scattering peak, suggesting a coexistence of hexagonal and cholesteric phases. The spacing and scattering profile at 150 mM SpmCl₄ is consistent with the cholesteric phase. The DNA pellet disappears at ∼180 mM.

The dependence of D_int on Co(NH₃)₆Cl₃ concentration is also shown in Fig. 2. Between 0.5 and 10 mM, D_int remains constant at 27.65 ± 0.05 Å. Between 10 and 250 mM (the highest concentration examined), D_int gradually increases to 28.2 Å. There is no observable change in the shape of the scattering profile over the entire range of concentrations.

The effect of anions on the hexagonal-cholesteric transition with spermidine

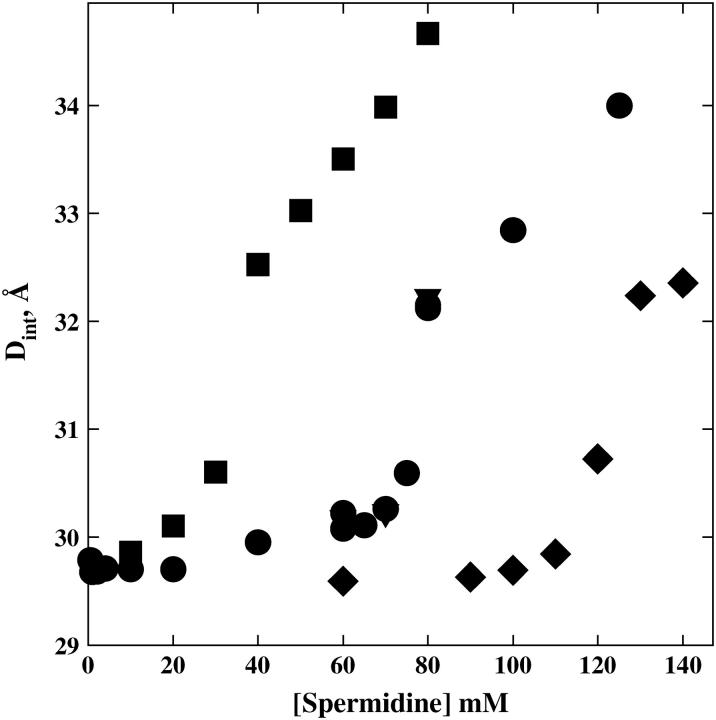
Fig. 3 shows the dependence of the scattering peak spacing on the total spermidine concentration for spermidine base neutralized with HCl, HOAc (acetic acid), or H₂SO₄. The Spd·3HCl data overlaps the SpdCl₃ salt data shown in Fig. 2. The transition with acetate anion does not occur until 125 mM spermidine. The transition with 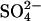occurs at a nominal spermidine concentration of ∼30 mM. The scattering profiles on either side of the transition are very similar for the three anions.

FIGURE 3.

The critical spermidine concentration at the abrupt change in interaxial spacing is strongly dependent on the nature of the anion. D_int is shown as a function of spermidine concentration for the salt SpdCl₃ (•) and for spermidine base neutralized with stoichiometrically added acid, H₂SO₄ (▪), HCl (▾), and CH₃CO₂H (♦). Interaxial spacings were determined as described in Fig. 2. The final pH for the acid-neutralized samples was ∼6.8.

This strong dependence of the transition on the anion identity is not consistent with the overcharging model and is consistent with an incomplete ion dissociation mechanism in which the consequent competition between +2 and +3 charged species underlies the hexagonal-cholesteric transition. The osmotic coefficient, Φ, is defined as the ratio of the measured osmolal osmotic pressure, Π, and the molal concentration, m, of species usually assuming total dissociation for salts, Φ = Π/m. Osmotic coefficients are approximate measures of the interactions and associations among species. Electrostatic attraction between anions and cations leads to Φ < 1 even at very low concentrations. For the trivalent salts CrCl₃ and LaCl₃, Φ = 0.81 and 0.79, respectively, at 0.1 M. The dissociation constant of LaCl²⁺ has been reported as ∼330 mM (37). Even this comparatively weak association leads to an expected 44 mM of the ion-paired divalent species at 100 mM total LaCl₃. Co(NH₃)₆Cl₃, which has a known dissociation constant for the ion-pair Co(NH₃)₆Cl²⁺ of ∼20 mM (33,34), has an osmotic coefficient at 0.1 M of 0.67. The measured osmotic coefficient of SpdCl₃ at 0.1 M (0.102 molal) is 0.68; Φ = 0.71 at 0.1 M SpdOAc₃; and Φ = 0.62 at 0.1 M Spd(SO₄)_1.5. The similar osmotic coefficients for the Spd³⁺ salts and for Co(NH₃)₆Cl₃ suggests that association constants are also similar and significantly larger than for CrCl₃ and LaCl₃. The apparent increase in association for the series SpdOAc₃, SpdCl₃, and Spd(SO₄)_1.5 inferred from their osmotic coefficients correlates their concentration at the hexagonal-cholesteric transition midpoint.

Interdependence of spermidine and NaCl concentrations at the transition midpoint

Fig. 4 shows the change of the critical SpdCl₃ concentration at the hexagonal-cholesteric transition point as the NaCl concentration is varied. Considering only the ion binding contribution, the variation of total SpdCl₃ concentration at the transition point with NaCl concentration is given by the difference in the number of ions associated with DNA between the two phases. At the transition point,

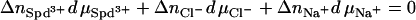(1)

or

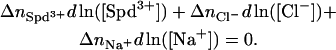(2)

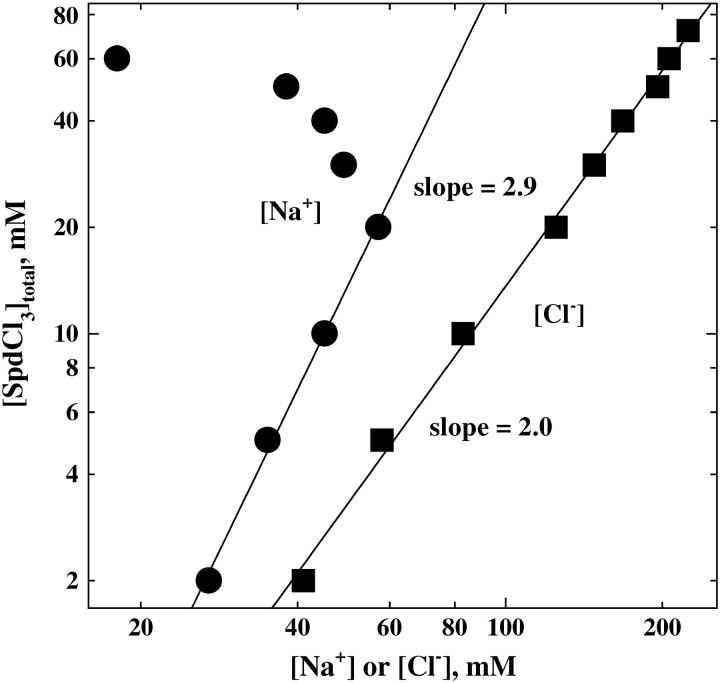
Electroneutrality requires that 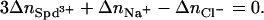Electroneutrality also prevents us from independently varying Spd³⁺, Na⁺, and Cl⁻ concentrations. The separate contributions from differences in spermidine, Na⁺, and Cl⁻ binding to the two phases over the entire range of concentrations, therefore, cannot be easily parsed. We have plotted log([Spd]_total) against both log([Na⁺]) and log([Cl⁻]_total). The regions to the left of these curves are in the hexagonal phase and to the right in the cholesteric phase. At salt concentrations greater than 55 mM NaCl, only the cholesteric phase is accessible with SpdCl₃. We have not examined the cholesteric-to-isotropic phase transition.

FIGURE 4.

The interdependence of SpdCl₃ and NaCl concentrations is shown for the hexagonal-to-cholesteric transition. The critical total spermidine concentration at the abrupt change in interaxial spacing is shown as a function of either the Na⁺ (•) concentration or the total Cl⁻ (▪) concentration from SpdCl₃, NaCl, and TrisCl. The hexagonal phase is stable in the regions to the left of the curves. The cholesteric phase is seen in the regions to the right of the curves. We have not mapped out the cholesteric-to-isotropic phase transition that occurs even further to the left of the curves. All samples also contained 10 mM TrisCl (pH 7.5) and were equilibrated at 20°C.

The log([Cl⁻]_total) plot is remarkably linear over the entire concentration range examined with a slope of ∼2. Within the overcharging model neglecting Spd³⁺-Cl⁻ ion-pairing, increased NaCl would favor extra Spd³⁺ binding because of increased charge shielding due to the higher Cl⁻ concentration. If we ignore Na⁺ ion-binding in the limit of small NaCl and high SpdCl₃ concentrations and consider only the increased number of Cl⁻ ions needed within the cholesteric phase to neutralize the excess Spd³⁺ charge, then a slope d log([Spd³⁺])/d log([Cl⁻]) = −3 is expected from Eq. 2 and the electroneutrality condition for the overcharging mechanism rather than the +2 value observed.

At low SpdCl₃ and NaCl concentrations (low ionic strength), the contribution of extra Cl⁻ binding can be neglected. In this limit, electroneutrality requires that the slope d log([Spd])/d log([Na⁺]) = 3, as is observed in Fig. 4. In this region, the hexagonal-cholesteric transition seems coupled to the simple displacement of Spd³⁺ with Na⁺.

Considering Spd³⁺-Cl⁻ ion-pairing complicates the analysis by adding at least one more component, SpdCl²⁺ in addition to Spd³⁺ (there is no reason to neglect the possible formation of 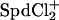), then

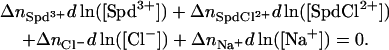(3)

To further make matters more difficult, the Cl⁻ binding-constant may be dependent on ionic strength. If we neglect the possible ionic-strength sensitivity of the ion-pair complex dissociation constant, then the equilibrium reaction, Spd³⁺ + Cl⁻ = SpdCl²⁺, connects changes in Spd³⁺, SpdCl²⁺, and Cl⁻ concentrations:

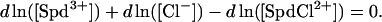(4)

If we again neglect the contribution of Na⁺ inclusion in the cholesteric phase at low NaCl concentrations, then at the transition point Eqs. 3 and 4 can be combined with the electroneutrality condition to give

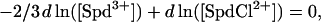(5)

or that [SpdCl²⁺]/ [Spd³⁺]^2/3 is constant.

Estimation of K_d for SpdCl²⁺ and Δn

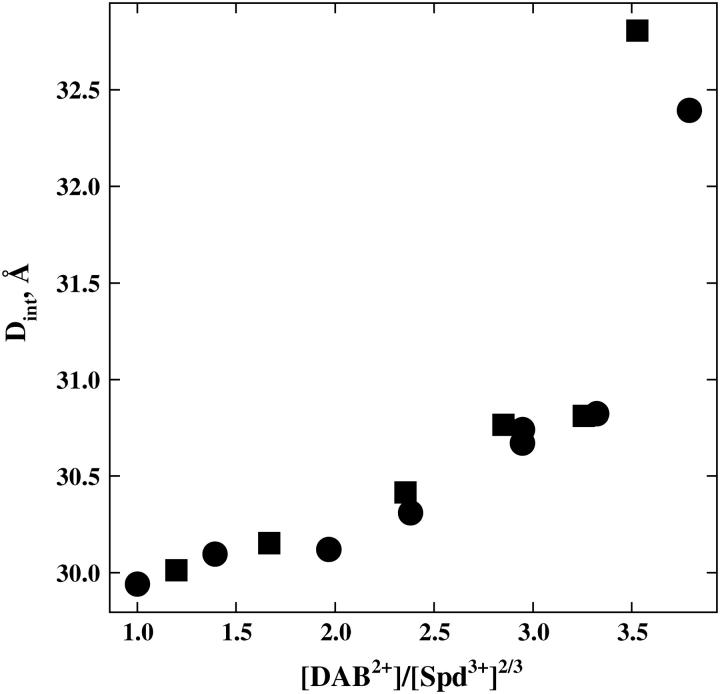
We can estimate the value of [SpdCl²⁺]/[Spd³⁺]^2/3 in the bulk solution at the transition point from the dependence of Spd³⁺ concentration at the transition point on putrescine or 1,4-diaminobutane concentration (DAB²⁺, essentially a truncated Spd³⁺), assuming that DAB²⁺ binds to DNA with an affinity similar to SpdCl²⁺. Fig. 5 shows the change in interaxial spacing as the ratio Spd³⁺/DAB²⁺ is changed while keeping the total Cl⁻ concentration constant (12 and 32 mM). At this low salt concentration we assume that essentially all the spermidine is present as Spd³⁺. The Cl⁻ concentration is held constant so that at the transition point d ln([Cl⁻]) = 0 and, therefore,

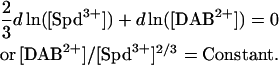(6)

The transition occurs at [DAB²⁺]/[ Spd³⁺]^2/3 ∼3.5. The same ratio for [SpdCl²⁺]/[Spd³⁺]^2/3 at the 70 mM SpdCl₃ transition point corresponds to a dissociation constant, K_d, for the reaction SpdCl²⁺ ↔ Spd³⁺ + Cl⁻ of ∼150 mM.

FIGURE 5.

The interdependence of SpdCl₃ and 1,4 diaminobutane·2HCl (DABCl₂ or putrescineCl₂) concentrations at the hexagonal-to-cholesteric transition. We use the divalent diamine DAB²⁺ to estimate SpdCl²⁺ binding. The total Cl⁻ concentration from SpdCl₃, DABCl₂, and TrisCl is held constant at 12 mM (•) or 32 mM (▪) to neglect changes in Cl⁻ binding that might accompany the transition. The ratio [DAB²⁺]/[Spd³⁺]^2/3 at the transition point is the same for these two Cl⁻ concentrations, as expected for a simple binding competition. At 12 mM total Cl⁻, the transition point occurs at ∼0.3 mM SpdCl₃ and 1.55 mM DABCl₂; at 32 mM total Cl⁻, [SpdCl₃] ∼3.2 mM and [DABCl₂] ∼7.2 mM. All samples also contain 10 mM TrisCl (pH 7.5) and were equilibrated at 20°C.

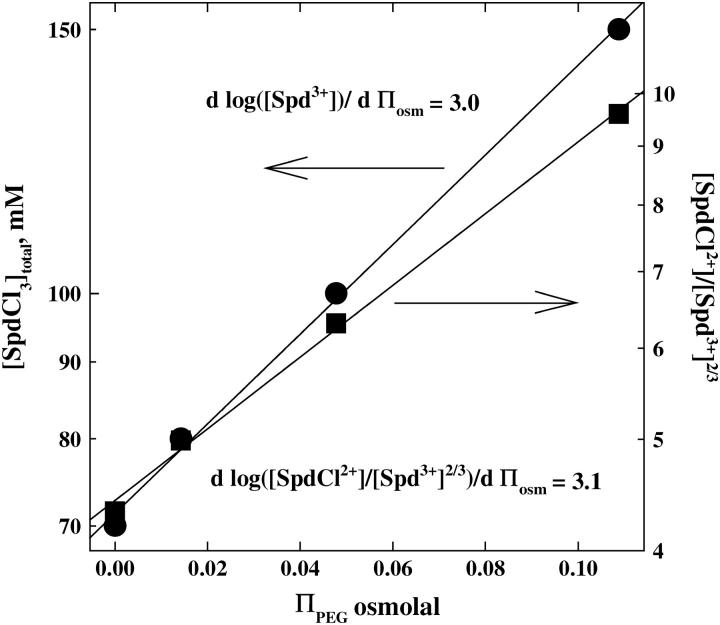
Within the ion-pairing scheme, we can also estimate the number of ions displaced in the transition from the sensitivity of the total spermidine concentration at the transition midpoint on the PEG osmotic pressure acting on the DNA array. High-molecular-weight polyethylene glycols are excluded from the DNA phase and apply an osmotic pressure on the condensed array (38). Since water is taken up by the DNA phase in the hexagonal-to-cholesteric transition, there is an osmotic ΠΔV work that opposes the transition. At the transition point, the balance of chemical and osmotic energies gives

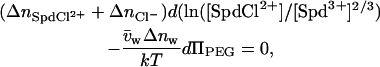(7)

where 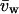is the volume of a water molecule (assumed constant), Δn_w is the difference in the number of water molecules per DNA base between the hexagonal and cholesteric phases, and Π_PEG is the PEG osmotic pressure. Fig. 6 shows the dependence of Π_PEG on both the overall SpdCl₃ concentration and the ratio [SpdCl²⁺]/[Spd³⁺]^2/3 calculated assuming that K_d = 150 mM and that K_d is insensitive to PEG concentration. The highest PEG osmotic pressure corresponds to a polymer weight fraction of 0.12. For PEG osmotic pressures expressed as osmolal concentrations, the slope is given by

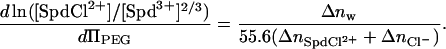(8)

A change in spacing between DNA helices from 30 to 32 Å for the transition corresponds to Δn_w ∼6 water molecules/DNA-phosphate. The observed slope gives 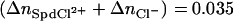ions/DNA-phosphate. This difference in numbers of bound ions is insensitive to the value of K_d used to calculate [SpdCl²⁺]/[Spd³⁺]^2/3, changing by <10% between K_d = 50 and 250 mM. Within the ion-pairing framework, replacement of <10% of the bound Spd³⁺ initially present in the hexagonal phase (∼0.33/ DNA-phosphate, assuming charge neutralization) with SpdCl²⁺ is sufficient to cause the transition to the cholesteric phase.

FIGURE 6.

The interdependence of SpdCl₃ concentration and PEG osmotic pressure is shown for the hexagonal-to-cholesteric phase transition. The osmotic pressure of excluded PEG acts to oppose the increase in spacing that accompanies the transition. On the left-hand axis the variation of the total SpdCl₃ concentration (•) with osmotic pressure is shown. On the right-hand axis, the ratio [SpdCl²⁺]/[Spd³⁺]^2/3 (▪) calculated using K_d = 150 mM is shown as dependent on PEG osmotic pressure. All samples also contain 10 mM TrisCl (pH 7.5) and were equilibrated at 20°C.

DISCUSSION

The observation of resolubilization of spermidine-compacted DNA at higher spermidine concentrations led to the proposal of overcharging DNA or charge reversal at high counterion concentrations (see, for example, Refs. 30 and 32). Apparent overcharging of polystyrene sulfonate beads has been reported at high concentrations of La(NO₃)₃ (39) using electrophoresis. At the salt concentrations necessary for apparent charge reversal, La³⁺ binding sites are well screened from one another. This is unlike the situation with condensed DNA. To our knowledge, there has been no demonstration of charge reversal for DNA helices. The nonideality of solutions of multivalent ions such as spermidine, particularly at high concentrations, however, has not been well appreciated. The electrostatic energies gained from ion-pairing are substantial for these ions. Much of the work is in the older literature (see, for example, Refs. 40 and 41). The reported dissociation constant of the 1-3 complex 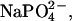for example, is 6.8 mM and for the 1–4 complex NaEDTA³⁻, K_d = 22 mM. Even for the 1-2 complex 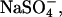K_d = 190 mM. Dissociation constants are naturally sensitive to the nature of the ions involved. From conductivity measurements, the dissociation constant of Co(NH₃)₆Cl²⁺ has been reported as 32 mM and of 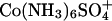as 0.28 mM (33). From changes in absorbance, the dissociation constant of Co(NH₃)₆Cl²⁺ has been reported as 14 mM and of Co(NH₃)₆I²⁺ as 60 mM (34). At the higher concentrations needed for resolubilization of DNA, multivalent ions should not be expected to be fully dissociated and there will be a DNA binding competition among the fully charged ions and their ion-paired complexes of lesser charge. Of course, no one would be surprised that DNA can be resolubilized by adding competing +1 or +2 ions to a solution of +3 condensing ions.

We have investigated here the hexagonal-cholesteric transition of Spd-DNA assemblies. This transition precedes the resolubilization step. In the hexagonal phase, x-ray scattering from DNA gives comparatively sharp peaks centered at a spacing of 29.7 Å. The interaxial scattering peak from the cholesteric phase is much broader and spans a range of spacings from ∼32 to 35 Å before the DNA pellet dissolves. Over a narrow range of spermidine concentrations, the two phases coexist. The observed scattering peak can be adequately described as a simple sum of the hexagonal and cholesteric peaks. This coexistence could reflect different packing energies of scattering domains or, perhaps, the presence of DNA domains with different spermidine binding affinities.

The concentration of spermidine at the hexagonal-cholesteric transition midpoint is strongly dependent on the nature of the anion, ranging from 30 mM with 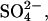to 70 mM with Cl⁻, to 125 mM with acetate (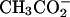). This sensitivity indicates that spermidine-anion complex formation very likely underlies the transition. The effect of 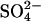is particularly notable. The competition would be between the trivalent, fully dissociated Spd³⁺ and the univalent ion 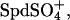rather than a more strongly binding divalent ion as with bound Cl⁻ or 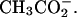If we crudely estimate that 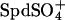binds with an affinity similar to Na⁺, then the data in Fig. 4 would indicate that only ∼2 mM of the 30 mM total spermidine is present as Spd³⁺ and ∼28 mM as 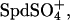for K_d ∼1 mM. The approximate 100-fold difference in Spd³⁺ binding inferred between 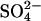and Cl⁻ (estimated as ∼150 mM from the data in Fig. 5) is consistent with the 100-fold difference in measured 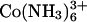binding constants between 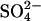and Cl⁻ given above.

Complex formation is difficult to measure directly for an ion such as spermidine, since its flexibility precludes straightforward interpretation of conductivity measurements and little change is expected in the absorption spectrum—two techniques that are commonly used to measure ion-pairing. Osmotic coefficients, however, are consistent with Spd³⁺-Cl⁻ binding and are comparable to those for Co(NH₃)₆Cl₃ at the same concentration. Osmotic coefficients for the different anions with spermidine correlate with their ability to induce the hexagonal-cholesteric transition.

At the higher spermidine concentrations, there would seem to be significant concentrations of SpdCl²⁺. We presume that as for divalent putrescine (1,4 diaminobutane, DAB²⁺), forces between DNA helices with bound SpdCl²⁺ in water are repulsive (42). As the SpdCl²⁺ concentration increases, it becomes energetically more and more costly to preferentially bind Spd³⁺ over SpdCl²⁺ to maintain interhelical attraction. Since the ratio of [SpdCl²⁺]/[Spd³⁺] increases as the spermidine concentration increases, at some point the difference in interhelical interaction energies between DNA with bound Spd³⁺ and SpdCl²⁺ will become comparable to the energy of preferentially binding Spd³⁺. This is essentially the basis of the Gibbs-Duhem relation shown in Eqs. 1–3 and 7. Since the activities of all ions must be the same in the bulk solution and DNA phase, formally the dissociation constant K_d is the same in the two phases. The activities of ions in the DNA phase, however, include the contribution from their interactions with DNA, essentially their binding constants. This means that even though the activities of tri- and divalent ions are necessarily the same in the two phases, the ratios of [SpdCl²⁺]/[Spd³⁺] will be quite different in the bulk and condensed phases.

The observation of an abrupt, discrete transition between the hexagonal and cholesteric is somewhat unexpected. We did not observe such a transition previously for the titration of DNA in 0.25 M NaCl with Co(NH₃)₆Cl₃ (5). Only a transition from solution to the hexagonal phase was apparent in the absence of an externally applied osmotic pressure. It is possible the cholesteric phase is stable only over a very narrow range of Co(NH₃)₆Cl₃ concentrations under these conditions. We have characterized differences between the cholesteric and hexagonal phases for Na-DNA (35,43,44). Except for very high NaCl concentrations (∼1.2 M and above), a discrete transition between the two phases is not observed. The cholesteric phase is characterized by increased DNA configurational fluctuation and positional disorder. The increased structural entropy may be accompanied by an increased disorder in the correlation of ions bound on one helix with phosphate groups on apposing helices. There is still, however, a slight attractive force between helices in the cholesteric phase with SpdCl₃. The transition is a complicated interplay of configurational entropy, ion-binding competition, and interhelical forces that will be difficult to unravel.

We also mapped the dependence of SpdCl₃ concentration at the midpoint of the hexagonal-cholesteric transition on NaCl concentration. At NaCl concentrations low enough that the inclusion of Na⁺ in the cholesteric phase is negligible, the overcharging mechanism would predict a slope d(log[Spd³⁺])/d(log[Cl⁻]) = −3 compared with the observed slope of +2. Considering a simple Spd³⁺ + Cl⁻ ↔ SpdCl²⁺ reaction and neglecting the additional binding reaction to form 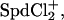the dependence of the transition point on SpdCl₃ and NaCl concentrations translates into the condition that d(log([SpdCl²⁺]/[Spd³⁺]^2/3)) = 0. Again this is only valid in the limit of low NaCl concentrations and neglects any dependence of the dissociation constant on ionic strength.

If SpdCl²⁺ binds to DNA with an affinity comparable to the diamine putrescine²⁺ (1,4 diaminobutane), then the estimated dissociation constant for SpdCl²⁺ is ∼150 mM, a value significantly larger than other trivalent ions as 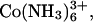but smaller than for La³⁺ (37). Since there may be a loose coordination of a Cl⁻ anion by two charged amino groups in the ion-pair, it is likely that SpdCl²⁺ binds less tightly than putrescine²⁺ so that the dissociation constant is likely smaller than 150 mM. The close similarity of SpdCl₃ and Co(NH₃)₆Cl₃ osmotic coefficients at 0.1 M would indeed suggest a smaller dissociation constant. From the dependence of the critical SpdCl₃ concentration at the transition midpoint on the osmotic pressure of a PEG solution acting to compress the condensed DNA array, we infer that only a very small number of Spd³⁺ ions are displaced in the transition (<10% of the total bound Spd³⁺). A large change in the ratio of [SpdCl²⁺]/[Spd³⁺] in the bulk solution is necessary for a small change in this ratio in the DNA phase due to the difference in DNA binding constants. This again indicates the delicate balance among interhelical forces, ion binding, and configurational freedom.

The dependence of the interaxial spacing on spermine concentration seen in Fig. 2 can also be rationalized by Cl⁻ binding to Spm⁴⁺ and a consequent competition between ions for DNA binding and compaction. Spm⁴⁺ should bind Cl⁻ more strongly than Spd³⁺. The K_d for SpmCl³⁺ is likely similar to the 20-mM value tabulated for the NaEDTA³⁻ complex (see Table 14.5 in Ref. 41). We presume that SpmCl³⁺ binding is similar to Spd³⁺ and also confers attractive forces between DNA helices. The continuous increase in spacing as the spermine concentration increases is then due to a gradual replacement of tetravalent Spm⁴⁺ with trivalent SpmCl³⁺. The abrupt transition at ∼140 mM SpmCl₄ is likely the result of further reaction of SpmCl³⁺ to form 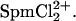Since this transition occurs at higher concentrations than for SpdCl₃, the dissociation constant of 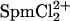would seem higher than SpdCl²⁺, as might be expected.

The dependence of interaxial spacing on Co(NH₃)₆Cl₃ concentration curve seen in Fig. 2 is also quite interesting, showing unexpected behavior. From the overcharging viewpoint, since 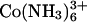binds DNA more tightly than Spd³⁺ (45), one might have anticipated that overcharging and resolubilization would occur more readily with Co(NH₃)₆Cl₃ than with SpdCl₃. Yet DNA assemblies remain tightly packed up to 250 mM (the limit of solubility is ∼300 mM). The dissociation constant of Co(NH₃)₆Cl²⁺ has been reported as ∼20 mM (33,34). At 100 mM there should be little 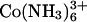left in solution, yet the spacing between helices only changes by some 0.7 Å between 0.5 and 250 mM. It would seem that similar to the divalent transition metals Mn²⁺ and Cd²⁺ (42) Co(NH₃)₆Cl²⁺ also confers attractive forces between DNA helices. Many other di- and trivalent transition metals such as Cu²⁺, Ni²⁺, Fe³⁺, and Fe²⁺ will also precipitate DNA, but destroy the helical structure in the process as these ions coordinate directly with DNA bases (42,46). Presumably, the tight coordination with NH₃ prevents this with Co³⁺. The increase in spacing seen with increasing concentrations of Co(NH₃)₆Cl₃ likely reflects a weakening interhelical attraction as 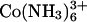is displaced with Co(NH₃)₆Cl²⁺. We have no indication whether 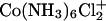is present in significant concentrations at 200 mM Co(NH₃)₆Cl₃ or not.

CONCLUSIONS

The hexagonal-cholesteric transition of condensed DNA seen with increasing concentration of SpdCl₃ and, consequently, the resolubilization of Spd·DNA aggregates, most likely results from anion binding of Spd³⁺ and not from DNA overcharging. We have concentrated here on changes or differences in ion binding between the hexagonal and cholesteric condensed phases of DNA. It is a general result of the Gibbs-Duhem equation, however, that any dependence of DNA interactions as inferred, for example, from changes in the spacing between helices on salt concentration necessarily means the distribution of ions associated with DNA changes with the spacing between helices. Differences in energy between two condensed states of DNA depend not only on the difference in their direct physical interactions but also on differences in the numbers of ions associated with each state.