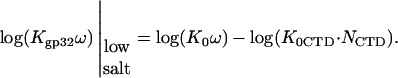Theory of Electrostatically Regulated Binding of T4 Gene 32 Protein to Single- and Double-Stranded DNA

Abstract

Bacteriophage T4 gene 32 protein (gp32) is a single-stranded DNA binding protein, which is essential for DNA replication, recombination, and repair. In a recent article, we described a new method using single DNA molecule stretching measurements to determine the noncooperative association constants K_ds to double-stranded DNA for gp32 and *I, a truncated form of gp32. In addition, we developed a single molecule method for measuring K_ss, the association constant of these proteins to single-stranded DNA. We found that in low salt both K_ds and K_ss have a very weak salt dependence for gp32, whereas for *I the salt dependence remains strong. In this article we propose a model that explains the salt dependence of gp32 and *I binding to single-stranded nucleic acids. The main feature of this model is the strongly salt-dependent removal of the C-terminal domain of gp32 from its nucleic acid binding site that is in pre-equilibrium to protein binding to both double-stranded and single-stranded nucleic acid. We hypothesize that unbinding of the C-terminal domain is associated with counterion condensation of sodium ions onto this part of gp32, which compensates for sodium ion release from the nucleic acid upon its binding to the protein. This results in the salt-independence of gp32 binding to DNA in low salt. The predictions of our model quantitatively describe the large body of thermodynamic and kinetic data from bulk and single molecule experiments on gp32 and *I binding to single-stranded nucleic acids.

INTRODUCTION

In a recent article (1), we have measured the equilibrium binding constants of T4 gene 32 protein (gp32) and *I, a truncation of gp32 lacking 48 C-terminal residues, to double-stranded DNA (dsDNA; K_ds) and single-stranded DNA (ssDNA; K_ss) as a function of salt concentration using single molecule force spectroscopy (2–5). It was shown that, in contrast to the high salt conditions, where the affinities of gp32 and *I for single-stranded nucleic acids are very similar (6), below 0.2 M salt the binding constants of these two proteins strongly diverge. Although binding of gp32 to both ss- and dsDNA saturates, the binding of *I continues to increase, though somewhat less steeply, with decreasing solution ionic strength. This is in contrast to the situation in high salt, where both proteins exhibit similarly steep salt-dependencies.

In this article, we propose and develop a model that describes the structural origin of the dramatic difference between the binding of these proteins to nucleic acids (NA) in low salt. This model includes the release of small ions from both the NA and the protein, as well as the strongly salt-dependent removal of the C-terminal domain (CTD) of gp32 from its NA surface on the core domain. We hypothesize that unbinding of the CTD is associated with the counterion condensation (CC) of Na⁺ ions onto this part of the protein, which compensates for Na⁺ release from single-stranded (ss) NA upon its binding to gp32. This results in the salt-independence of gp32 binding to NA in low salt, suggesting an electrostatic equivalence of the CTD and the segment of NA that binds gp32. This model is tested against the large body of experimental data from the literature on equilibrium and kinetic measurements of ssNA binding to gp32 *I, and *III (core domain, residues 22–253, containing the nucleic acid binding site). The predictions of our model quantitatively describe all of the available data. We will also discuss the structural basis for the counterion condensation on the CTD. The similarity of the salt dependence of protein binding to ss and to double-stranded (ds) DNA observed in this study suggests that the same conformational change in gp32 is also a prerequisite for its binding to dsDNA. As was shown in our previous work (3), it is the magnitude of the gp32 binding constant to dsDNA that controls the protein's dsDNA helix-destabilizing activity. This provides an explanation for the much stronger dsDNA melting ability of *I as compared to gp32 and the extremely high salt sensitivity of the melting ability of the full-length protein.

The results presented below are divided into eight sections. In the first section, we introduce the model of electrostatic regulation of gp32 binding to single-stranded nucleic acids. In the second section, we quantify this model and obtain expressions that relate the electrostatic and nonelectrostatic binding constants of gp32 and *I as a function of both NaF and NaCl, as well as its nonelectrostatic salt-independent component. In addition, we also obtain the binding constant for binding of the C-terminal domain of gp32 to its core domain, as well as a binding constant for Cl⁻ anions binding to gp32. We also obtain the number of anions and cations bound and released upon gp32 and *I binding to DNA, and the binding constant for Cl⁻ anions binding to gp32.

In the third and fourth sections, we use these parameters to describe the salt dependence of N-terminal domain mutants of gp32 binding to single-stranded nucleic acids, and the binding of *I and *III to single-stranded nucleic acids.

In the fifth section, the same parameters are used to describe available data on the kinetics of gp32 association and dissociation from various single-stranded nucleic acids. In the sixth and seventh sections, we discuss the physical origin of the counterion condensation on CTD of gp32. We conclude with a summary and discussion of the importance of this salt-dependent conformational change in gp32 for DNA replication processes.

RESULTS AND DISCUSSION

T4 gene 32 protein binding to single-stranded nucleic acids is regulated by the strongly salt-dependent opening of its C-terminal domain

A schematic showing the general trends observed in binding data for gp32 and *I binding to ssNA is presented in Fig. 1 a. The new information obtained in single DNA molecule stretching experiments (1) includes the binding constants to ss λ-DNA in low salt ([Na⁺] < 0.2 M) for both gp32 and *I. The high salt data in Fig. 1 b for gp32 binding to φx174 ssDNA were measured in high salt (>0.4 M [Na⁺]) by Newport et al. (7). In high salt the binding constants of gp32 and *I are strongly salt-dependent, and, most importantly, the slopes of the log K-log [NaCl] plots are in both cases ∼−7 in NaCl (the magnitude of the *I binding constants are only 2–4 times higher than those of gp32). Our new data obtained in lower salt shows that the binding constants of the two proteins significantly diverge below 0.2 M Na⁺. The slope of the log-log plot for *I is reduced to ∼−3. The change in slope of the full-length protein is even more dramatic: there is essentially no salt dependence at [Na⁺] < 0.2 M. This agrees with the salt dependence of the relatively weak binding to poly(adenylic acid) by wild-type and N-domain mutant proteins measured in bulk experiments, which clearly show a flattening of the log K versus log[NaCl] plots below 0.2 M salt (8). (In the case of wild-type protein, the cooperativity parameter, ω, was not directly determined at low salt conditions, and was assumed to be invariant, as it is at >0.2 M NaCl.) In addition, the salt dependence of the association kinetics of the protein to single-stranded polynucleotides show a nonmonotonic behavior between 0.1 and 0.2 M NaCl (9); below 0.1 M, the log k_a versus log [NaCl] plot has a positive slope, and above 0.2 M the slope is negative. Villemain and Giedroc (8) characterized gp32 binding to poly(A) at low salt using salt-back titrations, as shown in Fig. 1 b. In addition, it was established (8) that the slope at high salt of K_gp32 and K_*I is much smaller if NaF is used instead of NaCl. This prompted Villemain and Giedroc (8) to attribute the strong nonlinearity in log(K_gp32) versus log([NaCl]) to additional anion and cation association with the protein upon binding ssNA. They calculated that the total number of cation binding sites, m_tot, on the protein that undergo a change of ionic environment from bulk solvent to the milieu of the nucleic acid, where the concentration is higher, m_tot, is ∼5. This corresponded to an uptake of ∼4 Na⁺ ions in the vicinity of the cationic binding groove of gp32. Inspection of the core domain crystal structure (10) does not readily identify such a large number of Na⁺-binding anionic residues near the binding groove. More critically, protein cationic uptake does not provide an explanation for our new data, where the salt dependence for *I binding to ssDNA below 0.2 M (slope ∼−3.3) is of much greater magnitude than for gp32 binding (slope ∼ 0). We note that the ssDNA binding groove is shared by the full length protein and all its truncated variants.

FIGURE 1.

(a) Calculation of the salt dependence of all binding constants discussed in the text with the plausible values of parameters, extrapolated to various salt conditions. Black and green dashed lines are the hypothetical binding constant of *I in high NaCl and NaF, respectively. The actual binding constant (pink solid line) of *I in NaCl interpolates between its value in NaCl in high and in NaF in low salt. The dashed blue and red lines are hypothetical binding constants of gp32 in NaCl and NaF, respectively. The latter curves converge with the *I binding constant curves in high salt, but saturate in low salt. (b) Binding constant and their fits to our binding model for *I as a function of NaCl (solid circles and squares, and curve I) and gp32 (open circle, triangle, and solid diamond and curves II–III) as function of NaCl or NaF (solid triangle and curve IV). The red circles associated with curves I and II were obtained in this study for ss λ-DNA in low NaCl for gp32 and *I, respectively, and the violet diamonds for φx174 ssDNA (Newport et al. (7)) in high NaCl for gp32. The open blue triangles associated with curve III are from Villemain et al. (8) for gp32 binding to poly(A) and the green squares from Lonberg et al. (6) for *I binding to poly(rA) in NaCl. The closed blue triangles associated with curve IV are from Villemain et al. (8) measured for gp32 binding to poly(A) in NaF. These two sets of curves were fit using Eqs. 4b, 8, and 9, with a common set of parameters: n = 2.95 ± 0.30, m = 3.70 ± 0.30, K_Cl = 2 ± 0.5 M⁻¹, and (1/2.3) · (ΔG_0CDT/k_BT) = −log (K_0CTD · N_CTD) = 1.4 ± 0.2. The only difference between the binding curves for ss λ-DNA and poly(A) is the vertical shift due to the difference in (K₀ · ω), which was log (K₀ · ω) = 6.50 ± 0.1 for ss λ-DNA and log (K₀ · ω) = 5.75 ± 0.10 for poly(A).

With these considerations, we present an alternative model of gp32 binding to ssNA. In accord with other researchers, and based on the extensive evidence from the proteolytic accessibility of the CTD in the free and bound forms of gp32 (11–14), we suggest that unbinding of the CTD from the protein is required before gp32 binding to the NA. The primary new feature of our model is that we hypothesize that CTD unbinding from a cationic surface of gp32 into solution is accompanied by the strong association of Na⁺ cations with the CTD. The salt insensitivity of gp32 binding in low salt can then be explained by the fact that upon gp32 binding NA, as many small ions become associated with the CTD as there are released from the NA and the protein. For the CTD to bind these Na⁺ ions in low salt it must be electrostatically comparable to the NA that gp32 binds. In other words, there should be a counterion condensation (CC) (15–18) on the negatively charged CTD, as its environment changes to the bulk low-salt solution. The specific features of CC as opposed to the more conventional cation binding to independent binding sites, as well as the structural basis for CC on the CTD, will be discussed on pages 1952 and 1953. In the next four sections we will concentrate on the direct quantitative consequences of this model for both the thermodynamics and kinetics of gp32 binding to ssNA. It will be shown that our model allows us to reconcile most of the data obtained in the course of ∼30 years of studies on the affinities of gp32, *I, and *III for their nucleic acid binding sites, and offers an explanation for the kinetic regulation of the DNA duplex unwinding activity of the full-length protein. In addition, this study provides a convincing and quite unusual example of a strongly salt-dependent conformational change within a protein, which regulates its ability to bind to nucleic acids.

Quantitative description of gp32 and *I binding to single-stranded nucleic acids

In the proposed model, the C-terminal domain (CTD) is bound to a cationic surface on the protein in low salt, blocking binding to single-stranded nucleic acid. This implies that the net association constant for gp32 binding to an isolated site, K_gp32, can be described as a product of the *I association constant, K_*I, and the probability that the CTD is open, P_op,

(1)

where

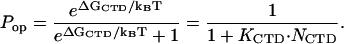(2)

We have assumed that the free energy of CTD binding to its protein binding site, ΔG_CTD, is given by

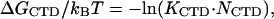(3)

where K_CTD is the CTD binding constant to the gp32 cationic surface, and N_CTD is the effective local concentration of the CTD in the vicinity of its binding site. It is determined by the conformational freedom of the unbound CTD, such that 1/N_CTD is a measure of the volume available for the CTD in its unbound state. We can roughly estimate N_CTD ∼10⁻¹–10⁻⁴ M⁻¹.

Our main assumption of the electrostatic equivalence between the CTD and the NA means that the binding constant of the CTD and the NA to the cationic groove in the absence of CTD are proportional to each other, such that

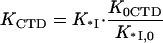(4a)

or

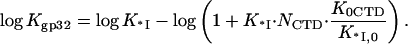(4b)

Here K_0CTD and K_*I,0 are the salt-independent nonpolyelectrolyte components of the CTD and nucleic acid binding to the protein binding groove, respectively.

When the salt concentration is high, the CTD-groove binding constant is small, such that 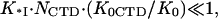and K_*I([Na⁺]) converges to K_gp32([Na⁺]). At the same time, when the salt concentration is low, the binding constant K_*I is high, such that 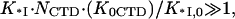and the gp32 binding becomes salt-independent (1),

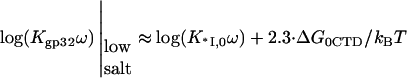(5)

(note that in equations relating binding constants, ω cancels out; however, when necessary to express the full binding free energy, we reintroduce ω as a factor to the binding constant), where

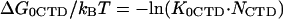(6)

is the nonpolyelectrolyte part of the CTD binding free energy and the nonelectrostatic part of the NA binding constant is K₀ω.

The latter quantity can be found independently by fitting the experimental data for *I, i.e., K_*I ([Na⁺]), which, due to this study, is available over a broad range of salt concentrations. However, fitting K_*I ([Na⁺]) also requires a model that would explain the change in the slope of the salt dependence plot from −(6–7) in high [NaCl] to ∼−3 in low salt. The significantly stronger salt dependence seen in NaCl compared to NaF (at [Na⁺] > 0.3) (8) provides a lead into the nature of this effect, which we will show is related to the additional release of anions from a cationic surface on the full-length protein. Among common anions, Cl⁻ binds relatively tightly to cationic sites on proteins, whereas F⁻ binds weakly (19–22). In our model, we assume that only anions are released from the cationic protein binding site upon its NA binding in NaCl. This hypothesis is supported by our new data showing the similarity of the log-log DNA binding slopes of *I in low salt and of both *I and gp32 proteins in high salt, i.e., under the conditions when only Na⁺ cations are displaced upon binding, as shown in Fig. 1. At the same time, binding in NaF is not associated with anion release at any solution ionic strength due to the much weaker association of F⁻ with the cationic protein site, as compared to Cl⁻,

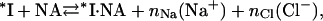(7)

where n_Na is the number of Na⁺ released into the solvent from the nucleic acid and n_Cl the number of Cl⁻ released from the protein upon complex formation. If the affinity of each of the n_Cl Cl⁻ ions for their protein cationic sites is K_Cl, then the binding constant of *I in the presence of Cl⁻ can be written as

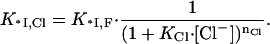(8)

Here 1/(1 + K_Cl · [Cl⁻]) is the probability of one ion removal, and we assumed that all n_Cl Cl⁻ ions have identical and independent binding sites within the protein binding groove. K_*I,Cl and K_*I,F are the association constants of *I to NA in NaCl and NaF, respectively. The term 1/(1 + K_Cl [Cl⁻]) is the probability of a Cl⁻ not to be bound to its site on the protein. K_*I,Cl is a function of K_*I,0,F, the nonelectrostatic binding constant at 1M NaF, and the ionic concentrations, [Cl⁻] = [Na⁺],

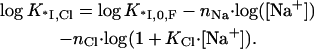(9)

Since no F⁻ ions are released upon nucleic acid binding (since K_F ≪ K_Cl), in NaF the only small ions released are the n_Na Na⁺ ions from NA. Thus,

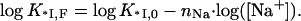(10)

Here K_*I,0,F = K_*I,0 is the nonpolyelectrolyte protein binding constant at 1 M NaF. It is also assumed in Eqs. 8–10, and everywhere in this article, that the binding of small ions to nucleic acid or protein occurs much more rapidly than reactions involving macromolecular associations or conformational changes; thus, small ion binding is in equilibrium as these changes occur. This assumption is always fulfilled because of the rapid diffusion of the small ions, the lack of any need for orientation before binding, and the fact that their concentrations are always in excess compared to the macromolecules. Analyzing Eq. 9 for the protein binding constant in NaCl we see that in high salt, when K_Cl · [Cl⁻] ≫ 1, Eq. 9 reduces to

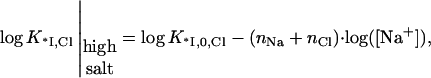(11)

where 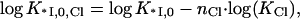and the apparent slope becomes −(n_Na + n_Cl), i.e., involves release of n_Na cations from nucleic acid and n_Cl anions from the protein binding site. At the same time, in low salt, when K_Cl · [Cl⁻] ≪ 1, i.e., all Cl⁻ ions dissociate from the protein binding site, K_*I,Cl reduces to K_*I,F, i.e.,

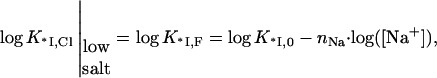(12)

such that the slope becomes −n_Na. Each of these situations is illustrated as a separate line in Fig. 1 a, where each line is extrapolated to all salt concentrations to show the effect of changing salt on the expected slopes in each case.

A summary of the available data for the binding of *I and gp32 to ssDNA in both NaF and NaCl is shown in Fig. 1 b, along with fits to the data using the electrostatic binding model presented above. These curves were fit to the data using Eq. 4b and Eqs. 8–10, with a common set of parameters: n_Na = 2.95 ± 0.30, n_Cl =3.70 ± 0.30, K_Cl = 2.00 ± 0.50 M⁻¹, and 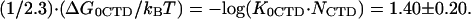The only difference between the binding curves for ss λ-DNA and poly(A) is the vertical shift due to the difference in log(K_0,Clω), which was log(K_0,Clω) = 6.50 ± 0.20 for ss λ-DNA and log(K_0,Clω) = 5.75 ± 0.20 for poly(A). As expected, the difference in type of NA similarly affects only the nonpolyelectrolyte part of both gp32 and *I proteins binding to NA.

Out of five independent parameters, n_Na, n_Cl, K_Cl, log(K₀ω), and ΔG_0CTD/k_BT, important for *I and gp32 binding to NA, only the first four are needed to describe the binding of *I. These four parameters could be determined independently of the CTD term (which requires knowledge of K_gp32([Na+]), if good data were available for *I binding to NA over a broad range of [NaCl] and [NaF]. However, comparative binding data in NaF and NaCl is available only for gp32 (8). Therefore we fit all four curves presented in Fig. 1 b simultaneously to characterize binding of both proteins. Although there are a large number of parameters, several factors allow for a reliable fit. The number of Na⁺ and Cl⁻ ions released upon binding can be inferred from comparison of gp32 binding in NaCl and NaF in high salt. The obtained values of n_Na and n_Cl can then be used as a first guess for fitting our new binding data obtained in low [NaCl]. The log-log slope of the low salt data for *I yields a good estimate of the number of Na⁺ ions released from DNA upon binding of either gp32 or *I. Fitting of the nonlinear log(K_*I)-log[Na⁺] dependence at intermediate salt yields an estimate of K_Cl; we would expect this to be independent of base or sugar composition. Also, fits of log(K_*I) versus log[Na⁺] for all tested nucleic acids provide log(K₀) for each of them. Finally, given log(K₀), the salt-independent value at low [Na⁺] of K_gp32 provides an estimate of log(K_0CTD · N_CTD), independent of the rest of the parameters. Any additional binding data fitted simultaneously should further improve the reliability of our parameter determination. Below, we will analyze additional literature data for the binding of gp32, *I, *III, and several mutants to various polymeric nucleic acids. With only minimal changes necessary for particular experimental conditions, these binding data are well fit with the same set of parameters. A schematic diagram showing the behavior of gp32 and *I at high and low salt using the values for n_Na and n_Cl that were obtained from our model is shown in Fig. 2.

FIGURE 2.

Schematic depiction of model for electrostatic regulation of DNA binding. (a) *I lacks the C-terminal domain, so in low salt its DNA binding site is always available for binding to DNA. (b) In low salt, the gp32 C-terminal domain spends a significant amount of time bound to the cationic DNA binding site, thus preventing binding to DNA. (c) In high salt, four Cl⁻ ions are condensed onto the cationic binding site of *I. (d) In high salt, the C-terminal domain of gp32 is unbound from the core, so gp32 resembles *I, with four Cl⁻ ions bound to the cationic DNA binding site on the core. (e) When full-length gp32 is bound to DNA, the gp32 C-terminal domain is exposed to solution. Three sodium ions are condensed onto the gp32 C-terminal domain.

To conclude this section we will use our fitted parameter values to calculate the probability of opening of the CTD from its binding site to a cationic surface on gp32. Fig. 3 a represents P_op(log[Na⁺]), calculated according to its definition in Eq. 2 with K_CTD calculated according to Eq. 4a using our fitted parameters. In addition, Fig. 3 b presents the free energy of CTD intramolecular association versus [Na⁺], calculated as

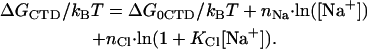(13)

The latter expression can be obtained by substituting Eqs. 4a and 9 into Eq. 3. In the same panel we present as data points ΔG_CTD/k_BT obtained directly from our measured low salt binding constants (1) for *I and gp32 as

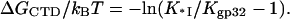(14)

All of the parameters for calculating ΔG_CTD/k_BT according to Eq. 13 were the same as those used to fit the data in Fig. 1 b. The positive fitted ΔG_0CTD value, once again, emphasizes the fact that the CTD interaction with the protein binding site is attractive for purely electrostatic reasons. We anticipate that this favorable electrostatic free energy involves primarily the entropy of Na⁺ ion release from the CTD upon its binding to the cationic surface of the protein. As the salt concentration increases, the entropy change due to small cation release becomes smaller, until at [Na⁺] ≈ 0.2 M, i.e., log[Na⁺] ≈ −0.7, the unfavorable nonelectrostatic portion of the free energy change of internal CTD interaction wins over the entropic segment, and results in CTD unbinding. One of many possible explanations for a positive free energy change associated with nonelectrostatic binding is the formation of an α-helix or other structure within the anionic CTD upon its binding to the cationic surface. In any case, CTD opening results in the binding behavior of gp32 and *I becoming almost indistinguishable in higher salt.

FIGURE 3.

(a) The measured (symbol) probability of CTD unbinding from the gp32 binding groove (P_op) as a function of salt [NaCl]. The measured values of P_op were obtained for ss (solid red diamond) and ds (solid blue triangle) λ-DNA, according to Eq. 1. The solid line is the calculated value of P_op obtained using Eq. 2, where ΔG_CTD/k_BT was calculated according to Eq. 13 with the globally fitted values of small ions binding parameters: n_Na = 2.95 ± 0.3, n_Cl = 3.70 ± 0.30, K_Cl = 2 ± 0.5 M⁻¹, and (1/2.3) · (ΔG_0CDT/k_BT) = −log(K_0CTD · N_CTD) = 1.4 ± 0.2. (b) Free energy of CTD binding to a cationic surface on gp32 protein as a function of solution ionic strength in NaCl. Data for gp32 and *I binding to ss (solid red diamond) and ds (solid blue triangle) λ-DNA, derived from our measurements according to Eq. 14. The solid line is ΔG_CTD/k_BT calculated from Eq. 13 with the same parameter values as P_op.

Finally, it is interesting to directly compare the nonpolyelectrolyte portions of the binding constant of the CTD, K_0CTD, and of ssNA, K₀. We expect that K_0CTD ≪ K₀. Indeed, given the high local CTD concentration around the binding groove, and the similar electrostatic part of the binding free energy, it is only the more favorable nonpolyelectrolyte part of the groove-nucleic acid interaction that allows for the preferential binding of ssNA as compared to CTD at μM-to-nM nucleic acid concentrations within the studied salt range. Given the fitted value of the nonpolyelectrolyte free energy of CTD binding from Eq. 6, K_0CTD · N_CTD ∼ 10^−(1–2), and assuming N_CTD = 10^−(2–3) M, we estimate K_0CTD ∼ 10^−(1–2)/10^−(2–3) ∼ 1–100 M⁻¹. This value must be compared to 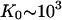M⁻¹, determined as log(K₀) = log(K₀ω) − log(ω) = 6.5 − 3 = 3.5. Thus, K₀/K_0CTD ∼ 10¹–10³, i.e., the nonpolyelectrolyte interaction of ssNA within the ss-NA binding groove is 10¹–10³ times stronger than the nonpolyelectrolyte binding of CTD to the protein. At least part of the nonpolyelectrolyte interaction of ssNA may result from interactions with as many as five tyrosine residues and nucleobases (23,24). Each of these five interactions contributes 0.3–0.7 kcal/mol of the binding free energy (23). This amounts to a total of −(1.5–3.5) kcal/mol ∼−(2–4) k_BT attraction. At the same time, the unfavorable nonpolyelectrolyte interaction of CTD with the groove is ΔG_0CTD = −2.3 · k_BT · log(K_0CTD · N_CTD) ≈ 3k_BT. Therefore the net nonpolyelectrolyte preference of gp32 for single-stranded nucleic acids over its own CTD is δG₀ ∼ (5 − 7)k_BT. This yields 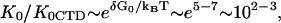in accord with our direct estimate of this ratio above.

Binding of N-terminal domain (NTD) gp32 mutants to poly(rA)

Fig. 4 represents the observed dependence of K_ssω on [Na⁺] obtained by Villemain and Giedroc (8) for gp32 and two N-terminal domain (NTD) mutants binding to ss poly(A) in NaCl and NaF, and the predicted dependence based on our model. In our calculations we assumed that the release of small ions from the protein binding site was the same for the mutants, i.e., n_Na = 2.95, n_Cl = 3.70, and K_Cl = 2.00 M⁻¹, as obtained in our fit of the data in Fig. 1 b. The new parameters that were varied to fit the three data sets in Fig. 4, and which characterize the specificity of each of the studied proteins, are summarized in Table 1, along with the analogous parameters for gp32 binding to ss λ-DNA. First, our hypothesis that the exchange of the small ions remains the same in all of the mutants is definitely confirmed. Secondly, whereas the values of K₀ω varies between these mutants by up to two orders of magnitude, the nonpolyelectrolyte component of the free energy of CTD binding to NA remains constant within our accuracy. As can be seen in Table 1, the nonpolyelectrolyte component of the binding free energy of CTD is unfavorable by ∼2 kcal/mol for gp32 and both of its mutants. Is this a reasonable result for these particular proteins?

FIGURE 4.

Salt dependence of gp32 and N-domain mutant proteins binding poly(A). Data for gp32 (blue diamond) and N-terminal domain mutants K3A (red square) and R4T (green triangle) in NaCl (solid symbols) and NaF (open symbols) from Villemain et al. (8) The lines are fits of these data to Eqs. 4b, 8, and 9 with the same fitting parameters for n_Na, n_Cl, and K_Cl as in Fig. 1 b, except for the values of log (K₀ · ω) and log (K_0CTD · N_CTD), which are given in Table 1.

TABLE 1.

Parameters describing the nonelectrostatic binding of gp32 and its mutants to single-stranded nucleic acids and to the gp32 C-terminal domain

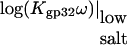		log(K0ω)	−log(K0CTDNCTD)	ΔG0CTD kcal/mol
gp32/ss λ-DNA	7.90	6.50 ± 0.20	1.4 ± 0.2	1.93 ± 0.20
gp32/poly(A)	7.15	5.75 ± 0.20	1.4 ± 0.2	1.93 ± 0.20
K3A/poly(A)	6.72	5.02 ± 0.20	1.7 ± 0.2	2.40 ± 0.20
R4T/poly(A)	6.10	4.10 ± 0.20	2.0 ± 0.2	2.60 ± 0.20

In Table 1, we have used Eq. 5: The value ΔG_0CTD was calculated as ΔG_0CTD = −k_BT · ln(K_0CTD · N_CTD), and we took into account that at room temperature (T_r), k_BT_r = 0.59 kcal/mol.

Each of the two mutants studied by Villemain and Giedroc (8) had one positively charged residue in its NTD mutated to an uncharged amino acid, i.e., Lys³ → Ala (K3A), and Arg⁴ → Gln (R4Q). Mutations in this region are expected to mostly affect the cooperativity of gp32 binding to ssNA, ω. However, the authors have shown that whereas ω indeed decreases for these two mutants, a noticeable change in the intrinsic binding constant K was also observed. In Table 1, the differences in the calculated fitted log(K₀ω) values reflects changes in both the intrinsic binding constant and ω from one protein to the other, as well as two different nucleic acids for gp32. On the other hand, the invariance in the value of the calculated free energy of CTD opening implies that the mutations in the NTD do not affect this opening.

Our interpretation of the data presented in Fig. 4 differs from its original interpretation by Villemain and Giedroc (8). Both models assume Cl⁻ ion release and Na⁺ ion association with gp32, as well as Na⁺ release from DNA upon gp32-DNA binding. However, whereas the authors assume a weak association of ∼5 Na⁺ cations with the binding site of gp32 upon its DNA binding, we suggest that ∼3 Na⁺ cations associate with the anionic CTD, as it unfolds into solution upon its binding to DNA. Our model is based on our new single molecule DNA stretching data, showing that Na⁺ ions associate with gp32, but not with *I, as it binds DNA. Comparison of the low salt binding slopes of gp32 and *I allows for the direct estimate of the number of Na⁺ cations (∼3), associated with the CTD of gp32, but not with *I upon DNA binding. Moreover, assumption of the local electrostatic equivalence of the CTD of gp32 and DNA suggests strong binding of Na⁺ to the CTD, thereby eliminating the Na⁺-CTD binding constant from the number of fitting parameters. Besides being much better justified by the experiment, this assumption makes our global parameter fit much better defined than in the model of Villemain and Giedroc. Thus, our model can be considered as a further development of Villemain and Giedroc's picture of gp32-DNA binding, which uses both new and previous data to fully characterize the small ion exchange accompanying gp32-DNA association.

*III binding to single-stranded nucleic acids differs from *I binding only by the absence of a cooperative protein-protein interaction

Binding of the proteolytically defined core domain of gp32, which lacks both the N- and C-terminal domains, denoted *III, was initially studied by Lonberg et al. (6) In contrast to *I and gp32 proteins, the interaction of *III with ssNA is completely noncooperative. The occluded site size of ∼5.5 derived from fitting the *III binding data to the McGhee and von Hippel isotherm was somewhat smaller than the analogous site size ∼7 for *I or gp32 binding. The similar spectroscopic changes upon complex formation (tryptophan fluorescence in the case of protein, ultraviolet absorbance and circular dichroism in the case of nucleic acid) of the three forms of the protein as well as the similar dependencies of affinity on nucleic acid base composition suggest that the nucleic acid binding sites are essentially identical. Since *III binding was found to be much weaker than that of gp32 or *I, data were obtained at a lower salt range, 0.05 M < [Na⁺] < 0.5 M. The average slope of the log K versus log[salt] binding plot was ∼−3 to −4, significantly smaller than the slopes of −6 to −7 observed for *I or gp32, which were measured at higher levels, 0.3 M < [Na⁺] < 1 M. Similar to *I and gp32, the dependence of the binding constant on NaF concentration was significantly weaker than on NaCl. In this section we will use our model for *I binding to ssNA to test the hypothesis that the electrostatic part of the *III and *I binding is the same, and that the only difference is that the binding of *I is cooperative.

Fig. 5 shows the results of fitting all of the *III binding data in NaCl and NaF (6), together with our single molecule data for *I (1). The curves were calculated according to Eqs. 9 and 10 with fixed values of n_Na = 2.95, n_Cl = 3.70 and K_Cl = 2.00 M⁻¹. The only parameter that was varied between the calculated curves was the nonpolyelectrolyte component of binding, log(K₀). We see that whereas the original parameters were chosen to optimize the fit for the *I salt dependence in the broad range of NaCl and NaF salts (Fig. 5, red data points and red line as a fit, logK₀ = 6.30), the same parameters work reasonably well for describing the salt dependence of *III binding to poly(dT) in both NaCl and NaF with log(K₀) = 7.50, to poly(rɛA) with log(K₀) = 7.00, and to poly(dA) with log(K₀) = 5.50. We note that the variation with base and sugar type seen in our calculated K₀ essentially parallels the results obtained by Lonberg et al. (6) for *I and Newport et al. (7) for gp32 in high salt. This observation further supports the notion that it is the interaction of the core domain (*III) with the nucleic acid that determines the value of the intrinsic binding constant to ssNA, K_ss, which is similar for all three proteins: gp32, *I, and *III. In our previous work we have shown that the salt dependence of *I becomes weaker in lower salt, such that the log-log slope becomes −(2–3). In this work, we have shown that this slope comes from the release of ∼2.9 Na⁺ cations from DNA upon *I binding. At the same time, in higher salt the apparent log-log slope of −(6–7) also includes the release of ∼4 Cl⁻ anions from the protein binding site. Here we have shown that this is similarly true of *III binding.

FIGURE 5.

Salt dependence of *III binding various single-stranded nucleic acids. *I binding data in NaCl from λ-DNA stretching experiments (open red diamond, our measurements) and for poly(dA) (solid green diamond from Lonberg et al. (6). *III binding data in NaCl for poly(dT) (open blue square), poly(dA) (open pink triangle), and poly(rεA) (black cross) from Lonberg et al. (6). *III binding data in NaCl for poly(dT) (solid blue square) in NaF from Lonberg et al. (6) The lines are the fits of these data according to Eqs. 9 or 10 with the number of cations and anions released fixed at n = 2.95 and m = 3.7, and the binding constant for Cl− to the protein binding site, K_Cl = 2 M⁻¹, as optimized in our earlier fits of the *I and gp32 protein binding. The only fitting parameter for each curve was the value of the nonpolyelectrolyte factor to the binding constant of the proteins to particular NA at 1 M salt, K₀. Best-fit values log (K₀) are given in the text.

Kinetics of gp32 association and dissociation from single-stranded nucleic acids

So far we have shown that our proposed mechanism of electrostatic regulation of gp32 binding to nucleic acids describes the available data on the salt dependence of the equilibrium binding constants of gp32, *I, and *III very well. There is also a significant amount of kinetic data for gp32 association with and dissociation from ssDNA and ssRNA (8). Our model of gp32 binding to nucleic acids, in which the interaction is regulated by the strongly salt-dependent opening of the CTD, makes very specific predictions for the kinetics of gp32 association and dissociation. In this section, we will re-analyze the extensive data on the kinetics of gp32 binding in the context of our model. It will be shown that all of the unexplained or arguable features of the salt dependence of gp32 kinetics follow directly from this model. All rates can be calculated essentially without fitting parameters using our measured equilibrium binding constants of gp32 and *I to ssDNA. This provides a complete, self-consistent picture of the equilibrium and kinetic features of gp32 interaction with nucleic acids.

Association rate

The association rate in the experiments by Lohman and Kowalczykowski (9) was measured by rapid mixing of protein and nucleic acid using the stopped-flow method. The dissociation rates of gp32 from ssDNA and ssRNA were measured by Lohman (25), using a stopped-flow salt-jump method as well as trapping of the protein with excess poly(rɛA). The salt dependence of both the association and dissociation kinetics was quite unusual. For the association reactions, two exponential decays were observed, with the more rapid decay accounting for ∼90% of the amplitude. Only the kinetic data of the rapid decay were analyzed. The measured association rate constants of gp32 are presented as data points in Fig. 6. One can see that the association rate constant behaves nonmonotonically as a function of salt, with a positive dlog k/dlog [NaCl] of ∼2.5 in low salt, i.e., at [NaCl] ≤ ∼0.1 M, and a negative slope of between −4.5 and −5.3 in high salt. These two different types of behavior were associated with “strong” and “weak” binding regimes and can be represented by the following schemes (9),

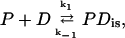(15)

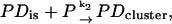(16)

where P is gp32, D is the single-stranded nucleic acid, PD_is is a noncontiguous complex, and PD_cluster is a complex of two or more contiguous proteins bound to the nucleic acid.

FIGURE 6.

The measured (symbol) salt dependence of association rate constant for gp32 binding ss nucleic acid. The data are shown for the association rate constant of gp32 binding to poly(dT) (black diamond) at [gp32] = 0.125 μM from Lohman et al. (9) The solid line is 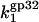calculated according to Eq. 22 using the values of K_*I and K_gp32 fitted to our measured binding constants using Eqs. 9 and 4b, as shown in Fig. 1 b. The salt-independent value reached by in higher salt was the only fitting parameter, 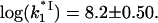Dashed line is our measured K_gp32ω (units in M⁻¹).

The rate-determining step of the low salt “strong” binding was shown to be the three-dimensional diffusional search of the protein for any isolated site on the ssNA, as represented in Eq. 15. Indeed, in this regime the association is bimolecular, and has a viscosity and temperature-dependence typical of diffusion-controlled reactions (9). The high salt regime has a salt dependence similar to that of the binding constant. In this “weak” binding regime, the noncooperative binding of the protein is in pre-equilibrium to the rate-limiting search for the boundary of the domain of bound proteins assisted by one-dimensional diffusion on NA (contiguous, i.e., cooperative binding; Eq. 16). Since these two processes, the three-dimensional diffusion to any site followed by the one-dimensional search for the boundary, generally work sequentially, the net association time, τ_net, for the majority of the binding proteins after mixing is determined as a sum of the times of these two processes,

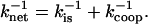(17)

Under pseudo-first-order conditions (where [ssNA] ≫ [protein]), and at low salt (strong binding conditions, where k₁ ≫ k₋₁),

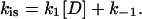(18)

Here, [D] is the ssNA concentration in the units of moles of gp32 binding sites. For the weak binding regime, the rate is equal to k_coop[P], and

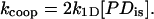(19)

Here [PD]_is is the concentration of the noncontiguous binding sites on NA, and k_1D is the rate of protein finding this noncontiguous site assisted by one-dimensional sliding along NA. According to Eq. 18, the slowest of the two processes always dominates the net rate. In low salt, the three-dimensional diffusion appears to be much slower than the one-dimensional search, whereas at higher salt the situation is reversed. This happens primarily due to the strong increase in the magnitude of the protein dissociation rate constant, k₋₁, in higher salt, which makes the one-dimensional search less effective, as discussed in the next subsection.

Association in low salt. In low salt, the dissociation constant k₋₁ is small, and therefore three-dimensional diffusion to any site on the NA is rate-limiting and, according to Eq. 18, k_is = k₁[D]. But why does k₁ increase so strongly with salt concentration below 0.2 M NaCl (Fig. 6)? The authors (9) suggested that charge repulsion between the net negatively charged (pI ∼5) gp32 and DNA decreases the diffusion rate of the two macromolecules, but this effect is reduced as the salt increases, due to the screening effect of the Na⁺ and Cl⁻. However, the traditional theory of this effect (16) predicts the dependence of

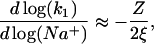(20)

due to the very weak residual electrostatic interaction between the ligand with net charge Z, and the DNA, which is almost completely neutralized due to counterion condensation up to the residual fractional charge of 1/ξ. Here ξ = l_B/b is the so-called Manning parameter, which is the dimensionless linear charge density on the nucleic acid with the unit charge per length b, and 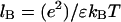is the Bjerrum length. For ssDNA, ξ ∼ 2. The nominal net charge of gp32 at pH = 7 is ∼−12, such that the slope in Eq. 20 cannot be larger than ∼12/4 = 3. Although this would seem to explain the observed slope, in reality this slope should be much smaller, since the protein is not a point charge, and only the fraction of its charge close to its binding site, which should be mostly positive charges, contributes to the salt dependence (18).

The model of protein binding that we propose here, however, suggests that the strongly salt-dependent unbinding of the CTD from its protein binding site is in pre-equilibrium to the three-dimensional diffusion-limited protein-DNA association. In other words, 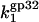is the product of the diffusional rate of finding the nucleic acid for *I, 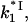and the probability of flap opening, P_op,

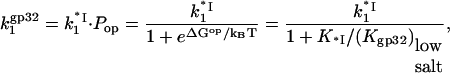(21)

or

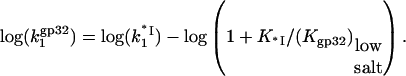(22)

Here we took into account that 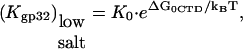as follows from Eqs. 5 and 6. Equation 21 is correct as long as the rate of CTD closing is much greater than the rate of finding the binding site, i.e., or that the CTD opening/closing step is effectively in pre-equilibrium relative to the binding reaction, which is always the case as long as the flap is mostly closed. In even lower salt, where the closed conformation is thermodynamically strongly favored, the closing of the CTD is much faster than its opening, i.e., k_cl ≫ k_op, or and Eq. 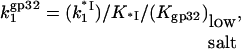21 reduces to such that

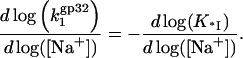(23)

In other words, the three-dimensional diffusion-controlled association rate of gp32 with NA in low salt is predicted to behave as a function of salt in the same way as a reciprocal of the binding constant of the protein without CTD, i.e., of *I. At the same time, in higher salt, when 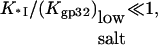Eq. 22 reduces to 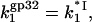i.e., the three-dimensional diffusion-controlled binding rates of both proteins are predicted to converge. In Fig. 6, we present 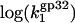calculated according to Eq. 22 with 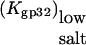values taken from our measurements. As predicted in low salt, i.e., [Na⁺] < 0.1 M, 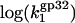has a slope ∼3 (the same magnitude for K_*I in this salt range), which is slightly higher than the slope ∼2.5 observed experimentally. In higher salt the calculated 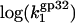saturates at a constant value of 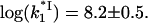This was the only parameter used to match experimental data points for k₁ with calculated 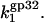This fitted value is quite reasonable for the three-dimensional diffusion-controlled association rate of the protein (26).

Association rate in high salt. Also shown in Fig. 6 is the log of the gp32 binding constant to ssDNA in the units of M⁻¹ along with the net association rate measured in Lohman and Kowalczykowski (9). We show this data here to illustrate the point that the association rate has almost the same salt dependence as K in higher salt. Under high salt conditions k₋₁ grows, such that k_is, as given by Eq. 18, becomes larger than k_coop. In other words, it is k_coop that becomes rate-limiting in the net association rate in Eq. 19 and determines its salt dependence.

The rate that determines the salt dependence of all of the other rates involved, as well as of K, is the dissociation rate k₋₁. Indeed, for any highly charged protein binding to NA it is 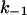that has the strongest salt dependence. The basic theory (16) predicts that practically all of the salt dependence of the equilibrium binding constant of the protein, K = k₁/k₋₁, resides in the dissociation rate constant, k₋₁. In the simplest case, when n_Na Na⁺ ions are released upon protein binding only from the nucleic acid, the salt dependence of the dissociation rate constant is predicted to parallel the reciprocal of the salt dependence of the equilibrium binding constant, i.e.,

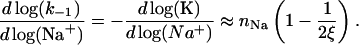(24)

For ssDNA with ξ ∼ 2 this slope is close to n_Na, i.e., has almost the same magnitude and the opposite sign to the slope of K. This strong salt dependence of k₋₁ should be the same for both gp32 and *I proteins, because the CTD refolding can happen only after the dissociation of the protein from NA.

The exact salt dependence of k_coop in the “weak” binding regime is a complicated function of k₋₁. According to Eq. 21, k_coop depends on k₋₁ through both k_1D and [PD]_is. When the noncontiguous protein binding to NA is very weak, k_1D is rate-limited by conventional mixed one- to three-dimensional diffusion: k_1D = k₁ · (k_sk₋₁)^1/2 (27). Here k_s is the sliding rate of the protein along NA. At the same time, the concentration of noncontiguously bound proteins is itself a function of the binding constant [PD_is] 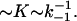Thus, Eq. 19 predicts that 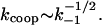This would yield a slope of k_coop equal to the 1/2 of the slope of K, i.e., ∼−3.5. This is somewhat smaller in magnitude than the experimental slope of −4.5 to −5.3. We believe that this discrepancy comes from the deviation of the k_coop behavior from the bimolecular one given by Eq. 19 at higher protein binding densities. As was shown both theoretically and experimentally in our recent study (3), at higher protein saturation the mechanism of a protein finding another protein on NA switches from mixed one- to three-dimensional diffusion (27) to pure one-dimensional diffusion. The latter is a much stronger function of K, and therefore of k₋₁.

Dissociation rate of gp32 from single-stranded nucleic acids

Lohman performed a series of experimental and theoretical studies, in which he analyzed the dissociation rate of gp32 from ssNA after a salt-jump, as a function of the final salt concentration (25,28). Typical experimental results are presented as data points in Fig. 7. In contrast to the association rate, the dissociation k_d depends strongly on the type of NA at all salt concentrations. A plot of log k_d versus log [NaCl] shows slopes of ∼5–7 at high salt (thus behaving as ∼1/K), and ∼2 in low salt. Lohman (25,28) provided an extensive theory of gp32 dissociation kinetics. Most importantly, in analyzing the dissociation rate as a function of initial NA saturation with the protein, he proved that the great majority of gp32 proteins dissociate directly from the ends of the cooperative clusters. Such a dissociation rate of the individual protein molecules is equal to the dissociation rate of the noncontiguously bound protein, k₋₁, slowed down by the cooperativity factor ω. Taking into account that not all of the proteins are bound at the boundaries, but only a small fraction, 2(1 − p₀) (in Ref. 25's notation), we can write the apparent dissociation rate constant as

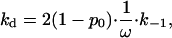(25)

where k₋₁/ω is the rate constant for dissociation of a single contiguously bound protein.

FIGURE 7.

(a) 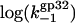versus log([Na⁺]) dependence. This was calculated according to Eq. 27 with 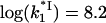obtained by fitting the association rate in Fig. 6, and K_*I calculated according to Eq. 9 with all parameters obtained by fitting of equilibrium binding data above. (b) The measured (symbol) dissociation constant log(k_d) as a function of log([NaCl]). The data were obtained by Lohman (25,28) using salt-jump and RNA competition methods for gp32 dissociation from poly(A) (circle). The solid line is log(k_d) calculated according to Eq. 25 using log(k₋₁) calculated according to a, (1 − p₀) = 0.24 (from Lohman for the specific experimental conditions f_sat = 0.09), and ω = 10³. No fitting parameters were used. Dashed line is k_d,s(Na⁺) calculated according to Eq. 28 with 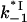(Na) from a.

Because ω does not appear to vary with [salt], k_d is predicted to follow the salt dependence of k₋₁. Rather than assume linearity (this is clearly not the case, see Fig. 7), we can now calculate k₋₁(Na⁺) directly using our measured K_*I(Na⁺). Indeed, since protein dissociation precedes closing of the CTD in gp32, the latter should have no effect on the protein dissociation rate. Therefore, the *I and gp32 unbinding rates should be the same, i.e.,

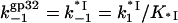(26)

or

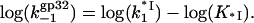(27)

Here 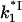is the association rate of *I with NA that is determined by three-dimensional diffusion and is almost salt-independent. In Fig. 7 a, we present the 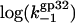versus log([Na⁺]) dependence calculated according to Eq. 27, with obtained by fitting the association rate in the previous section, and K_*I calculated according to Eq. 9 with all parameters obtained by the fitting of equilibrium binding data above. Also, in Fig. 7 b, we have used the 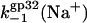dependence from Fig. 7 a to calculate k_d(Na⁺) according to Eq. 25, with ω = 10³, and the fraction of the boundary proteins (1 − p₀) ≈ 0.24. The latter was estimated for the particular fractional saturation of polyA with the protein, f_sat ≈ 0.09, which was used by Lohman (28) to obtain the data shown in Fig. 7. Comparing the results of our k_d(Na⁺) calculations with Lohman's data, we see reasonably good quantitative agreement. It is worth noting here that this agreement was obtained without using any fitting parameters, but instead by employing our experimentally determined K_*I(Na⁺). Thus the slower variation of K_*I(Na⁺) with salt in lower [Na⁺] explains the analogous behavior of k₋₁(Na⁺).

In 1984 there was no data available for K_*I(Na⁺) or k₋₁(Na⁺) in low salt. Therefore, Lohman suggested another explanation for the observed k_d(Na⁺) behavior (28). Specifically, he considered the possibility of an alternative dissociation pathway, when the protein first slides from the boundary without dissociation with the rate k_s/ω, and then dissociates with the probability (k₋₁/k_s)^1/2. This pathway should contribute the additional rate 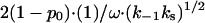to k_d, such that Eq. 25 should be replaced by

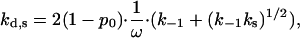(28)

where k_d,s is the dissociation rate enhanced by sliding. The second term 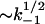should dominate in low salt when k₋₁ is small, explaining the smaller curvature of k₋₁(Na⁺) in this salt range. The value k_d(Na⁺), calculated according to Eq. 28 with 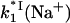from Fig. 7 a, is also presented in Fig. 7 b. One can see that in the studied salt range this calculated k_d,s(Na⁺) is much higher than the measured dissociation rate and varies much more slowly with salt. This means that the sliding pathway does not significantly contribute to the rate of gp32 dissociation from ssNA. We believe this occurs for the following reason. In deriving the result given by Eq. 28, Lohman assumed that the protein slides from the boundary onto an infinite protein-free NA. Then the probability of escaping a single boundary is proportional to the reciprocal of the effective size of the boundary, yielding an effective boundary size of

(29)

This effective boundary size is simply the distance that the protein can diffuse on NA before its dissociation after the time 1/k₋₁. Here we took into account that the sliding rate can be expressed through the one-dimensional diffusion constant D₁ and the length per nucleotide b as 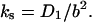However, if the NA saturation with the protein is not infinitely small the typical length of the protein-free NA can easily become smaller than x. Indeed, in our experimental salt range, 10⁰ ≤ k₋₁ ≤ 10⁴ s⁻¹ (see Fig. 7 a). Also, k_s ∼ 10⁶ s⁻¹, as estimated by Lonberg et al. (6) Therefore, for the protein not to be captured by the other boundary, this boundary has to be more than (k_s/k₋₁)^1/2 ∼ 10^1–3 nucleotides away. This condition can only be fulfilled for an extremely small initial fractional protein saturation, f_sat. In the lower salt, k₋₁ is smaller, so the role played by the sliding pathway in the protein dissociation at any finite f_sat becomes much smaller in low salt. In addition, the peculiar k_d(Na⁺) shape was observed for all f_sat up to fractional protein saturation, f_sat = 1 (28). Thus, we conclude that the sliding cannot measurably enhance the dissociation of gp32 from NA. We note that Lohman (25) considered the possibility that the slope of k_d in low salt decreases simply due to the fact that ∼4 Cl⁻ ions associate with gp32 upon its unbinding from ssNA in low salt. However, this was just a qualitative statement, which was dismissed based on the fact that the break in the slope of log(k_d) versus log(Na⁺) appears at different [Na⁺] for different ssNA. Here we calculate k_d(Na⁺) directly with no fitting parameters, using the experimental value of K_*I(Na⁺) and 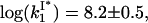which is in agreement with the direct measurements of this quantity. This calculated log-log slope of the k_d(Na⁺) is in very reasonable agreement over all salt concentrations with the measured k_d(Na⁺) (25) as shown in Fig. 7.

Concluding our discussion of the kinetics of gp32 association with dissociation from single-stranded nucleic acids, we can see that the very peculiar salt dependence of both processes follows directly from the idea of the required pre-equilibrium unfolding of the CTD from the protein binding site, which becomes exponentially less probable in lower salt. In fact, this model, in combination with our measured equilibrium binding constants of gp32 and *I over a broad range of solution conditions, allows a quantitative description of the kinetics of the association and dissociation rates of these proteins without fitting parameters.

Physical reason for the strong salt dependence of CTD binding

What is the physical basis for this strong salt dependence of CTD-ssNA binding? In general, a strong salt dependence of the binding of two macroions is a sign of counterion condensation on at least one of them. The main contribution to the binding free energy, ΔG, comes not from establishing the ionic contacts between the macroions with complementary charges, but rather from the entropy of release of n small ions TΔS = n · k_BT · ln(N_s/I) from either or both macroions, which yields the binding constant K:

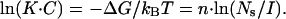(30)

Here N_s and I are the small cation (or anion) concentrations at the macroion surface and in the bulk solution. The reason that the direct electrostatic attraction between the macroions does not significantly contribute to ΔG is that each macroion is almost completely screened by the small ions even before the macroion binding. Most important, the neutralizing charge of the small counterions is contained within a thin layer λ at the concentration N_s at the macroion surface (18,29), with both quantities being independent of the bulk solution ionic strength I. N_s is independent of [salt], which results in the conventional log-log dependence of the binding constant on salt given by Eq. 30. The accumulation of such a salt-independent counterion atmosphere, termed counterion condensation, was first described by Oosawa (30,31) and Manning (15) for the hypothetical case of an infinite line charge. This approximation, in fact, can be used for a long finite radius polyelectrolyte in the limit of very low salt. The application of this idea to the interpretation of the salt dependence of NA binding of cationic ligands was further developed in the work of Record and Lohman (22,32). In addition, it was shown that similar counterion condensation exists on a macroion of arbitrary size and shape, within a certain range of solution ionic strength (18,33–35). The only requirement for counterion condensation (CC) is that of a local high surface charge density on the macroion, which creates a nearby region with counterion energy larger than k_BT (18,29). This effectively results in a situation in which the protein or nucleic acid has a binding site for the neutralizing counterions with a strong, salt-dependent binding constant. This is always the case for polymeric nucleic acids, both ds and ss. Therefore, the binding of the cationic ligands to NA is always strongly salt-dependent. A somewhat smaller CC occurs on short nucleic acid oligonucleotides (32). This study also argues that a similar CC occurs on the CTD of gp32 in its unbound form in solution. Thus, the main driving force for the CTD binding to a cationic surface on gp32 is the release of Na⁺ ions condensed on the CTD into solution.

This situation can be contrasted with the case of weakly charged macroions (or, more precisely, macroions with small surface charge density), which do not have CC. The free energy of interaction between such macroions is proportional to their Coulombic attraction screened by the Debye-Huckel ion atmosphere. Such free energy depends on the solution ionic strength though the Debye screening length, 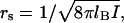as 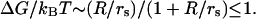Here I is the ionic strength, l_b is the Bjerrum length, given by l_b = e²/ɛk_BT, and R is the distance between ions in the bound state. This results in a much smaller, and much less salt-dependent, electrostatic contribution to the binding constant. In the case of gp32 protein, an example of such interaction is probably the association of its cationic N-terminal domain with (presumably) an anionic patch on the neighboring gp32 molecule, possibly the negatively charged “arm” at the C-end of the core (36), which is most likely responsible for the cooperativity of gp32 binding ssDNA. Although occurring between the complementary charged parts of the two molecules, this interaction is largely salt-independent (9,37–39).

Structural reason for counterion condensation on the C-terminal domain of gp32

Is there any structural reason for the CTD to have CC on it? In Fig. 8, the complete 301-amino-acid (aa) sequence of gp32 is presented. The 21 aa of the N-terminal domain and the 48 aa of the CTD are separated from the core-domain sequences using a box. In red are shown the negative charges of aspartic and glutamic acid. In blue are the positive charges of lysine and arginine. There are 38+ and 50− charges in the whole protein, such that its net charge at pH = 7 is −12. Without the CTD the protein has 35+ and 35− charges, which makes for a net-zero charge on *I. The 48-aa CTD, as defined by proteolytic digestion at the unstructured coil regions of the proteins, has 15− and 3+ charges, which makes a total of −12. However, these charges are distributed nonuniformly within the CTD. Specifically, five Asp are located within the stretch of seven amino acids between residues 290 and 296. Since the length per amino acid along an unstructured polypeptide backbone is ∼2.9 Å, this piece of the protein is an ∼20 Å length oligo-anion with the total charge of −5, i.e., an average linear charge density of one charge per ∼4 Å. This is quite similar to an ∼6-nt-long piece of ssDNA with a linear charge density of one charge per ∼3.4 Å. From the studies by Ballin et al. (40) we know that the CC on such a short ss oligonucleotide is approximately two times smaller than on a polymer; i.e., we can roughly estimate it as ∼2–2.5 Na⁺ ions condensed. However, in the case of the CTD, this counterion condensation must also be somewhat enhanced by the flanking of less highly charged, but still anionic sequences. Overall, it seems quite plausible that approximately three condensed Na⁺ get released into solution from the CTD as it binds the cationic groove of gp32. The above estimate was done for the completely unstructured CTD. Any structuring of the CTD would likely result in a higher surface charge density, and therefore, more Na⁺ ions condensed on it. However, no CTD structure in solution has been observed so far either by CD or NMR.

FIGURE 8.

The complete 301-aa sequence of gp32. The core domain lacks the 21 aa N-terminal (B domain) and 48 aa CTD (A domain), which are shown in the blue and red boxes, respectively. The negatively charged aspartic acid (D) and glutamic acid (E) are shown in red, whereas the positively charged lysine (K) and arginine (R) are shown in blue.

Is there CC on the cationic groove of the core domain of gp32? The fact that approximately four Cl⁻ ions associate with the cationic groove of gp32 with a binding constant of ∼2 M⁻¹ means that there is CC on this groove, but it is significantly weaker than on the CTD, most likely due to the smaller charge density within this groove.

gp32 binding to double-stranded DNA

So far, we have discussed the salt dependence of gp32 binding to single-stranded nucleic acids only. Indeed, whereas much data is available on gp32 binding to ssNA, there is very limited data for dsDNA binding from more conventional biochemical studies (41,42). However, recent results obtained in single molecule studies (3) argue convincingly that the intrinsic binding constant of both gp32 and *I to dsDNA is only ∼10 times weaker than the corresponding binding constant to ssDNA. The same factor of ∼10 follows from the limited data by Jensen et al. (24) The other factor of ω ∼ 10³ in the net binding constant to ssDNA as compared to dsDNA comes from the cooperative protein-protein interaction between the gp32 molecules bound to ssDNA. This cooperative interaction does not appear to exist for dsDNA-bound gp32, which results in an affinity ∼10⁴-fold lower than the overall affinity for ssDNA. This is the key factor in the identity of gp32 as an ssDNA binding protein and its biological functioning in DNA replication, recombination, and repair.

Moreover, according to our new single molecule measurements (1), the salt dependence of binding of both proteins to dsDNA parallels their binding to ssDNA, at least at the low levels of salt studied. This similarity between gp32 binding to ds- and ssDNA, together with our extensive analysis of ssDNA binding discussed above, suggests that the strongly salt-dependent conformational change in gp32 protein required for its binding to ssDNA is also a prerequisite for its binding to dsDNA. However, whereas the binding of gp32, *I, and *III to ssDNA results in the partial unstacking, stretching, and rigidification of ssDNA, as followed by the changes in the CD and UV spectra of NA (43), this presumably does not occur when the protein binds dsDNA. The changes in ssDNA structure may result, at least in part, from the partial stacking of five Tyr residues with NA bases. However, whereas none of the Tyr side chains are at the surface of the binding groove in the core-domain structure (10), the cationic residues are well exposed. If dsDNA binds to essentially the same binding site on the protein as ssDNA, its larger diameter (twice that of ssDNA) would prevent it from penetrating the binding groove without significant distortion. However, the flexible side chains of groove lysine and arginine residues could make contact with the dsDNA and still be able to minimize electrostatic free energy.

The biological role of gp32 binding to dsDNA and the kinetics of replication fork movement

Since the biological role of gp32 is believed to be its polymerization on all exposed regions of ssDNA in the moving replication fork (44), as well as binding to ssDNA during strand exchange (45,46), why should one be interested in gp32 binding to dsDNA? Despite the extensive studies of gp32 protein binding to ssDNA for over 30 years, the mechanism of its action in the cell remains unclear. For example, it was not understood why such an effective ssDNA binder as gp32 does not result in the melting of dsDNA within the cell. It was realized quite early (24) that the inability of the full-length protein to melt dsDNA (in contrast to *I) is related to some kinetic block in the former. However, if gp32 binding to ssDNA is slow, as suggested by the kinetic block model, how is it able to rapidly polymerize on ssDNA at the replication fork (covering up to 1000 bp/s; see Ref. 44), allowing it to keep up with the unwinding of dsDNA by the helicase?

We believe that we are now able to understand the kinetic mechanism of the latter process, based on our single DNA molecule stretching studies (1–3). In our previous work (3), our experiments mimicked the unwinding action of the helicase by the force-induced melting of dsDNA in the presence of gp32,*I, and *III proteins. This study has shown that the rate-determining step in protein-supported dsDNA melting is the simultaneous opening of seven basepairs from the duplex end, which should occur as a result of thermal fluctuations. If the basepairs are rather stable, then such an event is highly improbable. However, if such melting occurs, the melted conformation gets immediately trapped by *I. At the same time, gp32 needs much more time to trap the melted conformation. It, therefore, requires a much lower stability of DNA duplex to show any significant effect on DNA melting. The rate of protein finding the new binding site on ssDNA, which appears as a 7-bp melting fluctuation at the boundary between the protein-covered ssDNA and dsDNA, is, in fact, very fast. We have shown that this rate grows quadratically with protein concentration and for *I even exceeds the three-dimensional diffusion limit, a consequence of one-dimensional diffusion of the protein along dsDNA. As occurs in the cell, in our DNA stretching experiment the magnitude of the affinity of gp32 for dsDNA assures that a small but non-zero number of protein molecules are always bound to dsDNA. As the new ssDNA site appears, these molecules diffuse to it along dsDNA. The rate of finding the new site, k_a, is determined by the average distance from this site to the closest protein molecule bound to dsDNA. This distance, in turn, is governed by the protein concentration, and its binding constant to dsDNA, K_ds. As it is the pure one-dimensional diffusion that dominates this rate, it varies as the square of the fractional DNA saturation with the protein, Θ, i.e., k_a ∼ Θ². Also, since Θ ∼ K_ds, the association rate varies as 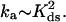Thus, it is the binding of gp32 to dsDNA that is most important for its DNA melting ability. At the same time, as long as ssDNA binding is much stronger than the dsDNA binding, such that polymerization of gp32 on ssDNA is irreversible, the magnitude of the affinity of gp32 binding to ssDNA does not affect the melting rate.

In this work, we have shown that the binding constants of gp32 and *I converge in high salt ([NaCl] ≥ 0.2 M), and strongly diverge in lower salt. The reason for such behavior is extensively discussed above for the case of gp32 binding to ssDNA. Yet, we expect it to similarly apply to this protein binding dsDNA. Thus, already at 0.1 M NaCl the dsDNA binding constant of *I is ∼50 times higher than for gp32 (1). This difference in K_ds amounts to the 50² = 2500-fold difference in the rate of protein finding the melted region of ssDNA, and explains the inability of gp32 to melt dsDNA.

This extreme sensitivity of the DNA melting ability to the presence of the CTD below 0.2 M NaCl stems from the strong salt dependence of CTD removal from its protein binding site. This, in turn, opens the possibility of fine-tuning gp32 DNA melting ability with other proteins of the replication fork, which are known to interact with the gp32 CTD.

CONCLUSIONS

In a recent article, we determined the equilibrium binding constants of gp32 and *I to dsDNA (K_ds) and ssDNA (K_ss) in different salt concentrations using single molecule force spectroscopy.(1) We showed that whereas the *I binding constant continues to grow with decreasing salt, the binding constants of gp32 to dsDNA and ssDNA saturate at [Na] < 0.2 M. We found a pronounced difference between the equilibrium binding constants for *I and gp32 in low salt, whereas at higher salt levels the affinities and salt-dependencies are similar.

In this article, we have proposed and developed a model that describes the structural and biophysical origin of the dramatic difference between the nucleic acid binding activities of these proteins based on our observations and the observations of other studies of gp32, its proteolytic fragments, and some mutants. Our model includes the release of small ions from both NA and the protein, as well as the strongly salt-dependent removal of the C-terminal domain (CTD) of gp32 from its NA binding site. We showed that unbinding of the CTD is associated with the counterion condensation (CC) of Na⁺ ions onto it, which compensates for Na⁺ release from ssNA upon its binding to gp32, and which results in the salt-independence of gp32 binding to NA in low salt. The predictions of our model quantitatively describe the large body of data collected during approximately 30 years of studies of gp32 binding to various types of single-stranded nucleic acids as a function of salt concentration over the entire available range of salt concentrations. Excellent fits to the salt dependence of gp32 and *I equilibrium binding to all types of nucleic acids were obtained simply by varying the nonelectrostatic binding constants of the proteins. In addition, the resulting fitting parameters could be used to describe most of the available data on the association and dissociation kinetics of gp32 binding to single-stranded nucleic acids without altering the values of these parameters. We also showed that the salt dependence of gp32 and *I binding to dsDNA is similar, which suggests that the same electrostatic regulation mechanism governs the binding of the protein to dsDNA.

As was shown in our previous study (3), it is the binding constant of gp32 and *I to dsDNA that determines the rate of protein-induced DNA duplex melting. Since the dsDNA melting rate varies as the square of the protein binding constant to dsDNA, the increasing difference in the K_ds of gp32 and *I leads to the dramatic ∼10³–10⁴-fold difference in the DNA melting rates by these proteins at physiological salt levels. This study relates the profound difference in *I and gp32 DNA melting ability to the salt-regulated unfolding of the C-terminal domain of gp32. Previous studies have shown that the C-terminal domain interacts with several other replication proteins (11–14,47,48), suggesting that the properties of gp32 at the replication fork can be regulated by such binding. This simple regulatory mechanism, based on the strongly salt-dependent conformational change within the protein, may be relevant to other DNA-protein systems that have not been as well studied as gp32. For example, the binding of T7 gene 2.5 protein to ssDNA also appears to be regulated by a negatively charged C-terminal domain, which interacts with other replication proteins (49).