Abstract
We have studied the catalytic efficiency of acetylcholinesterase (AChE) in various solutions with ion-disturbed water structure to explore the role that the water structure plays in the substrate-enzyme encounter. The extent of water structuring in the different aqueous solutions was determined by near-infrared spectroscopy. The influence of water structure on the degree of solvation and on the intramolecular mobility of AChE was investigated for different aqueous ionic solutions by small-angle x-ray scattering technique and depolarization fluorescence spectroscopy. It was found that the encounter process between AChE and acetylthiocholine was promoted in solutions with less structured water. In these solutions it was also found that AChE is less solvated coinciding with higher intramolecular mobility. The found experimental results suggest that the water structure may influence the substrate-enzyme encounter process by diminishing the AChE solvation shell and may help diffusion of the substrate through the gorge by enhancing the intramolecular mobility of AChE.
INTRODUCTION
During biological evolution some enzymes have reached the so-called “catalytic perfection”. Such enzymes operate at, or close to, the diffusion control limit, because of their ability to catalyze the reaction almost at every encounter with a substrate molecule (1). Because the active site of an enzyme is generally located on a small fraction of its total surface area and the molecules diffuse randomly in a solution, one could expect that the substrate is directly or indirectly guided to the active site during the encounter process leading to the maximal catalytic efficiency. Therefore, the understanding of the guidance of a substrate to the active site is of interest from academic and protein-design point of view.
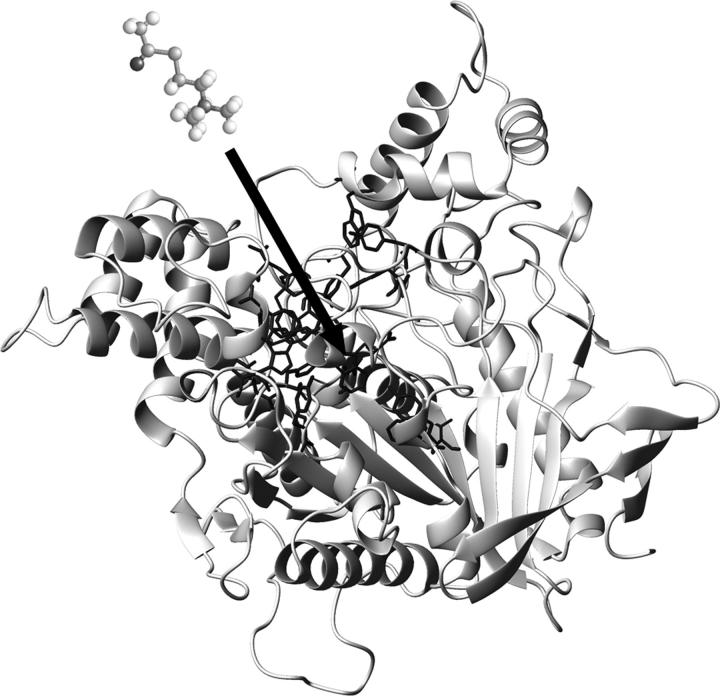
In the case of acetylcholinesterase ((AChE) EC 3.1.1.7), the encounter process is even more interesting since its active site cannot be easily reached because it is at the bottom of a deep and narrow gorge (20 × 6 Å (2); Fig. 1). AChE is a classic example of a perfect enzyme with very high catalytic efficiency (3,4). In earlier decades, electrostatic steering based on the ionic strength-dependent kinetics was mostly emphasized as a reason for the high efficiency of AChE (5). The positive group of the natural substrate acetylcholine (ACh) was assumed to bind at a highly negative site (six to nine negative charges) denominated as the anionic subsite (5,6). More recently, however, crystallographic studies have emphasized the aromaticity around the active site of the enzyme and the presence of only one negative charge (E199, TcAChE) in the “anionic subsite” (W84, E199, F330 (7,8)), thus decreasing the impact of the electrostatic attraction (2). Moreover, the importance of this residue for binding of the substrate has been questioned. It has been shown that site-directed mutations in the residue E202 (mAChE), in comparison with the aromatic residue W86, affect the catalytic efficiency only slightly (9–12). Crystallographic data of the complex of AChE with analogs of the transition state (13) have confirmed the importance of the residue W84 for the binding of the acetylcholine to the active site. Additionally, computational simulations (14) suggested that the size/shape complementarities affected the docking energy between ACh and AChE more than electrostatic interactions. Finally, the Km values for the charged substrate acetylthiocholine (AcSCh) and for its isosteric uncharged analog (DBTA) agree within a factor of two (15) suggesting that the initial encounter rate is charge independent (16). So far, all the experimental and theoretical efforts and the different techniques employed have not provided a full explanation of the high efficiency of AChE. The nonexpected aromaticity of the gorge as well as its influence on the electrostatic steering has been intensively discussed. On one hand, the ionic strength-dependent kinetics, the presence of negatively charged residues at the rim of the gorge and the computational simulations manifest the electrostatic steering hypothesis (1,5,17,18). On the other hand, the importance of aromatic residues in the “anionic subsite”, as opposed to the expected negative groups (7,8,14,19), and kinetic studies on mutants with neutralized surfaces have raised the question of the role of the electrostatic attraction in the guidance of the substrate to the active site. Even more, these mutants have shown ionic strength-dependent kinetics (16).
FIGURE 1.
Structure of AChE from Electrophorus electricus, Protein Data Bank code 1C2B. The active site is shown at the bottom of the deep and narrow gorge (20 × 6 Å). The arrow represents schematically the critical distance.
Antosiewicz and collaborators (20) remark that not only the formal charges contributed to the electrostatics interaction, but the dipole moment of the enzyme also played a significant role in the steering of the substrate. They have shown that the dipole moment of the neutralized mutants are only slightly modified and might still contribute to the attraction. The dipole moment created by charges in the entire enzyme has been proposed to be the origin of an electrostatic mechanism for substrate guidance (21). Nevertheless, AChE is mainly found in its dimeric and tetrameric forms ((22) Protein Data Bank, 1C2O, 1MAA) (23,24). Note, that in such an arrangement the monomer dipole moments might compensate each other.
Inspired by the ionic strength-dependent kinetics of the neutralized AChE mutants and interested in the influence of further physical parameters on the bimolecular rate constant, we decided to study the effect of the water structure on AChE kinetics. The effect of ions on water structure has been widely investigated (25–27). The influence of water structure on functions of proteins has been only recently discussed and attributed to effects on alteration or stabilization of the protein structure (28–31) or to the dynamics of the protein (32,33).
In the last decade the protein solvation has gained importance, but the role of the water in biological function is not entirely understood. In this work we investigate the role of the water structure on the encounter of AChE and its substrate without necessarily modifying the protein conformation. We have found that the structure of the H-bonding network of the water can modify protein solvation and protein intermolecular mobility without modification of the protein structure itself, but with consequences for the AChE kinetics.
To study the solvent structure influence on the enzyme function, we have modified the water structure by adding different monovalent ions and investigated the effect on the encounter rates of the enzyme and substrate by observing the enzymatic kinetics. The degree of water (dis)ordering was investigated by near-infrared (NIR) absorption measurements. The so-called Jones-Dole B coefficient for the different ionic solutions, which is widely used to indicate the ion disturbance of the water structure (25–27), was also used in our study. Spectroscopic and x-ray scattering techniques were employed to investigate the effect of the solvent on AChE structure, solvation, and intramolecular mobility. The influence of the bulk water structure on the solvation of acetylcholinesterase was determined by small-angle x-ray scattering experiments. The intramolecular mobility and its dependence on the solvation were investigated by fluorescence polarization spectroscopy. We have found a correlation between the disturbance of the water structure, the substrate guidance (“critical distance”), the solvation (radius of gyration, Rg), and the molecular mobility (diffusional rotation, Dr). This reveals that the water structure is able to modify the AChE enzymatic kinetics by changing the intramolecular mobility and the solvation of acetylcholinesterase. Because of these findings, we propose that the network of the water molecules around the protein and the substrate, as well as the mobility of the protein itself, should also be taken into account within the model for guiding of the substrate to the active site.
MATERIALS AND METHODS
Materials
Acetylcholinesterase type V-S from Electrophorus electricus, the salts (>99.9%): LiCl, NaCl, KCl, RbCl, CsCl, KBr, KI, CsI, and the reagents acetylthiocholine (AcSCh) and 5,5′-dithiobis(2-nitrobenzoic acid) (DTNB) were purchased from Sigma-Aldrich (St. Louis, MO). Absolute ethanol was purchased from Merck (Darmstadt, Germany). The enzyme was purified as described previously (34) and stored in 4 mM potassium phosphate buffer, pH 8.0, at concentrations ≥1 mg/ml and T = −20°C.
Enzymatic assay
The AChE activity was determined according to the method of Ellman (35). The assays contained 2 mM potassium phosphate buffer, pH 8.0, 10−10 M AChE, 1.25–600 μM enzymatic substrate AcSCh and 333 μM DTNB (ɛ412 = 14,150 M−1 cm−1 (36)). The ionic strength varied from 9.4 to 311.4 mM by addition of the following salts: LiCl, NaCl, KCl, RbCl, CsCl, KBr, KI, CsI, separately. The experiments were carried out in controlled temperature at 5°C. The increasing absorption at 412 nm was detected in the spectrophotometer Cary-5E (Varian Australia, Victoria, Australia) and registered during ∼60 s with a resolution of 0.033 s.
Near-ultraviolet circular dichroism
Circular dichroism (CD) spectra were recorded on a Jasco 720 spectropolarimeter equipped with a Peltier temperature controller (20°C) over the range of 250–350 nm in a 1-cm pathlength cuvette. The bandwidth and spectral resolution were 1 and 0.5 nm, respectively. Twenty scans were averaged and corrected for the respective buffer/salt solution spectrum.
Absorption in the near-infrared region
Absorption spectra were recorded using a Cary-5E UV-VIS-NIR spectrophotometer (Varian Australia). The slits were adjusted for a bandwidth of 2 nm, the spectral resolution was 0.5 nm, and the pathlength of the cuvettes was 1 cm. The spectra were corrected by subtracting a reference spectrum corresponding to that of the cuvette in the cell. All measurements have been carried out in nitrogen atmosphere and at 5°C. The spectra were normalized for the concentration of water in the respective ionic solutions.
Water structure determination
Fraction of free OH-group
The water fraction of the so-called “free OH-group” was estimated by the Luck method (37–39). The fraction of free OH-group (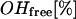 ) is directly antiproportional to the extent of H-bonding network in water and is defined as:
) is directly antiproportional to the extent of H-bonding network in water and is defined as:
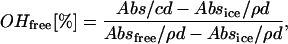 |
(1) |
where Absfree is the absorption of the water at 1143 nm at the critical point (40), Absice is the absorption of the ice at 1143 nm (40), Abs is the measured absorption of the ionic solution at 1143 nm, c is the concentration of the water in the ionic solutions (g/ml), ρ is the density of the water (g/cm3), and d is the distance of the light in the cuvette (cm). Further explanations will be given in the following section.
Jones-Dole B coefficient
The Jones-Dole B coefficient is related to the effect of the ions on the water structure. Positive B coefficients indicate water structuring and negative B coefficients indicate the disturbance of the water structure (25–27). The Jones-Dole B coefficient was calculated by fitting the viscosity data (41) of the ionic solutions by the Jones-Dole equation: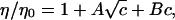 where η is the viscosity of the ionic solution; η0 is the viscosity of pure water at the same temperature; A and B are empirical parameters; and c is the concentration in mol/l.
where η is the viscosity of the ionic solution; η0 is the viscosity of pure water at the same temperature; A and B are empirical parameters; and c is the concentration in mol/l.
Small-angle x-ray scattering
Small-angle x-ray scattering was measured with a Krakty compact small-angle x-ray system (Anton Paar Germany GmbH, Ostfildern, Germany) at a controlled temperature of 278 K in a vacuum chamber. The scattered intensity was measured as function of the scattering vector 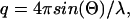 with 2Θ = scattering angle and λ = 1.54 Å, in the range from q = 0.005–0.1855 Å−1. The measurements were undertaken with solutions of 0.9–3.6 mg/ml of acetylcholinesterase in phosphate buffer 2 mM, pH 8, in sealed glass capillaries (diameter = 1.0 mm) as well as with solutions containing 1.8 mg/ml of AChE and 300 mM of the various salts. As reference, the buffer/ion solvents were used for background correction. After the small-angle x-ray scattering (SAXS) experiments the quality of the samples was checked by determining the enzymatic activity before and after the SAXS experiments. The radii of gyration were calculated by the Guinier equation:
with 2Θ = scattering angle and λ = 1.54 Å, in the range from q = 0.005–0.1855 Å−1. The measurements were undertaken with solutions of 0.9–3.6 mg/ml of acetylcholinesterase in phosphate buffer 2 mM, pH 8, in sealed glass capillaries (diameter = 1.0 mm) as well as with solutions containing 1.8 mg/ml of AChE and 300 mM of the various salts. As reference, the buffer/ion solvents were used for background correction. After the small-angle x-ray scattering (SAXS) experiments the quality of the samples was checked by determining the enzymatic activity before and after the SAXS experiments. The radii of gyration were calculated by the Guinier equation: 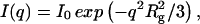 where
where 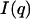 is the net scattered intensity at q and
is the net scattered intensity at q and 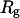 is the radius of gyration (42,43). To correct the concentration effect in the SAXS profile, the
is the radius of gyration (42,43). To correct the concentration effect in the SAXS profile, the 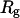 was extrapolated to zero concentration of the protein (42,44).
was extrapolated to zero concentration of the protein (42,44).
Fluorescence and fluorescence depolarization spectroscopy
Fluorescence emission measurements
The fluorescence spectra of AChE have been measured with a Fluorolog 3-22 (JOBIN YVON-SPEX, Munich, Germany). For the general emission experiments, the emission spectra were taken in 0.5-nm steps at a fixed excitation wavelength of 280 nm. The slits were adjusted to 2-nm bandwidth for both excitation and emission. The recorded spectra were automatically corrected for the wavelength dependence of the lamp intensity, monochromator transmission, and photomultiplier response. The concentrations in the solution were 300 mM of salt and 1 μM of AChE in the same buffer as used for the enzymatic essay.
For the depolarization measurements, the emission spectra were taken in 0.5-nm steps at a fixed excitation wavelength of 297 nm, avoiding tyrosine excitation. Because the anisotropy of the AChE fluorescence is constant for the measured wavelength interval (300–380 nm) and to obtain higher emission intensity on the detector the slits were adjusted to 2-nm bandwidth for excitation and to 12 nm for emission. The recorded spectra were automatically corrected for the wavelength dependence of the lamp intensity, monochromator transmission, polarizer, analyzer, and photomultiplier response. The solution concentrations used were 300 mM of salt and 4.15 μM of AChE in 2 mM potassium phosphate buffer, pH 8.0. For the limiting anisotropy (R0) measurements (as reference) the AChE was dried on a quartz plate. This method guaranteed that the rotational movement of the tryptophans in the solidified sample was hindered. All measurements were carried out at T = 5°C using a thermally controlled sample holder.
Lifetime of the AChE tryptophans
In the nanosecond range, the fluorescence decay curves were recorded on a standard time-correlated single-photon counting apparatus (Edinburgh Instruments, Livingston, UK) with a deuterium flash lamp as excitation source. An interference filter was used to select the excitation wavelength, with a maximum of 298 nm and a half-width of 1–2 nm, avoiding tyrosine excitation. The data were analyzed by applying a deconvolution technique and fitted with a nonlinear least-squares fitting method based on the Levenburg-Marquardt algorithm to mono/multiexponential decay laws such as 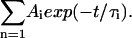 The accuracy was ±0.5 ns with χ2 ≅ 1.8).
The accuracy was ±0.5 ns with χ2 ≅ 1.8).
Determination of the rotational correlation time
Anisotropy was obtained by the fluorescence measurements using a polarizer and an analyzer in parallel and perpendicular alignment geometry. The anisotropy, the rotational correlation time, and the rotational diffusion were calculated by the Perrin equations (45):
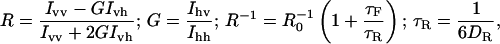 |
(2) |
where R is the anisotropy, R0 is the limiting anisotropy, I the fluorescence intensity, v and h assign the vertically and horizontally polarized light (position of polarizer and analyzer), G corresponds to the correction factor, τF (s−1) is the fluorescence lifetime, τR is the rotational correlation time (s−1), and DR is the rotational diffusion (rad2 s−1).
Statistical analysis
The results from the various experiments were compared and the empirical correlations found were linearized and statistically analyzed (46). To evaluate the significance of the correlations, the product-moment correlation coefficient was calculated as follows (47):
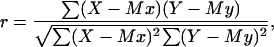 |
where r is the product-moment correlation coefficient, X is the observed values for the parameter x, Mx is the mean value for X, Y is the observed value for the parameter y, and My is the mean value for Y.
To judge the empirical correlations the t-test has been employed:
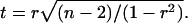 |
Here, n is the number of points.
The r-values and the values for t were compared with the statistical tables for critical values of r and of the t-distribution, respectively (48). If the calculated values are greater than the critical values for 5% of significance (depending of the number of measured points), the null hypothesis (for the case of no-correlation) can be rejected, i.e., the correlation is accepted as being significant. The probability of obtaining each value of t by random sampling (the P-value) can be consulted from the table “t-table for estimating P-values” (48).
RESULTS AND DISCUSSION
Enzymatic kinetics
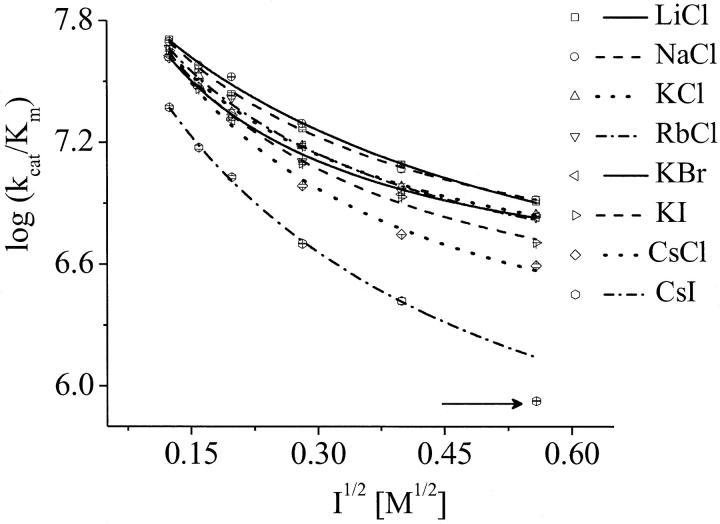
In accordance with a diffusion-controlled enzymatic reaction, the catalytic efficiency, kcat/Km, was considered to be the bimolecular rate constant (3). In this way, we can separately analyze the chemical (kcat) and the diffusive steps (kcat/Km) of the reaction. Table 1 shows that the ions alter Km, but not kcat, which demonstrates that the ions do not have any influence on the chemical step of the reaction by allosteric regulation. This suggests no conformational alteration of the enzyme, which is also supported by further investigations on the tertiary structure of AChE by fluorescence spectroscopy and near-ultraviolet (UV) circular dichroism experiments. The salt CsI, as an exception, altered the kcat at higher concentration (0.3 M). Hence, this point was excluded from the analysis in Fig. 2 (arrow). The general low values for kcat are due to the low temperature of the experiments (5°C).
TABLE 1.
Kinetic parameters for eelAChE in the ethanol and ionic solutions
| LiCl | |||
|---|---|---|---|
| Ic (M) | kcat (s−1) | Km (μM) | kcat/Km(M−1 s−1 × 10−7) |
| 0.0154 | 745.4 ± 13.2 | 14.71 ± 0.09 | 5.07 ± 0.06 |
| 0.0254 | 876.6 ± 23.6 | 24.13 ± 0.61 | 3.63 ± 0.01 |
| 0.0394 | 678.7 ± 0.01 | 24.89 ± 0.40 | 2.73 ± 0.04 |
| 0.0794 | 830.6 ± 9.5 | 44.91 ± 0.75 | 1.85 ± 0.05 |
| 0.1594 | 869.4 ± 5.8 | 70.46 ± 2.90 | 1.23 ± 0.06 |
| 0.3114 | 711.1 ± 1.9 | 87.88 ± 3.06 | 0.81 ± 0.03 |
|
|
NaCl
|
||
| Ic (M) | kcat (s−1) | Km (μM) | kcat/Km(M−1 s−1 × 10−7) |
| 0.0154 | 743.1 ± 11.0 | 14.97 ± 0.13 | 4.96 ± 0.12 |
| 0.0254 | 880.6 ± 11.8 | 23.20 ± 0.09 | 3.80 ± 0.07 |
| 0.0394 | 888.1 ± 0.02 | 26.73 ± 0.04 | 3.32 ± 0.01 |
| 0.0794 | 880.0 ± 25.2 | 42.13 ± 1.67 | 1.96 ± 0.02 |
| 0.1594 | 993.1 ± 16.8 | 83.99 ± 3.96 | 1.17 ± 0.08 |
| 0.3114 | 968.6 ± 6.5 | 117.17 ± 7.15 | 0.83 ± 0.06 |
|
|
KCl
|
||
| Ic (M) | kcat (s−1) | Km (μM) | kcat/Km(M−1 s−1 × 10−7) |
| 0.0154 | 773.9 ± 20.4 | 18.12 ± 0.33 | 4.27 ± 0.05 |
| 0.0254 | 876.6 ± 7.5 | 23.07 ± 0.54 | 3.37 ± 0.17 |
| 0.0394 | 920.9 ± 8.9 | 41.41 ± 1.06 | 2.22 ± 0.11 |
| 0.0794 | 967.8 ± 9.9 | 63.61 ± 1.44 | 1.52 ± 0.07 |
| 0.1594 | 813.9 ± 2.7 | 84.78 ± 2.82 | 0.96 ± 0.05 |
| 0.3114 | 920.6 ± 12.7 | 131.64 ± 0.76 | 0.70 ± 0.02 |
|
|
RbCl
|
||
| Ic (M) | kcat (s−1) | Km (μM) | kcat/Km(M−1 s−1 × 10−7) |
| 0.0154 | 839.9 ± 0.1 | 18.26 ± 0.75 | 4.60 ± 0.19 |
| 0.0254 | 774.6 ± 5.9 | 24.88 ± 1.59 | 3.12 ± 0.22 |
| 0.0394 | 762.1 ± 12.1 | 28.51 ± 0.43 | 2.63 ± 0.07 |
| 0.0794 | 821.8 ± 2.4 | 70.23 ± 1.97 | 1.17 ± 0.04 |
| 0.1594 | 922.8 ± 5.0 | 101.83 ± 7.65 | 0.91 ± 0.07 |
| 0.3114 | 874.0 ± 1. 8 | 129.05 ± 2.29 | 0.68 ± 0.01 |
|
|
CsCl
|
||
| Ic (M) | kcat (s−1) | Km (μM) | kcat/Km(M−1 s−1 × 10−7) |
| 0.0154 | 786.6 ± 0.1 | 19.03 ± 1.03 | 4.13 ± 0.22 |
| 0.0254 | 874.3 ± 6.8 | 29.61 ± 1.30 | 2.95 ± 0.10 |
| 0.0394 | 686.2 ± 4.7 | 33.00 ± 0.39 | 2.08 ± 0.04 |
| 0.0794 | 879.2 ± 14.0 | 90.72 ± 1.43 | 0.97 ± 0.03 |
| 0.1594 | 941.6 ± 35.4 | 168.94 ± 5.98 | 0.56 ± 0.01 |
| 0.3114 | 730.5 ± 8.9 | 187.23 ± 4.83 | 0.39 ± 0.01 |
|
|
KBr
|
||
| Ic (M) | kcat (s−1) | Km (μM) | kcat/Km(M−1 s−1 × 10−7) |
| 0.0154 | 861.5 ± 25.8 | 19.46 ± 0.34 | 4.43 ± 0.08 |
| 0.0254 | 897.6 ± 8.1 | 21.74 ± 0.15 | 4.13 ± 0.06 |
| 0.0394 | 889.4 ± 3.9 | 42.83 ± 0.70 | 2.08 ± 0.04 |
| 0.0794 | 898.6 ± 0.9 | 59.20 ± 0.67 | 1.52 ± 0.02 |
| 0.1594 | 996.9 ± 4.1 | 113.20 ± 1.80 | 0.88 ± 0.02 |
| 0.3114 | 882.3 ± 14.4 | 129.73 ± 1.75 | 0.68 ± 0.02 |
|
|
KI
|
||
| Ic (M) | kcat (s−1) | Km (μM) | kcat/Km(M−1 s−1 × 10−7) |
| 0.0154 | 710.9 ± 24.0 | 15.86 ± 0.75 | 4.48 ± 0.06 |
| 0.0254 | 748.6 ± 10. 5 | 25.79 ± 0.22 | 2.90 ± 0.02 |
| 0.0394 | 750.3 ± 4.9 | 34.80 ± 0.26 | 2.16 ± 0.02 |
| 0.0794 | 804.4 ± 4.7 | 64.44 ± 1.12 | 1.25 ± 0.03 |
| 0.1594 | 756.7 ± 0.7 | 88.72 ± 1.90 | 0.85 ± 0.02 |
| 0.3114 | 612.0 ± 7.8 | 120.32 ± 1.51 | 0.51 ± 0.01 |
|
|
CsI
|
||
| Ic (M) | kcat (s−1) | Km (μM) | kcat/Km(M−1 s−1 × 10−7) |
| 0.0154 | 587.3 ± 2.9 | 24.95 ± 0.51 | 2.35 ± 0.06 |
| 0.0254 | 639.9 ± 4.2 | 42.86 ± 1.23 | 1.49 ± 0.05 |
| 0.0394 | 651.4 ± 2.4 | 61.12 ± 1.92 | 1.07 ± 0.03 |
| 0.0794 | 630.4 ± 8.1 | 125.64 ± 0.48 | 0.50 ± 0.01 |
| 0.1594 | 446.9 ± 2.5 | 170.44 ± 9.67 | 0.26 ± 0.02 |
| 0.3114 | 274.4 ± 0.2 | 324.69 ± 2.41 | 0.08 ± 0.001 |
|
|
EtOH
|
||
| Ic (M) | kcat (s−1) | Km (μM) | kcat/Km(M−1 s−1 × 10−7) |
| 0.1 | 915.6 ± 2.1 | 18.32 ± 0.28 | 5.00 ± 0.07 |
| 0.2 | 733.5 ± 7.5 | 20.41 ± 0.04 | 3.60 ± 0.04 |
| 0.3 | 799.8 ± 4.6 | 24.74 ± 0.08 | 3.23 ± 0.03 |
| 0.4 | 718.8 ± 6.2 | 27.25 ± 0.07 | 2.64 ± 0.03 |
| 0.5 | 786.7 ± 0.1 | 28.93 ± 0.51 | 2.72 ± 0.05 |
| 0.6 | 781.4 ± 3.1 | 28.97 ± 0.11 | 2.70 ± 0.02 |
FIGURE 2.
Dependence of the bimolecular rate constant (kcat/Km) of AChE and AcSCh on the ionic strength square (I1/2). The data were fitted by the Brönsted-adapted Debye-Hückel equation (Eq. 3). The arrow indicates the excluded point of the fit in the solution of 0.3 M CsI, according to the discussion. Note that the error bars are within the size of the symbols.
Table 1 and Fig. 2 show that the kcat/Km depends not only on the ionic strength, as expected (5), but also on the ion type. To understand the influence of the individual properties of the ions on enzymatic efficiency we have analyzed the enzyme-substrate bimolecular rate constants by the Brönstedt-adapted Debye-Hückel equation (5,49,50). This equation describes the association kinetics of charged compounds (here, AChE and AcSCh) depending on the ionic strength 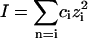 :
:
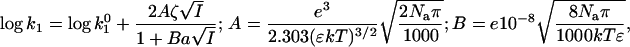 |
(3) |
where k1 is the bimolecular rate constant and 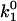 is k1 at I = 0, ζ = ZEZS, which are the net charge of the active site of the enzyme and the substrate (ZE = +1), I is the ionic strength, Na is the Avogadro number, e is the elementary charge, k is the Boltzmann constant, T is the temperature, ɛ is the dielectric constant of the medium, and a is the critical distance.
is k1 at I = 0, ζ = ZEZS, which are the net charge of the active site of the enzyme and the substrate (ZE = +1), I is the ionic strength, Na is the Avogadro number, e is the elementary charge, k is the Boltzmann constant, T is the temperature, ɛ is the dielectric constant of the medium, and a is the critical distance.
The data in Fig. 2 are within a very small experimental error range in agreement with Eq. 3, where the kcat/Km decreases with increasing ionic strength. The ion-type dependent kinetics found is not expected if one considers only the electrostatic aspect of the encounter process. Therefore, we conclude that the electrostatic steering is not the only important factor for the ES-encounter process, and that the particular properties of the ionic solutions influence the bimolecular rate constant, in addition to the increasing ionic strength.
The individual influence of the ions is described by the parameters a and ζ in Eq. 3. For this function the curvature corresponds to the parameters a, and the inclination corresponds to the parameter ζ. The critical distance obtained by Eq. 3 is defined as the distance at which enzyme and substrate encounter each other and the reaction takes place (Fig. 1). Diffusion-controlled reactions can be separated in two steps: the slow (diffusion) step and the fast (chemical transformation) step (51). Here, the critical distance is defined as the point, at which the fast step begins, i.e., at the distance of a few angstroms, where the encounter is as fast as the reaction itself. In summary, a great critical distance requires a facilitated encounter process. In contrast, a small critical distance suggests that short distances between the substrate and the active site are necessary to overcome the reaction barrier. In the resolved structure of the complex of TcAChE with the transition state analog TMTFA (1AMN (13)), the minimum distance between the charged group of the ligand (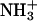 ), and the closest residue (W84) is ∼4 Å. Therefore, the minimum value for the critical distance is expected to be 4 Å and bigger values require an accelerated encounter.
), and the closest residue (W84) is ∼4 Å. Therefore, the minimum value for the critical distance is expected to be 4 Å and bigger values require an accelerated encounter.
It is also remarkable that the critical distances found are compatible with the length of the gorge (20 Å), indicating that the fast step begins when the substrate is very close to or in the gorge of the protein (Table 2). This result is also in agreement with the literature (12). It should be mentioned that close to the gorge there is the peripheral anionic site, which modulates the structure of the gorge and controls the catalytic activity (52).
TABLE 2.
Experimental parameter derived from the Brönsted-adapted Debye-Hückel model
| a (Å) | ζ | 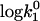 |
|
|---|---|---|---|
| LiCl | 13.38 ± 0.61 | 9.57 ± 0.56 | 8.47 ± 0.03 |
| NaCl | 7.66 ± 0.71 | 5.83 ± 0.34 | 8.25 ± 0.02 |
| KCl | 17.91 ± 2.08 | 13.67 ± 1.96 | 8.62 ± 0.08 |
| RbCl | 15.30 ± 1.13 | 12.02 ± 0.99 | 8.58 ± 0.04 |
| CsCl | 17.77 ± 1.06 | 17.49 ± 1.37 | 8.92 ± 0.08 |
| KBr | 22.98 ± 0.61 | 18.37 ± 0.57 | 8.79 ± 0.02 |
| KI | 17.07 ± 0.45 | 14.79 ± 0.45 | 8.72 ± 0.02 |
| CsI | 10.11 ± 0.97 | 11.43 ± 0.87 | 8.37 ± 0.06 |
| Na2HPO4* | 11.6 ± 2.9 | 8.5 ± 2.2 | 9.6 |
Data from Nolte et al. (5) at 25°C.
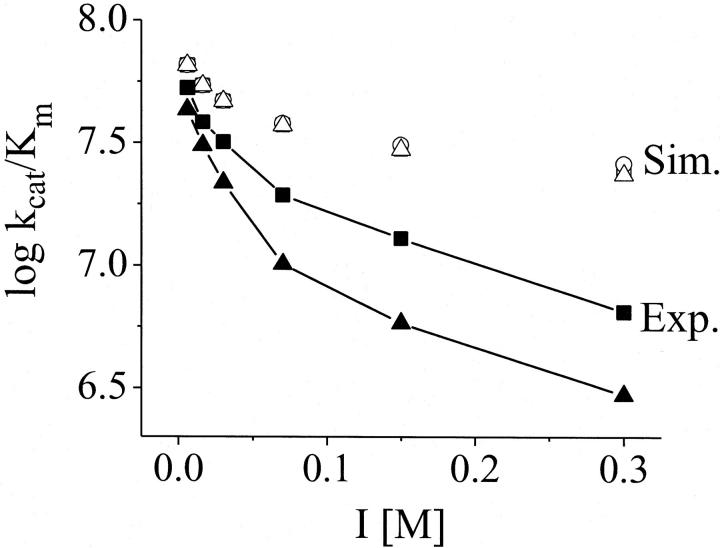
Ions are able to modify the dielectric constant (ɛ) and viscosity (η) of the aqueous medium, which are important parameters for the attraction between charged compounds (Eq. 3). Therefore, the effect of the ion-promoted variation of ɛ on the bimolecular rate constant (kcat/Km) was simulated using the Debye equations (Eq. 3) and it was found that the effect of the ions on these parameters is too small (one order of magnitude lower) to explain the difference between the curves shown in Fig. 2 (Fig. 3). In comparison with the experimental bimolecular rate constants the influence of the ions on the water viscosity is also negligible (Fig. 4, bottom). These small changes in ɛ and η are therefore not responsible for the ion-type dependence of the AChE kinetics.
FIGURE 3.
Simulation of the effect of the dielectric constant changes on the bimolecular constant k1. The simulations of k1 are shown in comparison to the experimental results for LiCl (▪) and CsCl (▴) from Fig. 2. The open squares, circles, and triangles are the simulated curves (Eq. 3) for LiCl solutions, pure water, and CsCl solutions, respectively. For the simulations, the experimental k1 value for I = 0 was used as an initial value (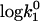 ). The parameters were chosen as a = 10, ζ = −3 and T = 278 K. The values of the dielectric constants for pure water and the ionic solutions at the specific ion concentrations were taken from literature (15,41).
). The parameters were chosen as a = 10, ζ = −3 and T = 278 K. The values of the dielectric constants for pure water and the ionic solutions at the specific ion concentrations were taken from literature (15,41).
FIGURE 4.
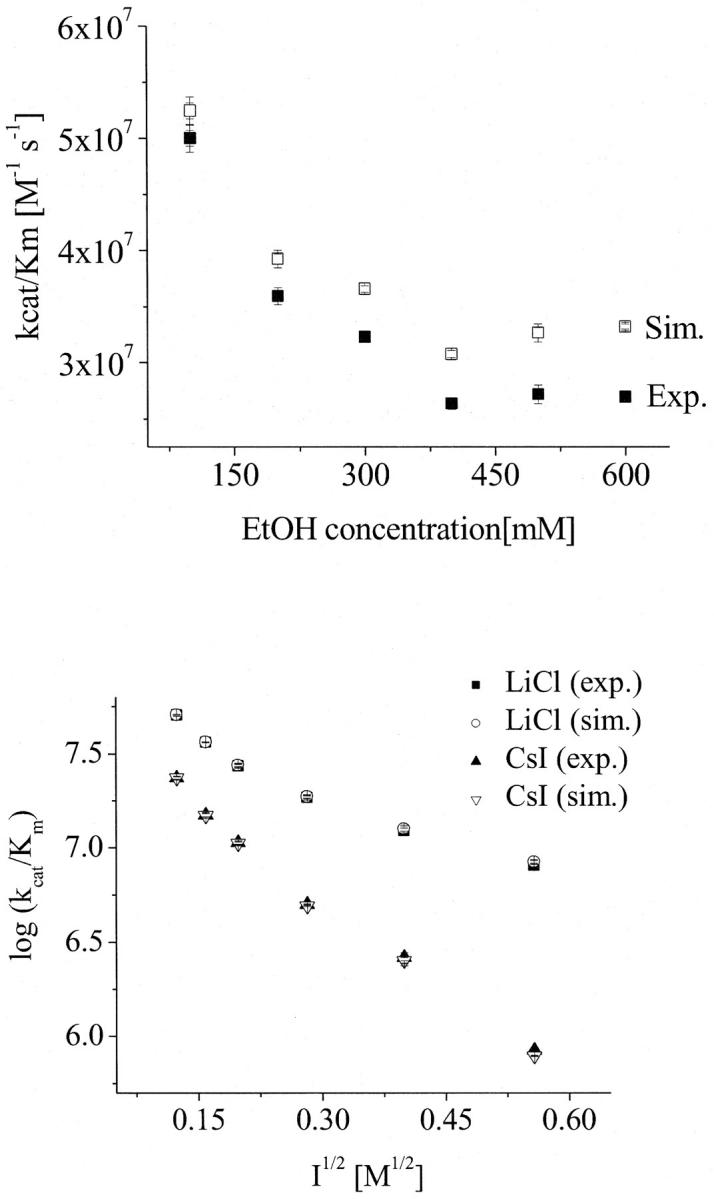
Influence of the viscosity changes on the bimolecular rate constant (kcat/Km) of AChE and AcSCh. (Top) Dependence of the bimolecular rate constant (kcat/Km) of AChE and AcSCh on the ethanol concentration. The solid squares represent the measured data and the open squares represent the simulated data according to Eq. 4 excluding the effect of viscosity changes. (Bottom) Dependence of the bimolecular rate constant (kcat/Km) of AChE and AcSCh on the ionic strength. The solid symbols represent the measured data (LiCl as squares and CsI as triangles) and the open symbols represent the simulated data according to Eq. 4 excluding the effect of viscosity changes (LiCl as circles and CsI as triangles). Note that the error bars are on the order of the size of the symbols.
The high values found for the parameter ζ in Table 2 lead to high charge values for the enzyme (ZE) in the various ionic solutions. A high value for ZE was also found in the experiments with Na2HPO4 reported in the literature (Table 2) (5), which emphasizes the limitation of the Debye equation for this system. It shows that the parameter ζ should not only be interpreted as the charge of the active site and the substrate (ZEZS), but as a more complex parameter (ζeff = α ζ), which includes the effect of the ionic strength (ζ = ZEZS) and the effect of the individual properties of the present ions on the kinetics (α).
Another important aspect is that the dielectric constant (ɛ) used for the fit (85.76) represents only the bulk and not the total dielectric constant. During the all-diffusion process, the substrate goes from the bulk solution through the solvation shell and the gorge to the active site. Each of these regions has a different value for ɛ. Because the ɛ of the gorge is much smaller than the bulk (3.72) (53) it is expected that the total ɛ is small compared to the bulk. In accordance with Eq. 3 it can lead to an overestimation of the value of the charges. However, even if the values found for ζ parameter were smaller, corresponding to the charges of the active site region, this parameter would include the individual properties of the ions, because different values for ζ were found.
In summary, the critical distance is related to the acceleration or facilitation of the ES-encounter at short distances. In the following analysis, the individual effect of the ion on the water structure will be considered for explaining the dependence of the kinetics on the ion type.
Effect of ethanol on AChE efficiency
Neumann and Nolte (54) have proposed that ions can decrease the Km by binding to the active site of the AChE. To investigate separately the effect of the water structure disturbance and the putative effect of cation binding, we have carried out systematic kinetic experiments with increasing concentrations of ethanol. Ethanol was chosen, because it does not present any charge, i.e., it does not bind at the anionic subsite, and because of its well-known effect on water structuring (55–57). The low concentrations of ethanol used were not deleterious for the protein structure as confirmed by investigations on the AChE conformation (see the next section). In Fig. 4, the dependence of kcat/Km on ethanol concentration is shown; the increasing ethanol concentrations up to a concentration of 400 mM decrease the kcat/Km. Considering that the dielectric constant decreases with increasing ethanol concentrations, a kcat/Km decay would not be expected for an electrostatic-dependent encounter process driven by Coulombic forces. This result shows that there must be a factor, possibly water structuring, which decreases the ES-encounter rates. Enhanced viscosity might be responsible for the decrease of the encounter rate, as expected for diffusion-dependent processes. Indeed, an increase in the ethanol concentration leads to an increase in the viscosity of the solutions (41), which results in a decrease of the diffusion coefficient of the substrate and of the enzyme, in accordance with the Stokes-Einstein diffusion equation (Eq. 5). Nevertheless, as shown in Fig. 4, this effect is too small to explain the decrease of kcat/Km. Fig. 4 also shows the normalized values of the bimolecular rate constant for the viscosity changes by applying the following equation:
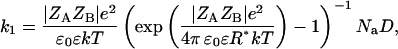 |
(4) |
with
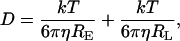 |
(5) |
where ɛ0 is the vacuum permittivity; D is the diffusion coefficient; RE is the enzyme radius; RL is the radius of the substrate (the ligand); η is the viscosity, and R* is the radius of the cross section of the collision between the enzyme and the ligand. Moreover, Fig. 4 emphasizes that the decay of the kcat/Km is similar.
Finally, we can conclude that parameters other than viscosity, dielectric constant, ionic strength, or binding of cations on the active site decrease the ES-encounter process. We propose that this effect is due to the structuring of water.
AChE structure maintenance
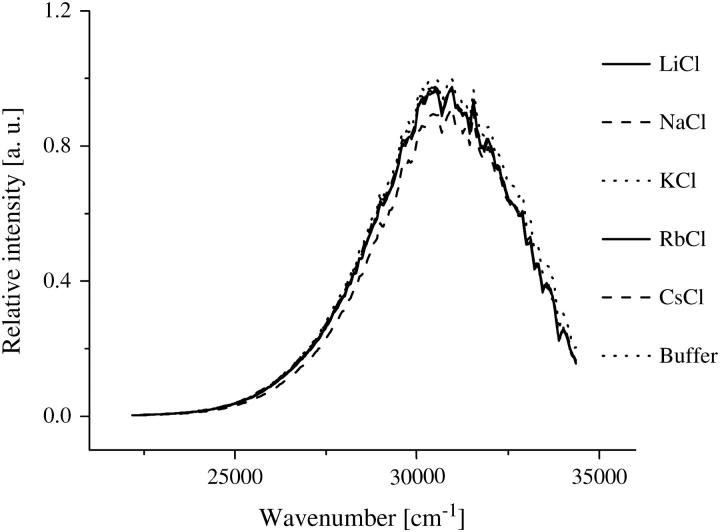
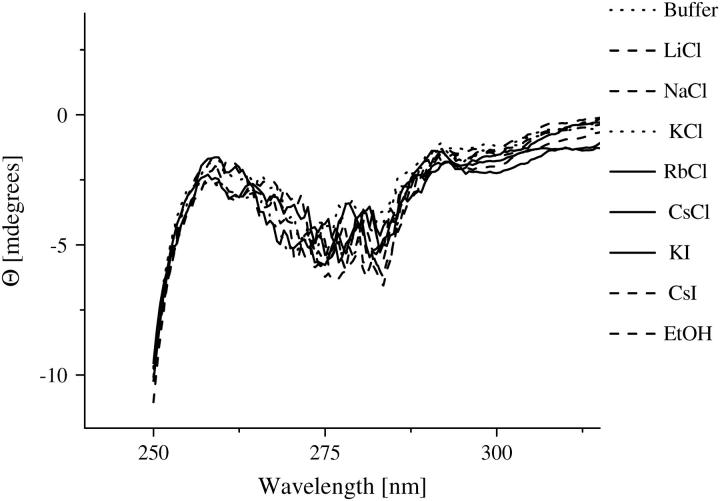
Investigations on the AChE structure by means of fluorescence spectroscopy and near- UV circular dichroism measurements indicate that the enzyme does not show any conformational changes in the presence of ethanol and the different ionic solutions. Due to its sensitivity to small perturbations of the environment of the aromatic side chains, near-UV circular dichroism and fluorescence are methods often applied to probe alterations in the tertiary structure of the proteins (58–60). Fig. 5 shows the fluorescence spectra of AChE in the various ionic solutions. The spectra remain essentially unchanged, with the exception of a small quenching found for the CsCl solution. However, this quenching was expected (61,62) and has also been confirmed by fluorescence lifetime measurements of tryptophan (data not shown). It is not attributed to an alteration of the AChE structure. The near-UV CD measurements are summarized in Fig. 6. The spectra are nearly constant within the sensitivity of the apparatus. The measurements strongly suggest that the AChE conformation is maintained in the ionic solutions studied. Consequently, the ions do not cause any direct conformational changes in AChE with the concentrations studied and the ion-disturbed water structure does not modify the AChE conformation.
FIGURE 5.
Fluorescence spectra of AChE (1 μM) in the indicated ionic solutions (300 mM) with potassium phosphate buffer 2 mM, pH 8.0. The spectra show no difference for the different ionic solution. The CsCl presents an exception due to expected quenching.
FIGURE 6.
Near-UV CD spectra of AChE (4 μM) in the ethanol (600 mM) and ionic solutions (300 mM) with potassium phosphate buffer 2 mM, pH 8.0.
Water structure
To find whether the structure of the liquid water in the solutions used is related to the individual influence of the ions on AChE kinetics, the degree of structuring of water was estimated and compared to the critical distances. The term “water structure” has to be used conscientiously, because the liquid water does not show a long-range order as it is known for solids (63). Contrary to the hexagonal structure of ice (Ih), the water molecules are not fully organized in a hexagonal structure with H-bondings in tetrahedral coordination in the liquid phase, but only part of the structure remains with distorted H-bondings, which are arranged irregularly. Consequently, some H-bondings are still tight, with favorable angle and distances and because of this they are called “ice-like” H-bondings; others are highly distorted, the so-called “weak” H-bondings; some water molecules even have OH-groups free of H-bonding. According to the “mixture model” for water, different water species involved in different numbers of H-bondings with different bond strengths coexist in liquid water (39). Therefore, the water structure can be represented by the strength of the H-bonding network of the aqueous solutions. Solutions presenting more and/or tighter H-bondings are considered to be more ordered or structured compared to solutions with less and/or weaker H-bondings.
Infrared spectroscopy has been widely used to study the structure of liquid water. The water molecule has three vibrational modes: the symmetric stretching (ν1), the bending (ν2), and the asymmetric stretching (ν3) mode. For isolated water molecules (monomer), the vibrational modes are excited at the frequencies: 3651.7 cm−1 (ν1), 1595.0 cm−1 (ν2), 3755.8 cm−1 (ν3) (64). On one hand, the bending mode (ν2) is known to be almost insensitive to H-bondings and therefore to undergo only minor changes from the vapor (1595 cm−1) to the liquid phase (1637.5 cm−1) (from 4 to 300°C (65)). On the other hand, the stretching vibrations (ν1 and ν3) are very sensitive to the surrounding strength of the H-bonding network (66) and can be used to probe the water structure. By the formation of an H-bonding network the force constant of the O-H bond decreases, which causes a shift of the frequency of the stretching modes (64,67):
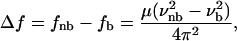 |
(6) |
where f is the force constant, μ = m1 m2/(m1 + m2) is the reduced mass of the oscillator (OH-group), and ν is the oscillating frequency. The subscripts b and nb stand for bonded and nonbonded, respectively. Because the effect of H-bonding on the force constant of the O-H bond is not yet quantifiable, this equation can be used to understand the wavenumber shift, but not to predict it (66).
Considering that the absorption bands of the water in liquid phase are broad, the vibrational frequencies of the symmetric and asymmetric stretching modes are indistinguishable and the assignment is done for both stretching modes, ν1 and ν3. Three principal bands are recognized in liquid water: ∼3220 cm−1; ∼3400 cm−1, and ∼3600 cm−1.
In literature, these bands are assigned to the different species of water, according to the theory used. Graener and Laubereau (68) attribute the bands to “ice-like”, “moderately strongly” H-bonded and “free” or “weakly bonded” OH-groups. Musto and collaborators (69) assign the bands to the number of hydrogen atoms (0, 1, or 2) of the water molecule involved in H-bonding. Franks (39) and Max and Chapados (67) attribute five bands to the number of H-bondings interacting with the molecule (from 0 to 4). Some other authors relate the different spectral position to different hydrogen bonding lengths OH…O or the enthalpy of H-bonding (70,71).
We have chosen the more general classification of the water species: free, strongly bonded, and weakly bonded OH-groups (72) because of the broadness of the absorption bands, which prevents a very accurate resolution of the peaks, and by the lack of theoretical values for the vibrational frequencies of each water species.
Combinational bands of the bending and stretching modes and overtones are excited at higher frequencies and can be measured in the near-infrared region. NIR spectroscopy technique offers advantages for the quantitative analysis of the water absorption. Because the pathlength and the penetration depth are well defined, the optical density is proportional to the concentration of the water species in accordance with the Lambert-Beer law (73).
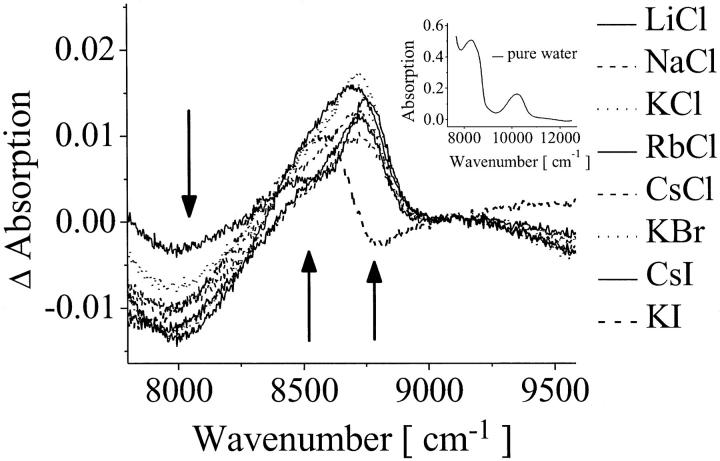
To investigate the disturbance of the water structure by the ions, we have quantified the water species by recording the difference spectra of the salt solutions obtained by subtracting the pure water spectrum (Fig. 7) at the NIR region of 8000–9000 cm−1 (combinational band ν1 + ν2 + ν3). The minimum of the difference absorption bands at 8000 cm−1 and the maxima at 8500 and 8750 cm−1 correspond to the water species: weakly bonded, strongly bonded, and free OH-group, respectively. Fig. 7 shows that the population of ice-like water molecules decreases (8000 cm−1), whereas the concentrations of weakly bonded populations (8500 cm−1) and of H-bonding free populations (8750 cm−1) increase. For all of the ions added an increase of the disorder of the H-bond network was found in comparison to pure water, converting tightly H-bonded water into weakly or non-H-bond water. It is important to remark that this investigation is not in contradiction to the classification of ions as so-called structure makers and structure breakers, because if an ion organizes the water molecules around itself, it creates a new structure in its local environment and existing H-bonding networks are broken during this process (74).
FIGURE 7.
Absorption difference spectra for the ionic solutions (300 mM) obtained by subtracting the pure water spectrum (inset) in the NIR region at 5°C. The arrows indicate the direction of change of the absorption in the presence of the ions.
The ion-disturbed water spectra were quantitatively analyzed by means of the Lambert-Beer law, where the difference of absorption (ΔAbs) is proportional to the difference of the concentration of each water species:
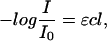 |
(7) |
where 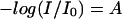 is the light absorption, ɛ is the extinction coefficient (M−1 cm−1), c is the chromophore concentration (M), and l is the pathlength (cm).
is the light absorption, ɛ is the extinction coefficient (M−1 cm−1), c is the chromophore concentration (M), and l is the pathlength (cm).
According to Eq. 7, ΔAbs = ɛΔc. The extinction coefficients of the water species could not be determined. Consequently, Δc cannot be calculated as an absolute value. Hence, the product ɛΔc was used for further analysis as it is directly proportional to the changes in the concentration of the water species.
For estimating the increase of weakly H-bonded OH-groups, the difference of absorption at 8500 cm−1 was used and for estimating the increase of broken H-bonding (free OH-groups) the difference of absorption at 8750 cm−1 was observed.
The Luck method was also employed. This method is based on the Lambert-Beer law and correlates the measured absorption at 1143 nm (8749 cm−1) with the absorption of the water at the critical point (without H-bonding) and in the solid phase (with 100% of tetrahedral coordination H-bonding) (37–39), so that the fraction of free OH-groups (broken H-bondings) can be determined.
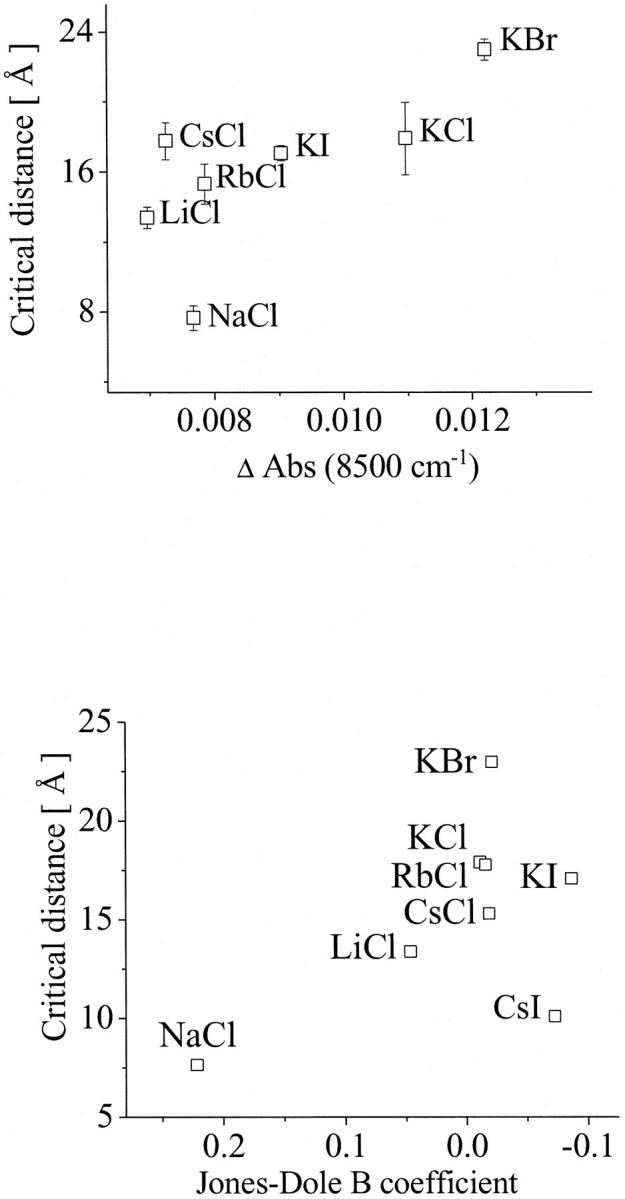
The quantitative results of our investigations have been compared with the critical distance and are summarized in Fig. 8. Fig. 8 (top) shows the dependence of the critical distances on the population of weakly H-bonded OH-groups represented by the difference of the absorption intensity at 8500 cm−1. The product-moment correlation coefficient for this relation was found to be r = 0.844, which is greater than the critical value of 0.669. Consequently, the empirical correlation can be considered to be significant. The t-test confirms this result. The t-value was 3.517, i.e., greater than the critical value of 2.015. The probability of obtaining such value of t by random sampling is P < 0.010.
FIGURE 8.
Dependence of the critical distances on the population of weakly H-bonded OH-groups represented by the difference of the absorption intensity at 8500 cm−1 (top) and on the water structure represented by the Jones-Dole B coefficient (bottom). For statistical analysis, see Discussion.
Because the relation between the Jones-Dole B coefficient and the water structure is well known (27), this parameter has also been compared to the kinetic data. The empirical correlation found is also significant. Here, the product-moment correlation coefficient was determined to r = 0.773, which is greater than the critical value of 0.621. The t-value was 3.223, i.e., greater than the critical value of 1.943. The probability of obtaining such value of t by random sampling is P < 0.010.
Fig. 8 shows that bigger critical distances for the ES-encounter in solutions are related to higher concentration of weakly H-bonded water molecules. The comparison with the Jones-Dole B coefficient shows the same tendency; at smaller B coefficient (more disordered water) bigger critical distances were found.
According to the analysis of the kinetic data, and from the dependences found, it is evident, that the perturbation of the water structure facilitates the ES-encounter and that the highly ordered water can hinder the encounter at short distances. In the investigated series, two extremes were found: NaCl, solutions of which present a more ordered water structure, is related to a small critical distance (7.7 Å); i.e., before ∼7.7 Å the substrate diffusion is not facilitated. On the other side, KBr heavily disturbs the water structure and this is related to a critical distance of 22.9 Å, meaning that, at greater distances, the diffusion of the substrate to the active site is strongly facilitated. We can, therefore, conclude that the less water is ordered, the more it is capable of providing an environment that facilitates the encounter between the substrate and the active site of AChE.
AChE solvation (SAXS measurements)
To get a more detailed understanding of the influence of the water structure on the ES-encounter, we have performed small-angle x-ray scattering experiments. SAXS is a well-established technique to study the solvation of proteins (43,75,76). SAXS measurements can, therefore, give information whether the ion-promoted disturbance of the bulk water structure can influence the solvation of the AChE or not.
The x-ray scattering of AChE was observed in the different ionic solutions. The AChE activity remains the same after the SAXS experiments, indicating that the enzyme was not damaged by the x-rays. The radii of gyration (Rg) obtained are related to the radii of the protein + hydration shell. The theoretical value for Rg of the AChE crystal structure could be estimated by analyzing the three-dimensional eelAChE crystallographic data (1C2O (23)) with the CRYSOL program (75), which lead to a radius of gyration of Rg = 45.78 Å for the dry AChE and to Rg = 48.88 Å for the protein plus 3-Å-wide hydration shell. The Rg of AChE for the different ionic solutions was found to range between Rg = 43.7 Å (±1.2 Å (SE value); ±2.2 Å (SD value)) in KI solutions and Rg = 63.2 Å (±1.1 Å (SE value); ±4.0 Å (SD value)) in CsCl solutions. The excess of the radius of gyration, as it has been obtained by the experiments, can therefore be related to the AChE hydration, which is attributed to the solvation, assuming a nonchanging overall structure of AChE as it was shown by the CD and fluorescence measurements. Association between the AChE tetramers is not expected at the low working concentrations of enzyme and the salts used.
A comparison between the water structure in the different ionic solutions from NIR measurements with the observed radii of gyration shows an evident relation between the radius of gyration and the fraction of free OH-group (Fig. 9). The absolute value of the product-moment correlation coefficient for this relation is |r| = 0.956, which is greater than the critical value of 0.669. Consequently, the correlation is considered to be significant. The t-test confirms this result, too. The absolute t-value is 7.295, i.e., greater than the critical value of 2.015. The probability of obtaining such t-value by random sampling is P < 0.0005. In KI solution the concentration of free OH-groups remains unchanged and is, therefore, not shown in Fig. 9.
FIGURE 9.
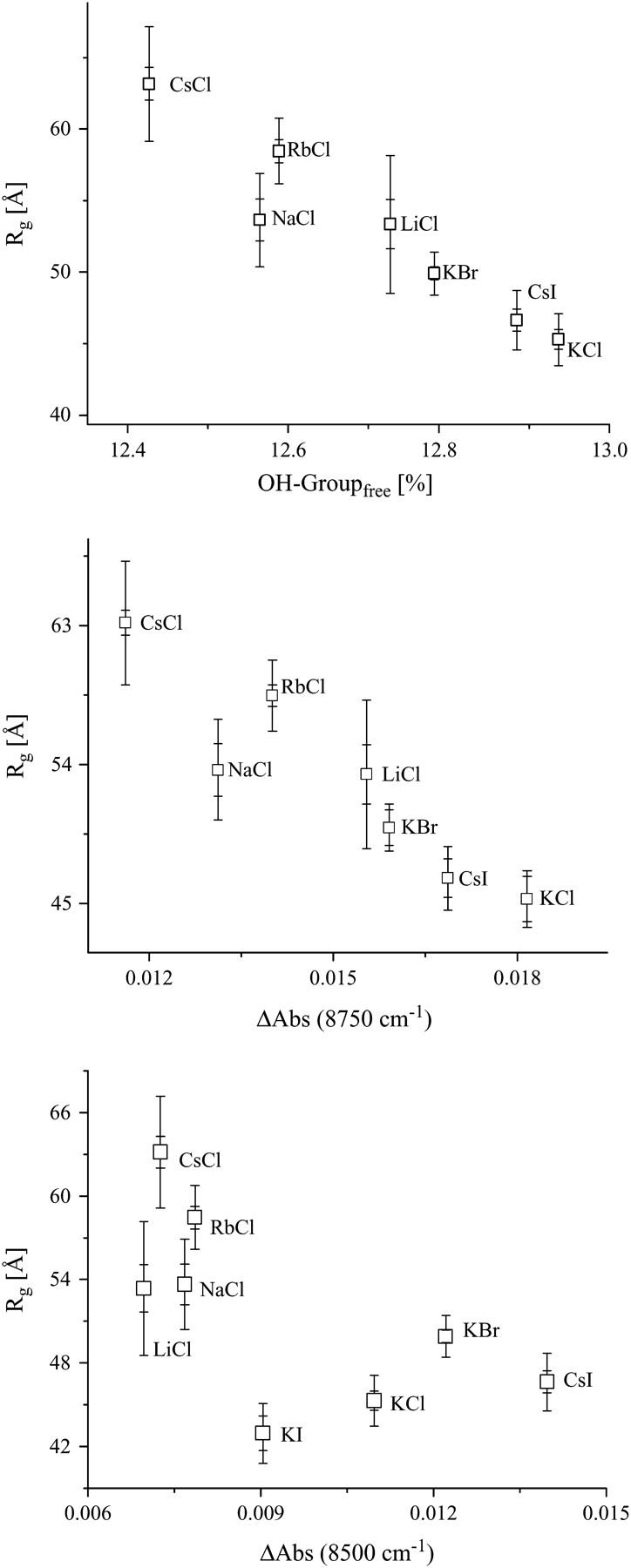
The correlation of the radius of gyration of AChE with the water structure, represented by the fraction of free OH-group (top), ΔAbs at 8750 cm−1 (middle), and ΔAbs at 8500 cm−1 (bottom; from Fig. 7). For statistical analysis, see Discussion.
Also the population of weakly H-bonded water shows a correlation to the radii of gyration (Fig. 9). For the absorption population at 8500 cm−1 the product moment correlation of r = 0.726 and a t-test value of t = 2.585 were found, which are greater than the critical values of 0.669 and 2.015, respectively. The probability of obtaining such values of t by random sampling is P < 0.025. The dependences found demonstrate that the ions not only modify the structure of the bulk water, but also the solvation of AChE. The solvation takes place in such a manner that less structured water leads to less hydrated AChE. In the case of less solvated AChE one can expect that the substrate can more easily reach the gorge.
Intramolecular mobility of AChE
To gain a more detailed understanding of the system we have additionally investigated the internal dynamics of AChE for the different solutions by applying the fluorescence depolarization technique. The measurements indicate that the intramolecular mobility of the enzyme is also affected by the structure of water. Because the fluorescence depolarization measurements monitor the rotational motions of the fluorophores, this technique has been widely used to investigate the flexibility and intramolecular mobility of protein segments by observing the tryptophan residue(s). For relatively small proteins, the rotational correlation time (τR) of tryptophan fluorescence is related to the segmental and whole protein. To resolve the two correlation times, time-resolved fluorescence depolarization experiments are required (77,78). In the case of AChE, because of the size (320 kDa) and its oblate form (23) the rotational correlation time of the whole protein is too large (322 ns (79)) to influence the anisotropy of the tryptophan fluorescence. According to Eq. 2, the τR corresponds to ∼200 ns for R ≈ R0, a value smaller than for the AChE rotation. Hence, the protein seems to be static in comparison with the fluorescence lifetime τF of Trp, and the measured anisotropy could be related only to segmental motions. AChE contains 14 Trp residues in each monomer, which are nearly homogenously distributed inside the whole protein. Although multitryptophan proteins can present a complex fluorescence behavior, the distribution of the Trp residues inside the AChE has two advantages: firstly, fluorescence depolarization probes the segmental motions of the whole protein and not only of one local segment. Secondly, because the fluorophores are inside the protein, their motions are coupled to the segment of the enzyme where they are inserted. A disadvantage of multitryptophan proteins for intramolecular mobility investigations could be the occurrence of energy transfer between the tryptophans; in this case, the anisotropy would no longer depend on the rotational motion of the fluorophore (45). Fortunately that is not the case for AChE because the measured anisotropy limit was found to be nearly 0.4 (0.386 ± 0.007) (45). Therefore, the measured anisotropy could exclusively be attributed to the rotational diffusion of the tryptophans.
The fluorescence polarization and the fluorescence lifetime of the tryptophans in AChE were measured under the same experimental conditions. The measured rotational correlation times were found to range between 1.5 and 2.5 ns.
The determined rotational correlation times and the rotational diffusion of the Trp residues in AChE were compared with the Jones-Dole B coefficients for the different ionic solutions and for the ethanol solution. Fig. 10 shows an increase in rotation correlation time and a decrease in rotational diffusion with increasing water structuring. Therefore, the AChE intramolecular mobility increases with increasing water disordering.
FIGURE 10.
Correlation of the rotational correlation time τr (top) and the rotational diffusion Dr (bottom) of tryptophan residues of the AChE with the water structure, represented by the Jones-Dole B coefficient for the various solutions. For statistical analysis, see Discussion.
The empirical correlations found for the rotational correlation time and the rotational diffusion were analyzed statistically. The values for the product moment correlation coefficient were found to be r = 0.749 and r = 0.754, respectively. Both values are above the critical value of 0.582 and therefore the correlation found is significant. The values of t = 2.995 and t = 3.0335 for the t-test also confirms this result, because both are above the critical value of 1.895. The probabilities of obtaining such t-values by random sampling are P ∼ 0.010 and P < 0.010, respectively.
The value found for ethanol in the plot supports the idea that the measured effect of the ion type on the kinetics is due to the water structure disturbance and not due to direct association (the ethanol binding to the active site of AChE is very unlikely). Furthermore, if one considers the charge density of the protein in comparison to the charge density of Cl− and I−, it is reasonable that the cations would preferentially bind to the anions rather than to the active site. Likewise, the anions would preferentially bind to the cations rather than to the substrate. It is known that the association rate of strong salts are very low in water solutions (26). According to this consideration, the association rate of the cations to AChE would be even lower compared to the association rates of halide anions.
In summary, we conclude that the protein has a faster intramolecular mobility in less structured water. It reveals that ion-promoted disturbance of the H-bonding network structure of the water affect the AChE intramolecular mobility.
It is interesting to remark that the mobility of the gorge has been proposed in computational simulation works to be important for the diffusion of substrate and inhibitors into the active site. Xu and collaborators (80) have shown in 5-ns molecular dynamics (MD) simulation that during 3 ns the gorge presents an “open” conformation with a minimum diameter of ∼6 Å, as opposed to 2 Å in the “close state”. Tai and collaborators (81) have also shown by 10-ns MD simulation that for ∼2.5 ns the gorge presents an open state (with larger radius). The order of magnitude of the measured rotational correlation times for the segmental motions (τR) is in reasonable agreement with the MD simulation time. Because the turnover number (kcat) for AChE is ∼800 s−1, one could conclude that the docking and release of the substrate is in the range of milliseconds and that because of this the nanosecond range would be negligible. Nevertheless, if one considers that the diffusion coefficient of the substrate in water is 4.5 × 10−6 cm2 s−1 (according to the Stokes-Einstein equation for diffusion), on a molecular scale it corresponds to 10 Å2 ns−1. Therefore, the distance of the gorge (20 Å) would be covered in the range of nanoseconds, if the viscosity of the gorge and the viscosity of the water have the similar order of magnitude. Hence, higher intramolecular mobility of AChE may facilitate the opening events of the gorge, allowing an easier passage of the substrate. Moreover, one can expect that during the opening of the gorge, an inward flux of water molecules is created, so that the substrate molecules at the vicinity could be sucked into the gorge.
A back door for the escape of the products has been proposed to contribute to the high efficiency by allowing a rapid flux of substrate (81,82). According to this hypothesis one should expect that higher mobility of AChE can contribute to opening the back door, allowing an easier release of the products and faster kinetics of AChE.
Another important aspect has been discussed by Xu and collaborators (80). In the 5-ns MD simulation they have examined the huperzine binding to AChE with and without water molecules and discussed the importance of the formation and breaking of the H-bonding of the buried water molecules in the gorge. Koellner et al. (83) compare the contribution of the H-bonding dynamics of the water to a lubricant for the substrate squeezing through the gorge. In the context of this work, one can imagine that less structured water around the protein allows a higher mobility of AChE, which can influence the water molecules buried in the gorge, where higher forming/breaking H-bonding rates facilitate the passage of the substrate through the gorge.
Two hypotheses for the influence on the ES-encounter can be proposed. Firstly, weaker H-bonding networks in the bulk water decrease the AChE solvation, which can be easily removed and reorganized (desolvation) during the substrate entrance. Secondly, weaker H-bonding networks of the water allow a higher intramolecular mobility, which facilitates the passage of the substrate through the gorge to the active site.
Moreover, the dependence of the intramolecular mobility on the water ordering can explain the reason of the ion type-dependent AChE kinetic and also the ion concentration (apparently ionic strength) dependence of the kinetics of neutralized AChE.
The results found reveal that not only the net charge and the structure of an enzyme are important for its function, but the solvation, the water structure by itself, and its influence on the dynamics also for the biological function of AChE.
CONCLUSION
In this work, we have investigated the influence of the H-bonding network structure of aqueous solutions on the AChE-substrate encounter process. The AChE kinetics in different ionic solutions was analyzed by the Brönstedt-adapted Debye-Hückel theory, which describes the bimolecular rate constant between charged compounds in dependence on the ionic strength of the medium. As the result of this analysis the critical distances of the reaction were determined for the different ionic solutions. The degree of water structure disturbance was investigated by near-infrared spectroscopy. The effect of the water disordering on the AChE solvation was observed by small-angle x-ray scattering. The intramolecular mobility of AChE was studied in solutions with different ion-disturbed water structure by fluorescence depolarization. We found that in solutions with less structured water (more content of broken and weak H-bonding), the ES-encounter process is facilitated (bigger critical distances), the solvation shell is thinner (smaller gyration radius), and the AChE presents faster intramolecular motions (shorter segmental rotational correlation time). The reorganization of the solvent during and after the entrance of the substrate into the gorge may be facilitated in an environment with less structured water. This process, in addition to the increase of the intramolecular mobility, may help the substrate to diffuse through the gorge of the enzyme.
Acknowledgments
We thank I. Dreger for technical assistance and J. Troe for permanent support of this work.
A.R. thanks the Deutsche Akademische Austauschdienst (PKZ, A/01/16759) and S.T. is grateful to Deutsche Forschungsgemeinschaft support (TE 347/1-2).
References
- 1.Elcock, A. H., R. R. Gabdoulline, R. C. Wade, and J. A. McCammon. 1999. Computer simulation of protein-protein association kinetics: acetylcholinesterase-fasciculin. J. Mol. Biol. 291:149–162. [DOI] [PubMed] [Google Scholar]
- 2.Sussman, J. L., M. Harel, F. Frolow, C. Oefner, A. Goldman, L. Toker, and I. Silman. 1991. Atomic structure of acetylcholinesterase from Torpedo californica: a prototypic acetylcholine-binding protein. Science. 253:872–879. [DOI] [PubMed] [Google Scholar]
- 3.Malany, S., M. Sawai, R. S. Sikorski, J. Seravalli, D. M. Quinn, Z. Radić, P. Taylor, C. Kronman, B. Velan, and A. Shafferman. 2000. Transition state structure and rate determination for the acylation stage of acetylcholinesterase catalyzed hydrolysis of (acetylthio)choline. J. Am. Chem. Soc. 122:2981–2987. [Google Scholar]
- 4.Quinn, D. M., A. N. Pryor, T. Selwood, B. H. Lee, S. A. Acheson, and P. N. Barlow. 1991. The chemical mechanism in acetylcholinesterase reactions. Biological catalysis at the speed limit. In Cholinesterases: Structure, Function, Mechanism, Genetics, and Cell Biology. J. Massoulié, F. Bacou, E. Barnard, A. Chatonet, B. P. Doctor, and D. M. Quinn, editors. American Chemical Society, Washington DC. 252–257.
- 5.Nolte, H. J., T. L. Rosenberry, and E. Neumann. 1980. Effective charge on acetylcholinesterase active sites determined from the ionic strength dependence of association rate constants with cationic ligands. Biochemistry. 19:3705–3711. [DOI] [PubMed] [Google Scholar]
- 6.Quinn, D. M. 1987. Acetylcholinesterase: enzyme structure, reaction dynamics, and virtual transition states. Chem. Rev. 87:55–105. [Google Scholar]
- 7.Harel, M., I. Schalk, L. Ehret-Sabatier, F. Bouet, M. Goeldner, C. Hirth, P. H. Axelsen, I. Silman, and J. L. Sussman. 1993. Quaternary ligand binding to aromatic residues in the active-site gorge of acetylcholinesterase. Proc. Natl. Acad. Sci. USA. 90:9031–9035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Taylor, P., and Z. Radić. 1994. The cholinesterases: from genes to proteins. Annu. Rev. Pharmacol. Toxicol. 34:281–320. [DOI] [PubMed] [Google Scholar]
- 9.Gibney, G., S. Camp, M. Dionne, K. MacPhee-Quigley, and P. Taylor. 1990. Mutagenesis of essential functional residues in acetylcholinesterase. Proc. Natl. Acad. Sci. USA. 87:7546–7550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Radić, Z., G. Gibney, S. Kawamoto, K. MacPhee-Quigley, C. Bongiorno, and P. Taylor. 1992. Expression of recombinant acetylcholinesterase in a baculovirus system: kinetic properties of glutamate 199 mutants. Biochemistry. 31:9760–9767. [DOI] [PubMed] [Google Scholar]
- 11.Shafferman, A., B. Velan, A. Ordentlich, C. Kronman, H. Grosfeld, M. Leitner, Y. Flashner, S. Cohen, D. Barak, and N. Ariel. 1992. Substrate inhibition of acetylcholinesterase: residues affecting signal transduction from surface to the catalytic center. EMBO J. 11:3561–3568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Radić, Z., P. Kirchoff, D. M. Quinn, J. A. McCammon, and P. Taylor. 1997. Electrostatic influence on the kinetics of ligand binding to acetylcholinesterase. Distinctions between active center ligands and fasciculin. J. Biol. Chem. 272:23265–23277. [DOI] [PubMed] [Google Scholar]
- 13.Harel, M., D. M. Quinn, H. K. Nair, I. Silman, and J. L. Sussman. 1996. The x-ray structure of a transition state analog complex reveals the molecular origins of the catalytic power and substrate specificity of acetylcholinesterase. J. Am. Chem. Soc. 118:2340–2346. [Google Scholar]
- 14.Kua, J., Y. Zhang, A. C. Eslami, J. R. Butler, and J. A. McCammon. 2003. Studying the roles of W86, E202, and Y337 in binding of acetylcholine to acetylcholinesterase using a combined molecular dynamics and multiple docking approach. Protein Sci. 12:2675–2684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ordentlich, A., D. Barak, C. Kronman, Y. Flashner, M. Leitner, Y. Segall, N. Ariel, S. Cohen, B. Velan, and A. Shafferman. 1993. Dissection of the human acetylcholinesterase active center determinants of substrate specificity. Identification of residues constituting the anionic site, the hydrophobic site, and the acyl pocket. J. Biol. Chem. 268:17083–17095. [PubMed] [Google Scholar]
- 16.Shafferman, A., A. Ordentlich, D. Barak, C. Kronman, R. Ber, T. Bino, N. Ariel, R. Osman, and B. Velan. 1994. Electrostatic attraction by surface charge does not contribute to the catalytic efficiency of acetylcholinesterase. EMBO J. 13:3448–3455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tara, S., A. H. Elcock, P. D. Kirchhoff, J. M. Briggs, Z. Radić, P. Taylor, and J. A. McCammon. 1998. Rapid binding of a cationic active site inhibitor to wild type and mutant mouse acetylcholinesterase: Brownian dynamics simulation including diffusion in the active site gorge. Biopolymers. 46:465–474. [DOI] [PubMed] [Google Scholar]
- 18.Wlodek, S. T., T. Shen, and J. A. McCammon. 2000. Electrostatic steering of substrate to acetylcholinesterase: analysis of field fluctuations. Biopolymers. 53:265–271. [DOI] [PubMed] [Google Scholar]
- 19.Saxena, A., J. M. Fedorko, C. R. Vinayaka, R. Medhekar, Z. Radić, P. Taylor, O. Lockridge, and B. P. Doctor. 2003. Aromatic amino-acid residues at the active and peripheral anionic sites control the binding of E2020 (Aricept) to cholinesterases. Eur. J. Biochem. 270:4447–4458. [DOI] [PubMed] [Google Scholar]
- 20.Antosiewicz, J., J. A. McCammon, S. T. Wlodek, and M. K. Gilson. 1995. Simulation of charge-mutant acetylcholinesterases. Biochemistry. 34:4211–4219. [DOI] [PubMed] [Google Scholar]
- 21.Ripoll, D. R., C. H. Faerman, P. H. Axelsen, I. Silman, and J. L. Sussman. 1993. An electrostatic mechanism for substrate guidance down the aromatic gorge of acetylcholinesterase. Proc. Natl. Acad. Sci. USA. 90:5128–5132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Massoulié, J., A. Anselmet, S. Bon, E. Krejci, C. Legay, N. Morel, and S. Simon. 1999. The polymorphism of acetylcholinesterase: port-translational processing quaternary associations and localization. Chem. Biol. Int. 119–120:29–42. [DOI] [PubMed] [Google Scholar]
- 23.Bourne, Y., J. Grassi, P. E. Bougis, and P. Marchot. 1999. Conformational flexibility of the acetylcholinesterase tetramer suggested by x-ray crystallography. J. Biol. Chem. 274:30370–30376. [DOI] [PubMed] [Google Scholar]
- 24.Bourne, Y., P. Taylor, P. E. Bougis, and P. Marchot. 1999. Crystal structure of mouse acetylcholinesterase. A peripheral site-occluding loop in a tetrameric assembly. J. Biol. Chem. 274:2963–2970. [DOI] [PubMed] [Google Scholar]
- 25.Jones, G., and M. Dole. 1929. The viscosity of aqueous solutions of strong electrolytes with special reference to barium chloride. J. Am. Chem. Soc. 51:2950–2964. [Google Scholar]
- 26.Robinson, R. A., and R. H. Stokes. 1958. Electrolyte Solution. 2. Revised Edition, Dover Publications Book News, Portland, OR.
- 27.Hribar, B., N. T. Southall, V. Vlachy, and K. A. Dill. 2002. How ions affect the structure of water. J. Am. Chem. Soc. 124:12302–12311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Colombo, M. F., D. C. Rau, and V. A. Parsegian. 1992. Protein solvation in allosteric regulation: a water effect on hemoglobin. Science. 256:655–659. [DOI] [PubMed] [Google Scholar]
- 29.Goldbeck, R. A., S. J. Paquette, and D. S. Kliger. 2001. The effect of water on the rate of conformational change in protein allostery. Biophys. J. 81:2919–2934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Friedman, R., E. Nachliel, and M. Gutman. 2003. The role of small intraprotein cavities in the catalytic cycle of bacteriorhodopsin. Biophys. J. 85:886–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Noinville, S., M. Revault, H. Quiquampoix, and M. H. Baron. 2004. Structural effects of drying and rehydration for enzymes in soils: a kinetics-FTIR analysis of alpha-chymotrypsin adsorbed on montmorillonite. J. Colloid Interface Sci. 273:414–425. [DOI] [PubMed] [Google Scholar]
- 32.Cordone, L., M. Ferrand, E. Vitrano, and G. Zaccai. 1999. Harmonic behavior of trehalose-coated carbon-monoxy-myoglobin at high temperature. Biophys. J. 76:1043–1047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gabel, F., M. Weik, B. P. Doctor, A. Saxena, D. Fournier, L. Brochier, F. Renault, P. Masson, I. Silman, and G. Zaccai. 2004. The influence of solvent composition on global dynamics of human butyrylcholinesterase powders: a neutron-scattering study. Biophys. J. 86:3152–3165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Li, F., and Z. Han. 2002. Purification and characterization of acetylcholinesterase from cotton aphid (Aphis gossypii Glover). Arch. Inst. Biochem. Physiol. 51:37–45. [DOI] [PubMed] [Google Scholar]
- 35.Ellman, G. L., D. Courtey, V. Andres, and R. M. Featherstone. 1961. A new and rapid colorimetric determination of acetylcholinesterase activity. Biochem. Pharmaceut. 7:88–95. [DOI] [PubMed] [Google Scholar]
- 36.Riddles, P. W., R. L. Blakeley, and B. Zerner. 1979. Ellman's reagent: 5,5′-dithiobis(2-nitrobenzoic acid): a reexamination. Anal. Biochem. 94:75–81. [DOI] [PubMed] [Google Scholar]
- 37.Luck, W. 1967. Spectroscopic studies concerning the structures and the thermodynamic behaviour of H2O, CH3OH and C2H5OH. Disc. Faraday Soc. 43:115–127. [Google Scholar]
- 38.Luck, W., and W. Ditter. 1968. Die Assoziation der Alkohole bis in überkritische Bereiche. [in German]. Bericht Bunsenges. Phys. Chem. 72:365–374. [Google Scholar]
- 39.Franks, F. 1972. Water. a comprehensive treatise. In Vol. 1: The Physics and Physical Chemistry of Water. Plenum Press, New York, NY and London, UK.
- 40.Luck, W. 1965. Zur Assoziation des Wassers III. Die Temperaturabhängigkeit der Wasserbanden bis zum kritischen Punkt. [in German]. Bericht Bunsenges. Phys. Chem. 69:626–637. [Google Scholar]
- 41.Landolt, H., and R. Boernstein. 1982. Zahlenwerte und Funktionen aus Naturwissenschaften und Technik: Neue Serie. [in German]. Springer, Berlin, Germany.
- 42.Glatter, O., and O. Krakty. 1982. Small Angle X-Ray Scattering. Academic Press. New York, NY.
- 43.Murthy, N. S., and J. R. Knox. 2004. Hydration of proteins: SAXS study of native and methoxy polyethyleneglycol (mPEG)-modified L-asparaginase and bovine serum albumin in mPEG solutions. Biopolymers. 74:457–466. [DOI] [PubMed] [Google Scholar]
- 44.Krebs, A., J. Lamy, S. N. Vinogradov, and P. Zipper. 1998. Lumbricus terrestris hemoglobin: a comparison of small-angle x-ray scattering and cryoelectron microscopy data. Biopolymers. 45:289–298. [DOI] [PubMed] [Google Scholar]
- 45.Cantor, C. R., and P. R. Schimmel. 1997. Biophysical Chemistry II, 1st Ed.. W. H Freeman and Company, New York, NY.
- 46.Haseloff, O. W., and H.-J. Hoffmann. 1968. Kleines Lehrbuch der Statistik. [in German]. Walter de Gruyter, Berlin, Germany.
- 47.Sokal, R. R., and F. J. Rohlf. 2001. Biometry. W. H. Freeman and Company, New York, NY.
- 48.http://fsweb.berry.edu/academic/education/vbissonnette/tables/tables.html. 2004. [online].
- 49.Debye, P. J. W. 1942. Reaction rates in ionic solutions. Trans. Electrochem. Soc. 82:265–272. [Google Scholar]
- 50.Kortüm, G. 1966. Lehrbuch der Elektrochemie. [in German]. Verlag Chemie GMBH, Weinheim, Germany.
- 51.Eigen, M. 1954. Über die Kinetik sehr schnell verlaufender Ionenreaktionen in wässriger Lösung. [in German]. Z. Phys. Chem. N.F. 1:176–200. [Google Scholar]
- 52.Bourne, Y., P. Taylor, Z. Radić, and P. Marchot. 2003. Structural insights into ligand interactions at the acetylcholinesterase peripheral anionic site. EMBO J. 22:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ramos, A. S. F., and S. Techert. 2003. A directly linked pyrene-dimethylaniline derivative as a potential biochemical sensor for the microenvironmental dielectric properties of the active site of enzymes. Phys. Chem. Chem. Phys. 5:5176–5181. [Google Scholar]
- 54.Neumann, E., and H. J. Nolte. 1981. Polyelectrolyte field effects. Bioelectrochem. Bioenerget. 8:89–101. [Google Scholar]
- 55.Wilson, M. A., and A. Pohorille. 1997. Adsorption and solvation of ethanol at the water liquid-vapor interface: a molecular dynamics study. J. Phys. Chem. B. 101:3130–3135. [DOI] [PubMed] [Google Scholar]
- 56.Lavelle, L., and J. R. Fresco. 2003. Enhanced stabilization of the triplexes d(C(+)-T)(6):d(A-G)(6);d(C-T)(6), d(T)(21):d(A)(21);d(T)(21) and poly r(U:AU) by water structure-making solutes. Biophys. Chem. 105:701–720. [DOI] [PubMed] [Google Scholar]
- 57.Pal, S. K., L. Zhao, and A. H. Zewai. 2003. Chemistry water at DNA surfaces: ultrafast dynamics in minor groove recognition. Proc. Natl. Acad. Sci. USA. 100:8113–8118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Matthews, J. R., J. Nicholson, E. Jaffray, S. M. Kelly, N. C. Price, and R. T. Hay. 1995. Conformational changes induced by DNA binding of NF-kappa B. Nucleic Acids Res. 23:3393–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Fasman, G. D. 1996. Circular Dichroism and the Conformational Analysis of Biomolecules. Plenum Press, New York, NY and London, UK.
- 60.Murray, T. A., M. P. Foster, and R. P. Swenson. 2003. Mechanism of flavin mononucleotide cofactor binding to the Desulfovibrio vulgaris flavodoxin. 2. Evidence for cooperative conformational changes involving tryptophan 60 in the interaction between the phosphate- and ring-binding subsites. Biochemistry. 42:2317–2327. [DOI] [PubMed] [Google Scholar]
- 61.Sau, A. K., and S. Mitra. 2000. Steady state and picosecond time-resolved fluorescence studies on native, desulpho and deflavo xanthine oxidase. Biochim. Biophys. Acta. 1481:273–282. [DOI] [PubMed] [Google Scholar]
- 62.Andi, B., A. H. West, and P. F. Cook. 2004. Stabilization and characterization of histidine-tagged homocitrate synthase from Saccharomyces cerevisiae. Arch. Biochem. Biophys. 421:243–254. [DOI] [PubMed] [Google Scholar]
- 63.Ben-Naim, A. 1974. Water and Aqueous Solutions. Introductions to a Molecular Theory. Plenum Press, New York, NY and London, UK.
- 64.Herzberg, G. 1991. Molecular Spectra and Molecular Structure: Infrared and Raman of Polyatomic Molecules, Vol. 2. Krieger Publishing, Melbourne, FL.
- 65.Ratcliffe, C. I., and D. E. Irish. 1982. Vibrational spectral studies of solutions at elevated temperatures and pressures. 5. Raman studies of liquid water up to 300 degrees. J. Phys. Chem. 86:4897–4905. [Google Scholar]
- 66.Vinogrado, S. N., and R. H. Linnell. 1971. Spectroscopic manifestations of hydrogen bonding. In Hydrogen Bonding, Chapter 3. Van Nostrand Reinhold, Florence, KY.
- 67.Max, J. J., and C. Chapados. 2004. Infrared spectroscopy of acetone-water liquid mixtures. II. Molecular model. J. Chem. Phys. 120:6625–6641. [DOI] [PubMed] [Google Scholar]
- 68.Graener, H., and A. Laubereau. 1991. Structural information on a hydrogen-bonded polymer from nonlinear infrared spectroscopy. J. Phys. Chem. 95:3447–3450. [Google Scholar]
- 69.Musto, P., G. Ragosta, and L. Mascia. 2000. Vibrational spectroscopy evidence for the dual nature of water sorbed into epoxy resins. Chem. Mater. 12:1331–1341. [Google Scholar]
- 70.Joesten, M. D., and L. J. Schaad. 1974. Hydrogen Bonding. Marcel Dekker, New York, NY.
- 71.Kropman, M. F., H.-K. Nienhuys, S. Woutersen, and H. J. Bakker. 2001. Vibrational relaxation and hydrogen-bond dynamics of HDO:H2O. J. Phys. Chem. A. 105:4622–4626. [Google Scholar]
- 72.Yalamanchili, M. R., A. A. Atia, and J. D. Miller. 1996. Analysis of interfacial water at a hydrophilic silicon surface by in-situ FTIR/internal reflection spectroscopy. Langmuir. 12:4176–4184. [Google Scholar]
- 73.Gottwald, W., and G. Wachter. 1997. IR-Spektroskopie für Anwender. [in German]. Wiley-VCH Verlag, Weinheim, Germany.
- 74.Botti, A., F. Bruni, S. Imberti, M. A. Ricci, and A. K. Soper. 2004. Ions in water: the microscopic structure of concentrated NaOH solutions. J. Chem. Phys. 120:10154–10162. [DOI] [PubMed] [Google Scholar]
- 75.Svergun, D., C. Barberato, and M. H. J. Koch. 1995. CRYSOL—a program to evaluate X-ray solution scattering of biological macromolecules from atomic coordinates. J. Appl. Crystallogr. 28:768–773. [Google Scholar]
- 76.Koch, M. H., P. Vachette, and D. I. Svergun. 2003. Small-angle scattering: a view on the properties, structures and structural changes of biological macromolecules in solution. Q. Rev. Biophys. 36:147–227. [DOI] [PubMed] [Google Scholar]
- 77.Kim, S. J., W. A. Beard, J. Harvey, D. D. Shock, J. R. Knutson, and S. H. Wilson. 2003. Rapid segmental and subdomain motions of DNA polymerase beta. J. Biol. Chem. 278:5072–5081. [DOI] [PubMed] [Google Scholar]
- 78.Sanchez, S. A., J. E. Brunet, D. M. Jameson, R. Lagos, and O. Monasterio. 2004. Tubulin equilibrium unfolding followed by time-resolved fluorescence and fluorescence correlation spectroscopy. Protein Sci. 13:81–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Berman, H. A., J. Yguerabide, and P. Taylor. 1985. Flexibility of the molecular forms of acetylcholinesterase measured with steady-state and time-correlated fluorescence polarization spectroscopy. Biochemistry. 24:7140–7147. [DOI] [PubMed] [Google Scholar]
- 80.Xu, Y., J. Shen, X. Luo, I. Silman, J. L. Sussman, K. Chen, and H. Jiang. 2003. How does huperzine A enter and leave the binding gorge of acetylcholinesterase? Steered molecular dynamics simulations. J. Am. Chem. Soc. 125:11340–11349. [DOI] [PubMed] [Google Scholar]
- 81.Tai, K., T. Shen, U. Borjesson, M. Philippopoulos, and J. A. McCammon. 2001. Analysis of a 10-ns molecular dynamics simulation of mouse acetylcholinesterase. Biophys. J. 81:715–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Gilson, M. K., T. P. Straatsma, J. A. McCammon, D. R. Ripoll, C. H. Faerman, P. H. Axelsen, I. Silman, and J. L. Sussman. 1994. Open “back door” in a molecular dynamics simulation of acetylcholinesterase. Science. 263:1276–1278. [DOI] [PubMed] [Google Scholar]
- 83.Koellner, G., G. Kryger, C. B. Millard, I. Silman, J. L. Sussman, and T. Steiner. 2000. Active-site gorge and buried water molecules in crystal structures of acetylcholinesterase from Torpedo californica. J. Mol. Biol. 296:713–735. [DOI] [PubMed] [Google Scholar]