Hydrogen Bonding Dynamics during Protein Folding of Reduced Cytochrome c: Temperature and Denaturant Concentration Dependence

Abstract

Folding dynamics of reduced cytochrome c triggered by the laser-induced reduction method is investigated from a viewpoint of the intermolecular interaction change. Change of the diffusion coefficient of cytochrome c during the refolding process is traced in the time domain from the unfolded value to the native value continuously at various denaturant (guanidine hydrochloride (GdnHCl)) concentrations and temperatures. In the temperature range of 288 K–308 K and GdnHCl concentration range of 2.5 M–4.25 M, the diffusion change can be analyzed well by the two-state model consistently. It was found that the m^‡-value and the activation energy of the transition state from the unfolded state for the hydrogen bonding network change are surprisingly similar to that for the local structural change around the heme group monitored by the fluorescence quenching experiment. This agreement suggests the existence of common or similar fundamental dynamics including water molecular movement to control the refolding dynamics. The nature of the transition state is discussed.

INTRODUCTION

In the protein folding research, kinetics of the refolding process is very important to reveal the molecular mechanism (1). Since there are many molecular properties that characterize the protein state and there are a huge number of degrees of freedom in the protein conformation, various properties should be monitored in a time domain. The observable dynamics should be different depending on the monitoring properties. For example, rather local structural change can be probed by the hydrogen/deuterium exchange rate, fluorescence, or ultraviolet-visible absorption change of a chromophore or localized vibrational bands. The secondary structure may be monitored by the amide bands in the vibrational spectroscopy or circular dichroism (CD) signal. The information of the kinetics of these properties is essential to construct the total view of the protein folding reaction. A protein, cytochrome c (cyt c), has served as a model protein to study the folding dynamics from various viewpoints (2–10). By using the laser-induced reduction method of cyt c, for example, the dynamics of the secondary structure (α-helices) construction of the reduced cyt c (Fe(II) cyt c) has been reported by the time-resolved CD experiment (11). Pascher measured the distance change between the Trp⁵⁹ and the heme by monitoring the fluorescence intensity change (12). Recently, we have developed a new method to monitor the dynamics of the intermolecular interaction (hydrogen bond networking) during the protein folding by using the pulsed laser-induced transient grating (TG) method and applying it to the cyt c folding reaction (13,14). We have discovered that the diffusion coefficient (D) of cyt c at the guanidine hydrochloride (GdnHCl) concentration of 3.5 M increases with the protein refolding process, and this dynamics was interpreted as the hydrogen bond networking changing from the intermolecular hydrogen bonding of the protein to the intramolecular one. It was found that the time dependence of the observed TG signal in a whole time range can be consistently reproduced well by the two-state model. The rate constants from the D change are different from that of the CD change or of the fluorescence change. On the basis of these results, a molecular picture of the refolding process of Fe(II) cyt c has been proposed (14).

Generally, the kinetics of reactions is characterized by the transition state, and the nature of the transition state can be investigated by the temperature dependence or denaturant concentration dependence measurements of the rate constant. If the dynamics monitored by various properties are different, the transition state associated with such dynamics should be different. Revealing the nature of the transition state is important to characterize the dynamics. In this work, we investigate the transition state for the change of the hydrogen bond network from the concentration dependence of GdnHCl and the temperature dependence of the D-dynamics. From the denaturant concentration dependence, information on the increase of the solvent accessible surface area (SASA) associated with the transition from the unfolded state to the transition state can be obtained. The temperature dependence of the rate constant provides the information on the energetic barrier. We compared our results on the transition state of the intermolecular interaction change with those of the local distance change between the Trp⁵⁹ residue and the heme group. We found that the nature of the transition state is very similar for both dynamics, even though the rate constants are different from each other more than one order of magnitude. This result suggests that a common or similar movement of the amino acid residues including water molecules controls the folding dynamics of the global conformation change and also rather local structural change.

EXPERIMENTAL METHODS

The experimental setup and the principle of the measurement were similar to that reported previously (13,15–19). Briefly, the third harmonic of an Nd:YAG laser (Spectra-Physics (Mountain View, CA) Quantum-Ray Model GCR-170-10) with a 10 ns pulse was used as an excitation beam and a photodiode laser (840 nm) as a probe beam for the refolding experiment. The excitation beam was split into two by a beam splitter and crossed inside a sample cell. A part of the probe beam was diffracted by the modulation of the refractive index induced by the light (TG signal). The signal was isolated from the excitation laser beam with a glass filter and a pinhole, detected by a photomultiplier tube, and recorded by a digital oscilloscope. The spacing of the fringe was measured by the decay rate constant of the thermal grating signal from a calorimetric standard sample, which releases all the photon energy of the excitation as the thermal energy within a time response of our system. All measurements were carried out under the oxygen purged condition by a nitrogen bubbling method.

Horse heart cyt c and ultrapure GdnHCl were purchased from Nakalai Tesque (Kyoto, Japan). β-Nicotinamide adenine dinucleotide (NADH) was obtained from Sigma (St. Louis, MO). They were used without further purification. Cyt c (66 μM) with NADH (650 μM) sample was prepared in a 100 mM phosphate buffer (pH = 7). The sample solution was filtered with a 0.2 μm filter to remove dust and transferred to a 1 cm optical path quartz cell. Since NADH is very sensitive to the light irradiation, the sample solution was changed to a fresh one after ∼150 shots of the excitation laser pulses. The temperature of the sample solution was controlled by flowing temperature-regulated methanol around a cell holder with a temperature control system (Lauda (Königshofen, Germany), RS-D6D).

PRINCIPLE AND THEORY

The principle of the diffusion coefficient measurement during the folding dynamics of cyt c has been reported previously (13,14). In the TG experiment, a photo-induced reaction is initiated by the spatially modulated light intensity that is produced by the interference of two excitation light waves. The sinusoidal modulations of the concentrations of the reactant and the product lead to the sinusoidal modulation in the refractive index (δn). This modulation can be monitored by the diffraction efficiency of a probe beam (TG signal). In this experiment, the refractive index change mainly comes from the thermal energy releasing (thermal grating) and created (or depleted) chemical species by the photoreaction (species grating). The species grating signal intensity is given by the difference of the refractive index changes due to the reactant (δn_r) and product (δn_p):

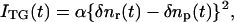(1)

where α is a constant. The sign of δn_p is negative because the phase of the spatial concentration modulation is 180° shifted from that of the reactant. The species grating signal intensity becomes weaker as the spatial modulation of the refractive index becomes uniform, which is accomplished by the translational diffusion. Temporal development and the spatial distribution of concentration of chemical species are calculated by solving a diffusion equation. If D is a constant during the observation time range, the time development of the TG signal can be expressed by a biexponential function (15–20):

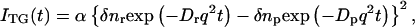(2)

where q is a grating wavenumber and D_r and D_p are diffusion coefficients of the reactant and the product, respectively. Furthermore, δn_r(>0) and δn_p(>0) are, respectively, the initial refractive index changes due to the presence of the reactant and the product. Similarly, the thermal grating signal decays with a rate constant of D_thq² (D_th; thermal diffusivity of the solution).

For analyzing the time profile of the TG signal in a case of the time-dependent D, the following two-state model is used (14). In this model, we consider that there are two types of conformations of cyt c having different D (D_U for unfolded protein and D_N for the native protein). By the populational transition between these two states, the observed D may be expressed by the population weighted average of D. If we assume that the conformational transition between two states occurs with a rate constant k, the time dependence of the refractive index is given by Eq. 3 (14):

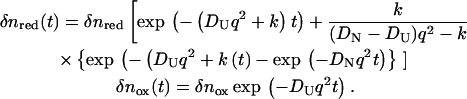(3)

The temporal profile of the TG signal based on this model is calculated from Eqs. 1 and 3.

RESULTS AND DISCUSSION

TG signal of diffusion at various concentrations of GdnHCl

Upon photoexcitation of NADH, the oxidized form of cyt c (Fe(III) cyt c) is reduced to the reduced form (Fe(II) cyt c) (21). This reduction initiates the refolding dynamics of cyt c because of the different stability of the protein against GdnHCl (6,10–12). The feature of the TG signal after the photoexcitation of NADH with cyt c in phosphate buffer solution at [GdnHCl] = 3.5 M and the analysis of the profile were described previously (13,14). Briefly, the essential feature is summarized. The TG signal appears immediately after the photoexcitation and decays with a rate constant of 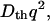which indicates that this initial signal is the thermal grating signal created by the thermal energy due to the nonradiative transition from the excited state. In the millisecond time range, a slower rise-decay signal was observed. Since the observable time range depends on the q²-value, this signal represents the diffusion process. The rise-decay curve (diffusion signal) clearly indicates that two species having different D contribute to the signal and they have positive and negative signs of the δn components. On the basis of the sign of δn, we found that the rise and decay components correspond to the presence of the product (Fe(II) cyt c) and the reactant (Fe(III) cyt c), respectively. Since the time-profile cannot be expressed by the biexponential function of Eq. 2 and the time profiles and the signal intensities depend on the observation time range significantly, we have concluded that these features should be interpreted in terms of the time-dependent D. Since D of the reactant (Fe(III) cyt c) is constant (D_U), the time dependence of D should come from the time dependence of D of Fe(II) cyt c. It was found that the time dependence of the observed TG signal at [GdnHCl] = 3.5 M in a whole time range can be consistently reproduced well by the two-state model (14). In this two-state model, we consider that there are two conformations with different D and the fraction of each conformation is changed. Although there might be small nontwo-state contributions in the kinetics, an excellent fitting in a wide time range strongly indicates that the D-change occurs dominantly by a two-state (cooperative) transition. However, it is worthy to stress here that the whole protein folding process is not the two-state transition, because there are a variety of rate constants depending on the monitoring properties (e.g., D-change, α-helix formation, or fluorescence intensity change; (14)). For example, the previously reported kinetics of transient absorption signals (22) and of fluorescence intensity from Trp (12), both of which may represent the ligand exchange reaction, are slower than the rate constants monitored by the α-helix formation (11) or that by the hydrogen bond networking change in this study as discussed later. The different timescale indicates that not all of the observed dynamics are determined by the ligand exchange process, so that several transition states for the folding reaction are involved in different time ranges depending on the monitored physical quantities. Furthermore, we have confirmed that the kinetics of D does not change even when we added imidazole (0.1 M), which can be a ligand to the heme (data not shown). This result indicates that the ligand exchange step does not control the kinetics of D. The absence of the ligand exchange contribution to the diffusion change may be explained by two factors: the rate of the D change is faster than the ligand exchange rate, and a diffusion coefficient of the misligated collapsed form is not much different from that of properly folded protein. The small difference in D between these states is not strange because D is only sensitive to the hydrogen bond networking. If the ligand exchange does not induce the change of the hydrogen networking, this process cannot be detected by the diffusion change. We will discuss the transition state for the hydrogen bond networking change in this study.

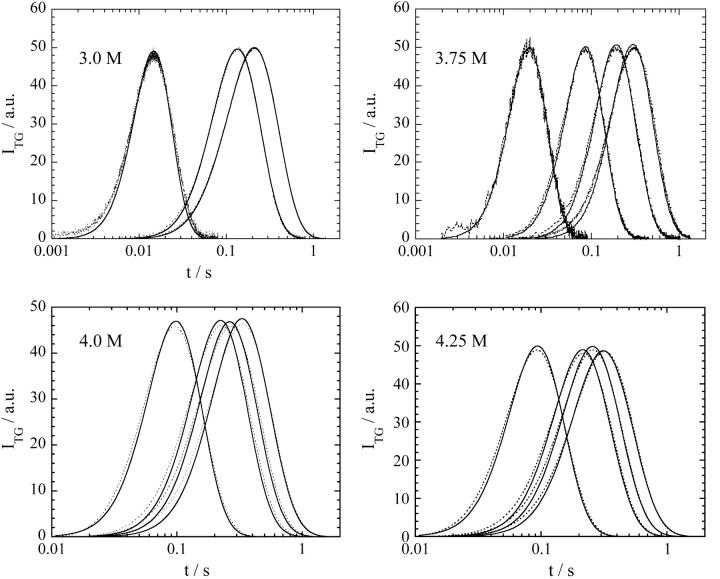
The essential features of the TG signal at various [GdnHCl] are similar to that at [GdnHCl] = 3.5 M. Typical examples of the time profiles of the diffusion signals at various q² are shown in Fig 1 at some [GdnHCl]. The signal is very weak in a range of [GdnHCl] < 2.5 M. The weak signal in the low concentration range of GdnHCl is reasonable because both Fe(II) cyt c and Fe(III) cyt c are folded at this concentration (Fig 2), and the photo-induced reduction does not initiate the folding reaction. The signal becomes stronger with increasing [GdnHCl] until [GdnHCl] = 3.5 M and then the intensity gradually decreases. The diffusion signal almost disappears in [GdnHCl] > 4.5 M. The disappearance of the diffusion signal in [GdnHCl] > 5.5 M is not surprising because both Fe(II) cyt c and Fe(III) cyt c are unfolded in this range (Fig. 2). However, no diffusion signal in 4.5 M < [GdnHCl] < 5.5 M was not expected, because Fe(II) cyt c is folded but Fe(III) cyt c is unfolded in a concentration range of 2 M < [GdnHCl] < 5.5 M (Fig. 2). Why does the diffusion signal disappear in 4.5 M < [GdnHCl] < 5.5 M?

FIGURE 1.

Observed TG signals (dotted lines) after photoreduction of Fe(III) cyt c in phosphate buffer at different q² at various GdnHCl concentrations. The signals are fitted by the two-state model described in the text (solid lines).

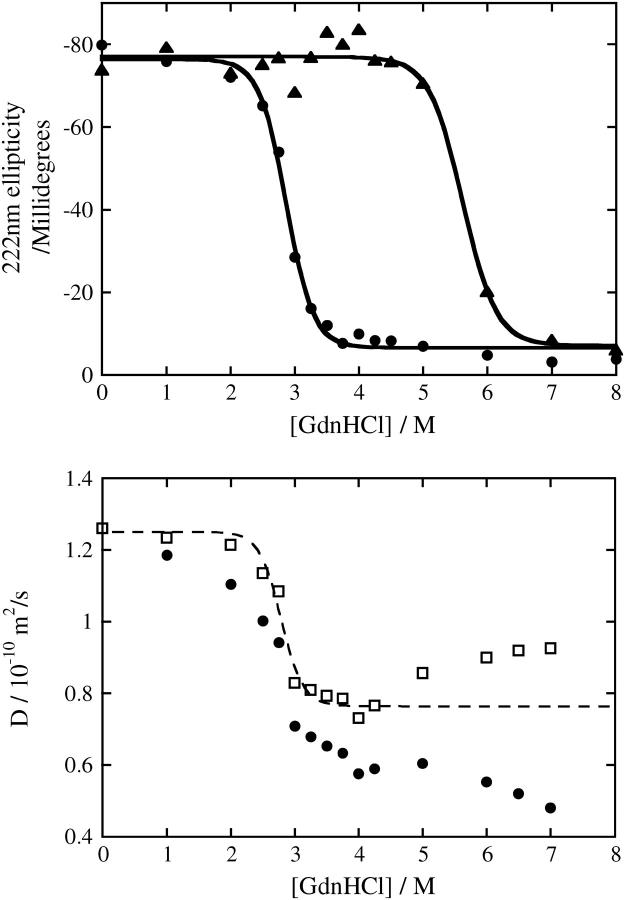
FIGURE 2.

(Top) Denaturation curves of Fe(III) cyt c (•) and Fe(II) cyt c (▴) against GdnHCl concentration in phosphate buffer solution monitored by CD at 222 nm and the best-fitted lines by the two-state model. (Bottom) Denaturation curve of Fe(III) cyt c monitored by the diffusion coefficient (D) and the best-fitted lines by the two-state model (dotted line). Circles and squares represent D of Fe(III) cyt c in the solution and that corrected by the viscosity increase due to the addition of GdnHCl.

To understand this behavior, we first investigate the [GdnHCl] dependence of D of Fe(III) cyt c. We measure D of Fe(III) cyt c in a wide concentration range of GdnHCl by the same method described before (14). Fig. 2 depicts the denaturation curve monitored by the CD intensity and monitored by D of cyt c. In a range of 0 < [GdnHCl] < 4 M, D decreases with increasing [GdnHCl]. The GdnHCl concentration dependence of D corrected by the solution viscosity is similar to the denaturation curve monitored by the CD intensity. Hence, destruction of the secondary structure (α-helices) should be the main origin of the D change in the low GdnHCl concentration range. However, in a range of 4.5 M < [GdnHCl], D of unfolded cyt c increases. The different D behavior suggests that the denatured state is different between 0 < [GdnHCl] < 4.5 M and 4.5 M < [GdnHCl].

It is interesting to note that Segel et al. previously observed two unfolded states (U₁ and U₂) by using the small angle x-ray scattering (SAXS) method (23). The relative population varies with a function of [GdnHCl]. The concentration range of GdnHCl, in which D decreases and the diffusion signal appears, agrees with the range where U₁ is populated. By decreasing the population of U₁ by increasing [GdnHCl], the relative populations of U₂ and D of cyt c increase. This tendency suggests that the U₁ state is responsible for the diffusion signal during the refolding process. According to the SAXS data, the U₁ and U₂ states have similar radii of gyration but differ in their degree of compactness. Whereas U₂ has a characteristic of a random coil, U₁ possesses some residual structure. The structure of the U₁ state is suggested to be nonspecific hydrophobic contact. As [GdnHCl] increases, the number of hydrophobic contact decreases to the favor for U₂. If increase of D in a range of 4.5 M < [GdnHCl] is originated from the different population of U₁ and U₂, D of U₂ should be larger than D of U₁. The larger D of U₂ compared with D of U₁ may be explained by a surrounding GdnHCl around the hydrophobic group and weakened intermolecular interaction between the protein and water molecules. This weakened intermolecular interaction for U₂ may be a possible origin for the faster diffusion of U₂ to lead the weak diffusion signal.

Generally it is believed that the denatured state of a protein consists of many random conformations. A combination of cyt c and SAXS technique is unique to show different denatured conformations (23). The D measurement in this study confirms the different conformations of the denatured cyt c. This result indicates that the D of proteins is a useful physical property not only to study the denaturation of a protein (24) but also to discriminate different denatured states from a viewpoint of the hydrogen bond networking.

GdnHCl concentration dependence

We analyzed the observed TG signals at various [GdnHCl] (Fig. 1) based on the two-state model. From the fitting in a wide time range at different q², the rate constant of the change of D, i.e., the hydrogen bond networking, are determined. The fitting parameters are only δn_red(= δn_ox) and k in Eq. 3. The reasonable fitting at different q² only using the two adjustable parameters (Fig. 1) ensures that the two-state model is appropriate. The calculated signals based on the two-state model can reproduce the TG signals at all concentrations we investigated.

We found that there is only one rate constant in the whole time range of the refolding process from the following reasons. First, the TG signal in the observation time range can be fitted by a single rate constant. Second, to examine if there exists dynamics faster than the time window of the TG signal in Fig. 1, we measured the TG signal in a faster time region by increasing q². If D has already changed before the signals in Fig. 1, a TG signal having two different D (Eq. 3) should appear. However, we observed the single exponential decay at higher q². A typical example has been presented previously (Fig. 2, top, in Nishida et al. (14)). This fact clearly indicates that D does not change before the observation time of Fig. 1. Third, to examine if there exists dynamics slower than the time window of the TG signal in Fig. 1, the signal sufficiently after this process, for instance, after ∼200 ms, is analyzed and it is found that the biexponential function with two time-independent D of native (D_N) and unfolded cyt c (D_U) can reproduce the signals well. Hence, the change in D completes until this time and there is no dynamics of D after the process shown in Fig. 1. Combining these facts, we conclude that the diffusion change can be expressed by the two-state model during a whole refolding process.

The denaturant concentration dependence of the folding rate has been explained by the concentration dependence of the activation Gibbs free energy (ΔG^‡). For the transition from the unfolded (U) states to the native (N) state, the activation Gibbs free energy is written as (1,25)

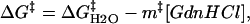(4)

where 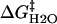is the activation free energy in water, and m^‡ is a constant. Combining this equation with the expression based on the transition state theory,

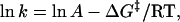(5)

where k is the rate constant and A is the so-called frequency factor of the Eyring equation, ln k is expected to be proportional to m^‡[GdnHCl]. An equation similar to Eq. 4 holds for reaction Gibbs free energy. It has been found experimentally that the m-value for the free energy of unfolding is proportional to the increase in degree of exposure of the protein to solvent (SASA) (26–28). On the basis of this result, m^‡-value has been also considered to be proportional to the increase in degree of SASA upon the transition from U state to the transition state.

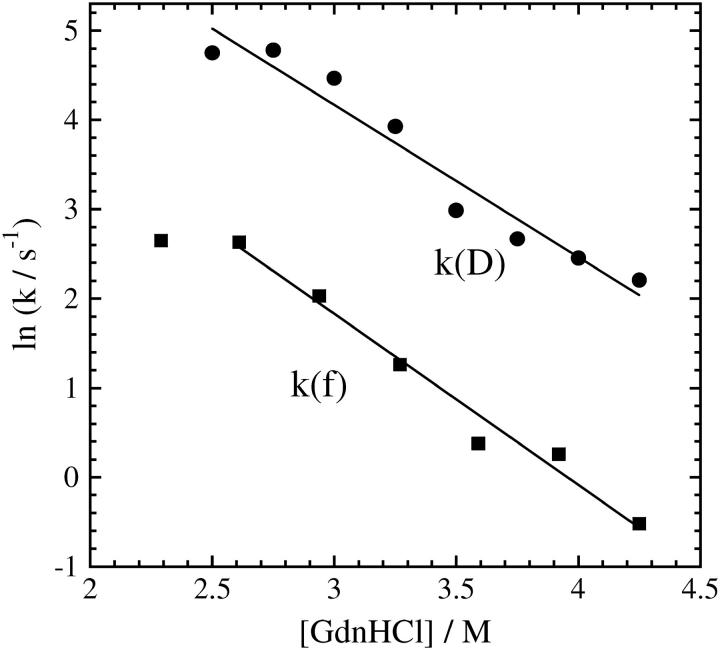
Fig 3 represents the [GdnHCl] dependence of the logarithm of the observed rate constant for the hydrogen bond networking (k(D)). The plot shows almost linear in the range of 2.5 M < [GdnHCl] < 4.3 M. The m^‡-value in this concentration range is determined to be −1.9. For comparison, the reported rate constants by monitoring the fluorescence intensity from Trp (k(f)) at 20°C (12) are also plotted. The rate constant of k(f) is smaller than k(D) more than one order of magnitude in any concentration. The slower dynamics of the Trp movement to the heme is consistent with a folding picture that the rearrangement of the hydrogen bonding network first occurs to form the protein frame and then local amino acid residues move to the native location. Surprisingly, although the monitoring properties and the absolute values of the rate constants are significantly different, we found that the slope of the [GdnHCl] dependence is almost the same for k(D) and k(f). (The fluorescence intensity change was measured in 1.63 M < [GdnHCl] < 4.9 M and found deviation from linearity in this wide concentration range. In particular, the deviation is observed at low [GdnHCl] and ln k is almost independent of [GdnHCl]. A similar trend is observable for k(D), too. However, we fitted the k(f) data by a linear function in a range of 2.5 M < [GdnHCl] < 4.3 M. The m^‡-value of k(f) in this concentration range is −1.7.) The similarity of the concentration dependence will be discussed later.

FIGURE 3.

Denaturant concentration dependence of the rate constants of the D change (k(D)) and those of fluorescence intensity change (k(f)).The rate constants in a range of 2.5 M < [GdnHCl] < 4.3 M are fitted by a linear function (solid lines).

Temperature dependence

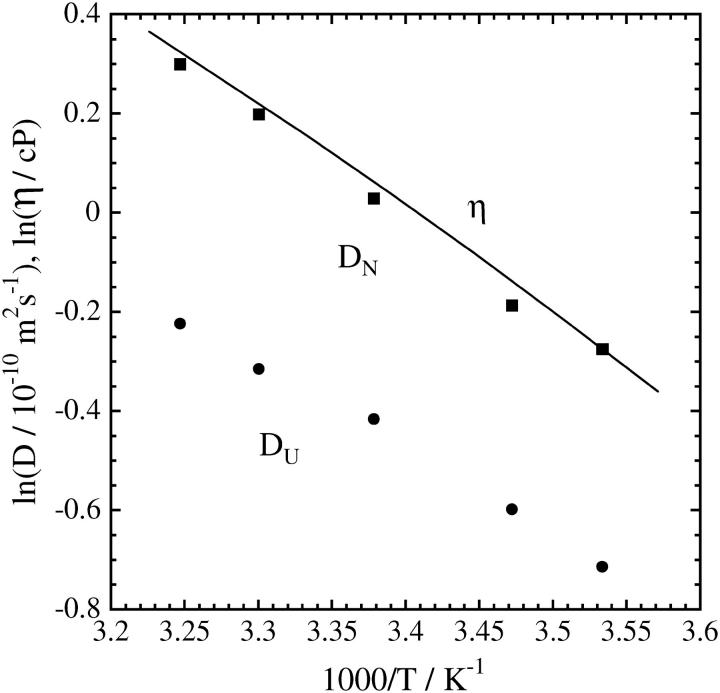
For investigating the temperature dependence of the dynamics of the hydrogen bond networking during the refolding reaction, we first measure D of native and the unfolded cyt c at various temperatures (Fig 4). Both D show the Arrhenius relationship with single activation energy, which is very close to that of the viscosity change. It indicates that the diffusion process is governed by the solution viscosity and the initial (unfolded) and final (native) conformations do not depend on temperature.

FIGURE 4.

Temperature dependence of D of native cyt c (▪) and unfolded cyt c (•). The line indicates the temperature dependence of the viscosity change.

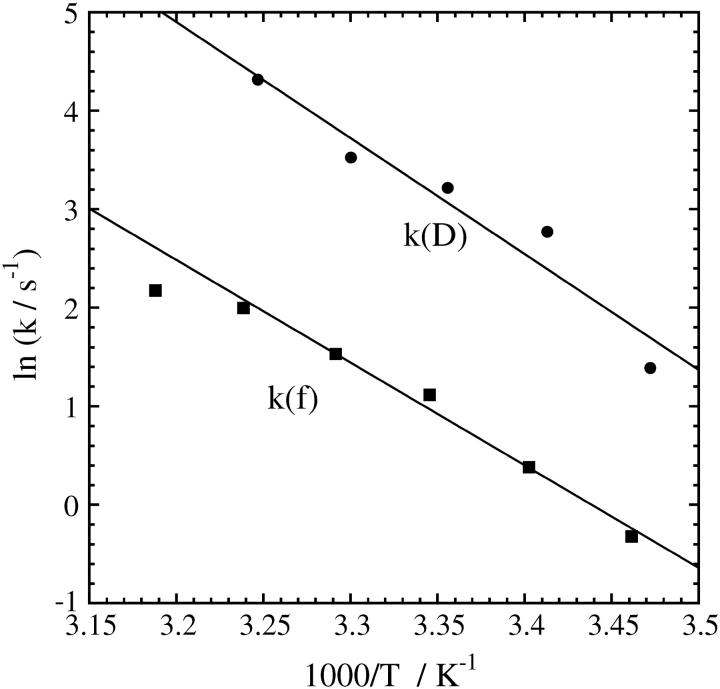
Essential features of the TG signal for the refolding reaction are similar to those described in the previous section. The signals can be fitted by the two-state model well in a temperature range of 288–308 K. The rate constants determined by the fitting are shown in Fig 5 against 1/T. The Arrhenius plot is almost linear in this range. For comparison purposes, we also plot k(f) measured at [GdnHCl] = 3.59 M (12). (Although the concentration of GdnHCl is not exactly the same as this experiment (3.5 M), the difference is negligible.) Pascher reported a nonlinear Arrhenius plot in a temperature range of 279–348 K and discussed possible origins. However, in a smaller temperature range of this study (288–308 K), the Arrhenius plot looks almost linear. Similar to the [GdnHCl] dependence, we found a strikingly similar temperature dependence for k(D) and k(f) although the absolute values of k are different.

FIGURE 5.

Temperature dependence of the rate constants of the D change (k(D)) and those of fluorescence intensity (k(f)). The solid line is the fitted line by the Arrhenius relation with the single activation energy.

Transition state of folding

It is extremely interesting to find that, although the folding rate constants monitored by the diffusion coefficient (k(D)) are ∼50 times larger than that monitored by the fluorescence (k(f)), the slope of the [GdnHCl] dependence and the temperature dependence are almost the same. As described above, the m^‡-value is considered to represent the increase of SASA by the transition from U to the transition state. The agreement from two different measurements might be an accidental coincidence. However, we furthermore found that the energetic barrier determined from the temperature dependence measurement of k(D) is very similar to that of k(f). Hence, it is hard to believe that this is just an accidental coincidence. How can we explain this similar transition state for two different processes?

A possible explanation is the following. For changing D, many hydrogen bonding rearrangements may be necessary. On the other hand, the fluorescence intensity change of Trp represents rather local dynamics. The similar characteristics of the transition state for both dynamics suggest that common or similar movement controls the global and local movement simultaneously. For example, the observed SASA increase step may be a fundamental movement of the protein to change the conformation, and this dynamics is the rate determining step for the change of D or the location of Trp. First, this movement triggers a cooperative change of many hydrogen bonding networks to result in the change of D. After this change, the same movement occurs with a less frequency factor to change the position of Trp, which leads the final adjustment of the Trp position to the native one. The similar temperature dependence for k(D) and k(f) indicates that the transition state has a similar energetic barrier as well. One plausible molecular origin of this fundamental movement is the solvent dynamics. If the movement of the protein is controlled by the solvent, the similar transition state for different dynamics can be rationalized. Recent theoretical and experimental studies on the protein folding suggested that structural collapse followed by desolvation of hydrophobic residues should play an important role in the course of protein folding process (29,30). The observed transition state in this and previous studies may represent this change of the solvation. Investigation of this fundamental movement in the future will be essential to understand the refolding dynamics.

CONCLUSION

Kinetics of the hydrogen bond networking between cyt c protein and solvent was studied during the protein refolding process at various denaturant concentrations and various temperatures from a viewpoint of diffusion coefficient D using the pulsed laser-induced TG technique. GdnHCl concentration dependence of D suggests two distinct unfolded states, which may be the same as those observed before by the SAXS measurement. The refolding dynamics monitored by D is expressed well by the two-state model at all GdnHCl concentrations and all temperatures we investigated. The m^‡-value and energetic barrier of the transition state from the unfolded state are determined from the [GdnHCl] and temperature dependences, respectively. Surprisingly, we found that these properties of the transition state are very similar for the diffusion change and the fluorescence intensity change, although the rate constants are different more than 50 times. The similar nature of the transition state for both dynamics suggests existence of common (or similar) fundamental protein motion, which controls the dynamics of the global hydrogen network change as well as the local movement such as Trp movement. At the transition state, the nonpolar region of the protein is exposed to water, which is suggested by the SASA increases. This process is the rate determining step and triggers a cooperative movement of much hydrogen bonding.