Abstract
A simple and complete derivation of the relation between concentration-based preferential interaction coefficients and integrals over the relevant pair correlation functions is presented for the first time. Certain omissions from the original treatment of pair correlation functions in multicomponent thermodynamics are also addressed. Connections between these concentration-based quantities and the more common molality-based preferential interaction coefficients are also derived. The pair correlation functions and preferential interaction coefficients of both solvent (water) and cosolvent (osmolyte) in the neighborhood of a macromolecule contain contributions from short-range repulsions and generic long-range attractions originating from the macromolecule, as well as from osmolyte-solvent exchange reactions beyond the macromolecular surface. These contributions are evaluated via a heuristic analysis that leads to simple insightful expressions for the preferential interaction coefficients in terms of the volumes excluded to the centers of the water and osmolyte molecules and a sum over the contributions of exchanging sites in the surrounding solution. The preferential interaction coefficients are predicted to exhibit the experimentally observed dependence on osmolyte concentration. Molality-based preferential interaction coefficients that were reported for seven different osmolytes interacting with bovine serum albumin are analyzed using the this formulation together with geometrical parameters reckoned from the crystal structure of human serum albumin. In all cases, the excluded volume contribution, which is the volume excluded to osmolyte centers minus that excluded to water centers in units of 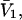 exceeds in magnitude the contribution of the exchange reactions. Under the assumption that the exchange contribution is dominated by sites in the first surface-contiguous layer, the ratio of the average exchange constant to its neutral random value is determined for each osmolyte. These ratios all lie in the range 1.0 ± 0.15, which indicates rather slight deviations from random occupation near the macromolecular surface. Finally, a mechanism is proposed whereby the chemical identity of an osmolyte might be concealed from partially ordered multilayers of water in clefts, grooves, and pits, and its consequences are noted.
exceeds in magnitude the contribution of the exchange reactions. Under the assumption that the exchange contribution is dominated by sites in the first surface-contiguous layer, the ratio of the average exchange constant to its neutral random value is determined for each osmolyte. These ratios all lie in the range 1.0 ± 0.15, which indicates rather slight deviations from random occupation near the macromolecular surface. Finally, a mechanism is proposed whereby the chemical identity of an osmolyte might be concealed from partially ordered multilayers of water in clefts, grooves, and pits, and its consequences are noted.
INTRODUCTION
The effects of weakly interacting osmolytes on the conformational equilibria and ligand binding reactions of biological macromolecules have been studied intensively over the past two decades (1–4). A major objective in many cases was to ascertain the difference between the number of water molecules “associated” with the products of a particular reaction on one hand and the corresponding number “associated” with its reactants on the other. The precise meaning, or interpretation, of the numbers of “associated” waters and the differences therein remains a subject of discussion and some debate (5–9). This general approach to studying changes in “associated” waters has come to be known as the osmotic stress method. In the case of a solution, consisting of water (solvent, component 1), dilute macromolecules (components 2J, J = 1, … M), and neutral osmolyte (cosolvent, component 3), the osmotic stress method yields the slope 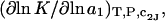 where K is the equilibrium constant for the reaction when written so as to take no account of either water or osmolyte, a1 is the activity of the water, and
where K is the equilibrium constant for the reaction when written so as to take no account of either water or osmolyte, a1 is the activity of the water, and 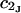 denotes the concentrations of each kind of macromolecule. This slope is extrapolated to the limit of infinite dilution,
denotes the concentrations of each kind of macromolecule. This slope is extrapolated to the limit of infinite dilution, 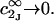 The difference in “associated” waters between products and reactants is sometimes taken to be the aforementioned slope,
The difference in “associated” waters between products and reactants is sometimes taken to be the aforementioned slope,
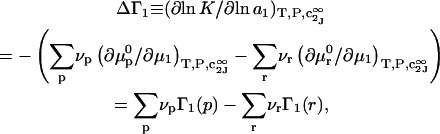 |
(1) |
where the index p or r denotes macromolecular products or reactants, respectively, 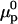 and
and 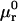 denote the respective standard state chemical potentials,
denote the respective standard state chemical potentials, 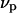 and
and 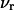 denote the respective stoichiometric coefficients of the reaction under consideration, and
denote the respective stoichiometric coefficients of the reaction under consideration, and
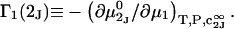 |
(2) |
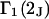 and the symmetrically defined
and the symmetrically defined  are concentration-based “preferential interaction coefficients”, which characterize the variation of that part of
are concentration-based “preferential interaction coefficients”, which characterize the variation of that part of 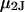 that does not depend upon
that does not depend upon 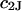 with either
with either 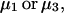 respectively.
respectively.
Alternative preferential interaction coefficients are defined in connection with equilibrium dialysis experiments and are usually molality based. The molalities of species 1, 2, and 3 are denoted by, respectively, 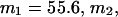 and
and 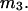 Two common molality-based preferential interaction coefficients are:
Two common molality-based preferential interaction coefficients are: 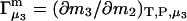 and
and 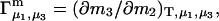 where the index J denoting the macromolecular conformation has been suppressed. Although relations between these and other molality-based preferential interaction coefficients have been intensively investigated, the connections between molality-based and concentration-based preferential interaction coefficients, like
where the index J denoting the macromolecular conformation has been suppressed. Although relations between these and other molality-based preferential interaction coefficients have been intensively investigated, the connections between molality-based and concentration-based preferential interaction coefficients, like 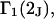 have received less attention. Clever and intuitive thermodynamic approaches indicate that for any given macromolecular species 2,
have received less attention. Clever and intuitive thermodynamic approaches indicate that for any given macromolecular species 2,
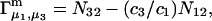 |
(3) |
where N12 and N32 denote the total number of water and osmolyte molecules, respectively, in a domain of sufficient size surrounding a single isolated macromolecule, and c1 and c3 denote the respective bulk concentrations in an exterior domain, no part of which is near any macromolecule (1–9). 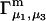 can be regarded as the excess number of osmolyte molecules in the vicinity of the macromolecule above the quantity that would be expected from the number of water molecules in that region and the bulk concentration ratio,
can be regarded as the excess number of osmolyte molecules in the vicinity of the macromolecule above the quantity that would be expected from the number of water molecules in that region and the bulk concentration ratio, 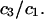
Although the analysis below indicates that Eq. 3 is correct, the rigor of the thermodynamic approaches used to derive it is debatable. For example, the neglect of the osmotic pressure due to the macromolecule within its local domain is justifiable only for a domain of very great size, yet in many cases that domain was assumed to extend no more than one or two hydration layers beyond the macromolecule. The likely resolution of this paradoxical circumstance is noted briefly below.
Recently several articles appeared in which 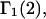 or the equivalent
or the equivalent 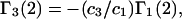 was expressed in terms of the so-called Kirkwood-Buff integrals (10),
was expressed in terms of the so-called Kirkwood-Buff integrals (10), 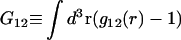 and
and 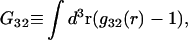 where g12(r) and g32(r) are the pair correlation functions, which are described in greater detail below (11–14). The derivation of the main relation followed an unusually circuitous, piecewise, and technically demanding route that took place over three different articles and a book that collectively spanned 26 years (11,15–17). Chitra and Smith combined two relations that appeared earlier in Ben-Naim's book (17), namely his Eq. 6.7.49 for
where g12(r) and g32(r) are the pair correlation functions, which are described in greater detail below (11–14). The derivation of the main relation followed an unusually circuitous, piecewise, and technically demanding route that took place over three different articles and a book that collectively spanned 26 years (11,15–17). Chitra and Smith combined two relations that appeared earlier in Ben-Naim's book (17), namely his Eq. 6.7.49 for 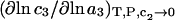 and Eq. 6.17.16 for
and Eq. 6.17.16 for 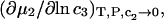 to obtain the final expression for
to obtain the final expression for 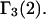 The Eq. 6.7.49 was explicitly derived in Ben-Naim's book, but the derivation of the much more difficult Eq. 6.17.16 was simply described as quite lengthy and omitted entirely. In fact, the first stage of that proof was presented in his 1975 article (15), and the second stage was presented in his 1988 article (16). Unfortunately, neither Chitra and Smith (11) nor Ben-Naim (17) referenced directly those earlier articles, from which the entire proof could be assembled. Chitra and Smith (11) demonstrated the approximate validity of their expression for
The Eq. 6.7.49 was explicitly derived in Ben-Naim's book, but the derivation of the much more difficult Eq. 6.17.16 was simply described as quite lengthy and omitted entirely. In fact, the first stage of that proof was presented in his 1975 article (15), and the second stage was presented in his 1988 article (16). Unfortunately, neither Chitra and Smith (11) nor Ben-Naim (17) referenced directly those earlier articles, from which the entire proof could be assembled. Chitra and Smith (11) demonstrated the approximate validity of their expression for 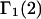 by molecular dynamics simulations of both the pair correlation functions and the free energies of insertion of different small species 2 into aqueous solutions over a wide range of concentrations of various cosolvents. Shimizu (13) suggested a way to obtain the separate G12 and G32 from the measured
by molecular dynamics simulations of both the pair correlation functions and the free energies of insertion of different small species 2 into aqueous solutions over a wide range of concentrations of various cosolvents. Shimizu (13) suggested a way to obtain the separate G12 and G32 from the measured 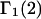 and
and 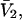 where
where 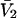 is the partial molecular volume. He employed a relation between
is the partial molecular volume. He employed a relation between 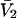 and G12 and G32 that was also first presented in Ben-Naim's book (17) (Eq. 6.17.22), but the derivation, described as quite lengthy, was also omitted entirely. Again, a two-stage proof of the relevant relation can be found in the same two earlier articles (15,16). Shimizu (12) also extended his idea to determine the changes, ΔG32 and ΔG12, accompanying a reaction of species 2 from the measured
and G12 and G32 that was also first presented in Ben-Naim's book (17) (Eq. 6.17.22), but the derivation, described as quite lengthy, was also omitted entirely. Again, a two-stage proof of the relevant relation can be found in the same two earlier articles (15,16). Shimizu (12) also extended his idea to determine the changes, ΔG32 and ΔG12, accompanying a reaction of species 2 from the measured 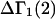 and
and 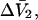 which was assumed to be the entire ΔV associated with the reaction. Shimizu and Smith (14) examined the differences between the effects of crowders, such as polyethylene glycol, and small osmolytes, such as glycerol, that stabilize native protein structures, on the separate G12 and G23. Schellman (18) undertook a related analysis in terms of the cross-second virial coefficients (
which was assumed to be the entire ΔV associated with the reaction. Shimizu and Smith (14) examined the differences between the effects of crowders, such as polyethylene glycol, and small osmolytes, such as glycerol, that stabilize native protein structures, on the separate G12 and G23. Schellman (18) undertook a related analysis in terms of the cross-second virial coefficients (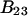 ).
).
The initial objective of this study is to provide a complete and much simpler derivation of the relevant expression for 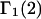 directly from the results of Kirkwood and Buff (10), as well as some important details that are missing from their original treatment of multicomponent thermodynamics. Such details include the choice of origin of the coordinate frame in a highly deformable macromolecule, its manifestation in the pair correlation functions, the invariance of the integrals of
directly from the results of Kirkwood and Buff (10), as well as some important details that are missing from their original treatment of multicomponent thermodynamics. Such details include the choice of origin of the coordinate frame in a highly deformable macromolecule, its manifestation in the pair correlation functions, the invariance of the integrals of 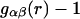 to that choice, a complete definition of the pair correlation function in the classical grand ensemble, and a derivation of the partial molecular volume. This derivation of
to that choice, a complete definition of the pair correlation function in the classical grand ensemble, and a derivation of the partial molecular volume. This derivation of 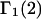 follows a considerably more direct line than the Ben-Naim-Chitra-Smith development, and is technically much simpler. All of the results of Kirkwood and Buff that are needed to derive
follows a considerably more direct line than the Ben-Naim-Chitra-Smith development, and is technically much simpler. All of the results of Kirkwood and Buff that are needed to derive 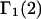 were rederived and found to be correct. In addition, a short proof of Ben-Naim's expression for
were rederived and found to be correct. In addition, a short proof of Ben-Naim's expression for 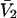 is provided in Appendix D.
is provided in Appendix D.
Connections between this concentration-based 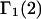 and the molality-based
and the molality-based 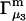 and
and 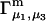 are derived via thermodynamic arguments that make use of certain expressions of Anderson et al. (19,20), which were also verified by rederivation.
are derived via thermodynamic arguments that make use of certain expressions of Anderson et al. (19,20), which were also verified by rederivation.
The main objective of this study is to clarify the meaning(s) of the 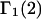 and
and 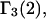 and especially to relate them to more familiar quantities such as excluded volumes and equilibrium constants for osmolyte-solvent exchange in the region surrounding the macromolecule (21–26). Although this development is more heuristic than rigorous, useful predictions and significant insights emerge. As an example, the experimental
and especially to relate them to more familiar quantities such as excluded volumes and equilibrium constants for osmolyte-solvent exchange in the region surrounding the macromolecule (21–26). Although this development is more heuristic than rigorous, useful predictions and significant insights emerge. As an example, the experimental 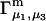 data for seven different osmolytes interacting with bovine serum albumin (BSA) are analyzed using this formulation in conjunction with geometrical parameters reckoned from the crystal structure of human serum albumin (HSA). The separate excluded volume and exchange contributions are evaluated. Under the assumption that only the surface-contiguous layer of osmolyte sites is important, the ratio of the average exchange constant to its neutral random value is obtained in each case.
data for seven different osmolytes interacting with bovine serum albumin (BSA) are analyzed using this formulation in conjunction with geometrical parameters reckoned from the crystal structure of human serum albumin (HSA). The separate excluded volume and exchange contributions are evaluated. Under the assumption that only the surface-contiguous layer of osmolyte sites is important, the ratio of the average exchange constant to its neutral random value is obtained in each case.
Finally, a mechanism is proposed whereby the chemical identity of the osmolyte may be concealed from partially ordered hydration multilayers in clefts, grooves, and pits, and its consequences are briefly noted.
A DERIVATION OF Γ1(2)
Let us consider a system comprising ν different molecular species, α, β, … η, at constant T, V. In this case, when each species j undergoes a change of 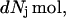
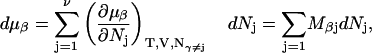 |
(4) |
where
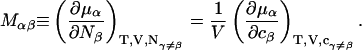 |
(5) |
Thus, the column vector containing the ν different dμk is related to the ν different dNj by the matrix relation dμ = M dN, where the elements of M are given by Eq. 5. Inversion of this matrix relation gives dN = M−1dμ, or
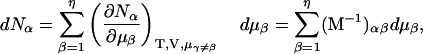 |
(6) |
where
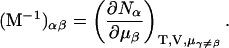 |
(7) |
Kirkwood and Buff (10) established that the 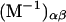 in Eq. 7 are directly related to integrals of the relevant pair correlation functions,
in Eq. 7 are directly related to integrals of the relevant pair correlation functions,
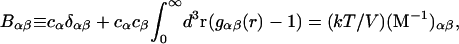 |
(8) |
where 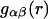 is the αβ-pair correlation function, or radial distribution function, and r = |r1 − r2| is the distance between the arbitrarily chosen central atom of an α-molecule at r1 and that of a β-molecule at r2, as indicated in Appendix A. A complete definition of gαβ(r12) in the grand ensemble (27) is given in Eq. A1 in Appendix A. It must be emphasized that gαβ(r12) pertains to no atoms other than the arbitrarily chosen central atom of each molecule, and will in general depend upon that choice. Because the relations presented here derive ultimately from fluctuations in the numbers of molecules in a volume V that is large enough to contain on average a great many molecules of each kind, those relations must be independent of the choice of central atom. It may be concluded from Eq. 8 that integrals of the gαβ(r) − 1 over the volume V, or at least from 0 out to a distance where gαβ(r) has converged to 1.0, are independent of the choice of central atom. The grand ensemble used to derive Eq. 8 can itself be derived by considering that the volume V is a tiny fraction of an enormously larger supersystem with a fixed number of molecules (27).
is the αβ-pair correlation function, or radial distribution function, and r = |r1 − r2| is the distance between the arbitrarily chosen central atom of an α-molecule at r1 and that of a β-molecule at r2, as indicated in Appendix A. A complete definition of gαβ(r12) in the grand ensemble (27) is given in Eq. A1 in Appendix A. It must be emphasized that gαβ(r12) pertains to no atoms other than the arbitrarily chosen central atom of each molecule, and will in general depend upon that choice. Because the relations presented here derive ultimately from fluctuations in the numbers of molecules in a volume V that is large enough to contain on average a great many molecules of each kind, those relations must be independent of the choice of central atom. It may be concluded from Eq. 8 that integrals of the gαβ(r) − 1 over the volume V, or at least from 0 out to a distance where gαβ(r) has converged to 1.0, are independent of the choice of central atom. The grand ensemble used to derive Eq. 8 can itself be derived by considering that the volume V is a tiny fraction of an enormously larger supersystem with a fixed number of molecules (27).
The pair correlation function has the following physical meaning. If the chosen central atom of a molecule of kind α is located at r1, then cβgαβ(r) is the probability per unit volume of finding the chosen central atom of a molecule of kind β at r2, such that r = |r1 − r2|. A completely random disposition of β-molecules in the vicinity of α corresponds to gαβ(r) = 1.0. In general, gαβ(r) is the factor by which the purely random probability per unit volume (i.e., cβ) must be multiplied to reckon the actual probability per unit volume of finding a β-molecule at distance r from an α-molecule. The pair correlation functions are by definition symmetric, so gαβ(r) = gβα (r), and also Bαβ = Bβα. We shall later regard cβgαβ(r) as the rotationally averaged mean density of centers of β-molecules at a distance r from the center of an α-molecule.
The matrix relation in Eq. 8 can be written as B = (kT/V)M−1, which can be inverted to give M = (kT/V)B−1, and
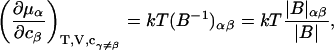 |
(9) |
where |B|αβ is the cofactor of Bαβ (i.e., (−1)α+β times the determinant of the matrix obtained by striking out the αth row and the βth column) and |B| denotes the determinant of B (10).
For the particular case of a three-component system held at constant T and V, the chemical potential μ2(T,c1,c2,c3) depends on all three concentrations, so
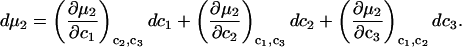 |
(10) |
The constant T subscript is suppressed in Eqs. 10–16 below. When 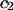 is held constant, then
is held constant, then 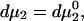 and it follows from Eq. 10 that
and it follows from Eq. 10 that
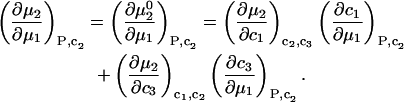 |
(11) |
An equation analogous to Eq. 10 holds for dμ1, from which it follows that
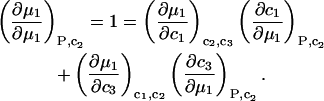 |
(12) |
The change in c1(T,P,c2,c3) at constant T,P,c2 is
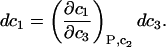 |
(13) |
It is shown in Appendix B that 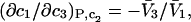 where
where 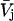 denotes the partial molecular volume (m3/molecule). Then Eq. 13 yields
denotes the partial molecular volume (m3/molecule). Then Eq. 13 yields
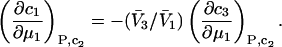 |
(14) |
After substituting Eq. 14 into Eq. 12 and rearranging one finds
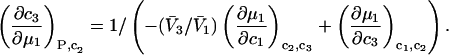 |
(15) |
After substituting Eqs. 14 and 15 into Eq. 11, and Eq. 11 into Eq. 2, there results
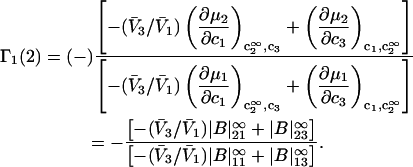 |
(16) |
Equation 9 was used to obtain the second line of Eq. 16 from the first, and the superscript ∞ on the |B|αβ indicates that they are to be evaluated in the limit 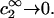 The
The 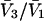 must be evaluated in the same limit.
must be evaluated in the same limit.
The right-hand side of Eq. 16 is partially evaluated by leaving the 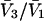 factors in place, but expanding the
factors in place, but expanding the 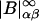 in terms of elements of the three-component B-matrix,
in terms of elements of the three-component B-matrix, 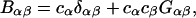 where
where
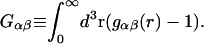 |
(17) |
Every term in both the numerator and denominator of the right-hand side of Eq. 16 contains at least one factor of c2, which can be divided out. Any remaining terms that still contain a factor of c2 will vanish in the limit  and are therefore omitted. After effecting some factorization and cancellation, the result can be expressed as
and are therefore omitted. After effecting some factorization and cancellation, the result can be expressed as
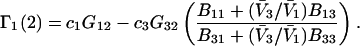 |
(18) |
It remains to evaluate the factor in parentheses on the right-hand side of Eq. 18. An expression for 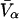 was presented by Kirkwood and Buff (10) without explicit derivation. That derivation is sketched briefly in Appendix C and the result is given in Eq. C6. Note that the denominator of Eq. C6 is independent of α, and cancels out of the ratio,
was presented by Kirkwood and Buff (10) without explicit derivation. That derivation is sketched briefly in Appendix C and the result is given in Eq. C6. Note that the denominator of Eq. C6 is independent of α, and cancels out of the ratio, 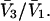 An important simplification is that
An important simplification is that 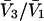 applies in the limit
applies in the limit 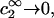 which leaves just a two-component (2 × 2), rather than a three-component (3 × 3) B-matrix, so the indicated cofactors become just elements of the two-component B-matrix. In fact, Eq. C6 gives the simple expressions,
which leaves just a two-component (2 × 2), rather than a three-component (3 × 3) B-matrix, so the indicated cofactors become just elements of the two-component B-matrix. In fact, Eq. C6 gives the simple expressions, 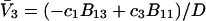 and
and 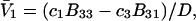 where D is the denominator, which cancels out of
where D is the denominator, which cancels out of 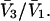 After performing straightforward algebra, invoking the symmetry, Bαβ = Bβα, and omitting any canceling terms, the entire factor in parentheses reduces to c1/c3, and Eq. 18 becomes simply
After performing straightforward algebra, invoking the symmetry, Bαβ = Bβα, and omitting any canceling terms, the entire factor in parentheses reduces to c1/c3, and Eq. 18 becomes simply
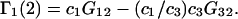 |
(19) |
INTERPRETATION AND DISCUSSION
From the definition of G12 in Eq. 17, it is clear that c1G12 is the excess number of 1-molecules in the vicinity of a 2-molecule beyond what would be expected from a random disposition of 1-molecules. An analogous meaning holds for c3G32. Although the c1G12 and c3G32 in Eq. 19 are explicitly excess numbers, rather than the total numbers of molecules in a domain surrounding the 2-molecule, Eq. 19 for 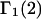 can be written in a form that is completely analogous to Eq. 3 for
can be written in a form that is completely analogous to Eq. 3 for 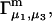 as will be seen.
as will be seen.
The pair correlation functions g12(r) and g32(r) must converge to the value 1.0 at large distances. Typically, for small osmolytes in a solution of dilute macromolecules, this occurs within, at most, a few nanometers beyond the maximum extension of the macromolecule (species 2). Thus, the upper limit of the integral in G12 or G32 can be reduced from ∞ to R, where R is any value sufficiently great that both g12(r) and g32(r) have converged to 1.0. Then Eq. 19 can be written as
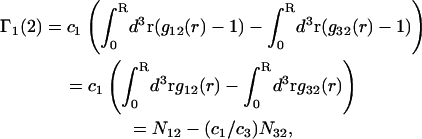 |
(20) |
where 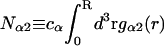 is the number of α-molecules within a sphere of radius R around the 2-molecule. The relevant criterion for the minimum size, Rmin, of the domain surrounding the macromolecule is clearly the convergence of the relevant pair correlation functions to 1.0 at all
is the number of α-molecules within a sphere of radius R around the 2-molecule. The relevant criterion for the minimum size, Rmin, of the domain surrounding the macromolecule is clearly the convergence of the relevant pair correlation functions to 1.0 at all 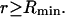 Because standard osmolytes are typically at least a few times larger than water, species 3 is typically excluded by the macromolecule from a larger volume than is species 1. Consequently, g32(r) cannot possibly converge to 1.0 within the volume defined by the centers of 1-molecules in the first hydration shell, and the minimum domain size generally must involve more water molecules than those in the first hydration shell in order for Eq. 20 to be valid.
Because standard osmolytes are typically at least a few times larger than water, species 3 is typically excluded by the macromolecule from a larger volume than is species 1. Consequently, g32(r) cannot possibly converge to 1.0 within the volume defined by the centers of 1-molecules in the first hydration shell, and the minimum domain size generally must involve more water molecules than those in the first hydration shell in order for Eq. 20 to be valid.
Equation 20 is rigorously valid for a finite domain size of radius 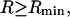 even though no account was taken of the osmotic pressure due to the macromolecule. This is likely a consequence of allowing the domain boundary to move with the macromolecule, so that it can never be contacted by the macromolecule and never experience its contribution to the osmotic pressure inside the macromolecular domain.
even though no account was taken of the osmotic pressure due to the macromolecule. This is likely a consequence of allowing the domain boundary to move with the macromolecule, so that it can never be contacted by the macromolecule and never experience its contribution to the osmotic pressure inside the macromolecular domain.
The preferential interaction coefficient can also be written in the simple form
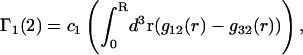 |
(21) |
which is most useful for our analysis. Corresponding expressions for  can also be obtained simply by replacing the index 1 by 3 and vice versa in Eqs. 2 and 3 and 19–21, which is permitted by the evident symmetry of the theory in regard to 1 ↔ 3 interchange. It follows from Eqs. 19–21 that
can also be obtained simply by replacing the index 1 by 3 and vice versa in Eqs. 2 and 3 and 19–21, which is permitted by the evident symmetry of the theory in regard to 1 ↔ 3 interchange. It follows from Eqs. 19–21 that
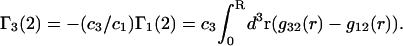 |
(22) |
The right-hand side of Eq. 22 is just 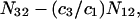 which matches the right-hand side of Eq. 3. Furthermore, it is shown by thermodynamic arguments in Appendix E that in the limit,
which matches the right-hand side of Eq. 3. Furthermore, it is shown by thermodynamic arguments in Appendix E that in the limit, 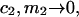
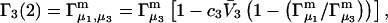 |
(23) |
where 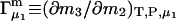 (c.f. Eqs. E16 and E19). The relations in Eq. 23 were obtained by assuming that
(c.f. Eqs. E16 and E19). The relations in Eq. 23 were obtained by assuming that 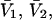 and
and 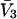 remain constant, independent of
remain constant, independent of 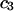 and
and 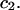 This should be a rather good approximation, when
This should be a rather good approximation, when 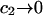 and
and 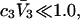 which correspond to prevailing conditions in many studies.
which correspond to prevailing conditions in many studies. 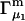 is obtained via vapor pressure osmometry, and
is obtained via vapor pressure osmometry, and 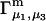 is measured by equilibrium dialysis. At typically low osmolyte volume fractions
is measured by equilibrium dialysis. At typically low osmolyte volume fractions 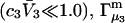 is quite close to
is quite close to 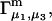 but
but 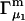 is rather different (5,19,20). In any case, most experimental work has reported
is rather different (5,19,20). In any case, most experimental work has reported 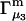 or
or 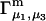 or both. Equation 23 thus provides the principal connections between these theoretical expressions for
or both. Equation 23 thus provides the principal connections between these theoretical expressions for 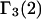 (or
(or 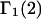 ) in terms of pair correlation functions and the experimentally measured quantities.
) in terms of pair correlation functions and the experimentally measured quantities.
We note that this 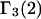 cannot be simply expressed as
cannot be simply expressed as 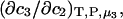 because there is no Maxwell relation equating
because there is no Maxwell relation equating 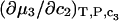 to
to 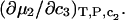 Moreover,
Moreover, 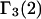 is also not equivalent to
is also not equivalent to 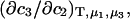 because direct evaluation of the latter in terms of
because direct evaluation of the latter in terms of 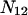 and
and 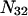 (9) yielded a result that is not equivalent to the right-hand side of Eq. 22.
(9) yielded a result that is not equivalent to the right-hand side of Eq. 22.
Radial distribution functions of multicomponent systems have not yet been treated rigorously and analytically, and no suitable approximate formulation in terms of basic quantities, such as excluded volumes and exchange constants for specific sites, was presented previously. Heuristic approximate evaluations of various contributions to c1g12(r), c3g32(r), 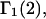 and
and 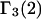 are presented in the following section.
are presented in the following section.
HEURISTIC EVALUATION OF Γ1(2) AND Γ3(2)
In general, both repulsive exclusion forces and attractive binding forces contribute simultaneously to 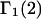 and
and 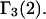 These contributions are evaluated approximately below. Comparisons with the models adopted by other workers will be discussed after this model is developed.
These contributions are evaluated approximately below. Comparisons with the models adopted by other workers will be discussed after this model is developed.
Repulsive exclusion forces
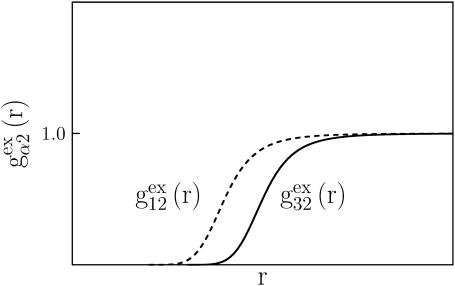
To simplify the discussion, let us first consider the effects of repulsive hard-core exclusion forces between the water (species 1) and the macromolecule (species 2). The superscript “ex” is used to indicate a contribution arising from such forces. A substantial void region, where  is expected around r = 0, as illustrated in Fig. 1. If both species 1 and 2 were perfectly spherical, then this void region would be followed at larger r by the region of the first coordination shell, where
is expected around r = 0, as illustrated in Fig. 1. If both species 1 and 2 were perfectly spherical, then this void region would be followed at larger r by the region of the first coordination shell, where 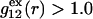 (11,17,28). This is true even in the case of hard spheres with no attractive interactions whatsoever. The first coordination shell would then be followed by a dip of g12(r) below 1.0, which in turn would be followed by a weaker second coordination shell, a second shallower dip, and so on, finally leveling off to g12(r) = 1.0. In the case of a nonspherical macromolecule, the dips and peaks associated with the void volumes and coordination shells arising from different parts of the surface are superposed with a distribution of relative “phases”, so that
(11,17,28). This is true even in the case of hard spheres with no attractive interactions whatsoever. The first coordination shell would then be followed by a dip of g12(r) below 1.0, which in turn would be followed by a weaker second coordination shell, a second shallower dip, and so on, finally leveling off to g12(r) = 1.0. In the case of a nonspherical macromolecule, the dips and peaks associated with the void volumes and coordination shells arising from different parts of the surface are superposed with a distribution of relative “phases”, so that 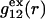 likely exhibits simply a more or less smooth rise to a plateau at 1.0, as indicated in Fig. 1. Because typical neutral osmolytes (species 3) are larger than water, the void regions of
likely exhibits simply a more or less smooth rise to a plateau at 1.0, as indicated in Fig. 1. Because typical neutral osmolytes (species 3) are larger than water, the void regions of 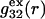 would extend outward somewhat farther than in the case of
would extend outward somewhat farther than in the case of 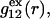 as indicated also in Fig. 1. The volumes excluded to the centers of species 3 and 1 can be expressed as
as indicated also in Fig. 1. The volumes excluded to the centers of species 3 and 1 can be expressed as 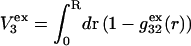 and
and 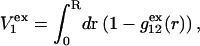 respectively. The difference between the volumes accessible to the centers of species 1 and 3 within the macromolecular domain is defined by,
respectively. The difference between the volumes accessible to the centers of species 1 and 3 within the macromolecular domain is defined by, 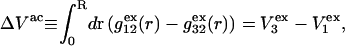 which is also the difference between the volumes excluded to species 3 and 1.
which is also the difference between the volumes excluded to species 3 and 1.
FIGURE 1.
Schematic illustration of 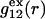 and
and 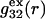 versus the distance r between the central atoms of species 2 and either 1 or 3, respectively. The
versus the distance r between the central atoms of species 2 and either 1 or 3, respectively. The 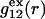 and
and 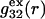 are those parts of the pair correlation functions that arise solely from repulsive exclusion forces between species 2 and either 1 or 3, respectively.
are those parts of the pair correlation functions that arise solely from repulsive exclusion forces between species 2 and either 1 or 3, respectively.
The 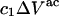 contribution to
contribution to 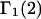 can be understood heuristically in terms of the osmotic pressure-volume work required to introduce a 2-molecule into the solution. The 2-molecule must effectively extrude the centers of the osmolytes (species 3) from a region occupied by the centers of the waters (species 1), which requires the input of work equal to
can be understood heuristically in terms of the osmotic pressure-volume work required to introduce a 2-molecule into the solution. The 2-molecule must effectively extrude the centers of the osmolytes (species 3) from a region occupied by the centers of the waters (species 1), which requires the input of work equal to 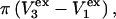 where π is the osmotic pressure of species 1 in the bulk solution. This work appears as a term in
where π is the osmotic pressure of species 1 in the bulk solution. This work appears as a term in 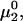 which is the increase in solution free energy upon adding a 2-molecule to the solution. The variation of the osmotic pressure of species 1 with its activity is given by
which is the increase in solution free energy upon adding a 2-molecule to the solution. The variation of the osmotic pressure of species 1 with its activity is given by 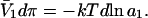 Thus, the osmotic work contribution to
Thus, the osmotic work contribution to 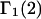 is
is 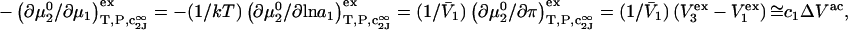 when
when 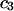 is sufficiently dilute that
is sufficiently dilute that 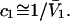 This simple analysis breaks down, when
This simple analysis breaks down, when 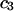 becomes comparable to
becomes comparable to 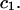
In the void regions, where 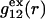 and
and 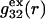 vanish,
vanish, 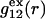 and
and 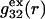 are practically independent of either
are practically independent of either 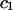 or
or 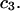 The contribution of repulsive exclusion forces to
The contribution of repulsive exclusion forces to 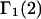 is obtained from Eq. 21 as
is obtained from Eq. 21 as
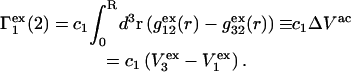 |
(24) |
Any variation of 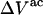 with c1 or c3 should be rather slight, due to the constancy of the void volumes, so
with c1 or c3 should be rather slight, due to the constancy of the void volumes, so 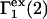 should remain nearly constant, so long as
should remain nearly constant, so long as 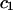 doesn't change much from the value,
doesn't change much from the value, 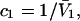 which will be the case, provided that
which will be the case, provided that 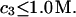 Due to the generally larger void volume of g32(r) in comparison to g12(r), both
Due to the generally larger void volume of g32(r) in comparison to g12(r), both 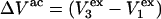 and
and 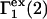 should be generally positive. In view of Eqs. 22 and 24, it is also expected that
should be generally positive. In view of Eqs. 22 and 24, it is also expected that
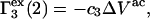 |
(25) |
where 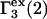 denotes the contribution of purely repulsive exclusion forces. Hence,
denotes the contribution of purely repulsive exclusion forces. Hence, 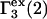 is expected to be proportional to c3 and negative.
is expected to be proportional to c3 and negative.
Generic long-range attractive forces
Let us now consider generic attractive forces, long-range van der Waals forces in particular, that may affect the densities of (centers of) species 1 and 3 in the region immediately beyond the void volume. Such mean densities are denoted by 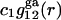 and
and 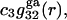 where the superscript “ga” denotes generic attractions. For simplicity it will be assumed here that such generic attractions do not discriminate significantly between species 1 or 3, so that the ratio of their densities at any r beyond the void volume matches that of the bulk solution, that is
where the superscript “ga” denotes generic attractions. For simplicity it will be assumed here that such generic attractions do not discriminate significantly between species 1 or 3, so that the ratio of their densities at any r beyond the void volume matches that of the bulk solution, that is 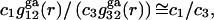 which implies that
which implies that 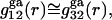 even though both may differ significantly from 1.0. In that case, the net contributions to
even though both may differ significantly from 1.0. In that case, the net contributions to 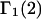 and
and 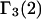 reckoned from Eqs. 21 and 22, respectively, are
reckoned from Eqs. 21 and 22, respectively, are 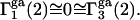 Thus, generic, but nondiscriminating, attractions may alter the local densities of species 1 and 3, but make no net contribution to the preferential interaction coefficients. Nonvanishing contributions of attractive interactions presumably arise from discriminatory exchange reactions, as indicated in the following section.
Thus, generic, but nondiscriminating, attractions may alter the local densities of species 1 and 3, but make no net contribution to the preferential interaction coefficients. Nonvanishing contributions of attractive interactions presumably arise from discriminatory exchange reactions, as indicated in the following section.
Osmolyte-water exchange reactions
Schellman (21–26) introduced the notion that the relevant reactions in solution were exchange reactions at sites or regions near the surface of the macromolecule (species 2). The objective here is to incorporate such exchanges within this formulation of the preferential interaction coefficients in terms of integrals over particular pair correlation functions.
Let us consider first the jth site, which may contain either a single osmolyte (species 3) or  water molecules (species 1). For osmolytes that do not bear charged groups, it is expected that
water molecules (species 1). For osmolytes that do not bear charged groups, it is expected that 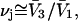 but that assumption need not be invoked at this point. The exchange reaction for this site is written as
but that assumption need not be invoked at this point. The exchange reaction for this site is written as
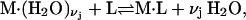 |
(26) |
where  denotes a complex with
denotes a complex with  bound waters on average in the jth site and M·L denotes a complex with a single bound osmolyte at the jth site. It is not required that
bound waters on average in the jth site and M·L denotes a complex with a single bound osmolyte at the jth site. It is not required that 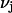 be an integer. When the macromolecule M (species 2) is sufficiently dilute, the equilibrium constant for Eq. 26 is
be an integer. When the macromolecule M (species 2) is sufficiently dilute, the equilibrium constant for Eq. 26 is
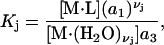 |
(27) |
where a1 = aw is the water activity for the mol fraction 1.0 standard state and 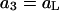 is the osmolyte activity for its hypothetical Henry's Law mol fraction 1.0 standard state, wherein each osmolyte experiences only the environment of its infinitely dilute solution (in water). The fraction of occupied (by osmolyte) j-sites is
is the osmolyte activity for its hypothetical Henry's Law mol fraction 1.0 standard state, wherein each osmolyte experiences only the environment of its infinitely dilute solution (in water). The fraction of occupied (by osmolyte) j-sites is
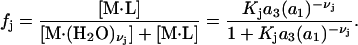 |
(28) |
The instantaneous density of the central atom of a 3-molecule in the jth site for any fixed configuration of the 2-molecule is a three-dimensional δ-function, δ(r − rj), where rj is the variable position of the central atom of the 3-molecule in the jth site in a coordinate frame originating on the central atom of the 2-molecule. When this density is averaged (with appropriate statistical weights) over the rj for all allowed positions and configurations of the 3-molecule in the site and over all configurations of the 2-molecule, and that result is in turn rotationally averaged about the chosen central atom of the 2-molecule, there results a distributed or smeared density function, 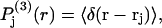 which depends only on the distance r from that central atom and should be peaked near the average distance
which depends only on the distance r from that central atom and should be peaked near the average distance 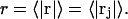 The preceding averages are taken only over those configurations, wherein rj lies within the somewhat arbitrarily defined boundaries of the jth exchange site for each configuration of species 2. This density function is still normalized, so
The preceding averages are taken only over those configurations, wherein rj lies within the somewhat arbitrarily defined boundaries of the jth exchange site for each configuration of species 2. This density function is still normalized, so 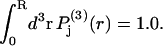
The density function for those 1-molecules that occupy the jth site, when the 3-molecule is absent, is defined in the following way. First the center of a 3-molecule with a fixed configuration is placed at rj in the jth site of a 2-molecule with a fixed configuration. The surrounding solution is assumed to consist entirely of 1-molecules. The density of all the η1 1-molecules in the solution, 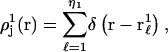 is then averaged over all positions and configurations of those same 1-molecules. The resulting mean density of 1-molecules will practically vanish over an excluded volume,
is then averaged over all positions and configurations of those same 1-molecules. The resulting mean density of 1-molecules will practically vanish over an excluded volume, 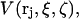 that depends upon the particular rj and fixed configurations ξ and ζ of the 2- and 3-molecules, respectively. The quantities ξ and ζ should be regarded as generalized vectors, or lists, of the coordinates of all the atoms in the 2-molecule and 3-molecule, respectively. Now, the 3-molecule is removed, but the configuration of the 2-molecule is held fixed at ξ. The 1-molecules are allowed to equilibrate with the 2-molecule in that same configuration ξ. The mean density of those 1-molecules, whose centers lie within the particular excluded volume,
that depends upon the particular rj and fixed configurations ξ and ζ of the 2- and 3-molecules, respectively. The quantities ξ and ζ should be regarded as generalized vectors, or lists, of the coordinates of all the atoms in the 2-molecule and 3-molecule, respectively. Now, the 3-molecule is removed, but the configuration of the 2-molecule is held fixed at ξ. The 1-molecules are allowed to equilibrate with the 2-molecule in that same configuration ξ. The mean density of those 1-molecules, whose centers lie within the particular excluded volume, 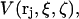 is defined by
is defined by 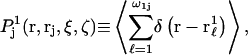 where the sum runs only over the
where the sum runs only over the 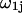 (variable) 1-molecules in each configuration, whose centers at
(variable) 1-molecules in each configuration, whose centers at 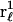 lie within V(rj,ξ,ζ), and the average is taken over all configurations of 1-molecules. This mean density of 1-molecules in V(rj,ξ,ζ) is further averaged over the rj (within the jth site), ξ, and ζ by repeating this initial averaging process for various rj, ξ, and ζ, and then averaging the results over rj, ξ, and ζ. One obtains
lie within V(rj,ξ,ζ), and the average is taken over all configurations of 1-molecules. This mean density of 1-molecules in V(rj,ξ,ζ) is further averaged over the rj (within the jth site), ξ, and ζ by repeating this initial averaging process for various rj, ξ, and ζ, and then averaging the results over rj, ξ, and ζ. One obtains 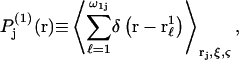 where the subscripts denote the final averages over rj, ξ, and ζ. By definition, the average value of
where the subscripts denote the final averages over rj, ξ, and ζ. By definition, the average value of 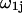 for the jth site is
for the jth site is 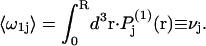 When species 3 has no charged groups, so electrostriction effects are negligible, it is expected that the average number of 1-molecules that occupy an empty exchange site is
When species 3 has no charged groups, so electrostriction effects are negligible, it is expected that the average number of 1-molecules that occupy an empty exchange site is 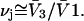 Finally, rotational averaging of
Finally, rotational averaging of 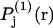 around the central atom of the 2-molecule yields
around the central atom of the 2-molecule yields 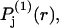 which depends only upon the scalar distance r from the central atom of the 2-molecule. The normalization integral remains unchanged, so
which depends only upon the scalar distance r from the central atom of the 2-molecule. The normalization integral remains unchanged, so 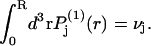 It is expected that the final smeared density,
It is expected that the final smeared density, 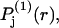 will normally be peaked near
will normally be peaked near 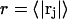 and exhibit a slightly greater width than
and exhibit a slightly greater width than 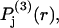 because the centers of multiple 1-molecules are involved.
because the centers of multiple 1-molecules are involved.
In light of the preceding remarks, the contribution of the jth site to the mean density of 1-molecules in the vicinity of the 2-molecule is
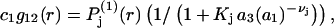 |
(29) |
and to the mean density of 3-molecules is
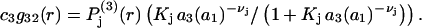 |
(30) |
The fraction of occupied sites, fj, from Eq. 28 appears in Eq. 30 and 1 − fj appears in Eq. 29. The contributions of the exchange reaction at the jth site to the preferential interaction coefficients follow from Eqs. 21 and 22 and the respective normalizations of 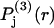 and
and  :
:
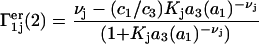 |
(31) |
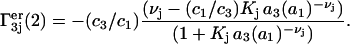 |
(32) |
The total contributions of exchange reactions at all such sites are 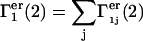 and
and 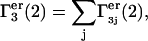 where the sums run over all sites (j), which lie beyond the macromolecular void volume.
where the sums run over all sites (j), which lie beyond the macromolecular void volume.
A model for preferential interactions
Let us now consider a model system that exhibits simultaneously all of the aforementioned repulsive exclusion forces, generic attractions, and discriminatory interactions that are responsible for exchange. For simplicity, we shall assume that the contributions of the various interactions to the total mean densities, c1g12(r) and c3g32(r), are additive. This important assumption is not generally valid and merits some discussion. For any given fixed configuration of species 2, the repulsive hard-core exclusion forces between 2 and either 1 or 3 affect the densities of species 1 and 3 in one region of space, whereas attractions or repulsions of longer range act on 1 and 3 in a different region (outside the hard core, but still inside the macromolecular domain of radius R). Hence, the effects of the short-range and longer-range interactions are largely spatially complementary, and would be expected to be nearly additive, even after configurational and rotational averaging of species 2. Nondiscriminatory generic attractions make no net contribution to 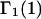 or
or 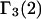 and are not considered further here. In regard to exchange reactions, some interaction between exchanging sites is generally expected. The neglect of such interactions renders this discussion oversimplified in an important regard, whenever
and are not considered further here. In regard to exchange reactions, some interaction between exchanging sites is generally expected. The neglect of such interactions renders this discussion oversimplified in an important regard, whenever 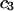 is not small compared to
is not small compared to 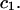 Nevertheless, useful insights may emerge, and quantitatively useful accuracy may be obtained whenever
Nevertheless, useful insights may emerge, and quantitatively useful accuracy may be obtained whenever 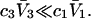
Under this additivity assumption
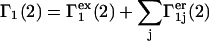 |
(33) |
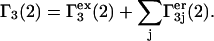 |
(34) |
Equations 24 and 25 give the 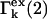 in terms of c1, c3 and
in terms of c1, c3 and 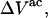 and Eqs. 31 and 32 express the
and Eqs. 31 and 32 express the 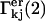 in terms of νj, Kj, a3, and a1.
in terms of νj, Kj, a3, and a1.
To examine the regime of small c3 in more detail, additional approximations are invoked. First, it is assumed that 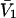 and
and 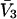 are independent of c3 (which has units of molecules/m3) up to a molar concentration of 1.0. To lowest order in c3, that gives
are independent of c3 (which has units of molecules/m3) up to a molar concentration of 1.0. To lowest order in c3, that gives 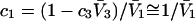 and
and 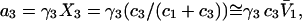 where γ3 is the activity coefficient of species 3. With these approximations, and the exact relation,
where γ3 is the activity coefficient of species 3. With these approximations, and the exact relation, 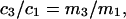 Eqs. 33 and 34 become,
Eqs. 33 and 34 become,
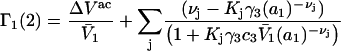 |
(35) |
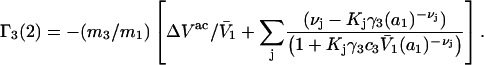 |
(36) |
Generalization of the exchange model
We imagine that a lattice of exchanging sites (or cells) with initial volume 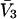 fills the entire osmolyte-accessible region of the macromolecular domain of radius R
fills the entire osmolyte-accessible region of the macromolecular domain of radius R 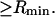 An osmolyte is regarded as bound to a particular site, when its central atom lies within that cell. The initial cell volume is taken as
An osmolyte is regarded as bound to a particular site, when its central atom lies within that cell. The initial cell volume is taken as 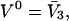 so the cell size matches the partial molecular volume of the osmolyte. Thus, if all of the initial sites were filled, species 3 would just fill the entire volume. The average number of 1-molecules that occupy a cell, when the osmolyte is absent, is assumed to be
so the cell size matches the partial molecular volume of the osmolyte. Thus, if all of the initial sites were filled, species 3 would just fill the entire volume. The average number of 1-molecules that occupy a cell, when the osmolyte is absent, is assumed to be 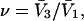 which is exact far from the macromolecular surface, and is almost certainly a fairly good approximation even near the macromolecular surface, except when electrostriction effects are large. Thus, the species 1 would just fill the lattice volume in the absence of species 3. While holding the overall lattice volume constant, one could now choose a smaller uniform cell size for the lattice of exchange sites, namely
which is exact far from the macromolecular surface, and is almost certainly a fairly good approximation even near the macromolecular surface, except when electrostriction effects are large. Thus, the species 1 would just fill the lattice volume in the absence of species 3. While holding the overall lattice volume constant, one could now choose a smaller uniform cell size for the lattice of exchange sites, namely 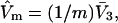 where
where 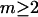 is an integer, provided that the contributions of each site to
is an integer, provided that the contributions of each site to 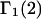 are reduced by the same factor,
are reduced by the same factor, 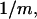 and that the j-sums in Eqs. 35 and 36 are extended from the original L sites of volume
and that the j-sums in Eqs. 35 and 36 are extended from the original L sites of volume 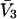 to the mL smaller sites of volume
to the mL smaller sites of volume 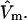 For some sufficiently large value of m, when
For some sufficiently large value of m, when 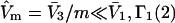 should become entirely independent of m or
should become entirely independent of m or 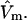 A lattice cell size in that range is adopted here. The center of the jth cell is taken at position q(j), and its exchange constant, Kq(j), may vary from one cell to the next in a limited way, so as to create a gradient of the Kq(j) along any reasonably smooth path in the discrete q(j) space. Both
A lattice cell size in that range is adopted here. The center of the jth cell is taken at position q(j), and its exchange constant, Kq(j), may vary from one cell to the next in a limited way, so as to create a gradient of the Kq(j) along any reasonably smooth path in the discrete q(j) space. Both 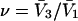 and the exchange constant, Kq(j), for each smaller cell of volume,
and the exchange constant, Kq(j), for each smaller cell of volume, 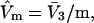 are taken as the values typical of a site with the initial volume,
are taken as the values typical of a site with the initial volume, 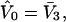 whose center lies within that smaller cell, with the understanding that m − 1 adjacent sites are closed, whenever an osmolyte binds to the smaller cell in question. In this way, any region of volume
whose center lies within that smaller cell, with the understanding that m − 1 adjacent sites are closed, whenever an osmolyte binds to the smaller cell in question. In this way, any region of volume 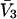 will bind one and only one osmolyte in approximately the same way as a function of a3 or a1, regardless of the number of cells into which is it subdivided, and the maximum densities of species 1 and 3 will remain unchanged. The smaller lattice cell volumes are employed simply to represent the spatial variation of the exchange constants at higher resolution than is afforded by cells of volume
will bind one and only one osmolyte in approximately the same way as a function of a3 or a1, regardless of the number of cells into which is it subdivided, and the maximum densities of species 1 and 3 will remain unchanged. The smaller lattice cell volumes are employed simply to represent the spatial variation of the exchange constants at higher resolution than is afforded by cells of volume 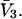 By suitable adjustment of the Kj associated with the various sites in the lattice, it is possible to create any conceivable mean densities c1g12(r) and c3g32(r) at a level of resolution set by the lattice cell size, subject to the implicit volume conservation rule invoked here (i.e.,
By suitable adjustment of the Kj associated with the various sites in the lattice, it is possible to create any conceivable mean densities c1g12(r) and c3g32(r) at a level of resolution set by the lattice cell size, subject to the implicit volume conservation rule invoked here (i.e., 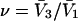 ). The approximate validity of this model is limited to the regime of small volume fraction of species 3, so that events in any one region of volume
). The approximate validity of this model is limited to the regime of small volume fraction of species 3, so that events in any one region of volume 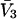 do not affect events in neighboring regions of the same size. The large anticooperativity associated with the closure of m − 1 binding sites surrounding a given site, when it becomes occupied, generally has a very strong influence on the system, except when the volume fraction of species 3 is small. In that special case, for a cell volume
do not affect events in neighboring regions of the same size. The large anticooperativity associated with the closure of m − 1 binding sites surrounding a given site, when it becomes occupied, generally has a very strong influence on the system, except when the volume fraction of species 3 is small. In that special case, for a cell volume 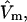 Eqs. 35 and 36 become
Eqs. 35 and 36 become
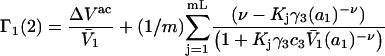 |
(37) |
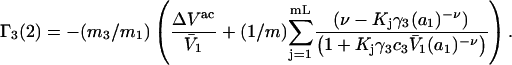 |
(38) |
Neutral binding
When the standard free energy change for an exchange reaction vanishes, Kj = 1.0. First, let us consider the limit of small c3, where, γ3 → 1.0 and 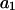 → 1.0, so the numerator of each term in the j-sums of Eqs. 37 and 38 becomes
→ 1.0, so the numerator of each term in the j-sums of Eqs. 37 and 38 becomes 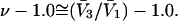 For typical small neutral osmolytes, excluding molecules the size of trehalose and sucrose, one expects that
For typical small neutral osmolytes, excluding molecules the size of trehalose and sucrose, one expects that 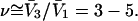 Note that, if
Note that, if 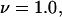 as was assumed in early treatments of exchange by Schellman (21–26), then
as was assumed in early treatments of exchange by Schellman (21–26), then 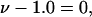 and the entire exchange contribution of the jth site would vanish. Although the condition, Kj = 1.0, is the point of neutrality in terms of vanishing standard state free energy change, it is not generally the point of neutrality in regard to purely random binding in the neighborhood of a 2-molecule, because ν 1-molecules are released for every 3-molecule bound. The point of neutrality in regard to random binding of 1- and 3-molecules at the jth site, when γ3 = 1.0 and
and the entire exchange contribution of the jth site would vanish. Although the condition, Kj = 1.0, is the point of neutrality in terms of vanishing standard state free energy change, it is not generally the point of neutrality in regard to purely random binding in the neighborhood of a 2-molecule, because ν 1-molecules are released for every 3-molecule bound. The point of neutrality in regard to random binding of 1- and 3-molecules at the jth site, when γ3 = 1.0 and 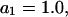 is clearly Kj = ν.
is clearly Kj = ν.
In general, sites that lie out in the bulk solution sufficiently far from the surface of the 2-molecule can make no net contribution to 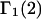 or
or 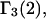 so for such sites it is absolutely required that
so for such sites it is absolutely required that 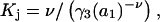 which can be taken as the general condition for neutrality of any site in regard to random binding of 1's and 3's. Smaller values of Kj yield a positive contribution of the jth site to
which can be taken as the general condition for neutrality of any site in regard to random binding of 1's and 3's. Smaller values of Kj yield a positive contribution of the jth site to 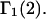
We consider next the limit, wherein 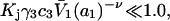 so the second terms in the denominators of Eqs. 37 and 38 can be ignored. The product,
so the second terms in the denominators of Eqs. 37 and 38 can be ignored. The product, 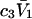 is unitless, and has the same value in any units, so one can take c3 in mol/L and
is unitless, and has the same value in any units, so one can take c3 in mol/L and 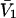 in L/mol. For small neutral osmolytes, one typically has
in L/mol. For small neutral osmolytes, one typically has 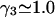 and
and 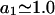 up to c3 = 1.0 M. Thus, for
up to c3 = 1.0 M. Thus, for 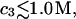 the inequality,
the inequality, 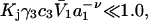 will be satisfied, when
will be satisfied, when 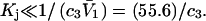 Hence, Kj could be as large as 10, and still satisfy this inequality for c3 = 1.0 M. In other words, K could be up to 2–3 times greater than the neutral random binding value,
Hence, Kj could be as large as 10, and still satisfy this inequality for c3 = 1.0 M. In other words, K could be up to 2–3 times greater than the neutral random binding value, 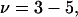 and still the second terms in the denominators of Eqs. 37 and 38 would be negligibly small for all c3 up to 1.0 M. In this limit, Eqs. 37 and 38 can be written as
and still the second terms in the denominators of Eqs. 37 and 38 would be negligibly small for all c3 up to 1.0 M. In this limit, Eqs. 37 and 38 can be written as
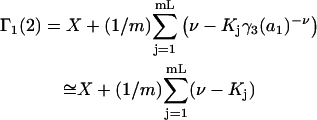 |
(39) |
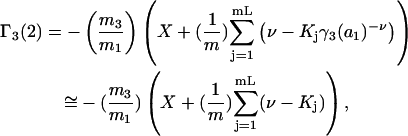 |
(40) |
where 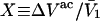 is the difference between the volumes accessible to 1 and 3 in units of
is the difference between the volumes accessible to 1 and 3 in units of 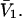 As noted above,
As noted above, 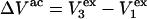 is generally positive, because the osmolyte generally exceeds the water in size, so X should also be generally positive. The j-sum (of binding terms) can in principle take either sign, depending upon the magnitude of Kj.
is generally positive, because the osmolyte generally exceeds the water in size, so X should also be generally positive. The j-sum (of binding terms) can in principle take either sign, depending upon the magnitude of Kj.
Variation of Γ1(2) and Γ3(2) with c3
Equations 39 and 40 predict that 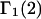 should be nearly constant independent of c3, and that
should be nearly constant independent of c3, and that 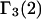 should vary nearly in proportion to
should vary nearly in proportion to 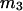 with constant slope, up to c3 = 1.0 M. In fact, for seven different osmolytes interacting with BSA, it was found that
with constant slope, up to c3 = 1.0 M. In fact, for seven different osmolytes interacting with BSA, it was found that 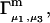 hence also
hence also 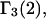 varied in proportion to m3 with a constant negative slope up to m3 = 1.0 molal (5,29,30; J. G. Cannon, personal communication, 2005). The negative slope implies that the total j-sum is either positive or not so negative that it overwhelms the positive value of X. The constant slope indicates that the second terms in the denominators of Eqs. 37 and 38 are negligible up to m3 = 1.0 m, which in turn implies that (in the case of BSA) most of the contribution from the j-sum must arise from sites with Kj-values that do not exceed by more than approximately threefold the random binding value,
varied in proportion to m3 with a constant negative slope up to m3 = 1.0 molal (5,29,30; J. G. Cannon, personal communication, 2005). The negative slope implies that the total j-sum is either positive or not so negative that it overwhelms the positive value of X. The constant slope indicates that the second terms in the denominators of Eqs. 37 and 38 are negligible up to m3 = 1.0 m, which in turn implies that (in the case of BSA) most of the contribution from the j-sum must arise from sites with Kj-values that do not exceed by more than approximately threefold the random binding value, 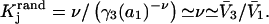
Because X derives from a shell volume with a thickness equal to the difference in radius between the osmolyte and water, it is expected to vary nearly in proportion to the area in the case of macromolecules with homologous surfaces. Likewise, the j-sum concerns primarily just the contact layer and a few additional layers of osmolyte or water, so that it too is expected to vary nearly in proportion to the area in the case of macromolecules with homologous surfaces. Courtenay et al. (6) noted that numerous globular proteins exhibit similar values of the ratio, 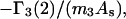 where
where 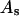 is the water accessible area.
is the water accessible area.
Analysis of Γ1(2)-values for BSA
Experimental values of 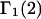 for different osmolytes interacting with BSA are obtained from the corresponding
for different osmolytes interacting with BSA are obtained from the corresponding 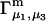 determined by the Record group (5,29,30; and J. G. Cannon, personal communication, 2005) via the relations Eqs. 22, 23, and 40, which are combined to give
determined by the Record group (5,29,30; and J. G. Cannon, personal communication, 2005) via the relations Eqs. 22, 23, and 40, which are combined to give
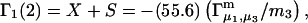 |
(41) |
where 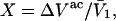 and
and 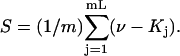 By combining the measured value of
By combining the measured value of 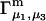 with an estimate of X obtained from the protein structure, it is possible to obtain an experimental estimate of S.
with an estimate of X obtained from the protein structure, it is possible to obtain an experimental estimate of S.
Although no crystal structure has been reported for BSA, it is assumed to be satisfactorily modeled by human serum albumin. BSA has 607 amino acid residues and HSA has 609, which are 76% homologous with the BSA sequence. Only 578 of the 609 residues of HSA are resolved in the crystal structure (31). Here the molecular volume reckoned for the crystal structure is simply scaled by 609/578 = 1.054 to estimate the corresponding volume for the full HSA (or BSA). However, the 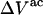 reckoned for the crystal structure corresponds to the volume of a relatively thin shell of a given thickness about the macromolecule, so it is scaled by the factor
reckoned for the crystal structure corresponds to the volume of a relatively thin shell of a given thickness about the macromolecule, so it is scaled by the factor 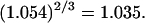 The osmolyte and water accessible areas are also scaled by 1.035 to estimate the corresponding areas for HSA (or BSA). The various volumes and areas are reckoned using the program MSROLL (32). The crystal structure contains an HSA dimer and seven water molecules. The nonhydrogen atoms of both the water molecules and the second dimer and their coordinates are deleted from the list of atomic coordinates, leaving just the atoms and coordinates of the 578 resolved residues of the first monomer. The program assigns a van der Waals radius to each atom or group of HSA. An effective radius,
The osmolyte and water accessible areas are also scaled by 1.035 to estimate the corresponding areas for HSA (or BSA). The various volumes and areas are reckoned using the program MSROLL (32). The crystal structure contains an HSA dimer and seven water molecules. The nonhydrogen atoms of both the water molecules and the second dimer and their coordinates are deleted from the list of atomic coordinates, leaving just the atoms and coordinates of the 578 resolved residues of the first monomer. The program assigns a van der Waals radius to each atom or group of HSA. An effective radius, 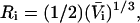 is assigned to water (i = 1) and to each osmolyte (i = 3).
is assigned to water (i = 1) and to each osmolyte (i = 3).
The molecular displacement volume (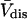 ) of HSA in water is determined by rolling a water-size sphere of radius
) of HSA in water is determined by rolling a water-size sphere of radius  Å around its exterior van der Waals surface in each of a series of closely spaced parallel planes. The program reckons the volume inside the continuous surface formed by the contact surface(s) of the sphere with the van der Waals surface of the protein plus the so-called reentrant surface(s) that bridge the gaps in the contact surface by following the interior surface of the bridging sphere. We obtain
Å around its exterior van der Waals surface in each of a series of closely spaced parallel planes. The program reckons the volume inside the continuous surface formed by the contact surface(s) of the sphere with the van der Waals surface of the protein plus the so-called reentrant surface(s) that bridge the gaps in the contact surface by following the interior surface of the bridging sphere. We obtain 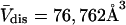 for HSA, which is then scaled by 1.054 to estimate
for HSA, which is then scaled by 1.054 to estimate 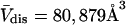 for BSA. This molecular displacement volume cannot be occupied by any part of the 1.48 Å sphere, and for numerous globular proteins is found to lie within 1–2% of the partial molecular volume
for BSA. This molecular displacement volume cannot be occupied by any part of the 1.48 Å sphere, and for numerous globular proteins is found to lie within 1–2% of the partial molecular volume 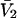 (S. Aragon, unpublished data). Courtenay et al. (5) report
(S. Aragon, unpublished data). Courtenay et al. (5) report 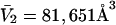 for BSA, which differs by ∼1% from the
for BSA, which differs by ∼1% from the 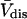 calculated above. This agreement provides an important check on the structure and computational protocols used, but does not pertain directly to the preferential interaction coefficients.
calculated above. This agreement provides an important check on the structure and computational protocols used, but does not pertain directly to the preferential interaction coefficients.
Next we obtain the volumes excluded by HSA to the centers of water-size or osmolyte-size spheres. This is the volume inside a surface that is traced out by the center of the osmolyte sphere or water sphere, as it rolls over the surface of the protein, and represents the void volume in 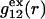 or
or 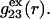 Although MSROLL does not calculate the volume inside the excluded-center surface directly, that volume can be reckoned by first inflating the atomic van der Waals radii by
Although MSROLL does not calculate the volume inside the excluded-center surface directly, that volume can be reckoned by first inflating the atomic van der Waals radii by 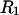 or
or 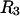 and using a probe sphere of zero radius. The resulting contact plus (vanishing) reentrant surface is the same surface traced out by the center of a sphere of radius
and using a probe sphere of zero radius. The resulting contact plus (vanishing) reentrant surface is the same surface traced out by the center of a sphere of radius 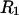 or
or 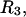 as it rolls over the uninflated van der Waals surface, and its interior volume is calculated by the program. The difference between the volume excluded to an osmolyte and that excluded to a water center is just
as it rolls over the uninflated van der Waals surface, and its interior volume is calculated by the program. The difference between the volume excluded to an osmolyte and that excluded to a water center is just 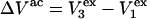 for that osmolyte, as illustrated in Fig. 2. After scaling
for that osmolyte, as illustrated in Fig. 2. After scaling 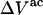 by 1.035, it is divided by the molecular volume of water,
by 1.035, it is divided by the molecular volume of water, 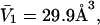 to obtain
to obtain 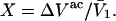 Then the exchange contribution,
Then the exchange contribution, 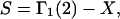 is finally evaluated. The results for X and S are presented for seven different osmolytes interacting with BSA in Table 1. In every case, X exceeds the magnitude of S. Thus, in the case of BSA, the largest contribution to
is finally evaluated. The results for X and S are presented for seven different osmolytes interacting with BSA in Table 1. In every case, X exceeds the magnitude of S. Thus, in the case of BSA, the largest contribution to 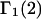 is simply a geometrical consequence of the fact that the osmolytes are substantially larger than water and therefore have a larger effective sphere radius. Four of the osmolytes, urea, glycerol, proline, and trehalose, exhibit a negative value of S, which indicates that
is simply a geometrical consequence of the fact that the osmolytes are substantially larger than water and therefore have a larger effective sphere radius. Four of the osmolytes, urea, glycerol, proline, and trehalose, exhibit a negative value of S, which indicates that 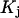 is on average greater than its neutral value,
is on average greater than its neutral value, 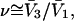 and implies a greater than random preference of the osmolyte for exchanging sites within the macromolecular domain. The remaining three osmolytes, trimethylamine N-oxide (TMAO), K+glutamate, and betaine glycine, exhibit a positive value of S, which indicates that
and implies a greater than random preference of the osmolyte for exchanging sites within the macromolecular domain. The remaining three osmolytes, trimethylamine N-oxide (TMAO), K+glutamate, and betaine glycine, exhibit a positive value of S, which indicates that 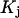 is on average less than its neutral value, and implies a lower than random preference of these osmolytes for the exchanging sites.
is on average less than its neutral value, and implies a lower than random preference of these osmolytes for the exchanging sites.
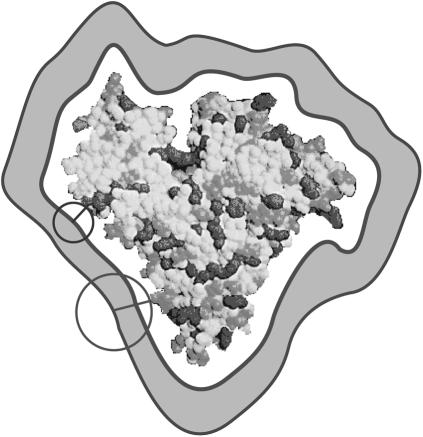
FIGURE 2.
Schematic illustration (not to scale) of the difference between the volume excluded to osmolyte (large sphere) and to water (small sphere) by human serum albumin. The desired volume is that of the shaded shell between the surfaces traced out by the center of an osmolyte-size sphere and that traced out by a water-size sphere, as those spheres are rolled over the surface of the protein. The sizes of the water and osmolyte relative to that of BSA are exaggerated for illustrative purposes.
TABLE 1.
Excluded volume (X) and exchange reaction (S) contributions to 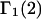 and
and 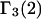 for osmolytes interacting with BSA
for osmolytes interacting with BSA
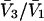 † †
|
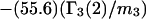 * *
|
X* | S | 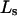 |
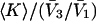 |
|
|---|---|---|---|---|---|---|
| Urea | 2.45 | 217 | 560 | −343 | 1364 | 1.10 |
| Glycerol | 3.92 | 250 | 777 | −527 | 932 | 1.15 |
| TMAO | 4.01 | 1389 | 888 | +501 | 911 | 0.86 |
| Proline | 4.60 | 778 | 981 | −203 | 820 | 1.05 |
| K+glu− | 5.03 | 1111 | 1048 | +63 | 755 | 0.95 |
| Betaine | 5.43 | 1283 | 1107 | +176 | 712 | 0.96 |
| Trehalose | 11.61 | 1167 | 1762 | −595 | 392 | 1.12 |
The 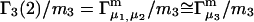 and
and 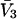 values for the different osmolytes were reported by Courtenay et al. (5), Felitsky et al. (29), Hong et al. (30), and J. Cannon (2005, personal communication). The X-values were reckoned using the MSROLL program with effective osmolyte radii (R): urea (2.09 Å), glycerol (2.45 Å), TMAO (2.47 Å), proline (2.58 Å), K+ glutamate (2.66 Å), betaine glycine (2.73 Å), and trehalose (3.52 Å), as described in the text.
values for the different osmolytes were reported by Courtenay et al. (5), Felitsky et al. (29), Hong et al. (30), and J. Cannon (2005, personal communication). The X-values were reckoned using the MSROLL program with effective osmolyte radii (R): urea (2.09 Å), glycerol (2.45 Å), TMAO (2.47 Å), proline (2.58 Å), K+ glutamate (2.66 Å), betaine glycine (2.73 Å), and trehalose (3.52 Å), as described in the text.
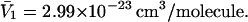
In previous work in this field, it was commonly assumed that 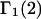 (or
(or 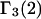 ) is determined primarily by exchange sites within the first surface-contact layer. We now also assume that the exchanging sites are confined to the first surface-contact layer. We take the number (
) is determined primarily by exchange sites within the first surface-contact layer. We now also assume that the exchanging sites are confined to the first surface-contact layer. We take the number (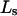 ) of surface-contiguous sites for species 3 to be the accessible area traced out by the center of a sphere of radius
) of surface-contiguous sites for species 3 to be the accessible area traced out by the center of a sphere of radius 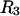 rolled over the van der Waals surface of HSA, scaled by the factor 1.035, and divided by the area,
rolled over the van der Waals surface of HSA, scaled by the factor 1.035, and divided by the area, 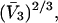 of a single site of volume
of a single site of volume 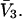 Values of
Values of 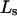 for the different osmolytes are also included in Table 1. For these sites, the cell volume is
for the different osmolytes are also included in Table 1. For these sites, the cell volume is 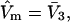 so m = 1.0, and mL = L =
so m = 1.0, and mL = L = 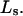 In this case,
In this case, 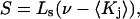 where
where 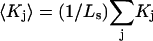 is the average exchange constant for the surface-contiguous sites of species 3. From the values of S,
is the average exchange constant for the surface-contiguous sites of species 3. From the values of S, 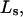 and
and 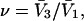 we estimate
we estimate 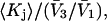 which is the ratio of the average exchange constant to its neutral (or random) value. These values are listed in the final column of Table 1. These
which is the ratio of the average exchange constant to its neutral (or random) value. These values are listed in the final column of Table 1. These 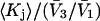 ratios are all remarkably close to 1.0, with a maximum deviation of <∼0.15. By this criterion the average interactions of these osmolytes with the BSA surface are all surprisingly similar.
ratios are all remarkably close to 1.0, with a maximum deviation of <∼0.15. By this criterion the average interactions of these osmolytes with the BSA surface are all surprisingly similar.
Comparisons with prior work
An advantage of this formulation for 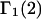 (or
(or 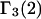 ) in terms of the pair correlation functions (Eqs. 21 and 22) in comparison to the thermodynamic formulation in terms of numbers of molecules in the macromolecular domain (Eq. 3) is that the excluded volume contribution is unambiguously given by
) in terms of the pair correlation functions (Eqs. 21 and 22) in comparison to the thermodynamic formulation in terms of numbers of molecules in the macromolecular domain (Eq. 3) is that the excluded volume contribution is unambiguously given by 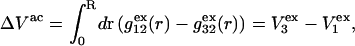 which is the volume of the shell in Fig. 2.
which is the volume of the shell in Fig. 2.
Shimizu (13) and Shimizu and Smith (14) employed a single “excluded” volume, 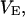 that is independent of the water or osmolyte, and is essentially the macromolecular displacement volume,
that is independent of the water or osmolyte, and is essentially the macromolecular displacement volume,  that is excluded to any part of a water or osmolyte molecule. Those authors approximated the excluded volume contribution to the numbers of water and osmolyte molecules in the macromolecular domain by
that is excluded to any part of a water or osmolyte molecule. Those authors approximated the excluded volume contribution to the numbers of water and osmolyte molecules in the macromolecular domain by 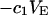 and
and 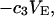 respectively. Their use of the same value,
respectively. Their use of the same value, 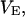 for both
for both 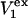 and
and 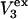 leads to complete cancellation of the excluded volume contribution to
leads to complete cancellation of the excluded volume contribution to 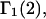 which is incorrect. However, the primary focus of their work was to determine
which is incorrect. However, the primary focus of their work was to determine 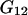 and
and 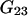 separately, and to interpret the excess quantities,
separately, and to interpret the excess quantities, 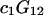 and
and 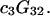 For that purpose, the use of
For that purpose, the use of 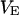 in place of
in place of 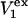 or
or 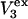 may be a reasonable approximation.
may be a reasonable approximation.
Schellman (18) evaluated the cross-second virial coefficient, 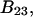 of the osmotic pressure for components 2 and 3 in terms of an integral over the potential of mean force between the osmolyte and macromolecule (averaged over all positions and numbers of the water molecules). The excluded volume contribution to that integral is the volume excluded by the macromolecule to the osmolyte centers, and is reckoned by a protocol identical to that employed here, except that the corresponding excluded volume for the water centers was not subtracted from that for the osmolyte. The exchange reaction of Schellman is the replacement of a single water molecule at a site by a single osmolyte at the same site, and its contribution to
of the osmotic pressure for components 2 and 3 in terms of an integral over the potential of mean force between the osmolyte and macromolecule (averaged over all positions and numbers of the water molecules). The excluded volume contribution to that integral is the volume excluded by the macromolecule to the osmolyte centers, and is reckoned by a protocol identical to that employed here, except that the corresponding excluded volume for the water centers was not subtracted from that for the osmolyte. The exchange reaction of Schellman is the replacement of a single water molecule at a site by a single osmolyte at the same site, and its contribution to 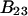 is expressed in terms of the exchange constant,
is expressed in terms of the exchange constant, 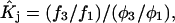 where
where 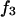 and
and 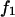 are the fractional occupations of the jth site by osmolyte and water, respectively, and
are the fractional occupations of the jth site by osmolyte and water, respectively, and 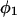 and
and 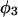 are the volume fractions of osmolyte and water, respectively, in the bulk solution. The exchange reaction contribution was then summed over all sites. The primary objective was to express the change,
are the volume fractions of osmolyte and water, respectively, in the bulk solution. The exchange reaction contribution was then summed over all sites. The primary objective was to express the change, 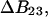 in
in 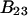 upon unfolding of the protein (species 2) in terms of the change in volume excluded to osmolyte centers and the change in the exchange reaction sum, and to assess their relative magnitudes. It was suggested that
upon unfolding of the protein (species 2) in terms of the change in volume excluded to osmolyte centers and the change in the exchange reaction sum, and to assess their relative magnitudes. It was suggested that 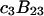 is “the total excess of cosolvent molecules in the neighborhood of the protein. Its identity with the preferential interaction coefficient (in the absence of nonideality) is thus completely explained at the molecular level”. In fact, Schellman's
is “the total excess of cosolvent molecules in the neighborhood of the protein. Its identity with the preferential interaction coefficient (in the absence of nonideality) is thus completely explained at the molecular level”. In fact, Schellman's 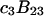 is not identical to the
is not identical to the 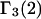 obtained here, or to
obtained here, or to 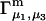 or to
or to 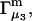 because
because 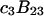 clearly lacks the contribution,
clearly lacks the contribution, 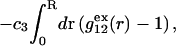 that is explicit in Eqs. 20 and 22. Provided that
that is explicit in Eqs. 20 and 22. Provided that 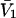 and
and 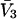 are independent of
are independent of  and
and 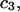 this
this 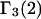 is identical to
is identical to 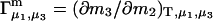 and very close to
and very close to 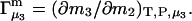 However, Schellman's osmotic pressure calculation is carried out (implicitly) for constant
However, Schellman's osmotic pressure calculation is carried out (implicitly) for constant 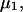 so that
so that 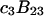 is conceivably identical to
is conceivably identical to 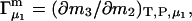 although a rigorous proof of that conjecture is lacking. As noted previously (5,19,20),
although a rigorous proof of that conjecture is lacking. As noted previously (5,19,20), 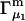 differs considerably from
differs considerably from 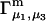 and also from
and also from 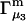 under the usual conditions of moderately low osmolyte concentration. In any case, Schellman's conclusion that urea occupation of the surface-contiguous layer exceeds the random value by modest amounts up to 15% for the five proteins analyzed (ribonuclease T, ribonuclease A, hen egg white lysozyme, staphylococcus nuclease, and T4 lysozyme) is consistent with the corresponding result of this analysis for urea interacting with BSA, where urea occupation exceeds the random value by 10% (c.f. Table 1).
under the usual conditions of moderately low osmolyte concentration. In any case, Schellman's conclusion that urea occupation of the surface-contiguous layer exceeds the random value by modest amounts up to 15% for the five proteins analyzed (ribonuclease T, ribonuclease A, hen egg white lysozyme, staphylococcus nuclease, and T4 lysozyme) is consistent with the corresponding result of this analysis for urea interacting with BSA, where urea occupation exceeds the random value by 10% (c.f. Table 1).
Record and co-workers applied the thermodynamic two-domain model to analyze their preferential interaction coefficients (9). They demonstrated that 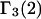 was proportional to
was proportional to 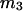 and presented evidence that
and presented evidence that 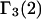 is correlated with the osmolyte accessible surface area (5,29,30). They introduced a local domain-bulk domain partition coefficient, instead of an osmolyte-water exchange constant, and initially proposed that the volume of the local domain was that of the surface-contiguous water molecules (5). Because the centers of the larger osmolytes lie entirely outside such a domain, the osmolyte number within such a local domain is either vanishing or not well defined without additional assumptions, so the local-bulk partition coefficient in such cases is not well defined. In general, the local-bulk partition coefficient depends upon the total volume of the local domain, much as the average exchange constant depends upon the total number of exchange sites of volume
is correlated with the osmolyte accessible surface area (5,29,30). They introduced a local domain-bulk domain partition coefficient, instead of an osmolyte-water exchange constant, and initially proposed that the volume of the local domain was that of the surface-contiguous water molecules (5). Because the centers of the larger osmolytes lie entirely outside such a domain, the osmolyte number within such a local domain is either vanishing or not well defined without additional assumptions, so the local-bulk partition coefficient in such cases is not well defined. In general, the local-bulk partition coefficient depends upon the total volume of the local domain, much as the average exchange constant depends upon the total number of exchange sites of volume 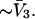 In their studies to date, Record and co-workers have made no attempt to treat the separate contributions of excluded volume on one hand and the exchange reactions, or osmolyte partitioning into the accessible local domain volume, on the other. They have investigated the positive correlation between
In their studies to date, Record and co-workers have made no attempt to treat the separate contributions of excluded volume on one hand and the exchange reactions, or osmolyte partitioning into the accessible local domain volume, on the other. They have investigated the positive correlation between 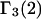 for betaine glycine and the fraction of the accessible macromolecular surface area that is associated with the anionic oxygen atoms of carboxylate or phosphate groups, and have proposed that the local domain includes two layers of more strongly bound water over those parts of the surface (29,30). That phenomenon can be analyzed in greater detail using this formulation and model, but that lies outside the scope of this article.
for betaine glycine and the fraction of the accessible macromolecular surface area that is associated with the anionic oxygen atoms of carboxylate or phosphate groups, and have proposed that the local domain includes two layers of more strongly bound water over those parts of the surface (29,30). That phenomenon can be analyzed in greater detail using this formulation and model, but that lies outside the scope of this article.
Strong water binding/weak osmolyte binding sites
It is conceivable that some macromolecules might exhibit a number of sites, wherein the water is rather more tightly bound and difficult to displace by common osmolytes. For such sites, Kj would lie far below the random binding value, 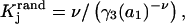 which declines with decreasing a1, up to moderately high values of c3 (or down to correspondingly low values of a1). For such sites, the
which declines with decreasing a1, up to moderately high values of c3 (or down to correspondingly low values of a1). For such sites, the 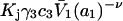 terms in the denominators of the j-sum (in Eqs. 35 and 36) are negligibly small compared to 1.0 up to rather high values of c3 (>1.0 M). Because the
terms in the denominators of the j-sum (in Eqs. 35 and 36) are negligibly small compared to 1.0 up to rather high values of c3 (>1.0 M). Because the 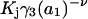 terms in the numerators are also negligibly small compared to their ν-terms, the ν-terms collectively provide the main contribution of such sites to the j-sum. Osmolytes of similar size should exhibit similar ν-values for any given site. Hence, for osmolytes of similar size, a dependence on osmolyte structure can enter the j-sum only through the Kj-terms. However, if those terms are negligibly small compared to ν, as is the case for strong water binding sites, then the contribution of such terms to the j-sum, to
terms in the numerators are also negligibly small compared to their ν-terms, the ν-terms collectively provide the main contribution of such sites to the j-sum. Osmolytes of similar size should exhibit similar ν-values for any given site. Hence, for osmolytes of similar size, a dependence on osmolyte structure can enter the j-sum only through the Kj-terms. However, if those terms are negligibly small compared to ν, as is the case for strong water binding sites, then the contribution of such terms to the j-sum, to 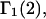 and to
and to 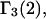 will be negligibly small. Thus, even though the Kj doubtless vary with osmolyte structure for osmolytes of comparable size, that variation will be negligible compared to the
will be negligibly small. Thus, even though the Kj doubtless vary with osmolyte structure for osmolytes of comparable size, that variation will be negligible compared to the 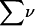 and to the total contributions of the strong water-binding sites to the j-sum, or to
and to the total contributions of the strong water-binding sites to the j-sum, or to 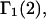 or to
or to 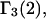 provided that neither c3 is too large, nor a1 too small.
provided that neither c3 is too large, nor a1 too small.
Upon increasing c3, al decreases, 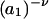 increases, and the
increases, and the 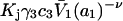 term in the denominator of each term in the j-sum increases toward (and eventually beyond) 1.0. In addition, the
term in the denominator of each term in the j-sum increases toward (and eventually beyond) 1.0. In addition, the 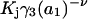 term in the numerator of each term in the j-sum increases toward its ν or beyond. Both effects act to decrease
term in the numerator of each term in the j-sum increases toward its ν or beyond. Both effects act to decrease 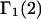 and also to shift the negative slope of
and also to shift the negative slope of 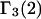 with respect to c3 toward less negative, or more positive, values. Such effects depend upon the Kj, and hence upon the chemical structure of the osmolyte. Thus, the contribution of strong water-binding sites to
with respect to c3 toward less negative, or more positive, values. Such effects depend upon the Kj, and hence upon the chemical structure of the osmolyte. Thus, the contribution of strong water-binding sites to 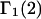 and
and 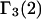 is expected to be independent of osmolyte structure only for osmolytes of comparable size in the regime of strong exclusion of 3-molecules, when c3 is not too large.
is expected to be independent of osmolyte structure only for osmolytes of comparable size in the regime of strong exclusion of 3-molecules, when c3 is not too large.
INTERPRETATION OF ΔΓ1(2) FOR HYDRATION COUPLED REACTIONS
In experimental studies of the effects of osmolytes on equilibrium constants (K) for macromolecular reactions, it is typically found that ln K varies in proportion to ln a1, when c3 is not too large. Thus, 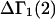 (c.f. Eq. 1) typically remains practically constant over the range of c3 examined. This is in accord with Eqs. 19–21, 35, 37, 39, and 41, when c3 is moderately small.
(c.f. Eq. 1) typically remains practically constant over the range of c3 examined. This is in accord with Eqs. 19–21, 35, 37, 39, and 41, when c3 is moderately small.
For simplicity we consider a conformational change of the macromolecule, 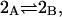 where the subscripts “A” and “B” denote different conformations of species 2. When
where the subscripts “A” and “B” denote different conformations of species 2. When 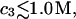 Eqs. 39–41 apply to 2A and 2B separately. We adopt identical space-filling lattices of exchange sites centered at q(j), j = 1,2, … , in the regions surrounding the hard-cores of species 2A and 2B. It is assumed that
Eqs. 39–41 apply to 2A and 2B separately. We adopt identical space-filling lattices of exchange sites centered at q(j), j = 1,2, … , in the regions surrounding the hard-cores of species 2A and 2B. It is assumed that 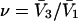 is the same for a given osmolyte in the lattices around both A and B. Then, Eq. 41 gives
is the same for a given osmolyte in the lattices around both A and B. Then, Eq. 41 gives
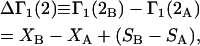 |
(42) |
where 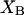 and
and 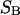 are the excluded volume and exchange reaction contributions for species
are the excluded volume and exchange reaction contributions for species 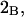 and
and 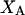 and
and 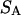 are the corresponding quantities for species
are the corresponding quantities for species 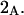 Equation 42 applies only in the small
Equation 42 applies only in the small 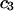 limit, where
limit, where 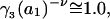 so
so 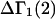 remains nearly constant with increasing
remains nearly constant with increasing 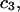 as found experimentally. We now divide the surfaces of both A and B into two regions, namely the “passive” regions that are the same in the B conformation as in the A conformation, and the “active” regions that differ between the two conformers. An active region may consist of surface that is either exposed or buried during the A
as found experimentally. We now divide the surfaces of both A and B into two regions, namely the “passive” regions that are the same in the B conformation as in the A conformation, and the “active” regions that differ between the two conformers. An active region may consist of surface that is either exposed or buried during the A  B transition, so that it is present in one species, but not in the other. It may also contain surface whose topography is reconfigured during the
B transition, so that it is present in one species, but not in the other. It may also contain surface whose topography is reconfigured during the 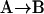 transition, so as to alter the number and/or exchange constants of the exchanging sites associated with that part of the surface. A particular example would be the widening or narrowing of the angle of a cleft during the A
transition, so as to alter the number and/or exchange constants of the exchanging sites associated with that part of the surface. A particular example would be the widening or narrowing of the angle of a cleft during the A  B transition. Under the assumption that the main contributions to
B transition. Under the assumption that the main contributions to 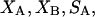 and
and 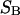 involve only regions of the solution that are reasonably proximal to the surface of A or B, the contribution of the passive parts of the surface to
involve only regions of the solution that are reasonably proximal to the surface of A or B, the contribution of the passive parts of the surface to 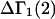 is expected to cancel. Furthermore, the sums over exchanging sites associated with the active parts of the surface can be divided into the terms arising from strong water-binding/weak osmolyte-binding sites, for which
is expected to cancel. Furthermore, the sums over exchanging sites associated with the active parts of the surface can be divided into the terms arising from strong water-binding/weak osmolyte-binding sites, for which 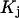 can be neglected in favor of ν, and those terms arising from more neutral water-binding sites. Then,
can be neglected in favor of ν, and those terms arising from more neutral water-binding sites. Then,
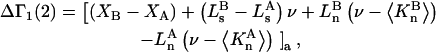 |
(43) |
where the subscript “a” on the square bracket indicates that all quantities therein pertain only to the active parts of the surface, 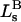 and
and 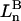 are the numbers of strong (s) and more neutral (n) water-binding sites of volume
are the numbers of strong (s) and more neutral (n) water-binding sites of volume 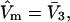 respectively, associated with the active part of the surface of conformer
respectively, associated with the active part of the surface of conformer 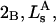 and
and 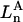 are the corresponding quantities for conformer
are the corresponding quantities for conformer 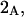 and
and 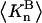 and
and 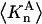 are the average equilibrium constants of the more neutral water-binding sites associated with the active surfaces of
are the average equilibrium constants of the more neutral water-binding sites associated with the active surfaces of 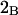 and
and 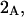 respectively. Weak water-binding/strong osmolyte-binding sites are not considered here, because, if significant, they would cause
respectively. Weak water-binding/strong osmolyte-binding sites are not considered here, because, if significant, they would cause 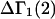 to vary with
to vary with 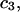 which is not observed. The
which is not observed. The 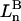 and
and 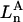 need count only those more neutral sites sufficiently near the surface that
need count only those more neutral sites sufficiently near the surface that 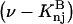 and
and 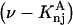 differ significantly from zero.
differ significantly from zero.
When is ΔΓ1(2) independent of the chemical structure of the osmolyte?
What are the conditions under which 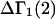 is or is not independent of the chemical structure of the osmolyte for osmolytes of comparable size? The
is or is not independent of the chemical structure of the osmolyte for osmolytes of comparable size? The 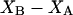 term in Eq. 43 depends on the osmolyte's size, but not on its chemical structure. The
term in Eq. 43 depends on the osmolyte's size, but not on its chemical structure. The 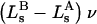 term also varies with the size, but not the chemical structure, of all those osmolytes that have a common set of strong water-binding sites around conformer
term also varies with the size, but not the chemical structure, of all those osmolytes that have a common set of strong water-binding sites around conformer 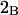 and another common set around conformer
and another common set around conformer 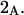 Nonionic, non-zwitterionic osmolytes of similar size, such as ethylene glycol and acetamide, should have the same set of strong water-binding/weak osmolyte-binding sites around a given conformer. In contrast, osmolytes of similar size, but different ionic character, such as glycerol and TMAO, may well have different sets of such sites around conformers
Nonionic, non-zwitterionic osmolytes of similar size, such as ethylene glycol and acetamide, should have the same set of strong water-binding/weak osmolyte-binding sites around a given conformer. In contrast, osmolytes of similar size, but different ionic character, such as glycerol and TMAO, may well have different sets of such sites around conformers  and
and 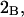 and would likely exhibit different
and would likely exhibit different 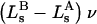 terms. In general, the
terms. In general, the 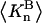 and
and 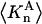 vary with both the osmolyte's size and its chemical structure, especially for surface-contiguous sites, and the
vary with both the osmolyte's size and its chemical structure, especially for surface-contiguous sites, and the 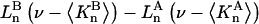 term is expected to vary from one osmolyte to another, except in the event of accidental cancellation, or in the event that active regions of the surface consist only of strong water-binding sites, in which case these terms vanish. Except in special cases, discussed below, one expects to find that
term is expected to vary from one osmolyte to another, except in the event of accidental cancellation, or in the event that active regions of the surface consist only of strong water-binding sites, in which case these terms vanish. Except in special cases, discussed below, one expects to find that 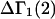 varies with both osmolyte chemical structure and size. Such variations of
varies with both osmolyte chemical structure and size. Such variations of 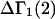 with the osmolyte's chemical structure and size have often been reported (2,6,33–36). For many of these processes the magnitude of
with the osmolyte's chemical structure and size have often been reported (2,6,33–36). For many of these processes the magnitude of 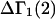 was found to increase with osmolyte size, as would be expected, if the
was found to increase with osmolyte size, as would be expected, if the 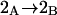 transition involved a significant change in macromolecular surface area, and if also
transition involved a significant change in macromolecular surface area, and if also 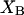 and
and 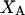 exceed
exceed 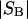 and
and 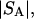 respectively, as is the case for BSA.
respectively, as is the case for BSA.
One scenario, wherein 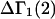 is independent of the osmolyte's chemical structure, occurs when the active regions of the surface almost completely enclose pockets or channels that cannot be penetrated by any osmolyte exceeding a certain size. In such a case, there are no exchanging sites of any kind within the pocket or channel, and
is independent of the osmolyte's chemical structure, occurs when the active regions of the surface almost completely enclose pockets or channels that cannot be penetrated by any osmolyte exceeding a certain size. In such a case, there are no exchanging sites of any kind within the pocket or channel, and 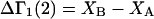 arises entirely from the excluded volume contribution. Because all osmolytes exceeding a certain size are completely excluded from the pocket or channel in
arises entirely from the excluded volume contribution. Because all osmolytes exceeding a certain size are completely excluded from the pocket or channel in 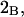 one has
one has 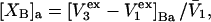 which is just the volume of the pocket or channel in
which is just the volume of the pocket or channel in 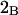 that is accessible to water centers, but excluded to osmolyte centers, divided by
that is accessible to water centers, but excluded to osmolyte centers, divided by 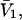 which is approximately the number of nondisplaceable water molecules within the pocket or channel of
which is approximately the number of nondisplaceable water molecules within the pocket or channel of 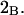 A similar relation applies to
A similar relation applies to 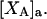 In this scenario,
In this scenario, 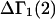 can be regarded as the change in the number of bound water molecules, or more precisely in the number of water molecules that cannot be displaced by any osmolyte above a certain size. This nondisplaceable water scenario is typically proposed to rationalize the observation that
can be regarded as the change in the number of bound water molecules, or more precisely in the number of water molecules that cannot be displaced by any osmolyte above a certain size. This nondisplaceable water scenario is typically proposed to rationalize the observation that 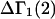 (or
(or 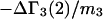 ) is independent of the chemical structure and size of the osmolyte over a significant range of osmolyte kinds and sizes (6,7,38–39). However, this scenario seems unlikely to account for the observations of Spink and Chaires (33), who studied the effects of ethylene glycol, acetamide, glycerol, and sucrose on DNA melting. The inverse melting temperature,
) is independent of the chemical structure and size of the osmolyte over a significant range of osmolyte kinds and sizes (6,7,38–39). However, this scenario seems unlikely to account for the observations of Spink and Chaires (33), who studied the effects of ethylene glycol, acetamide, glycerol, and sucrose on DNA melting. The inverse melting temperature, 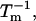 varied linearly with ln
varied linearly with ln 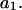 The slope,
The slope, 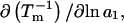 was similar for ethylene glycol, acetamide, and glycerol, corresponding to
was similar for ethylene glycol, acetamide, and glycerol, corresponding to 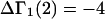 water molecules per basepair, but was substantially greater for the much larger sucrose, as expected, because it is unable to penetrate the minor groove and perhaps other nooks, as well. However, crystal structures of duplex B DNAs appear to provide no spaces in which to sequester water molecules so that they cannot in principle be displaced by osmolytes as small as ethylene glycol or acetamide, or even by glycerol. Recent and ongoing work in our lab (40) suggests that ethylene glycol and acetamide at 37°C induce a transition to an alternative duplex conformation within the B-family, and may do so in a similar, though not completely identical, manner as a function of ln
water molecules per basepair, but was substantially greater for the much larger sucrose, as expected, because it is unable to penetrate the minor groove and perhaps other nooks, as well. However, crystal structures of duplex B DNAs appear to provide no spaces in which to sequester water molecules so that they cannot in principle be displaced by osmolytes as small as ethylene glycol or acetamide, or even by glycerol. Recent and ongoing work in our lab (40) suggests that ethylene glycol and acetamide at 37°C induce a transition to an alternative duplex conformation within the B-family, and may do so in a similar, though not completely identical, manner as a function of ln 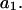 These findings suggest that another mechanism may exist by which osmolytes may exert effects that depend only weakly on their chemical structure or even size over a limited range.
These findings suggest that another mechanism may exist by which osmolytes may exert effects that depend only weakly on their chemical structure or even size over a limited range.
Water in small confined spaces, whether accessible to osmolytes or not, is likely to be at least partially ordered. When two atomically smooth cylindrical mica surfaces in aqueous media are pressed together with perpendicular orientation, the force at first rises smoothly with decreasing distance, and then for distances 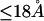 exhibits five to six oscillations, as successive water layers are squeezed out (41). This suggests that water molecules in clefts and grooves of width
exhibits five to six oscillations, as successive water layers are squeezed out (41). This suggests that water molecules in clefts and grooves of width 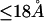 are likely to be at least partially ordered. In fact, high resolution x-ray diffraction studies at −110°C revealed some four layers of partially ordered water in and above the minor groove of a B-DNA (42,43). The absence of crystallographic evidence for more widespread occurrence of more than two layers of ordered water molecules in clefts, grooves, and pits might arise from the coexistence of two or a few different partially ordered water structures within the same cavity, which would appear to be disordered with a concomitant loss of resolution of the translationally ordered water. In any case, it would be premature, in our view, to conclude that water molecules in clefts and grooves of DNA and protein surfaces are not partially ordered on the basis of the extant reported crystal structures. If partially ordered multilayers exist in certain clefts and grooves, as we suspect, then there also exist multiple exchanging sites within that space, where the osmolyte does not contact the macromolecular surface. For such sites, the
are likely to be at least partially ordered. In fact, high resolution x-ray diffraction studies at −110°C revealed some four layers of partially ordered water in and above the minor groove of a B-DNA (42,43). The absence of crystallographic evidence for more widespread occurrence of more than two layers of ordered water molecules in clefts, grooves, and pits might arise from the coexistence of two or a few different partially ordered water structures within the same cavity, which would appear to be disordered with a concomitant loss of resolution of the translationally ordered water. In any case, it would be premature, in our view, to conclude that water molecules in clefts and grooves of DNA and protein surfaces are not partially ordered on the basis of the extant reported crystal structures. If partially ordered multilayers exist in certain clefts and grooves, as we suspect, then there also exist multiple exchanging sites within that space, where the osmolyte does not contact the macromolecular surface. For such sites, the 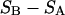 terms in
terms in 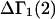 (Eq. 42) might vary much less with osmolyte chemical structure than is the case for surface-contiguous sites, as described below.
(Eq. 42) might vary much less with osmolyte chemical structure than is the case for surface-contiguous sites, as described below.
We speculate that the osmolyte is preferentially excluded from any partially ordered water multilayer, much as impurities are excluded from macroscopic crystalline ice. In such a case, the exchanging sites within the array are necessarily of the strong water-binding/weak osmolyte-binding variety. Hence, the exchange constant, 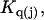 along an approaching trajectory should decline from its random value,
along an approaching trajectory should decline from its random value, 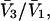 in bulk solution to a much smaller value typical of strong water-binding sites, as indicated in Fig. 3. Although the
in bulk solution to a much smaller value typical of strong water-binding sites, as indicated in Fig. 3. Although the 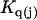 -values in the interior and bottom of the array (i.e., to the left of
-values in the interior and bottom of the array (i.e., to the left of 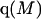 ) may depend strongly on the osmolyte's chemical structure, that will not matter much, because for those sites,
) may depend strongly on the osmolyte's chemical structure, that will not matter much, because for those sites, 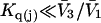 in any case. However, in the region immediately exterior to (i.e., to the right of)
in any case. However, in the region immediately exterior to (i.e., to the right of) 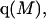 the
the 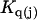 -values also depend on the osmolyte chemical structure and are large enough to make a significant contribution compared to the
-values also depend on the osmolyte chemical structure and are large enough to make a significant contribution compared to the 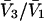 term for each site. Indeed, sufficiently far to the right of
term for each site. Indeed, sufficiently far to the right of 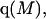 the
the 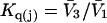 everywhere in the bulk solution, and the corresponding (
everywhere in the bulk solution, and the corresponding (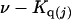 ) terms in S for those sites vanish altogether. It is conceivable that the deeper, strong water-binding sites in the cleft are much more numerous than the more neutral water-binding sites at the outer surface of the hydration multilayer, as illustrated in Fig. 4 a, so the
) terms in S for those sites vanish altogether. It is conceivable that the deeper, strong water-binding sites in the cleft are much more numerous than the more neutral water-binding sites at the outer surface of the hydration multilayer, as illustrated in Fig. 4 a, so the 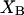 and
and 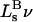 terms dominate the
terms dominate the 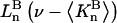 term in Eq. 43 for the B conformer, and a similar circumstance prevails for the A conformer. In such a case, the relative variation of
term in Eq. 43 for the B conformer, and a similar circumstance prevails for the A conformer. In such a case, the relative variation of 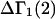 with osmolyte chemical structure for osmolytes of a similar size might be rather modest, because the largest terms,
with osmolyte chemical structure for osmolytes of a similar size might be rather modest, because the largest terms, 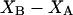 and
and 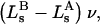 are practically invariant to osmolyte structure.
are practically invariant to osmolyte structure.
FIGURE 3.
Variation of the equilibrium constants for osmolyte/solvent exchange of two different neutral nonzwitterionic osmolytes of different size, αand β, along the same path passing from the bulk solution into a hydration multilayer from which the osmolytes are strongly excluded. The macromolecule (protein or DNA) exhibits two different conformations, A and B, and A has a more distant outer boundary of its hydration multilayer than does B. The larger osmolyte α is unable to exchange with sites as close to the outer edge of the hydration multilayer as those accessed by the smaller osmolyte β, and that is true for either conformation, A or B, of the macromolecule. Nevertheless, in this scenario, the difference in positions where the exchange constants turn down for the two conformations, namely 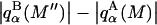 for osmolyte α and
for osmolyte α and 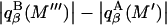 for osmolyte β, is practically the same for both osmolytes, regardless of their chemical composition or size. The positions,
for osmolyte β, is practically the same for both osmolytes, regardless of their chemical composition or size. The positions, 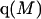 where the exchange constants turn downward, correspond to the position where the osmolyte would first contact the outermost hydration layer, if that layer did not melt.
where the exchange constants turn downward, correspond to the position where the osmolyte would first contact the outermost hydration layer, if that layer did not melt.
FIGURE 4.
(a) Schematic illustration of an osmolyte molecule approaching a partially ordered hydration multilayer in a cleft of a protein (or DNA) molecule. The maximum occupation positions of the water molecules are denoted by the ordered array of spheres in this diagram. The path of the osmolyte through the lattice of osmolyte/solvent exchange sites surrounding the protein-water complex begins at position 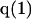 in the bulk solution and passes through a sequence of sites that are designated by
in the bulk solution and passes through a sequence of sites that are designated by 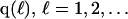 (b) As the osmolyte approaches the partially ordered hydration multilayer, the latter “melts” to form a liquid water film that wets the surface of the remaining partially ordered waters, and separates the osmolyte from the partially ordered water. Direct contact between the osmolyte and partially ordered water is thereby prevented, and the osmolyte remains surrounded by liquid everywhere along its advancing trajectory. The free energy cost to “melt” the ordered water resists the advance of the osmolyte toward the protein (or DNA), by decreasing the equilibrium constant for osmolyte/solvent exchange as the osmolyte begins to displace the partially ordered water.
(b) As the osmolyte approaches the partially ordered hydration multilayer, the latter “melts” to form a liquid water film that wets the surface of the remaining partially ordered waters, and separates the osmolyte from the partially ordered water. Direct contact between the osmolyte and partially ordered water is thereby prevented, and the osmolyte remains surrounded by liquid everywhere along its advancing trajectory. The free energy cost to “melt” the ordered water resists the advance of the osmolyte toward the protein (or DNA), by decreasing the equilibrium constant for osmolyte/solvent exchange as the osmolyte begins to displace the partially ordered water.
More complete invariance of 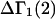 to the chemical structures of osmolytes of similar size requires that the identity of the osmolyte be concealed from the partially ordered water, as it approaches from bulk solution to the position,
to the chemical structures of osmolytes of similar size requires that the identity of the osmolyte be concealed from the partially ordered water, as it approaches from bulk solution to the position, 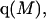 of the steep descent. We propose the following speculative mechanism. If the contact surface free energy between the hydration multilayer and the osmolyte sufficiently exceeds the sum of the surface free energy between the hydration multilayer and liquid water and that between liquid water and the osmolyte, then the hydration multilayer will “melt” in front of the advancing osmolyte to create an interposed liquid water film as indicated in Fig. 4 b. As an example, crystalline ice forms a stable liquid film at its interface with air, provided that the temperature is not too far below the freezing point (44,45). In this case, the chemical structure of the osmolyte is not directly sensed by the partially ordered water, from which it is separated by the liquid film. Of course, there may also be partially ordered water associated with the osmolyte. Under these conditions, for osmolytes of similar size, the
of the steep descent. We propose the following speculative mechanism. If the contact surface free energy between the hydration multilayer and the osmolyte sufficiently exceeds the sum of the surface free energy between the hydration multilayer and liquid water and that between liquid water and the osmolyte, then the hydration multilayer will “melt” in front of the advancing osmolyte to create an interposed liquid water film as indicated in Fig. 4 b. As an example, crystalline ice forms a stable liquid film at its interface with air, provided that the temperature is not too far below the freezing point (44,45). In this case, the chemical structure of the osmolyte is not directly sensed by the partially ordered water, from which it is separated by the liquid film. Of course, there may also be partially ordered water associated with the osmolyte. Under these conditions, for osmolytes of similar size, the 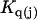 are practically independent of the osmolyte's chemical structure from position
are practically independent of the osmolyte's chemical structure from position 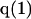 in the bulk to
in the bulk to 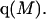 The
The 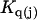 may vary with osmolyte structure at deeper sites to the left of
may vary with osmolyte structure at deeper sites to the left of 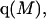 not only for those sites that place the osmolyte in contact with the macromolecular surface, but also for those where the liquid film cannot form, perhaps due to the higher free energy cost of melting those layers. However, those
not only for those sites that place the osmolyte in contact with the macromolecular surface, but also for those where the liquid film cannot form, perhaps due to the higher free energy cost of melting those layers. However, those 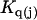 -values are very small compared to
-values are very small compared to 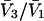 in any case, and contribute little to
in any case, and contribute little to 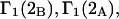 or
or 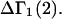 In this scenario,
In this scenario, 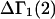 is practically independent of chemical structure for osmolytes of the same hydrated size, but it cannot be identified simply with a change in the amount of bound water in the multilayer, because some of the
is practically independent of chemical structure for osmolytes of the same hydrated size, but it cannot be identified simply with a change in the amount of bound water in the multilayer, because some of the 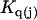 terms make a significant contribution.
terms make a significant contribution.
In an ideal case, 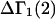 may also be largely independent of osmolyte size over a limited range of osmolyte sizes. To exhibit such behavior, both the excluded volume contribution,
may also be largely independent of osmolyte size over a limited range of osmolyte sizes. To exhibit such behavior, both the excluded volume contribution, 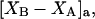 and the exchange reaction contribution,
and the exchange reaction contribution, 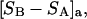 associated with the active part(s) of the surface must display practically the same values for two osmolytes, α and β, of different size. That is, one must have,
associated with the active part(s) of the surface must display practically the same values for two osmolytes, α and β, of different size. That is, one must have, 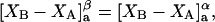 where
where 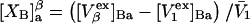 is the difference between the volume excluded by species B to osmolyte β and that excluded to solvent 1 in units of
is the difference between the volume excluded by species B to osmolyte β and that excluded to solvent 1 in units of 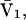 and similar definitions apply to
and similar definitions apply to 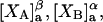 and
and 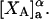 This condition is equivalent to
This condition is equivalent to 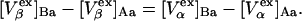 The difference volume,
The difference volume, 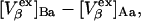 may well be nearly independent of the size of the osmolyte β over a limited range of sizes, because it corresponds to the volume of a partial “shell”, associated with the active parts of the surface, whose thickness is just the difference in the positions of the active surfaces of the B and A conformers relative to their own central atoms. In such a case,
may well be nearly independent of the size of the osmolyte β over a limited range of sizes, because it corresponds to the volume of a partial “shell”, associated with the active parts of the surface, whose thickness is just the difference in the positions of the active surfaces of the B and A conformers relative to their own central atoms. In such a case, 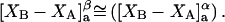 In addition, an osmolyte of smaller size (β) begins to penetrate the hydration multilayer at a closer distance to the surface of conformer B than does an osmolyte of larger size (α), so that its
In addition, an osmolyte of smaller size (β) begins to penetrate the hydration multilayer at a closer distance to the surface of conformer B than does an osmolyte of larger size (α), so that its 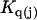 turns downward at a correspondingly smaller distance
turns downward at a correspondingly smaller distance 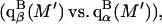 as indicated in Fig. 3. However, if the separation between the turndown positions for those two osmolytes (β and α) is the same for conformer A as for conformer B, as indicated in Fig. 3, then the contribution of the smaller osmolyte to
as indicated in Fig. 3. However, if the separation between the turndown positions for those two osmolytes (β and α) is the same for conformer A as for conformer B, as indicated in Fig. 3, then the contribution of the smaller osmolyte to 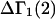 may be nearly the same as that of the larger osmolyte. This can be seen from the expression,
may be nearly the same as that of the larger osmolyte. This can be seen from the expression,  wherein
wherein 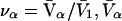 is the volume of the exchange sites, which is here taken as the partial molecular volume of the osmolyte α, and
is the volume of the exchange sites, which is here taken as the partial molecular volume of the osmolyte α, and 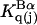 and
and 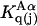 are the exchange constants for an osmolyte α with its center in the volume element
are the exchange constants for an osmolyte α with its center in the volume element 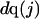 at position
at position 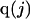 in the vicinity of the species B or A, respectively. The integral is taken over the volume of the osmolyte accessible region extending from the active part of the macromolecular surface out to the point, where both
in the vicinity of the species B or A, respectively. The integral is taken over the volume of the osmolyte accessible region extending from the active part of the macromolecular surface out to the point, where both 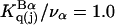 and
and  so the integrand vanishes. Analogous considerations apply for
so the integrand vanishes. Analogous considerations apply for 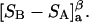 For the case illustrated in Fig. 3, where the difference between the downturn positions of the osmolyte β in the vicinity of B and A is very similar to the corresponding difference for the osmolyte α, the integrals may well take rather similar values for two osmolytes of somewhat different size, hence their
For the case illustrated in Fig. 3, where the difference between the downturn positions of the osmolyte β in the vicinity of B and A is very similar to the corresponding difference for the osmolyte α, the integrals may well take rather similar values for two osmolytes of somewhat different size, hence their 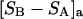 -values may also be nearly identical. Under these conditions, then,
-values may also be nearly identical. Under these conditions, then, 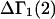 may become independent of osmolyte size, as well as osmolyte chemical structure, over a limited range of osmolyte sizes. However,
may become independent of osmolyte size, as well as osmolyte chemical structure, over a limited range of osmolyte sizes. However, 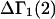 does not necessarily correspond to the change in the amount of ordered water, because some of the
does not necessarily correspond to the change in the amount of ordered water, because some of the 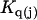 terms make a significant contribution.
terms make a significant contribution.
It is not known whether a liquid film actually is formed between a hydration multilayer and an osmolyte, or at what, if any, depth it ceases to form, because the free energy required to “melt” an interior layer is simply too high. Nevertheless, this scenario may merit consideration in those cases, where 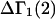 is found to be independent of osmolyte chemical structure for osmolytes of the same size, and perhaps also independent of osmolyte size over a limited range of sizes, but where also the crystal structure appears to provide no places to sequester water in such a way that it could not be displaced by those same osmolytes.
is found to be independent of osmolyte chemical structure for osmolytes of the same size, and perhaps also independent of osmolyte size over a limited range of sizes, but where also the crystal structure appears to provide no places to sequester water in such a way that it could not be displaced by those same osmolytes.
Possible biological relevance of highly excluded osmolytes
It is noteworthy that cells employ osmoprotectants that are zwitterionic (betaine glycine, glycine, proline, and trimethylamine N-oxide) or both ionic and zwitterionic (glutamate), and which are excluded from 2.3 to 5.3 times as much water-occupied volume as is glycerol, for which 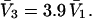 Cells also employ neutral nonzwitterionic species, such as trehalose, which has a larger
Cells also employ neutral nonzwitterionic species, such as trehalose, which has a larger 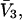 and is also excluded from three times as much water as glycerol. Such superexcluded osmolytes are unable to displace some of the innermost water molecules in clefts, grooves, and pits. It is conceivable that these osmolytes have been selected to lower a1 without displacing important inner water molecules associated with the cell's macromolecules, which may be the most strongly coupled to changes in macromolecular structure and function. Felitsky et al. (29) proposed that betaine glycine was commonly selected as an osmoprotectant, because it has the least effect on protein-unfolding equilibria for a given osmolality. It is not unlikely that both functions, namely preserving inner waters and minimally altering unfolding equilibria, are important for an osmoprotectant.
and is also excluded from three times as much water as glycerol. Such superexcluded osmolytes are unable to displace some of the innermost water molecules in clefts, grooves, and pits. It is conceivable that these osmolytes have been selected to lower a1 without displacing important inner water molecules associated with the cell's macromolecules, which may be the most strongly coupled to changes in macromolecular structure and function. Felitsky et al. (29) proposed that betaine glycine was commonly selected as an osmoprotectant, because it has the least effect on protein-unfolding equilibria for a given osmolality. It is not unlikely that both functions, namely preserving inner waters and minimally altering unfolding equilibria, are important for an osmoprotectant.
Acknowledgments
The authors thank Profs. Bob Mazo and John Schellman for pointing out an error in an earlier version of this manuscript, and Dr. Jonathan Cannon and Prof. Tom Record for providing recent experimental results before publication, and also for many helpful comments and suggestions.
This work was supported in part by grant RO1 GM61685 from the National Institutes of Health.
APPENDIX A: DEFINITION OF Gαβ(R) IN THE GRAND ENSEMBLE
The pair correlation function is defined in the following way. First, a particular atom at the same topological position in every molecule of a given kind is arbitrarily designated as its central atom. The coordinates of the central atom of the ith molecule of the αth kind are denoted by 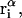 and the coordinates of its remaining
and the coordinates of its remaining 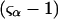 atoms are denoted by a generalized
atoms are denoted by a generalized 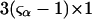 vector,
vector, 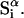 The full set of coordinates of all the atoms in the ith molecule of kind α are denoted by a generalized
The full set of coordinates of all the atoms in the ith molecule of kind α are denoted by a generalized 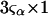 vector,
vector, 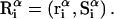 The full set of all of the coordinates of all the atoms in all the molecules in the volume V are denoted by a generalized vector R of dimension
The full set of all of the coordinates of all the atoms in all the molecules in the volume V are denoted by a generalized vector R of dimension 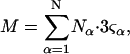 which has associated volume element dMR. The potential energy function U(R) depends upon all of the coordinates. The pair correlation function, or radial distribution function, for the central atom of a β-molecule at r2, given a central atom of an α-molecule at r1, is defined by
which has associated volume element dMR. The potential energy function U(R) depends upon all of the coordinates. The pair correlation function, or radial distribution function, for the central atom of a β-molecule at r2, given a central atom of an α-molecule at r1, is defined by
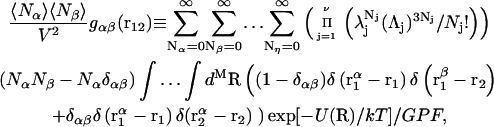 |
(A1) |
wherein  is the Kronecker δ, k is Boltzmann's constant, T is absolute temperature,
is the Kronecker δ, k is Boltzmann's constant, T is absolute temperature,  is the mass of the nth atom of an α-molecule, and GPF denotes the grand partition function,
is the mass of the nth atom of an α-molecule, and GPF denotes the grand partition function,
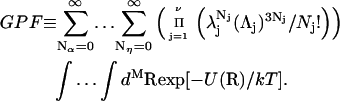 |
(A2) |
In the thermodynamic limit of extremely large systems, the terms in the sums of both the numerator and denominator on the right-hand side of Eq. A1 are strongly peaked near the mean values of the Nj, in which case the kinetic energy factors 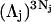 cancel out of the
cancel out of the 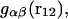 as expected in classical statistical mechanics.
as expected in classical statistical mechanics.
APPENDIX B: EVALUATION OF (∂c1/∂c3)T,P,c2
For the kth species, 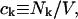 so
so 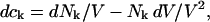 and
and 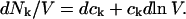 At constant T,
At constant T,
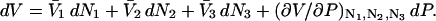 |
(B1) |
Dividing Eq. B1 by V and using the preceding relations for d Nk /V yields
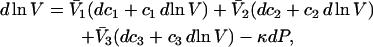 |
(B2) |
wherein the compressibility is defined by 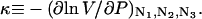 After collecting all of the dln V terms on the left-hand side, one has
After collecting all of the dln V terms on the left-hand side, one has 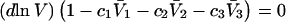 on that side. There remains then
on that side. There remains then
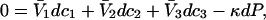 |
(B3) |
so at constant c2 and P one has finally
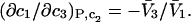 |
(B4) |
APPENDIX C: EVALUATION OF V̄α
At constant T, μj(T,c1, … ,cν) depends upon all the concentrations. Hence,
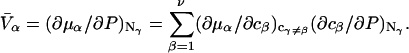 |
(C1) |
Using 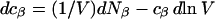 from Appendix B, one finds
from Appendix B, one finds
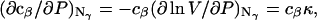 |
(C2) |
where κ is the compressibility defined in Appendix B. Use of Eq. C2 in Eq. C1 yields
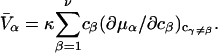 |
(C3) |
Equation C3 is multiplied by cα on both sides and summed over α=1, … , ν to give
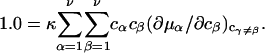 |
(C4) |
After inserting Eq. 9, there results
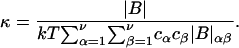 |
(C5) |
After inserting Eq. C5 into Eq. C3 and again using Eq. 9, there results
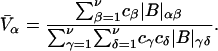 |
(C6) |
Equations C5 and C6 are precisely the expressions of Kirkwood and Buff (10).
APPENDIX D: VERIFICATION OF BEN-NAIM'S EXPRESSION FOR V̄2
We adopt Eq. 6.17.22 of Ben-Naim (17) as a conjecture for the three-component system at constant T:
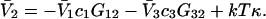 |
(D1) |
In the limit 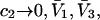 and
and 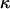 are properties of the two-component solution (1 + 3), whereas
are properties of the two-component solution (1 + 3), whereas 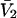 is a property of the three-component solution. Equation C3 with α = 3 can be written as
is a property of the three-component solution. Equation C3 with α = 3 can be written as
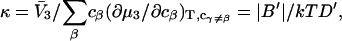 |
(D2) |
where the second equality was obtained from the first by using Eq. C6 for 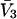 and Eq. 9 for
and Eq. 9 for 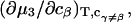 the primes denote quantities pertaining to the two-component system, and
the primes denote quantities pertaining to the two-component system, and
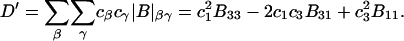 |
(D3) |
Use was made of the symmetry of the B-matrix to obtain the final equality of Eq. D3. After substituting equations D2 and C6 into the right-hand side (rhs) of Eq. D1 and expanding out the two-component sums for  and
and 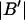 (in
(in 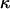 ) there results
) there results
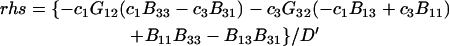 |
(D4) |
The left-hand side (lhs) of Eq. D1 is evaluated for the three-component system via Eq. C6, which after expansion of the various terms gives
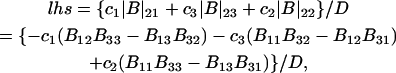 |
(D5) |
where
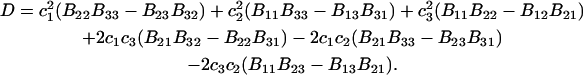 |
(D6) |
Every term in the numerator of lhs in Eq. D5 contains a single factor of  The terms in D in Eq. D6 all contain either one or two factors of
The terms in D in Eq. D6 all contain either one or two factors of  Hence, both numerator and denominator of lhs can be divided by
Hence, both numerator and denominator of lhs can be divided by  Any terms that still contain a factor of
Any terms that still contain a factor of 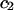 can be neglected against the constant terms in the limit
can be neglected against the constant terms in the limit 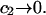 In this limit, D becomes identical to
In this limit, D becomes identical to  in Eq. D3, and finally
in Eq. D3, and finally
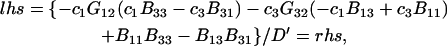 |
(D7) |
so the conjectured Eq. D1 is verified.
APPENDIX E: CONNECTION BETWEEN Γ2(3) AND OTHER PREFERENTIAL INTERACTION COEFFICIENTS
For a three-component system, 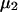 and
and 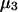 depend upon T, P, and the concentrations,
depend upon T, P, and the concentrations, 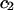 and
and 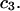 Thus, at constant T, P, and
Thus, at constant T, P, and 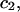
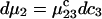 |
(E1) |
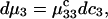 |
(E2) |
where 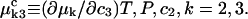 Dividing Eq. E1 by Eq. E2 yields
Dividing Eq. E1 by Eq. E2 yields
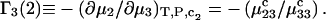 |
(E3) |
For the same system, 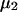 and
and 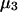 can also be expressed in terms of T, P, and the molalities,
can also be expressed in terms of T, P, and the molalities, 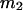 and
and 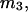 so at constant T, P,
so at constant T, P,
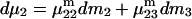 |
(E4) |
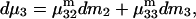 |
(E5) |
where 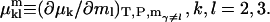 Hence, at constant T, P,
Hence, at constant T, P,
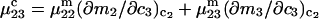 |
(E6) |
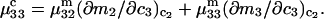 |
(E7) |
The subscripts denoting constant T and P of the slopes, 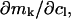 in Eqs. E6 and E7 are omitted for clarity and this convention applies in the sequel.
in Eqs. E6 and E7 are omitted for clarity and this convention applies in the sequel.
We assume for simplicity that the partial molar volumes, 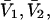 and
and 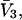 are constants independent of
are constants independent of 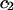 and
and 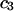 at constant T, P over the range of
at constant T, P over the range of 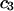 up to ∼1.0 M, which should be a good approximation, provided that
up to ∼1.0 M, which should be a good approximation, provided that 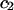 is sufficiently dilute.
is sufficiently dilute.
The molalities, 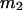 and
and 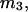 can be expressed in terms of the concentrations and solvent molar mass,
can be expressed in terms of the concentrations and solvent molar mass, 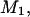 by
by
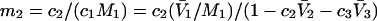 |
(E8) |
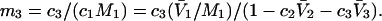 |
(E9) |
After performing the derivatives and collecting terms, we obtain
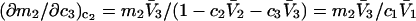 |
(E10) |
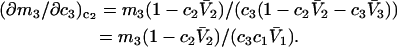 |
(E11) |
In the limit 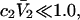 the
the 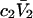 term in Eq. E11 may be neglected, and we obtain
term in Eq. E11 may be neglected, and we obtain
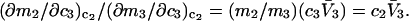 |
(E12) |
After dividing Eq. E6 by Eq. E7 in accord with Eq. E3, dividing both numerator and denominator of the resulting quotient by 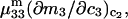 and rearranging somewhat, there results
and rearranging somewhat, there results
 |
(E13) |
The Maxwell relation, 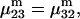 and the definition,
and the definition, 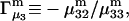 were used to obtain the first equality, and the definition,
were used to obtain the first equality, and the definition, 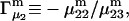 was used to obtain the second. In the limit of small
was used to obtain the second. In the limit of small 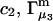 becomes independent of
becomes independent of 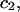 and the second term in the denominator may be neglected to obtain
and the second term in the denominator may be neglected to obtain
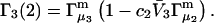 |
(E14) |
The second term in Eq. E14 cannot be neglected for small  as seen in Eq. E15 below. The definitions of
as seen in Eq. E15 below. The definitions of  and
and 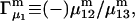 and their alternative representations used here are given in Table 1 of Anderson et al. (19). An exact expression linking
and their alternative representations used here are given in Table 1 of Anderson et al. (19). An exact expression linking 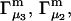 and
and 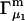 was also derived in Eq. 12 of that same article, and can be rearranged without approximation to give
was also derived in Eq. 12 of that same article, and can be rearranged without approximation to give
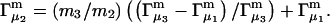 |
(E15) |
Inserting Eq. E15 into Eq. E14 and taking the limit 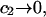 where
where 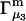 and
and 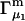 remain constant, yields
remain constant, yields
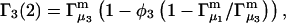 |
(E16) |
where 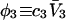 is the volume fraction of species 3.
is the volume fraction of species 3.
An expression relating the “dialysis” preferential interaction coefficient, 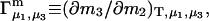 to
to  and
and  was derived by Anderson et al. (20) (their Eq. 20). In the limit
was derived by Anderson et al. (20) (their Eq. 20). In the limit 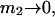 that relation becomes
that relation becomes
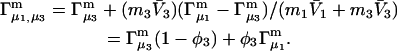 |
(E17) |
The relation between 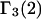 and
and 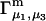 is obtained by solving Eq. E17 for
is obtained by solving Eq. E17 for 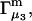
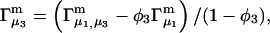 |
(E18) |
and inserting that into Eq. E16 in both places where 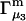 occurs. There results finally
occurs. There results finally
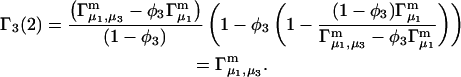 |
(E19) |
Thus, in the limit 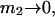 this concentration-based
this concentration-based 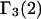 is equal to the molality-based
is equal to the molality-based 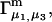 provided that
provided that 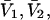 and
and  are constants independent of
are constants independent of  at constant T, P over the range considered.
at constant T, P over the range considered.
References
- 1.Timasheff, S. N. 1993. The control of protein stability and association by weak interactions with water: how do solvents affect these processes? Annu. Rev. Biophys. Biomol. Struct. 22:67–97. [DOI] [PubMed] [Google Scholar]
- 2.Parsegian, A., R. P. Rand, and D. C. Rau. 1995. Macromolecules and water: probing with osmotic stress. Methods Enzymol. 259:43–94. [DOI] [PubMed] [Google Scholar]
- 3.Record, M. T., Jr., W. Zhang, and C. F. Anderson. 1998. Analysis of effects of salts and uncharged solutes on protein and nucleic acid equilibria and processes: a practical guide to recognizing and interpreting polyelectrolyte effects, Hofmeister effects, and osmotic effects of salts. Adv. Protein Chem. 51:281–353. [DOI] [PubMed] [Google Scholar]
- 4.Timasheft, S. N. 1998. Control of protein stability and reactions by weakly interacting cosolvents: the simplicity of the complicated. Adv. Protein Chem. 51:355–432. [DOI] [PubMed] [Google Scholar]
- 5.Courtenay, E. S., M. W. Capp, C. F. Anderson, and M. T. Record Jr. 2000. Vapor pressure osmometry studies of osmolyte-protein interactions: implications for the action of osmoprotectants in vivo and for the interpretation of “osmotic stress” experiments in vitro. Biochemistry. 39:4455–4471. [DOI] [PubMed] [Google Scholar]
- 6.Parsegian, V. A., R. P. Rand, and D. C. Rau. 2000. Osmotic stress, preferential hydration, and binding: a comparison of perspectives. Proc. Natl. Acad. Sci. USA. 97:3987–3992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Timasheff, S. N. 2002. Protein-solvent preferential interactions, protein hydration, and the modulation of biochemical reactions by solvent components. Proc. Natl. Acad. Sci. USA. 99:9721–9726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Inoue, M., and S. N. Timasheff. 1972. Preferential and absolute interactions of solvent components in mixed solvent systems. Biopolymers. 11:737–743. [DOI] [PubMed] [Google Scholar]
- 9.Record, M. T., Jr., and C. F. Anderson. 1995. Interpretation of preferential interaction coefficients of nonelectrolytes and of electrolyte ions in terms of a two-domain model. Biophys. J. 68:786–794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kirkwood, J. G., and F. P. Buff. 1951. The statistical mechanical theory of solutions. J. Chem. Phys. 19:774–777. [Google Scholar]
- 11.Chitra, R., and P. E. Smith. 2001. Preferential interaction coefficients with hydrophobic solutes. J. Phys. Chem. B. 105:11513–11532. [Google Scholar]
- 12.Shimizu, S. 2004. Estimating hydration changes upon biomolecular reactions from osmotic stress, high pressure, and preferential interaction coefficients. Proc. Natl. Acad. Sci. USA. 101:1195–1199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shimizu, S. 2004. Estimation of excess solvation numbers of water and cosolvents from preferential interaction and volumetric experiments. J. Chem. Phys. 120:4989–4990. [DOI] [PubMed] [Google Scholar]
- 14.Shimizu, S., and D. J. Smith. 2004. Preferential hydration and the exclusion of cosolvents from protein surfaces. J. Chem. Phys. 121:1148–1154. [DOI] [PubMed] [Google Scholar]
- 15.Ben-Naim, A. 1975. Solvent effects on chemical equilibria. J. Chem. Phys. 63:2064–2073. [Google Scholar]
- 16.Ben-Naim, A. 1988. Theory of preferential solvation of nonelectrolytes. Cell Biophys. 12:255–269. [DOI] [PubMed] [Google Scholar]
- 17.Ben-Naim, A. 1992. Statistical Thermodynamics for Chemists and Biochemists. Plenum Press, New York, NY.
- 18.Schellman, J. A. 2003. Protein stability in mixed solvents: A balance of contact interaction and excluded volume. Biophys. J. 85:108–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Anderson, C. F., E. S. Courtenay, and M. T. Record Jr. 2002. Thermodynamic expressions relating different types of preferential interaction coefficients in solutions containing two solute components. J. Phys. Chem. B. 106:418–433. [Google Scholar]
- 20.Anderson, C. F., D. J. Felitsky, J. Hong, and M. T. Record Jr. 2002. Generalized derivation of exact relationship linking different coefficients that characterize the thermodynamic effects of preferential interactions. Biophys. Chem. 101–102:497–511. [DOI] [PubMed] [Google Scholar]
- 21.Schellman, J. A. 1987a. The thermodynamic stability of proteins. Annu. Rev. Biophys. Biophys. Chem. 16:115–137. [DOI] [PubMed] [Google Scholar]
- 22.Schellman, J. A. 1987b. Selective binding and solvent denaturation. Biopolymers. 26:549–559. [DOI] [PubMed] [Google Scholar]
- 23.Schellman, J. A. 1990. A simple model for solvation in mixed solvents. Applications to stabilization and destabilization of macromolecular structures. Biophys. Chem. 37:121–140. [DOI] [PubMed] [Google Scholar]
- 24.Schellman, J. A. 1993. The relation between the free energy of interaction and binding. Biophys. Chem. 45:273–279. [Google Scholar]
- 25.Schellman, J. A. 1994. The thermodynamics of solvent exchange. Biopolymers. 34:1015–1026. [DOI] [PubMed] [Google Scholar]
- 26.Schellman, J. A., and N. C. Gassner. 1996. The enthalpy of transfer of unfolded proteins into solutions of urea and quanidinium hydrochloride. Biophys. Chem. 59:259–275. [DOI] [PubMed] [Google Scholar]
- 27.Hill, T. L. (1960). Introduction to Statistical Thermodynamics. Addison-Wesley Publishing, Reading, MA.
- 28.McQuarrie, D. A. 1976. Statistical Mechanics. Harper and Row, New York, NY.
- 29.Felitsky, D. J., J. G. Cannon, M. W. Capp, J. Hong, A. W. Van Wynsberghe, C. F. Anderson, and M. T. Record Jr. 2004. The exclusion of glycine betaine from anionic biopolymer surface: why glycine betaine is an effective osmoprotectant but also a compatible solute. Biochemistry. 43:14732–14743. [DOI] [PubMed] [Google Scholar]
- 30.Hong, J., M. W. Capp, C. F. Anderson, R. M. Saecker, D. J. Felitsky, M. W. Anderson, and M. T. Record, Jr. 2004. Preferential interactions of glycine betaine and urea with DNA: implications for DNA hydration and for effects of these solutes on DNA stability. Biochemistry. 43:14744–14758. [DOI] [PubMed] [Google Scholar]
- 31.Sugio, S., A. Kashima, S. Mochizuki, M. Noda, and K. Kobayashi. 1999. Crystal structure of human serum albumin at 2.5 Å resolution. Protein Eng. 12:439–446. [DOI] [PubMed] [Google Scholar]
- 32.Connolly, J. L. 1993. The molecular surface package. J. Mol. Graph. 4:139–141. [DOI] [PubMed] [Google Scholar]
- 33.Spink, C. H., and J. B. Chaires. 1999. Effects of hydration, ion release, and excluded volume on the melting of triplex and duplex DNA. Biochemistry. 38:496–508. [DOI] [PubMed] [Google Scholar]
- 34.Preisler, R. S., H. M. Chen, M. F. Colombo, Y. Choe, B. J. Short, and D. C. Rau. 1995. The B-form to Z-form transition of poly (dG − m(5)dC) is sensitive to neutral solutes through an osmotic stress. Biochemistry. 34:14400–14407. [DOI] [PubMed] [Google Scholar]
- 35.Ruggiero-Neto, J., and M. F. Colombo. 2000. Water regulation of actinomycin-D binding to DNA: the interplay among drug affinity, DNA long-range conformation and hydration. Biopolymers. 53:46–59. [DOI] [PubMed] [Google Scholar]
- 36.Garner, M. M., and D. C. Rau. 1995. Water release associated with specific binding of gal repressor. EMBO J. 14:1257–1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Siderova, N. Y., and D. C. Rau. 1996. Differences in water release for the binding of EcoRI to specific and non-specific DNA sequences. Proc. Natl. Acad. Sci. USA. 93:12272–12277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Colombo, M. F., D. C. Rau, and V. A. Parsegian. 1992. Protein solvation in allosteric regulation: a water effect on hemoglobin. Science. 256:655–659. [DOI] [PubMed] [Google Scholar]
- 39.Vodyanoy, I., S. M. Bezrukov, and V. A. Parsegian. 1993. Probing alamecithin channels with water-soluble polymers. Size modulated osmotic action. Biophys. J. 65:2097–2105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rangel, D. P., C. A. Sucato, C. H. Spink, B. S. Fujimoto, and J. M. Schurr. 2004. Effects of small neutral osmolytes on the supercoiling free energy and intrinsic twist of p30δ DNA. Biopolymers. 75:291–313. [DOI] [PubMed] [Google Scholar]
- 41.Israelachvili, J. 1987. Solvation forces and liquid structure, as probed by direct force measurements. Acc. Chem. Res. 20:415–421. [Google Scholar]
- 42.Shui, X., C. C. Sines, L. McFail-Isom, D. Van Derveer, and L. D. Williams. 1998. Structure of the potassium form of CGCGAATTCGCG:DNA. Deformation by electrostatic collapse around inorganic ions. Biochemistry. 37:16877–16887. [DOI] [PubMed] [Google Scholar]
- 43.Shui, X., L. McFail-Isom, G. G. Hu, and L. D. Williams. 1998. The B-DNA dodecamer at high resolution reveals a spine of water on sodium. Biochemistry. 37:8341–8355. [DOI] [PubMed] [Google Scholar]
- 44.Elbaum, M., S. B. Lipson, and J. G. Dash. 1993. Optical study of surface melting on ice. J. Cryst. Growth. 129:491–505. [Google Scholar]
- 45.Wilen, L. A., J. S. Wettlaufer, M. Elbaum, and M. Schick. 1995. Dispersion force effects in interfacial premelting of ice. Phys. Rev. B. 52:12426–12433. [DOI] [PubMed] [Google Scholar]