A Computational Study of the Closed and Open States of the Influenza A M2 Proton Channel

Abstract

In this study, four possible conformations of the His-37 and Trp-41 residues for the closed state of the influenza M2 ion channel were identified by a conformation scan based on a solid-state NMR restraint. In the four conformations, the His-37 residue can be of either the t-160 or t60 rotamer, whereas Trp-41 can be of either the t-105 or t90 rotamer. These conformations were further analyzed by density functional theory calculations and molecular dynamics simulations, and the data indicate that the His-37 residue most likely adopts the t60 rotamer and should be monoprotonated at the δ-nitrogen site, whereas Trp-41 adopts the t90 rotamer. This result is consistent with published experimental data and points to a simple gating mechanism: in the closed state, the His-37 and Trp-41 residues adopt the (t60, t90) conformation, which nearly occludes the pore, preventing nonproton ions from passing through due to the steric and desolvation effects. Moreover, the His-37 tetrad interrupts the otherwise continuous hydrogen-bonding network of the pore water by forcing the water molecules above and below it to adopt opposite orientations, thus adding to the blockage of proton shuttling. The channel can be easily opened by rotating the His-37 χ₂ angle from 60 to 0°. This open structure allows pore water to penetrate the constrictive region and to form a continuous water wire for protons to shuttle through, while being still narrow enough to exclude other ions.

INTRODUCTION

The M2 protein of the influenza A virus is a transmembrane protein found in the virion membrane and infected host cells. It can adjust the pH by transporting protons across the membrane, which plays an important role during the virion-uncoating (1–3) and hemagglutinin-maturation processes (4,5). A large amount of evidence has confirmed that this functionality can be mainly ascribed to a proton channel (the M2 channel) formed by its transmembrane (TM) domain (6–9), which can be specifically inhibited by the antiflu drug amantadine (1-aminoadamantine hydrochloride) (10,11,7). Because of the essential roles of the M2 channel in the viral life cycle, studying its structure and illuminating its proton conductance mechanisms are of great interest to antiflu drug design, pharmacology, and medicine.

Considerable effort has been devoted to elucidating the M2 channel's structure. To date, experimental data have shown that the TM domain is a homotetramer, forming a parallel α-helix bundle in a (pseudo-) C₄ symmetrical fashion (12–14). A 25-residue peptide (M2-TMP) with the following amino acid sequence: NH₂-Ser-Ser-Asp-Pro-Leu-Val-Val-Ala-Ala-Ser-Ile-Ile-Gly-Ile-Leu-His-Leu-Ile-Leu-Trp-Ile-Leu-Asp-Arg-Leu-COOH, corresponding to the residues 22–46 (encompassing the segment for the TM domain, residues 25–43) in the M2 protein, has been shown to be able to form amantadine-sensitive proton channels in lipid bilayers with almost the same specificity and efficiency as the whole M2 protein (10). A backbone structure of the M2-TMP in dimyristoylphosphatidylcholine (DMPC) bilayer has been determined by both solid-state NMR and infrared dichroism spectra experiments (15–18), revealing that the M2-TMP peptide in lipid bilayer adopts a similar α-helix structure with a tilt angle of 30–38° and a rotational angle (ρ₀) of roughly −50°. This result is generally consistent with other structural information on the M2 channel (13), though the tilt angle was recently found to be slightly larger than that (25° ± 3) for the TM domain of the whole M2 protein (19,20). Despite this discrepancy, M2-TMP seems an excellent model system for studying the structure and mechanisms of the M2 channel.

Electrophysiological studies have shown that the M2 channel is highly proton selective, roughly 10⁶-fold more conductive than other monovalent cations (21,22). It is activated (open) when the pH at its N-terminal side (pH_out; the pH at the C-terminal side is herein denoted pH_in) goes lower than 6.0 (10,9). Mutagenesis studies have suggested that the 37th residue (His-37) plays a key role in the conductance mechanism (7,9). Modeling studies have also provided insights into the detailed structure (23–26). For the closed state, all models agree that the four His-37 residues are oriented such that their imidazole side chains are directed toward the lumen, occluding the pore. For the open state, two conductance mechanisms, namely the shutter (27) and the shuttle (13) mechanisms, have been proposed. The former suggests that the function of the His-37 residues is like a camera shutter: when two or more of them are protonated, they move apart under the electrostatic repulsion, and the pore is open to allow water molecules to form a continuous water wire for protons to hop through via Grotthuss hopping. The shuttle mechanism, on the other hand, suggests that His-37 is a part of the proton relay system, and therefore opening the pore for water molecules is not necessary. To date, both mechanisms have obtained some support from experimental and/or computational studies, and more evidence is needed to clarify this important issue about the M2 channel. (For more details of the mechanism see, e.g., Wu and Voth (28) for a recent review.)

A recent ultraviolet resonance Raman spectroscopy study of the M2-TMP in lipid bilayer indicated that the 41st residue (Trp-41) is involved in the gating via cation-π interactions with the protonated His-37 residues in the open state (29). The involvement of Trp-41 was also proposed for the closed state in a more recent mutagenesis study, revealing that replacement of Trp-41 with Ala, Cys, or Phe leads to a “leaky” channel that allows outward proton current (the wild type only conducts protons inwardly) (30).

The most detailed structural information about His-37 and Trp-41 has been obtained from a solid-state NMR study by Cross and co-workers (31), revealing that the distance (d_δ-γ) between the δ-nitrogen atom of His-37 and the γ-carbon atom of Trp-41 should be ≤3.9 Å for the closed state of the M2-TMP channel in DMPC lipid bilayer. This restraint considerably narrows down the conformational space accessible by the two residues. A conformation with the His-37's χ₁, χ₂, and Trp-41's χ₁, χ₂ angles being −177°, +172°, −177°, and −105°, respectively, has been proposed (Protein Data Bank identification, 1NYJ) (31).

This study, inspired by the work of Cross and co-workers, represents a reexamination of the structure for the closed state via a thorough conformation scan. Four rotameric states were identified, three of which cannot be further distinguished by the available structural information in contrast to the previous conclusion (31). These candidates were examined here for their structural stabilities via density functional theory calculations and classical molecular dynamics (MD) simulations. Our results suggest a different structure for the closed state than that proposed by Cross and co-workers. The new structure is consistent with published experimental data and implies a revised gating mechanism.

METHODS

Conformation nomenclature

In this article, the nomenclature from the penultimate rotamer library (PRL) (32) is adopted to describe side-chain conformations. For example, the notation “t-160” indicates that the χ₁ dihedral angle of an amino acid residue's side chain is roughly 180° (trans conformation), and its χ₂ is roughly and favorably −160°. A notation, for example (t-160, t-105), is used to describe the conformation of both His-37 and Trp-41, meaning that the His-37 and Trp-41 residues are in the t-160 and t-105 conformations, respectively. Wherever the monoprotonation state of the histidine residue is concerned, a notation, for example (t-160, t-105, ɛ), is used to indicate that the His-37 residue in the (t-160, t-105) conformation is monoprotonated at its ɛ-nitrogen.

Conformation scan

The conformation of the side chain of His or Trp can be defined completely with two dihedral angles: χ₁ and χ₂. With the presumption that the M2 channel is C₄ symmetrical, the conformation of the side chains of the His-37 and Trp-41 residues is thus determined by four dihedral angles, namely the histidine's χ₁, χ₂ and the tryptophan's χ₁, χ₂. Discretization of each angle by 10° gives 36 × 36 × 36 × 36 combinations, which were filtered through the following constraints:

1. There is no severe steric clash between any atom pair within the His-37 and Trp-41 residues and the backbone. The scan results reported in this article were obtained with the backbone structure from Cross and co-workers (31); no essential deviation in the scan results was found when small (within the experimental error bars) modifications in the ρ₀ and tilt angles were applied to that backbone structure. The atom radii defined by Richardson (33) were used to determine atomic contacts, with atom radius overlaps >0.35 Å considered severe steric clashes.

2. The d_δ-γ should be ≤3.9 Å to be consistent with the NMR restraint (31).

3. The conformations of the His and Trp should be ones of the PRL rotamers. This constraint accounts for the preference of the dihedral angles.

4. There is no unavoidable steric clash between the His-37–Trp-41 adduct and the other side chains. To this end, the surviving combinations were energy minimized with the His-37 and Trp-41 residues kept frozen, and then the atomic contacts were rechecked in the same way as specified in constraint 1.

Geometry optimizations

Geometry optimizations for the adduct formed by one histidine and one tryptophan were performed at the B3LYP level of theory with 6-31G** basis set using Gaussian 98 software. The initial structure of the adduct was obtained by cutting out one His-37 and one Trp-41 residue for which the d_δ-γ was <3.9 Å for a given conformation from the aforementioned M2-TMP structure (31). The C- and N-ends of each residue were capped by the −NH₂ and −COCH₃ groups, respectively, to mimic the peptide bonds. The atoms in the backbone were kept frozen in the optimizations. The optimization results were reproduced with slightly different starting structures for each conformation.

MD simulations

Our preliminary MD simulations indicated that with the tetrameric bundle of the M2-TMP channel structure is quite unstable with a tilt angle of 38° as proposed by Cross and co-workers. (31). Two of the four helices were observed to bend so much that the pore at the N-end became essentially sealed. This behavior contradicts the experimental observation that the backbones are almost ideal α-helices (15), and the instability can be considerably improved by reducing the tilt angle to 30° and increasing the ρ₀ angle by roughly 10° (both changes are still within the range of the experimental uncertainties). This backbone structure was used throughout the MD simulations. The remaining small distortion in the backbone was considered an artifact due to the force fields that were essentially parameterized for polar environments. Stiffer α-helices with stronger hydrogen bonds within the backbone have been observed for membrane peptides (34). To be consistent with the experimental observation that the α-helices have little distortion (15), harmonic position restraints with a small force constant (1.2 kcal/mol/Ų) were applied on the α-carbon atoms in our production simulations.

The channel structure with the desired conformation of the His-37 and Trp-41 residues were placed into a well-equilibrated and fully solvated DMPC bilayer. Additional waters were added into the channel lumen to solvate the pore, resulting in a system containing a complete M2-TMP channel, 82 DMPC lipid molecules (41 for each monolayer), 1 Na⁺ counter ion, and 2888 water molecules. To avoid artifacts due to a single force field, the MD simulations were independently performed with the Amber99 (parm99 data set (35) for the protein and the sodium plus an Amber-compatible force field for the DMPC lipid (36)) and OPLS-AA force fields (37). The simulations were run using DL_POLY version 2.13 (38) (with the Amber99 force field) and GROMACS version 3.1.4 (39) (with the OPLS-AA force field).

The MD simulation conditions were as follows: the system was placed into a periodic box and coupled with a Nosé-Hoover thermostat (40,41) and a Hoover barostat (42) (or a Berenderson barostat (43) in GROMACS) so that the temperature and pressure of the system could be maintained at 310 K and 1 atm with the relaxation times of 0.2 and 1 ps, respectively. Long-range Coulomb interactions were treated using the particle mesh Ewald method with a real space spherical cutoff (radius = 10.0 Å) and a computing precision of 10⁻⁵ (44). The short-range van der Waals interactions were described by the Lennard-Jones potential with a spherical cutoff (radius = 10.0 Å), and its long-range dispersion effects were compensated for both the energy and the pressure (45). All bond lengths were constrained with the SHAKE method (46) (or the LINCS method (47) in GROMACS). The equations of motion were integrated using the leapfrog algorithm with a time step of 2 fs.

The system was equilibrated for 400 ps with strong position restraints on both the backbone atoms and the heavy atoms of the side chains of the His-37 and Trp-41 residues, allowing the lipid, water, the ion, and the other protein side chains to fully relax. Then the equilibrated structure was used for 5-ns production runs without restraints on the side chains. To avoid artifacts due to a single starting structure, the production simulations were repeated with two different starting structures that were the snapshots at 300 and 400 ps of the equilibration trajectories.

RESULTS

Possible conformations for the closed state

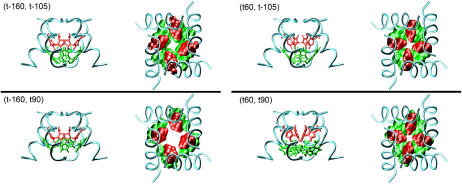
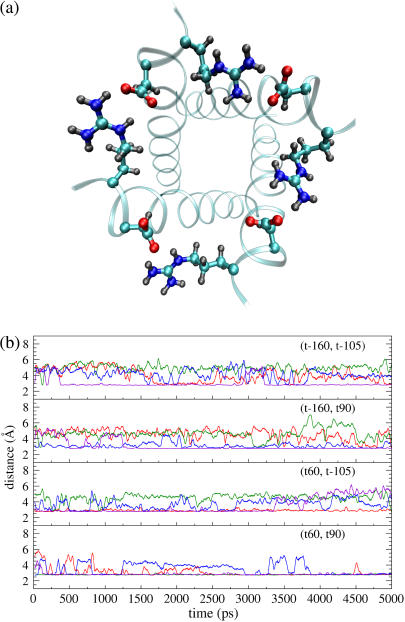
Based on the solid-state NMR restraint and Cross and co-workers' backbone structure (31), a conformation scan (see Methods) was performed in this study. This approach represents a more thorough search for possible conformations than that by the previous study (31), where only the χ₂ angle of His-37 was scanned, and the χ₁ angles of both His-37 and Trp-41 were fixed (presumably) to the ideal value (−177°), which leads to the exclusion of other possible rotameric states (see below). The scan reveals four possible conformations such that the His-37 residues can be in either the t-160 or t60 state, and Trp-41 in either the t-105 or t90 state (see Table 1; representative structures illustrated in Fig. 1). It was confirmed that the His-37 and Trp-41 residues must be from two neighboring helices to satisfy the NMR restraint (31). The pore radius profiles (supplementary Fig. S1) show that in all conformations the His-37 and Trp-41 residues form the only constrictive region where the overall pore radius quickly drops from >3 to <1.8 Å, implying that a considerable desolvation effect may be associated with ions passing the constrictive region. The minimal pore radius in (t-160, t90), in contrast to the other states, is slightly larger than the van der Waals radius of water (∼1.4 Å), implying that it may not be a closed state for protons.

TABLE 1.

Possible conformations of His-37 and Trp-41

Dihedral angles (°)
His-37		Trp-41		Rotamers
χ1	χ2	χ1	χ2	His-37	Trp-41
160–170	190–200	150–160	280–290	t-160	t-105
160–170	160–190	170–210	090–100	t-160	t90
150–160	50–70	150–170	270–290	t60	t-105
150–160	050–110	160–210	090–100	t60	t90

The dihedral angles were obtained via conformation scan with a discretization of each angle by 10°. These conformations do not have steric clashes and are consistent with both the NMR restraint (d_δ-γ ≤ 3.9 Å) (31) and the penultimate rotamer library (32). The PRL rotamer nomenclature is used here.

FIGURE 1.

The representative structures of the four possible conformations for the closed state. The coils represent the backbones. The left image of each pair is the side view with the side chains of the His-37 and Trp-41 residues depicted in the stick model. The right one of each pair is the top view (from the N-end to the C-end) with the side chains depicted in the space-filling model. The residues in red color are His-37, while those in green color are Trp-41. Note that the pore in the (t-160, t90) conformation is obviously larger than those in the other conformations.

A further constraint on the possible rotameric states can be imposed by examining the motionally averaged dipolar coupling between ¹⁵N_δ-His-37 and ¹³C_γ-Trp-41. Both (t-160, t-105) and (t-160, t90) satisfy the last constraint (note that (t-160, t90) was previously excluded in reference (31) by mistakenly assuming that the t90 state would result in severe steric clashes), whereas (t60, t-105) can be safely excluded because its dipolar coupling is too small. The dipolar coupling of (t60, t90) is, however, elusive due to its high sensitivity to the uncertainties in the structural parameters of the backbone, e.g., the tilt and ρ₀ angles and the interhelical distance (see supplementary Tables S1 and S2 for detailed comparison results). For this reason, these three candidates were further examined by their structural stabilities as described below; the (t60, t-105) state was also included (as a negative control) without prior distinction from the others.

Optimized geometries and energetics of the His-37–Trp-41 adduct in different conformations

To distinguish the internal conformational stability of the His-37–Trp-41 adduct in different conformations, the structures were optimized at the B3LYP level with the 6-13G** basis set for the four conformations and for both monoprotonation states (MPS) of the histidine. The results are summarized in supplementary Table S3; (t-160, t90, ɛ), (t60, t90, ɛ), and (t-160, t90, δ) experienced alterations in their rotameric state after the optimization—an indicator of instability of the original conformation, and therefore they were excluded from further consideration. The MPS can have a remarkable effect on the energetics of the adduct, and so the ones with lower energies were chosen for further consideration, giving the following states: (t-160, t-105, ɛ), (t60, t-105, δ), and (t60, t90, δ). Finally, the consistency with the NMR restraint (d_δ-γ ≤ 3.9 Å) is considered. The d_δ-γ's of the optimized structures for the remaining states are 4.6, 4.3, and 4.0 Å, respectively; (t60, t90, δ) is obviously in best agreement with the NMR result. Fig. 2 shows its optimized geometry, where the δ-hydrogen of His-37 is seen to be directed toward the hexamer ring of the indole moiety of the tryptophan, suggesting a stabilizing hydrogen-π interaction that is not observed for the other states. The prediction of the δ-MPS of His-37 is in agreement with the NMR result where a ¹H-¹⁵N_δ dipolar coupling has been detected (31).

FIGURE 2.

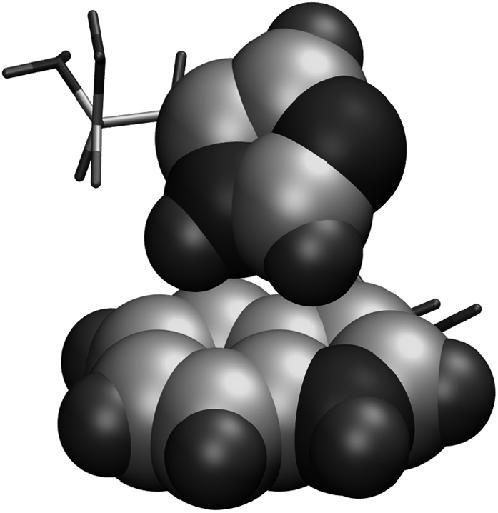
The structure of the (t60, t90) conformation that was optimized at the B3LYP level of theory with the 6-31G** basis set. The imidazole and indole moieties are depicted in the space-filling model with the carbon, nitrogen, and hydrogen atoms represented as large gray, large black, and small black balls, respectively. Note that the δ-hydrogen of the His-37 residue is pointed toward the hexamer ring of the indole moiety of the Trp-41 residue, implying a hydrogen-π interaction between the two side chains.

Equilibrium structures of the His-37 and Trp-41 residues in MD simulations

To further evaluate the stability of the different conformations with δ-MPS in the complete channel environment, MD simulations were performed. To avoid artifacts from a single force field, the simulations were conducted with two different force fields—Amber99 and OPLS-AA, as stated earlier. Very similar results were obtained, and hereby only those from the Amber99 force field are presented unless stated otherwise.

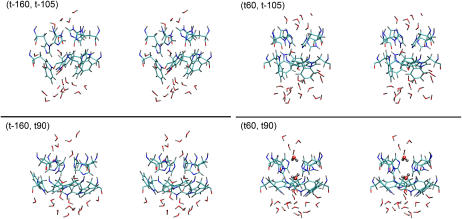
Fig. 3 illustrates the representative equilibrium structures of the His-37 and Trp-41 residues and nearby water molecules. The conformation of His-37 have dramatically changed in the (t-160, t-105) and (t-160, t90) simulations: the structure of the side chains of His-37 protrude into the channel lumen, occluding the pore, which is in striking contrast to the initial structures where the side chains stick to the channel wall (Fig. 1). Comparatively, the conformation of His-37 appears more stable in the (t60, t-105) and (t60, t90) simulations with much smaller deviation of the side-chain conformation from the starting structure. The side chains of Trp-41 in the t-105 state essentially changed their conformation by rotating themselves into the lumen so to minimize the free energy penalty of solvating the nonpolar bulky side chains by water, whereas in the t90 state, they are much less exposed to water and thus avoid such a free energy penalty, showing a consistent structure with the t90 state.

FIGURE 3.

The final structures (stereo views) of the His-37 and Trp-41 residues of the MD simulations. The residues are depicted in the stick model. The angled sticks are the water molecules. The elements C, N, O, and H are, respectively, in light blue, dark blue, red, and gray colors. The two water molecules above and below the His-37 tetrad in the (t60, t90) conformation are presented in the stick-and-ball model, and note their opposite orientations and the hydrogen bonds formed between the pore water molecules and the ɛ-nitrogen of the His-37 residues.

It should be noted that the pore water chain is completely interrupted in all structures. There are only a few water molecules in the constrictive region. Interestingly enough, the water molecules below and above the His-37 tetrad exhibit opposite orientations in (t60, t90), which has important implications for the gating mechanism for protons as will be discussed later.

Structural stability of the His-37 and Trp-41 residues in MD simulations

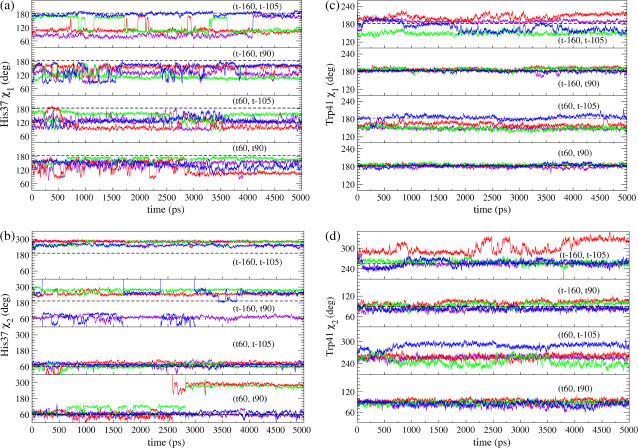
The dihedral angles of the side chains are shown in Fig. 4 as a function of time. In the (t60, t90) simulation, all His-37's χ₁ angles stay in the trans conformation (160°) for most of the time; whereas in the (t-160, t-105) simulation only one His-37 residue keeps the trans conformation, and the others are instead stabilized at 90°. The His-37's χ₂ angles are also much more stable in the t60 state than in the t-160 state. With the Amber99 force field, two of the four His-37 χ₂ angles in the simulation of the (t60, t90) conformation were observed to be unstable with a considerable change from 60° (or 120°) to 280° at roughly 2.6 ns, which is, however, not surprising given that the potential energy barrier for a dihedral angle is normally of the order of roughly 5 kcal/mol (48) and that the corresponding potential in the Amber99 force field is actually zero. This fluctuation was not observed with the OPLS-AA force field where the highest stability of the t60 conformation still holds.

FIGURE 4.

The dihedral angles of the side chains of the His-37 χ₁ (a) and χ₂ (b) and Trp-41 χ₁ (c) and χ₂ (d) residues as functions of time. Different colors correspond to different monomers. The black dashed lines indicate the favorable value of the corresponding rotamer in the penultimate rotamer library.

Trp-41's χ₁ and χ₂ angles are extremely stable in the t90 conformation, with almost no deviation from the original value throughout the whole length of simulation, whereas they fluctuate considerably in the t-105 conformation.

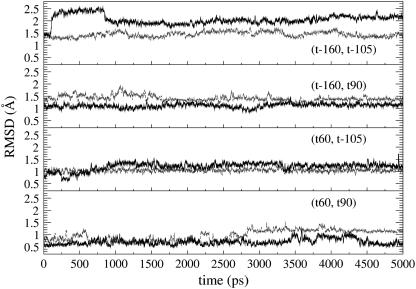
Root mean square deviations (RMSD) were calculated for the His-37 and Trp-41 residues with respect to their starting structure (Fig. 5). The (t60, t90) simulation has the smallest RMSDs (1.02 ± 0.21 Å and 0.77 ± 0.16 Å for His-37 and Trp-41, respectively), followed by (t60, t-105). The (t-160, t-105) simulation has the largest RMSDs (1.44 ± 0.10 Å and 2.06 ± 0.18 Å for His-37 and Trp-41, respectively). These data indicate that (t60, t90) is the most stable conformation among the four candidates, consistent with the above dihedral angle analysis.

FIGURE 5.

The root mean square deviation (RMSD) of the side chains of the His-37 (gray) and Trp-41 (black) residues for different conformations.

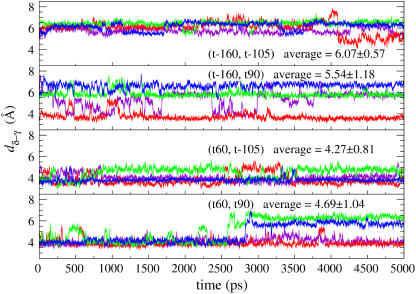
Reproduction of the solid-state NMR restraint was examined by calculating d_δ-γ as a function of time (Fig. 6). The average d_δ-γ's (over time and over the tetramer) of all conformations are >3.9 Å. The smallest average d_δ-γ is that of the (t60, t-105) simulation, followed by (t60, t90). The worst agreement with the NMR restraint is again the (t-160, t-105) simulation. For the (t60, t90) and (t60, t-105) simulations, there are two or three His-37–Trp-41 pairs whose d_δ-γ's are ∼3.9 Å throughout the whole length of simulations. A significant deviation was observed for two of the four His-37–Trp-41 pairs in the (t60, t90) simulation, which is due to the χ₂ angle change as shown in Fig. 4 b and was again not observed with the OPLS-AA force field.

FIGURE 6.

The distance (d_δ-γ) between the δ-nitrogen of His-37 and the γ-carbon of Trp-41 as functions of time for different conformations. The value in each panel is the average d_δ-γ over the time and monomers.

Asp-44–Arg-45 salt bridges and their stability

It was found from our simulations that the Asp-44 and Arg-45 residues could form interhelical salt bridges. To our knowledge, this has not been noticed in earlier simulation studies, probably due to the fact that the ρ₀ angle was improperly defined whereas our backbone model is based on the experimental data (16,18). Incorrect ρ₀ angles often result in intrahelical salt bridges or no bridges at all according to our previous simulations. Fig. 7 a shows a representative structure of the salt bridges taken from the (t60, t90) simulation. In this structure, both residues adopt extended conformations so that the 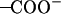group of Asp-44 approach and form a salt bridge with the 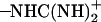group of Arg-45 from a neighboring helix, implying that they may play important roles in stabilizing the overall tetrameric architecture.

FIGURE 7.

(a) The final snapshot of the (t60, t90) simulation, demonstrating well-formed salt bridges between the Asp-44 and Arg-45 residues, where the coils represent the backbone structure and the elements C, N, O, and H are, respectively, in light blue, dark blue, red, and gray colors. (b) The minimal distance between the 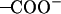group of Asp-44 and the 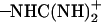group of Arg-45 as functions of time for different conformations. The different colors in b correspond to different monomers.

The stability of the salt bridges could be greatly influenced by conformations of the nearby residues (e.g., Trp-41 and His-37), which arises because the bulky side chain of the tryptophan residue is close to, and therefore may interfere, with the salt bridges due to the steric effects. For example, it was observed from the simulation trajectories that with the t-105 conformation the side chains of Trp-41 can stay in between the Asp-44 and Arg-45 residues, breaking the salt bridges. The strength of salt bridges can be quantitatively represented by the minimal distance between the two charged groups. In Fig. 7 b, the minimal distance between the 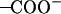and 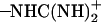groups are plotted as a function of time for each conformation. This quantity in the (t60, t90) simulation is very small (3–4 Å) for all Asp-44–Arg-45 pairs, whereas only one or two pairs in the other simulations could keep the minimal distance under 4 Å, which suggests that the salt bridges in the (t60, t90) conformation are stronger than those in the other conformations, thus lending additional support to the proposition that (t60, t90) is the most stable state.

A possible open structure corresponding to the (t60, t90) closed structure

The correct closed structure should also allow for an open structure to be accessible through reasonable conformational changes of the residues. As mentioned above, it was noticed that the (t-160, t90) conformation seems like an open structure, which can be formed from the (t60, t90) conformation simply via rotating the His-37's χ₂ angle by roughly 100–140°. A very similar open structure could be obtained from the (t-160, t90) conformation by flipping the imidazolium moiety by 180° around the bond connecting the β-carbon and γ-carbon atoms of the histidine. Changing to the latter conformation (denoted (t0, t90) in this article; note t0 is not a standard rotamer in the PRL) from (t60, t90), the His-37's χ₂ angle only needs to rotate by roughly 40–80°.

To compare the stabilities of the two conformations, geometry optimizations were performed for the His⁺-Trp adduct using the same density functional theory methodology as mentioned earlier. The energies of the relaxed structures indicate that the (t0, t90) conformation is roughly 5 kcal/mol more stable than the (t-160, t90) conformation. Therefore, (t0, t90) seems more likely to be the open structure for (t60, t90).

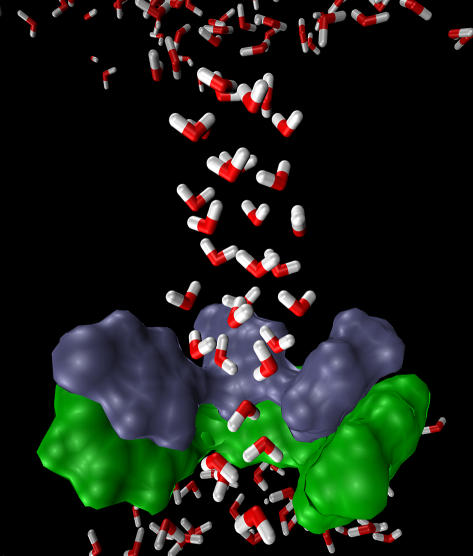
An MD simulation was performed to examine if the (t0, t90) conformation actually corresponds to an open structure. In the simulation, the heavy atoms of the His-37 and Trp-41 residues were restrained to their ideal positions, and all His-37 residues were protonated. The simulation lasted for 950 ps. A representative equilibrium structure of the pore water molecules is shown in Fig. 8, demonstrating a continuous water column throughout the channel. The pore radius of the narrowest region is still very small—only one water molecule can be accommodated, suggesting that transport of nonproton ions may be blocked due to a large desolvation penalty. The selectivity of this channel can therefore be rationalized with this open structure.

FIGURE 8.

The final snapshot of the MD simulation for the (t0, t90) conformation where the four His-37 residues are all protonated, demonstrating the structure of the pore water (highlighted angled sticks in the picture). The His-37 (blue) and Trp-41 (green) residues are depicted as van der Waals surfaces. For the sake of clarity, one pair of His-37 and Trp-41 is not shown. Note that the pore water is able to penetrate the constrictive region lined by the His-37 and Trp-41 residues and that the ordered pore water structure may be restrictive for protons to hop into the channel.

Fig. 8 also reveals an ordered pore water structure that can impede protons from hopping into the channel, which is mainly due to the fact that all of the His-37 residues are positively charged in this simulation. The exact protonation state of the four His-37 residues for the open channel is still unknown. The implication of the extremely ordered pore water structure on this point will be discussed in the next section.

DISCUSSION

Our conformation scan has revealed four possible conformations for the closed state structure of the M2 channel, i.e., the (t-160, t-105), (t-160, t90), (t60, t-105), and (t60, t90) rotameric states. In all of these conformations, a narrow pore region is formed by the His-37 and Trp-41 residues. The simulated dipolar coupling calculation indicates that the (t60, t-105) state can be safely excluded, whereas the other states cannot be distinguished (see supplementary Tables S1 and S2 for details). This result contradicts the previous conclusion that (t-160, t-105) was the only state consistent with the NMR distance restraint and the ¹⁵N_δ-His-37–¹³C_γ-Trp-41 and ¹H–¹⁵N_δ-His-37 dipolar couplings (31), which, we believe, was mistakenly drawn from an incomplete search through the conformational space. More specifically, it seems that in the previous study, only one value (177°) of the trans state for the χ₁ angles of both His-37 and Trp-41 was taken into account; in addition, the effects of the uncertainties in the backbone structure on the dipolar coupling are significant.

In this study, the further distinction of the conformations was based on their respective structural stability. Our data consistently indicate that (t60, t90) is the most stable state of the four candidates. In addition, the interhelical salt bridges formed by the Asp-44 and Arg-45 residues are found to be most stable with the (t60, t90) state. Therefore, (t60, t90) seems likely to be the most probable structure for the closed state over the other candidates.

In the (t60, t90) state, possible hydrogen-π interactions between His-37 and Trp-41 have been noticed (Fig. 2). This interaction may stabilize the (t60, t90) conformation and lead to cooperative motion of the two residues. Mutating out either residue would thus destabilize or even destruct the wild-type conformation of the other residue, which in turn results in a more open and/or weakly selective channel. This analysis is in good agreement with mutagenesis results. In particular, it has been shown that replacing His-37 with Ala, Glu, or Gly results in a large increase in proton conductance and loss of pH-induced gating behavior (7,9), and with Glu it can also weaken the selectivity (9). Furthermore, the structure of Trp-41 can hide the side chains of the His-37 residues from the C-end bulk water, assuring that the histidine residues are not accessible by ions coming from the C-end. Replacement of Trp-41 with Phe, Cys, Tyr, or Ala enables the channel to be more easily activated by pH_in (30). One phenomenon observed in experiments for the Trp-41Tyr mutant is that, unlike the other mutants, it cannot be activated by low pH_in (30). This can be well explained with the (t60, t90) closed state structure: Tyr-41 can provide a hydroxyl group to form a hydrogen bond with the δ-hydrogen of His-37. The hydrogen bond resembles the hydrogen-π interaction, and thus a similar structure of the His-37 and Tyr-41 residues to (t60, t90) can be adopted such that the side chains of the His-37 residues can be well covered by Tyr-41 and thus avoid being exposed to the water at the C-end.

The (t60, t90) closed-state structure demonstrates that the constrictive region of the channel is formed by both His-37 and Trp-41. This region is narrow enough to prevent nonproton ions from passing through the channel due to steric and desolvation effects. It is noted that the pore water molecules below and above the His-37 tetrad adopt opposite orientations (Fig. 3), forming hydrogen bonds with the ɛ-nitrogens of the His-37 residues rather than with the water molecule at the other side of the tetrad. This structure suggests that protons cannot go through the constrictive region without protonating at least one of the His-37 residues first. The four ɛ-nitrogens of the His-37 residues are unprotonated and are pointed toward the center of the channel. The distance between two ɛ-nitrogen atoms in the diagonal corner is roughly 4.8–6 Å, which suggests that the His-37 tetrad in the (t60, t90) conformation could be a good chelating site for a Cu²⁺ ion, providing a reasonable explanation to the observation that the M2 channel can be inhibited by Cu²⁺ ions (49).

The orientation of the imidazole ring of the His-37 residues in the (t60, t90) conformation is worth special attention: The ɛ-nitrogen atoms are pointed toward the center and are the only acceptors of the protons coming from the N-end, whereas the δ-nitrogen atoms are pointed to the indole ring of Trp-41 and cannot form hydrogen bonds with pore water. This characteristic of the (t60, t90) structure does not support the shuttle mechanism that requires both nitrogen atoms of the imidazole side chain of His-37 to be able to form hydrogen bonds with the pore water so that the imidazole moiety can accept a proton at one side and release another proton at the other side. To change to the required orientation from the t60 state, relatively large conformational change involving both χ₁ and χ₂ angles of His-37 has to occur. Moreover, the tautomerization of the imidazole moiety of His-37, as being used in the shuttle mechanism to explain how the next proton would be transported, is difficult to justify from the atomic details. A variant of the shuttle mechanism could be a load-flip-deliver cycle: for instance, the imidazole moiety accepts a proton from one side, and then the imidazolium ring is flipped so that the proton can be released to the other side, after which the imidazole ring is flipped back to the original orientation and ready for “shuttling” the next proton. Though reasonable, this picture requires much more complicated conformational behavior of the His-37 residues. Due to these issues, the shuttle mechanism is less favored than the much simpler shutter mechanism by the (t60, t90) conformation.

A correct closed structure should allow a reasonable open structure to be found to which the closed one can change without an obviously large energy penalty. This is a favorable characteristic of the (t60, t90) conformation. Our results suggest that such an open structure can be obtained via a minimal conformational change—simply rotating each His-37's χ₂ angle roughly from 60 to 0°. This open structure allows the pore water molecules to penetrate through the constrictive region while still narrow enough to preserve the proton selectivity (Fig. 8). Furthermore, this structure does suggest that there can be cation-π interaction between protonated His-37 and Trp-41, which is consistent with the ultraviolet resonance Raman spectroscopy data (29). In contrast, a reasonable open structure that can preserve the proton selectivity and allow the cation-π interaction seems very difficult for the (t-160, t-105) conformation unless the Trp-41 residues change to the t90 state.

An extremely ordered pore water structure is noted when all four His-37 residues are charged (Fig. 8). Obviously, the ordered structure should be mainly ascribed to the electrostatic field due to the charged His-37 residues rather than to their conformation. This orientation of the pore water does not favor proton transport into the channel, suggesting that the open state may not be fully protonated, which is in agreement with previous MD simulation results (24), which observed that a four-protonated or three-protonated M2 channel resulted in a distorted backbone. Moreover, a more recent MD simulation study has shown that the M2 channel with only one protonated His-37 residue can indeed open for proton transport (25).

CONCLUSIONS

The conformation scan in this work has revealed four possible conformations of the His-37 and Trp-41 residues, namely the (t-160, t90), (t-160, t-105), (t60, t-105), and (t60, t90) rotameric states, for the closed state of the M2 channel. The latter three states cannot be further distinguished by the available structural information, but our results indicate that the (t60, t90) state is the most stable one that is also consistent with nearly all experimental data so far. Furthermore, an open structure consistent with the shutter mechanism can be found for (t60, t90).

The (t60, t90) conformation and the above analyses suggest a modified gating mechanism that can be proposed as follows: the channel is in the (t60, t90) conformation in its closed state, and when one (or two) of the four His-37 residues is protonated, the conformation of His-37 and Trp-41 is changed, e.g., to the (t0, t90) conformation, which opens the pore for water molecules to penetrate the constrictive region, thus allowing protons to be transported by hopping through the resulting water wire via the Grotthuss mechanism. Future experimental and computational studies will be needed to provide additional insight into the ion conductance properties of the M2 channel.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.