Temperature Dependence and Thermodynamic Properties of Ca²⁺ Sparks in Rat Cardiomyocytes

Abstract

To elucidate the temperature dependence and underlying thermodynamic determinants of the elementary Ca²⁺ release from the sarcoplasmic reticulum, we characterized Ca²⁺ sparks originating from ryanodine receptors (RyRs) in rat cardiomyocytes over a wide range of temperature. From 35°C to 10°C, the normalized fluo-3 fluorescence of Ca²⁺ sparks decreased monotonically, but the Δ[Ca²⁺]_i were relatively unchanged due to increased resting [Ca²⁺]_i. The time-to-peak of Ca²⁺ sparks, which represents the RyR Ca²⁺ release duration, was prolonged by 37% from 35°C to 10°C. An Arrhenius plot of the data identified a jump of apparent activation energy from 5.2 to 14.6 kJ/mol at 24.8°C, which presumably reflects a transition of sarcoplasmic reticulum lipids. Thermodynamic analysis of the decay kinetics showed that active transport plays little role in early recovery but a significant role in late recovery of local Ca²⁺ concentration. These results provided a basis for quantitative interpretation of intracellular Ca²⁺ signaling under various thermal conditions. The relative temperature insensitivity above the transitional 25°C led to the notion that Ca²⁺ sparks measured at a “warm room” temperature are basically acceptable in elucidating mammalian heart function.

INTRODUCTION

Intracellular Ca²⁺ transients that control muscle contractions and other cell activities are composed of the elementary Ca²⁺ events, Ca²⁺ sparks, originated from ryanodine receptor (RyR) Ca²⁺ release channels in the sarcoplasmic reticulum (SR) (for review, see Bers (1) and Berridge et al. (2)). Since their discovery (3), Ca²⁺ sparks have been found in cardiac, skeletal, and smooth muscle cells, glias, and neurons (4–8) and provide molecular interpretations for intracellular Ca²⁺ signal transduction. However, despite extensive studies of Ca²⁺ sparks during the past decade, most measurements of Ca²⁺ sparks were performed under room temperature (22 ∼ 25°C). One of a few studies that measured Ca²⁺ sparks with temperature control, to our knowledge, was reported by Wier et al. (9), who demonstrated Ca²⁺ sparks in quiescent rat trabeculae at 33°C and suggested that Ca²⁺ sparks can occur above room temperature and are not restricted to dissociated myocytes. A comparison of Ca²⁺ sparks at different temperatures was not seen until the recent work by Ferrier et al. (10), who showed that a temperature increase from 22°C to 37°C significantly reduces the normalized fluo-3 fluorescence (ΔF/F₀), time-to-peak, and frequency of Ca²⁺ sparks in mouse cardiomyocytes. Their data provide valuable information for Ca²⁺ sparks at mammalian body temperature (although we have different results in this study), yet the full picture of temperature dependence of Ca²⁺ sparks is not known.

Temperature has comprehensive influence on most (if not all) biochemical processes, including intracellular Ca²⁺ signaling. In mammals, neural transmission, muscle contraction, and heart beating, which depend heavily on intracellular Ca²⁺ dynamics, are most vigorous at their normal body temperature. Lowering temperature not only slows down the kinetics of neuromuscular activities but also causes metabolic and functional problems. In humans and dogs, for example, a hypothermia lower than 25 ∼ 28°C usually results in severe ventricular fibrillation and cardiac arrest (11), a problem that has restricted the clinical application of cryo-anesthesia. When isolated and bathed in an artificial environment, cardiac myocytes from rats and rabbits exhibit slower contractions at lower temperatures and gradually lose contractility when the temperature is below ∼20°C (12,13). Measurement of intracellular free Ca²⁺ concentration ([Ca²⁺]_i) showed that the amplitude of Ca²⁺ transient decreases dramatically at low temperatures, implying a dysfunction of the excitation-contraction coupling apparatus (14). Because Ca²⁺ sparks represent the elementary Ca²⁺ release events, understanding the temperature dependence of Ca²⁺ sparks is fundamental for elucidating the cardiac function under various physiological conditions, including euthermia and hypothermia.

In this study, we measured Ca²⁺ sparks in rat ventricular myocytes over a wide temperature range from 35°C to 10°C. We quantified the temperature sensitivity of Ca²⁺ spark morphology and kinetics and analyzed the underlying determinants from the thermodynamic point of view.

METHODS

Cell preparation

Ventricular cardiac myocytes from adult Sprague-Dawley rats (age, 2–3 months; weight, 225–300 g) were prepared as previously reported (15,16). Briefly, the hearts were rapidly excised from the animals under ether anesthesia and perfused for 5 min at 37°C with a calcium-free buffer containing (in mM): 110 NaCl, 4 KCl, 1.2 MgCl₂, 1.2 NaH₂PO₄, 20 NaHCO₃, 30 taurine, 10 glucose, aerated with 95% O₂ + 5% CO₂, pH 7.35. The tissue was then digested in a buffer containing 0.5 mg/ml collagenase (Sigma (St. Louis, MO), Type 1A), 1% bovine serum albumin (Sigma, fraction V), and 75 μM Ca²⁺ for 15 min. The ventricle was then cut into small pieces and incubated in digesting solution. Finally the myocytes were harvested and stored in Tyrode's solution which contained (in mM): 135 NaCl, 4 KCl, 1.0 CaCl₂, 1.2 MgCl₂, 1.2 NaH₂PO₄, 10 glucose, 5 HEPES, pH 7.35 adjusted by NaOH. Ca²⁺ indicators were loaded into cells before experiments by exposing the cells to 2.5 μM fluo-3 acetoxymethyl ester or indo-1 acetoxymethyl ester (Molecular Probes, Eugene, OR) in Tyrode's solution for ∼5 min or 20 min, respectively, in the dark at 37°C.

Recording and analysis of Ca²⁺ sparks

In Ca²⁺ spark recording, the fluorescence of fluo-3-loaded cells was measured with a Zeiss LSM510 confocal microscope equipped with an argon laser and a 40×, 1.3 numerical aperture oil immersion objective and adjusted to axial and radial resolutions of 1.5 and 0.5 μm, respectively. The cells were scanned with a 488 nm laser, and the fluorescence was separated by a 495-nm dichroic mirror in combination with a 500-nm long-pass filter. Line-scan (x-t) imaging was performed with a sampling rate of 0.78 ms per scan line.

Ca²⁺ spark analysis was performed using an IDL routine as reported previously (17,18). In brief, after a minimal (3 × 3) smooth, the original fluorescent data (F) were normalized by resting fluorescence (F₀). The threshold for the program to pick up events was set at 1.25 F/F₀. The amplitude, full width at half-maximum (FWHM), full duration at half-maximum (FDHM), time-to-peak, rate-of-rise, and half-decay time of Ca²⁺ sparks were determined automatically with the routine. When necessary, the Δ[Ca²⁺]_i of Ca²⁺ sparks were calculated using the formula

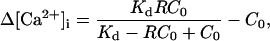(1)

in which R = F/F₀, C₀ is the resting [Ca²⁺]_i measured as described below, and K_d is the dissociation constant of fluo-3 (3). As the K_d of fluo-3 is almost temperature independent at physiological pH (19), taking into account the influence of intracellular environment on K_d of fluo-3 (20), an approximate value of 1 μM was used to calculate the Δ[Ca²⁺]_i.

Measurement of resting Ca²⁺ concentration

Most previous calculations of the intracellular free Ca²⁺ concentration ([Ca²⁺]_i) corresponding to Ca²⁺ sparks were based on an assumed value of resting [Ca²⁺]_i (usually set at 100 nM). However, the resting [Ca²⁺]_i itself changes significantly with temperature (14,21). To access the [Ca²⁺]_i profile of Ca²⁺ sparks at different temperatures, we used the ratiometric Ca²⁺ indicator, indo-1, to determine the resting [Ca²⁺]_i in ventricular myocytes under otherwise the same experimental settings as in spark measurement. Cells were loaded with indo-1 by exposure to 2.5 μM indo-1/AM in Tyrode's solution for ∼15 min in the dark at 37°C. The indo-1 fluorescence was visualized and measured by an ASCS Meridian 575 UV confocal microscope equipped with a UV laser. The fluorescence was separated by a 450-nm dichroic mirror into two channels with 485/45 nm and 405/45 nm bandpass filters, respectively. The intracellular Ca²⁺ concentration was calculated by the formula

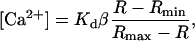(2)

in which R is the ratio of fluorescence detected at 405 nm versus that detected at 480 nm, R_max and R_min were the R in Ca²⁺-free and Ca²⁺-saturated buffers, respectively, and β is the ratio of 480 nm fluorescence in Ca²⁺-free versus in Ca²⁺-saturated buffers. The dissociation constant, K_d, of indo-1 at different temperatures was determined as previously reported (15).

Temperature control

To control the bathing temperature while using an inverted confocal microscope, we designed a temperature-control chamber in which a circular glass cannula was fixed on the center of a coverslip-bottomed petri culture dish. The glass cannula formed a 0.5 ml reservoir for bathing the cells. Temperature was controlled by perfusing the circular glass cannula with a Cole-Parmer refrigerated circulator. A tiny bithermal thermistor probe was attached on the glass bottom of the dish to monitor the temperature. When there was 0.3 ml solution in the chamber, the temperature difference between the center and the periphery of the useful area of the coverslip was <0.5°C. In the experiments, temperature was altered alternately from 35°C to 10°C and from 10°C to 35°C to avoid time-dependent effects. At each temperature, cells were allowed at least 5 min for equilibrium.

Statistics

The data are presented as mean ± SE. One-way analysis of variation with repeated measures was used to analyze the significance of the effects of temperature and other factors. p < 0.05 was considered significant.

RESULTS

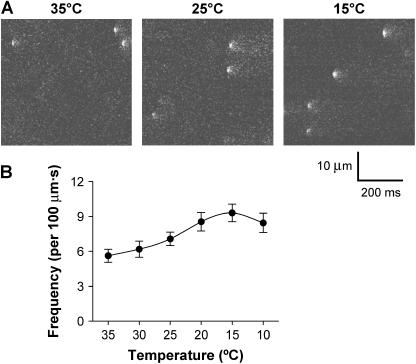
Using confocal microscopy in line-scan mode, spontaneous Ca²⁺ sparks were recorded at every 5°C from 35°C to 10°C. Fig. 1 A shows typical line-scan images recorded at 35°C, 25°C, and 15°C, respectively. With the decrease in temperature from 35°C, the frequency of Ca²⁺ sparks increased progressively until reaching a maximum at 15°C (Fig. 1 B). For a clear demonstration of the temperature-dependent change of Ca²⁺ spark morphology, we averaged 64 Ca²⁺ sparks randomly sampled at 35°C, 25°C, and 15°C, respectively, which would improve the signal/noise ratio by eightfold. The two-dimensional and three-dimensional images of the averaged data (Fig. 2) show that temperature modified both amplitude and spatiotemporal features of Ca²⁺ sparks.

FIGURE 1.

Confocal imaging of spontaneous Ca²⁺ sparks. (A). Representative line-scan images recorded in a rat ventricular myocyte at 35°C, 25°C, and 15°C (from left to right), respectively. For each image, time runs horizontally, and space runs vertically. (B). Temperature dependence of Ca²⁺ spark frequency (n = 17 cells each; p < 0.05). The frequency was calculated by dividing the total number of Ca²⁺ sparks by the product of distance (μm) and time (s) of line scanning.

FIGURE 2.

Two-dimensional and three-dimensional demonstration of the averages of 64 original Ca²⁺ sparks recorded at 35°C, 25°C, and 15°C, respectively. The original events were aligned by their takeoff times and spatial mass centers.

The amplitude of Ca²⁺ sparks

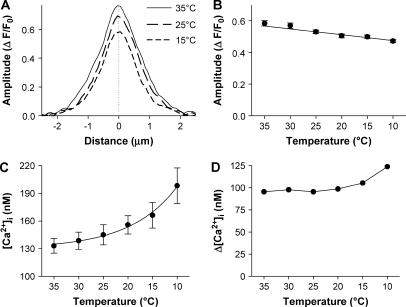
Fig. 3 A illustrates the local Ca²⁺ profiles at 35°C, 25°C, and 15°C when the averaged sparks reached their peaks, which demonstrated that the lower the temperature, the lower the spark amplitude. Original data show that the amplitude of Ca²⁺ sparks, when expressed in ΔF/F₀, was decreased significantly from 0.58 ± 0.02 at 35°C to 0.47 ± 0.01 at 10°C (Fig. 3 B, p < 0.05).

FIGURE 3.

Temperature dependence of spark amplitude. (A). An overlay of the spatial profiles at the peak of the averaged sparks shown in Fig. 2. (B). Temperature dependence of spark amplitude (F/F₀). Each data point represents an average of more than 240 sparks from 17 cells in six animals (p < 0.05). (C). Temperature dependence of resting [Ca²⁺]_i in rat ventricular myocytes (n = nine cells from three animals; p < 0.01). (D). Ca²⁺ spark amplitude in terms of Δ[Ca²⁺]_i was calculated from the data in B and C using Eq. 1.

During the decline in temperature, the baseline (visualized as F₀) of intracellular free Ca²⁺ concentration ([Ca²⁺]_i) would not remain constant (14,21). Therefore, the change of ΔF/F₀ of Ca²⁺ sparks may not be comparable among different temperatures. To assess the underlying Δ[Ca²⁺]_i of Ca²⁺ sparks, we determined the resting [Ca²⁺]_i by ratiometric confocal microscopy using indo-1 as the Ca²⁺ indicator. The measurement showed that resting [Ca²⁺]_i increased monotonically with lowering temperature (Fig. 3 C). Based on this measurement, we calculated the Δ[Ca²⁺]_i of spark amplitude. As shown in Fig. 3 D, the Δ[Ca²⁺]_i of Ca²⁺ sparks remained constant above 20°C and gradually lifted up at lower temperature range.

Spatiotemporal properties of Ca²⁺ sparks

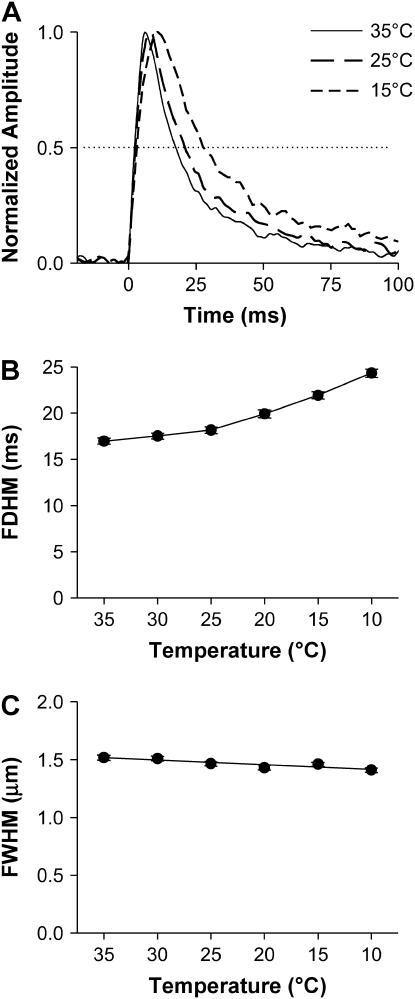
It can be seen in the time courses of Ca²⁺ sparks (Fig. 4 A) that both the rise and decay became slower when the temperature was lowered. The FDHM, a commonly employed index of Ca²⁺ spark kinetics, increased monotonically from 17.0 ± 0.4 ms at 35°C to 24.3 ± 0.5 ms at 10°C (Fig. 4 B). By contrast, the FWHM of Ca²⁺ sparks, which reflexes spatial dispersion of Ca²⁺ sparks, changed little with temperature (Fig. 4 C).

FIGURE 4.

Temperature dependence of the temporal and spatial properties Ca²⁺ sparks. (A). An overlay of the time courses of the averaged sparks shown in Fig. 2. (B). Temperature dependence of FDHM of spark amplitude (F/F₀) (p < 0.01). (C). Temperature dependence of FWHM of Ca²⁺ sparks (p > 0.05).

Time-to-peak of Ca²⁺ sparks

During a Ca²⁺ spark, Ca²⁺ is released from a small number of RyRs and accumulates over time. The data showed that the time-to-peak of Ca²⁺ sparks exhibited bell-shaped distributions, which shifted rightward when temperature went down (Fig. 5 A). The average of time-to-peak increased from 9.7 ± 0.3 ms at 35°C to 13.4 ± 0.3 ms at 10°C (Fig. 5 B).

FIGURE 5.

Thermodynamic analysis of RyR Ca²⁺ release duration. (A). Histograms showing the distributions of time-to-peak of Ca²⁺ sparks at 35°C, 25°C, and 15°C, respectively. (B). Temperature dependence of the time-to-peak of Ca²⁺ sparks (p < 0.01). Note the break of trend at ∼25°C. (C). Arrhenius plot of the reciprocal of time-to-peak. The data were fitted by a combination of two lines with Eq. 3. Best fit was achieved by lines intersecting at 24.8°C.

We noticed in Fig. 5 B that there was a break in slope at ∼25°C. The ratio for every 10°C change (Q₁₀) was 1.05 between 25°C and 35°C but was increased to 1.19 between 10°C and 25°C. A similar phenomenon has previously been described for kinetic parameters of many membrane proteins, such as the turnover rate of sodium pumps (22) and the gating properties of ion channels (23). The discontinuous temperature dependence in Arrhenius plots has been attributed to a phase transition of membrane lipids, which alters the apparent activation energy (E_a) associated with the conformational change of membrane proteins. We speculated that a similar analysis might provide information about the energetic aspects of Ca²⁺ release channels. We plotted the natural logarithm of the kinetic index (k) of the RyR opening (represented by the reciprocal of time-to-peak) against the corresponding reciprocal of absolute temperature (1/T) (Fig. 5 C). The resulting Arrhenius plot could be best fit by two intersecting lines, each described by the Arrhenius equation

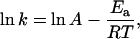(3)

in which R is the gas constant and A is a fitting parameter. The intersection of fitted lines suggested that a transition of SR membrane might occur at 24.8°C. The fitting determined that the apparent E_a for RyR Ca²⁺ release is 5.2 or 14.6 kJ/mol, respectively, at temperatures higher or lower than the transition temperature.

Diffusion of local Ca²⁺

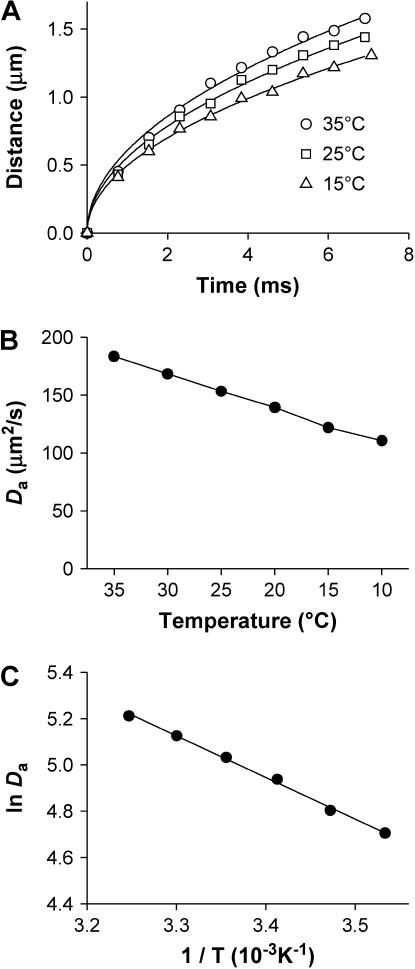
After being released from RyRs, Ca²⁺ diffuses from its origin to adjacent intracellular space. To assess the effect of temperature on Ca²⁺ diffusion, we tracked the apparent wavefronts of Ca²⁺ spark by constructing mono-side contours that cut through the bottom 10% of the averaged Ca²⁺ sparks (Fig. 6 A, symbols). Before Ca²⁺ sparks reached their peak, the distance (x) of the apparent wavefront away from the Ca²⁺ origin was a function of time (t) that could be well described (Fig. 6 A, lines) by the Einstein Diffusion Equation:

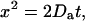(4)

in which D_a is the apparent diffusion coefficient. By fitting the contour data to Eq. 4, we observed that D_a decreased monotonically with temperature (Fig. 6 B). By replacing the kinetic parameter k with dx/dt, the Arrhenius equation (Eq. 3) can be transformed to

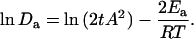(5)

Linear fitting of lnD_a determined an E_a of 8.4 KJ/mol, corresponding to Q₁₀ of 1.12 (Fig. 6 C).

FIGURE 6.

Temperature dependence of the spatial dispersion of spark wavefronts at bottom 10%. (A). Spatiotemporal wave front profiles of the Ca²⁺ sparks, each from the average of 64 original events. The curves represent the fitting to the data with Eq. 4. (B). Temperature dependence of the apparent diffusion coefficient D_a determined as in A (p < 0.01). (C). Thermodynamic analysis of D_a. The solid lines represent linear fitting with Eq. 5.

Recovery of Ca²⁺ sparks

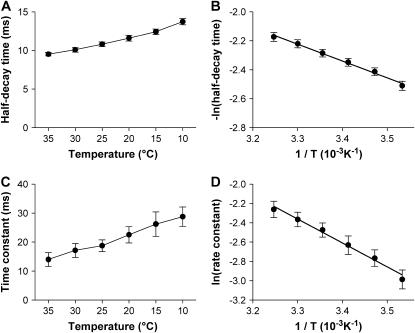
After the closure of RyRs, the local [Ca²⁺]_i declines with time due to diffusion and, possibly, active transports by SR Ca²⁺-ATPase and Na⁺-Ca²⁺ exchange. As Ca²⁺ diffusion and active transports have distinct thermodynamic properties, analysis of the temperature dependence may provide clues regarding how they contribute to the recovery from intracellular Ca²⁺ events. For this purpose, we measured the half-decay time, a commonly employed index of recovery kinetics. As shown in Fig. 7 A, the half-decay time increased monotonically with the decrease in temperature, indicating a slowing down in Ca²⁺ recovery. To quantify its thermodynamic property, we plotted the natural logarithm of its reciprocal against the reciprocal of absolute temperature. Fitting this Arrhenius plot (Fig. 7 B) yielded an apparent E_a of 9.2 kJ/mol, corresponding to Q₁₀ of 1.14. This temperature sensitivity is similar to that of Ca²⁺ diffusion, but differs essentially with those of active transports. Therefore, Ca²⁺ diffusion is the major determinant in the early recovery process of Ca²⁺ sparks.

FIGURE 7.

Thermodynamic analysis of recovery kinetics of Ca²⁺ sparks. (A and C). Temperature dependence of half-decay time (A) and late time constant (C) of Ca²⁺ sparks (p < 0.01). (B and D). Arrhenius plot of the reciprocal of half-decay time (B) and late time constant (D). The solid lines represent linear fitting with Eq. 3.

How about the late recovery phase? We then determined a late time constant by fitting the second half of decay in Ca²⁺ sparks. As shown in Fig. 7 C, the late time constant of Ca²⁺ sparks was prolonged by ∼1-fold from 35°C to 10°C at a Q₁₀ of 1.33. The Arrhenius plot of the corresponding rate constant (reciprocal of the time constant) determined that the apparent E_a for late recovery of Ca²⁺ sparks was 20.6 kJ/mol (Fig. 7 D), well above that of Ca²⁺ diffusion. Therefore, the role of active transports (24) is more important in determining the kinetics of the late, slow phase of Ca²⁺ spark recovery.

DISCUSSION

In this study, by characterizing Ca²⁺ spark properties over a range of temperatures, we have analyzed the factors that shaped up the temperature dependence of Ca²⁺ sparks and revealed relevant thermodynamic parameters involved in intracellular Ca²⁺ signals. The data provide a quantitative basis for interpreting intracellular Ca²⁺ signaling under various thermal conditions, including normal mammalian body temperature and hypothermia.

Gating properties of RyRs reflected in Ca²⁺ sparks

RyR is the Ca²⁺ release channel that mediates Ca²⁺ sparks in heart cells. Because its intracellular location prevents direct electrophysiological measurement, most of our knowledge about its channel properties has been based on in vitro measurements in artificial lipid bilayers (for review, see Fill and Copello (25)). In situ operation of RyRs could not be measured until the finding of Ca²⁺ spark, whose time-to-peak was suggested as an index of RyR open duration. Although an early mathematical deconvolution study of Ca²⁺ flux underlying a Ca²⁺ spark (26) raised a possibility that RyR Ca²⁺ release may outlast the rise phase of Ca²⁺ sparks, it was also pointed out that Ca²⁺ flux reconstruction from individual spark records is problematic due to a low signal/noise ratio (27). With improved quality of imaging enabled by the new generation of confocal microscopic technology, it was recently shown that the rise phase of in-focus Ca²⁺ sparks has the exponential kinetics expected from a square-waveform Ca²⁺ flux (28). Measurement of spark Ca²⁺ flux with a fast, low-affinity Ca²⁺ indicator combined with a slow Ca²⁺ buffer showed that Ca²⁺ release duration and spark time-to-peak are of the same value (29). Therefore, time-to-peak of Ca²⁺ sparks is by far the best approximation of RyR open duration in situ.

Temperature has been used as a tool to understand the kinetics and thermodynamics of ion channels (23,30,31). It has been found that, for most ion channels, the temperature dependence of conductance does not differ significantly from that of a diffusion-limited process; the Q₁₀ usually ranges between 1.1 ∼ 1.5, whereas the gating, in general, shows much greater sensitivity to temperature with Q₁₀ values ranging between 1.5 and 6 (32). For RyRs from sheep cardiac muscle incorporated in lipid bilayers, a decrease in temperature from 23°C to 5–10°C increases single RyR open probability (P_o) from 0.13 to 0.69 in the presence of 10 μM activating Ca²⁺ (33). As the increase in P_o results exclusively from an increase in channel open duration rather than the frequency of channel opening (33), the apparent Q₁₀ for open duration of RyRs in vitro should be ∼3. This value contrasts with the Q₁₀ of 1.25 for RyRs gating in situ in a similar temperature range revealed by time-to-peak measurement in this study.

The difference in the temperature dependence of RyR in situ and in vitro parallels their distinct patterns in gating kinetics. It is known that a single RyR incorporated in lipid bilayers, as almost all other known ion channels, exhibits an exponential open duration distribution (34). This type of open duration distribution is determined by the thermodynamic reversibility of stochastic transition of channel status and is generally shared by all Markovian channels or channel groups that are usually uncoupled from external free energy (35,36). Even coupled gating of multiple RyRs in vitro still satisfies the thermodynamic reversibility, although the synchronized open duration is much prolonged compared to that of a single RyR (37). However, the time-to-peak of Ca²⁺ sparks usually exhibits a bell-shaped distribution, which cannot be explained based on any thermodynamic reversible scenario. We have therefore postulated a model in which the Ca²⁺-induced Ca²⁺ release among adjacent RyRs in situ may couple a certain source of external energy, resulting in a thermodynamically irreversible mode of gating (28,29). In this study, we show that the apparent E_a (14.6 kJ/mol) for RyR Ca²⁺ release is indeed much lower than that estimated for RyRs gating in vitro (∼70 kJ/mol, calculated based on Sitsapesan et al. (33)). We speculate that, among other possibilities, the difference of apparent E_a may possibly reflect the external free energy that drives the irreversible gating.

Temperature dependence involves multiple processes

At any temperature, the Ca²⁺ spark parameters, including amplitude, kinetics, and spatial dispersion, depend on the rates of many different processes, including RyR Ca²⁺ release, Ca²⁺ diffusion and buffering within intracellular microdomains, and Ca²⁺ transports by pumps and exchangers. Some of these rates, such as those of Na⁺-Ca²⁺ exchangers (38,39) and SR Ca²⁺-pumps (40) depend strongly on temperature, with apparent Q₁₀ values ranging between 2 ∼ 4, whereas others (e.g., Ca²⁺ diffusion) are likely to be far less sensitive to temperature with Q₁₀ values <1.3. In the recovery phase of Ca²⁺ sparks, for example, both Ca²⁺ diffusion and active transports contribute to the decay of local [Ca²⁺]_i (24). However, the Q₁₀ of the first half of recovery is similar to that of ion diffusion, whereas that of the second half becomes larger. This phenomenon indicates that Ca²⁺ spark recovery is initially dominated by fast equilibration of local Ca²⁺. The role of active transports becomes more important in the slower phase of recovery.

When two or more rates contribute significantly in a process, their effects could be synergistic or offsetting. For example, due to slowed Ca²⁺ diffusion, the spatial dispersion became narrowed when temperature was lowered. However, this effect was largely compensated by prolonged Ca²⁺ release. As the result, the FWHM of Ca²⁺ sparks changed little with temperature. On the other hand, both prolonged Ca²⁺ release and slowed Ca²⁺ diffusion tend to facilitate the local accumulation of Ca²⁺. They are synergistic in determining the amplitude of Ca²⁺ sparks. However, the amplitude of Ca²⁺ sparks appears to be insensitive to temperature, implying that the Ca²⁺ release flux is attenuated when temperature is lowered. Although it is not presently known whether the number of RyRs participating in sparks is changed, in vitro studies have shown that the unitary current of RyRs in lipid bilayers indeed changes with temperature at a Q₁₀ of 1.5 (33).

Temperature sensitivity of Ca²⁺ sparks and heart function

One of the common issues that have been discussed since the inception of Ca²⁺ sparks is the validity to interpret mammalian cardiac and muscular function using room temperature-measured Ca²⁺ sparks. This issue was recently visited by Ferrier et al. (10), who showed that Ca²⁺ sparks in mouse cardiomyocytes measured at 22°C are >1000% more in spark frequency, 42% higher in amplitude (ΔF/F₀), and 43% longer in time-to-peak than those measured at 37°C, with half-decay time unchanged. Their results contrast with the 50% increase in frequency, 13% decrease (rather than increase) in ΔF/F₀, 14% increase in time-to-peak, and 21% increase (rather than being unaltered) in half-decay time in our rat data during a comparable change in temperature. Several factors may be implicated in the high discrepancy between these two studies:

1. SR Ca²⁺ load. In resting cardiac myocytes from all tested species, including rats and mice, lowering temperature results in increased SR Ca²⁺ content (10,41,42). However, this does not mean that low temperature fortified the SR capability to uptake Ca²⁺; rather, the increased SR load has to do with inhibited Na⁺-pump activity at low temperature. The attenuated Na⁺ handling (22) will shift the Ca²⁺ flux via Na⁺-Ca²⁺ exchange. The resulted [Ca²⁺]_i elevation, which tends to load the SR even when Ca²⁺-pump activity slows down at low temperature. Interestingly, the cooling-induced increase in spark frequency, which is sensitive to SR load, correlates well with the progressive elevation in resting [Ca²⁺]_i in rat cells but not in mouse cells (10).

2. Species-related difference. The relative strength of Na⁺-Ca²⁺ exchange and SR Ca²⁺ pumping varies with species (1). Although the relative contributions of these two mechanisms in removing cytosol Ca²⁺ are similar in rat and mouse cardiomyocytes at 23°C (1), it is not known whether they differ at higher temperature. Besides, possible species difference in Ca²⁺-sensing, gating, and luminal regulation of RyRs should also be taken into consideration.

3. Number of observations. In connection with the extreme infrequency of Ca²⁺ sparks at 37°C in mouse cardiomyocytes, only 19 sparks could be compared with those at 22°C (10). Given the highly variable nature of Ca²⁺ sparks, some of the observed temperature responses, such as the temperature insensitivity of half-decay time, may not be conclusive without further examination.

To ensure the accuracy of results, we measured >240 sparks for each data point in this study. We found that spark amplitude (Δ[Ca²⁺]_i) and FWHM are relatively insensitive to temperature. Although the resting [Ca²⁺]_i, time-to-peak and half-decay times, and therefore FDHM, increase significantly from 35°C to 10°C, they are only altered by 8%, 5%, 10%, and 7%, respectively, during the first 10°C change. Therefore, our data suggest that when cardiac Ca²⁺ sparks are measured at a room temperature around or above the transitional 25°C (so-called “warm room”), they are basically acceptable to account for the heart function in mammals.

Below the critical temperature of 25°C, where the phase transition of membrane lipids occurs, membrane protein-mediated processes, including RyR gating, Ca²⁺ transport by Ca²⁺ pumps, and exchangers, encountered increased energetic barriers in conformational transitions and become more sensitive to temperature. A comparable change in temperature would cause more profound changes in Ca²⁺ spark kinetics and much more profound changes in kinetics of Ca²⁺ transients (14). As the result of prolonged and increased RyR Ca²⁺ release and truncated capability of intracellular Ca²⁺ handling, resting [Ca²⁺]_i becomes inhomeostatic (Fig. 3 C). In addition, low temperature also leads to a progressive loss in resting membrane potential (43), which will promote Ca²⁺ entry through the window current of L-type Ca²⁺ channels. These factors additively lead to Ca²⁺ overload in cytosol, resulting in incomplete relaxation and, eventually, loss of myocardial contractility. In hibernating mammals, however, the contractility can be maintained at a temperature near freezing point (13). It is thus intriguing how the cell system in hibernators is adapted to cope with these temperature-dependent issues.

CONCLUSIONS

In this study, we have characterized Ca²⁺ sparks systemically over a wide temperature range that covers both euthermic and hypothermic conditions. Whereas the amplitude and spatial dispersion of Ca²⁺ sparks are relatively insensitive to temperature, the spark kinetics slows down significantly due to prolonged RyR Ca²⁺ release duration and slowed Ca²⁺ diffusion under low temperature conditions. The temperature dependence of Ca²⁺ release duration reveals a lowered apparent E_a for RyRs gating in situ compared with that in vitro. The relative temperature insensitivity of Ca²⁺ spark parameters above ∼25°C suggests that Ca²⁺ sparks measured at “warm room” temperatures are basically acceptable in elucidating mammalian heart functions.