Ligand-Induced DNA Condensation: Choosing the Model

Abstract

We test and compare different models for ligand-induced DNA condensation. Using ¹⁴C-labeled spermidine³⁺, we measure the binding to condensed DNA at micromolar to molar polyamine concentrations. DNA aggregates at a critical polyamine concentration. Spermidine³⁺ binding becomes highly cooperative at the onset of aggregation. At higher concentrations, spermidine³⁺ binding to condensed DNA reaches a plateau with the degree of binding equal to 0.7 (NH⁴⁺/PO³⁻). Condensed DNA exists in a wide range of spermidine concentrations with the roughly constant degree of ligand binding. At greater concentrations, the degree of binding increases again. Further spermidine penetration between the double helices causes DNA resolubilization. We show that a simple two-state model without ligand-ligand interactions qualitatively predicts the reentrant aggregation-resolubilization behavior and the dependence on the ligand, Na⁺, and DNA concentrations. However, such models are inconsistent with the cooperative ligand binding to condensed DNA. Including the contact or long-range ligand-ligand interactions improves the coincidence with the experiments, if binding to condensed DNA is slightly more cooperative than to the starting DNA. For example, in the contact interaction model it is equivalent to an additional McGhee-von Hippel cooperativity parameter of ∼2. Possible physical mechanisms for the observed cooperativity of ligand binding are discussed.

INTRODUCTION

DNA is stored in vivo inside the small volumes of chromosomes, viral capsids, and bacterial nucleoids in a compact ordered state. DNA packing may be also achieved in vitro by adding either a neutral polymer in the presence of a monovalent salt (1), or charged ligands—for example, natural polyamines (2,3). This process is usually called DNA condensation (4). DNA condensation in vitro is a good model system to study its functioning in living systems (5–9). In addition, DNA condensation is becoming important for pharmaceutics, because the formation of compact particles is one of the possible ways for DNA delivery in gene therapy (10). Another proposed application of DNA condensation is the construction of biosensors based on the liquid-crystalline properties of condensed DNA (11).

In vitro studies

DNA condenses upon addition of a critical ligand concentration. Long enough DNA may form ordered particles (toroids, rods, or more sophisticated structures) either as a collapse of an individual macromolecule (12–14), or an intermolecular aggregation (15). DNA molecules shorter then the persistence length do not form structures like toroids (16), but their condensed phase is still ordered and has liquid-crystalline properties (17,18). If one continues to increase the ligand concentration, a second critical concentration exists, at which the DNA aggregates resolubilize (18–20). In the case of long DNA molecules the resolubilization is associated with the decondensation of individual molecules (6,21).

The effect of reentrant aggregation-resolubilization with increasing ligand concentration has been observed both for short or long DNA molecules, single-stranded or double-stranded, small or high DNA concentrations (17–22). The corresponding bell-shaped condensation curves have attracted much attention of the experimentalists and theoreticians (6,18,19,22–27). However, this picture is incomplete without the curves of ligand binding coupled to DNA aggregation-resolubilization. The polyamine binding to DNA was measured previously at small ligand concentrations (28,29) and at the intermediate concentrations in the regime of DNA condensation (30,31). The determination of polyamine binding curves in the whole interval of ligand concentrations including the onset of DNA aggregation and the beginning of resolubilization is carried out in the present study. We use these curves for testing the theoretical models.

Theoretical modeling

There are several approaches for the description of DNA condensation caused by ligand binding. The first one is based on the classical methods of polymer physics (e.g., 12,14,15,32). The pure polymer approach usually considers the system as consisting of only two components, DNA and a solvent, without a microscopic treatment of the molecular interactions. Another approach focuses on the rearrangements of water molecules in the vicinity of a double helix that may cause attractive hydration forces between DNAs (33). Many groups are investigating the electrostatic forces that drive condensation of negatively charged DNA molecules surrounded by monovalent and multivalent counterions (19,23–25,34–39). However, even for spherelike ligands there are ion-specific effects beyond simple electrostatics. For example, Mn²⁺, but not Mg²⁺, can condense supercoiled circular DNA (40). The situation is even more complicated for linear flexible polyamines. The polyamine chain length and the positions of the charged groups strongly influence the polyamine-induced DNA condensation (41). In addition, the condensation also depends on the DNA sequence (42,43). Computer simulations constitute one possible approach to investigate these problems (27,44,45). Another possibility is to use phenomenological experimentally accessible parameters to construct the thermodynamical ligand binding models (26,46–49). In the following sections we will concentrate on the latter formalism.

Ligand-binding approaches

The principles of the calculation of equilibrium binding of large ligands to DNA were formulated in the late 1960s into the 1970s (50–52). This formalism usually uses an important concept of cooperativity: binding of one ligand to DNA may affect binding of another ligand. Different cooperative and noncooperative models have been applied for the description of ligand binding and its influence on the conformational transitions of nucleic acids, their folding, melting, etc. (53). DNA condensation is one of the processes that may be treated using this formalism.

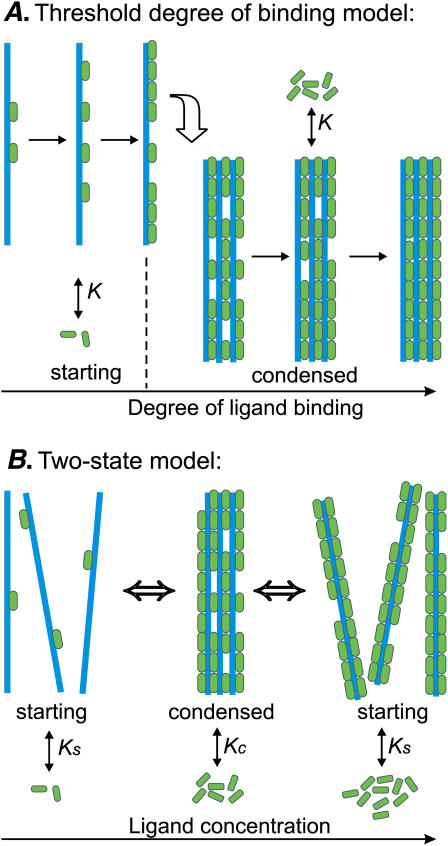
There are several possible descriptions of DNA condensation caused by ligand binding. The first one is the threshold-degree-of-binding model (46,48,49). It assumes that the ligand binding is noncooperative. DNA condenses when the degree of binding reaches a certain threshold value (Fig. 1 A). The condition of the abrupt condensation at a threshold degree of binding is quite artificial here—it is taken from the electrostatic models, which state that the DNA charge should be neutralized to ∼90% to allow condensation (3).

FIGURE 1.

Schematic representation of the models for ligand-induced DNA condensation. (A) The threshold degree of binding model. Starting DNA (blue) binds ligands (green) until the degree of ligand binding reaches a threshold value (0.8 in this example). After reaching the threshold degree of binding, DNA condenses and continues to bind ligands with the same binding constant K and the same stoichiometry. (B) The two-state model. DNA may be in the two states: starting and condensed. The two DNA states bind ligands with different binding constants, K_s and K_c, and different stoichiometries. Without the ligands, the transition from the starting to condensed state is characterized by a very small equilibrium constant S_sc. Adding the ligands shifts the thermodynamic equilibrium, and at high enough ligand concentrations, the condensed phase is favored. At yet higher concentrations the condensates may redissolve, if uncondensed DNA binds more ligands at saturation.

Another way to calculate DNA condensation induced by ligand binding is available in the frame of the two-state models (Fig. 1 B). These models imply that DNA may be in the two states, starting or condensed, and the transition between the two states is governed by the different modes of ligand binding to each state (26,47,54,56). Both intermolecular and intramolecular DNA condensation has been observed experimentally (15). Several two-state models have been constructed to calculate the intermolecular association of two double helices due to ligand crosslinking (47,55,56). On the other hand, our previous model considered ligand-induced intramolecular condensation of a single DNA molecule (26,54). We will show below that this model is also applicable for the description of condensed phase consisting of many short DNAs.

In the next sections we start from the latter model: perform calculations and compare them with the known experimental dependencies of DNA condensation on Na⁺, polyamine, and DNA concentrations. It appears that the theoretical predictions agree qualitatively with the experimental condensation-decondensation curves. However, the measurements of the corresponding curves of ligand binding to condensed DNA are lacking in the literature. We perform the experiments to fill this gap, and then use the obtained binding and condensation curves to test the theoretical models. It becomes clear from the analysis that the ligand-ligand interactions should be introduced in the model to be consistent with the experiments. We consider different models, trying to choose the right one and to understand the physical mechanisms of the experimentally observed ligand-binding cooperativity.

MATERIALS, METHODS, AND THEORY

Measurement of spermidine binding and DNA condensation

Spermidine 3HCl was obtained from Fluka (Buchs, Switzerland); ¹⁴C-spermidine 3HCl was obtained from Amersham Biosciences (4.14 GBq/mmol, 1.85 MBq/ml; Freiburg, Germany). The stock solutions were prepared using TE buffer (10 mM Tris HCl, 1 mM EDTA, pH = 7.5) and stored at −21°C. Mononucleosomal double-stranded DNA extracted from calf thymus (57) was given by Dr. F. Livolant (Université Paris Sud, Orsay, France). We solubilized the DNA pellet and dialyzed it for 48 h against TE buffer. The mean length of the fragments is 146 basepairs (bp). All experiments were performed in the 1.7 ml low-binding microcentrifuge tubes (Marsh Biomedical Products, Rochester, NY) coated with a methyl brush to decrease DNA adsorption on the walls as described in Goldar and Sikorav (58).

Solutions of TE buffer, spermidine³⁺, DNA, and ¹⁴C-spermidine³⁺ were added one after another to achieve in total 200 μl, 20,000 cpm per tube. The tubes were shaken, incubated for 12 h, and centrifuged at 15,000 × g for 5 min to sediment the aggregated DNA. Then the solution from each tube was divided into the three parts. The first part, 10 μl of the supernatant taken by a micropipette from the top of the tube, was diluted by TE buffer and used to determine the concentration of soluble DNA via measurement of adsorption at 260 nm by a Beckman UV spectrophotometer (Beckman-Coulter, Fullerton, CA). The second part, 40 μl of supernatant, was used to determine the radioactivity, A_top, of spermidine molecules, which are free in solution or bound to soluble DNA. The rest of the solution in the tube was used to determine the radioactivity, A_bot, of the spermidine molecules, which are free in solution, plus those bound to DNA in the soluble state, plus those bound to condensed DNA in the precipitate.

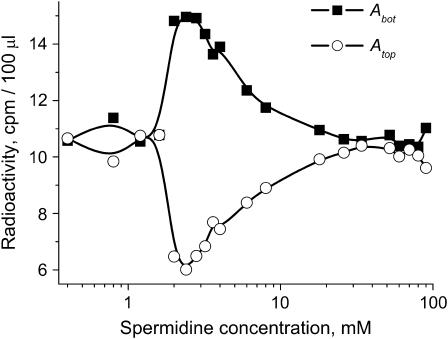
The radioactivity of the labeled polyamine solutions was measured by adding 1 ml of Pico-Fluor 40 scintillation cocktail (Beckman-Coulter) and counting after 5 h of preequilibration in a Beckman LS3801 liquid scintillation counter. The counting changes with time after addition of Pico-Fluor, but after several hours of preequilibration, the changes are negligible. Fig. 2 shows the typical curves for the radioactivity (cpm/100 μl) of the supernatant (A_top) and the aggregated phase (A_bot) as a function of spermidine concentration.

FIGURE 2.

Radioactivity of the supernatant (A_top) and the aggregated phase (A_bot) as a function of spermidine concentration. 2.5 mM DNA (bp), TE buffer.

The difference between A_top and A_bot gives the radioactivity corresponding to spermidine molecules bound only to condensed (aggregated) DNA. The degree of spermidine binding to condensed DNA expressed in spermidine nitrogens per DNA phosphate, NH⁴⁺/PO³⁻, was calculated as

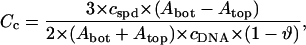(1)

where ϑ is the degree of DNA condensation, ϑ = OD/OD_init, OD is the optical density of the supernatant determined at 260 nm, OD_init is the optical density at 260 nm extrapolated to zero concentration of spermidine, c_spd is the total molar concentration of spermidine added to the solution, and c_DNA is the molar concentration of DNA basepairs.

Previous studies of polyamine-induced aggregation of ³²P-labeled highly diluted DNA using the same centrifugation technique as above indicate that up to 10% of DNA is not pelleted from the supernatant in the middle of the condensation regime (18). Having in mind that our experiments are performed at millimolar DNA concentrations, when even better pelleting is expected, we can set 10% as an upper limit for the experimental error due to the remnants of the condensed phase in the supernatant.

Calculation of ligand binding and DNA condensation in the frame of the two-state model

This model assumes that a DNA molecule is either in the starting (soluble) or condensed (aggregated) state, intermediate states being forbidden. The ligands may reversibly bind each DNA state with different binding constants and different stoichiometric parameters (Fig. 1 B). Although the model was originally proposed for a monomolecular condensation (54), it is applicable also for the transition of a DNA molecule from solution to a condensed phase formed by many short DNAs, which is considered in the experimental section of the current article. Indeed, in this case it is reasonable to assume that the energy of a DNA molecule in the aggregate does not depend on the aggregate size. (Such an assumption may be not true for the case of a toroid formation from several DNA molecules (59). In this case, one has to use a model for ligand-governed formation of an n-mer macromolecular aggregate (60). The n-mer aggregation model should tend asymptotically to the two-state model considered here.)

Let us introduce the following notation (26). The parameters corresponding to the starting (s) or condensed (c) DNA state are denoted by the subscript i = (s, c). F_i is the free energy of an i-state DNA molecule in the absence of ligands. S_sc = exp[(F_s − F_c)/(R × T)] is the equilibrium constant for s → c transition of a DNA molecule in the absence of ligands, T is the temperature (in degrees Kelvin), and R is the gas constant. L is the DNA length (bp). ϑ is the degree of DNA condensation, which is equal to the ratio of condensed to the total number of DNA molecules, c_o is the molar concentration of free ligands in solution, m the number of DNA basepairs covered by one bound ligand, K_i the ligand binding constants for DNA in state i, c_i the degrees of ligand binding (ligand per bp), and r_i is equal to the number of i-state DNA double helices interacting with one ligand. This stoichiometric parameter is connected with the maximum degree of ligand binding, 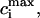as

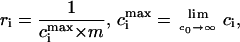(2)

where r_i = 1/2 means that a bound ligand interacts with only one DNA strand. The value r_i = 1 means that a ligand interacts with two DNA strands (for example, by winding along a groove of the double helix and not allowing another ligand to be bound to the same place). In the condensed phase, r_c may depend on the particular type of the liquid crystal-like lattice formed by DNA.

Let us consider two types of ligand-ligand interactions. The first one is the conventional contact cooperativity between the ligands bound to adjacent basepairs (52). The second one is the long-range interaction between the ligands bound to DNA sites far from each other. The extreme case of long-range interactions is the infinite-range interaction that may be described by a mean-field potential covering all the ligands bound to DNA. This changes the free energy of the system by an energetic term G_i per each ligand bound to DNA in the i^th state. Let us assume that G_i does not depend on the ligand-ligand distances and depends only on the degree of ligand binding (G_i = G_i(c_i)), as was first introduced by Scatchard (61) for proteins and then adopted by Nechipurenko (62) for DNA. Then minimizing the free energy of the system analogously to Lando and Teif (26) and Teif et al. (63), we obtain equations for the determination of the equilibrium degrees of ligand binding and the degree of DNA condensation (see the derivation in the Appendix),

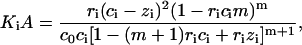(3)

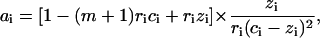(4)

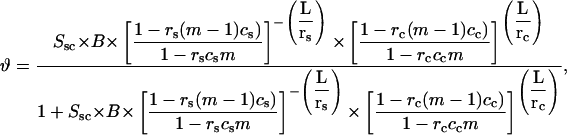(5)

where 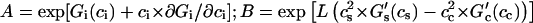; z_i is the number of direct contacts between the ligands bound to DNA (per basepair); a_i = exp[−ɛ_i/(k_B × T)] is the McGhee-von Hippel contact cooperativity parameter; and ɛ_i is the energy of the ligand-ligand contact. The value a_i > 1 corresponds to positive cooperativity (effective binding constant increases with increasing the number of bound ligands), a_i < 1, negative cooperativity and a_i = 1, no contact interactions. Analogously, G_i(c_i) > 0 corresponds to positive long-range cooperativity, G_i(c_i) < 0, negative, and G_i(c_i) = 0, no long-range interactions.

A standard condition of mass conservation (Eqs. 6–7) should be added to Eqs. 3–5, to get the final system of equations:

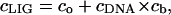(6)

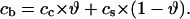(7)

Here c_LIG is the total molar concentration of ligands added to a test tube, c_DNA is the molar concentration of DNA (bp), and c_b is the degree of ligand binding to DNA molecules in both states. It should be noted that c_i values are expressed in ligands per basepair, whereas the C_i values are expressed in spermidine nitrogens per DNA phosphate (NH⁴⁺/PO³⁻). C_i shows the degree of DNA charge neutralization due to polyamine binding. There is a simple relation between these values: C_i = c_i × m/2, and 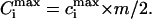For the case of spermidine, C_i = 3/2 × c_i, and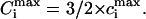

In the presence of a monovalent salt, the ligand binding constants are changed. For uncondensed DNA the equation of Record and co-authors (64) predicts the dependence

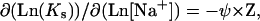(8)

where [Na⁺] is the Na⁺ concentration in solution, ψ equals to the number of thermodynamically released Na⁺ ions per phosphate upon ligand binding, and ψ ≈ 0.88 for helical DNA. More exact solutions to this problem are available (e.g., 65), but they do not change the main trend. For some ligands widely used as DNA condensing agents, the situation is even simpler, since the experimental K_s([Na⁺]) dependencies are available in the literature. The equilibrium dialysis studies performed for spermidine³⁺ (28) give Log(K_s) = −2.5 × Log[Na⁺] + 0.2. For another trivalent DNA-condensing ligand one can use the calorimetric data: Log(K_s) = −2.9 × Log[Na⁺] −2.9 (our linear fit of Table 3 from Matulis et al. (66)). These data allow us to obtain K_s values that may be inserted directly into Eqs. 3–5 to calculate DNA condensation for each Na⁺ concentration.

Calculation of ligand binding and DNA condensation in the frame of the threshold-degree-of-binding model

To make a comparison between the different models, we have changed here the notations of Porschke (46,47) and Nechipurenko et al. (48,49), who introduced the threshold degree of binding model before, and we have added the equations for C_s and C_c calculation. It is possible to reformulate this model in the same language as the two-state model was formulated above. Indeed, this model as well as the previous one assumes that a DNA molecule may be in the two states, starting and condensed (Fig. 1 A). But now these two states have the same ligand binding properties: 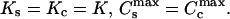We assume that DNA molecules, which have less than C_lim degree of ligand binding, are in the starting state, and those with higher degrees of binding are condensed. Then in the absence of ligand-ligand interactions the following equations should be evaluated numerically to get ϑ and C_i:

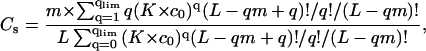(9)

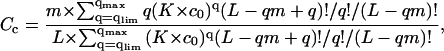(10)

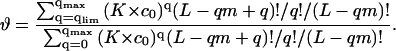(11)

Here q is the number of ligands bound to one DNA molecule, q_lim = C_lim × L/m; q_max = L/m.

RESULTS

Calculations in the frame of the two-state model without ligand-ligand interactions

Let us assume first that the ligands do not interact with each other, and the ligand bound to DNA is covering m = 3 nucleotides. This may be the case of spermidine³⁺. Spermidine³⁺ binding to soluble DNA is mainly electrostatic with charge neutralization at saturation, therefore In the condensed phase, neighboring DNA molecules are tightly packed and aligned, and the maximum number of bound ligands is smaller than that for the same uncondensed DNA molecule due to geometrical obstacles. Spermidine³⁺ binding to soluble DNA has been measured previously using equilibrium dialysis (28). One can take K_s ≈ 10³ M⁻¹ as a characteristic value from this study. Condensed DNA binds ligands more strongly than the uncondensed one, due to the higher charge density in the condensate, and because additional DNA-ligand bonds may be formed (67). The free energy difference between the starting and condensed DNA may be estimated as 0.04 k_B × T/bp (33), and correspondingly one can use S_sc ≈ 0.001 as an estimate for the DNA fragments of length L = 146 bp used in our experiments.

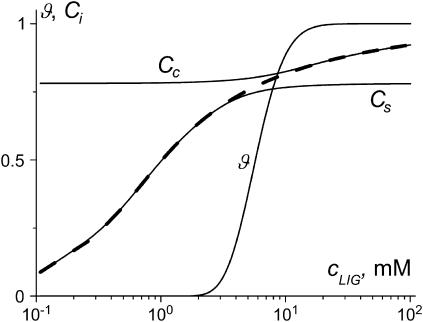
Fig. 3 shows the condensation and binding curves calculated using the system of Eqs. 3–7 for the set of parameters chosen above. The ϑ(c_LIG) curve undergoes two transitions: condensation at small spermidine³⁺ concentrations and decondensation at high concentrations. Ligand binding to the starting (C_s) and condensed (C_c) DNA states is described by noncooperative curves. The C_c(c_LIG) curve reaches a saturation at a lower level in comparison with the C_s(c_LIG) curve due to the different stoichiometry of binding to soluble and condensed DNA. The overall ligand binding to DNA in both states, C_b(c_LIG), is cooperative due to the cooperativity of ϑ(c_LIG) curve on which it depends according to Eq. 7.

FIGURE 3.

DNA condensation and ligand binding curves calculated in the frame of the two-state model without taking into account ligand-ligand interactions. Here and in Figs. 8–10: ϑ, degree of DNA condensation; C_s, degree of ligand binding to soluble DNA; C_c, degree of ligand binding to condensed DNA; and C_b (dashed line), binding to the both states of DNA. Parameters used: L = 146, S_sc = 10⁻³, m = 3, r_s = 0.5, r_c = 0.7, K_s = 10³ M⁻¹, K_c = 5 × 10³ M⁻¹, c_DNA = 2.5 mM (bp), G_i = 0, and a_i = 1.

Let us assume a simple relation between the stoichiometries and the binding constants in the condensed DNA state. It is reasonable to consider that the geometry of the condensate allows only one ligand to penetrate between the two DNAs. Then the adjacent DNA segments share the ligands, and the maximum number of ligands that can be bound to a condensed DNA molecule would be two-times smaller than that for the same uncondensed DNA molecule (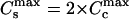). The energy of binding of a ligand to DNA may be estimated as two-times higher in the condensate and the binding constants are then linked as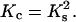

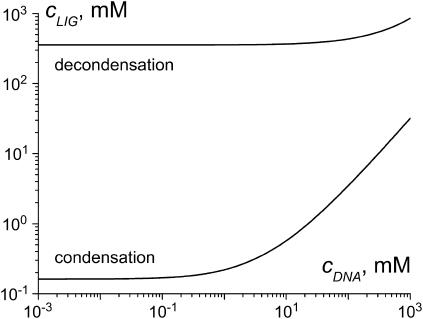
Fig. 4 shows the dependencies of the ligand concentration at the condensation and decondensation midpoints on DNA concentration, calculated according to Eqs. 3–7 using the assumptions above. The ligand concentration at the condensation midpoint increases linearly with DNA concentration (the line is curved in Fig. 4 due to log-log scale). The decondensation midpoint is almost unaffected by DNA concentration. This is consistent with the experimental data in the literature (3,18,19,46,48). Our estimates and 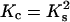used in this calculation do not pretend for a high accuracy, but this does not change the main trends in Fig. 4.

FIGURE 4.

Dependence of the ligand concentration at the midpoint of DNA condensation and decondensation on DNA concentration calculated in the frame of the two-state model.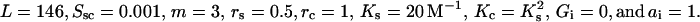

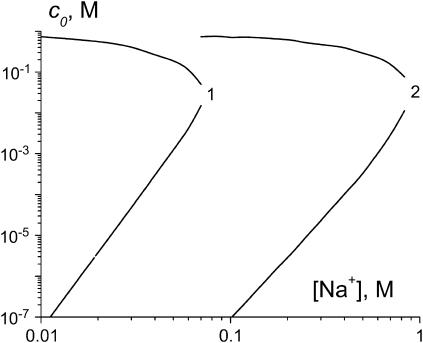
Fig. 5 shows the results of the calculation of free ligand concentration in solution at the condensation and decondensation midpoints as a function of Na⁺ concentration. It is seen that addition of Na⁺ prohibits DNA condensation. Sufficiently high Na⁺ concentrations completely suppress DNA condensation at any ligand concentration. The ligand concentration at the midpoint of condensation transition increases linearly with increasing Na⁺ concentration, while the decondensation midpoint is almost completely unaffected. These trends are consistent with the experimental data (13,18–20).

FIGURE 5.

The dependencies of free ligand concentration at the midpoint of DNA condensation on Na⁺ concentration, calculated in the frame of the two-state model. K_s values are taken from the literature as described in the text: (66), 2 = spermidine³⁺ (28). Other parameters: L = 146, S_sc = 0.001, m = 3, r_s = 0.5, r_c = 1, K_c = 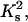G_i = 0, and a_i = 1.

Experimental measurement of spermidine³⁺ binding to condensed DNA

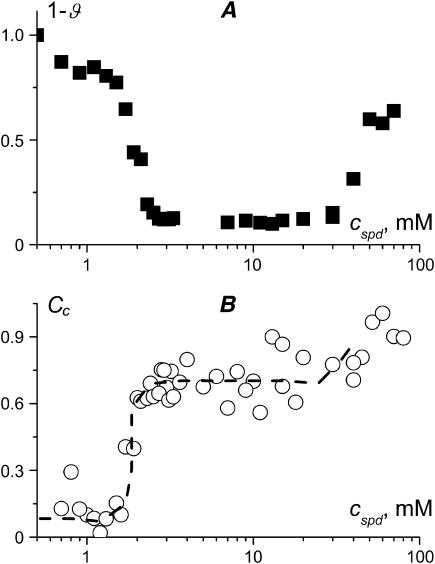
Fig. 6 A shows the fraction of uncondensed DNA in solution, determined by UV adsorption of the supernatant, as a function of the total spermidine concentration. The corresponding degree of spermidine binding to condensed DNA (NH⁴⁺/PO³⁻), determined using radioactivity measurements, is shown in Fig. 6 B. We have performed these experiments at 2.5 mM DNA (bp). The condensation curve exhibits two well-defined transitions: aggregation at 2 mM spermidine and resolubilization after 50 mM. The binding curve increases very sharply at the onset of condensation, but we are able to observe the intermediate degrees of binding. When all the DNA molecules are transformed into the condensed form the binding curve comes to a plateau. The height of this plateau allows us to measure the limiting stoichiometry of spermidine binding to condensed DNA as 0.7 NH⁴⁺/PO³⁻. This is close to the limiting stoichiometry of one spermidine³⁺ ion per four DNA phosphates reported earlier by Heby and Agrell (30). We have performed several series of experiments in the same conditions to check for the systematic errors. The final error may be estimated as 15% (see Materials, Methods, and Theory, above, for discussion of the method accuracy).

FIGURE 6.

(A) Fraction of uncondensed DNA molecules and (B) corresponding degree of spermidine³⁺ binding to condensed DNA (NH⁴⁺/PO³⁻) as a function of the total spermidine³⁺ concentration. The curve is a guide for the eye. Mononucleosomal DNA, 146 bp, 2.5 mM (bp), TE buffer.

It is seen from Fig. 6 that the degree of spermidine binding to condensed DNA increases close to the resolubilization transition. Big measurement errors in the region of high spermidine concentrations do not allow our analyzing this region quantitatively. It is possible to increase the signal/noise ratio by using higher DNA concentration. Fig. 7 shows spermidine binding to condensed DNA measured at 10 mM DNA. The C_c curve in Fig. 7 B confirms that spermidine binding increases at the onset of condensation and then again during decondensation. The plateau between these two steep increases is lower than that in Fig. 6 B. That the plateaus in Fig. 6 B and Fig. 7 B do not coincide may be due to non-equilibrium effects (e.g., large equilibration time for 10 mM DNA solution). However, this difference is within the experimental error.

FIGURE 7.

(A) Fraction of uncondensed DNA molecules and (B) corresponding degree of spermidine³⁺ binding to condensed DNA (NH⁴⁺/PO³⁻) as a function of the total spermidine³⁺ concentration. The curve is a guide for the eye. Mononucleosomal DNA, 146 bp, 10 mM (bp), TE buffer.

The binding curves shown in Fig. 6 B and Fig. 7 B represent the degree of ligand binding to condensed DNA, C_c. This value should be distinguished from the degree of ligand binding to the soluble DNA, C_s, and the DNA in the both states, C_b. The three degrees of binding, i.e., C_s, C_c, and C_b, are related through the degree of DNA condensation, ϑ, according to Eq. 7. The molar concentration of free ligands in solution, c_o, is linked to the relative degrees of binding by the condition of mass conservation (Eq. 6). This means that of five measurable variables, c_o, C_s, C_c, C_b, and ϑ, any three would be enough to characterize the system completely, knowing the input molar concentrations of DNA (i.e., c_DNA) and ligands (i.e., c_LIG). Our experiments allowed us to determine only two variables, C_c and ϑ. We tried to determine the concentration of free polyamines, c_o, by filtrating the supernatant through a membrane, which is permeable to water and polyamines but impermeable to DNA, and using centrifugation to quicken the filtration. Unfortunately this method did not allow our measuring c_o correctly. One can also think, in the future, of measuring C_b using the dialysis technique or C_s using spectroscopy methods. The advantage of our experiments is that it was possible to measure two independent variables, C_c and ϑ, for the same tube. Having three variables would be better, but even now we have two-times more information than just the aggregation-resolubilization curves and can test the theoretical models on a new level.

Theory versus experiments: testing the models

Two-state model

Fig. 3 shows the calculations performed in the frame of the two-state model without ligand-ligand interactions. The parameters used in this calculation correspond to our experimental system in Fig. 6. Thus the two figures may be compared directly. It is seen that the two-state model predicts reentrant DNA condensation consistent with the experimental Fig. 6 A. The ligand binding to condensed DNA (C_c(c_LIG) curve) comes to a saturation at 0.7 NH⁴⁺/PO³⁻ in both the theoretical Fig. 3 and the experimental Fig. 6 B. However, at the onset of condensation, the experimental C_c(c_LIG) curve increases stepwise; the theoretical one does not show such a cooperativity. The condensation transition predicted theoretically at a small degree of ligand binding to condensed DNA (Fig. 3) requires, experimentally, a higher degree of binding (Fig. 6 B).

Threshold-degree-of-binding model

Fig. 8 shows the condensation and binding curves calculated using Eqs. 9–11 in the frame of the threshold-degree-of-binding model. This model does not take into account ligand-ligand interactions as well as our previous calculations. The threshold degree of binding is taken as equal to 0.8 (NH⁴⁺/PO³⁻) according to Wilson and Bloomfield (3) and Porschke (46). Now the C_b curve exhibits a noncooperative binding. The C_s curve starts from zero and tends to the threshold degree of binding at saturation. The C_c curve is starting not from zero, but from the threshold value C_c = 0.8 (NH⁴⁺/PO³⁻), and saturates at C_c = 1. This is not what we observe in the experiments, where the C_c curve changes from zero to the plateau 0.7 (NH⁴⁺/PO³⁻) at the onset of DNA condensation (Fig. 6 B). Thus the naïve interpretation that the stepwise change in the experimental C_c(c_LIG) curve is directly due to DNA condensation at the threshold degree of binding would be wrong. Since both the two-state and the threshold-degree-of-binding models fail to describe the experimental binding and condensation curves without ligand-ligand interactions, we have to consider the ligand-ligand interactions explicitly.

FIGURE 8.

DNA condensation and ligand binding curves calculated in the frame of the threshold degree of binding model. Notation is the same as in Fig. 3. Parameters used: C_lim = 0.8, L = 146, m = 3, K = 103 M⁻¹, and c_DNA = 2.5 mM (bp).

Contact interactions

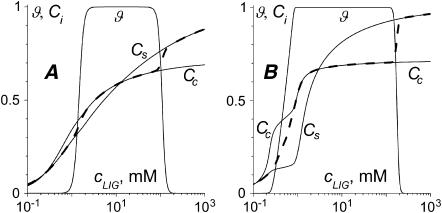
Let us return to the two-state model. Now assume that the difference in the ligand binding properties between the starting and condensed DNA arises not because of the different binding constants as in Fig. 3, but because of the different contact cooperativity parameters. Our calculations show that the behavior of the system is governed by the ratio of the contact cooperativity parameters, a_c/a_s. If a_c/a_s < 1.8 there is no DNA condensation at all. DNA is soluble at any ligand concentration. At a_c/a_s > 2.3 we obtain condensation at a critical ligand concentration, but the reverse resolubilization transition is obtained at more than molar spermidine concentrations, which is not consistent with the experiments. Only inside a narrow interval between these two extremes can one find the binding and condensation curves consistent with the experiments. Holding a_c/a_s ≈ 2 we are able to obtain the aggregation-resolubilization effect for any particular a_c and a_s pair.

The two examples of such calculations are shown in Fig. 9, A (a_s = 0.6, a_c = 1.2) and B (a_s = 1, a_c = 2). In both cases, the C_c(c_LIG) curve cooperatively increases at the onset of condensation and intersects the ϑ(c_LIG) curve at >0.5 (NH⁴⁺/PO³⁻). Then the C_c(c_LIG) curve reaches a plateau at C_c = 0.7 (NH⁴⁺/PO³⁻). The C_c(c_LIG) curve is not as steep as the experimental one (Fig. 6), but if we increase the contact cooperativity parameter further, the coincidence with the experimental condensation curve will be lost. The anticooperative binding in Fig. 9 A leads to an unusual form of the C_b curve. There is no data on the existence of such type of binding to DNA in the literature. Although additional experiments may be considered to check for this possibility, it is hardly probable that the experimentalists have overlooked such an unusual curve. Thus, the situation represented in Fig. 9 B (cooperative binding to condensed DNA and noncooperative or slightly cooperative binding to the starting DNA) fits the experimental data better.

FIGURE 9.

DNA condensation and ligand binding curves calculated in the frame of the two-state model with contact ligand-ligand interactions. Notation is the same as in Fig. 3. Parameters used: L = 146, S_sc = 10⁻³, m = 3, r_s = 0.5, r_c = 0.7, K_s = K_c = 10³ M⁻¹, c_DNA = 2.5 mM (bp), and G_i = 0. (A) a_s = 0.6, a_c = 1.2; and (B) a_s = 1, a_c = 2.

Long-range interactions

Let us suppose now that the ligand binding to DNA is characterized by a linear attractive potential: G_i(C_i) = W_i × c_i, where W_i is a cooperativity parameter. As in the case of contact interactions, a small but nonzero difference between W_s and W_c is required to get the aggregation-resolubilization effect consistent with the experiments. Fig. 10 shows two examples of the condensation and binding curves calculated for W_s = −3, W_c = 0 (Fig. 10 A), and W_s = 0, W_c = 5 (Fig. 10 B). The comparison between Fig. 3 (no ligand-ligand interactions) and Fig. 10 (long-range interactions) now shows that ligand binding to condensed DNA changes dramatically. Both the anticooperative (Fig. 10 A) and cooperative (Fig. 10 B) interactions solve the problem of DNA condensation at a too-low degree of ligand binding, which is encountered without ligand-ligand interactions (Fig. 3). However, cooperative (Fig. 10 B) rather than anticooperative (Fig. 10 A) interactions provide a stepwise change in the ligand binding at the onset of DNA condensation, consistent with the experiments (Fig. 6). The cooperative long-range interactions in Fig. 10 B determine a steep increase in the C_c(c_LIG) binding curve from zero to C_c = 0.5 (NH⁴⁺/PO³⁻) at the onset of DNA condensation. At the condensation midpoint there is a concavity in the C_c(c_LIG) curve. Such a concavity is not observed in the experimental Fig. 6 B, although it could be too small to be detected. The concavity of the C_c(c_LIG) curve arises during the condensation transition because the number of condensed DNA molecules sharply increases in this regime, and the increase in molar ligand concentration c_LIG is used mainly to maintain the ligand binding to condensed DNA at the same level. When all the molecules are converted to the condensed state, the increase in c_LIG again results in a cooperative increase in the C_c(c_LIG) binding curve.

FIGURE 10.

DNA condensation and ligand binding curves calculated in the frame of the two-state model with long-range ligand-ligand interactions. Notation is the same as in Fig. 3. Parameters used: L = 146, S_sc = 10⁻³, m = 3, r_s = 0.5, r_c = 0.7, K_s = K_c = 10³ M⁻¹, c_DNA = 2.5 mM (bp), a_i = 1, and G_i = W_i × c_i. (A) W_s = −3, W_c = 0; and (B) W_s = 0, W_c = 5.

DISCUSSION

Is it possible to construct a self-sufficient model for DNA condensation in the language of lattice-ligand binding? To answer this question, we look at the main experimental features of the process—the reentrant behavior, the dependence on salt, ligand, and DNA concentrations and sizes, and the cooperativity of ligand binding—from the point of view of different models.

Reentrant behavior

Several explanations have been proposed in the literature for the experimentally observed DNA resolubilization at high ligand concentrations. A very high ligand concentration in this regime determines that almost all ligand-binding sites on DNA are filled. From the point of view of electrostatics, this means that the multivalent ion distribution along DNA becomes homogeneous and the attractive forces between the double helices that were created by correlated (inhomogeneous) ligand distribution are lost (56,25). The forces between the double helices covered by ligands may even become repulsive if the total number of positive charges coming with ligands is more than the bare DNA negative charge—the so-called DNA charge reversal (24,27). It should be noted, however, that DNA charge reversal has been observed in direct electrophoresis measurements only for large ligands such as poly(propylene imine) dendrimers (68), but not for polyamines (19).

Another explanation of DNA resolubilization is that, at high concentrations, ligands penetrate inside the aggregates and create an osmotic pressure pushing the double helices to move apart (20). This explanation is suitable both for charged and neutral ligands. Our experimental data, showing that the degree of spermidine binding to condensed DNA increases at the onset of DNA resolubilization (Figs. 6 and 7), seem to support this explanation. This interpretation is also consistent with the recently found increase of the interhelical distances in polyamine-condensed DNA at high polyamine concentrations close to the resolubilization of the aggregates (69).

The electrostatic and the osmotic stress explanations of DNA resolubilization do not contradict each other, and just highlight the different sides of the same phenomenon. Yet one more explanation is available in the frame of the two-state model (Fig. 1 B). The decondensation is entropically driven due to the higher number of ligand binding sites (and therefore the higher number of ligand rearrangements) in decondensed DNA in comparison with the condensed molecules (26). We have now shown experimentally that spermidine binding to condensed DNA saturates at 0.7 NH⁴⁺/PO³⁻ (Figs. 6 and 7), whereas soluble DNA may bind more ligands. This brings an argument in support to the above explanation.

Our estimate of the limiting spermidine stoichiometry in the aggregates is close to the value 0.75 (NH⁴⁺/PO³⁻) determined by Heby and Agrell using thin-layer chromatography (30). Both of these values are below the 0.8–0.85 degree of spermidine binding calculated by Wilson and Bloomfield (3) on the basis of the two-variable Manning model (70). It was shown later that this value may vary significantly with increasing Na⁺ concentration (13), but again at the 13 mM Na⁺ concentration used in our study a higher degree of spermidine binding is expected from their calculations. This difference may arise from nonelectrostatic effects that are not considered by the Manning model. Earlier experiments also showed that spermidine³⁺ binding to DNA deviates from the Manning model (71).

The explanation of DNA resolubilization due to the different stoichiometry of ligand binding to condensed and uncondensed DNA has been in the literature for some time (32,47,55,56). In particular, Porschke has constructed a two-state model to consider the intermolecular DNA association induced by protamines, large natural ligands with charges up to +20 per molecule (47). It was established in the recent experiments that, as well as for polyamine-induced DNA condensation (this work), one can observe reentrant behavior for protamine-induced DNA condensation (E. Raspaud, Université Paris-Sud, personal communication, 2004). However, this was not known when Porschke published his article. Even for polyamines, the reentrant behavior was discovered only in 1996 (18). Thus Porschke, in fact, predicted the resolubilization at high ligand concentrations but could not compare his model with experiments. He argued that the protamine system is principally different from the polyamine case. We believe that this statement should be reexamined, now having new experimental data.

The reentrant behavior is not limited to the case of DNA condensation. Some recent examples are divalent metal-ion-induced reversible hypercondensation-decondensation of chromatin (72), and aggregation-resolubilization of F-actin and filamentous viruses (44). Furthermore, at least in 1908, it was already known that upon increasing the concentration of a multivalent salt in solution one gets aggregation (agglutination) of erythrocytes, which is followed by resolubilization at much higher salt concentration (73). Several models for the description of ligand-induced protein and cellular aggregation and resolubilization have been considered later (60,74–76). A similar stoichiometry effect leading to the reentrant behavior was described for the helix-coil transition of DNA-ligand complexes (77,78). These studies showed that the ligands that bind more strongly to helical DNA, but that have fewer sites with which to bind in comparison with the single-stranded molecules, stabilize the double helix at small concentrations and destabilize it at high concentrations. Interestingly, the monomolecular two-state model considered for DNA condensation (26) resembles the models for ligand-induced protein conformational transition (79). So, in principle, one can expect to find a similar ligand-governed reentrant behavior for protein conformational transitions.

Effects of DNA length and ligand size

The measurement of DNA charge neutralization using pulse gel electrophoresis (71) revealed that spermidine binding after onset of DNA condensation depends on DNA length. This means that our experimentally determined stoichiometry of binding might be limited to DNA of similar length. From the point of view of the two-state model, DNA length enters Eqs. 3–5 as a parameter, but this parameter by itself may only change the steepness of the condensation transition (26). On the other hand, it is known that DNA of different lengths may produce different types of the condensates (59,80). Different alignments of DNA in the condensed phase may affect the stoichiometry of binding through Eq. 2. This could explain the dependence of spermidine binding on DNA length found in Li et al. (71).

An even stronger effect on the stoichiometry of binding comes from the geometrical sizes of the ligands. In addition to the direct action through Eq. 2, the ligand length also acts as a parameter decreasing the cooperativity of binding (63). In general, the ligand-binding models predict that, for two ligands with equal binding constants, the one with the larger size would be the weaker binder of DNA. Therefore, one can expect that large ligands have a smaller DNA condensing efficiency. This is in line with the experimental data that polyamines are less effective DNA condensing agents (higher concentration is required to induce condensation) than inorganic cations of the same valence (20,66). But in many cases, this effect is masked because the ligand size also correlates with the binding constant through the cation structure (81), hydrophobicity (82), and the number and positions of the charged groups (41).

DNA concentration dependence

It is known experimentally that polyamine concentration at the midpoint (18,46,83) or at the onset of DNA condensation (19) increases almost linearly with the increase of DNA concentration. An electrostatic theory including three different regimes has been proposed initially to account for the observed DNA concentration dependence (19). However, it was shown recently that a single linear regime is enough to describe this system (23).

Fig. 4 shows that this linearity is quite natural in our approach. The law of mass action uniquely determines the numbers of free and bound ligands at the condensation midpoint. This turns the condition of mass conservation (Eq. 6) into a linear dependence of the total ligand concentration on DNA concentration. This linear dependence reflects the fundamental assumption about the reversible ligand binding at a thermodynamic equilibrium, and should be true for any ligand-binding model until the law of mass action holds. In particular, the analysis of the dependence of the condensation midpoint on DNA concentration has been already performed in the framework of the threshold-degree-of-binding model (46), and allowed the author to obtain a reasonable spermine⁴⁺ binding constant to DNA. Since DNA resolubilization takes place in the regime when most of the binding sites on DNA are filled, the degrees of ligand binding C_i tend to their saturation values 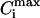and no longer depend on the ligand concentration (Fig. 4). In this regime, the increase in the total ligand concentration, c_LIG, results mainly in the increase of the concentration of the free ligands in solution, c_o, and the dependence on DNA concentration is lost. This trend is in accordance with the experiments (19,20).

Na⁺ dependence

Monovalent ions cannot induce DNA condensation by themselves, but they influence DNA condensation induced by multivalent ligands, changing the binding constants. A simple two-state model without ligand-ligand interactions shows that the ligand concentration required to induce DNA condensation increases with increasing Na⁺ concentration, while the ligand concentration at the midpoint of DNA resolubilization is almost unaffected by Na⁺ (Fig. 5). Similar Na⁺ dependence was observed experimentally for polyamine-induced condensation (13,18–20).

It is interesting to compare our approach to study the [Na⁺] and [DNA] effects on DNA condensation with the recent articles addressed to the same issue (23,39). We started from the ligand binding formalism, which naturally includes ligand sizes, competitive binding, etc., and connected it to the polyelectrolyte properties of DNA using the Record-Manning concepts. Burak and co-authors (23,39), on the other hand, started from the electrostatic Poisson-Boltzmann approach, and modified it to allow competition between monovalent and multivalent ion binding to DNA. It is clear that the system under consideration bears both polyelectrolyte and specific ligand binding properties. Therefore, the description of this system should be a hybrid of polyelectrolyte and ligand binding approaches. Investigations of this type have, in fact, been performed (25,55,56). The problem is that, for large ligands that cover several DNA phosphates, it is difficult to provide an exact electrostatic solution. It is easier to proceed with electrostatics if one considers simple ligand geometry, such as pointlike or spherelike (25) or rigid rodlike ligands (84). However, in this case, focusing on the electrostatics one usually lacks the entropic contribution due to the rearrangement of large ligands along DNA and DNA-mediated ligand-ligand interactions.

Ligand-ligand interactions

Neither the two-state (Fig. 3) nor the threshold degree of binding model (Fig. 8) can explain the experimentally observed cooperative ligand binding to condensed DNA (Fig. 6) without ligand-ligand interactions. Assuming the existence of the contact (Fig. 9) or long-range (Fig. 10) interactions between the ligands bound to DNA allows our improving the coincidence between the two-state model and the experiments.

The contact interaction model shows that the cooperativity parameter corresponding to the condensed DNA state should be approximately two-times higher then the one corresponding to the starting DNA state. An analogous difference between the cooperativity parameters is required in the case of long-range interactions. Interestingly, such a condition may hold even if both DNA states bind ligands anticooperatively. That the overall anticooperative ligand binding may lead to a highly cooperative effect of DNA condensation is not a trivial result. Is it realized in the experiments? We leave this question open. What is important for us now is that the ligand binding to the condensed state should be more cooperative in comparison with the starting state to be consistent with the experiments. And the second important point is that this additional cooperativity is very small. In the contact interaction model, it is equivalent to a McGhee-von Hippel cooperativity parameter equal to 2. This is much lower than the typical cooperativity parameters reported for protein binding to DNA. Evidently, the origin of contact cooperativity in our case is different from the protein-protein interactions. Homogeneously charged polyamines do not have sticky-ends that would allow them to interact with each other as proteins do (53), nor do they exhibit hydrophobic interactions that would allow them to bind condensed DNA cooperatively like cationic lipids (67,82). It is also probably not the case of an allosteric cooperativity through DNA conformational transition, since the majority of the literature reports that DNA remains in the B-form upon condensation by polyamines. What is really being changed during the condensation is the entropy associated with the DNA/ligand positioning. For a long DNA molecule, when a loop is being formed during its compaction, there is a tension at the last ligand crosslinking the loop and the DNA end coming out from the loop. A new ligand would try to bind DNA next to already liganded site to decrease this tension. This mechanism can lead to a contact cooperativity, mathematically equivalent to a standard McGhee-von Hippel cooperativity. Analogously, in the case of short DNA molecules, the formation of new nonliganded volumes inside the condensed phase is unfavorable both energetically (leaving an uncompensated DNA charge) and entropically (breaking the liquid-crystalline order). As a result, ligands would tend to rearrange so as to bind DNA close to already bound ligands.

Now let us look at the long-range interaction model (Fig. 10). Although anticooperative (repulsive) long-range interactions may result in the reentrant aggregation-resolubilization behavior (Fig. 10 A), the cooperative (attractive) interactions in Fig. 10 B better correspond to a sharply increasing binding curve in the experimental Fig. 6. What could be the physical nature of the attractive long-range potential? It may come only from electrostatics, but at a first glance positively charged polyamines would repel each other both in solution and on DNA. Ligand binding reduces the DNA charge and thus decreases the DNA affinity for the next ligands. This would result in the anticooperativity (effective binding constant decreases with increasing degree of binding). Such an anticooperative behavior has, in fact, been observed for electrostatic binding to DNA in solution. For example, anticooperative binding of divalent metal ions to the double helix may be well described by a linear potential G_s = W_s × c_s (85,86). A similar dependence would be true for polyamine binding at small concentrations. However, somehow the anticooperative polyamine binding to soluble DNA turns to cooperative when DNA is condensed. One can propose that the explanation of the long-range cooperativity lays in the correlated distribution of ligands along DNA, which creates attractive forces between the double helices and mediates the ligand-ligand interaction through DNA. Thus the cooperative interaction between the bound ligands is a unique feature of condensed DNA, whose physical properties are principally different from soluble DNA. Equations 3–7 allow one to take the long-range interaction potential in any form (and also in combination with the contact interactions). Several possible types of electrostatic potentials for condensed DNA have been considered in the literature (e.g., 24,27,87). It would be interesting to compare the effects of different potentials on the form of the binding curves, and choose the most suitable one.

That at least part of the ligand-binding cooperativity comes from electrostatics is manifested by the experiments where poly-L-lysine binding to condensed DNA may be either cooperative or noncooperative depending on Na⁺ concentration (88). In addition, between the two extremes of the contact and infinite-range cooperativity lays an intermediate case of the interactions involving the ligands separated by a large but fixed number of basepairs. For example, the experimentally observed cooperativity in a cationic antimicrobial agent polyhexamethylene biguanide binding to condensed DNA has been explained by the crosslink formation between distant sites of the polymer (89).

To summarize, we have considered different ligand binding models for the description of DNA condensation. A simple two-state model without ligand-ligand interactions is enough to describe qualitatively the dependencies of the aggregation-resolubilization curves on the polyamine, Na⁺, and DNA concentrations. Our experimental measurements of the stoichiometry of spermidine binding to condensed DNA provide an argument in support of the stoichiometry-dependent mechanism for the resolubilization transition proposed by the two-state model. However, the experiments show that polyamine binding to condensed DNA exhibits a cooperative behavior not consistent with the models of noninteracting ligands. We have considered the contact and the long-range ligand-ligand interactions and have showed that both types of interactions may be used to describe the experimental binding and condensation curves. Several physical mechanisms leading to cooperative ligand binding to condensed DNA are proposed. New experimental data are required to discriminate between the proposed models. In particular, the two-state model predicts an increase in the total ligand binding curve C_b during the resolubilization (Figs. 3, 9, and 10). This prediction could be verified experimentally using equilibrium dialysis (28) or titration microcalorimetry (90). Another possibility is to look into the cooperativity of ligand binding and DNA condensation using fluorescent spectroscopy (89) or capillary electrophoresis (91).

A Windows application for calculation of DNA condensation and ligand binding in the framework of the models considered above is available upon request.

APPENDIX: DERIVATION OF EQS. 3–5

Let the DNA molecule may be in the two states, starting (s) or condensed (c). Let n_i DNA molecules of type i (i = (s, c)) bind k_i ligands forming b_i ligand-ligand contacts. Then, analogously to Lando and Teif (26) and Teif et al. (63), we write the expression for the free energy of the system ΔF:

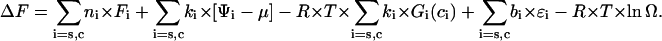(A1)

The first sum in Eq. A1 gives the free energy of n_s DNA molecules in the starting and n_c molecules in the condensed state without ligand contributions. Here F_i is the energy per DNA molecule in the state i. The second sum in Eq. A1 is the energy change arising directly due to binding of ligands to DNA without taking into account ligand-ligand interactions. Ψ_i is the free energy of binding of a ligand to DNA, and μ the chemical potential of a free ligand in solution, μ = μ_o + R × T × ln(c_o), where μ_o is the standard chemical potential. It is the difference between μ_o and Ψ_i that determines the binding constant: K_i = exp[(μ_o − Ψ_i)/(R × T)]. The third and fourth sums in Eq. A1 take into account the long-range and contact ligand-ligand interactions correspondingly. Here G_i(c_i) is the long-range interaction potential taken in units of R × T, where R is the universal gas constant, T the temperature (in degrees Kelvin). The last term in Eq. A1 is the entropy of the system, which depends on the number of possible realizations, Ω, of the same energetic state:

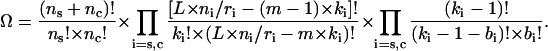(A2)

The first multiplier in Eq. A2 corresponds to the rearrangements of n_s starting and n_c condensed DNA molecules, the second multiplier is the number of rearrangements of k_i ligands of length m along L × n_i/r_i available sites on the DNA molecule, and the third multiplier is the number of possible rearrangements of b_i contacts between these ligands.

For sufficiently long DNA molecules, one can find the equilibrium values of n_i, k_i, and b_i from the Stirling's expression, ln(n!) ≈ n × [ln(n) − 1], and the conditions of ΔF minimum given by Eqs. A3–A5:

(A3)

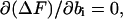(A4)

(A5)

Solving Eqs. A3–A5, one obtains the final system of Eqs. 3–5 for the equilibrium values of ϑ and c_i.