Translational-Entropy Gain of Solvent upon Protein Folding

Abstract

We show that even in the complete absence of potential energies among the atoms in a protein-aqueous solution system, there is a physical factor that favors the folded state of the protein. It is a gain in the translational entropy (TE) of water originating from the translational movement of water molecules. An elaborate statistical-mechanical theory is employed to analyze the TE of water in which a protein or peptide with a prescribed conformation is immersed. It is shown that if the number of residues is sufficiently large, the TE gain is powerful enough to compete with the conformational-entropy loss upon folding. For protein G we have tested over 100 compact conformations generated by a computer simulation with the all-atom potentials as well as the native structure. A significant finding is that the largest TE is attained in the native structure. The translational movement of water molecules is quite effective in achieving the tight packing in the interior of a natural protein. These results are true only when the solvent is water whose molecular size is the smallest among the ordinary liquids in nature.

INTRODUCTION

One of the defining characteristics of a living system is the ability of its component molecular structures to self-assemble with precision and fidelity. Uncovering the mechanisms through which such processes occur is a central subject for understanding life at the molecular level. The most fundamental and universal example of the biological self-assembly is protein folding, and investigating this complex process will provide a new physical insight into the other processes as well (1). However, the elucidation of the folding mechanism is one of the most difficult tasks in modern science, and despite an enormous amount of effort devoted, the elucidation has not been achieved yet. It appears that a breakthrough is not likely to be obtained unless a unique concept, which is different from the conventional approaches, is employed. On the other hand, water is believed to play critical roles in the living system and to be indispensable in sustaining life. However, it has not yet been made clear how water is critical in the concrete. In this article, we are concerned about presenting a new view of protein folding and highlighting an aspect of the critical importance of water from an interesting standpoint.

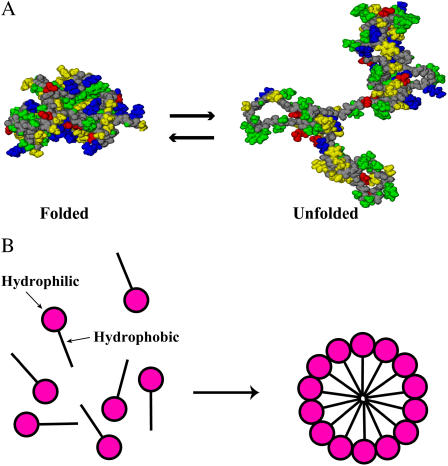
A protein spontaneously folds into a unique native structure from numerous denatured conformations. A feature common to the native structures of proteins is that the backbone and side chains are tightly packed and the interior contains little space (2–7). This means that protein folding undergoes a very large loss of the conformational entropy (CE) of a protein molecule. Then a question arises: “What is the major factor competing with the CE loss in the folding?” The formation of intramolecular hydrogen bonds, one of the previously suggested factors, is accompanied by the serious energetic penalty of dehydration (8–11). This is also true for the formation of salt bridges, contacts of unlike-charged atoms, in the interior. The prevailing view is that water adjacent to a hydrophobic group is entropically unstable due to the ordering of water molecules with an increase in the number of hydrogen bonds and that the folding is driven mainly by the so-called hydrophobic effect through the burial of nonpolar side chains (12,13). We note, however, that a protein is characterized by the heterogeneity that hydrophobic and hydrophilic atoms and groups are rather irregularly distributed in the molecule. Hence, the burial of nonpolar side chains is unavoidably accompanied by the burial of polar and charged groups. Fig. 1 A compares the folded, native structure and an unfolded conformation of barnase. In the figure the polar backbone, nonpolar side chains, polar side chains, positively charged side chains, and negatively charged side chains are marked in different colors. It is observed that none of the colors is appreciably more buried or exposed to water upon unfolding or folding. The database shows that when proteins fold, 83% of the nonpolar side chains, 82% of the peptide groups, 63% of the polar side chains, and 54% of the charged side chains are buried in the interior (7,14). Thus, protein folding is in contrast to the aggregation of surfactant molecules as micelles illustrated in Fig. 1 B where the nonpolar groups are almost completely buried whereas the charged groups are all exposed (15). In protein folding the hydrophobic effect works much less effectively than in the micelle formation. Thus, none of the previously suggested factors is powerful enough to compete with the very large CE loss. Actually, the experimental and theoretical results are quite inconsistent and controversial. For example, the salt bridges act both as stabilizers (16) and as destabilizers (17), the exposed area of the hydrophobic surface is not always correlated with the conformational stability of a protein (18), and the polar group burial contributes more to the stability of the native structure than the nonpolar group burial (7,19). There must be another powerful driving force in the folding.

FIGURE 1.

(A) The folded, native structure (left) and an unfolded conformation (right) of barnase. The constituent atoms are represented by the solid model. The polar backbone, nonpolar side chains, polar side chains, positively charged side chains, and negatively charged side chains are marked in gray, yellow, green, blue, and red, respectively. (B) Cartoon illustrating the micelle formation by surfactant molecules in water.

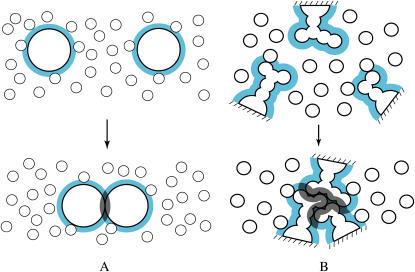
Most of the discussions concerning protein folding have been focused on contributions to the free-energy change upon folding from potential energies among the atoms in the system including the solvent (1). A view lacking in earlier studies is that the translational movement (the thermal motion) of the solvent molecules should critically influence the folding process. We start with the concept illustrated in Fig. 2 A, which was first presented by Asakura and Oosawa (20). Suppose that large particles are immersed in small particles and the number density of the small particles is much higher than that of the large particles. The small and large particles are hard spheres with diameter d_S and those with diameter d_L, respectively, and there are no soft interactions (e.g., van der Waals and electrostatic interactions) among the particles at all. In such a system, all allowed configurations have the same energy and the system behavior is purely entropic in origin. The presence of a large particle generates the volume from which the centers of the small particles are excluded. The excluded volume is the spherical volume with diameter (d_L + d_S) that is the sum of the volumes of the large particle and of the envelope colored in blue. When two large particles contact each other, the excluded volumes overlap (the overlapped volume is shadowed), and the total volume available to the translational movement of the small particles increases by this amount. The increase leads to a gain in the translational entropy (TE) of the small particles. We remark that the resultant free-energy change takes the same value in both of the isochoric and isobaric processes. Within the framework of the Asakura and Oosawa (AO) theory, the free-energy change is given as −(ΔV/V_S)η_Sk_BT = −3(d_L/d_S)η_Sk_BT/2 (20,21) where η_S is the packing fraction of the small particles, ΔV the increase in the total volume available to the small particles defined above, V_S the volume (size) of a small particle, and k_BT Boltzmann's constant times the absolute temperature. In the isochoric process, the TE gain exactly equals the free-energy change divided by −T. In the isobaric process, there is a slight decrease in the system volume accompanying a corresponding decrease in the enthalpy. That is, part of the TE gain is converted into the enthalpic gain. Irrespective of the process, the free-energy decrease originates purely from the TE effect in the model system considered (20,21). In the original discussion by Asakura and Oosawa, the large particles are colloidal particles and the small particles are macromolecules. In colloidal mixtures (21,22) to which the AO theory have been applied, the larger and smaller colloidal particles are regarded as the large and small particles, respectively. In general, the large particles can be solutes immersed in solvent of the small particles.

FIGURE 2.

(A) Illustration of the concept first presented by Asakura and Oosawa (20). (B) Application of the concept to protein folding occurring in solvent. In this example, the three side chains are packed against one another. We remark that the excluded volume generated by a solute molecule is physically different from the partial molar volume (see the text).

An important point of the concept described above is that the large particles are driven to contact each other for increasing the TE and decreasing the free energy of the small particles. Besides the highly specific interactions of steric and chemical nature, this entropic effect is omnipresent in a biological system. We apply the concept to protein folding occurring in a dense solvent where the solvent molecules energetically move round. In our application, the small particles are from the solvent and the large particles correspond to protein subunits. In Fig. 2 B, three side chains are considered to illustrate an example of intramolecular contacts. The excluded volume for the solvent molecules and the overlapped volume are represented in the same manner as in Fig. 2 A. The gain in the TE of the solvent arising from the contact is dependent not on the absolute value of the overlapped volume but on the overlapped volume scaled by the size of the solvent molecules. The geometric features of the side chains lead to a much larger overlapped volume than in the case of simple spheres (compare Fig. 2, A and B). The solvent in the biological system is water whose molecular size is exceptionally small. For these reasons, the TE gain occurring in this particular system is expected to be quite substantial.

To exclusively investigate the TE effect in protein folding, we model solvent molecules as hard spheres and treat a protein molecule as a set of fused hard spheres accounting for the geometric features of the backbone and side chains at the atomic level (23). We employ the three-dimensional (3D) integral equation theory (24–26), an elaborate statistical-mechanical approach, which allows us to calculate the density structure of the solvent near a protein molecule in a prescribed conformation and its solvation free energy (SFE). Two peptides (Met-enkephalin and the C-peptide fragment consisting of the 1–13 residues of ribonuclease A) and two proteins (protein G and barnase) are treated and a number of different conformations are considered. The key quantity we analyze is the TE of the solvent in which a peptide or protein molecule is immersed. The TE, which is strongly dependent on the molecular conformation, can readily be extracted from the SFE in our model system. The TE gain upon folding is compared with the CE loss, and the effects due to the number of residues of a peptide or protein molecule, the temperature, the size of solvent molecules, and the solvent packing fraction are investigated. We show that when the number of residues is sufficiently large and the solvent is water, the TE gain is a powerful driving force in the folding and well competes with the very large CE loss. Based on an exhaustive analysis for protein G, it is found that the native structure allows the surrounding water to win almost the largest TE, and the significance of this result is discussed in detail. Last, it is argued that the formation of ordered structures and the occurrence of self-assembling processes in a living system, which are critical in sustaining life, are made possible only in water.

MODEL AND THEORY

The integral equation theory is a statistical-mechanical theory that is popular in liquid state physics (27). It was originally developed for a spherically symmetric system. The 3D integral equation theory we employ is an extension to general systems described using the x-y-z coordinate system. The great advantage of the 3D version is that details of the polyatomic structure of a solute molecule can explicitly be taken into account. Similar approaches have been employed by several authors (28–32) to analyze the solvation properties of a solute molecule. In our case, the 3D integral equation theory is applied to the special model system described below.

Solute I, a protein molecule with a prescribed conformation, is immersed in small spheres forming the solvent at infinite dilution. Solute I consists of a set of fused atoms. In the 3D integral equation theory, the Ornstein-Zernike equation in the Fourier space (24–26) is expressed by

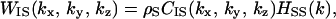(1)

and the closure equation (24–26) is written as

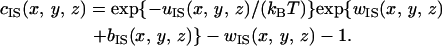(2)

Here, the subscript S denotes the solvent, c is the direct correlation function, h the total correlation function, w = h − c, u the potential, k_BT Boltzmann's constant times the absolute temperature, and ρ_S the solvent number density. The capital letters (C, H, and W) represent the Fourier transforms. is calculated using the integral equation theory for spherical particles and served as part of the input data. In the hypernetted-chain approximation employed in this study, the bridge function b is set at zero. The reliability of the hypernetted-chain closure equation has already been verified (24,33).

Equations 1 and 2 are numerically solved on a cubic grid. The x-y-z coordinates of the protein atoms in the native structure are taken from the Protein Data Bank (PDB). As for the protein atoms in an unfolded conformation, the coordinates are obtained in the following manner. First, a conformation is generated by randomly assigning dihedral angles of the backbone. Second, to eliminate all the unreasonable overlaps, the constituent atoms are moved to the locally optimized coordinates by employing a standard energy-minimization method with the all-atom potentials. The center of the protein molecule (x_C, y_C, z_C) is calculated from

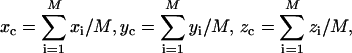(3)

where M denotes the total number of the atoms. The center is then chosen as the origin of the coordinate system and the x-y-z coordinates of the protein atoms are recalculated as (x_i − x_C, y_i − y_C, z_i − z_C) (i = 1, …, M). The numerical procedure is briefly summarized as follows.

1. Calculate u_IS(x, y, z) at each 3D grid point.

2. Initialize w_IS(x, y, z) to zero.

3. Calculate c_IS(x, y, z) using Eq. 2.

4. Transform c_IS(x, y, z) to C_IS(k_x, k_y, k_z) using the 3D fast Fourier transform (3D-FFT).

5. Calculate W_IS(k_x, k_y, k_z) from Eq. 1.

6. Invert W_IS(k_x, k_y, k_z) to w_IS(x, y, z) using the 3D-FFT.

7. Repeat steps 3–6 until the input and output functions become identical within convergence tolerance.

The solvent molecules are modeled as hard spheres and solute I is treated as a set of fused hard spheres. On grid points where the solvent particle and at least one of the atoms overlap, exp{−u_IS(x, y, z)/(k_BT)} is zero. Otherwise, it is unity. The grid spacing (Δx, Δy, and Δz) is set at 0.2d_S and the grid resolution (N_x × N_y × N_z) chosen, which is dependent on the solute size and the solute conformation, is in the range from 64 × 64 × 64 to 512 × 512 × 512. It has been verified that the spacing is sufficiently small and the box size (N_xΔx, N_yΔy, and N_zΔz) is large enough.

The density structure of the solvent near solute I is obtained as g_IS(x, y, z) (g = h + 1). A great advantage of our theory is that the solvation free energy of solute I, Δμ_I, is obtained from the simple integration of the direct and total correlation functions (25) expressed by

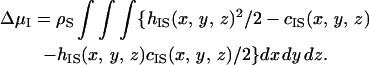(4)

The SFE is “the excess free energy of the solvent in which solute I is immersed” minus “the excess free energy of pure solvent”. In our system, both the solvent particles and the fused atoms constituting solute I are modeled as hard spheres, and there are no soft interactions at all. Moreover, the solvent is a monoatomic fluid. Consequently, the excess energy of solvent is zero and the SFE equals −TΔS_I where ΔS_I is “the translational entropy of the solvent in which solute I is immersed” minus “the TE of pure solvent”. (The most important quantity is the solvation free energy that is independent of the solute insertion process. Here we conveniently consider the isochoric process.)

As explained in the Introduction, the solvent drives solute particles to contact each other, and this effect is physically described in terms of the potential of mean force (PMF) between the solute particles (24). Earlier analyses (33,34) showed that due to the density structure of the solvent formed near the solute particles, the PMF reaches several solvent diameters. Moreover, it is oscillatory (i.e., attraction and repulsion appear alternately) and has multiple local minimums and maximums. A smaller excluded volume or a smaller accessible surface area (ASA) does not always lead to a lower value of the PMF. This feature of the PMF cannot be described by the AO theory (20). Because a protein molecule has the polyatomic structure, the SFE, which is dependent on the PMF between every pair of protein atoms, exhibits complex behavior. The smallest excluded volume or the smallest ASA does not always give the lowest SFE. Hence, neither the simple treatment based on the ASA (35,36) nor the scaled particle theory (37) is capable of evaluating the SFE correctly. This is particularly true for a rather compact conformation in which many of protein atoms near the surface are close together but not completely in contact with one another. This is why an elaborate statistical-mechanical approach such as the 3D integral equation theory is required.

We are especially interested in water as the solvent. The diameter d_S of a water molecule employed in earlier studies is in the range from 0.275 to 0.28 nm. The packing fraction 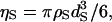where ρ_S is the experimental value for water at 25°C, is 0.3630 for d_S = 0.275 nm, and 0.3831 for d_S = 0.28 nm. In this study, d_S and η_S are set at 0.28 nm and 0.3665, respectively, as the reference condition. The diameter of each atom in the peptide or protein molecule is chosen to be the Lennard-Jones sigma of ECEPP/2 (38,39) (for Met-enkephalin and the C-peptide) or AMBER99 (for the C-peptide, protein G, and barnase). It is not easy to extract the TE for a real system accurately in a quantitative sense. However, semiquantitative evaluation of the TE can reasonably be made. We have performed many test calculations using different values of the atomic diameters. Here, we describe the TE or SFE difference between a fully extended conformation and the α-helix structure of the C-peptide as examples. The TE difference calculated using ECEPP/2 does not differ from that calculated using AMBER99. When the atomic diameters are set smaller by 10%, for instance, the TE difference decreases by ∼24% but the α-helix structure still gives much larger TE. When an attractive interaction is incorporated in the solvent-solvent potential, the absolute value of the SFE decreases considerably for both the extended conformation and the α-helix structure. However, the SFE difference, which is much more important, does not change significantly by the incorporation of the attractive interaction: The change is always <±10% (as the attractive interaction incorporated becomes stronger, the SFE difference first increases and then decreases). Thus, for the peptides and proteins in the conformations tested, it has been verified that our conclusions are robust regardless of the atomic diameters and the solvent-solvent attractive interaction.

RESULTS AND DISCUSSION

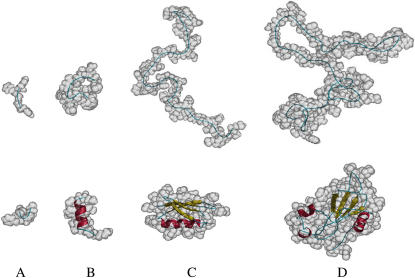
We test Met-enkephalin, the C-peptide, protein G, and barnase. The number of residues of these peptides and proteins are, respectively, 5, 13, 56, and 110. For Met-enkephalin, some extended and compact conformations are considered. One of the compact conformations is the lowest-energy conformation in vacuum determined in an earlier work (38). For the C-peptide, protein G, and barnase, we consider the native structure taken from the PDB (the structure for the C-peptide is the corresponding segment of the native protein forming an α-helix structure) and an unfolded conformation is generated in the manner described above. A fully extended conformation is also considered for the C-peptide. It is experimentally known that the C-peptide has a high propensity to form the α-helix structure and even for the isolated C-peptide the α-helix partially (∼30%) remains in aqueous solution (40). We consider this peptide to study the feature of the α-helix formation in terms of the TE effect. For protein G, we consider a number of additional, very compact conformations taken from the local-minimum and global-minimum states of the energy function in computer simulations using all-atom potentials (39).

Translational-entropy gain of solvent upon folding

The values of ΔS_I calculated under the reference solvent condition, “d_S = 0.28 nm and η_S = 0.3665”, for some representative conformations of the peptides and proteins are collected in Table 1. In the analysis on the TE, the solvent under the reference condition is a good model of water. Representative conformations of the peptides and proteins are illustrated in Fig. 3. As observed from Table 1, for Met-enkephalin the translational entropy of the solvent tends to be larger for a more compact conformation. However, it is not significantly dependent on the conformation and the largest difference observed is only ∼10k_B. For the C-peptide, the TE is the smallest for the fully extended conformation and the largest for the α-helix structure, and the difference is quite large (∼54k_B). The TE for the α-helix structure is larger than that for the unfolded conformation by ∼23k_B. Thus, the formation of an α-helix structure involves a large gain in the TE of the solvent, which has been overlooked in earlier studies. The TE gain of ∼23k_B corresponds to the free-energy change of ∼−14 kcal/mol at 25°C. Baldwin (11) argued that the enthalpy change in the formation of an intramolecular hydrogen bond between “O” and “N” in –CONH– groups in water, CO⋯W + NH⋯W → CO⋯HN + W⋯W, is 0 ± 1 kcal/mol. Even if the enthalpy change was negative and as large as −1 kcal/mol, the contribution to the α-helix formation would be ∼−9 kcal/mol. This suggests that in the α-helix formation the TE gain is more substantial as a driving force than the intramolecular hydrogen bonding that unavoidably accompanies the dehydration penalty. This never means that the intramolecular hydrogen bonding is unimportant. Sufficiently many intramolecular hydrogen bonds must be formed in the interior to compensate the dehydration penalty. As argued in recent articles (26,41), the formation of the helical structure by a long backbone, which features the α-helix structure, leads to a significant decrease in the excluded volume for the solvent molecules. The formation of the β-sheet structure also results in the excluded-volume decrease due to the lateral contact of backbones (26). The TE gain arising from the formation of these secondary structures should be dependent on the amino acid sequence, and the examination of the sequence effects is an interesting task for the future.

TABLE 1.

ΔS_I calculated under “d_S = 0.28 nm and η_S = 0.3665” for representative conformations of Met-enkephalin, the C-peptide, protein G, and barnase

Peptide or protein (conformation)	Parameters	ΔSI/kB
Met-enkephalin (compact)	ECEPP/2	−221 (10)
Met-enkephalin (extended)	ECEPP/2	−231 (0)
C-peptide (native)	AMBER99	−582 (54)
C-peptide (unfolded)	AMBER99	−605 (31)
C-peptide (extended)	AMBER99	−636 (0)
C-peptide (native)	ECEPP/2	−577 (54)
C-peptide (extended)	ECEPP/2	−631 (0)
Protein G (native)	AMBER99	−2179 (207)
Protein G (unfolded)	AMBER99	−2386 (0)
Barnase (native)	AMBER99	−4128 (518)
Barnase (unfolded)	AMBER99	−4646 (0)

ΔS_I is “the translational entropy of the solvent in which solute I is immersed” minus “the TE of pure solvent”. The number in the parenthesis denotes the value relative to ΔS_I/k_B of the extended conformation (for Met-enkephalin and the C-peptide) or of the unfolded conformation (for protein G and barnase). For example, the TE of the solvent in which barnase is immersed is larger for the native structure by 518k_B than for the unfolded conformation.

FIGURE 3.

Representative conformations of Met-enkephalin, the C-peptide, protein G, and barnase. The constituent atoms are represented by the shaded model in transparency. The backbone atoms are shown by the ribbon model. The coil, α-helix, and β-strand are colored in blue, red, and yellow, respectively. (A) Met-enkephalin. An extended conformation (top) and a compact conformation obtained as the lowest-energy conformation in vacuum (bottom). (B) The C-peptide. An unfolded conformation (top) and the native α-helix structure (bottom). (C) Protein G. An unfolded conformation (top) and the native structure (PDB code, 2GB1) (bottom). (D) Barnase. An unfolded conformation (top) and the native structure (PDB code, 1BNR) (bottom).

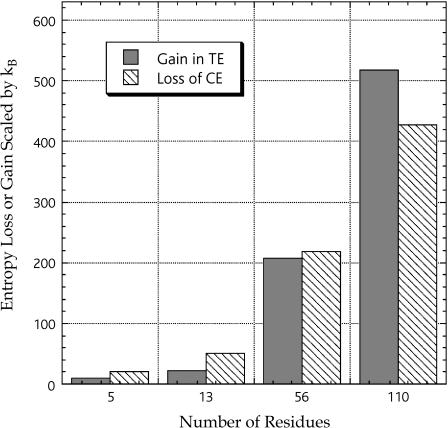
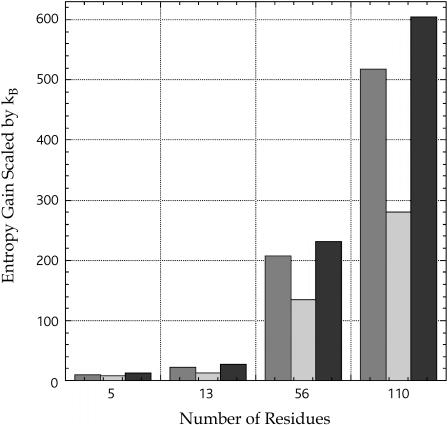
Our next concern is to check if the TE gain of the solvent upon folding is large enough to compete with the conformational-entropy loss that is quite large. Let ΔS_N and ΔS_D be ΔS_I for the native structure and ΔS_I for the unfolded conformation, respectively. (In the case of Met-enkephalin whose stabilized conformation is extended (42), ΔS_I for the compact conformation and ΔS_I for the extended conformation shown in Fig. 3 are regarded as ΔS_N and ΔS_D, respectively.) The CE change upon unfolding ΔS_C,N→D (i.e., the CE loss upon folding) can roughly be estimated as the sum of (ln9)N_Rk_B and 1.7N_Rk_B, which, respectively, represent the contributions from the backbone and the side chains (43). Fig. 4 is prepared to compare (ΔS_N − ΔS_D) and ΔS_C,N→D for the peptides and proteins. The estimation of the CE change is not quantitatively accurate. We can generate a number of different unfolded conformations on a computer and the TE gain calculated should be variable, depending on the unfolded conformation chosen. For these reasons, the comparison illustrated in Fig. 4 gives just an idea of the magnitudes of the TE gain and the CE loss upon folding as functions of N_R. The values of the ratio (ΔS_N − ΔS_D)/ΔS_C,N→D are ∼0.53, ∼0.45, ∼0.95, and ∼1.2 for Met-enkephalin, the C-peptide, protein G, and barnase, respectively. It can be concluded that if N_R becomes sufficiently large, the TE gain is powerful enough to compete with the CE loss.

FIGURE 4.

Gain in the translational entropy (TE) of the solvent calculated under the reference condition (“d_S = 0.28 nm and η_S = 0.3665”) and loss of the conformational entropy (CE) of the peptide or protein molecule. The TE gain and the CE loss upon folding are compared.

Here, it is worthwhile to refer to the temperature dependence of the CE loss and the TE gain. The experimental measurements (44) have shown that the CE loss increases considerably as the temperature increases. This evidence can physically be interpreted as follows. The CE is closely related to the torsion energy of a protein molecule. The dihedral angle giving high torsion energy is not allowed at a low temperature. As the temperature increases, the allowed range of the dihedral angle becomes increasingly wider, leading to larger CE of an unfolded conformation. The CE of the native structure does not become significantly larger due to its conformational constraints. It follows that the CE loss becomes larger with increasing temperature. On the contrary, the TE gain becomes smaller as the temperature increases because the solvent packing fraction, which has a large effect on the TE gain, becomes slightly lower upon heating. In other words, the TE gain increases as the temperature becomes lower, whereas the opposite is true for the CE loss.

Characteristics of native structure

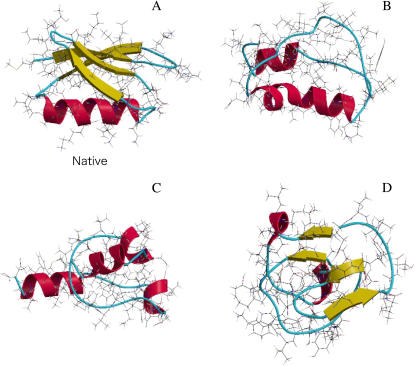
For protein G, we have tested over 100 conformations with great compactness, which were taken from those in the trajectories of exhaustive computer simulations (39). Three of them (structures 1, 2, and 3) are compared with the native structure in Fig. 5. It has been found that there are significantly many conformations giving lower intramolecular energy than the native structure. Strikingly, we have found no conformation giving larger TE than the native structure. We now discuss the TE for the specific structures shown in Fig. 5. The values of ΔS_I calculated under the reference condition, “d_S = 0.28 nm and η_S = 0.3665”, for the four structures are given in Table 2. The absence of the β-sheet in structure 1 causes smaller TE. Although the α-helix formation leads to a large stabilization as shown above, the TE of structure 2 with four α-helices is smaller than that of the native structure. This result indicates that the nonlocal intramolecular contacts play important roles in the formation of the native structure. If a solute has a smooth surface, for a fixed volume the spherical shape gives the smallest excluded volume for solvent molecules and the largest TE. However, this is not true for a protein with the complex polyatomic structure. For example, the conformation of structure 3 is more spherical than the native conformation as observed from Table 3 in which the parameters representing overall shapes of the four structures and the unfolded conformation are compared. Nevertheless, structure 3 gives considerably smaller TE than the native structure. The tight packing specific to the amino acid sequence of protein G gives rise to the asphericity of the native structure. Thus, among the conformations that are probable in terms of the intramolecular energy, the native structure can be characterized as the structure allowing the surrounding water to win almost the largest TE.

FIGURE 5.

Bond representation of four example conformations of protein G. The ribbons of the backbone atoms are colored in the same manner as in Fig. 3. (A) The native structure. (B) A conformation in which the α-helix in agreement with the native structure is formed but the β-sheet is absent (structure 1). (C) A conformation with four α-helices (structure 2). (D) A nearly spherical conformation with an incomplete β-sheet (structure 3).

TABLE 2.

ΔS_I calculated under “d_S = 0.28 nm and η_S = 0.3665” for representative conformations of protein G

Conformation	Parameters	ΔSI/kB
Native	AMBER99	−2179 (207)
Unfolded	AMBER99	−2386 (0)
Structure 1	AMBER99	−2225 (161)
Structure 2	AMBER99	−2212 (174)
Structure 3	AMBER99	−2255 (131)

The number in the parenthesis denotes the value relative to ΔS_I/k_B of the unfolded conformation. For example, the TE of the solvent in which protein G is immersed is larger for the native structure by 207k_B than for the unfolded conformation.

TABLE 3.

Overall shapes estimated for representative conformations of protein G

Conformation	l1/l3	l1/l2
Native	1.40	1.32
Unfolded	2.04	1.85
Structure 1	1.25	1.05
Structure 2	1.27	1.15
Structure 3	1.19	1.08

The overall shape of a protein molecule can be characterized by the three principal moments of inertia, λ₁, λ₂, and λ₃. These moments are given as the eigenvalues of the matrix of radii of gyration (15). The asphericity can be measured by monitoring the parameters, l₁/l₂ and l₁/l₃ (l₁ ≥ l₂ ≥ l₃), where l_i is defined as 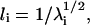(i = 1, 2, 3). For a complete sphere, l₁/l₃ = 1 and l₁/l₂ = 1. For a cylinder with length greater than diameter and for a prolate, l₁/l₃ > 1 and l₁/l₂ > 1. For a disk with length smaller than diameter and for an oblate, l₁/l₃ > 1 and l₁/l₂ = 1.

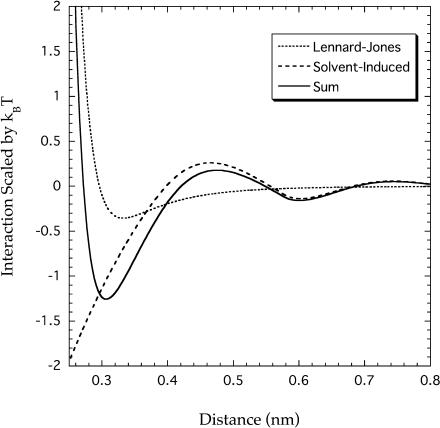
The tight packing in the interior of a protein molecule is necessary to ensure that the native structure be stable and that partially denatured, inactive structures have negligible probability at ambient temperatures (5,45). Pace (7) claimed that the tight packing in the native structure is ascribed to the van der Waals interactions among protein groups in the interior, which are more favorable than the interactions of the same groups with water in an unfolded protein. To examine his claim, we consider the oxygen atom in the –CONH– group that has the largest value of the Lennard-Jones (LJ) epsilon. In Fig. 6, the LJ interaction between oxygen atoms, whose attractive part is the van der Waals interaction, is compared with the interaction entropically induced in solvent. The former is calculated using the AMBER99 parameters. The latter is theoretically calculated as the interaction between hard spheres, the diameter of which equals the LJ sigma of the oxygen atom (0.29 nm), immersed in solvent hard spheres with diameter 0.28 nm. The integral equation theory incorporating accurate bridge functions (46) is employed in the calculation. The total interaction, the sum of the two interactions, is also shown in the figure. It is apparent that the solvent-induced interaction predominates over the LJ interaction. The minimum of the LJ interaction occurs at ∼0.33 nm (the distance between two centers) with the minimum interaction energy of −0.35k_BT, whereas the total interaction has the minimum of −1.26k_BT at ∼0.30 nm. We note that the incorporation of an attractive interaction in the solvent-solvent potential causes a downward shift of the induced interaction, even enhancing its predominance. Thus, the induced interaction makes a dominant contribution to the unexpectedly tight packing (2–7) leading to a very large stabilization.

FIGURE 6.

Direct Lennard-Jones interaction and solvent-induced interaction between oxygen atoms. The solvent-induced interaction, which is entropic in origin, is represented in terms of the potential of mean force. The sum of the two interactions is also shown.

Effects due to molecular size and packing fraction of solvent

The conformation of a protein is quite variable depending on the solvent species. The TE effect, which plays essential roles in the conformational stability, is governed by the two key parameters, the molecular diameter d_S and the packing fraction η_S of the solvent. Here, we make a quantitative examination of the effects due to d_S and η_S. As for the TE gain arising from the contact of spherical solutes, within the framework of the AO theory (20), it increases in proportion to η_S and 1/d_S. However, the TE gain upon folding calculated by the 3D integral equation theory for the polyatomic structure exhibits more complex behavior. We have chosen two additional conditions, “d_S = 0.42 nm and η_S = 0.3665” and “d_S = 0.28 nm and η_S = 0.3927” (the reference condition is “d_S = 0.28 nm and η_S = 0.3665”), and analyzed the TE effect for the peptides and proteins. The values of ΔS_I calculated under “d_S = 0.42 nm and η_S = 0.3665” are given in Table 4 that is to be compared with Table 1. The TE gains upon folding (ΔS_N − ΔS_D) obtained from the three different conditions are compared in Fig. 7. The ∼7% increase in η_S leads to the TE gain that is larger by ∼21, ∼17, ∼12, and ∼17%, respectively, for Met-enkephalin, the C-peptide, protein G, and barnase. The ∼33% decrease in 1/d_S results in the TE gain that is smaller by ∼27, ∼46, ∼35, and ∼46%, respectively. The effects due to η_S and 1/d_S are much larger than the AO theory predicts and significantly dependent on the peptide or protein species. An impressive result is that for barnase the TE gain under “d_S = 0.42 nm and η_S = 0.3665” is far smaller than the CE loss ((ΔS_N − ΔS_D)/ΔS_C,N→D ∼ 0.65). We have found for barnase that the TE gain is much smaller than the CE loss even when η_S is increased to 0.4189 with d_S = 0.42 nm. The packing fraction of a pure solvent in liquid phase at ambient temperatures and pressures does not vary greatly from solvent to solvent, whereas the variation of the molecular size is much larger: Whenever d_S increases, η_S/d_S becomes much smaller. Water exists, thanks to the hydrogen-bonding network, in a dense liquid state despite its exceptionally small molecular size. This feature of water is crucially important in protein folding.

TABLE 4.

ΔS_I calculated under “d_S = 0.42 nm and η_S = 0.3665” for representative conformations of Met-enkephalin, the C-peptide, protein G, and barnase

Peptide or protein (conformation)	Parameters	ΔSI/kB
Met-enkephalin (compact)	ECEPP/2	−81 (7)
Met-enkephalin (extended)	ECEPP/2	−88 (0)
C-peptide (native)	AMBER99	−208 (30)
C-peptide (unfolded)	AMBER99	−220 (18)
C-peptide (Extended)	AMBER99	−238 (0)
C-peptide (native)	ECEPP/2	−207 (28)
C-peptide (extended)	ECEPP/2	−235 (0)
Protein G (native)	AMBER99	−744 (135)
Protein G (unfolded)	AMBER99	−879 (0)
Barnase (native)	AMBER99	−1384 (280)
Barnase (unfolded)	AMBER99	−1664 (0)

The number in the parenthesis denotes the value relative to ΔS_I/k_B of the extended conformation (for Met-enkephalin and the C-peptide) or of the unfolded conformation (for protein G and barnase). For example, the TE of the solvent in which barnase is immersed is larger for the native structure by 280k_B than for the unfolded conformation.

FIGURE 7.

TE gains of the solvent upon folding calculated under three different conditions, “d_s = 0.28 nm and η_S = 0.3665” (dark shaded), “d_S = 0.42 nm and η_S = 0.3665” (light shaded), and “d_S = 0.28 nm and η_S = 0.3927” (solid).

Comments on solute hydrophobicity

The hydration free energy (HFE) of a nonpolar solute has a positive value. In a conventional interpretation, the physical origin of the positive value is the entropic loss arising from the ordering of water molecules around the solute (12,13). Hereafter, this is simply referred to as the entropic loss. The entropic loss originates from the situation in which water molecules interact through strongly attractive potential whereas the water-solute attractive interaction is much weaker. However, the TE loss upon the insertion of the solute into water, which arises from the restriction of the translational movement of water molecules, also makes a significantly large contribution to the positive HEF (47). An important point to be emphasized is that the TE loss is always present regardless of the physicochemical properties of the solute, whereas the entropic loss is present only around a nonpolar solute. The entropic loss increases roughly in proportion to the accessible surface area. Therefore, when the entropic loss dominates, the HFE can be scaled by the ASA and this scaling is experimentally known to be valid for small solute molecules. However, by employing a realistic molecular model for water, Cann and Patey (48) showed for sufficiently large nonpolar solutes that the TE loss, which strongly depends on the excluded volume, makes a dominant contribution to the HFE and that the scaling by the ASA does not hold at all. We remark that the TE loss of water upon the insertion of a solute must explicitly be included in the interpretation of the solute hydrophobicity.

Even when the concern is just the free-energy change associated with the conformational change of a protein, the hydration properties of small solute molecules cannot be extended to those of large proteins in a straightforward manner as shown below. The solvation free energy Δμ_S can be decomposed into two terms. One of them is the contribution from the molecular volume Δμ_S0 and the other is the contribution from the solute surface structure Δμ_SA: Δμ_S = Δμ_S0 + Δμ_SA. Let us consider different structures of a protein. Because the molecular volume is constant against the structure change, Δμ_S0 = Δμ_S − Δμ_SA is independent of the structure and the following equation holds: (Δμ_S)_I − (Δμ_S)_J = (Δμ_SA)_I − (Δμ_SA)_J (the subscripts I and J denote values for two different structures, structures I and J). In the ASA method applied to our model system, Δμ_SA is considered proportional to the ASA (the ASA is denoted by A). If this consideration is valid, D_IJ = {(Δμ_S)_I − (Δμ_S)_J}/(A_I − A_J) takes the same value for any structures. For the four structures of protein G shown in Fig. 5 and explained in Table 3, we have calculated the ASA (49) and D_IJ (I = 1, 2, 3) where the native structure is chosen as structure J. The values of D_IJ/(k_BT) are ∼−980, ∼110, and ∼−550 nm⁻³, respectively. D_IJ is quite variable and even its sign is changeable. Thus, the ASA method fails for a large solute molecule like protein G for which the TE effect dominates.

CONCLUDING REMARKS

We have pointed out the importance of the translational movement of water molecules as a major driving force in protein folding. Even in the complete absence of potential energies among the atoms forming a protein-solvent system, there is a gain in the translational entropy of the solvent, which favors the protein folding. The TE gain upon folding becomes the largest when the solvent is water that exists, thanks to the hydrogen-bonding network, in a dense liquid state at ambient temperatures and pressures despite its exceptionally small molecular size. We note that the TE gain is physically different from the entropic gain arising from the burial of nonpolar groups followed by the release of highly ordered water molecules adjacent to the groups. For a sufficiently large peptide and a protein immersed in water, the TE gain upon folding is powerful enough to compete with the conformational-entropy loss that is quite large. In another solvent whose molecular size is significantly larger, the TE gain is no longer capable of competing with the CE loss even for a protein.

The formation of an α-helix structure involves a TE gain of water contributing to a significantly large free-energy decrease. For the C-peptide, which has a high propensity to form the α-helix, it has been shown that the contribution is considerably larger than that from the intramolecular hydrogen bonding plus the dehydration penalty. For protein G we have tested over 100 compact conformations generated by a computer simulation with the all-atom potentials as well as the native structure and have found that the largest TE of water is attained in the native structure. Though this result is to be examined in further studies for other proteins, it is suggestive that the native structure can be characterized as the structure allowing the surrounding water to win almost the largest TE. Another finding is that the TE effect predominates over the van der Waals attractive interactions among protein groups in the interior and seems to be the most effective in achieving the tight packing in the interior required for a protein to function.

Protein folding is the most fundamental example of the biological self-assembly (1). A variety of ordered structures are formed and self-assembling processes occur in a living system. Good examples are the molecular recognition between guest ligands and host enzymes, which is often referred to as the lock-key interaction (24,50,51), the association of protein molecules, and the burial of protein molecules into a membrane. The formation of amyloid fibrils (25,26) is no exception though it is quite unfavorable and causes various diseases. It is generally believed that these processes are driven by a great energy gain at a large expense of the entropy. However, we claim that the entropy of the whole system including the surrounding water does not necessarily decrease during the processes: even when it decreases, only a moderate energy gain can overcome the total entropic loss. (It has been shown in recent experiments that the amyloid-fibril formation (52) and the lock-key interaction (53) are entropically driven. We believe that the translational movement of water molecules is a powerful driving force in these processes though the authors in Ohtaka et al. (53) give a different interpretation of their experimental results.) However, this is not true in solvents other than water. A conspicuous aspect of the crucial importance of water in sustaining life can thus be understood.