Quantitative Multiphoton Spectral Imaging and Its Use for Measuring Resonance Energy Transfer

Abstract

Protein labeling with green fluorescent protein derivatives has become an invaluable tool in cell biology. Protein quantification, however, is difficult when cells express constructs with overlapping fluorescent emissions. Under these conditions, signal separation using emission filters is inherently inefficient. Spectral imaging solves this problem by recording emission spectra directly. Unfortunately, linear unmixing, the algorithm used for quantifying individual fluorophores from emission spectra, fails when resonance energy transfer (RET) is present. We therefore sought to develop an unmixing algorithm that incorporates RET. An equation for spectral emission incorporating RET was derived and an assay based on this formalism, spectral RET (sRET), was developed. Standards with defined RET efficiencies and with known Cerulean/Venus ratios were constructed and used to test sRET. We demonstrate that sRET analysis is a comprehensive, photon-efficient method for imaging RET efficiencies and accurately determines donor and acceptor concentrations in living cells.

INTRODUCTION

Imaging of proteins that have been genetically altered to express spectrally distinct fluorescent isoforms has revolutionized cell biology. Experiments probing the interactions of proteins, formerly limited to in vitro preparations and fixed specimens, can now be conducted inside living cells (1,2). In vivo imaging of protein interaction falls into two general categories, colocalization and resonance energy transfer (RET). Fluorescence imaging can be used to map intracellular distributions of putative interacting proteins labeled with specific members of the green fluorescent protein family (FPs) (3,4). Spatial overlap between distributions can suggest intermolecular relationships (5,6). The validity of colocalization analysis is limited by the ability to obtain quantitative measurements of the abundance of each fluorescent species and by the resolution of light microscopy.

RET imaging measures the nonradiative transfer of energy from the excited state of a fluorophore (called the donor) to an adjacent acceptor molecule (7). Specifically, RET imaging measures RET efficiency, the fraction of donor excitation events that results in excitation of the acceptor. For RET to occur, three requirements must be met. First, the emission spectrum of the donor molecule must overlap with the absorbance spectrum of the acceptor. Second, the emission transition dipole of the donor must not be oriented perpendicular to the absorbance transition dipole of the acceptor and, most importantly, the donor and acceptor molecules must reside within ∼100 Å of each other. Because the RET efficiency can be used to measure distances on the 10–100 Å scale, this technique has been exploited to study protein-protein interactions. The validity of RET-based distance measurements, however, is limited by knowledge of the donor-acceptor dipole orientation, by knowledge of the donor-acceptor complex stoichiometry, and by the accuracy of the measured RET efficiency. In turn, RET efficiencies are typically estimated by measuring changes in the fluorescence intensity of the donor in the presence or absence of the acceptor. Alternatively, RET efficiency can also be estimated by measuring changes in the fluorescence lifetime of a donor in the presence or absence of an acceptor. To verify that energy lost by the donor is indeed transferred to the acceptor, a decrease in the fluorescence intensity of a donor should be matched by an increase in the fluorescence intensity of the acceptor. For fluorescence lifetime decay curves, the lifetime of the donor molecule should decrease with RET, and a new kinetic component with a “negative lifetime” should appear in the acceptor decay curve. Because of the difficulty in isolating an acceptor's fluorescent signal from a donor's signal, fluorescent lifetime analysis generally monitors the donor lifetime only. Two technical difficulties often encountered measuring RET efficiency are contamination of the acceptor's fluorescent signal with the donor's (bleed-through) and the difficulty of exciting a donor without also directly exciting the acceptor. Spectral imaging can potentially overcome both of these problems (8,9).

Excitation and emission spectra of most FP members overlap (10). Thus, they are excellent fluorophores for RET imaging studies. The overlap of emission spectra, however, makes it both difficult and inefficient to use conventional filter technology to acquire uncontaminated fluorescent signals of individual FPs in mixed populations. Spectral imaging, an imaging modality that allows for the accurate measurement of the abundance of fluorophores with overlapping emission spectra, can potentially overcome this limitation. In this study, we demonstrate that by accounting for the effects of RET in the complex fluorescent emission spectra emanating from mixtures of potential donors and acceptors, spectral imaging can be used to accurately measure donor and acceptor concentrations and their RET efficiencies.

MATERIALS AND METHODS

Cloning and purification of 6XHis-tagged proteins

Polymerase chain reaction (PCR) mutagenesis (11) was used to generate 6XHis-tagged Cerulean and Venus. PCR primers that hybridize to all FPs (sense CTTCGAGCTGGACGGCGAC and antisense CTCCAGCAGGACCATGTGATCG) were synthesized (Invitrogen, Carlsbad, CA) and used in a first PCR to generate 620 bp fragments from either Cerulean or Venus (gift from Dr. H. Puhl and Dr. S. Ikeda, NIAAA, NIH). These fragments were purified (PCR purification kit from Qiagen, Valencia, CA) and used as the primer in a second PCR where 6XHis-tagged enhanced cyan fluorescent protein (ECFP) or enhanced yellow fluorescent protein (EYFP) (generous gifts from Dr. G. Patterson (10)) were used as templates. The PCR products were digested with Dpn I (New England Biolabs, Ipswich, MA) and used to transform TOP 10 bacterial cells (Invitrogen). Cells were plated onto Lauria-Bertani medium agar plates containing ampicillin (Fermentas, Hanover, MD), and His-tagged Cerulean and Venus clones were picked and sequenced.

For protein purification, 6XHis-tagged Cerulean and Venus constructs were transformed into BL21 Star (DE3) pLysS cells (Invitrogen) and grown in 200 ml cultures for 4 h at 37°C. Isopropyl thio galactoside (IPTG) (1 mM) was then added, and cells were incubated at room temperature overnight. Cells were spun down, resuspended in Lysis buffer (50 mM NaH₂PO₄, 300 mM NaCl, 10 mM imidazole; pH 8.0) and flash frozen and thawed twice. Insoluble debris from the cell lysate was removed by centrifugation, and the supernatant was collected. Nickel nitroilotriacetic acid magnetic agarose beads (50 μl, Qiagen) were added to each 0.5 ml aliquot of supernatant and incubated at room temperature for 30 min. Magnetic beads were then washed 1× in wash buffer (50 mM NaH₂PO₄, 300 mM NaCl, 20 mM imidazole; pH 8.0). His-tagged proteins were eluted with 50μl of elution buffer (50 mM NaH₂PO₄, 300 mM NaCl, 250 mM imidazole; pH 8.0). The eluate was concentrated using Centricon filters (Amicon, Bedford, MA) and resuspended in 10 mM Tris-HCl at pH 8.0. The concentrations of the isolated FPs were determined using a spectrophotometer and Beers Law. Absorption coefficients and excitation wavelengths used were 43,000 M⁻¹cm⁻¹ at 433 nm for Cerulean (12) and 92,200 M⁻¹cm⁻¹ at 515 nm for Venus (13).

Construction of expression vectors encoding RET-stoichiometry standards

Cerulean-C1 and Venus-C1 expression vectors were generated by mutagenesis of ECFP-C1 and EYFP-C1 (Clonetech, Mansfield, UK) as described above. These clones were sequenced and used as precursors for the construction of all RET-stoichiometry standards. Standards composed of multiple FPs required removal of internal start and stop codons. To generate constructs with two FPs, a sense primer containing a BglII site (GCAGATCTGTGAGCAAGGGCGAGGAGCTGTTCACC) and an antisense primer containing EcoRI site (GCGAATTCCTTGTACAGCTCGTCCATGCCGAGAGTG) were used (high fidelity Ultra-Pfu, Stratagene, La Jolla, CA). The resultant Cerulean or Venus PCR products were purified and digested using BglII (NEB) and EcoRI (NEB). Fragments were ligated into either Venus C1 or Cerulean C1 to generate VC or CV. The two fluorophores are separated by a five amino acid linker in these constructs. Clones were selected by size and confirmed by restriction analysis. Furthermore, both blue and yellow fluorescent emission was detected from N1E cells transfected with these constructs.

To generate constructs with three FP domains, we amplified full-length Cerulean and Venus with SalI sense (GCGTCGACGGGTGAGCAAGGGCGAGGAGCTGTTCACCG) and BamHI antisense primers (GCGGATCCCTTGTACAGCTCGTCCATGCCGAGAGTGATC). Purified Cerulean PCR product was digested with SalI (Roche, Indianapolis, IN) and BamHI (NEB) and ligated into the CV construct (described above) to generate CVC. Likewise, purified Venus PCR product was digested with and ligated into the VC construct to generate VCV. This resulted in proteins in which the second and last FP domains were separated by a six amino acid linker. Clones were selected by size and confirmed by restriction analysis. Blue and yellow fluorescent emission was detected from cells transfected with these constructs.

A tumor necrosis factor receptor associated factor (TRAF) domain (229 amino acid) was PCR amplified from CFP-TRAF2TRAF-YFP (a gift from Dr. L. He, NIAMS, NIH) primers flanked by BspE1 (sense: AACTCCGGAGAGAGCCTGGAGAAGAAG, antisense: AACTCCGGAGAGCCCTGTCAGGTCCAC) sites (14).The purified PCR product was digested with BspEI (NEB) and ligated into either Cerulean C1 or CV to generate the CT and CTV constructs. Clones were selected by size and confirmed by restriction and sequence analysis.

Construction of γ-Venus and β-Cerulean

ECFP-γ- and EYFP-β-subunits of trimeric G-proteins (gifts from S. Ikeda (15)) were used to construct N-terminally tagged γ-Venus and β-Cerulean. The γ-Venus construct was generated by removing ECFP from ECFP-γ and replacing it with Venus. ECFP-γ and Venus C1 were digested with Eco47III (Roche) and BspEI (NEB). The Venus and γ-vector products were gel purified (QiaExII gel purification kit, Qiagen), ligated (Rapid ligation kit, Roche), and transformed into Top 10 bacteria. The cDNA coding for the β-subunit was digested using EcoRI and ligated into Cerulean C1. Clones expressing γ-Venus and β-Cerulean were selected based on restriction analysis. Sequencing confirmed the presence of the respective G-protein subunits, and the fluorescent emission from transfected cells confirmed the presence of the appropriate FP.

Cell culture and transfection

N1E-155 mouse neuroblastoma cells were cultured in 89% Dulbecco's modified Eagle's medium, 10% fetal bovine serum, and 1% penn/strep (Invitrogen, Carlsbad, CA). Lipofectamine 2000 (Invitrogen) was used to transfect all constructs using the protocol provided by the manufacturer, and cells were imaged the following day.

Imaging

All imaging was performed using a Carl Zeiss (Jena, Germany) 510 META nonlinear optics (NLO) scan head attached to an upright Zeiss Axioplan 2 microscope. A mode-locked Ti:sapphire laser (Coherent Chameleon, Coherent, Santa Clara, CA), tunable from 710 to 950 nm was attached to the NLO laser in-port of the scan head through an acoustic optic modulator. Imaging of capillaries was performed using a 10 × 0.3 numerical aperture (NA) air objective, and live-cell imaging was performed with a 20× NA 0.5 water objective. For two-photon spectral imaging, all 32 channels of the internal META photomultiplier array were used, spanning an emission range of 388–719 nm. A BG39 filter was placed in the detection light path to prevent Ti:sapphire laser emissions from entering the detector assembly. For linear unmixing, between four and eight spectral image scans were averaged to reduce noise. Time-domain fluorescence lifetime imaging (FLIM) and spectroscopy were performed using the time-correlated single-photon counting technique (TCSPC) (7,16). For donor lifetime analysis, Cerulean was excited with a mode-locked laser tuned to 850 nm. Emitted photons were filtered through a BG39 filter, a polarizer set to 54.7°, a 700 nm short-pass filter (Chroma Optical (Rockingham, VT), e700sp-2p), and a 460–490 nm band-pass filter, and detected on a bialkali microchannel plate photomultiplier (∼10% quantum efficiency at 500 nm; Hamamatsu (Hamamatsu City, Japan) R3809U-52) attached to a Zeiss 510 nondescanned detector port placed in the transmitted light pathway. For FLIM analysis, photons were counted and correlated with excitation laser pulses and XY scan head position using a Becker and Hickl (Berlin, Germany) SPC830 module. The FLIM system was verified using calcium green (Molecular Probes, Eugene, OR) in the presence and absence of calcium as lifetime standards (17). For fluorescence lifetime spectroscopy, the laser was scanned over a region of interest, and detected photons were pooled, counted, and correlated with excitation laser pulses to generate a single fluorescence lifetime decay curve.

Image processing and analysis

Image acquisition was controlled using Zeiss software release 3.2, and for FLIM analysis, single photon counting module acquisition software from Becker and Hickl was also used. Fluorescent lifetime decay curves for each pixel were fit to exponential decay models convolved with an estimate of our system response function using single photon counting Image software from Becker and Hickl. The average decay constant (τ_avg) for each pixel was calculated and used to create pseudocolor mapped τ_avg images as well as histograms of the distribution of average lifetimes in an image. Where appropriate, RET efficiencies were calculated from decay constants or average decay constants using E_construct = 1 − τ_construct/τ_Cerulean. Linear unmixing of 32-channel spectral data sets was performed with custom software written using Igor Pro (WaveMetrics, Lake Oswego, OR). This software performed linear unmixing as described in Eq. 1 for three channels—donor (Cerulean), acceptor (Venus), and background—to create apparent donor and acceptor images with estimated standard deviations calculated for each pixel. Reference spectra for unmixing were obtained by imaging two square capillaries (100 μm × 100 μm inner dimensions, Vitrocom, Mt. Lakes, NJ) containing either pure donor or pure acceptor at equal concentrations. Reference spectra were automatically baseline corrected to remove dark counts. Similar results were obtained using linear unmixing software from Zeiss, but reference baseline correction had to be performed manually, and estimated deviations for each unmixing channel were not calculated. Software for sRET analysis was also custom written using Igor Pro. Paired spectral data sets were first linearly unmixed as described above to produce excitation wavelength-specific apparent donor and acceptor images. Linear unmixing errors as estimated by the Levenberg-Marquardt fitting algorithm were propagated (assuming no correlated errors (18)), and pixel values with errors >50% of their value were discarded. Equations 5, 6, and 7 were applied to the apparent donor and acceptor images to generate RET corrected donor images, acceptor images, and RET efficiency images.

RESULTS

Spectral imaging utilizes microscopes that collect fluorescent emission spectra for each pixel in an image. The complex spectrum (F_complex) emitted by samples containing multiple fluorophores is assumed to be the linear sum of individual component spectra (F_i, F_j, …) weighted by their abundance (i, j, …) (19–21):

(1)

Equation 1 is only valid in the absence of mechanisms that selectively alter individual component spectra, such as RET. Barring RET, and with knowledge of the types of fluorescent species present as well as their individual unit emission spectra, the abundance of each fluorescent species in a sample can be mathematically extracted from a complex spectra. (Unit emission spectra are defined as the spectra emitted from a fixed amount of fluorophore under defined conditions e.g., excitation wavelength, excitation power, the spectral characteristics of detection pathway components). This process, called linear unmixing, has been shown to qualitatively separate the distribution of cyan fluorescent protein (CFP)-, green fluorescent protein-, and yellow fluorescent protein (YFP)-labeled proteins in cells (22). Using unit reference spectra for linear unmixing instead of the more commonly used normalized emission spectra, obviates the need for factors that take into account differences in absorption and quantum yield of the molecules being quantified.

The RET problem

Because the emission and excitation spectra of most members of the FP overlap, proteins labeled with these fluorophores can potentially transfer energy between each other by nonradiative RET (23) if they reside within 100 Å of each other (24). Under these circumstances, the observed emission spectra (F_complex) from a mixture containing d molecules of a donor fluorophore with unit emission spectra F_d and a molecules of an acceptor fluorophore with unit emission spectra F_a will be

(2)

A detailed derivation of Eq. 2 is presented in the Appendix. If Eq. 2 is valid and RET is not accounted for, linear unmixing will underestimate the abundance of the donor, d, by a factor of 1 − E (where E is the RET efficiency), and the abundance of acceptor molecules, a, will be overestimated by the product of d × E × (Φ_a/Φ_d) × k(λ). For mixed populations containing free donor, free acceptor, as well as donor-acceptor complexes, the RET efficiency, E, in Eq. 2 becomes the weighted average RET efficiency of free donors (E = 0) and donors transferring energy to acceptors (E > 0). By definition, a donor's fluorescence quantum yield (Φ_d) is the number of photons emitted per photons absorbed. For two-photon excitation, the quantum yield is the number of photons emitted per twice the number of photons absorbed. The energy absorbed by an acceptor, even if acquired by RET, will be emitted by both the radiative and nonradiative pathways of the acceptor. Thus, the fluorescence emitted from an acceptor's excited state is proportional to its absorbed energy multiplied by its quantum yield (Φ_a). For energy transferred by RET, we must account for the fraction of energy that normally would have been lost by nonradiative pathways of the donor but were instead transferred to the acceptor and attenuated by its nonradiative pathways. Therefore a correction factor of Φ_a/Φ_d is needed to correct for the energy transferred in Eq. 2. This ratio is a wavelength-independent constant specific for any particular pair of fluorophores. The transfer factor k is an excitation wavelength-dependent constant, specific for each donor-acceptor pair and imaging system (k = ∫F_ddλ/∫F_adλ). Essentially, k is the ratio of a donor's detected fluorescence intensity (in the absence of an acceptor) divided by an acceptor's detected fluorescence intensity (in the absence of a donor) for equal concentrations of donor and acceptor. RET efficiency typically is not affected by excitation wavelength (excluding red-edge effects (25)).

The ratio of the number of photons transferred per photons absorbed remains constant. In contrast, the probability for exciting a fluorophore does change with excitation wavelength. In a population, more donor molecules will be excited at the peak of their absorption spectrum than when excited at less efficient wavelengths. Thus, whereas RET efficiencies do not change with excitation wavelength, the number of donor molecules excited and consequently the net amount of energy being transferred to the acceptor pool are a function of excitation wavelength. The spectral manifestation of energy transfer is a decrease in the magnitude of the donor component of the complex emission spectrum, with a concomitant increase in the acceptor component. These changes are observed as additions or subtractions from the spectral emission of directly excited donors and acceptors. The magnitudes of these directly excited spectral components are also functions of the excitation wavelength. Equation 2 was derived assuming conservation of photons. The k transfer factor is used to incorporate photon conservation in Eq. 2. To achieve this, the integral of the decrease in the donor spectrum should equal the integral of the increase in the acceptor spectrum (before adjusting for different quantum yields). The k transfer factor adjusts for the fact that different fluorophores have different shaped emission spectra. If Eq. 2 is correct, linear unmixing using Eq. 1 will only produce valid estimates of fluorophore concentrations in the absence of RET. Our goal was to use Eq. 2 to develop a method for accurate quantitative linear unmixing despite the presence of RET.

The development of RET standards of known donor/acceptor stoichiometry

Controls with defined RET efficiencies and stoichiometries were needed to test the validity of Eq. 2, as well as to develop and test a new comprehensive linear unmixing algorithm. We genetically engineered a set of four DNA constructs encoding donor and acceptor FPs at specific ratios and different RET efficiencies. To rigorously test unmixing algorithms under a wide range of RET efficiencies and stoichiometries, we wanted specifically 1), RET-positive and -negative constructs with the same acceptor/donor stoichiometry, 2), constructs with similar RET efficiencies but different acceptor/donor ratios, and 3), a construct with a high RET efficiency and excess acceptor. Cerulean, a blue FP derivative, was used as a RET donor in these constructs because of its high absorbance coefficient 43,000 M⁻¹cm⁻¹, quantum yield 0.62, and because its fluorescence decays with a single exponential facilitating fluorescence lifetime analysis (12). Venus, a yellow FP derivative, was used as an acceptor in these constructs because of its high absorbance coefficient 92,200 M⁻¹cm⁻¹, quantum yield 0.57 (13), and because the Cerulean to Venus Förster radius is 54 Å (D. Piston, Vanderbilt University, personal communication, 2005). The two-photon excitation-evoked emission spectra of Cerulean and Venus are nearly identical to the emission spectra of CFP and YFP. Changes in their intensity as a function of excitation wavelength are shown (see Fig. 2). Two constructs with a Venus/Cerulean stoichiometry of 1:1 were generated, termed “CTV” and “CV” (Fig. 1 a). In the CTV construct the Cerulean domain is separated from the Venus domain using a 229 amino acid linker encoding the TRAF domain of human TRAF2 (26). The crystal structure of a TRAF domain has been solved and predicts at least an 80 Å distance between Cerulean and Venus in the CTV construct (26).

FIGURE 2.

(a) Excitation wavelength-dependent changes in the two-photon emission spectra of Cerulean (15 μM) and Venus (15 μM). Purified FPs were placed in square microcapillaries and were excited with a mode-locked Ti:sapphire laser tuned to emit at 850, 870, 890, 920, and 940 nm. At all wavelengths the laser power exiting the objective was adjusted to 37 mW. Individual spectra are the average of 49 individual pixels, and each pixel's spectrum was the average of 16 scans. Standard Zeiss calibration of the META photomultiplier array compensated for nonuniform detection efficiencies at different wavelengths, and a dark noise adjustment was made by subtracting values in the lowest emission channel (385 nm) from all other channels. Potential changes in laser pulse width and in the two-photon excitation volume (36) as a function of laser wavelength were not accounted for in this figure. Although these factors can significantly alter the shape of the emission spectra as reported here, they were not a factor in our linear unmixing analysis because Cerulean and Venus reference standards were measured always at laser settings identical to when cells were spectrally imaged. (b) The integral of Cerulean (blue circles) and Venus (yellow diamonds) emission spectra, as well as k (red squares), the ratio of these integrals, are plotted as a function of a two-photon excitation wavelength.

FIGURE 1.

Characterization of RET efficiency standards with known donor/acceptor stoichiometries. (a) Construct maps of fluorescence lifetime controls (C and CT) as well as constructs with 1:1 Venus/Cerulean stoichiometry (CTV and CV), 1:2 stoichiometry (CVC), and 2:1 stoichiometry (VCV). (b) Cerulean fluorescence lifetime decay curves using a 475 ± 15 nm emission filter obtained from cells expressing the six constructs. Dark count values were subtracted from each curve. (c) Two-photon laser scanning spectral images acquired at 870 nm (CTV and CV) or 890 nm (CVC and VCV) excitation. Size bars are 10 μm. (d) Cells expressing the RET-positive CV construct (circles) or the RET-negative CTV constructs (squares) were spectrally imaged. These images were processed by linear unmixing as described by Eq. 1 to generate apparent concentrations for Cerulean (blue symbols) and Venus (yellow symbols) from each construct. Each point is mean ± SD, n = 3 cells.

A construct similar to CTV but using CFP and YFP as donor and acceptor has been generated and expressed little if any RET (14). The RET efficiency of the CTV construct was measured using fluorescence lifetime spectroscopy. N1E cells were transfected with DNA encoding either CTV, Cerulean alone (Fig. 1 a, “C”), or Cerulean ligated to the TRAF2 domain, “CT” (but without Venus). Fluorescence lifetime spectroscopy was used to measure decay times of the Cerulean fluorescence using these constructs. The fluorescent decays observed were all well fit by a single exponential decay model. The decay curves for C and CT were identical, whereas that of CTV was slightly faster (Fig. 1 b), suggesting that a small amount of RET was occurring in the CTV construct. The fluorescent decay constants (τ) of CTV and CT constructs were used to calculate a RET efficiency for the CTV construct: 6.3% ± 2.6% (mean ± SD, n = 30). RET efficiency is expressed as the percentage of energy transferred from donor to acceptor (E × 100). In contrast, the CV construct was generated by ligating Cerulean to Venus using a five amino acid linker. The fluorescence lifetime decay of Cerulean fluorescence emanating from cells transfected with the CV construct was faster than the fluorescent decay of Cerulean alone (Fig. 1 b), indicating that the CV construct is undergoing RET. Its decay was poorly fit by a single exponential model, suggesting that a distribution of separation distances exists between Cerulean and Venus in this construct (7). Nonetheless, an estimate of the CV average RET efficiency can be calculated by measuring its average decay time (7). Its decay was well fit by a double exponential and yielded an average RET efficiency of 43.1% ± 6.1% (n = 20) when compared to the decay time of Cerulean alone. To generate a construct with the same RET efficiency as the CV construct, but with a different Venus/Cerulean stoichiometry, CVC was constructed by ligating Cerulean cDNA to the N- and C-terminus of Venus (Fig. 1 a). The Venus/Cerulean stoichiometry of this construct is 1:2. For quantitative fluorescence microscopy to be accurate, it is essential that only small fractions of fluorescent molecules be excited at any instant. Cerulean emission count rates, measured through a 475 ± 15 nm filter, were always below 20,000 photons/s (the recommended limit of the Hamamatsu R3809U-52 detector).

The excitation frequencies in our experiments were set by the laser pulse rate (90 MHz). Essentially, <1 out of every 4500 laser excitation pulses resulted in a detected emission. We reasoned that under these imaging conditions, it is unlikely that more than a single fluorescent protein domain of any individual CVC molecule will be excited in response to a single laser pulse. A low probability for fluorescence excitation was confirmed by the invariance of the fluorescence lifetime of Cerulean in the CVC construct when excited at different laser powers (1.5–7.2 mW at 850 nm measured through a 20 × 0.5 NA objective at the sample; see Supplemental Fig. 1). Accordingly, the infrared excitation power typically used in all live-cell lifetime experiments was kept below 5 mW. Because the distance from each Cerulean domain to the central Venus domain is comparable and likely composed of a distribution of separation distances (and almost certainly a distribution of transition dipole angles), the CVC RET efficiency should be comparable to that of CV. As expected, the CVC fluorescent decay curve was virtually identical to the decay curve of the CV construct (Fig. 1 b) and yielded an average RET efficiency of 41.4% ± 3.2% (n = 20). Finally, we assembled VCV (Fig. 1 a), with a Venus/Cerulean stoichiometry of 2:1. We reasoned that a Cerulean domain flanked on both sides with Venus domains should have a higher RET efficiency than CVC because in its excited state, Cerulean would have two RET de-excitation pathways instead of just one. As expected, the VCV fluorescence decayed faster than fluorescence emanating from all of the other constructs (Fig. 1 b). The VCV fluorescent decay was poorly fit by a single exponential but was well fit by a double exponential. Its average RET efficiency was found to be 64.5% ± 3.2% (n = 20). N1E cells transfected with these four constructs and imaged by two-photon excitation showed even fluorescence throughout the cytoplasm (Fig. 1 c). Unlike the other three constructs, CTV appeared to be occluded from the nucleus. This suggests that the central TRAF2 domain of CTV facilitates the formation of large rigid trimeric structures consistent with the literature that effectively separate Cerulean from Venus in this construct.

Linear unmixing produces erroneous result in the presence of RET

Having measured RET efficiencies in our constructs through lifetime analysis, we next wanted to test the validity of Eq. 2 using our RET- negative and positive standards. Linear unmixing of a spectral data set yields an apparent donor concentration (d_apparent) and an apparent acceptor concentration (a_apparent). If Eq. 2 is valid, the apparent donor concentration, measured by linear unmixing, will remain constant at all excitation wavelengths:

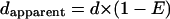(3)

In contrast, the apparent acceptor concentration will vary with excitation wavelength if RET is occurring:

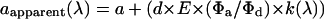(4)

To test these predictions, we transfected cells with DNA encoding either CTV or CV. Both constructs have a Venus/Cerulean stoichiometry of 1:1, but CTV was virtually RET negative whereas CV is RET positive. Transfected cells were excited by two-photon absorption at 850, 880, 920, and 940 nm and emission spectra collected for linear unmixing analysis. As predicted, the apparent Cerulean concentration from the CTV and CV constructs did not change with excitation wavelength (Fig. 1 d). Similarly, the apparent Venus concentration of CTV, the low RET construct, did not change with excitation wavelength. In contrast, the apparent Venus concentration of CV, the RET-positive construct, did change with excitation wavelength (Fig. 1 d). The apparent Venus and Cerulean concentrations of the CTV construct were identical as expected for a 1:1 stoichiometry, supporting the conclusion that in the absence of RET, apparent concentrations generated by linear unmixing are accurate estimates of the true concentrations. In stark contrast, stoichiometries calculated using the apparent Venus and Cerulean concentrations of the RET-positive CV construct were different at each excitation wavelength tested and ranged from 4:1 (940 nm excitation) to 20:1 (850 nm excitation). Because the predictions of Eq. 2 were observed, we conclude that it is a valid model which describes the complex emission spectra generated by a mixture of a RET donor and acceptor. Furthermore, we conclude that linear unmixing with Eq. 1 will produce erroneous values if RET is occurring.

Spectral RET analysis

Having demonstrated the failure of linear unmixing in the presence of RET, we then focused on developing a method based on Eq. 2 to accurately measure the concentration of spectrally overlapping FPs even if they are close enough to transfer energy by RET. Equation 2 has three unknowns, d, the donor concentration, a, the acceptor concentration, and E, the RET efficiency. Linear unmixing at any excitation wavelength yields two observables, d_apparent and a_apparent. The apparent donor concentration is a function of d and E, whereas a_apparent is a function of a, d, E, and of the excitation wavelength through the k constant. Thus, it is clear that the information embedded in a single spectral data set is insufficient to solve for all three unknowns. In contrast, two spectral data sets acquired at two different excitation wavelengths with different k values should have sufficient information to solve for all three unknowns. Emission spectra and excitation wavelength-dependent k values for two-photon excitation of Cerulean and Venus are shown in Fig. 2. The normalized emission spectra of the individual FPs, acquired at different excitation wavelengths, were indistinguishable (data not shown).

We derived solutions for d, a, and E by solving the simultaneous equations that describe the values of d_apparent and a_apparent when acquired at excitation wavelengths A and B:

Simplified by substitutions,

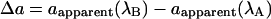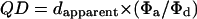we solved for d, a, and E:

(5)

(6)

(7)

A computer algorithm that combines linear unmixing of two spectral data sets with these three equations was developed to generate images of the RET-corrected donor distribution, the RET-corrected acceptor distribution, and the RET efficiency. We call this new algorithm spectral RET or sRET. Furthermore, the RET-corrected acceptor image can be divided by the RET-corrected donor image to generate a pixel stoichiometry image. Accurate sRET analysis is dependent on the precision of the unit emission spectra used for linear unmixing at any specific combination of excitation wavelength and laser power. It also requires an accurate measurement of fluorophore concentration when these experimental parameters are determined. Theoretically, unit emission spectra and the k-factors derived from them are constants that can be measured once for any given microscope setup and imaging condition. In practice, however, variance in emission power, wavelength, bandwidth, or pulse width of a Ti:sapphire laser, particularly upon wavelength tuning, precludes the use of predetermined unit emission spectra. To circumvent this instrumental limitation, unit emission spectra are measured immediately before and after an sRET determination. A typical sRET measurement involves tuning the excitation laser to the first of the two wavelengths used and adjusting the excitation power. A slide containing two capillaries with either 7.8 μM Cerulean or 7.8 μM Venus is spectrally imaged to obtain unit reference spectra for both fluorophores. This slide is removed and replaced with a dish containing transfected cells. These are spectrally imaged under the identical conditions. Next, the laser is tuned to the second wavelength and the power is adjusted. The cells are again spectrally imaged at this second wavelength. Finally, the dish with the transfected cells is removed and replaced with the same capillary slide previously used. This slide is spectrally imaged at the second wavelength. Capillary slide spectral images, obtained at the two wavelengths, are used to generate unit reference spectra at each wavelength for both Cerulean and Venus, as well as to generate k-factors for each excitation wavelength. The unit spectra obtained at the two excitation wavelengths are used to linearly unmix the corresponding spectral images of the cells. The k-factors measured at each wavelength are used in Eqs. 5, 6, and 7 to calculate donor concentration, acceptor concentration, and RET efficiency. An overview of the major data processing steps involved in sRET analysis is shown in Fig. 3.

FIGURE 3.

sRET image processing (from left to right). Two spectral image stacks are acquired at two different excitation wavelengths, along with unit reference spectra of isolated Cerulean and Venus in capillaries (not shown in diagram). Excitation wavelengths are selected to maximize different k(λ) values at each wavelength while maintaining strong donor and acceptor signals relative to the noise level. Linear unmixing produces an apparent donor and acceptor image from each image stack. The apparent donor images for both excitation wavelengths should be identical and are averaged to produce the donor apparent image (not shown). Equations 5, 6, and 7 are used to process the apparent donor and acceptor images and yield a donor, acceptor, and RET efficiency image. Finally, the acceptor image is divided by the donor image to produce a stoichiometry image (a/d).

Evaluation of sRET analysis

To test the validity of sRET analysis, we transfected cells with DNA encoding the CTV, CV, CVC, and VCV constructs. Spectral data sets were acquired at 890 and 940 nm excitation for the CTV and CV data sets and at 870 and 920 nm excitation for the CVC and VCV data sets. Although theoretically any two wavelengths with different k values should yield similar results from linear unmixing (see Fig. 2), selection of excitation wavelengths that excites one fluorophore much better than the other will impair the precision of these measurements. The VCV sample when excited at 940 nm displayed a very high yellow signal resulting from its high RET efficiency and from its stoichiometry. The large yellow component of its complex spectrum dictated the dynamic range of our acquisition, and thus limited the accuracy of measuring the relatively weak blue signal of VCV. By shifting excitation wavelengths down by 20 nm, we could boost the VCV blue signal relative to its yellow signal and thus acquire more precise measurements of d_apparent. Spectral data sets were linearly unmixed to generate Cerulean_apparent and Venus_apparent images. The Venus_apparent images acquired at 870 or 890 nm were used as a_apparent(λ_A) in Eqs. 5, 6, and 7, whereas the Venus_apparent images acquired at 920 or 940 nm were used as a_apparent(λ_B).? The Cerulean_apparent images acquired at each excitation wavelength were similar (data not shown, but see Fig. 1 d), and an average of both apparent Cerulean images were used as d_apparent. Application of Eqs. 5, 6, and 7 using the apparent Venus and Cerulean images produced donor images (Fig. 4 a, top row; Cerulean), acceptor images (second row; Venus), and RET efficiency images (bottom row) for each construct. Dividing the Venus image by the Cerulean image produced a V/C ratio image (third row). Because Cerulean and Venus are linked at set stoichiometries in all four constructs, the images mapping the distribution of Cerulean and Venus for each construct were similar. The ratio image of Venus divided by Cerulean (Fig. 4 a, third row) reveals each constructs' stoichiometry. The yellow images of CTV and CV indicated a 1:1 Venus/Cerulean (V/C) stoichiometry. The CVC image was orange, whereas the VCV image was green. These colors indicate that CVC has a 1:2 Venus/Cerulean stoichiometry and VCV has a 2:1 stoichiometry. Histograms of the V/C pixel values (acceptor/donor) of these images are shown in Fig. 4 b. The V/C stoichiometries of the constructs are revealed by the position of the peaks in these histograms. The average peak ratio of cells transfected with CTV had a Venus/Cerulean ratio of 0.89 ± 0.40 (mean ± SD, n = 12 experiments); this was indistinguishable from a ratio of 1 as determined by a one-sample t-test. Likewise, cells transfected with CV had a V/C ratio of 1.01 ± 0.29 (mean ± SD, n = 12). Cells transfected with CVC or VCV had V/C ratios of 0.49 ± 0.26 (mean ± SD, n = 6) and 2.09 ± 0.96 (n = 6), respectively, in good agreement with the theoretical values for these constructs of 0.5 and 2. ANOVA analysis indicated that CTV and CV had the same V/C ratio but differed from the V/C ratios of CVC and VCV.

FIGURE 4.

Validation of sRET analysis. (a) After spectral imaging and linear unmixing, paired apparent donor and acceptor images were used to generate RET-corrected Cerulean images (top row), Venus images (second row), and RET efficiency images (bottom row) for each of the four RET and stoichiometry standards characterized in Fig. 2. A V/C ratio image was also generated by dividing the Venus images by the Cerulean images (third row). Pixel values were mapped to the color look-up tables presented to the right of each row. (b) A histogram of acceptor to donor pixel values for each of the four constructs generated from the V/C images shown above. (c) A histogram of RET efficiency pixel values for each of the four constructs generated from the RET efficiency images shown above. Dashed black line indicates 0 RET.

RET efficiency images generated by sRET analysis were mapped to a red-white-blue color map with red indicating positive RET efficiencies, white indicating no RET, and blue indicating negative RET values. Cells expressing CTV mapped white, CV and CVC expressing cells mapped pink, and VCV expressing cells mapped red (Fig. 4, a bottom row). Histograms of these RET efficiency images reveal that CTV had a RET efficiency of 0%, CV and CVC had RET efficiencies of ∼40%, and VCV had a RET efficiency of almost 70% (Fig. 4 c). On average, cells transfected with CTV had RET efficiencies of 1.7% ± 7.0% (mean ± SD, n = 12), in agreement with the value of 6.3% ± 2.6% obtained from lifetime analysis. Cells transfected with CV and CVC had RET efficiencies of 45.3% ± 5.4% (n = 12) and 41.2% ± 4.5% (n = 6), respectively. These values were indistinguishable from each other and from the RET efficiencies measured for these constructs by lifetime spectroscopy (as determined by ANOVA). The VCV RET efficiency measured by sRET analysis was 69.7% ± 5.7% (n = 6) and compared well with the efficiency measured by fluorescence lifetime spectroscopy (64.5% ± 3.2%). Because sRET analysis predicted the correct V/C ratio and RET efficiency (as determined by fluorescence lifetime spectroscopy) of all four constructs, we conclude that sRET is a valid algorithm for measuring the abundance of donor and acceptor molecules in the presence and absence of RET.

RET analysis with variable donor/acceptor stoichiometries

We next wanted to demonstrate the utility of sRET in conditions where the acceptor and donor molecules were not covalently linked. For this purpose, we used β- and γ-subunits of trimeric G-proteins since crystal structures reveal that they form dimers (27). Further, both β- and γ-subunits are biologically active when FPs are attached to their N-termini (15). Transfection of β-Cerulean and γ-Venus into N1E cells showed that RET does indeed occur between these two constructs; FLIM similarly confirms the presence of RET (Fig. 5). Similarities between RET efficiency as determined through sRET or FLIM are remarkable considering that two entirely different approaches to measuring RET efficiency were applied (Fig. 5, b and c). Nevertheless, it is important to point out that sRET, unlike FLIM, was not limited to measuring RET efficiencies; concentrations of Cerulean and Venus are also revealed using sRET analysis (Fig. 5 a).

FIGURE 5.

sRET analysis accurately detects RET in samples with low RET efficiencies and independent donors and acceptors. Cells were transfected with the β-Cerulean, γ-Venus, and unlabeled α-subunits of trimeric G-proteins. (a) sRET donor and acceptor images showing different intracellular distributions of β-Cerulean and γ-Venus. (b) RET efficiency images generated by sRET analysis (left) and FLIM-RET analysis (right). Note the absence of signal over the nucleus and near the cell surface in the FLIM-RET image. (c) A histogram of RET efficiency pixel values generated by sRET analysis (red) and FLIM-RET analysis (blue). Dashed black line indicates 0 RET.

The interpretation of RET imaging in general is severely limited when proteins of interest or their binding partners are endogenously expressed. Under these conditions, individual cells will contain an unknown number of unlabeled binding partners for labeled donors, resulting in underestimates of the true RET efficiency of any given molecular complex. The cell imaged in Fig. 5 a is an example of this circumstance because in this cell the donor concentration was greater than the acceptor concentration. Nevertheless, knowledge of donor and acceptor concentrations as provided by sRET analysis adds considerably to the ability to interpret RET efficiencies in terms of protein-protein interactions.

DISCUSSION

We have shown that linear unmixing produced erroneous results in samples that transferred energy by RET (Fig. 1 d). To overcome this limitation, we developed and tested a new algorithm for the analysis of spectral data that accounts for RET activity. Using standards with known donor/acceptor stoichiometries and with RET efficiencies measured by fluorescent lifetime analysis, sRET analysis accurately measured donor and acceptor stoichiometries in the presence of 0%, 40%, and 70% RET (Fig. 4). Thus, spectral imaging with sRET analysis is an ideal method for measuring the abundance of two fluorophores with overlapping excitation and emission spectra when the possibility of RET cannot be eliminated.

Although sRET analysis was primarily developed as a method for quantifying overlapping FP signals in living cells, it is also a straightforward method for measuring RET activity. RET efficiency values for our constructs, as determined by sRET analysis, was virtually identical to the values generated by fluorescence lifetime decay analysis (for example, compare Figs. 1 b and 4 c). In some previous studies, RET efficiency, as well as the abundance of donors and acceptors, have been measured from data sets acquired using conventional filter-based data acquisition systems (28–30). Analyses of these data sets utilize complex correction factors to compensate for spectral bleed-through, and the direct excitation of an acceptor at the donor's excitation wavelength. In contrast, sRET analysis is based on a linear-unmixing algorithm using spectral data sets. Linear unmixing inherently corrects for bleed-through artifacts, which plague filter-based RET measurements. Furthermore, rather than being hindered by simultaneous direct excitation of both donor and acceptor, sRET analysis exploits this phenomenon. Equation 2, the basis for sRET analysis, models the complex spectra emitted from a population containing a mixture of two fluorophores.

The equation has three terms that are added to define the complex emission spectrum. The first term accounts for the emission from the donor population. The second term accounts for acceptor emission stimulated by direct excitation. The third term accounts for acceptor emissions stimulated by RET. Because the direct excitation of both donors and acceptors are accounted for in Eq. 2, theoretically RET should be measurable under conditions that excite both donors and acceptors, even when the majority of the donor emission is stimulated by direct excitation. Practically, however, sRET analysis is limited by the signal/noise ratio of the measured experimental spectra and by the dynamic range and resolution of the data acquisition hardware. When either the donor's or the acceptor's emission component is significantly brighter than the other's, its fluorescent signal will determine the dynamic range for data acquisition. As the magnitude of the weaker signal approaches the data acquisition digitization resolution, the accuracy of that component's signal will be compromised. In the imaging system used in this study, data were acquired at 12 bit resolution. Thus, with a reasonable signal/noise ratio, it should be possible to accurately measure the emission from both donors and acceptors, even when one is 10 times as bright as the other. Judicious selection of excitation wavelengths for a particular sample can alter the intensities of the emissions from the two fluorophores. An evaluation of the signal processing statistics for sRET analysis is warranted to identify the dominant sources of noise in the system, to optimize the procedure, and to better define its operation limits. Finally, because spectral imaging utilizes photons spanning the complete emission spectrum of a sample, sRET analysis is intrinsically more efficient than filter-based methods that use only a fraction of the emission spectrum.

Several methods have been developed for RET imaging in living cells (29,31–34). Of these, FLIM-RET is one of the most widely accepted. In our study we show how spectral imaging can be used to measure RET efficiencies. FLIM-RET analysis was used as a control to validate our spectral method, and for the same samples both sRET and FLIM-RET yielded similar RET efficiencies. At this point, it is unclear if a general evaluation of the relative merits of spectral imaging and FLIM for RET analysis can be reached. Different laboratories and manufacturers are actively working to optimize the efficiency of these techniques, but few microscopes exist that incorporate the latest optimizations for both technologies. For our study FLIM was incorporated into a commercial multiphoton spectral imaging system (Zeiss META/NLO) using off the shelf time-domain FLIM components (Becker and Hickl and Hamamatsu). No modifications were made to optimize photon efficiency in the spectral detector light path. Similarly, the FLIM detector light path was implemented per the manufacturers design. Time-domain FLIM using streak cameras and frequency-domain FLIM were not evaluated to optimize FLIM efficiencies. Direct comparison of the photon efficiency of FLIM and sRET is complicated by the fact that different excitation wavelengths are used for these analyses. To maximize Cerulean and minimize Venus fluorescence (see Fig. 2 b), 850-nm excitation was used for FLIM analysis. Accurate FLIM measurements require the isolation of the donor signal from the acceptor signal, particularly in samples containing either high concentration of acceptor or high RET efficiencies. Signal isolation is achieved by thoughtful selection of excitation wavelength, as well as by the use of band-pass filters. These, however, decrease the photon efficiency of the process by limiting FLIM data acquisition to a fraction of the donor's emission spectrum. In contrast, sRET analysis utilized excitation wavelengths between 870 and 940 nm to maximize excitation of both Cerulean and Venus, and the full emission spectrum of both the donors and the acceptors were collected. Furthermore, the average laser power in FLIM measurements was typically limited to <7 mW because of the maximum allowable photon count rate of the FLIM detector (Hamamatsu R3809U-52; 20,000 cps), as well as by pile-up errors caused by detector dead-time counting statistics at high count rates. Because the spectral detector used in the Zeiss META system is not operated in a photon-counting mode, these limitations do not directly apply for sRET analysis. For live-cell spectral imaging, excitation power was limited to <10 mW, primarily to prevent fluorophore bleaching and to avoid photodamage.

Despite the differences in excitation wavelength and power used in FLIM and sRET experiments, our study places us in a unique situation to compare the practical merits of these two methods for live-cell RET imaging. Obviously, any comparison is limited to our specific implementation of these two methods. In our experiments, the times required for sRET imaging and FLIM imaging were significantly different. The spectral data sets used to produce sRET images (as in Fig. 5) consisted of two sets of 32 ∼ 10 nm wide wavelength channels spanning emissions from 388 to 719 nm. Each 32-channel spectral data set was acquired in 25 s, thus 50 s were required, not including time for tuning the laser between data sets (typically 7.5 ± 1.4 s, n = 6) or the time to image reference capillaries containing donor or acceptor (∼50 s at each wavelength for both wavelengths). Potentially, this time can be significantly shortened. Linear unmixing does not significantly suffer from a reduction in the number of spectral channels used (35). On our imaging system, a reduction from 32 spectral channels to 8 would reduce the acquisition time from 50 to 12.5 s. Furthermore, a system with two Ti:sapphire lasers pretuned to the required excitation wavelengths would eliminate the time required for laser tuning and also allow premeasurement of reference spectra for each fixed excitation wavelength, albeit at great expense. In contrast, the FLIM data set used to generate the image in Fig. 5 b was acquired in 300 s. Additionally, binning of pixels (3 × 3) was required to produce decay curves with sufficient photon counts for curve fitting to a single-exponential lifetime model. A data set with enough photon counts for fitting a multiexponential lifetime model would require significantly longer acquisition times. The effects of binning, a form of spatial averaging that sacrifices resolution to increase signal strength, can be seen in the FLIM-RET image in Fig. 5 b. The sRET image, with its higher spatial resolution, appears speckled. In contrast, the spatially averaged FLIM image appears as a uniform, solid color. Furthermore, even with binning, there were insufficient numbers of photons detected over the nucleus and cell periphery to measure fluorescent lifetimes (compare sRET and FLIM-RET in Fig. 5 b). The acquisition time for FLIM imaging could potentially be reduced by using a gallium-arsenide-phosphide photomultiplier tube (40% quantum efficiency at 550 nm), though temporal resolution would decrease.

Compared to FLIM, sRET analysis has several important advantages for imaging protein-protein interactions in living cells. As mentioned above, sRET analysis required less time than fluorescent lifetime imaging. Thus, to minimize phototoxicity or bleaching or to achieve higher temporal resolutions in time-lapse studies, sRET analysis was preferable on our microscope. FLIM analysis typically monitors RET efficiencies by measuring changes in the fluorescence lifetime of the donor alone, whereas spectral imaging and sRET analysis monitors intensity changes in both the donor and the acceptor. As a result, RET images generated by sRET analysis are less susceptible to artifacts caused by nonspecific quenchers. Multiexponential analysis of lifetime data can potentially discriminate between components transferring energy by RET from those that do not (7). Likewise, the ratio of fast and slow decay constant amplitudes from such an analysis can yield the ratio of components undergoing RET from those that are not (7). Multiexponential curve fitting is integral to this form of analysis and requires many more detected photons than were acquired in our FLIM analysis in Fig. 5. Thus, the relative photon efficiency would be much worse if such an analysis was conducted. Furthermore, multiexponential lifetime analysis is problematic in samples containing a distribution of donor-acceptor distances. This, evidently, was the case for our CV, CVC, and VCV constructs (as indicated by the curved decay traces in Fig. 1 b). In contrast, sRET analysis yielded the correct donor and acceptor concentrations for these constructs as well as the correct RET efficiencies.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX: DERIVATION OF EQ. 2

For quantitative spectral analysis, it is assumed that fluorescence excitation is conducted under nonsaturating conditions; only a small fraction of the fluorophores present are excited at any instant in time. Furthermore, emission from individual fluorophores must not be altered during the course of an experiment (e.g., no quenching, bleaching, or excimer formation). Under these conditions, an equation describing the shape and magnitude of the complex emission spectrum, F_complex, of a sample composed of two fluorophores in the absence of RET requires two summed terms. Each term consists of a scalar to describe the magnitude of the emission from each fluorophore and a unit emission spectrum that describes the wavelength-dependent distribution of the emission for a fixed amount of that fluorophore at a set excitation wavelength and power and for a defined instrumental setup. The complete equation can be described as the abundance-weighted sum of the emission spectra of the two independent spectral components:

(A1)

The first term, d × F_d, accounts for the emission of the donor and scales with the abundance of the donor; d is proportional to the abundance of the donor, and F_d is the unit emission spectrum of the donor. The second term, a × F_a, accounts for the emission of the acceptor as a result of its direct excitation. It scales with the abundance of the acceptor; a is proportional to the abundance of the acceptor, and F_a is the corresponding unit emission spectrum of the acceptor.

A description of the complex emission spectrum of a sample containing two fluorophores when RET is occurring requires three terms to define the three types of emission events that can occur. The first term must account for emission by the donor. The second accounts for emission by the acceptor as a result of direct excitation. Finally, the third term must account for emission by the acceptor resulting from RET. Each of these summed terms will consist of a scalar and an appropriate unit emission spectrum. Because the first term involves emission by donors and the last two terms describe emission by acceptors, the first term must use the unit emission spectrum of the donor, whereas the last two terms must use the unit emission spectrum of the acceptor. An expression for each of these three scalars terms will be derived.

The first term accounts for emission by the donor after a fraction of its absorbed energy has been transferred to acceptors. Let E equal the RET efficiency, defined as the fraction of donor excitation events that result in energy transfer to the acceptor. Then, 1 − E equals the fraction of donor excitation events that are not transferred to acceptors, and the scalar of the new first term is

and the complete term (scalar multiplied by the unit emission spectrum) is

(A2)

As expected, in the absence of RET, E = 0, and this term reduces to its original form described in the first half of Eq. A1.

The scalar for the second term of Eq. A1 described the magnitude of the directly excited emission of acceptors. It is not altered by RET and at any specific excitation wavelength and power remains simply proportional to the abundance of acceptor molecules in the sample, a. The second term remains

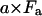(A3)

RET requires an interaction between a donor molecule in its excited state with a neighboring acceptor molecule in its ground state. After RET the donor is in its ground state, and the acceptor is in its excited state. RET is nonradiative; it does not involve the emission of a photon by the donor or the absorption of a photon by the acceptor. The third term of a comprehensive equation describing the shape and magnitude of the complex emission spectrum of a sample containing two fluorophores must account for energy transferred from donors to acceptors and ultimately emitted by the acceptor. Because this term describes emission from acceptors, it too, like the previous term (Eq. A3), will have the form of a scalar multiplied by the unit emission spectrum of the acceptor. The amount of energy transferred by RET will be a function of the donor concentration (d) and the RET efficiency (E). The scalar for this term must incorporate these variables without violating conservation of energy. To this end, differences in the quantum yields of donors (Φ_d) and acceptors (Φ_a) must be considered, as well as differences in the shapes and magnitudes of the unit emission spectra of donors (F_d) and acceptors (F_a). To derive this scalar, we will begin by determining how many quanta of energy a donor absorbs in the absence of RET. If d × F_d describes the shape and magnitude of a donor's emission in the absence of RET, then d × ∫F_ddλ is proportional to the number of photons emitted as fluorescence. Division by the donor's quantum yield, Φ_d, produces d × ∫F_ddλ/Φ_d, proportional to the number of photons absorbed. When RET occurs, the fraction of quanta absorbed, whose energy is transferred to acceptors is

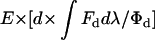The fraction of this energy emitted by the acceptor as fluorescence, however, will be attenuated by the acceptor's nonradiative pathways. Thus, the energy transferred from the donor to the acceptor and emitted as fluorescence will be proportional to

(A4)

To convert this expression into a scalar (to be multiplied by the unit emission spectrum of the acceptor) requires a conversion factor equating photon-energy and scalar magnitude. This conversion factor will be unique for specific acceptors imaged under defined conditions. Because photon energy is proportional to a scalar × ∫Fdλ, conversion requires division by ∫Fdλ. Thus, the scalar for the third term of our equation is Eq. A4 divided by ∫F_adλ:

(A5)

Rearrangement of Eq. A5 yields

where we define the k transfer factor, k(λ), as ∫F_ddλ/∫F_adλ. This transfer factor is a function of the excitation wavelength (as well as of the properties of the imaging system) and must be evaluated for each specific donor-acceptor pair.

The complete third term, scalar multiplied by the unit emission spectrum, is

(A6)

As expected, in the absence of RET, E = 0, and the entire third term is eliminated.

The complex emission spectrum of a sample composed of donors and acceptors, even if they transfer energy by RET, is defined by the sum of the three emission terms. The first term accounts for emission by the donor (Eq. A2), the second accounts for acceptor emission stimulated by direct excitation (Eq. A3), and the third term accounts for acceptor emission resulting from RET (Eq. A6). Thus, the complex spectrum is described by

(A7)

Equation A7 is identical to Eq. 2 in the main text and reduces to Eq. A1 when RET does not occur.