Variable Incidence Angle Fluorescence Interference Contrast Microscopy for Z-Imaging Single Objects

Abstract

Surface-generated structured illumination microscopies interrogate the position of fluorescently labeled objects near surfaces with nanometer resolution along the z axis. However, these techniques are either experimentally cumbersome or applicable to a limited set of experimental systems. We present a new type of surface-generated structured illumination fluorescence microscopy, variable incidence angle fluorescence interference contrast microscopy (VIA-FLIC), in which the fluorescent sample is assembled above a reflective Si surface and the incidence angle of excitation light is varied by placing annular photomasks with different radii in the aperture diaphragm plane of the microscope. The variation in incidence angle alters the interference pattern of excitation light, and hence the intensity of detected fluorescence. Quantitative VIA-FLIC is tested by using a set of fluorophore-containing supported membranes separated from the Si surface by SiO₂ layers of variable thicknesses. The resulting fluorescence intensity versus incidence angle curves depends on the separation from the Si surface and when fit with an appropriate model yield precise SiO₂ thicknesses that are accurate with respect to the known SiO₂ thicknesses. Since only a simple modification to a standard epifluorescence microscope is required, VIA-FLIC offers a versatile method to produce z-reconstructions with high resolution for a wide range of biological systems.

INTRODUCTION

The availability of genetically encoded fluorophores (1) and increasingly sophisticated optical microscopes and imaging systems has spurred the development of significant new approaches for improving the spatial resolution beyond the diffraction limit (2). A few methods, most notably stimulated emission depletion microscopy (3), provide subhundred nanometer z-resolution by directly imaging a narrowed point-spread function. Although somewhat more limited in their applicability, surface-generated structured illumination techniques produce very high z-resolution (nanometer or tens of nanometers) reconstructed images through the appropriate processing of a series of images. Surface-generated structured illumination techniques are especially useful for an important subset of experimental systems that involve fluorescent objects near a microscope slide with fluorophores in or associated with supported lipid bilayers or cells in contact with the surface. It would be desirable to obtain information on the distance of these fluorescent objects or time-dependent changes in their distance from the surface with the highest possible spatial resolution in the direction normal to the surface, the z axis. To reconstruct images with high z-resolution, surface-generated structured illumination techniques structure the excitation intensity in a well-defined way such that the intensity of the fluorescence is related to its distance from the interface. Two such methods, fluorescence interference contrast microscopy (FLIC) and variable incidence angle total internal reflection fluorescence microscopy (VIA-TIRFM), have been developed to achieve z-resolution on the nanometer scale, and they are illustrated schematically in Fig. 1. As discussed in detail below, each of these surface-generated structured illumination techniques has advantages and disadvantages. In an effort to capture the simplicity of FLIC and the versatility of VIA-TIRFM, we have developed a new technique, VIA-FLIC, that combines the advantages of both.

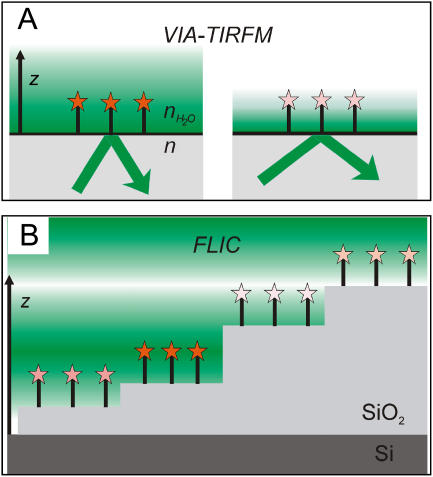
FIGURE 1.

(A) Schematic of VIA-TIRFM. In VIA-TIRFM, the characteristic 1/e distance of the exponentially decaying evanescent is modulated by varying the incidence angle at the TIR interface. (B) Schematic of FLIC. In FLIC, an interference pattern is created by reflection from the Si surface. By assembling the object of interest on many different SiO₂ steps, its position relative to the nodes and antinodes of the interference pattern is modulated. In these schematic diagrams, high intensity excitation light is denoted by a dark green background, shading to low excitation intensity in white.

To obtain the positions of fluorescent objects with high z-resolution, surface-generated structured illumination techniques create a variation in excitation intensity with z and modulate this excitation intensity function. The presence of an excitation intensity function influences the rate of absorption of a fluorescent object such that this rate will strongly depend on the object's location in z. Because the object's resulting fluorescence intensity is directly related to its absorption rate, distance information can be decoded from measurements of the object's fluorescence intensity. A single measurement of the fluorescence intensity with surface-generated structured illumination does not yield unique distance information because the absolute fluorescence intensity for a given excitation intensity function depends on many parameters in addition to its z-position, such as the number of fluorophores in the object, the intensity of incident light (independent of the surface-generated structured illumination), and the reflective losses in the detection optics. Varying the excitation intensity function changes the relationship of fluorescence intensity and z, whereas these other difficult-to-determine parameters remain, in principle, constant. The z-position is then determined by fitting the fluorescence intensity change due to the change in the excitation intensity function to an appropriate model. In the context of surface-generated structured illumination techniques, reconstructed resolution is the minimum z displacement between two fluorescent objects that can be separately identified by numerical processing of images obtained with different excitation intensity functions. The level of this attainable resolution depends strongly on the maximal gradient of the excitation intensity function and the signal/noise ratio of the images.

TIRFM forms the basis for VIA-TIRFM (4–7), also referred to as multiple angle-TIRFM or variable angle-TIRFM (Fig. 1 A). In TIRFM, the evanescent field of the excitation light decays exponentially from the total internal reflection (TIR) interface with a characteristic 1/e distance. TIRFM is exquisitely surface sensitive because only fluorophores within ∼200 nm of the TIR interface are excited to an appreciable extent. In VIA-TIRFM, the characteristic 1/e distance of the evanescent field is modulated by varying the incidence angle at the TIR interface. The attainable reconstructed resolution in VIA-TIRFM depends on the minimum 1/e distance of the evanescent field, which is fundamentally limited by the refractive index of the solid support relative to the medium in which the fluorophore is located. When used with glass (5,6) (n = 1.5), Al₂O₃ (4) (n = 1.8), or LiNbO₃ (7) (n = 2.3) solid supports, VIA-TIRFM can achieve reconstructed resolution on the order of 46 nm, 26 nm, or 14 nm, respectively, assuming a 30% difference in intensity can be differentiated. (For this calculation, the dependence of the amount of fluorescence emission that is detected on z-position (4,7) has been ignored, and these numbers should only be taken as approximate measures of relative resolving ability.) The major disadvantage of VIA-TIRFM is its experimental difficulty. Because of the range of incidence angles required, a through-prism TIRFM geometry must be used rather than through-objective TIRFM (8). Through-prism excitation requires separate excitation and detection optics and careful alignment between those two optical paths. Stock et al. (5) developed a novel setup to improve the ease of doing VIA-TIRFM with glass, but because of the scarcity of index-matching fluids above 1.6, it is not straightforward to extend this to higher refractive index materials that would allow significantly better reconstructed resolution.

In contrast, FLIC, developed for biological microscopy by Fromherz and co-workers (9–12), uses a very simple experimental setup to achieve very high reconstructed z-resolution. In FLIC (Fig. 1 B), the sample is assembled on a series of SiO₂ steps of different thickness on a highly reflective and flat Si surface. These FLIC chips can be fabricated using relatively straightforward lithographic methods. Interference between the incoming and reflected excitation light creates a very well defined variation in the excitation intensity, and the different SiO₂ step thicknesses move the fluorescent molecules in z relative to the interference pattern. Thus a series of excitation intensity functions, related by constant displacements in z, results from the FLIC chip architecture. The emitted fluorescence also undergoes interference. Since the wavelength difference between the excitation and emission light is relatively small, the overall dependence of the fluorescence intensity on position goes approximately as the square of the excitation intensity variation. An unmodified epifluorescence microscope is used to measure the fluorescence intensity on many different SiO₂ step heights (typically at least 16). In addition to its experimental simplicity, FLIC can resolve distances on the order of 2 nm through reconstruction (9,13). To date, FLIC has been very effective in studies of biomimetic membranes, such as DiI-labeled cell membranes (11,12,14), lipid components in tethered supported membranes (15,16), and intermembrane junctions between a membrane patch and a supported membrane (17–19). Although spatial and temporal variations in the z-position of an object have been visualized as variations in fluorescence intensity on a single SiO₂ step (17–19), to quantitatively determine these changes in z-position, a fluorescence intensity calibration is required, the object must be uniformly fluorescently labeled, and it must extend over several microns in xy. There are no proven methods to use FLIC to image objects whose density of fluorophores varies laterally or for objects that are smaller than the diffraction limit and whose position, particularly in the z direction, varies from object to object. This class of objects, which we refer to as single objects, includes many objects of biological interest such as individual vesicles at a neuronal synapse, focal contacts of a cell adhering to a protein-coated surface, membrane proteins in a cell membrane, and fluorescent single molecules, i.e., cases in which there is no correlation in the density of fluorophores on different steps or even regions of a single step. In the case of VIA-TIRFM, individual objects or regions can be observed while the incidence angle and penetration depth of the evanescent field are modulated, but alignment issues make this far from straightforward to apply quantitatively.

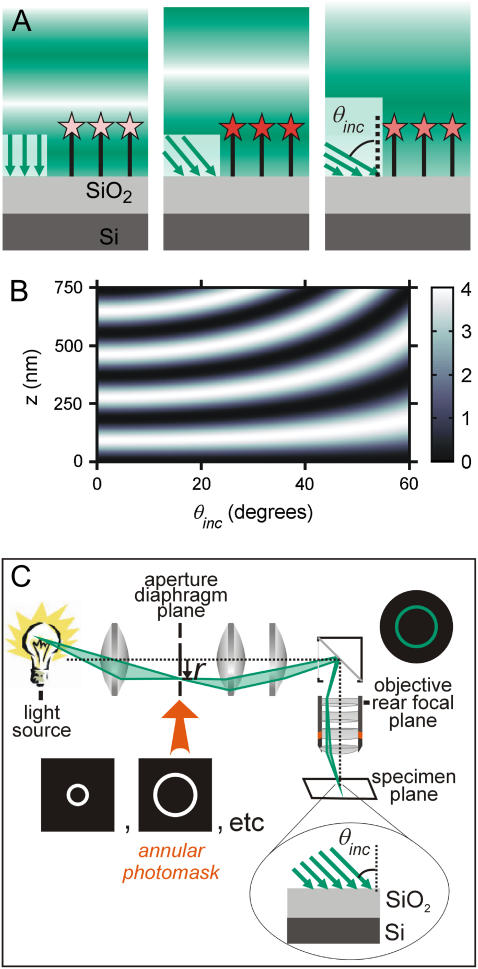
Here we present a novel imaging technique, VIA-FLIC, which preserves the experimental simplicity of FLIC, but adds the ability to image isolated objects like VIA-TIRFM. As in FLIC, VIA-FLIC uses interference from a very flat Si mirror to create structured illumination. However, instead of using SiO₂ steps to displace the interference pattern experienced by the fluorophores, the periodicity of the interference is changed by varying the incidence angle, θ_inc (Fig. 2 A). Fig. 2 B shows a surface plot of the variation in excitation intensity with z-position from a mirror surface and θ_inc, calculated using a simplified model described in detail below, which illustrates that the excitation intensity at different distances from the Si mirror surface can be modulated with θ_inc. Thus we would predict that measuring the fluorescence intensity as a function of θ_inc would allow a unique determination of the z-position. Different values of θ_inc can be obtained simply by placing a photomask that only transmits a thin annulus of light into the aperture diaphragm plane of the microscope so that an image of this annulus is formed at the objective's back focal plane (Fig. 2 C). Thus only a hollow cone of epi-illumination rays with a given narrow range of θ_inc values is focused at the specimen plane; the range of values of θ_inc is dictated by the size of the annulus on the photomask and the objective. Because θ_inc values less than the critical angle are used, only this relatively simple and inexpensive modification to a standard epifluorescence microscope is required, similar to that used in through-objective TIRFM (8). We demonstrate that this method of varying θ_inc creates contrast between fluorophores at defined positions in supported membranes at different z-positions and that the changes in intensity with θ_inc can be used to determine the z-position of fluorescent objects with high accuracy and precision.

FIGURE 2.

(A) Schematic of VIA-FLIC. The angle between incoming rays and the normal to the mirror surface is the incidence angle, θ_inc. Modulation of θ_inc varies the period of the interference pattern. Intensity of excitation light as a function of z is denoted by shading (dark green for high intensity, white for low intensity) as in Fig. 1. (B) A surface plot of the light intensity near a mirror as a function of z and θ_inc, calculated using Eq. 3 and λ = 370 nm. The relative intensity at any abscissa and ordinate is given by the color bar on the right. (C) Schematic of VIA-FLIC apparatus. In an epifluorescence microscope, an annular photomask replaces the aperture diaphragm. Since each radial position in the aperture diaphragm plane, r, corresponds to a particular θ_inc (Eq. 2), a hollow cone of excitation light comprising a narrow range of θ_inc values is focused at the specimen plane. The fluorescently labeled sample is assembled on an SiO₂/Si substrate, and the emitted fluorescence is collected with the full NA of the objective.

MATERIALS AND METHODS

Because several different SiO₂ thicknesses on Si were used for the calibration experiments described below, we used FLIC chips for these experiments. However, we emphasize that intensity data for each thickness are fit independently, i.e., a single SiO₂ thickness on Si is sufficient for the VIA-FLIC method. FLIC chips, composed of a series of 16 SiO₂ steps on Si, were fabricated by standard photolithographic procedures. After RCA cleaning, an ∼400 nm thick layer of SiO₂ was grown on Si using thermal oxidation in the presence of O₂ (g). Four rounds of photoresist development and buffered hydrofluoric etching were used to produce 16 5 × 5 mm SiO₂ steps. A transparency mask of alternating transparent and opaque stripes was used to mask exposure of the photoresist; this relatively low-resolution mask created patterned borders between SiO₂ steps. For each round of etching, the hydrofluoric concentration and etch time were adjusted to match the desired depth of etching. Before use, the FLIC chips were soaked in 90°C 7× detergent (diluted 1:5 in Millipore water; MP Biomedicals, Irvine, CA), rinsed extensively in double distilled water, and baked at 400°C for 4 h. After use, the FLIC chips were sonicated in water, isopropanol, and chloroform and cleaned in piranha solution (75% by volume concentrated H₂SO₄ and 25% by volume 30% H₂O₂, heated to 70°C), and the SiO₂ thicknesses of individual steps were measured by ellipsometry (Auto-nulling Imaging Ellipsometer, Nanofilm Technologie, Goettingen, Germany). The parameters n_Si = 4.1562, κ_Si = 0.0419, and 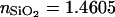at 532 nm were used to determine the SiO₂ thickness; ellipsometric measurements of the SiO₂ thickness were made over regions near the intersections of the steps, closely corresponding to regions where fluorescence intensity was measured. The accuracy of ellipsometric measurement is quoted as <0.1 nm; however, repeated measurements of the same SiO₂ step on the same chip yielded variations in thickness of as much as 1 nm, possibly indicative of some variation in thickness arising from the etch process. The SiO₂ thickness determined by ellipsometry is therefore reported to 1 nm.

To narrow and vary the range of excitation θ_incs, the aperture diaphragm of a Nikon E800 epifluorescence microscope was replaced by a photomask that only transmits a thin annulus of light (see Fig. 2 C). A set of photomasks (Delta Mask, Enschede, The Netherlands), with transparent annuli of 0.5 mm width and median radii (halfway between the inner and outer radii), r, of 0.25, 0.75, 1.25, 1.75, 2.25, 2.75, 3.25, 3.75, 4.25, 4.75, 5.25, and 5.75 mm, was fabricated on a single soda lime glass plate patterned with a 98 nm thick, opaque layer of chrome. The photomasks were mounted on an xy stage and a home-built support for manual alignment of the first annulus with respect to the optical axis in the aperture diaphragm plane; the entire apparatus was attached to a motorized linear stage to drive subsequent photomasks into the optical path. The finite annular width of these photomasks produces a range of θ_inc values to excite the sample. Therefore the fluorescence intensity is reported as a function of the median θ_inc, i.e., the angle corresponding to the median radius of the photomask.

Note that it would be possible to modulate the emission intensity in a similar manner by placing an annular photomask in a plane in the imaging path conjugate to the objective rear focal plane. However, selection of a narrow range of emission angles would greatly reduce the ratio of detected photons to excitation photons, increasing the likelihood of sample photobleaching. As demonstrated by Braun and Fromherz (12), photobleaching can cause systematic errors in the determination of z-position by FLIC, making the emission variation approach less attractive.

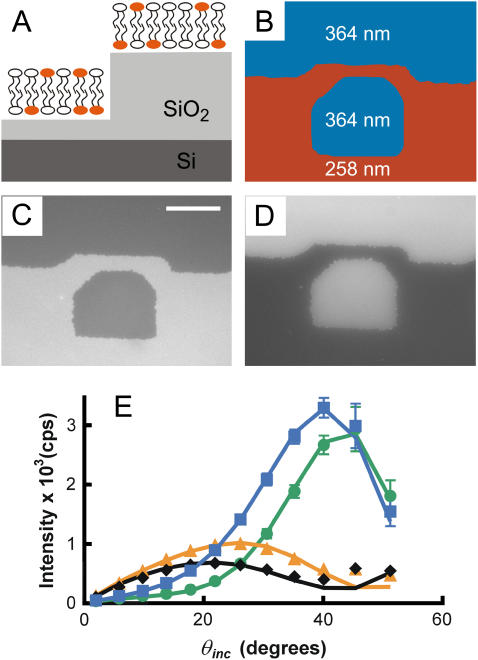
As a demonstration of the VIA-FLIC technique, an egg PC-supported membrane containing 1 mol % 1,1′-dioctadecyl-3,3,3′,3′-tetramethylindocarbocyanine (DiI) on different thicknesses of SiO₂ on Si was imaged using VIA-FLIC. Small unilamellar vesicles composed of egg PC (Avanti Polar Lipids, Alabaster, AL) and 1 mol % DiI (Molecular Probes, Eugene, OR) were prepared by vesicle extrusion through 50 nm polycarbonate filters. The supported membranes were formed by vesicle fusion onto the FLIC chip, and two small strips of double-sided tape were used to seal the FLIC chip-supported membrane to a glass coverslip (∼0.1 μm thickness), trapping an ∼100 μm thick bulk layer of water. The VIA-FLIC images were acquired by positioning the appropriate photomask in the aperture diaphragm plane, imaging through the glass coverslip and water layer with a 40× NA = 1.30 oil immersion objective. A high-pressure mercury arc lamp (1020DH, Ushio, Cypress, CA) was used as the light source. Light from the arc was passed through a light scrambler (1 mm diameter single silica fiber, Technical Video, Port Townsend, WA), thus entering the microscope optics as if from a homogeneous disk-shaped source. Images were acquired with a CoolSNAP CCD (Roper Scientific, Tucson, AZ) and processed with the Metamorph software package (Universal Imaging Corp., Downingtown, PA). Membranes were imaged using a DsRed filter set (HQ546/12×, Q560LP, HQ605/75m, Chroma Technology, Battlesboro, VT) for all excitation conditions. The images shown in Fig. 4, C and D, were linearly contrast adjusted using Adobe PhotoShop.

FIGURE 4.

VIA-FLIC of DiI-containing supported membranes located at different distances from the Si mirror surface. (A and B) Schematic illustration of the experiment. DiI-containing supported membranes are formed on different SiO₂ steps of different thicknesses, creating objects with the same density of fluorophores positioned at different distances in z from the Si surface. There are 364 nm and 258 nm of SiO₂ on Si on the top and bottom steps, respectively. The puzzle piece-shaped border between the SiO₂ steps is a result of the transparency photomask used to create the SiO₂/Si surface (see Materials and Methods). (C and D) VIA-FLIC images of two supported membranes that contain 1 mol % DiI separated by different distances from the Si by two different SiO₂ thicknesses. (C) Illumination with θ_inc centered around 9.8°. (D) The same position with θ_inc centered around 35.2°. (E) Intensity of 1% DiI-supported membranes located at different positions in z on a SiO₂/Si surface as a function of θ_inc. The symbols and lines are intensity measurements for different SiO₂ thicknesses and calculated best fits using Eq. 9, respectively: 255 nm (black diamonds, fit 254 nm, black line), 276 nm (orange triangles, fit 280 nm, orange line), 364 nm (blue squares, fit 358 nm, blue line), and 385 nm (green circles, fit 380 nm, green line).

To calibrate the intensity of excitation light as a function of radius in the aperture plane, the intensity of incident light was measured with each photomask positioned in the aperture diaphragm plane using a laser power meter positioned at the focal point of a 10× NA = 0.45 air objective. Intensities are reported as a function of r, the median radius of the photomask. The excitation filter and dichroic mirror from the DsRed filter set were used to narrow the wavelength range of the incident light.

THEORY

Relation between incidence angle and radial position in the aperture diaphragm plane

The relationship between θ_inc and the radial position in the aperture diaphragm plane in mm, r, is given by

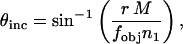(1)

where M is the magnification from the aperture diaphragm plane to the objective rear focal plane, n₁ is the refractive index of the medium (we consider n₁ = 1.475 corresponding to a lipid membrane), and f_obj is the focal length of the objective. For the Nikon E800, M = 1. For infinity-corrected microscopes, the focal length of the objective is related to the tube lens focal length, f_tube, and the magnification of the objective, m_obj: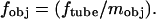 For Nikon microscopes, f_tube = 200 mm. For our experimental setup, Eq. 1 simplifies to

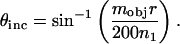(2)

Modulation of interference by θ_inc: a simplified model

To provide some intuition for the shape of VIA-FLIC curves, we first consider single slit interference above a mirror, a situation known as Lloyd's mirror, as a simplified model for the excitation intensity in VIA-FLIC. This description does not account for imperfect reflection of the Si surface or the dependence of the absorption probability on the angle between the transition dipole moment and the direction of the excitation light electric field (see the full model below). Equation 3 describes the light intensity, I, in air above a mirror as a function of its initial intensity (I₀), θ_inc, the wavelength in air (λ), and distance from the mirror (z):

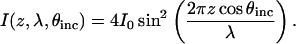(3)

Using Eq. 3, the dependence of I on z and θ_inc is shown as a surface plot in Fig. 2 B, where the value of I is indicated by the color bar on the right. The wavelength used in this calculation, λ = 370 nm, corresponds to the typical absorption of a red-emitting dye embedded in a membrane, and the values of θ_inc correspond to the range incident in lipid membrane (n = 1.475) focused by a numerical aperture (NA) = 1.30 objective. Note that one could also vary λ to modulate the interference pattern, but this variation is likely to be less useful than the varying θ_inc. Plotting I as a function of z and λ for λ = 325–400 nm, a reasonable absorption range for a red-emitting fluorophore embedded in a lipid membrane, with fixed θ_inc shows that modulation of λ would be significantly less sensitive to changes in z than modulation of θ_inc. Additionally, a specialized light source such as tunable dye laser or monochromator would be required to illuminate the sample with monochromatic light of different wavelengths, and the absorption spectrum of the fluorophore in the actual sample would have to be determined.

To determine the z-position of a fluorescent object with high precision, the I versus θ_inc curves for z and z + dz should have sufficiently different shapes. By this we mean that the curves should be distinguishable by least squares fitting using Eq. 9 (see below). Specifically, as the quantity 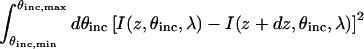increases, the curves are more different, and it is easier to distinguish small changes in z-position. As can be seen by comparing slices of I along the abscissa for slightly different values of z, Fig. 2 B predicts that this condition will hold for VIA-FLIC. Note that even though this requirement is necessary for accurate distance determination, it is not sufficient, since the error in experimental data and in the fitting of the scale factor, b′ (see Eq. 9), also contribute to the uncertainty in the determination of z-position.

Several trends in Fig. 2 B are of note and carry over to the full electromagnetic model. For θ_inc = 0°, the period between adjacent maxima corresponding to total constructive interference is 185 nm or λ/2. Fig. 2 B also shows that as θ_inc increases, the z-positions of the first and successive maxima increase. These trends occur because as θ_inc increases, the change in the path length difference decreases, and the period of the interference pattern, 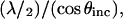increases. Thus, Fig. 2 B can be visualized as a series of sine-squared functions along z that have increasing periods as θ_inc increases.

Modulation of interference by θ_inc: a full electromagnetic model

To quantitatively model and fit FLIC data, Fromherz and co-workers developed an electromagnetic model to describe steady-state fluorescence near a multilayer interface that includes absorptive losses, nonradiative decay, and near-field losses. The equations derived by Lambacher and Fromherz (10) are more general cases of equations derived by Hellen and Axelrod (20), Sullivan and Hall (21), and Mertz (22), among others. Since only minor adjustments to this model are required to model and fit VIA-FLIC data, we use the notation of Lambacher and Fromherz (10) herein. For VIA-FLIC, the observed fluorescence intensity per unit time for a fluorophore near the SiO₂/Si surface, J^layer, depends on the rate of absorption by the fluorophore when excited by a range of θ_inc values, 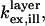the rate of detection of emitted fluorescence through a fixed aperture, 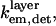the rate of emission at the surface, 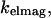and the rate of deexcitation due to nonradiative processes:

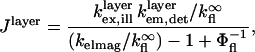(4)

where 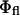is the quantum yield of the fluorophores and 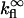is the rate of fluorescence emission in the absence of the surface. The full expressions for 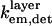and 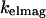can be found in Lambacher and Fromherz (10) (Eqs. A24 and A22, respectively). The expression for 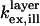is identical to 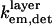except that the limits of integration over θ_inc are from the smallest θ_inc to the largest θ_inc dictated by the annular photomask, instead of from 0 to 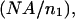and the fluorophore's absorption wavelength range and appropriately weighted excitation wavelengths are used instead of its emission and appropriately weighted detection wavelengths.

To provide a reference for the magnitude of variations in 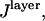the intensity of a fluorescent object on the SiO₂/Si surface is normalized by the intensity under identical conditions in homogeneous media (10):

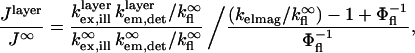(5)

where 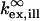and 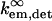refer to the rate of absorption by the fluorophore illuminated through a fixed aperture and the rate of emission detected through a fixed aperture when the fluorophore is embedded in a single homogeneous medium, respectively. The expressions for 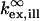and 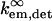can be derived from Ford and Weber (23).

Introduction of an empirical aperture function

In the established analysis of FLIC data, it is assumed that the incident light intensity as a function of θ_inc, referred to as the aperture function, is constant and the NA for excitation is treated as a fitting parameter. This simplification cannot be used in quantitative VIA-FLIC analysis because each data point is produced by illumination over a narrow range of θ_inc values and the real aperture function affects the shape of the intensity curves to be fit. The intensity of incident light through each annular photomask, independent of interference effects, can be measured directly using a power meter placed at the focal point of an objective lens with an appropriately long focal distance. The incident light intensity through the nth annular photomask, I_n, is given by

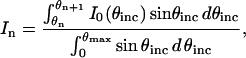(6)

where θ_n and θ_n+1 are the lowest and highest angles, respectively, transmitted by the nth photomask and θ_max is the highest angle transmitted. A step function approximating the radial aperture function I₀(θ_inc) can be calculated by dividing the measured intensity by the angular weighting for each annulus (i.e., it is assumed that the incident intensity is constant within the angle range transmitted by each annular photomask).

Numerical modeling and fitting

The numerical modeling codes used to produce the predictions and fits in Figs. 2–4 were written in MATLAB (The MathWorks, Natick, MA). The refractive indices of Si, SiO₂, and H₂O as a function of wavelength are taken from Palik (24), and the refractive index of the hydrocarbon region of the membrane was taken to be 1.475, independent of wavelength. The thickness of the hydrocarbon region of an egg phosphatidylcholine (PC) bilayer is 3.78 nm (25,26). Cobalt quenching has demonstrated that 55% of the DiI is located in the top leaflet of the bilayer and 45% is located in the bottom leaflet (13); the fluorophore in DiI is located 1.75 nm from the hydrocarbon center of the bilayer (27). The absorption transition dipole of DiI is 76.5° from normal of the bilayer plane (28,29). This parameter was allowed to vary for some fits (see below). The thickness of the water layer between the lower leaflet of the supported bilayer and the SiO₂ surface is 1.4 nm (13). The absorption and emission spectra of DiI were obtained from the manufacturer. The output spectrum of the mercury arc lamp and the transmission spectra of the excitation filters, emission filters, and dichroic mirrors were obtained from the respective manufacturers. In our model a continuous approximation of the aperture function was generated from the measured step function by interpolating a fifth order polynomial, and this polynomial was used to weight the excitation light as a function of θ_inc.

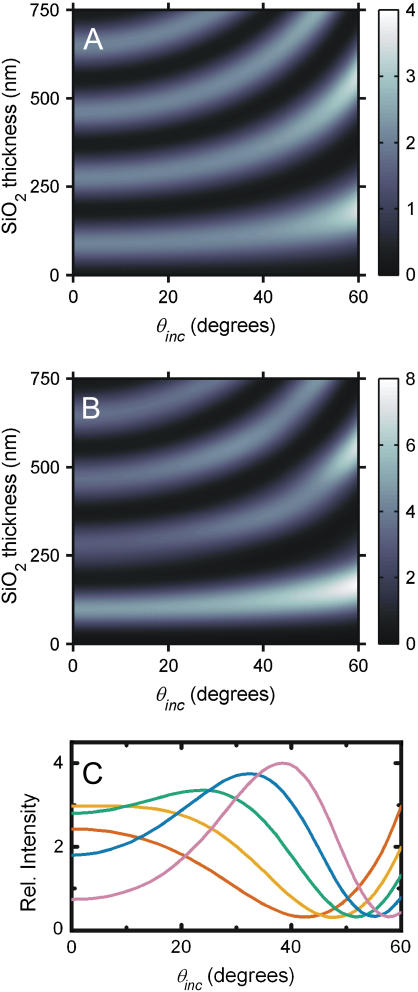
FIGURE 3.

(A and B) Surface plots of the calculated relative power as a function of θ_inc and SiO₂ thickness for fluorophores located in the center of a supported bilayer. The relative intensity at any abscissa and ordinate is given by the color bar to the right of each plot. The absorption transition dipole moment and the emission transition dipole moment are both 90° relative to the surface normal. (A) Calculation of relative absorbed power, 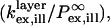for bandpass excitation at 546 nm with a width of 50 nm. (B) Calculation of relative detected fluorescence power, 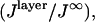assuming 546 nm bandpass excitation as in A, and bandpass detection at 588 nm with a width of 50 nm and NA = 1.30. (C) The relative detected fluorescence power as calculated in B for several SiO₂ thicknesses, 250 nm (red line), 275 nm (orange line), 300 nm (green line), 325 nm (blue line), and 350 nm (purple line).

For our experimental conditions, the distance of the fluorophore from the Si mirror is far enough that the approximation 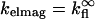can be used with minimal effect on the accuracy of the model. Equation 4 for J^layer thus reduces to (10)

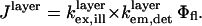(7)

This equation gives J in units of energy/s; however, since the fluorescence intensity is measured in counts/s, a scaling factor, b, is introduced that is constant for all values of θ_inc:

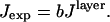(8)

Furthermore, the values of 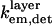and 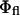are also constant under variations of θ_inc, meaning that the experimental data can be fit to (for constant b′)

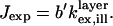(9)

Best fit parameters of scale factor and oxide thickness were extracted by least squares fitting of the model to the data. Each data point was calculated by averaging the measured fluorescence intensity over the area imaged by the charge-coupled device (CCD) camera and contained within a field diaphragm iris and given a weighted importance in the fit according to its intensity standard deviation.

RESULTS

Principles of VIA-FLIC

To illustrate the principles underlying VIA-FLIC and compare it to FLIC, we consider a few examples, which correspond closely to the examples presented by Lambacher and Fromherz (10). Fig. 3 A predicts how the relative intensity absorbed by a fluorophore in a supported membrane on SiO₂/Si depends on θ_inc and the SiO₂ thickness. The relative intensity is calculated as the power corresponding to a fluorophore in a supported membrane on SiO₂/Si normalized by the power of a fluorophore in a membrane surrounded by semiinfinite regions of the same refractive index; this is the quantity 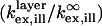in Eq. 5. This calculation assumes bandpass excitation centered ∼546 nm in air (corresponding to 372 nm in SiO₂), orientation of the absorption and emission transition dipole moments of the fluorophore parallel to the membrane plane, a single plane of fluorophores located in the center of the hydrocarbon region of the supported membrane, and a water-filled gap of 1.4 nm between the lower leaflet of the bilayer and the SiO₂ surface (13). Similarly to Fig. 2 B, Fig. 3 A shows that for θ_inc = 0° the period between maxima of absorbed power corresponds to 186 nm, or λ/2 in SiO₂, and that the z-positions of the maxima increase as θ_inc increases. As in the simplified model, these effects are caused by the increasing period of the interference pattern with increasing θ_inc. Unlike the simplified model, Fig. 3 A predicts that the magnitude of the maxima should increase with increasing θ_inc. This occurs because a larger percentage of the light is reflected at grazing incidence angles in the full model, whereas the simplified model assumes perfect reflection independent of incidence angle. Also, bandpass excitation decreases the sharpness of the interference pattern: the absorbed power difference between maxima and minima decreases, and the change in absorbed power as a function of SiO₂ thickness is more gradual.

We also consider the effect of broadband detection with a large NA objective in Fig. 3 B. This calculation uses Eq. 5 to fully model a realistic experimental setup. Just as the excitation intensity is structured by the architecture of the SiO₂/Si surface, so the intensity of emitted fluorescence also depends on the distance of the fluorophore from the Si surface. The emitted light interferes strongly when the SiO₂ thickness is small, but as a result of the competing contributions from many θ_inc values, the emission interference is relatively damped out after ∼250 nm of SiO₂. Thus, as shown in Fig. 3 B, the greatest increase in intensity occurs at the first maximum with an SiO₂ thickness of ∼95 nm. Nonetheless, Fig. 3 B illustrates that for optimal VIA-FLIC experiments a larger SiO₂ thickness is generally favored over smaller SiO₂ thickness because the intensity changes more dramatically with θ_inc for successive maxima. (Note, however, that the coherence length of light from a mercury arc source and more imperfections in the SiO₂ layer with increased thickness act as upper bounds on the optimal oxide thickness.) Additionally, the SiO₂ thickness should be either slightly smaller or larger than an SiO₂ thickness which gives a maximum of intensity at θ_inc = 0°. This criterion ensures maximal signal/noise and a sensitive dependence of fluorescence intensity on θ_inc. Fig. 3 C illustrates the relative intensity as a function of θ_inc for a set of SiO₂ thicknesses (250, 275, 300, 325, and 350 nm) near the second maxima at θ_inc = 0° (280 nm SiO₂). The emission characteristics contribute to the height of intensity maxima and influence signal/noise and therefore determine which oxide thicknesses would give the largest variation in intensity with θ_inc for a given distance of a fluorophore above the surface. However, the curve shape is independent of emission and depends entirely on absorption properties, as in Eq. 9. For the purposes of model fits to data, only the excitation intensity component of the calculation is required.

An experimental test of VIA-FLIC

To demonstrate the effect that Fig. 3 C predicts, namely that intensity measurements as a function of θ_inc reflect differences in the distance of fluorescent objects from the Si surface, we chose a 1 mol % DiI-containing supported membrane on different SiO₂ steps. This system has been used as a calibration for FLIC by Fromherz and co-workers (10). As schematically illustrated in Fig. 4 A, it provides a set of well-defined fluorescent objects whose position is systematically varied with respect to the Si-mirror surface. Fig. 4, C and D, show the VIA-FLIC images of DiI-labeled membranes separated from the Si surface by different thicknesses of SiO₂ (Fig. 4 B) for two different ranges of excitation angles. When the range of excitation incidence angles is near 10° (median θ_inc = 9.8°), Fig. 4 C shows that the fluorescence intensity of a supported membrane closer to the Si surface (SiO₂ thickness = 258 nm) is brighter than the fluorescence intensity of a membrane farther from the Si surface (SiO₂ thickness = 364 nm). Fig. 4 D shows that the situation is reversed for excitation incidence angles near 35° (θ_inc = 35.2°): the fluorescence intensity of the DiI-supported membrane is brighter farther from the Si surface. These images demonstrate that changing θ_inc differentially modulates the fluorescence intensity of fluorescent objects located at different positions in z.

As a demonstration that VIA-FLIC can quantitatively determine the z-position of a fluorescent object, the fluorescence intensity of DiI-containing supported membranes at four different z-positions was measured for 12 ranges of incidence angles, and the resulting VIA-FLIC curves were fit to determine the SiO₂ thickness. Fig. 4 E plots the fluorescence intensities of a typical sample of DiI-containing supported membranes on four SiO₂/Si surfaces (SiO₂ thicknesses = 255 nm, 276 nm, 364 nm, 385 nm) as a function of θ_inc (θ_inc = 1.9°, 5.8°, 9.8°, 13.7°, 17.8°, 21.9°, 26.1°, 30.6°, 35.2°, 40.1°, 45.4°, and 51.2°). For this test, a sequence of images (one for each photomask) was acquired on a single bilayer region at low light intensities to minimize photobleaching. Reversing the sequence of image acquisition, and so presumably the effect of photobleaching on the data, had minimal effect on the data points and fitting parameters obtained (data not shown). By including the experimentally determined aperture function in the calculation of J^layer, the SiO₂ thicknesses of the four steps were determined by least squares fitting of the measured data with Eq. 9. The SiO₂ thicknesses as determined by VIA-FLIC showed good agreement with the SiO₂ thicknesses as determined by ellipsometry: 254 ± 5 nm (255 nm), 280 ± 4 nm (276 nm), 358 ± 2 nm (364 nm), and 380 ± 3 nm (385 nm), where the ellipsometric thicknesses are in parentheses and the error in fitted oxide thickness is the formal standard deviation as derived from the measured fluorescence intensity distribution. Thus, oxide thicknesses determined by VIA-FLIC are accurate to within 6 nm of the ellipsometric thicknesses with precision of a few nanometers. Possible sources of systematic error whose elimination would improve fit accuracy are discussed below.

DISCUSSION

Fitting dependence on the aperture function

The aperture function is an important component of the quantitative fitting model. The design of many commercial microscopes, including the Nikon E800 used in these experiments, causes an image of the lamp to be formed in the aperture diaphragm plane, meaning that the light intensity in the aperture diaphragm plane may vary dramatically as a function of radial position (and hence excitation intensity varies with θ_inc even in a homogeneous medium). The form of this variation is highly dependent on the shape of the arc, which is not known a priori but needs to be determined to fit experimental data using a VIA-FLIC model. In our setup, using a mercury arc, the aperture function generally differs by a factor of ∼10 from largest to smallest intensity (innermost to outermost annular photomask), a variation on the same order as the variation in intensity with θ_inc due to interference (Fig. 3). Therefore, if a simple mercury arc is used as the light source, the curve to be fit is affected by the shape of the arc to the same extent as the interference effects that encode distance information.

To reduce the dependence of the measured intensity on the aperture function, the light from the mercury arc lamp was focused into and transmitted through a silica fiber, resulting in a disk-shaped source such that the aperture diaphragm plane and the objective rear focal plane (entrance pupil) were uniformly illuminated. With this setup, it is possible to fit experimental data using a rectangular aperture function to an accuracy of ∼20 nm (see Supplementary Material). However, more precise quantitative fits require an empirical description of the aperture function of the fiber optic source. A stepped approximation to this aperture function was calculated using measured intensities transmitted through each photomask, which were then compared to values predicted for a constant aperture function. The set of ratios of measured/predicted intensities was interpolated to give a continuous function; when incorporated into the fitting model this function considerably improved fit accuracy (see Supplementary Material). Measuring the absolute incident light intensity directly is quite straightforward; however, the interpolated step function derived from the measurement may not be an entirely accurate description of the radial aperture function. Imaging the rear objective focal plane using a CCD chip placed just outside the specimen plane would give a direct measurement of the aperture function. This would reduce uncertainty in the intensity of incident light at a given angle.

It should be noted that VIA-FLIC does not require the use of a modified light source. A stepwise description of the image of the mercury arc at the objective rear focal plane, obtained using a power meter, can be used to fit fluorescence intensity data obtained using a direct arc lamp source with accuracy approaching that of the fits obtained using a uniform disk source (not shown). However, the effect of the aperture function on the intensity curve shape is much more drastic with an arc source, with the result that even approximate curve fitting is impossible without a description of the aperture function. Furthermore, experiments are less reproducible due to arc wandering, and problems with arc alignment (in particular that the most homogeneous illumination of the field of view may not exactly correspond to the sharpest image of the arc in the aperture diaphragm plane) make fluorescence inhomogeneity more problematic.

Although the objective rear focal plane is not uniformly illuminated, especially with an unmodified mercury arc source, the equations used by Fromherz (10) to fit FLIC data assume that it is, and instead treat the excitation NA as a free parameter. Since FLIC integrates over the entire range of incidence angles, the contribution of the arc shape to the predicted intensity curves is relatively small. However, changing the NA changes the range of θ_inc values rather than the relative weights of these values; and despite very good fits between FLIC calculations and experiment presented by Lambacher and Fromherz, there are some discernible systematic discrepancies. Our calibration provides a simple method of avoiding the incorrect assumption of uniform illumination and thus removes one free parameter from FLIC fitting. This has the potential to improve the FLIC fits.

Fitting dependence on the absorption dipole orientation

As with many other quantitative absorption techniques (including the parent methods FLIC and VIA-TIRFM), quantitative analysis in VIA-FLIC incorporates a description of the orientation of the transition dipole of the absorbing species. The description used in our quantitative fitting model treats the absorption dipole as perfectly oriented at 76.5° to the bilayer normal, the value for the DiI absorption dipole in a perfectly oriented planar membrane determined by Axelrod and co-workers (29), leaving only the oxide thickness and a scale factor as free parameters. To assess the importance of dipole orientation to the fit parameters extracted, the absorption dipole orientation was allowed to vary in the model as an additional free parameter. Using two sets of data for the same four oxide thicknesses presented in this study (i.e., n = 8), the best fit absorption dipole angle is 64 ± 4° (see Supplementary Material). This result differs from the value used for the oxide fitting and is more similar to the empirical absorption dipole angle result of 62° obtained by Lambacher and Fromherz for DiI (10). The two-variable model also gives oxide thickness parameters that are closer (by 1 ± 2 nm) to the thicknesses determined by ellipsometry.

Two conclusions should be drawn from this analysis. First, it is a simplification to treat the absorption dipole of DiI as completely well oriented with respect to the surface normal; rather, fluctuations in overall membrane orientation or DiI within the membrane contribute to fluorophore disorder. This is consistent with the observations of DiI orientation in supported lipid bilayers by Lambacher and Fromherz (10) and Sund et al. (29). Second, although VIA-FLIC is sensitive to dipole orientation and could even be used as a probe of approximate dipole orientation, the primary effect modulating fluorescence intensity is excitation intensity, a function of distance from the silicon mirror. At least in this case, calculated distances in z are precise and in good agreement with expected values even when using models with a simple description of the fluorophore's absorption dipole orientation. Allowing the transition dipole orientation to be refined, and so taking account of the more complex dynamics of DiI in the membrane, improves the z fits and may be necessary when very high accuracy is required.

Use of large annular radii photomasks

Fig. 4 E shows that for large θ_inc values, i.e., large annular radii, the best fits deviate from measured fluorescence intensities and that the measured fluorescence intensities at large θ_inc have a larger standard deviation. This observation raises concern about possible sources of systematic error, especially for the larger annular photomasks.

The DiI-labeled membrane, comprised of two well-defined layers of evenly distributed fluorophores, is one of the most stringent tests of illumination homogeneity available. Some inhomogeneity in illumination is expected for all fluorescence microscopes; we regard 10% standard deviation as an acceptable level of homogeneity. Significant (>10%) differences in the measured fluorescence intensities between different regions of the image were consistently observed for the two largest annular photomasks. The significant inhomogeneity in fluorescence intensity at high θ_inc values results in part from the dim edge of the illumination field partially encroaching on that portion of the field imaged by our CCD. In addition, very bright and dark regions were consistently observed for the largest annular photomask. These inhomogeneities, observed even after the direct arc source had been replaced with homogeneous illumination via a silica fiber, suggest that factors not described in Eq. 9 are affecting the measured light intensity. These inhomogeneities may be an effect of inaccurate alignment of the center of the photomask with the optical axis in the rear objective focal plane. At large annular radii any effect of incorrect photomask alignment, especially tilting, would be magnified. There may also be unanticipated imperfections in the microscope optics, including additional stray light arising from our insertion of a photomask into the optical path, that are magnified for high angle light paths. These possibilities suggest that the fitting model should be applied with caution at high radii and that the experiment performed here could also be treated as a calibration of the useful range of mean radii, i.e., 0–5 mm.

Future experimental improvements

An experimental modification that may improve data quality and accuracy of fit parameters for future experiments could be to use a larger number of narrower θ_inc ranges while avoiding median radii >5 mm. Such a data set would give a more accurate representation of the curve shape where the model most accurately matches the data and the standard deviation of measured fluorescence is small. These modifications could be accomplished by simply using narrower annular photomasks with smaller radii. Alternatively, the light intensity in the rear objective focal plane could be patterned and these patterns could be modulated through use of a small programmable micromirror device or by galvonometer-based deflection of a laser spot. Either of these approaches would allow excitation with an almost arbitrary number of median θ_incs each with a narrow range. As discussed below, both of these alternatives have additional benefits in terms of increased time resolution.

Additionally, it would be advantageous to modify the existing VIA-FLIC apparatus to make time-resolved z-distance measurements. In the setup described herein, a single height measurement takes ∼1 min. Based on exposure times of hundreds of milliseconds and the speed of the motorized linear stage, the maximum achievable time resolution for a completely automated data acquisition process with 12 annuli would be on the order of 5–10 s. The time resolution scales with the number of annular photomasks used for each height determination, and so reducing the number of annular photomasks would improve the possibilities for dynamic measurement. Since there are always at least two free variables (a scaling factor and a z-position), a minimum of three photomasks is required for the least squares fitting process to be meaningful. Fitting SiO₂ thicknesses using data only from three annular photomasks results in fits that are quite similar to those obtained with the full complement of photomasks (see Supplementary Material). However, the reproducibility and precision of fits using fewer data points would need more thorough investigation before quantitative analysis of changes in z-position with time could be performed. Nonetheless, we project that the maximum time resolution with VIA-FLIC would be ∼3× slower than the maximum time resolution of an unmodified wide field imaging system. With existing light sources and CCD cameras, this time resolution could be video rate.

Another improvement would be to use a thicker layer of SiO₂ on Si, ∼625 nm for objects located within tens of nanometers of the SiO₂ surface. As the oxide thickness increases, it is expected that the rate of change in curve shape with change in z should increase. Starting with a reasonable estimate for the object of interest's distance from the surface, the SiO₂ thicknesses for a VIA-FLIC experiment can be chosen such that small changes ∼±10 nm around that distance give very different intensity versus θ_inc curves. After calibration of the aperture function, VIA-FLIC data could be collected, corrected, and fit to Eq. 9.

Our quantitative demonstration of contrast between identical DiI-containing supported membranes located at different distances from the Si surface when θ_inc is varied indicates the level of accuracy possible with VIA-FLIC, as well as providing a nanometer calibration for VIA-FLIC. The method allows the accurate measurement of the height of well-oriented fluorophores that are narrowly distributed in z, but that need not be uniformly laterally distributed, by way of a straightforward experiment using a modified standard epifluorescence microscope. VIA-FLIC also permits assay of z structure when replicating structures or identical manipulation of the sample over many SiO₂ steps is impractical. For example, multiple SiO₂ steps could perturb the structure of thin films prepared by spin coating and would complicate the fabrication of multilayered structures prepared by various nanofabrication methods. Additionally, the edges between adjacent SiO₂ steps on a FLIC chip have been demonstrated to affect the structure of thin films created by Langmuir-Blodgett deposition (16). Other surface modifications such as microcontact printing or microfludics flow patterning are difficult to implement such that all the SiO₂ steps of a FLIC chip have identical final structures. Finally, it should be possible to position an Si mirror near a freestanding lipid bilayer either by using a precision stage or the fabrication of an integrated system, so that membranes and membrane protein structural changes could be measured. Such measurements are in progress.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.