Dynamical Mechanisms of Pacemaker Generation in I_K1-Downregulated Human Ventricular Myocytes: Insights from Bifurcation Analyses of a Mathematical Model

Abstract

Dynamical mechanisms of the biological pacemaker (BP) generation in human ventricular myocytes were investigated by bifurcation analyses of a mathematical model. Equilibrium points (EPs), periodic orbits, stability of EPs, and bifurcation points were determined as functions of bifurcation parameters, such as the maximum conductance of inward-rectifier K⁺ current (I_K1), for constructing bifurcation diagrams. Stable limit cycles (BP activity) abruptly appeared around an unstable EP via a saddle-node bifurcation when I_K1 was suppressed by 84.6%. After the bifurcation at which a stable EP disappears, the I_K1-reduced system has an unstable EP only, which is essentially important for stable pacemaking. To elucidate how individual sarcolemmal currents contribute to EP instability and BP generation, we further explored the bifurcation structures of the system during changes in L-type Ca²⁺ channel current (I_Ca,L), delayed-rectifier K⁺ currents (I_K), or Na⁺/Ca²⁺ exchanger current (I_NaCa). Our results suggest that 1), I_Ca,L is, but I_K or I_NaCa is not, responsible for EP instability as a requisite to stable BP generation; 2), I_K is indispensable for robust pacemaking with large amplitude, high upstroke velocity, and stable frequency; and 3), I_NaCa is the dominant pacemaker current but is not necessarily required for the generation of spontaneous oscillations.

INTRODUCTION

The cardiac biological pacemaker (BP) was recently created by genetic suppression of the inward-rectifier K⁺ current (I_K1) in guinea pig ventricular myocytes (1), suggesting possible development of the functional BP as a therapeutic alternative to the electronic pacemaker. A first step for creation of the functional BP would be engineering of single BP cells, which requires deep understanding of the BP mechanisms. Using the Luo-Rudy guinea pig ventricle model (2), Silva and Rudy (3) simulated BP activity by reducing I_K1 conductance (g_K1) and investigated the ionic mechanisms of BP generation in the I_K1-downregulated ventricular myocyte. They reported that BP activity was yielded by 81% suppression of I_K1, concluding that Na⁺/Ca²⁺ exchanger current (I_NaCa) was the dominant pacemaker current. However, the mechanistic difference between ventricular pacemaking and natural sinoatrial (SA) node pacemaking, as well as whether I_K1 downregulation also induces BP activity in human ventricular myocytes (HVMs), remains to be clarified.

The aim of this study was to elucidate the mechanisms of BP generation in I_K1-downregulated HVMs and the roles of individual sarcolemmal currents in HVM pacemaking in terms of the nonlinear dynamics and bifurcation theory. In previous studies (4–11), bifurcation structures of ventricular or SA node models, i.e., ways of changes in the number or stability of equilibrium and periodic states of the model systems, were investigated for elucidating the mechanisms of normal and abnormal pacemaker activities. These theoretical works indicate that the mathematical approach provides a convenient way of understanding how individual currents contribute to pacemaker activities. In this study, therefore, local stability and bifurcation analyses, as well as numerical simulations, were performed for a mathematical model of the HVM. We constructed bifurcation diagrams by calculating equilibrium points (EPs), periodic orbits, stability of the EP, and saddle-node or Hopf bifurcation points as functions of bifurcation parameters (for details, see Theory and Methods). During I_K1 suppression, BP activity abruptly emerged around an unstable EP via a saddle-node bifurcation at which a stable EP corresponding to the resting state disappeared. Our results suggested that BP activity could be developed by reducing I_K1 alone in HVMs as well and that the instability of an EP at depolarized potentials is essentially important for BP generation.

To elucidate the ionic mechanisms of EP destabilization and BP generation in the I_K1-downregulated HVM, we further explored bifurcation structures of the I_K1-reduced BP system during decreases or increases in an L-type Ca²⁺ channel current (I_Ca,L), delayed-rectifier K⁺ currents (I_K), and I_NaCa, which appear to be essentially important for pacemaker generation (3,11). Moreover, we determined stability of the BP system at the steady-state potential (V₀) during applications of the constant bias current (I_bias) and how the unstable V₀ and I_bias regions, where BP oscillations occur, change with decreasing or increasing the sarcolemmal currents. This would reveal the contributions of each current to EP instability and robustness of BP activity to hyperpolarizing or depolarizing loads (11). Our study suggests that the dynamical mechanism of the ventricular pacemaking is essentially the same as that of the natural SA node pacemaking as reported by Kurata et al. (11).

This article clearly shows that bifurcation analyses of a mathematical model allow us to notice the essential importance of EP instability for pacemaker generation and to elucidate the roles of individual ionic currents in pacemaking. Thus, the nonlinear dynamical approach is useful for general understanding of the mechanisms of normal and abnormal pacemaker activities and may also be applicable to engineering of a functional BP as a therapeutic alternative to the electronic pacemaker. Definitions of the terms specific to the nonlinear dynamics and bifurcation theory are provided at the end of the Theory and Methods section to help understand the theory and methods for bifurcation analysis as well as our results and conclusions. Abbreviations and acronyms repeatedly used in this article are listed in Table 1.

TABLE 1.

Abbreviations and acronyms

AP	Action potential
APA	Action potential amplitude
APD(90)	Action potential duration (at 90% repolarization)
βAS	β-adrenergic stimulation
BP	Biological pacemaker
CL	Cycle length
C-LTCC	High voltage-activated L-type Ca2+ channel
D-LTCC	Low voltage-activated L-type Ca2+ channel
EP	Equilibrium point
hESC	Human embryonic stem cell
HVM	Human ventricular myocyte
Ibias	Constant bias current
ICa,L	L-type Ca2+ channel current
IK	Delayed-rectifier K+ current
IKr	Rapidly activating component of IK
IKs	Slowly activating component of IK
IK1	Inward-rectifier K+ current
INa	Na+ channel current
INaCa	Na+/Ca2+ exchanger current
Ito	4-Aminopyridine-sensitive transient outward current
IX,b	Background current carried by ion X
Ih	Hyperpolarization-activated current
MDP	Maximum diastolic potential
ODE	Ordinary differential equation
PB	Priebe-Beuckelmann
POP	Peak overshoot potential
SA	Sinoatrial
SR	Sarcoplasmic reticulum
V	Membrane potential
V0	Steady-state potential at an EP
[Ca2+]rel	Free Ca2+ concentration in the junctional SR
[Ca2+]up	Free Ca2+ concentration in the network SR
[X]i	Intracellular concentration of ion X
[X]o	Extracellular concentration of ion X

THEORY AND METHODS

Development of a modified HVM model

A mathematical model of cardiac myocytes is described as an n-dimensional nonlinear dynamical system, i.e., a set of ordinary differential equations of the form

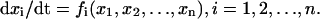(1)

This is usually written in the vector form

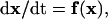(2)

where the state variable x is a vector-valued function of time t, and the vector field f is a function of the state variable x (12–14). For a model system to be suitable for bifurcation analysis, the vector field f should be continuous and smooth (i.e., sufficiently differentiable) and should not depend on time or initial conditions but depend only on the state variable x. Such a system is called an “autonomous” system (see also Definitions of Terms at the end of this section).

On the basis of single-cell patch-clamp data from undiseased and failing HVMs, Priebe and Beuckelmann (15) have first developed a single HVM model (referred to as the Priebe-Beuckelmann (PB) model) as a modified version of the Luo-Rudy phase II model for the guinea pig ventricle (2). Recently, ten Tusscher et al. (16) and Iyer et al. (17) developed more elaborate HVM models based on detailed experimental data. Their models appear to be superior to the PB model in reproducing experimental data but less suitable for bifurcation analyses for the following reasons: 1), the ten Tusscher et al. model has the vector field containing many complex functions that are not continuous or smooth, thus they are not always differentiable or yield noncontinuous derivatives; and 2), the Iyer et al. model (n = 67) is much larger than the PB model (n = 15) or the ten Tusscher et al. model (n = 17), making bifurcation analyses practically much harder. We have therefore chosen to modify the PB model on the basis of recent experimental findings as well as other human or animal heart models. The original PB model explicitly contains time t in the formula for the sarcoplasmic reticulum (SR) Ca²⁺ release, making it nonautonomous. Thus, modifications of the PB model were required for converting it into an autonomous system, as well as for improving the capability of reproducing experimental data.

The standard model for the normal activity is described as a nonlinear dynamical system of 15 first-order ordinary differential equations. The membrane current system includes I_Ca,L, the rapid and slow components of I_K (denoted I_Kr and I_Ks, respectively), 4-aminopyridine-sensitive transient outward current (I_to), Na⁺ channel current (I_Na), I_K1, background Na⁺ (I_Na,b) and Ca²⁺ (I_Ca,b) currents, Na⁺-K⁺ pump current (I_NaK), I_NaCa, and Ca²⁺ pump current (I_pCa). The expressions for I_Ca,L and I_Ks as well as SR Ca²⁺ release were reformulated, whereas the formulas for other ionic currents and intracellular Ca²⁺ handling are essentially the same as those in the original PB model or adopted from other existing models (16,18–20). Modifications of the model are summarized in Table 2; details on major modifications are described below. All expressions (Eqs. 3–64) and the standard parameter values used are provided in Appendix 1 and Table 5, respectively.

TABLE 2.

Equations and parameter values adopted for individual components of the HVM model

Component	Expressions	Parameter values		PB*	TNNP*
ICa,L	dL,∞, fL,∞: Bénitah et al. (21)	gCa,L (nS/pF)	0.2496	0.064
	τdL: Same as the TNNP model (16)
	τfL: Original formula based on Bénitah et al. (21)
IKr	pa,∞: Li et al. (24)	gKr (nS/pF)	0.012	0.015	0.096
	pi,∞: Same as the CRN model (19)†
	τpa: Same as the CRN model (19)†
IKs	n∞: Li et al. (24)	gKs (nS/pF)	0.036	0.02	0.245
	τn: Original formula based on Virág et al. (34)
Ito	Same as the PB model (15)	gto (nS/pF)‡	0.3/0.4	0.3	0.294
INa	Same as Bernus et al. (18)§	gNa (nS/pF)	7.8	16	14.838
IK1	Same as the PB model (15)	gK1 (nS/pF)	3.9	2.5	5.405
INa,b	Same as the PB model (15)	gNa,b (nS/pF)	0.001	0.001	0.00029
ICa,b	Same as the PB model (15)	gCa,b (nS/pF)	0.00051	0.00085	0.000592
INaK	Same as the PB model (15)	INaK,max (pA/pF)	0.884	1.3	1.362
INaCa	Same as the PB model (15)	kNaCa	1000	1000	1000
IpCa	Same as the CRN model (19)¶	IpCa,max (pA/pF)	0.11	0	0.025
Jrel	Modified formulas base on Faber and Rudy (20)	Prel	50	22	24.696
Jup	Same as the TNNP model (16)¶	Pup	0.00221	0.0045	0.000425
Jtr	Same as the PB model (15)	τtr	180	180
Ca2+ buffers	Same as the PB model (15)

^*Parameter values used for the PB model (15) and ten Tusscher et al. (TNNP) model (16) are given for comparison. Values are shown in italics or not shown, when the formula is different from that of the current model and thus direct comparison is impossible.

^†Formulas of the Courtemanche et al. (CRN) model for human atrial myocytes (19) were used. For details, see text.

^‡The g_to (nS/pF) was set equal to 0.4, the value for epicardial cells (18), for the simulation of paced APs, and to 0.3, the value of the original PB model, for the BP simulations and bifurcation analyses.

^§Formulas for I_Na were adopted from Bernus et al. (18) to reduce the number of state variables as well as to avoid the use of noncontinuous functions.

^¶To reduce the diastolic [Ca²⁺]_i during pacing at 0.25–2 Hz to <0.3 μM, 1), a small amount of I_pCa was added, and 2), the formula for SR Ca²⁺ uptake was adopted from the TNNP model (16).

Formulation of I_Ca,L

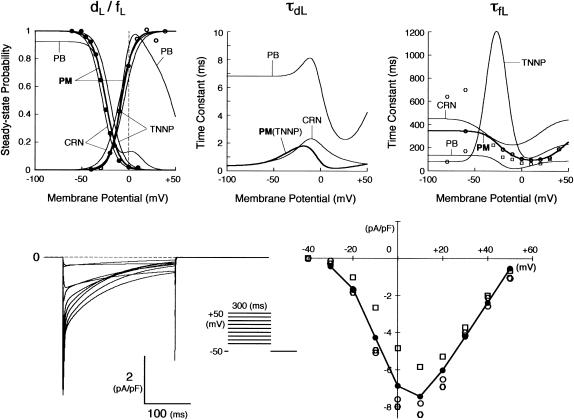
The kinetics of I_Ca,L was described by Eqs. 3–8 with the activation (d_L), voltage-dependent inactivation (f_L), and Ca²⁺-dependent inactivation (f_Ca) gating variables. Voltage dependences of I_Ca,L gating kinetics in the current (modified) and original human heart models are shown in Fig. 1 (top), together with temperature-corrected experimental values for comparison. As ten Tusscher et al. (16) pointed out, the steady-state activation and inactivation curves (d_L∞, f_L∞) yielded by the original PB formulas were somewhat unusual for unknown reasons (see Fig. 1, left top), resulting in a very large window current. We therefore renewed the expressions for I_Ca,L. For the steady-state activation and inactivation (d_L∞, f_L∞), we used the data of Bénitah et al. (21). The expression of the activation time constant (τ_dL) was adopted from the ten Tusscher et al. model (16). The formulas for the time constants of the voltage-dependent inactivation and recovery (τ_fL) employed by the original models appeared not to fit the experimental data for single HVMs from Bénitah et al. (21) or other articles (see Fig. 1, right top, and also Fig. 2 E of ten Tusscher et al. (16)). Therefore, we originally formulated τ_fL from the data of Bénitah et al. (21), which were corrected for a temperature of 37°C with a Q₁₀ of 2.2 and [Ca²⁺]_o-dependent factor (16). The τ_fL data were fitted to a function similar to that used by Courtemanche et al. (19) for their human atrial model, using a least square minimization procedure. The formula for the Ca²⁺-dependent inactivation (f_Ca,∞) is also the same as used by Courtemanche et al. (19). Maximum I_Ca,L was formulated as a fully selective Ca²⁺ current, with its reversal potential (E_Ca,L) fixed at a constant value of +52.8 mV as reported by Bénitah et al. (21) and the maximum conductance (g_Ca,L) set equal to 249.6 pS/pF at 2 mM [Ca²⁺]_o.

FIGURE 1.

Kinetics of I_Ca,L. (Top) Voltage dependence of steady-state probabilities (d_L∞, f_L∞) and time constants for I_Ca,L activation (τ_dL) and inactivation (τ_fL). Equations used for the current (modified) model are shown with the thick lines (labeled “PM”). For comparison, those for existing (original) models are also shown with the thin lines: PB, Priebe and Beuckelmann (15); TNNP, ten Tusscher et al. (16); CRN, Courtemanche et al. (19). The experimental data for d_L∞, f_L∞, and τ_fL are from Bénitah et al. (21) (circles), Pelzmann et al. (22) (squares), and Li et al. (23) (hexagons). (Bottom) Computed voltage-clamp records for I_Ca,L (left) and peak I_Ca,L-V relationship (right). Currents were evoked by 300-ms step pulses from a holding potential of −50 mV to test potentials ranging from −30 to +50 mV in 10 mV increments. Simulating the whole-cell perforated-patch recording, [Ca²⁺]_i was not clamped, whereas [Na⁺]_i and [K⁺]_i were fixed at 5 and 140 mM, respectively. The experimental data for the peak I_Ca,L-V relation are from Bénitah et al. (21) (open circles), Pelzmann et al. (22) (squares), and Li et al. (23) (hexagons).

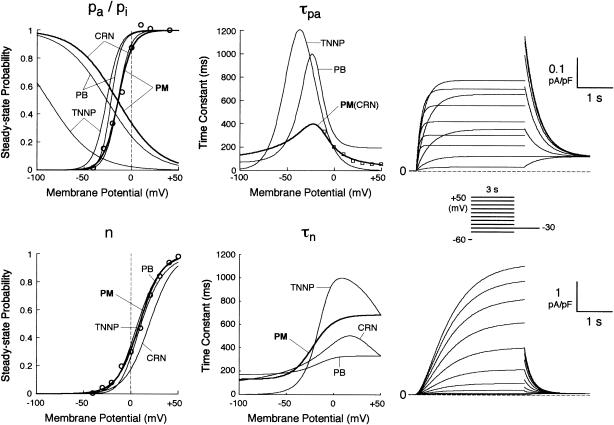
FIGURE 2.

Kinetics of I_Kr (top) and I_Ks (bottom). (Left, middle) Voltage dependence of steady-state probabilities and time constants of I_Kr activation (p_a,∞, τ_pa) and inactivation (p_i,∞) as well as I_Ks activation (n_∞, τ_n). The thick lines are for this study (PM); the thin lines are from the existing models (PB, TNNP, CRN). The experimental data for p_a,∞, τ_pa, and n_∞ are from Li et al. (24) (circles) and Wang et al. (25) (squares). (Right) Computed voltage-clamp records for I_Kr and I_Ks. Currents were elicited by 3-s step pulses from a holding potential of −60 mV to test potentials ranging from −50 to +50 mV in 10 mV increments.

The model-generated I_Ca,L during voltage-clamp pulses and peak I_Ca,L-V relationship are depicted in Fig. 1 (bottom). The simulated peak I_Ca,L-V relation is comparable to the experimental data from Bénitah et al. (21), Pelzmann et al. (22), and Li et al. (23).

Formulation of I_Kr

The kinetics of I_Kr was described by Eqs. 9–14 with the activation (p_a) and inactivation (p_i) gating variables. Voltage dependences of I_Kr activation and inactivation in the current and original human heart models are shown in Fig. 2 (top), together with experimental data for comparison; the model-generated I_Kr during voltage-clamp pulses are also depicted. There are limited experimental data available for the gating kinetics of native I_Kr channels in HVMs. Nevertheless, experimentally observed activation of native I_Kr in human cardiac myocytes (24,25) appeared to be faster than the I_Kr activation simulated by the original PB formulas. To formulate I_Kr kinetics, the recently developed HVM models (16,17) employed the experimental data from human ether-a-go-go-related gene (HERG) channels expressed in human embryonic kidney (HEK) cells (26,27), Chinese hamster ovary cells (28), or Xenopus oocytes (29). However, voltage- and time-dependent kinetics of expressed HERG channels appear to depend on cell lines or conditions for expression, as well as conditions for current recordings such as temperatures, and thus may be different from those of native I_Kr channels in human hearts (26–28,30–32). We therefore adopted the data from HVMs of Li et al. (24) for the steady-state activation curve (p_a,∞) and the formula of Courtemanche et al. (19) based on the data from human atrial myocytes of Wang et al. (25) for the activation time constant (τ_pa). We also employed the expression of Courtemanche et al. (19) for the steady-state inactivation curve (p_i,∞). No detailed experimental data are available on the time constant of I_Kr inactivation (τ_pi) in intact HVMs. Inactivation and recovery of native I_Kr in animal hearts or expressed HERG channels are very rapid (28,33); thus, we assumed that I_Kr inactivation is instantaneous. The maximum I_Kr conductance (g_Kr) was set equal to 12 pS/pF, according to the data of Li et al. (24). With this g_Kr value, the complete block of I_Kr prolonged the action potential duration (APD) of the model HVM paced at 1 Hz by 34.6–48.9%; the simulated APD prolongation by I_Kr block is comparable to the experimentally observed effects of the selective I_Kr blocker E-4031 as reported by Li et al. (24).

Formulation of I_Ks

On the basis of the recent data from Li et al. (24) and Virág et al. (34), the kinetics of I_Ks was reformulated as Eqs. 15–18. Voltage dependences of I_Ks kinetics in the current and original models are shown in Fig. 2 (bottom), together with experimental data for comparison; the model-generated I_Ks during voltage-clamp pulses are also depicted. Steady-state I_Ks activation curve (n_∞) is from Li et al. (24). Virág et al. (34) recently reported that I_Ks in HVMs slowly activates and rapidly deactivates. According to their report, therefore, we reformulated the time constant of I_Ks activation (τ_n) as Eq. 18. The expression of E_Ks is the same as for the PB model. The maximum conductance (g_Ks) was set equal to 36 pS/pF so as to yield the APD at 90% repolarization (APD₉₀) during 1 Hz pacing of 336 ± 16 ms, as reported by Li et al. (24).

Formulation of SR Ca²⁺ release

In the original PB model, SR Ca²⁺ release kinetics was represented by the formula that explicitly contains time t and also Δ[Ca²⁺]_i,2, which is not a state variable but the sum of net Ca²⁺ influx during the first 2 ms after initiation of the action potential (AP). Thus, the original PB model is a nonautonomous system, the vector field of which depends on time and initial conditions, not suitable for bifurcation analysis. We had therefore to renew the SR Ca²⁺ release formula to convert the model into an autonomous system. Owing to the lack of available data for updating the kinetic formulation of SR Ca²⁺ release in HVMs, we utilized simple expressions, Eqs. 47–51. The formula for conductance of the Ca²⁺ release channel (g_rel) was adopted from Faber and Rudy (20), with the P_rel value reduced to one-third of the original value to obtain the peak [Ca²⁺]_i transient of ∼1 μM during APs elicited at 1 Hz. For gating behaviors of the Ca²⁺ release channel (d_R, f_R), we used the expressions similar to those for the I_Ca,L gating variables to make the model an autonomous system suitable for bifurcation analyses.

Ion concentration homeostasis

The model also includes material balance expressions to define the temporal variation in [Ca²⁺]_i, [Na⁺]_i, and [K⁺]_i, whereas [Ca²⁺]_o, [Na⁺]_o, and [K⁺]_o were fixed at 2, 140, and 5.4 mM, respectively. As pointed out by Hund et al. (35) and Krogh-Madsen et al. (36), the second-generation models incorporating ion concentration changes have two major problems: 1), drift, with very slow long-term trends in state variables; and 2), degeneracy, with nonuniqueness of steady-state solutions. The current model did not show a long-term drift in the intracellular ion concentrations but reached a steady state during pacing, as well as during BP oscillation, when the principle of charge conservation was taken into account (35).

An n-dimensional fully differential system formulated as a cardiac second-generation model can usually be converted into a differential-algebraic system composed of n − 1 differential equations and one algebraic equation, resulting in n − 1 equations for n unknowns (35,36). In such a system, the Jacobian matrix of which is singular, the EP or limit cycle is not unique but depends on initial conditions; e.g., our full system has a continuum of EPs, because Eq. 65 can be derived from Eqs. 66, 69, and 70 (see Appendix 2). Thus, second-generation models including our full system exhibit degeneracy not suitable for bifurcation analysis to be applicable to isolated equilibria. As suggested by Krogh-Madsen et al. (36), one of the ways to remove degeneracy and thus allow bifurcation analyses of isolated equilibria is to make some ionic concentrations fixed. Variations in [K⁺]_i during changes in parameters or stimulation rates (0.25–2 Hz) were relatively small (<5 mM), being too small to significantly alter the model cell behaviors. For stability and bifurcation analyses, therefore, [K⁺]_i was fixed at 140 mM. The degenerate system with the fixed [K⁺]_i has the finite number of EPs and limit cycles, being suitable for bifurcation analyses.

Determination and validation of model HVM dynamics

Numerical methods for dynamic simulations of HVM behaviors

Dynamic behaviors of the model HVM were determined by solving a system of nonlinear ordinary differential equations numerically. Numerical integration, as well as bifurcation analyses, were performed on Power Macintosh G4 computers (Apple Computer, Cupertino, CA) with MATLAB 5.2 (The MathWorks, Natick, MA). We used the numerical algorithms available as MATLAB ODE solvers: 1), a fourth-order adaptive-step Runge-Kutta algorithm which includes an automatic step-size adjustment based on an error estimate (37), and 2), a variable time-step numerical differentiation approach selected for its suitability to stiff systems (38). The former (named ode45) is the best function for most problems. However, the latter (named ode15s) was much more efficient than ode45 and both solvers usually yielded nearly identical results. Therefore, ode15s was usually used, and ode45 was only sometimes used to confirm the accuracy of calculations. The maximum relative error tolerance for the integration methods was set to 1 × 10⁻⁶.

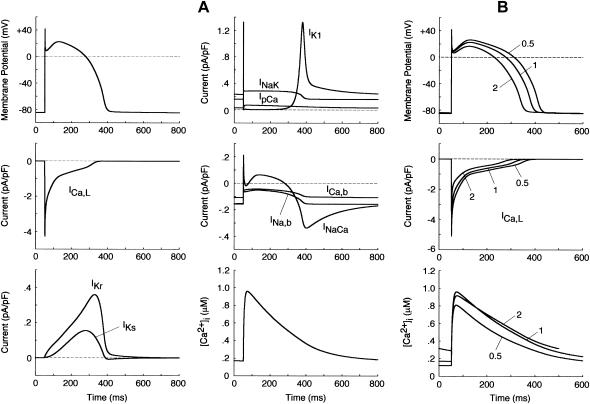
Dynamic properties of the model HVM: simulated APs, ionic currents, and [Ca²⁺]_i dynamics

The steady-state AP, sarcolemmal currents, and [Ca²⁺]_i transient of the current model paced at 1 Hz with the standard parameter values are shown in Fig. 3 A. According to the report of Hund et al. (35), the stimulus current was assumed to carry K⁺ ions into the cell for charge conservation. During pacing, the model cell dynamics reached a steady state, with no long-term drift in the state variables. Steady-state values of the resting potential, maximum upstroke velocity, and APD₉₀ during 1 Hz pacing were −84.9 mV, 411 V/s, and 338 ms, respectively. The diastolic [Ca²⁺]_i and peak [Ca²⁺]_i transient in the model HVM paced at 1 Hz were 0.169 and 0.961 μM, respectively. The simulated AP parameters and [Ca²⁺]_i dynamics of the current and original HVM models are listed in Table 3, together with corresponding experimental data for comparison. The AP parameters and [Ca²⁺]_i dynamics of the current model appear to be in reasonable agreement with the mean experimental values recently determined for single HVMs, as well as those of the original PB and other HVM models. The values of [Ca²⁺]_rel and [Ca²⁺]_up were 0.41 mM (identical) for the resting state and 0.59–2.68 and 2.84–2.92 mM, respectively, in a steady state during 1 Hz pacing. These values are comparable to the experimental data from rat and rabbit ventricular myocytes (40,41), as well as those in the original PB model, although experimental values for HVMs are unknown.

FIGURE 3.

Simulated dynamics of the model HVM. (A) Steady-state behaviors of the AP, underlying sarcolemmal currents, and [Ca²⁺]_i transient. The model HVM was paced at 1 Hz with 1-ms stimuli of 80 pA/pF. Differential equations (Eqs. 55–64) were numerically solved for 20 min with the initial conditions appropriate to a resting state, which were determined by Eqs. 65–69 with [K⁺]_i fixed at 140 mM. Model cell behavior after the last stimulus (during the last AP) is depicted. (B) Rate dependence of APD, I_Ca,L, and [Ca²⁺]_i transients. The model HVM was paced at 0.5, 1, and 2 Hz with 1-ms stimuli of 80pA/pF. The differential equations were numerically solved for 20 min at each pacing rate; model cell behaviors after the last stimulus are depicted.

TABLE 3.

AP parameters and [Ca²⁺]_i dynamics for single HVMs paced at 1 Hz: model-generated values and experimentally observed values

	[Ca2+]o (mM)	[K+]o (mM)	[Na+]i* (mM)	RP (mV)	Vmax (V/s)	APD90 (ms)	[Ca2+]i,r† (nM)	Δ[Ca2+]i (nM)
Model values	2.0	4.0	10	−91.2	385	357	200	900
Priebe-Beuckelmann (15)‡	2.0	4.0	10	−90.2	386	357	400	0
Bernus et al. (18)	2.0	4.0	10	−90.4	369	333	119	784
Sachse et al. (39)	2.0	5.4	>11.5	−87.3	288	276	70	930
Ten Tusscher et al. (16)	2.0	4.0	9.80	−90.7	350	322	68	797
Iyer et al. (17)	2.0	5.4	9.18	−84.9	411	338	169	792
Current (modified) model
Experimental values
Peeters et al. (90)	1.2	4.0		−84 ± 6		381 ± 94
Li et al. (24)	1.0	5.4	10	−83 ± 3		336 ± 16
Li et al. (42)	2.0	5.4	10	−82 ± 2		298 ± 17
Péréon et al. (91), epicardium	2.7	4.0		−86 ± 1	196 ± 20	324 ± 19
Péréon et al. (91), midmyocardium	2.7	4.0		−86 ± 1	446 ± 46	432 ± 19
Piacentino et al. (92)	1.0	5.4	12.5				153 ± 20	804 ± 197

^*The steady-state mean [Na⁺]_i values during 1 Hz pacing are shown for the TNNP (16), Iyer et al. (17), and the current model; the resting state or fixed value is shown for others. The experimental values were for the perforated- or ruptured-patch recording. A [Na⁺]_i value was unknown (not shown) when the conventional microelectrode method was used.

^†Minimum [Ca²⁺]_i values during the diastolic phase, i.e., [Ca²⁺]_i values at the end of phase 4.

^‡Data for AP parameters are from Table 3 of Bernus et al. (18). The values of [Ca²⁺]_i,r (200) and Δ[Ca²⁺]_i (900) are only approximations from the original figures.

Abbreviations: RP, resting potential; V_max, maximum upstroke velocity.

Rate dependence of APD, I_Ca,L, [Ca²⁺]_i transients, and [Na⁺]_i

We also tested the rate dependence of APD (dynamic restitution), as well as that of the I_Ca,L waveform, [Ca²⁺]_i transients and [Na⁺]_i (Fig. 3 B). The steady-state values of APD₉₀ at 0.5, 1, and 2 Hz were 369, 338, and 298 ms, respectively, compatible with the averaged experimental values (23,42). I_Ca,L attenuated with increasing the pacing rate as observed in the AP clamp experiment of Li et al. (23). The values of [Na⁺]_i during stimuli at 0 (resting state), 0.25, 0.5, 1, and 2 Hz averaged 6.14, 7.47, 8.26, 9.22, and 9.57 mM, respectively, comparable to experimental data (43,44).

The peak [Ca²⁺]_i transient predicted by the current model was a little smaller at 2 Hz than at 1 Hz. In most experiments, however, the peak [Ca²⁺]_i transient and/or developed tension increased as the pacing rate increased up to 2.5 Hz (45–47). This inconsistency may result from the lack of intracellular modulating factors such as those involved in the rate-dependent potentiation of I_Ca,L (48,49). Alternatively, the kinetic formulation of I_Ca,L and/or SR Ca²⁺ handling may be inappropriate. We found that the use of the τ_fL formula from the ten Tusscher et al. model (16) led to the successful reproduction of the rate-dependent increase in the peak [Ca²⁺]_i transient. Nevertheless, their τ_fL formula was not used, because it appeared not to fit the experimental data as shown in Fig. 1 and because a very large I_Ks (>8 times larger than the experimental values) was required to counteract the large I_Ca,L during phase 2 (16). In the preliminary study, BP dynamics or bifurcation structures of the HVM model were not essentially altered by the use of different formulas for I_Ca,L (τ_fL) or the change in the rate dependence of [Ca²⁺]_i transients.

Stability and bifurcation analyses

Constructing bifurcation diagrams

We examined how the stability and dynamics of the model cell alter with changes in bifurcation parameters and constructed bifurcation diagrams for one or two parameters. Bifurcation parameters chosen in this study were the maximum conductance of the ionic channels (g_K1, g_Ca,L, g_Kr, g_Ks) and amplitude of I_NaCa or I_bias; the maximum conductance and I_NaCa amplitude are expressed as normalized values, i.e., ratios to the control values.

In the HVM model with the fixed [K⁺]_i, 14 state variables define a 14-dimensional state point in the 14-dimensional state space of the system. We calculated EPs and periodic orbits in the state space. An EP was determined as a point at which the vector field vanishes (i.e., f(x) = 0); steady-state values of the state variables were calculated by Eqs. 65–69 (see Appendix 2). Asymptotic stability of the EP was also determined by computing 14 eigenvalues of a 14 × 14 Jacobian matrix derived from the linearization of the nonlinear system around the EP (for more details, see Vinet and Roberge (7)). Periodic orbits were located with the MATLAB ODE solvers. When spontaneous oscillation (BP activity) appeared, the AP amplitude (APA) as a voltage difference between the maximum diastolic potential (MDP) and peak overshoot potential (POP), as well as the cycle length (CL), was determined for each calculation of a cycle. Numerical integration was continued until the differences in both APA and CL between the newly calculated cycle and the preceding one became <1 × 10⁻³ of the preceding APA and CL values. Potential extrema (MDP, POP) and CL of the steady-state oscillation were plotted against bifurcation parameters. When periodic behavior was irregular or unstable, model dynamics were computed for 60 s; all potential extrema and CL values were then plotted in bifurcation diagrams.

Codimension one and two bifurcations to occur in the model system were explored by constructing bifurcation diagrams with one and two parameters, respectively (10,11). For construction of one-parameter bifurcation diagrams in which values of a state variable at EPs or extrema of periodic orbits are shown as a function of one bifurcation parameter, a bifurcation parameter was systematically changed while keeping all other parameters at their standard values. The membrane potential (V) at EPs (steady-state branches) and local potential extrema of periodic orbits (periodic branches) were determined and plotted for each value of the bifurcation parameter. The saddle-node bifurcation point at which two EPs coalesce and disappear was determined as a point at which the steady-state current-voltage (I/V) curve and zero-current axis come in touch with each other. The Hopf bifurcation point at which the stability of an EP reverses was also detected by the stability analysis as described above. For construction of two-parameter bifurcation diagrams in which codimension one bifurcation points are plotted in a parameter plane, the secondary parameter was systematically changed with the primary parameter fixed at various different values. The path of saddle-node and Hopf bifurcation points was traced in the parameter plane; i.e., bifurcation values for the secondary parameter were plotted as a function of the primary parameter.

Definition and evaluation of structural stability for the BP system

We also evaluated the structural stability of the BP system, which is defined as the robustness of pacemaker activity to various interventions or modifications that may cause a bifurcation to quiescence or irregular dynamics (11). Interventions or modifications leading to quiescence or irregular dynamics include injections of I_bias, electrotonic loads of normal HVMs, current leakage via myocardial injury, and intrinsic changes in channel conductance or gating kinetics. In this study, the structural stability of the BP system was tested for hyperpolarizing and depolarizing loads by exploring bifurcation structures during applications of I_bias.

The way of evaluating the structural stability to I_bias is essentially the same as in our previous study for the SA node pacemaker (11). Changes in V₀ and its stability with I_bias applications were depicted as the I_bias-V₀ curve (for more details, see Fig. 1 of Kurata et al. (11)). There are one or two Hopf bifurcation points and two saddle-node bifurcation points corresponding to the current exrema in the I_bias-V₀ curve. In the unstable I_bias region between two Hopf (or a Hopf and saddle-node) bifurcation points, the system has an unstable EP only, usually exhibiting stable limit cycles without annihilation (6,8). When the system removes to the stable I_bias region, it would come to rest at the stable EP via gradual decline of limit cycles, annihilation, or irregular dynamics, as reported by Guevara and Jongsma (8). Note that system A is considered structurally more stable than system B when the amplitude of I_bias required for stabilizing an EP or causing a bifurcation to quiescence is greater in system A than in system B (11). Thus, the larger the unstable I_bias range over which limit cycles continue is, the more structurally stable the system is.

The Hopf and saddle-node bifurcation points, as well as the control V₀ at I_bias = 0, in the I_bias-V₀ curve were determined as functions of bifurcation parameters and plotted on both the potential and current coordinates, as in previous studies (7,11). Exploring how the unstable V₀ and I_bias regions change with decreasing or increasing the sarcolemmal currents would enable us to determine the contribution of each current to the structural stability of the BP system to hyperpolarizing or depolarizing loads, as well as to EP instability itself, which is evaluated by positive real parts of eigenvalues of Jacobian matrices (see Fig. 4 of Kurata et al. (11)).

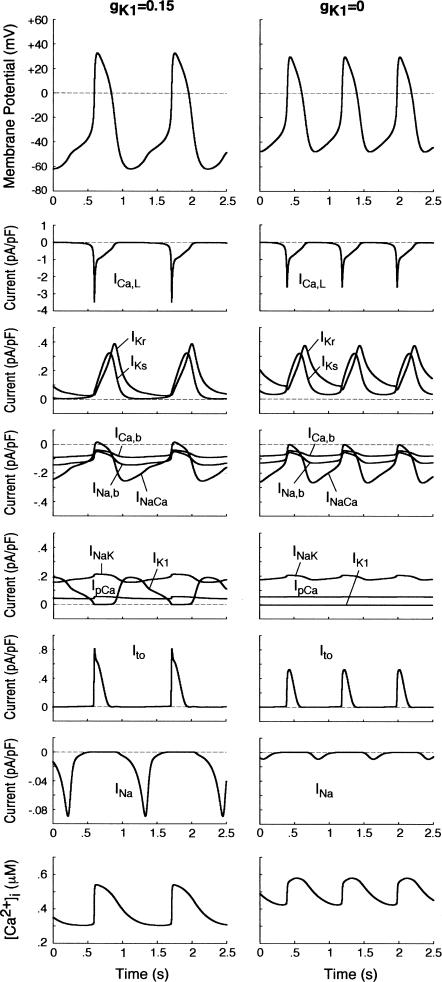
FIGURE 4.

Simulated steady-state BP activities (spontaneous APs, ionic currents, and [Ca²⁺]_i dynamics) in the model HVM at g_K1 = 0.15 (left) and 0 (right). Differential equations (Eqs. 55–63) were numerically solved for 20 min at each g_K1 with initial conditions appropriate to an EP and a 1-ms stimulus of 1 pA/pF for triggering an AP; model cell behaviors during the last 2.5 s starting from MDP are depicted. Note the differences in the ordinate scales for individual currents.

Definitions of terms specific to nonlinear dynamics and bifurcation theory

Autonomous system

An nth-order “autonomous” continuous-time dynamical system is defined by the state equation dx/dt = f(x), where the vector field f, a smooth function of the state variable x = x(t), does not depend on time, but depends only on the state variable x (13).

Nonautonomous system

An nth-order “nonautonomous” continuous-time dynamical system is defined by the state equation dx/dt = f(x, t), where the vector field f depends on time, i.e., explicitly contains time t (13).

EP

A time-independent steady-state point at which the vector field vanishes (i.e., dx/dt = 0) in the state space of an autonomous system, constructing the steady-state branch in one-parameter bifurcation diagrams. This state point corresponds to the zero-current crossing in the steady-state I/V curve, i.e., a quiescent state of a cell if it is stable.

Periodic orbit

A closed trajectory in the state space of a system, constructing the periodic branch in one-parameter bifurcation diagrams.

Limit cycle

A periodic limit set onto which a trajectory is asymptotically attracted in an autonomous system. A stable limit cycle corresponds to an oscillatory state, i.e., pacemaker activity, of a cell.

Bifurcation

A qualitative change in a solution of differential equations caused by altering parameters, e.g., a change in the number of EPs or periodic orbits, a change in the stability of an EP or periodic orbit, and a transition from a periodic to quiescent state. Bifurcation phenomena we can see in cardiac myocytes include a generation or cessation of pacemaker activity and occurrence of irregular dynamics such as skipped-beat runs and early afterdepolarizations.

Hopf bifurcation

This is a bifurcation at which the stability of an EP reverses with emergence or disappearance of a limit cycle, occurring when eigenvalues of a Jacobian matrix for the EP have a single complex conjugate pair and its real part reverses the sign through zero.

Saddle-node bifurcation

This is a bifurcation at which two EPs (steady-state branches) or two periodic solutions (periodic branches) emerge or disappear. The saddle-node bifurcation of EPs occurs when one of eigenvalues of a Jacobian matrix is zero.

Codimension

The codimension of a bifurcation is the minimum dimension of the parameter space in which the bifurcation may occur in a persistent way (12,50). In other words, the codimension is the number of independent conditions determining the bifurcation (14). A bifurcation with codimension one is a point in one-parameter bifurcation diagrams such as Fig. 6 or a line in two-parameter bifurcation diagrams such as Fig. 7, whereas a bifurcation with codimension two is a point in the two-parameter space.

FIGURE 6.

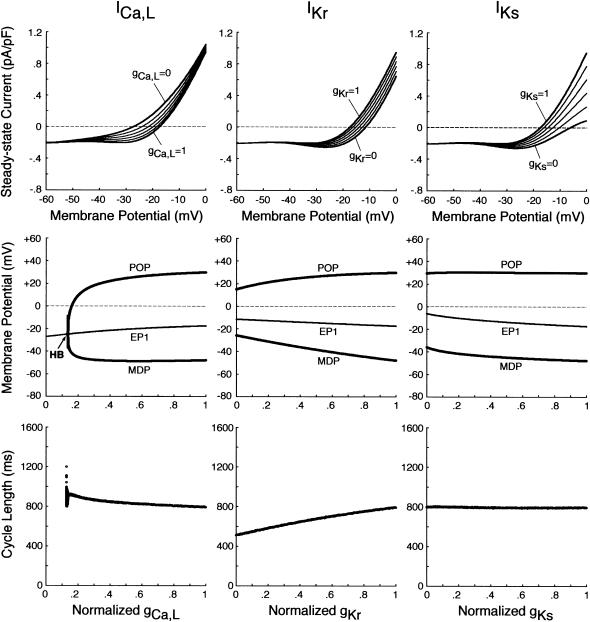
EP stability and BP dynamics of the I_K1-removed system during inhibition of I_Ca,L, I_Kr, or I_Ks. (Top) Steady-state I/V relations for g_Ca,L = 0 − 1 (left), g_Kr = 0 − 1 (middle), and g_Ks = 0 − 1 (right), depicted at an interval of 0.2. (Middle, bottom) Bifurcation diagrams with the steady-state (EP1) and stable periodic (MDP, POP) branches (middle), as well as CL (bottom), are shown as functions of g_Ca,L, g_Kr, or g_Ks, which was reduced at an interval of 0.001. The differential equations were numerically solved for 2–3 min at each conductance value. A Hopf bifurcation occurred at g_Ca,L = 0.134 (labeled HB), with the loci of MDP and POP converging at the bifurcation point.

FIGURE 7.

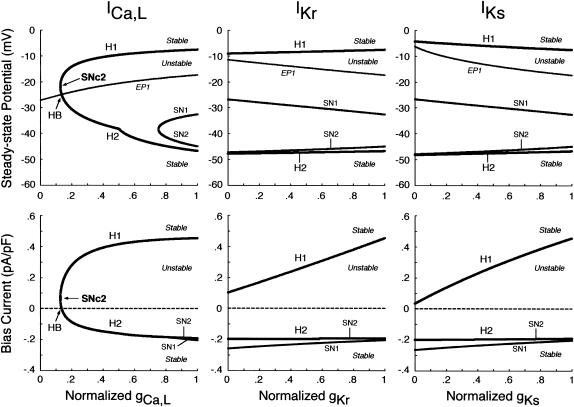
Changes in the unstable regions of the I_bias-V₀ curve during inhibition of I_Ca,L, I_Kr, or I_Ks. Displacements of Hopf (H1, H2) and saddle-node (SN1, SN2) bifurcation points in the I_bias-V₀ curve with decreasing g_Ca,L, g_Kr, or g_Ks at an interval of 0.001 are shown for the I_K1-removed BP system. Values of V₀ and I_bias at the bifurcation points were plotted on the potential (top) and current (bottom) coordinates, respectively, as functions of the conductance. The path of the control V₀ at I_bias = 0 (i.e., EP1 in Fig. 6) is also shown on the potential coordinates, intersecting the locus of H2 at g_Ca,L = 0.134 (labeled HB). Note that the unstable region exists between H1 and H2 (or H1 and SN2), where spontaneous oscillations occur. A codimension two saddle-node bifurcation at which the loci of H1 and H2 merge together, i.e., the unstable region disappears occurred at g_Ca,L = 0.126 (labeled SNc2).

RESULTS

BP generation in I_K1-downregulated HVM

BP activity appears in model HVM during I_K1 suppression

We first examined whether I_K1 downregulation leads to BP generation in the model HVM by decreasing g_K1 at an interval of 0.01 (1%). Spontaneous oscillations (BP activity) abruptly appeared when g_K1 was reduced to 0.15 (15%). Fig. 4 shows the simulated BP activity of the I_K1-downregulated HVM with g_K1 of 0.15 or 0, depicting the membrane potential oscillations, underlying sarcolemmal currents, and [Ca²⁺]_i transients in steady state. The values of MDP, POP, APA, CL, and maximum upstroke velocity were determined for the BP oscillations at each g_K1 value. The simulated AP parameters are listed in Table 4, together with the data from the guinea pig ventricle (3) and rabbit SA node (51) models, as well as from real BP systems (1,52), for comparison. The average [Na⁺]_i during the BP oscillations at g_K1 of 0.15 and 0 were 6.55 and 6.42 mM, respectively. Decreasing g_K1 caused the decrease of APA with depolarization of MDP, decrease of CL, increase of [Ca²⁺]_i, and decrease of [Na⁺]_i. Consistent with the result from the guinea pig ventricular model (3), I_NaCa was the dominant inward current during phase 4 depolarization in the HVM pacemaking. In contrast, I_Ca,L was very small during the early phase of the depolarization, although predominantly contributing to phase 0 upstroke. I_Na was also very small due to the voltage-dependent inactivation.

TABLE 4.

AP parameters for pacemaker systems: Model-generated values and experimental values

	Normalized gK1	MDP (mV)	POP (mV)	APA (mV)	CL (ms)	Vmax (V × s−1)
Model values
Silva and Rudy (3)*	0.19	−67.3			594	15
	0				366
This study	0.15	−61.9	+32.7	94.7	1117	3.2
	0.10	−54.3	+31.6	86.0	938	2.8
	0	−47.9	+29.8	77.7	795	2.3
Kurata et al. (51)†	0	−58.6	+16.6	75.2	308	6.4
Experimental values
Miake et al. (1)*	0.20	−60.7			600
Plotnikov et al. (52)‡					1091

^*Data from the model and real guinea pig ventricular myocytes.

^†Primary pacemaker model for the rabbit SA node.

^‡Data for Purkinje myocytes expressing I_h (HCN2) in the canine left ventricle.

Ionic basis of phase 4 depolarization in simulated BP activity

Before investigating the dynamical mechanisms of BP generation via bifurcation analyses of the HVM model, we examined the ionic basis of phase 4 depolarization of the BP activity. The contributions of I_Kr and I_Ks deactivation, as well as individual inward currents (I_Ca,L, I_Na, I_NaCa, I_Na,b, I_Ca,b), to the pacemaker depolarization were assessed by the conventional freezing and blocking methods (53–55). Phase 4 depolarization of the I_K1-reduced BP system disappeared on clamping I_Kr deactivation (gating variable p_a) at the time of MDP, but not on clamping I_Ks deactivation (gating variable n). Thus, the g_Kr-decay theory for the natural SA node pacemaker (53–55) appears to be applicable to the HVM pacemaker as well. Removal of I_Ca,L at the time of MDP little altered the initial phase of pacemaker depolarization, although reducing the rate of the later phase depolarization with cessation of BP activity. Eliminating I_Na did not significantly affect BP oscillations. Furthermore, in the I_K1-removed system, eliminating I_NaCa (the most dominant pacemaker current) at the MDP abolished phase 4 depolarization, leading to cessation of BP activity, whereas the removal of I_Na,b (the second dominant pacemaker current) or I_Ca,b only reduced the depolarization rate.

Bifurcation structure of HVM system during I_K1 suppression

BP activity abruptly appears around unstable EP via saddle-node bifurcation

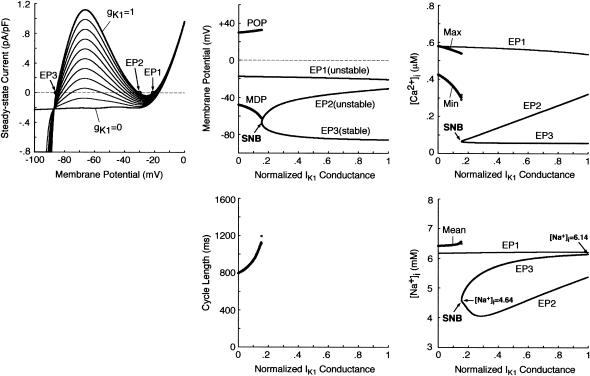
To elucidate the dynamical mechanisms of BP generation, we explored EP stability, dynamics, and bifurcation structures of the HVM system during I_K1 suppression by constructing bifurcation diagrams for g_K1. As shown in Fig. 5, the zero-current potential in the steady-state I/V curve, as well as steady-state [Ca²⁺]_i and [Na⁺]_i, was plotted as a function of g_K1; when BP activity appeared, AP parameters (MDP, POP, CL), extrema of [Ca²⁺]_i, and average [Na⁺]_i were also plotted. There are three EPs corresponding to the zero-current crossings of the I/V curve in the state space of the system at g_K1 = 1 (denoted as EP1, EP2, and EP3). The stability analysis revealed that EP1 with the most depolarized potential as well as EP2 is unstable, whereas EP3 with the most negative potential corresponding to the resting state is stable. The zero-current potential at EP3 positively shifted with decreasing g_K1; the stable EP3 (and EP2) disappeared via a saddle-node bifurcation when g_K1 reduced to 0.154. After the bifurcation, the system has only one EP at depolarized potentials (EP1), which is always unstable, not stabilized during g_K1 decreases. Limit cycles (BP oscillations) abruptly emerged around the unstable EP1 on occurrence of the saddle-node bifurcation, with APA and CL gradually decreasing during further reductions in g_K1.

FIGURE 5.

Bifurcation structure of the model HVM during g_K1 decreases. (Left) Steady-state I/V relations for g_K1 = 0 − 1, depicted at an interval of 0.1 with [K⁺]_i fixed at 140 mM. The zero-current crossings, corresponding to EPs, are designated by EP1, EP2, and EP3. (Middle) A bifurcation diagram for g_K1 with the steady-state (EP1–3) and stable periodic (MDP, POP) branches (top), and CL plotted as a function of g_K1 (bottom). EPs were determined by the algebraic equations (Eqs. 65–69). The model cell dynamics were computed by numerically solving the differential equations (Eqs. 55–63) for 10 min at each g_K1, which was reduced at an interval of 0.001, with the initial [Na⁺]_i at g_K1 = 1 set equal to 6.14 mM. The saddle-node bifurcation point at which EP2 and EP3 merge together and disappear is located (labeled SNB at g_K1 = 0.154). (Right) Steady-state [Ca²⁺]_i (top) and [Na⁺]_i (bottom) at EPs as functions of g_K1. The minimum (Min) and maximum (Max) of [Ca²⁺]_i, as well as average [Na⁺]_i, during the BP oscillations are also plotted. Note that the steady-state [Na⁺]_i at EP3 reduces with decreasing g_K1.

Decrease in [Na⁺]_i accelerates BP generation

The steady-state [Na⁺]_i, 6.14 mM in the control resting state (at g_K1 = 1), reduced as g_K1 decreased, reaching 4.64 mM just before the saddle-node bifurcation at g_K1 = 0.154 (see Fig. 5, right bottom). This reduction in [Na⁺]_i during I_K1 suppression was due to the enhancement of Na⁺ efflux via the Na⁺-K⁺ pump, as well as decrease of Na⁺ influx via the Na⁺/Ca²⁺ exchanger and I_Na,b, with resting potential depolarization. To determine how the [Na⁺]_i decrease affects BP generation, we constructed bifurcation diagrams for g_K1 using the reduced system with [Na⁺]_i fixed at the control value of 6.14 mM or critical value of 4.64 mM (data not shown). The critical g_K1 at which BP activity emerges via a saddle-node bifurcation was larger in the system with the reduced [Na⁺]_i of 4.64 mM (0.153) than with the control [Na⁺]_i of 6.14 mM (0.117), suggesting that the [Na⁺]_i reduction facilitates BP generation during I_K1 suppression.

Ionic bases of EP instability and BP generation in I_K1-downregulated HVM

Instability of the EP at depolarized potentials (EP1) appears to be essentially important for BP generation. To elucidate the ionic mechanisms of EP instability and BP generation, therefore, we further explored how modulating individual sarcolemmal currents or [Ca²⁺]_i transients affects EP stability, oscillation dynamics, and bifurcation structures of the BP system. We focused on I_Ca,L, I_K, and I_NaCa, which appear to be essentially important for BP generation.

Influences of blocking I_Ca,L or I_K on stability and dynamics of the BP system

Fig. 6 shows the effects of reducing the maximum conductance of I_Ca,L (g_Ca,L), I_Kr (g_Kr), or I_Ks (g_Ks) on EP stability and BP dynamics of the I_K1-removed system. The zero-current potential (EP1) negatively shifted with decreasing g_Ca,L; the EP became stable via a Hopf bifurcation when g_Ca,L was reduced by 86.6%. During the g_Ca,L decreases, a limit cycle (BP oscillation) gradually contracted in size and finally disappeared at the Hopf bifurcation point. In contrast, a Hopf bifurcation to abolish BP activity did not occur during decreases in g_Kr or g_Ks, although APA significantly reduced with decreasing g_Kr. Spontaneous oscillation continued even when I_Kr or I_Ks was completely blocked, whereas it was abolished by eliminating both I_Kr and I_Ks.

As shown in Fig. 7, we also examined the effects of blocking I_Ca,L, I_Kr, or I_Ks on the unstable V₀ and I_bias regions in the I_bias-V₀ curve for further clarifying the contributions of the individual currents to EP instability and structural stability to depolarizing or hyperpolarizing loads of the BP system. Hopf and saddle-node bifurcation points in the I_bias-V₀ curve determined with decreasing conductance values were plotted on the potential and current coordinates to display how blocking each current shrinks the unstable ranges where BP oscillations occur (for more details, see Theory and Methods). The more prominent shrinkage in the unstable V₀ region is, the greater the contribution of the current to EP instability is; the more prominent shrinkage in the unstable I_bias region is, the greater the contribution to the robustness to depolarizing or hyperpolarizing loads is. The unstable regions, shrinking with decreases in g_Ca,L, disappeared via a codimension two saddle-node bifurcation at a 87.4% reduction of g_Ca,L. Pacemaker activity never appeared in the system with g_Ca,L reduced to less than the saddle-node bifurcation value. In contrast, reducing g_Kr or g_Ks little affected the unstable V₀ range, eigenvalues of Jacobian matrices at V₀ being not significantly altered. The unstable I_bias region shrunk with decreasing g_Kr or g_Ks, though it did not disappear even when I_Kr or I_Ks was completely blocked; the robustness to depolarizing I_bias was attenuated by decreasing g_Kr or g_Ks.

Effects of incorporating various K⁺ currents on stability and automaticity of an I_K-removed system

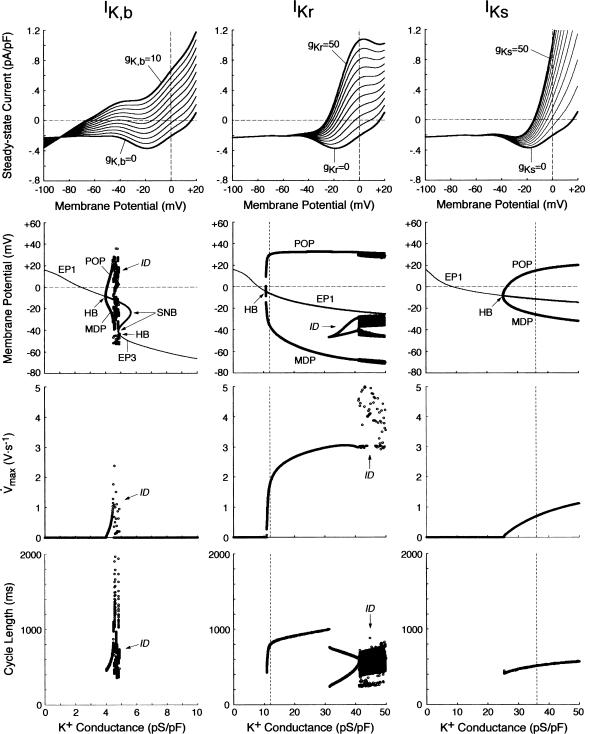
The results shown in Figs. 6 and 7 suggest that I_Kr or I_Ks contributes little to the instability of the EP leading to the generation of spontaneous oscillations. To elucidate the roles of I_Kr and I_Ks in the HVM pacemaking, we tested how the stability and dynamics of the reduced BP system not including either I_Kr or I_Ks are affected by incorporating different K⁺ currents. Both I_Kr and I_Ks were first removed from the standard I_K1-eliminated BP system, and the background K⁺ current of linear I/V relation (I_K,b) or the original I_Kr or I_Ks (one of the three) was then incorporated. Eliminating both I_Kr and I_Ks abolished BP activity, with the model cell coming to a rest at a stable zero-current potential of +16.15 mV. Fig. 8 shows how EP stability and automaticity of the reduced system change with increasing the K⁺ current conductance up to 10–50 pS/pF. As the K⁺ conductance increased, the zero-current potential was negatively shifted and eventually destabilized via a Hopf bifurcation, with limit cycles emerging at the bifurcation. It should be noted that all the K⁺ currents, including I_K,b, could individually create an unstable EP and induce spontaneous oscillations. However, I_K,b, the effect of which was very similar to the electrotonic influence of the adjacent normal HVM in a coupled-cell system (data not shown), produced the oscillation of relatively small amplitude and low upstroke velocity, as well as unstable CL and irregular dynamics. The I_K,b conductance (g_K,b) range where an EP is unstable and spontaneous oscillations occur was very limited, with further increases in g_K,b leading to quiescence via emergence of a stable EP. In contrast, I_Kr could yield the large amplitude oscillation with relatively high upstroke velocity and stable CL; however, I_Kr caused irregular dynamics at higher g_Kr values (>31.5 pS/pF), whereas I_Ks did not.

FIGURE 8.

Effects of incorporating various K⁺ currents with different kinetics (I_K,b, I_Kr, or I_Ks) on EP stability and dynamics of the I_K-removed model cell (g_K1 = 0). (Top) Steady-state I/V relations for g_K,b = 0–10 pS/pF (left), g_Kr = 0–50 pS/pF (middle), and g_Ks = 0–50 pS/pF (right), depicted at an interval of 1 or 5 pS/pF. (Middle, bottom) Oscillatory behaviors, as well as zero-current potentials and their stability, of the model system, calculated during increases in g_K,b, g_Kr, or g_Ks at an interval of 0.01–0.1 pS/pF. Bifurcation diagrams with the steady-state (EP1–3) and periodic (MDP, POP) branches, as well as Hopf bifurcation (HB) and saddle-node bifurcation (SNB) points, were constructed for g_K,b, g_Kr, or g_Ks (middle). Maximum upstroke velocity (V_max) and CL of the potential oscillations were also plotted against g_K,b, g_Kr, or g_Ks (bottom). The vertical lines for I_Kr and I_Ks represent the standard values of g_Kr (12 pS/pF) and g_Ks (36 pS/pF). The symbol “ID” designates the irregular dynamics.

We further examined how incorporating the K⁺ currents affects the structural stability of the reduced model to depolarizing or hyperpolarizing loads. The unstable regions in the I_bias-V₀ curve were determined for individual K⁺ currents with the conductance increased up to 50 pS/pF (data not shown). Note that the structural stability to hyperpolarizing or depolarizing loads is considered as improved when the unstable I_bias region is enlarged, i.e., when larger I_bias is required to cause a bifurcation to quiescence. The results are summarized as follows: 1), Increasing I_Kr (g_Kr) continuously enlarged the unstable I_bias region, sufficiently improving the structural stability to depolarizing I_bias; 2), I_Ks could also enlarge the unstable I_bias region, but did not improve the structural stability as efficiently as I_Kr; and 3), I_K,b could not enlarge the I_bias region of instability; with increasing g_K,b, the unstable regions shrunk and finally disappeared via a codimension two saddle-node bifurcation. These findings are essentially the same as those reported for the SA node pacemaker (see Fig. 9 of Kurata et al. (11)).

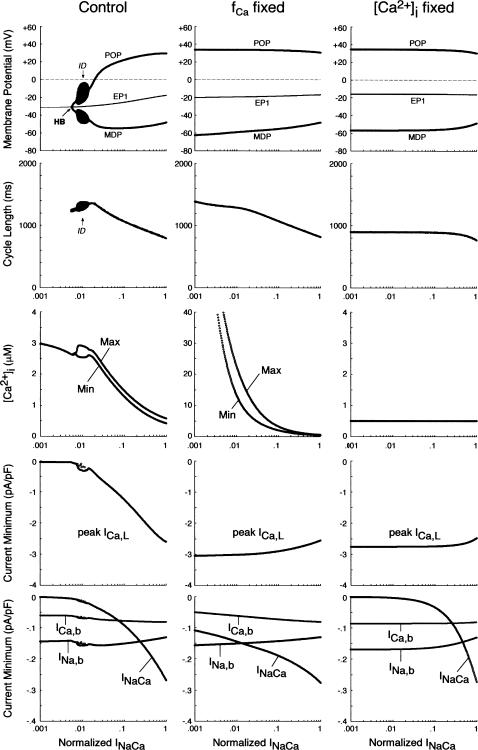
FIGURE 9.

EP stability and BP dynamics of the I_K1-removed system during I_NaCa inhibition, determined for the unmodified system (left) and the modified system in which f_Ca was fixed at 0.412, the value for [Ca²⁺]_i = 0.5 μM (middle), or [Ca²⁺]_i itself was fixed at 0.5 μM (right). The amplitude of I_NaCa as a ratio to the control value was decreased from 1 (control) to 0.001 (0.1%); practically, the log(I_NaCa) value was reduced from 0 (I_NaCa = 1) to −3 (I_NaCa = 1 × 10⁻³) at an interval of 0.01. The zero-current potential (EP1) and BP dynamics (MDP, POP, CL), as well as the minimum (Min) and maximum (Max) of [Ca²⁺]_i and minimum values of the inward currents (I_Ca,L, I_NaCa, I_Na,b, I_Ca,b), are plotted as functions of log(I_NaCa). Note that a Hopf bifurcation to abolish BP activity occurred only in the unmodified system (HB at I_NaCa = 0.0056).

Influences of blocking I_NaCa or [Ca²⁺]_i transients on the stability and dynamics of the BP system

SR Ca²⁺ release, [Ca²⁺]_i transients, and activation of I_NaCa possibly play an important role in the generation and regulation of BP activity; as in the guinea pig ventricular pacemaking (3), I_NaCa was the dominant pacemaker current in the HVM pacemaking (Fig. 4). We therefore assessed the contributions of I_NaCa and [Ca²⁺]_i transients (SR Ca²⁺ release) to the EP instability and oscillation dynamics of the BP system by decreasing I_NaCa and/or clamping [Ca²⁺]_i. As shown in Fig. 9 (left), BP oscillation ceased via a Hopf bifurcation when I_NaCa was reduced by 99.44% in the I_K1-removed system. However, this may be due to the Ca²⁺-dependent inactivation of I_Ca,L after the induction of Ca²⁺-overload conditions, rather than the decrease of I_NaCa itself. Therefore, we further tested the stability and dynamics during I_NaCa inhibition of the modified BP system for which [Ca²⁺]_i or Ca²⁺-dependent I_Ca,L inactivation (f_Ca) was fixed at a control value. In the modified systems, inhibition of I_NaCa caused neither EP stabilization nor BP cessation, with I_Ca,L being not attenuated, although I_NaCa was still the dominant pacemaker current in control (Fig. 9, middle, right). Eliminating [Ca²⁺]_i transients or blocking SR Ca²⁺ release little altered BP dynamics.

We also examined the contributions of I_NaCa or [Ca²⁺]_i dynamics to the EP instability and structural stability to depolarizing or hyperpolarizing loads of the BP system by determining the unstable regions in the I_bias-V₀ curve during decreases in I_NaCa or [Ca²⁺]_i transients. As shown in Fig. 10 (left), inhibition of I_NaCa significantly shrunk the unstable regions, though a codimension two saddle-node bifurcation did not occur. When [Ca²⁺]_i or f_Ca was fixed at the control value, however, the unstable regions did not shrink during I_NaCa reduction (Fig. 10, middle, right). The influences of eliminating [Ca²⁺]_i transients or blocking SR Ca²⁺ release on the unstable regions were very small.

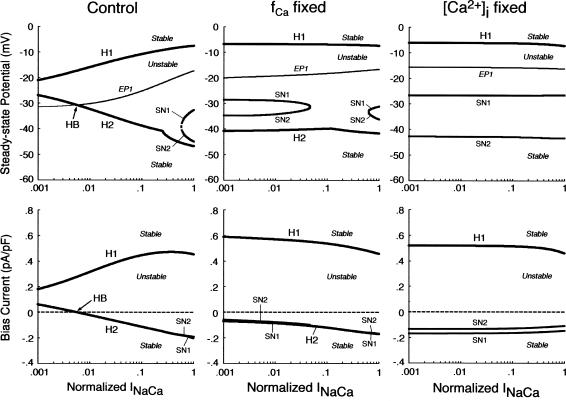
FIGURE 10.

Changes in the unstable regions of the I_bias-V₀ curve during I_NaCa suppression in the I_K1-removed systems. Displacements of the bifurcation points (H1–2, SN1–2), as well as the control V₀ at I_bias = 0 (EP1), in the I_bias-V₀ curve with decreasing I_NaCa are shown for the unmodified system (left) and the modified system with f_Ca fixed at the value for [Ca²⁺]_i = 0.5 μM (middle) or [Ca²⁺]_i itself fixed at 0.5 μM (right). The log(I_NaCa) value was reduced from 0 to −3 at an interval of 0.01. As in Fig. 7, values of V₀ and I_bias at the bifurcation points are plotted on both the potential (top) and current (bottom) coordinates as functions of log(I_NaCa). In the unmodified system, the path of EP1 intersected the locus of H2 at I_NaCa = 0.0056 (labeled HB).

DISCUSSION

Mechanisms of BP generation in I_K1-downregulated HVM

Nonlinear dynamical aspects of BP generation

This study shows that pacemaker activity appears in the I_K1-downregulated HVM system via a saddle-node bifurcation (disappearance of a stable EP) or Hopf bifurcation (destabilization of an EP) and that the instability of an EP at depolarized potentials underlies the stable HVM pacemaking. The term “mechanisms of pacemaker generation” is usually interpreted as meaning how individual sarcolemmal currents drive or contribute to phase 4 depolarization. From the viewpoint of the nonlinear dynamics and bifurcation theory, however, “EP instability” seems to be most important for the generation of robust pacemaking: if the system has a stable EP, it will be quiescent at the stable EP or in a bistable zone where stable steady states and periodic states coexist and thus annihilation occurs (for details on bistability and annihilation, see Landau et al. (6) and Guevara and Jongsma (8)). When considering the pacemaker mechanisms, therefore, one must elucidate the ionic mechanism of EP destabilization, which may be different from that of phase 4 depolarization. In the HVM pacemaker, I_Ca,L is responsible for EP instability, whereas I_NaCa as well as I_Kr deactivation most contributes to phase 4 depolarization. Our study also suggests that the question “which current is dominant during phase 4” is relevant to the ionic mechanism not for EP instability as a requisite to stable pacemaking, but for the regulation of the destabilization rate (Figs. 4, 9, and 10). These viewpoints would be important particularly for engineering of functional BP cells to exhibit robust pacemaking.

It should be noted that the EP with the most depolarized potential (EP1) is always unstable, not stabilized during I_K1 suppression (Fig. 5). The saddle-node bifurcation may also be yielded by increasing inward currents such as I_Na,b or I_Ca,b. Nevertheless, increasing the inward currents would not lead to BP generation, because the positively shifted EP1 becomes stable via a Hopf bifurcation, resulting in an arrest at depolarized potentials. Another approach to create a BP cell may be overexpression of the hyperpolarization-activated current (I_h), which has been reported to induce BP activity in canine atrial or Purkinje myocytes (52,56). However, incorporating I_h did not cause a saddle-node bifurcation nor BP generation in the HVM model with normal I_K1, although accelerating BP generation during I_K1 suppression via shifting the saddle-node bifurcation point toward higher g_K1 values (data not shown). This discrepancy is at least in part due to the difference in I_K1 density, which is much higher in ventricular cells than in atrial or Purkinje cells (56,57). These findings suggest that I_K1 downregulation, ensuring both the occurrence of a saddle-node bifurcation and instability of EP1, is necessary and sufficient for constructing BP cells from HVMs.

Roles of individual sarcolemmal currents in HVM pacemaking

I_Ca,L

I_Ca,L contributes little to the initial phase of pacemaker depolarization, although it contributes significantly to the terminal phase of the depolarization as well as to phase 0 upstroke (Fig. 4). Nevertheless, I_Ca,L appears to be indispensable for the HVM pacemaking in that it is responsible for EP instability as a requisite to stable pacemaking (Figs. 7 and 8). The Ca²⁺ channel responsible for I_Ca,L in the current model and original ventricular or SA node models corresponds to the high voltage-activated subtype (C-LTCC) formed by an α_1C subunit (Ca_v1.2), which is a major component in the heart of mouse or other species (58–60). However, the low voltage-activated subtype (D-LTCC), the α-subunit of which is α_1D (Ca_v1.3), activating at the pacemaker potential range, has recently been reported to contribute to phase 4 depolarization in the mouse SA node (61–63) and possibly in the rabbit SA node as well (64). Nevertheless, it is unlikely that D-LTCC plays an important role in the ventricular pacemaking, because Ca_v1.3 m-RNA is not present in the mouse or human ventricle (58,63).

I_K

In contrast to I_Ca,L, I_Kr or I_Ks was suggested to be inessential for EP destabilization leading to spontaneous activity, because 1), eliminating I_Kr and/or I_Ks did not significantly attenuate the EP instability as evaluated by positive real parts of eigenvalues of Jacobian matrices, little shrinking the unstable V₀ region in the I_bias-V₀ curve (Fig. 7); and 2), the I_K-removed BP system, quiescent in control (at g_K = 0), resumed automaticity when an EP was destabilized by incorporation of I_K,b (Fig. 8) or electrotonic influences of adjacent normal HVMs (data not shown). Although I_Kr or I_Ks is not necessarily required for the generation of spontaneous oscillations, the K⁺ currents appear to play pivotal roles in the modulation of BP dynamics. As suggested by Fig. 8, I_K would be necessary for the BP generation with large amplitude, high upstroke velocity, and stable frequency. Decreasing I_Kr or I_Ks shrunk the unstable I_bias region in the I_bias-V₀ curve, i.e., it attenuated the structural stability to depolarizing loads of the BP system (Fig. 7). The K⁺ conductance region, as well as the I_bias region, where EPs are unstable and thus spontaneous oscillations occur, was much larger for the I_K-incorporated system than for the I_K,b-incorporated system (Fig. 8). Therefore, I_K may also contribute to the robust maintenance of BP activity, i.e., prevention of a bifurcation to quiescence.

I_NaCa

As in the guinea pig ventricular pacemaking (3), I_NaCa was suggested to be the dominant pacemaker current in the HVM pacemaking, with its removal leading to cessation of BP activity via a Hopf bifurcation (Figs. 4 and 9). However, the stabilization of an EP and cessation of BP activity during I_NaCa decreases appear to be a consequence of the Ca²⁺-dependent inactivation of I_Ca,L, rather than the I_NaCa decrease itself: when f_Ca was fixed or when [Ca²⁺]_i was kept low by rapid Ca²⁺ buffering or tentative electroneutral Ca²⁺ transport, BP activity did not cease, being quite stable, during I_NaCa suppression (Fig. 9). It is also suggested that I_NaCa is not required for the destabilization of an EP or generation of spontaneous oscillations (Fig. 10). Thus, the major role of I_NaCa would be the maintenance of relatively low [Ca²⁺]_i to prevent Ca²⁺-dependent inactivation of I_Ca,L as well as cellular remodeling under Ca²⁺-overload conditions, rather than the contribution to phase 4 depolarization as a pacemaker current. In all existing heart models, the Na⁺/Ca²⁺ exchanger is assumed to mediate only the current I_NaCa via the 3Na⁺:1Ca²⁺ transport mode. However, it is also reported to carry a significant part of I_Na,b via the Na⁺-conducting mode (65,66). The background inward current I_Na,b is the second dominant pacemaker current in the HVM model and the most dominant pacemaker current in most SA node models (51). Thus, the Na⁺/Ca²⁺ exchanger may also contribute to pacemaker depolarization by generating I_Na,b.

Comparisons of HVM pacemaker with other pacemaker systems

Conditions for BP generation and BP dynamics

Real and model guinea pig ventricular myocytes exhibited spontaneous activities on 80–81% suppression of I_K1 channels (1,3). In the HVM model, BP activity appeared when I_K1 was suppressed by 84.6%, which is close to the critical values for BP generation in the guinea pig ventricle. The BP rates of the I_K1-reduced HVM (54–75 bpm), lower than those of the real or model guinea pig ventricular myocytes (100–164 bpm), appear to be in reasonable agreement with the mean human heart rate under normal conditions (refer to Table 4).

Pacemaker mechanisms

It has been reported for the rabbit SA node primary pacemaker that 1), I_Ca,L is, but I_K is not, responsible for EP instability leading to spontaneous oscillations (11); 2), I_Kr contributes to the robust pacemaking with large amplitude and stable frequency (11); 3), I_Kr deactivation is crucial for phase 4 depolarization (53–55); and 4), I_Na,b and I_NaCa are the predominant inward currents during phase 4 depolarization, with I_Ca,L contributing only to the terminal phase of the depolarization as well as to phase 0 upstroke (51,55). These findings for the SA node pacemaker are in good agreement with our conclusions for the HVM pacemaker. As mentioned in the preceding section, the low voltage-activated I_Ca,L mediated by D-LTCC may serve as a pacemaker current in the SA node pacemaking, but not in the ventricular pacemaking (61–63). However, the knockout of D-LTCC did not lead to sinus arrest, but led only to sinus bradycardia and arrhythmias (61–63), whereas the deletion of C-LTCC caused fetal death (60). These findings and our study suggest that the roles of C-LTCC and D-LTCC in pacemaking are different: C-LTCC would contribute mainly to EP destabilization as a requisite for basal pacemaking, whereas D-LTCC is not necessary for basal pacemaking, rather playing a pivotal role in pacemaker regulation by contributing mainly to phase 4 depolarization. Thus, the dynamical mechanism of the HVM pacemaking appears to be essentially the same as that of the basal SA node pacemaking. This consistency may reflect that cardiac myocytes, both pacemaker and nonpacemaker cells, in different regions or species share the common mechanism for the generation of basal pacemaking. Nevertheless, previous reports suggest the regional difference in pacemaker mechanisms. Blocking I_Ca,L abolished spontaneous activity in central SA node tissues, but not in peripheral tissues (67,68); in the peripheral SA node, I_Na might contribute to EP destabilization and pacemaker generation. I_h is also suggested to play a predominant role in the subsidiary pacemaker mechanism (69,70). Bifurcation analyses of mathematical models for various regions or species are required for further investigations of the regional difference in pacemaker mechanisms.

Because there is transmural heterogeneity of electrophysiological properties of ventricular myocytes (16,18,71), one may also expect the transmural difference in BP mechanisms. Electrophysiological differences between epicardial, midmyocardial, and endocardial cells are attributable mainly to the differences in density and kinetics of I_to or I_Ks, and possibly I_NaCa, as summarized by ten Tusscher et al. (16). Reducing g_to only increased POP without affecting other AP parameters or EP stability (data not shown). Changing g_Ks or I_NaCa exerted only minor effects on stability and dynamics of the BP system (Figs. 6, 7, 9, and 10). These results suggest that bifurcation structures of epicardial, midmyocardial, and endocardial cells are essentially the same; thus we do not expect the transmural difference in BP mechanisms.

Responsiveness to β-adrenergic stimulation

As suggested by Silva and Rudy (3), a potential advantage of the BP over the electronic pacemaker is responsiveness to β-adrenergic stimulation (ßAS). In the guinea pig ventricular model, BP responsiveness to ßAS was very limited (3). We did not show the data on this issue, which is very important but out of the aim of this study. Nevertheless, we also found in the simulations according to the method of Silva and Rudy (3) that the HVM pacemaker did not exhibit a significant rate increase in response to ßAS, suggesting that the ventricular pacemaker is less sensitive to ßAS than the SA node pacemaker. The low sensitivity to ßAS of the ventricular pacemaker may be at least in part due to the lack or low density of the regulatory inward currents, such as the low voltage-activated I_Ca,L, sustained-inward current (I_st) and I_h, which are known to be enhanced by ßAS and abundant in SA node primary pacemaker cells (11,51,61–63,72–74).

Significance of applying bifurcation theory to BP system analysis and engineering

In this study, we used stability and bifurcation analyses to investigate the mechanisms of BP generation. As mentioned in the Introduction, the nonlinear dynamical approach is known to be useful for general understanding and systematic descriptions of the mechanisms of normal and abnormal pacemaker activities (4–11), as well as reentrant arrhythmias or conduction block (75–78). This study demonstrates that bifurcation theory also provides a reliable way of elucidating the roles of individual currents in pacemaker generation of I_K1-downregulated ventricular myocytes.

Our work suggests that exploring bifurcation structures of model cells can reveal the conditions and ways for oscillatory behavior to emerge or disappear in cardiac myocytes and possibly allow us to accurately predict and properly control the dynamics of real cells. Thus, the mathematical approach would also be applicable to engineering BP cells from native myocytes in vivo (1,52,56) or from human embryonic stem cells (hESCs) ex vivo (79–81) for the gene or cell therapy of bradyarrhythmias usually requiring implantation of an electronic pacemaker (for review, see Gepstein et al. (80)). Bifurcation analyses of model systems may lead to appropriate design of a functional BP, like the SA node, as a therapeutic alternative to the electronic pacemaker. Further investigations based on the bifurcation theory will possibly find out the most efficient ways to 1), create BP cells, 2), control BP dynamics, 3), improve the robustness of BP activity as well as BP sensitivity to ßAS, and 4), improve BP ability to drive surrounding nonpacemaker tissues via modulating the existing currents or newly expressing the regulatory inward currents.

Limitations and perspectives of the study

Incompleteness of the HVM model

One limitation of this study is the incompleteness of the HVM model due to the lack of experimental data from HVMs. The formulas for I_Ca,L, I_Kr, SR Ca²⁺ release, and others were partly adopted from human atrial or animal heart models (see also Priebe and Beuckelmann (15)). In addition, for simplicity, the current model does not incorporate detailed descriptions of intracellular Ca²⁺ dynamics, SR Ca²⁺ handling, or the intracellular modulating factors such as cAMP and protein kinases, as in recently developed models (73,82–84). More elaborate HVM models have recently been developed (16,17); however, these models with the larger number of equations and/or very complex formulas are less suitable for bifurcation analyses than the current model (for more details, see Theory and Methods). We believe that the current model is valuable and highly appropriate for exploring the essential mechanisms of BP generation. Nevertheless, further sophisticated but simplified HVM models with refinements of the formulas based on the data from HVMs, as well as incorporating more detailed descriptions of the intracellular Ca²⁺ handling and modulating factors, would have to be developed for future investigations.

The recently developed HVM models (16,17) are based mainly on the data from expressed channels whose electrophysiological properties may be different from those of native channels in HVMs. As suggested recently (79,81,85), hESCs would provide an unlimited and renewable source of human cardiomyocytes for basic research as well as implantation therapies. Thus, cell system engineering to establish hESC-derived experimental models of HVMs may facilitate the development of more sophisticated HVM models.

Lack of experimental evidence

The conclusions in this study are of course the predictions from the model system; thus, they must be verified and supported by experimental works using real HVMs. However, there is no experimental study on BP activity in genetically modified HVMs. The hESC-derived experimental models of ventricular or nodal cells may also be useful for future investigations of BP mechanisms and thus verification of the model predictions. We hope that this study provides a stimulus to further experimentation on this issue.

Requirement of multicellular models involving electrotonic interactions

As suggested by Silva and Rudy (3), it should be recognized that the engineering of single BP cells is only a first step toward creation of the functional BP. Pacemaker mechanisms of the intact SA node are reported to involve electrotonic interactions with the atrium (86–88). BP cells in vivo would also suffer hyperpolarizing loads of adjacent nonpacemaker cells, which may abolish BP activity. Thus, BP ability to drive the heart would depend on its architecture to facilitate optimization of the electrical loading by the surrounding atrial or ventricular tissue (86,87). Recently, hESC-derived pacemaking cardiomyocytes implanted into the guinea pig ventricle in vivo have been found to integrate with the host tissue via forming gap junctions and drive the quiescent ventricle with nearly the same rate as in the isolated state (81). This suggested that the engrafted BP could efficiently interact with the surrounding nonpacemaker tissue to minimize the electrotonic load. However, the hESC-derived pacemaker may not be as robust to excessive hyperpolarizing loads as the native SA node pacemaker. Multicellular models such as for the SA node tissue (68,86,89) are required for further investigating the roles of electrotonic interactions in BP mechanisms in vivo and how to create a real functional BP with robust pacemaking.

APPENDIX 1: MODEL EQUATIONS

The mathematical expressions used in this study are given below. Units are mV, pA, nS, ms, nF, mM, and L. The temperature assumed for the model is 37°C. The symbols used and their definitions are the same as those in our rabbit SA node model (51) or the original PB model (15). The stimulus current I_stim in Eqs. 55 and 64 was assumed to carry K⁺ ions into the cell for charge conservation during paced AP simulations, being set equal to zero for BP simulations. Standard parameter values and initial conditions for computations are given in Tables 5 and 6, respectively.

TABLE 5.

Standard parameter values

Parameters	Values	Parameters	Values
F	96485 (C/mol)	IpCamax	0.11 (pA/pF)
R	8.3144 (J/mol/K)	KmCap	0.0005 (mM)
T	310.15 (K)	Prel	50 (ms−1)
Cm	153.4 (pF)	Pup	0.00221 (mM/ms)
Vcell	38 (pL)	Pleak	0.00026 (ms−1)
Vi	25.84 (pL)	Kup	0.00025 (mM)
Vrel	0.182 (pL)	τtr	180 (ms)
Vup	2.098 (pL)	[CM]tot	0.05 (mM)
[Na+]o	140 (mM)	[CQ]tot	10 (mM)
[K+]o	5.4 (mM)	[TC]tot	0.07 (mM)
[Ca2+]o	2.0 (mM)	KdCM	0.00238 (mM)
gCa,L	0.2496 (nS/pF)	KdCQ	0.8 (mM)
gKr	0.012 (nS/pF)	KdTC	0.0005 (mM)
gKs	0.036 (nS/pF)	kfTC	400 (mM−1 × ms−1)
gto	0.3 or 0.4 (nS/pF)	kbTC	0.2 (ms−1)
gNa	7.8 (nS/pF)
gK1	3.9 (nS/pF)
gNa,b	0.001 (nS/pF)
gCa,b	0.00051 (nS/pF)
ECa,L	+52.8 (mV)
KmfCa	0.00035 (mM)
INaKmax	0.884 (pA/pF)
KmNap	10 (mM)
KmKp	1.5 (mM)
kNaCa	1000 (pA/pF)
ksat	0.1
rNaCa	0.35
KmNaex	87.5 (mM)
KmCaex	1.38 (mM)

TABLE 6.

State variable initial conditions for simulations of paced APs and BP oscillations

State variables	APs during 1 Hz pacing*	BP activity at gK1 = 0.15†	BP activity at gK1 = 0†
V	−84.86	−61.91	−47.88
dL	4.941 × 10−6	1.862 × 10−4	1.714 × 10−3
fL	0.8873	0.5298	0.3868
pa	9.095 × 10−3	0.3382	0.5371
n	1.974 × 10−2	0.1350	0.2321
q	0.9997	0.9890	0.8999
h	0.9925	0.2811	1.640 × 10−2
[Ca2+]i	1.691 × 10−4	3.502 × 10−4	4.889 × 10−4
[Ca2+]rel	2.683	5.207	6.378
[Ca2+]up	2.843	5.349	6.473
[Na+]i	9.224	6.548	6.418
[K+]i	136.4	140	140
dR	4.941 × 10−6	1.866 × 10−4	1.718 × 10−3
fR	0.9998	0.9954	0.9645
fTC	0.2529	0.4125	0.4949

^*Initial conditions for simulations of paced APs in the standard system (g_K1 = 1), obtained at 30 min during 1 Hz pacing, i.e., just before the 1801st stimulus, starting from a resting state.

^†Initial conditions for simulations of BP activity in the I_K1-reduced systems, obtained at MDP after 15 min calculations starting from an EP.

Sarcolemmal ionic currents

L-type Ca²⁺ channel current (I_Ca,L)

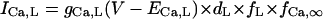(3)

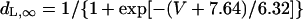(4)

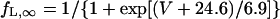(5)

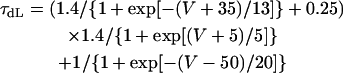(6)

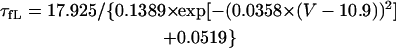(7)

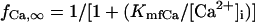(8)

Rapidly activating delayed-rectifier K⁺ current (I_Kr)

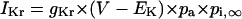(9)

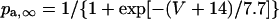(10)

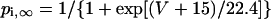(11)

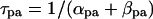(12)

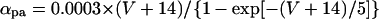(13)

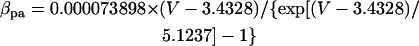(14)

Slowly activating delayed-rectifier K⁺ current (I_Ks)

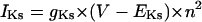(15)

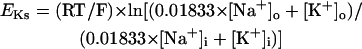(16)

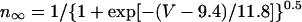(17)

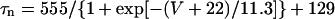(18)

Transient outward current (It_o)

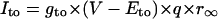(19)

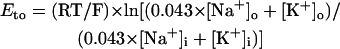(20)

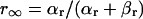(21)

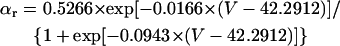(22)

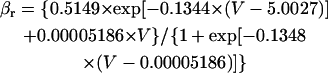(23)

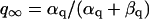(24)

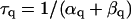(25)

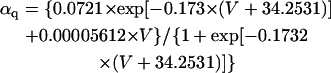(26)

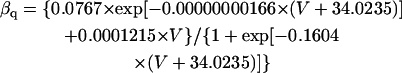(27)

Na⁺ channel current (I_Na)

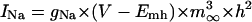(28)

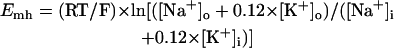(29)

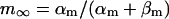(30)

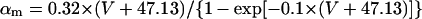(31)

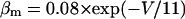(32)

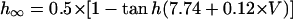(33)

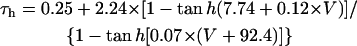(34)

Inward-rectifier K⁺ channel current (I_K1)

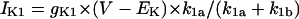(35)

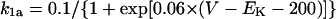(36)

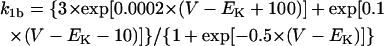(37)

Background Na⁺/Ca²⁺ currents (I_Na,b, I_Ca,b)

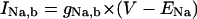(38)

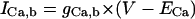(39)

Na⁺-K⁺ pump current (I_NaK)

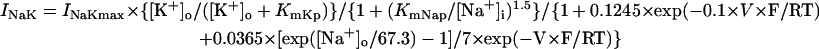(40)

Na⁺/Ca²⁺ exchanger current (I_NaCa)

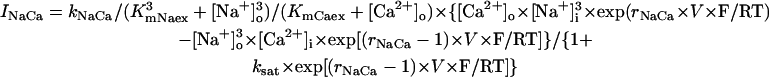(41)

Sarcolemmal Ca²⁺ pump current (I_pCa)

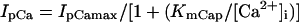(42)

Total membrane current (I_total)

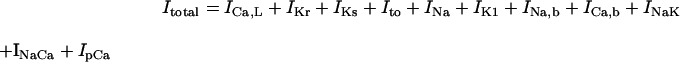(43)

Net ion fluxes

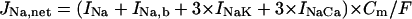(44)

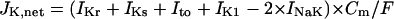(45)

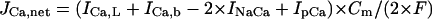(46)

Intracellular Ca²⁺ dynamics (SR Ca²⁺ handling)

SR Ca²⁺ release

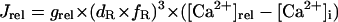(47)

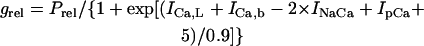(48)

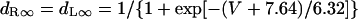(49)

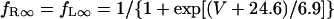(50)

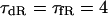(51)

SR Ca²⁺ uptake via Ca²⁺ pump

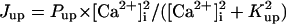(52)

SR Ca²⁺ transfer and leak

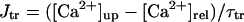(53)

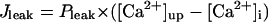(54)

Differential equations for state variables

Membrane potential (V)

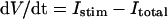(55)

Gating variables

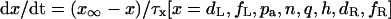(56)

Ca²⁺ buffering flux

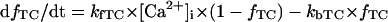(57)

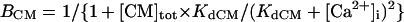(58)

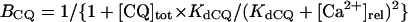(59)

Intracellular ion concentrations

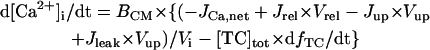(60)

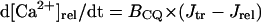(61)

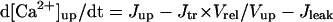(62)

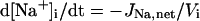(63)

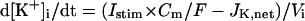(64)

APPENDIX 2: DETERMINATION OF EPS AS INITIAL CONDITIONS

To determine an EP (resting state) of the HVM system as initial conditions for AP simulations, steady-state values of the state variables V, [Ca²⁺]_i, [Na⁺]_i, [K⁺]_i, [Ca²⁺]_rel, and [Ca²⁺]_up were calculated numerically by the differential or algebraic method of Hund et al. (35). Differential equations given in Appendix 1 (Eqs. 55, 60–64) were used for the differential method with the MATLAB ODE solvers, whereas the following algebraic equations derived from the differential equations were used for the algebraic method with a nonlinear equation solver available in MATLAB.

(65)

(66)

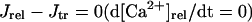(67)

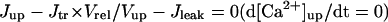(68)

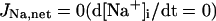(69)

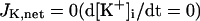(70)

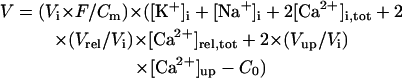(71)

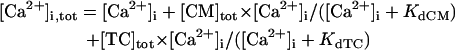(72)

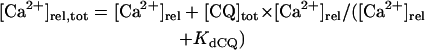(73)

The symbol C₀ in Eq. 71 is a constant of integration determined by initial conditions (35). Note that Eq. 65 can be derived from Eqs. 66, 69, and 70 (see Eqs. 43–46). The algebraic method for the full system with variable [K⁺]_i practically used Eqs. 66–70 and Eqs. 71–73 instead of Eq. 65, assuming that [K⁺]_i is equal to 140 mM under control conditions (e.g., at g_K1 = 1). The differential and algebraic methods yielded nearly identical results. For BP simulations and bifurcation analyses using the [K⁺]_i-fixed system, steady-state values of the state variables were calculated by Eqs. 65–69.