The Entropic Cost of Protein-Protein Association: A Case Study on Acetylcholinesterase Binding to Fasciculin-2

Abstract

Protein-protein association is accompanied by a large reduction in translational and rotational (external) entropy. Based on a 15 ns molecular dynamics simulation of acetylcholinesterase (AChE) in complex with fasciculin 2 (Fas2), we estimate the loss in external entropy using quasiharmonic analysis and histogram-based approximations of the probability distribution function. The external entropy loss of AChE-Fas2 binding, ∼30 cal/mol K, is found to be significantly larger than most previously characterized protein-ligand systems. However, it is less than the entropy loss estimated in an earlier study by A. V. Finkelstein and J. Janin, which was based on atomic motions in crystals.

Entropic changes upon noncovalent binding are difficult to estimate because extensive phase space sampling is required (1). For example, to calculate the external (translational and rotational) entropy, the range of residual motion in the complex must be known. Finkelstein and Janin (2) were the first to estimate residual motion; using the average fluctuation of crystal atoms they estimated an entropy loss of 50 cal/mol K. Many studies since have calculated the external entropy of protein-ligand systems (3–5), but none to date has targeted protein-protein association. Here, we estimate the external entropy loss using molecular dynamics sampling and integrating over different forms of the probability distribution function (PDF).

We apply our methods on a 15 ns molecular dynamics trajectory of mouse acetylcholinesterase (AChE) in complex with fasciculin-2 (Fas2) (6,7). AChE, which catalyzes the hydrolysis of the neurotransmitter acetylcholine in cholinergic synapses, is inhibited by the snake toxin Fas2, a high affinity binder with a slow dissociation rate. The initial external entropy for AChE-Fas2 is given by the Sackur-Tetrode equation and a rotational entropy term (8). For the final state, the entropy of restricted modes is estimated using the Gibbs entropy for translational and rotational modes. Assuming no change in momenta and moments of inertia upon binding, the entropic change is

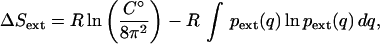where C° is standard concentration (1 molecule/1660 ų) and 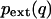is the external mode PDF.

Molecular dynamics simulations of the AChE-Fas2 complex have been previously described (6,7). The proteins are assumed to be bound over the course of the simulation. After 1.1 ns of equilibration, snapshots from every 10 ps of a 14.9 ns trajectory were superimposed according to the C_α atoms of an alignment molecule, either AChE or Fas2, allowing a reference structure to be defined by their average. Translational coordinates were defined by the center of mass of the other (hereafter referred to as the test) molecule. Quaternions were used for least-squares alignment of the test molecule with respect to the reference structure, and were converted to Euler angles through the small-angle approximation (5). Principal components analysis was performed by diagonalizing the zero-mean covariance matrices for the rotational and translational motions. The calculations were performed using either two 3 × 3 or a single 6 × 6 covariance matrix. The eigenvalues are equivalent to the variances in each principal axis.

In quasiharmonic (QH) analysis (9), the molecule is assumed to have a Gaussian distribution, leading to a Gibbs entropy of for each dimension. The PDF was also estimated by direct histogram analysis of the simulation. After projecting the coordinates into principal component space, histograms were constructed with 70 bins in each dimension, allowing 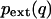to be calculated by normalizing the histogram and numerically integrating the configurational integral using the composite Simpson's rule. In Gaussian fit methods, a single Gaussian (sGF) or the sum of two Gaussians (dGF) was fitted to the histogram using nonlinear least-squares regression. The configuration integrals were numerically evaluated by adaptive Lobatto quadrature over three standard deviations from the extrema. To validate the integration procedure, it was tested on the sGF and found to match the analytical result.

In the AChE-Fas2 simulation, most of the external coordinate histograms are singly peaked, except for the doubly peaked most important components (Fig. 1). Thus, the dGF PDF more closely follows the simulation histogram than other PDFs. The histogram shape is due to sampling of several local minima over time (see Supplementary Material). The similarity between dGF and direct histogram entropies is advantageous in the limit of extensive ensemble sampling. However, in this limit, the value of the harmonic oscillator assumption is debatable. A multiple Gaussian fit may be most applicable in cases where multiple nearby energy wells are sparsely sampled.

FIGURE 1.

Probability distributions of translational and rotational degrees of freedom, AChE as alignment molecule. Black dots signify the histogram-derived probabilities; the dashed blue line is the QH distribution; the green line is sGF; and the red line is dGF. Translation units are angstroms and rotational units are radians.

When there are multiple energy wells, the accuracy of QH analysis is questionable (10). If the wells are distant from one another, the assumption of a normal distribution will lead to an overestimated entropy. To illustrate this principle, the entropy of a double-well distribution was compared to the QH value (Fig. 2). As separation is increased, the double well entropy stabilizes while the QH entropy continues to increase.

FIGURE 2.

QH (green) and Gibbs (blue) entropies as a function of well separation. The double-well distribution was generated using the sum of two equally weighted Gaussians and varying the distance between peaks.

Calculated entropies are qualitatively similar for every technique (Table 1). Entropy losses are slightly lower, by <1 cal/mol K, when a single Gaussian is used, in agreement with Fig. 2 calculations. If Fas2 is used as the alignment molecule (see Supplementary Material), the rotational entropy of the complex is estimated to be ∼2 cal/mol K higher. This may be due to difficulty of accurately aligning to a smaller reference molecule, leading to artifactual phase space excursions. One way to remove this artifact is to treat the six external modes all together.

TABLE 1.

External entropy changes (cal/mol K), AChE as alignment molecule

Method	Translation	Rotation	External	Decoupled
Hist	−18.7(0.02)	−10.9(0.02)	−29.5(0.03)	−31.7(0.19)
QH	−18.2(0.01)	−10.6(0.10)	−28.8(0.15)	−31.1(0.16)
sGF	−17.7(0.03)	−10.4(0.02)	−28.1(0.03)	−31.2(0.26)
dGF	−18.3(0.48)	−11.0(0.11)	−29.3(0.50)	−31.9(0.55)

Decoupled entropies denote values obtained from a 6 × 6 covariance matrix. Error values, enclosed in parentheses, are the standard deviation of 500 entropy calculations from 500 randomly selected snapshots.

The degree of coupling between translational and rotational modes is given by 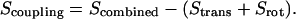Entropic analysis was performed for a 6 × 6 covariance matrix encompassing all external modes. Because generating this matrix combines angular and Cartesian coordinates, the eigenvectors are extremely sensitive to the units used in the equation. Therefore, dimensionless units of length and angle were used to generate the matrix and histograms (see Supplementary Material). In the QH method, when either AChE or Fas2 was used as the alignment molecule, the entropy change estimate is −31.1 cal/mol K. The similarity of external entropy values evinces the successful decoupling of translational and rotational entropy terms. The coupling terms for AChE and Fas2 alignment molecules are 2.4 and 5.0 cal/mol K, respectively. Retrospectively, it is clear that considering the translational and rotational degrees of freedom separately led to artifactual motions in rotational phase space.

Molecular dynamics simulations provide evidence for enhanced conformational fluctuations of AChE-Fas2 in complex in comparison to apo form (7). These fluctuations may lead to increased internal entropy to compensate for the external entropy loss upon binding. The external entropy loss upon protein-protein complexation is of greater magnitude than for protein-water binding (0–7 cal/mol K) (11) and protein-small molecule systems (3–5). For example, Swanson et al. estimated that for FK506 binding protein and 4-hydroxy-2-butanone, association leads to translational and rotational entropy changes of 10.6 and 2.0 cal/mol K, respectively (5). With protein-protein complexation, the larger interaction surface leads to a more substantial reduction of the external entropy, particularly for the rotational degrees of freedom. However, the entropy loss estimated is less than expected from analysis of atomic motions in crystals (2), even for the tight binding AChE-Fas2 complex. This is a reasonable result reflecting the enhanced fluctuations of proteins in solution.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.