Mechanochemical Model of Microtubule Structure and Self-Assembly Kinetics

Abstract

Microtubule self-assembly is largely governed by the chemical kinetics and thermodynamics of tubulin-tubulin interactions. An important aspect of microtubule assembly is that hydrolysis of the β-tubulin-associated GTP promotes protofilament curling. Protofilament curling presumably drives the transition from tip structures associated with growth (sheetlike projections and blunt ends) to those associated with shortening (rams' horns and frayed ends), and transitions between these structures have been proposed to be important for growth-shortening transitions. However, previous models for microtubule dynamic instability have not considered such structures or mechanics explicitly. Here we present a three-dimensional model that explicitly incorporates mechanical stress and strain within the microtubule lattice. First, we found that the model recapitulates three-dimensional tip structures and rates of assembly and disassembly for microtubules grown under standard conditions, and we propose that taxol may stabilize microtubule growth by reducing flexural rigidity. Second, in contrast to recent suggestions, it was determined that sheetlike tips are more likely to undergo catastrophe than blunt tips. Third, partial uncapping of the tubulin-GTP cap provides a possible mechanism for microtubule pause events. Finally, simulations of the binding and structural effects of XMAP215 produced the experimentally observed growth and shortening rates, and tip structure.

INTRODUCTION

Microtubules are intracellular filaments essential for cell division and thus have been targeted by several anti-cancer strategies (reviewed in (1)). Microtubules exhibit dynamic instability, where sustained periods of microtubule growth make stochastic transitions (called catastrophes) to sustained periods of shortening, and vice versa (called rescues) (reviewed in (2) and (3)). Although microtubules have been the subject of intensive study, there are key questions that remain, including how microtubules maintain a metastable character with transitions between growth and shortening, and how they change this character to bias for long, stable microtubules in nondividing cells, or bias for short, unstable microtubules in dividing cells.

Assembled tubulin structures assume various conformations other than blunt-ended tubes, including curled protofilaments during microtubule shortening (rams' horns), GDP rings formed under rapid depolymerization conditions, and curved sheetlike extensions during growth (4,5). Furthermore, microtubules stabilized by assembly with the slowly hydrolyzable GTP-analog, GMPCPP, have an extended dimer length along the axis of the microtubule (6), and microtubules stabilized by assembly with taxol have been reported to be less rigid and appear to have less-organized protofilament associations in electron micrographs (7). Observed structural features of microtubules are likely to have an important role in their metastable character (8), but the previous chemical kinetics simulations have not explicitly considered the mechanical and structural features of the microtubule.

Questions about the metastable character of microtubules have been addressed experimentally, but models for these behaviors have proven difficult to validate because high-resolution observation of dimer arrivals and departures is currently unavailable. Computational models are presently the only way to test different models at the scale of individual dimers. For example, the seminal five-start helical model (9) and the lateral cap model (10–12) both considered the various possible tubulin-tubulin interactions that may be attributed to dimer position at the tip of a two-dimensional microtubule lattice, and these models were used to examine assembly dynamics. More recently, a more abstract model that considers only the net association of dimers was used to examine assembly dynamics (13). None of these previous models, however, have explicitly accounted for the structure of the tip and the mechanical energy changes associated with tubulin deformation.

Our previous effort to simulate microtubules resulted in a model for microtubule dynamic instability that combined individual models for assembly and disassembly with rules for switching between states that considered mechanical features of microtubules (14,15). Using this pseudo-mechanical model allowed estimation of the bond energies between tubulin dimers within the microtubule lattice and reproduced microtubule dynamic instability in close agreement with the experimentally observed parameters of microtubule dynamics at 10 μM tubulin, including growth rate, shortening rate, catastrophe frequency, and rescue frequency. However, the pseudo-mechanical model cannot represent observed microtubule three-dimensional tip structures and behaviors. To represent microtubule behaviors more accurately, it is necessary to consider mechanical forces explicitly. Recently, mechanical models for microtubules have been constructed that accurately reproduce the experimentally observed tip structures (8,16–18). However, these models did not integrate tubulin addition/loss and GTP hydrolysis to relate mechanics to the chemical kinetics and thermodynamics.

The aim of this work was to produce an integrated mechanochemical model that accurately represents microtubule behaviors in diverse experimental conditions. The model relates conformational changes in tubulin heterodimers to the standard Gibbs free energy of tubulin-tubulin noncovalent interactions. This relationship between energy and dimer position in the model postulates that thermodynamically favorable interactions at the tubulin-tubulin interfaces are antagonized by destabilizing elastic forces that promote curling within the tubulin dimers. To simplify calculations in a coarse-grained representation of microtubule structure and dynamics, tubulin monomers are given as points along a vector axis representing a dimer, with preferred distances and angles specified with regard to neighboring monomers.

METHODS

Mechanical and structural modeling

For concreteness we assume that microtubules have 13 protofilaments in a B-lattice, which has a left-handed helical pitch of 1½ dimers per helical turn, and thus has a seam of interactions between unlike monomers (α-β and β-α), whereas most neighboring protofilaments share like-like lateral interactions (α-α and β-β). Monomers in a single simulated protofilament are positioned as connected vectors, where two rotations are possible for each dimer, θ-rotation and φ-rotation. The rotation in the θ-direction may be thought of as curling radially outward from the microtubule lattice (Fig. 1 A). For example, a dimer in a typical rams' horn formation would have a combined θ-rotation of 22°, as measured previously by others (19). Twenty-two degrees (22°) is assumed to be the preferred angle, θ, for tubulin-GDP in our model. The GTP cap model suggests that tubulin-GTP dimers maintain a straight conformation at the end of a microtubule, as determined by studies with tubulin-GMPCPP showing that GTP hydrolysis is accompanied by an increase in curvature of the protofilaments (19), so for tubulin-GTP dimers in our model, θ = 0° is preferred.

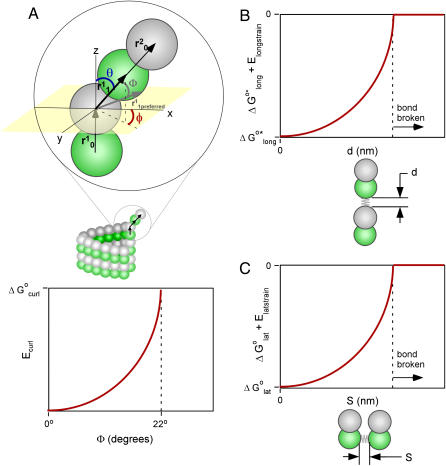
FIGURE 1.

Schematic representation of how bending and stretching affects energy in the model. In each graph, the standard free-energy change (ΔG°) is measured on the Y axis. (A) Subunit curling and torsion. The preferred curling angle, θ, is 0° for tubulin-GTP and 22° is the preferred θ for tubulin-GDP. The preferred torsion angle, φ, is 0° for both tubulin-GTP and tubulin-GDP. These preferences are described by direction cosines, and the actual dimer position is similarly described (see Methods). The angle between the preferred orientation (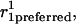 shaded arrow) and the actual orientation ( 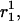bold black arrow) is Φ. The relationship between Φ and E_curl obeys a Hookean spring law, where energy is minimized at the preferred orientation (Φ = 0°) and energy increases with increased deviation from this preferred orientation (Φ > 0°). Note that Φ measures deviation of an actual orientation from a preferred orientation, so that, e.g., a tubulin-GDP held in a straight conformation would have Φ = 22°, the same value for Φ as a tubulin-GTP would have when held curled to 22°. Although not explicitly shown in the figure, curling may also occur at the centroid of the α-tubulin monomer to relieve mechanical stress propagated throughout the microtubule lattice by curling events at the β-tubulin monomers. (B) Longitudinal strain. Longitudinal strain (E_longstrain) is minimized when longitudinal stretching (d) is zero. Energy follows a Hookean spring law, where energy increases with longitudinal stretching squared. (C) Lateral strain. Lateral stretching energy (E_latstrain) is minimized when lateral stretching (S) is zero. Energy follows a Hookean spring law, where energy increases with longitudinal stretching squared. S is a derived position descriptor for the purpose of evaluating energetics; θ, φ, and D give a complete description of dimer positions in the microtubule lattice.

The angle φ represents torsion about the protofilament axis (Fig. 1 A), where rotation about φ accommodates lateral interactions concomitant with outward protofilament curling, as seen with protofilament extensions (5). Rams' horns appear to bend outward radially relative to the center of the microtubule, suggesting that φ = 0° is the preferred angle of rotation. Protofilament extensions (of 2–12 protofilaments) have been observed to have curvature which would suggest that, although φ = 0° is preferred, other values for φ must be permitted (5,16). Torsion must exist to accommodate persistence of lateral bonds when protofilaments curl outwards; simply curling radially outward would break lateral bonds. Janosi et al. (16) modeled the elastic properties of microtubules as a continuum based on observed curvatures of protofilament extensions viewed in electron micrographs. In their model, protofilament extensions had curvature that is dependent on the number of protofilaments in each extension. Predicted curvatures from their simulations were given by mechanical energy minimization, and energies computed as a function of length and number of protofilaments in an extension. The curvatures predicted by Janosi et al. (16) provide some clues about the proper constraints to be used when searching for configurations that minimize the mechanical energy. In particular, the maximum expected torsion (φ) can be estimated from the curvature of the various protofilament extensions they measured and modeled (see below).

In addition to φ and θ, a third structural variable, longitudinal monomer length (D), was introduced to provide a complete three-dimensional description of each monomer's orientation and position in the microtubule lattice. Monomer length D is the sum of the preferred monomer length (d₀ = 4 nm) and the amount of longitudinal stretching (d). The model relies on energy minimization to determine the orientation and position (θ, φ, and D) of dimers in the vicinity of the microtubule tip.

The fourth structural variable, S, is the lateral distance between center points of adjacent monomers, which modulates the standard Gibbs free energy of lateral interactions, ΔG°_lat (Fig. 1 C). Lateral stretching, S, is derived from θ, φ, and D.

Lateral stretching, represented by S, and longitudinal stretching, represented by d, account for two of the three kinds of mechanical energy considered by our model (E_latstrain and E_longstrain, respectively). The final type of mechanical energy (E_curl) considered is curling/torsion, which is parameterized by Φ (the fifth and final structural variable), the angle at which a monomer deviates from a preferred orientation (Fig. 1 A). The exchangeable guanine nucleotide of tubulin binds the β-tubulin polypeptide of the heterodimer at the longitudinal interface (20). The state of this nucleotide (i.e., whether it is GDP or GTP) affects the mechanical energy state by changing the conformational preference of the monomer (θ_preferred = 0° for GTP and θ_preferred = 22° for GDP). In this model, the lateral bond energy of dimers is offset by some fraction of the curling energy (ΔG°_curl) that depends on combined lateral strain and curling. Curling energy is evaluated in the model by considering the difference between a preferred orientation and the actual orientation of a dimer, given by the angle Φ between the two vectors that define the preferred and actual orientations (Fig. 1 A). The difference in direction between the two vectors can be characterized by using direction cosines (l, m, and n), which are derived from the spherical coordinates D, φ, and θ. Dimers are represented by a vector, r₀, which begins at the centroid of the α-tubulin (minus (−) end) and points to the intradimer β-tubulin centroid. When another dimer is bound to the longitudinal plus (+) end (β-tubulin) of the dimer represented by r₀, then a second vector, r₁, describes this connection where the origin of r₁ is the head of r₀, and r₁ points to the centroid of the interdimer α-tubulin (Fig. 1 A). Any dimer curling occurs where two vectors meet. The Cartesian coordinates (x, y, and z) of each monomer are calculated from the spherical coordinates (θ, φ, and D) via

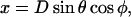(1)

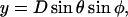(2)

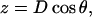(3)

where monomer length D is the magnitude of a vector, r₀ or r₁. The angle Φ between the preferred and actual orientation is then given by

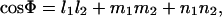(4)

where subscripts 1 and 2 denote each of the two dimer orientation vectors forming an angle at the origin, and l, m, and n are the direction cosines given by

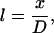(5)

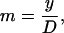(6)

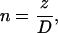(7)

where x, y, and z are the coordinates of the vector head (plus (+) end) with respect to the vector origin (minus (−) end), and D is the length of the vector. The angle Φ that results from these calculations was then used in Hooke's Law to determine the energy of curling deformation,

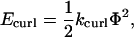(8)

where k_curl is the spring constant. The spring constant, k_curl, was determined by substituting ΔG°_curl for E_curl and substituting Φ_Deformed for Φ, and then solving for k_curl,

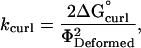(9)

where ΔG°_curl is the energy of conformational strain for a tubulin-GDP held in a straight conformation (aligned with the microtubule axis) and Φ_Deformed is the angular difference between the straight and the preferred curling conformations for a tubulin-GDP.

Our model postulates that the changes that promote curling occur in close proximity to the GTP hydrolysis (i.e., at the centroid of the β-tubulin monomer), although the model could be calibrated for other possible hinge points without changing the main conclusions reached here. As the estimation of flexural rigidity (EI) is model-dependent (see below), however, our estimation of EI is expected to be slightly influenced by the choice of hinge points in our simulations. Note that curling may also occur at the centroid of the α-tubulin monomer to relieve lattice strain in our model. Curling is thus not isolated to the β-tubulin monomer, and the assumption of asymmetric curling forces (where curling at the α-tubulin results from stress transfer) gives an additional source of polarity to microtubules in our model. Earlier simulations with our pseudomechanical model (14,15) have suggested to us that differences in the parameters of dynamic instability between the plus (+) and minus (−) ends of the microtubule may not be entirely explained by differences in GTP hydrolysis. We therefore include this additional source of polarity to be more fully examined in future modeling attempts. Another possible source of polarity that has yet to be introduced to our model are differences in the strength of α-α and β-β interactions. Interaction modeling (21) has suggested that β-β interactions may be up to twofold stronger than α-α interactions, although the authors note that taxol-stabilization for acquiring the crystal structure and other limitations of the crystal structure (moderate structure resolution and loss of residues 35–60 in the α-subunit) are confounding factors that may influence that finding.

Chemical thermodynamic and kinetic modeling

The equilibrium association constant, K, is related to rate constants by

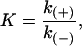(10)

where k₍₊₎ is the bimolecular on-rate constant for a reaction and k₍₋₎ is the unimolecular off-rate constant for a reaction. The bimolecular rate constant is multiplied by the tubulin-GTP concentration to give a pseudo first-order on-rate constant

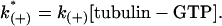(11)

The equilibrium constant is then used to calculate unimolecular off-rate constants (k₍₋₎), given an assumed association constant (k₍₊₎) of 2 × 10⁶ M⁻¹ s⁻¹ (10) or 4 × 10⁶ M⁻¹ s⁻¹. The unimolecular off-rate constant k₍₋₎ is independent of tubulin concentration and is given by

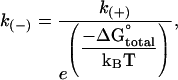(12)

where ΔG°_total is the total standard free energy of binding that includes both the chemical and the mechanical energies.

The standard free energy change obtained by a longitudinal association of two dimers is given by 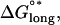and includes the entropy of immobilizing a dimer in the microtubule lattice as well as the energy of longitudinal surface interactions (14,15). To find the mechanochemical energy of a particular longitudinal association, Hooke's law, E_longstrain = 1/2(k_longd²), is used to convert the length of longitudinal stretching (d) into the longitudinal elastic stretching energy, which is then added to the chemical binding energy, 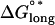(Fig. 1 B). Longitudinal standard free energy increases with increasing stretch until the mechanical spring energy plus longitudinal chemical bond energy equals zero, which means that the bond has broken.

Modulation of lateral standard free energy (ΔG°_lat) by S takes the form of a Hookean spring law equation, E_latstrain = 1/2(k_latS²). Free energy increases as the distance S increases. As with longitudinal energy, lateral free energy increases with increased stretching until spring energy plus lateral bond energy is zero, and bond breakage occurs (Fig. 1 C).

Integration of mechanics, thermodynamics, and kinetics

Total energy for a dimer is equal to the sum of the component energies. The mechanical strain energy is computed from the stretching, torsion, and curling of the neighbors present. For each dimer, there are four possible lateral-binding energies, as well as a longitudinal energy, and a bending energy. For simplicity, when a dimer dissociates from the lattice or changes orientation, the effect of this is propagated to all dimers above it (closer to the tip) within the same protofilament. Energy contributions from vacant lateral positions are zero. Total energy can be calculated for any of the various dimer positions by summing all the chemical and mechanical energies, which is given by

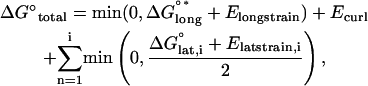(13)

where i is the number of monomeric lateral bonds considered (0, 1, 2, 3, or 4 bonds per dimer considered). The energy of each lateral bond is divided to distribute energy equally between the two neighbors sharing that association. For cases where individual bond energy plus strain energy for that bond is greater than zero, the bond is considered broken (i.e., the energy sum for that bond = 0). Total energy for various test positions may then be compared to find the optimal position, or the position with the minimum total free energy. As the sum of energies considered includes propagated changes to (or breakage of) the lateral bonds of dimers, orientation changes or dissociation are very unlikely for dimers buried deep in the microtubule lattice (Eq. 13).

Simulation procedure

The simulation procedure is as follows:

1. Determine all possible kinetic events at the tip of the microtubule (this is the event list).

2. Determine how long it will take each kinetic event to occur stochastically.

3. Implement the event that takes the shortest amount of time.

4. Determine positional changes that result from the occurrence of the new event.

5. Return to step 1.

For step 1, possible events include association and dissociation at every protofilament end, breakage of any intraprotofilament longitudinal bonds and hydrolysis of any tubulin-GTP dimers. The time taken for each event to occur, for use in step 2, is determined with the equation

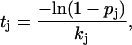(14)

where the value of k_j is the first-order rate constant of the event j (if an association event, the pseudo first-order rate constant), p_j is a random number from 0 to 1, and t_j is the time the event takes. After events are assigned times as described above, the event with the shortest time is implemented. The mechanical energy minimization routine (described below) is then used to determine the new orientations/positions of dimers. If the event was an association event, then the position of the new dimer is also determined in the mechanical energy minimization.

Mechanical energy minimization

Different strategies for energy minimization were developed and tested, and a local minimization strategy was chosen for our simulations. Global energy minimization ultimately fails to capture the metastable character of microtubules, since the calculated global minimum when using a GTP cap model is a completely disassembled microtubule. Local energy minimization for repositioning individual dimers was performed with stochastic ordering, so that there were 3n visits to randomly selected dimers in the lattice, where n is the total number of lattice dimers under consideration. Approximately 95% (1−e^(−3n/n)) of the dimers in the lattice were visited for energy minimization at least once during each round of minimization. The entire local minimization procedure was performed after each association or dissociation event. This procedure for energy minimization implicitly assumes a timescale for conformational changes in the simulations, which is fast compared with association/dissociation events. Conformational changes without a free energy barrier occur at a rate equal to the vibrational frequency of a covalent bond, v = k_BT/h, where v = 6.5 × 10¹² s⁻¹ at 37°C (22). Conformational changes are thus very fast compared with association events, which are simulated with a pseudo first-order rate of 20 s⁻¹ per protofilament tip in 10 μM tubulin (k₍₊₎ = 2 × 10⁶ M⁻¹ s⁻¹). The fastest dissociation events occur at a rate of 165 s⁻¹ (a single longitudinal interaction with 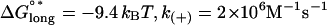), and conformational changes are thus expected to occur at a rate at least 3.9 × 10¹⁰-fold faster than other simulated events. Therefore, for simplicity, conformational changes are assumed to occur arbitrarily fast and the amount of time taken by these events is not recorded during the simulation. The reason the global minimum is not expected to be reached quickly is that realizing the global minimum requires large energy barriers to be overcome (see Results).

Dimer positions are adjusted to accommodate the energy minimum found by the algorithm. Energy minimization is performed using the fmincon algorithm provided by the Optimization Toolbox in MatLab, Vers. 6, Rel. 12 (The MathWorks, Natick, MA), and takes the form of a function minimization problem, where a function is written that takes the descriptive variables of monomer positions (θ, φ, and d) as input, builds the microtubule from that description, and evaluates and returns the energy as output. Parameters describing the convergence criteria and constraints (convergence tolerances set to 1 × 10⁻³, φ constrained to ±1.6°, θ constrained to 0 to 22°) are provided to the algorithm and a new set of variables describing the tubulin monomer positions are returned when these criteria are satisfied. MatLab, Vers. 6, Rel. 12, was used to develop and perform all simulations in this work. Simulation run times were on the order of one day per processor per minute of simulated microtubule assembly using a 300-MHz Macintosh G3 computer. Given resources available to us at the time these simulations were performed, it was not practical to derive transition frequencies between growth and shortening from our simulations.

Mechanical parameter estimation

Large parameter sets for models introduce at least two difficulties: 1), exhaustive combinatorial trials of large parameter sets may be impractical; and 2), large parameter sets may often be easily fit to experimental data, and multiple sets of parameter values may fit the data equally well, thus making it more difficult to interpret parameters or have confidence that their values reflect some property of the system modeled. In the interest of maintaining a small and self-consistent parameter set, we used the Young's modulus of tubulin to derive all of the elastic mechanical properties of tubulin used in the model, including dimer flexural rigidity (EI_p), the lateral bond spring constant (k_lat), and the longitudinal bond spring constant (k_long). Due to the nonhomogenous atomic structure of tubulin, its Young's modulus is not clearly defined, so the value of Young's modulus was adjusted to produce the observed shortening velocity for an uncapped microtubule. We used two values for the bimolecular on-rate constant of tubulin, 2 × 10⁶ M⁻¹ s⁻¹ (12) and 4 × 10⁶ M⁻¹ s⁻¹, and we predicted a flexural rigidity of 3.4 × 10⁻²⁴ Nm² and 4.7 × 10⁻²⁴ Nm², respectively (discussed in detail below). Both of these predictions fall within the range of experimentally measured values for the flexural rigidity of microtubules (summarized in Table 1) (23–28). Our estimation of EI is model-dependent, where modeling choices such as the use of spring models for tubulin deformation and concentrating the effect of curling on lateral associations are likely influences on this prediction. Our estimate thus cannot be used as a general verification of the correct value of EI, although the model's ability to recapitulate observed microtubule tip structures does lend some support to this estimate (see Results).

TABLE 1.

Published values for the flexural rigidity of microtubules (EI_MT)

Publication	Method	Microtubule type	EIMT (× 1024 Nm2)
(23)	Thermal fluctuations	Pure tubulin	18.5 ± 2.0
		With XMAP215	17.5 ± 2.2
(24)	Optical trapping, RELAX method	Pure tubulin	3.7 ± 0.8
		With taxol	1 ± 0.3
		With MAPs	16 ± 3
	Optical trapping, WIGGLE method	Pure tubulin	4.7 ± 0.4
		With taxol	1.9 ± 0.1
		With MAPs	18 ± 3
(25)	Optical trapping	With MAPS	43
		With taxol	5.9
(26)	Thermal fluctuations	Cap-stabilized	26 ± 2
		With taxol	32 ± 2
(27)	Hydrodynamic flow	Pure tubulin	8.5
	Thermal fluctuations	Pure tubulin	4.6
		With taxol	2.5
(28)	Thermal fluctuations	With taxol	21.9 ± 0.14

There are at least three important sources of information concerning the mechanical features of microtubules, including 1), measurements of the flexural rigidity of microtubules; 2), thermodynamic studies that infer mechanical stress; and 3), electron micrographs demonstrating the curvature of sheetlike microtubule ends and other protofilament extensions. Below we describe how flexural rigidity is used as a parameter in the model to derive the Young's modulus of tubulin and define the modeled elastic properties of tubulin dimers in the microtubule, including ΔG°_curl (the intradimer mechanical strain energy) and spring constants for dimer lateral and longitudinal stretching (which are used to calculate the energy of interdimer mechanical strain energy). Predictions for ΔG°_curl were compared to Caplow and Shanks' (29) thermodynamic estimate (∼2.8 k_BT) for the elastic strain energy stored in a tubulin-GDP dimer in the core of the microtubule lattice, and the bimolecular on rate 2 × 10⁶ M⁻¹ s⁻¹ was chosen for further simulations, as this rate produces closer agreement with their experiment (see Results).

The flexural rigidity (EI) of an object is equal to the product of Young's modulus (E) and the second moment of area (I) for the object in question. Mickey and Howard (26) estimate the second moment of area for a 14-protofilament microtubule (I_MT) to be 1.8 × 10⁻³² m⁴. They modeled a protofilament with a rectangular cross-section of thickness a = 2.7 nm and a width of b = 5.15 nm, with a second moment of area for a single protofilament given by

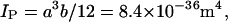(15)

where I_p is the second moment of area of a protofilament.

Several groups have measured the flexural rigidity of microtubules using various experimental methods (Table 1). These methods have produced measurements that differ by two orders of magnitude in the range of 4.5 × 10⁻²⁵ to 2.6 × 10⁻²³ Nm². As there is not yet agreement on the correct value for the flexural rigidity of microtubules, we tested a range of flexural rigidity for values that produce the experimentally observed rate of disassembly for an uncapped microtubule using the measurements of Walker et al. (30). It is expected that a large range of values for Young's modulus would produce the correct assembly rate for capped microtubules, so measuring the accordance of predicted assembly rate to experimentally observed assembly rate may be thought of as a secondary test.

To calculate Young's modulus for tubulin, we solve for E in

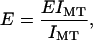(16)

where EI_MT is the flexural rigidity measured by experiment and I_MT is the calculated second moment of area for a microtubule. Young's modulus is given by

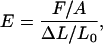(17)

where F is the force, A is the cross-sectional area perpendicular to the force, ΔL is the change in length from rest, and L₀ is the original length. Solving for force (F) gives

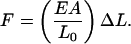(18)

This is Hooke's Law, where

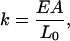(19)

giving F = kΔL, where F is the restoring force. The work (energy) required to stretch a spring is given by integrating F = kΔL, which gives

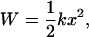(20)

where x = ΔL.

Spring constants k_lat and k_long, for lateral stretching and longitudinal stretching, respectively, were calculated from a range of values for Young's modulus (which, as stated above, come from measurements of flexural rigidity by others), and using the dimer dimensions described by Mickey and Howard (26) to calculate A and L₀, Eq. 19 was used to find

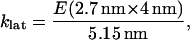(21)

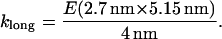(22)

We next consider how bending is modeled in our simulations. The flexural rigidity for a single protofilament is

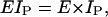(23)

where I_P is the second moment of area estimated for a protofilament. The work required per monomer to bend a protofilament into an arc with radius R is given by

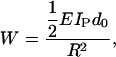(24)

where d₀ is the length of a monomer.

The value for the work required to bend a protofilament into an arc with radius R in Eq. 24 is used in the same context as the energy of curling applied in a previous pseudo-mechanical model of microtubule assembly dynamics (14,15). In this earlier model, ∼2.5 k_BT/dimer was predicted to be required to straighten a tubulin-GDP or to curl out a tubulin-GTP to 22°. This angle was measured from electron micrograph evidence demonstrating that the principle difference between a tubulin-GTP and a tubulin-GDP was that the former has a conformational preference to be straight (aligned with the microtubule axis), and the latter has a conformational preference for curling outwards radially at 22° (4,5,31–33). Additionally, we posit in this model, as we did in our earlier pseudomechanical model, that this difference in conformational preference is literally the driving force for disassembly, as the conformational preference of tubulin-GDP for curling would put mechanical stress on lateral bonds in the microtubule lattice. Table 1 gives experimental measurements of EI_MT by various groups, and Table 2 gives our predictions for EI_MT. The value of ΔG°_curl may be substituted for work (W) in Eq. 24, so given an experimentally determined value for ΔG°_curl, we have a convenient means of estimating EI. For example, Caplow and Shanks (29) estimated that ∼1.7 kcal mol⁻¹ (∼2.8 k_BT/dimer) of elastic strain energy is stored in the microtubule lattice by tubulin-GDP (our definition for ΔG°_curl). This value for ΔG°_curl predicts an EI of ∼2.6 × 10⁻²⁴ Nm² (Eq. 24), falling within the range of experimentally measured values. This prediction from experiment was used as a guide for comparison to predictions for EI made by disassembly simulations.

TABLE 2.

Predictions for EI_MT made with the mechanochemical model

Bimolecular on-rate (k(+))	EIMT (× 10−24 Nm2)
2 × 106 M−1 s−1	3.4
4 × 106 M−1 s−1	4.7

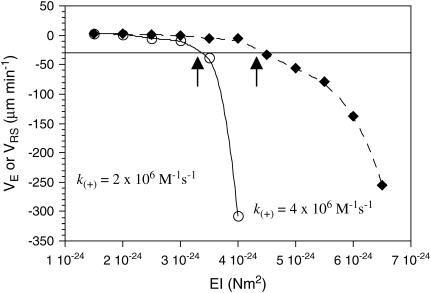
To determine an appropriate value of EI to use in our simulations, microtubules were simulated without GTP caps in 10-μM tubulin-GTP (Fig. 2). Flexural rigidity (EI) was thus calibrated to the shortening rate, rather than to the growth rate, since it is expected that the growth rate and associated tip structures are less sensitive to EI than the shortening rate, where a wide range of values for EI could produce the same maximal growth rate. Simulations were performed using either k₍₊₎ = 2 × 10⁶ M⁻¹ s⁻¹ or k₍₊₎ = 4 × 10⁶ M⁻¹ s⁻¹ and their associated predictions for lateral (ΔG°_lat; −3.2 k_BT and −5.7 k_BT, respectively) and longitudinal (ΔG°*_long; −9.4 k_BT and −6.8 k_BT, respectively) bond energies for the assembly state (as calculated in (14,15)). Simulations of 250 events were performed 10 times and the mean shortening or growth velocity was calculated at EI intervals of 0.5 × 10⁻²⁴ Nm². At the observed disassembly rate of −30 μm min⁻¹, these simulations predict an EI of ∼3.4 × 10⁻²⁴ Nm² at k₍₊₎ = 2 × 10⁶ M⁻¹ s⁻¹, and an EI of ∼4.7 × 10⁻²⁴ Nm² at k₍₊₎ = 4 v 10⁶ M⁻¹ s⁻¹. These values for EI predict values for ΔG°_curl of ∼3.7 k_BT and ∼4.2 k_BT, respectively. The value of ΔG°_curl = 3.7 k_BT predicted at k₍₊₎ = 2 × 10⁶ M⁻¹ s⁻¹ is closer to the value Caplow and Shanks (29) calculated for the energy stored in the microtubule lattice, suggesting that 2 × 10⁶ M⁻¹ s⁻¹ is closer than 4 × 10⁶ M⁻¹ s⁻¹ to the correct value for k₍₊₎. Further simulations were therefore performed with k₍₊₎ = 2 × 10⁶ M⁻¹ s⁻¹. Parameters used in our simulations are summarized in Tables 3 and 4.

FIGURE 2.

Shortening velocities that result from simulations performed at a range of values for EI. Increasing stiffness causes a larger amount of strain energy to be stored in the lattice, which in turn increases the tendency to depolymerize. Arrows indicate points where EI produces the observed disassembly rate.

TABLE 3.

Model parameters

Parameter	Definition	Comments
EIMT	Flexural rigidity of a microtubule.	Used to calculate all elastic properties of tubulin in the model.
k(+)	Bimolecular on rate constant.	Required constant to predict k(−) at various microtubule tip sites.
ΔG°Lat	Standard free energy change for lateral association.	Antagonized by ΔG°curl for tubulin-GDPs.
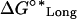	Standard free energy change of longitudinal association plus the free energy of immobilizing a dimer in the microtubule lattice.	Requires the assumption that dimers in the microtubule lattice always have at least one longitudinal bond.
kH	Hydrolysis rate constant.	Only for dimers with tubulin bound to their β-tubulin end.

TABLE 4.

Constants and derived model parameters

Parameter	Definition	Comments
klat	Spring constant for lateral stretching.	Derived from EIMT.
klong	Spring constant for longitudinal stretching.	Derived from EIMT.
ΔG°curl	Standard free energy change for mechanical strain of a tubulin-GDP held in an unrelaxed straight position.	Derived from EIMT. May also be defined as the energy required to bend a tubulin dimer 22° from its preferred conformation.
θDpref	The preferred angle for tubulin-GDP.	Constant. Observed in EMs. May also be described as the amount of angular deviation that G°curl can cause.
θTpref	The preferred angle for tubulin-GTP.	Constant. Observed in EMs.

RESULTS

Microtubule tip structure during growth and shortening

When examined in electron micrographs, growing microtubules in pure 10-μM tubulin-GTP exhibit blunt ends or sheetlike projections, whereas shortening microtubules have frayed or blunt ends (4,5). To test whether our model could naturally give rise to these observed tip structures, we examined the simulated tip structures for both assembling and disassembling microtubules grown in 10-μM tubulin-GTP. A hydrolysis rate (k_H) of 0.95 s⁻¹ was used in these and all subsequent simulations, a value estimated previously with the pseudo-mechanical model (14,15).

There are multiple lines of evidence that the minimal stable GTP-cap is a monolayer (29,34,35). It should be emphasized that this is a minimal requirement, and the authors make no claim that a single monolayer GTP-cap is the typical or average condition of a growing microtubule. Our previous work (14,15) predicted an average GTP-cap size of ∼55 dimers, and simulated dilution experiments showed that the time to catastrophe after dilution was consistent with the observed rate (36). Here and in subsequent simulations, GTP-capped microtubules were simulated with a 52-dimer GTP-cap (four layers' deep), which is close to the cap-size range predicted by Voter et al. (36) (23–44 dimers).

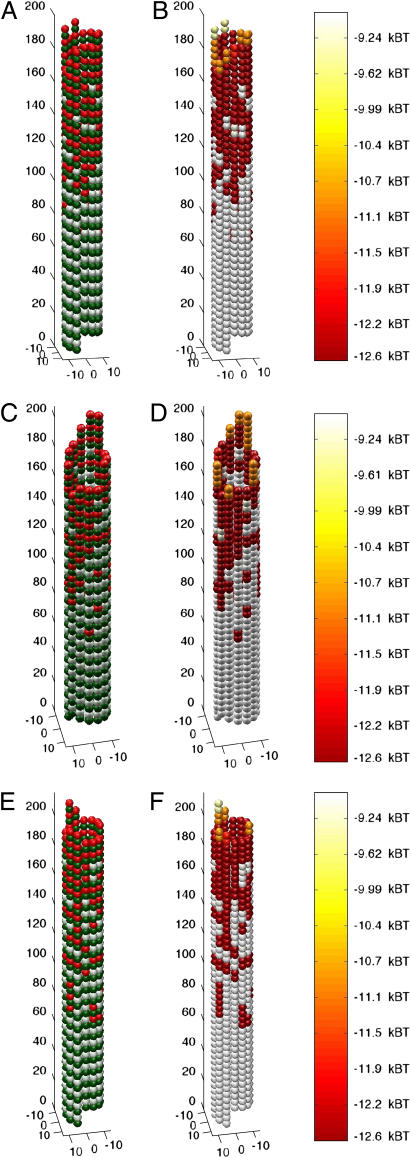
Simulations of growing microtubules started with a blunt-end and a GTP-cap as described above were allowed to assemble for 1000 events, which could include association, dissociation, and hydrolysis events, with rates assigned as described in the Methods. Shortening microtubules were simulated in the same manner, with the exception that shortening microtubules began without a GTP-cap. Growing microtubules at k₍₊₎ = 2 × 10⁶ M⁻¹ s⁻¹ typically displayed blunt ends, whereas short sheetlike protofilament extensions were sometimes formed (Fig. 3). There was no apparent bias in the appearance of these sheetlike extensions with respect to the location of the seam. Shortening microtubules at k₍₊₎ = 2 × 10⁶ M⁻¹ s⁻¹ displayed either frayed or blunt ends (Fig. 4), consistent with electron microscopy observations of disassembling microtubules. Growing and shortening microtubules at k₍₊₎ = 4 × 10⁶ M⁻¹ s⁻¹ were similar to microtubules at k₍₊₎ = 2 × 10⁶ M⁻¹ s⁻¹, with the exception that extensions did not form on growing microtubules (not shown). Long sheetlike extensions were not observed for simulated growing microtubules, although this may be reflective of the relatively short simulation interval (1000 events).

FIGURE 3.

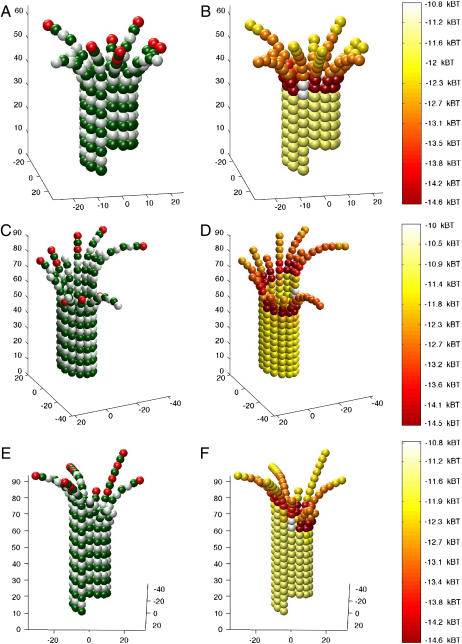
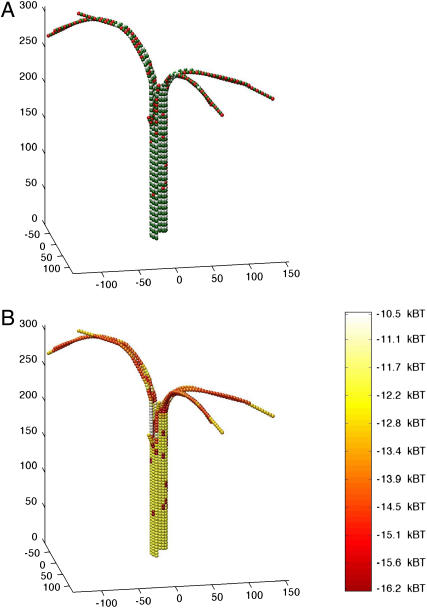
Simulated growing microtubule tips have either blunt ends or short sheetlike extensions. Microtubules started in a blunt, GTP-capped configuration in the presence of 10 μM tubulin-GTP (k₍₊₎ = 2 × 10⁶ M⁻¹ s⁻¹). GTP-caps were initialized to four layers of dimers (52 dimers total) and simulations were allowed to run for 1000 events, including association, dissociation, and hydrolysis, to produce the final configurations shown. (A, C, and E) Structure and GTP state of growing microtubule tips, three typical examples of assembly. Green monomers are α-tubulin. White monomers are β-tubulin with GDP content. Red monomers are β-tubulin with GTP content. (B, D, and F) Mechanochemical energy state of microtubule tips. The same microtubules represented in A, C, and E, respectively, are used to show mechanochemical energy state. Spectral color-coding indicates total chemical and mechanical energy for each dimer as given in the color scale to the right, with red being most stable and white the least.

FIGURE 4.

Simulated shortening microtubule tips have either frayed or blunt ends. Microtubules started in a blunt, uncapped configuration in the presence of 10 μM tubulin-GTP (k₍₊₎ = 2 × 10⁶ M⁻¹ s⁻¹). Simulations were allowed to run for 500 events, including association, dissociation, and hydrolysis, to produce the final configurations shown. (A, C, and E) Structure and GTP state of shortening microtubule tips. Three typical examples of disassembly are shown. Green monomers are α-tubulin. White monomers are β-tubulin with GDP content. Red monomers are β-tubulin with GTP content. (B, D, and F) Mechanochemical energy state of shortening microtubule tips. The same microtubules represented in A, C, and E, respectively, are used to show mechanochemical state. Spectral coding indicates total chemical and mechanical energy for each dimer, with red being most stable and white the least.

Microtubules with sheetlike extensions are more likely to undergo catastrophe than microtubules with blunt ends

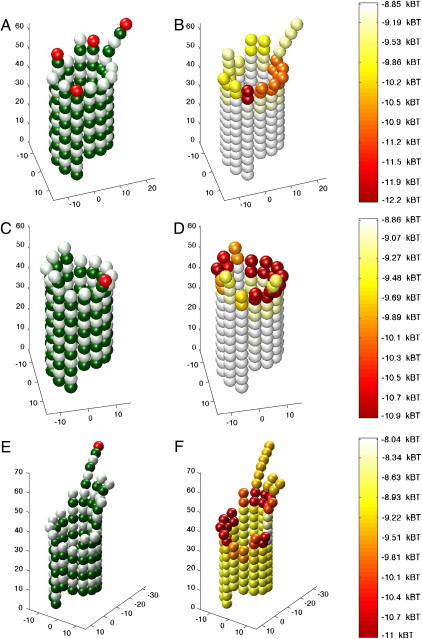
Arnal et al. (37) proposed that oncoprotein 18 (Op18) promotes catastrophe by supporting the switch of a microtubule tip from a sheetlike extension to a closed blunt-end. This hypothesis was consistent with an earlier proposal that blunt-end microtubules are under greater mechanical stress than relaxed sheets, and that this greater strain forces the end to fall into disassembly (5). We tested this idea with the model by simulating catastrophes with two representative configurations for a blunt end and a sheetlike end, and calculated the mechanical energy changes required to reach a state of rapid shortening. The tip of the blunt-end microtubule ends with a complete level of one helical turn, so that there is one protofilament that lacks three monomeric neighbors on one side, with the rest of the end closed (Fig. 5 A). The tip of the sheetlike end is tapered to create a fissure on one side (Fig. 5 F), with dimers along the tapered-edge lacking neighbors.

FIGURE 5.

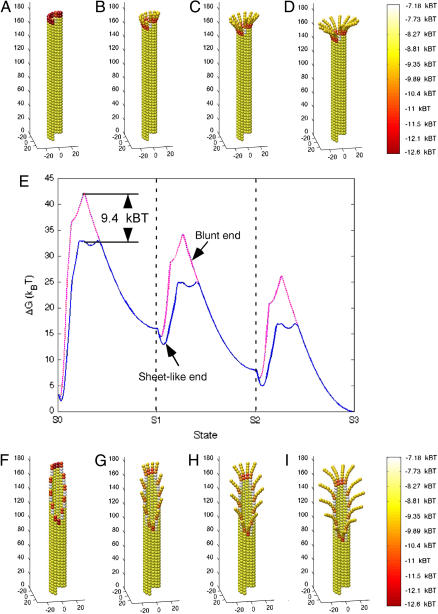
Energy analysis of blunt-end and sheetlike microtubule tips undergoing catastrophe. Simulated microtubules with a tubulin-GTP cap one-layer-deep were adjusted (i.e., peeled outward) to produce a catastrophe-like final state (S3). State 1 (S1) was achieved by curling the second layer from the top radially outwards at 22° (B and G). Subsequent states were achieved by repeating this step one-layer-deeper per state (C, D, H, and I). Energy was calculated at 100 intervals between states to produce the energy plot in E. Diagrams of each state (A–D (blunt end) and F–I (sheetlike end)) are aligned with the energy plot (E). Blunt-end microtubules (dashed magenta line) pass through a higher energy intermediate (∼9.4 k_BT higher) than sheetlike microtubules (solid blue line) as the catastrophe progresses from state 0 (S0) to state 1 (S1) (E). This analysis indicates that sheetlike microtubules are e^9.4 (∼22,000) times more likely to undergo a catastrophe by this particular pathway (see text for details).

Fig. 5, A–D and F–I, display a graphical representation of these microtubules, where there is a tubulin-GTP cap of one dimer per protofilament (13 dimers total, tubulin-GTP not indicated in figure). Splaying is imposed in a stepwise procedure, where the second layer of dimers from the tip are curled to 22° to produce microtubules as seen in Fig. 5, B and G. The next step is to curl-out the third layer from the end 22° to produce microtubules as in Fig. 5, C and H. Finally, the fourth layer from the end is curled-out 22° to produce microtubules as in Fig. 5, D and I. Total energy was calculated at 100 intervals between states for both the blunt-end and sheetlike microtubule. Energy is spectrally coded in Fig. 5, A–D and F–I, where the total energy is the sum of the total chemical thermodynamic energy of binding and the total energy of mechanical strain. Note that there is a collar of low-energy dimers at the point where dimers peeled away from the microtubule lattice (as predicted by Janosi (8)). The energy state of the dimers in this collar is lower than other dimers because dimers in the collar can simultaneously relax mechanical stress by curling and maintain lateral bonds by remaining in close proximity to neighboring dimers.

The relative probabilities of these structures undergoing catastrophe was evaluated by analyzing their respective energetics. Fig. 5 E shows the standard free energy change (ΔG°) plotted as a function of the microtubule state. The likelihood (L_A) of being in one state (A) relative to another state (B) is given by Boltzmann's Law as

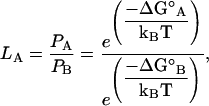(25)

where ΔG° indicates the energy change each event would incur upon the system. For example, if L_A = 4, then state A is four-times more likely than state B. This likelihood was calculated for microtubules transitioning from a starting configuration associated with growth S0 (Fig. 5, A and F) to a configuration associated with rapid shortening S1, where protofilaments are splayed outwards at 22° per dimer (Fig. 5, B and G). Transitions for both structures had a high-energy intermediate between S0 and S1. This transition intermediate was 9.4 k_BT higher for the blunt-end microtubule than its counterpart for the sheetlike microtubule, indicating that the sheetlike microtubule is e^9.4 (∼22,000) times more likely to undergo catastrophe in this manner than the blunt-end microtubule (Fig. 5 E). This analysis indicates that sheetlike microtubules are more likely to be an intermediate to catastrophe than blunt-end microtubules.

Partial GTP-cap configurations cause pauses in microtubule assembly

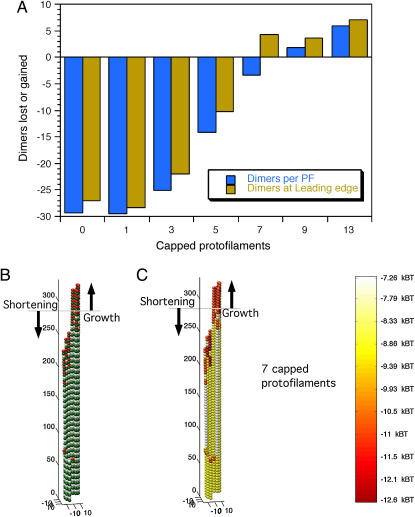
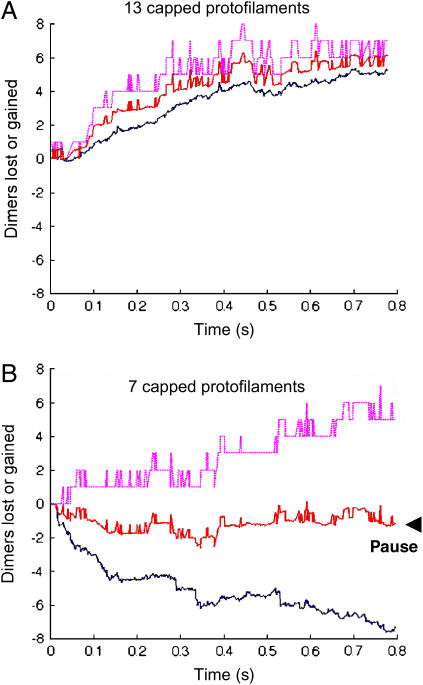
To assess GTP-cap requirements for the persistence of assembly, microtubules were simulated with GTP-caps over a range of cap integrity levels. Caps were placed at the ends of simulated blunt-end microtubules with a cap-depth of four dimers. The number of capped protofilaments varied from 0 to 13 as follows: 0, 1, 3, 5, 7, 9, and 13. For experiments with more than one capped protofilament, all capped protofilaments were assigned positions adjacent to each other. These starting configurations were then each simulated for 500 events to determine which configurations would result in net assembly and which would result in net disassembly of polymer. Simulated partial caps were observed to render stability to a portion of the microtubule end, so a simple metric was developed to examine this behavior. Microtubule polymer assembly or disassembly was calculated by counting the total dimers lost or gained. The leading-edge position was also calculated, and this was defined as the length of the longest protofilament. Total polymer assembly was normalized to the leading-edge metric by dividing the total loss or gain of dimers by the number of protofilaments. These simulations indicate net polymer assembly with nine or more protofilaments capped, and net polymer disassembly with five or fewer protofilaments capped (Fig. 6 A). Simulated microtubules with seven capped protofilaments grew their leading edge, although they had a net loss of polymer, meaning that a section of the microtubule grew, whereas another section shortened (Fig. 6, B and C). Length-versus-time plots demonstrate the relationship between the leading edge and overall polymer loss or gain for microtubules with 13 capped protofilaments (a full cap) and for microtubule with seven capped protofilaments (a partial cap) (Fig. 7). The leading edge and the total polymer gain or loss was averaged to approximate the measurement that would be made by video-enhanced differential interference contrast (VE-DIC) microscopy. This approach demonstrates a pause for the microtubule with seven capped protofilaments compared to the microtubule with 13 capped protofilaments, which grew at ∼2 μm min⁻¹ (Fig. 7).

FIGURE 6.

Effects of partial GTP cap configurations. Simulations were run for 500 events with caps that were initialized to four-dimers-deep on microtubule blunt end tips and had varying numbers of capped protofilaments. (A) There is net polymer gain and growth of the leading edge for microtubules with nine or more capped protofilaments and net polymer loss and shortening of the leading edge for microtubules with five or fewer capped protofilaments. (B and C) Final state of a simulated microtubule with seven capped protofilaments. The horizontal shaded lines indicate the starting length of the blunt-ended microtubule. Note simultaneous growth of the leading edge and the overall loss of polymer (A, B, and C).

FIGURE 7.

The number of dimers lost or gained for 13 capped protofilaments (A) and for seven capped protofilaments (B) was simulated. Simulations began with tubulin-GTP four layers deep in each experiment, with 13 × 4 = 52 total tubulin-GTPs in A and 7 × 4 = 28 total tubulin-GTP in B. Solid blue lines indicate total dimers gained or lost per protofilament. Dashed magenta lines indicate dimers lost or gained when measuring the leading edge, or longest protofilament. It is reasonable to suppose that the microtubule length recorded by VE-DIC microscopy would be approximately the average of the leading edge and the average polymer loss or gain (red lines). The experimentally recorded growth rate in A would thus be ∼2 μm min⁻¹, but in B there would appear to be a pause, without growth or shortening.

Simulated XMAP 215 can enhance growth to rates measured experimentally without invoking special mechanisms and promotes formation of protofilament extensions

We examined the effects of introducing XMAP215 to simulations of growing and shortening microtubules. First, the predicted energetic effects of XMAP215 (14,15) were applied to simulations of disassembling microtubules to ensure that the correct rate of disassembly was achieved. We previously predicted that XMAP215 supports longitudinal tubulin associations by −3.6 k_BT and antagonizes lateral associations by 0.35 k_BT per dimeric lateral association via promotion of curling (14,15). For this model, using the previously predicted longitudinal support estimation (−3.6 k_BT) and modestly increasing the energetic preference for dimer curling by 0.85 k_BT produced the observed shortening rate (−60 μm min⁻¹) for microtubules with XMAP215 present. Note that differences in how we account for energy effects on lateral associations in these two models largely account for the apparent energy discrepancy; in the previous model we attributed the energy change caused by XMAP215 directly to lateral associations (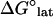) as a fixed amount per dimeric association, whereas in this model we attribute the energy change caused by XMAP215 to the curling energy (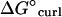), thereby stressing lateral associations rather than directly weakening them. The appearance of simulated shortening microtubules matched observations with the formation of rams' horns peeling away at the microtubule tip (unpublished observations; see also Fig. 8).

FIGURE 8.

Simulated microtubule disassembly in the presence of XMAP215. Simulated disassembly, with an XMAP215-induced change in standard free energy of −3.6 k_BT for longitudinal bonds, and +0.85 k_BT for curling energy, promotes rapid disassembly (∼−60 μm min⁻¹) of uncapped microtubules. Simulations were allowed to run for 500 events to produce the final states shown, which recapitulate the observed appearance of rams' horns during disassembly in the presence of XMAP215.

With the above adjustment to extrinsic curling energy, simulations showed that XMAP215 strongly enhances a kinetic preference for assembling microtubules to form pronounced protofilament extensions compared to that observed with pure tubulin. At k₍₊₎ = 2 × 10⁶ M⁻¹ s⁻¹, multiple protofilament extensions formed during assembly in the presence of XMAP215 (Fig. 9).

FIGURE 9.

Simulated microtubule assembly in the presence of XMAP215. Assembly with XMAP215 was simulated for 1000 events to produce the final state shown. Simulated XMAP215 speeds assembly approximately fivefold and promotes the formation of long, curved protofilament extensions. Parameter values used were the same as in Fig. 8.

DISCUSSION

Here we described a computer simulation of microtubule assembly dynamics that can serve as a tool with which to analyze the interplay between mechanics, kinetics, and thermodynamics. The simulation was used to assess models and make specific predictions, including:

1. Making a prediction of the flexural rigidity of microtubules.

2. Growing blunt ends are less likely to undergo catastrophe than growing sheetlike ends.

3. Partial uncapping leads to pausing.

4. XMAP215 strengthens longitudinal bonds (by ∼3.6 k_BT) ands weakly antagonizes lateral bonds (via supporting curling by ∼0.85 k_BT).

Microtubule rigidity and stability

Predictions made by the mechanical model for flexural rigidity agree well with the work of Felgner et al. (24), and with the work of Venier et al. (27) (Tables 1 and 2). Interestingly, our simulations show that a decrease in intrinsic flexural rigidity would cause an increase in microtubule kinetic stability, causing a rapid transition to growth with a less-than-twofold decrease in flexural rigidity. We use the term intrinsic here to distinguish the flexural rigidity that is intrinsic to the tubulin polymer from the flexural rigidity that results from cross-bridging tubulin interactions, as some MAPs are expected to do. Taxol, however, does not cross-bridge dimers and so can be thought of as a modulator of intrinsic flexural rigidity. There is a consensus that taxol reduces the flexural rigidity of microtubules by approximately one-half (with the exception of Mickey and Howard (26), although the absolute measure of flexural rigidity varies across different labs (7,24,25,27)). This is consistent with our simulations showing that lowering EI_p causes increased microtubule stability. Given the relationship between EI_p and stability, we predict that taxol's entire stabilizing effect on microtubule assembly results from its ability to decrease intrinsic flexural rigidity (Fig. 2).

Likelihood of catastrophe for blunt and sheetlike growing microtubule tips

Simulations comparing the likelihood of two different structures, sheets and blunt ends, to undergo a catastrophe, demonstrated that sheetlike ends can more easily transition to catastrophe than blunt ends. Arnal et al. (37), however, have proposed that blunt ends are a more likely intermediate to catastrophe. That proposal was based on electron micrograph (EM) evidence showing that a greater proportion of microtubules were blunt-ended compared to controls when Op18 was added to the Xenopus egg extracts. They proposed that Op18 somehow causes a preference for blunt-ended microtubules, which was thought to be a likely intermediate to catastrophe. We propose that the Arnal EM data show the structures remaining after catastrophes occurred, rather than intermediates to catastrophe. Contrary to the authors' interpretation, this would suggest instead that the blunt-end microtubules are the most catastrophe-resistant in the presence of Op18. This latter interpretation is consistent with our analysis.

The idea that seam closure, or the formation of a blunt microtubule end, portends a catastrophe has also previously been put forward as an interpretation of EM data of growing microtubules, where most growing microtubules were observed with a sheetlike appearance in which sheet length increased and broadened over time (5). The seam-closure model was proposed to explain the loss of GTP subunits, which are conceived to undergo forced hydrolysis upon closure at the seam. This model is problematic, because there is no reason why the blunt ends formed at the beginning of the growth phase should remain growing, whereas blunt ends formed later due to seam closure should undergo catastrophe. According to this model, microtubules would never grow. Contrary to the model proposed by Chretien et al. (5), our model supports an interpretation where sheetlike microtubules are the most likely candidates for catastrophe, and that the sheetlike portion of the microtubule is quickly lost at the onset of shortening, as dimers at the sheet tip edge are expected to dissociate more quickly than dimers composing the closed portion of the microtubule. Dimers on the sheet tip edge of the microtubule are subject to a greater frequency of loss because they have fewer thermodynamic chemical interactions with the lattice (i.e., they lack one of their potential neighbors), making them more readily lost from the microtubule tip and less resistant to curling propagated by tubulin-GDP dimers below them in the lattice (Fig. 5). Thus, the GTP cap likely starts out as a blunt ring that is very stable early in the growth phase, then eventually evolves to a sheetlike projection (e.g., via partial uncapping as in Figs. 6 and 7) that is relatively less stable owing to terminal tubulin-GTP subunits having a single lateral neighbor. At this later point in its growth phase, the GTP cap is now far more prone to catastrophic loss than it was in the earlier blunt configuration. This explanation is also consistent with the observation that nascent microtubules (i.e., blunt) are less likely to undergo catastrophe than older (i.e., sheetlike) microtubules (38–41). Therefore, our model explains both the EM data, where microtubules start out blunt and evolve sheetlike projections over time, and the in vitro assembly data, where catastrophe rate increases during a growth phase.

Partial uncapping as the origin of pauses in microtubule growth

Pauses in microtubule assembly have been observed in vivo and in vitro, but the molecular events occurring during a pause have not been previously explained. We found that simulated microtubules with a partial GTP cap could enter a pause state, without apparent net growth or shortening. Although these microtubules did have a net loss of total polymer, they had a net growth of the leading edge. It is likely that measurements made with VE-DIC microscopy would detect no net change in length for microtubules in this state. This analysis provides the first explanation of the pause state, and may yield insight into possible mechanisms for microtubule-stabilizing drugs such as nocodazole (42) and vinblastine (43) that induce a sustained pause state.

Effect of XMAP215 on microtubule assembly and disassembly

XMAP215 has been observed to both increase the growth rate (stabilize) and increase the shortening rate (destabilize) of microtubules (44). More recently, XMAP215 has been identified as a potent destabilizer of microtubules grown with GMPCPP (45). The mechanism of microtubule stabilization by GMPCPP may be ascribed to mimicry of the GTP-bound state or the intermediate GDP-P_i-bound state (46). It is thus reasonable to suppose that tubulin dimers with bound GMPCPP have weaker interactions than dimers with bound GTP, but have stronger interactions than those formed by dimers with bound GDP. A simple model consistent with the observation that XMAP215 causes rapid depolymerization of GMPCPP-stabilized microtubules (45) is that GMPCPP-stabilized microtubules have weaker lateral interactions between dimers than microtubules grown with GTP, and that further weakening of lateral interactions by XMAP215 (14,15) causes rapid disassembly.

Some models for the enhancement of microtubule growth rate by XMAP215 invoke special mechanisms for the rapid assembly achieved. One model suggests that XMAP215 may come preloaded with dimers and deliver dimers when it binds to microtubules (47). Another model suggests that XMAP215 binds microtubules and allows dimer loading on XMAP215 away from the leading edge of the microtubule tip, a so-called guidance model (47,48). Both of these models were suggested to account for the rapid rate of assembly induced by XMAP215. A third model, which invokes no special mechanism, proposes that XMAP215 simply provides additional bonding interactions for incoming dimers as they bind to the microtubule tip (14,15). This may be thought of as a simple guidance model, where k₍₋₎ is reduced by the additional bonding interactions. We tested the feasibility of this third model by adjusting bond parameters in the mechanical model to account for the presence of XMAP215 (see above), and found that the experimentally observed assembly rate behavior could be achieved by adding the predicted energetic support for longitudinal associations. When XMAP215 was present in these simulations, growth rate increased from 2 μm min⁻¹ to 9 μm min⁻¹ at k₍₊₎ = 2 × 10⁶ M⁻¹ s⁻¹, compared with pure 10-μM tubulin. These results demonstrate the feasibility of a simple guidance model for the action of XMAP215 on assembly and disassembly. We propose this model as the simplest model consistent with the published data, although our simulations do not eliminate more complex models from consideration. It will be interesting to see whether high-resolution observation of tubulin addition and loss events (on the nanoscale) can discriminate between these competing models.

Further applications of the mechanical model

Seams in the microtubule lattice are thought to be energetically weaker than other lateral interactions in the microtubule, and recent theoretical analysis of interprotofilament interaction energies supports this claim by showing that B-lattice interactions are stronger than A-lattice interactions (21). Based on those findings, it can be estimated that monomeric α-β and β-α lateral interactions (seam) are ∼2.5 k_BT weaker than α-α or β-β lateral interactions (non-seam). Potential effects of different lattice types and of the B-lattice seam may be analyzed by contrasting simulations of the B-lattice with simulations of the A-lattice, and by simulating microtubules with weaker lateral interactions at the seam, respectively.

The mechanical model presented here may be further refined to model timescales long enough to enable estimation of transition frequencies. Our earlier pseudo-mechanical model showed a steep dependence of transition frequencies on tubulin-GTP concentration that is not consistent with the measured values (14,15), and this remains an open problem. The pseudo-mechanical model must lack a representation of some important aspect of assembly. This representation could be the full mechanical representation presented here in the mechanical model.

One alternative is that surface area changes at dimer interfaces increase the complexity of the dynamics. Ravelli et al. (49) have recently shown significant differences in the surface area of interacting dimers, including a change in longitudinal interfaces from ∼3000 Ų for straight dimers to a surface of ∼2000 Ų for curled dimers. This new data remains to be incorporated in the model and may introduce unforeseen complexities.

A third possibility is that there is some mechanism related to the speed of assembly that promotes a shallow dependence of transition frequencies on tubulin-GTP concentration. For example, the occurrence of lattice defects could increase with increased speed of assembly. At higher tubulin-GTP concentrations, more lattice defects would accumulate, possibly making the microtubule tip more susceptible to catastrophe. Conversely, microtubules grown at lower concentrations may grow more slowly and accurately, and hence would be less likely to undergo catastrophe than predicted by the pseudo-mechanical model. This presents an attractive explanation for the discrepancy between modeled and observed transition frequencies over a range of concentrations, but one that is difficult to test because of the problem of precisely defining “lattice defect” for incorporation in the algorithm. The many possibilities make any attempt at modeling challenging, as it is uncertain how to ascertain the frequency of particular types of defects and relate them to tubulin-GTP concentration. Incorporation of lattice defects in microtubule assembly remains as an interesting open problem for future modeling attempts.