A Model for Diffusion in White Matter in the Brain

Abstract

Diffusion of molecules in brain and other tissues is important in a wide range of biological processes and measurements ranging from the delivery of drugs to diffusion-weighted magnetic resonance imaging. Diffusion tensor imaging is a powerful noninvasive method to characterize neuronal tissue in the human brain in vivo. As a first step toward understanding the relationship between the measured macroscopic apparent diffusion tensor and underlying microscopic compartmental geometry and physical properties, we treat a white matter fascicle as an array of identical thick-walled cylindrical tubes arranged periodically in a regular lattice and immersed in an outer medium. Both square and hexagonal arrays are considered. The diffusing molecules may have different diffusion coefficients and concentrations (or densities) in different domains, namely within the tubes' inner core, membrane, myelin sheath, and within the outer medium. Analytical results are used to explore the effects of a large range of microstructural and compositional parameters on the apparent diffusion tensor and the degree of diffusion anisotropy, allowing the characterization of diffusion in normal physiological conditions as well as changes occurring in development, disease, and aging. Implications for diffusion tensor imaging and for the possible in situ estimation of microstructural parameters from diffusion-weighted MR data are discussed in the context of this modeling framework.

INTRODUCTION

Nuclear magnetic resonance imaging (MRI) has demonstrated that the diffusion coefficient of water in brain tissue decreases quickly after stroke and other brain injuries by ∼30–40% (1). The fact that diffusion effects can be visualized within minutes, much earlier than any other imaging modality (1,2), has life-saving implications (3). Diffusion tensor imaging (DTI) (4) for noninvasive imaging of the fiber tracts in white matter has become an indispensable tool for studying the brain and managing stroke and other disorders such as tumors, Alzheimer's disease, multiple sclerosis, dyslexia, and schizophrenia (4–7). A better exploitation of diffusion MRI will come from a better understanding of diffusion in tissues.

Biological tissues are multicompartmental heterogeneous media composed of cellular and subcellular domains. Diffusion of water is very sensitive to the local environment in tissues, and is affected by the packing geometry of the cells and their membrane permeability that controls the exchange of molecules across the membranes (8,9). The cellular structures of tissues are in the micron range whereas conductivity and diffusion measurements are generally made over a macroscopic length scale, typically in the millimeter range (5,10,11). The measured signal originates from all the molecules that are present, i.e., both from the molecules diffusing within the cells and the molecules exchanging between these microcompartments. The term apparent diffusion coefficient (ADC) was coined to reflect the fact that the measured diffusion coefficient of water in tissues is reduced from its bulk value due to geometrical restrictions and permeation across cell membranes. A change in the measured macroscopic transport properties (in millimeter range) reflects the underlying property changes of these compartments.

The primary purpose of this article is to provide analytical results for the long-time ADC (actually apparent diffusion tensor (ADT)) in a simplified model of brain white matter, to probe the dependencies of the ADT on tissue structure and composition. In principle, the diffusion coefficient in individual compartments, packing geometry, intercellular spacing, axon diameter, myelin sheath thickness, and permeability of membranes should all affect the measured apparent diffusion coefficient ADC, yet the relationship between these microstructural quantities and parameters, and the macroscopic ADC remains obscure. This gap has hindered the full exploitation of diffusion-weighted nuclear-magnetic-resonance-based techniques (NMR) for studying the brain and its disorders. Specifically, we compute the macroscopic diffusion coefficient both parallel and perpendicular to the axis of symmetry of a neuronal bundle and relate these quantities to microstructure and compositional parameters.

Water diffusion in tissue has been studied previously both analytically and numerically by many and it is not possible to review the literature here. Some relevant references can be found in Nicholson (10), Sotak (12), Norris (13), Beaulieu (14), and other articles (8,15–26). Szafer et al. (19) considered a periodic array of boxes (cells) surrounded by partially permeable membranes, embedded in an extracellular medium. The fact that intracellular and extracellular diffusion coefficients may differ was taken into account. The results were applied to the changes occurring in ADC after ischemic insults to brain tissue. They found that although membranes affect ADC significantly, the change results from the combined effect of changes in cellular volume fraction, and extracellular and intracellular diffusion. Ford et al. (17,18) modeled white matter as a bundle of cylinders and used a numerical simulation of water self-diffusion among permeable cylinders to predict the dependence of MR-based apparent diffusion coefficients on axonal separation, barrier permeability, and diffusion time t. Recently, Hwang et al. (27) employed the finite-difference method on histological images for simulating restricted diffusion in myelinated axons. The literature had been reviewed well by Hwang et al. (27), who stated that the thickness of the myelin sheath had been ignored in all studies before theirs. They (27) validated their finite-difference scheme against known analytic solutions for diffusion in a cylindrical pore and in a hexagonal array of cylinders that do not possess thick skins. Specifically, Hwang et al. compared their simulation for cases: a), of a cylindrical pore surrounded by an impermeable medium, and b), hexagonal arrays of permeable cylinders using the results of Perrins et al. (28,29) for uncoated cylinders. Presumably, such numerical studies would benefit from the solutions provided here in which analytical results for the thick-walled tube pack are provided. Here, among other things, we present results for hexagonal packs of coated cylinders that could serve as a test system to validate such numerical calculations.

Anatomical sections of white matter reveal that the myelin sheath on neurons is thick; see Fig. 1. To model myelin, we incorporate a finite coating thickness having transport properties represented by its fluid concentration and diffusion coefficient. The limit of infinitesimal layer thickness is just a special case, characterized by a lumped permeability parameter, κ. In our study we consider composite cylinders with an inner core of radius r_c and an outer radius r_s such that the thickness r_s − r_c of the sheath can vary. The separation between the centers of cylinders is L. In the model, we treat the myelin and membrane as a composite and the permeability is determined by the combined effect of the membrane and the myelin sheath. The myelinated axon is actually a heterogeneous structure having long myelinated links interrupted by short nodes of Ranvier; see Fig. 1. Both these segments contribute significantly to the electrical properties of the myelinated axon, and are presumed to do the same for the water diffusion properties. None of the previous works described above nor our work, adequately attributes the overall water diffusion properties to the nodal membrane, membrane of the myelinated axon, or the myelin itself.

FIGURE 1.

A schematic diagram of a myelinated axon. The axonal membrane contains short active regions, nodes of Ranvier, which are joined by long passive segments insulated by myelin. The outer radius of the axon is r_s; its inner radius r_c. Diffusion across myelin is hindered by layers of lipid bilayers (in addition to the myelin sheath). A separate membrane skin can be added to our calculation, but is not considered here. In the model, we treat the myelin and membrane as a composite and the permeability is determined by the combined effect of the membrane and the myelin sheath.

Clearly, the parameter space is too large to explore completely using numerical simulations. In this case, analytical expressions for the parallel and perpendicular ADCs, ADT, and other related quantities, are useful in assessing whether some variables are more important than others in determining the aggregate diffusion behavior within a biological range of parameters. This we illustrate by performing a sensitivity analysis that computes a fractional change in a macroscopic dependent variable for a given fractional change in an independent variable or parameter.

GENERAL FORMULATION

Analysis of transport processes, such as diffusion, electrical conduction, heat transfer, etc., in composite media is a large and well-developed subject (30,31). Interestingly, the similarity in structure and form of their governing equations allows solutions for one type of transport process to be mapped to another, provided that the analogous variables in the constitutive equations can be identified (30,31). In the case of diffusion, what is often neglected is that the relevant constitutive parameter—that can be likened to electrical conductivity or the dielectric constant—is the product of the concentration and the diffusion coefficient (32,33). This extra factor of concentration comes from the thermodynamic formulation of the diffusion process, discussed below.

Many methods are available for measuring the diffusion coefficient (34). The results derived here can readily be used to analyze a diffusion experiment that measures concentration directly, by releasing a precise amount of a nonabsorbing marker (10) from a point source and measuring the resulting concentration at a known distance, or by use of other markers such as tritium or fluorescent dyes (34). In NMR measurements, the diffusion is measured from the part of the signal decay that is due to incoherent diffusive motion in the presence of an external magnetic field inhomogeneity. However, it is generally entangled with relaxation of magnetization (T₁, T₂). The relaxation processes of a given spin (typically proton) that arise from the fluctuating field of the other spins are important, and can be different in different regions in general (22). However, for long diffusion times, the relaxation appears to be single exponential (22). Chin et al. (35) concluded that for white matter, the overall relaxation is given by a single exponential (at long times), the sensitivity of measured ADC to relaxation is small, and the difference in rate of relaxation in different compartments can be neglected (17,18,35). Thus, the overall relaxation of magnetization is factored out and the steady state (i.e., long times) diffusion coefficient in these tissues can be measured by NMR.

Diffusion currents are driven by gradients in the Gibbs chemical potential,

(1)

Here R is the gas constant, T is the temperature, C is the concentration of the substance that is diffusing, a is the activity coefficient, and μ⁰ is the chemical potential of the substance in its standard state. A thermodynamic view of diffusion and a discussion of how the gradient of chemical potential acts like a force can be found in any standard thermodynamics book (36). The variable μ⁰ is independent of position; we will assume either the substance is ideal (ln a ≡ 0) or ln a does not vary with position, and the temperature is uniform throughout. To be explicit, the particle current density is given by the constitutive relation

(2)

We use the analogy of Eq. 2 and the corresponding constitutive relations between electric currents (displacement or conduction) and electric potential gradient via dielectric constant or electrical conductivity. We can apply the solutions for electrical conductivity or dielectric constants for composite media made up of coated cylinders (37,38) (for spheres, see Torquato and Rintoul (39)) by replacing the electrical potential, V(r, θ), by a chemical potential, μ(r, θ) = μ⁰ + RT ln [C(r, θ)], (we lump position-independent R T ln a with μ⁰). For the corresponding diffusion problem, the conductivities or dielectric constants of each region are replaced by the product of the diffusion coefficient and the concentration of the corresponding region. There are other terms in the chemical potential that are not displayed here explicitly—the initial equilibrium concentration differences in different regions are maintained by such differences in chemical potentials for the corresponding regions. Here, as in the other transport problems, we need to consider perturbations around the initial chemical potentials (36,33).

The additional factor of concentration plays an important role in the tortuosity factor of the effective diffusion coefficient (32,40). In a well-connected porous medium made up of impenetrable grains, the measured diffusion coefficient, D, of the interstitial fluid approaches, at long times, a nonzero finite value, that is the bulk diffusion coefficient, D₀, reduced by a geometrical factor, known as the tortuosity α. For an isotropic medium,

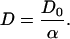(3)

The coefficient α is a dimensionless number that defines the dc limit of diffusion and conductivity in a restrictive geometry in terms of diffusion and conductivity of the bulk fluid, Eq. 4, below. The tortuosity plays an important role in various transport processes in porous media. In porous media made of insulating grains, the conductivity of the medium σ is proportional to the conductivity of the interstitial fluid σ_w through a geometrical factor F, which also relates to α = Fφ, where φ is the porosity, i.e., the volume fraction of fluid,

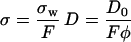(4)

(5)

The extra factor of φ for D, in Eq. 4, comes from the fact that concentration enters into a transport problem involving diffusion (32) and not one involving electrical conduction. We use the symbol φ to be consistent with the literature and to draw attention to a basic difference between φ and the corresponding volume fraction of extra axonal fluid in our model, 1 − f, where f is the fraction of volume occupied by the coated cylinders. Note that in Eq. 4, the only conducting phase is the interstitial fluid, in contrast to the case of white matter where the intraaxonal fluid may also be conducting. The details of the computation of the effective diffusion coefficient for packs of coated cylinders are discussed in Appendix I.

We use a subscript c to denote the core, s to denote the sheath, and b to denote extraaxonal (bath) material; see Fig. 2. The equilibrium concentration and diffusion coefficients of the molecules under investigation inside the core are C_c0 and D_c, those inside the myelin sheath are C_s0 and D_s, and those outside are C_b0 and D_b. We will use C_c(r), etc., to denote perturbations to the corresponding equilibrium concentrations C_c0, etc. (33). The perturbations are due to an externally imposed concentration or chemical potential gradient, which can be likened to an electric field, E_ext, that is used in the corresponding problem of electrical conductivity or dielectric constant of composite media (28,37,38). D_b, the diffusion in the extraaxonal bath is hindered, due to the presence of glial cells and other tissues, and is presumably lower that the free diffusivity of water. We believe that the presence of glia in the extracellular space is consistent with an isotropic medium with a diffusion coefficient that is lower than that of free water.

FIGURE 2.

The unit cell for a square array of coated cylinders representing white matter with a myelin sheath. The equilibrium concentrations such as C_s0, etc., and corresponding diffusion coefficients D_s, etc., of each region as well as the inner and outer radii, r_c, and r_s, respectively, can be different. The cylinders can be made to touch each other by taking

We will consider both a square pack, Fig. 2, and a hexagonal pack of cylinders, Fig. 3. In both cases, the cylinder centers are separated by a distance L, the radius of the inner cylinder is r_c, and that of the outer is r_s, and thus the sheath thickness is given by Δt = r_s − r_c. Only the ratios of these lengths will appear in the answer. We do not expect to be able to infer the packing geometry from DTI experiments. We use the hexagonal geometry because the square lattice arrangements do not admit the high packing densities consistent with what has been reported in axon bundles in vivo (10). The hexagonal packing geometry permits regular but higher packing densities. The square lattice packing geometries are included for completeness.

FIGURE 3.

Nearest neighbors around the central cylinder of a portion of a hexagonal array of coated cylinders. To simplify, only one cylinder is depicted as coated, and only the outer radius is shown for the others. The Wigner-Seitz cell is shown by dashed lines (inner hexagon). Centers of cylinders are separated by a distance L, hence where r_s is the outer radius.

The boundary conditions are such that chemical potentials and normal particle currents are continuous at the interfaces:

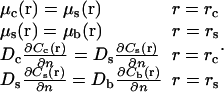(6)

Mathematical details are considered in Appendix I. If we denote the products of concentration and diffusion by ε, i.e., C_s0D_s = ε_s, etc., we can directly use the previous results (28,29,37,38), to compute the effective concentration times the effective transverse diffusion coefficient C_eff D_t,eff. Here, the effective concentration C_eff is:

(7)

The effective properties for coated cylinders depend on what Nicorovici et al. (37,38) call γ, the crucial quantity:

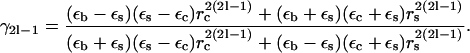(8)

The longitudinal effective diffusion coefficient D_l,eff is given by the volume averages:

(9)

for all packing geometries.

Before giving results for transverse diffusion coefficients for a specific packing geometry, a few general comments that hold for all packing geometries are useful. A reasonable measure of diffusion anisotropy can be given by the ratio D_l,eff/D_t,eff, which can be obtained from the ratio of Eqs. 9 and 27. Note that this ratio is independent of C_eff. Moreover, using the longitudinal and transverse ADCs, we can obtain an estimate for the angular profile of ADC as a function of the polar angle, θ,

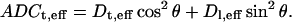(10)

This relationship, first introduced by Boss and Stejskal (41) results in a peanut- or pumpkin-shaped ADC profile when plotted versus the polar angle, θ. A rotationally invariant quantity that is proportional to the orientationally averaged bulk diffusivity is the trace of the diffusion tensor

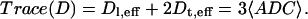(11)

〈ADC〉, the mean apparent diffusion coefficient, and the degree of anisotropy, are two very useful parameters routinely used in characterizing white matter.

In square (see Fig. 2) and hexagonally symmetric packs (see Fig. 3), the symmetry dictates (42) that the diffusion tensor be described by two principal diffusivities—one parallel to the axis of the cylinders and another perpendicular to it, lying in the transverse plane (i.e., diffusion is isotropic in the transverse plane and two transverse components of the tensor are identical). The form of the ADT in the principal frame of reference is given by

(12)

Square array

For a square array, 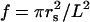is the fraction of volume occupied by the coated cylinders. As explained in Appendix I, to the lowest order in multipolar expansion, we obtain the Maxwell-Garnett formula:

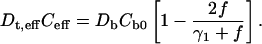(13)

A truncation to third order gives (37,38),

(14)

The higher-order corrections can be obtained in the manner outlined in Appendix I.

Hexagonal array

Although for the square lattice geometry, the maximum value of f is π/4 ≈ 0.785, published values of the intracellular space based on iontophoretic measurements are typically higher, ∼0.82 (10). To treat the physiological range of axon spacing, we must consider hexagonal (and possibly other) packing geometries that afford higher packing densities.

For a hexagonal array,

(15)

Thus, the maximum packing density is about f = 0.907. To the lowest order in multipolar expansion, we obtain again the Maxwell-Garnett formula, Eq. 13, the same as that for a square array. In fact, the Maxwell-Garnett formula holds for all structures, including disordered systems and is accurate for small f, i.e., in the dilute limit. Next to the same degree of accuracy as in Eq. 14 gives:

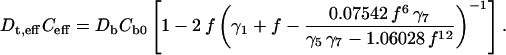(16)

In the absence of a sheath, Eq. 24 holds, and we recover Eq. 13 of Perrins et al.

SPECIAL CASES

Although the formulas given here are straightforward, they are still quite complex, and it is useful to consider a few limiting cases that give additional insight. For example, when the diffusivity of the molecules in myelin is extremely small compared to those of the intra- or extraaxonal fluid, the contributions from the interior part of the axon will be “screened out”, as shown below.

Thin myelin: permeability approximation

In the usual permeability approximation, the limit of thin skin is used where with 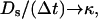giving rise to a jump condition:

(17)

Now we can see that Eq. 8 gives, with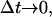

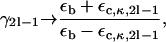(18)

where

(19)

All the results for longitudinal and transverse diffusion coefficients are easily generalized for the thin myelin case using Eq. 18 instead of the full Eq. 8.

Nearly impermeable myelin

Because a thick myelin sheath is nearly impermeable, and acts as a diffusion barrier, we expand the factor γ_2l−1 in Eq. 8 in a series (D_sC_s0)/(D_bC_b0),

(20)

to the linear order in (D_sC_s0)/(D_bC_b0).

All the results for longitudinal and transverse diffusion coefficients are easily generalized for the nearly impermeable myelin case by using Eq. 20 instead of the full Eq. 8. Note that Eq. 20 does not depend on properties of the core. This is intuitively obvious; when the diffusivity in the sheath is practically zero, it acts as a barrier so that D_t,effC_eff is dominated by diffusion outside the sheath and the core contribution drops out (is shielded out). In the electrical problem, this limit corresponds to an array of insulating cylinders with γ_2l−1 ≡ 1 and the effective conductivity is given by that of the extraaxonal fluid reduced by a formation factor determined completely by the geometrical structure factors {S_2l−1} and by f. Similarly, for diffusion, cellularity (i.e., the factor f and the geometrical structure factors ) determines D_t,effC_eff. Thus, the core properties drop out (in the lowest approximation); however, the effective concentration C_eff involves the properties of the core.

In the extreme limit, when C_c D_c = C_s D_s = 0, all transport comes from the bath molecules–but they have a tortuous path to follow in the transverse direction. The Maxwell-Garnett form for transverse diffusivity is D_t,eff = D_b/(1 + f), whereas D_l,eff = D_b. Note that for the case of electrical conductivity, the volume fraction of the conductive material will enter the expression for the longitudinal conductivity, but not for D_l,eff, due to the additional concentration factor mentioned earlier. In this approximation we can write the tortuosity tensor (we use a caret to distinguish it from the scalar counterpart) as

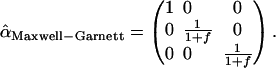(21)

To be explicit,

(22)

Similarly, for insulating cylinders of volume fraction f immersed in a bath of conductivity σ_w having a volume fraction φ = 1 − f, the overall conductivity tensor is

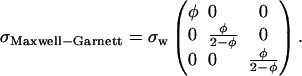(23)

No myelin

The results from Rayleigh (28) and Perrins (29) of uncoated cylinders can be used in this case. To be explicit if or the myelin sheath is effectively absent:

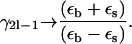(24)

All the results for longitudinal and transverse diffusion coefficients are easily generalized for the nonmyelin case using Eq. 24 instead of the full Eq. 8.

The diffusion tensor can still be anisotropic, even in the absence of a myelin sheath. Let us illustrate this using the lowest order of the Maxwell-Garnett form, Eq. 13, for transverse diffusivity:

(25)

Note that in Eq. 25 above, the system will be anisotropic even when D_b = D_c, but C_b ≠ C_c; the anisotropy vanishes only when C_b D_b = C_c D_c.

That there can be anisotropy even in the absence of a myelin sheath (and membrane) is obvious, although, as Beaulieu (14) notes, there is much confusion in the literature. To understand the anisotropy in absence of a sheath or membrane, consider, for example, the case when cylinders with high values of C_c D_c (containing highly diffusive molecules) are inserted in a bath with small values of C_b D_b (containing poorly diffusive molecules). The longitudinal transport, mainly dominated by the cylinders, can be high; whereas the transport perpendicular to the cylinder axes will be low, as the molecules within the cylinders have to diffuse through the bath in the transverse direction but not in the longitudinal direction. This phenomenon can be likened to resistors in series (transverse direction) and resistors in parallel. Recall that in our model, the sheath is a composite of membrane and myelin. Even without a membrane or myelin, one can observe anisotropy as long as the bundles are aligned and have different diffusivity from the “bath” material.

It is obvious how to incorporate terms involving higher powers in f, and refine the above formulas for effective diffusion or conductivity. We do not pursue that here because our main point is that the presence of the myelin sheath is not essential to cause the anisotropy in diffusion or conductivity.

RESULTS AND DISCUSSIONS

Analytical solutions for the ADT and quantities derived from it, such as the mean ADC, 〈ADC〉, and the degree of diffusion anisotropy, can be used to explore the effects of small changes in model parameters associated with normal conditions as well as a number of developmental and disease processes known to affect myelinated axon structure and function. For a particular set of assumed parameters, we can assess the relative importance of each microstructural parameter by computing the fractional change in the 〈ADC〉 or degree of diffusion anisotropy for a unit fractional change in a parameter of interest. This result provides us with a way to compare the relative importance of different independent experimental parameters in the model. We can also consider the effect of changes in these different parameters on the 〈ADC〉 and anisotropy ratio for tissue swelling accompanying vasogenic edema (increasing L) or deswelling (decreasing L) accompanying hydrocephalus. We can consider the effect of redistribution of fluid from the extracellular to intracellular space that occurs in acute stroke or cytotoxic edema (decreasing L, increasing r_c and r_s). We can also consider the effects of myelination occurring in normal development (increasing r_s), or dysmyelination (decreasing D_s) and demyelination (decreasing r_s) that occur in diseases like leukodystrophy and multiple sclerosis, respectively.

For comparing the relative importance of different independent experimental parameters, it is useful to choose parameters that are representative of white matter in the central nervous system (CNS), and then consider perturbations in these parameters associated with various developmental and disease states. For the analysis of sensitivity to perturbations, we assume the initial values for diffusion coefficients and concentrations, as we do not know their exact values. These assumed numbers are either based on values known for other cells, such as erythrocyte (33), or based on reasonable guess. The sensitivity of measured diffusion to the changes in underlying parameters, rather than their actual values, is what we wish to emphasize.

Specifically, we perform a sensitivity analysis on the mean 〈ADC〉 and the anisotropy ratio with respect to variations in microstructural dimensions and compositional parameters. The results are qualitatively similar for both packing geometries and are provided in Tables 1 and 2 for the square packing geometry, and in Tables 3 and 4 for the hexagonal packing geometry. In the case of the normal myelinated axon, as well as for vasogenic edema, hydrocephalus, cytotoxic edema, and dysmyelination cases, the microstructural parameters whose effects are most pronounced are L (axon spacing), r_s (outer radius of the axon), and f (volume fraction of axons). The observed fractional change in both the 〈ADC〉 and the anisotropy ratio for a unit fractional change in these parameters is significant, and an order of magnitude larger than for the other independent parameters in the model. This result is reasonable, because the intraaxonal region is largely screened out due to the use of conservative values of myelin and bath dimension, intraaxonal diffusivities, and water concentrations, so that the behavior of 〈ADC〉 and the degree of anisotropy are dominated by the extraaxonal dimensions.

TABLE 1.

Square pack: sensitivity function for 〈ADC〉, the mean ADC (top row) ∂ ln((2D_t,eff + D_l,eff)/3) / ∂ ln X with corresponding parameter X values (bottom rows) for normal situations and various physiologically or clinically relevant perturbations

	Db	Dc	Ds	Cb0	Cc0	Cs0	L	rc	rs	f	〈ADC〉/Dw
Normal	0.71	0.20	0.080	0.39	−0.22	−0.17	6.29	0.21	−6.51	−3.15	0.18
	20	7.5	0.3	0.95	0.88	0.5	17.66	6.0	8.57	0.74	–
Vasogenic edema	0.80	0.14	0.06	0.40	−0.23	−0.16	3.91	0.081	−3.99	−1.96	0.22
	20	7.5	0.3	0.95	0.88	0.5	18.56	6.0	8.57	0.67	–
Hydrocephalus	0.65	0.25	0.099	0.36	−0.20	−0.16	8.33	0.32	−8.65	−4.66	0.14
	20	7.5	0.3	0.95	0.88	0.5	17.31	6.0	8.57	0.78	–
Cytotoxic edema	0.52	0.33	0.15	0.26	−0.27	0.004	7.45	0.88	−0.88	−3.72	0.16
	20	7.5	0.3	0.95	0.88	0.5	17.20	7.2	8.57	0.78	–
Demyelination	0.97	0.06	−0.03	0.20	−0.26	0.05	0.67	−0.07	−0.59	−2.64	0.47
	20	7.5	0.3	0.95	0.88	0.5	17.66	6.0	4.28	0.74	–
Dysmyelination	0.41	0.28	0.31	0.12	−0.17	0.04	4.20	0.38	−4.59	−2.1	0.24
	20	7.5	3.0	0.95	0.88	0.5	17.20	6.0	8.57	0.78	–

The last column gives the 〈ADC〉 normalized wrt that of water. Concentrations are with respect to unit molarity of bulk water, lengths are in micrometers, and diffusion coefficients are in units of 10⁻¹⁰m²/s.

TABLE 2.

Square pack: sensitivity function for anisotropy (top row) ∂ ln(D_l,eff/D_t,eff) / ∂ ln X with corresponding parameter X values (bottom rows) for normal situations and various deviations

	Db	Dc	Ds	Cb0	Cc0	Cs0	L	rc	rs	f	Anisotropy
Normal	−0.12	0.31	−0.19	−0.12	0.31	−0.19	−9.61	0.14	9.46	4.80	3.23
	20	7.5	0.3	0.95	0.88	0.5	17.66	6.0	8.57	0.74	–
Vasogenic edema	−0.14	0.25	−0.11	−0.14	0.25	−0.11	−4.14	0.21	3.93	2.07	2.37
	20	7.5	0.3	0.95	0.88	0.5	19.94	6.0	8.57	0.67	–
Hydrocephalus	−0.07	0.34	−0.28	−0.07	0.347	−0.28	−16.57	0.003	16.57	10.44	4.68
	20	7.5	0.3	0.95	0.88	0.5	17.3	6.0	8.57	0.78	–
Cytotoxic edema	0.03	0.41	−0.44	0.028	0.41	−0.44	−15.32	−1.53	1.53	7.66	4.18
	20	7.5	0.3	0.95	0.88	0.5	17.20	7.2	8.57	0.78	–
Demyelination	−0.18	0.13	0.053	−0.18	0.13	0.05	−0.73	0.099	0.63	30.13	1.43
	20	7.5	0.6	0.95	0.88	0.5	17.66	6.0	4.28	0.74	–
Dysmyelination	0.30	0.12	−0.42	0.30	0.12	−0.42	−2.85	−0.44	3.29	1.43	1.68
	20	7.5	3.0	0.95	0.88	0.5	17.20	6.0	8.57	0.78	–

The last column gives the anisotropy for the case considered. Concentrations are with respect to unit molarity of bulk water, lengths are in micrometers, and diffusion coefficients are in units of 10⁻¹⁰m²/s.

TABLE 3.

Hexagonal pack: sensitivity function for 〈ADC〉, the mean ADC (top row) ∂ ln((2D_t,eff + D_l,eff)/3) / ∂ ln X with corresponding parameter X values (bottom rows) for normal situations and various physiologically or clinically relevant perturbations

	Db	Dc	Ds	Cb0	Cc0	Cs0	L	rc	rs	f	〈ADC〉/Dw
Normal	0.69	0.24	0.077	0.43	−0.23	−0.20	5.53	0.23	−5.77	−2.77	0.17
	20	7.5	0.3	0.95	0.88	0.5	18.25	6.0	8.57	0.8	–
Vasogenic edema	0.82	0.13	0.048	0.41	−0.24	−0.17	3.06	0.046	−3.11	−1.53	0.24
	20	7.5	0.3	0.95	0.88	0.5	19.94	6.0	8.57	0.67	–
Hydrocephalus	0.59	0.31	0.10	0.39	−0.19	−0.20 9	7.66	0.39	−8.05	−3.83	0.14
	20	7.5	0.3	0.95	0.88	0.5	17.71	6.0	8.57	0.85	–
Cytotoxic edema	0.49	0.38	0.13	0.31	−0.28	−0.24	6.14	0.86	−0.86	−3.07	0.15
	20	7.5	0.3	0.95	0.88	0.5	17.71	7.2	8.57	0.85	–
Demyelination	0.97	0.06	−0.03	0.21	−0.27	0.06	0.70	−0.08	−0.62	−1.83	0.46
	20	7.5	0.6	0.95	0.88	0.5	18.48	6.0	4.28	0.78	–
Dysmyelination	0.47	0.27	0.26	0.21	−0.20	−0.01	3.23	0.30	−3.53	−1.62	0.25
	20	7.5	3.0	0.95	0.88	0.5	18.25	6.0	8.57	0.8	–

The last column gives the 〈ADC〉 normalized wrt that of water. Concentrations are with respect to unit molarity of bulk water, lengths are in micrometers, and diffusion coefficients are in units of 10⁻¹⁰m²/s.

TABLE 4.

Hexagonal pack: sensitivity function for anisotropy (top row) ∂ ln(D_l,eff/D_t,eff) / ∂ ln X with corresponding parameter X values (bottom rows) for normal situations and various physiologically or clinically relevant perturbations

	Db	Dc	Ds	Cb0	Cc0	Cs0	L	rc	rs	f	Anisotropy
Normal	−0.23	0.39	−0.16	−0.23	0.39	−0.16	−5.27	0.35	4.92	2.64	2.77
	20	7.5	0.3	0.95	0.88	0.5	18.25	6.0	8.57 3	0.8	–
Vasogenic edema	−0.16	0.25	−0.09	−0.16	0.25	−0.09	−2.13	0.27	1.86	1.06	2.07
	20	7.5	0.3	0.95	0.88	0.5	19.94	6.0	8.57	0.67	–
Hydrocephalus	−0.23	0.47	−0.23	−0.23	0.47	−0.23	−9.69	0.33	9.36	4.84	3.43
	20	7.5	0.3	0.95	0.88	0.5	17.71	6.0	8.57	0.85	–
Cytotoxic edema	−0.19	0.53	−0.34	−0.19	0.53	−0.34	−8.04	−8.11	8.11	4.02	3.39
	20	7.5	0.3	0.95	0.88	0.5	17.71	7.2	8.57	0.85	–
Demyelination	−0.19	0.13	0.056	−0.19	0.13	0.06	−0.78	0.10	0.67	9.51	1.46
	20	7.5	0.6	0.95	0.88	0.5	18.48	6.0	4.28	0.78	–
Dysmyelination	0.13	0.18	−0.31	0.13	0.18	−0.31	−0.65	−0.22	0.87	0.32	1.47
	20	7.5	3.0	0.95	0.88	0.5	18.25	6.0	8.57 3	0.8	–

The last column gives the anisotropy for the case considered. Concentrations are with respect to unit molarity of bulk water, lengths are in micrometers, and diffusion coefficients are in units of 10⁻¹⁰m²/s.

Many studies suggest the existence of diffusion anisotropy in white matter before the appearance of myelin (14,43–45). To address this issue, we can use Eq. 25 above to assess whether diffusion anisotropy can be expected in a bundle of unmyelinated axons.

When present, myelin is the major barrier to diffusion and the cause of anisotropy. In normal white matter development, the thickness of the myelin sheath increases. We can recapitulate this process heuristically by considering the case where the normalized thickness of the myelin sheath, (r_s − r_c)/r_c, grows from zero to a finite value (∼0.5), which is somewhat larger than that reported histologically by Rushton (46). Fig. 4 shows the mean 〈ADC〉 as a function of the radius of the myelin sheath. As myelin thickness increases, the mean ADC progressively drops, which is in qualitative agreement with findings by Neil et al. (43). In Fig. 5, the anisotropy ratio is plotted versus the radius of the myelin sheath. Some diffusion anisotropy is observed when no myelin is present, but the fact that anisotropy increases with increasing myelin thickness supports the hypothesis that, although not the only determinant of diffusion anisotropy in white matter, myelin significantly contributes to it (14). Recall, in the model, we treat the myelin and membrane as a composite and the permeability is determined by the combined effect of the membrane and the myelin sheath.

FIGURE 4.

Mean diffusion coefficient 〈ADC〉 = (2D_t,eff + D_l,eff)/3 as a function of the myelin sheath radius r_s develops from its minimum value of r_c to that allowed by hexagonal close pack. Here, r_c = 6 μm, D_b = 2 × 10⁻⁹m²/s, C_b0 = 0.95, D_c = 7.5 × 10⁻¹⁰m²/s, C_c0 = 0.88, D_s = 3 × 10⁻¹¹m²/s, C_s0 = 0.5, L = 18.2 μm.

FIGURE 5.

Degree of diffusion anisotropy D_l,eff/D_t,eff as a function of the myelin sheath radius r_s develops from its minimum value of r_c to that allowed by hexagonal close pack. Here r_c = 6 μm, D_b = 2 × 10⁻⁹m²/s, C_b0 = 0.95, D_c = 7.5 × 10⁻¹⁰m²/s, C_c0 = 0.88, D_s = 3 × 10⁻¹¹m²/s, C_s0 = 0.5, L = 18.2 μm.

Fig. 6 shows the orientational ADC profile (41) using the parameters for normal tissue, computed using the formula given in Eq. 40. Some features of microstructure can be gleaned from this figure. First, the narrow wasp waist of this peanut is indicative of a very low effective diffusivity in the transverse direction. The anisotropy ratio can be estimated from this construction. However, it not clear, from the form of Eq. 40 and the shape of this profile, how to relate ADC to the numerous microstructural, compositional, and physical parameters that characterize even this simplified model of white matter. We view these diffusion peanuts as glyphs that summarize gross features of the diffusion process, but do not provide insight into tissue microstructure, composition, or physical properties therein.

FIGURE 6.

Angular profile of ADC_t,eff = D_t,eff cos² θ + D_l,eff sin² θ in units of D_b as a function of the polar angle, θ in a hexagonal close pack. Here the parameters r_c = 7.2 μm, r_s = 9.77 μm, D_b = 2 × 10⁻⁹m²/s, C_b0 = 0.95, D_c = 7.5 × 10⁻¹⁰m²/s, C_c0 = 0.88, D_s = 3 × 10⁻¹¹m²/s, C_s0 = 0.5, L = 17.71 μm are chosen to represent cytotoxic edema.

One advantage of formulating this model of diffusion in a pack of axons, is that some of the results can be applied to other transport processes occurring in white matter. For instance, the diffusion tensor data obtained in a DTI experiment can be scaled to describe the electrical conductivity tensor required to calculate electric field and current density distributions (6). This is particularly important in developing a realistic electrical model of the brain in EEG (11) and in magnetic stimulation (47) applications.

Next we wish to comment on how our calculations relate to DTI. In these measurements, in one way or another, there is an attenuation in the measured magnetization due to random phases the spins acquire during their Brownian diffusive motion. In the lowest order of approximation, the attenuation exponent depends on the mean-square displacement. Here we have considered only the long-time limit of the diffusion coefficient. The diffusion coefficient, by definition, is the mean-square displacement divided by time. In general, the mean-square displacement and the diffusion coefficient are time dependent (48). However, if the mean-square displacement becomes finite at long time, the diffusion coefficient goes to zero upon dividing by time, and one can no longer assess the attenuation exponent from the diffusion coefficient (zero).

When the particles inside the axon are trapped by an impermeable myelin sheath, their mean-square displacement eventually saturates and the diffusion coefficient goes to zero. One needs to take this fact explicitly into account when computing the attenuation of magnetization that depends on the mean-square displacement. The mean-square displacement has to be computed directly (48) and not via (zero) diffusion coefficient. For the model considered here, the attenuation of magnetization has been computed explicitly in a recent article (49). To characterize water diffusion in brain white matter, Assaf et al. (49) proposed a framework that incorporates both hindered and restricted models of water diffusion and an experimental methodology that embodies features of diffusion tensor and q-space MRI. They propose a model of white matter diffusion anisotropy that contains a hindered extraaxonal compartment, whose diffusion properties are characterized by an effective diffusion tensor, and an intraaxonal compartment, whose diffusion properties are characterized by a restricted model of diffusion within cylinders. The hindered model primarily explains the Gaussian signal attenuation behavior observed at low b (or q) values; the restricted non-Gaussian model does so at high b (or q).

The full time dependence when the particles are exchangeable between core and the bath has been investigated in a simulation by Ford et al. (18), but analytical results are still not available.

Care must be taken in using the results for diffusion directly in DTI. It is the mean-square distribution of the accumulated phase that matters and this depends on the pulse sequence used. Often the relationship between root mean-square phase and root mean-square displacement is not straightforward. For an extremely hard gradient pulse, of strength g and duration δ, the decay exponent from the restricted axonal fluid will be time independent where q = γgδ. The free part of the fluid gives the decay exponent ∼q²D_efft, where q = γgδ. But when the duration δ of the gradient is long compared to the diffusion time across the core, the usual motional narrowing arguments that are based on the Gaussian phase approximation may be invoked and the decay exponent from the restricted axonal fluid will be 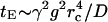where t_E is the echo time. These points still need to be fully developed in the context of DTI.

CONCLUSIONS

Here we have presented a simplified, but self-consistent modeling framework for predicting the long-time apparent diffusion coefficients of water parallel and perpendicular to a “pack” of myelinated axons. Values assumed for white matter suggest that the orientationally averaged 〈ADC〉 and the diffusion anisotropy ratio are fairly insensitive to intracellular dimensions and diffusion properties, and is primarily affected by changes in the outer diameter of the axons, the extracellular volume fraction, and interaxonal spacing.

The main conclusion of our model is that the low diffusion coefficient in the myelin sheath makes it a diffusion barrier for the axonal fluid. In that case, the bath or the extraaxonal fluid mainly determines the overall diffusion coefficient, although the concentration factor is affected by the axonal fluid; ADC and the anisotropy are dominated by the f and type of packing.

APPENDIX I: HIGHER-ORDER CORRECTIONS AND MATHEMATICAL DETAILS

This appendix is to fill in the gaps in the text and to show how to compute more accurate results than those given above.

The chemical potential is expanded in terms of multipoles, as in any standard electrostatics problem (28). For example,

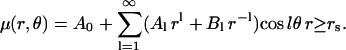(26)

There are corresponding expansions in other regions with different coefficients that are eliminated by the use of boundary conditions, Eq. 6, as worked out by Nicorovici et al. (37,38) and by Perrins et al. (29). If we denote the products of concentration and diffusion by ε, i.e., C_s0D_s = ε_s, etc., we can directly use the previous results (29,37,38) to compute the effective transverse diffusion coefficient D_t,eff

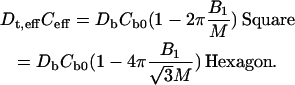(27)

Here, the effective concentration, C_eff, is given by Eq. 7.

C_eff is the volume average of concentrations. In Eq. 27, M is the local chemical field, where M = M_ext + M_pol, the sum of the external field M_ext and the “polarization” field M_pol. M_ext is the applied chemical field, analogous to the applied electric field of Rayleigh's problem. M_pol, the depolarization field, drops out by assuming that the sample has a long needle shape (see below).

Both for hexagonal and square packs, due to symmetry, only the multipole coefficients B_2l−1, l = 1, 2, 3, … of odd orders survive. In a hexagonal pack all B_2l−1 = 0 for 2l − 1 = 3, 6, 9, .. i.e., the multipoles that are multiples of 3, also vanish (see below). Rayleigh found the recursion relation below between the coefficients:

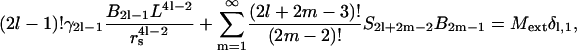(28)

where S_2l+2m−2 are the lattice sums (28,29,37,38) or the structural constants that depend on the specific lattice used. These are of the form:

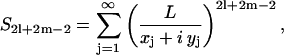(29)

where {x_j, y_j} denote the coordinates of center of the j^th cylinder and The sum runs over all the cylinders. As noted by Lord Rayleigh (28), for a square array S₂ = π and S₆ = S₁₀ = S₁₄ = … = 0, etc. In hexagonal packs (29), on the other hand, and only other nonzero S_2l+2m−2 have 2l + 2m − 2 as a multiple of 6, for example, S₆ = −5.86303, etc.

The effective diffusion coefficient is given by B₁ alone in Eq. 27, but its value is affected by all multipole coefficients B_2m−1, m = 1, 2, …, N, which all are functions of composite properties. As in Rayleigh (28) or in Nicorovici et al. (37,38), by a suitable choice of sample shape, we make M_pol = 0 so that M_ext, in turn, drops out because the ratio B₁/M determines the effective diffusion coefficients.

To keep the calculation to a reasonable size, the recursion relation is generally truncated. This is most conveniently done using the method of Nicorovici et al. (37,38) using a symmetric matrix w with elements

(30)

This equation corresponds to Eq. 21 of Nicorovici et al. (37); we change the indexing notation slightly making it explicit that W_{2l−1,2m−1} = w[2l − 1, 2m − 1] relates B_2l−1 and B_2m−1. Matrix W and the diagonal matrix together define their matrix A = D^Nic(γ) + W. The effective diffusion coefficient is given by the first element of A⁻¹.

Square array

For a square array, Eq. 27 gives (37):

(31)

which upon simplification becomes:

(32)

Here 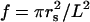is the fraction of volume occupied by the coated cylinders. To the lowest order in multipolar expansion, we obtain the Maxwell-Garnett formula by truncating at N = 1 for l = 1, and using γ₁ as given by Eq. 8:

(33)

A truncation to N = 3 gives:

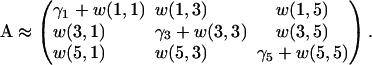(34)

Using this in Eq. 32 and the known values of structure constants (37,38), gives

(35)

As the intercylinder spacing decreases, or the contrast between the products of D_iC_i among different components i become disparate, the higher and higher-order terms become more important. This change can be accommodated easily by making the dimensions of the matrix A larger and larger. For example, to obtain results to N = 4 one needs to consider:

(36)

Hexagonal array

For a hexagonal array (29),

(37)

which upon simplification, using

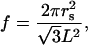(38)

gives,

(39)

which is the same form as Eq. 32, but with completely different structural constants. To the lowest order in the multipolar expansion, we obtain the Maxwell-Garnett formula by truncating at N = 1 for l = 1:

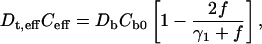(40)

which is the same as for a square array Eq. 33; and, as before, γ₁ as given by Eq. 8. The Maxwell-Garnett formula holds for all structures, including for disordered systems and is accurate for small f. We now consider the higher-order terms.

We note above (29) that in hexagonal packs terms with only odd multipoles, except those that are multiples of 3, survive. Apart from only nonzero S_l have l as a multiple of 6, for example, S₆ = −5.86303, etc. In this case, to degree N = 3, we need to consider the inverse of this matrix:

(41)

We emphasize again that for the hexagonal pack, matrix elements, w(2l − 1, 2m − 1), are completely different from the corresponding ones for the cubic pack. Similarly, all the structure factors S_2l+2m−2 are different in the two different structures.

(42)

to the same degree of accuracy (N = 3) as before in Eq. 35.

This extends Perrins et al.'s calculation (29) to the case where the cylinders are coated. In the absence of a sheath, Eq. 24 holds, and we recover Eq. 13 of Perrins et al.

D_t,effC_eff depends on three quantities: the volume fraction f of myelinated axons, the sets of geometrical factors {S_2l−1}, and the material property dependent parameter set {γ_2l−1}. Note that the specific properties of axon core, sheath, etc., appear via the set {γ_2l−1}. In other words, for a given lattice the results have the same geometrical or structural factors, the specific form of Eq. 8 distinguishes one case from another.

It is interesting to note that Eq. 18 does depend on 2l − 1, the order of dipole. Equation 3 in Latour et al. (33) implies that only the dipolar term l = 1 was kept, which is correct for the Maxwell-Garnett approximation, as noted above. For l = 1, Eq. 18 implies that the core diffusion coefficient was augmented by a term that is proportional to the skin permeability times the radius of the core region. A similar result applies for a stack of flat membranes (9) with r_c replaced by intermembrane separation. Higher-order multipoles become increasingly important as the cylinders begin to touch. Incorporating the higher-order multipoles requires using the new “crucial” Eq. 18 that is a function of the order 2l − 1. Neglecting them may be the cause of the discrepancy reported by Ford (17,18) between the simulated values (17,18), and the values estimated using the formula of Latour et al. (33) that sets l = 1.