Abstract
Fluid membranes containing charged lipids enhance binding of oppositely charged proteins by mobilizing these lipids into the interaction zone, overcoming the concomitant entropic losses due to lipid segregation and lower conformational freedom upon macromolecule adsorption. We study this energetic-entropic interplay using Monte Carlo simulations and theory. Our model system consists of a flexible cationic polyelectrolyte, interacting, via Debye-Hückel and short-ranged repulsive potentials, with membranes containing neutral lipids, 1% tetravalent, and 10% (or 1%) monovalent anionic lipids. Adsorption onto a fluid membrane is invariably stronger than to an equally charged frozen or uniform membrane. Although monovalent lipids may suffice for binding rigid macromolecules, polyvalent counter-lipids (e.g., phosphatidylinositol 4,5 bisphosphate), whose entropy loss upon localization is negligible, are crucial for binding flexible macromolecules, which lose conformational entropy upon adsorption. Extending Rosenbluth's Monte Carlo scheme we directly simulate polymer adsorption on fluid membranes. Yet, we argue that similar information could be derived from a biased superposition of quenched membrane simulations. Using a simple cell model we account for surface concentration effects, and show that the average adsorption probabilities on annealed and quenched membranes coincide at vanishing surface concentrations. We discuss the relevance of our model to the electrostatic-switch mechanism of, e.g., the myristoylated alanine-rich C kinase substrate protein.
INTRODUCTION
The lipid bilayer, constituting the central structural element of biological membranes, is a two-dimensional fluid mixture, composed typically of many lipid species. Owing to the lateral mobility of lipids at physiological temperatures, the membrane can respond to interactions with integral and peripheral macromolecules by mobilizing those lipids interacting favorably with the macromolecule into the interaction zone. This process leads to local changes in lipid composition around the guest molecules which, under certain conditions, may evolve into larger-scale reorganization of membrane components, resulting in domain formation. The molecular composition and phase characteristics of the domains, as in lipid rafts, are different from those of the surrounding membrane (1–3).
The ability of integral proteins to induce local and global changes in lipid composition has been extensively documented experimentally (4), and amply analyzed theoretically (5,6). Similarly, experiments reveal that when charged macromolecules, such as certain kinds of proteins or DNA, are adsorbed onto a mixed membrane containing a small amount of oppositely charged lipids, the charged species migrate toward the adsorbed macromolecule (7–9), tending to achieve local electrical neutrality. Although lowering the electrostatic (free) energy of the system, the segregation of charged lipids induced by the peripheral macromolecule may involve a non-negligible entropic penalty. Several recent theoretical studies have carefully analyzed the energetic-entropic balance associated with electrostatic adsorption of rigid macromolecules (e.g., DNA and globular protein) onto fluid membranes (10–16). It was shown, for instance, that the extent of lipid segregation, the corresponding entropy loss, and the interaction free energy depend sensitively on the shape, charge, and concentration of the adsorbing macromolecule (17,18).
This work focuses on the energetic and structural characteristics of the interaction between flexible, electrically charged, macromolecules (polyelectrolytes), and mixed, oppositely charged, fluid membranes. We shall consider three-component membranes composed of one electrically neutral species and two differently charged lipids. Electrostatic adsorption on such membranes may involve significant changes in the spatial configuration of the adsorbing polyelectrolyte and, consequently, a substantial loss of conformational entropy. The two kinds of entropy loss, those associated with lipid segregation and those which lower the macromolecule's conformational freedom, tend to offset the gain in electrostatic interaction energy between the oppositely charged molecules. It should be noted, however, that both degrees of freedom, namely, lipid mobility and macromolecule flexibility, enable the interacting complex to select, with higher probability, those mutual membrane-macromolecule configurations of lowest free energy.
A delicate balance between the energetic and entropic contributions to the adsorption free energy on mixed fluid membranes is exhibited in various biological processes (19,20). One important example is the electrostatic-switch mechanism underlying the operation of the myristoylated alanine-rich C kinase substrate (MARCKS), and several other proteins (21,22). MARCKS is a prominent protein C kinase substrate, implicated in a variety of signaling pathways involving, for instance, the control of lipid second messengers and the regulation of cytoskeletal actin. This natively unfolded (and thus flexible) protein binds electrostatically to anionic lipids in the inner leaflet of the plasma membrane. Of special importance in this binding is the multivalent (here z = −4, but generally varying between −3 and −5) anionic lipid (phosphatidylinositol 4,5 bisphosphate, PIP2). The average membrane concentration of PIP2 is typically ∼1%, yet it tends to localize in viral envelopes and membrane rafts, as well as in the binding zones of various proteins involved in signal transduction pathways. Among these proteins is MARCKS, which binds to the plasma membrane through its relatively small (25-residue) but strongly charged effector domain that comprises 13 basic residues. A 150-residue-long flexible polypeptide chain separates the effector domain from the myristoylated N-terminus, and a comparably long and flexible peptide chain connects the effector domain with the C-terminus (for more details, see e.g., Gambhir et al. (9)). The myristoyl chain inserts into the hydrophilic core of the lipid bilayer, serving to anchor MARCKS to the membrane.
Experiments reveal that the effector domain sequesters approximately three PIP2 molecules (9,23,24), suggesting that these multivalent (z = −4) lipids provide most of the negative charge required for neutralizing the 13 basic charges of the MARCKS' effector domain (25). Considering the small average PIP2 concentration in the membrane (∼1%), versus the 10–30% abundance of monovalent acidic lipids (primarily phosphatidyl-serine, PS), it is clear that the protein must import the multivalent lipids from remote membrane regions. Another significant observation is that upon lowering the net charge of the effector domain from +13 to +7, MARCKS detaches from the membrane, thereby exposing PIP2 to cleavage by phospholipase C and initiating a series of signal transduction events (26,27). The change in charge is generally achieved through phosphorylation of three serine residues in the basic domain by protein kinase C.
In addition to electrostatic interactions, MARCKS interacts with the membrane hydrophobically as well, through the myristoyl anchor at the N-terminus and via five phenylalanine side chains within the effector domain (28). A subtle interplay between the electrostatic and hydrophobic interactions, as well as the entropies associated with the long flexible chains on both sides of the effector domain, governs the intricate electrostatic switching process involving MARCKS and PIP2. Motivated by this notion, our goal in this study is to examine the coupling between electrostatic interactions, membrane composition, lipid mobility, and polymer flexibility, and elucidate its role in the adsorption of charged macromolecules onto oppositely charged membranes. Although inspired by the biological relevance of these interactions and processes, our present calculations do not attempt to mimic in detail the behavior of any particular biological system. In fact, our simulations involve a rather short (20-segment) flexible polyelectrolyte chain, interacting with a three-component fluid membrane containing neutral, monovalent, and tetravalent lipids. More specific simulations, modeling MARCKS-membrane interaction, are in progress.
To demonstrate the important role of lipid mobility, our results for the fluid (i.e., annealed) membrane are compared to those obtained for a frozen (i.e., quenched) membrane of the same average lipid composition. The structural and energetic characteristics of a polyelectrolyte interacting with a fluid membrane are qualitatively and quantitatively different from those pertaining to any specific quenched lipid membrane. However, from the purely formal-computational aspect, as argued in the next section, the statistical aspects of polymer adsorption on a fluid membrane can also be derived using a biased superposition of statistical averages corresponding to polymer adsorption on an ensemble of quenched membranes. We shall also show that, in the limit of vanishing polymer concentration (in the bulk solution and hence also on the membrane surface), the average adsorption probability on a Boltzmann-weighted ensemble of quenched membranes equals the adsorption probability on an annealing, fluid membrane. Differences between the two kinds of membranes appear at nonzero concentrations of macromolecules, and will be accounted for using a simple cell model.
In addition to the fluid and quenched lipid membranes, some of our calculations describe polyelectrolyte adsorption on uniformly charged surfaces, such as those of metal oxides or metal electrodes (29,30). We shall see that, in general, uniformly charged surfaces adsorb more weakly than either a quenched or a fluid lipid membrane. Another limiting case of interest is that of a stiff polyelectrolyte interacting with a charged membrane. Contrasting the adsorption behavior of such a molecule with that of a self-avoiding freely jointed chain will emphasize the role of polyelectrolyte flexibility. As we shall see, weak electrostatic interaction may not suffice to overcome the loss of chain flexibility upon adsorption. This will be demonstrated by considering the limiting cases of a weakly charged polyelectrolyte and a membrane containing only monovalent lipids.
In the next section we first describe the basic statistical-thermodynamic background underlying the adsorption of a flexible macromolecule onto the various types of lipid membranes mentioned above. Later in that section we introduce the model system and describe our extended version of the Rosenbluth Monte Carlo (MC) simulation scheme (31,32), which enables efficient simulation of polymer adsorption on annealing, fluid, membranes. We then present and analyze the results of the simulations and close with a brief summary of the main conclusions.
THEORY
The lipid molecules comprising a fluid (annealed) membrane are mobile and can thus diffuse into and out of the interaction region with the adsorbing macromolecule. The statistical thermodynamics of macromolecule adsorption onto such membranes involves simultaneous averaging over all the polymer and lipid degrees of freedom. In a frozen membrane, on the other hand, the lipids are immobile, and thermodynamic averaging is obtained by tracing over many quenched arrangements of the membrane lipids. Qualitative differences between these two membrane types are reflected in various structural and thermodynamic properties, such as the local lipid composition around the adsorbed macromolecule, and the average adsorption free energies. Formally, however, it can be shown that the various characteristics of macromolecule-lipid interaction on a fluid membrane, can be derived by a biased averaging of the same property over a Boltzmann-weighted ensemble of quenched membranes. (This suggests an indirect way of simulating adsorption onto the fluid membrane using quenched membrane simulations.) We shall see that the differences between average macromolecule adsorption characteristics on fluid and quenched membranes are substantial at nonzero concentrations of macromolecules, but disappear in the limit of vanishing concentration. We open this section with a detailed discussion of the relevant thermodynamic background, and then describe the model system and our method of simulation.
Adsorption thermodynamics
All our simulations involve one adsorbed macromolecule, as formally appropriate to low surface concentrations. However, using a simple cell model, the simulations can also be used to account for the adsorption behavior at higher surface concentrations. In this model, the membrane area A is divided into an array of A/a noninteracting cells, all with the same area, a, and the same lipid composition. The cell area is large enough to comfortably accommodate one adsorbed macromolecule. The model thus, approximately, accounts for excluded area effects but ignores other intermacromolecule interactions. Note that to contain a flexible macromolecule, e.g., an unfolded protein, a membrane cell should typically consist of several hundreds of lipid molecules. For the three-component membranes of interest here, this implies an enormous number of two-dimensional lipid arrangements.
Single molecule partition functions
We treat the quenched membrane as an ensemble of independent cells, each characterized by a specific frozen lipid configuration, m. To compare the quenched membrane with a fluid membrane having the same lipid composition, we equate the fraction, Pq(m), of quenched membranes in configuration m, with the Boltzmann weight, P(m), of m in the bare fluid membrane, i.e.,
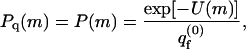 |
(1) |
where 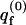 is the partition function per cell of a bare fluid membrane,
is the partition function per cell of a bare fluid membrane,
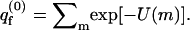 |
(2) |
In these equations and below we use the subscripts q and f for the quenched and fluid membranes, respectively. Also, the potential energy U(m) of the lipids in configuration m, as well as all other energies are hereafter expressed in units of kBT, the thermal energy, where T is the temperature and kB is the Boltzmann constant.
The partition function, per cell, of a fluid membrane occupied by an adsorbed macromolecule is given by
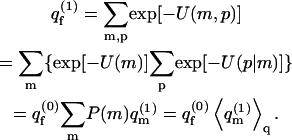 |
(3) |
Here U(m,p) = U(m) + U(p|m) is the potential energy corresponding to the membrane-polymer configuration m,p. The term U(p|m) stands for the energy of a polymer in state p, interacting with a membrane in a given configuration m. It includes the self-energy of the polymer (i.e., the sum of its intersegment potentials), and its interaction energy with a membrane in state m. By p = α,r we refer to the polymer chain conformation, α, and the position, r, of the polymer relative to the membrane plane (see below). The sum over p thus (tacitly) involves integration over r, implying that 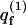 is a configurational partition function, bearing the dimensions of volume. As above, U(m) is the interlipid interaction energy.
is a configurational partition function, bearing the dimensions of volume. As above, U(m) is the interlipid interaction energy.
The sum of Boltzmann factors,
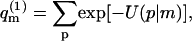 |
(4) |
introduced in the third equality in Eq. 3, is, of course, the partition function of a macromolecule adsorbed onto a membrane of a specific lipid configuration m. From Eq. 3 it thus follows that the partition function of a macromolecule interacting with a fluid membrane can be expressed as a Boltzmann average of the partition functions corresponding to the ensemble of quenched environments. Note that the constant lipid energy, U(m), is not included in our definition of 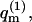 i.e., the energy of the occupied m-cell is measured relative to the ground state energy U(m). On this energy scale we obtain
i.e., the energy of the occupied m-cell is measured relative to the ground state energy U(m). On this energy scale we obtain 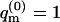 for the empty cell. The quantity
for the empty cell. The quantity 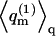 introduced in the last equality of Eq. 3 may be interpreted as the average partition function, per cell, in a Boltzmann-weighted ensemble of quenched membranes.
introduced in the last equality of Eq. 3 may be interpreted as the average partition function, per cell, in a Boltzmann-weighted ensemble of quenched membranes.
From Eq. 3, it also follows that the average of any property A (e.g., adsorption energy, polymer radius of gyration, etc.) of a polymer adsorbed on a fluid membrane, can, in principle, be evaluated as a biased average of A in the ensemble of quenched membranes. Explicitly, let
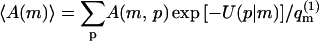 |
(5) |
denote the average (over polymer conformations) of A, for a polymer adsorbed on a quenched membrane in configuration m. Using Eqs. 1–4, we find
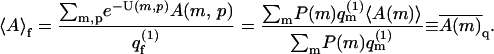 |
(6) |
Note that all quantities on the right-hand side of this equation depend only on quenched membrane properties. The second equality thus offers a way of calculating 〈A〉f as a weighted average of the polymer conformational averages, 〈A(m)〉, in the ensemble of quenched membranes. In this biased average, here denoted as 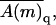 the weight, (
the weight, (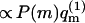 ), of the quenched membrane configuration m, is the product of the fraction of such membranes (P(m)) with the statistical weight (∝
), of the quenched membrane configuration m, is the product of the fraction of such membranes (P(m)) with the statistical weight (∝ 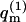 ) of all polymer conformations on this membrane. It will be shown below that this formal relationship between fluid and quenched membrane averaging may be given a physical meaning in the limit of vanishing macromolecule concentration. In this limit the probability of finding a macromolecule adsorbed onto a quenched membrane m is proportional to
) of all polymer conformations on this membrane. It will be shown below that this formal relationship between fluid and quenched membrane averaging may be given a physical meaning in the limit of vanishing macromolecule concentration. In this limit the probability of finding a macromolecule adsorbed onto a quenched membrane m is proportional to  and hence
and hence 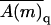 is the average of A(m,p) in the ensemble of quenched membranes. Note, however, that this average differs from the simple average
is the average of A(m,p) in the ensemble of quenched membranes. Note, however, that this average differs from the simple average 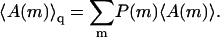
Membrane partition functions
To account for the adsorption behavior at nonzero surface concentrations we should consider a many-cell membrane in equilibrium with a solution of macromolecules. Suppose the bulk solution is of volume V, and contains Nb macromolecules of chemical potential μ. For simplicity we assume dilute solution behavior, in which case μ = −ln qb + ln ϕb, where ϕb = Nb/V is the bulk density of macromolecules, and
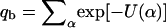 |
(7) |
is the internal partition function of a macromolecule in the bulk solution. Note that the summation here is over all possible conformations of the macromolecule, ensuring that its center of mass (or one of its segments) is kept fixed in space. Note also that qb, like all partition functions in our treatment, is a configurational partition function. The momentum factors in the partition function cancel out identically in all relevant expressions (33). Note, however, that μ refers here to the configurational part of the chemical potential, also known as the excess chemical potential (32).
The cells comprising a fluid membrane are identical. Treating the membrane as an open system with respect to macromolecule exchange, the grand-canonical partition function of the membrane is
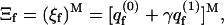 |
(8) |
where γ = exp(μ) is the absolute activity, and  is the two-state (i.e., empty and occupied) partition function of a membrane cell. Using Ns to denote the number of macromolecules adsorbed on the membrane surface, the fraction, θf = Ns/M = Nsa/A, of the membrane area occupied by macromolecules (or, the surface coverage), is given by
is the two-state (i.e., empty and occupied) partition function of a membrane cell. Using Ns to denote the number of macromolecules adsorbed on the membrane surface, the fraction, θf = Ns/M = Nsa/A, of the membrane area occupied by macromolecules (or, the surface coverage), is given by 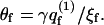 We thus obtain a Langmuir-like adsorption equation
We thus obtain a Langmuir-like adsorption equation
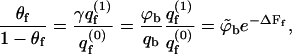 |
(9) |
where in the second equality we have used the dilute solution limit of the activity, γ = ϕb/qb = exp(μ). In the third equality we have introduced the dimensionless bulk concentration 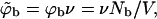 where v is a volume per macromolecule defined in more detail below. Thus,
where v is a volume per macromolecule defined in more detail below. Thus, 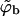 may be regarded as the volume fraction of polymers in solution.
may be regarded as the volume fraction of polymers in solution.
The grand partition function of the quenched membrane is given by
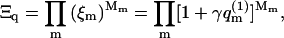 |
(10) |
where Mm = P(m)M is the number of membrane cells with a two-dimensional lipid distribution m. The probability of finding an m-cell occupied by a macromolecule is 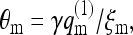 so that
so that
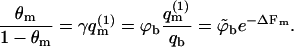 |
(11) |
Averaging over all the quenched configurations, m, and using Eqs. 3, 9, and 11, we find
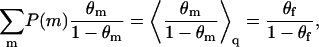 |
(12) |
or, equivalently,
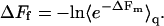 |
(13) |
Actually, with the definitions of ΔFf and ΔFm given in Eqs. 9 and 11, the last equality follows directly from Eq. 3.
Both θm/(1 − θm) and exp(−ΔFm) are convex functions of their arguments. Using Jensen's inequality of convex functions (34), it thus follows from Eqs. 12 and 13 that
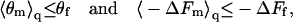 |
(14) |
for any probability distribution P(m). In other words, on average, macromolecule adsorption onto an ensemble of quenched membranes (whose lipid configurations appear with probabilities P(m)) is always weaker (lower θ and smaller −ΔF) than adsorption onto a fluid membrane of the same lipid composition.
From Eq. 12 it follows that the equality 〈θm〉q = θf is obtained only in the limit of vanishing surface coverage, i.e., when 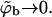 (〈ΔFm〉q → ΔFf requires that all ΔFm are negligibly small, as can be seen from Eq. 13.) Underlying the limiting behavior 〈θm〉q = θf is the fact that although the lipid molecules of a quenched membrane are, indeed, immobile, the adsorbed macromolecules can nevertheless explore all membrane states, m. This may be achieved via lateral diffusion on the membrane surface and/or by desorption from one local membrane region and adsorption into another. Note also that in the limit
(〈ΔFm〉q → ΔFf requires that all ΔFm are negligibly small, as can be seen from Eq. 13.) Underlying the limiting behavior 〈θm〉q = θf is the fact that although the lipid molecules of a quenched membrane are, indeed, immobile, the adsorbed macromolecules can nevertheless explore all membrane states, m. This may be achieved via lateral diffusion on the membrane surface and/or by desorption from one local membrane region and adsorption into another. Note also that in the limit 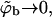 we obtain
we obtain 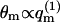 (see Eq. 11). Thus, in a Boltzmann-weighted ensemble of quenched membranes, the number of macromolecules bound to membranes of lipid configuration m, is proportional to P(m)θm and hence to
(see Eq. 11). Thus, in a Boltzmann-weighted ensemble of quenched membranes, the number of macromolecules bound to membranes of lipid configuration m, is proportional to P(m)θm and hence to 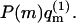 If measured over an ensemble of quenched membranes, the average of a physical observable A(m,p) would then be given by
If measured over an ensemble of quenched membranes, the average of a physical observable A(m,p) would then be given by 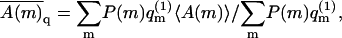 which, as noted in Eq. 6, is equal to 〈A〉f. Thus, in the θ → 0 limit, both the average surface concentration, and the θ-weighted average of A(m,p) over the quenched membrane ensemble, approach the corresponding quantities in the fluid membrane.
which, as noted in Eq. 6, is equal to 〈A〉f. Thus, in the θ → 0 limit, both the average surface concentration, and the θ-weighted average of A(m,p) over the quenched membrane ensemble, approach the corresponding quantities in the fluid membrane.
A physical interpretation of the last conclusion can be given in terms of the cell model, as follows. When θ → 0 (and in the absence of kinetic constraints), each of the adsorbed macromolecule can freely and independently visit all membrane environments m, thereby sampling all possible lipid-polymer configurations m,p. Furthermore, since none of the cells is blocked, all m and hence all m,p are sampled according to their Boltzmann weights, just like the states sampled by a macromolecule on a fluid membrane. The difference is, of course, that a macromolecule adsorbed on a fluid membrane need not migrate from one cell to another to sample the entire configuration space. Consequently, θ = θf is the same for all cells of the fluid membrane, whereas a wide distribution of θm values characterizes the ensemble of quenched membranes. Note however, that in practice, even this formal equivalence between a fluid membrane and an ensemble of quenched membranes may not materialize, even when θ → 0, because of kinetic barriers to macromolecule mobility.
Interestingly, it is possible that for some quenched membrane states m, ΔFm ≤ ΔFf (and hence, θm ≥ θf). This may appear surprising in view of the fact that the free energy, Ff (not ΔFf), of a macromolecule interacting with a fluid membrane is invariably lower than the free energy, Fm, of a macromolecule adsorbed onto any quenched membrane, m. (This is because 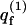 involves summation over both m and p and is therefore larger than any
involves summation over both m and p and is therefore larger than any 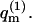 ) Hence,
) Hence, 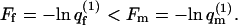 After adsorption, however, the distribution of lipid arrangements in the fluid membrane is no longer the Boltzmann distribution before adsorption, implying a loss of lipid-mixing entropy. Of course, no loss of lipid entropy is involved upon adsorption onto a quenched membrane, which explains why certain quenched states can be more attractive to macromolecule adsorption than the fluid membrane.
After adsorption, however, the distribution of lipid arrangements in the fluid membrane is no longer the Boltzmann distribution before adsorption, implying a loss of lipid-mixing entropy. Of course, no loss of lipid entropy is involved upon adsorption onto a quenched membrane, which explains why certain quenched states can be more attractive to macromolecule adsorption than the fluid membrane.
Upon increasing the concentration of macromolecules in solution, the more strongly adsorbing m-values of the quenched membrane will be occupied first. Once these favorable local environments (or cells) are populated, further adsorption is necessarily suppressed. This implies 〈θm〉q ≤ θf, because in the fluid membrane every cell can independently anneal its lipid distribution, thereby enhancing adsorption.
Our conclusions regarding the relationship between macromolecule adsorption on quenched versus fluid membranes agree with previous works pertaining to polymer statistics in random media. Cates and Ball (35) have studied the behavior of a single long polymer chain in a random medium and concluded that, as long as the environment is infinite, the quenched and annealed averaging will yield the same statistical chain properties. Our fluid and frozen membranes are analogous to the annealed and quenched random potentials in the treatment above. Inequalities valid for the multichain adsorption, analogous to Eq. 12, have been obtained by Andelman and Joanny (36,37) for neutral chains adsorbing on annealed and quenched flat surfaces. The main conclusion there is that the density of polymers on an annealed surface (membrane) is always higher than in the frozen case.
The adsorbed state
The MC simulations presented in the following sections enable evaluation of all the partition functions encountered above, as well as a variety of relevant structural properties. First, however, we have to clarify what distinguishes an adsorbed macromolecule from a free macromolecule in solution.
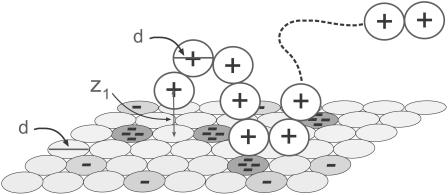
We noted above that the sum over p in Eqs. 2 and 3 involves all possible chain conformations, α, as well as all possible positions, r, of the macromolecule, relative to some arbitrary point on the membrane. Identifying the membrane surface with the (x,y) plane, the only relevant coordinate is the distance, z, of the macromolecule from the membrane surface. This distance can be expressed in terms of the normal displacement of any chain segment (or the center of mass) from the membrane plane. In the simulations, we find it convenient to measure this distance in terms of z1, the normal displacement of the first (more precisely, terminal) chain segment (see Fig. 1). Beyond a certain distance from the membrane surface, comparable to the range of membrane-macromolecule interactions, the macromolecule is not affected by the membrane. This cutoff distance, λ, may be defined in terms of z1, such that for z1 ≤ λ, the macromolecule is considered adsorbed, and otherwise as free in solution. An alternative, yet practically equivalent definition of λ can be given in terms of the average segment density profile (see below).
FIGURE 1.
A schematic drawing of the simulation model. A 20-segment long chain of spherical segments, each carrying a single point charge in its center, interacts with a mixed membrane composed of neutral, singly charged and tetravalent anionic lipids, which occupy the sites of a two-dimensional hexagonal lattice. Lipid charges are concentrated in the centers of the corresponding discs. The lipids can diffuse (exchange positions) within the membrane plane. The polymer chain is flexible, but subjected to electrostatic and short-range spatial repulsion between its constituent segments. The diameters, d, of polymer segments and lipid disks are equal.
With p ≡ z1, α, we find from Eq. 3 that the partition function of a macromolecule adsorbed on a fluid membrane is given by
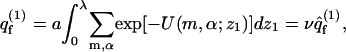 |
(15) |
with v ≡ λa, and
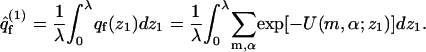 |
(16) |
In the last equation we have introduced qf(z1), the partition function of a macromolecule whose first segment is fixed at z1. The factor a in Eq. 15 results from the fact that the partition function per molecule must be proportional to the cell's area. The volume element, v = aλ, may now be interpreted as the volume of a membrane cell. Thus, 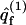 represents the (average) partition function per unit volume of an adsorbed macromolecule, or, equivalently, the average partition function per unit length along the membrane normal. Note that for large z1 (practically for z1 ≥ λ) we have U(m,α;z1) = U(m) + U(α), and hence
represents the (average) partition function per unit volume of an adsorbed macromolecule, or, equivalently, the average partition function per unit length along the membrane normal. Note that for large z1 (practically for z1 ≥ λ) we have U(m,α;z1) = U(m) + U(α), and hence 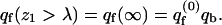
We may now rewrite Eq. 9 in the form
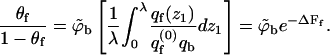 |
(17) |
Similarly, for the quenched membrane
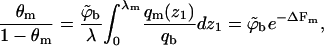 |
(18) |
where qm(z1 > λ) = qm (∞) = qb. In Eq. 18, to enable straightforward comparison with the fluid membrane, we keep using the same concentration units, 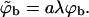
For chain molecules composed of L segments, the segment density in the bulk solution is ρ(z = ∞) = ρb = Lϕb. Near the membrane surface the segment density, ρ(z), is different from ρb and is given by
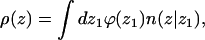 |
(19) |
where ϕ(z1) is the density of macromolecules whose first segment is at z1, and n(z|z1)dz is the average number of chain segments between z and z + dz due to chains originating at z1.
The surface excess of adsorbed macromolecule is, by definition,
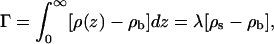 |
(20) |
where, in the second equality, 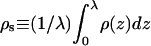 is the average (three-dimensional) density of chain segments within the surface layer. Note that the upper limit in the integral defining Γ can be replaced by λ (or any larger value). The second equality may also be regarded as the definition of the surface layer thickness λ. Note that in the limit of vanishing surface density, λaρs/L = θ.
is the average (three-dimensional) density of chain segments within the surface layer. Note that the upper limit in the integral defining Γ can be replaced by λ (or any larger value). The second equality may also be regarded as the definition of the surface layer thickness λ. Note that in the limit of vanishing surface density, λaρs/L = θ.
A slightly different definition of λ, useful in our numerical calculations, can be given in terms of the ratio q(z1)/q(∞) = ϕ(z1)/ϕb. Namely, we can choose λ as the smallest value of z1, beyond which this ratio is practically 1. In practice, the two definitions are indistinguishable, because 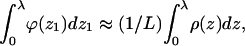 so that the integral over ρ(z) in Eq. 20 can be replaced by the integral over ϕ(z). The equality of the two integrals follows from the fact that for practically all z1 within λ, all chain segments will be found inside the surface layer. For chains originating near λ, say at z1 = λ − δ (δ ≪ λ), some conformations will cross the z = λ surface, contributing less than L segments to the surface layer density. By symmetry, however, chains originating at z1 = λ + δ will compensate for the loss of segments from the z1 = λ − δ chains. The near-equivalence of chains originating at z1 = λ ± δ follows from the fact that these chains are hardly affected by the membrane.
so that the integral over ρ(z) in Eq. 20 can be replaced by the integral over ϕ(z). The equality of the two integrals follows from the fact that for practically all z1 within λ, all chain segments will be found inside the surface layer. For chains originating near λ, say at z1 = λ − δ (δ ≪ λ), some conformations will cross the z = λ surface, contributing less than L segments to the surface layer density. By symmetry, however, chains originating at z1 = λ + δ will compensate for the loss of segments from the z1 = λ − δ chains. The near-equivalence of chains originating at z1 = λ ± δ follows from the fact that these chains are hardly affected by the membrane.
Equations 19 and 20 are applicable to the fluid membrane, as well as any quenched membrane state m. For small values of θ we can use ϕ(z1) = ϕbq(z1)/q(∞) with q(z1)/q(∞) derived from our single-chain simulations. Approximate density profiles for nonzero surface concentrations can be derived by expressing ρ(z) as the product of the probability (θ) to find the cell occupied and the normalized density profile corresponding to one adsorbed molecule. With the aid of Eqs. 17–19 we then find that for z ≤ λ,
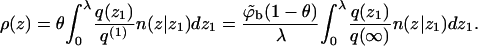 |
(21) |
For z > λ we must require ρ(z) = ρb. Note that this equation applies to the fluid membrane, as well as to any quenched membrane in state m.
The model system
Our model system consists of a single polyelectrolyte interacting with a finite size membrane, large compared to the size of the polymer and the range of intermolecular potentials. With the exception of several limiting test cases, in all simulations we consider polyelectrolyte chains composed of L = 20 spherical segments of diameter d, interacting with a considerably larger two-dimensional membrane cell consisting of M = 2500 lipid headgroups. The lipid membrane is modeled as a perfectly flat and impenetrable two-dimensional hexagonal lattice, with lipid headgroups occupying all its lattice sites. The lattice constant is set equal to d. The membrane may thus be regarded as an hexagonal array of closely packed disks of diameter d, as illustrated schematically in Fig. 1. Using a typical lipid headgroup area of 65 Å2 we find d = 8.66 Å. We simulate three-component membranes, composed of electrically neutral (z = 0), monovalent (z = −1), and tetravalent (z = −4) headgroups. These may be regarded as representing, respectively, the phosphatidyl-choline (PC), phosphatidyl-serine (PS), and phosphatidylinositol 4,5 bisphosphate (PIP2) lipids mentioned in the previous section. The lipid charges are treated as point charges residing at the grid points of the hexagonal lattice, and the electrostatic repulsion between them is modeled in the Debye-Hückel (DH) approximation. Explicitly, the interaction potential between lipids of valences z1 and z2 at distance r apart, and in units of kBT, is
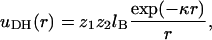 |
(22) |
where lB = e2/ɛ kBT is the Bjerrum length, and κ−1 is the Debye screening length; e denotes the elementary charge and ɛ is the dielectric constant. In all calculations we use lB = 7.14 Å, appropriate for water (ɛ = 78) at room temperature, and κ−1 = 10 Å, which corresponds to typical physiological conditions (monovalent ionic strength of ∼0.1 M). Note that κ−1 is comparable to the other relevant length scale in our system, namely, the distance (d = 8.66 Å) between adjacent lipid charges, as well as between adjacent polymer charges.
In the simulations each polymer bead carries a unit positive charge (z = +1), localized at its center. Although the polymer bond length d is fixed, there are no other restrictions on bond angles, except for those implied by electrostatic and spatial (excluded volume) repulsion between nonbonded segments. For the electrostatic interaction between polymer charges we again use DH potentials. The spatial repulsion is modeled using the shifted and truncated Lennard-Jones potential:
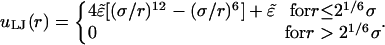 |
(23) |
Note that only the short-range repulsion of the 6:12 Lennard-Jones potential is retained. Setting 21/6 σ = d and 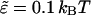 ensures the onset of steep repulsion as soon as r falls below d (38).
ensures the onset of steep repulsion as soon as r falls below d (38).
The electrostatic attraction between the oppositely charged polymer and membrane is also modeled using screened DH potentials. In addition, the membrane surface is treated as an impenetrable wall to the polymer, implying a minimal distance of d/2 between polymer and lipid charges. At this distance the electrostatic attraction between a polymer (z = +1) segment and a monovalent (z = −1) lipid headgroup is 1.07 kBT. For comparison, the electrostatic repulsion between neighboring monovalent lipids or adjacent polymer beads, taking the distance of closest approach to be r = d, is 0.35 kBT.
Since the distances between charges in the system are either comparable to or larger than the Debye length, i.e., r ≥ d ≈ κ−1, screening by counterions is expected to be effective. Under physiological conditions, when κ−1 is small (of the order of few Ångströms), the long-range character of the electrostatic interactions is screened and DH potentials offer a reasonable approximation. These potentials are commonly employed in simulation and theoretical studies of polyelectrolyte-surface interactions (see, e.g., (39,40)).
Henceforth, we shall measure all distances in units of d. Recall also that energies are measured in units of kBT.
Simulation method
The Rosenbluth MC method (31), or its configurational-bias variant, provides an efficient means for simulating polymer statistics (32). In this approach, chain conformations are generated, segment after segment, with preference for conformations of large statistical weight. Based on these ideas we present below our extension of the Rosenbluth scheme for modeling polyelectrolyte adsorption on fluid, as well as frozen and uniform membranes.
Frozen membrane
Consider first a polymer interacting with a membrane of quenched lipid configuration m. The simulation begins by placing the first chain segment at distance z1 above the center of the membrane cell, where its interaction energy with membrane lipids is u(z1,m) (see Fig. 1). We then sample k random directions (and hence positions, r2) for segment 2 and select one, say 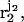 with probability
with probability 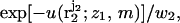 where
where 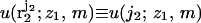 is the interaction energy of segment 2 with segment 1 and the membrane, and
is the interaction energy of segment 2 with segment 1 and the membrane, and 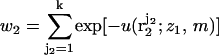 is a local partition function. This procedure is continued until all segments of the chain are generated. Repeated applications of this scheme (for the given (m, z1)) yield an ensemble of conformations {α = r2,…,rL;z1,m} with probabilities
is a local partition function. This procedure is continued until all segments of the chain are generated. Repeated applications of this scheme (for the given (m, z1)) yield an ensemble of conformations {α = r2,…,rL;z1,m} with probabilities
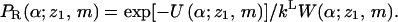 |
(24) |
As above, 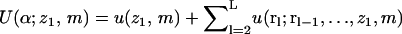 is the total interaction energy of polymer segments with each other and with the membrane. The partition function,
is the total interaction energy of polymer segments with each other and with the membrane. The partition function,
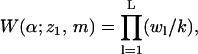 |
(25) |
with w1 ≡ k exp[−u(z1,m)], is the complete Rosenbluth factor of the polymer-membrane configuration (α;z1,m). Note that W becomes independent of k in the limit k → ∞. In our calculations we generally use k = 50. Note also that some of the k vectors pointing from segment l to l + 1 may cross the membrane interface, especially if segment l is near the surface. Their probability, and likewise their contribution to wl+1 (and hence to W) is zero, reflecting the loss of entropy associated with the presence of the hard membrane wall.
Since every possible conformation α is sampled with probability proportional to exp[−U(α)]/W(α), proper Boltzmann averaging requires weighting each α by its Rosenbluth factor W(α); i.e., the average (over α, for the given z1,m) of any structural or energetic polymer property A is given by
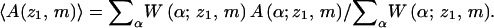 |
(26) |
Note also that the partition function corresponding to all polymer conformations originating at z1 is
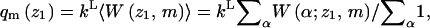 |
(27) |
where it should be stressed that the sum runs over all the α generated by the Rosenbluth scheme.
For z1 > λ we have qm(z1) = qm(∞) ≡ qb. Averaging 〈A(z1,m)〉 over all z1 ≤ λ we obtain the average of A (over all conformations) for molecules adsorbed on a frozen membrane of lipid configuration m,
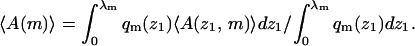 |
(28) |
Similarly,
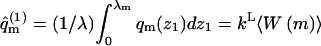 |
(29) |
is the partition function of the adsorbed polymer (see Eq. 18).
Fluid membrane
From Eqs. 3 and 6 we know that the thermodynamic and structural properties of a fluid membrane can be modeled based on simulating an ensemble of quenched membranes. However, this procedure is rather indirect and often impractical. Alternatively, adsorption on the fluid membrane could be simulated by combining the Rosenbluth and Metropolis methods. That is, after generating a polymer in conformation p = (α;z1) for a given lipid configuration m, the membrane is allowed to relax to a new configuration m′ through a series of Metropolis moves. Another polymer conformation p′ can then be generated for m′, letting the membrane relax to m″, and so on. The problem here is that the relaxed membrane is no longer the one which served to generate the last polymer conformation. A retracing procedure (32) can be used to improve this scheme, but not fully eliminate its inconsistencies. We have adopted, therefore, an alternative simulation method for the fluid membrane whereby, in the spirit of the Rosenbluth sampling scheme, we generate simultaneously both polymer conformations p and membrane configurations m, as follows.
Any joint polymer-membrane configuration p,m is fully specified by the coordinates of K = L + M(−1) + M(−4) particles; that is, L polymer segments, M(−1) monovalent lipids, and M(−4) tetravalent lipids (M(0) = M – M(−1) – M(−4) neutral lipids occupy all other membrane sites). We now generate a joint (p,m) configuration by randomly adding either a polymer segment or a charged lipid, until all particles have been placed. More explicitly, suppose the new configuration is already partly grown, consisting of a polymer chain of length l, and a partially charged membrane containing m(−1) and m(−4) anionic lipids. One of the remaining (K – l – m(−1) – m(−4)) particles is now randomly selected and added to the system. If this is a polymer segment it is added as the (l + 1)th segment of the chain. As before, this segment is placed in one of k possible positions, with probability exp[−u(l+1;l,m(−1),m(−4))]wl+1, and u(l+1;l,m(−1),m(−4)) is the interaction potential of the added particle with all those already placed, and wl+1 is defined as usual. If the new particle is, say, a monovalent lipid, it is placed with probability 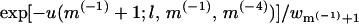 in one of n randomly chosen membrane sites, where u(m(−1) + 1;l,m(−1),m(−4)) is the interaction energy of this lipid with the rest of the system, and
in one of n randomly chosen membrane sites, where u(m(−1) + 1;l,m(−1),m(−4)) is the interaction energy of this lipid with the rest of the system, and 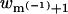 is the sum of the Boltzmann factors corresponding to the n membrane sites. (In the simulations we usually sample n = 1000 sites, some of which are possibly occupied already and thus do not contribute to w.) This procedure is repeated until all chain segments and all charged lipids are placed, resulting in a statistical distribution of p,m configurations, whose probabilities are
is the sum of the Boltzmann factors corresponding to the n membrane sites. (In the simulations we usually sample n = 1000 sites, some of which are possibly occupied already and thus do not contribute to w.) This procedure is repeated until all chain segments and all charged lipids are placed, resulting in a statistical distribution of p,m configurations, whose probabilities are
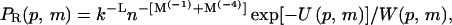 |
(30) |
where
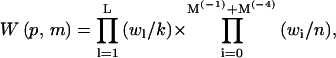 |
(31) |
is the (generalized) Rosenbluth factor of configuration p,m.
As for the quenched membrane, we generally sample many polymer-membrane configurations corresponding to various z1 values and only then average over this variable. The averaging procedure is analogous, e.g., the average of A for a given z1 is
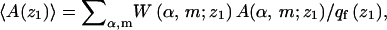 |
(32) |
where
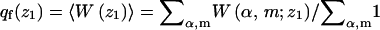 |
(33) |
is the partition function introduced in Eq. 16. Similarly,
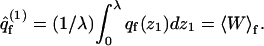 |
(34) |
RESULTS AND DISCUSSION
From the simulations we have derived the basic thermodynamic characteristics of macromolecules interacting with fluid, quenched, and uniformly charged membranes. In parallel, for every system considered we have calculated a variety of structural properties, such as the two-dimensional distribution of charged lipids in the membrane plane, or the density profile of chain segments along, as well as perpendicular to, the membrane normal. Two membrane compositions were analyzed in detail:
PC:PS:PIP2 = 98:1:1 membrane, i.e., a membrane containing 98% neutral (z = 0, or PC) lipids, 1% monovalent (z = −1, PS) lipids, and 1% tetravalent (z = −4, PIP2) lipids.
PC:PS:PIP2 = 89:10:1.
Note that the average charge, per lipid, corresponding to these membranes (hereafter also referred to as the weakly-charged and the strongly-charged membranes) is 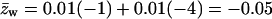 and
and  respectively.
respectively.
For both compositions, simulations were performed for fluid, quenched, and uniformly charged membranes. In the uniformly charged membrane all lipids carry the same partial charge, 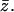
We repeat the numerical values of the various parameters in our model: The polyelectrolyte is a freely jointed homopolymer chain composed of L = 20 spherical segments, each carrying a z = +1 charge (see Fig. 1). The membrane cell is an hexagonal array of M = 50 × 50 lipid molecules. The headgroup diameter, 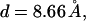 is equal to the polymer's bond length. The distance d also marks the onset of steep excluded volume repulsion between nonbonded chain segments (see Eq. 23 where σ = d/21/6 ≈ 7.72 Å and
is equal to the polymer's bond length. The distance d also marks the onset of steep excluded volume repulsion between nonbonded chain segments (see Eq. 23 where σ = d/21/6 ≈ 7.72 Å and  ). The Bjerrum and Debye lengths are lB = 7.14 Å and κ−1 = 10 Å, respectively.
). The Bjerrum and Debye lengths are lB = 7.14 Å and κ−1 = 10 Å, respectively.
For the sake of comparison, we have also performed a limited number of simulations for a stiff (rodlike) polymer, as well as for a weakly charged 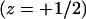 polymer. Recall that simulations are performed for varying values of the first segment position, z1, and that
polymer. Recall that simulations are performed for varying values of the first segment position, z1, and that 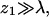 corresponds to a free polymer in solution. For the three-dimensional case of a polymer in solution we have also carried out, for comparative reasons, one set of simulations for an electrically neutral polymer.
corresponds to a free polymer in solution. For the three-dimensional case of a polymer in solution we have also carried out, for comparative reasons, one set of simulations for an electrically neutral polymer.
The number of chain-membrane conformations generated for each z1 value of a polymer adsorbed on a fluid membrane is ∼106. The number of chain conformations generated for each z1 value of a given quenched membrane m is ∼103, and the number of membrane configurations is 104. The increments in chain origin positions are Δz1 = 1. (Recall that distances are measured in units of d.) The number of possible bond directions when generating polymer conformations is k = 50. The number of possible positions for lipid addition in our simulation scheme of the fluid membrane is n = 1000.
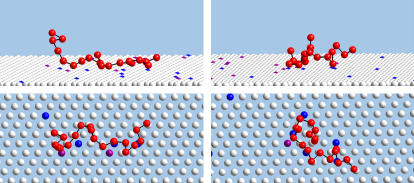
A pictorial illustration of the polymer-membrane configurations generated by our simulations is given in Fig. 2. The figure shows top and side views of two (rather arbitrary) simulation snapshots of a polyelectrolyte interacting with a fluid membrane of composition PC:PS:PIP2 = 98:1:1. Only part of the membrane is shown, yet it is apparent that the local concentration of charged lipids in the vicinity of the polymer significantly exceeds the membrane average.
FIGURE 2.
Side and top views of two, rather arbitrary, simulation snapshots (left and right), of a polyelectrolyte interacting with a weakly charged fluid membrane (1% PIP2, and 1% PS). For visual clarity only a section of the membrane is shown, and polymer segments and lipid headgroups are depicted as small spheres, (recall, however, that short range repulsions keep these segments at distance ≥ d). PIP2 and PS lipids are represented by blue and purple spheres, respectively. Note the localization of the charged lipids in the vicinity of the polymer.
Adsorption thermodynamics
Potential of mean force
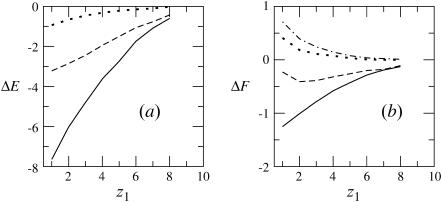
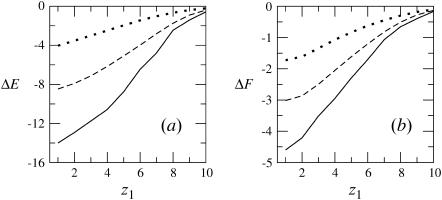
Fig. 3 shows how ΔF(z1), the differential adsorption free energy, and ΔE(z1), the differential adsorption energy, vary with the distance (z1) of the chain origin from the surface of the weakly charged (PC:PS:PIP2 = 98:1:1) membrane. Fig. 4 shows the same quantities for the strongly charged (PC:PS:PIP2 = 89:10:1) membrane. The value ΔF(z1) is the free energy change, or, the potential of mean force, associated with bringing the first segment of the macromolecule from the bulk solution to distance z1 from the membrane. Then ΔE(z1) and TΔS(z1) = ΔE(z1) − ΔF(z1) are the energetic and entropic components of this free energy difference. More explicitly, for the fluid and uniformly charged membranes ΔEf(z1) = 〈U(α,m;z1)〉f − 〈U(α)〉b − 〈U(m)〉f and ΔEu(z1) = 〈U(α,z1)〉 − 〈U(α)〉b, respectively. For the quenched membrane we show here the average energy change corresponding to the Boltzmann-weighted ensemble of quenched membranes,
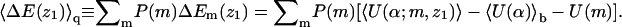 |
(35) |
The differential adsorption free energy onto the fluid membrane is given by 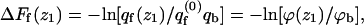 with a similar definition of ΔFu(z1). The corresponding free energy change for the quenched membrane is defined here as
with a similar definition of ΔFu(z1). The corresponding free energy change for the quenched membrane is defined here as 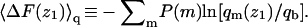 It should be noted that the net (or integral) adsorption energy of the quenched membrane is not a simple integral of
It should be noted that the net (or integral) adsorption energy of the quenched membrane is not a simple integral of 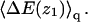 Similarly, the net free energy change of all membranes is not a direct integral of ΔF(z1). These issues will be clarified after analyzing Figs. 3 and 4 .
Similarly, the net free energy change of all membranes is not a direct integral of ΔF(z1). These issues will be clarified after analyzing Figs. 3 and 4 .
FIGURE 3.
The differential energy of adsorption (a), and free energy of adsorption (b), of a flexible macromolecule adsorbing on a membrane of lipid composition PC:PS:PIP2 = 98:1:1. The value z1 is the distance of the first polymer segment from the membrane plane. The solid, dashed, and dotted curves correspond to the fluid, frozen, and uniformly charged membranes, respectively. The dotted-dashed curve in b is for a weakly charged (z = +1/2) polymer interacting with a fluid membrane. The free energy change corresponding to this polymer is not shown because it very nearly overlaps the dotted curve in a.
FIGURE 4.
The differential energy of adsorption (a), and free energy of adsorption (b), of a flexible macromolecule interacting with a lipid membrane of composition PC:PS:PIP2 = 89:10:1. The solid, dashed, and dotted curves correspond to the fluid, frozen, and uniformly charged membranes, respectively.
Figs. 3 and 4 reveal, as expected, that the interaction (potential of mean force) between the polyelectrolyte and all three types of oppositely charged membranes is attractive, i.e., ΔE(z1) < 0. In Fig. 3 we also show the results for a weakly charged polymer (z = +1/2) interacting with a fluid membrane. This figure reveals that although in all cases ΔE(z1) < 0, this attractive interaction may not suffice to ensure adsorption. More explicitly, we note that in the case of a z = +1 polymer interacting with the uniformly ( ) charged membrane, as well as in the case of a weakly charged (z = +1/2) polymer interacting with a fluid membrane, the free energy change is positive, ΔF(z1) > 0. This is because the electrostatic attraction cannot counterbalance the repulsive depletion interaction resulting from the loss of conformational entropy experienced by any flexible molecule near a rigid wall. The weakly charged quenched membrane is, on average, nonadsorbing as well. Only the fluid membrane appears attractive to the peripheral macromolecule, owing to its ability to recruit charged lipids into the interaction zone. However, even this membrane is repulsive when the polymer charge is reduced to z = +1/2. Fig. 4 reveals that, upon increasing the membrane charge (to
) charged membrane, as well as in the case of a weakly charged (z = +1/2) polymer interacting with a fluid membrane, the free energy change is positive, ΔF(z1) > 0. This is because the electrostatic attraction cannot counterbalance the repulsive depletion interaction resulting from the loss of conformational entropy experienced by any flexible molecule near a rigid wall. The weakly charged quenched membrane is, on average, nonadsorbing as well. Only the fluid membrane appears attractive to the peripheral macromolecule, owing to its ability to recruit charged lipids into the interaction zone. However, even this membrane is repulsive when the polymer charge is reduced to z = +1/2. Fig. 4 reveals that, upon increasing the membrane charge (to 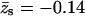 per lipid), all membranes become attractive. The strongest binding is to the fluid membrane and the weakest corresponds to the uniformly charged one.
per lipid), all membranes become attractive. The strongest binding is to the fluid membrane and the weakest corresponds to the uniformly charged one.
The entropy losses, TΔS(z1) = ΔE(z1) − ΔF(z1), associated with polyelectrolyte adsorption are quite substantial. In the quenched and uniform membrane cases these entropy losses reflect the lower conformational entropy of the adsorbed molecule, compared to that of a polymer in solution. The entropy loss is even higher, reaching ∼70% in the case of the fluid membrane, see Figs. 3 and 4. The origin of the enhanced entropy deficit experienced by this membrane is the additional loss of lipid mixing entropy.
From Eq. 13 we know that 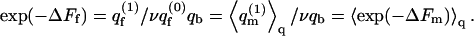 An analogous equality is also valid for the differential partition functions, q(z1). That is,
An analogous equality is also valid for the differential partition functions, q(z1). That is,
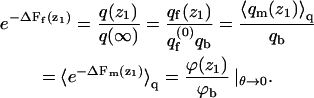 |
(36) |
The last equality here is a reminder that, in the limit of low surface coverage, q(z1)/q(∞) is equal to the ratio between the density of chain molecules (more precisely, chain termini) at distance z1 from the membrane, and the corresponding density in the bulk solution. From Eq. 36 we also note that 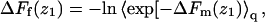 explaining why
explaining why 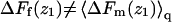 in Figs. 3 and 4.
in Figs. 3 and 4.
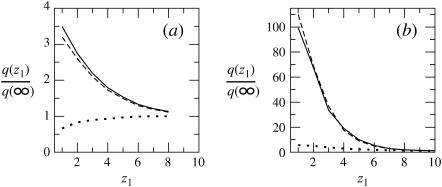
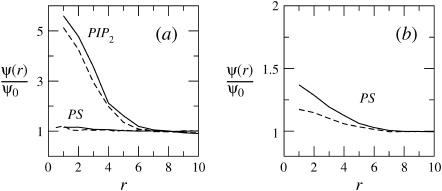
In Fig. 5 we show, for our three model membranes, how the partition function (equivalently, the first segment density) ratio defined in Eq. 36 varies with z1. It should be emphasized that the partition functions corresponding to the quenched and fluid membranes have been obtained using the two different MC simulation schemes described in the previous section. Apart from the small numerical noise, we indeed find that the partition functions corresponding to the fluid and the ensemble of quenched membranes are essentially identical, reassuring that the different simulation methods indeed yield identical results.
FIGURE 5.
The partition function ratio, 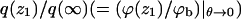 for a macromolecule interacting with weakly charged membranes of composition PC:PS:PIP2 = 98:1:1 (a), and strongly charged membranes where PC:PS:PIP2 = 89:10:1 (b). Solid, dashed, and dotted curves correspond to the fluid, quenched, and uniformly charged membranes, respectively.
for a macromolecule interacting with weakly charged membranes of composition PC:PS:PIP2 = 98:1:1 (a), and strongly charged membranes where PC:PS:PIP2 = 89:10:1 (b). Solid, dashed, and dotted curves correspond to the fluid, quenched, and uniformly charged membranes, respectively.
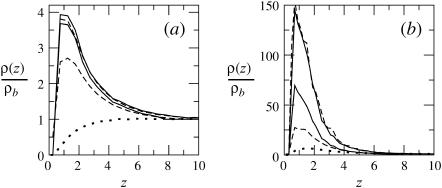
The ratio q(z1)/qb = ϕ(z1)/ϕb reveals, as expected, the stronger attraction of the polyelectrolyte to the strongly charged membrane (Fig. 5 b). Similar behavior is shown by the average segment density profiles, ρ(z), as defined in Eq. 19 and shown in Fig. 6. Again we see that for θ → 0, the density profiles corresponding to the fluid and quenched membranes are the same.
FIGURE 6.
Segment density profiles along the membrane normal, ρ(z), relative to the segment density in the bulk solution ρb = ρ(∞). The membrane composition is PC:PS:PIP2 = 98:1:1 (a), and PC:PS:PIP2 = 89:10:1 (b). The solid, dashed, and dotted curves correspond to the fluid, quenched, and uniformly charged membranes, respectively. Two curves are shown for each type of membrane; the upper curve corresponds to the low density limit 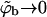 (and hence θ → 0), and the lower one is for
(and hence θ → 0), and the lower one is for 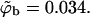
Figs. 5 and 6 convey similar information. Fig. 5 displays the density profile of chain termini, whereas Fig. 6 shows the average density due to all chain segments (see Eq. 19). Indeed, apart from small differences at the very small (i.e., near the membrane) and large (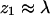 ) values of z1, the two profiles are quite similar. Unlike ϕ(z1) (∝ q(z1)), which decreases monotonically with z1, the maximum in ρ(z) occurs slightly away from the membrane surface. This is probably due to the fact that terminal segments can more easily attach and detach from the surface. Comparing Figs. 5 and 6 we also note that ϕ(z1) (∝ q(z1)) decays slightly more slowly than ρ(z), reflecting the fact that although one chain-end may reside relatively far from the membrane, other segments are attracted to the membrane (see Fig. 2). Of course, all end effects become negligible for very long chains and we then expect similar density distributions for all chain segments.
) values of z1, the two profiles are quite similar. Unlike ϕ(z1) (∝ q(z1)), which decreases monotonically with z1, the maximum in ρ(z) occurs slightly away from the membrane surface. This is probably due to the fact that terminal segments can more easily attach and detach from the surface. Comparing Figs. 5 and 6 we also note that ϕ(z1) (∝ q(z1)) decays slightly more slowly than ρ(z), reflecting the fact that although one chain-end may reside relatively far from the membrane, other segments are attracted to the membrane (see Fig. 2). Of course, all end effects become negligible for very long chains and we then expect similar density distributions for all chain segments.
In Fig. 6, we also show representative density profiles corresponding to high surface concentrations of macromolecules (see Eq. 21). Under these conditions we expect different adsorption probabilities on the fluid and quenched membrane. Indeed, for a macromolecule bulk density of 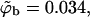 Eq. 17 yields θf = 0.5 for the strongly charged fluid membrane, whereas Eq. 18 implies a much smaller surface density for the quenched membrane,
Eq. 17 yields θf = 0.5 for the strongly charged fluid membrane, whereas Eq. 18 implies a much smaller surface density for the quenched membrane, 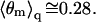 Additional values are given in Table 1. Note that the average free energy of adsorption in the ensemble of quenched membranes is zero, indicating that some membrane environments must be repulsive (see below). Also repulsive is the weakly charged uniform membrane, as clearly seen in Fig. 3 b. Indeed, the ratio
Additional values are given in Table 1. Note that the average free energy of adsorption in the ensemble of quenched membranes is zero, indicating that some membrane environments must be repulsive (see below). Also repulsive is the weakly charged uniform membrane, as clearly seen in Fig. 3 b. Indeed, the ratio 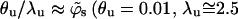 ), which may be interpreted as the three-dimensional density of macromolecules very near the membrane, is
), which may be interpreted as the three-dimensional density of macromolecules very near the membrane, is 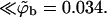
TABLE 1.
Adsorption properties
PC:PS:PIP2 = 89:10:1 (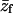 = −0.14) = −0.14)
|
PC:PS:PIP2 = 98:1:1 (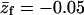 ) )
|
|||||
|---|---|---|---|---|---|---|
| Fluid | Quenched | Uniform | Fluid | Quenched | Uniform | |
| ΔE | −12.5 | −7.4 | −3.1 | −5.0 | −2.4 | −0.7 |
| ΔF | −3.5 | −1.4 | −1.0 | −0.7 | 0 | 1.3 |
| θ | 0.5 | 0.28 | 0.09 | 0.06 | 0.05 | 0.01 |
Adsorption energies and free energies for the 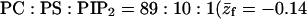 ) and
) and 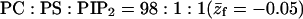 membranes. For the quenched lipid membrane we list 〈ΔEm〉q and 〈ΔFm〉q. The surface concentrations, θ, in the bottom row (〈θm〉q for the quenched membrane) are for a bulk concentration of macromolecules
membranes. For the quenched lipid membrane we list 〈ΔEm〉q and 〈ΔFm〉q. The surface concentrations, θ, in the bottom row (〈θm〉q for the quenched membrane) are for a bulk concentration of macromolecules 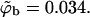
Adsorption free energies
The adsorption free energy and related thermodynamic functions are calculated using the partition functions appearing in Eqs. 15–18 and 21, whose values depend on the cutoff distance λ. We have determined 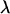 as the distance beyond which ρ(z)/ρb ≤ 1.1 for attractive membranes (ΔF < 0), or >0.9 for repulsive ones. (This criterion closely satisfies the second equality in Eq. 20.)
as the distance beyond which ρ(z)/ρb ≤ 1.1 for attractive membranes (ΔF < 0), or >0.9 for repulsive ones. (This criterion closely satisfies the second equality in Eq. 20.)
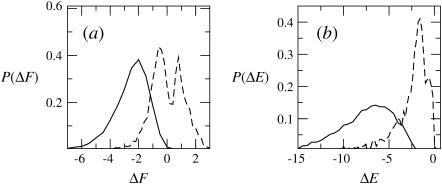
Given the λ-values we have calculated, the integral adsorption energies, free energies, and surface concentrations θ for the fluid, quenched, and uniform membranes. Fig. 7 shows the distributions, P(ΔF) and P(ΔE), of adsorption free energies, ΔFm, and energies, ΔEm, for the ensemble of quenched membranes. The adsorption energies are defined here by 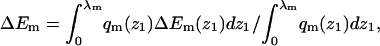 and their average is
and their average is 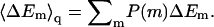 The integral adsorption energies for the fluid and uniformly charged membranes are
The integral adsorption energies for the fluid and uniformly charged membranes are 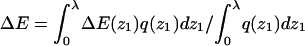 where ΔE(z1) are the differential adsorption energies shown in Figs. 3 and 4. The adsorption free energies are given by
where ΔE(z1) are the differential adsorption energies shown in Figs. 3 and 4. The adsorption free energies are given by 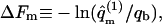 with
with 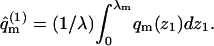 Their average is
Their average is 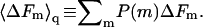 In Figs. 3 and 4 we have shown
In Figs. 3 and 4 we have shown 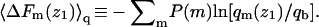 Thus, as noted above,
Thus, as noted above, 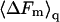 is not simply the integral of
is not simply the integral of 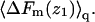 The relationship between ΔF(z1) and ΔF of the fluid membrane is different, namely,
The relationship between ΔF(z1) and ΔF of the fluid membrane is different, namely, 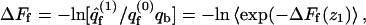 with a similar relationship for the uniform membrane.
with a similar relationship for the uniform membrane.
FIGURE 7.
Probability distributions of adsorption free energies P(ΔF) (a), and adsorption energies P(ΔE) (b), for a Boltzmann-weighted ensemble of quenched membranes. Solid and dashed curves correspond to membranes with PC:PS:PIP2 = 89:10:1 and PC:PS:PIP2 = 98:1:1, respectively. See Table 1 for more details.
The numerical values of ΔF and ΔE for the fluid, quenched, and uniform membranes are listed in Table 1. Again we note that the adsorption energy is largest for the fluid membrane and smallest for the uniform membrane. In fact, no adsorption takes place on the weakly charged uniform membrane, (ΔFu > 0), and the weakly charged quenched membrane is, on average, nonadsorbing as well. Note, however, that in this case P(ΔF) is bimodal. From Fig. 7 a, we note that although ΔEm < 0 for all m values, the bimodal distribution of ΔFm reflects two distinct classes of quenched environments, corresponding to attractive (ΔFm < 0) and repulsive (ΔFm > 0) membranes.
The distributions, P(θ), of surface concentrations for the ensembles of weakly and strongly charged quenched membrane are shown in Fig. 8. Also mentioned there (and in Table 1) are the average values of θ for the fluid and uniform membranes, confirming that adsorption onto the fluid membrane is, indeed, the strongest of all. In accordance with the results in Fig. 7 a, we note in Fig. 8 a that a large fraction of the local environments comprising a weakly charged quenched membrane are repulsive. On the other hand, a weakly charged fluid membrane is everywhere attractive. This is of course due to the ability of its charged lipids to diffuse and localize at the macromolecule adsorption site. In biological systems, where the interactions are often weak, such subtle differences could be of crucial importance.
FIGURE 8.
The distribution of surface concentrations, θ, for an ensemble of quenched membranes of composition PC:PS:PIP2 = 98:1:1 (a) and PC:PS:PIP2 = 89:10:1 (b). Also listed are the average surface coverages of the fluid, quenched, and uniformly charged membrane. In a, the solid curve is the overall distribution of θ values, whereas the dashed and dash-dotted curves correspond to the distributions of θ-values for membranes with ΔFm < 0 and ΔFm > 0, respectively. In all cases the volume fraction of macromolecules in the bulk solution is 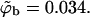
Structural properties
The structural and thermodynamic properties of the adsorbed macromolecules are intimately related to each other. For instance, the density profile of chain termini, ϕ(z1), enters the calculation of partition functions and free energies. In this subsection we present additional information, pertaining to the configurational statistics of the adsorbed polymer and the concomitant changes in the two-dimensional distribution of membrane lipids. Since changes in lipid distribution can only occur in fluid membranes, the discussion in this subsection involves only fluid membranes.
Polymer dimensions
In Table 2, we present the results of our simulations for some of the basic conformational characteristics of the 20-segment polyelectrolyte chain, when adsorbed onto the weakly and strongly charged membranes. For the sake of comparison we also list the corresponding values of the charged polyelectrolyte, as well as for the corresponding neutral chain, in an isotropic bulk solution.
TABLE 2.
Macromolecule conformational properties
 |
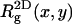 |
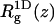 |
σ(z) | ξp | |
|---|---|---|---|---|---|
| Solution | 2.97 (2.50) | 2.42 (2.04) | 1.72 (1.45) | 1.72 (1.45) | 4.70 (3.15) |
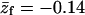 |
2.91 | 2.80 | 0.79 | 2.13 | 8.23 |
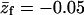 |
2.91 | 2.63 | 1.25 | 4.00 | 5.37 |
Conformational properties of the polymer in solution and when adsorbed on the weakly (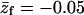 ) and strongly (
) and strongly (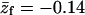 ) charged membranes. The numbers in parentheses are for an electrically neutral polymer. The value
) charged membranes. The numbers in parentheses are for an electrically neutral polymer. The value 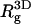 is the three-dimensional radius of gyration of the polymer,
is the three-dimensional radius of gyration of the polymer, 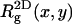 is the two-dimensional radius of gyration in a plane parallel to the membrane surface,
is the two-dimensional radius of gyration in a plane parallel to the membrane surface, 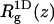 is the z-component of the radius of gyration (measured, as usual, with respect to the center of mass), σ(z) is the width of the segment density distribution along z, and ξp is the persistence length.
is the z-component of the radius of gyration (measured, as usual, with respect to the center of mass), σ(z) is the width of the segment density distribution along z, and ξp is the persistence length.
Owing to the electrostatic repulsion between chain segments, 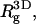 the radius of gyration of the polymer in solution, is significantly larger than that of the neutral polymer (41,42). We find
the radius of gyration of the polymer in solution, is significantly larger than that of the neutral polymer (41,42). We find 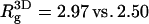 for the neutral polymer; the corresponding end-to-end distances are
for the neutral polymer; the corresponding end-to-end distances are 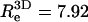 and 6.36, respectively. The ratio
and 6.36, respectively. The ratio 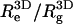 is close to the theoretical value,
is close to the theoretical value,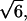 for an ideal chain (43). Recall that
for an ideal chain (43). Recall that 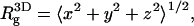 where
where 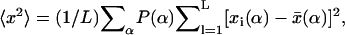 with
with 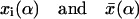 denoting, respectively, the x coordinates of segment l, and the center of mass of a polymer in conformation α. In an isotropic solution
denoting, respectively, the x coordinates of segment l, and the center of mass of a polymer in conformation α. In an isotropic solution 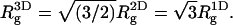 From Table 2 it is apparent that the polymer's three-dimensional radius of gyration, (
From Table 2 it is apparent that the polymer's three-dimensional radius of gyration, (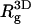 ), does not change much upon adsorption. Yet,
), does not change much upon adsorption. Yet, 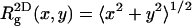 (the two-dimensional radius of gyration in a plane parallel to the membrane surface) and
(the two-dimensional radius of gyration in a plane parallel to the membrane surface) and 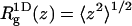 (the one-dimensional radius of gyration along the membrane normal) are quite different from the corresponding bulk values. As expected, upon adsorption, the polymer flattens parallel to the membrane plane (see also Fig. 2), resulting in larger
(the one-dimensional radius of gyration along the membrane normal) are quite different from the corresponding bulk values. As expected, upon adsorption, the polymer flattens parallel to the membrane plane (see also Fig. 2), resulting in larger 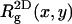 and smaller
and smaller 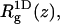 with enhanced anisotropy on the strongly adsorbing membrane. We also note a substantial increase in the persistence length, ξp, upon adsorption, reflecting the stretching of the polymer chain along the membrane plane.
with enhanced anisotropy on the strongly adsorbing membrane. We also note a substantial increase in the persistence length, ξp, upon adsorption, reflecting the stretching of the polymer chain along the membrane plane.
In Table 2 we also list the width, 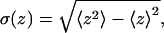 of the chain density profile along the membrane normal, where
of the chain density profile along the membrane normal, where
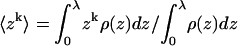 |
(37) |
is the kth moment of the segment density 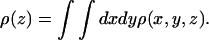 Here ρ(r) is the same quantity defined in Eq. 19, and
Here ρ(r) is the same quantity defined in Eq. 19, and 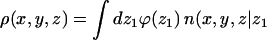 ) is the segment density at x,y,z, where n(x,y,z|z1)dxdydz is the number of segments in dxdydz around x,y,z, due to chains originating at z1. Note that in calculating n(x,y,z|z1), and hence ρ(x,y,z), we average over many chain conformations, ensuring that their centers of mass reside on one z axis. With
) is the segment density at x,y,z, where n(x,y,z|z1)dxdydz is the number of segments in dxdydz around x,y,z, due to chains originating at z1. Note that in calculating n(x,y,z|z1), and hence ρ(x,y,z), we average over many chain conformations, ensuring that their centers of mass reside on one z axis. With 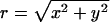 denoting the distance from the z axis, the function
denoting the distance from the z axis, the function
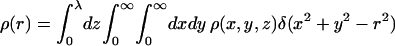 |
(38) |
defines the integrated radial distribution of chain segments, relative to the membrane normal, δ(x) being the δ-function. Equivalently, ρ(r) is the projection of the segment density distribution on the membrane plane. Note 
It is not difficult to show that if the centers of mass of all chain conformations are superimposed onto the same point (say x,y,z = 0), then
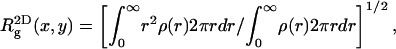 |
(39) |
and (because now  Eq. 39 remains valid if the centers of mass no longer reside at one point, but are still restricted to the z axis. On the other hand,
Eq. 39 remains valid if the centers of mass no longer reside at one point, but are still restricted to the z axis. On the other hand, 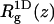 is no longer equal to σ(z). We expect (see Table 2),
is no longer equal to σ(z). We expect (see Table 2), 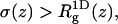 since the width of the distribution is a convolution of the center-of-mass distribution and the distribution of chain segments around the center of mass (only the latter contributes to the radius of gyration).
since the width of the distribution is a convolution of the center-of-mass distribution and the distribution of chain segments around the center of mass (only the latter contributes to the radius of gyration).
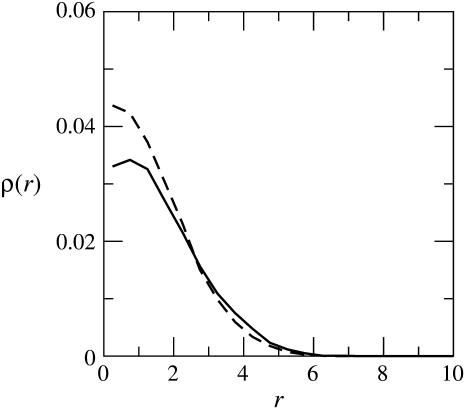
Fig. 9 shows ρ(r) for a macromolecules adsorbed on the weakly and the strongly charged membranes, indicating a radial span of approximately five segment diameters in both cases. As noted already in Table 2, and as follows by comparing Figs. 6 and 9, the lateral dimensions of the adsorbed macromolecule are approximately twice-larger than its extension along the membrane normal.
FIGURE 9.
The integrated two-dimensional density, ρ(r), of chain segments as a function of the radial distance from the membrane normal. The solid and dashed curves are for the strongly and weakly charged fluid membranes, respectively.
Lipid redistribution
The lateral dimensions of the adsorbed macromolecule are expected to correlate with the lateral distribution of charged lipids in the membrane. One important characteristic of the two-dimensional lipid distribution is the enrichment factor 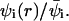 This is the ratio between the local concentration of lipid species i at distance r from the (projection on the membrane plane) of the polymer's center of mass, and the average (or bulk) concentration of this lipid in the membrane. The enrichment factor thus measures the change in local lipid composition after macromolecule adsorption.
This is the ratio between the local concentration of lipid species i at distance r from the (projection on the membrane plane) of the polymer's center of mass, and the average (or bulk) concentration of this lipid in the membrane. The enrichment factor thus measures the change in local lipid composition after macromolecule adsorption.
In Fig. 10, we show the enrichment factor for two ternary membranes, PC:PS:PIP2 = 89:10:1, and 98:1:1 (left); and two binary membranes, PC:PS = 90:10 and 99:1 (right). Comparing Figs. 9 and 10 we find that the range of the lipid region enriched with charged lipids, namely, approximately five lipid diameters, correlates closely with the lateral dimensions of the adsorbed polymer.
FIGURE 10.
The enrichment factor of charged lipids associated with macromolecule adsorption on a ternary lipid mixture of PC/PS/PIP2 (a), and a binary mixture PC/PS (b), as a function of the radial distance from the polymer's center of mass. The bulk molar fraction of PIP2 in a is, in all cases, 0.01. Solid curves and dashed curves, in both figures, correspond to PS molar fractions of 0. 1 and 0.01, respectively.
Another view of the lipid density profile is shown in Fig. 11 a, which displays the distribution of tetravalent lipids around the projection onto the membrane plane of the polymer's center of mass. Fig. 11 b, shows, for comparison, the results corresponding to a stiff, rodlike polymer of the same length and charge. For both cases shown the lipid composition is PC:PS:PIP2 = 98:1:1, but it should be noted that the PIP2 distribution in the PC:PS:PIP2 = 89:10:1 membrane is very similar. The interaction energy of the rod with the membrane (Fig. 11 b) shows a very steep minimum near the surface, with ΔE(z = 1) = −10 and ΔF(z = 1) = −6. The entropy loss here, TΔS = −4, is entirely due to lipid demixing. For comparison, the results shown in Fig. 11 a are for a flexible polymer whose first (or last) segment is at z1 = 1. In this case we find ΔE(z1 = 1) = −7.8 and ΔF(z1 = 1) = −1.3, implying a substantially larger entropy loss, TΔS = −6.3, which in this case involves a loss of polymer conformational entropy in addition to the loss of lipid mixing entropy. (After averaging over all z1, we find for polymer adsorption: ΔE = −5 and ΔF = −0.7, and hence TΔS = −4.3.)
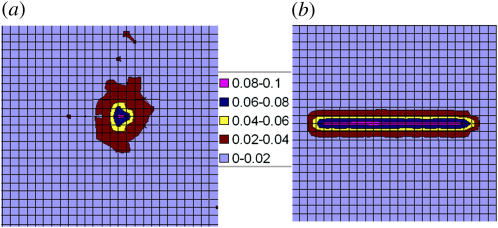
FIGURE 11.
Contour maps of PIP2 density in the membrane plane. The area per square of the grid corresponds to one lipid molecule. (The square grid is used here just for display; the simulations were carried out using a two-dimensional hexagonal lattice.) The figure on the left, a, is for a flexible 20-segment chain interacting with a fluid membrane of average composition PC:PS:PIP2 = 98:1:1. The figure on the right, b, is for a rodlike polymer of the same length and charge. The rod is placed at distance z = 1 from the membrane. The polymer's first segment is fixed at z1 = 1. The numbers labeling the color code indicate the local mole fractions of PIP2. The average membrane concentration is 0.01.
Figs. 10 a and 11 a reveal a rather dramatic enrichment of the interaction zone by the tetravalent lipids, and essentially no change in the local concentration of the monovalent lipids. This phenomenon has been discussed and analyzed both theoretically and experimentally (9,11,15). Qualitatively, its origin involves two basic physical principles. The first is that the electrostatic interaction free energy between a charged macromolecule and a charged surface is minimal at isoelectricity, i.e., when the net amounts of negative (in our case lipid) and positive (in our case polymer) charges are equal (44–46). Thus, when a highly charged polymer is brought into contact with a weakly charged fluid membrane, oppositely charged lipids tend to migrate toward the polymer, attempting to achieve the desired charge matching. In the case of a flexible polyelectrolyte on a mixed membrane this tendency is partly opposed by the entropic penalties associated with the loss of polymer flexibility and lipid mixing freedom. The second physical fact is that importing one tetravalent lipid into the interaction zone involves a much lower entropy loss as compared to that of bringing four monovalent lipids.
The entropy change upon transferring one lipid molecule of type i from a region where its molar fraction is 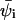 into a region of local mole fraction ψi(r) is, (for small
into a region of local mole fraction ψi(r) is, (for small 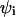 ),
),
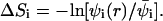 |
(40) |
A crude estimate of the average lipid charge within the interaction zone can be obtained by calculating the amount of charge required to neutralize the charge of the adsorbed polymer. Our simulations of a fluid membrane containing 1% PIP2 and 10% PS reveal that, on average, most of the 20 polymer charges reside within a rather thin surface layer (see Fig. 6, and Table 2). The radius of the lipid interaction zone is approximately five headgroup diameters, corresponding to a membrane patch containing ∼80 lipids. The simulations show that the total lipid charge within this patch is ∼−20. Approximately eight charges are provided by the monovalent lipids (corresponding to their average fraction in the membrane) and the remaining 12 × 3 tetravalent lipids, implying an average enrichment factor of 3 (see Fig. 10). The entropic cost of bringing the three tetravalent lipids into the interaction region is thus −3 ln(0.03/0.01) ≈ −3.3 (which is nearly one-half of the total entropy loss in adsorption; see Table 1). In the absence of tetravalent lipids, effective charge neutralization would require the import of 12 additional monovalent lipids into the interaction region. In this case the entropic penalty would be intolerably high, −12 ln(20/8) ≈ −11, comparable to the gain in electrostatic energy (Fig. 7). Supporting this conclusion are our simulations of polymer adsorption on a binary membrane containing only neutral and monovalent lipids, whose results are shown in Fig. 10 b. Owing to the severe entropic penalty, PS enrichment in these membranes is very small and the adsorption energy is small for 10% PS and positive for 1% PS.
In the case of the weakly charged (1% PIP2 and 1% PS) membrane, complete charge neutralization would require the recruitment of five tetravalent lipids, implying a substantially higher entropic penalty as compared to the strongly charged membrane. Here we found that, on average, only 12 lipid charges have accumulated in the interaction zone and that a similar number of polymer charges reside within the narrow surface layer (see Fig. 2). In other words, in this case, the system settles on less than complete neutralization of all polymer charges, thereby retaining more lipid translational freedom and polymer flexibility. Finally, we note that a membrane containing a large amount of monovalent lipids to begin with, need not relocate lipids upon polymer adsorption. For our case, using the same, rather crude, estimates as above, we conclude that a membrane containing ∼20–25% PS need not recruit additional molecules into the interaction region. These qualitative conclusions appear consistent with experiments, measuring the interaction between the MARCKS effector domain (and similar peptides) and mixed PC:PS:PIP2 membranes (9,15).
CONCLUDING REMARKS
Our major objective in this work has been to study the role of lipid mobility and composition in the nonspecific electrostatic adsorption of charged flexible macromolecules. Based on computer simulations and qualitative theoretical considerations we have shown that a fluid membrane, enabling lipid lateral diffusion, is substantially more effective in mediating macromolecule binding than a frozen or a uniform membrane carrying the same average charge. We also found that multivalent lipids, even if in small amounts, can substantially enhance the electrostatic adsorption of flexible macromolecules. The crucial role of these lipids in mediating membrane binding is a direct consequence of the fact that, in the fluid lipid membrane, their localization in the macromolecule's adsorption zone provides efficient electrostatic binding at a minimal cost of lipid demixing entropy.
A strongly charged membrane can bind an oppositely charged macromolecule even if all the charged lipids are monovalent, because in this case there is no need for lipid segregation, thus avoiding the entropic lipid demixing penalty. On the other hand, previous theoretical studies suggest that a fluid membrane containing relatively small (yet biologically relevant) amounts, say 10–20%, of monovalent lipids may effectively bind rigid charged macromolecules (e.g., folded globular proteins) (13,18). In such cases the electrostatic binding free energy outbalances the lipid entropy loss. On the other hand, in the case of a flexible macromolecule, binding involves the additional loss of conformational entropy. Our calculations indeed suggest that in this case, 10% of monovalent lipids hardly suffice to mediate polymer binding and the presence of multivalent lipids in the membrane, whose localization in the interaction zone involves just a small entropy loss, thus appears critical. Our conclusions regarding the ability of a medium-size macromolecule to sequester multivalent lipids upon membrane binding appear consistent with recent experimental observations. Qualitatively, they also agree with more detailed, atomic-level calculations—modeling, for instance, MARCKS adsorption on several quenched environments of a mixed membrane (15).
From the more technical-theoretical aspect, we have presented an extended version of the Rosenbluth Monte Carlo sampling scheme, enabling the simultaneous generation of polymer and membrane configurations. In addition, we have shown that, in principle, the statistical aspects of polymer adsorption on a fluid membrane can be obtained by biased superposition of simulation data of an ensemble of quenched membranes. An approximate cell model has been presented to account for the different adsorption probabilities on fluid and quenched membranes. In the limit of vanishing macromolecule concentrations, the average adsorption probabilities become equal.
Notwithstanding the inherent approximations of our model (e.g., the use of DH potentials), our results suggest that the electrostatic binding free energies of flexible macromolecules onto lipid membrane are generally small and depend on a subtle interplay of several factors. These include lipid mobility and composition on the one hand, and macromolecule charge, shape, and flexibility on the other hand. Finally, as noted in the Introduction, the work presented here is currently being extended to model the adsorption of heterobiopolymers. As a specific model system we are studying the adsorption of MARCKS on a fluid lipid membrane, with particular emphasis on elucidating the roles of polymer chain entropy, electrostatic and hydrophobic interactions, lipid fluidity and composition, whose complex interplay underlies the electrostatic switch mechanism.
Acknowledgments
We thank David Andelman for many stimulating discussions, suggestions, and encouragement. We also thank Sylvio May, Daniel Harries, Igal Szleifer, Diana Murray, Barry Honig, Stuart McLaughlin, Bill Gelbart, and the reviewers of this manuscript for helpful advice.
The financial support of the Israel Science Foundation (grant No. 227/02) and the US-Israel Binational Science Foundation (grant No. 2002-75) is gratefully acknowledged. The Fritz Haber center is supported by the Minerva Foundation, Munich, Germany.
References
- 1.Edidin, M. 2003. The state of lipid rafts: from model membranes to cells. Annu. Rev. Biophys. Biomol. Struct. 32:257–283. [DOI] [PubMed] [Google Scholar]
- 2.Simons, K., and E. Ikonon. 1997. Functional rafts in cell membranes. Nature. 387:569–572. [DOI] [PubMed] [Google Scholar]
- 3.Simons, K., and D. Toomre. 2001. 2000. Lipid rafts and signal transduction. Nature Rev. Mol. Cell Biol. 1:31–39. Erratum in. Nat. Rev. Mol. Cell Biol. 2:216. [DOI] [PubMed] [Google Scholar]
- 4.Sackmann, E. 1995. Biological membranes architecture and function. In Structure and Dynamics of Membranes. R. Lipowsky and E. Sackmann, editors. Elsevier, Amsterdam, The Netherlands. 1–64.
- 5.Sens, P., and S. A. Safran. 2000. Inclusion induced phase separation in mixed lipid film. Eur. Phys. J. E. 1:237–248. [Google Scholar]
- 6.Mouritsen, O. G. 1998. Self-assembly and organization of lipid-protein membranes. Curr. Opinions Colloid Interf. Sci. 3:78–87. [Google Scholar]
- 7.Mitrakos, P. M., and P. M. Macdonald. 2000. Polyelectrolyte molecular weight and electrostatically induced domains in lipid bilayer membranes. Biomacromolecules. 1:365–376. [DOI] [PubMed] [Google Scholar]
- 8.Bazzi, M. D., and G. L. Nelsestuen. 1990. Extensive segregation of acidic phospholipids in membranes induced by protein kinase C and related proteins. Biochemistry. 30:7961–7969. [DOI] [PubMed] [Google Scholar]
- 9.Gambhir, A., G. Hangyás-Mihályné, I. Zaitseva, D. S. Cafiso, J. Y. Wang, D. Murray, S. N. Pentyala, S. O. Smith, and S. McLaughlin. 2004. Electrostatic sequestration of PIP2 on phospholipid membranes by basic/aromatic regions of proteins. Biophys. J. 86:2188–2207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Murray, D., A. Arbuzova, G. Hangyás-Mihályné, A. Gambhir, N. Ben-Tal, B. Honig, and S. McLaughlin. 1999. Electrostatic properties of membranes containing acidic lipids and adsorbed basic peptides: theory and experiment. Biophys. J. 77:3176–3188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Haleva, E., N. Ben-Tal, and H. Diamant. 2004. Increased concentration of polyvalent phospholipids in the adsorption domain of a charged protein. Biophys. J. 86:2165–2178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Harries, D., S. May, W. M. Gelbart, and A. Ben-Shaul. 1998. Structure, stability and thermodynamics of lamellar DNA-lipid complexes. Biophys. J. 75:159–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.May, S., D. Harries, and A. Ben-Shaul. 2000. Lipid demixing and protein-protein interactions in the adsorption of charged proteins on mixed membranes. Biophys. J. 79:1747–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Murray, D., A. Arbuzova, B. Honig, and S. McLaughlin. 2001. The role of electrostatic and nonpolar interactions in the association of peripheral proteins with membranes in peptide-lipid interactions. In Current Topics in Membranes: Peptide-Lipid Interactions. S. Simon and T. McIntosh, editors. Academic Press, New York.
- 15.Wang, J. Y., A. Gambhir, S. McLaughlin, and D. Murray. 2004. A computational model for the electrostatic sequestration of PI(4,5)P2 by membrane-adsorbed basic peptides. Biophys. J. 86:1969–1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fleck, C., R. R. Netz, and H. H. von Grünberg. 2001. Poisson-Boltzmann theory for membranes with mobile charged lipids and pH-dependent interaction of a DNA molecule with a membrane. Biophys. J. 82:76–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.May, S., D. Harries, and A. Ben-Shaul. 2002. Macroion-induced compositional instability of binary fluid membranes. Phys. Rev. Lett. 89:268102–268105. [DOI] [PubMed] [Google Scholar]
- 18.Mbamala, E. C., A. Ben-Shaul, and S. May. 2005. Domain formation induced by the adsorption of charged proteins on mixed lipid membranes. Biophys. J. 88:1702–1714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hosaka, M., R. E. Hammer, and T. C. Sudhof. 1999. A phospho-switch controls the dynamic association of synapsins with synaptic vesicles. Neuron. 24:377–387. [DOI] [PubMed] [Google Scholar]
- 20.Ono, A., S. D. Ablan, S. J. Lockett, K. Nagashima, and E. O. Freed. 2004. Phosphatidylinositol (4,5) bisphosphate regulates HIV-1 GAG targeting to the plasma membrane. Proc. Natl. Acad. Sci. USA. 101:14889–14894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.McLaughlin, S., and A. Aderem. 1995. The myristoyl-electrostatic switch: a modulator of reversible protein-membrane interactions. Trends Biochem. Sci. 20:272–276. [DOI] [PubMed] [Google Scholar]
- 22.Murray, D., L. Hermida-Matsumoto, C. A. Buser, J. Tsang, C. T. Sigal, N. Ben-Tal, B. Honig, M. D. Resh, and S. McLaughlin. 1998. Electrostatics and the membrane association of SRC: theory and experiment. Biochemistry. 37:2145–2159. [DOI] [PubMed] [Google Scholar]
- 23.Wang, J., A. Arbuzova, G. Hangyás-Mihályné, and S. McLaughlin. 2001. The effector domain of myristoylated alanine-rich C kinase substrate binds strongly to phosphatidylinositol 4,5-bisphosphate. J. Biol. Chem. 276:5012–5019. [DOI] [PubMed] [Google Scholar]
- 24.Laux, T., K. Fukami, M. Thelen, T. Golub, D. Frey, and P. Caroni. 2000. GAP43, MARCKS, and CAP23 modulate PI(4,5)P2 at plasmalemmal rafts, and regulate cell cortex actin dynamics through common mechanism. J. Cell Biol. 149:1455–1471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.McLaughlin, S., J. Wang, A. Gambhir, and D. Murray. 2002. PIP2 and proteins: interactions, organization and information flow. Annu. Rev. Biophys. Biomol. Struct. 31:151–175. [DOI] [PubMed] [Google Scholar]
- 26.Arbuzova, A., A. A. P. Schmitz, and G. Vergeres. 2002. Cross-talk unfolded: MARCKS proteins. Part I. Biochem. J. 362:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Murray, D., and B. Honig. 2005. To B or not to B: PIP2 answers the question. Dev. Cell. 8:138–139. [DOI] [PubMed] [Google Scholar]
- 28.Victor, K., J. Jacob, and D. S. Cafiso. 1999. Interactions controlling the membrane binding of basic protein domains: phenylalanine and the attachment of the myristoylated alanine-rich C-kinase substrate protein to interfaces. Biochemistry. 38:12527–12536. [DOI] [PubMed] [Google Scholar]
- 29.Fleer, G., M. C. Stuart, J. M. H. M. Scheutjens, T. Cosgrove, and B. Vincent. 1998. Polymers at Interfaces. Chapman & Hall, New York.
- 30.Netz, R. R., and D. Andelman. 2003. Neutral and charged polymers at interfaces. Phys. Rep. Rev. Phys. Lett. 380:1–95. [Google Scholar]
- 31.Rosenbluth, M. N., and A. W. Rosenbluth. 1955. Monte Carlo simulations of the average extension of molecular chains. J. Chem. Phys. 23:356–359. [Google Scholar]
- 32.Frenkel, D., and B. Smit. 1996. Understanding Molecular Simulation: From Algorithms to Applications. Academic Press, New York.
- 33.Ben-Shaul, A., and W. M. Gelbart. 1994. Statistical thermodynamics of amphiphile self-assembly: structure and phase transitions in micellar solutions. In Micelles, Membranes, Microemulsions and Monolayers. W. M. Gelbart, A. Ben-Shaul, and D. Roux, editors. Springer, New York. 359–402.
- 34.David, S. 1994. Elementary Probability. Cambridge University Press, Cambridge, UK.
- 35.Cates, M. E., and R. C. Ball. 1998. Statistics of a polymer in a random potential with imperfection for a nonlinear growth model. J. Phys. (Fr.). 49:2009–2018. [Google Scholar]
- 36.Andelman, D., and J. F. Joanny. 1993. Polymer adsorption on surfactant monolayers and heterogeneous solid surfaces. J. Phys. II (Fr.). 3:121–138. [Google Scholar]
- 37.Andelman, D., and J. F. Joanny. 1991. On the adsorption of polymer solutions on random surfaces: the annealed case. Macromolecules. 22:6040–6042. [Google Scholar]
- 38.Gerroff, I., A. Milchev, K. Binder, and W. Paul. 1993. A new off-lattice Monte Carlo model for polymers—a comparison of static and dynamic properties with the bond-fluctuation model and application to random-media. J. Chem. Phys. 98:6526–6539. [Google Scholar]
- 39.Yamakov, V., A. Milchev, O. Borisov, and B. Dunweg. 1999. Adsorption of a polyelectrolyte chain on a charged surface: a Monte Carlo simulation of sealing behaviour. J. Phys. Cond. Mater. 11:9907–9923. [Google Scholar]
- 40.Kong, C. Y., and M. Muthukumar. 1998. Monte Carlo study of adsorption of a polyelectrolyte onto charged surfaces. J. Chem. Phys. 109:1522–1527. [Google Scholar]
- 41.Odijk, T. 1977. Polyelectrolytes near rod limit. J. Pol. Sci. B Pol. Phys. 15:477–483. [Google Scholar]
- 42.Skolnick, J., and M. Fixman. 1977. Electrostatic persistence length of a wormlike polyelectrolyte. Macromolecules. 10:944–948. [Google Scholar]
- 43.Rubinstein, M., and R. Colby. 2003. Polymer Physics. Oxford University Press, Oxford, UK.
- 44.Parsegian, V. A., and D. Gingell. 1972. On the electrostatic interaction across a salt solution between two bodies bearing unequal charges. Biophys. J. 12:1192–1204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nardi, J., R. Bruinsma, and E. Sackmann. 1998. Adhesion-induced reorganization of charged fluid membranes. Phys. Rev. E. 58:6340–6354. [Google Scholar]
- 46.Wagner, K., D. Harries, S. May, V. Kahl, J. O. Rädler, and A. Ben-Shaul. 2000. Counterion release upon cationic lipid-DNA complexation. Langmuir. 16:303–306. [Google Scholar]