Variability in Couplon Size in Rabbit Ventricular Myocytes

Abstract

Variation in couplon size is thought to be essential for graded Ca²⁺ transients in cardiac myocytes. We examined this variation by investigating spark appearance in rabbit ventricular myocytes at various locations and at potentials from −20 to 0 mV. At 0 mV, sparks appeared at the beginning of the voltage step with a probability of unity. On the other hand, at −20 mV, sparks appeared later during the voltage step with a lower probability. The cumulative spark probabilities at various potentials were fitted with exponential functions of both time and voltage. Spark latency became longer as spark probability decreased at more negative potentials. At −20 mV, the cumulative spark probability and the mean spark latency were not only variable among locations but also inversely related. Under the assumption that a single opening of an L-type Ca²⁺ channel triggers a spark, we suggest a simple mathematical explanation for the distribution of spark appearance. The variation in spark probability and latency with location suggests that the couplon size, and hence the number of L-type Ca²⁺ channels in a couplon is variable.

INTRODUCTION

During excitation-contraction coupling, Ca²⁺ release from sarcoplasmic reticulum (SR) is triggered by transmembrane Ca²⁺ influx and produces a Ca²⁺ transient (see, for example, London and Krueger (1)). This transient is believed to consist of many local Ca²⁺ release events (or Ca²⁺ sparks) from SR release channels (or ryanodine receptors; RyRs) (2). In ventricular myocytes, L-type Ca²⁺ channels (LCCs) and RyRs are co-localized at SR junctions, which are mostly associated with T-tubules (3,4). Moreover, both LCCs and RyRs are distributed in clusters at the junctions (5). The term “couplon” has been coined to describe these functional clusters of dihydropyridine receptors and RyRs that produce sparks; this was defined by Stern et al. (6) as the functional grouping of dihydropyridine receptors and RyRs (and other functional proteins), which act in concert during excitation-contraction coupling. Here the term was applied to skeletal myocytes. Franzini-Armstrong et al. (4) pointed out that “Dyads and peripheral couplings are constituted of a single couplon. All junctions, dyads, triads, and peripheral couplings are called Ca²⁺ release units.” The couplon is, therefore, currently considered to be the fundamental structure underlying excitation-contraction coupling in both cardiac and skeletal myocytes.

A Ca²⁺ spark is thought to consist of Ca²⁺ release from 10 to 40 ryanodine receptors (7–11), although Franzini-Armstrong et al. (4) have suggested that a couplon may consist of as many as 200 RyRs. To account for the high probability of spark appearance, we recently concluded that a couplon contains three or more LCCs (12).

The size of a couplon is determined by the number of both LCCs and RyRs and there is no a priori reason to think that its size is fixed. Moreover, it is not entirely clear whether the stoichiometric relationship between LCCs and RyRs within a couplon is fixed. However, at least two groups have produced evidence suggesting this is the case (13,14). If this ratio is fixed, larger couplons contain both greater numbers of LCCs and RyRs. Regardless of whether the stoichiometry of LCCs and RyRs is fixed, two important consequences follow if couplon size is increased by increasing the number of LCCs. First, the chance that a couplon will produce a spark is increased simply because, with more LCCs, the chance that RyRs are triggered increases. Secondly, because the chance of a short first latency associated with an LCC responsible for triggering an RyR must increase if the number of LCCs increases, the variance of first spark latency will decline if more LCCs are available to trigger sparks.

So far it has only been possible to demonstrate variation in couplon size from direct measurement of foot processes using electron microscopy (4). In fact, Franzini-Armstrong et al. (4) have suggested that in mouse skeletal myocytes the variation in couplon size might produce a 10-fold variation in spark size. Mathematical modeling (15) has been used to infer variation in couplon size. Bondarenko et al. (15) have shown that homogeneous Ca²⁺ release subsystems (or couplons with fixed size) produce no gradation of Ca²⁺ release as a function of voltage, but that heterogeneous subsystems produce graded Ca²⁺ release as observed experimentally (see, for example, Cannell et al. (16)). It appears then that variation in couplon size is a structural necessity, which, besides other factors, ensures graded Ca²⁺release from the SR.

In this study we have taken advantage of the expected variation in spark probability and latency that should occur if the couplon size displays variation with location. We examined variability of spark probability and latency with voltage-clamp at 0 to −20 mV. The amplitude of unitary Ca²⁺ current is relatively large at these potentials so that the chance that a single LCC opening will trigger an RyR is greater. The way that spark probability varies with latency suggests the couplon size does indeed vary with location.

METHODS

Animals and cell isolation

We used adult New Zealand White rabbits housed according to the National Institutes of Health guidelines (NIH, Guide for the Care and Use of Laboratory Animals). Cell isolation was based on that previously described by Cordeiro et al. (17). Rabbits (2.0–3.0 kg) were completely anesthetized with intravenous administration of sodium pentobarbital (50 mg/ml). The hearts were excised quickly and perfused by Langendorff's method at 37°C with a Ca²⁺-free solution for 5 min. This solution contained 126 mM NaCl, 22 mM dextrose, 5 mM MgCl₂, 4.4 mM KCl, 20 mM taurine, 5 mM creatine, 5 mM Na-pyruvate, 1 mM NaH₂PO₄, and 24 mM HEPES (pH 7.4 with NaOH). They were then digested for 10–15 min by perfusion with an enzyme solution containing 1.0 mg/ml collagenase type 2 (Worthington Biochemical, Lakewood, NJ) and 0.1 mg/ml protease (Sigma-Aldrich, St. Louis, MO) with 0.1 mM CaCl₂ added to the Ca²⁺-free solution. Finally, the enzyme was washed out by perfusion with a solution containing 0.1 mM CaCl₂ added to the Ca²⁺-free solution. Ventricles were then cut out, minced, and shaken gently at 37°C for 10 min. The dissociated myocytes were filtered and kept at room temperature (22–24°C) in a solution containing 0.5 mM CaCl₂ added to the Ca²⁺-free solution.

Voltage-clamp and confocal imaging

Myocytes were placed in a laminin-coated chamber perfused with the bath solution containing 138 mM NaCl, 8 or 10 mM CaCl₂ (dependent on Ca²⁺ tolerance of the myocytes), 1 mM MgCl₂, 4.4 mM KCl, 11 mM Dextrose, and 24 mM HEPES (pH 7.4 with NaOH). We used pipettes with resistance of 2.0–3.0 MΩ filled with a solution containing 110 mM KCl, 5 mM K₂ATP, 5 mM MgCl₂, 2 mM EGTA, 0.54 mM CaCl₂, 10 mM NaCl, 20 mM HEPES, and 0.1 mM fluo-3 (Molecular Probes, Eugene, OR) (pH 7.1 with KOH). We added EGTA to the pipette for the purpose of buffering [Ca²⁺]_i weakly (∼0.1 μM) to improve spark resolution (12,18). Voltage-step commands (0, −5, −10, −15, −20 mV) were applied for 200 ms from holding potential at −40 mV at 0.2 Hz. Series resistance (<10 MΩ) was compensated by >75%. Data were filtered at 10 kHz and acquired with a Digidata 1320 acquisition system and pClamp8 software (Axon Instruments, Foster City, CA). All experiments were performed at room temperature.

Fluorescent images were observed with a BioRad MRC-1024 laser-scanning confocal-microscope system simultaneously with voltage-clamp (BioRad, Hercules, CA). Myocytes were viewed with a Nikon DIAPHOT 200DV inverted microscope and a 40× oil immersion objective lens (Nikon, Tokyo, Japan). Intracellular fluo-3 was excited at 488 nm with a krypton/argon laser and the emission passed through an OG515 longpass filter into a photomultiplier tube. Myocytes were placed with their long axis within ±10° along the longitudinal axis of the imaging window. All images were acquired digitally in line-scan mode with 0.15 μm and 2 ms per pixel resolution. As the confocal system could not perfectly synchronize images with the external trigger, we also recorded signals of myocyte stimuli simultaneously with line-scan fluorescence images. This allowed us to align the line-scan images with the stimuli after they were acquired.

Data analysis

We analyzed fluorescence images with the public domain NIH Image program (developed at NIH and available on the internet at http://rsb.info.nih.gov/nih-image/) and its custom-made macros (12). We constructed self-ratioed (F/F₀) images by dividing every pixel value (F) by the average (F₀) of > 20 pixels at the corresponding location before every stimulation. To measure Ca²⁺ sparks, we processed self-ratioed (F/F₀) images with a 5 × 5 average filter. We accepted fluorescence measurements as sparks if their peak F/F₀ values were >1.3. By setting the threshold to F/F₀ = 1.3 we could distinguish sparks from the noise (baseline F/F₀ = 1.00 ± 0.05, mean ± SD). This was small enough to minimize the possibility of missing sparks (peak F/F₀ = 1.60 ± 0.14, mean ± SD, at all locations at −20 mV). We then measured spark appearance at the half-rise point of the F/F₀ values because this point seems least affected by filtering. However, apparently a spark is activated before it reaches its half-rise point. Because we did not observe any spark reaching its half-rise point within 5 ms of the onset of the voltage step, we measured spark latencies from 5 ms after the onset of the voltage step. This 5-ms period is consistent with our detailed spark analysis in rabbit ventricular myocytes that indicated an averaged spark reaches its half-rise point in 5 ms (Inoue and Bridge (12), their Fig. 3)). Data were processed with Microsoft Excel (Microsoft, Redmond, WA) and statistically analyzed with SPSS software (SPSS, Chicago, IL).

FIGURE 3.

Sparks evoked at −20 mV among various locations. (A) Sparks evoked with repeated 50 voltage steps to −20 mV. Spark appearances were measured at various locations in the myocyte. (B) Spark appearances at locations a and b of A displayed in tiled images. The numbers to the left of the images were sequential numbers of the 50 voltage steps. (C) (Dotted lines) Cumulative spark probabilities (P_spark) at eight locations plotted versus time (t). (Solid lines) Curves of P_spark versus time fitted with the exponential equation P_spark = 1 − exp(−m × t). (D) P_spark at 50 ms versus mean spark latencies of measured sparks at eight locations. Error bars represent SE. Dotted ellipses indicate two groups (see Results). The grouping of the point indicated by the arrow is explained in the text (see Results).

RESULTS

We investigated the hypothesis that the number of the LCCs in a couplon varies with location. If a couplon contains a single LCC and every LCC opening triggers a spark, we expect that spark probability will be identical to the probability with which the first LCC opens and the latency of sparks will reflect the first latency of LCCs. If, on the other hand, a single LCC triggers a spark but a couplon contains several or many LCCs, the probability of spark activation must increase. This is because the chance of a single LCC opening will increase. Moreover, since the chance of an LCC opening with a short latency must also increase, we expect larger couplons to exhibit not only an increase in their probability of activation but also a decline in their first latency of activation. We therefore first investigated the conditions most suited to measure spark latencies. (For a clear idea of our notion of the nature of a couplon, see Fig. 1.)

FIGURE 1.

An illustration of a couplon. An LCC cluster faces an RyR cluster on the surface of the SR. Our assumption that openings of LCCs will produce sparks does not involve geometric relationships between individual LCCs and individual RyRs. Thus our definition of couplon size only reflects the number of RyRs and LCCs. In this study we mainly consider variation of the number (n) of LCCs as a determinant of couplon size. We will explain why n is variable in the Discussion. P_channel(t) is the cumulative probability of the first opening of a single LCC and P_spark(t) is the cumulative probability of spark appearance.

Spark probability and latency versus voltage

Spark probability and latency is affected by LCC openings, which are voltage-dependent (19). We examined how the voltage affects the probability and latency of spark appearance within the range of 0 to −20 mV. Fig. 2 displays spark appearance at a fixed location with voltage steps to various potentials. At 0 mV, sparks appeared at the beginning of the voltage step with a probability of unity (Fig. 2 B, left panel). On the other hand, at −20 mV, sparks appeared later during the voltage step with a lower probability (Fig. 2 B, right panel). Spark amplitudes were larger at 0 mV (peak F/F₀ = 1.82 ± 0.03, mean ± SE at the location of Fig. 2 A) than those at −20 mV (peak F/F₀ = 1.36 ± 0.01, mean ± SE at the same location), consistent with larger transmembrane current amplitude at 0 mV (−4.4 pA/pF at negative peak) than that at −20 mV (−0.4 pA/pF) (Fig. 2 B, bottom). Sparks often appeared more than once with each step command at the same location presumably because a repetitive spark was evoked after a refractory period (20). To avoid measuring second sparks, we limit measurements to the first 50 ms of a voltage step (Fig. 2, C and D). Thus we observed at most one spark during this interval at every voltage step. Fig. 2 C shows the different time-dependences of spark appearance as a function of the voltage. These curves could be fit with an empirical equation P_spark = 1 − exp(−m × t). As the voltage becomes negative, the fit parameter m becomes smaller. This exponential voltage dependence was also observed at four other cell locations. Plots of P_spark and mean spark latency (Fig. 2 D) indicate that, as the membrane potential becomes more negative, spark latency becomes longer, and spark probability decreases. This is consistent with the idea that spark appearance shows exponential properties with different voltage fit parameters. We concluded that −20 mV provides a suitable voltage to measure latencies as they can be easily resolved.

FIGURE 2.

Sparks evoked at various potentials. (A) Sparks evoked with five voltage steps (0 to −20 mV). The myocyte was clamped with a set of five voltage steps, repeated 20 times (100 steps in total). Spark appearance was measured at a fixed location (right arrow). (B) Spark appearance at 0 and −20 mV displayed in tiled images. The numbers to the left of the images were sequential numbers of the 100 voltage steps. Averaged transmembrane currents at respective potentials were shown below the tiled images. The cell capacitance was 160 pF. (C) (Dotted lines) Cumulative spark probabilities (P_spark) at various potentials plotted versus time (t). (Solid lines) Curves of P_spark versus time fitted with the exponential equation P_spark = 1 − exp(−m × t); m = 0.409 ± 0.036 (0 mV), 0.320 ± 0.018 (−5 mV), 0.177 ± 0.013 (−10 mV), 0.096 ± 0.004 (−15 mV), 0.024 ± 0.002 (−20 mV), mean ± SE. (D) P_spark at 50 ms versus mean spark latencies of measured sparks at five potentials of the voltage steps. Error bars represent SE.

Spark probability and latency among locations

It is clear that, at −20 mV, both spark probability is lower and spark latency is longer than at more positive potentials. Interestingly, the empirically derived fit parameter m used to describe the exponential relationship between spark probability and latency varies with location. We therefore hypothesized that it would be possible to demonstrate variations in spark probability and latency at different locations. This is facilitated at −20 mV because spark latency becomes sufficiently long to resolve easily. We expected to observe an inverse relationship between spark probability and latency at different locations if couplon size and hence the number of LCCs in a couplon varies with location. Therefore, we examined the variation in spark probability and latency among locations evoked with repeated −20 mV voltage steps (Fig. 3). Sparks appearance was different at different locations (Fig. 3 B). Specifically, m in the equation P_spark = 1 − exp(−m × t) varies among locations (Fig. 3 C). Plots of P_spark(50 ms) and mean spark latency (Fig. 3 D) indicates that spark latency becomes longer as spark probability decreases. This suggests that the number of LCCs in a couplon varies with location.

The relationship between P_spark(50 ms) and mean spark latency appears to fall into two distinct groups (Fig. 3 D; dotted ellipses). (In Fig. 3 D we included the point indicated by the arrow in the lower group for convenience, although it could be included in the upper group. In the discussion, we will explain why this point could possibly be included in both groups. This will not alter our conclusions.) Although spark probability and latency differs between both groups, spark amplitude was similar; i.e., there was no statistically significant difference with an unpaired t-test (Fig. 3 D, upper group, peak F/F₀ = 1.61 ± 0.02, mean ± SE, n = 60; and Fig. 3 D, lower group, 1.58 ± 0.03, mean ± SE, n = 16). Members of each group have a strong negative correlation between P_spark(50 ms) and mean spark latency (Fig. 3 D, upper group, −0.961, n = 5; and Fig. 3 D, lower group, −0.995, n = 3). Although both groups appear to display an inverse relationship between P_spark(50 ms) and mean spark latency, this finding requires explanation. If two spark generators coincide in location, we expect that P_spark(50 ms) roughly doubles, but that the mean spark latency would not change significantly. This is because the spark probability from two spark generators is the sum of the spark probabilities from each spark generator and the mean spark latency from two spark generators is the weighted average of the mean spark latencies from each spark generator. Here we explain this point more fully.

During n voltage steps, the first spark generator produces sparks x times and the second spark generator produces sparks y times. The spark probability from the first spark generator is P_a = x/n and that from the second spark generator is P_b = y/n. We observe (x + y) sparks from these two spark generators during n voltage steps. On the other hand, we limit measurements to the first 50 ms of a voltage step to avoid measuring second sparks from a single spark generator (see Methods). As a result, we observed, at most, one spark during this interval at every voltage step. Thus, we observe sparks in (x + y) voltage steps out of n voltage steps, so that the spark probability is P = (x + y)/n. Therefore, P ≈ P_a + P_b.

The latencies of sparks from the first spark generator are a₁, a₂,…, a_x and those from the second spark generators are b₁, b₂,…, b_y; the mean spark latency from the first spark generator is a = (a₁ + a₂ +…+ a_x)/x and that from the second spark generator is b = (b₁ + b₂ +…+ b_y)/y. We will measure latencies from (x + y) sparks and these are a₁, a₂,…, a_x, b₁, b₂,…, b_y so that the overall mean spark latency is m = (a₁ + a₂ +…+ a_x + b₁ + b₂ +…+ b_y)/(x + y). Because a₁ + a₂ +…+ a_x = a × x and b₁ + b₂ +…+ b_y = b × y, therefore m ≈ (a × x + b × y)/(x + y).

It is possible that each of two generators produces a spark at the same time during a voltage step. In this case we can only observe a single spark because two sparks are fused. Thus we will miss one spark measurement so that P is decreased by 1/n. This will not affect m significantly, because this decreases both the sum of the latencies measured (the numerator of m) and the number of sparks observed (the denominator of m). At −20 mV, however, because each spark appears with relatively low probability and sparsely throughout the voltage steps, the chance of simultaneous sparks from two spark generators will be rare, so that this will not affect our discussion significantly. Moreover, we did not observe any sparks with double amplitudes, which consist of fused sparks from two spark generators.

Thus, the upper group in Fig. 3 D can be explained if each of these locations had two spark generators, whereas the lower group in Fig. 3 D were measured from single spark generators. However, these spark measurements from single or double spark generators still display variability in size with location. There is no a priori reason to assume that two spark generators exist in some locations. However, our ad hoc assumption of two generators provide a reasonable explanation of our results (see Discussion). In addition, the properties of spark generators in both groups seems similar because there were no significant differences in spark amplitude between the groups. We will discuss our ideas without assuming any difference in the properties of spark generators between groups.

We conclude from the results that there is an inverse relationship between spark probability and latency and that this varies with location. From this we infer that the couplon size can vary with location.

DISCUSSION

Our main conclusion is that the number of LCCs in a couplon varies with location. Since it is likely that the stoichiometric relation between LCCs and RyRs is fixed (13,14), we think that the couplon size varies with location. This conclusion hinges on our hypothesis that, under the simplest circumstances, we expect larger couplons to produce sparks with a higher probability than smaller couplons. Moreover, the higher the probability, the shorter the first latency. This conclusion is complicated by numerous factors—most notably, that more than one spark generator could exist at a location. The idea that an inverse relation exists between spark probability and latency requires additional justification.

Our interpretation of the results is based on the idea that openings of LCCs are required to trigger RyRs, and hence, evoke sparks under normal circumstances (21). This is true regardless of the presence or absence of Na⁺-Ca²⁺ exchange (22). It may be a simplification for spontaneous sparks or Ca²⁺ waves. Moreover, the exchange is also likely to be involved in triggering (23). We will first calculate spark probability from LCC activity and demonstrate time- and voltage-dependence of spark appearance. Then we will explain the relationship between spark probability and spark latency. From these, we conclude that the variation of spark probability and latency among locations results from variation of the number of LCCs in a couplon.

Time- and voltage-dependence of spark appearance

Under the assumption that openings of LCCs trigger RyRs and hence evoke sparks (Fig. 1), spark appearance is dependent on time and voltage because openings of LCCs are time- and voltage-dependent. Our results are consistent with this idea. Moreover, the number of LCCs in a couplon should affect spark appearance as a couplon, because more LCCs will produce sparks with higher probability. Can we propose a quantitative basis for the dependence of spark probability on time, voltage, and the number of LCCs is a couplon?

For simplicity, we first assume that any short opening of LCCs can evoke sparks. This is because Ca²⁺ influx through an LCC is large at 0 mV or negative potentials and high external calcium concentration. Moreover, the SR is probably highly loaded. Under a simple two-state transition (close → open), the cumulative probability of the first LCC opening (P_channel(t)) is a single exponential function of time (t) (24),

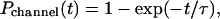(1)

where τ is the time constant for the transition. This transition is voltage-dependent (19). If this is the case and there are n LCCs in a couplon, cumulative spark probability (P_spark(t)) can be calculated as follows. Because the chance of obtaining no openings from an LCC (null events) is 1 − P_channel(t), the chance of obtaining no open events from n LCCs is {1 − P_channel(t)}ⁿ. P_spark(t) is the probability of obtaining at least one open event from n LCCs: P_spark(t) = 1 − {1 − P_channel(t)}ⁿ. Because 1 − P_channel(t) = exp(−t/τ) (Eq. 1), it follows that

(2)

Equation 2 is a function of t, n, and τ. The empiric fit function P_spark = 1 − exp(−m × t) we used in our results is analogous to Eq. 2, and our results showed time-dependent exponential properties of spark appearance. Since LCC activity for this transition is voltage-dependent (19), the time constant τ for LCC availability (Eq. 1) varies at different potentials. In this case, cumulative spark probably (Eq. 2) varies for different τ values, i.e., at different potentials. Our results showed that spark appearance is voltage-dependent and consistent with Eq. 2. Eq. 2. also suggests that spark appearance is dependent on n, the number of LCCs in a couplon. If n is variable among couplons, spark appearance should be variable among locations. We will deal with this issue later.

We assumed a two-state LCC transition for simplicity, although several multiple-state LCC models have been proposed (15,25). They include multiple close states so that P_channel(t) will be a sum of exponential functions. In that case, P_spark(t) will be a more complicated expression composed of multiple exponential functions. However, this will not significantly alter our discussion.

The exponential property of spark appearance was also previously demonstrated by Collier et al. (26). They, however, offered a different explanation for this exponential property. They concluded that this resulted from the exponential decay of I_ca, which is dependent on L-type Ca²⁺ channel inactivation. They assumed that P_spark was dependent on P_o, the LCC open probability. Their assumption is different from ours, because it seems to imply that each opening will have an equal chance of evoking a spark, whereas we assume the first LCC opening is more likely to evoke a spark (27). However, their explanations seem reasonable, considering their experimental conditions, which were different from ours. They evoked sparks at −30, +20, and +30 mV with Nifedipine and +50 mV with and without Nifedipine. At very positive potentials, e.g., +50 mV, the unitary L-type Ca²⁺ current is so small that the chance that a single LCC opening will evoke a spark may be low. In that case, the first LCC opening will not be “privileged” (28) to evoke a spark, but any opening is equally likely to evoke sparks. At potentials more negative than +50 mV, e.g., +20 and +30 mV, they evoked sparks with Nifedipine present. Under the condition that Nifedipine lowers the chance of LCC opening, LCC activity observed during a short interval will reveal that most LCC openings are likely to be first openings because of the low chance of any LCC opening. Therefore, their implication that each opening is equally likely to evoke a spark is equivalent with our assumption that the first LCC opening evokes a spark. At negative potentials like −30 mV they also argued that spark appearance was constant with time. They explained this result by proposing that I_Ca is constant with time. Our assumption can also explain this because our exponential curve P_spark = 1 − exp(−m × t) resembles a straight line when m is small. On the other hand, we evoked sparks at 0 to −20 mV without Nifedipine. Under our experimental conditions where the chance that a single LCC opening is relatively large, it seems reasonable that the first LCCs openings are likely to evoke sparks and, consequently, later LCC openings cannot evoke sparks due to their refractory period (20).

Relation between spark probability and latency

Data from various locations show that spark appearance differs among these locations. At a specific potential, the time constant τ for the Eq. 1 is constant among locations. If n varies among locations, P_spark(t) (Eq. 2) also varies among locations. This can explain the difference in spark probability and latency among locations at −20 mV. However, the difference in spark probability can also be explained if there is more than one spark generator in a location and the number of spark generators differs among locations. In that case, apparent spark probability will be a multiple of single spark probabilities, although apparent spark latency will be within the range of single spark latency (see Results). Therefore, we plotted spark probability versus mean spark latency (Fig. 3 E) among various locations. We explain these plots as follows:

We define p_spark(t) as the probability density of spark appearance. Thus p_spark(t) is the derivative of P_spark(t), 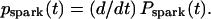Because P_spark(t) = 1 − exp(−t × n/τ) (Eq. 2),

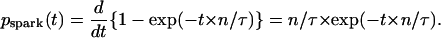(3)

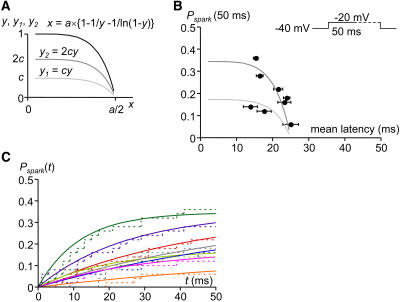
When we plot mean spark latency (x) versus cumulative probability (y) of spark appearance within 0 < t ≤ a, 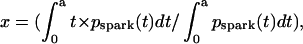and because p_spark(t) = n/τ × exp(−t × n/τ) (Eq. 3) and

(4)

and

(5)

Solving Eq. 5 for τ and n yields

(6)

Inserting Eq. 5 into Eq. 4 followed by elimination of τ and n with Eq. 6 yields

(7)

Here x is expressed as a function of y (this cannot be explicitly solved for y). This equation is independent of τ and n. Therefore, although both spark latency (x) and cumulative probability (y) is variable and dependent on LCC activity (τ) and the number (n) of LCCs in a couplon, x,y plots of spark measurements should follow Eq. 7, which is independent of different LCC activity (τ) or the number (n) of LCCs in a couplon. The curve corresponding to the relationship between spark probability and mean spark latency as a function of voltage (Fig. 2 D) should be consistent with Eq. 6, which is independent of τ (Fig. 4 A). Experimental plots of P_spark(50 ms) and mean spark latency at the same location and various voltages seem to fit this curve with the exception of the single point at −20 mV (Fig. 4 B). Thus, experimental plots at various locations at −20 mV do not fit Eq. 6, which is drawn under the assumption that any short opening of an LCC can trigger an RyR. If this assumption is not true, however, we can apply a coefficient (c; 0 < c ≤ 1) to y. This coefficient is introduced to account for the possibility that some short openings of LCCs fail to trigger RyRs. At negative potentials (−20 mV), although the amplitude of a single LCC is larger, open time is shorter due to voltage-dependent inactivation (19). Thus spark probability could be reduced by c because of trigger failure. When LCC activity is low at −20 mV, c can be considered to be a coupling fidelity between an LCC and RyRs (21). In that case, spark probability y₁ is reduced by c. If there are two spark generators at the same location and they act independently, as described before (see Results), spark probability from two spark generators will be the sum of those from each generator but mean spark latency from two spark generators will not be significantly changed. Supposing that spark probability y₂ is twice that of y₁,

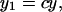(8)

(9)

when the relationship between x and y is x = a × {1−1/y − 1/ln(1−y)} (Eq. 7). With this coefficient c, cumulative spark probability P_spark(t) at −20 mV is reduced by c or 2c compared with Eq. 2 (when a single spark or double spark generators exist at a location, respectively),

(10)

or

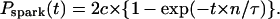(11)

The experimental plots of P_spark(50 ms) and the mean spark latency at various locations and −20 mV appears to fit the curves for Eq. 7 (Fig. 5 B). Exponential curves versus time, which include c or 2c for Eqs. 10 and 11 give better fits among various locations (Fig. 5 C) than those not including these coefficients (Fig. 3 D). At more positive potentials, as shown in Eq. 2, c is not required for P_spark(t). The open time of an LCC is longer and bursting LCC activity is likely at more positive potentials (19). If clustered LCCs in a couplon are located together, opening of adjacent LCCs may also contribute to triggering an RyR when LCCs are more active at more positive potentials.

FIGURE 4.

(A) Curve representing Eq. 7. (B) A curve of Eq. 7 (gray line; x = mean spark latency, y = P_spark, a = 50 ms) drawn over plots of P_spark(50 ms) versus mean-spark latencies at various potentials shown in Fig. 2 D. The arrow indicates the point at −20 mV (see Discussion).

FIGURE 5.

(A) Curves representing Eq. 7 (solid line), Eqs. 8 and 9 (light gray line (y₁) and dark gray line (y₂)). (B) Curves of Eqs. 8 and 9 (light gray line (y₁) and dark gray line (y₂); x = mean spark latency, y₁ and y₂ = P_spark, a = 50 ms) fitted with plots of P_spark(50 ms) versus mean spark latencies at eight locations shown in Fig. 3 D. Estimated c = 0.172 ± 0.007. (C) (Dotted lines; the same as Fig. 2 C) Cumulative spark probabilities (P_spark) at eight locations plotted versus time (t). (Solid lines) Curves of P_spark versus time fitted with exponential curves including c or 2c (P_spark = c × {1 − exp(−m × t)} and P_spark = 2c × {1 − exp(−m × t)}). See Discussion.

Our estimation of c will be variable in differently loaded myocytes (29). Moreover, an increase or decrease in SR load during a protocol may result in an increase or decrease in c. However, the relationship between spark probability and spark latency described above is maintained as long as we compare measurements in the same myocyte.

Variable number of L-type channels in a couplon

Our results at −20 mV revealed that some locations may have double spark generators. Clearly sparks can appear from two spark generators with one above and one below the confocal plane. It seems possible that large numbers of spark generators with relatively low probability at the same location produce a very high probability of spark appearance at 0 mV. However, this cannot explain the variability in spark latency and the negative correlation between P_spark(50 ms) and mean spark latency among locations. We observed sparks of larger amplitude at 0 mV than at −20 mV. Several factors affect measurements of spark amplitude. Larger transmembrane Ca²⁺ influx at 0 mV will affect larger background fluorescence of sparks than at −20 mV. At 0 mV, sparks appear with a probability of unity simultaneously at the beginning of the voltage step. In that case, summation of Ca²⁺ diffusion from spark generators at adjacent locations may also increase apparent spark amplitude. Moreover, as discussed before, there can be double spark generators at one location. Two sparks cannot be dissociated when they appear at the same time. However, spark probability for each spark generator must still be approximately unity because we did not observe late sparks, which will appear when P_spark(t) is, much less than unity. Apparent spark latency for double spark generators will reside between two individual spark latencies. These factors does not alter our conclusions. Even though double spark generators make P_spark(50 ms) double at −20 mV, there still is a variation in spark latency. This variation should be explained by variation of n, the number of LCCs in a couplon.

Physiological significance of the variability in couplon size

The variation of couplon size, which is, at least in part, due to the variation of the number of LCCs in a couplon, seems to be involved in the regulation of Ca²⁺ release. Smaller couplons with fewer LCCs will provide sparks with lower probabilities and longer latencies (see Eq. 2). Thus, such couplons are less likely to contribute to the Ca²⁺ transient. This effect will be more apparent when the probability of sparks is low and therefore their latency is long, i.e., at the negative portion of the relationship between voltage and the Ca²⁺ release.

Bondarenko et al. (15) modeled the idea that the couplon size varies among locations. They assumed that couplon sizes vary with 1–8 LCCs and 10–80 RyRs, which gives a 1:10 ratio of the number of LCCs to that of RyRs. With their calculations, they demonstrated that variation in couplon size is necessary for smoothly graded Ca²⁺ release as a function of voltage.

We recently concluded that multiple (three or more) LCCs are involved in evoking a spark (12). The variability of couplon size supports the idea that more than one LCC can exist in a couplon. On the other hand, the variability in couplon size does not seem to affect spark probability under normal conditions because our recent data suggests that all couplons are activated at the beginning of an action potential (12). However, under conditions where the function of LCCs is modulated, the variability in couplon size can be revealed. For example, ventricular myocytes of the failing heart shows spatial heterogeneity in Ca²⁺ release (30). This can be explained if the number of functional LCCs are reduced (31). In this case, smaller couplons with fewer LCCs are more likely to produce sparks with longer latencies and a probability <100%. Thus spark latency increases and spark probability decreases at locations where smaller couplons are found and this could explain the heterogeneous pattern of Ca²⁺ release.

In conclusion, the number of LCCs in a couplon is variable. Because the size of a couplon is determined by the number of both LCCs and RyRs, this indicates the couplon size is variable. This variability is not only necessary for explanations of experimental results for smoothly graded Ca²⁺ transients versus voltage but may be involved in altered mechanisms of excitation-contraction coupling in diseased myocytes. An explanation of this variability gives us insight into couplon structure.