Elementary Steps of the Cross-Bridge Cycle in Fast-Twitch Fiber Types from Rabbit Skeletal Muscles

Abstract

To understand the molecular mechanism underlying the diversity of mammalian skeletal muscle fibers, the elementary steps of the cross-bridge cycle were investigated in three fast-twitch fiber types from rabbit limb muscles. Skinned fibers were maximally Ca²⁺-activated at 20°C and the effects of MgATP, phosphate (P, P_i), and MgADP were studied on three exponential processes by sinusoidal analysis. The fiber types (IIA, IID, and IIB) were determined by analyzing the myosin heavy-chain isoforms after mechanical experiments using high-resolution SDS-PAGE. The results were consistent with the following cross-bridge scheme:

where A is actin, M is myosin, D is MgADP, and S is MgATP. All states except for those in brackets are strongly bound states. All rate constants of elementary steps (k₂, 198–526 s⁻¹; k₋₂, 51–328 s⁻¹; k₄, 13.6–143 s⁻¹; k₋₄, 13.6–81 s⁻¹) were progressively larger in the order of type IIA, type IID, and type IIB fibers. The rate constants of a transition from a weakly bound state to a strongly bound state (k₋₂, k₄) varied more among fiber types than their reversals (k₂, k₋₄). The equilibrium constants K₁ (MgATP affinity) and K₂ (=k₂/k₋₂, ATP isomerization) were progressively less in the order IIA, IID, and IIB. K₄ (=k₄/k₋₄, force generation) and K₅ (P_i affinity) were larger in IIB than IIA and IID fibers. K₁ showed the largest variation indicating that the myosin head binds MgATP more tightly in the order IIA (8.7 mM⁻¹), IID (4.9 mM⁻¹), and IIB (0.84 mM⁻¹). Similarly, the MgADP affinity (K₀) was larger in type IID fibers than in type IIB fibers.

INTRODUCTION

Skeletal muscles are composed of various fibers to fulfill functional needs. This diversity is caused by specific myofibrillar protein isoforms that result in different fiber types (for review, see Pette and Staron (1) and Schiaffino and Reggiani (2)). Fiber types are generally categorized according to their myosin heavy chain (MHC) isoforms. Three fast-twitch fiber types have been identified in limb muscles of adult rodents: types IIB, type IID (or IIX), and type IIA; they, respectively, contain MHC-IIb, MHC-IId(x), and MHC-IIa. In contrast, only one slow-twitch fiber type (type I) to date has been identified, and it contains MHC-I. However, there are increasing lines of evidence that type I fibers may not represent a homogeneous population, but they contain multiple fiber types (3–5).

During last decades a variety of mechanical and energetic parameters were measured on different fiber types of mammalian skeletal muscles. Investigations on neuronally stimulated leg muscles of rat at 35°C revealed ∼1.4-fold difference in the curvature of the force-velocity relationship, and two- to threefold difference in the rates of activation and relaxation and in maximal shortening velocity depending on fiber type composition (6). In these studies, it was suggested that type IIB fibers were fastest, type IID and IIA fibers were in between, and type I fibers were slowest. Many more experiments were carried out in single skinned fiber preparations. These are muscle fibers in which the sarcolemmal and intracellular membranes are functionally destroyed while keeping the contractile apparatus intact. In these preparations the intracellular milieu bathing the contractile apparatus can be controlled. After the mechanical experiments, skinned fibers can be analyzed by biochemical techniques to relate the mechanical parameters to protein isoforms (7).

The frequently measured mechanical parameter is the unloaded shortening velocity (V_u). As reviewed by Schiaffino and Reggiani (2), the unloaded shortening velocity (V_u) is less in slow-twitch fibers than in fast-twitch fibers (8). Among fast-twitch fibers, average V_u is largest in type IIB, intermediate in type IID, and smallest in type IIA fibers (9–12). However, a large overlap of V_u values of different fiber types existed in these reports. Another important functional parameter determined is the ATP hydrolysis rate of fibers during isometric contraction. It was found that a correlation between the ATP hydrolysis rate and the fiber types exists in rat skeletal muscle (13). Maximal Ca²⁺-activated tension was found to be lower in slow-twitch fibers than in fast-twitch fibers (10,14,15), however, within fast-twitch fiber types no consistent difference was found.

Among all mechanical parameters investigated, the kinetics of force response after a rapid change of the fiber length show the best separation between different fiber types. It was reported that a 10- to 20-fold difference exists in skinned fiber preparations of fast frog muscles and slow tortoise muscles (16). For rabbit skeletal muscles, a 30-fold difference was found between slow-twitch and fast-twitch fibers (17). In studies of skeletal muscle fibers from the mouse, the rat, the rabbit, and the human, a strong correlation between the kinetics of stretch-induced delayed force increase (stretch activation) and the myosin heavy-chain isoforms has been reported (12,14,15). Furthermore, a variation in the stretch activation kinetics was found in flight muscles of Drosophila where the myosin head was genetically modified (18,19).

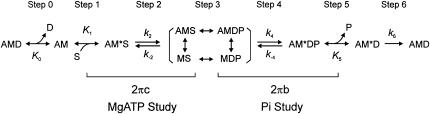
Although the measurement of V_u, the ATP hydrolysis rate, and the force response after a rapid length change may reveal important information about mechanical and energetic properties of different fiber types, these parameters give only a partial insight in the elementary processes of the cross-bridge cycle. One method to determine a detailed difference in the cross-bridge cycle of different fiber types is the application of sinusoidal analysis under varying concentrations of MgATP, phosphate (P_i), and MgADP. Using this approach, the affinities of MgATP, MgADP, and P_i to the cross-bridges of fast-twitch fibers of rabbit psoas (20) and slow-twitch fibers of rabbit soleus were determined (21). Furthermore, the rate constants of the forward and backward reactions of the force-generation step, and of the transition of cross-bridges from strong-binding to weak-binding states (ATP isomerization step) were deduced in the same studies. This approach was not carried out to identify fast-twitch fiber types IIA, IID, and IIB, except for rabbit psoas, which consists of type IID fibers. Therefore, we carried out sinusoidal analysis on rabbit fast-twitch muscle fibers of known MHC isoforms to deduce the kinetic constant of elementary steps in the cross-bridge cycle, which is shown as follows. where A is actin, M is myosin, D is MgADP, S is MgATP, and P is P_i; k₂, k₄, and k₆ represent the rate constants of individual elementary steps in the forward direction; k₋₂ and k₋₄ represent the rate constants in the backward direction; K₀ is the association constant of MgADP to AM, K₁ is the association constant of MgATP to AM, and K₅ is the association constant of phosphate to AM*D. These as a whole are called kinetic constants of elementary steps. This scheme was initially derived to account for the data of rabbit psoas fibers (20). Our analysis indicates that the rate constants of elementary steps are progressively faster in the order of type IIA, type IID, and type IIB fibers. The difference among fiber types is found to be much larger in skinned fibers than in the extracted and reconstituted protein system in solution (22).

MATERIALS AND METHODS

Muscle fiber preparations

New Zealand white rabbits of 3.5–5 kg were killed by injecting 150 mg/kg sodium pentobarbital into an ear vein. Strips of the extensor digitorum longus (EDL), adductor magnus, and soleus muscles were excised and placed in ice-cooled skinning solution (Table 1). Fiber bundles of ∼15 mm in length and 2 mm in diameter were tied to bamboo sticks at in situ length using silk thread. The bundles were kept in ice-cooled skinning solution (Table 1) for 24 h and then transferred to a storage solution (in millimolar) 5 EGTA, 2 MgATP, 5 free ATP, 132 potassium propionate, 6000 glycerol, 10 MOPS (3-(N-morpholino)propanesulfonic acid), pH 7.0. The bundles were stored at −20°C without freezing.

TABLE 1.

Solutions used for this report

	K2EGTA	K2CaEGTA	CaPr2	Na2MgATP	Na2K2ATP	MgPr2	Na2CP	NaADP	K1.5Pi	KPr	NaPr	NaN3	A2P5	CK
Solutions	mM	mM	mM	mM	mM	mM	mM	mM	mM	mM	mM	mM	mM	unit/ml
Skinning	5	–	–	2	5	–	–	–	–	–	132	–	–	–
Relax	5.03	0.97	–	2	5	–	–	–	8	55	51	10	–	–
Rigor	–	–	–	–	–	–	–	–	8	102	75	–	–	–
WP	–	–	–	5.83	1.45	–	15	–	0	109	0.4	10	–	320
5S0P	–	6	0.179	5.83	1.45	–	15	–	0	91	0.5	10	–	320
5S32P	–	6	0.170	5.70	1.45	–	15	–	32	17	0.7	10	–	320
WS	–	–	–	–	0.84	–	15	–	8	103	13	10	–	320
0S8P	0.017	5.98	–	–	–	0.85	15	–	8	88	15	10	–	320
5S8P*	–	6	0.174	5.79	1.45	–	15	–	8	73	0.5	10	–	320
WD	–	–	–	2.78	0.10	–	–	–	8	116	39	10	0.2	–
0D2S	–	6	0.055	2.72	0.182	–	–	–	8	97	39	10	0.2	–
3D2S	–	6	0.205	2.86	–	2.786	–	11.9	8	62	21	10	0.2	–

CP = creatine phosphate, P_i = phosphate, Pr = propionate, CK = creatine kinase, A₂P₅ = P₁,P₅-diadenosine pentaphosphate. In addition to the above, 10 mM MOPS (morpholinopropane sulfonic acid) is added to all solutions, and pH adjusted to 7.00. The ionic strength of all solutions is 200 mM. pCa of relaxing solution is 7.00; pCa of all activating solutions is 4.40. Mg²⁺ concentration of all activating solutions is 0.5 mM. nSmP notation indicates activating solution composition, where n = [MgATP²⁻] and m = [P_i]_total. *5S8P solution is the same as the standard activating solution, and it contains 5 mM MgATP²⁻ and 8 mM total P_i.

Single fibers ∼10 mm in length were dissected from the bundles and doubly knotted at both ends. After transferring a fiber to the experimental chamber, one end was connected to the length driver, and the other end to the force transducer. The sarcomere length was adjusted to 2.5 μm as measured by optical diffraction of a He-Ne laser beam (632.8 nm), and then the fiber length (L₀) was determined under the light microscope. L₀ ranged 3–4 mm. Using a medium power (200×) Nomarski optics (Diavert, Leitz, Bielefeld, Germany), the fiber was carefully monitored rejecting damaged fibers. Both the major diameter (maximum width) and the minor diameter (minimum width) were measured by ocular micrometer (fibers were often mounted twisted by 1/4–1/2 turn), and the cross-sectional area was estimated by assuming an elliptical shape.

Solutions

Solutions used in the experiments are listed in Table 1. The pH was adjusted to 7.00 at 20°C. The pCa of all activating solutions was 4.40, and the free Mg²⁺ concentration was 0.5 mM. The temperature of the bath solutions was controlled to 20.0 ± 0.2°C, and they were continuously stirred to minimize local heterogeneities in the concentration and temperature; 10 mM NaN₃ was included to inhibit mitochondrial ATPase. Activating solutions used in the P_i and MgATP studies included 15 mM creatine phosphate (CP) and 320 U/ml creatine kinase (CK). The strength of the ATP regenerating system was tested by changing the CP (15 and 25 mM) and CK (80, 160, and 320 U/ml) concentrations, and 15 mM CP and 160 U/ml CK were judged to be more than sufficient in psoas fibers. In activating solutions of the MgADP study, 0.2 mM P¹,P⁵-di(adenosine-5′) pentaphosphate (A₂P₅) was included to inhibit the adenylate kinase, and CP/CK was deleted. Activating solutions for specific experiments were made as a variation of the standard activating solution. The WP solution was used to remove EGTA and P_i before Ca²⁺ activation in the P_i study. The WS solution was used to remove EGTA and MgATP before Ca²⁺ activation in the MgATP study. The removal of EGTA before activation is necessary to reduce the Ca²⁺ buffer capacity within the fiber (23); this allows fast and homogeneous activation and facilitates the maintenance of the striation pattern. The WD solution was used to remove EGTA before Ca²⁺ activation in the MgADP study. Rigor was induced by three washes with the rigor solution. The ionic strength of all solutions was 200 mM.

Experimental procedure

A detailed description of the mechanical apparatus used in this study was previously published (24). For obtaining complex modulus data, the length of the fiber was changed in sinewaves at 0.07–187 Hz (type IIA fibers) or 0.25–500 Hz (type IID and type IB fibers), and the tension transient data were collected. The amplitude of the length change was 0.125%, which corresponds to 1.6 nm per half-sarcomere. The complex modulus Y(f) is defined as the ratio between the tension (stress) change to the length (strain) change in the frequency (f) domain. Y(f) consists of the complex number and it is displayed on the Cartesian coordinate system with the real part on the abscissa and the imaginary part on the ordinate, hence Y(f) constitutes a vector. When the frequency is used as an intervening parameter, the display is called the Nyquist plot (Fig. 2, C–E). The length of the vector |Y(f)| (dynamic modulus) is related to the fiber stiffness. The angle of the vector from the abscissa (arg[Y(f)]) represents the phase shift between force and length changes and is related to the work absorption (or production) by the fiber. The projection of the vector to the abscissa (real part) is called “elastic modulus”, the projection to the ordinate (imaginary part) is called “viscous modulus”.

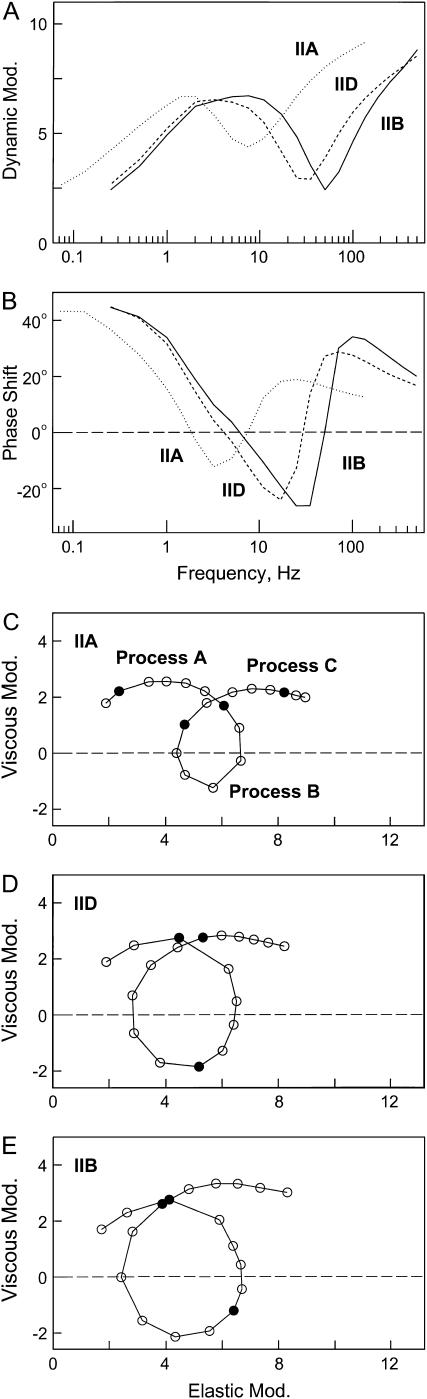
FIGURE 2.

Complex moduli (Y(f)) of three muscle fiber types IIA, IID, and IIB as labeled. (A) Dynamic modulus versus frequency; (B) phase-shift versus frequency; (C–E) Nyquist plots (viscous modulus versus elastic modulus). The viscous modulus is defined as Imag(Y(f)), the elastic modulus as Real(Y(f)), dynamic modulus as |Y(f)|, and the phase shift as Arg(Y(f)). The unit of all moduli is in MPa (Pa = Nm⁻²). Frequencies used are as follows: Type IIA fibers, 0.07, 0.13, 0.25, 0.35, 0.5, 0.7, 1, 1.4, 2, 3, 5, 7, 11, 17, 25, 35, 50, 70, 100, 135, and 187 Hz; Type IID and IIB fibers, 0.25, 0.5, 1, 2, 3, 5, 7, 11, 17, 25, 35, 50, 70, 100, 135, 187, 250, 350, and 500 Hz. Underlined frequencies are entered with solid circles in the Nyquist plots (C–E). The complex moduli were obtained in the standard activating solution at 20°C. Type IIA fibers, average of seven preparations. Type IID fibers, average of 16 preparations. Type IIB fibers, average of 15 preparations. In panel C, the hemicircle that defines each process is indicated.

Single muscle fibers were maximally activated under the isometric condition at different concentrations of P_i (P_i study), MgATP (MgATP study), or MgADP (MgADP study). Complex modulus data were collected when the force reached a steady state. Each activation was preceded by a rinse in a wash solution and followed by an exposure to an activating solution (Table 1). In the beginning and at the end of an experimental series, the preparation was tested by the standard activating solution (5S8P). Only the data from preparations, in which tension decline was <20% and the sarcomere length was unchanged from the initial setting (2.5 μm), were further analyzed. All modulus data were corrected against those from rigor of the same fiber as described (24).

Biochemical analysis

After the completion of mechanical measurements, muscle preparations were removed from the apparatus for biochemical analysis as described (15). The muscle preparations were dissolved in SDS lysis buffer (62 mM TRIS-HCl, pH 6.8, 10% (v/v) glycerol, 5% (w/v) SDS, 5% (v/v) 2-mercaptoethanol) and heated at 90°C for 5 min. Subsequently, a part of this extract (∼0.1 μg protein) was applied to the SDS polyacrylamide gel system (4% polyacrylamide in stacking and 7.5% in running gel). For electrophoresis, a SE 600 chamber (Hoefer, San Francisco, CA) with 16-cm-long glass plates was used. A constant voltage of 180 V was applied for 35 h. After electrophoresis, gels were silver stained.

RESULTS

Myosin heavy-chain isoforms and fiber types

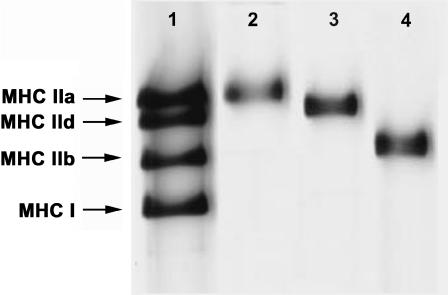
Fig. 1 shows an electrophoresis pattern of MHC isoforms of single fibers. The first lane represents a mixture of rabbit gastrocnemius and diaphragm muscles, which serves as a marker for the MHC isoforms. In this lane four distinct MHC isoforms are seen from the top: MHC-IIa, MHC-IId, MHC-IIb, and MHC-I. The three following lanes represent single muscle fibers that have been used for mechanical experiments. Fibers containing MHC-IIa (type IIA, lane 2), MHC-IId (type IID, lane 3), and MHC-IIb (type IIB, lane 4) are shown. About one-quarter of all fast-twitch fibers studied contained two MHC isoforms. These hybrid fibers were not used for further analysis. Because only a small number (=7) of type IIA fibers was found in the EDL muscles, the type IIA fibers found in slow-twitch muscle soleus (25) were also used in some of our study (limited to Fig. 3). It has been known that a small fraction of soleus fibers exhibits fast kinetics. The majority of soleus exhibits a slow-twitch response (25–27). Type IIA fast-twitch fibers from soleus contain MHC-IIa (28), and Fig. 3 demonstrates that they exhibit the same kinetics to type IIA fibers of EDL.

FIGURE 1.

Silver-stained polyacrylamide gel electrophoresis pattern of myosin heavy-chain (MHC) isoforms from rabbit skeletal muscle fibers. Lane 1 represents a mixture of extracts from rabbit gastrocnemius and diaphragm muscles and serves as marker for MHC-IIb, MHC-IId, MHC-IIa, and MHC-I as indicated. The other lanes represent single fibers for which mechanical properties were measured: lane 2, type IIA (EDL); lane 3, type IID (adductor magnus); lane 4, type IIB (adductor magnus).

FIGURE 3.

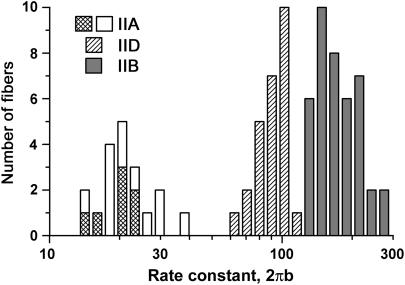
Distribution of the apparent rate constant 2πb among three fiber types. The ordinate is the number of fibers, and the abscissa is 2πb. Shaded areas represent fibers that were tested with SDS-PAGE, and their fiber types confirmed based on MHC. White areas represent fast-twitch fibers of soleus (type IIA) that were not tested with SDS-PAGE, but their fiber type was identified based on frequency plots.

Kinetic differences of muscle fiber types

Single fibers were maximally activated at pCa 4.4 under the isometric condition with the standard activating solution (5S8P; Table 1). When the tension reached a stable plateau (typically 150–170 kPa; Table 2), sinusoidal length changes of 19–21 different frequencies were applied. The resulting force time course was collected, and the complex modulus data were calculated. The averaged frequency dependence of the dynamic modulus and the phase shift is shown in Fig. 2, A and B. The plots are similar in shape, but displaced along the x axis to the higher frequency in the order of type IIA, type IID, and type IIB fibers (marked). This implies that the cross-bridge kinetics are slowest in type IIA, intermediate in type IID, and fastest in type IIB fibers. Fig. 2, C–E, shows the corresponding Nyquist plots. The general appearance of the Nyquist plots of three fiber types is similar, and they consist of three hemicircles each of which represents one exponential process (24,29). The slowest hemicircle is called exponential process A, the intermediate one is called exponential process B, and the fastest one is called exponential process C. These are called exponentials, because their time domain expression uses exponential functions (24). The complex modulus data are fitted to Eq. 1 (24):

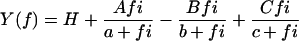(1)

where f is the frequency and 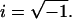Lowercase letters a, b, and c represent characteristic frequencies of exponential processes A, B, and C, respectively. Uppercase letters A, B, and C represent their respective magnitudes. Y_∞ is the elastic modulus at infinite (∞) frequency and is defined by Eq. 2:

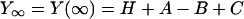(2)

TABLE 2.

Tension (P₀), stiffness (Y_∞), and parameters of exponential processes

Parameters	Units	Type I*	Type IIA	Type IID	Type IIB
P0	kPa	150 ± 20	157 ± 7	157 ± 7	157 ± 4
Y∞	MPa	8.6 ± 0.7	10.0 ± 0.8	9.2 ± 0.6	8.9 ± 0.3
P0/Y∞	%L0	1.74 ± 0.23	1.63 ± 0.10	1.77 ± 0.05	1.80 ± 0.04
H	MPa	0.75	2.0 ± 0.1	1.4 ± 0.1	1.1 ± 0.1
A	MPa	3.90	9.2 ± 0.7	7.0 ± 0.5	6.0 ± 0.2
B	MPa	5.55	7.9 ± 0.7	7.6 ± 0.6	7.7 ± 0.2
C	MPa	7.94	6.7 ± 0.5	8.5 ± 0.6	9.4 ± 0.3
2πa	s−1	1.90	4.4 ± 0.4	5.50 ± 0.16	6.48 ± 0.15
2πb	s−1	4.11	21 ± 2	85 ± 2	168 ± 6
2πc	s−1	26.1	238 ± 16	596 ± 23	813 ± 19
2πfmin	s−1	6	62.3 ± 2.6	196 ± 3	305 ± 5
N	–	7	9	26	43
†Vu	s−1	0.72	1.46	2.25	2.45

These values were obtained at the standard activating condition (5 mM MgATP, 8 mM P_i) at 20°C. The mean ± SE and the number of experiments (number of fiber preparations) are shown by N.

^*From Wang and Kawai (21) except for V_u.

^†From Andruchov et al. (15) given in fiber length per second; the data were obtained at 22°C in the absence of added P_i, pCa 4.5.

Exponential processes of sinusoidal analysis and “phases” of step analysis (16,30) are intimately related: Y_∞ corresponds to the instantaneous force change induced by a rapid change of the fiber length (phase 1), process C corresponds to the quick force recovery after the length change (phase 2), process B corresponds to the reversal of the force recovery (phase 3), and process A corresponds to the final slow force recovery (phase 4). By fitting the data to Eq. 1, magnitude parameters and characteristic frequencies of three exponential processes were obtained.

When the characteristic frequencies are multiplied by 2π, they are called the apparent rate constants (24). These are given for three fiber types in Table 2. The unpaired t-test indicates that all three apparent rate constants are significantly different (P < 0.001) among different fiber types. The apparent rate constants are fastest in type IIB fibers, intermediate in type IID fibers, and slowest in type IIA fibers under the same activating condition. The rate constant 2πb exhibits the largest separation among different fiber types, followed by the rate constant 2πc. The rate constant 2πa exhibits the smallest separation. The ratio of the apparent rate constants of type IIB/type IID fibers is 1.2 (2πa), 2.0 (2πb), and 1.4 (2πc). The ratio of the apparent rate constants of type IID/type IIA fibers is 1.3 (2πa), 4.0 (2πb), and 2.5 (2πc). The magnitudes are also given in Table 2. It can be seen that the magnitude A decreases in the order of type IIA, type IID, and type IIB, whereas the magnitude C increases in the same order (P < 0.001). The magnitude B is similar in all type II fibers. Table 2 also includes 2πf_min. f_min is the frequency that gives the minimum dynamic modulus that was often used to indicate the “cross-bridge kinetics” by some investigators (31–33). As expected, f_min is smallest in type IIA fibers, intermediate in type IID fibers, and fastest in type IIB fibers. All apparent rate constants and f_min are larger in type IIA fibers than in type I fibers (Table 2). The data on type I fibers were taken from an earlier report (21).

Fig. 3 shows the distribution of 2πb of all fibers investigated in this study; no hybrid fibers were included. It can be seen that there is no overlap of the 2πb values among different fiber types. The figure also shows that the seven type IIA fibers from EDL that were identified by MHC analysis are located in the central range of the type IIA fibers of soleus that were not characterized by MHC analysis. Therefore, we conclude that the type IIA fibers of both muscles exhibit the same kinetics.

Effect of phosphate (P_i)

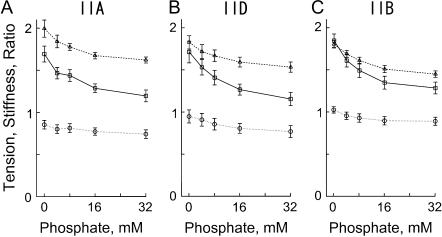
To investigate the effect of P_i on three fiber types, skinned fibers were maximally Ca²⁺-activated at five different P_i concentrations ranging from 0 (no added P_i) to 32 mM. The MgATP concentration was kept constant at 5 mM. The MgADP concentration was kept low (<20 μM) (34) by use of the ATP regenerating system (CP and CK). In all fiber types, the tension and stiffness decreased with an increase in the P_i concentration, whereas the tension/stiffness ratio changed less (Fig. 4). The complex modulus data were collected during Ca²⁺ activation. Although not individually shown in this report, both the dynamic modulus plot and the phase shift plot shifted to a larger frequency with increasing P_i concentration in all fiber types as reported (35). This indicates that the cross-bridge kinetics became faster with an increasing concentration of P_i. The Nyquist plots obtained under different P_i concentrations maintained three hemicircles indicating that three exponential processes were universally present. The product Bb increased with the P_i concentration that indicates a larger power output at higher P_i concentration.

FIGURE 4.

The effect of phosphate on isometric tension, stiffness, and their ratio (tension/stiffness) in three fiber types. The unit of tension (solid line, □) is 100 kPa, the unit of stiffness (dotted line, ○) is 10 MPa, and the unit of the ratio (dashed line, ▵) is %L₀. (A) Average of five type IIA fibers from EDL. (B) Average of seven type IID fibers. (C) Average of 15 type IIB fibers. The mean and ± SE are shown.

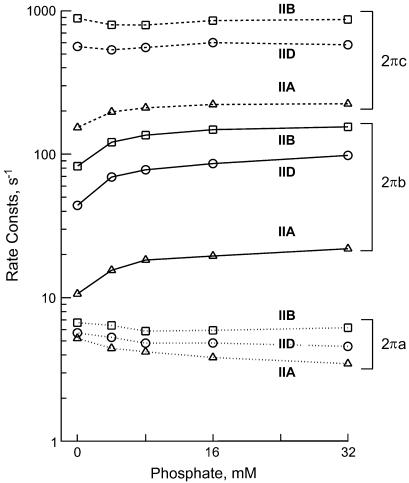
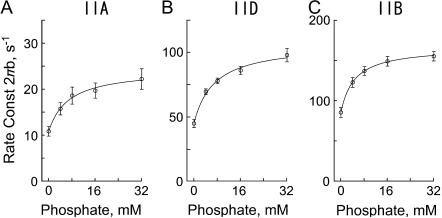
Fig. 5 demonstrates the effect of P_i on the apparent rate constants in the log scale. For this diagram, the data of individual fibers of the same type were averaged and plotted against the P_i concentration. It can be seen in this figure that 2πb is most affected by the P_i concentration in all fiber types. Fig. 6 demonstrates the P_i dependence of 2πb in the linear scale. It can be seen from this figure that the plot is hyperbolic in shape for all fiber types. This is consistent with earlier results of rabbit psoas muscle fibers (20,36–38). As discussed in these reports, the P_i dependence can be explained by a portion of the cross-bridge Scheme 1 labeled with “P_i study”. Equation 3 is the analytical form of the apparent rate constant 2πb (20).

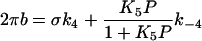(3)

where P is the total P_i concentration; k₄ and k₋₄ are the forward and backward rate constants of step 4, and K₅ is the P_i association constant to AM. K₄ (=k₄/k₋₄) is the equilibrium constant of step 4; σ (0 < σ ≤ 1) is placed in Eq. 3 to account for a presence of fast equilibria to the left of step 4 (σ is defined later in Eq. 5); σ = 1 if there is no fast equilibria, which is an assumption used by other investigators (36,37).

FIGURE 5.

The effect of phosphate on the apparent rate constants in three fiber types. Type IIA fibers from EDL, average of five experiments; type IID fibers, average of seven experiments; and type IIB fibers, average of 15 experiments. The means are shown; ± SE is about the same or smaller than the symbol size in log plots, hence not shown.

FIGURE 6.

The effect of phosphate on the apparent rate constant 2πb in three fiber types. (A) Type IIA fibers from EDL, average of five experiments. (B) Type IID fibers, average of seven experiments. (C) Type IIB fibers, average of 15 experiments. The mean and ± SE are shown. Continuous lines represent Eq. 3 with best-fit parameters. Note the change in the ordinate scaling in three panels.

SCHEME 1.

The effects of P_i on 2πa or 2πc were smaller than that on 2πb, and in the opposite direction (Fig. 5) for most cases except for 2πc of type IIA fibers. These results are a direct proof that process B represents step 4 (Eq. 3 demonstrates that 2πb is a linear combination of k₄ and k₋₄), and it is influenced by equilibrium constants of the neighboring steps that are faster. The cross-bridge Scheme 1 and Eq. 3 is the simplest and direct way to explain the effects of P_i on 2πb in different fiber types. No other scheme of the same degree of simplicity can describe the data. To deduce the kinetic constants of the elementary steps, the data were fitted to Eq. 3. The kinetic constants were averaged for fibers of the same type. The mean values ± SE of k₄, k₋₄, K₄ (=k₄/k₋₄), and K₅ of the three fiber types are listed in Table 3. An application of these constants to Eq. 3 results in continuous lines shown in Fig. 6, indicating a good fit of the data in all fiber types. The rate constants of step 4 (k₄, k₋₄) differ significantly (P < 0.001) among three fiber types. They are largest in type IIB, intermediate in type IID, and least in type IIA fibers. The equilibrium constant of step 4 (K₄) decreases from type IIB to type IID fibers, but there is hardly any difference between type IID and type IIA fibers. Similarly, the P_i association constant (K₅) decreases from type IIB to type IID fibers, but there is hardly any difference between type IID and type IIA fibers.

TABLE 3.

Kinetic constants and related parameters of the elementary steps of four fiber types

Constants	Units	Type I*	Type IIA	Type IID	Type IIB
K0	mM−1	18 ± 4 (7)	ND	18.0 ± 6.6 (4)	5.0 ± 0.5 (10)
K1	mM−1	1.2 ± 0.3 (8)	8.7	4.9 ± 1.0 (6)	0.84 ± 0.13 (9)
K2	none	1.6 ± 0.3 (8)	3.9	3.6 ± 0.6 (6)	1.8 ± 0.4 (9)
σ	none	0.34	0.79	0.70 ± 0.06 (6)	0.308 ± 0.050 (9)
K4	none	1.37 ± 0.13 (9)	1.21 ± 0.28 (5)	1.11 ± 0.23 (7)	2.03 ± 0.30 (15)
K5	mM−1	0.18 ± 0.01 (9)	0.18 ± 0.04 (5)	0.16 ± 0.02 (7)	0.26 ± 0.03 (15)
K4/K5	mM	7.6 ± 0.8 (9)	7.0 ± 1.0 (5)	7.1 ± 1.2 (7)	8.0 ± 0.8 (15)
ΔG4	kJ mol−1	−0.77	−0.46	−0.25	−1.73
ΔG45	kJ mol−1	0.13	0.33	0.29	0.0
k2	s−1	21 ± 3 (8)	198	352 ± 23 (6)	526 ± 76 (9)
K1k2	μM−1s−1	0.025 ± 0.007	1.72	1.72 ± 0.37	0.44 ± 0.09
k−2	s−1	14.1 ± 1.0 (8)	51	121 ± 30 (6)	328 ± 32 (9)
k4	s−1	5.7 ± 0.5 (9)	13.6 ± 1.3 (5)	58 ± 4 (7)	143 ± 10 (15)
k−4	s−1	4.5 ± 0.5 (9)	13.6 ± 2.7 (5)	63 ± 9 (7)	81 ± 6 (15)

The mean ± SE and the number of experiments (N) are shown. Where there is no ±, the best-fit constants are shown. ND = not determined; σ was calculated according to Eq. 5 and at S = 5 mM, P = 8 mM.

^*From Wang and Kawai (21), ΔG₄ = −RT ln K₄ was used to calculate ΔG₄, and ΔG₄₅ = −RT ln K₄/K₅P was used to calculate ΔG₄₅ for P = 8 mM.

Effect of MgATP

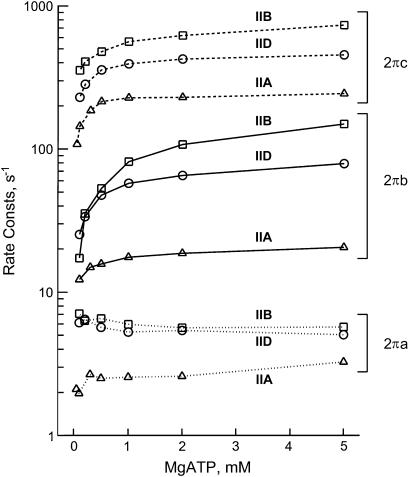
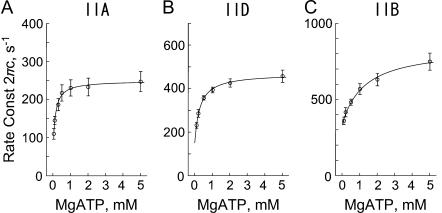
To investigate the effects of MgATP on different fiber types, the preparations were maximally Ca²⁺-activated at six to seven different MgATP concentrations ranging from 0.05 to 5 mM. The P_i concentration was kept constant at 8 mM and MgADP at <20 μM by the CP/CK system. The high P_i concentration was used to populate cross-bridges around the AM*S and AMS states (see Scheme 1, which should be effectively open at step 6), so that the resolution of step 2 becomes better. If physiological P_i concentration (1–2 mM) is used, the equilibrium shifts heavily to the AM*D state (note that the P_i dissociation constant 1/K₅ is 4–6 mM from Table 3), resulting in cross-bridges poorly populated around the AM*S state and the AMS state. The complex modulus data were collected during Ca²⁺ activation. Although not individually shown in this report, both the dynamic modulus plot and the phase shift plot shifted to a higher frequency with an increase in the MgATP concentration, indicating that the cross-bridge kinetics became faster. In all fiber types the product Bb increased with the MgATP concentration, indicating that more oscillatory power came out with a higher MgATP concentration. Fig. 7 demonstrates the effect of MgATP on the apparent rate constants 2πa, 2πb, and 2πc in the log scale. It can be seen that 2πb and 2πc increase with an increase in the MgATP concentration in all fiber types. The apparent rate constant 2πa is affected differently in different fiber types, and the net effect is smaller.

FIGURE 7.

The effect of MgATP on the apparent rate constants in three fiber types. Type IIA fibers from EDL, average of four experiments; type IID fibers, average of six experiments; and type IIB fibers, average of nine experiments. The means are shown; ± SE is about the same or smaller than the symbol size in log plots, hence not shown.

Fig. 8 plots 2πc as the function of the MgATP concentration in the linear scale. It can be seen from this figure that 2πc is a hyperbolic function of the MgATP concentration in all fiber types. This is consistent with earlier results with rabbit psoas fast twitch (type IID) fibers (39) and soleus slow twitch (type I) fibers (25). As shown in these reports, the MgATP dependence can be explained by the partial cross-bridge scheme labeled with “MgATP study” in Scheme 1. It can be assumed that step 2 is monitored by process C. Equation 4 relates the rate and association constants of elementary steps to the apparent rate constant 2πc (39).

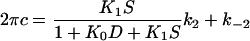(4)

where S is the MgATP concentration, and D is the MgADP concentration; k₂ and k₋₂ are the forward and backward rate constants of step 2; K₂ (=k₂/k₋₂) is the equilibrium constant of step 2; K₀ and K₁ are the association constants of MgADP and MgATP, respectively. For the MgATP study, the K₀D term is omitted because [MgADP] < 0.02 mM in the presence of CP/CK as described. The part of Scheme 1 labeled with “MgATP study” and Eq. 4 is the simplest way to explain the effects of MgATP on different fiber types. Note that 2πc is a linear combination of k₂ and k₋₂ (Eq. 4), hence 2πc is a direct measure of step 2 that is influenced by equilibrium constants of neighboring steps that are faster (K₀ and K₁). Therefore, to deduce kinetic constants of the elementary steps, the data were fitted to Eq. 4 for each individual fiber and averaged. The mean values ± SE of K₁, k₂, k₋₂, and K₂ are listed in Table 3 for three fiber types. Application of these constants to Eq. 4 results in the continuous lines in Fig. 8 indicating that the fits are satisfactory. All kinetic constants (K₁, K₂, k₂, k₋₂) are significantly different (P < 0.001) among different fiber types. The equilibrium constants K₁ and K₂ decrease, and the rate constants k₂ and k₋₂ increase in the order of type IIA, type IID, and type IIB fibers.

FIGURE 8.

The effect of MgATP on the apparent rate constant 2πc in three fiber types. (A) Type IIA fibers from EDL, average of four experiments. (B) Type IID fibers, average of six experiments. (C) Type IIB fibers, average of nine experiments. The mean and ± SE are shown. Continuous lines represent Eq. 4 with best-fit parameters. Note the change in the ordinate scaling in three panels.

The equilibrium constants of the MgATP study were used to determine σ (Eq. 5) which was used in Eq. 3 to account for the presence of fast equilibria to the left of step 4 (Scheme 1) in the P_i study.

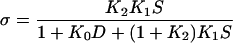(5)

This equation was obtained from Eq. 6 of Zhao and Kawai (40). For our experimental conditions, K₀D ≪ 1, hence this term can be omitted from Eq. 5. The presence of fast equilibria to the left of step 4 diminishes the number of cross-bridges that can undergo step 4, because they occupy states AM, AM*S, etc., hence, σ < 1; σ was calculated for S = 5 mM and listed in Table 3. As it is evident in Eqs. 3 and 5, 2πb also depends on S, and the hyperbolic nature of 2πb vs. S plot (Fig. 7) may appear to fit to Eq. 3. However, we did not attempt this fitting, because we are not able to resolve step 3 (ATP cleavage step), hence, steps 1–2 monitored by process B (step 4) would have an error.

Effect of MgADP

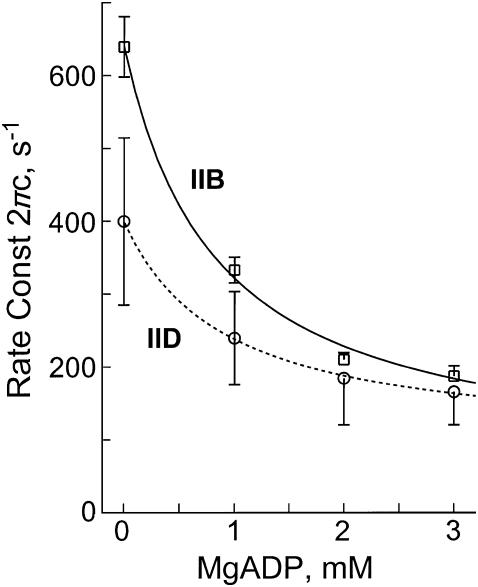
To study the effect of MgADP on the complex modulus Y(f), fibers were maximally Ca²⁺-activated at four different MgADP concentrations ranging from 0 (no added MgADP) to 3 mM. The MgATP concentration was kept constant at 2 mM and the P_i concentration at 8 mM. Tension increased with an increase in the MgADP concentration. We noticed a frequent deterioration of fibers in the ADP solution. Thus, a considerable number of fibers had to be discarded because too much tension was lost (>20%) during the experimental sequence. With an increase in the MgADP concentration, both dynamic modulus and phase shift plots shifted to the left indicating that the cross-bridge kinetics became slower. The magnitude of process B diminished and disappeared with an increase in the MgADP concentration, indicating that there was less power output at higher MgADP concentration. Fig. 9 shows the effect of MgADP on 2πc of type IID and type IIB fibers. It can be seen that 2πc decreases hyperbolically with an increase in the MgADP concentration. This result is consistent with earlier results on fast-twitch fibers of rabbit psoas (39) and slow-twitch fibers of rabbit soleus (25). As discussed in these reports, the MgADP dependence can be explained by a part of the cross-bridge Scheme 1 that includes AMD, AM, AM*S, and MS. Step 0 represents the release of MgADP from cross-bridges.

FIGURE 9.

The effect of MgADP on the apparent rate constant 2πc. Type IID fibers, average of four experiments; Type IIB fibers, average of 10 experiments. The mean and ± SE are shown. Continuous lines represent Eq. 4 with best-fit parameters.

Equation 4 relates rate and association constants of elementary steps to the apparent rate constant 2πc in the presence of MgADP. The data of the ADP study were fitted to this equation and the association constant of MgADP (K₀) was determined by using K₁ obtained from the ATP study and S = 2 mM. The results are listed in Table 3; K₀ is significantly larger in type IID fibers than in type IIB fibers (P < 0.001). Application of these constants to Eq. 4 results in the continuous lines of Fig. 9, indicating that the fits are satisfactory.

Based on Eq. 4, it is not entirely impossible to obtain k₂ and k₋₂ from the ADP study, however, we did not attempt this because of the deterioration of fibers in ADP solutions as mentioned. In other words, k₂ and k₋₂ obtained from the ADP study are less reliable than those obtained from the ATP study. For the same reason, K₀ obtained from the ADP study is least reliable among all kinetic constants we obtained. However, this is a minor problem for characterizing the cross-bridge cycle, because D (ADP concentration) is smaller than 0.02 mM in the presence of CP/CK, hence cross-bridge occupancy in the AMD state (proportional to K₀D) is <1% and small.

DISCUSSION

This is the first comprehensive investigation of the elementary steps of the cross-bridge cycle of three fast-twitch fiber types of mammalian skeletal muscles. A comparable investigation on slow twitch fibers was carried out previously (21,25). Sinusoidal analysis is undoubtedly a powerful approach to characterize elementary steps of the cross-bridge cycle including the force-generation step. After mechanical experiments, a high-resolution SDS-PAGE analysis of the MHC isoforms was employed to identify the fiber types. Previously, it was shown that the kinetics of stretch activation based on step analysis correlates with the MHC isoforms in studies on mouse, rat, rabbit, and human skeletal muscle fibers (12,14,15) and on rat heart muscle fibers (41). From these results, it has been hypothesized that the major contributing factor of the mechanical response is myosin. This hypothesis is consistent with reports on Drosophila melanogaster fibers in which genetic modifications in the myosin heads resulted in a difference in kinetics (18,19). At the same time, it has been known that the regulatory proteins, troponin and tropomyosin, modify the kinetics as reported in muscle fibers (42,43) and in in vitro motility assays (44–46). The histogram of the distribution of log(2πb) of sinusoidal analysis (Fig. 3) exhibits similar distributions and similar separations among three fiber types to the histogram reported by Andruchov et al. (15) (in their Fig. 2 b), which plotted log (t₃) in the abscissa instead of 2πb. This result is expected, because t₃ (in an earlier report, the term t₂ was used (12)) is the time to the peak of the delayed force increase induced by a rapid stepwise stretch, and it approximates 1/2πb. In the log scale, these plots are mirror images to each other.

The exponential processes A, B, and C of three fiber types

The general appearance of the Nyquist plot (Fig. 2, C–E) is the same for all three fast-twitch fiber types within the range of frequencies examined. This observation implies that the underlying molecular mechanism and the elements of the cross-bridge cycle are the same in all fiber types, except that their speeds may be different. An analysis of the complex modulus Y(f) with Eq. 1 demonstrates that all apparent rate constants are largest in type IIB fibers, intermediate in type IID fibers, less in type IIA fibers, and least in type I fibers. These differences imply that some of the kinetic constants of the elementary steps are different. Table 2 demonstrates that the apparent rate constant 2πb exhibits the largest difference (IIB/IIA = 8.0) among different fiber types (P < 0.001), which is followed by 2πc (IIB/IIA = 3.4), and 2πa (IIB/IIA = 1.5). This pattern is in accord with correspondingly different speeds of force recovery after a quick release of fiber length in fiber types of other skeletal muscle preparations as reported in rat (47), and rabbit and mouse (48). The latter report, however, did not carry out biochemical analysis. For interpreting these findings, the molecular events underlying the processes A, B, and C have to be considered.

The significance of processes B and C were reported by a large number of publications from this laboratory (20,21,39,49,50,51). Process C is the fastest of three processes, and it represents the transition of the myosin heads from a strongly bound state to a weakly bound state (step 2 of Scheme 1). This process is initiated by the binding of MgATP to the nucleotide-binding pocket on the myosin head. This hypothesis was derived by the MgATP sensitivity of process C (39,52).

Process B is slower than process C, and it represents the force-generation step that is based on an isomerization of the weakly bound AMDP state to the strongly bound AM*DP state (step 4). Once force is generated, P_i is released subsequently (step 5) and the same force is maintained. This hypothesis was deduced by the effect of P_i on 2πb and isometric tension, and by the lack of the effect of P_i on 2πc (20,50). Similar lines of investigation using pressure-release (36) and caged P_i (37) in muscle fibers, and isometric tension on myofibrils (54) resulted in the same conclusion. In the pressure-release experiment (36), a reduction in the pressure from 10 to 0.1 MPa accelerates the force generation step (step 4). In the caged P_i experiment (37), an increase in the P_i concentration by photolysis of caged P_i increases the number of cross-bridges in the AM*DP state, thereby accelerating the reversal of step 4. The transient change of the cross-bridge occupancy in the AM*DP and AM*D states results in a transient change in force.

Because the reaction of step 4 is slower than step 2 (k₄ + k₋₄ < k₂ + k₋₂), 2πc is not very sensitive to the phosphate concentration, which is consistent to the data (Fig. 5) (53). The insensitivity is because a slow reaction (step 4) isolates a fast reaction (step 2) from being affected by the P_i concentration (step 5). Conversely, the slow reaction of step 4 is affected by the MgATP concentration via the fast reaction of step 2, hence both 2πb and 2πc are sensitive to MgATP as observed (Fig. 7).

Process A is the slowest event. This process does not represent an elementary step of the cross-bridge cycle, because the magnitude parameter A diminishes and disappears without changing the cross-bridge kinetics when the sarcomere structure is made rigid by a partial cross-linking of cross-bridges to the thin filament (55). Process A is absent in cardiac (31,32,42,49,58–61) and in insect (18,19,56,57) muscle fibers when cross-bridges cycle normally and shortening takes place. Process A may include information on sarcomere dynamics, as it is the process that slowly recovers force (phase 4 of step analysis) when the length of active muscle is released (62).

It would be of interest to compare the processes A, B, and C with other physiological properties of skeletal muscle fiber types. The unloaded shortening velocity (V_u) of rabbit fast-twitch muscle fibers investigated at 12°C exhibits the following ratios between fiber types: IIB/IID = 1.40, IID/IIA = 1.45 (63). The ATP hydrolysis rate of rat fast-twitch muscle fibers investigated at the same temperature exhibits the following ratios between fiber types: IIB/IID = 1.29, IID/IIA = 1.06 (13). Thus, among the three processes A, B, and C, the apparent rate constant 2πa shows the closest correlation with the ATP hydrolysis rate or with V_u, although this correlation may be fortuitous.

The measurement of both the ATP hydrolysis rate and V_u involves many cross-bridge cycles, and therefore, they may provide information about the rate-limiting step 6 (the slowest step in the cross-bridge cycle). The ATP hydrolysis rate measured by Bottinelli et al. (13) is an indicator for the rate-limiting step of the cross-bridge cycle under isometric conditions, whereas V_u may indicate the duration of cross-bridges attached to actin and their subsequent detachment under the unloaded condition. The fact that the kinetics of the elementary steps of the cross-bridge cycle expressed by 2πb and 2πc differ considerably more among fast-twitch fiber types than the ATP hydrolysis rate or V_u, is consistent with the idea that the transient analysis method detects fast reactions in the cross-bridge cycle, whereas ATP hydrolysis rate or V_u detects the rate-limiting (slowest) reaction of the cross-bridge cycle. The correlation between the ATP hydrolysis rate and k₆ was established, and in fact, k₆ was deduced from the ATP hydrolysis rate measurement (20,40).

Elementary steps of the cross-bridge cycle of different fiber types

The apparent rate constants 2πb and 2πc characterize the transitions of the cross-bridges at the given solution condition. To determine the individual rate constants of forward and backward reactions during these transitions, sinusoidal analysis was performed on maximally activated fibers, and 2πb and 2πc were determined as the functions of the P_i, MgATP, and MgADP concentrations. From the effect of P_i on 2πb, the rate constant of the force-generation step (k₄), the rate constant of its reversal step (k₋₄), and the P_i association constant (K₅) are characterized (Eq. 3).

From the effect of MgATP on 2πc, the rate constant of the ATP isomerization step (k₂), the rate constant of its reversal step (k₋₂), and the MgATP association constant (K₁) are characterized (Eq. 4). More precisely, the step characterized by k₂ is the transition of cross-bridges from a strongly bound state to a weakly bound state, which represents isomerization of the ATP-bound state. From the MgADP study, the MgADP association constant (K₀) is characterized (Eq. 4).

Most rate constants and equilibrium constants determined in this study (Table 3) are ordered according to the three fiber types. For comparative purpose, previous data on rabbit soleus slow-twitch fibers (type I) (21) are also entered in Table 3.

As seen in this table, all rate constants of elementary steps (k₂, k₋₂, k₄, k₋₄) increased in the order of type I, type IIA, type IID, and type IIB fibers. Among four individual rate constants, k₄ exhibited the largest difference between fast fiber types: IIB/IID = 2.5 and IID/IIA = 4.3. Consequently, it can be concluded that the force-generating transition occurs at considerably different speeds among three fiber types. The difference in its backward reaction (k₋₄) is less prominent (IIB/IID = 1.3 and IID/IIA = 4.6). The backward reaction of the ATP isomerization step (k₋₂) is very different in different fiber types: IIB/IID = 2.7 and IID/IIA = 2.4. In this sense, it may be interesting to point out that both k₄ and k₋₂ represent a transition from a weakly bound state to a strongly bound state. The ATP isomerization step itself (k₂) varies least among different fiber types (IIB/IID = 1.5 and IID/IIA = 1.8). The rate constants of rabbit slow-twitch type I fibers are considerably less than those of type IIA fibers of this study (Table 3). When these are compared, k₂ is 9.4×, k₋₂ is 3.6×, k₄ is 2.4×, and k₋₄ is 3.0× faster in type IIA fibers than in type I fibers.

Two equilibrium constants K₁ and K₂ are ordered according to the fiber types within the fast-twitch category. K₁ and K₂ decrease in the order IIA, IID, and IIB (Table 3). The decrease is larger in K₁: IIA/IID = 1.8 and IID/IIB = 5.8. Thus, the myosin head of type IIA fibers binds MgATP more tightly than that of type IID fibers. The lowest MgATP affinity is seen in type IIB fibers. Similarly, our determination of K₀ showed that MgADP binds 3.6× more tightly in type IID fibers than in type IIB fibers. The fact that the order of MgATP affinity and MgADP affinity is the same in different fiber types is consistent with the assumption that MgATP and MgADP compete for the same binding site as shown in Scheme 1. It would be of interest to point out that K₁ for type I fibers is 1.2 mM⁻¹ (Table 3), which is much less than type IIA fibers (1/7×) or type IID fibers (1/4×), but similar to type IIB fibers. Wang and Kawai (64) argued that this difference may be related to a sequence difference of loop 1, which is the junction between 27k and 50k domains and which comes close to the nucleotide binding site on the myosin head (65). Loop 1 is more positively charged in type I fibers (3 Lys⁺, 1 Arg⁺, 2 Asp⁻) than in type II fibers (4 Lys⁺, 3 Glu⁻), attracting the negatively charged MgATP molecule more in type I fibers than in type II fibers. The P-loop, that binds the nucleotide's phosphate group and is located in the 27k domain, has the same sequence between type I and type II fibers. The same applies for the rest of amino acids building the nucleotide-binding pocket. The variation in K₂ is smaller than that of K₁: IIA/IID = 1.1 and IID/IIB = 2.0, and K₂ of type I fibers is similar to that of type IIB fibers.

Two additional equilibrium constants K₄ and K₅ are largest in type IIB fibers, and similar in type IID, type IIA, and type I fibers. The largest variation in K₄ is 1.8× and that of K₅ is 1.6×. These observations are consistent with the idea that the force generation step has a similar free-energy change (ΔG₄ = −RT ln K₄) among various fiber types, and their maximum variation is ∼0.6 RT (=1.5 kJ mol⁻¹) and not significant (Table 3). These results indicate that force generated per cross-bridge must be similar among these fiber types. This conclusion is consistent with our observation that force generated per cross section (P₀) is just about the same among different fiber types (Table 2). Because the P_i affinity (K₅) is not markedly different, K₄/K₅ is not very different among the four fiber types, indicating that the free-energy change of force generation through P_i release steps (steps 4 and 5, ΔG₄₅ = −RT ln(K₄/K₅P)) is not significantly different in all fiber types; Table 3 demonstrates the maximum variation of ΔG₄₅° is <0.2 RT (=0.5 kJ mol⁻¹) and very small. It is sometimes convenient to lump K₄ and K₅ together such as in K₄/K₅, because step 4 has not been recognized in solution biochemistry, and it is presumably lumped together with the subsequent P_i release step.

Comparison with solution studies

In the solution study reported (22), myosin of single rat skeletal muscle fibers of different types was purified and used in experiments where actomyosin was dissociated by an increase in the MgATP concentration induced by ultraviolet-flash photolysis of caged ATP at 22°C. From the time course of the actomyosin dissociation monitored by light scattering, the second order rate constant (K₁k₂) was determined. The mean K₁k₂ values (in μM⁻¹s⁻¹) of this study were 0.84 (=4200/5000) in type IIA, 1.04 (=5200/5000) in type IID, and 1.04 (=5200/5000) in type IIB fibers after the ionic strength correction to 200 mM. The corresponding values of our study in rabbit skeletal muscle fibers were (in μM⁻¹s⁻¹) 1.7 in type IIA fibers, 1.7 in type IID fibers, and 0.44 in type IIB fibers at 20°C (Table 3). Thus, the overlap of the values obtained from both studies is impressive. From this comparison, it can be concluded that muscle fibers exhibit much higher variation (3.9×) among fiber types than the extracted and reconstituted protein system in solution (1.2×). Note that the K₁k₂ value in rabbit psoas myofibrils has been reported to be 1 μM⁻¹s⁻¹ (66) (their k₂/K₁), a value in the midrange among fast-twitch fibers of this report. However, the myofibril study was performed at 4°C, hence the agreement should be considered as approximate. In the study of Weiss et al. (22), the MgADP dissociation constant was also determined. Their corrected value to 200 mM ionic strength is 5.6 mM⁻¹ (=10,000/1790) in type IID fibers and 4.5 mM⁻¹ (=10,000/2220) in type IIB fibers. This compares with 18 mM⁻¹ in type IID fibers and 5.0 mM⁻¹ in type IIB fibers of our study (K₀ of Table 3).

The different results of the two studies are likely caused by a vast difference in the experimental conditions. In the fiber study, the contractile machinery of the muscle fibers was intact; the experiments were carried out near or at isometric conditions. The MgATP concentration ranged between 0.05 and 5 mM and the ionic strength was 200 mM. In the solution study of Weiss et al. (22), purified proteins were used and the ionic strength was ∼500 mM to keep myosin soluble (they performed the ionic strength correction). The ATP concentration induced by photolysis of caged ATP ranged between 10 and 40 μM, whereas in our skinned fiber study the MgATP concentration ranged between 50 μM and 5 mM. In addition, the myosin heads are integrated in a well-ordered and highly packed protein network in muscle fibers. Consequently, neighboring proteins interact to result in a cooperative activation at various levels. This apparently is not the case in the solution system where the orientation of actin and myosin is not fixed, and the interaction between actin and myosin is less frequent than in fibers. Most importantly, the energy of ATP hydrolysis is lost as heat in the solution studies, whereas a large part of the energy is retained in elastic elements of the lattice structure in fiber studies. Because of these differences, it is not surprising that the kinetic constants are found to be somewhat different in the two methods.

In conclusion, our study demonstrates that there are four distinctively different cross-bridge kinetics associated with four different myosin heavy chains to fulfill various functional needs. The rate constants are different mostly in the force generation step (k₄) and the reversal of the ATP isomerization step (k₋₂). Our study further demonstrates that the difference among fiber types is larger in skinned fibers than in the extracted and reconstituted protein system in solution.