Abstract
A general method is presented that allows the separation of the rigid body motions from the nonrigid body motions of structural subunits when bound in a complex. The application presented considers the motions of the tRNAs: free, bound to the ribosome and to a synthase. We observe that both the rigid body and nonrigid body motions of the structural subunits are highly controlled by the large ribosomal assembly and are important for the functional motions of the assembly. For the intact ribosome, its major parts, the 30S and the 50S subunits, are found to have counterrotational motions in the first few slowest modes, which are consistent with the experimentally observed ratchet motion. The tRNAs are found to have on average ∼72–75% rigid body motions and principally translational motions within the first 100 slow modes of the complex. Although the three tRNAs exhibit different apparent total motions, after the rigid body motions are removed, the remaining internal motions of all three tRNAs are essentially the same. The direction of the translational motions of the tRNAs are in the same direction as the requisite translocation step, especially in the first slowest mode. Surprisingly the small intrinsically flexible mRNA has all of its internal motions completely inhibited and shows mainly a rigid-body translation in the slow modes of the ribosome complex. On the other hand, the required nonrigid body motions of the tRNA during translocation reveal that the anticodon-stem-loop, as well as the acceptor arm, of the tRNA enjoy a large mobility but act as rigid structural units. In summary, the ribosome exerts its control by enforcing rigidity in the functional parts of the tRNAs as well as in the mRNA.
INTRODUCTION
The ribosome is a molecular machine responsible for the biosynthesis of peptides of sequence specified according to the messenger RNA. The Thermus thermophilus ribosome is comprised of two major multicomponent subunits of unequal size, the large (50S) and the small (30S) subunits, which are associated with each other through intermolecular interactions. The tRNAs are the adaptor molecules that move through the ribosome through coordinated motions during the elongation cycle. Understanding the motions of tRNAs through the ribosome could be key to understanding the molecular mechanism of the ribosome. In the study of the functional motions of large biological complexes comprised of multiple separate molecular components such as the ribosome, one natural question arises. How does the motion of a single component within the complex relate to its motions as a fully independent molecule unencumbered by its binding partner(s)? Can there be independent motions of the components during the functional motions of the complex? Are the motions intrinsic to the individual component or completely different? We explore the answers to these fundamental questions here for the motions of the tRNA bound to the three sites in the ribosome during the elongation cycle.
The functional motions of proteins and biological complexes typically represent large domain motions having strong internal cohesion. This cohesiveness is likely a cooperative hydrophobic effect. One of the most successful computational models for the study of the large-scale correlated motions is the elastic network models originally proposed by Tirion (1) and further developed, articulated, and applied extensively to many problems by Bahar and Jernigan (2–11) and many others (12–21). The elastic network models include the Gaussian network model (GNM) (3,4,8) and the anisotropic network model (ANM) (2); the former provides the magnitudes of motions and the latter yields also the directions of motions. The elastic network models use coarse-grained representations for the protein or the biological complex. The most common approach has been to use one site per residue or one site for several sequential residues (7). There is abundant evidence to indicate that coarse graining of structures is appropriate, insofar as the overall molecular shape is retained, because the slowest, most important motions are robust and depend principally on the shape of the structure. Individual motions of the structures are usually extracted with normal mode analyses. This approach avoids the limitations of atomic molecular dynamics in accessing the slowest large domain motions, as well as the problems with atomic potentials not adequately representing the large-scale cohesiveness of proteins and other large biomolecules. It has also been shown that these simplified models are adequate to recover the low-frequency motions (3,4). Several studies have demonstrated that the direction of these slow modes closely relate to known conformational changes for a number of proteins (14,11,18,21). There is growing interest in applying these elastic network models to study the cooperative motions of proteins within complex biological assemblies, given their demonstrated abilities to better reproduce crystallographic thermal factors than atomic molecular dynamics, and strong evidence that the cohesiveness of these structures is one of the most important factors in determining their motions.
We have recently applied the elastic network model (the ANM) to obtain the modes of motion of the entire 70S ribosome, which includes a short sequence of mRNA and three tRNAs bound at the A, P, and E sites (22). The predicted slow modes of motion correspond closely to the experimentally observed conformational change in the ribosome during the elongation cycle, namely, the ratchet-like motion observed by cryo-electron microscopy (cryo-EM) (23). However, the direct comparison of the predicted modes of the motions with the cryo-EM data were not pursued because the modes predicted represent the “equilibrium” fluctuations near the native structures. The actual conformational change during the elongation step can either be represented as a sum of these normal modes with appropriate weights or perhaps obtained through other approaches such as the targeted molecular dynamics simulations. One may, however, extract dynamic quantities that would be of interest for understanding some details of the functioning of the ribosome by examining the predicted fluctuations near the native state, which is our purpose here.
We present here a general methodology that can be applied to analyze the motion of separable molecules in any complex. This method can reveal the interesting motions of the individual molecules within the complexes and in this case can inform us about the roles of the tRNAs in their various complexes. In particular, we examine various aspects of the motions of the tRNA that relate to the elongation cycle.
METHODS
Details of elastic network models used for the ribosome
We use the ANM version of the elastic network models. For the ribosome, we use the crystal structure, having a resolution of 5.5 Å, reported by Yusupov et al. (Protein Data Bank (PDB) code 1GIX and 1GIY) (24), except that the L9 protein has been removed from the original reported structure because its observed position was not consistent with other experimental evidence (25). The structure has then been simplified by coarse graining to have one point for each Cα atom of every amino acid and one site for each P atom of every nucleotide, a level of detail consistent with the reported resolution. All of these sites are then assumed to have the same molecular weight, an approximation well established by many of the applications referenced above. The cutoff distance chosen to define contacts is 24 Å between P-P sites and 15 Å between other types of sites. The total number of all types of sites in this representation of the ribosome is 9746, of which 3915 sites are on the 30S subunit, 5599 sites on the 50S subunit, and 76 sites on the A site tRNA (A-tRNA), 76 sites on the P site tRNA (P-tRNA), and 74 sites on the E site tRNA (E-tRNA), with six sites on the small fragment of mRNA; thus the 30S is ∼2/3 the size of the 50S in this coarse-grained model. We will use the symbol L to designate these substructures, L = 30S, 50S, A-tRNA, P-tRNA, E-tRNA, or mRNA.
The normal modes of motion computed for the ribosome are indicated by the column eigenvectors Uk of length 3N (N = 9746 is the total number of sites in the ribosome) where k is the mode index. These vectors Uk are normalized and orthogonal. Each column vector Uk specifies the directions and relative magnitudes in the kth mode for the fluctuations of each of the N sites in Cartesian coordinates specified by ΔX1, ΔX2, ΔX3, …. ΔX3N-1, ΔX3N-2, ΔX3N. Because Uk is normalized, each number in the column vector, Uik, is small. We will use 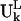 to denote the motion of the Lth substructure within the ribosome in the kth mode. Note that the vector
to denote the motion of the Lth substructure within the ribosome in the kth mode. Note that the vector 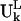 has different lengths for the different L substructures.
has different lengths for the different L substructures.
We have also performed an ANM calculation of tRNA bound to synthase (PDB code: 1GTR) (26) to illustrate the difference between the tRNA bound to synthase and tRNA bound at the three sites in the ribosome. For the synthase-tRNA we have used one site on the Cα atom per amino acid, and two sites on the P and O4* atoms per nucleotide. The cutoff distance between all sites is 19 Å in this system because the system is more uniformly represented in units of spatial volume than the ribosome has been in our computations. These robust approaches are usually quite insensitive to such details.
Contributions of each mode to the possible fluctuations observed in experiments
Let ΔX denote the column vector of an actual fluctuation of the protein. The probability of finding this fluctuation according to the harmonic approximation is given by
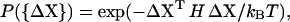 |
(1) |
where H is the Hessian matrix, kB is the Boltzmann constant, and T is the temperature. The Hessian matrix can be diagonalized by H = U−1ΛU, where the kth column of U is the eigenvector Uk and Λ is a diagonal matrix of eigenvalues λk. If ΔX is expanded in the basis set Uk as
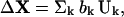 |
(2) |
then the probability of observing a fluctuation ΔX is proportional to
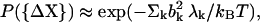 |
(3) |
where λk is the eigenvalue associated with the kth normal mode. Here the total energy associated with the fluctuation vector 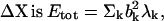 and the total magnitude of fluctuation
and the total magnitude of fluctuation 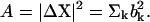 If the conformational change arises solely from the thermal fluctuations, one may apply the equipartition rule, i.e., every site will have a thermal kinetic energy of (3/2)kBT. This would allow one to set the Etot = (3/2)N kBT. To achieve a large conformational change, but within the constraint of the total cost of Etot, an economical way is to have larger contribution from the modes having lower frequencies. In the absence of any knowledge of ΔX, a reasonable assumption is to set
If the conformational change arises solely from the thermal fluctuations, one may apply the equipartition rule, i.e., every site will have a thermal kinetic energy of (3/2)kBT. This would allow one to set the Etot = (3/2)N kBT. To achieve a large conformational change, but within the constraint of the total cost of Etot, an economical way is to have larger contribution from the modes having lower frequencies. In the absence of any knowledge of ΔX, a reasonable assumption is to set 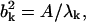 the contribution of each mode is inversely proportional to its eigenvalue. With this assumption, one may compute the B factor of each residue as (3,4,19):
the contribution of each mode is inversely proportional to its eigenvalue. With this assumption, one may compute the B factor of each residue as (3,4,19):
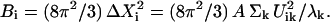 |
(4) |
Here we give the B factor along the three Cartesian coordinates separately. The experimentally reported B factor is the sum over contributions along the three Cartesian directions for each residue. A can be determined by normalizing the computed B factor against the experimentally determined B factor. It has been shown that simple elastic network models such as GNM or ANM can reproduce the experimental reported B factors remarkably well (8), usually better than atomic molecular dynamics, despite the approximations that lead to Eq. 4.
Correlation of substructure motions bound in the complex with motions of unbound substructures
To correlate the motions of substructures in the ribosome with the motions of the free unbound substructures, we determine the normal modes of the free unbound substructure (for example, tRNA). We will specify the normal modes of the unbound substructure as Vh, h = 1,2, … 3M, where M is the total number of sites of the substructure. The first six modes will be the translational and rotational modes of the substructure, which all have zero eigenvalues. However, the numerical vectors determined from diagonalization of the Hessian matrix are not always pure translation or pure rotational, but can be linear combinations of these six modes. We replace these first six modes with a translational eigenvector, Tx, Ty, Tz, and a rotational eigenvector Rx, Ry, Rz of the substructure (27,28). These six eigenvectors along with the 3M-6 normal modes of Vh form a complete basis for the 3M dimensional space. The motion of the substructure in any bound state can then be projected onto this 3M dimensional space. Therefore, we have the following expansion:
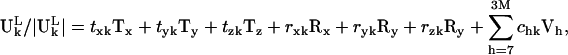 |
(5) |
where 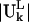 denotes the magnitude of the vector
denotes the magnitude of the vector 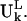 The sum of the squares of the coefficients on the right-hand side of Eq. 5 equals one. Each coefficient squared,
The sum of the squares of the coefficients on the right-hand side of Eq. 5 equals one. Each coefficient squared, 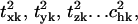 represents the fractional contribution of that independent mode to the motion of the Lth substructure in the kth mode of the ribosome. We define the fractional contribution of translational motion,
represents the fractional contribution of that independent mode to the motion of the Lth substructure in the kth mode of the ribosome. We define the fractional contribution of translational motion, 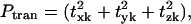 the fractional contribution of the rotational motion,
the fractional contribution of the rotational motion, 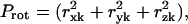 and the sum of the two will be called the fractional contribution of all the rigid body motions, Prigid = Ptran + Prot. Weighted averages of Ptran, Prot, Prigid, over the modes of the complex with the eigenvalue λk used as the weight are also obtained. The coefficients
and the sum of the two will be called the fractional contribution of all the rigid body motions, Prigid = Ptran + Prot. Weighted averages of Ptran, Prot, Prigid, over the modes of the complex with the eigenvalue λk used as the weight are also obtained. The coefficients 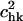 are also called overlap coefficients in the literature (13), which represent the degree of overlap of the motion of the substructure in its kth normal mode within the complex with the hth normal mode of the independent substructure. Moreover, the coefficients txk, tyk, tzk specify the direction of the translational vector of the subunit, and rxk, ryk, rzk specify the rotational axis that passes through the center of the substructure (see Appendix). These expansion coefficients completely specify the direction and the extent of rigid body motion of the subunits in the complex. On the other hand, the term
are also called overlap coefficients in the literature (13), which represent the degree of overlap of the motion of the substructure in its kth normal mode within the complex with the hth normal mode of the independent substructure. Moreover, the coefficients txk, tyk, tzk specify the direction of the translational vector of the subunit, and rxk, ryk, rzk specify the rotational axis that passes through the center of the substructure (see Appendix). These expansion coefficients completely specify the direction and the extent of rigid body motion of the subunits in the complex. On the other hand, the term 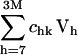 specifies the nonrigid body motion of the substructure within the complex during the functional motions. Hence, the expansion in Eq. 5 permits us to examine both the contributions of the rigid body and nonrigid body motions of the substructure as manifested during the functional motions within the complex. In this study, we have applied such analyses to study the motions of tRNA bound to the synthase and to the ribosome.
specifies the nonrigid body motion of the substructure within the complex during the functional motions. Hence, the expansion in Eq. 5 permits us to examine both the contributions of the rigid body and nonrigid body motions of the substructure as manifested during the functional motions within the complex. In this study, we have applied such analyses to study the motions of tRNA bound to the synthase and to the ribosome.
RESULTS AND DISCUSSIONS
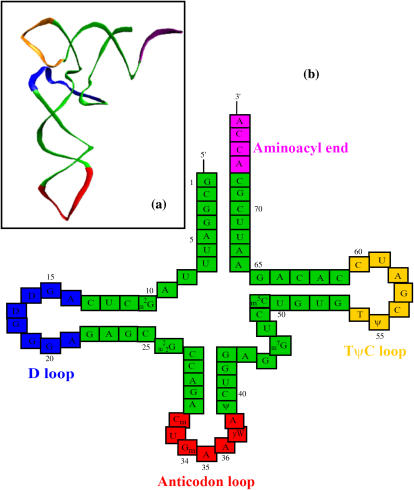
The transfer RNAs in general have sizes ranging from 73 to 93 nucleotides in length, all with the characteristic cloverleaf secondary structure and L-shaped three-dimensional structures, as illustrated in Fig. 1. The secondary structure consists of four stems and four loops (D loop, anticodon loop, and TψC loop plus an additional variable loop at positions 40–50). Of particular interest is the anticodon-stem-loop ((ASL) nucleotides from 27 to 43). Experiments have shown that ASLs with as few as four basepairs in the stem are stable and can bind to the ribosomal A and P sites as does the full length of the tRNA, and it can translocate from the A site to the P site catalyzed by the elongation factor EF-G (29,30). Studies have strongly suggested the tRNAs are related to each other through common simple structural rules rather than sequence-specific characteristics (31). Such simple structural rules could arise from the dynamic motions required during translation.
FIGURE 1.
The tertiary structure (a) and the secondary structure (b) of yeast tRNAphe with the D loop shown in blue, the anticodon loop in red, the TψC loop in yellow, and the aminoacyl end (CCA) in purple.
Calculated B factors
tRNA-synthase complex
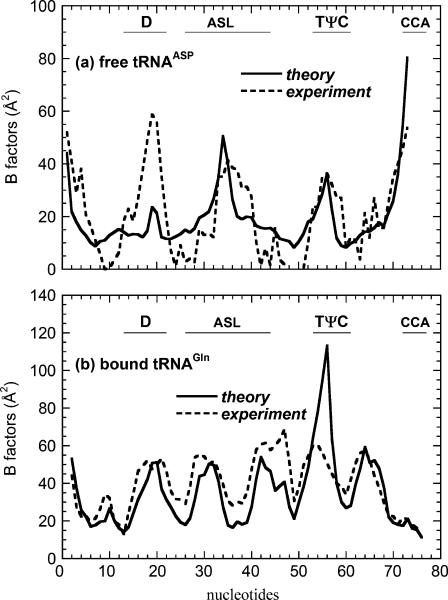
In Fig. 2 we compare the computed B-factors with the experimental B-factors of the unbound tRNA (yeast tRNAAsp, (32)), and tRNA (yeast tRNAGln) bound to the synthase (26). The figure illustrates the large changes in the mobilities of the nucleotides when it is bound to synthase. In the unbound form, the 3′ end, which is the attachment locus for the amino acid (also called CCA end), has much greater mobility, as does the anticodon of the tRNA (residues 34–36). When bound to synthase, the 3′ end is docked into the binding site on the synthase and the anticodon is also in direct contact with the synthase. Therefore, their mobilities are reduced significantly. The ANM model was able to capture this drastic change of mobilities upon binding, just as that reported earlier using the GNM model (5). The small discrepancy between the computed and experimental values is similar to that seen in the earlier study using the GNM model. Notably the ANM predicts a higher mobility of the first anticodon base (nucleotide 34) and the CCA end, and as a result underestimates the mobility in the D loop for the unbound form. In the bound form, ANM overestimates the mobility in the TψC loop (here ANM slightly underperforms compared to GNM in reproducing the experimental B factors). Possible origins of these discrepancies between the computed and experimental B factors were discussed in the earlier study (5) and could be due to the crystal packing effects not considered here. It is remarkable that this extremely simple model of the structures can closely reproduce the large changes in mobilities within the different parts of the structure upon binding.
FIGURE 2.
Computed and experimental B factors for the unbound tRNAphe (PDB code, 1TRA) and tRNAGln bound to Gln-synthase (PDB code, 1GTR). The significant differences in the B factors between the bound and unbound forms are closely reproduced by the calculations. The meanings of the symbols used are: D stands for the D-loop, ASL stands for the anticondon-stem-loop, TψC stands for the TψC loop, and CCA stands for the aminoacyl end. Same notations are used in Figs. 3, 9, and 10.
tRNA-ribosome complex
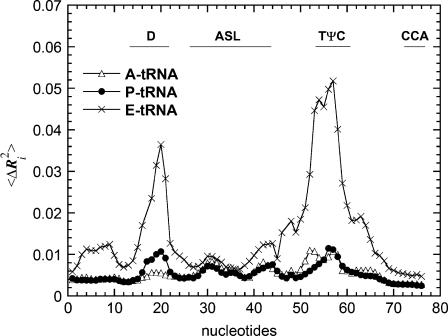
Similarly we found that when tRNA is bound to the ribosome at the three different sites, the mobility of the residues in the tRNAs are very different from one another (Fig. 3) as well as from the unbound tRNA and tRNA bound to the synthase. The E-tRNA on average has a much higher mobility than does the A-tRNA or P-tRNA. The D and TψC stem-loops on the E-tRNA have extremely large mobilities. These residues are located at the elbow of the L-shaped tRNA, as shown in Fig. 1. In the ribosome, the CCA end of the tRNA interacts with the 50S subunit, and the anticodon stem interacts with the mRNA and the 30S subunit. The elbow of the L-shaped tRNAs are mostly in contact with the 50S subunit. For the E-tRNA, the elbow is in contact with the highly mobile L1 stalk of the 50S subunit. Hence, the large mobility of these residues is directly linked to the mobility of the L1 stalk on the 50S subunit, and it appears that the L1 stalk actually pulls strongly on the E-tRNA. The A-tRNA and P-tRNA, being buried more deeply between the 30S and 50S interface, are much less mobile than the E-tRNA.
FIGURE 3.
The calculated B factors (in units of kT/γ, γ being the spring constant) for A-tRNA, P-tRNA, and E-tRNA embedded in the ribosome assemblage. The large mobilities in the E-tRNA at nucleotides ∼20, 50–60 are associated with the large mobility of the L1 stalk of the ribosome. Note data have not been normalized. They report the relative magnitudes of motion, which reflect the ribosome environment for each of the three tRNA sites. The E-tRNA is remarkably more mobile than the other two.
Contributions of rigid body motions
tRNA-synthase complex
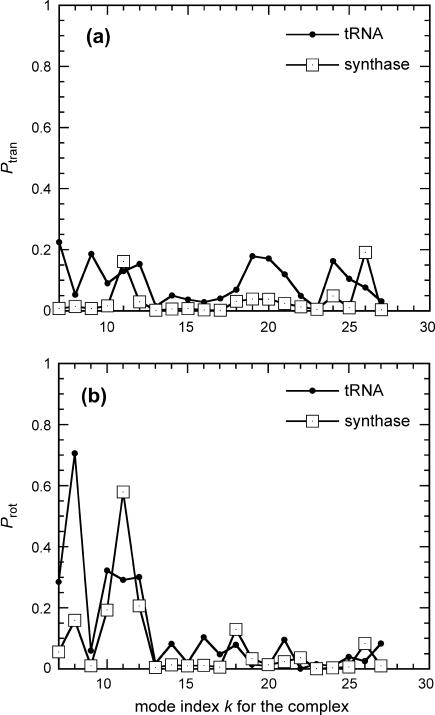
We now examine the contributions of rigid body motions of tRNA when bound to synthase. The first six modes of the bound complex are not of interest because they are simply the overall translation and rotation of the whole complex. The slow modes of the complex, starting from mode k = 7 (k = 1–6 being rigid body motions), are of interest. We project the motion of the bound tRNA in the complex onto the modes of the unbound tRNA according to Eq. 5 and similarly for the synthase. Fig. 4 presents the fraction of translation and rotational motions for the tRNA and synthase in the first 20 slow modes. The fractions of overall rigid body motions, which is the sum of translational and rotational motions, are large only in the first few slow modes, and they quickly drop to zero for the high modes (data not shown). Also tRNA has more rigid body motions, mostly rotation, in the complex than the synthase does for most of the slow modes—the relative sizes affect the relative amounts of observed rigid body motion. Most of the rigid body motions of these two subunits are rotational motions, especially in the eighth mode for tRNA and the eleventh mode for the synthase. This will contrast with the results to be shown for the case of tRNA in the ribosome. The fraction of translational, rotational, and the sum of the two averaged over 100 slowest modes for the two structural components are summarized in Table 1. The bound tRNA has an average of ∼24% rigid body motions whereas the synthase has ∼8% rigid body motions. The relative percent of the rigid body motions may be linked to the relative sizes of the components in the complex.
FIGURE 4.
Fraction of rotational (a) and translational (b) motion of bound tRNA and synthase in the first 10 slow modes of motion of the complex.
TABLE 1.
Contribution of rigid body motions of the structural components in the bound complex averaged over the 100 slowest modes
| tRNA- synthase* | Translational | Rotational | Sum |
|---|---|---|---|
| tRNA | 0.080 | 0.157 | 0.237 |
| Synthase | 0.018 | 0.069 | 0.087 |
| Ribosome | Translational | Rotational | Sum |
| 30S | 0.101 | 0.303 | 0.404 |
| 50S | 0.029 | 0.101 | 0.130 |
| A-tRNA | 0.517 | 0.207 | 0.725 |
| P-tRNA | 0.543 | 0.211 | 0.754 |
| E-tRNA | 0.519 | 0.214 | 0.733 |
| mRNA | 0.838 | 0.124 | 0.963 |
Values shown are the weighted average, 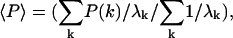 where k is the mode index, λk is the eigenvalue of the kth mode of the complex.
where k is the mode index, λk is the eigenvalue of the kth mode of the complex.
The contribution of the rigid body motions of the subunits within the complex can partially explain the observed dramatic difference in the B factors for the bound and unbound tRNA. In the unbound tRNA, the B factors contain contributions only from the internal (nonrigid body) modes, but in the bound tRNA, the B factors contain significant contributions from the rigid body motions, i.e., the rigid independent-body modes. Of course the translational modes would not affect the B factor shape because in the translational motions all residues move together in the same direction with the same magnitude. However, in the rotational motions, the amplitudes of motion for different residues depend on their relative distances from the rotational axis.
tRNA-ribosome complex
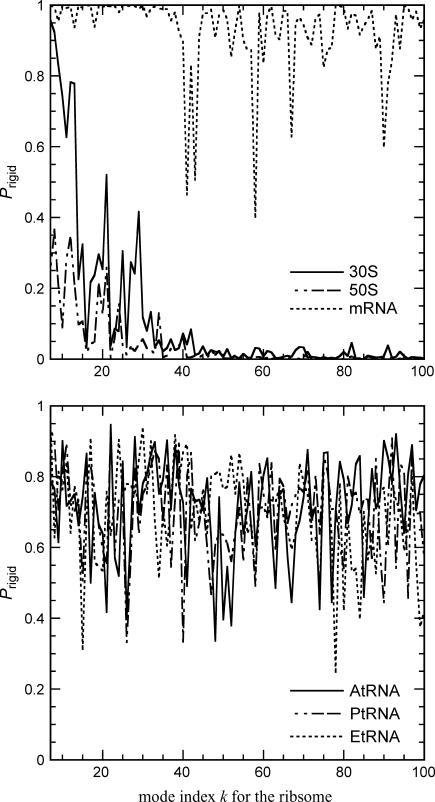
Next we turn our attention to the rigid body motions of the structural components in the ribosome. The projection method used here offers a convenient way to assess the extent of the rigid body motions of these subunits moving in the slow modes of the ribosome. Fig. 5 shows the contributions of rigid body motions of these subunits in the first 100 slow modes of the ribosome. The 30S has quite significant rigid body motions in the first few slow modes, and then these contributions diminish for higher modes. The 50S has a smaller contribution from rigid body motions in the first few slow modes compared with the 30S subunit. The mRNA has overall almost entirely rigid body motions in the slow modes, and only in higher modes such as k ∼ 40, 60, etc., do we see the mRNA exhibiting nonrigid body motions. Table 1 presents the weighted average of the fractional contributions of translation, rotation, and the sum of two for these structural components in the intact ribosome averaged over the 100 slowest modes. The weighted average of rigid body motion for the mRNA is 96%, which is mostly translational. The three tRNAs have ∼72–75% rigid body motions, of which ∼50% is translational. The 30S and 50S have small contributions from translation. Their motions, especially for the 30S, appear to be mostly rotation, which is consistent with the cryo-EM snapshots (23).
FIGURE 5.
Fraction of the rigid body motions of the structural components within the ribosome in the slow modes of motion of the ribosome. (Top) The small (30S) and large (50S) ribosome subunits and the mRNA; (bottom) the three tRNAs in their different sites.
These results show that in the slow modes of the ribosome, the tRNAs and the mRNA mostly move as rigid bodies, and this is especially true for the mRNA. This may indicate that the mRNA may be held rather rigidly in a tightly controlled environment during the translational steps of the ribosome. This is logical, because reading the code on the mRNA, ought to require tightly controlled motions of the nearly linear code to assure that it does not undergo much internal flexible motion, which could introduce reading errors. Because the mRNA is the most intrinsically flexible mobile component, it is noteworthy that it is the most controlled in its motions within the ribosome. We note that the translocation of the A site tRNA to the P site would requires a 28.5-Å translation along the interface between the two subunits. The observed dominance of the translational motions of the tRNA within the ribosome is a reflection of the fact that the tRNA must undergo a significant translational motion during the ribosomal translocation step.
Direction of translational motions of tRNAs in the ribosome complex
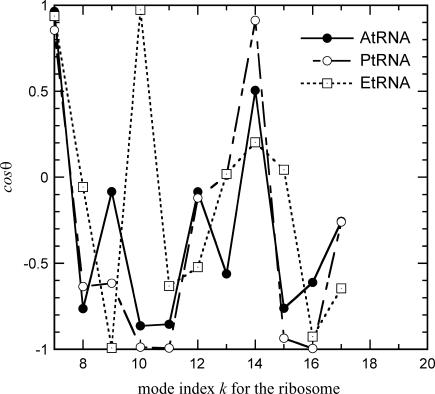
We further examine the directions of the translational motions of the tRNAs to see if they are along the directions of translocation from the A site, to the P site, and the P site to the E site. We define the vector RAP as the vector pointing from the center of mass of the A-tRNA, to the P-tRNA, and the vector RPE as the vector pointing from the center of mass of the P-tRNA, to the E-tRNA. The two vectors, RAP and RPE are almost parallel; the cosine of the angle between them is 0.84, confirming the nearly linear path for the tRNAs. For the A-tRNA, we monitor cosθ between its translation vector and RAP, for P-tRNA and E-tRNA, we monitor cosθ of their translational vectors along RPE. For the E-tRNA, we might possibly measure its motion along the direction of exit. However, because we do not have a clear geometrical pathway for exiting, we instead will monitor its motion along RPE. Fig. 6 shows the variation of cosθ for the three tRNAs thus defined in the first few slow modes of the ribosome. Either values of cosθ = +1 or −1 would imply that in a given mode the translational motion of the tRNA coincides with the direction of the translocation step from A to P, or P to E, because the nature of the normal modes means that either direction along the normal modes determined in the theoretical calculations is equally probable. Fig. 6 shows that in the first slowest mode (mode k = 7), the motions of the three tRNAs coincide almost perfectly with the direction of the translocation. In the next few slow modes, there are still good correlations between the translational motions and the directions of the translocations, but not simultaneously for all three tRNAs. The averages 〈|cosθ|〉 over the 100 slowest modes are 0.551, 0.624, and 0.521 for A-tRNA, P-tRNA, and E-tRNA, respectively, not significantly different from each other, but on average indicating that all three tRNAs move along the direction of the translocation step. It is also clear from the figure that the motions of the A-tRNA and the P-tRNA are positively correlated, and that they move generally in the same direction, but this is not true for the E-tRNA. Notice that in mode k = 9 (the third slowest internal mode), the A-tRNA is clearly not moving along the direction of the translocation step; whereas the E-tRNA is. For the E-tRNA, we notice that in mode k = 10, the E-tRNA is moving strongly in the translocation direction and the P-tRNA goes in the opposite direction. Generally the motions between the P-tRNA and the E-tRNA are not as strongly correlated as between the A-tRNA and the P-tRNA. These data give an indication that the translocation between the A-tRNA and the P-tRNA may be coupled, but not so with the E-tRNA.
FIGURE 6.
Orientations given as cosθ where the θ-values are the angles between the direction of the translational motion of the tRNA and either the vector pointing from the center of mass of the A site to the P site (RAP), or the P site to the E site (RPE). Motion of the A-tRNA is measured against the vector RAP, and motion of the P-tRNA and E-tRNA against the vector RPE. In the first slowest mode, the translational motions of the three tRNAs are in perfect alignment with the translocation direction.
Contributions of nonrigid body motions
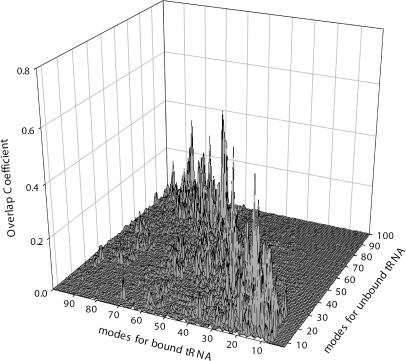
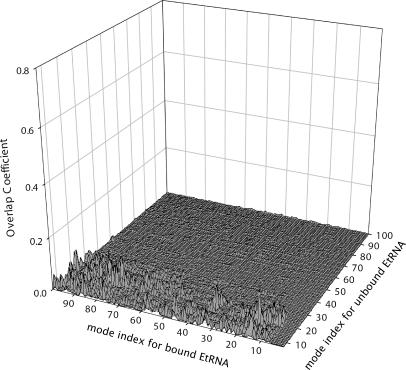
Although the contributions of the rigid body motions of the bound tRNAs in the complex are important to the functional motions of the ribosome, there are required nonrigid body motions of the tRNAs, albeit smaller in magnitude, during the translocation. We first illustrate the difference in the extent of contributions of the nonrigid body motions in the tRNA-synthase and tRNA-ribosome complexes. Fig. 7 presents a three-dimensional view of all the overlap coefficients between the modes of the bound tRNA and the modes of nonrigid motions of free tRNA. For the tRNA-synthase, there are significant contributions of the nonrigid body motions in the tRNA bound to the synthase. In general, the largest overlaps occur in the vicinity of the diagonal in the plot. This indicates that the high-frequency modes of free tRNA become increasingly important in the high-frequency modes of the bound tRNA. A completely different behavior is observed for the E-tRNA in the ribosome. Fig. 8 presents the overlap coefficients between the nonrigid modes of the free tRNAs with the modes the E-tRNA in the ribosome (similar results were obtained for A-tRNAs and P-tRNA). The nonrigid body motions constitute on average a total of only ∼30% to the motions of bound tRNAs, not a significant amount. It is also evident from the figure that only the first few slow modes of the independent tRNA contribute to any nonrigid body motions of these bound tRNAs, quite different from the tRNA bound to synthase (see Fig. 7). This indicates that the flexibilities of the individual components in the complex are severely restrained. Only a small set of the slow modes of motion of the individual components need to be considered when it is bound to the large ribosome complex. The constrained circumstances apparently conspire to filter out all of the higher frequency internal motions intrinsic to tRNA—a surprising result and one that strongly simplifies any study of the ribosomal tRNA motions.
FIGURE 7.
The three-dimensional view of the overlap coefficients, 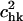 between the modes of tRNA bound to the synthase with the modes of the free unbound tRNA. There is, in general, a large overlap between the modes along the diagonal of the plot, indicating that the high-frequency modes of the free tRNA resemble the corresponding motions of the tRNA bound to the synthase.
between the modes of tRNA bound to the synthase with the modes of the free unbound tRNA. There is, in general, a large overlap between the modes along the diagonal of the plot, indicating that the high-frequency modes of the free tRNA resemble the corresponding motions of the tRNA bound to the synthase.
FIGURE 8.
Overlap coefficients, 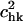 between the modes of the E-tRNA bound to the ribosome with the modes of the free unbound form of the tRNA. The z axis is set to the same range as in Fig. 7, for the purpose of illustrating the small contributions of only the first few nonrigid modes of the unbound E-tRNA to the motions of the E-tRNA bound in the ribosome.
between the modes of the E-tRNA bound to the ribosome with the modes of the free unbound form of the tRNA. The z axis is set to the same range as in Fig. 7, for the purpose of illustrating the small contributions of only the first few nonrigid modes of the unbound E-tRNA to the motions of the E-tRNA bound in the ribosome.
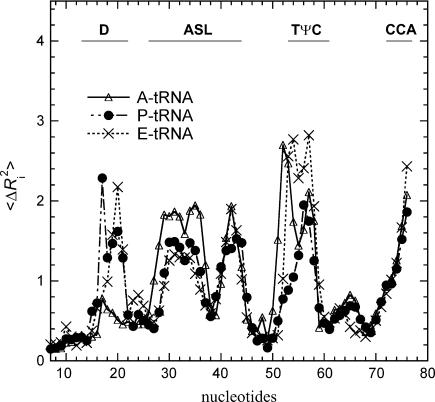
We further examine whether there are any similarities in the observed nonrigid body motions of the tRNAs at the three sites. For this purpose, we calculate the average B factors contributed only by the nonrigid body motions as shown in Fig. 9. The apparent large differences among the B factors for the three tRNAs shown in Fig. 3 are now absent, instead all three now all have remarkably similar B factor profiles. Large mobilities are seen at the D loop, ASL, TψC loop, and CCA end. It is interesting to note that the nucleotides 37–39, right after the anticodon, have low mobilities, whereas the rest of the ASL have large mobilities. This implies that the motion of the ASL is not symmetric with respect to the anticodon. The separation of the nonrigid body motions from the rigid body motions also allow us to calculate the deformation energy sustained by the structural subunit during the functional motion of the complex (14,22). The deformation energy Di at ith site on a substructure in mode k is calculated according to
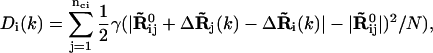 |
(6) |
where nci is the number of sites within the cutoff distance from the ith site, 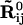 is the distance vector between the ith and jth site in the original x-ray crystal structure,
is the distance vector between the ith and jth site in the original x-ray crystal structure, 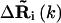 and
and 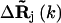 are the fluctuation vectors for the ith and jth sites in the kth mode, γ is the spring constant that is taken as one in this study, and N is the total number of sites in a substructure. Here
are the fluctuation vectors for the ith and jth sites in the kth mode, γ is the spring constant that is taken as one in this study, and N is the total number of sites in a substructure. Here 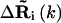 and
and 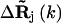 do not assume the values of the elements in the column vector
do not assume the values of the elements in the column vector 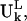 but assume the values of the elements in the expansion of the vector
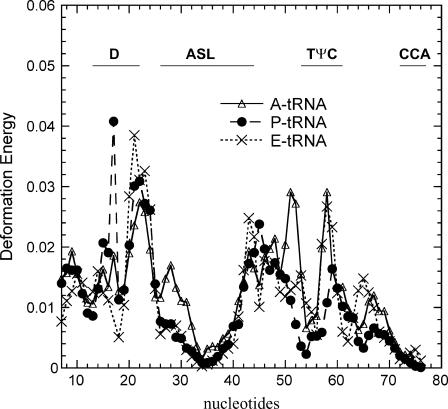
but assume the values of the elements in the expansion of the vector 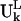 by the term, ΣhchkVh in Eq. 5. The deformation energy measures the local structural distortion from the original equilibrium structure and differs from the measure of the mobility (14,22). Fig. 10 shows that the deformation energy, which represents local structural changes, is lowest at the first anticodon position 34, and rises on both sides of the ASL. Large deformation energies are found on the D loop and the TψC loop. These two figures together show that the anticodon loop is rather mobile (supported by large mobility in Fig. 9) but internally rigid (supported by the low deformation energy in Fig. 10). The stem above the ASL, however, has to sustain large structural distortion. Earlier GNM analysis also identified nucleotides 22, 46, and 48 as forming the hinge region of the tRNA in the first global motion (5). Experiments have shown that the ASL with only four basepairs in the stem (sequence of ASL from 28 to 42) could translocate from the ribosomal A site to the P site efficiently (29). As the number of basepairs in the stem is increased beyond the D loop and TψC loop, the translocation efficiency is significantly impaired. Our results are consistent with this experimental finding. The ASL with fewer basepairs in the stem would not experience large deformation energy penalties during the translocation step, and hence could be efficiently translocated from the A site to the P site. As the stem length increases, however, the tRNA must sustain larger deformation energy at a cost that might interfere with translocation. In another computational study, the dynamics of transfer RNA was analyzed in terms of the fluctuation in the dihedral angle space of the main chain (33). It was found that the anticodon loop has large mobility but was rather rigid in the first seven slowest modes, consistent with what we have observed here.
by the term, ΣhchkVh in Eq. 5. The deformation energy measures the local structural distortion from the original equilibrium structure and differs from the measure of the mobility (14,22). Fig. 10 shows that the deformation energy, which represents local structural changes, is lowest at the first anticodon position 34, and rises on both sides of the ASL. Large deformation energies are found on the D loop and the TψC loop. These two figures together show that the anticodon loop is rather mobile (supported by large mobility in Fig. 9) but internally rigid (supported by the low deformation energy in Fig. 10). The stem above the ASL, however, has to sustain large structural distortion. Earlier GNM analysis also identified nucleotides 22, 46, and 48 as forming the hinge region of the tRNA in the first global motion (5). Experiments have shown that the ASL with only four basepairs in the stem (sequence of ASL from 28 to 42) could translocate from the ribosomal A site to the P site efficiently (29). As the number of basepairs in the stem is increased beyond the D loop and TψC loop, the translocation efficiency is significantly impaired. Our results are consistent with this experimental finding. The ASL with fewer basepairs in the stem would not experience large deformation energy penalties during the translocation step, and hence could be efficiently translocated from the A site to the P site. As the stem length increases, however, the tRNA must sustain larger deformation energy at a cost that might interfere with translocation. In another computational study, the dynamics of transfer RNA was analyzed in terms of the fluctuation in the dihedral angle space of the main chain (33). It was found that the anticodon loop has large mobility but was rather rigid in the first seven slowest modes, consistent with what we have observed here.
FIGURE 9.
The parts of the calculated B factor (in units of kT/γ) for the tRNA bound to the ribosomal A, P, and E sites contributed only by the internal nonrigid body motions. The three tRNAs show highly similar mobility patterns after elimination of the rigid body motions. The large mobilities are seen for the D loop, the anticodon loop, the variable loop, the TψC loop, and the aminoacyl end.
FIGURE 10.
The calculated deformation energies (in units of kT) for the tRNA bound to the ribosomal A, P, and E sites sustained in the internal nonrigid body motions during the 10 slowest modes of motions of the ribosome complex. High deformation energies are found at the two sites of the ASL.
CONCLUDING REMARKS
The focus of this study is to present a general method with which one can study the motions of the subunits in a large biological assembly during its functional motions. By means of an expansion, we show that we can readily separate the rigid body motions and nonrigid body motions of the subunits sustained during the functional motions of the assembly. We have shown through an analysis of the motions of the tRNA structural subunits in the complex with synthase and with the ribosome that both allowed rigid and nonrigid body motions are important for the functional joint motions of the assembly. In the intact ribosome, it was revealed that the 30S and the 50S subunits undergo largely counterrotational motion, a motion that has been observed in cryo-EM experiments. At the same time, the tRNAs are found to undergo largely translational motions along the direction of the translocation. The mRNA is found to be held almost completely rigid in these slow modes and undergoes mostly rigid translation. These are strong indications that the allowed rigid body motions of the subunits are controlled within the assemblage.
The allowed nonrigid body motions of the tRNA are also found to be strongly dependent on the assembly structure. In the ribosome, only the low-frequency motions of the tRNAs are observed, whereas in the synthase, there is a general correlation between most modes of the complex and most modes of the free unbound tRNA. The allowed nonrigid body motions of the tRNAs at the three sites are found to be similar. In particular, we found that the anticodon-stem-loop moves like a rigid unit during translocation, a phenomenon that can be linked with the experimental observation that the ASL with a short stem can translocate from the ribosomal A site to the P site efficiently.
From this study, we propose that the rigid body motions of the structural components in a biological complex relate closely to the functional motions and make the following interesting suggestions. First, the functional motions of large biological complexes are not so critically dependent on the detailed atomic level interactions between the subunits, a point of view advocated in the use of the elastic network models (1,10,34). The rigid body motion of the structural units certainly does not depend on the detailed atomic interactions within the unit and perhaps not so strongly on the interactions between the units either. Second, the rigid body motions can depend on the shape and mass distribution within the complex of its structural components. The mass distribution determines the rotational axis of an object. The ribosome has many proteins located on its periphery. The functions of these proteins are not clear. Could they be acting to balance and fine tune these rigid body motions of the tRNAs and the mRNA within the ribosome? Studies on the motions of the subunits in the presence and absence of these proteins are underway. Preliminary calculations have suggested for example that the L7/L12 stalk somehow controls the direction of motions of the tRNAs. Results related to this will be presented in the future.
On the other hand, the allowed nonrigid body motions of structural units must impose some restrictions on the flexibility of the structural units. The structure of a subunit must be sufficiently stable so that it can sustain forces imposed by the remainder of the structure during the functional motion of the assembly. Anything that interferes with the rigidity of the subunits or their essential motions could interfere with the proper functioning of the assembly, unless these essential motions conform to the intrinsic feasible deformations of the subunits, as appears to be the case here.
Acknowledgments
The rotational axis passes through the center of mass of the subunit.
APPENDIX
Consider a substructure that contains N sites, each with mass mi, i = 1, 2…N, having Cartesian coordinates dix, diy, and diz. The total mass of the structure is M = Σimi. The rotational and translation vectors, Tx, Ty, Tz, Rx, Ry, Rz, are of length 3N. We will denote their elements as Tμi,ν, Rμi,ν where μ and ν = x, y, z.
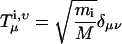 |
(A.1) |
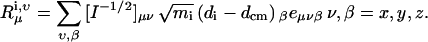 |
(A.2) |
Iμ,ν is the elements of the moment of inertia tensor I, which is a positive definite symmetric matrix, eμνβ is the permutation symbol, dcm is the Cartesian coordinate of the center of mass of the subunit. After the motion of the subunit in the complex is projected onto the modes of the free subunits according to Eq. 5, one obtains the expansion coefficients, tx, ty, tz, which specify the translational vector of the subunits in the Cartesian coordinate, t = txx + tyy + tzz. The rotational vector of the subunit, ω = ωxx + ωyy + ωzz, is related to the coefficients rx, ry, and rz through
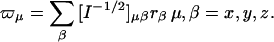 |
(A.3) |
References
- 1.Tirion, M. M. 1996. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 77:1905–1908. [DOI] [PubMed] [Google Scholar]
- 2.Atilgan, A. R., S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin, and I. Bahar. 2001. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 80:505–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bahar, I., A. R. Atilgan, and B. Erman. 1997. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 2:173–181. [DOI] [PubMed] [Google Scholar]
- 4.Bahar, I., B. Erman, T. Haliloglu, and R. L. Jernigan. 1997. Efficient characterization of collective motions and interresidue correlations in proteins by low-resolution simulations. Biochemistry. 36:13512–13523. [DOI] [PubMed] [Google Scholar]
- 5.Bahar, I., and R. L. Jernigan. 1998. Vibrational dynamics of transfer RNAs: comparison of the free and synthetase-bound forms. J. Mol. Biol. 281:871–884. [DOI] [PubMed] [Google Scholar]
- 6.Bahar, I., and R. L. Jernigan. 1999. Cooperative fluctuations and subunit communication in tryptophan synthase. Biochemistry. 38:3478–3490. [DOI] [PubMed] [Google Scholar]
- 7.Doruker, P., R. L. Jernigan, and I. Bahar. 2002. Dynamics of large proteins through hierarchical levels of coarse-grained structures. J. Comput. Chem. 23:119–127. [DOI] [PubMed] [Google Scholar]
- 8.Haliloglu, T., I. Bahar, and B. Erman. 1997. Gaussian dynamics of folded proteins. Phys. Rev. Lett. 79:3090–3093. [Google Scholar]
- 9.Keskin, O., I. Bahar, D. Flatow, D. G. Covell, and R. L. Jernigan. 2002. Molecular mechanisms of chaperonin GroEL-GroES function. Biochemistry. 41:491–501. [DOI] [PubMed] [Google Scholar]
- 10.Keskin, O., R. L. Jernigan, and I. Bahar. 2000. Proteins with similar architecture exhibit similar large-scale dynamic behavior. Biophys. J. 78:2093–2106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kundu, S., and R. L. Jernigan. 2004. Molecular mechanism of domain swapping in proteins: an analysis of slower motions. Biophys. J. 86:3846–3854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chacon, P., F. Tama, and W. Wriggers. 2003. Mega-dalton biomolecular motion captured from electron microscopy reconstructions. J. Mol. Biol. 326:485–492. [DOI] [PubMed] [Google Scholar]
- 13.Hinsen, K. 1998. Analysis of domain motions by approximate normal mode calculations. Proteins. 33:417–429. [DOI] [PubMed] [Google Scholar]
- 14.Hinsen, K., A. Thomas, and M. J. Field. 1999. Analysis of domain motions in large proteins. Proteins. 34:369–382. [PubMed] [Google Scholar]
- 15.Kundu, S., J. S. Melton, D. C. Sorensen, and G. N. J. Phillips. 2002. Dynamics of proteins in crystals: comparison of experiment with simple models. Biophys. J. 83:723–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ming, D., Y. Kong, and J. Ma. 2003. Substructure synthesis method for simulating large molecular complexes. Proc. Natl. Acad. Sci. USA. 100:104–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tama, F., and C. L. Brooks. 2002. The mechanism and pathway of pH induced swelling in cowpea chlorotic mottle virus. J. Mol. Biol. 318:733–747. [DOI] [PubMed] [Google Scholar]
- 18.Tama, F., and Y.-H. Sanejouand. 2001. Conformational change of proteins arising from normal mode calculations. Protein Eng. 14:1–6. [DOI] [PubMed] [Google Scholar]
- 19.Tama, F., M. Valle, J. Frank, and C. L. Brooks. 2003. Dynamic reorganization of the functionally active ribosome explored by normal mode analysis and cryo-electron microscopy. Proc. Natl. Acad. Sci. USA. 100:9319–9323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tama, F., W. Wriggers, and C. L. Brooks. 2002. Exploring global distortions of biological macromolecules and assemblies from low-resolution structural information and elastic network theory. J. Mol. Biol. 321:297–305. [DOI] [PubMed] [Google Scholar]
- 21.Zheng, W., and S. Doniach. 2003. A comparative study of motor-protein motions by using a simple elastic network model. Proc. Natl. Acad. Sci. USA. 100:13253–13258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang, Y., A. J. Rader, I. Bahar, and R. L. Jernigan. 2004. Global ribosome motions revealed with elastic network model. J. Struct. Biol. 147:302–314. [DOI] [PubMed] [Google Scholar]
- 23.Frank, J., and R. K. Agrawal. 2000. A ratchet-like inter-subunit reorganization of the ribosome during translocation. Nature. 406:318–322. [DOI] [PubMed] [Google Scholar]
- 24.Yusupov, M. M., G. Z. Yusupova, A. Baucom, K. Lieberman, T. N. Earnest, J. H. Cate, and H. F. Noller. 2001. Crystal structure of the ribosome at 5.5 A resolution. Science. 292:883–896. [DOI] [PubMed] [Google Scholar]
- 25.Cate, J. H., M. M. Yusupov, G. Z. Yusupova, T. N. Earnest, and H. F. Noller. 1999. X-ray crystal structures of 70S ribosome functional complexes. Science. 285:2095–2104. [DOI] [PubMed] [Google Scholar]
- 26.Rould, M. A., J. J. Perona, and T. A. Steitz. 1991. Structural basis of anticodon loop recognition by glutaminyl-tRNA synthetase. Nature. 352:213–218. [DOI] [PubMed] [Google Scholar]
- 27.Li, G., and Q. Cui. 2002. A coarse-grained normal mode approach for macromolecules: an efficient implementation and application to Ca2+-ATPase. Biophys. J. 83:2457–2474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Papousek, D., and M. R. Aliev. 1982. Molecular Vibrational-Rotational Spectra. Elsevier/North Holland, Amsterdam, The Netherlands.
- 29.Joseph, S., and H. F. Noller. 1998. EF-G-catalyzed translocation of anticodon stem-loop analogs of transfer RNA in the ribosome. EMBO J. 17:3478–3483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Phelps, S. S., O. Jerinic, and S. Joseph. 2002. Universally conserved interactions between the ribosome and the anticodon stem-loop of A site tRNA important for translocation. Mol. Cell. 10:799–807. [DOI] [PubMed] [Google Scholar]
- 31.Steinberg, S., F. Leclerc, and R. Cedergren. 1997. Structural rules and conformational compensation in the tRNA L-form. J. Mol. Biol. 266:269–282. [DOI] [PubMed] [Google Scholar]
- 32.Westhof, E., P. Dumas, and D. Moras. 1988. Restrained refinement of two crystalline forms of yeast aspartic acid and phenylalanine transfer RNA crystals. Acta Crystallogr. A. 44:112–123. [PubMed] [Google Scholar]
- 33.Matsumoto, A., M. Tomimoto, and N. Go. 1999. Dynamical structure of transfer RNA studied by normal mode analysis. Eur. Biophys. J. 28:369–379. [DOI] [PubMed] [Google Scholar]
- 34.Keskin, O., S. R. Durell, I. Bahar, R. L. Jernigan, and D. G. Covell. 2002. Relating molecular flexibility to function: a case study of tubulin. Biophys. J. 83:663–680. [DOI] [PMC free article] [PubMed] [Google Scholar]