Direct Mechanical Force Measurements during the Migration of Dictyostelium Slugs Using Flexible Substrata

Abstract

We use the flexible substrate method to study how and where mechanical forces are exerted during the migration of Dictyostelium slugs. This old and contentious issue has been left poorly understood so far. We are able to identify clearly separate friction forces in the tip and in the tail of the slug, traction forces mostly localized in the inner slug/surface contact area in the prespore region and large perpendicular forces directed in the outward direction at the outline of contact area. Surprisingly, the magnitude of friction and traction forces is decreasing with slug velocity indicating that these quantities are probably related to the dynamics of cell/substrate adhesion complexes. Contrary to what is always assumed in models and simulations, friction is not of fluid type (viscous drag) but rather close to solid friction. We suggest that the slime sheath confining laterally the cell mass of the slug experiences a tension that in turn is pulling out the elastic substrate in the direction tangential to the slug profile where sheath is anchored. In addition, we show in the appendix that the iterative method we developed is well adapted to study forces over large and continuous fields when the experimental error is sufficiently low and when the plane of recorded bead deformations is close enough to the elastomer surface, requirements fulfilled in this experimental study of Dictyostelium slugs.

INTRODUCTION

Coordinated movements of cells are the topic of a great deal of investigation because of their intrinsic interest in morphogenesis and embryonic development and because of their medical importance (1). The social amoeba Dictyostelium discoideum provides an experimentally accessible and simple model system to investigate chemotaxis and cell signaling, and to compare individual and coordinated cell movements (2). When the environment becomes depleted of nutrients, amebas stop dividing and aggregate to form a mound of cells. The mound elongates to become a finger-like structure called slug that migrates in response to light or heat. Both the aggregation of free living single amebas and the movements in multicellular aggregates including slugs are controlled by the concentration gradient of the chemoattractant cAMP produced and relayed by the cells (3–4).

Over the last decade, a large amount of information has been obtained on the distribution of cell movements along slug axis both in normal three-dimensional (3D) slugs (5–7) and in two-dimensional (2D) slugs formed at the oil water/interface (8,9). There is a characteristic pattern of movements in slugs: cells in the anterior prestalk zone show vigorous lateral movement by constantly changing their relative position, whereas cells in the central prespore zone move straight forward in the direction of slug migration in a generally periodic fashion (5–7,9). In 3D slugs, motion of prestalk cells is often helical around the central core of the tip (5,7). Siegert and Weijer (5) proposed then that the prestalk cell movement is organized by a rotating scroll wave of cAMP, which serves as pacemaker for the formation of planar cAMP waves, which in turn direct periodic forward movement of prespore cells. Periodic motions and optical waves with the same period have been observed in 3D slugs of many Dictyostelium strains (10) and in 2D slugs (9).

The distribution of mechanical forces exerted by the migrating slug was never directly measured. Hence the mechanisms by which motive force is transmitted to the substrate and their location have been subject to numerous speculations and hypotheses. According to Dormann et al. (7), anterior prestalk cells do not contribute to slug migration because the tip is often raised, only prespore cells propel the slug forward due to their close contact to the substrate. On the other hand, other studies suggested that the anterior cells exert larger forces than the posterior ones (11–13) and this is proposed to be the primary cause of the anteroposterior pattern of prestalk and prespore cells in the slug (14,15). Some models assumed that migration involves coordinated force of a special group of peripheral cells (16,17). The only indirect measurement of motive force was made by Inouye et al. (11,18,19). Assuming a viscous drag in their analysis of the experimental data, the total motive force was found proportional to slug volume suggesting that the sum of the crawling movements of the whole cells is propelling the slug forward. Many models of slug migration have since then simply postulated that the motive force is volumetric (14,15,20,21). However, the mechanisms by which interior cells can transfer forces to the substrate remain unclear. Recently, Dallon and Othmer (22) predicted that only cells in contact with the substrate can reasonably gain traction to produce a motive force for the slug. All these models take friction forces (cell/cell and cell/substrate) proportional to the relative velocity between object considered. This assumption has never been verified experimentally. The role of extracellular matrix surrounding the slug (slime sheath) made of cellulose and glycoproteins (23) was also never investigated in models.

It has been shown experimentally that the slug velocity is correlated to the slug length (14). One of the motivations of this work came from our own measurements of this relation over extended ranges of lengths, using both 2D and 3D slugs (9). To understand the origin of this relation and more generally the mechanisms of the slug migration, one must have an idea of the force distribution along slug axis which is clearly not the case presently. Therefore, we apply here for migrating slugs the flexible substrate method which was so far only used to measure mechanical forces exerted by single cells like fibroblasts or keratocytes (24). The method lies on the observation of the deformations of fluorescent beads embedded inside an elastomer substrate. Complex calculations are necessary to invert the system of coupled integral equations given by linear elasticity theory that relate the substrate deformations to the forces (25). It was demonstrated that this inverse problem is ill-posed (i.e., the solution is highly sensitive to small changes in the deformation data) for usual levels of noise and that regularization in general cannot be neglected (26). Regularization is the process of solving these problems numerically by introducing some additional information about the solution, such as an assumption on its localization, on its smoothness, or a bound on the norm.

In the Appendix of this article, we show using simulations that for slug force fields and for our range of experimental parameters (low noise level and close plane of recorded deformations), regularization is not necessary using our iterative method. Taking the advantage that slugs often have a linear steady trajectory, the deformation field is averaged in the moving slug frame. This average reduces the displacement error drastically especially for long slugs (L > 1 mm) for which the lower magnification increases bead position error. We discuss the relevance of the averaging procedure in the results section. We measure the forces exerted by migrating 3D slugs of various lengths ranging between 400 and 1100 μm. The force patterns confirm our preliminary measurements on 2D slugs (9). We find resistive forces in the slug tip and tail, traction in the central prespore area and large perpendicular forces on the sides. In addition, we find that traction and friction stresses are decreasing function of slug velocity.

MATERIALS AND METHODS

Cells and culture

Wild-type Dictyostelium discoideum NC-4 amebas were grown according to the standard protocol of two-member culture (3). For development of three-dimensional slugs, 10 μl of a suspension at 10⁷ cells/ml was dropped on polyacrylamide gel and incubated for 16 h before observations at 21°C.

Polyacrylamide gels

Flexible polyacrylamide gel sheets were prepared with 10% acrylamide, 0.03% bis, ammonium persulfate (10% w/v solution, 1:138 v/v), TEMED (1:1380 v/v; all products of Bio-Rad, Hercules, CA), and either 1-μm fluorescent beads (1:54 v/v) or 4-μm fluorescent beads (1:9 v/v; all beads are 2% solid; products of Molecular Probes, Eugene, OR). The mixture (450 μl) was poured on treated glass slides (25) and the droplet was flattened using a nontreated slide glass and 400-μm spacers. After polymerization (15–30 min), the nontreated slide glass was removed, the elastomer was covalently coated with type I collagen (Wako Chemicals, Osaka, Japan) using Sulfo-SANPAH (Pierce Chemical, Rockford, IL) (25). The Young's modulus of the elastomer was characterized using the method described in Wang et al. (27). We found values in the range 5–8.5 kPa. The Poisson ratio v of polyacrylamide gels was taken as 0.5 (25).

Detection of substrate deformations

We visualized simultaneously with a confocal microscope (Olympus IX70-KrAr-SPI, Tokyo, Japan) the ventral portion of the slug (transmission channel) and the beads (fluorescence channel, 488-nm line). We selected a field of view with the slug approaching on the side and we took the initial image as the undisturbed position to calculate the displacement vector of each bead. The focus plane Z_M was fixed just underneath the elastomer/cell surface and was carefully measured at the end of the experiments. After thresholding and binarizing images, all bead centroids and sizes (fluorescent area) were first recorded at every time using Scion-Image (http://www.scioncorp.com, Scion, Frederick, MD). The threshold was chosen to eliminate beads <2 pixels (or sometimes larger depending on experimental conditions). We then reconstructed bead trajectories using our own C codes. Briefly, for each bead, we examine all possible corresponding beads next image (typically 1 min later) with the following criteria: i), the fluorescent area change of the bead should be <75% to eliminate beads coming into contact; ii), relative bead displacement between two successive images should be less than a value determined for each experiment (typically 2 μm, i.e., less than the larger absolute bead displacements between a given time and the initial undisturbed position because it takes several minutes to reach maximal substrate deformation at a given location); iii), if several bead pairs fulfill the previous criteria, we stop at that time the bead trajectory to avoid mixing trajectories.

The efficiency of this code depends greatly on the image resolution that is fixed by the microscope objective, the bead size, the confocal scan, and photomultiplier settings. In case of the slug A displayed in Figs. 1 and 2, which is recorded with a 20× objective and a large density of 1-μm beads (>3200 beads are in the field of view), 580 beads (i.e., 18%) could be followed until t = 45 min (Fig. 1 B). However, many beads were lost in the inner slug area where large displacements induce blinking or collisions between beads. It is possible to mark manually several hundreds of beads in the slug area using the brush tool of Scion image for interesting experiments. In case of the slug B recorded with a 40× objective, the efficiency of the tracking code is very good because the bead density is lower and the focus plane is closer to the surface (Fig. 3, A and B). More than 75% of the 440 beads could be followed during the whole experiment. Bead centroids are measured with an accuracy of about δ_XY = 0.15 ∼ 0.5 μm depending on the experimental conditions. The error σ_B on the displacement vector (i.e., nearly twice) was measured experimentally from nondeflected beads far from the slug.

FIGURE 1.

(A) Bead displacement vector field created by an intermediate length slug (slug A; L = 670 μm, V = 23.2 μm/min) at t = 22 min. The background image (transmission channel) shows general slug shape and in particular the inner close contact area that is lighter. (B) Same slug at t = 45 min. Arrowheads illustrate the large perpendicular deformation remaining in the collapsed slime sheath trail; dotted lines delimitate the area used to compute the displacement field averaged in the slug frame (Fig. 2). (C) Parallel deformation profiles as a function of the parallel distance; (D) parallel and perpendicular deformation profiles as a function of the perpendicular distance at two different times and averaged over time in the slug frame. Legend is indicated in panel C. (E) Autocorrelation function Z(t) of the parallel bead displacement U_P in the central traction area (between −250 and −450 μm from the tip) as a function of time: Z(t) = C(t)/C(0), where C(t) = 〈U_P (t₀ + t) × U_P (t₀)〉.

FIGURE 2.

Optimal force field at slug A calculated at #4 (see Appendix) at (A) t = 22 min, (B) t = 28 min. Force is null outside the slug except in the trail region; the larger forces are perpendicular to the slug boundary (tip and sides), and forces mostly parallel to slug axis exist only in the central closed contact area. (C and D) Parallel and perpendicular stress profiles as a function of the parallel and perpendicular distances at two different times and averaged over time in slug frame. Legend is indicated in panel C. (E) Bead displacements averaged over time in moving slug frame using a grid spacing Δ = 20 μm. (F) Corresponding optimal calculated stress field at #6. (G) Recalculated optimal stress field at #4 when adding both lateral noise σ_XY = 0.15 μm in the lateral bead displacements and perpendicular noise σ_Z = 1.7 μm in the recorded bead depth (bootstrap method).

FIGURE 3.

(A) Central part of the bead displacement vector field created by the long slug B, (L = 1085 μm, V = 34.4 μm/min) visualized with a 40× objective at t = 30 min. (B) Enlarged bead displacement vector field of slug B in the tip area at t = 10 min. The background image (fluorescence channel) shows the optical resolution on such 1-μm beads. The slug external and contact area outlines are also delimited. (C) Bead displacements averaged over the time in the moving slug frame and (D) corresponding optimal stress field at #7 for slug B. (E) Bead displacements averaged over the time in the moving slug frame and (F) corresponding optimal stress field at #6 for the small slug C (L = 492 μm; V = 17.4 μm/min). (G and H) Parallel and perpendicular stress profiles for slug B (·) and slug C (○).

We performed a time average of the displacement field in the slug frame as follows. At every time, we adjust a grid divided in unit cells of Δ = 20 μm side whose origin is fixed at slug tip. The grid is moving and crossing the recorded field of view. The mean displacement in each cell unit corresponds then to an average displacement over the set of beads N_B belonging at a given time to the moving unit cell (typically N_B ≈ 30). This average over a large number of beads reduces greatly the error σ_XY on the average displacement vector in each unit cell as Experimentally, we measured typically σ_XY ∼ 0.15 μm far from the slug. There is also an uncertainty in the relative bead depth that affects the Green functions (see below). This error, arises from the finite depth of field of the objective (2δ_ZF) and from the eventual geometrical roughness of the elastomer surface (δ_ZG). With δ_ZF ∼ 2 μm for a 20× objective and a probably overestimated roughness of the elastomer surface (at the millimeter scale) δ_ZG ∼ 5 μm, we obtain σ_Z ∼ 1.7 μm.

Calculations of forces

In the framework of linear elasticity theory (25), the deformation field u(r) inside a semiinfinite elastic medium caused by a distribution of forces F(r) on the surface is described by a Fredholm integral equation of the first kind:

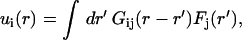(1)

where i and j refer as the components x,y,z of the vectors and G_ij are the Green functions scaling as (r − r′)⁻¹ (25,28). If one makes the reasonable assumption that there are no vertical forces, there are four Green functions Gxx, Gxy, Gyx, and Gyy. Our method is an unconstrained method (29): we calculate the forces at the sites where deformations are measured but at finite depth Z_M and we do not impose the calculated force to be zero outside the slug area. The integral equation from Eq. 1 becomes a set of linear equations, u = GF, in which u = (u_x(r₁), u_y(r₁), u_x(r₂), u_y(r₂), . . .), and F = (F_x(r₁), F_y(r₁), F_x(r₂), F_y(r₂), . . .) are 2N-vectors and G is a 4N²-matrix (typically N ∼ 2 × 10³ and the matrix has >10⁷ terms). To solve these equations, we run a numerical program based on iterative biconjugate gradient method generally used to invert large sparse matrix (30). Of course, here the matrix is dense but this method is known to give good results especially for 2D problems because, in this case, direct solution of Eq. 1 is hopeless because the matrix G is too large (30). It takes typically 5 min to invert a 10⁷-terms matrix using a personal computer with a 1.6-GHz microprocessor.

We start from a zero initial force solution at iteration zero (#0) and the solution progressively builds up with increasing iterations. At every iteration (#), we record the force field, the mean error per site on the calculated displacements Er = |u − GF| (in micrometers or nanometers) and the mean force per unit area |P_out| and |P_in| outside and inside the slug area. Experimentally, the optimal # is chosen when Er reaches the experimental error for Δ/Z_M is large (typically ≥4), or when Er is minimal within the range #1–10 for Δ/Z_M low. In the Appendix, we show using simulations that, for slug force pattern (extended force area with rather smooth variations), the minimum of ø_ext = |P_out|/|P_in| provides a good estimation of the optimal # and of the accuracy of the calculated force pattern. Indeed, the study performed on simulated force pattern (see Appendix) shows that ø_ext ∼ ΔF where ΔF = |F_real − F(#)|_slug/|F_real|_slug is the mean force deviation from the original real simulated pattern in the slug area. Typically it takes <10 iterations to reach the optimal #. At higher #, chaotic solutions may exist for large recorded bead depth (see Appendix), but they are easy to distinguish from regular solutions.

Deformation and stress profiles

When forces are calculated from time-averaged deformations in the moving slug frame, forces are divided by the lattice site area to obtain stress components. Parallel and perpendicular stress profiles are obtained by averaging stress over slug width W and a central band half-slug length, respectively. Parallel direction is the direction of the slug migration. When forces are calculated from raw data, parallel and perpendicular stress profiles in slug frame are calculated by first summing up forces over slug width W and a central band half-slug length, respectively, and then by dividing these sums by ΔxW and ΔyL/2, respectively, where Δx = 25 μm and Δy = 15 μm are the bin sizes. Error on stress profiles is determined in the Appendix using the bootstrap analysis (25,26). We have computed the parallel and perpendicular deformation components in the slug frame using the same definition. The statistical error (number of beads in each bin) and the geometrical error due to the slug angle choice are used to estimate the error on the deformation profiles. We recorded as a function of slug velocity the following characteristic features of stress profiles: the mean net traction per unit area T (often simply referred to as traction) is the average traction over the length L_T of the traction area where stress is negative, including arches when present; the tip and tail frictions per unit area f_P and f_R are also averaged over the length L_P and L_R, respectively, of the friction peaks (peaks of positive stress in the tip and tail parts).

RESULTS

Substrate deformations

Dictyostelium cells are able to aggregate on polyacrylamide substrata treated with type I collagen. The resulting slugs migrate at the same speed than on agar (9). We have recorded the deformations created by 3D slugs ranging between 400 μm and 1100 μm. These slugs induce large displacements of fluorescent beads. Fig. 1, A and B, shows the displacement fields for intermediate length slug A at two different times (see also Supplementary Material (Movie 1)). Substrate deformations present for all slugs a characteristic pattern in the slug frame. The bead displacements are oriented in the direction of migration in the tip region and opposite to this direction in the central region with a perpendicular component directed centrifugally (Fig. 1 A). In Fig. 2 E, we present the deformation field averaged over time in the slug frame using a 20-μm grid spacing. The linear portion of the trajectory between the dotted lines (see in Fig. 1 B) was used for the average. The noise level is estimated to σ_B = 0.5 μm for nonaveraged deformations (Fig. 1, A and B) and to σ_XY ∼ 0.15 μm for time-averaged deformations (Fig. 2 E). The maximal deformations are u_max ∼ 9 and 6.6 μm for nonaveraged and time-averaged deformations, respectively.

In Fig. 1, C and D, we computed the parallel and perpendicular component of these deformations. The parallel deformation presents some important fluctuations larger than the error bar, the tip friction peak is sometimes sharper (i.e., at 22 min) but the characteristic shape of the profile described by the time average is well conserved (Fig. 1 C). As a function of the perpendicular direction (Fig. 1 D), the parallel deformation is maximal in the inner area corresponding to the lighter area of the slug clearly visible in the transmission images (Fig. 1, A and B). This inner lighter area is presumably the region of close contact between cells and the substrate. For the perpendicular deformation, instantaneous and averaged profiles are all identical (Fig. 1 D). It is maximal just after the inner lighter outline. After that maximum, both the parallel and perpendicular components of the deformation field decrease continuously with perpendicular distance with no sign of break-off at slug external black outline. Far behind the slug, the beads returned slowly to their initial positions in the parallel direction but not in the perpendicular direction (see arrowheads in Fig. 1 B). The transmission image shows that the elastomer presents wrinkles in this area (see Supplementary Material (Movie 1, late times)). This surprising result indicates that the slime trail has enough mechanical stiffness to keep the substrate in a stretched state.

Typical migrating slug force pattern

The force field of the slug A is first calculated from raw data at different times when the slug is mostly entirely within the field of view (Fig. 2, A and B). The force pattern has the same characteristic properties as the force field calculated from the averaged deformation field (Fig. 2 F): large perpendicular forces, friction in the tip and in the tail, and traction in the central prespore area. It is easy to demonstrate using simulations that all these ingredients are absolutely necessary to retrieve the recorded deformation patterns (not shown). Unlike the deformation field, force (Fig. 2, A and B) or stress vectors (Fig. 2 F) are almost absent outside the slug. Fig. 2 G shows the force field recalculated after adding supplementary in-plane and vertical Gaussian noises (bootstrap method) with zero mean ± SD σ_XY ∼ 0.15 and σ_Z ∼ 1.7 μm (values discussed in the Materials and Methods section). The similarity between Fig. 2, F and G, demonstrates the robustness of the solution.

Largest forces are exerted at the outline of the lighter close contact area perpendicular to slug axis (Fig. 2 D) where the bead deformations are larger (Fig. 1 D). These perpendicular forces decrease almost to zero at the external black outline of the slug. The parallel stress profiles (Fig. 2 C) present large fluctuations with time but at every time we found two positive peaks in the anterior (tip) and very posterior region of the slug indicating resistive forces there. Although smaller than in the tip, parallel and perpendicular stresses in the posterior region extend beyond the tail of the slug in the trail left by the collapsed sheath (see arrowheads in Fig. 2 F) and are responsible for the deformations already commented in this area (Fig. 1 B). In average, the remaining parallel component in the trail is always resistive (see Fig. 2 F and also 3D).

In the central prespore zone of the slug, parallel stress is negative in average indicating dominance of traction here (Fig. 2 C). Note also the presence of two distinctive traction zones at 75 and 600 μm from the tip separated by a central zone with almost vanishing parallel forces. This traction free zone is often but not always present in other investigated slugs. It corresponds probably to the presence of a steady arch as found previously (9). The overall sum of parallel or perpendicular stresses is not significantly different from zero as expected for a slowly moving body (25). However, to satisfy exactly the force balance it would be necessary to sum up the forces along the full slug trajectory due to the remaining friction forces in the trail.

Fluctuations, correlations, and waves of forces

When we averaged deformations over time in the moving slug frame, we selected portions of their trajectory where slugs are moving straight at constant velocity with a constant shape. However, before presenting the slug velocity dependence of time-averaged forces, we must question the statistical validity of our averaging procedure.

Only two times are represented in Fig. 2, A–D, but we calculated at 12 different times the force field from raw displacement data with a slug almost entirely in the field of view. We found always a perfect correspondence between instantaneous and time-averaged perpendicular forces (Fig. 2 D). Instantaneous parallel force profiles although presenting fluctuations follow also the characteristic averaged profile described above (Fig. 2 C). In particular, we always find the two distinctive traction zones separated by a central traction free zone that is also present in the force calculated from the time-averaged displacements. When averaging the force profiles obtained at different times, central fluctuations are smoothed and we obtain almost exactly the force calculated from the time-averaged displacements. For our purpose of measuring the mean traction and friction forces (averaged over traction and friction areas, respectively) as a function of slug velocity, we can state that the time-averaged deformations and subsequent force calculations are well representative of slug behavior. They are also robust as we used different time intervals and different portions of the slug trajectory, and we never observed significant difference between the resulting force or deformation patterns.

We may now ask whether the large fluctuations present in the parallel deformations and stresses are correlated (Figs. 1 C and 2 C). Do they correspond to waves of forces? We know that optical waves and periodic motions with the same period have been observed in 3D slugs of many Dictyostelium strains (10) and in 2D slugs (9). Although a direct chemical demonstration is still required, it was proposed that these waves of motion correspond to periodic cAMP waves originating in the prestalk tip and progressing backward toward the tail (5). Whatever their exact origin, waves may just polarize the cell deformations in the migrating direction or increase the motive force of the cells or both.

Obviously, to detect waves of forces, it is necessary first that some periodicity could be detected in the deformation raw data. We performed for that purpose an autocorrelation-function calculation for the parallel component of deformation. The results indicate that a weak oscillatory component of a 6-min period may exist (Fig. 1 E). However, by identifying the amplitude of the oscillation with the calculated amplitude of the autocorrelation function of u = u_dc + u_ac cos(ω t), we found that the experimental u_ac is as small as 10% of u_dc. This estimation is comparable with the estimated error bars: in the central traction area of Fig. 1 C, mean deformation is 〈u〉 = 2.7 μm and error that originates from experimental resolution is 〈Δu〉 = 0.24 μm. Fluctuations larger than 10% from the time-averaged deformation exist in the parallel direction (Fig. 1 C) but they are not correlated temporally.

Assuming, however, that the 10% u_ac oscillation is meaningful, can we calculate the oscillatory part f_ac of the force from which it originates? For that, we used a realistic force pattern keeping the same features with the experimental pattern of Fig. 2 (same tip and tail friction; same perpendicular forces) but symmetric with respect to slug to avoid any effect from the perpendicular direction. We introduced a parallel force modulation f = f_dc + f_ac cos(2πx/λ + φ) in the central traction area, keeping the total traction force constant, equal to our experimental result from time-averaged data (see supplemental Fig. 9, Supplementary Material). We tested several ratio p = f_ac / f_dc and found that u_dc/u_ac = 10% corresponds roughly to p = 25%. This estimation is comparable to the estimated error on force ΔF from time-averaged data (case Δ/Z_M = 2; see Appendix) but lower than the one for nonaveraged data. From the series of the 12 different times we calculated forces for the slug A, we never observed any indication of correlated or propagating forces. Therefore, at that moment, there are no clues for the existence of oscillatory forces due to chemical waves. However, if they exist they are certainly smaller than the uncorrelated forces. The irregular tip lift-landing events clearly visible in the supplemental Movie 1 (see Supplementary Material) seem responsible for these uncorrelated fluctuations.

Measurements of the stress field as a function of the slug velocity

The stress fields for a long fast slug (slug B, L = 1085 μm) and a small slow slug (slug C, L = 592 μm) are displayed in Fig. 3. The deformation fields (at a given time for slug B in Fig. 3 A; averaged over time in Fig. 3, C and E) have been recorded at a similar mean bead depth (Z_M = 3 and 5 μm, respectively) with the same grid spacing Δ = 20 μm. The force profiles are qualitatively similar to those of the slug of intermediate length (Fig. 2, C and D). Friction in the tip is generally larger than in the tail. Perpendicular stresses are larger than parallel ones. But, surprisingly, both the parallel and the perpendicular forces are larger for the smaller slug (Fig. 3, G and H).

We have reported in Fig. 4 the characteristic features of the parallel stress profiles as a function of the slug velocity for nine investigated slugs. Both the absolute value of the negative traction T and frictions are decreasing functions of slug velocity (Fig. 4, A and B). The reported friction is the mean overall friction on both tip and tail defined as F = (L_P × f_P + L_R × f_R)/(L_P + L_R), where L_P and L_R are the lengths of the tip and the tail + trail friction areas. Traction is best fitted by a power law relation ∼V^−1.36 (solid line in Fig. 4 A) but, due to the large experimental error bars, an inverse velocity form ∼V⁻¹ (dotted line) that is used in the discussion to model the length dependence of the slug velocity also fits the data. Tip and tail frictions may be fitted by the power law decreasing functions ∼V^−1.31 and ∼V^−0.96 (not shown), respectively. The overall friction scales as ∼V^−1.26 (see solid line in Fig. 4 B).

FIGURE 4.

(A) Amplitude of the traction stress as a function of the slug velocity. Solid line is the power-law best fit V^−1.36, dotted line is an inverse velocity fit V⁻¹. The slugs presented in Figs. 1–3 are indicated. (B) Amplitude of overall (tip + tail) friction (see text) as a function of slug velocity. Solid line is the power-law best fit ∼V^−1.26.

The choice to plot the mean forces as a function of the slug velocity will be discussed below, but, because a monotonic relation exists between slug length and slug velocity, qualitatively same curves are obtained for the forces as a function of the slug length. As the mean traction, tip and tail frictions are averaged over the friction lengths, these quantities are little affected by the error on the bead positions. On the other hand, the force magnitude is very sensitive to the mean plane Z_M of recorded bead deformation. Error in Z_M induces directly error in the amplitude of the stress field. Indeed, for a given recorded deformation field, the deeper we estimate the beads, the higher are the calculated forces. The control of the microscope focusing plane and the calibration of the elastomer Young's modulus are the most important points to obtain reliable quantitative forces. Each contributes to ∼20 and 12%, respectively, on the relative error on mean parallel stress components: mean traction (Fig. 4 A) and tip and tail frictions. The overall friction F (Fig. 4 B) has a supplementary error due to the determination of L_P and L_R. The amplitude of perpendicular stress, calculated from the maximum of the vertical stress profile, is also decreasing function of slug velocity (not shown). But due to the difficulty of finding sharp forces when noise increases (as discussed in the second section of the Appendix), perpendicular forces suffer large errors.

We also measured the lengths of the traction area (L_T), of the tip (L_P) and of the tail + trail (L_R) friction areas (Fig. 5). L_T is clearly linearly increasing with slug length L (not with slug velocity V). L_P and L_R values are close to the slug width W (thick gray line). But the large scatter in the data for L_P, L_R, W, and the overall friction length L_F = L_P + L_R prevents conclusion about the dependence of these quantities with L (or with V).

FIGURE 5.

Lengths of the traction area (•), tip friction area (▵), tail friction area (▾), and sum of tip + tail friction area (○) as a function of the slug length. Thick gray line is the slug width. Solid lines are linear fits (see Discussion).

DISCUSSION

Role of slime sheath in the transmission of forces to the substrate

The existence of large forces perpendicular to the direction of slug migration, symmetric with respect to this axis, already observed in the case of 2D slugs (9) is confirmed by this work for all 3D slugs investigated (Fig. 3 A). Symmetric lateral movements from the slug axis toward periphery have never been reported in 3D or 2D slugs. In 2D slugs, cells presented sometimes alternatively elongated shapes but mostly in the slug migration direction (9). Therefore, the observed perpendicular forces do not result from the lateral movements of the cells; they are likely the result from the mechanical forces transmitted by the slime sheath to the substrate. New surface sheath made of cellulose and glycoproteins is continuously formed in the tip (31). It is smooth and extremely thin, only 10–50 nm as measured by electron microscopy, but acts as a protective shell for the slug. Once it makes contact with the substrate, it attaches strongly to it and is left behind as a collapsed tube (slug trail). It is known that newly formed sheath in the tip part of the slug can be deformed by anterior cells but in the posterior part cells move in is a rigid and immobile tube (32).

Our current view of sheath/substrate force transmission mechanism is described in Fig. 6. As the slug advances, sheath production and sheath/substrate anchorage in the tip create a resistive force f_P pushing the elastomer forward in the direction of slug migration and possibly also with a component in a direction normal to the hemispherical tip (Fig. 6, A and B). Although sheath is not moving, it is probably stretched and pulled forward by the moving cell mass. This forward stretching force may cause the parallel friction f_R in the tail (Fig. 6, A and B). We can postulate that the motive force of the slug is supplied by cell traction T mostly in the central prespore region in the inner lighter contact area between slug and substrate, and that this traction is essentially independent from perpendicular forces P and from the sheath. This hypothesis is consistent with the calculated forces (Figs. 2 and 3) and with the measured localization of maximum parallel and perpendicular bead deformations (Fig. 1 D). We will examine below in more details the force balance equation between parallel traction and friction forces. Before that, we are now presenting possible mechanisms responsible for the large perpendicular forces.

FIGURE 6.

Model of a migrating slug. The surface sheath covering the slug is produced in the tip; it immediately anchors to the substrate at various attachment points. In the tip, this anchorage combined with the slug migration creates a force f_P pushing the elastomer forward (A and B). In the central prespore region, a motive force T due to cell traction along slug migration direction is localized in the inner close contact area (A and B). The perpendicular force P visualized by the flexible substrata method is the in-plane component of the stretching force tangential to the slug profile exerted by the sheath at the various lateral attachment points (C). In the tail, the collapse of the sheath creates a resistive force f_R (A and B). Frozen sheath only partially realizes the perpendicular force in the trail of the slug (B and C).

We previously postulated that the observed perpendicular forces were due to a mechanism analog to the capillary force acting at the contact line of a liquid droplet placed on a solid surface (9). We assumed that due to its tension, the sheath can pull out the elastic substrate in the direction tangential to the slug profile where it is anchored in the vicinity of the contact line (Fig. 6 C). There are several possible origins of the sheath tension. One possibility is that frustrated cell movements in the lateral direction cause an internal pressure on the sheath. Another is that slug/substrate adhesion induces sheath tension in a mechanism analogous to the lipid membrane tension induced by the adhesion of vesicles to surfaces (33). As the elastic substrate assays do not visualize vertical bead displacements, we visualize only the in-plane component of the stretching forces. In case of slugs, there is evidence that the slug has a flattened cylindrical shape from the visualization of the slug ventral profile using the confocal microscope (see also the relative size of the lighter inner and dark areas of the slug in Fig. 1). If slug/substrate contact angle Θ (Fig. 6 C) is much larger than 90°, an in-plane stretching force directed outward exists. The localization of deformations and perpendicular forces in the vicinity of the outline of the inner lighter contact area (Figs. 1 D and 2 D) supports this hypothesis. Note that a broad distribution of attachment points between sheath and substrate in this area may spread the perpendicular forces. However, this mechanism does not explain the remaining perpendicular deformations and forces often observed far from the slug in the collapsed sheath trail (arrowheads in Figs. 1 B and 2 F). Here, it is possible the substrate is kept stretched by the frozen sheath (32).

Forces are decreasing with slug velocity

The most important result of this article is that traction and friction forces per unit area are decreasing with the slug length or the slug velocity.

We can draw several important consequences from these measurements. First, traction is not constant with slug length or slug velocity (Fig. 4 A) contrary to what is usually assumed in models (14,15,20–22). As a result, the total motive force TL_TW is roughly constant at −5 μN (not shown). Second, friction is not a viscous fluid friction increasing with slug velocity as always assumed in these models, but it is probably close to solid friction, stick-slip, or other mechanisms (see below). Moreover, this finding has a very important consequence on the interpretation of the experimental measurements of motive force of Inouye et al. (11,18,19). They indeed assumed a fluid-type resistive force to extrapolate the force. As we show that friction is decreasing with the slug velocity (Fig. 4 B), we believe that the measured motive force is erroneous and the conclusion that motive force is volumetric is not founded. We cannot conclude, however, from our measurements whether traction is a volume or a surface force; it will be necessary for that to measure carefully forces as a function of height for a given slug length.

A velocity dependence of cell traction forces was never directly reported to our knowledge, however, several independent observations suggest that for single cells the same relation probably holds. During ameboid migration, traction forces are generated by the actin-myosin cytoskeleton (24) and coordinated with other events: extension of protrusions at the leading edge, attachment/detachment to the substrate, translocation of the cell body (34). In slowly moving fibroblasts (V ∼ 0.5 μm/min), the force pattern has been resolved to a resolution of ∼2 μm (25). Traction at the leading edge is balanced by friction in the tail caused by the passive stretching of stationary adhesive linkages as the cell moves forward. Mean traction stress is ∼2 kPa. In fast-moving keratocytes (V ∼ 30 μm/min), significantly smaller traction forces are detected (i.e., 0.2 kPa) (35). Moreover, it was found that fibroblast cell speed and traction force depend on the rigidity of the substrate. Fibroblasts move slower but exert a significantly higher traction force on stiffer polyacrylamide substrates (36).

Dictyostelium single cells are also fastly moving but forces are more difficult to resolve due to the small cell size and the fast cell shape changes. It was recently observed by Uchida and Yumura that cell velocity is inversely proportional to the number of active cell/substrate adhesion sites referred to as actin foci (37). They suggested that actin foci constitute the active feet of Dictyostelium cells. The parallel between these observations and ours is striking. The fact that friction and traction forces are decreasing with slug velocity (Fig. 4, A and B) suggest that the dynamics of the cell/substrate adhesion sites may regulate the slug velocity. Too many sites create large traction but also large friction; as a result the cell is slowly moving like fibroblasts. On the other hand, once the cell is moving fast, the probability for an actin bundle to make an adhesion site with the surface is inversely proportional to the velocity.

In dry solid frictional sliding between a rough surface and a smooth surface, one observes often a stick-slip regime in the range of low velocities. In this regime, the friction coefficient is described by a logarithmic decreasing function of V due to a logarithmically strengthening of adhesive joints when aging at rest (stick) and their more frequent rejuvenation when slipping fast (38). At higher velocity (V > 60 μm/min), the friction coefficient increases again logarithmically. The fact that we are measuring a friction decreasing with slug velocity in the range 10 ∼ 30 μm/min suggests that cell/substrate and/or sheath/substrate friction is compatible with a stick-slip mechanism.

Both in the study of actin foci or of solid friction cited here, the velocity of the moving or sliding object is playing a central role, but not the macroscopic size of the object. Substrate/moving object interactions indeed always occur at the scale of the micrometric size asperities or adhesion sites. This justifies fully our assumption for the scaling relations derived below that forces depend on slug velocity but not on slug length.

Scaling relations of slug migration

One of the important questions related to slug migration is why the slug velocity V correlates with the slug length L (14). We have reported in Fig. 7 our measurements of 2D and 3D slug velocities on acrylamyde (9) as well as 3D results on agar (14). Several numerical models addressed this point. They found that slug speed increases with slug length L but saturates when L is larger than the wavelength of chemoattractant waves (21,39). However experimentally, slug speed still increases by a factor of 8 ∼ 10 between the wavelength, i.e., ∼250 μm (9), and the larger 3D slugs observed (Fig. 7).

FIGURE 7.

Slug speed as a function of slug length. Open and solid circles correspond, respectively, to 2D (9) and 3D slugs (this study) on elastomer. Squares correspond to the measurements of Inouye and Takeuchi (14) for 3D slugs on agar. Solid line corresponds to the predicted relation using force balance equation and experimentally fitted force lengths and amplitudes.

Simple phenomenological models are useful because they allow a quick examination and estimate of the relevant parameters describing the phenomena. We propose the following simple 1D model based on the force balance equation:

(2)

where F is the overall friction on both tip and tail. We already discussed the relation between traction and slug velocity V. We used the simple form T = −t₁/V = −1467/V (V in micrometers per minute, T in Pascal), which fits satisfactorily the experimental data (dotted line in Fig. 4 A). The overall friction relation is probably not exactly symmetric to the traction relation. Friction is not only affected by the resistance of the actin foci, but also by other sources: cell membrane/substrate (or cell membrane/sheath) friction or old adhesion complexes no more linked to the actin cytoskeleton. Actin foci are, indeed, temporary structures that disappear after 20 s on average, but adhesion complexes may persist even after actin foci disappear (37). In dry solid friction, friction decreases and then increases logarithmically with V (38). Here, we found that the simplest form that captures the saturation of the slug velocity is a decreasing function of V, which saturates at high velocities. The relation F = f₀ + f₁/V = 60 + 1036/V is therefore used (f₁ is a free parameter of the fit and f₀ was chosen to retrieve the experimental saturation of the velocity).

We postulate now that the lengths of the traction and friction area are proportional to L (not to V). Experimentally, L_T shows an almost perfect linear increase with L (Fig. 5, L_T = B_TL = 0.75L, in micrometers) not with V (not shown). L_F is probably also governed by slug geometry. Tip friction occurs where the newly produced sheath attaches to the substrate, in the contact area between the flattened hemispherical tip and substrate. Tail and trail frictions are caused by collapsed sheath resistance that should occur on a length roughly proportional to the slug lateral dimension. Experimentally, L_P, L_R, and slug width W are clearly of the same order but it is hard to find a correlation with L due to the large scatter of the data (Fig. 5). Extensive studies of slug morphology for a large population of NC-4 slugs showed that W is increasing with L (40). The fact that W is not clearly increasing with L for the selected slugs of this study is not surprising with respect to the small number of experiments analyzed and the large scatter inherent to such measurements (40). Finally, we use the following relation for the friction length L_F = A_F + B_FL = 120 + 0.25L (in micrometers) where A_F was fitted (see Fig. 5) and B_F was chosen to satisfy a sum L_T + L_F −L = 120 μm independent of L. This value represents the characteristic friction length remaining outside the slug in the trail of the slime sheath.

By injecting the experimental fits of L_F(L), L_T(L), F(V), and T(V) into Eq. 2, we obtain the length dependence of the velocity (solid line in Fig. 7). The agreement with the experimental velocity data for the full range of slug lengths is reasonably good except for very small slugs. The reason why the velocity saturates for large slugs (L > 3 mm) is mainly due to the dissymmetry at large V between slug friction that is constant (F_∞ = f₀) and traction that is decreasing to zero. The maximum velocity (V_∞ = [B_T × t₁ − B_F × f₁]/B_Ff₀ ≈ 50 μm/min) is positive because the traction force decreases faster than the friction forces when the slug size increases (i.e., B_T × t₁ > B_F × f₁). Of course, the choice of the scaling relations is not unique. In particular, logarithmic or power-law decreasing functions of the stresses may satisfy as well the force balance equation (Eq. 2). The important point to be kept in mind is that forces decreasing with slug velocity satisfy both the force balance equation and the relation between slug length and slug velocity.

In conclusion, we directly measured for the first time the distribution of mechanical forces of migrating slugs of different sizes. We found that traction forces as well as friction forces decrease with the slug velocity. In addition, we found a large force perpendicular to slug migration direction. Our measurements and scaling relations propose a new explanation of the well-known relation between slug velocity and slug length. We suggest that it will be interesting to integrate these new findings in numerical models of slug migration taking explicitly forces into account (15,20–22).

SUPPLEMENTARY MATERIAL

A supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX: AN ITERATIVE METHOD TO CALCULATE FORCES FROM ACCURATELY COLLECTED DEFORMATIONS

As described in the Materials and Methods section, we run a numerical program based on iterative biconjugate gradient method (30) to solve the coupled equations of elasticity (Eq. 1). In this Appendix, we address the details of our computational method. We show first how the iteration and the solution are chosen and we then study the influence on the solutions of the experimental parameters such as the noise on bead deformations σ_XY (simply referred to as “noise”) or the mean recorded bead depth Z_M. To find the validity range of our computational method, i.e., the range of the experimental parameters for which our method gives robust and accurate solution, we simulated two very different force patterns.

The first artificial force pattern mimics the experimental force pattern of migrating Dictyostelium slug (supplemental Fig. 9 A, Supplementary Material). In the traction area, we introduced a parallel force modulation f = f_dc + f_ac cos(2πx/λ + φ) (f_ac/f_dc = 0.5), keeping the total traction force constant and balanced by friction forces. One test of our force reconstruction will be whether these “waves of forces” can be retrieved when changing experimental parameters. We took a Young modulus of 5 kPa giving a maximal deformation u_max = 8.6 μm at Z_M = 5 μm.

The second simulated force pattern mimics forces exerted by a fish keratocyte with sharp high traction forces directed inward at the edge of the cell and low forces in the middle separated by 3 μm (supplemental Fig. 10, Supplementary Material). This second pattern allows an exploration of the applicability of our method to measure forces exerted by single cells. We also took here a Young modulus of 5 kPa giving a maximal deformation u_max = 3 μm at Z_M = 0.75 μm with the typical forces measured in Doyle et al. (35).

Starting from the simulated force pattern, we use Eq. 1 to calculate the displacement field at different Z_M. We add Gaussian noise of zero mean ± SD σ_XY to the displacement field and then we run our numerical program to reconstruct the forces. This process is often termed as a “Monte Carlo” simulation. In simulations, contrary to experiments, the force deviation ΔF is exactly known.

Choice of the optimal iteration

For all simulated force patterns and for all slug experiments, we always found two classes of behavior of the solutions as a function of the iteration number (#). These two classes depend mostly on the mean plane of recorded bead deformations Z_M.

The first class is represented in Fig. 8 A and corresponds to the case of low Z_M. Actually the important parameter is the ratio between the spatial resolution Δ (the distance between two neighboring sites of deformation) and Z_M, which should be larger than or equal to Δ/Z_M ∼ 4 (the precise estimate depends on the type of the force pattern). In that case, the displacement error Er decreases monotonically to zero; it crosses the experimental level of noise σ_XY approximately when the force deviation ΔF presents its minimum, typically between #5 and #10 depending on the level of noise. The fact that E_r is continuously decreasing toward zero with # indicates that the code is able to find a solution that accommodates any added noise. Of course, such a solution is not physical and we should not exceed the iteration at which E_r = σ_XY. E_r = σ_XY defines then the criterion to choose the optimal # in experiments when Δ/Z_M is large. Here, it gives the #8, which is slightly different than #6 where ΔF is minimal. However, solutions at iterations 5–8 are really difficult to distinguish from each other (supplemental Fig. 11, A and B, Supplementary Material).

FIGURE 8.

(A and B) Error landscapes as a function of the iteration number at Z_M =5 μm, σ_XY =0.15 μm (A) and at Z_M =10 μm and σ_XY = 0.15 μm in log scale (B) |P_in| and |P_out| are not displayed for more clarity in panel B. Legend is displayed in panel A. Arrows indicate the minimum of ΔF (optimal iteration #). Dotted lines are the level of Gaussian noise (in nanometers) added to deformation field. (C and E) Reconstructed stress fields calculated at (C) Z_M =5 μm, σ_XY = 0.15 μm, #6 (optimal iteration); (D) Z_M = 10 μm, σ_XY = 0.15 μm, #6 (optimal iteration); (E) Z_M = 10 μm, σ_XY = 0.15 μm, #23 (chaotic solution). Slug external boundary is represented by a thick gray line. Scale is the same for all stress patterns. Bar, 200 μm.

The smaller the noise, the larger the optimal #, and the smaller ΔF is. With σ_XY = 0.15 μm (u_max/σ_XY = 60), Δ/Z_M = 4 and in the case of the slug pattern, the optimal solution at #6 (as given by the minimum of the force deviation ΔF) has a ΔF = 15%. This solution (Fig. 8 C) is very close to the original one (supplemental Fig. 9 A, Supplementary Material). It is robust when changing or increasing the noise. The stress noise outside the slug area is low and the slug boundary is sharp. At low # (i.e., #1–3), the stress pattern is still not fully reconstructed and resembles the deformation pattern in the sense that there is no sharp vanishing of the stress vectors after the slug boundary (see the stress profiles in supplemental Fig. 11, A and B, Supplementary Material). The mean stress inside |P_in| the slug area increases up to #6–7 and then remains constant. On the other hand, ΔF increases until #13–14 because directional noise on stress vector increases although |P_in| is nearly constant (Fig. 8 A). The remaining stress outside the slug area |P_out| also increases until #13–14. As a result the proportion of external stress ø_ext shows a minimum at 5 iterations, increases, and finally stabilizes at large iterations (Fig. 8 A). Although the minima are not exactly at the same #, the similarity between the curves of ø_ext and ΔF is striking and is observed for all slug-type force patterns and all Z_M. It indicates that the minimum of ø_ext provides a good estimate of the force deviation at the optimal #. Note finally that after #15 and until the last iteration we could investigate (#190 where Er = 10⁻²⁷ μm !), the code converged to a stable solution as |P_in|, |P_out| and the calculated pattern no more change.

The error landscape is very different at same noise for a larger Z_M = 10 μm (Δ/Z_M = 2; Fig. 8 B). E_r is a nonmonotonic function of the # and presents a series of minima separated by large peaks (note the log scale in Fig. 9 B). The first minimum of E_r at #6 corresponds to the lower ΔF in the range #0–30. At this optimal # given by ΔF, the reconstructed stress pattern (supplemental Fig. 8 D, Supplementary Material) is reasonably close to the original one (supplemental Fig. 9 A, Supplementary Material). The force deviation ΔF = 25.4% is larger than the one found for Z_M = 5 μm and E_r does not reach the added noise σ_XY = 0.15 μm. It is possible to find large # for which the absolute minimum of E_r is smaller. But after #12, the solutions are in fact completely erratic (Fig. 8 E). The criterion to find the optimal # in experiments when Δ/Z_M is low is therefore to take the minimum of E_r within the range 1–10 iterations. We indeed never found optimal solutions at higher iterations for a level of noise consistent with experiments. Again, here for large Z_M, ø_ext ∼ ΔF and its minimum provides good estimate of the experimental accuracy without any prior knowledge of ΔF.

To show that these results do not depend on a given type of pattern, we reconstruct now a very different keratocyte-type force pattern (supplemental Fig. 10 A, Supplementary Material). The error landscape (supplemental Fig. 10 B, Supplementary Material) is qualitatively similar than the one of the slug at similar geometrical and signal/noise ratios (Δ/Z_M = 4 and u_max/σ_XY = 60). Although less marked, a minimum ΔF = 13.4% at #11 exists, and Er decreases monotonically well below the noise level. The criterion Er = σ_XY gives #7, but ΔF is only 15.2% at this # and the reconstructed force patterns are not distinguishable within this # range #6–∞. Both |P_in| and |P_out| are indeed perfectly constant after #12. The real force vectors of smaller amplitude within the cell area can be clearly distinguished from external force noise at a lower noise σ_XY. At Δ/Z_M = 2, even for much lower noise, the sharp traction forces at the edges of the keratocyte are dramatically spread over the two or three next neighboring sites. The required range of parameters of our method for single-cell experiments seems presently difficult to fulfill experimentally, contrary to the slug case. Details and a more complete discussion will be given in a forthcoming article.

To summarize this first Appendix section, our iterative algorithm is numerically stable in a large range of parameters. For signal/noise ratio u_max/σ_XY > ∼20, and a geometrical ratio Δ/Z_M ≥ ∼2 for slugs and 4 for keratocytes, it gives always an optimal solution characterized by a minimum of the force deviation ΔF from the original simulated force in the range 10–30%. This solution is robust when adding or changing noise contrary to that we could expect for erratic and nonregularized solutions. Therefore, we confirm here what was already implicitly demonstrated that regularization is less relevant for low noise level and lower spatial resolution (26).

Accuracy of slug force measurements

We already briefly discussed that there is little quantitative difference in terms of ΔF between the optimal and the neighboring iterations. However, the parallel profile shows little difference between all # investigated in supplemental Fig. 11 A (Supplementary Material) (except #3 in the tip friction peak). A small difference on the perpendicular stress profiles between #5 and optimal #6 is on the other hand detectable and the difference is huge with #3 (supplemental Fig. 11 B, Supplementary Material). Note also that the perpendicular profile of #6 itself is slightly more spread than the real simulated pattern at the slug external boundary. This means that in the regions of the field where forces are abruptly changing, one may lose the sharpness of the real solution and this effect is enhanced when choosing a low iteration or with larger Z_M (supplemental Fig. 11 D, Supplementary Material). On the other hand, the parallel profile remains little affected by large Z_M (supplemental Fig. 11 C, Supplementary Material).

As expected, increasing the noise σ_XY on the displacement field increases the noise on the stress profiles. However, even for the larger presented value σ_XY = 0.6 μm (signal/noise ratios u_max/σ_XY = 15), the oscillations in the central traction area are clearly visible and the perpendicular stress profile did not loose its sharpness (supplemental Fig. 11, E and F, Supplementary Material). For larger Z_M, increasing σ_XY tends to worsen the effect of spreading the perpendicular component.

In the time-averaged slug experiments, we used a spatial resolution of Δ = 20 μm. For experiments at given times with a random bead configuration, the bead density also fixed a similar spatial resolution. We adjusted the Young modulus of the elastomer around 5 kPa to measure maximal bead displacements u_max = 5 ∼ 10 μm with a lateral resolution σ_XY = 0.3 ∼ 0.5 μm. Lateral resolution is generally fixed by the ratio between the large recorded field of view and the maximal number of pixels. Thus, for measurements at instantaneous times, the signal/noise ratio is u_max/σ_XY = 15 ∼ 30, a value that is close to the limit of our method. To keep a reasonable resolution while measuring long slugs including their trail, we averaged over time bead displacements in the moving slug frame. We could reduce the error on bead displacements to ∼0.15 μm, i.e., u_max/σ_XY = 60, a ratio large enough to avoid regularization and get fairly good parallel stress profile even for Δ/Z_M > 2 (supplemental Fig. 11 C, Supplementary Material). However, we always used at least Δ/Z_M ∼ 2 (slug A, Figs. 1 and 2) and often Δ/Z_M = 4 (slug B and C, Fig. 3).

Finally, even if the tip friction peak may sometimes lose its sharpness, even if force noise may exist in the traction area, as we are averaging mean friction and mean traction over the width of these area, the values given in Fig. 4 do not suffer any significant error due to the computational method. As stated in the body of the article, errors on mean stresses have essentially an experimental origin: error in the measurement of the Young modulus and of Z_M.

Miscellaneous remarks on traction force calculations

The inverse problem of calculating forces from displacements, i.e., inverting Eq. 1, is a complex computational problem because this kind of equation is generally ill-posed for a usual noise level (26). The long-range spatial extend of the Green function (it scales inversely with distance) smoothes the information. Ill-posed inverse problems can be solved by regularization methods that enforce smooth solutions and suppress erratic solutions of high frequency and possible high amplitude (25,26). One can then ask how we could avoid regularization?

The first reason is that the signal/noise ratio in our slug experiments (especially those time averaged, u_max/σ_XY = 60) is much lower than in any previous experiments at a single-cell level (24). The second reason is due to the geometrical ratio Δ/Z_M between the grid spacing Δ and the recorded plane of deformation Z_M. We show that the larger the ratio Δ/Z_M, the easier the force calculations. For slug-type force pattern, Δ/Z_M ∼ 2 allows a reasonably good quantitative measurement of the force even if at interfaces where real forces are sharply changing calculated ones may be spread a little (supplemental Fig. 11, C and D, Supplementary Material). For single-cell type force pattern, Δ/Z_M ∼ 2 induces a dramatic spreading of the point-like forces. This influence of Z_M on the calculations was never reported in other methods to our knowledge. Recently, it is has been suggested that the inverse problem becomes computationally more efficient when being solved in Fourier space and that regularization is not needed (29). However, the authors did not perform a detailed analysis of the noise level and they took Z_M = 0. Thus, the efficiency of their method may also arise from low noise or from an infinite Δ/Z_M ratio. In most single-cell traction force experiments or simulations, a value Δ/Z_M ∼ 2 was used, which justifies the need for regularization. The third reason is that the iterative method does not try to find directly a “perfect” solution. The approached solution at optimal # is generally characterized by an error ΔF ∼ 10–20% (estimate from various simulations).

Our method is an unconstrained method (29). We measure displacements in a large field around slug and we do not impose the calculated force to be zero outside the slug area. Of course, the internal force might be slightly biased by the substantial remaining outside force. On the other hand, if we constrained the solution to the slug area, we could miss the important forces remaining in the slime sheath trail of the slug. More generally the presence of small random forces outside their supposed location allows examining quickly the level of force noise. If those forces are not random, it indicates that data collection suffers some systematic bias. The latter bias may arise due to elastomer inhomogeneity or the presence of real forces outside the recorded field of view.