Morphology of the Lamellipodium and Organization of Actin Filaments at the Leading Edge of Crawling Cells

Abstract

Lamellipodium extension, incorporating actin filament dynamics and the cell membrane, is simulated in three dimensions. The actin filament network topology and the role of actin-associated proteins such as Arp2/3 are examined. We find that the orientational pattern of the filaments is in accord with the experimental data only if the spatial orientation of the Arp2/3 complex is restricted during each branching event. We hypothesize that branching occurs when Arp2/3 is bound to Wiskott-Aldrich syndrome protein (WASP), which is in turn bound to Cdc42 signaling complex; Arp2/3 binding geometry is restricted by the membrane-bound complex. Using mechanical and energetic arguments, we show that any membrane protein that is conical or trapezoidal in shape preferentially resides at the curved regions of the plasma membrane. We hypothesize that the transmembrane receptors involved in the recruitment of Cdc42/WASP complex has this property and concentrate at the leading edge. These features, combined with the mechanical properties of the cell membrane, explain why lamellipodium is a flat organelle.

INTRODUCTION

Actin polymerization produces the major propulsive force that drives eukaryotic cell motility (1–5). When animal cells such as the fish keratocyte crawl over a substratum, a leaflike extension filled with a dense and highly branched actin filament network, the lamellipodium, is observed (6–9). This network is composed of polarized filaments, which play a crucial role in the directional motion of the cell. The fast growing ends (barbed/plus ends) of the filaments are oriented toward the membrane and the slow growing ends (pointed/minus ends) are oriented toward the cell center (10). Electron microscopy (EM) suggests that, in addition to their polarization, the filaments at the leading edge are oriented in a well-defined pattern: most of the filaments make a 35° angle with respect to the local normal to the plasma membrane (11–13). The observed F-actin organization results from a delicate balance between the activity of Arp2/3 complex, which nucleates new F-actin branches from existing filaments, and that of capping proteins which stop the growth of existing filaments. In this article, we address the origin of this organization by simulating the growth of the actin filament network in three dimensions. The molecular geometry of the Arp2/3-actin branch is taken into account explicitly. We also consider the origin of the nonuniform distribution of the Arp2/3 complex at the leading edge, which is explained by physical arguments based on the energetics of proteins in curved membranes. We examine how Arp2/3 localization and its geometrical constraints lead to the observed F-actin patterns. Possible experimental verifications of our predictions are described.

Several types of external stimuli can activate cell movement (7). Presumably, transmembrane proteins such as G protein coupled receptors (GPCR) (14) in specific areas of the cell membrane recruit actin-associated proteins (AAP) and locally mediate actin polymerization and activate other signaling molecules near the membrane (15). Many AAPs have been identified (16,17). Among them, Arp2/3 complex is responsible for forming new branches from mother filaments with a 70° branching angle (18–20). Arp2/3 alone is inactive; members of the Wiskott-Aldrich syndrome protein (WASP) family are required for Arp2/3 activity (16,17,21). WASP proteins are themselves activated by the phospholipid PIP₂ and the small Rho GTPase Cdc42, which is recruited by GPCRs (22). This chain of biochemical events leads to the growth of new F-actin network in the lamellipodium. Capping proteins are also indispensable for cell motility (7,23). Because of capping, actin filaments cannot grow indefinitely, although long (>1 μm) actin filaments are sometimes observed. Other AAPs are responsible for bundling/crosslinking (24,25), regulated depolymerization of actin filaments, and sequestering of actin monomers (7). The dendritic morphology of the actin filament network within the lamellipodium is the result of these structural and signaling proteins working in concert.

Electron microscopy (EM) of fish keratocyte lamellipodia suggests that the filaments are oriented in a well-defined pattern: most of the filaments make a ±35° angle with respect to the leading-edge normal (11–13) (Fig. 1). This spatial organization of actin filaments was studied theoretically by Maly and Borisy (11). These authors argued that this pattern is the result of the interplay between Arp2/3-mediated branching and the action of capping proteins. Filaments pointing away from the leading edge are rapidly capped, and the competition between capping and branching favors the filaments in the ±35° directions. Therefore, in conjunction with 70° branches mediated by the Arp2/3 complex, evolution and selection of the filaments produce the observed pattern.

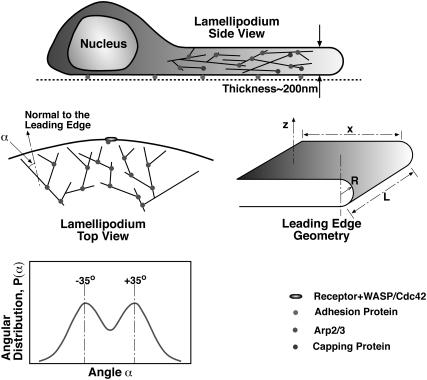
FIGURE 1.

Geometrical patterns of actin filaments at the leading edge of a crawling cell. The lamellipodium is a broad and extremely flat organelle filled with a dense actin filament network. The lamellipodium thickness is not drawn to scale with the rest of the cell. Looking from above, the actin filaments are polarized. The angle, α, is defined as the angle between the filament and the vertical normal. EM of the lamellipodium suggests that the angular probability distribution, P(α), has distinct peaks at ±35°.

Mogilner and co-workers (26,27) have considered two-dimensional mathematical models of a motile cell based on Maly and Borisy's arguments. Carlsson also performed computer simulations of actin filament network growth against a rigid object (28,29). Although the arguments presented above have considerable appeal, they do not completely explain the origin of the actin filament patterns in the lamellipodium. It was assumed a priori that branching occurs at the very leading edge (specifically on the membrane) and no backward branching was considered. (We note that Carlsson has considered the effect of backward branch initiation in the context of Listeria monocytogenes motility.) In reality, the branching process is inherently three-dimensional. Actin filaments are helical structures; new branches can potentially form in all directions. Typically, EM shows a projection of the three-dimensional filaments onto a two-dimensional surface. The thickness of the lamellipodium is ∼200 nm (16). Therefore, the network morphology should contain a substantial three-dimensional component. Unanswered questions are:

• Why do the two-dimensional projections of the filaments show this remarkably organized pattern?

• Why are the filaments predominantly pointed in the forward direction in the xy-plane and do not grow significantly in the z-direction (Fig. 1)?

• What are the roles of the cell membrane, transmembrane receptors complexed with WASP and Cdc42, Arp2/3, and capping proteins in generating the observed pattern?

In this article, a computational algorithm is developed to simulate the growth, branching, and capping of F-actin in three dimensions. The direction and orientation of each monomer in F-actin are tracked. By incorporating capping proteins, and realistic branching geometries, we produce F-actin orientational distributions comparable to the experimental data. Our results show that the details of Arp2/3 binding to F-actin play an important role in the observed organization.

Arp2/3 has to be activated by WASP/Cdc42 to nucleate new actin filaments. However, the details of the branching processes are not known. There are two main possibilities:

1. Arp2/3 complex is free to diffuse in the cytoplasm after its activation and can bind to any filaments; and

2. Arp2/3-mediated branching occurs while it is attached to the WASP/Cdc42 membrane complex and only binds to filaments directly underneath the membrane.

The most important difference between these two cases is that the orientational freedom of Arp2/3 is restricted in the latter because of its physical attachment to the membrane, whereas in the former, it is free to diffuse and orient in any direction. We vary the geometrical constraints during Arp2/3 binding to F-actin in our simulation and compare the results with experiments.

In addition to geometrical constraints during branching, we find that Arp2/3 must be concentrated at the very leading edge (tip) of the lamellipodia. We hypothesize that membrane proteins aggregate because of the preferential solvation of receptor proteins in highly curved regions of the membrane. Consequently, WASP and Arp2/3 are localized at the leading edge. We support this idea by computing the solvation energy of hypothetical membrane proteins in membranes of varying curvature. Our membrane elastic energy estimates also show that the preferred thickness of the lamellipodium is ∼100 nm, close to experimental observations.

MEMBRANE ENERGY AND AN ESTIMATE OF LAMELLIPODIUM THICKNESS

To understand the role of the cell membrane in determining lamellipodium morphology, we quantify membrane properties using a coarse-grained theory. The mechanical energy of a curved membrane, E₀, can be written in the Canham-Helfrich form (30,31)

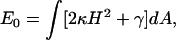(1)

where H is the mean curvature of the membrane and dA is an area element. The values κ and γ are the bending modulus and the surface tension of the membrane, respectively. Contributions due to the Gaussian curvature can be neglected for the present purpose (32). A schematic of the shape of the membrane at the leading edge of a crawling cell is depicted in Fig. 1. If the leading edge is a half-cylinder, then the curvature is a constant, and a straightforward application of Eq. 1 gives

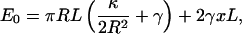(2)

where R is the radius of the half-cylinder, L is the length of the lamellipodium (Fig. 1), xL is the area of the leading edge, and πRL is the area of the half-cylinder. The values x and L are maintained by the growing F-actin network and therefore are held fixed. If we minimize the energy with respect to the radius, we obtain

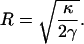(3)

Using reasonable estimates of the bending modulus and surface tension, κ = 20 k_BT and γ = 0.005 k_BT/nm² (33,34), we find R ≈ 50 nm, implying that the thickness of the lamellipodium is 100 nm. This is in agreement with experimental observations. Our estimate shows that there is a preferred lamellipodium thickness and the elasticity of the plasma membrane may partly explain lamellipodium morphology. Actual cell membranes will exhibit substantial thermal fluctuations (35). However, because the cell moves slowly, the average membrane shape will be close to the equilibrium geometry. Due to features such as focal adhesions and tethering of filaments to the membrane (36–38), the actual leading edge may not be a perfect half-cylinder, as we have assumed here. Thus, R should be considered as the average radius of the leading edge, and the elastic energy is an estimate.

Growing actin filaments within the lamellipodium also determine the lamellipodium thickness. To maintain a thickness of ≈100 nm, actin filaments should predominantly grow at the leading edge in the xy-plane. If the filaments grew significantly in the z-direction, then the thickness would not be maintained. In The Model Studied and Actin Network Morphology, we propose a mechanism where the growth patterns of actin filaments are maintained.

It is important to note that we are not suggesting that actin filaments cannot grow in the z-direction at all. If the density of z-pointing filaments is sufficiently low, then, the resistive force of the membrane will cause the single actin filament to buckle. Only bundled filaments, such as in a filopodium, can extend significantly beyond the lamellipodium F-actin network (39). The critical buckling force depends on the filament stiffness and length. If the actin filament is directly underneath and perpendicular to the membrane, a single filament cannot extend for >100 nm. This suggests that for the lamellipodium to maintain a thickness of 100–200 nm, few filaments can grow in the z-direction. The mechanisms behind this three-dimensional arrangement of the actin filaments within the lamellipodium are further discussed in The Model Studied and Actin Network Morphology.

The argument presented above does not explain how lamellipodium extension is initiated. We believe that lamellipodium initiation is related to the physical properties of membrane-bound proteins, which we describe in the next section. In the discussion, some plausible scenarios of lamellipodium initiation are presented.

LOCALIZATION OF MEMBRANE-BOUND PROTEINS

In Results, we will find that a necessary but not sufficient condition to generate the actin network pattern is that Arp2/3 must be localized at the leading edge. A possible mechanism of this localization is one where Arp2/3 is bound to a membrane signaling complex (involving WASP, Cdc42, and transmembrane receptors), and the membrane complex is localized at the leading edge due to the preferential solvation of the transmembrane receptor protein in regions of high curvature. Chemical and mechanical signals from the extracellular milieu activate the receptors, and with the subsequent recruitment of Cdc42, WASP eventually localizes Arp2/3 to the leading edge. In this section, we use statistical mechanics to quantitatively compute the membrane energy and show that localization is possible with simple assumptions and the membrane protein geometry.

The overall energy of the membrane with a solvated protein can be written as

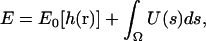(4)

where Ω is the protein-membrane boundary and s is the arc-length along the boundary, h(r) is the shape of the membrane, and r = (x, y) is a point on the membrane. The interaction energy between the protein and the membrane, represented by U(s), is strongly hydrophobic (40). The protein and membrane would like to maintain contact at their interface. As a result, the midplane of the membrane is perpendicular to the outer surface of the protein. This overall effect can be treated as a boundary condition on the membrane (41–45). Thus, the membrane shape can be obtained by minimizing E₀ with respect to h, subject to the boundary condition

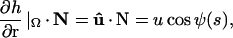(5)

where 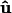is the tangent vector of the membrane along the boundary, and N is the unit orientation vector of the membrane protein. The value ψ(s) is the contact angle between the protein and the membrane on the boundary, and is related to the geometry of the protein outer surface (Fig. 2).

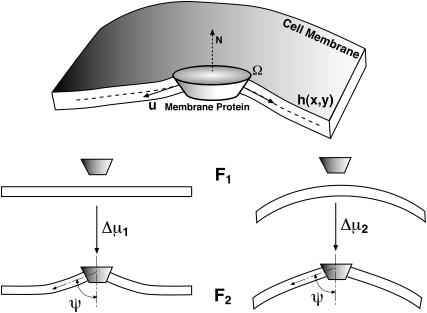
FIGURE 2.

Transmembrane proteins such as G protein-coupled receptors (GPCR) can be asymmetrical in shape. The hydrophobic contact energy between the membrane and the protein enforces a boundary condition at the protein-lipid interface. We compute the solvation energy of such a protein into a flat/curved membrane region, Δμ_1,2, which is the difference between free energies, F₂ − F₁. The symbols in the upper-panel are explained in the text.

The solvation energy, Δμ, of a membrane protein is the difference between the free energies before and after protein insertion into the membrane,

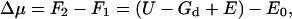(6)

where E is the membrane energy in the presence of the protein, U is the interaction free energy between the membrane and the protein, and G_d is the free energy of carving out a space in the membrane to accommodate the protein, F₂ = U − G_d + E. The value E₀ is the energy of the membrane without the protein. If the protein configuration is unchanged during solvation, then Eq. 6 is an exact expression.

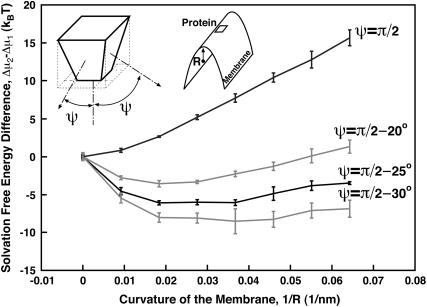
Let us consider a wedge-shaped protein, solvated in a highly curved region of the membrane (such as the cell leading edge), and compare it to the solvation of the same protein into a flat region (Fig. 2). U is not affected by the membrane curvature. However, Δμ for these two situations will be different due to the change in the local membrane geometry. It is more favorable to solvate a wedge-shaped protein into a curve region. Fig. 3 shows the solvation free energy for a membrane protein as a function of the curvature of the membrane region. The details for computing this plot are given in Appendix A. For a flat membrane region (zero curvature), the solvated protein induces a bump in the membrane and the solvation energy is positive. As the membrane becomes curved, the solvation energy becomes progressively less positive, that is, more favorable. The difference in Δμ between a curved membrane and a flat one, i.e., Δμ₂ − Δμ₁, is >5 k_BT per protein for ψ = π/2 − 25°. Since membrane proteins are generally free to diffuse throughout, we can regard their spatial distribution in the membrane to be in thermal equilibrium. Thus, the spatial distribution of receptor proteins follows the Boltzmann distribution 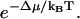The Δμ of several k_BT will completely localize the membrane protein and concentrate it in regions of high membrane curvature.

FIGURE 3.

Solvation free energy, Δμ, of membrane proteins as a function of the membrane curvature, 1/R. The protein is ≈5 nm in diameter and has a shape shown in the figure. All four interfaces with the membrane make an angle ψ with respect to N. For ψ = 70°, the most favorable curvature corresponds to a radius of 50 nm. In this case, the free energy difference between solvating in a flat region versus a curved one is ≈4 k_BT. Thus, the relative probability of seeing the protein in the flat region versus the leading edge (R = 50 nm) is low, i.e., e⁻⁴ = 0.02.

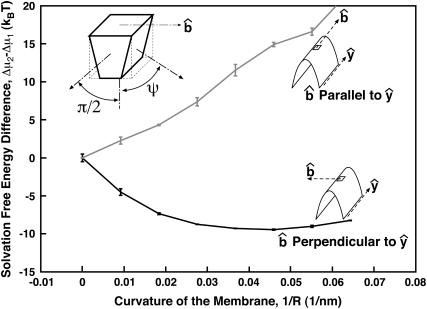
Depending on the shape of the protein, the membrane curvature can have additional organizational effects. Consider a membrane protein that is rotationally asymmetric around N (Fig. 4). Two of the four interfaces with the membrane imposes an angle of ψ = π/2 (Eq. 5). The other two interfaces have the condition ψ = π/2 − 25°. For this protein, its orientation in a flat region is equally probable in all directions. However, if the same protein is solvated in a curved region with no rotational symmetry, such as the surface of a cylinder, membrane curvature tends to align the protein along the curvature axis (Fig. 4).

FIGURE 4.

Solvation free energy of an asymmetric protein in a curved membrane. Two of the membrane interfaces impose an angle of ψ = π/2. The two other interfaces impose an angle of ψ = π/2 − 25°. We see that the membrane protein has a preferred orientation so that 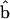is perpendicular to the y-axis. For a membrane curvature of 1/50 nm⁻¹, the protein energy difference between two orientations is >6 k_BT.

Experiments indicate that proteins can localize at membrane edges and ruffles (46–48). Similar aggregation has been observed in membrane-tether experiments involving aquaporin (49). To our knowledge, our estimate presented here is the first computation of membrane solvation free energy as a function of curvature. We note that the detailed structure of the membrane protein is unimportant; generic properties such as the protein shape and membrane elasticity determine the solvation energy. We hypothesize that the receptor protein connected to an activated Arp2/3 complex has this property, and is concentrated at the tip of the lamellipodium. We examine the consequence of this hypothesis in the next section.

THE MODEL STUDIED AND ACTIN NETWORK MORPHOLOGY

F-actin is a double-stranded helical filament where each monomer can potentially bind to Arp2/3 and nucleate new filament branches (daughter filaments). As shown in Fig. 5, the branching geometry of F-actin is not random and depends on the location and the orientation of the actin monomer where Arp2/3 binds. In Appendix B, the connection geometry between mother and daughter filaments is explained in detail. In our three-dimensional simulations, we treat actin filaments as rigid rods and account for volume exclusion. We simulate the processes of polymerization, depolymerization, branching, and capping using a continuous-time Markov algorithm (Appendix C). The leading-edge membrane protrudes with a velocity proportional to the number of contacting filaments, although we note that the velocity cannot be a linear function of the filament density if the density is very high. For filament densities encountered in our simulation, the linear relationship is reasonable. Other processes such as debranching, hydrolysis, and Pi-release are omitted since these processes are slow compared to actin growth and they should not affect network morphology. More details about the simulation and the construction of the network can be found in Appendix C.

FIGURE 5.

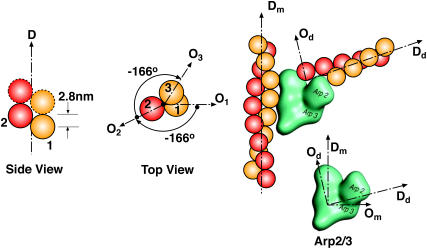
Order of the actin monomers in the helical filament structure and branching geometry. D_m, D_d are the direction vectors of mother and daughter filaments. O_m, O_d are the orientation vectors of mother and daughter monomers. All the vectors D_m, D_d and O_m, O_d lie in the same plane. O_m, O_d and D_m, D_d also define the orientation of the Arp2/3 complex at the branching point. Note that D_m⊥O_m and D_d⊥O_d and ∠(D_d, D_m) = 70°.

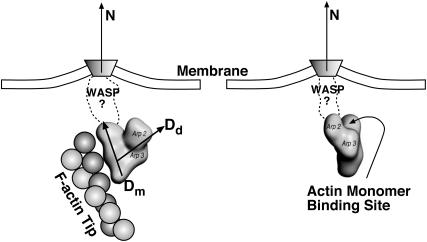
The parameters in our model simulation can be categorized into three cases. In all cases, we assume that Arp2/3 can only nucleate new filaments near the leading edge. In Case 1, we consider the situation where Arp2/3 unbinds from the membrane complex and freely diffuses after activation; nucleation of new filaments occurs in a region d nm away from the tip. Hence, all F-actin monomers in the region can initiate branches with a rate k_b (unless they already have bound Arp2/3). In Case 2 and Case 3, we assume that branching can only occur directly beneath the membrane while Arp2/3 is bound to the membrane protein complex. Hence, Arp2/3 cannot diffuse into the cytoplasm, but it is free to diffuse on the membrane at the leading edge. Due to preferential solvation of the membrane complex, Arp2/3 is also localized at the leading edge. Because of its physical attachment, Arp2/3 orientational freedom will be constrained. We describe this orientational constraint mathematically.

The spatial orientation of a rigid three-dimensional object can be specified by two linearly independent body-fixed vectors. The vectors will define three angular variables, {θ, φ, ω}. In our model, {θ, φ, ω} define the Arp2/3 orientation at the instant of branch nucleation (Fig. 6 b). {D_d, O_d} are chosen to be the body-fixed reference frame of the Arp2/3 molecule. N is the local normal vector defined by the average membrane shape. The value θ is the azimuthal angle, and φ is the amount of rotation of O_d around D_d in relation to N′, N′ = (D_d × N) × D_d. The value ω is the rotational angle of the whole complex around N, measured by the angle between the y-axis parallel to the leading edge and the projection of D_d on the tangent plane to the surface (Fig. 6 c).

FIGURE 6.

The definitions of the variables used to describe the orientation of Arp2/3 with respect to the leading edge normal, N. {θ, φ, ω} are used in our model to define the geometry of a branching event. (a) Regardless of how Arp2/3 is attached to the membrane complex, the orientation of Arp2/3 can be specified by either (D_m, O_m) or (D_d, O_d). We chose (D_d, O_d), which are defined by {θ, φ, ω} with respect to the normal vector N. (b and c) The three-dimensional definitions of {θ, φ, ω}. The curved surface in c is the leading-edge membrane. (d) In our simulation, the average shape of the leading edge remains constant and N is defined with respect to the lab-frame, {x, y, z}.

As described in Appendix B, the direction and geometry of a new branch are not random. The orientation of Arp2/3 should align with the orientation of the filament tip at the branching point (Fig. 7). Stated mathematically, each F-actin monomer also defines D′_d and O′_d vectors, which describe the orientation of a possible Arp2/3 after a binding event. Similarly, we also define {θ′, φ′, ω′}. For binding to occur between the F-actin tip and Arp2/3, primed coordinates and unprimed coordinates should match exactly: {θ′, φ′, ω′} = {θ, φ, ω}. If all the objects are rigid and not fluctuating, then the occurrence of a branching event would be unlikely. However, thermal fluctuations of the F-actin tip, membrane, and Arp2/3 complex are present. To account for these fluctuations, we introduce probability distributions P(θ), P(φ), and P(ω),

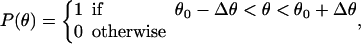(7)

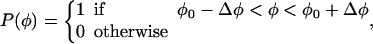(8)

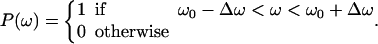(9)

FIGURE 7.

Branching can only occur if the filament and Arp2/3 orientation are compatible with each other. Structure of WASP-Cdc42 complex is not known. We describe the orientation of Arp2/3 using probability distributions P(θ), P(φ), and P(ω). The orientation of the F-actin tip, described by (θ′, φ′, ω′), must fall within the nonzero regions of the probability distribution.

The centers of these distributions, {θ₀, φ₀, ω₀}, correspond to the equilibrium geometry of the Arp2/3 complex; and deviations from these centers, {Δθ, Δφ, Δω}, account for the possible thermal fluctuations. Since the structure of the Arp2/3 complex and the exact geometry of the leading edge are unknown, these probability distributions should be considered as a gross approximation of the actual structure. The exact details of the distributions do not affect the conclusions. Thus, for branching to occur, {θ′, φ′, ω′} should be in the nonzero range of P(θ), P(φ), and P(ω).

In the simulations presented here, we compare the filament distributions for different choices of {θ₀, φ₀, ω₀} and Δθ, Δφ, and Δω. A kinetic Monte Carlo scheme has been developed to simulate the growth of the lamellipodium (Appendix C). We keep track of the direction of every actin filament and orientation of every monomer in each filament. The probability of branching at a particular monomer is determined by the branching rate, k_b; the distance of the monomer to the leading edge, d; the orientation of a possible Arp2/3 that can bind to the monomer, (θ′, φ′, ω′); and assumed distributions of Arp2/3, P(θ), P(φ), and P(ω). To simulate the orientational dependence of the branching processes, branching rate k_b is modified to k_bP(θ)P(φ)P(ω). Note that for Case 1, P(θ)P(φ)P(ω) = 1, since Arp2/3 is free to rotate in any direction. The capping probability also depends on the filament geometry: if there is sufficient space between the membrane and the tip, then capping can proceed; otherwise, capping is not allowed. The F-actin network produced by the simulation is histogrammed and analyzed.

RESULTS

Case 1: no orientational constraints for Arp2/3

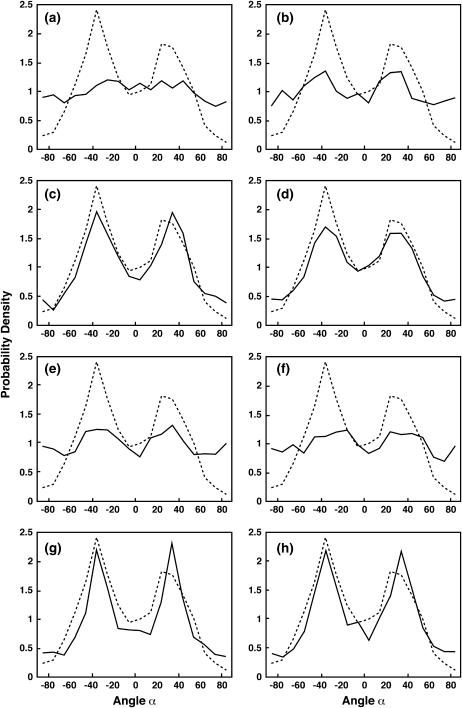
Apr2/3 can bind actin filaments without any geometrical restriction imposed on its orientation, but branching is restricted to a region d nanometers away from the leading edge. This represents the commonly assumed situation where Arp2/3 is detached from the membrane complex and diffusively binds to available actin filaments (16). The result for d = 50 nm is shown in Fig. 8 a. Dashed lines in Fig. 8 are the experimental data (11) and full lines are the distributions from our simulation. We also compute the results for d > 50 nm. For all values of d, the distributions resemble the one shown in Fig. 8 a. The simulated results are not in accord with the experimental angular distribution.

FIGURE 8.

The probability distribution, P(α), for growing actin filaments in the lamellipodium. The dashed line is the experimental data from Maly and Borisy (11), which shows the histogram of α with respect to the normal of the leading edge. The angle α is computed from the projection of the filaments in the xy plane. The distributions are normalized. The solid lines are the results from our simulations. (a) Case 1: no geometrical restriction on the values of θ and φ. Arp2/3 branching occurs with the rate k_b in a region 50-nm from the leading edge. (b) Case 1: no restriction on θ, φ, and ω, but branching occurs directly underneath the membrane, i.e., within 5 nm. (c and d) Two successful examples from Case 2. (e and f) Two failed examples from Case 2. See Table 1 for the values of θ₀, φ₀, Δθ, and Δφ. (g and h) Case 3: θ₀ = 45°, φ₀ = 45°, and ω is constrained. ω₀ = ±90° and Δω = 45°. (g) Δθ = Δφ = 45°. (h) Δθ = Δφ = 90°. We see that agreement between simulation and experiment is achieved in c–f. The detailed description of these panels are given in the text.

An extreme situation of this case is when Arp2/3 cannot diffuse far from the membrane (d = 5 nm), but its orientational freedom is completely free. Fig. 8 b shows a representative distribution from our simulation. Even though some preference exists for the ±35° directions, the tails of the distributions do not match, and the peaks are not sharp enough. Hence, we conclude that these conditions do not yield a good agreement with the experimental distribution.

The results are not unexpected. Indeed, filaments with an orientation of ∼±35° directions are favored due to their ability to rapidly follow the moving leading edge. However, if all branching events are considered, and especially backward branching, then 35° filaments will nucleate 105° filaments as well as −35° filaments. As a result, we see an accumulation of filament orientations at ±105° directions. Note that ±105° corresponds to ±75° in Fig. 8, near the tail regions of the distributions.

The relationship between the three-dimensional network and the two-dimensional projected network can be complex. On the curved surface of the leading edge, N is not always in the xy-plane. Hence, the relationship between the projected filaments and the three-dimensional network is nontrivial. We examined the situation where the leading edge is flat (and therefore N is always in the xy-plane). The projected angular distributions for this situation are similar to Fig. 8 b. A flat leading edge approximates a two-dimensional description of actin network. Thus, in two dimensions, if backward branching is included, the results would not agree with experimental patterns.

Case 2: orientational constraints for Arp2/3

Arp2/3 is bound to membrane proteins via WASP, and consequently its orientational freedom is restricted. Due to membrane attachment, d is set to 5 nm from the leading edge. (Note that 5 nm is assumed to be the approximate size of the membrane complex. The exact value of d is not critical.) In this case, we choose P(ω) = 1, which is equivalent to assuming that the membrane complex is free to rotate around N. Only θ and φ determine the branching event. We systematically change θ₀ and φ₀ by 45° increments and Δθ is chosen to be equal to Δφ (see Table 1). Δθ and Δφ are the amounts of possible deviation away from θ₀ and φ₀, or the amounts of fluctuations during the branching event. The values we have chosen are estimates. We aim to cover all possible and reasonable combinations of θ and φ, and Δθ and Δφ. The results are tabulated in Table 1: G denotes good agreement between simulated network and experimental distribution; F denotes poor agreement; and C denotes a collapsed actin network. A collapse during simulation occurs when the network fails to grow steadily, speed drops to zero, and all filaments are eventually capped. Fig. 8, c and d, show two successful agreements, and Fig. 8, e and f, show two failed ones from Table 1 (superscripts in Table 1 correspond to the panels in Fig. 8).

TABLE 1.

Summary of the results from our simulations for Case 2

	Δθ = Δφ = 45°						Δθ = Δφ = 90°
φ0\θ0	0°	45°	90°	135°	180°	φ0\θ0	0°	45°	90°	135°	180°
±0°	F	G	F	C	C	±0°	Gd	Ff	F	F	C
±45°	F	Gc	Fe	C	C	±45°	G	F	F	F	C
±90°	C	C	C	C	C	±90°	G	F	F	F	C
±135°	C	C	C	C	C	±135°	F	F	F	F	C
±180°	C	C	C	C	C	±180	C	C	C	C	C

G denotes good agreement with the experimental data, F denotes failure in agreement, and C denotes collapse, i.e., the network does not continuously extend and the system stops protruding without producing any ordered pattern. The superscripts c, d, e, and f correspond to the panels of Fig. 8.

The summarized results from Table 1 show that only certain specific intervals of θ and φ give rise to the observed organization. If the maximum possible values of θ = θ₀ + Δθ exceed 90°, we observe higher probabilities in the ±90° region of the distributions shown in Fig. 8. Hence, P(θ) must be zero for θ > 90° for the simulations to agree with experiments.

If θ₀ = 0° and Δθ = 45°, and φ₀ is changed (Table 1, left side), the results are either F or C. We found that in this column, even if P(φ) = 1, we obtain F. Thus, θ is the most critical parameter in generating the correct network pattern. If we change Δθ and allow for greater fluctuations (Table 1, right side), agreement between simulation and experiment is obtained. These results suggest that θ₀ is somewhere between 0° and 90°. The exact value of θ₀ is difficult to pinpoint from our model, since the fluctuations of the combined complex is important and we do not have a well-defined structure for the membrane complex. If we assume that Δθ = 45°, then θ₀ = 45°. The results also give information regarding P(φ). Table 1 suggests that if P(φ) does not cover the range (−45°:45°), the F-actin network fails to resemble the experimental patterns.

In summary, different probability distributions for P(θ) and P(φ) were studied using our computational model. Since P(θ) and P(φ) are directly related to the structure of the membrane complex, our simulation results suggest that the preferred configuration of the complex, θ₀ and φ₀, are in the intervals (0°:90°) and (−90°:90°), respectively.

Case 3: additional constraints on angle ω

Case 3 is similar to Case 2, but we include additional constraints on ω. We imagine a membrane protein with a shape shown in Fig. 4. Due to the shape of the leading edge and the protein complex, the energetically favorable configuration of the membrane protein is where the y-axis and the straight side of the protein are aligned. Therefore, the solvation energy imposes constraints on the probability distribution P(ω). According to the definition of ω described in the previous section and Fig. 6 c, the favorable configuration corresponds to ω₀ = ±90°. We varied the probability distribution, P(ω), as was done for Case 2. We found that P(ω) has a small effect on the network patterns. The results are similar to Case 2, except we observed relatively sharper peaks at ±35° in the filament distributions. Two representative patterns are shown in Fig. 8, g and h.

Other properties of the network morphology

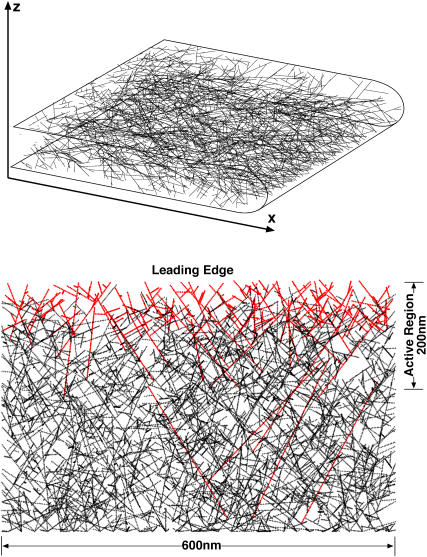
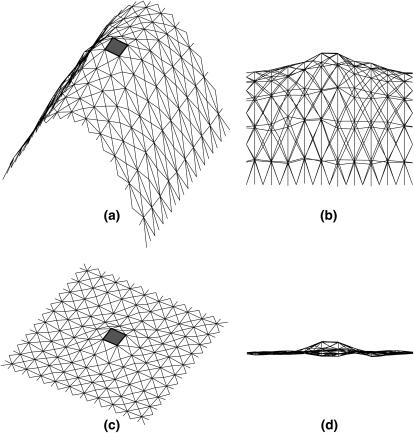
A representative actin filament network from Case 2 is shown in Fig. 9. The red filaments are uncapped whereas the black filaments have stopped growing. The actively growing (red) region spans a 200–300-nm region from the leading edge. Although the exact size of this region depends on the capping and branching rates. The filament density can be measured from our simulation: for constant x, we find, on average, 120 filaments crossing the yz-plane, which correspond to a density of 0.0013 filaments per nm² in the yz-plane for the given branching and capping rate constants.

FIGURE 9.

A representative three-dimensional actin filament network from our simulation (upper panel). The projection of three-dimensional filament in the xy-plane is shown (lower panel). Case 2 conditions are applied (see Fig. 8). The red filaments are uncapped and growing. The black filaments are no longer growing. The actively growing region is the 200–300-nm zone directly behind the leading edge. The filament diameters are not to scale.

The filament network obtained from the simulation has many features similar to those observed under EM. For instance, due to capping and branching, most of the filaments are quite short. Short filaments also do not show a great deal of angular organization. Longer filaments are invariably confined to the xy-plane. The longer filaments are also likely to point in the ±35° directions. However, there are many more short filaments and their contribution to the final probability distribution cannot be neglected.

DISCUSSION AND CONCLUSION

Experiments show that there is a distinct orientational pattern generated by the growing actin filaments in the lamellipodium of keratocytes (11–13). In this article, we presented a plausible mechanism of this pattern generation. Our important result is that the spatial location and orientation of Arp2/3 must be restricted to produce the observed network patterns. We surmise that the spatial localization is possibly due to attachment of Arp2/3 to a membrane-bound complex. If the transmembrane protein is asymmetrical in shape as shown in Figs. 3 and 4, then it is preferentially localized at the leading edge. The assumption of membrane attachment also explains why the orientation of Arp2/3 might be restricted: when bound, Arp2/3 is not free to diffuse and only a subset of orientational degrees of freedom is allowed. Thus, the hypothesis of Arp2/3 membrane attachment during the branching event seems to explain localization and orientational restriction simultaneously. Of course, other yet undiscovered proteins or mechanisms may be able to explain the observed patterns as well. Our computational model shows that it is possible to explain the observed pattern with simple assumptions.

Possible experiments

The hypothesis that active Arp2/3 is bound to the plasma membrane could be tested experimentally. Binding of Arp2/3 to WASP-activated Cdc42 can be demonstrated using the live-cell assay developed by Hahn and co-workers (50,51). In that assay, activated Cdc42 is detected in cells by injection of a biosensor, which consists of a portion of the CRIB domain of WASP conjugated to a dye (I-SO) designed to probe protein interactions. Upon activation of Cdc42 and binding of the biosensor to Cdc42, the dye becomes fluorescent. The interaction of Arp2/3 complex to activated Cdc42, which is bound to the membrane, could be tested using fluorescence resonance energy transfer (FRET) (52,53). Labeled-Arp2/3 would be the donor and activated Cdc42 would be the receptor; significant FRET above background would signify a high probability of interactions between Arp2/3 and activated Cdc42. Further co-localization of Arp2/3 and plasma membrane can be assessed via confocal microscopy by labeling the membrane with specific fluorescent dyes and fluorescently labeling Arp2/3 complex.

Experimental evidence suggests that the localization of membrane proteins can be influenced by local membrane curvature. Plasma membrane tethers generated by micropipette suction promote the aggregation of fluorescently labeled aquaporin water channels in regions of high curvature (49). Aquaporin has the proper asymmetric structure (54), which would promote its recruitment to the tethers. A similar micromanipulation assay could be used to test our hypothesis that high-curvature regions of the plasma membrane of a migrating cell, such as those present at the leading edge, can recruit signaling proteins. To probe the recruitment of activated Cdc42 and active Arp2/3 complexes to regions of high curvature, membrane tethers could be pulled from cells injected with Hahn's biosensor and aggregation could be visualized in live cells under fluorescence microscopy.

Neglected factors in the present model

Several factors are neglected in our simulation. For example, we do not consider the possibility of fluctuations at the Arp2/3 joint (55), although fluctuations of the membrane leading edge and the tips of growing filaments are included by considering the distribution P(θ, φ, ω). The distributions considered are also estimates, not based on a known structure. Resolving the Arp2/3/WASP complex will go a long way toward quantifying the model further. We also do not directly simulate how actin filaments push the membrane, and therefore our results are independent of the mechanism of force generation. Models of force generation, such as the elastic Brownian ratchet (4) or formin-capped filament growth (37,38), are equally applicable. The actin filament network pattern results from how the branching process is initiated and how the membrane receptors are organized at the leading edge.

A possible scenario of lamellipodium initiation after cell spreading

Sensitivity of receptor proteins to curvature might explain lamellipodium initiation. Before a cell is adhered to the substrate and starts to crawl, it is approximately spherical in shape with equal curvature everywhere. The membrane receptors are distributed uniformly throughout the membrane. After adhering to the substrate through focal adhesions, the spherical symmetry is broken. The regions of higher curvature are directly near the substrate (Fig. 10). Receptors will tend to accumulate in this region. The timescale of this accumulation will depend on the diffusion constant of the receptors. (GPCRs have been shown to diffuse rapidly (56–58); see next section.) Extracellular signals will activate the membrane receptors and recruitment of Cdc42, WASP, and Arp2/3 begins. These events then initiate filament growth and branching, which drive the protrusion of the leading edge. During this phase, receptors will remain in the leading edge, nucleating further growth. This process, coupled with capping, can perhaps maintain the lamellipodium during the crawling motion. Experimental test of this hypothesis will involve the identification and tracking of the signaling proteins.

FIGURE 10.

The process of lamellipodium initiation can be related to curvature sensitivity of the membrane receptors. Our scenario: Initially receptors are distributed on the surfaces of the cell body. Cell sticks to the substrate and that results in high curved regions closer to the substrate. If the receptor proteins are asymmetrical in shape as shown in Fig. 3 or Fig. 4, then they are localized at the regions close to the substrate. Signaling occurs and the recruitment of Cdc42, WASP, and Arp2/3 initiates lamellipodium protrusion. During the protrusion process, the transmembrane receptors resides in the curved region due to favorable solvation energy (Fig. 4). These combination of factors maintains lamellipodium thickness and growth.

Can transmembrane receptors aggregate?

We have computed the solvation energy of hypothetical transmembrane receptors in the presence of membrane curvature. The energetic arguments are valid if the membrane proteins are in equilibrium with respect to their membrane location. Thus, diffusion of these membrane proteins must be rapid to establish equilibrium. Diffusion constants of membrane proteins vary widely. A GPCR such as rhodopsin, which is close to 5 nm in size, has a diffusion constant of 0.4 μm²/s (59). In 1 s, such a protein can traverse a mean distance of 1.3 μm. Other GPCRs and membrane proteins have been shown to diffuse rapidly as well (56–58,60). On the other hand, if the membrane proteins are anchored to the cytoskeleton web beneath the membrane, diffusion could become very slow. However, once the receptors have accumulated at the leading edge, diffusion becomes less important. The protruding actin network can push the receptors forward along with the leading edge. Observations of fluorescently labeled receptors responsible for generating motility would answer this question.

Mechanosensitivity of membrane proteins in general

Mechanosensitivity of membrane protein is also a generic phenomenon not limited to cellular motility. Ion channels and other membrane receptors should have a similar response to membrane curvature (61,62). We presented a method to compute the solvation energy using a phenomenological model (Appendix A). Careful experiments can ultimately measure the solvation energy difference and observe this organizational effect in a wide variety of systems.

APPENDIX A: COMPUTATION OF PROTEIN SOLVATION ENERGY IN THE MEMBRANE

The plasma membrane exhibits strong thermal fluctuations at the length scales of nanometers. The mechanical equilibrium geometry corresponds to the lowest energy configuration of the membrane. However, due to thermal fluctuations, higher energy membrane configurations are sampled as well. Therefore, free energies, not elastic energies, are the driving force for change. The elastic energy of a two-dimensional isotropic membrane can be modeled using the Canham-Helfrich energy, E₀(h) (Eq. 1), where h describes the shape of the membrane and H is its mean curvature. The values κ and γ are the bending modulus and surface tension, respectively. The free energy, F, of the plasma membrane is defined as (35)

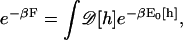(A1)

where represents the functional integral over all possible membrane configurations.

In computational implementations of membrane statistical mechanics, the membrane surface, h, is tiled by a triangular lattice of finite elements. Each triangle, indexed by i and characterized by a vector normal to the triangle, a_i, can change its size and orientation. Equation 1 can be written in a discretized form (35,63,64),

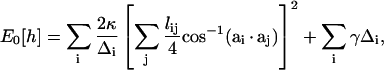(A2)

where the i-summation is over all the triangles in the membrane. For each triangle, the j-summation is over all the neighboring triangles of i; l_ij is the length of the edge shared by i and j triangles; and Δ_i is the area of the i^th triangle. The membrane geometry can be varied by changing the positions of the vertices. By moving the vertices, all possible membrane configurations can be sampled.

To compute the solvation energy of a membrane protein, we need the reversible work of inserting the protein while imposing the boundary condition of Eq. 5. The solvation energy is the free-energy difference between two systems, connected by a reversible parameter λ. For λ = 0, E(0) corresponds to the complete membrane energy without the protein, E₀. For λ = ∞, E(∞) = E₁ where E₁ is the energy of the membrane with a hole at the center and the appropriate boundary condition has been applied. Thus, if Γ represents the physical region occupied by the protein, Ω represents the triangles immediately next to Γ, and Θ_ij = cos⁻¹(a_i · a_j), we can define E(λ, ψ) as

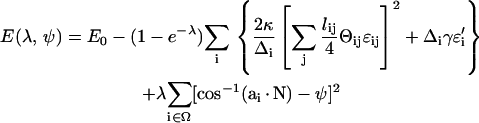(A3)

where

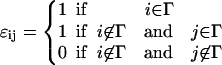(A4)

and

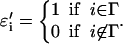(A5)

The subtracted term corresponds to carving out a hole for the membrane protein. The last term corresponds to the boundary condition of the membrane around the protein. E(λ, ψ) reversibly connects E₀ to E₁. The solvation free energy corresponds to the free-energy difference,

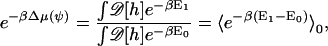(A6)

where the average is with respect to the protein-less membrane. The solvation energy can be computed using thermodynamic integration (65),

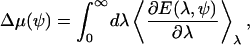(A7)

where the average is with respect to the system describes by E(λ, ψ). Metropolis Monte Carlo is used to compute the average energy in Eq. A7.

In the simulations, the edges of the triangles are ∼3-nm in length. The transmembrane protein is ∼5 nm in diameter (Fig. 11). The protein is rectangular in shape (Figs. 3 and 4). The only variation is the geometrical shape related to ψ. To investigate the dependence of the solvation energy with membrane curvature, a fixed boundary condition is imposed on the outer edges of the membrane. Thus, the edge of the membrane is held fixed, mimicking the effect of focal adhesions and other membrane attachments. During the simulation, the region immediately next to the protein is typically slightly distorted. However, the rest of the simulation region preserves the curvature. Therefore, isolated membrane proteins only perturb the membrane locally.

FIGURE 11.

Representative configurations of the membrane with a transmembrane protein at the center. The triangular finite elements are shown, along with the transmembrane protein (depicted as the shaded box). Panels a and b are different views of the same curved membrane. Panels c and d are different views of the same flat membrane. The boundary condition of Eq. 5 is applied to the triangles immediately next to the central hole.

APPENDIX B: THE GEOMETRY OF ARP2/3-MEDIATED ACTIN BRANCHING

Actin polymerizes into double-stranded helical filaments where the actin monomers in different strands are spaced 2.8-nm apart. The neighboring monomer is oriented 166° in the opposite direction (66) (Fig. 5). There is no evidence that Arp2/3 locally alters the structure of actin filament, and therefore we assume that the monomer geometries are unchanged near a branching point (67).

From Fig. 5, we see that the daughter filament's elongation direction and the orientation around its axis depends on the orientation and direction of its mother filament. Arp2/3 can be considered a junction that transforms the direction and orientation of the mother filament into the daughter filament. We represent the geometry of the filament by two orthogonal unit vectors: D is in the direction of elongation and O is the orientation of the monomer around the filament axis, or D. If the orientation of the first actin subunit is taken as the reference (O₁ in Fig. 5), orientation of all other units can be defined with the rule depicted in Fig. 5. For n^th monomer in the same filament, the position of the monomer along the filament will be 2.8(n − 1) nm; the angular difference between the orientational vectors ∠(O₁, O_n) will be −166°(n − 1) (Fig. 5).

The atomic structure of Arp2/3 complexed with actin filament is unresolved (68). It is unclear whether Arp2/3 binds to the sides or the tip of the mother filament. Two groups have compared the length of mother and daughter filaments beyond the branch point to find the correlation between the lengths. If branching happens at the tip, the ratio of the lengths of the mother/daughter filaments from the branch point should be close to 1. Pantaloni et al. (69) have reported data in agreement with this prediction, based on the measurements of the branched filaments in electron micrographs. On the other hand, using fluorescence microscopy, Pollard and co-workers directly observed that activated Arp2/3 binds to the sides of existing filaments (55,67,68). In this article, we follow the findings of Volkmann et al. (68), where it is reported that new actin filament branches are only slightly out of plane with respect to the mother filament. The branching geometry that we have implemented is shown in Fig. 5. Note that all vectors associated with direction and orientation of the mother and the daughter filaments lie in the same plane. The role of Arp2/3 can be simply stated as a mathematical transformation, a rotation, that takes (D_m, O_m) to (D_d, O_d):

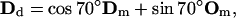(B1)

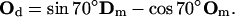(B2)

Note that D vectors are the same for the monomers of the same filament. However, O vectors depend on where the monomers are located along their filaments. In the above transformation rule, O_m is the orientation vector of the monomer where Arp2/3 binds, and O_d is the orientation vector of the first monomer of the daughter filament. Given this Arp2/3 geometry, we can now define the orientation of the vectors (D_m, O_m, D_d, O_d) with respect to the leading-edge normal.

APPENDIX C: MARKOV SIMULATION OF ACTIN FILAMENT NETWORK GROWTH

The simulations are carried out in three dimensions, starting with randomly oriented filaments. The actin monomers are treated as spheres 2.8-nm in radius. The volume exclusion effect is included, i.e., a monomer cannot grow into the space already occupied by another monomer. We simulate the growing actin network between two parallel planes, 150-nm apart (Fig. 6). The tip of the lamellipodium (shown as Leading Edge in Fig. 6), is assumed to be constant in shape (parabolic), but it moves with a speed proportional to the number of filaments in contact with it. The exact shape of the leading edge is unimportant. The proportionality constant in the protrusion velocity is adjusted to achieve an average protrusion speed of 100–180 nm/s. During the simulation, the number of filaments in contact with the leading edge fluctuates, but the average number (and therefore the protrusion speed) remain steady. We note that if the filament density is very high, the velocity is not strictly a linear function of the number of contacting filaments. This regime is not encountered in our model.

We treat the filaments as growing rigid polymer. The length of the actin rods change in 2.8-nm units with rates k₊(actin) and k₋, where k₊ is monomer addition rate, k₋ is the depolymerization rate and (actin) is the concentration of free monomers in the cytoplasm. Arp2/3 complex can nucleate filament branches with the rate k_b(actin). Filaments can also be capped with the rate k_c(cap), where (cap) is the capping protein concentration. The numerical values of these rate constants are listed in Table 2. We omit debranching, hydrolysis, and Pi-release of the polymerized units because these processes are relatively slow compared to actin growth and should not affect the network morphology.

TABLE 2.

The relevant rate constants used in our simulations

Actin concentration: (actin)	12 μM	(74)
ATP-actin addition to barbed end: k+	11.6 μM−1 s−1	(74)
ATP-actin drop from barbed end: k−	1.4 s−1	(74)
Branching: kb	3.4 μM−1 s−1	(19)
Capping: kc(cap)	1 s−1	(75)

Filament polymerization, depolymerization, branching, and capping are all treated in a continuous-time Markov algorithm. Given the current state of the system σ, we tabulate the rate constants, k_σ→σ′, for transition to all possible destination states, σ′. The time to change the current state is randomly picked from the distribution P(Δt) ∝ e^−KΔt, where

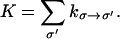(C1)

Depending on what σ′ is, k_σ→σ′ could be the polymerization, depolymerization, capping, or branching rates. We also keep track of the configurations of the filament and the average configuration of the cell membrane. If there are geometric obstacles to an event, then the rate constant is set to zero. This determines the time when the transition will take place. The identity of the destination state is determined by another random number uniformly distributed in (0, K). This kinetic Monte Carlo scheme was first used for simulating spin systems (70).

The probability distribution of the angle α is obtained by projecting the three-dimensional filaments into the xy-plane, whose dimension is 600 × 2000 nm. The direction with respect to x and the projected length of the filaments is recorded. As described by Maly and Borisy (11), the probability in the direction α is weighted by the projected length of the filament.